-
Neutron stars are one of the densest objects in the universe. The structure and properties of neutron stars are sensitive to EOS, making them ideal laboratories for testing theories of dense matter physics [1−4]. However, owing to the uncertainty of the EOS, predicting the unobservable or difficult to observe properties of neutron stars is difficult. Fortunately, groundbreaking observations from detectors such as NICER, LIGO, and VIRGO have provided new insights into the properties of neutron stars. Since the observation of GW170817 [5, 6], there have been many promising results from astronomical observations of neutron stars, such as the PSR J0030+0451 [7], PSR J0740+6620 [8], GW190814 [9]. These observations have made it possible to constrain the unobservable properties of neutron stars and the EOS of high-density asymmetric nuclear matter [10, 11].
Several approaches can be used to constraint the properties of neutron stars based on astronomical observations. Bayesian analysis methods are a standard method. For example, using this method, Steiner
$ et \; al. $ inferred the radius range of a canonical neutron star from six neutron star observations [12]; Güven$ et \; al. $ deduced both the EOS and the canonical neutron star radius [13]. Universal relations provide another way to constrain the properties of a neutron star through astronomical observations. This method has established the EOS-independence relations of the global properties of neutron stars. Early in 1994, Ravenhall and Pethick proposed the universal relation between the normalized moment of inertia$ I/MR^2 $ and the compactness C [14]. This relation was refined by Lattimer & Prakash [15] and Bejger & Haensel [16], and later used by Lattimer & Schutz to estimate the radius of neutron stars in binary systems [17]. Breu and Rezzolla switched to the dimensionless moment of inertia$ I/M^3 $ to establish a more precise relation with C [1], which was confirmed at the maximum rotation sequence by Ref. [18]. In 1998, Andersson and Kokkotas proposed a classical universal relation between the frequency of the f-mode$ \omega_f $ and the average density of a neutron star in the field of asteroseismology [19]. This relation has received attention up to recent years [20−24]. In 2013, the notable relation,$I - LOVE - Q$ , was established by Yagi and Yunes [25]. Pappas and Apostolatos found that this relation breaks down for conditions with rapid rotation [26]. Soon after, Doneva$ et \; al. $ and Chakrabarti$ et \; al. $ proposed the$I - LOVE - Q$ relation for rotating neutron stars and rotating quark stars [27, 28], respectively. In more recent years, the relation between the macroscopic properties of neutron stars and the nuclear matter parameters was established [10, 29], and the universal relations related to the rotational parameters of neutron stars were also introduced [30−33].By leveraging the
$I - LOVE - Q$ relations, measurements of the moment of inertia of PSR J0737-3039A were used to obtain its radius and tidal deformation with precise mass data. This was important for dense matter EOS studies[3]. In contrast, Sulieman and Read have emphasized that these universal relations are not sufficiently precise in constraining the properties of neutron stars, especially the radius [34], which raises the question if whether more precise universal relations can be established.It is well understood that the properties of neutron stars exhibit EOS dependence [16, 32] and that the global properties mass-radius of neutron stars and the EOS pressure-density of dense nuclear matter have a one-to-one correspondence[35]. In a sense, the EOS dependence is equivalent to the mass-radius dependence. For different EOSs, we find that the points corresponding to a certain property of a neutron star are almost located on the same surface in 3-dimensional space with the mass and radius as the base coordinates. By describing the surface, we can obtain the universal relation between a property and the mass and radius. The resulting universal relations have been shown to have greater precision. This method is called mass-radius projection. In this study, the mass-radius projection method is used to establish several high-precision universal relations that are related to the moment of inertia, f-mode frequency, and tidal deformation. Using the observation data of neutron star masses and radii from NICER, the properties related to the observed neutron stars can be constrained more precisely.
This paper is organized as follows. Sec. II introduces the EOS model and the basic formulas for neutron star properties. In Sec. III, the universal relations of static-neutron-star properties are established through the mass-radius projection method, where Sec. III. A, Sec. III.B, and Sec. III.C present the universal relation of the moment of inertia, f-mode frequency, and tidal deformation, respectively. Sec. III.D introduces the application of affine transformation in establishing the universal relations, where the universal relation between I and
$ \omega_f $ is established as an example. Sec. IV. summarizes the paper.Unless stated otherwise, we assume the gravitational units
$ G = c = 1 $ in our equations. -
A set of representative EOSs is necessary to prove the existence of a universal relation. This includes: (1) the piecewise-polytropic (PP) model [36]; (2) the microscopic and phenomenological nuclear many-body model, such as APR [37], APR3 [37], APR4 [37], ALF2 [38], ENG [39], DDLZ1 [40], DD-ME1 [41], DD-ME2 [42], MPA1 [43], PKA1 [44], PKO3 [44], SLy [45], WFF1 [46], WFF2 [46], soft-EOS [47], and stiff-EOS [47]; (3) the first-order phase transitions model, which combines APR3 with quark EOS and DD-ME2 with quark EOS, exhibiting first-order phase transitions at densities of
$ 1\ \rho_0 $ (saturation density),$ 1.5\ \rho_0 $ ,$ 2\ \rho_0 $ .For the PP model, each segment is represented by a different density
$ \rho _i $ and pressure$ P_i $ , which can be written as$ P = K_i\rho ^{\varGamma _i}\,\,\left( \rho _i\leqslant \rho \leqslant \rho _{i+1} \right), $

(1) where
$ K_i $ is the polytropic constant defined as$ K_i = \frac{P_i}{\rho _{i}^{\varGamma _i}}, $

(2) and the adiabatic index
$ \varGamma _i $ defined as$ \varGamma _i = \frac{\log _{10}\left( P_{i+1}/P_i \right)}{\log _{10}\left( \rho _{i+1}/\rho _i \right)}. $

(3) Here, we use BPS+NV EOSs [48, 49] as the crust segment. The core segment is parameterized starting at 0.375
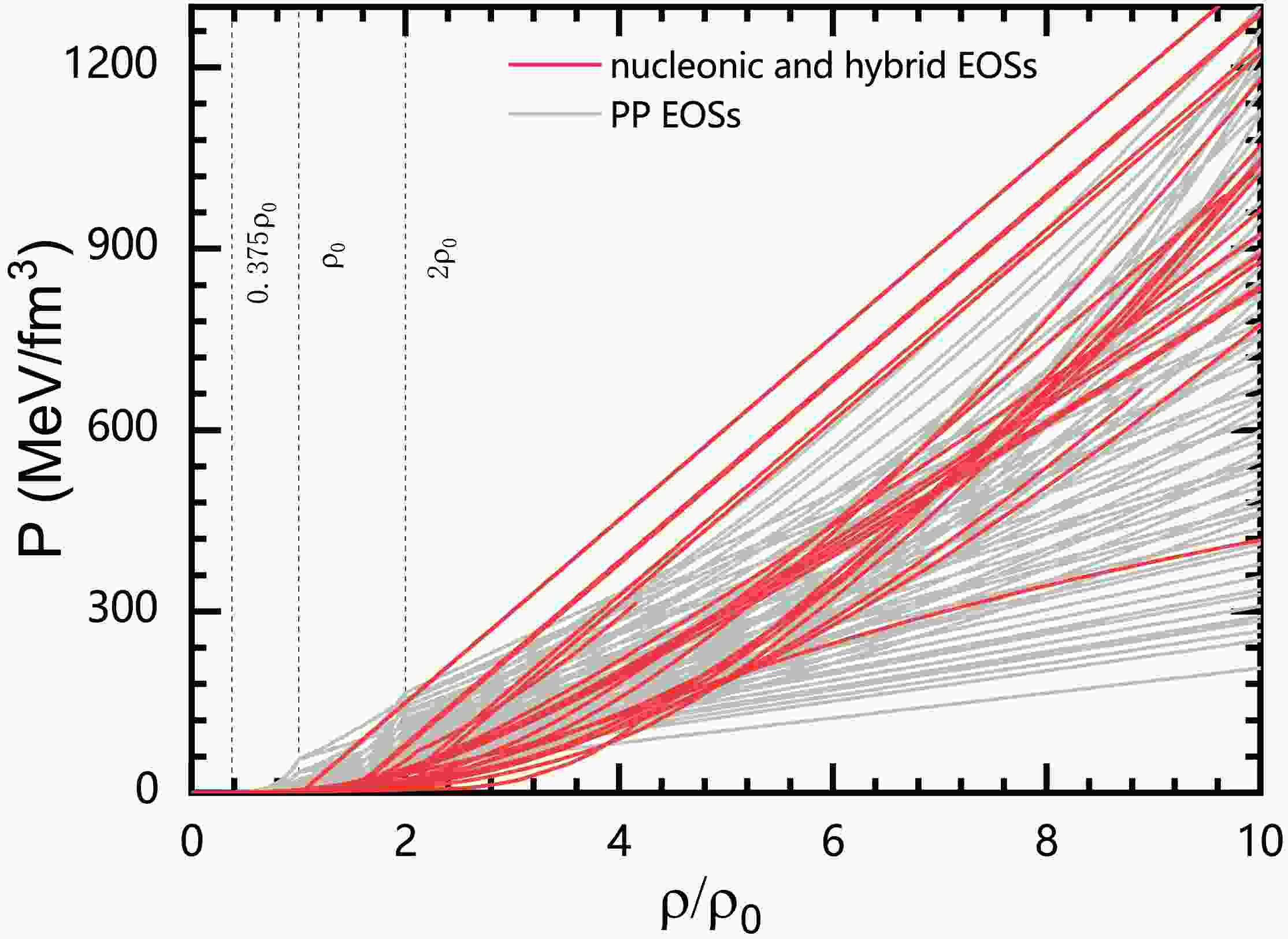
$ \rho_0 $ with an adiabatic index$ \varGamma _i $ in the range$ \left[ 1, \ 5 \right] $ . Figure 1 shows the EOSs included in our collection, which can be considered to be broadly representative based on the distribution of pressure-density. Additionally, the causality condition ($\sqrt{{\rm d}P/{\rm d}\rho}\leqslant 1$ ) and maximum mass condition ($ M_{\rm max}\geqslant 2.14\ M_{\odot} $ [50]) are satisfied for the constructed 63 piecewise-polytropic EOSs.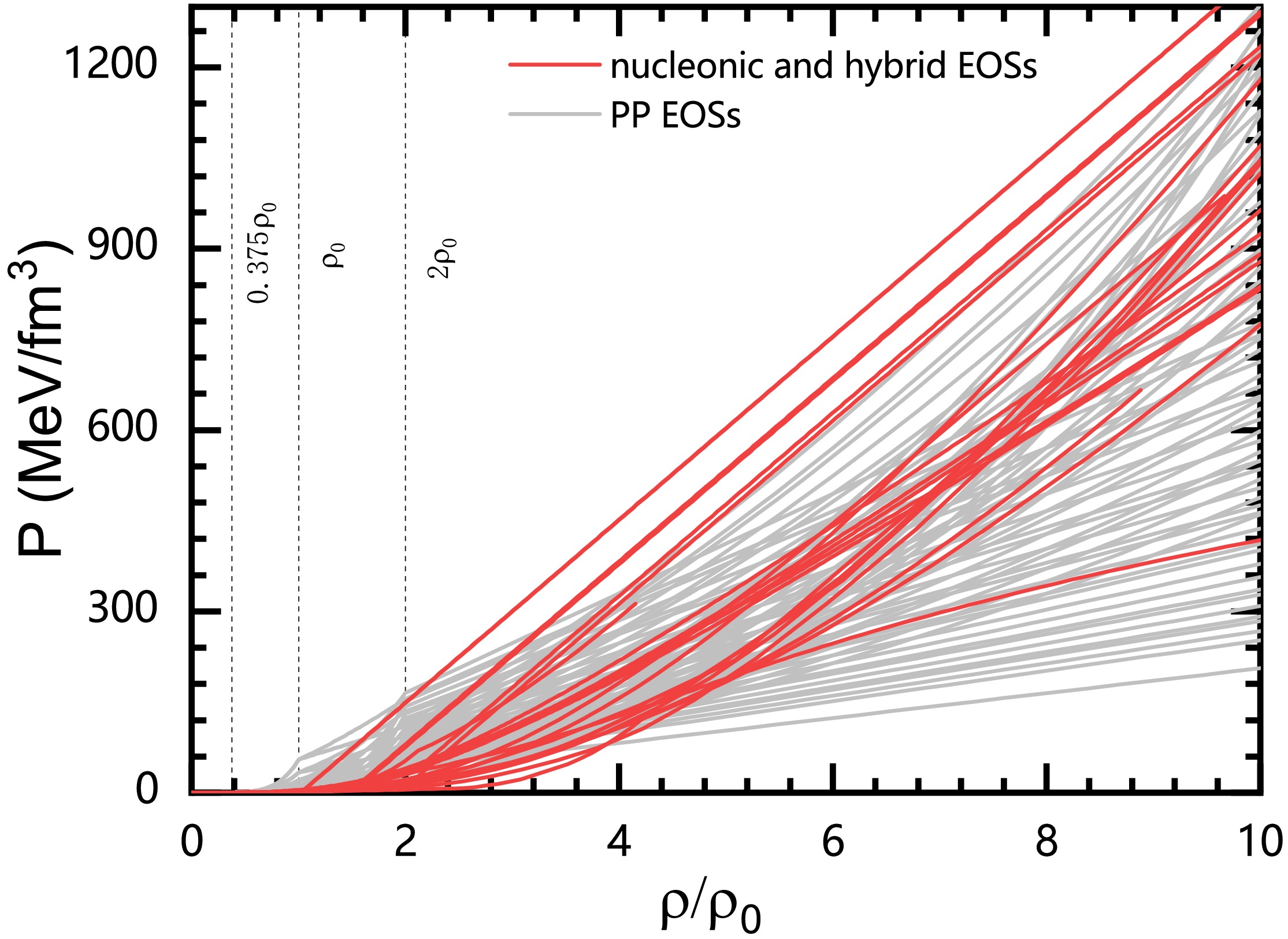
Figure 1. (color online) The
$P-\rho$ relations of the adopted EOS models, where$\rho_0$ denotes the saturation density. The gray curves represent PP EOSs, while the vertical dashed lines indicate the transition of points between different PP segments. The red coloured curves represent nucleonic and hybrid EOSs. -
The moment of inertia of the neutron star reflects the particles content of matter, the mass associated with the energy required to compress the matter to a given density, and the effective energy of the gravitational interactions between different parts of the star [51]. In General Relativity, the moment of inertia is defined as
$ I = J/\varOmega, $

(4) where J and Ω represent the angular momentum and the spin frequency, respectively. We adopt the moment of inertia of spherically symmetric neutron stars in general relativity from Ref. [52] in calculations, expressed as
$ \frac{{\rm d}I}{{\rm d}r} = \frac{8}{3}\pi r^4\rho \left( 1+\frac{P}{\rho} \right) \left( 1-\frac{5I}{2r^3}+\frac{I^2}{r^6} \right) \left( 1-\frac{2m}{r} \right) ^{-1}, $

(5) where m is the mass as a function of radius r, given by the TOV equation. This approach has been verified to be in basic agreement with the results of the conventional algorithm [51, 53].
The tidal deformation λ is defined by the star's induced quadrupole moment
$ Q_{ij} $ in response to the external tidal field$ \varepsilon_{ij} $ ,$ Q_{ij} = -\lambda \varepsilon _{ij}. $

(6) The second tidal-Love-number
$ k_2 $ is defined as$ k_2 = \frac{3}{2}\lambda R^{-5}, $

(7) which can be solved together with the TOV equation [54, 55]. Once
$ k_2 $ is determined, the dimensionless tidal deformation Λ can be determined by the relation$ \varLambda = \frac{2k_2}{3C^5}, $

(8) where
$ C = M/R $ is the compactness.The f-mode is the lowest-frequency quadrupole oscillation of neutron stars [56]. The basic formulas to calculate f-mode oscillation can be found in Refs. [56−58]. The numerical solution method used in this work is the Detweiler-Lindblom method [56, 58].
-
The properties mass-radius of neutron stars and the EOS pressure-density of dense nuclear matter are known to have a one-to-one correspondence [35]. This correspondence implies that the EOS-dependent neutron star properties also embodies mass-radius dependence. We find that for different EOSs the points corresponding to a certain property of neutron star are almost located in the same surface in 3-dimensional space with mass and radius as the base coordinates. Describing the surface can yeild the accurate universal relation between a property and mass-radius. Our calculations show that the resulting universal relations have greater precision. In this section, using the mass-radius projection of the moment of inertia, f-mode frequencies, and tidal deformation, the precise universal relations of these properties with the mass-radius of neutron stars are presented. Based on these universal relations, combining with the astronomical observations from NICER, such as the mass and radius constraints of PSR J0030+0451 [7] and PSR J0740+6620 [8], relative precise predictions of the star's related properties are made.
-
Many universal relations have been constructed for the moment of inertia, such as the well-known
$I - LOVE - Q$ [25, 27, 28],$I - C$ [14, 15],$I - BE$ [59], where$ BE $ is the binding energy. These relations require the use transformed quantities such as$ I/M^3 $ and$ I/R^3 $ for I. For example, Breu and Rezzolla improved the precision of predicting the moment of inertia by using$ I/M^3 $ in the universal relation [1]. Here, we attempt to build a more precise universal relation for the moment of inertia using the mass-radius projection method. In addition, since the masses and radii of neutron stars can be more easily observed, they can be used to more precisely constraint the moments of inertia of observed neutron stars.Figure 2 illustrates the moment of inertia (globular dots) as a function of the the masses and radii if neutron stars in 3-dimensions. For different EOSs, almost all of the points are located on the same fitting surface, indicating that the moment of inertia can be described accurately using the mass and radius as independent variables. Through describing the surface, we can obtain the universal relation between the moment of inertia and mass-radius as
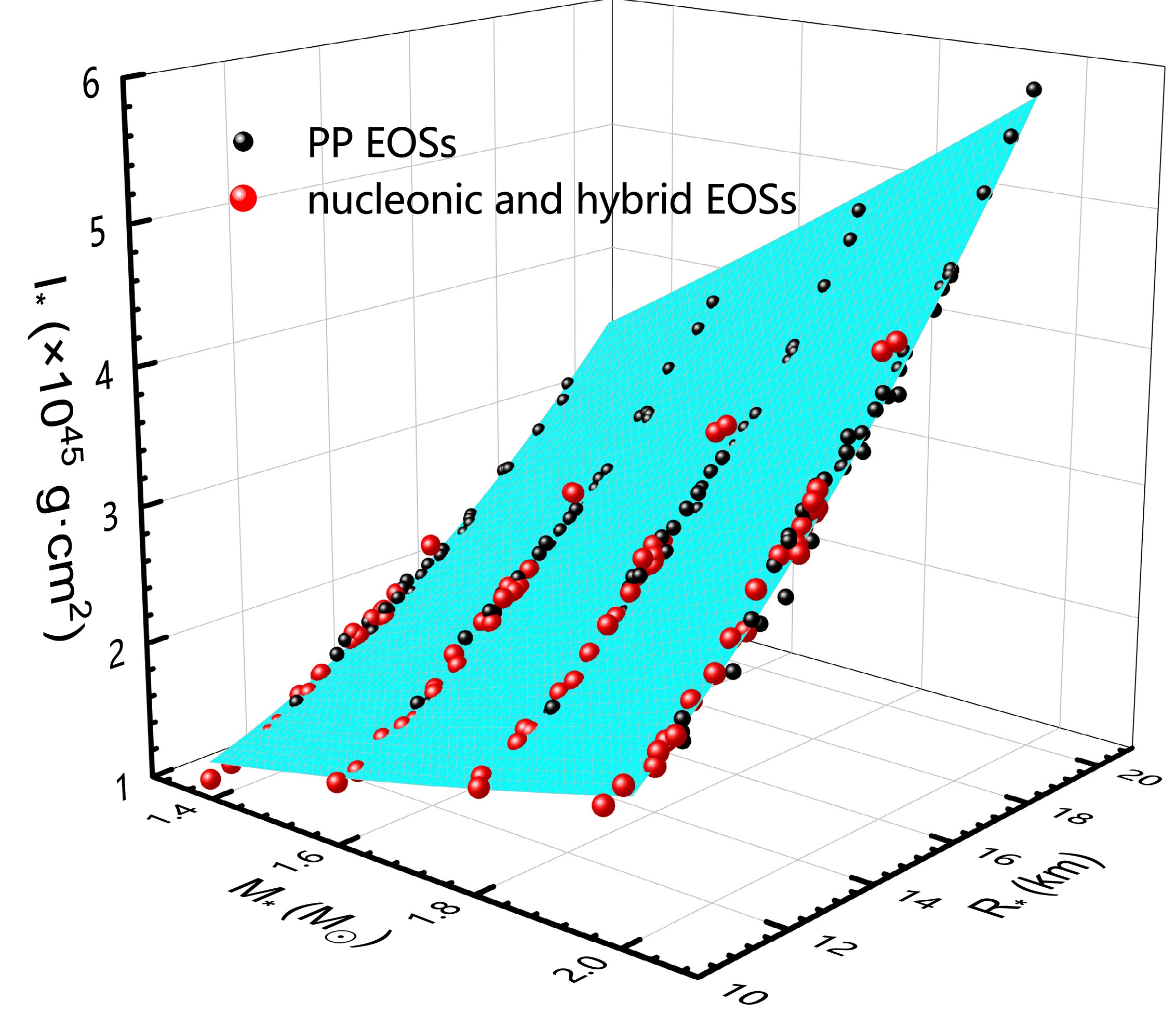
Figure 2. (color online) The moment of inertia as a function of the stellar mass and radius, where the black dots represent the results of the piecewise-polytropic EOSs, the red dots represent the results of nucleonic and hybrid EOSs, and the cyan surface is the fitting surface.
$\begin{aligned}[b] I_* =\;& 4.417-2.696M_*-0.513R_*+0.427{M_*}^2\\&+0.014{R_*}^2+0.249M_*R_*,\end{aligned} $

(9) in terms of the dimensionless parameters
$I_* = \dfrac{I}{10^{45}\ {\rm{g}}\cdot {\rm cm}^2}$ ,$ M_* = \dfrac{M}{M_{\odot}} $ , and$ R_* = \dfrac{R}{\mathrm{km}} $ .To investigate the precision of
$I_* - \left( M_*,\ R_* \right)$ , we employed the commonly used universal relation between the dimensionless moment of inertia$ \overline{I}( = I/M^3) $ and compactness C for comparison [14, 15]. Figure 3 shows the$\overline{I} - C$ universal relation for the EOS set used in Fig. 2. By using a polynomial of the same order, the universal relation$\overline{I} - C$ can be expressed as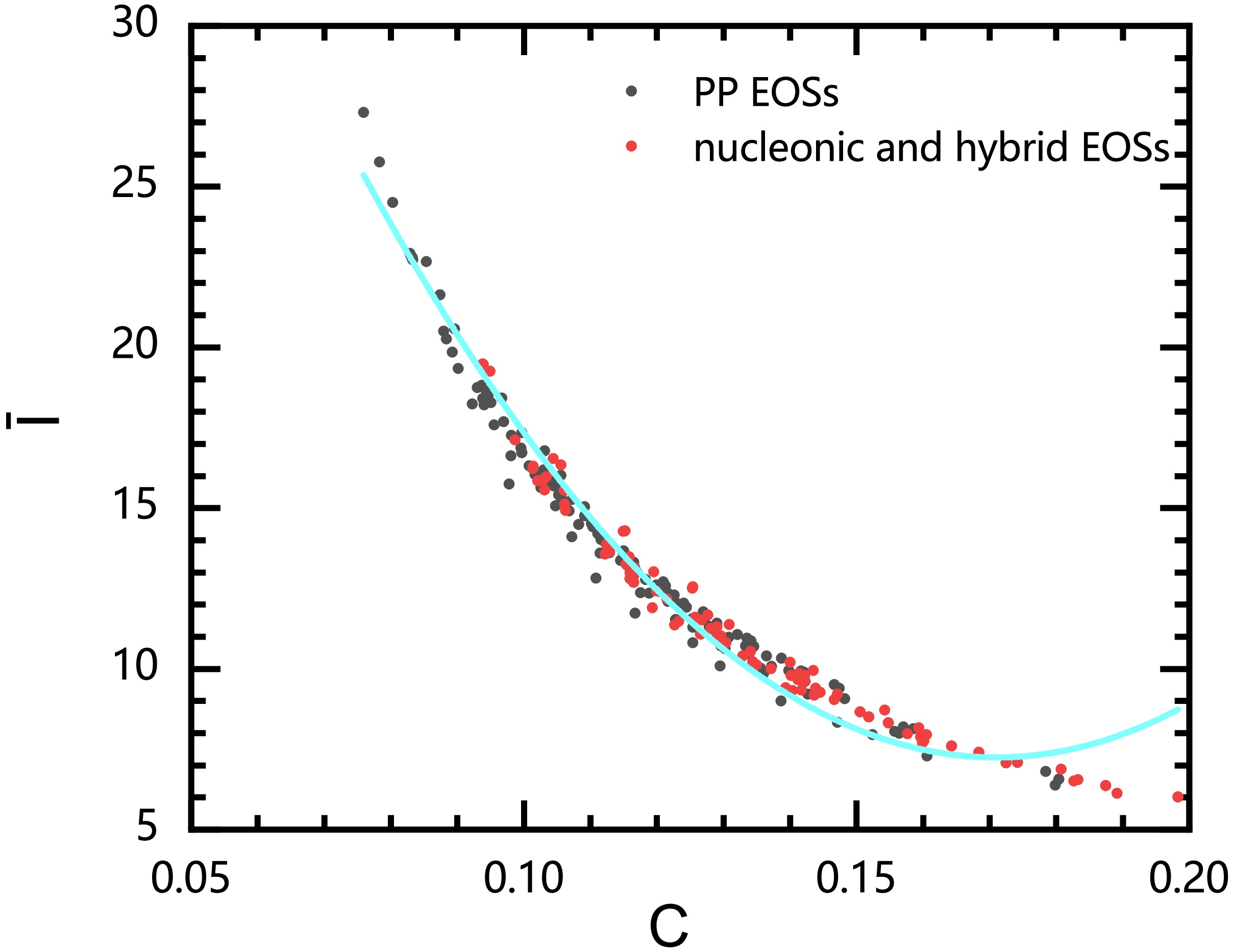
Figure 3. (color online)
$ \overline{I} $ –C relation with different EOSs with the fitting curve (cyan). Black dots represent the results of the piecewise-polytropic EOSs. Red dots represent the results of nucleonic and hybrid EOSs.$ \bar{I} = 65.857-685.567C+2004.727C^2. $

(10) To quantitatively compare the accuracy of these two universal relations, the means of the relative errors are presented in Table 1. Clearly, the universal relation described by Eq. (9) has much better precision.
$I_* - \left( M_*,\ R_* \right)$ 

$\overline{I} - C$ 

Mean $\left( \dfrac{1}{n}\displaystyle\sum_{i=1}^n{X_i} \right)$ 

0.019 0.774 Table 1. Mean of relative errors for
$I_* - \left( M_*,\ R_* \right)$ and$\overline{I} - C$ , where$ X_i $ represents the value of the relative error.According to Eq. (9) and the NICER data of stellar masses and radii, a relative precise constraint on the moment of inertia for the observed neutron star can be predicted. For instance, the moment of inertia of PSR J0030+0451, which has a mass of
$ 1.44\pm 0.15\ M_{\odot} $ and radius of$\left[ 11.2- 13.3 \right]\ \mathrm{km}$ at 90% credibility [7], can be constrained to a range of$\left[0.980-3.408\right] \times{10^{45}\ {\rm{g}}\cdot {\rm{cm}}^2}$ . This result is in basic agreement with the prediction ($1.43_{-0.13}^{+0.3}\ \times {10^{45}\ {\rm{g}}\cdot {\rm{cm}}^2}$ ) in Ref. [60]. Similarly, for PSR J0740+6620, which has a mass of$ 2.08\pm 0.07\ M_{\odot} $ and radius of$ \left[ 12.2-16.3 \right]\ \mathrm{km} $ at 95% credibility [8], the moment of inertia should be in the range of$\left[1.859- 7.364\right]\times {10^{45}\ {\rm{g}}\cdot {\rm{cm}}^2}$ . -
In recent years, many universal relations have been established for the f-mode frequencies. These relations include
$\omega_f - D _t$ [23],$\omega_f - C$ [61],$\omega_f - \varLambda$ [62], where$ \omega_f $ and$ D _t $ are the f-mode frequency and damping time, respectively. In particular, the universal relation$ \omega _f\left( \mathrm{kHz} \right) = a+b\sqrt{M_*/{R_*}^3} $ has received long and continuous attention, where the constants a and b are different for different studies [19−24].Similar to the treatment of universal relation
$I_* - \left( M_*,\ R_* \right)$ , the f-mode frequencies$ \omega_f $ as a function of the stellar mass and radius are presented in Fig. 4. By fitting this surface, the universal relation of$\omega_f - \left( M_*,\ R_* \right)$ can be written as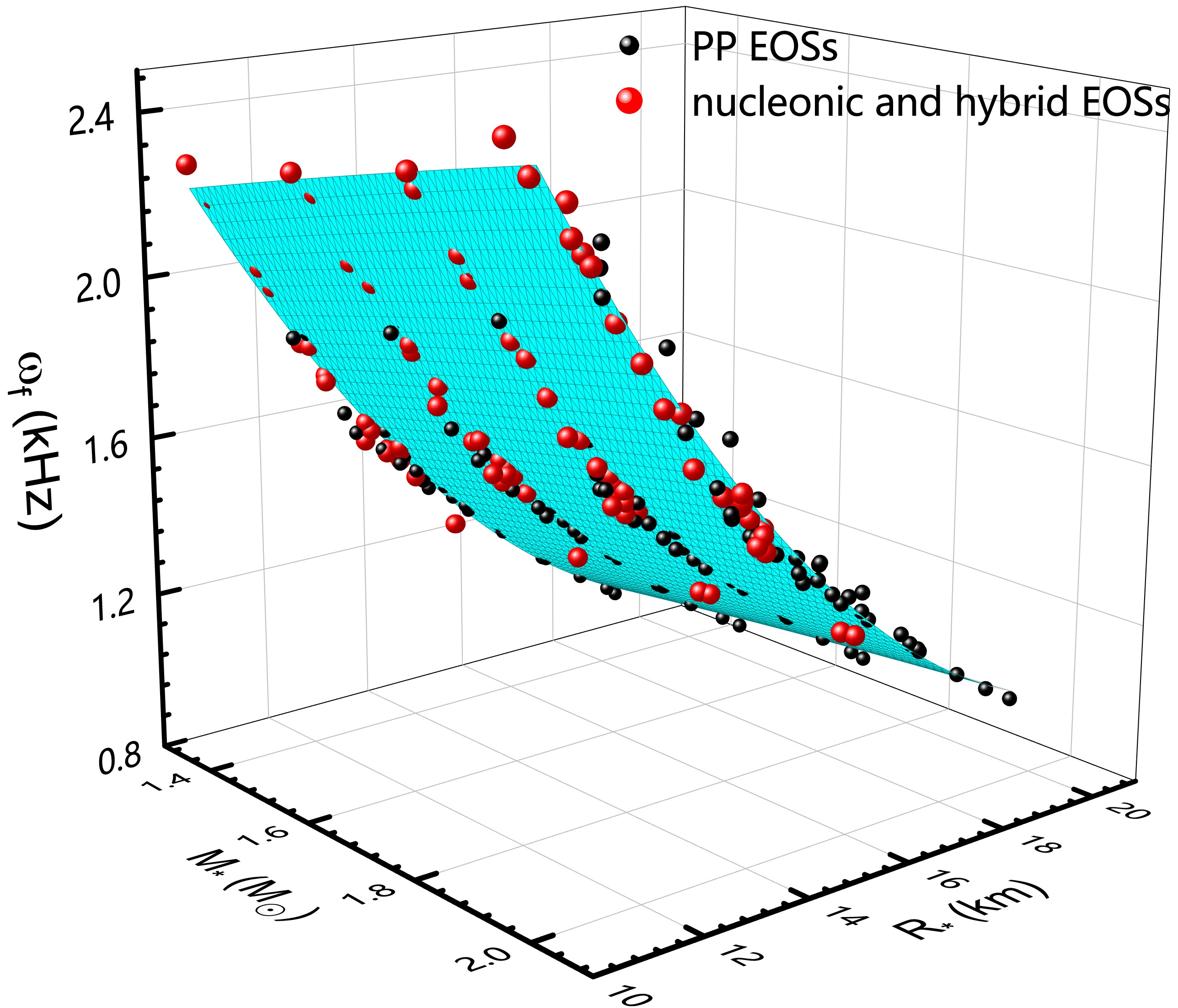
Figure 4. (color online) Similar to the Fig. 2, but for
$\omega_f - \left( M_*,\ R_* \right)$ .$\begin{aligned}[b] \omega _f\left( \mathrm{kHz} \right) =\;& 4.66+0.838M_*-0.416R_*-0.0471{M_*}^2\\&+0.0106{R_*}^2-0.0267M_*R_*,\end{aligned} $

(11) where
$ M_* = \dfrac{M}{M_{\odot}} $ and$ R_* = \dfrac{R}{\mathrm{km}} $ .Here, we adopt the classical universal relation
$\omega_f - \sqrt{M_*/{R_*}^3}$ as an example to compare the precision of the universal relations. Adopting the same set of EOSs, the universal relation between$ \omega_f $ and$ \sqrt{M_*/{R_*}^3} $ is displayed in Fig. 5. This universal relation can be fitted by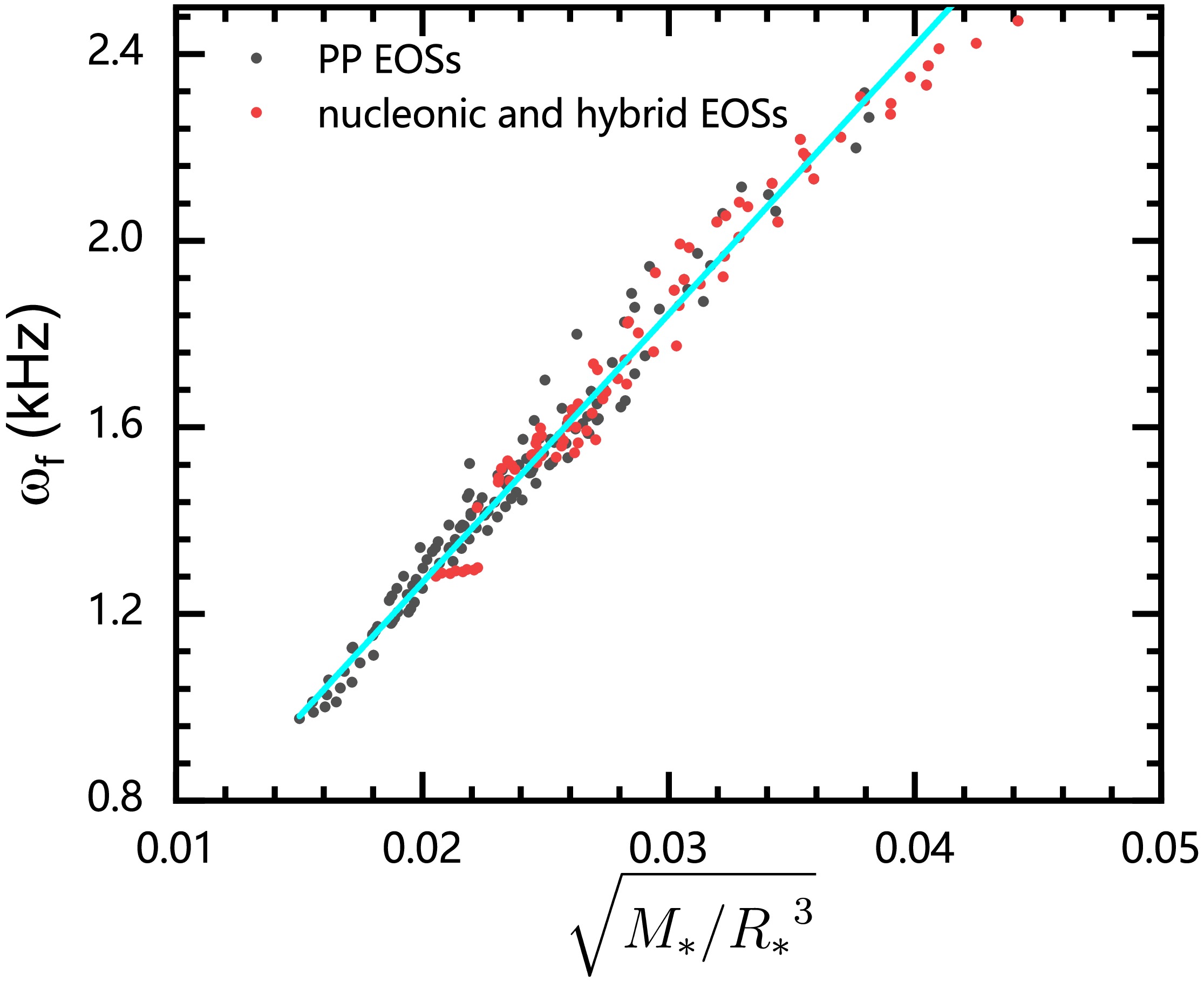
Figure 5. (color online) Similar to the Fig. 3, but for
$\omega_f - \sqrt{M_*/{R_*}^3}$ .$ \omega _f\left( \mathrm{kHz} \right) = 0.118+57.478\sqrt{M_*/{R_*}^3}. $

(12) Quantitative comparisons of the accuracy of these two universal relations are shown in Table 2. Again, the universal relation described by Eq. (11) has a better precision. The lack of a separate
$ R_* $ term in Eq. (12) may lead to a higher relative error for the$\omega_f - \sqrt{M_*/{R_*}^3}$ relation.$\omega_f - \left( M_*,\ R_* \right)$ 

$\omega_f - \sqrt{M_*/{R_*}^3}$ 

Mean $\left( \dfrac{1}{n}\displaystyle\sum_{i=1}^n{X_i} \right)$ 

0.0698 0.106 Table 2. Same as Table 1, but for
$\omega_f - \left( M_*,\ R_* \right)$ and$\omega_f - \sqrt{M_*/{R_*}^3}$ Similarly, based on Eq. (11) and the NICER observations, the f-mode frequencies of PSR J0030+0451 [7] and PSR J0740+6620 [8] can be constrained in the ranges of
$ \left[1.296-2.111\right]\ {\rm{kHz}} $ and$ \left[0.966-2.479\right]\ {\rm{kHz}} $ , respectively. The constraint of PSR J0030+0451 is largerly consistent with the prediction of ($ 1.67 - 2.18\ {\rm{kHz}} $ ) for canonical neutron stars presented in Ref. [23]. These constraints may provide useful guidance for the future detection of gravitational radiation from neutron star oscillations. -
Since the observation of GW170817, dimensionless tidal deformation Λ has become an attractive neutron start observational property for constraining the EOS. Establishing the universal relation between Λ and mass-radius provides an approach for validating these three observable properties. Similarly, the mass-radius projection method can be used to construct a precise universal relation between the tidal deformation and mass-radius of a neutron star. Figure 6 shows the universal relation between Λ and the mass-radius. Here, we express this universal relation using the following polynomial fitting
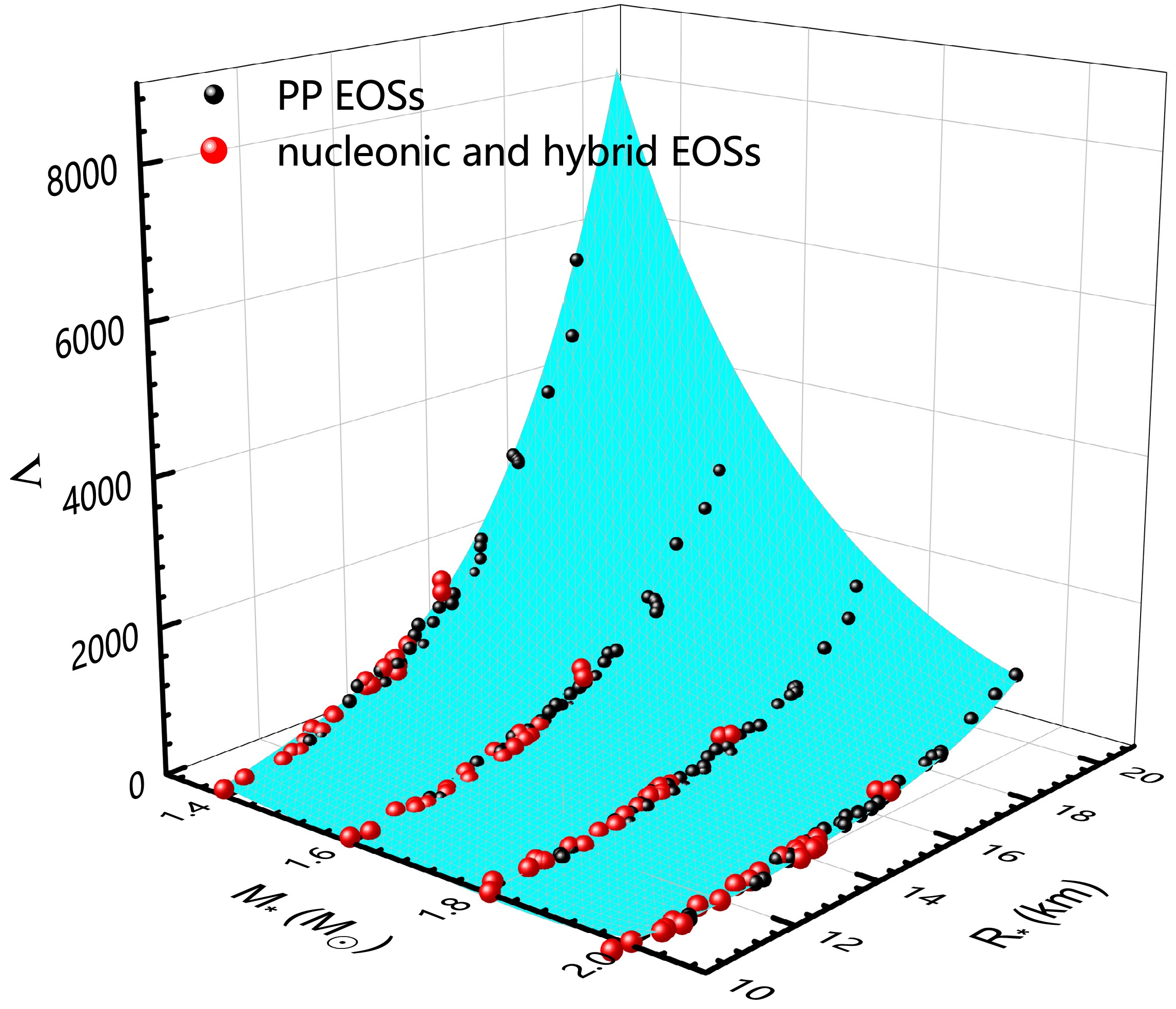
Figure 6. (color online) Similar as Fig. 2, but for
$ \varLambda\ - \ \left( M_*,\ R_* \right) $ .$ \begin{aligned}[b] \varLambda =\;& 108757.7751-299645.88054M_*+4654.63671R_*\\&-5931.14445M_*R_*+289044.79877{M_*}^2 \\ &-80.98134{R_*}^2-127741.20618{M_*}^3\\&+18.16444{R_*}^3+5789.65511{M_*}^2R_*\\&-342.04328M_*{R_*}^2 +23162.31504{M_*}^4\\&+0.35154{R_*}^4+295.79953{M_*}^2{R_*}^2\\&-2493.99688{M_*}^3R_*-18.85851M_*{R_*}^3, \end{aligned}$

(13) where
$ M_* = \dfrac{M}{M_{\odot}} $ and$ R_* = \dfrac{R}{\mathrm{km}} $ .In addition, to compare the accuarcy of the obtained relation, we use the universal relation between the dimensionless tidal deformation Λ and compactness C[63]. Employing the same set of EOSs, The universal relation
$ \varLambda\ -\ C $ with the EOSs used for the Λ and mass-radius universal relation is displayed in Fig. 7. This universal relation can be fitted by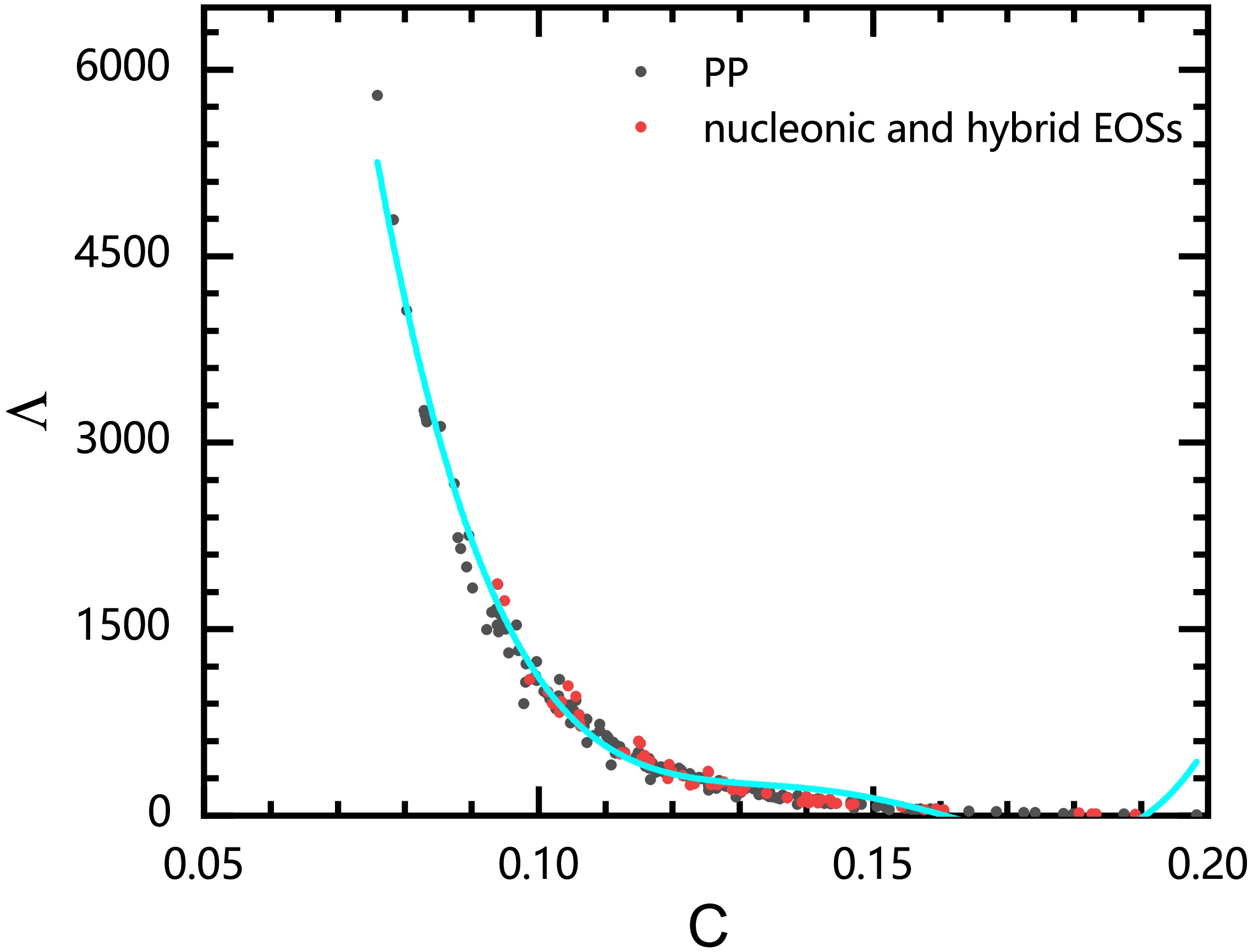
Figure 7. (color online) Similar as Fig. 3, but for
$\varLambda - C$ .$\begin{aligned}[b] \varLambda =\;& 1.009\times 10^5-2.786\times 10^6C+2.878\times 10^7C^2\\&-1.312\times 10^8C^3+2.223\times 10^8C^4.\end{aligned} $

(14) The accuracies of these universal relations are compared in Table 3. The universal relation described by Eq. (13) is shown to have better accuracy.
$\varLambda -\left( M_*,\ R_* \right)$ 

$\varLambda - C$ 

Mean $\left( \dfrac{1}{n}\displaystyle\sum_{i=1}^n{X_i} \right)$ 

0.0798 0.213 Table 3. Same as Table 1, but for
$\varLambda - \left( M_*,\ R_* \right)$ and$\varLambda - C$ .According to the above fitting equation and tidal deformation observational constraint
$ \varLambda _{1.4} = 190_{-120}^{+390} $ of GW170817 [6], the radius of a canonical neutron star ($ 1.4\ M_{\odot} $ ) should be constrained in the range of$ 10.707_{-0.668}^{+1.967}\ {\rm{km}} $ . This result is in basic agreement with the prediction ($11 - 12\ \mathrm{km}$ ) of Steiner [12]. In addition, by employing the mass and radius observational data from NICER, the tidal deformations of PSR J0030+0451 [7] and PSR J0740+6620 [8] can be constrained to$ \left[ 284.713- 2833.076 \right] $ and$ [<1885.358] $ , respectively. -
Establishing the universal relation can be viewed as constructing a functional relation between two neutron star properties, that is,
$ Y = F(X) $ , where X and Y represent any neutron star properties. Theoretically, if we have precise universal relations$ X\left( M_*,\ R_* \right) $ and$ Y\left( M_*,\ R_* \right) $ , we can establish the universal relation between$ X-Y $ by projecting one of the 3-dimensional surfaces to another surface. This projection process is called 3-dimensional affine transformation. Appendix A demonstrates the numerical solution of the process.As an example, we will construct the universal relation between the dimensionless moment of inertia
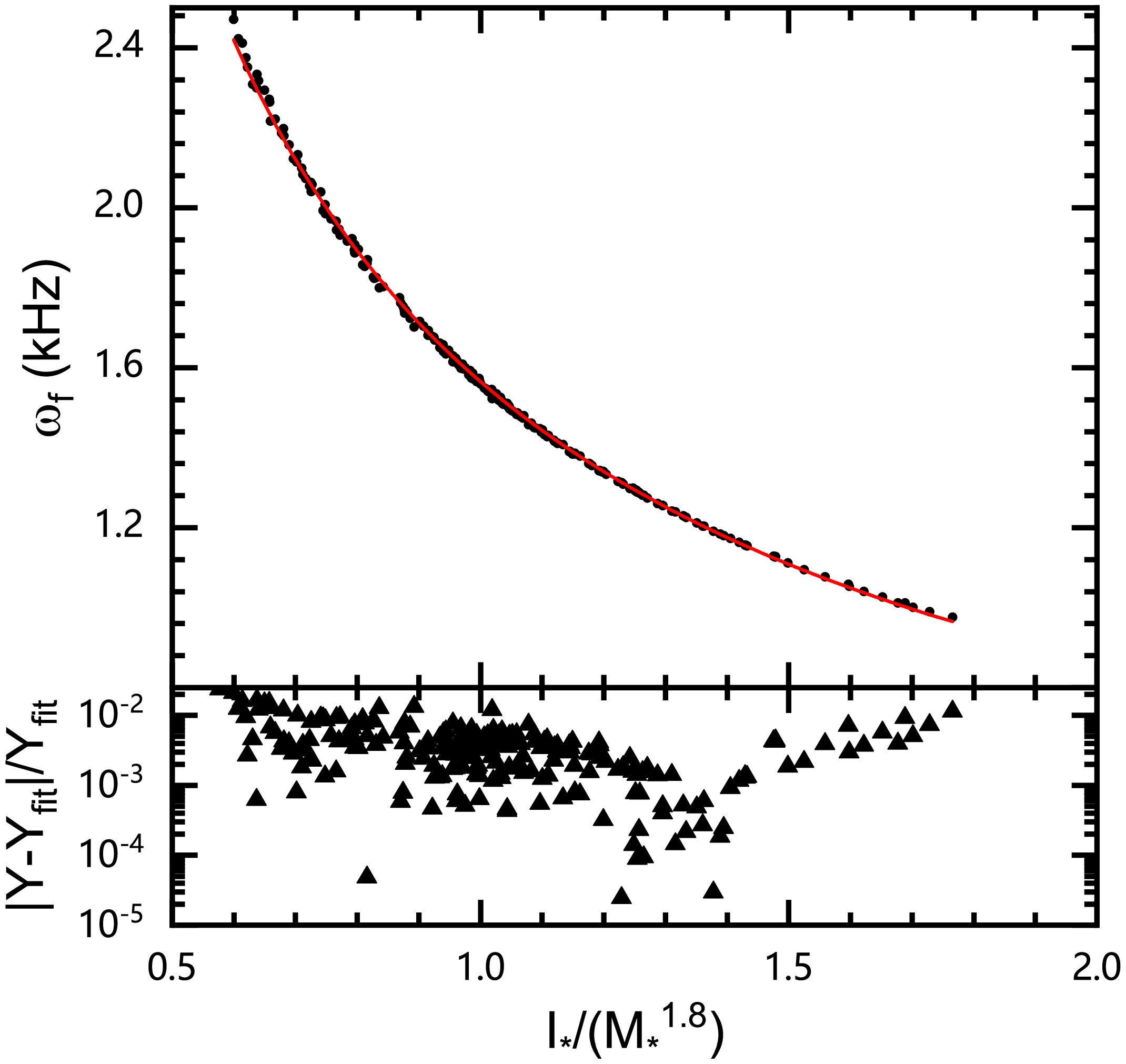
$ I_{*} $ and f-mode the frequency$ \omega_f $ using the projection method based on Eqs. (9) and (11). Operationally, making the universal relation$ \omega_f\left( {\rm{kHz}} \right) = F(I_*) $ hold is equivalent to overlapping the 3-dimensional surfaces$ \omega_f \left( M_*,\ R_* \right) $ and$ I_* \left( M_*,\ R_* \right) $ . In mathematical transformation, the most likely transformation factors for this projecting operation should be$ {M_*}^n $ and$ {R_*}^n $ . That is, we can roughly achieve the overlap of the 3-dimensional surfaces$ I_* \left( M_*,\ R_* \right) $ and$ \omega_f \left( M_*,\ R_* \right) $ by using Eq. (9) (or Eq. (11)) multiplied by the transformation factor. Through analysis and trial, we find that for Eq. (9) divided by$ {M_*}^{1.8} $ , the projected surface$ I_{*}(M_*,\ R_*) $ overlaps well with$ \omega_f(M_*,\ R_*) $ . Using this transformation, we can obtain a precise universal relation between$ I_{*} $ and$ \omega_f $ and express it as$ \omega _f\left( \mathrm{kHz} \right) = 1.565\left( I_*/{M_*}^{1.8} \right) ^{-0.851}. $

(15) This universal relation is illustrated in Fig. 8. It is shown that the maximum relative error for all EOSs is within 2% and the mean relative error is only 0.37%.
-
This study proposes the mass-radius projection method to establish the precise universal relations between neutron star global properties. Our constructed universal relations have greater precision than conventional universal relations. Since our universal relations are expressed using the masses and radii of neutron stars, they can constrain global properties, such as the moment of inertia, the frequency of f-mode and the tidal deformation, through stellar mass and radii observations. Combing these relations with NICER observations can provide a useful approach to precisely constraining properties of observed neutron stars. In addition, we establish a new perspective on constructing the universal relations; namely, constructing universal relations through a 3-dimensional affine transformation based on the mass-radius projection.
The established universal relations are only applicable to non-rotating static neutron stars. Theoretically, this projection method can be extended to the rotating cases. For rapidly rotating neutron stars, since the rotating frequency
$\varOmega $ will significantly effect the structure and properties of the stars [64−66], the process of establishing the universal relations should be extended to a 4-dimensional projection, where the extra dimension accounts for the rotation frequency$\varOmega $ . Correspondingly, the transformation factors should be rewritten as$ {M_*}^n $ ,$ {R_*}^n $ , and$ \varOmega^n $ . A discussion of establishing the universal relations of rotating neutron stars using the$ \varOmega$ factor can be found in Refs. [27, 28, 32, 33]. We plan to pursue further studies with the aim of validating the above ideas. -
This section presents an approach for numerically solving the new universal relation. Establishing the universal relation is equivalent to finding the function
$ Y = F(X) $ . In this context, we consider the universal relations$ X\left( M_*,\ R_* \right) $ and$ Y\left( M_*,\ R_* \right) $ as two-variable polynomials in the variables$ M_* $ and$ R_* $ . Consequently, the process of establishing the universal relation can be viewed as analogous to performing multivariate polynomial division (MPD) [67]. At this point,$ Y = F(X) $ can be expressed as$ Y\left( M_*,\ R_* \right) = {\rm d}\left( M_*,\ R_* \right) X\left( M_*,\ R_* \right) +r\left( M_*,\ R_* \right) , $

(A1) where
$ {\rm d}\left( M_*,\ R_* \right) $ represents the divisor and$ r\left( M_*,\ R_* \right) $ is the remainder. By performing MPD on Eq. (9) and Eq. (11), the universal relation between$ I_{*} $ and$ \omega_f $ can be expressed as$ \omega_f\left( \mathrm{kHz} \right) = {\rm d}\left( M_*,\ R_* \right) I_* + r\left( M_*,\ R_* \right), $

(A2) $ {\rm d}\left( M_*,\ R_* \right) = -\frac{471}{4270}, $

(A3) $\begin{aligned}[b] r\left( M_*,\ R_* \right) =\;& \frac{327}{247000} M_* R_* + \frac{577111}{1067500} M_* \\&+ \frac{463}{38125} R_* - \frac{2017943}{4270000} R_* \\&+ \frac{3139801}{610000}.\end{aligned} $

(A4) The mean relative error for this relation was 1.4%. Due to the inherent errors in the universal relation of the mass-radius projection, MPD numerical solutions may not minimize error.
Precisely constraining the properties of neutron stars using new universal relations and astronomical observations
- Received Date: 2024-08-23
- Available Online: 2025-04-15
Abstract: Given the significant uncertainty in the equation of state (EOS) of high-density nuclear matter, establishing EOS-independent universal relations between global properties of neutron stars provides a practical method to constraining unobservable or difficult-to-observe properties using astronomical observations. Constructing universal relations between EOS-dependent properties (e.g., moment of inertia, tidal deformation, etc.) or combined properties (e.g., compactness) is common, and improving the precision of the universal relations may provide stricter constraint on the properties of neutron star. We find that in 3-dimensional space with mass and radius as the base coordinates, the points corresponding to properties of a neutron star described by different EOSs are almost located on the same surface. Thus, the universal relation between the property and the stellar mass-radius can be expressed through describing the surface. We demonstrate that the resulting universal relations have greater precision. For example, we construct high-precision universal relations for the moment of inertia, the f-mode frequency, and the dimensionless tidal deformation with respect to the mass-radius. With the increase in the size and accuracy of NICER observational data for neutron star masses and radii, these universal relations allow for more precise constraints on the unobservable or difficult-to-observe properties.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: