Fixing the AdS₃ metric from pure state entanglement entropies of CFT₂

The Anti-de Sitter (AdS)/conformal field theory (CFT) correspondence plays a central role in modern theoretical physics. This conjecture states that a weakly coupled gravitational theory in a $ d+1 $ dimensional AdS space is equivalent to a strongly coupled d dimensional CFT on its conformally flat boundary [1]. It provides a testable realization of the holographic principle [2, 3].

Quantum entanglement is a manifestation of the non-local property of quantum mechanics. For the simplest configuration, a quantum system is divided into two parts: A and B. Thus, the Hilbert space is decomposed into $ {\cal{H}}={\cal{H}}_{A}\otimes{\cal{H}}_{B} $. The entanglement entropy (EE) of region A is defined as the von Neumann entropy, $ S_{A}=-\mathrm{Tr}\left(\rho_{A}\ln\rho_{A}\right) $, where $ \rho_{A} $ is the reduced density matrix of region A: $ \rho_{A}=\mathrm{Tr}_{{\cal{H}}_{B}}\rho $. Evidently, $ S_{A}=S_{B} $ for this pure state. One of the most successful supports of the AdS/CFT correspondence is the Ryu-Takayanagi (RT) formula, which asserts the equality of the EE of the boundary CFT and the accordingly defined minimal surface area in the bulk AdS [4−6]. In these studies, the geodesic length (minimal surface area) in AdS$ _{3} $ is calculated and found to agree with the EE of CFT₂. This identification has been extensively verified by subsequent studies, as summarized in a review [7] and the references therein.

Motivated by the success of the RT formula, a conjecture has been proposed suggesting that gravity can be interpreted as an emergent structure, determined by the quantum entanglement of the dual CFT [8, 9]. This concept was further developed by Maldacena and Susskind, who proposed an equivalence between the Einstein-Rosen (ER) bridge and Einstein-Podolsky-Rosen (EPR) experiment [10]. Building on this framework, a crucial question arises: Can we determine the leading behavior of the dual bulk geometry, specifically the metric, from the EEs of the CFT?

This question has attracted considerable interest in recent years. The primary challenge lies in determining the metric of the holographic dimension that extends into the bulk. It is widely accepted that this hidden extra dimension is generated by the energy cut-off of the CFT and oriented perpendicular to the boundary, as achieved using the holographic principle [11]. To date, two major approaches have been developed to solve this problem. The first one is the tensor network, which generates a logarithmic geodesic length from boundary states, leading to a discretized AdS space [12]. These networks provide an intuitive connection between entanglement and spatial geometry. The second method resorts to kinematic space. This method maps geodesics in AdS₃ to points in a kinematic space. Specifically, the Crofton form, defined as the second derivative of EE with respect to two distinct points (without taking the coincidence limit), plays a crucial role. A codimension-1 locus, or "point curve", in kinematic space corresponds to a family of geodesics that intersect at a single point in AdS₃. The geodesic length between any two points in the bulk is then obtained by integrating the Crofton form over the area between the corresponding point curves in the kinematic space [13]. The advantage of this approach lies in its clear correspondence between Crofton's formula and field theory, enabling operator product expansion (OPE) blocks to be derived from local operators in AdS via the Radon transformation [14, 15]. However, despite its elegance, this method is not straightforward with respect to fixing the leading behavior of the spacetime metric in an unknown bulk geometry. In contrast to these approaches, our method introduces a key difference: we impose the limit $ x \to x' $ after taking the derivatives. This procedure enables us to directly obtain the metric from the geodesics, offering a more immediate pathway to deducing the bulk geometry. In addition to these advancements, significant progress has been made in the dynamics of the system, such as deriving linearized Einstein equations from EE [16].

In this study, we develop a method to explicitly determine the leading behavior of the dual geometry from the free $ \mathrm{CFT_2} $. At first glance, we might consider this problem trivial, citing symmetry arguments because both $ \mathrm{CFT_2} $ and AdS₃ share the same $ S O(2,2) $ symmetry. However, as is commonly known, all d-dimensional CFTs share the same $ S O(2,d) $ symmetry, which their dual geometries must also respect. Therefore, symmetry matching is a necessary condition but not a sufficient one. Therefore, methods that go beyond symmetry arguments must be developed and a more robust framework provided. The approach we propose in this study satisfies several key requirements: The first requirement of the expected new method is to reproduce pure AdS$ _{d+1} $ uniquely from the free $ \mathrm{CFT_d} $, ensuring a solid foundation for the correspondence. The second step is to reconstruct nontrivial topologies from the dual CFT. The next step is to build one-to-one correspondences between the excited states of the CFT and their associated bulk geometries. The final step is to derive the dynamics, namely the Einstein equation, directly from the CFT data. These steps form a systematic pathway toward not only confirming the duality but also deepening our understanding of the holographic principle and its applications in emergent spacetime physics.

In contrast to previous efforts in the literature, our strategy is based on two key distinctions: Synge's world function [17] and the infrared entanglement entropy (IR EE) ¹. Constructing the geodesic length is inherently simpler than directly deriving the metric, a point acknowledged in earlier research on integral geometry and kinematic space [13]. However, the significance of Synge's world function appears to have been ignored in these approaches. While previous authors utilized derivatives with respect to two distinct points along geodesics, they did not apply the coincidence limit to extract the metric. In classical gravity, Synge's world function, defined as one half of the squared geodesic length, is a fundamental tool for studying the motion of a self-drived particle in a curved background. Almost all significant two-point quantities in classical gravity are derived from this function. For our current problem, the critical importance of Synge's world function lies in its ability to compute the metric directly. By taking second derivatives of the function and applying the coincidence limit, we can bypass irrelevant complexities and obtain the desired results with precision. This approach eliminates the ambiguities often associated with reconstructing the bulk geometry. Additionally, the parallels between the kinematic space formalism and Synge's world function are noteworthy. Although the two frameworks have distinct focuses, their similarities could inspire further developments.

The second critical quantity we incorporate is the IR EE of a perturbed CFT₂. Traditionally, attempts to construct the dual geometry have relied only on the UV EE but have not been successful. Intuitively, reducing from a higher-dimensional system to a lower-dimensional one is straightforward, whereas reconstructing higher-dimensional information from lower-dimensional data is inherently more challenging. On the surface, the UV EE is fully expressed in terms of flat CFT quantities, with no apparent signature of the hidden bulk dimension. This suggests that the UV EE alone is insufficient for reconstructing the dual geometry. A possible explanation is that the UV EE inherently depends on a UV cut-off, intrinsic to quantum field theories. However, on the (bulk) classical gravity side, this UV cut-off can, in principle, be removed. Although a massless CFT has no intrinsic IR cut-off, the correlation length diverges, rendering the IR EE not directly expressible. This observation leads us to conjecture that introducing a finite IR cut-off could be useful. By progressively pushing this cut-off to infinity, we can extract meaningful results without introducing inconsistencies on the gravity side. This approach is similar to the Pauli-Villars regularization in quantum field theory, where a large cut-off is introduced to isolate finite physical results. For a perturbed CFT with a finite IR cut-off, we anticipate that the leading-order behavior of the dual geometry corresponds to an asymptotic AdS space. The finite IR cut-off provides a natural framework for encoding the bulk geometry, bridging the gap between the perturbed CFT and its holographic dual.

Our derivations demonstrate that the frequently used UV EE of $ \mathrm{CFT_2} $can provide only partial information about the asymptotic behavior of the boundary directions. It does not offer any direct insights into the energy-generated direction. Remarkably, we observe that the EE in the IR region of a perturbed CFT₂ provides the sufficient condition to determine both the energy-generated direction and the residual freedom in the boundary directions. This is because the IR EE is determined by both the UV and IR energy scales, which correspond to different values along the energy-generated direction. Therefore, by combining both the UV and IR EEs, we can uniquely determine the asymptotic form of the geodesic length in the bulk. This leads to the determination of the metric of the dual geometry, which is found to be the anticipated asymptotic AdS₃. The pure AdS₃, which serves as the gravity dual of the massless CFT₂, is obtained by taking the mass scale of the perturbed CFT₂ to the massless limit. This corresponds to taking the correlation length of the perturbed CFT₂ to infinity. Moreover, the covariant case can be derived using the same approach, following the same underlying pattern.

Before starting the discussion, we summarize the methods and steps.

Main Equation: Synge's World Function. Synge's world function is instrumental in extracting the spacetime metric from geodesics. Note that the geodesics referred here are those in the bulk geometry, whereas the known EEs correspond to boundary-attached geodesics. Therefore, our strategy involves deducing the general expression for bulk geodesics based on boundary-attached geodesics and then employing Synge's world function to obtain the metric. Our steps are given as follows:

1. Use the RT formula to determine two types of boundary-attached geodesics from the EEs.

2. Write the general expression for the bulk geodesics.

3. Fix the free coefficients and functions of the bulk geodesics using the known boundary-attached geodesics.

4. Use Synge's world function to compute the spacetime metric.

In classical gravity, Synge's world function is fundamental to investigating the radiation back-reaction (self-force) of a particle moving in a curved background. All the bi-tensors are defined by Synge's world function. A comprehensive review on this subject is available in [18]. We only list some useful results here. Given a fixed point on a manifold M and another point $ x^{\prime} $ that connects to x through a single geodesic $ x=x\left(\tau\right) $, with $ \tau\in\left[0,t\right] $, such that $ x\left(0\right)=x $ and $ x\left(t\right)=x^{\prime} $, Synge's world function is defined as the square of the geodesic length:

where $ L_{\gamma_{A}} $ is the geodesic length connecting the points x and $ x^{\prime} $. This function is a bi-scalar for the points x and $ x' $, respectively. Throughout this paper, we use i and $ i^{\prime} $ to distinguish the two points x and $ x' $. The first derivative with respect to x or $ x' $ is the ordinary derivative, denoted as $ \sigma_{i}=\dfrac{\partial\sigma}{\partial x^{i}} $ or $ \sigma_{i^{\prime}}=\dfrac{\partial\sigma}{\partial x^{i^{\prime}}} $. Note that $ \sigma_{i}(x,x') $ $ (\sigma_{i^{\prime}}) $ is a vector for point x $ (x') $ but a scalar for point $ x' $ $ (x) $. We easily find that

As usual, the second derivative at a single point is interpreted as the covariant derivative: $ \sigma_{ij}\equiv\nabla_{j}\sigma_{i} $ and $ \sigma_{i^{\prime}j^{\prime}}\equiv\nabla_{j^{\prime}}\sigma_{i^{\prime}} $. A key quantity in our derivation is the derivative with respect to different points: $ \sigma_{i^{\prime}j}\equiv\partial_{i^{\prime}}\sigma_{j}= \dfrac{\partial\sigma}{\partial x^{j}\partial x^{i^{\prime}}} $ and $ \sigma_{ij^{\prime}}=\sigma_{j'i} $.The notation for coincidence limits of an arbitrary function is defined as

We easily observe that

Remarkably, the coincidence limits of the second derivatives lead to the metric

To better understand this formula, note that along a geodesic, the norm of the tangent vector $ g_{ij}\dot{X}^{i}\dot{X}^{j} $ is constant. Thus, as $ t\to0 $, we find

The advantage of $ \sigma_{ij^{\prime}} $ over $ \sigma_{ij} $in Eq. (5) is that we need not know the connection (geometry). Therefore, we only need to determine the geodesic length of the yet-to-be-determined dual geometry.

Note that the geodesic length here refers to a geodesic in the bulk, with its endpoints not fixed on the boundary. To address this, we must use two types of known EEs to fix the leading behavior of this geodesic length, as shown in Fig. 1.

Figure 1.  (color online) Two types of entanglement entropies to determine the leading behavior of the bulk geodesic.

We begin by assuming no prior knowledge of the emerged geometry. From the RT formula, our analysis relies only on the CFT EE, which we identify with the geodesic length, along with the holographic principle. In this work, we focus on a CFT₂ with infinite length. For simplicity, we first consider the static scenario, as generalizing the results to the covariant case is straightforward. To begin, we define a quantity with length dimension:

where c is the central charge of the CFT₂, and $ G_{N}^{(3)} $ is the Newton constant in three dimensions. The EE of the $ \mathrm{CFT_{2}} $ in the UV region is given by

where $ \ell=x-x^{\prime} $ represents the length of the entanglement sub-region in the CFT, and a is the UV cutoff or lattice spacing. Note that this expression for the UV EE is valid only when $ \ell\gg a\rightarrow0 $. Thus, the geodesic length of the dual geometry ending on the boundary is

In contrast, when the CFT₂ is perturbed by a relevant perturbation, the correlation length (IR cutoff) ξ becomes finite. In this case, the UV EE expression (8) is no longer valid for $ \ell\ge\xi $. In the large $ \ell $ IR region, with the condition $ a\ll\xi\ll\ell $, the IR EE becomes independent of $ \ell $ and is instead completely determined by the ratio of the IR and UV cutoffs [19, 20],

where $ \xi\equiv1/m $, and m is the mass gap of the perturbed CFT₂. Note the crucial factor $ 1/6 $, which is key to deriving the expected geometry, a point we will return to later. This confirms that the RT formula also applies in the IR region [4, 5]. Therefore, the geodesic length for the IR region, based on the perturbed CFT IR EE, is

The energy scale of a CFT is widely recognized to result in a hidden holographic dimension, denoted as y in this paper [11]. In the UV EE (9), $ \ell $ represents the boundary dimension x, whereas a introduces the holographic dimension $ y=a $. Eq. (9) is valid for geodesics that end on the boundary. Our objective is to generalize the expression ${(x-x')^{2}}/{y^{2}}$ in (9) to the bulk. To generalize it, we replace $ a^{2} $ with a regular function $ h\left(x,x^{\prime},y,y^{\prime}\right) $. The general extension of the proper length $ \ell^{2}=(x-x')^{2} $ to include the holographic dimension y is

where $ k\left(x,x^{\prime},y,y^{\prime}\right) $ and $ p\left(x,x^{\prime},y,y^{\prime}\right) $ are arbitrary regular functions. Note that odd powers of $ (x-x') $ or $ (y-y') $ are prevented by the symmetry between $ x(y) $ and $ x'(y') $. Possible higher order even powers of $ (x-x') $ or $ (y-y') $ are grouped into $ k\left(x,x^{\prime},y,y^{\prime}\right) $ and $ p\left(x,x^{\prime},y,y^{\prime}\right) $. Cross terms between $ (x-x') $ and $ (y-y') $ are excluded by the widely accepted viewpoint that the energy-generating holographic direction y is perpendicular to the boundary direction x.

Therefore, to match (9) and (11), we can generalize the geodesic as

for large $ \eta^2 $, where

Note that the functions k, p, and h must be invariant under the exchange $ \left(x^{\prime},y^{\prime}\right)\leftrightarrow\left(x,y\right) $. To recover Eq. (9) in the limit $ y=y'=a\to0 $, we must have $ k\left(x,x^{\prime},a,a\right)/ h\left(x,x^{\prime},a,a\right)\sim1/a^{2} $ and $ \left(y-y^{\prime}\right)^{2}p\left(x,x,y,y^{\prime}\right)\to0 $. These conditions ensure the generality of $ \eta^{2} $. The expression for η can be simplified by dividing $ p(x,x',y,y') $ from both the numerator and denominator ²:

In contrast, when the endpoints of the geodesic approach each other ($ \eta\rightarrow0 $), the geodesic length must vanish. Therefore, the function $ \chi\left(\eta\right) $ must take the form

In summary, we have

Here, $ C_{i} $ and α are constants to be determined. Thus, the next step is to fix the functions $ f(x,x',y,y') $, $g(x,x', y,y')$, and the constant α.

The next step is to determine the functions $ f(x,x',y,y') $ and $ g(x,x',y,y') $ from Eq. (15):

We will substitute this expression into the general form of the geodesic length, given by Eq. (17), to ensure it is consistent with Eqs. (9) and (11) in both the UV and IR regions, corresponding to boundary-attached geodesics.

1) $\boldsymbol{ y=a} $, $ \boldsymbol{y^{\prime}=\xi} $, and $ \boldsymbol{x=x^{\prime}} $ (Fixing $ \boldsymbol{g(x,x',y,y')} $)

In this case, the IR EE condition is given by Eq. (11):

Here, both a and ξ are energy scales corresponding to the two points in the holographic direction, $ y=a $ and $ y^{\prime}=\xi $, respectively. Additionally, $ x-x^{\prime}\rightarrow0 $. The geometry corresponding to this scenario is illustrated in Fig. 2. Referring to the large η limit in the general expression (17) and (15), we find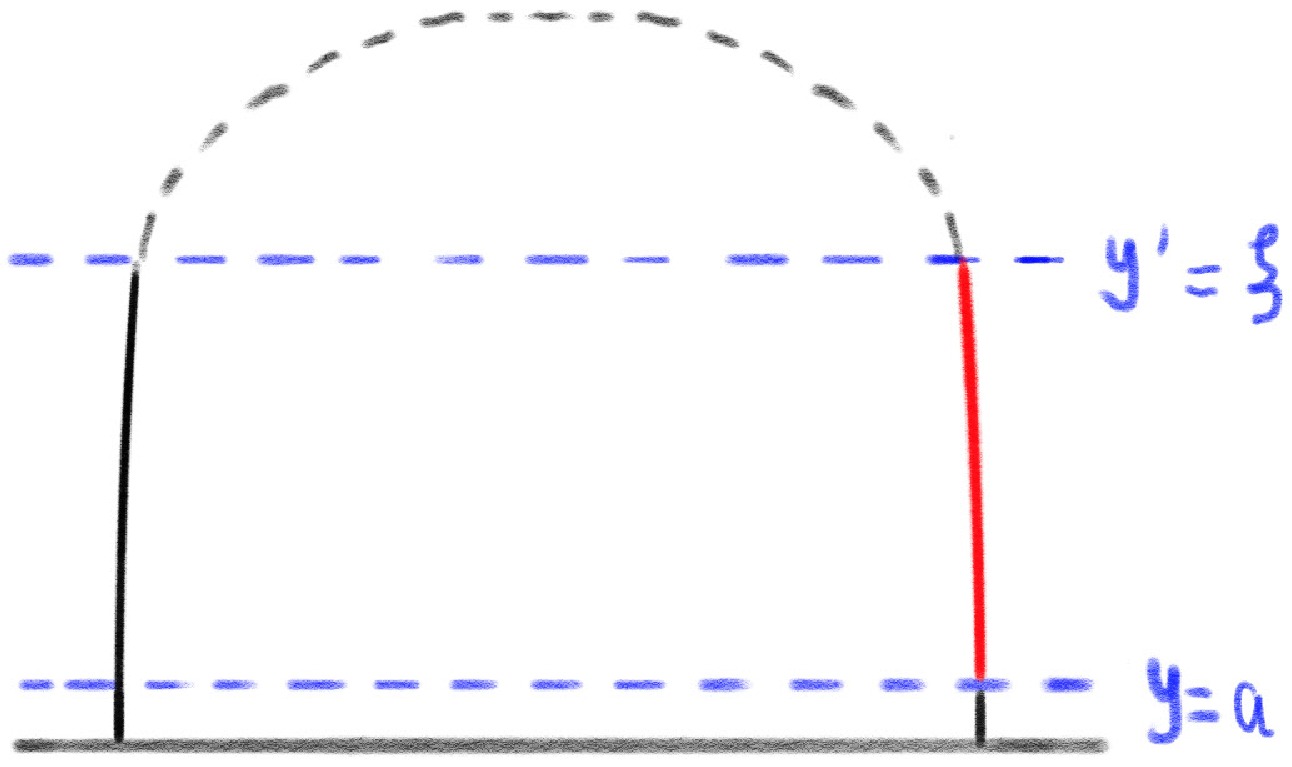

Figure 2.  (color online) Entanglement entropy with IR cut-off gives the geodesic connecting $ y=a $, $ y^{\prime}=\xi $, and $ \Delta x=0 $.

where we take the limit $ \triangle x\rightarrow0 $ and use $ y\left(=a\right)\ll y^{\prime}\left(=\xi\right) $. In this limit, for the numerator, we have

Comparing this with

we can now fix the leading behavior of the denominator:

where ξ is introduced to make the expansion parameter dimensionless. Note that $ \triangle x\rightarrow0 $ and $ \xi\rightarrow \infty $ in the expansion. The function with arbitrary endpoints can be extracted from this limit result (23):

2) $ \boldsymbol{y=y^{\prime}=a\ll\ell\ll\xi} $ (Fixing $ \boldsymbol{f(x,x',y,y')} $)

In this scenario, we are in the UV regime, and the EE is given by

Because $ y=y^{\prime}=a $, we have $ y-y^{\prime}=0 $, and the general geodesic length expression becomes

For consistency with Eq. (25), we must have $ f\left(x,x^{\prime},a,a\right)/ g\left(x,x^{\prime},a,a\right)\sim1/a^{2} $. This condition ensures that we recover the expected UV behavior as $ y=y'=a\to0 $. The corresponding geometry is shown in Fig. 3. From the determined function $ g(x,x',y,y') $ in Eq. (24), we immediately obtain

Figure 3.  (color online) Entanglement entropy with UV cut-off supports the geodesic connecting $ y=y^{\prime}=a $ with arbitrary $ \Delta x $.

Here, $ \triangle x $ is finite, and $ y=y^{\prime}=a\ll \ell \ll\xi $. In this limit, we can expand the function $ f\left(x,x^{\prime},y,y^{\prime}\right) $ as

where $ \mu_{i}\left(x,x^{\prime}\right) $ are regular functions. Now, recall the expression for the geodesic length,

where

As $ \eta\rightarrow0 $ ($ \triangle x\rightarrow0 $ and $ \triangle y\rightarrow0 $) and $ \xi\rightarrow \infty $, if we require y, $ y^{\prime}\ll\xi\rightarrow \infty $, the expressions for $ g\left(x,x^{\prime},y,y^{\prime}\right) $ (24) and $ f\left(x,x^{\prime},y,y^{\prime}\right) $ (28) still hold. Therefore, we have

where the order of $ {\cal{O}}\left[A,B,\ldots\right]^{2} $ denotes the higher order of $ {\cal{O}}\left[A^{2}\right] $, $ {\cal{O}}\left[B^{2}\right] $, $ {\cal{O}}\left[AB\right] $....

We now aim to calculate the metric by using the geodesic length. Hence, we can apply the following relation based on Synge's world function:

where we must determine the value of α. Through some computation, we obtain the following results:

This implies that only $ \alpha=1 $ yields a physical solution. Therefore, we can now extract the nonvanishing components of the metric:

The functions $ s\left(x,x^{\prime},0,0\right) $ do not contribute to the metric. Thus, the background metric is

This is the asymptotic form of static AdS$ _{3} $ with radius $ C_{1}R $. This is the asymptotic form of static $ \mathrm{AdS_{3}} $ and the central charge c of $ \mathrm{CFT_{2}} $ [21]: $ c=\dfrac{3R_{\rm AdS}}{2G_{N}^{\left(3\right)}} $; we identify

Therefore, we finally determine the leading terms of the series (17) ³:

Thus, the metric becomes

To recover pure AdS₃, we introduce the IR cut-off scale defined as

In the massless limit $ m\rightarrow0 $ (or equivalently $ \xi\rightarrow \infty $), we recover the pure AdS₃ metric:

When including the time-like direction, the UV EE is

The procedure follows the same pattern as in the static case. To generalize this, when expressing η as in Eq. (15), we introduce an arbitrary function multiplying $ (\Delta t)^{2} $. After performing a similar analysis, we obtain the covariant AdS metric:

where

As $ \xi\rightarrow \infty $, we recover pure AdS₃:

The result is consistent with the holographic RG flow discussed in [22]. To illustrate this, we consider the action for a bulk scalar field $ \phi_{a} $:

where $ G_{ab} $ is the metric of the internal space of the scalar field. When the potential $ V\left(\phi_{a}\right) $ reaches its critical value $ V\left(0\right)=-\dfrac{2}{R^{2}} $, the solution for the metric is

Near the boundary $ y=0 $, we obtain the asymptotic expansion

where μ is a mass scale. This is a special case of Eq. (42) under the condition $ G(t,x,y)=F(t,x,y) $.

We begin by recalling the two types of EEs and their corresponding geodesic lengths in the context of AdS/CFT:

These results follow directly from the AdS/CFT correspondence. However, if we do not assume the AdS/CFT framework, meaning we do not have a direct relation between the AdS radius and central charge, we have difficulty explaining why the first formula has a squared term while the second formula does not. To address this, we propose that the IR EE is multiplied by a constant factor $ {\cal{A}} $, and we identify this factor as modifying the corresponding geodesic length:

We can straightforwardly verify that for this modified IR EE to be compatible with the UV EE in the form given by Eq. (9), the function η must take the form

where $ g(x,x',y,y')=(yy')^{{\cal{A}}}(1+\Delta x^{2}s(x,x',y,y')/\xi^{2}+\cdots) $, $ \: $ and $ f(x,x',0,0)=(yy')^{{\cal{A}}-1}(1+\Delta x^{2}s(x,x',0,0)/\xi^{2}+\cdots) $. When substituting this expression for η into Eq. (5) for the metric, we find that $ g_{yy} $ behaves as follows:

Thus, we conclude that there is no dual gravity for $ {\cal{A}}\not=1 $, which provides a necessary condition for determining whether a CFT₂ is holographic. Furthermore, $ {\cal{A}}=1 $ is a necessary condition for any holographic CFT. This is consistent with the fact that, although a single interval has two boundary points, the holographic dual IR EE only counts one point.

We are deeply indebted to Bo Ning for several illuminating discussions and suggestions. This study could not have been conducted without her help. We are also very grateful to S. Kim, J. Lu, H. Nakajima, and S. He for very helpful discussions and suggestions.