ρ meson form factors and parton distribution functions in impact parameter space

I. INTRODUCTION

• I. INTRODUCTION
• II. FORM FACTORS
•      A NJL model
•      B FFs
• III. IMPACT PARAMETER DEPENDENT PDFs
•      A The width distribution
• IV. SUMMARY AND CONCLUSION
• APPENDIX A: USEFUL FORMULAS

The investigation into the inner structure of matter and the fundamental laws governing interactions has consistently been at the forefront of natural science research. This pursuit not only enables humanity to comprehend the underlying principles of nature but also fosters significant advancements in various technologies. Multidimensional imaging of hadrons has generated significant interest over the past several decades. It is widely acknowledged that generalized parton distributions (GPDs) [1−20] and transverse momentum dependent parton distribution functions (TMDs) [21−34] are a powerful tool for elucidating the hadronic structure of a system. This efficacy is because GPDs inherently encapsulate information pertaining to both form factors (FFs) [35−50] and parton distribution functions (PDFs) [51−62], thereby providing insights into system complexities. TMDs encapsulate the crucial information regarding the three-dimensional internal structure of hadrons, particularly the spin-orbit correlations among the quarks they contained [63−66].

FFs encapsulate fundamental information regarding the extended structure of hadrons, as they represent matrix elements of conserved currents between hadronic states. The electromagnetic interaction serves as a distinctive tool for probing the internal structure of the hadron. Measurements of electromagnetic FFs in both elastic and inelastic scattering, along with assessments of structure functions in deep inelastic scattering of electrons, have provided a wealth of information regarding the hadron's structure. A deficiency in precise information regarding the shapes of various form factors derived from the first principles of Quantum Chromodynamics (QCD) has been, and continues to be, a significant challenge in hadron physics. The electromagnetic FFs play a crucial role in elucidating nucleon structure and are essential for calculations involving the electromagnetic interactions of complex nuclei.

The elastic electromagnetic FFs of hadrons are fundamental quantities that represent the probability of a hadron absorbing a virtual photon with four-momentum squared $Q^2$. These FFs serve as essential tools for investigating the dynamics of strong interactions across a broad spectrum of momentum transfers [67, 68]. Their comprehensive understanding is crucial for elucidating various aspects of both perturbative and nonperturbative hadron structures. At high momentum transfers, they convey information regarding the quark substructure of a nucleon as described by QCD. Conversely, at low momentum transfers, these quantities are influenced by the fundamental properties of the nucleon, such as its charge and magnetic moment. The FFs also provide crucial insights into nucleon radii and the coupling constants of vector mesons.

The electromagnetic structure of the spin-1 ρ meson as revealed in elastic electron–hadron scattering is parametrized in terms of the charge $G_C$, magnetic $G_M$, and quadrupole $G_Q$ form factors. The comprehension of these form factors is crucial in any theoretical framework or model pertaining to strong interactions.

The work presented here is an update and extension of our previous work of Ref. [14]. In that paper, we studied the $5$ unpolarized and $4$ polarized GPDs in the Nambu–Jona-Lasinio (NJL) model of Refs. [69−75]. Through the GPDs, we studied the form factors of ρ meson, which related to the Mellin moments of GPDs. In this paper, we study the charge $G_C$, magnetic $G_M$, and quadrupole $G_Q$ form factors of ρ mesons and compare them with the lattice data in Refs. [76, 77]. Using the three form factors, we studied the structure functions $A(Q^2)$ and $B(Q^2)$, and the tensor polarization function $T_{20}(Q^2,\theta)$ appeared in the Rosenbluth cross section of elastic electron scattering. In addition, we studied the PDF of ρ mesons in impact parameter space. The diagrams of $x \cdot q_C(x, {{\boldsymbol{b}}}_{\perp}^2)$, $x \cdot q_Q(x, {{\boldsymbol{b}}}_{\perp}^2)$, and $x \cdot q_M(x, {{\boldsymbol{b}}}_{\perp}^2)$ for various values of x and $b_{\perp}$ are presented. The width distribution of the three distributions in the ρ meson for a given momentum fraction x are studied. The width distributions of $q_C(x, {{\boldsymbol{b}}}_{\perp}^2)$, $q_Q(x, {{\boldsymbol{b}}}_{\perp}^2)$, and $q_M(x, {{\boldsymbol{b}}}_{\perp}^2)$ provide insights into the sizes of the charge, magnetic moment, and quadrupole moment, respectively, in impact parameter space.

This article is structured as follows: In Sec. II, we introduce the NJL model and subsequently present the form factors of the ρ meson derived from the Mellin moments of GPDs. In Sec. III, we examine the properties of ρ meson PDFs in impact parameter space. A concise summary and outlook are provided in Sec. IV.

II. FORM FACTORS

• I. INTRODUCTION
• II. FORM FACTORS
•      A NJL model
•      B FFs
• III. IMPACT PARAMETER DEPENDENT PDFs
•      A The width distribution
• IV. SUMMARY AND CONCLUSION
• APPENDIX A: USEFUL FORMULAS

A NJL model

• I. INTRODUCTION
• II. FORM FACTORS
•      A NJL model
•      B FFs
• III. IMPACT PARAMETER DEPENDENT PDFs
•      A The width distribution
• IV. SUMMARY AND CONCLUSION
• APPENDIX A: USEFUL FORMULAS

The $S U$(2) flavor NJL Lagrangian is as follows:

where $\hat{m}={\rm{diag}}\left(m_u,m_d\right)$ denotes the current quark mass matrix, while $\vec{\tau}$ represents the Pauli matrices used to describe isospin. For perfect isospin symmetry, $m_u = m_d = m$. The 4-fermion coupling constants associated with each chiral channel are $G_{\pi}$, $G_{\omega}$, and $G_{\rho}$.

By solving the gap equation, we derive the dressed quark propagator within the framework of the NJL model:

The interaction kernel of the gap equation is local, leading us to derive a constant dressed quark mass M that satisfies

where the trace is greater than the Dirac indices. When the coupling constant exceeds a critical threshold, specifically when $G_{\pi} > G_{\rm critical}$, dynamical chiral symmetry breaking can occur, leading to a nontrivial solution with $M > 0$.

The NJL model is non-renormalizable, necessitating the application of a regularization method to fully define the framework. In this context, we adopt the proper time regularization (PTR) scheme [78−80].

where X represents a product of propagators combined through Feynman parametrization. The infrared cutoff is expected to be on the order of $\Lambda_{{\rm{QCD}}}$, and we select $\Lambda_{{\rm{IR}}} = 0.240$ GeV. The parameters utilized in this study, including the coupling strength $G_{\pi}$, the momentum cutoff $\Lambda_{{\rm{UV}}}$, and the current quark mass m, are determined through the Gell-Mann–Oakes–Renner (GMOR) relation given by

and gap equation

where $m_{\pi}=0.140$ GeV represents the physical pion mass, $f_{\pi}=0.092$ GeV denotes the pion decay constant, the current quark mass is given by $m=0.016$ GeV, the ultraviolet cut off $\Lambda_{{\rm{UV}}} = 0.645$ GeV and the constituent quark mass is specified as $M=0.4$ GeV, Additionally, $\langle\bar{\psi}\psi \rangle$ refers to the two-quark condensate derived from QCD sum rules. The pseudoscalar bubble diagram

where $\sigma_1=M^2+x(1-x)Q^2$and $\mathcal{C}_0$ and $\bar{\mathcal{C}}_1$ are defined in Eq. (A1) of the appendix. The mass of the pion aligns with the value derived from the pole condition given by $1+2G_{\pi} \Pi_{PP} (-m_{\pi}^2)=0$. The coupling constants $G_{\omega}$ and $G_{\rho}$ are determined using the masses $m_{\omega}=0.782$ GeV and $m_{\rho}=0.770$ GeV through the relation $1+2G_i \Pi_{VV} (-m_i^2) =0$, where $i=(\omega,\rho)$. Here, $\Pi_{VV} (Q^2)$ represents the vector bubble diagram as defined in Eq. (13). The parameters utilized in this study are presented in Table 1.

Table 1

Table 1.  Parameter set used in the study. The dressed quark mass and regularization parameters are in units of GeV, while coupling constant are in units of GeV⁻², and quark condensates are in units of GeV³.

$\Lambda_{{\rm{IR}}}$	$\Lambda _{{\rm{UV}}}$	M	m	$G_{\pi}$	$Z_{\rho}$	$m_{\rho}$	$G_{\omega}$	$G_{\rho}$	$\langle\bar{u}u \rangle^{1/3}$
0.24	0.645	0.4	0.016	19.0	6.96	0.77	10.4	11.0	−0.173

DownLoad: CSV

Show Table

The quark charge operator in the NJL model is

where $e_u$ and $e_d$ represent the electric charges of the up and down quarks, respectively. This indicates that the quark-photon vertex possesses both isoscalar and isovector components. Consequently, the dressed quark-photon vertex and effective vertex can be respectively, articulated as follows:

and

where $i=(\omega,\rho)$. For a point-like quark, we have $P_{1i}(Q^2) = 1$ and $P_{2i}(Q^2) = 0$. The inhomogeneous Bethe-Salpeter equation (BSE) governing the quark-photon vertex is expressed as follows:

where $\sum_{\Omega}K_{\Omega}\Omega_{\alpha\beta} \bar{\Omega}_{\gamma\delta}$ denotes the interaction kernels. Among these, only the isovector-vector term, $-2{\rm i}G_{\rho}(\gamma_{\mu}\vec{\tau })_{\alpha\beta}(\gamma_{\mu}\vec{\tau })_{\gamma\delta}$ and the isoscalar-vector term, $-2{\rm i}G_{\omega}(\gamma_{\mu})_{\alpha\beta}(\gamma_{\mu})_{\gamma\delta}$, can contribute significantly.

From the inhomogeneous BSE, the dressed quark form factors associated with the electromagnetic current described in Eq. (10) are [11]

where $i=(\omega,\rho)$, and $\Pi_{VV}$ is the bubble diagram

The subsequent sections employ the Gamma functions and notations presented in Eq. (A1).

In the light-cone normalization, the ρ meson vertex function is defined as

where $Z_{\rho}$ is the square of the effective meson-quark-quark coupling constant, which is defined as follows:

B FFs

• I. INTRODUCTION
• II. FORM FACTORS
•      A NJL model
•      B FFs
• III. IMPACT PARAMETER DEPENDENT PDFs
•      A The width distribution
• IV. SUMMARY AND CONCLUSION
• APPENDIX A: USEFUL FORMULAS

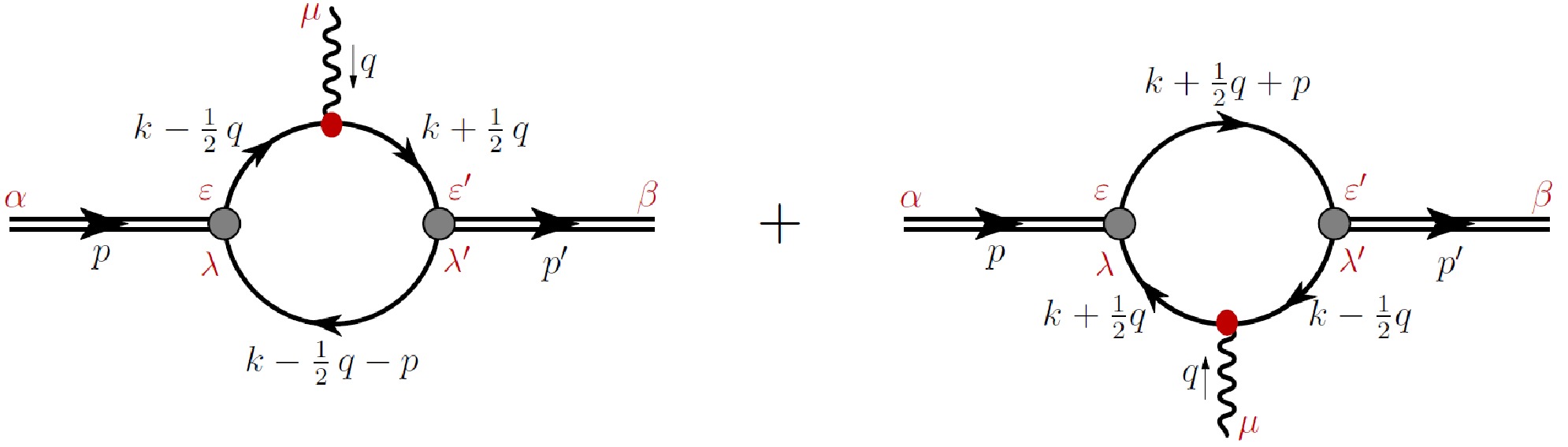
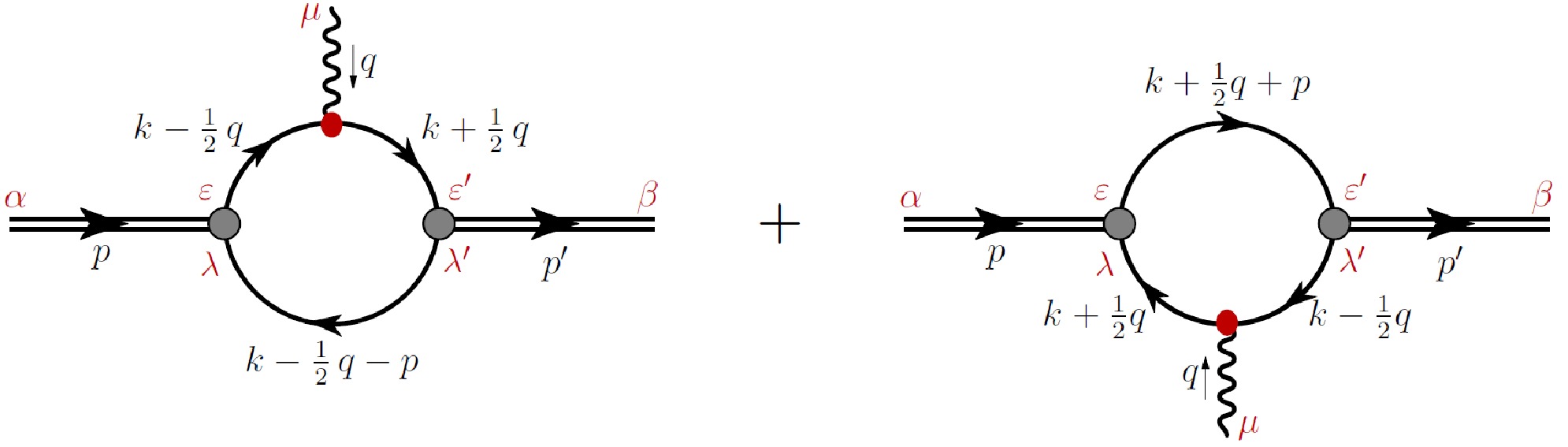
The Feynman diagrams representing the GPDs of the ρ meson are illustrated in Fig. 1. In the NJL model, the GPDs of the quark in the ρ meson are defined as follows:

Figure 1

Figure 1.  (color online) Feynman diagrams representing the $\rho^+$ meson GPDs.

DownLoad: Full-Size Img PowerPoint

where ${\rm{tr}}_{{\rm{D}}}$ indicates a trace over spinor indices, $\delta_n^x (k)= \delta (xP^+-k^+)$, $k_{+q}=k+\frac{q}{2}$, $k_{-q}=k-\frac{q}{2}$. p is the incoming and $p'$ the outgoing ρ meson momentum. In this study, we use the symmetry notation. Hence, the kinematics of this process and the related quantities are defined as

ξ is the skewness parameter, and in the light-cone coordinate,

For any four-vector, n is the light-cone four-vector defined as $n=(1,0,0,-1)$in the light-cone coordinate

The vector quark correlator can be decomposed as follows:

where the expressions for $H_i$ are derived in Ref. [14]. The general form of the vector current associated with the ρ meson is presented as follows:

Integrating over x allows one to derive

The expressions for $F_1(Q^2)$, $F_2(Q^2)$, and $F_3(Q^2)$ are presented in Ref. [14].

The Sachs-like charge, magnetic, and quadrupole form factors for the ρ meson are presented as follows:

where $\eta=Q^2/(4m_{\rho}^2)$. The dressed Sachs-like charge, magnetic, and quadrupole form factors are defined as $G_C^D(Q^2)=G_C(Q^2)P_{1\rho}(Q^2)$, $G_M^D(Q^2)=G_M(Q^2)P_{1\rho}(Q^2)$, and $G_Q^D(Q^2)=G_Q(Q^2)P_{1\rho}(Q^2)$, respectively. Here, $P_{1\rho}(Q^2)$ is specified in Eq. (12).

We compare our results with the lattice QCD (LQCD) findings presented in Refs. [76, 77] in Fig. 2. The figure illustrates that the general trends of both the bare and dressed charge factor are consistent with the lattice results. The error bars of the 2015 lattice data in Ref. [77] are quite short, particularly at large values of $Q^2$; hence, they as dots when plotted. The various points without uncertainties for the same kinematic conditions represent different initial and final ρ meson momenta. It is important to note that form factors corresponding to different initial and final ρ meson momenta at the same $Q^2$ may overlap.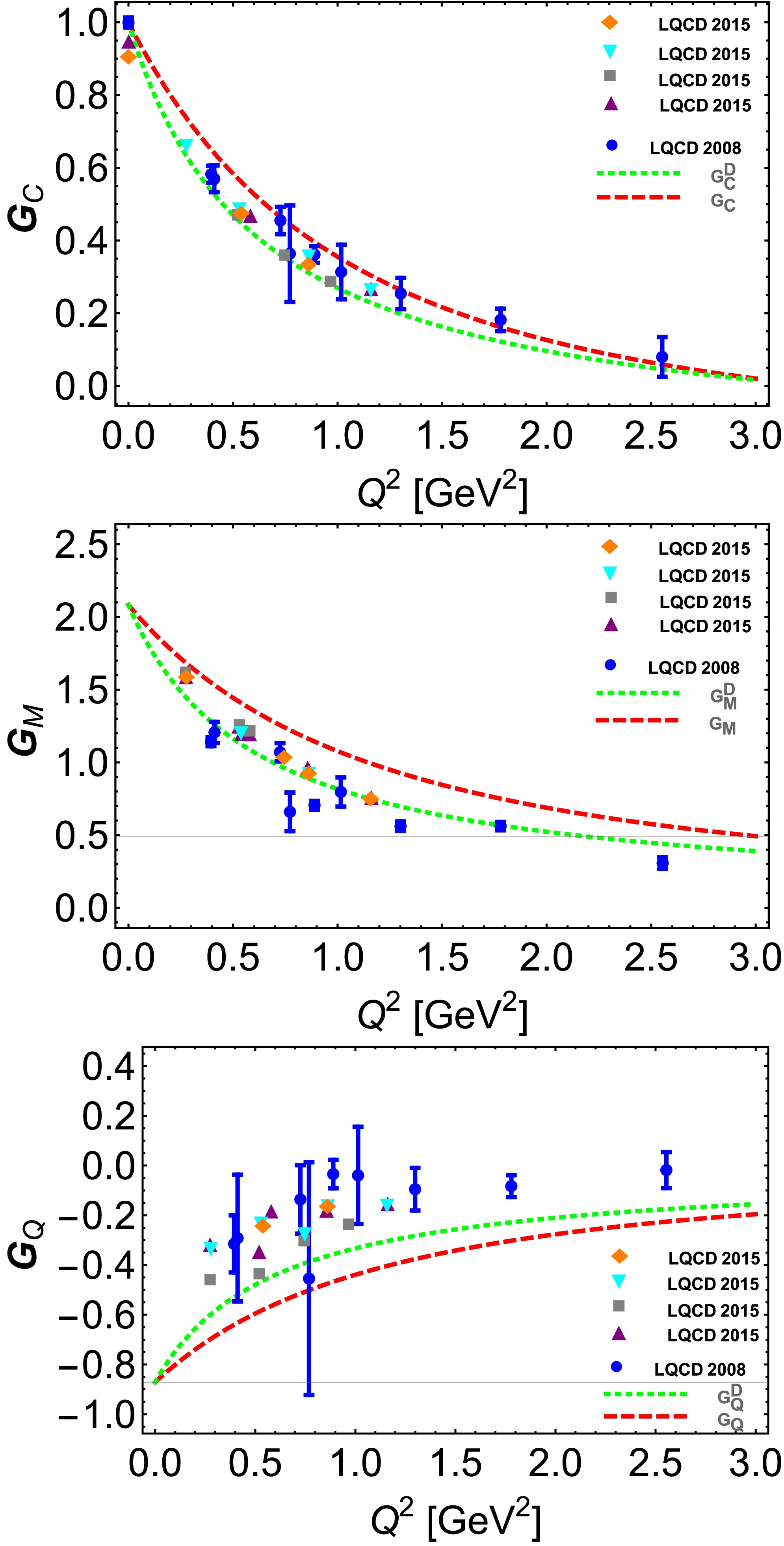

Figure 2

Figure 2.  (color online) The upper, middle, and lower panels show the bare and dressed charge, magnetic, and quadrupole form factors, respectively. The bare and dressed form factors are denoted by the red dashed line and green dotted line, respectively. The LQCD predictions from 2008 [76] are denoted by blue solid lines accompanied by error bars. Additionally, LQCD predictions from 2015 [77] are represented by yellow diamonds, cyan inverted triangle, gray squares, and purple triangles.

DownLoad: Full-Size Img PowerPoint

For the magnetic form factor, as shown in the middle diagram, we observe that the bare $G_M$ is harder than reported in lattice studies; conversely, the dressed $G_M^D$ aligns more closely with the lattice results from [77], although it remains harder than those from [76].

For the quadrupole form factor $G_Q$, both bare and dressed form factors exhibit a hardness greater than that observed in Refs. [76, 77].

In Ref. [39], a relationship was derived for the form factors of spin-$1$ particles at large $Q^2$. Specifically, in the regime of large timelike or spacelike momenta, the ratio of form factors for the ρ meson is expected to exhibit the following behavior:

where the corrections are of the orders $\Lambda_{{\rm{QCD}}}/Q$ and $\Lambda_{{\rm{QCD}}}/m_{\rho}$. In Fig. 3, we present a diagram illustrating the ratios of the three form factors. These figures demonstrate that the ratios $G_C/G_M$ and $G_C/G_Q$ exhibit a good fit, while the ratio $G_M/G_Q$ remains below $-2$ and approaches a finite value of $-2.52$ as $Q^2$ increases.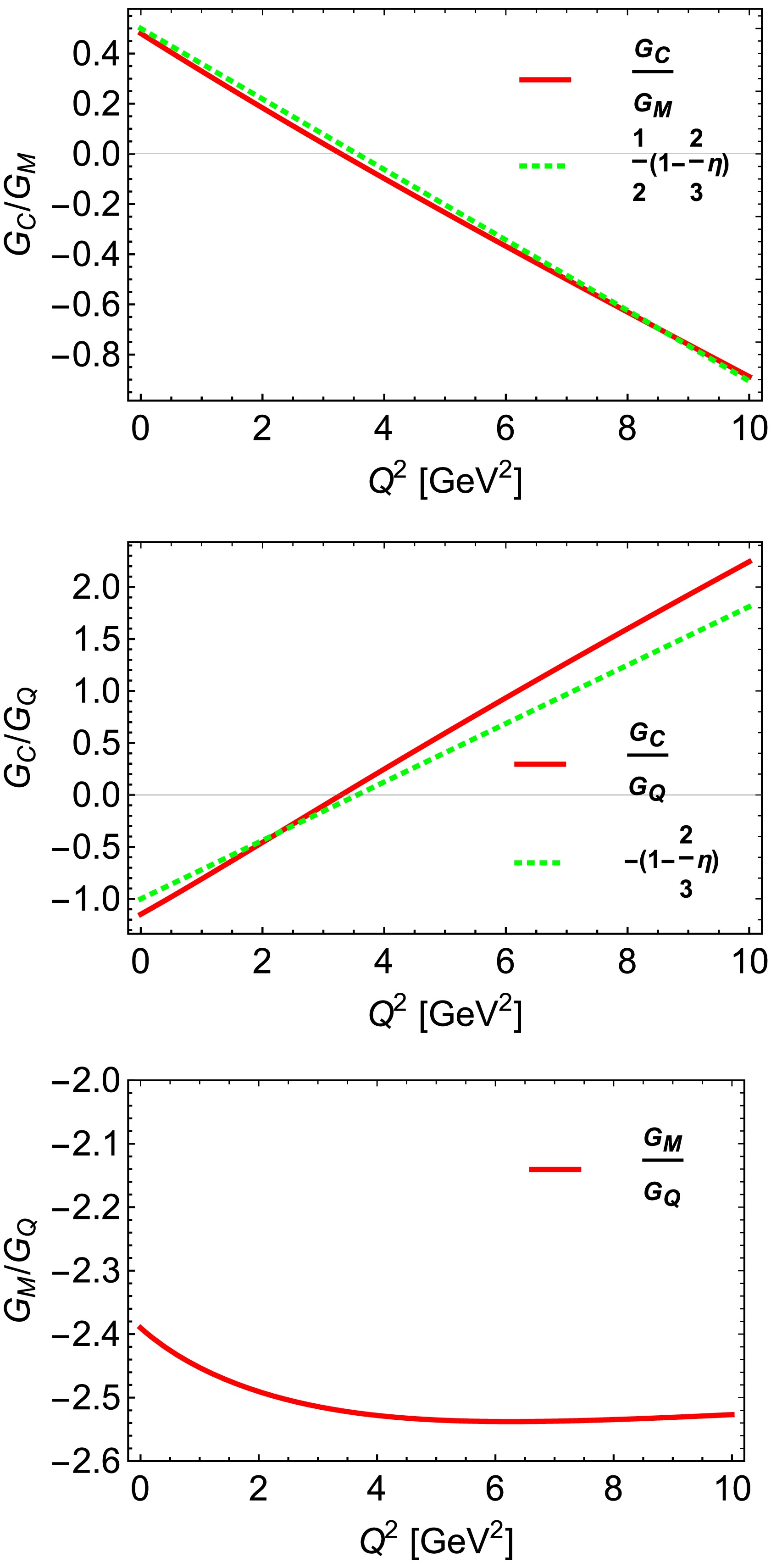

Figure 3

Figure 3.  (color online) Upper panel: The red solid line represents the ratio of $G_C/G_M$, while the green dotted line denotes $\frac{1}{2}(1-\frac{2}{3}\eta)$. Middle panel: The red solid line illustrates the ratio of $G_C/G_Q$, and the green dotted line indicates $-(1-\frac{2}{3}\eta)$. Lower panel: The red solid line depicts the ratio$G_M/G_Q$.

DownLoad: Full-Size Img PowerPoint

Further, one can define the helicity-conserving matrix elements $(G_{11}^+,G_{00}^+)$ and helicity nonconserving matrix elements $(G_{0+}^+,G_{-+}^+)$, respectively, in terms of $G_C$, $G_M$, and $G_C$ as in Refs. [81−83]

In Fig. 4, we present the diagrams for both the bare and dressed helicity-conserving matrix elements $(G_{11}^+, G_{00}^+)$, as well as the helicity non-conserving matrix elements $(G_{0+}^+, G_{-+}^+)$. For $G_{00}^+$, the contact interaction renders the form factor hard; as Q approaches infinity, $G_{00}^+$ approximates a non-zero constant value. The dressed version, $G_{00}^{D+}$, is softer than its bare counterpart $G_{00}^+$; when $Q > 4$ GeV, it remains nearly constant at approximately $G_{00}^{D+}\simeq 0.54$. Compared to Refs. [82, 83], which demonstrates $G_{00}^+$ approaching zero as Q increases, our findings suggest harder behavior.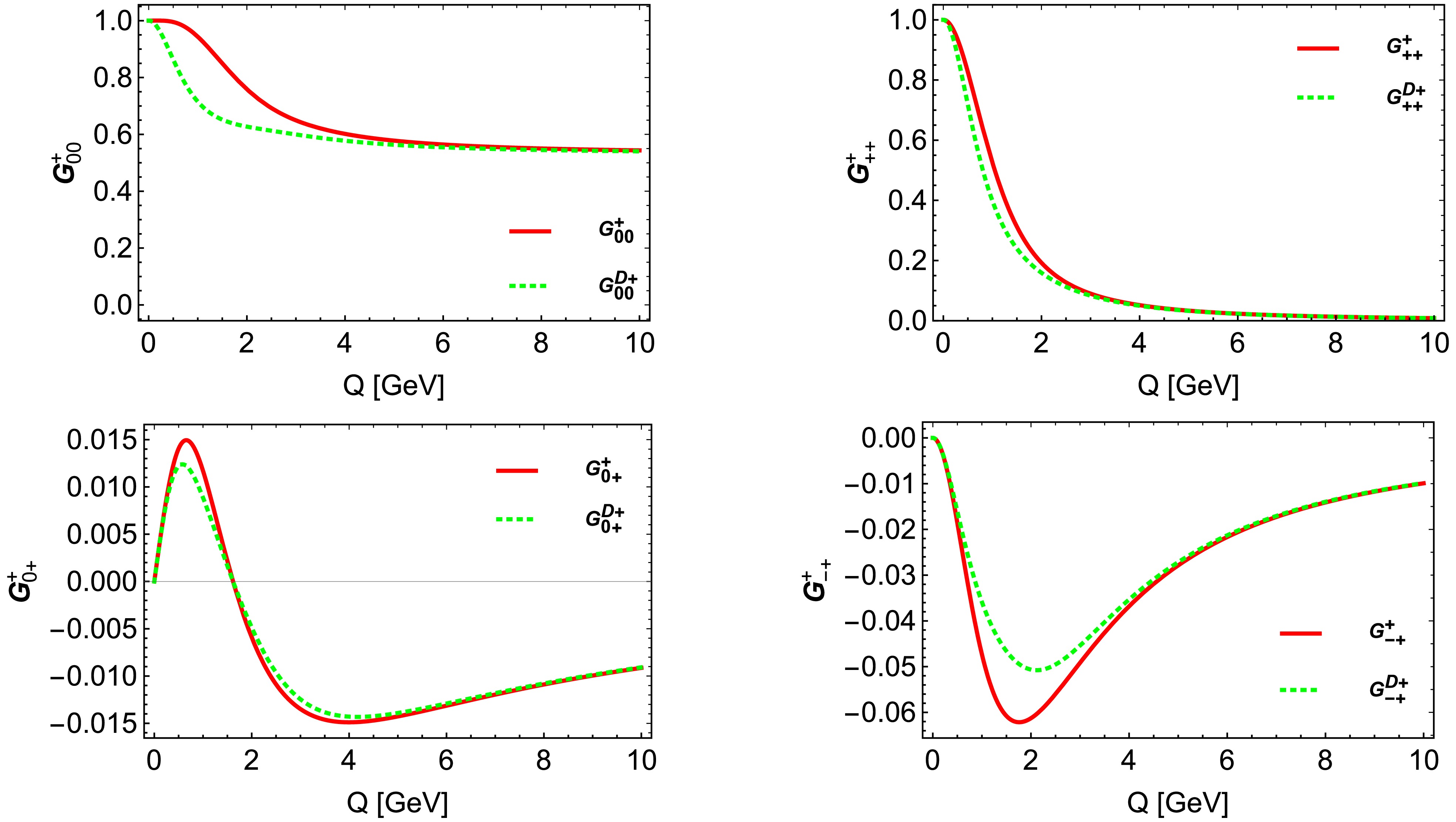

Figure 4

Figure 4.  (color online) The red solid line represents the helicity-conserving and helicity non-conserving matrix elements, which are denoted as $G_{00}^+$, $G_{11}^+$, $G_{0+}^+$, and $G_{-+}^+$. The green dotted line illustrates the dressed helicity-conserving and helicity non-conserving matrix elements, indicated as $G_{00}^{D+}$, $G_{11}^{D+}$, $G_{0+}^{D+}$, and $G_{-+}^{D+}$.

DownLoad: Full-Size Img PowerPoint

The helicity-conserving element $G_{11}^+$ tends to zero with increasing Q, consistent with Refs. [82, 83].

The matrix element $G^{+}_{0+}$ displays a peak around $Q\simeq 0.7$ GeV, aligning with observations from Ref. [82]. The concavity observed in our model occurs at approximately $Q \simeq 3.8$ GeV. Furthermore, the peaks of the dressed $G^{D+}_{0+}$ are smaller than those of $G^{+}_{0+}$.

$G^{+}_{-+}$ had a minimum -0.06 at $Q\simeq 1.8$ GeV, which is larger than that reported in Ref. [82]. For the dressed $G_{- +}^{D+}$, a minimum value of -0.05 occured at $Q\simeq 2$ GeV.

The standard Rosenbluth cross section [84] for elastic electron scattering on a target of arbitrary spin in the laboratory frame is given by

In the context of invariants, it is:

The structure functions $A(Q^2)$, $B(Q^2)$ and tensor polarization [85] $T_{20}(Q^2,\theta)$ are defined as

In Fig 5, we present diagrams for both the bare and dressed forms of $A(Q^2)$ and $B(Q^2)$. In our analysis, as $Q^2$ increases, $A(Q^2)$ decreaes, ultimately stabilizing at a finite value of approximately $0.14$ for the bare $A(Q^2)$ and around $0.12$ for the dressed $A^D(Q^2)$.

Figure 5

Figure 5.  (color online) The bare structure functions $A(Q^2)$ and $B(Q^2)$ and dressed structure functions $A^D(Q^2)$ and $B^D(Q^2)$of ρ mesons represended by the red solid line and green dotted line, respectively.

DownLoad: Full-Size Img PowerPoint

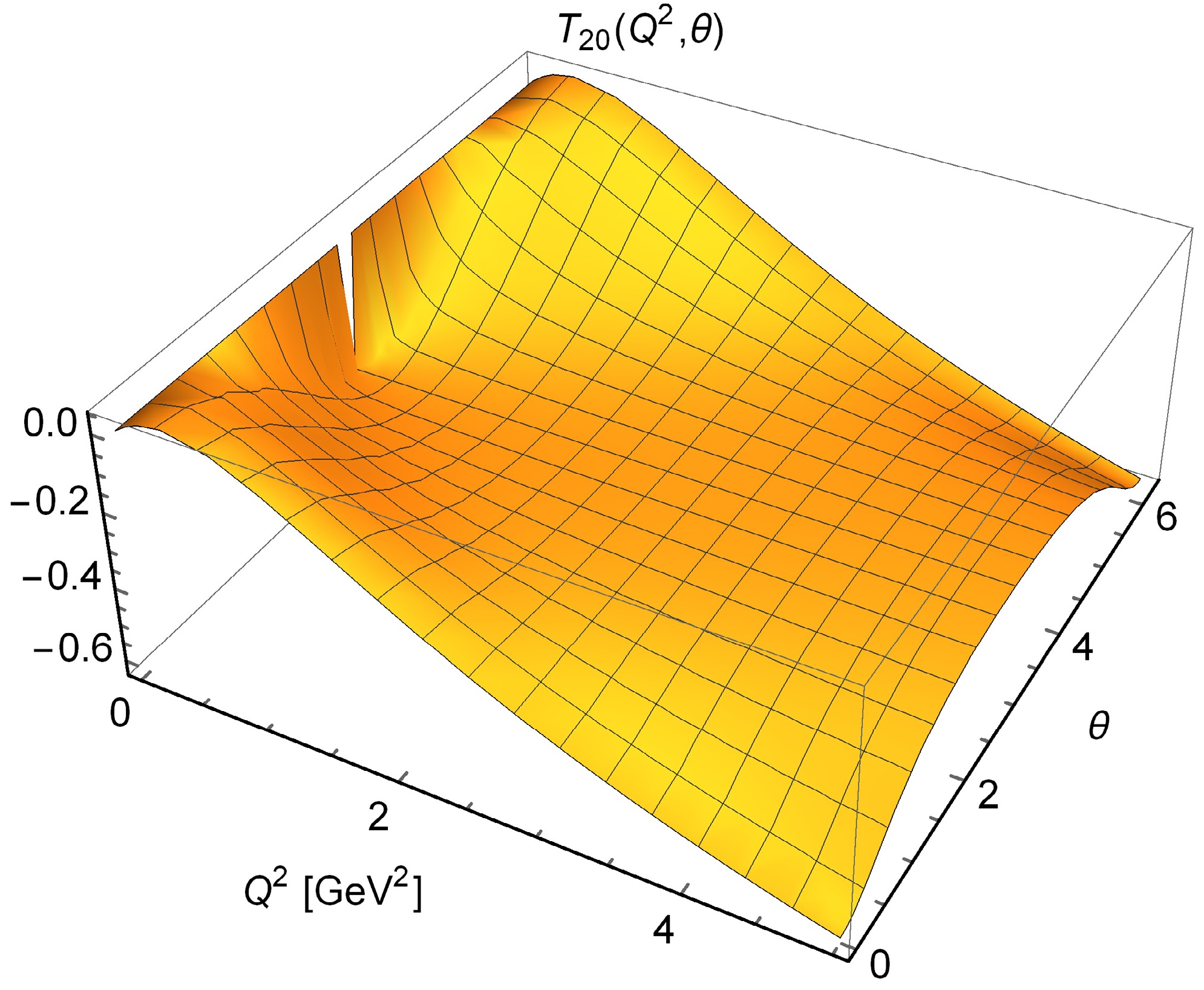
For small values of $Q^2$, $B(Q^2)$ initially increases with rising $Q^2$, reaching a peak at approximately $Q^2\simeq 1.5$ GeV$^2$. Then, it declines as $Q^2$ increases. At sufficiently large values of $Q^2$, it approaches a finite limit of about 0.7. In contrast, the dressed form, denoted as $B^D(Q^2)$, does not exhibit a maximum; instead, it remains nearly constant when $Q^{2} > 1$ GeV$^2$, stabilizing at approximately 0.6.

In Fig. 6, we present the three-dimensional diagram of $T_{20}(Q^2,\theta)$. When $Q^2$ is small, $T_{20}(Q^2,\theta)$ is larger values for $\theta\rightarrow 0$ and $\theta\rightarrow 2\pi$, while it is comparatively smaller near $\theta\simeq \pi$. At $\theta\simeq \pi$, as $Q^2$ increases, there is minimal change in $T_{20}(Q^2,\theta)$. Conversely, at both limits of $\theta\rightarrow 0$ and $\theta\rightarrow 2\pi$, an increase in $Q^2$ results in a gradual decrease of $T_{20}(Q^2,\theta)$. The dressed $T_{20}^D(Q^2,\theta)$ remains consistent with $T_{20}(Q^2,\theta)$.

Figure 6

Figure 6.  (color online) The ρ meson tensor polarization $T_{20}(Q^2,\theta)$.

DownLoad: Full-Size Img PowerPoint

Thus, the domain for leading-power perturbative QCD predictions regarding the ρ meson form factors is characterized by $Q^2 \gg 2m_{\rho}\Lambda_{{\rm{QCD}}} \sim 0.35$ GeV$^2$. Within this domain, one obtains

In the extreme limit, $\eta\gg1$, namely, $Q^2 \gg 4m_{\rho}^2=2.37$ GeV$^2$, these reduce to

For $\eta \ll 1$, namely, $Q^2 \ll 2.37$ GeV$^2$, one obtains

The fundamental assumption underlying all of these findings is that the $G_{00}^+$ amplitude defined in Eq. (26) is dominant.

In Fig. 7, we present the ratio of $A(Q^2)$ to $B(Q^2)$. From the diagram, it is evident that when $Q^2$ is small, the results align with theoretical predictions. As $Q^2$ increases, the value of $B/A$ exceeds $4$, approaching approximately $B/A \simeq 5$.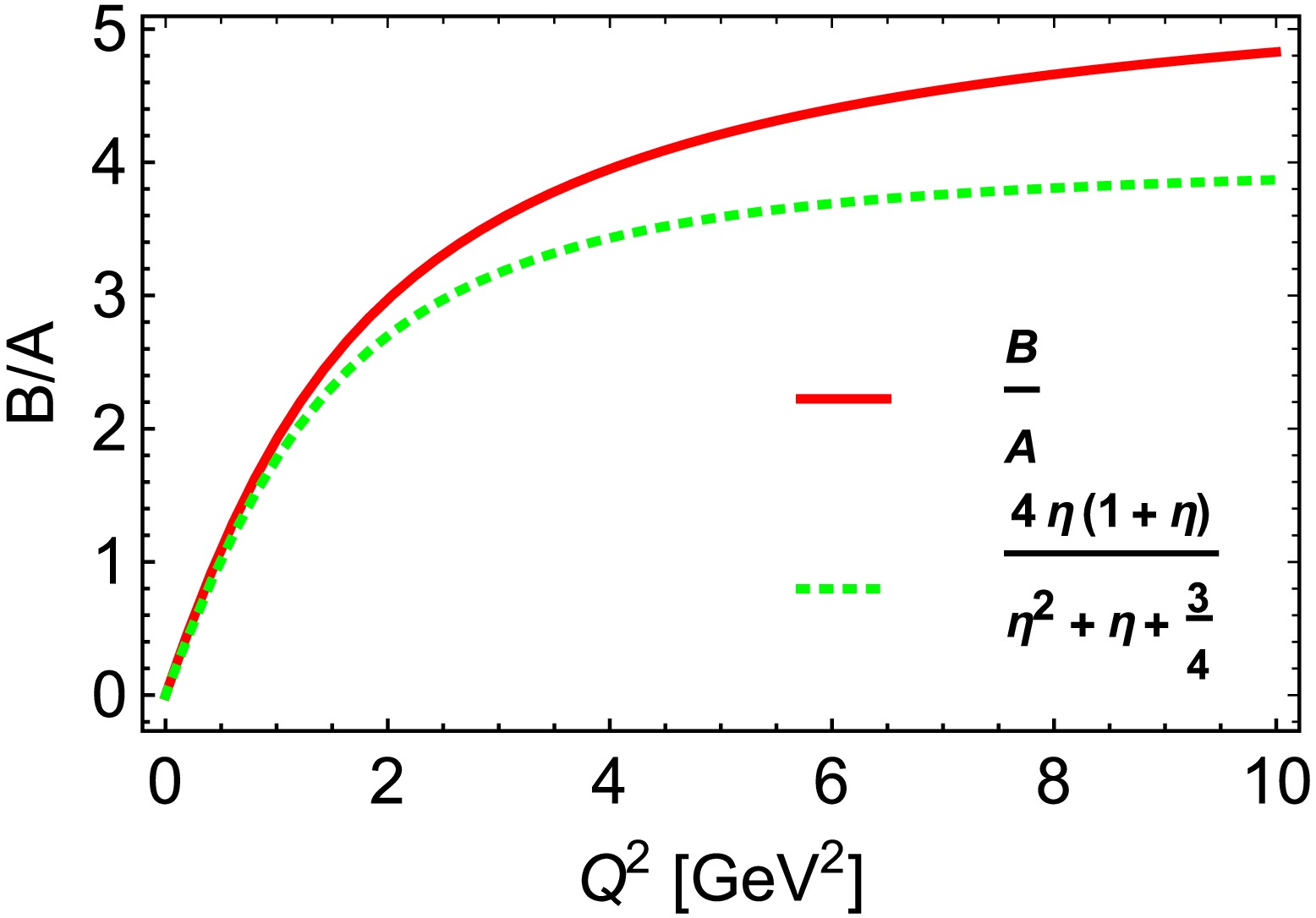

Figure 7

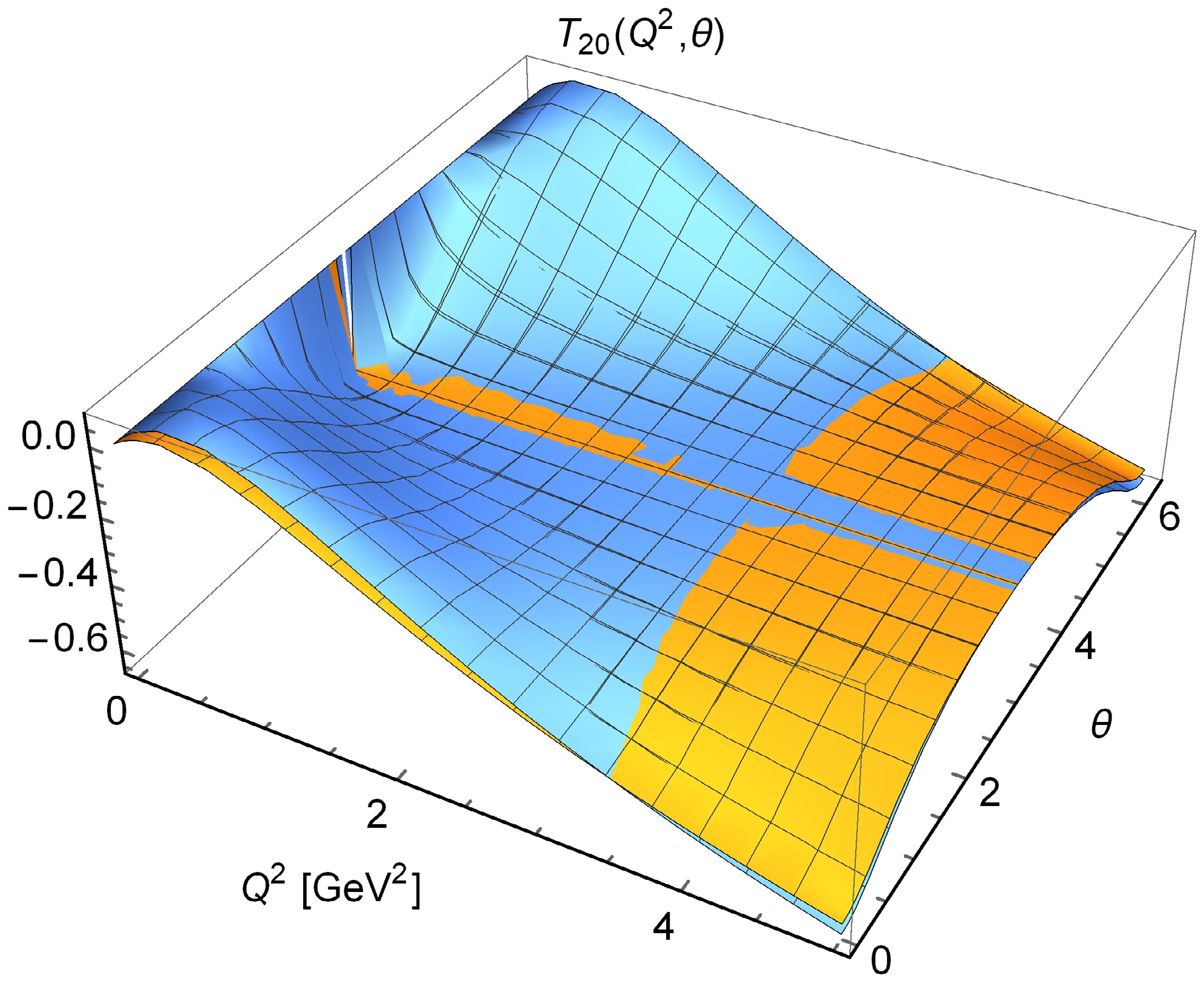
Figure 7.  (color online) The red solid line represents the ratio $B/A$, while the green dotted line illustrates the expression $\frac{4\eta(1+\eta)}{\eta^2+\eta+3/4}$ for the ρ meson.

DownLoad: Full-Size Img PowerPoint

In Fig. 8, we illustrate the graphs of $T_{20}(Q^2,\theta)$ and $T_{20}(\theta)$, as described in Eq. (33). The diagrams indicate that our calculated values for $T_{20}(Q^2,\theta)$ closely coincide with those predicted by theory.

Figure 8

Figure 8.  (color online) The tensor polarization $T_{20}(Q^2, \theta)$ is depicted in yellow, accompanied by the approximate value of the ρ meson as presented in Eq. (33), which is illustrated in blue.

DownLoad: Full-Size Img PowerPoint

III. IMPACT PARAMETER DEPENDENT PDFs

• I. INTRODUCTION
• II. FORM FACTORS
•      A NJL model
•      B FFs
• III. IMPACT PARAMETER DEPENDENT PDFs
•      A The width distribution
• IV. SUMMARY AND CONCLUSION
• APPENDIX A: USEFUL FORMULAS

The impact parameter dependent PDFs are defined as

indicating that the impact parameter dependent PDFs are the Fourier transform of GPDs at $\xi=0$. We examine the quantities $q_C$, $q_M$, and $q_Q$ as discussed in Ref. [14]. In this section, we further investigate these parameters within the context of the impact parameter space.

The diagrams of $x\cdot q_C$, $x\cdot q_M$, and $x\cdot q_Q$ are presented in Fig. 9. The diagrams indicate that as $b_{\perp}$ increases, the values of $x\cdot q_{C,M,Q}$ decrease, while the corresponding x-value at which the peak occurs gradually diminishes. It is important to note that in the large x region, for small $b_\perp$, the value of $x \cdot q_Q$ exhibits oscillatory behavior around zero. The sign issue is of numerical origin.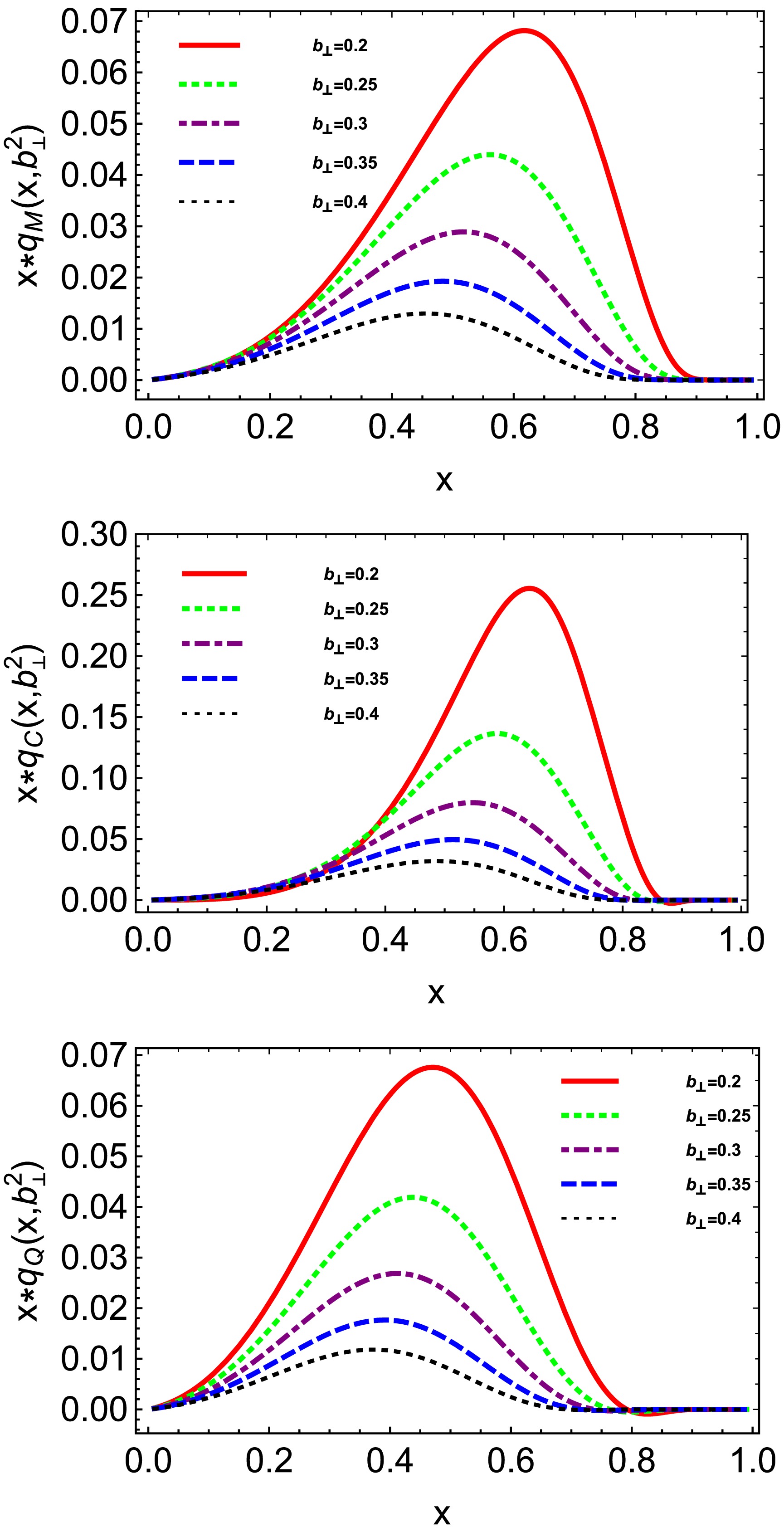

Figure 9

Figure 9.  (color online) The three distinct impact parameter-dependent PDFs are multiplied by the momentum fraction x for varying values of $b_{\perp}$. The thick red solid line represents $b_{\perp}=0.2$ fm; the thick green dotted line corresponds to $b_{\perp}=0.25$ fm; the thick purple dot-dashed line indicates $b_{\perp}=0.3$ fm; the thick blue dashed line signifies $b_{\perp}=0.35$ fm; and the thin black dotted line illustrates $b_{\perp}=0.4$ fm.

DownLoad: Full-Size Img PowerPoint

A The width distribution

• I. INTRODUCTION
• II. FORM FACTORS
•      A NJL model
•      B FFs
• III. IMPACT PARAMETER DEPENDENT PDFs
•      A The width distribution
• IV. SUMMARY AND CONCLUSION
• APPENDIX A: USEFUL FORMULAS

The distribution of parton widths for a specified momentum fraction x is

When $x\rightarrow 1$, the impact parameter should approach zero. This is because the struck quark moves closer to the center of momentum as its momentum increases.

The width distributions for the three datasets are illustrated in Fig. 10. It is evident that all of them satisfy the condition $\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_1=0$. When x is small, $\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_x^C$ exhibits the largest value, while $\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_x^Q$ shows the smallest. This indicates that in impact parameter space, the charge distribution is the broadest, whereas the quadrupole distribution is the narrowest.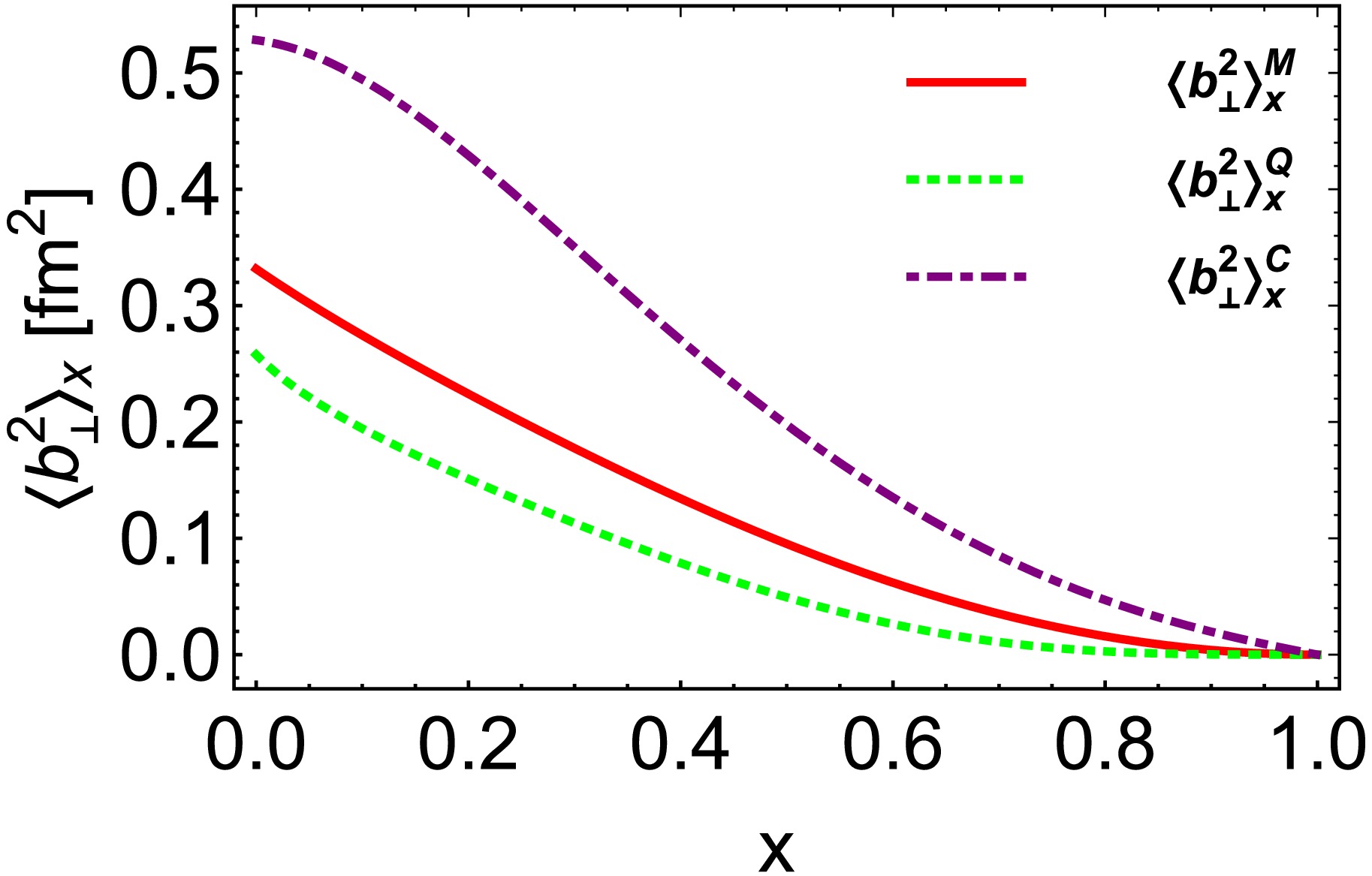

Figure 10

Figure 10.  (color online) The width distribution for a given momentum fraction x is defined in Eq. (39). The red solid line represents $\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_x^M$, the green dotted line denotes $\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_x^Q$, and the purple dot-dashed line illustrates $\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_x^C$.

DownLoad: Full-Size Img PowerPoint

In Fig. 11, we present a three-dimensional representation of the function described in Eq. (39). This illustration highlights the x-dependence of the transverse magnetic, charge, and quadrupole radii of the ρ meson, as referenced in Ref. [86]. The diagram reveals that the transverse quadrupole radius is minimized across the region where $x\in[0,1]$. Additionally, it is observed that the transverse charge radius exhibits its maximum breadth.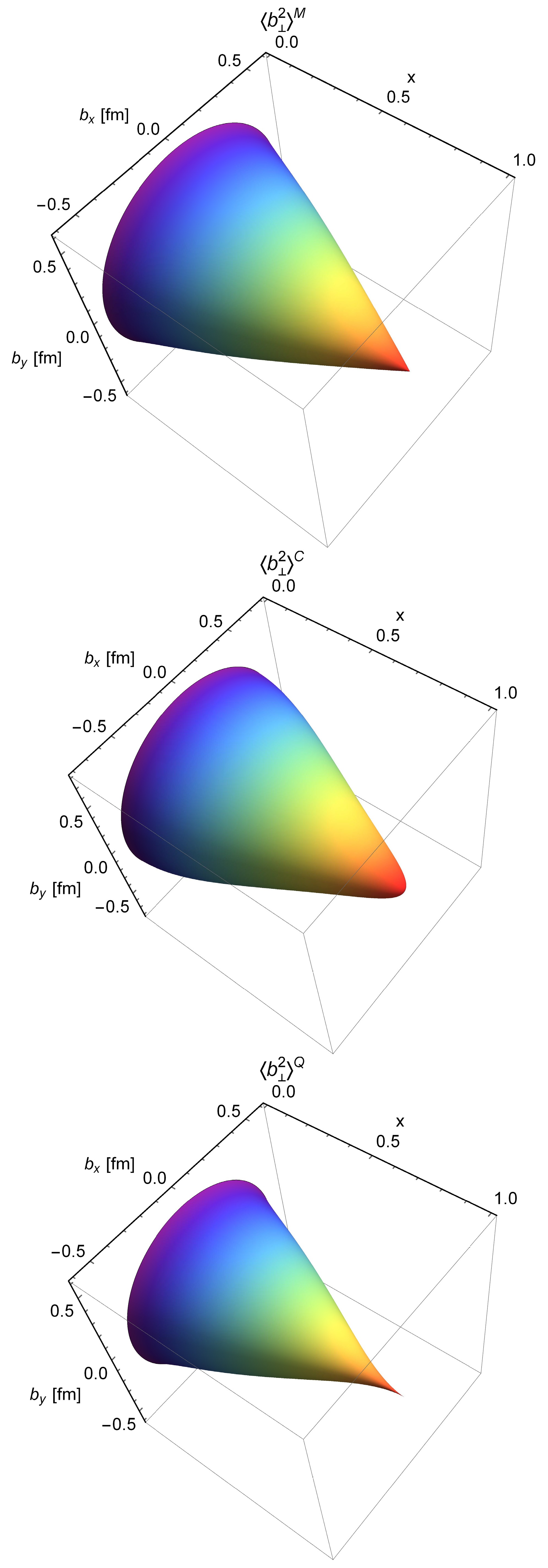

Figure 11

Figure 11.  (color online) Three-dimensional representation of the function of Eq. (39), showing the x-dependence of the ρ meson’s transverse magnetic, charge, and quadrupole radii.

DownLoad: Full-Size Img PowerPoint

The squared radius is determined from $\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_x$ by computing the following average over x:

In Table 2, we present the $\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_x$ at $x=0$, which indicates the ranges of various distributions. In impact parameter space, the range of the charge distribution $q_C$ is the most extensive, while the quadrupole distribution $q_Q$ exhibits the narrowest range. The observed values$\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_0$ are the same as those of the pseudoscalar mesons in Refs. [12, 20] and quarks in the proton of Ref. [86].

Table 2

Table 2.  Comparison of the x-averaged squared radius for $\langle {{\boldsymbol{b}}}_{\bot}^2\rangle$ and the value of $\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_x$ at $x=0$ in the NJL model in fm².

	$\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_0^{C}$	$\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_0^{M}$	$\langle {{\boldsymbol{b}}}_{\bot}^2\rangle_0^{Q}$	$\langle {{\boldsymbol{b}}}_{\bot}^2\rangle^{C}$	$\langle {{\boldsymbol{b}}}_{\bot}^2\rangle^{M}$	$\langle {{\boldsymbol{b}}}_{\bot}^2\rangle^{Q}$
NJL	0.528	0.332	0.258	0.220	0.126	0.094

DownLoad: CSV

Show Table

IV. SUMMARY AND CONCLUSION

• I. INTRODUCTION
• II. FORM FACTORS
•      A NJL model
•      B FFs
• III. IMPACT PARAMETER DEPENDENT PDFs
•      A The width distribution
• IV. SUMMARY AND CONCLUSION
• APPENDIX A: USEFUL FORMULAS

In this study, we assess the form factors and impact parameter space parton distribution functions (PDFs) derived from the GPDs of the ρ meson within the framework of the NJL model, employing proper time regularization. We select the NJL model due to its ability to provide qualitatively sound initial conditions for exploring physical possibilities in domains where more realistic frameworks have yet to yield insights or predictions.

For the Sachs-like charge, magnetic, and quadrupole form factors of the ρ meson, we compare our results with lattice QCD data. The findings indicate that the dressed $G_C^D$ and $G_M^D$ align well with the lattice QCD data; however, for the quadrupole form factors, both the dressed $G_Q^D$ and bare $G_Q$ exhibit harder behaviors than those observed in lattice results.

We also examine the structure functions $A(Q^2)$, $B(Q^2)$, and tensor polarization $T_{20}(Q^2,\theta)$. The values obtained are in good agreement with those derived under various limits of $Q^2$. Furthermore, we investigate helicity-conserving matrix elements such as $G_{00}^+$ and $G_{11}^+$ alongside helicity non-conserving matrix elements like $G_{0+}^+$ and $G_{-+}^+$. Both bare and dressed cases have been studied, yielding results consistent with other findings.

The impact parameter dependent PDFs are analyzed. The diagrams of $x\cdot q_C$, $x\cdot q_M$, and $x\cdot q_Q$ are illustrated in Fig. 9. A closer examination reveals several intriguing characteristics regarding the distributions of valence constituents within the ρ meson. The diagrams indicate that as $b_{\perp}$ increases, $x\cdot q_{C,M,Q}$ decreases and the x values at which the peak occurs also decrease.

We also investigate the width distributions corresponding to the three PDFs in impact parameter space. The radius of the magnetic distribution $q_M$ is between the charge distribution $q_C$ and quadrupole distribution $q_Q$.

To obtain a more realistic form factor for the ρ meson, the contributions of gluons must be considered. We can compute the Sachs-like charge, magnetic, and quadrupole form factors of the ρ meson using Dyson-Schwinger equations (DSEs) and subsequently compare these results with those obtained from this model as well as lattice QCD data.

Additionally, we can evaluate the gravitational form factors, which related to higher Mellin moments of ρ meson GPDs within the NJL model and verify whether these GPDs satisfy polynomial conditions. Furthermore, we will assess the twist-2 chiral odd quark transversity GPDs for the ρ meson in the NJL model. Finally, we aim to examine unpolarized, polarized, and transversity GPD polynomial sum rules associated with the ρ meson.

APPENDIX A: USEFUL FORMULAS

• I. INTRODUCTION
• II. FORM FACTORS
•      A NJL model
•      B FFs
• III. IMPACT PARAMETER DEPENDENT PDFs
•      A The width distribution
• IV. SUMMARY AND CONCLUSION
• APPENDIX A: USEFUL FORMULAS

Here, we use the gamma-functions ($n\in \mathbb{Z}$, $n\geq 0$)

where $\tau_{uv,ir}=1/\Lambda_{{\rm{UV}},{\rm{IR}}}$ are, respectively, the infrared and ultraviolet regulators described above, with $\Gamma (\alpha,y )$ being the incomplete gamma-function.

References