Unstable mode of the net-baryon density near the spinodal decomposition region

The exploration of the Quantum Chromodynamics (QCD) phase structure is one of the important frontiers in both theoretical and experimental research of strongly interacting matter. Simulations of the lattice QCD have revealed a crossover transition from the quark-gluon plasma phase (QGP) to the hadronic phase at the vanishing baryon chemical potential ($ \mu_B $) [1−4]. Extensive studies based on the effective theories of QCD conjectured a first-order phase transition at large $ \mu_B $, together with a critical point between them [5−8].

The characteristic feature of the phase transition is the large fluctuations and divergence of variables. After being created in relativistic heavy-ion collisions, the QGP fireball is driven across the QCD phase transition region, and several final observables potentially preserve the non-trivial behavior induced by phase transition. Non-monotonic behavior of net-proton multiplicity fluctuations with respect to the colliding energy is believed to be one of the most important signatures of QCD phase transition in relativistic heavy-ion collisions [9, 10]. The Beam Energy Scan (BES) program at RHIC has been dedicated to searching for the QCD critical point, and the preliminary non-monotonic behavior of net-proton fluctuations has been observed in the first phase of the program (BES-I) [11, 12]. However, the statistic of net-proton fluctuations is insufficient to conclude the observation of non-monotonic behavior at BES-I, and researchers are anticipating the higher statistic measurement at the second phase of the BES program (BES-II).

In addition, the theoretical modeling requires further improvement for a better description of the fireball system near the QCD phase transition region. The QGP fireball created in relativistic heavy-ion experiments is a complex system, in which the critical fluctuations significantly deviate from the ones at an ideal and equilibrium context. In particular, the finite time effects induced by the expanding fireball have been revealed to significantly modify the critical fluctuations. For example, the magnitude of the fluctuations is suppressed [13, 14], the sign can be reversed [15], and the largest fluctuations do not necessarily correspond to the trajectory closest to the critical point [16]. Consequently, several dynamical models have been built to incorporate the dynamics of the critical effects (see e.g., Refs. [17−22] for recent reviews). Typically, the dynamics of the critical fluctuations are considered an additional degree of freedom and couples with the conventional dynamical model (e.g., relativistic hydrodynamics), such as the dynamics of the order parameter field in non-equilibrium chiral hydrodynamics [23−25] and the slow mode in the hydro+ [26]. In particular, the dynamics of the conserved net-baryon density have been investigated [27−31] and the non-monotonic behavior of multiplicity fluctuations was observed with respect to the detector acceptance window [29−31].

However, researches on the dynamics of the fluctuations near the first-order phase transition side is relatively deficient [20] owing to its complexity. The characteristic property of the system near the first-order phase transition is the existence of the unstable mode, which may result in nucleation or spinodal decomposition. In relativistic heavy-ion collisions, the spinodal decomposition has been investigated within the framework of dissipative hydrodynamics using an approximate equation of state for the coexistence region [32−36]. In these works, the unstable mode in the coexistence region was studied, with the increasing density moments as the consequence. In contrast, the acceptance dependence of the net-proton fluctuations is feasible in heavy-ion experiments [37]. With the fluctuations within a specific detector acceptance window (e.g., $ \Delta y $), the collision energy dependence of the multiplicity fluctuations scans different regions of the QCD phase diagram. From another perspective, varying the acceptance window (e.g., $ \Delta y $) at specific collision energy $ \sqrt{s_{NN}} $ enables us to study the multiplicity fluctuations with an increasing particle number involved. For example, Refs. [38, 39] studied the multiplicity fluctuations of protons with an increasing detector acceptance window (transverse momentum $ p_T $ range and rapidity range $ \Delta y $) near the critical point and observed the acceptance dependence as a consequence of the long-range correlation. However, the multiplicity fluctuation with respect to the acceptance at the first-order phase transition side has not been addressed yet. This paper focuses on the consequence of the unstable mode in the spinodal decomposition region on the acceptance dependence of the multiplicity fluctuations. We find that the unstable mode results in the correlation function dominating at a much harder mode compared with the ones outside the spinodal decomposition. This effect selects the harder mode and exhibits oscillating behavior with increasing acceptance.

Describing the dynamics near the QCD phase transition requires the dynamics of the relevant degree of freedom. Relativistic hydrodynamics considers the dynamics of several slow degrees of freedom and achieves extraordinary success in relativistic heavy-ion collisions. Unstable mode analysis near the spinodal decomposition region has been performed [32−36] within the framework of relativistic hydrodynamics, with the equation of state constructed by performing a suitable spline between two idealized systems (either a gas of pions and interacting nucleons or a bag of gluons and quarks). In this framework, the thermal noise has not been considered, but it is essential for the region near the critical point of the coexistence side. As several relevant degrees of freedom exist in fluctuating hydrodynamics near the coexistence region, this is challenging for a comprehensive study both theoretically and numerically.

As an alternative framework to study the dynamics near the QCD phase transition, model B evolves the conserved quantities only near the critical point and is much easier to implement. Near the QCD phase transition, the order parameter field (chiral condensate $ \sigma\equiv \bar{q}q-\langle \bar{q}q\rangle $) is a slow mode and couples with other slow hydrodynamic modes, such as the conserved baryon number density $ n_B $, as well as densities of energy e and momentum $ \pi^i $ [40, 41]. Additionally, the baryon density mode evolves much slower than the σ mode and plays a more important role near the phase transition [40]. This enables us to study only the dynamics of $ n_B $ as an approximation, which is the so-called model B. On the crossover side of the QCD critical point, several phenomenological studies with the conserved quantity in heavy-ion collisions have been implemented [27−31] and the multiplicity fluctuations with respect to the increasing acceptance have been investigated [29−31]. Therefore, this work focuses on the extension of this model to the system near the critical point on the coexistence side and theoretically studies the corresponding multiplicity fluctuations with increasing system size.

The coupling between order parameter field σ and $ n_B $ transmits the effects of phase transition to the baryon number density field, and the conventional Landau-Ginzburg free energy can be considered a good approximation of the effective potential of net-baryon density:

where K is the coefficient of surface tension. As one type of first-order phase transition, spinodal decomposition is an important mechanism for phase separation in many areas of physics. One of the characteristic properties of the spinodal decomposition is that the corresponding effective potential exhibits a convex anomaly, $ v<0 $ and $ u>0 $ in this case [42]. The small deviation from uniformity in this convex anomaly region is amplified and eventually results in phase separation.

To study the phenomenological consequence of the spinodal decomposition in relativistic heavy-ion collisions, the coefficients in Eq. (1) must be specified from the QCD theory. The pressure P can be obtained from the effective potential (1); therefore, the coefficients in Eq. (1) can be expressed in terms of various orders of baryon number susceptibility, as performed in Refs. [30, 31]. However, the surface tension K is essential near the first-order phase transition (which we see later) and the knowledge of K (as well as other coefficients) is insufficient to make a conclusive comparison with experiments. This work focuses on the theoretical consequence of unstable spinodal decomposition on the multiplicity fluctuations without specifying parameters of strongly interacting matter. A more comprehensive and realistic analysis is left for future research.

The basic theory of spinodal decomposition is the Cahn-Hilliard equation [43], which has been widely studied in metallurgy. The dynamics of conserved net-baryon density $ n_B(t, x) $ at space-time $ (t, x) $ near the phase transition can be described [27, 28]:

where the noise term employed in this work is white noise and its moments have the relations

The coefficient of the second moment of $ \zeta(t, x) $ is determined by the fluctuation-dissipation relation. The notation $ \langle \cdots \rangle $ represents the averaging over the noise configuration. D denotes as the diffusion coefficient, and T is the temperature.

The diffusion equation in Eq. (2) with non-linear effective potential cannot be solved analytically. Nevertheless, it still can be analyzed by assuming the small perturbations $ \tilde{n}_B $ near the minima of free energy $n_{\min, B}$:

and the evolution of $ \tilde{n}_B $ takes the form

This equation of $ \tilde{n}_B $ has a formal solution in Fourier k-space:

with the initial condition $ \tilde{n}(t_0, k) $ at $ t=t_0 $. The notation $\tilde{D}(t_0, t, k)\equiv \int^t_{t_0}{\rm d} t'D[(v+3un^2_{\min, B})k^2+Kk^4]$ is used for convenience. We can observe that the mean value of perturbation for the conserved quantity $ \langle \tilde{n}_B(t, k)\rangle $ decays exponentially from the initial fluctuations $ \langle \tilde{n}_B(t_0, k)\rangle $, without contribution from the noise, as shown in Eq. (3). In the limit of the zero mode $ k=0 $, corresponding to the entire system, the fluctuations are constant as a function of time, which is the characteristic of the dynamics of the conserved quantity (model B).

The initial condition is required to obtain the two-point correlation function. We can assume that the system is thermalized and the correlation is expressed as [29]

With the initial condition of the correlation function and performing the averaging over the noise configuration, the correlation function in Fourier space can be obtained as

Typically, the system is assumed to be homogeneous, namely, the correlation function $ \langle \tilde{n}_B(t, x_1)\tilde{n}_B(t, x_2)\rangle $ only depends on the distance $ x_1-x_2 $, not on the abstract value $ (x_1+x_2)/2 $. Therefore, $ \delta(k_1+k_2) $ appears in the correlation function.

As in the case of perturbation $ \langle \tilde{n}_B(t, k)\rangle $, the correlation

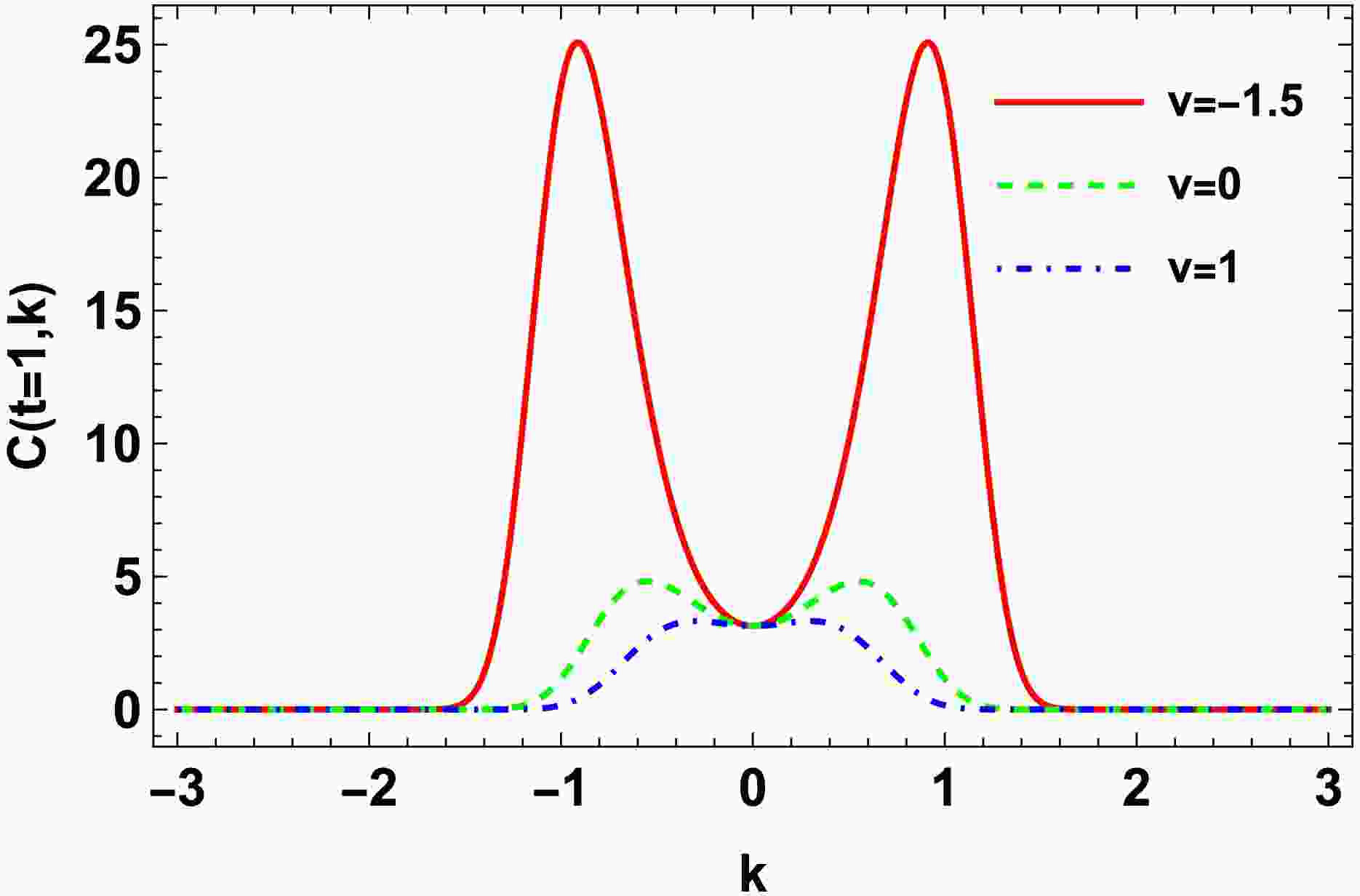
decays exponentially from the initial value $ \chi(t_0) $. However, the second moment of noise in Eq. (2) is non-zero and contributes to the two-point correlation function $ C(t, k) $ (the second term of Eq. (8)). Because of the noise contribution, the correlation $ C(t, k) $ tends to develop a stronger correlation at larger mode k. Outside the spinodal region ($ v>0 $), $ \tilde{D}(t_0, t, k) $ is always positive (the diffusion coefficient D, surface tension coefficient K and fourth order coupling constant u are typically positive), and the correlation function decays rapidly for the hard mode k and dominates at the small mode k. In contrast, $ \tilde{D}(t_0, t, k) $ could be negative in the spinodal region ($ v<0 $) owing to the convex anomaly, and the correlation function significantly enhances at the hard mode k, if the surface tension K is neglected. The correlation function accumulates as a function of time and diverges eventually, i.e., it becomes unstable. Therefore, the surface tension is essential for the stability of the system near the phase transition. The effects of surface tension have been addressed in Refs. [32−34, 36] and introduced as a gradient term in the equation of state to describe the finite range of interaction. In other words, the surface tension K stabilizes the system, but the negative contribution of v in the spinodal region results in the largest $ C(t, k) $ at the harder mode k, comparing outside spinodal region ($ v>0 $). For the illustration, the correlation function $ C(t=1, k) $ in k-space is shown in Fig. 1 with $D=1, \;\chi(t_0)= {1}/{2}, T=1,\; t_0=0, \;t=1, \; u=0.1,\; n_{\min, B}=1$, and $ K=1 $. As shown in Fig. 1, the correlation function has the largest values at the harder mode k for $ v<0 $ than for $ v>0 $.

Figure 1.  (color online) Correlation function of net-baryon density in Fourier space for the system in the spinodal region ($ v=-1.5 $) and outside the spinodal region ($ v=0 $ and $ v=1 $).

To illustrate the effects of the unstable mode on the multiplicity fluctuations acceptance $ \Delta x $, we must transform the correlation function in Fourier space Eq. (8) into the coordinate space. After performing the spatial integration with interval $ (-\Delta x/2, \Delta x/2) $, the correlation function becomes

where the function $ f(k, \Delta x) $ is defined as

The function $ f(k, \Delta x) $ results from the inverse Fourier transformation and spatial integration with a finite range. In the slow mode limit (small k), the function $ f(k, \Delta x) $ is simply a quadratic function of $ \Delta x $: $ f(k, \Delta x)\approx 5\Delta x^2 $, whereas $ f(k, \Delta x) $ is a trigonometric function in the limit of large k: $ f(k, \Delta x)\approx 4\dfrac{\Delta x}{k}\sin(k\Delta x) $. As shown in Fig. 2, the function $ f(k, \Delta x) $ for small k behaves as a quadratic function with increasing $ \Delta x $. In contrast, the function has oscillating behavior with larger k. This is consistent with the conventional picture that the harder mode varies with smaller wavelengths. In this case, the criteria of the existence of oscillating behavior are determined by the negative second order derivative of $ f(k, \Delta x) $ with respect to $ \Delta x $: $ f''(k, \Delta x)=10\cos(k\Delta x)-4k\Delta x\sin(k\Delta x)<0 $. As shown in Fig. 3, the curvature $ f''(k, \Delta x) $ is positive at a small spatial interval $ \Delta x $ for the slow mode $ k=0.1 $, i.e., no oscillating behavior of $ f(k, \Delta x) $. In contrast, for the hard mode ($ k=1 $ in Fig. 3), the second term $ -4k\sin(k\Delta x) $ plays a more important role (oscillating behavior appears), and $ f''(k, \Delta x) $ can be negative with small spatial interval $ \Delta x $.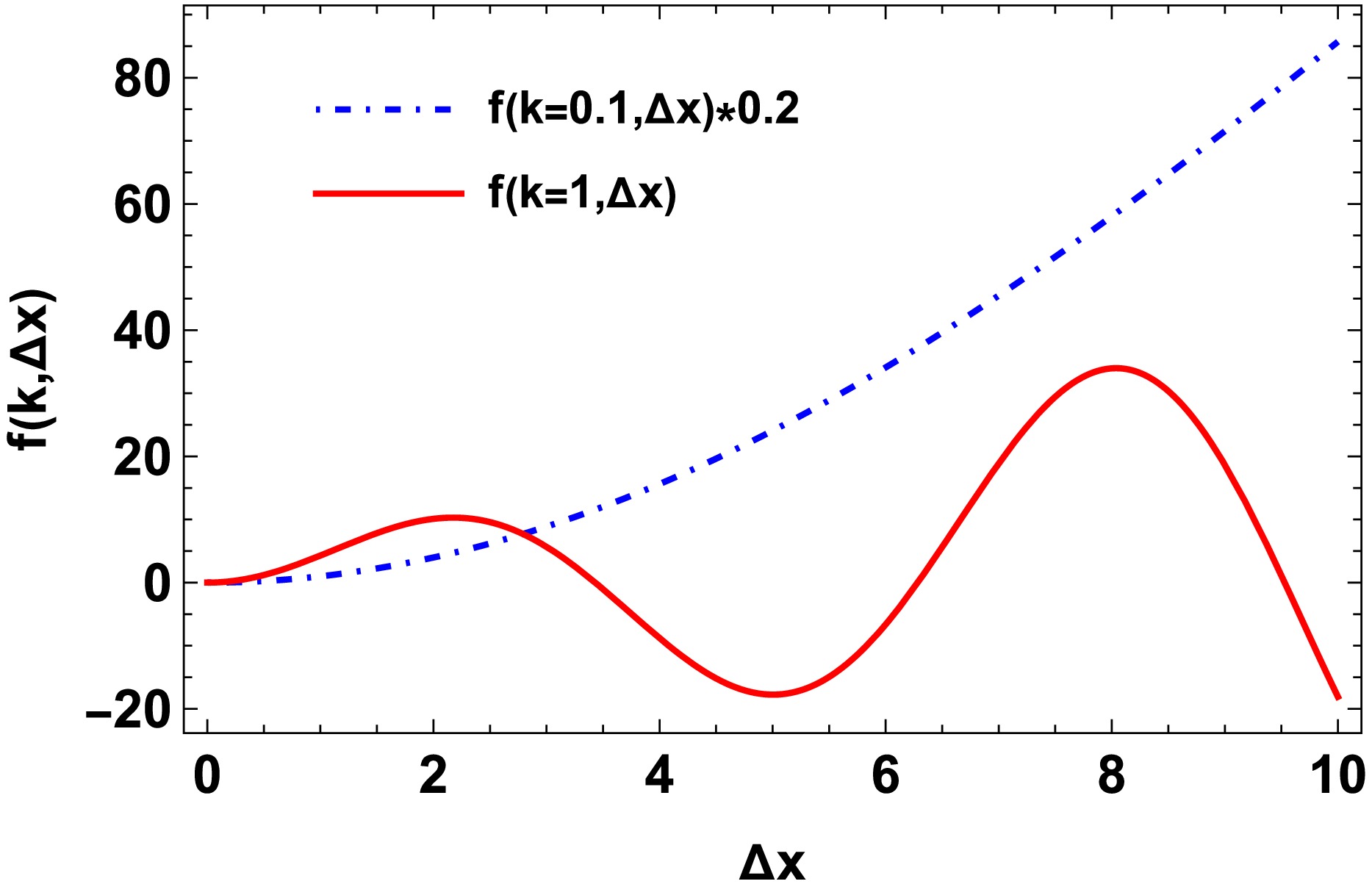

Figure 2.  (color online) Function related to the inverse Fourier transform as a function of spatial integration interval $ \Delta x $ (see Eq. (10) for the definition of $ f(k, \Delta x) $). The blue dotted dashed curve corresponds to $ 0.2f(k, \Delta x) $ with the slow mode $ k=0.1 $, and the red solid one represents the harder mode $ k=1 $.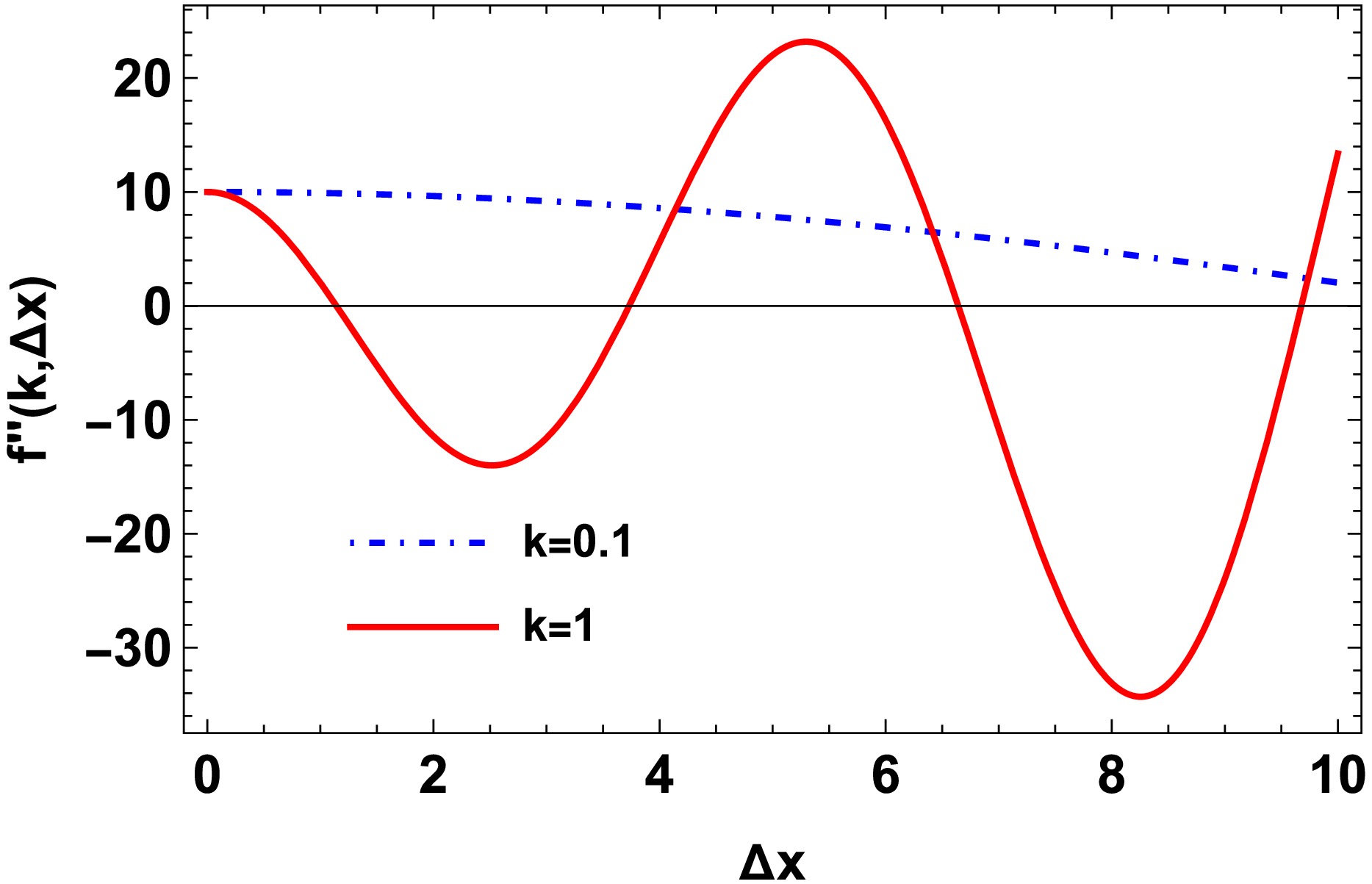

Figure 3.  (color online) Similar with Fig. 2, but for the second derivative of $ f(k, \Delta x) $ with respect to $ \Delta x $: $ f''(k, \Delta x) $.

As emphasized, the unstable mode in the spinodal decomposition region ($ v<0 $) derives the correlation function in Fourier space $ C(t, k) $ dominates at large k, whereas $ C(t, k) $ rapidly decays at large k outside the spinodal region. Owing to the property of $ f(k, \Delta) $, we naturally expect that the correlation function $ C_2(\Delta x) $ exhibits oscillating behavior with increasing system size $ \Delta x $ in the spinodal region, which does not exist outside the spinodal region. As an illustration, the correlation function with increasing system size $ \Delta x $ is shown in Fig. 4. Note that the values of v in Fig. 4 are selected for illustrative purposes. The oscillating behavior continuously smears to the ones of $ v=0 $ with decreasing absolute value of negative v. The oscillating behavior of $ C_2(\Delta x) $ for $ v<0 $ indicates the existence of an unstable mode induced by spinodal decomposition, which is difficult to achieve outside the spinodal region ($ v>0 $) at a small $ \Delta x $.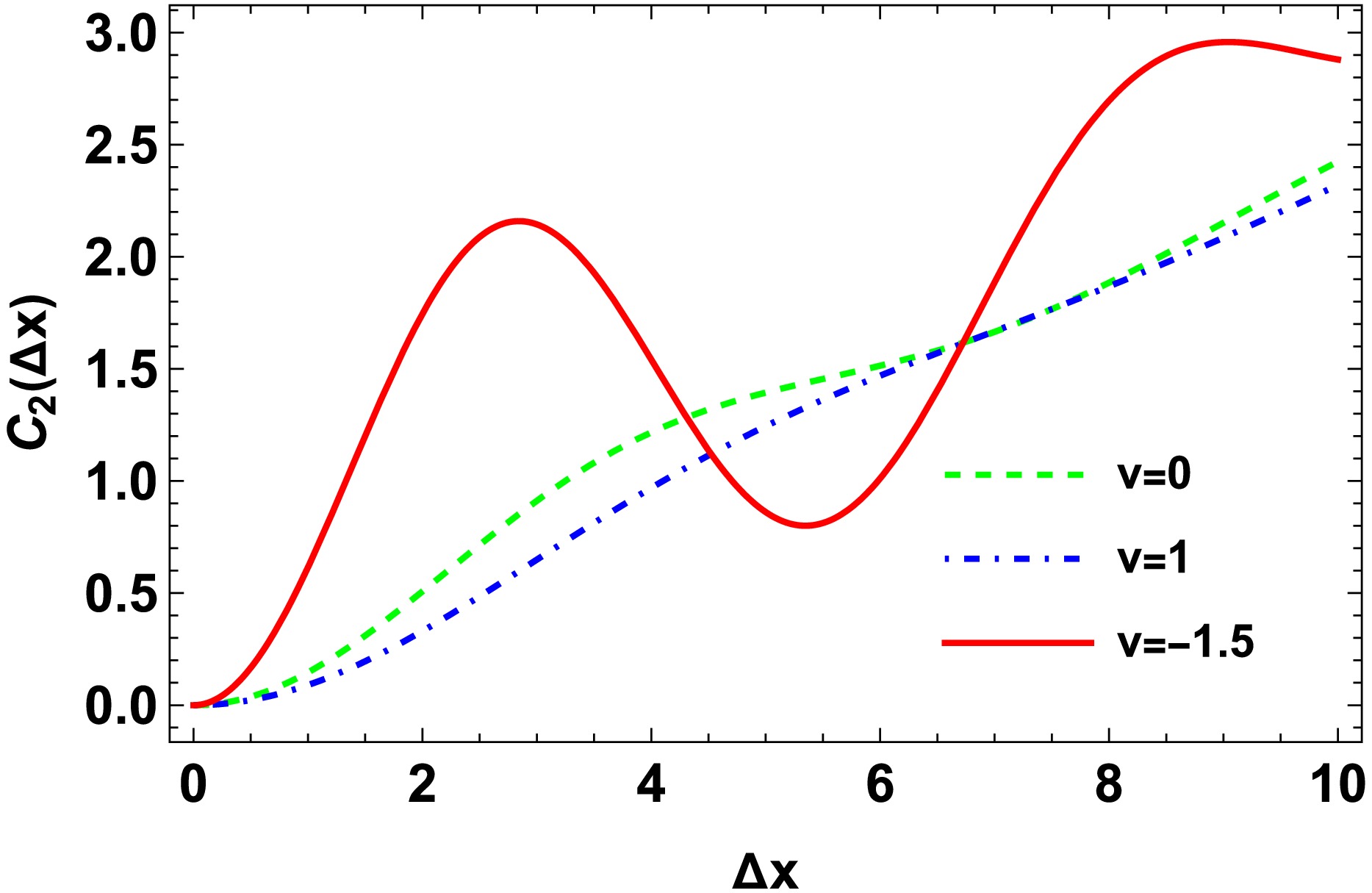

Figure 4.  (color online) Correlation function of net-baryon density with increasing spatial integration interval $ \Delta x $ for the system in the spinodal region ($ v=-1.5 $) and outside the spinodal region ($ v=0 $ and $ v=1 $).

In this work, $ \Delta x $ refers to the interval of spatial integration. Such analysis can also be performed in the relativistic frame ($ \tau, x, y, \eta $), where the integration is performed in the space-time rapidity space η. For the system with large collision energy, the space-time rapidity η equals the momentum rapidity y because of the boost-invariance. A detector with a wider momentum rapidity window $ \Delta y $ approximately corresponds to the integration of the system with a larger system size. This so-called acceptance dependence with non-monotonic behavior of multiplicity fluctuations has been studied near the critical point on the crossover side [29−31]. As addressed in this paper, the acceptance dependence with oscillating behavior of second-order multiplicity fluctuations is observed near the first-order phase transition side.

Based on the conserved dynamics near the phase transition, model B, this work studies the conserved net-baryon multiplicity fluctuations near the spinodal decomposition region. We find that the convex anomaly induces an unstable mode in the Fourier space, and the correlation function dominates at harder mode, comparing the one outside the spinodal region. As a result, this property picks up the higher mode with oscillating behavior at finite spatial interval. Such oscillating behavior of net-baryon multiplicity fluctuations with increasing detector acceptance could be the possible signature of the convex anomaly of spinodal decomposition.

Note that this work focused on studying the possible consequence of the unstable mode in spinodal decomposition with respect to the acceptance. A more comprehensive and phenomenological investigation is required in heavy-ion experiments in a more realistic context. An essential aspect to evaluate is which mode of the correlation function dominates the realistic setup and estimate the possibility of the survival of the unstable mode. For instance, the QGP fireball created in relativistic heavy-ion collisions is a rapidly expanding system, which derives the system passing through the spinodal decomposition. Such finite time effects have not been considered in this work, which is important for future research to address the possible existence of such a signature of spinodal decomposition.