Strong decays of the fully charmed tetraquark states with explicit P-waves via QCD sum rules

Recently, the fully heavy hadrons have become a research hot-spot in high energy physics, and the first fully heavy tetraquark candidates were reported by the Large Hadron Collider beauty (LHCb) collaboration in 2020 [1]. The LHCb collaboration observed a narrow structure $ X(6900) $ and a broad structure above the di-$ J/\psi $ threshold ranging from 6.2 to 6.8 GeV in the $ J/\psi J/\psi $ invariant mass spectrum using the proton-proton collision data at $ \sqrt{s}=7 $, $ 8 $ and $ 13\,{\rm{TeV}} $, which corresponds to an integrated luminosity of $ 9\, {\rm{fb}}^{-1} $ [1].

Subsequently, in 2023, a toroidal LHC apparatus (ATLAS) collaboration confirmed the $ X(6900) $ and observed several resonances (R) in the $ J/\psi J/\psi $ and $ J/\psi\psi^\prime $ invariant mass spectra based on the proton-proton collision data at $\sqrt{s}=13\,\;{\rm{TeV}}$, corresponding to an integrated luminosity of $140\,\; {\rm{fb}}^{-1}$ [2]. The fitted Breit-Wigner masses and widths are given as follows:

or

in the di-$ J/\psi $ mass spectrum, and

or

in the $ J/\psi \psi^\prime $ mass spectrum.

In the same year, the compact muon solenoid (CMS) collaboration studied the $ J/\psi J/\psi $ invariant mass spectrum produced in the proton-proton collisions at a center-of-mass energy of $ \sqrt{s} = $ 13 TeV, which corresponds to an integrated luminosity of $ 135\;{\rm{ fb}}^{-1} $ [3]. In this study, they observed three resonant structures with fitted Breit-Wigner masses and widths of

and local significance of $ 6.5 $, $ 9.4 $ , and $ 4.1 $ standard deviations, respectively.

The quantum numbers $ J^{PC} $ of the newly observed resonances have not been determined until now and their inner structures are still under hot debate. On the theoretical side, the fully charmed tetraquark states were investigated using several phenomenological approaches, such as the potential quark model [4−18], quantum chromodynamics (QCD) sum rules [19−31], lattice QCD [32], dynamical rescattering mechanism [33], Bethe-Salpeter (BS) equation [34], and coupled-channel final state interactions [35−37]. However, none of them can explain all the resonances consistently and more experimental data are required to figure out the nature of the fully charmed tetraquark states unambiguously.

Previously, we studied the mass spectrum of the ground state and first radial excited tetraquark states (which are constructed by the axial vector diquarks $ \varepsilon^{ijk}Q_j^T C\gamma_\mu Q_k $ $ (A) $) using the spin-parity-charge-conjugation $ J^{PC}=0^{++} $, $ 1^{+-} $, $ 1^{--} $ and $ 2^{++} $ [19, 21, 22]. In [26], we considered the updated experimental data and re-studied the mass spectrum of the ground, first, second, and third radial excited $ A\bar{A} $-type fully charmed tetraquark states with the spin-parity-charge-conjugation $ J^{PC}=0^{++} $, $ 1^{+-} $ and $ 2^{++} $. Subsequently, this work was extended to explore the strong decays of the ground states and first radial excited tetraquark states via the QCD sum rules [29]. Combining the masses and decay widths, we reached the conclusion that the $ X(6552) $ can be assigned as the first radial excitation of the $ A\bar{A} $-type scalar tetraquark state.

In [23], we introduced a relative P-wave to construct the doubly charmed vector diquarks $ \varepsilon^{ijk}Q^T_j C\gamma_5 \overset\leftrightarrow{\partial}_\mu Q_k $ $ (\widetilde{V}) $ and constructed the $ \widetilde{V}\overline{\widetilde{V}} $-type tetraquark currents to study the mass spectrum of the ground state of the fully charmed tetraquark states with the spin-parity-charge-conjugation $ J^{PC}=0^{++} $, $ 1^{+-} $ and $ 2^{++} $ via the QCD sum rules. The numerical results indicate that the ground state $ \widetilde{V}\overline{\widetilde{V}} $-type tetraquark states and first radial excited $ A\bar{A} $-type tetraquark states have almost degenerated masses.

As the assignments by the masses alone are imprecise, in the present work, we explore the decay widths of the scalar, axial vector, and tensor $ \widetilde{V}\overline{\widetilde{V}} $-type tetraquark states in the framework of the QCD sum rules, which worked well in several studies on the hadronic coupling constants and decay widths [38−45], whereby more credible assignments were made based on the masses and widths to diagnose the nature of the fully charmed tetraquark states.

This article is organized as follows: in Sec. II, the hadronic coupling constants of the $ \widetilde{V}\overline{\widetilde{V}} $-type tetraquark states for seven decay channels are obtained; in Sec. III, discussions are presented on the numerical results; and finally, the conclusion of this study is presented in Sec. IV.

The fully charmed interpolating currents with two P-waves are constructed as,

where i, j, k, m, and n are color indices [23], and the currents,

interpolate the conventional mesons $ \eta_c $, $ J/\psi $, $ \chi_{c1} $ and $ h_c $, respectively.

Based on the above currents, we adopted the three-point correlation functions,

to study the hadronic coupling constants and hence the widths of the decay channels,

where the subscripts denote the spins $ 0 $, $ 1 $ , and $ 2 $, respectively. In the present work, we chose the supposedly dominant decays, which occur through the Okubo-Zweig-Iizuka super-allowed fall-apart mechanism and ignored the tiny contributions of the other non-dominant (Okubo-Zweig-Iizuka suppressed) decays, such as the decays $ X_0 \to D\bar{D} $ or $ D^*\bar{D}^* $, which can occur by annihilating a $ c\bar{c} $ pair and creating a $ q\bar{q} $ pair.

In the next step, the complete sets of intermediate hadronic states with the same quantum numbers were inserted as currents into the hadron side of the correlation functions [46, 47], to obtain explicit expressions of the ground state contributions (isolated in the charmonium channels),

where the projector

The decay constants or pole residues are defined by

$ \tilde{\lambda}_{X_1}m_{X_1}=\lambda_{X_1} $, and the hadronic coupling constants are defined by

where the $ \xi_\mu $, $ \zeta_\mu $, $ \varepsilon_{\mu} $, and $ \varepsilon_{\mu\nu} $ denote the polarization vectors of the corresponding charmonium or tetraquark states. As the currents $ J_{\alpha\beta}^{h_c}(x) $ and $ J^1_{\alpha\beta}(x) $ potentially couple to the charmonia/tetraquarks with both quantum numbers $ J^{PC}=1^{+-} $ and $ 1^{-} $, we introduce the projector $ P_{A}^{\mu\nu\alpha\beta}(p) $ to project the states with $ J^{PC}=1^{+-} $ [23], as further explained in the Appendix.

On the hadron side, there exists a factor,

in the components $ \Pi_i(p^{\prime2},p^2,q^2) $ with $ i=1-7 $, whereas on the QCD side, a pole term is obtained:

with $ u\geq 4m_c^2 $. If the chiral limit $ m^2_{\eta_c} \to 0 $, $ m^2_{J/\psi}\to 0 $, and $ u \to 0 $can be taken, we expect the hadron side to match the QCD side in the limit $ q^2 \to 0 $ with respect to a pole,

on both sides; therefore we can only retain the ground state contribution as a good approximation. In the case of the current $j_5(x)=\bar{u}(x){\rm i}\gamma_5 u(x)-\bar{d}(x){\rm i}\gamma_5 {\rm d}(x)$, the ground state and first radial excitation are the π and $ \pi(1300) $, respectively, and the energy gap is very large. Therefore, we can take the chiral limit and neglect the excited states (see Sec. 5.3 in [47]). However, in the present case, as the masses of$ \eta_c $, $ J/\psi $, $ \eta_c^\prime $, and $ \psi^\prime $ are of the same order, we cannot take the chiral limit and have to resort to other tricks to match the two sides.

The hadronic spectral densities $ \rho_H(s^\prime,s,u) $are straightforward to be obtained through the triple dispersion relation,

where

and the subscript H denotes the hadron side. According to the discussions in [48, 49], the four quark currents $ J^0(x) $, $ J^1_{\alpha\beta}(x) $, and $ J^2_{\alpha\beta}(x) $ are local currents, and couple potentially to the tetraquark states, not to the two-meson scattering states. Although the variables $ p^\prime $, p, and q obey conservation of the momentum $ p^\prime=p+q $, we can obtain a nonzero imaginary part for all the variables $ p^{\prime2} $, $ p^2 $, and $ q^2 $ by taking the $ p^{\prime2} $, $ p^2 $, and $ q^2 $ as free parameters to determine the spectral densities.

On the QCD side, we contract all the quark fields using the Wick's theorem and consider the perturbative terms and gluon condensate contributions in the operator product expansion, as the three-gluon condensate contributions are diminished by additional inverse powers of Borel parameters and play a tiny role. Then, the QCD spectral densities of the components $ \Pi_{i}(p^{\prime2},p^2,q^2) $ with $ i=1-7 $ can be directly obtained through the double dispersion relation,

as

Naively, we expect to obtain the triple dispersion relation,

to match with the hadron side, $ \Pi_{H}(p^{\prime2},p^2,q^2)= \Pi_{\rm QCD}(p^{\prime2},p^2,q^2) $( see Eq. (30)).

The triple dispersion relation in Eq. (30) on the hadron side cannot match the double dispersion relation in Eq. (32) on the QCD side. Therefore, we have to match the hadron side with the QCD side of the correlation functions according to the rigorous quark-hadron duality suggested in [38, 39],

and perform the integral over $ ds^\prime $ first on the hadron side. As the higher resonances and continuum states in the $ s^\prime $ channels are unclear, allowing only transitions to the ground state meson pairs, we introduce the free parameters $ C_{i} $ with $ i=1-7 $ to denote the contributions of the higher resonances and continuum states in the $ s^\prime $ channel. For example,

where $ \rho_{H}(s^\prime,m_{\eta_c}^2,m_{\eta_c}^2)=\tilde{\rho}_{H}(s^\prime,s,u) \delta(s-m_{\eta_c}^2)\delta(u-m_{\eta_c}^2) $. We suggested such a scheme in [38, 39] as a conjecture, and applications indicate that this scheme works well.

To present the hadron representation more clearly,

The variables $ p^{\prime2} $ in Eq. (35) can be set as $ p^{\prime2}=\alpha p^2 $, where α is a constant. According to the mass poles at $ s^\prime=m^2_{X_{0,1,2}} $ and $ s=m^2_{\eta_c,J/\psi,\chi_c,h_c} $, an approximate relation $ s^\prime=4s $, can be obtained; therefore, it is reasonable to set $ \alpha=1\sim4 $ in the present work. This is just a phenomenological trick, $ p^{\prime2}=(1\sim4) p^2 $, as the $ p^{\prime2} $, $ p^2 $, and $ q^2 $ are free parameters after performing the operator product expansion. In numerical calculations, the optimal value $ \alpha=2 $ was obtained in all the QCD sum rules via trial and error, which is consistent with our previous studies [29].

Then, performing the double Borel transform with respect to variables $ P^2=-p^2 $ and $ Q^2=-q^2 $ and setting the double Borel parameters as $ T_1^2=T_2^2=T^2 $ we expect flat Borel platforms to appear, which is one criterion of the QCD sum rules. Finally, we obtain seven QCD sum rules. As an example,

where the notation is defined by,

The other six QCD sum rules are ignored for simplicity, and readers can obtain them by contacting us via email. In numerical calculations, we assumed the $ C_{i} $ are unknown parameters and searched for suitable values to obtain the flat Borel platforms for the hadronic coupling constants via trial and error [38−45]. This is just an assumption and should be examined based on the experimental data to dettermine whether it is feasible. In detail, endpoint divergences appear at the thresholds $ s=4m_c^2 $ and $ u=4m_c^2 $ because of the factors $ s-4m_c^2 $ and $ u-4m_c^2 $ in the denominators. The routine replacements $s-4m_c^2\to s-4m_c^2+\Delta^2$ and $ u-4m_c^2\to u-4m_c^2+\Delta^2 $ with $ \Delta^2=m_c^2 $ are performed to regularize the divergences because of the tiny contributions of the gluon condensates [29, 50, 51].

On the QCD side, we take the standard gluon condensate $ \langle \dfrac{\alpha_s GG}{\pi}\rangle=0.012\pm0.004\,{\rm{GeV}}^4 $ [46, 47, 52] and the $ \overline{MS} $ mass $ m_{c}(m_c)=(1.275\pm0.025)\,{\rm{GeV}} $ from the Particle Data Group [53]. In addition, we also allow for the energy-scale dependence of the $ \overline{MS} $ mass,

where $ t=\log \dfrac{\mu^2}{\Lambda^2} $, $ b_0=\dfrac{33-2n_f}{12\pi} $, $ b_1=\dfrac{153-19n_f}{24\pi^2} $, $b_2= ({2857-\dfrac{5033}{9}n_f+\dfrac{325}{27}n_f^2})/({128\pi^3})$, $ \Lambda=213\,{\rm{MeV}} $, $ 296\,{\rm{MeV}} $ and $ 339\,{\rm{MeV}} $ for the flavors $ n_f=5 $, $ 4 $, and $ 3 $, respectively [53]. In the present work, the flavor number was set as $ n_f=4 $ to study the fully charmed tetraquark states.

On the hadron side, the parameters are taken as $m_{\eta_c}=2.9834\,\,{\rm{GeV}}$, $m_{J/\psi}=3.0969\,\,{\rm{GeV}}$, $m_{h_c}=3.525\,\,{\rm{GeV}}$, $m_{\chi_{c1}}=3.51067\,\,{\rm{GeV}}$ from the Particle Data Group [53], $s^0_{h_c}=(3.9\,\,{\rm{GeV}})^2$, $ s^0_{\chi_{c1}}=(3.9\,{\rm{GeV}})^2 $, $ s^0_{J/\psi}=(3.6\,{\rm{GeV}})^2 $, $ s^0_{\eta_c}= (3.5\,{\rm{GeV}})^2 $, $ f_{h_c}=0.235\,{\rm{GeV}} $, $ f_{J/\psi}=0.418 \,{\rm{GeV}} $, $f_{\eta_c}= 0.387 \,{\rm{GeV}}$ [54], $ f_{\chi_{c1}}=0.338\,{\rm{GeV}} $ [55], $ m_{X_0}=6.52\,{\rm{GeV}} $, $ \lambda_{X_0}=6.17\times 10^{-1}\,{\rm{GeV}}^5 $, $ m_{X_1}=6.57\,{\rm{GeV}} $, $ \lambda_{X_1}=5.17\times 10^{-1}\,{\rm{GeV}}^5 $, $ m_{X_2}=6.60\,{\rm{GeV}} $, $ \lambda_{X_2}=7.95\times 10^{-1}\,{\rm{GeV}}^5 $ from the QCD sum rules [23].

At the beginning, we set the free parameters $ C_i=0 $ but could not obtain a stable platform, which indicates that the contributions of the higher resonances and continuum states are considerable. Therefore, we tried to obtain stable platforms by varying the values of the unknown parameters $ C_i $ via trial and error. Finally, we obtained the values,

which can lead to Borel platforms,

where the subscripts $ X_0\eta_c \eta_c $, $ X_0J/\psi J/\psi $, $ X_0\chi_c \eta_c $, $ X_1 J/\psi\eta_c $, $ X_1 h_c\eta_c $, $ X_2\eta_c \eta_c $, and $ X_2J/\psi J/\psi $ denote the corresponding channels (modes). Therefore, seven flat platforms with uniform intervals $T^2_{\rm max}-T^2_{\rm min}=1\,{\rm{GeV}}^2$ were obtained as in our previous works [38−45], where the max and min denote the maximum and minimum, respectively.

Before analyzing the numerical results, it is crucial that the uncertainties of the hadronic coupling constants be established. These uncertainties originate not only from the decay constants (or pole residues) but also from the parameters on the QCD side. Therefore, we should avoid overestimating the uncertainties. Specifically, the uncertainties of the channel $ X_0 \rightarrow J/\psi + J/\psi $, are presented as an example, $\lambda_{X_0}f_{J/\psi}^2G_{X_0J/\psi J/\psi} = \bar{\lambda}_{X_0}\bar{f}_{J/\psi}^2\bar{G}_{X_0J/\psi J/\psi} + \delta\,\lambda_{X_0}f_{J/\psi}^2G_{X_0J/\psi J/\psi}$, $ C_{2} = \bar{C}_{2}+\delta C_{2} $,

where the short overline $ \bar{} $ denotes the central value. Then, by approximately setting $ \delta C_{2}=0 $ and $\dfrac{\delta f_{J/\psi}}{\bar{f}_{J/\psi}} = \dfrac{\delta \lambda_{X_0}}{\bar{\lambda}_{X_0}}= \dfrac{\delta G_{X_0J/\psi J/\psi}}{\bar{G}_{XJ/\psi J/\psi}}$, we can obtain the uncertainties of the hadronic coupling constants.

Finally, we obtain the values of the hadronic coupling constants:

In Fig. 1, as an exmple, the curves of the hadronic coupling constants $ G_{X_0\chi_c\eta_c} $ and $ G_{X_0 J/\psi J/\psi} $ with variations of the Borel parameters $ T^2 $ are plotted in the Borel windows. Clearly, flat platforms appear. Thus, we can extract the hadronic coupling constants reasonably.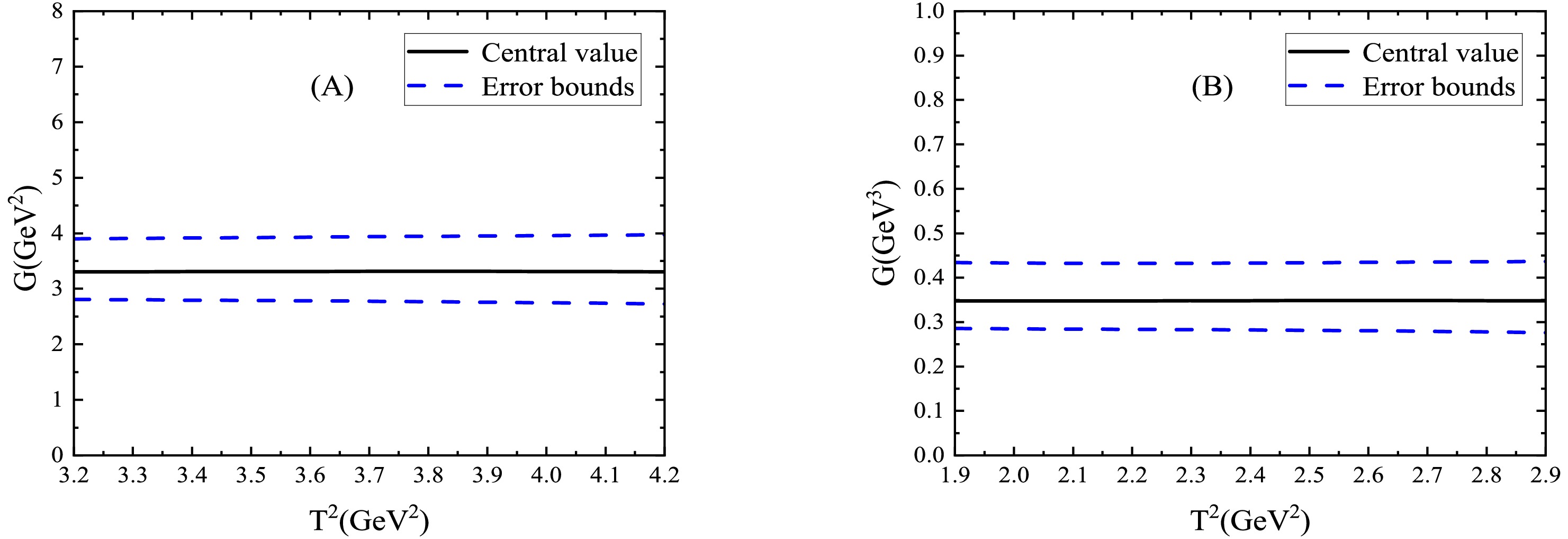

Figure 1.  (color online) Central values of the hadronic coupling constants with variations of the Borel parameters $ T^2 $, where (A) and (B) denote the $ G_{X_0 \eta_c \chi_c} $ and $ G_{X_0 J/\psi J/\psi} $, respectively.

Then, taking the masses $ m_{X_0}= $ 6.52 GeV, $m_{X_1}= 6.57\;{\rm{GeV}}$, and $ m_{X_2}=6.60\,{\rm{GeV}} $ obtained from the QCD sum rules [23], we obtained the partial decay widths,

and consequently the full widths,

In our previous studies, the mass spectrum of the ground states and first/second/third radial excitations and the decay widths of the ground states and first radial excitations of the $ A\bar{A} $-type fully charmed tetraquark states were studied via the QCD sum rules, and the results showed that the $ X(6552) $ can be assigned as the first radial excitation of the $ A\bar{A} $-type scalar tetraquark state, considering both the masses and decay widths [26, 29]. In Ref. [23], we studied the mass spectrum of the ground state $ \widetilde{V}\bar{\widetilde{V}} $-type scalar, axial vector, and tensor fully charmed tetraquark states using the QCD sum rules. The numerical results indicate that the ground state $ \widetilde{V}\overline{\widetilde{V}} $-type tetraquark states and first radial excited states of the $ A\bar{A} $-type tetraquark states have almost degenerated masses, appoximately $0.35\pm0.09 \; {\rm{GeV}}$ above the $ J/\psi J/\psi $ threshold.

In the present work, the predicted width $\Gamma_{X_0}= 70.18^{+82.53}_{-51.43}\;{\rm{MeV}}$ is compatible with the experimental data $\Gamma_{X(6552)} = 124^{+32}_{-26}\pm33 \;{\rm{ MeV}}$ from the CMS collaboration [3] within uncertainties, which supports assigning the $ X(6552) $ as the ground state $ \widetilde{V}\overline{\widetilde{V}} $-type scalar tetraquark state, whereas the widths of the tetraquark states with higher spins $\Gamma_{X_1}=28.37^{+16.12}_{-12.42}\;{\rm{MeV}}$ and $\Gamma_{X_2}=4.89^{+3.91}_{-2.76}\; {\rm{MeV}}$ are too small to match the experimental data.

As a hadron has several Fock states, the $ X(6552) $ may have both the 1S $ \widetilde{V}\overline{\widetilde{V}} $-type and 2S $ A\bar{A} $-type scalar tetraquark components. Furthermore, the relative branching ratios are quite different from each other,

which indicate that the main decay channels are $ X_0\to \eta_c \eta_c $ for the 1S $ \widetilde{V}\overline{\widetilde{V}} $-type scalar tetraquark state and $ X_0\to J/\psi J/\psi $ for the 2S $ A\bar{A} $-type scalar tetraquark state. More experimental data are required to diagnose the nature of the fully charmed tetraquark states. Other predictions serve as meaningful guides for the high energy experiments, awaiting to be examined in the future.

In the present study, a relative P-wave was introduced to construct the doubly charmed vector diquark and hence the scalar and tensor four-quark currents to investigate the decay widths of the fully charmed tetraquark states with the $ J^{PC}=0^{++} $, $ 1^{+-} $ and $ 2^{++} $ via the QCD sum rules. We consider the perturbative terms and gluon condensate contributions in the operator product expansion to match the hadron side with the QCD side based on rigorous quark-hadron duality. The predicted width of the ground state scalar tetraquark state $ \Gamma_{X_0}=70.18^{+82.53}_{-51.43}\,{\rm{MeV}} $ is compatible with the experimental data $\Gamma_{X(6552)} = 124^{+32}_{-26}\pm 33 \,{\rm{ MeV}}$ from the CMS collaboration within the range of uncertainties, which supports assigning the $ X(6552) $ as the ground state $ \widetilde{V}\overline{\widetilde{V}} $-type scalar tetraquark state. The relative branching ratios of the ground state $ \widetilde{V}\overline{\widetilde{V}} $-type scalar tetraquark state and first radial excitation of the $ A\bar{A} $-type scalar tetraquark state are quite different, which can be used to clarify the nature of the $ X(6552) $. We expect that the other predictions will be confirmed in future experiments.

For simplicity, we introduce the notation $ J_{\alpha\beta}(x) $ to denote the $ J_{\alpha\beta}^{h_c}(x) $ and $ J^1_{\alpha\beta}(x) $, and resort to the two-point correlation function $ \Pi_{\mu\nu\alpha\beta}(p) $,

to illustrate how to project the pertinent tensor structures. On the hadron side, we isolated the ground state contributions,

where

the A and V stand for the $ J^{PC}=1^{+-} $ and $ 1^{--} $ mesons, respectively. Introducing the operators $ P_{A}^{\mu\nu\alpha\beta}(p) $ and $ P_{V}^{\mu\nu\alpha\beta}(p) $,

and projecting the components $ \Pi_{A}(p^2) $ and $ \Pi_{V}(p^2) $ unambiguously,

and

Therefore, in Eqs. (15)−(17), we project the contributions of the $ h_c $ and $ X_1 $ using the $ J^{PC}=1^{+-} $and projectors $ P_{A}^{\mu\nu\mu^\prime\nu^\prime}(p) $ and $ P_{A}^{\alpha\beta\alpha^\prime\beta^\prime}(p^\prime) $, respectively,