Thermodynamics of Barrow Einstein-power-Yang-Mills AdS black hole in the restricted phase space

As is well known, black holes are both thermodynamic and quantum systems [1−3]. Black hole thermodynamics is a very important research field because it can provide some clues for exploring the nature of quantum gravity. Since Bekenstein and Hawking proposed the Bekenstein-Hawking entropy [3, 4] for black holes, the corresponding thermodynamic laws of black holes [3, 5] were presented by analogy with ordinary thermodynamic systems. Subsequently, the study of black hole thermodynamic properties has garnered substantial interest, with particular focus on the thermodynamics of asymptotically anti-de Sitter (AdS) black holes. Through the AdS/CFT correspondence [6], the thermodynamical properties of an AdS black hole with a finite temperature can be described by the dual conformal field theory (CFT). When an AdS black hole is in thermal equilibrium with its surrounded radiation field, the famous Hawking-Page (HP) phase transition [5, 7] survives. For the RN-AdS black hole, in 1999 Chamblin found the first-order phase transition of this system [8]. It should be noted that by identifying the negative cosmological constant to the positive thermodynamical pressure [9], traditional black hole thermodynamics were extended to the extended phase space where black hole mass is regarded as enthalpy. In the extended phase space AdS black holes have richer phase structure and thermodynamical properties: the Van de Waals-like phase transition [10−12], the reentrant phase transitions [13, 14], superfluid [15], the polymer-like phase transition [16], the triple points [17, 18], the novel dual relation of HP phase transition [19], and the topological structure [20, 21]. Furthermore, the proposed extended phase space for AdS black holes reduces to the appearance of other novel dual thermodynamical quantities related to model parameters [22] and to the investigation of some black hole heat engines [23, 24]. These developments are in the subdiscipline of black hole chemistry [25].

From the holographic viewpoint [26, 27], the explanation of black hole chemistry via AdS/CFT [28, 29] is somewhat elusive: i) For an AdS black hole, changing the cosmological constant $ \delta\Lambda $ corresponds to changing both the central charge and CFT volume. This leads to an inconsistency between the first law of thermodynamics in the extended phase space and that in the dual field theory [30, 31]. ii) $ \delta\Lambda $ (or $ \delta P $) implies a change in the model of gravity. The corresponding ensemble does not describe a collection of black holes from the same gravity model, where the microstates are identical. Instead, it describes a collection of gravity models with the same or similar black hole solutions. iii) The Smarr relation for an AdS black hole in the extended phase space is not a homogeneous function of order one with respect to all independent dual thermodynamic quantities. This discrepancy has prompted efforts to seek a more expanded first law of thermodynamics. Recently, the central charge and chemical potential, which are considered as a new pair of dual thermodynamical quantities, were introduced in the first law of thermodynamics [32, 33], that is, the extended phase space is extended to the restricted phase space. Both the corresponding Newton's gravitational constant and the cosmological constant can change, leading to profound consequences for the chemical potential and its holographic interpretation. In the restricted phase space, a new thermodynamic phenomenon arises for AdS black holes, which is fundamentally different from the first-order phase transition observed in AdS black holes in the extended phase space and in ordinary thermodynamic systems: the supercritical phase transition [34−36]. In this work, for the Einstein-Power-Yang-Mills (EPYM) AdS black hole [37−40], we demonstrate the process of establishing the thermodynamical first law in the restricted phase space.

In contrast, black hole thermodynamics is the most important tool in investigating quantum gravity in spacetime with a horizon [41]. Hawking radiation provides valuable insight, revealing that the Hawking entropy is proportional to the black hole horizon area, while the Hawking temperature is proportional to the surface gravity of the black hole horizon [42]. This indicates a strong relationship between thermodynamic systems and gravitational systems. In 2020, Barrow proposed that due to quantum gravitational effects, the surface of a black hole can be altered, leading to the emergence of Barrow entropy [43]. The black hole horizon area can be represented as a discontinuous and potentially fractal structure in the geometry of the horizon. Based on the concept of the "Koch snowflake," Barrow suggested that the Schwarzschild black hole horizon is surrounded by NNN smaller spheres, with their radii having a specific ratio relative to the original sphere. After an infinite number of iterations, the total area and volume are the sums of all the intricate structures, which are finite and infinite, respectively. Consequently, the corresponding entropy becomes very large. Subsequently, the idea of Barrow entropy has been further used to investigate dark energy [44, 45], cosmology [46−48], and black hole thermodynamics [49−52]. This study investigates the thermodynamics and stability of AdS black holes with the a black hole horizon with a fractal structure.

Additionally, linear charged black holes in AdS spacetime, exhibiting a second-order phase transition, show a scaling symmetry: at the critical point, the state parameters scale with respect to the charge q, that is, $ S\sim q^2,\; P\sim q^{-2},\; T\sim q^{-1} $ [53]. It is natural to inquire whether scaling symmetry exists in non-linear charged AdS black holes. As a generalization of the charged AdS Einstein-Maxwell black holes, it is intriguing to explore new non-linear charged systems. Due to the infinite self-energy of point like charges in Maxwell's theory [54−58], Born and Infeld proposed a generalization when for strong fields by introducing non-linearities [59, 60]. An interesting non-linear generalization of charged black holes involves a Yang-Mills field exponentially coupled to Einstein gravity, known as the Einstein-Power-Yang-Mills (EPYM) theory. This theory possesses conformal invariance and allows for the construction of analogues to the four-dimensional Reissner-Nordström black hole solutions in higher dimensions. Unlike the Maxwell-Einstein coupling, which has an infinite range, the coupling between Einstein gravity and the Yang-Mills (YM) field is crucial in systems such as nuclei and highly dense matter, justifying its inclusion in black hole applications. Several features of EPYM gravity in extended thermodynamics have recently been studied [26, 61, 62]. On the holographically dual side, the effects of non-linear sources on the strongly coupled dual gauge theory, within the context of AdS/CFT correspondence, have also been reported [63].

This work is organized as follows: In Sec. II, we provide a brief description of the EPYM AdS black hole in the restricted phase space. In Sec. III, we present the phase structure of the EPYM AdS black hole with a fractal structure on the black hole horizon in the restricted phase space. In Sec. IV, we analyze the stability of the EPYM AdS black hole with the fractal structure on the black hole horizon in the restricted phase space. Furthermore, the effects of the fractal parameter and the non-linear YM charge parameter on the phase structure and stability are also examined. A brief summary is provided in Sec. V.

For the four-dimensional AdS Einstein-power-Yang-Mills (EPYM) black hole, the spherically symmetric static spacetime's parameterization approach is as follows

the metric function can be described as [64]

Here, $ d\Omega_{2}^{2} $ is the metric on unit $ 2 $-sphere with volume $ 4\pi $ and q is the YM charge, l is related to the cosmological constant and $ l^2=-\dfrac{3}{\Lambda} $, G is the gravitational constant, and γ is the non-linear YM charge parameter and satisfies $ \gamma>0 $ [38]. Additionally, the event horizon $ r_+ $ corresponds to the largest root by solving the expression $ f(r_+)=0 $. Thus, the mass parameter of the black hole can be expressed in terms of the horizon radius as

From the classical Boltzmann-Gibbs statistics, the famous Bekenstein-Hawking entropy is proportional to the surface area of the black hole horizon: $ S=\pi r_+^2/G $. It is important to emphasize that although entropy S is commonly used in relativistic theory, it remains essentially a classical concept. According to the principle of maximum entropy, S is maximized when a thermodynamic equilibrium system is described by the Maxwell-Boltzmann distribution, which belongs to the classical Boltzmann-Gibbs statistical framework. However, arguments from various perspectives suggest that Boltzmann-Gibbs statistics may not be the most suitable framework for investigating black hole thermodynamics.

In Ref. [43], Barrow proposed that quantum gravitational effects may give rise to a complex structure on the black hole horizon surface, extending down to microscopic scales. These effects manifest as modifications to the black hole horizon area, which can be described using a fractal structure. By incorporating the influence of quantum gravity and fractal geometry, Barrow challenges the conventional view of the event horizon as smooth and uniform. This fractal nature implies that the event horizon undergoes intricate structural transformations. While thermodynamics suggests that black holes are infinitely complex systems, the modification of the horizon area having a finite volume but an infinite (or finite) surface area leads to a new entropy relation, known as Barrow entropy , which is given by

where Δ represents the quantum effect and is in the range of $ (\Delta\in[0,1]) $. For $ \Delta=0 $, the well-known Bekenstein-Hawking entropy is restored, signifying the absence of a fractal structure. Conversely, when $ \Delta=1 $, the black hole horizon surface is its most deformed and has the most complex fractal structure. Additionally, the Barrow entropy is associated with Tasllis entropy execution [65, 66] and is different from the logarithmically corrected quantum entropy [44, 67, 68]. Furthermore, other entropy functions such as Renyi entropy [69], Sharma-Mittal entropy [70], and Kaniadakis entropy [71] have been proposed. In the following, we investigate the Barrow entropy of the EPYM AdS black hole and its associated thermodynamics within the restricted phase space. Additionally, the Barrow temperature of the EPYM AdS black hole can be obtained from Eqs. (3) and (4), as follows

In the extended phase space (setting $ G=1 $), the thermodynamical first law for the EPYM AdS black hole reads

Considering Eq. (3) and $ P=\dfrac{3}{8\pi l^2} $, the corresponding thermodynamical volume and potential are

The corresponding thermodynamical properties of the EPYM AdS black hole in the extended phase space were exhibited in Refs. [62, 72] and optical properties such as the photon sphere and shadow were also presented in Refs. [73, 74].

Note that from the Holographic interpretation of the thermodynamical first law (6) in the extend phase space there exist some issues [23, 75, 76]. In boundary conformal field theory (CFT),$ V\delta P $ can become two terms in the first law of thermodynamics: one is the central charge of the boundary CFT, and the other is the thermodynamical pressure of the boundary CFT caused by a change in the AdS radius. The way of addressing this problem is to invoke the form of the central charge from the AdS/CFT dictionary, which is related to the AdS radius l as in Ref. [30]

The partition function of AdS spacetime is related to the Euclidean action [77, 78] by

where for the EPYM AdS black hole, $I_E=\dfrac{1}{2}\int {\rm d}^4x\sqrt{g} (R- 2\Lambda-\mathcal{F}^\gamma )$. The Yang-Mills (YM) invariant $ \mathcal{F} $ and YM field $ F_{\mu \nu}^{(a)} $are

Here, R and γ are the scalar curvature and a positive real parameter, respectively; $ C_{(b)(c)}^{(a)} $ represents the structure constants of a three-parameter Lie group G; and ξ is the coupling constant. $ A_{\mu}^{(a)} $ are the $S O(3)$ gauge group Yang-Mills (YM) potentials defining by the Wu-Yang (WY) ansatz [79]. Note that the internal indices $ {a,b,c,...} $are the same in covariant or contra-variant form. Implementing the variation of the action with respect to the spacetime metric $ g_{\mu\nu} $produces the gravitational field equations:

Through the variation with respect to the YM gauge potentials, $ A_{\mu}^{(a)} $, and the traceless condition, the $ 2 $-forms YM equations yields

where $\boldsymbol{F}^{(a)}=\dfrac{1}{2}F_{\mu \nu}^{(a)}dx^\mu\wedge dx^\nu,\; \boldsymbol{A}^{(b)}=A_{\mu }^{(b)}\wedge dx^\mu$, and $ { }^{\star} $ represents duality. It is clear that for $ \gamma=1 $, the EPYM theory reduces to the standard Einstein-Yang-Mills (EYM) theory [80]. Note that the non-Abelian property of the YM gauge field is expressed with its YM potentials

where q is the YM charge and the indices ($ a,\; i,\; j $) are in the range $ 1\leq a,\; i,\; j\leq3 $. The coordinates $ x_i $ take the following forms: $ x_1=r \cos\phi \sin\theta,\; x_2=r \sin\phi \sin\theta,\; x_3= r \cos\theta. $ Since we have utilized the WY ansatz for the YM field, the invariant for this field takes the form [81, 82]

Under the Wu–Yang (WY) ansatz, the structure constants − responsible for the non-Abelian nature of the Yang–Mills (YM) gauge field—disappear. As a result, the focus shifts from the non-Abelian character to the role of the non-linear YM charge parameter γ. To ensure that the system satisfies the Weak Energy Condition (WEC), Strong Energy Condition (SEC), Dominant Energy Condition (DEC), and the Causality Condition (CC), the physically meaningful range for the non-linear YM charge parameter γ must lie between $ 3/4 $ and$ 3/2 $ (see Ref. [39]).

From the formulation of the AdS/CFT correspondence, the partition function of AdS spacetime is equal to the CFT dual one, $Z_{\rm AdS}=Z_{\rm CFT}$. The CFT partition function is related to the free energy by

where T represents temperature. As shown in Ref. [33], the free energy is in terms of the central charge and chemical potential as follows:

One can infer that the free energy is correlated with the parameters characterizing EPYM AdS black holes:

Here, S corresponds to the Bekenstein-Hawking entropy and Φ is the electric potential on the black hole event horizon due to the electric charge $ Q=q^{\gamma}\sqrt{C} $. The corresponding Smarr relation within the restricted phase space can be written as

The first law of thermodynamic for the EPYM AdS black hole in the restricted phase space reads as follows (more details see Ref. [83])

Since $ S_B=S^{1+\Delta/2} $ and the Hawking temperature $ T= \partial M/\partial S $, one can establish the relationship between the modified quantities ($ T_B,\; S_B $) and ordinary ones ($ T,\; S $) as

Substituting the above equation into Eq. (20), we can obtain the Smarr relation in terms of the modified quantities

This result contradicts the conventional Smarr relation in the restricted phase space under normal conditions, where the mass parameter is a homogeneous function of degree one with respect to all relevant thermodynamic quantities. The influence of quantum gravity, encapsulated by the fractal paramete Δ destroy the homogeneous of Smarr relation in the restricted phase space. As $ \Delta=0 $, Eq. (23) can recover the Smarr relation of the ordinary restricted phase space. With the definition of Barrow temperature $ T_B=\dfrac{\partial M}{\partial S_B} $, one can obtain $ T_B=\dfrac{\partial M}{\partial S}\dfrac{\partial S}{\partial S_B}=T\dfrac{\partial S}{\partial S_B} $, that is, $ TdS=T_BdS_B $. Thus the corresponding thermodynamics first law for the Barrow EPYM AdS black hole in the restricted phase space becomes as

In this section, we examine the thermodynamical properties of the Barrow Einstein–power Yang-Mills (EPYM) AdS black hole within the framework of the restricted phase space. We begin by defining the relevant thermodynamic quantities and formulating the equations of state. Utilizing Eqs. (3), (4), and (8), the black hole mass parameter can be expressed in terms of the modified thermodynamic variables and the fractal parameter becomes

Since $ T_B=\left(\dfrac{\partial M}{\partial S_B}\right)_{C, Q,\Delta} $ and $ \mu=\left(\dfrac{\partial M}{\partial C}\right)_{S_B, Q,\Delta} $, the equations of state describing the EPYM AdS black hole in the presence of quantum gravity effects are as follows

According to Ehrenfest's classification of phase transitions in thermodynamical systems, the critical point can be determined by satisfying the following equations:

Considering Eq. (26), we can obtain the critical thermodynamical quantities as follows

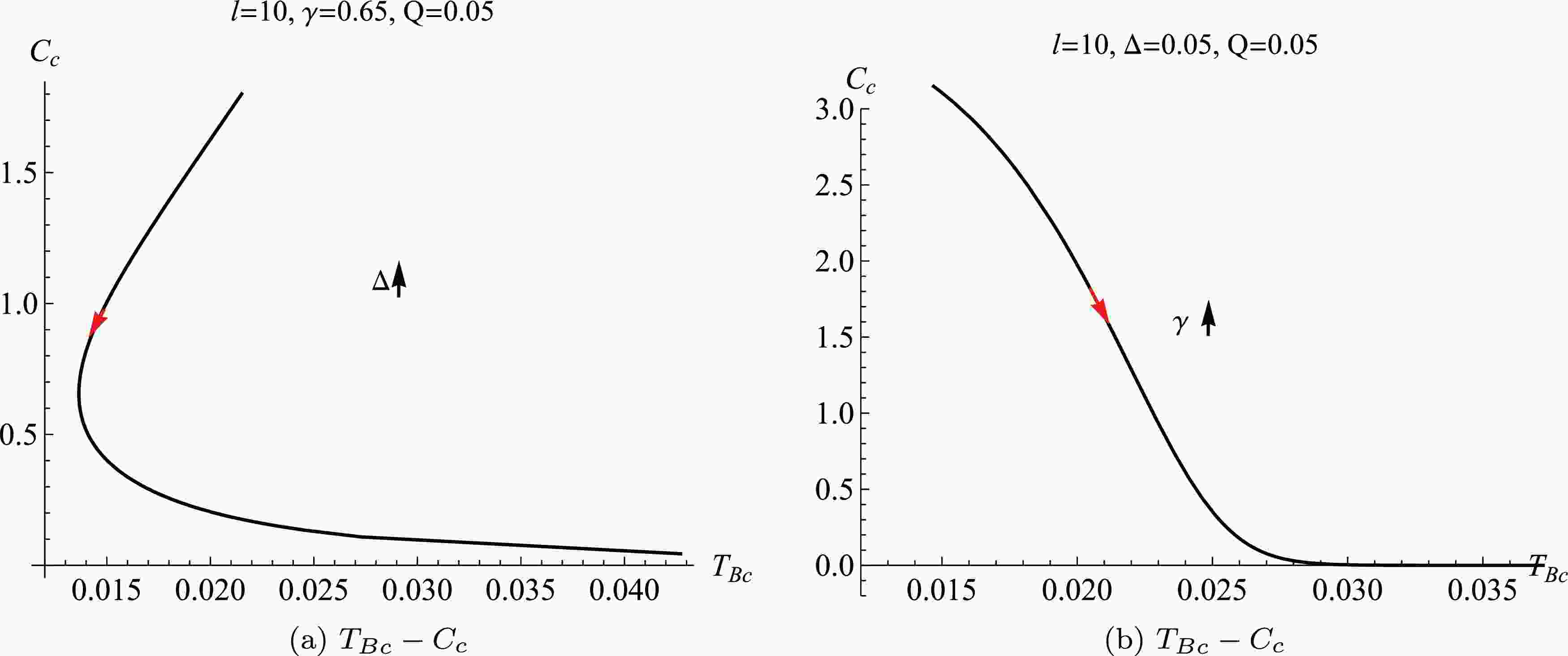
The results indicate that the critical point is determined by the non-linear YM parameter γ, the fractal parameter Δ, the AdS spacetime radius l, and the electric charge Q. The corresponding behaviour of the critical center charge with respect to the critical Barrow's temperature under different parameters have been depicted in Fig. 1. When the parameters ($ l,\; \gamma,\; Q $) are fixed, the critical center charge increases with the critical Barrow's temperature for the small value of the fractal parameter Δ, and for the large values of Δ it decreases with $ T_{Bc} $, see Fig. 1(a). For small values of the non-linear YM charge parameter γ the critical center charge monotonically and rapidly decays with the critical Barrow's temperature until to zero, while it tends to zero and does not changes with the critical Barrow's temperature, see Fig. 1(b).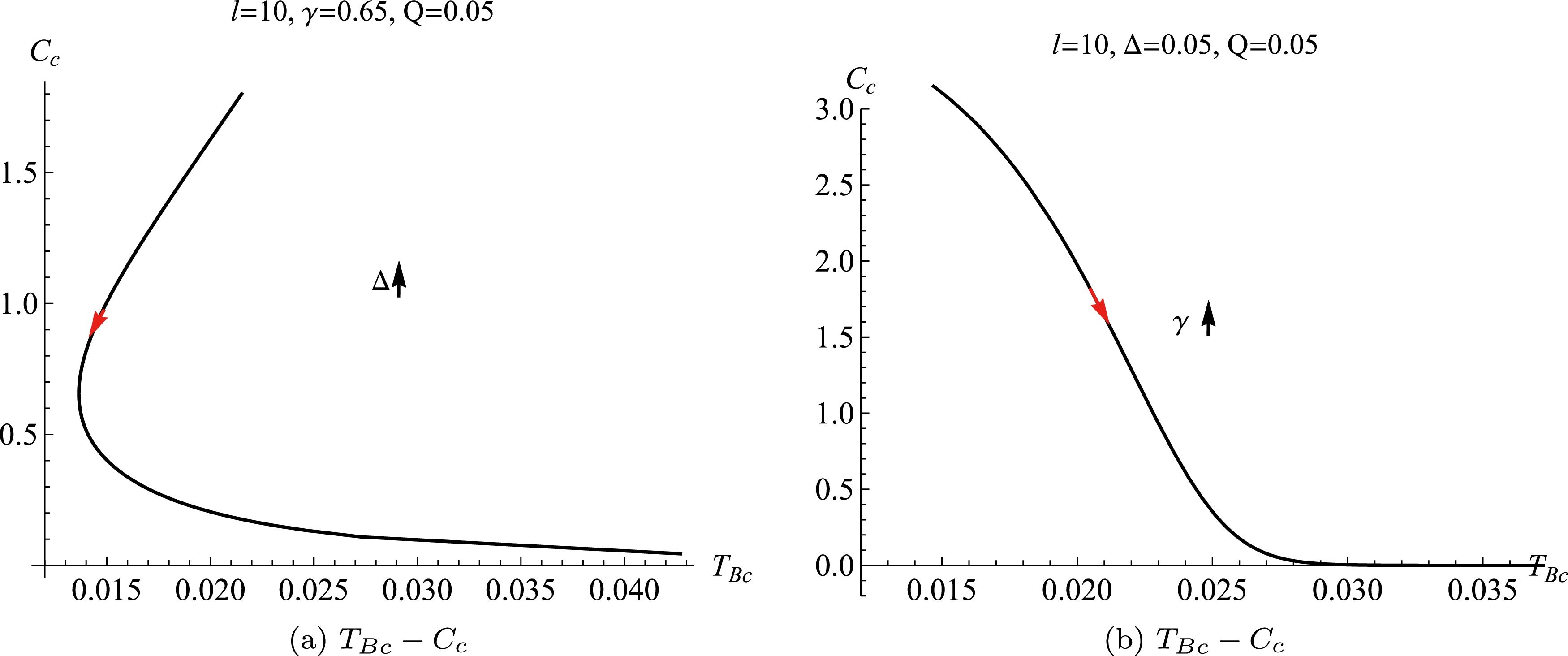

Figure 1.  (color online) The behaviors of the center charge respects to the Barrow's temperature $ T_{Bc} $ with different non-linear charge parameter γ and the fractal parameter Δ.

To investigate the first-order phase transition and obtain the analyzed results, we consider the case of $ \gamma=1 $ and solve the equation $\dfrac{\partial T_B}{\partial S_B}=0$. With the definitions $ s=S_B/S_{Bc},\; c=C/C_c $, there are two solutions of the normalized Barrow entropy:

where $ s_1 $ stands for the solution of $ '+' $ and $ s_2 $ is the solution of $ '-' $. Note that these two solutions are related to the first-order phase transition and their behaviours with respect to the fractal parameter are depicted in Fig. 2. With an increasing fractal parameter Δ, both dimensionless solutions decrease. When the fractal structure is maximized, $ \Delta=1 $, $ s_1=\sqrt{2c} $, and $ s_2=0 $. Here, we should point out that for the maximum fractal structure, there is one the critical point, $ s_c=s_{1,2}=0 $, which is meaningless and can be ruled out. Additionally, when this system is without the fractal structure $ \Delta=0 $, $ s_1=s_2=c=1 $ as $ Q^2=1/36 $. This case is consistent with that of the EPYM AdS black in the restricted phase space with $ \gamma=1 $ (see Ref. [83]). Note that at the critical point, we have $ Q^2=q^2/C_c=1/36 $ for $ \gamma=1 $, that is, $ q^2=C_c/36 $. This relation between the YM charge and the critical center charge is captured in Eq. (29). From the above analysis, it is evident that the fractal structure induced by quantum gravity plays a significant role in the critical phenomena and first-order phase transitions. When the fractal structure reaches its maximum extent, no phase transition can occur. Therefore, the fractal structure, as a manifestation of quantum gravity effects on the black hole horizon surface, effectively serves as a probe for detecting phase transitions.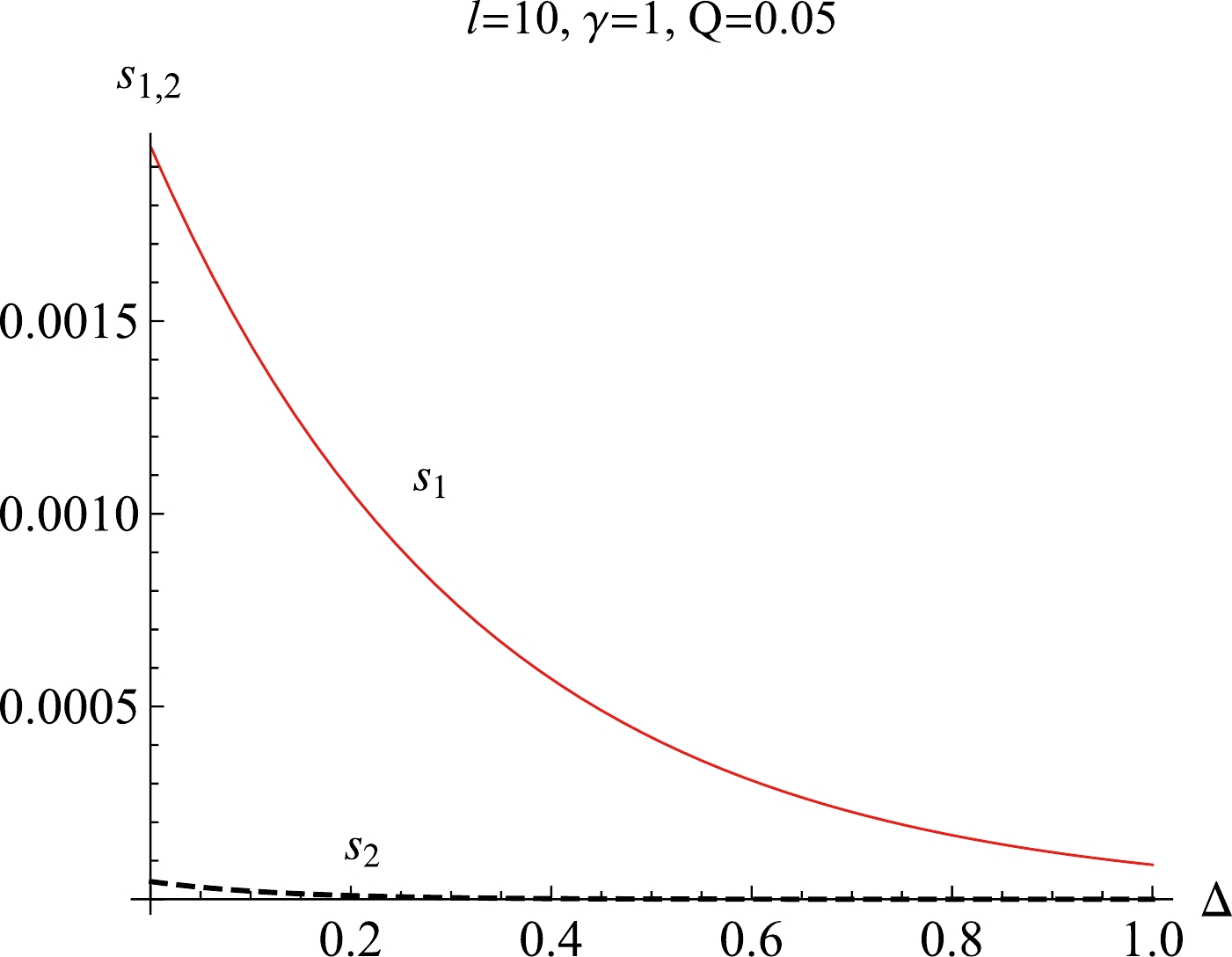

Figure 2.  (color online) The behaviors of the center charge with respect to the Barrow's temperature $ T_{Bc} $ with different non-linear charge parameters γ and fractal parameters Δ.

We can investigate the first-order phase transition from the perspective of the Maxwell's equal area law in the $ T_B-S_B $ phase diagram: $\int_{S_{B1}}^{S_{B2}} T_B {\rm d} S_B= T_{B0}(S_{B2}-S_{B1})$ with the first-order phase temperature $ T_{B0} $ and the boundary entropies $ S_{B1,B2} $ in the two-phases coexistence. Since there is no analytic expression for different values of Δ and γ, here, we will only numerically give the corresponding phase diagram. For convenience, with the normalized parameter $ t=T_B/T_{Bc} $, one can obtain

From the above equation, we plot the normalized Barrow's temperature as a function of the normalized Barrow entropy with different parameters in Fig. 3. The results show that for the Barrow EPYM AdS black hole in the restricted phase space, there exists a supercritical phenomenon of the phase transition: when $ c<1 $, it is a monotonic curve of $ s-t $, where no phase transition occurs; for $ c=1 $, the critical point appears. This system undergoes a first-order phase transition for $ c>1 $. In contrast, from the Gibbs free energy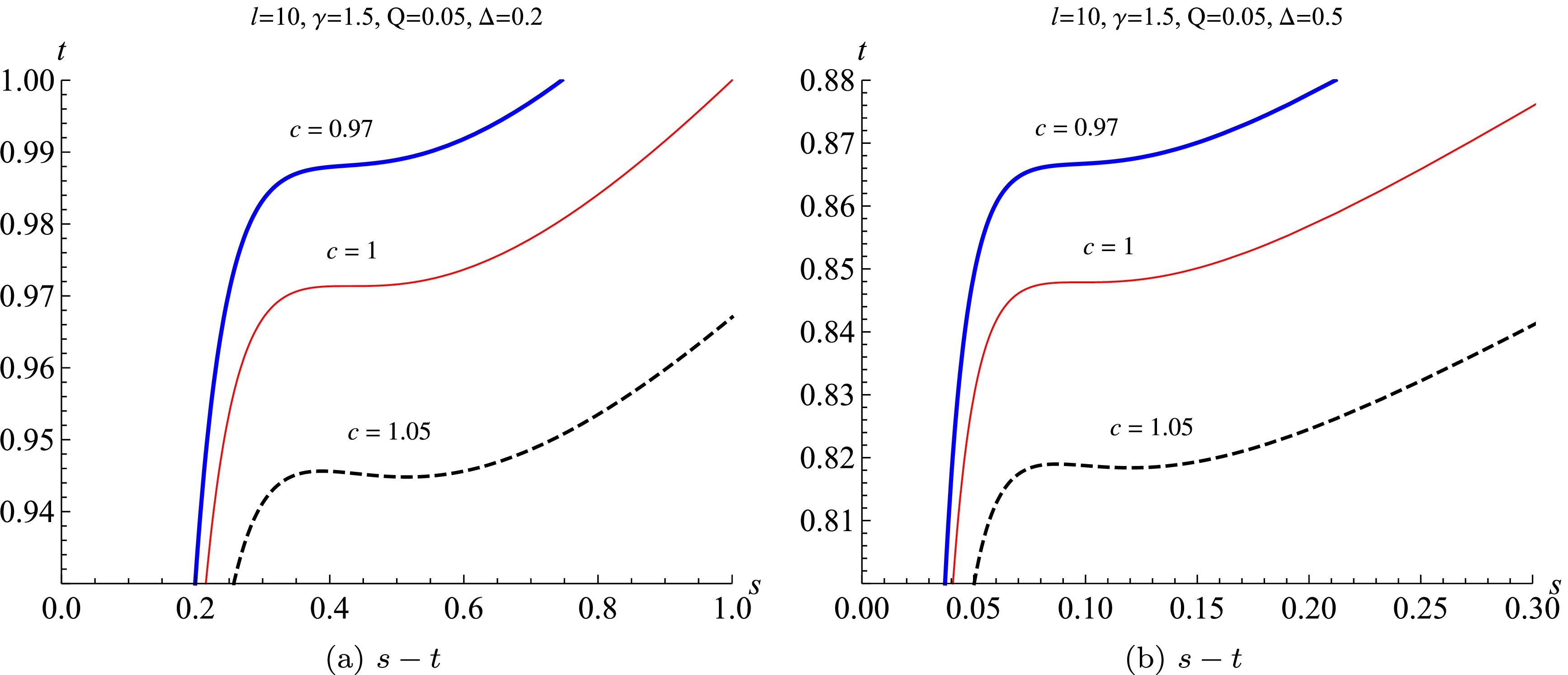

Figure 3.  (color online) The phase diagram of $ t-s $ with different normalized center charge c and fractal parameter Δ.

the corresponding phase structure is also exhibited in Fig. 4. At the first-order phase transition point, the temperature of the Barrow EPYM AdS black hole in the restricted phase space decreases with increasing normalized center charge c. Conversely, for smaller values of the fractal parameter Δ, the phase transition temperature increases with Δ. This behavior suggests that, within the restricted phase space framework − where quantum gravity effects modify the event horizon area − the thermodynamics of the EPYM AdS black hole resemble those of Van der Waals systems. Specifically, in the temperature–entropy phase diagram, monotonic curves signify the absence of phase transitions, while non-monotonic or multi-valued curves indicate the presence of first-order phase transitions. From the perspective of Gibbs free energy, the appearance of swallowtail structures confirms the occurrence of first-order phase transitions, with the vertices of these structures corresponding to critical points.

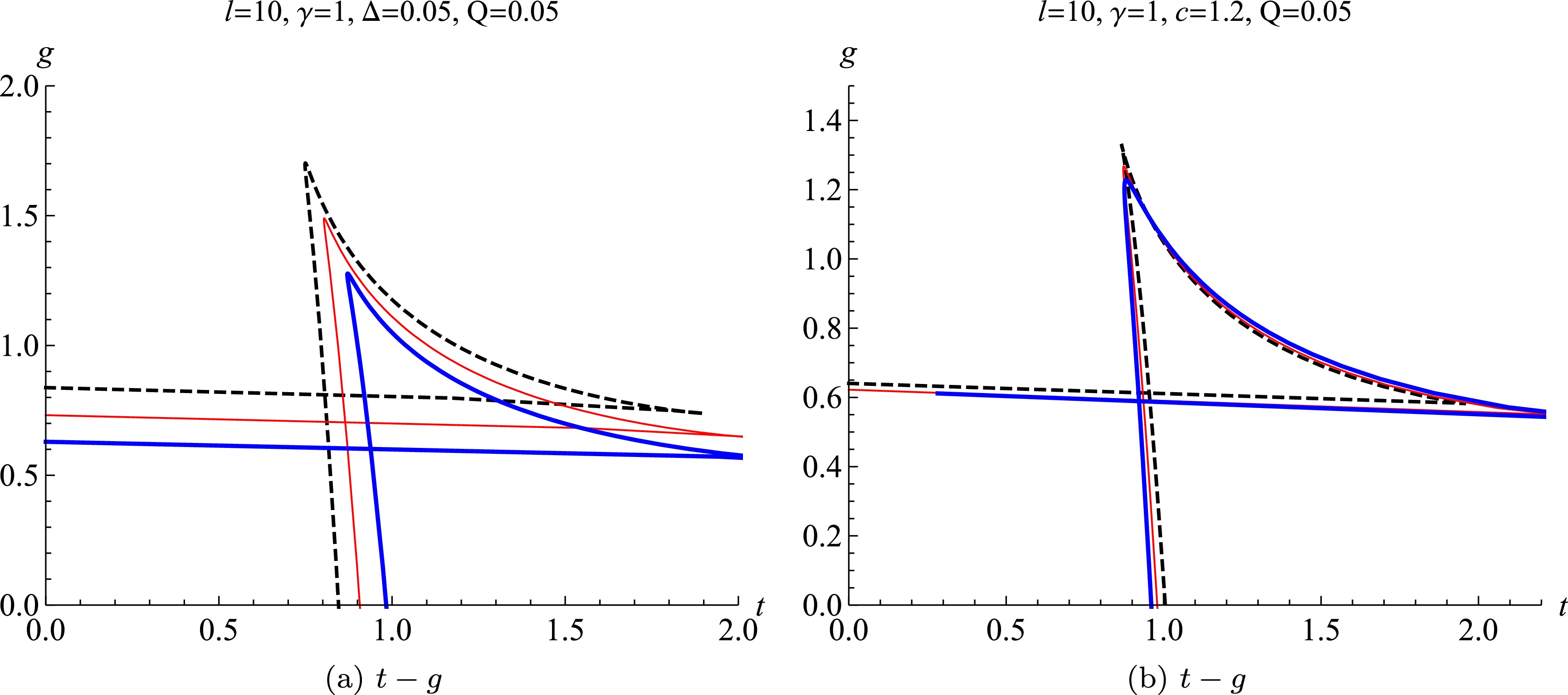
Figure 4.  (color online) The first-order phase transition in the phase diagram of $ t-g $ with different normalized center charges c and fractal parameters Δ. In the left pane, the parameter is set to $ c=1.2 $ (the blue thick line), $ c=1.4 $ (the red thin line), and $ c=1.6 $ (the dashed black line); in the right file, the fractal parameter is set to 0 (the blue thick line), 0.06 (the red thin line), and 0.11 (the dashed black line).

In black hole thermodynamics, a central aspect is the investigation of black hole stability, which can be effectively analyzed through the behavior of the heat capacity. A positive heat capacity signifies a thermodynamically stable black hole, whereas a negative heat capacity implies instability. To explore the stability of the Barrow EPYM AdS black hole within the restricted phase space, and to assess the influence of the fractal parameter Δ and the non-linear YM charge parameter γ on the stability, one can derive the heat capacity under conditions of constant parameters ($ l,\; Q $), as the follows:

whose behaviors with different parameters Δ and γ are shown in Fig. 5. We can conclude that when $ c>1 $, the EPYM AdS black hole in the restricted phase space with a black hole horizon with a fractal structure undergoes a first-order phase transition among the large/intermediate/ small black hole phases. The corresponding heat capacities of the large/small black hole phases are positive and are stable, while the heat capacity of the intermediate one is negative and is unstable. For $ c=1 $, that is, a second-order phase transition between the large/small black hole phases, the heat capacities are positive and the corresponding black hole systems are stable. When $ c<1 $, this black hole system has positive heat capacity and one single stable phase. Furthermore, with an increasing non-linear YM charge parameter γ and fractal parameter Δ, the region of the unstable intermediate phase also expands. The value of heat capacity also increases for $ c\le1 $.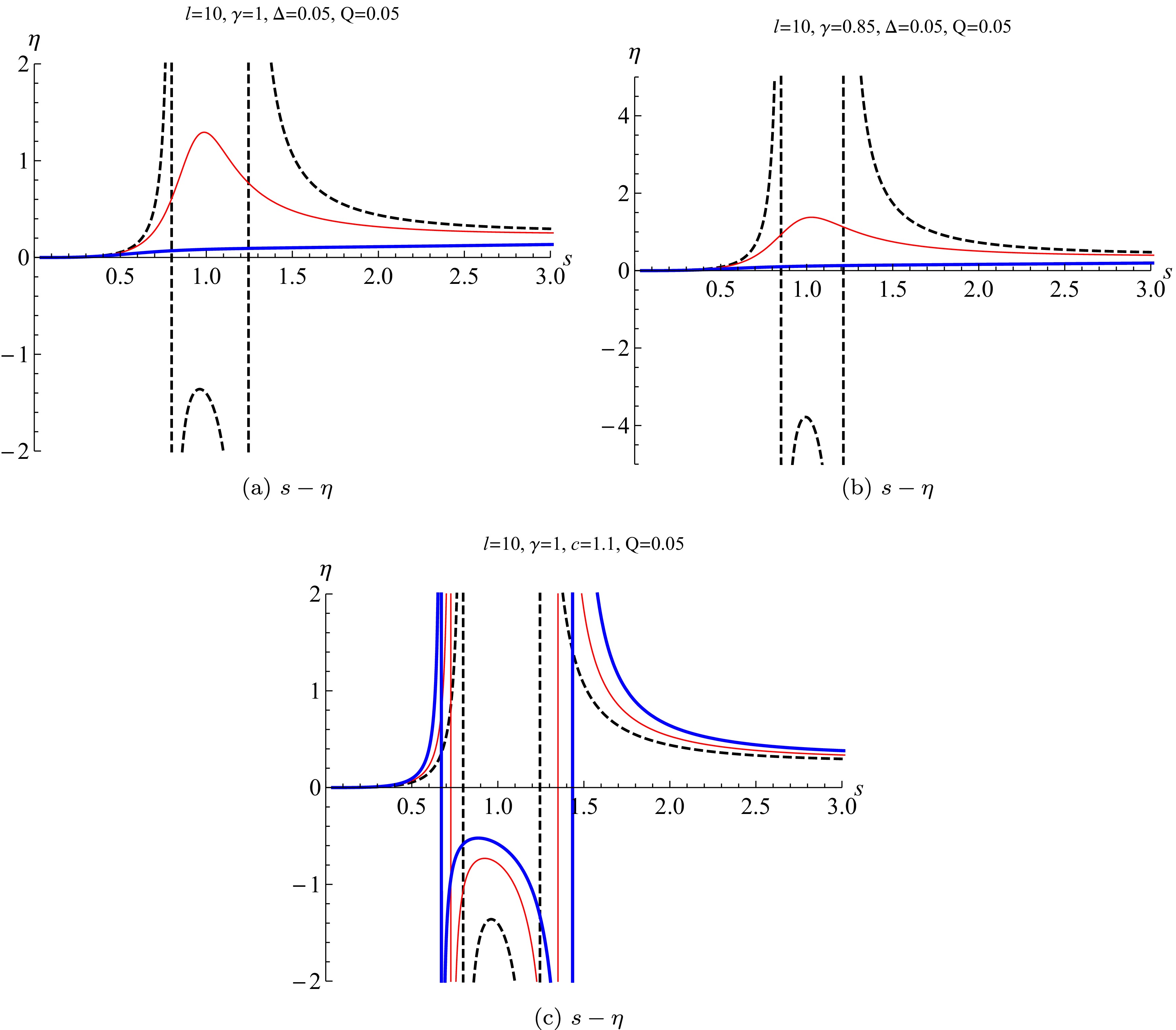

Figure 5.  (color online) The heat capacity of Barrow EPYM AdS black hole in the restricted phase space. In the top figures, the normalized center charge is set to $ c=1.1 $ (the dashed black lines), $ c=1 $ (the red thin lines), and $ c=0.5 $ (the blue thick lines). In the bottom figure, the fractal parameter is set to $ \Delta=0.05 $ (the dashed black line), $ \Delta=0.1 $ (the red thin line), and $ \Delta=0.15 $ (the blue thick line).

In this manuscript, we have studied the thermodynamics of the EPYM AdS black hole in the restricted phase space, considering the fractal structure of the black hole horizon. We have uncovered the influence of quantum gravity and its impact on black hole thermodynamics. The results reveal several remarkable characteristics, similar to those of the RN-AdS black hole in the restricted phase transition [34]. Compared to the RN-AdS black hole in the expanded phase space, the results are summarized as follows:

● The mass parameter is to be understood as the internal energy. Due to the fractal structure of the black hole horizon, the Smarr relation for this black hole in the restricted phase space is not restored, unlike in an ordinary thermodynamic system;

● The EPYM AdS black hole with a fractal structure in the restricted phase space exhibits a unique thermodynamic phenomenon: a supercritical phase transition. When the system has a higher center charge, a first-order phase transition appears; however, it vanishes when the normalized center charge is less than one. This supercritical phase transition is governed by the degrees of freedom in the conformal field theory;

● When the fractal structure is maximum ($ \Delta=1 $), regardless of the normalized central charge parameter value, there is no physical phase transition in the EPYM AdS black hole. For the other values of the fractal structure parameter $ 0\leq\Delta<1 $, there are non-zero thermodynamical quantities at the critical and first-order phase points. Hence, the fractal structure can be regarded as a phase transition probe;

● When$ \Delta=0 $, the phase transition properties of the EPYM AdS black hole in the restricted phase space are the same as those in the extended phase space. This means that when a black hole lacks the fractal structure, its thermodynamic properties are independent of the choice of the corresponding phase space;

● From the perspective of heat capacity, the EPYM AdS black hole in the restricted phase space with a black hole horizon with a fractal structure is always stable when the normalized center charge is equal to or less than one. In contrast, for $ c>1 $, this system is of one unstable intermediate black hole phase and two stable large/small black hole phases. These results are consistent with those in the extended phase space, where there is no fractal structure on the black hole horizon. Specifically, when the EPYM AdS black hole system undergoes a first-order phase transition, the heat capacities of the two stable large/small black hole phases are always positive, while the heat capacity of the unstable intermediate black hole phase is negative. However, when the black hole system is not undergoing a phase transition, the corresponding heat capacity is always positive (more details see Ref. [84]).

We would like to thank Prof. Ren Zhao and Meng-Sen Ma for their indispensable discussions and comments.