Evidence of the negative-parity linear-chain states in ¹⁶C

Clustering is a universal phenomenon occurring at every hierarchical layer of the matter universe, including the nuclear system [1−7]. According to the Ikeda diagram, cluster structures tend to be formed at the vicinity of the cluster-separation threshold [8]. This idea has been extended to the neutron-rich unstable nuclei where much more abundant molecular-type cluster states can be formed owing to the "glue"-effect of the excess valence neutrons [1].

One of the most intriguing clustering structures is the linear-chain configuration, which was initially proposed in the 1950s [9] and has recently been confirmed through intensive theoretical and experimental studies [6, 7, 10]. A linear-chain configuration requires at least three aligned cluster cores [11, 12]. The famous Hoyle state, $ {\rm{^{12}}C(0_2^+)} $, was first considered as a triple-α linear chain [9] but was later proved to be a gas-type condensation state [13−16]. In ¹³C, the existence of the linear-chain structure has been studied with a microscopic 3$ \alpha + n $ model, and two rotational bands with chain-like properties were suggested [17, 18]. For ¹⁴C, numerous theoretical and experimental studies have been performed to search for molecular-like linear-chain structures [15, 16, 19−31], with the latest measurement demonstrating the clear spin assignments to the member states [32]. For ¹⁶C with more valence neutrons, state-of-the-art antisymmetrized molecular dynamics (AMD) calculations have revealed the possible existence of the triangular and linear-chain configurations together with their characteristic decay properties [33−35]. The significant linear-chain configurations can further be classified into three types of molecular rotational bands: positive-parity $ (3/2_\pi^-)^2(1/2_\sigma^-)^2 $-bond, negative-parity mixed bond, and positive parity $ (1/2_\sigma^-)^2(1/2_\sigma^+)^2 $-bond, with a few MeV energy gap in between these bands [34, 35]. Here, the π-bond represents the distribution of the valence neutron mainly surrounding the symmetry axis defined by the aligned cores, while the σ-bond for valence neutrons is mainly distributed in between of the aligned cores, as defined in the standard molecular model [1]. Experimentally, although the positive-parity linear-chain molecular states have been evidenced in both ¹⁴C and ¹⁶C nuclei [10, 32, 36], the search for the negative-parity linear-chain configuration is still very limited. This is partially due to the more probable fragmentation of the negative-parity clustering state, as revealed by the theoretical model [33, 34]. Fortunately, the negative-parity linear-chain states in ¹⁶C may still have partial decay widths comparable to those of the positive parity states [34]. We emphasize that the establishment of the negative-parity molecular band is crucial to the existence of exotic molecular structure because, in a reflection asymmetric system, such as the $ (\pi^2\sigma^2) $-bond system, the parity-inversion doublet should appear simultaneously [1, 33, 34, 37, 38]. Therefore, search for the negative-parity linear-chain molecular band would be a necessary supplement to the previous work on the positive-parity states.

In this study, we aim to investigate the negative-parity linear-chain molecular band in ¹⁶C. Becuase this band is situated a few MeV above the previously reported $ (\pi^2\sigma^2) $-bond positive-parity band [10, 36], the available energy in the reaction and acceptance of the detection system should be expanded to the higher excitation-energy range. The experimental setup is described in Section II, followed by the report of the data analyses and experimental results in Section III. Section IV is dedicated to the discussion of the observed new phenomena, and Section V provides a brief summary.

The experiment was carried out at the Radioactive Ion Beam Line at the Heavy Ion Research Facility in Lanzhou (HIRFL-RIBLL1) [39]. A 60 MeV/nucleon ¹⁸O⁸⁺ primary beam was impinged on a 3500-$ {\rm{\mu m}} $-thick ⁹Be target. One of the reaction products, ¹⁶C, was collected and transported to the secondary (physics) target through the RIBLLl beam line, together with some other isotopes as impurities. The identification of the ¹⁶C beam was realized using the typical method relying on the time-of-flight (TOF) and energy loss ($ \Delta E $) measurements along the beam line [39]. The resulting ¹⁶C-beam purity is as high as 98.5% by applying a gate on the TOF spectrum (the $ \Delta E $ beam-detector must be removed during the physics measurements). The ¹⁶C secondary beam, at an energy of approximately 28 MeV/nucleon and average intensity of approximately 3$ \times $$ 10^{4} $ particles per second (pps), was impinged on a 9.53-mg/cm² $ ({\rm{CD}}_2)_n $ target, where ¹⁶C can be excited and decayed into daughter fragments. As schematically shown in Fig. 1, each incident particle was tracked by three parallel plate avalanche chambers (PPACs) installed upstream of the physical target, providing the reaction position on the target with a precision of approximately 1 mm in either the X or Y direction. In this experiment, we adopted a combined data acquisition (DAQ) system including both the traditional VME system and XIA digital system [40]. However during the ¹⁶C beam time, the XIA system accidentally failed to work and only the VME system recorded data. This resulted in the loss of the PPAC information, and we had to employ another method to determine the reaction point on the target, as described below.

Figure 1.  (color online) Schematic view of the experimental setup (see the text for details).

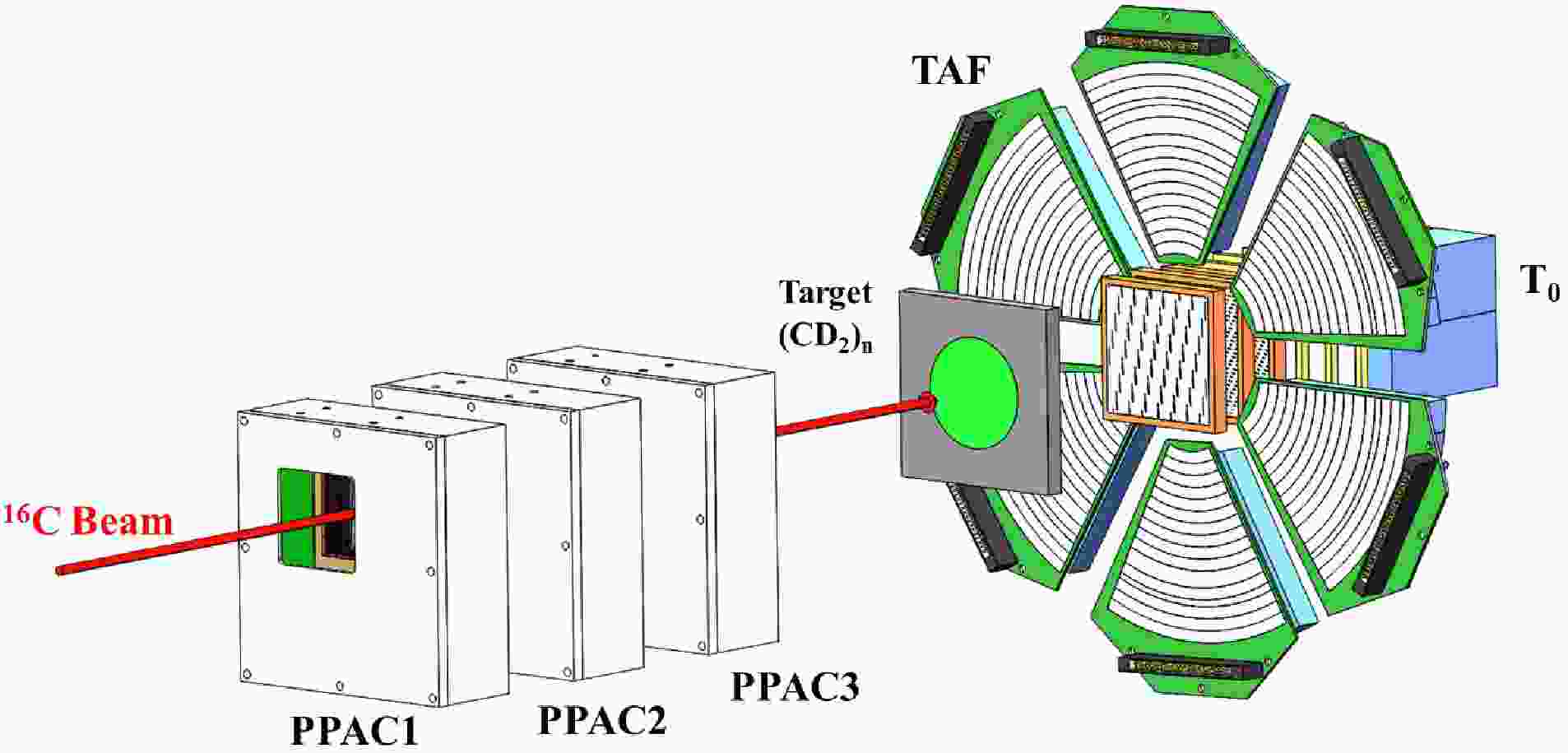
The reaction-decay channels of interest in this experiment were ²H(¹⁶C, ¹⁶C^* $ \to $ ⁴He + ¹²Be)²H and ²H(¹⁶C, ¹⁶C^* $ \to $ ⁶He + ¹⁰Be)²H. Due to the inverse kinematics, the two decaying fragments from ¹⁶C were basically emitted to the forward angles, which were detected by zero-degree telescope (T₀, see Fig. 1) [10, 32, 36]. Inspired by the previous work, it is also crucial to detect the recoil deuteron to deduce the reaction Q-value with high precision. Therefore, we also installed an annual telescope array at larger forward angles (TAF, see Fig. 1) around T₀. The T₀ telescope consists of three layers of Double-sided Silicon-strip Detectors (DSSDs) with thicknesses of approximately 1000, 1500, and 1500 $ {\rm{\mu m}} $, respectively, three large size Single-sided Silicon Detectors (SSDs) with a similar thickness of approximately 1500 $ {\rm{\mu m}} $, and a 2 $ \times $ 2 CsI(Tl) scintillator array (4.1 $ \times $ 4.1 $ \times $ 4.0 cm³ for each unit). Each side of the DSSD is divided into 64 or 32 strips for the 1000 or 1500 $ {\rm{\mu m}} $-thick silicon-strip layer, providing excellent energy and position resolutions [41, 42]. Comparing to our previous work [10, 32], we reduced the distance between the front face of the T₀ telescope and physical target from 160 mm to 100 mm, enlarging the angle-acceptance up to ±24.35°. To retain the high position resolution, we replaced the previous first layer DSSD (BB7 type, 32 strips on each side) with a higher resolution one (BB28 type, 64 strips on each side). These modifications to the T₀ setup allowed the detection sensitivity to be expanded to a much higher excitation-energy range for ¹⁶C (refer to Fig. 2 below). In addition, the heavier break-up fragments, such as the beryllium isotopes, can be fully stopped in the first three DSSD layers, while the lighter fragments, such as helium or hydrogen isotopes, could penetrate the SSD or CsI(TI) detector without the need for double hit discrimination. Using the self-uniform calibration method described in [42], energy matching for different strips in one DSSD was achieved. Then, the energy-loss matching among the hits on both sides of each DSSD, hit-position matching between different layers of DSSDs (tracking method), and particle identification (PID) matching for the acceptable hit combination were applied to discriminate multiple hits in the T₀ telescope [10, 32]. These methods were checked by known reaction-decay channels, such as ¹²C(0$ _2^+ $)$ \rightarrow 3\alpha $ and ⁸Be(g.s.)$ \rightarrow 2\alpha $, and Monte Carlo simulation [10, 32]. Thanks to the excellent energy resolution of the silicon detectors, the T₀ telescope provides clear PID for all helium and beryllium isotopes to be used in the present invariant mass (IM) analysis. The TAF array is composed of six pieces of Annular Double-sided Silicon Strip Detector (ADSSD), each with a thickness of approximately 150 $ {\rm{\mu m}} $, and is divided into sixteen 6.4-mm-wide ring strips on the front side and eight wedge-shaped strips on the back side, providing position sensitivity. Each ADSSD is backed by two large size wedge-shaped CsI(Tl) scintillators [43, 44]. TAF covered the scattering angle from ±26.4° to ±56.26° (Fig. 1) and can clearly discriminate the hydrogen isotopes.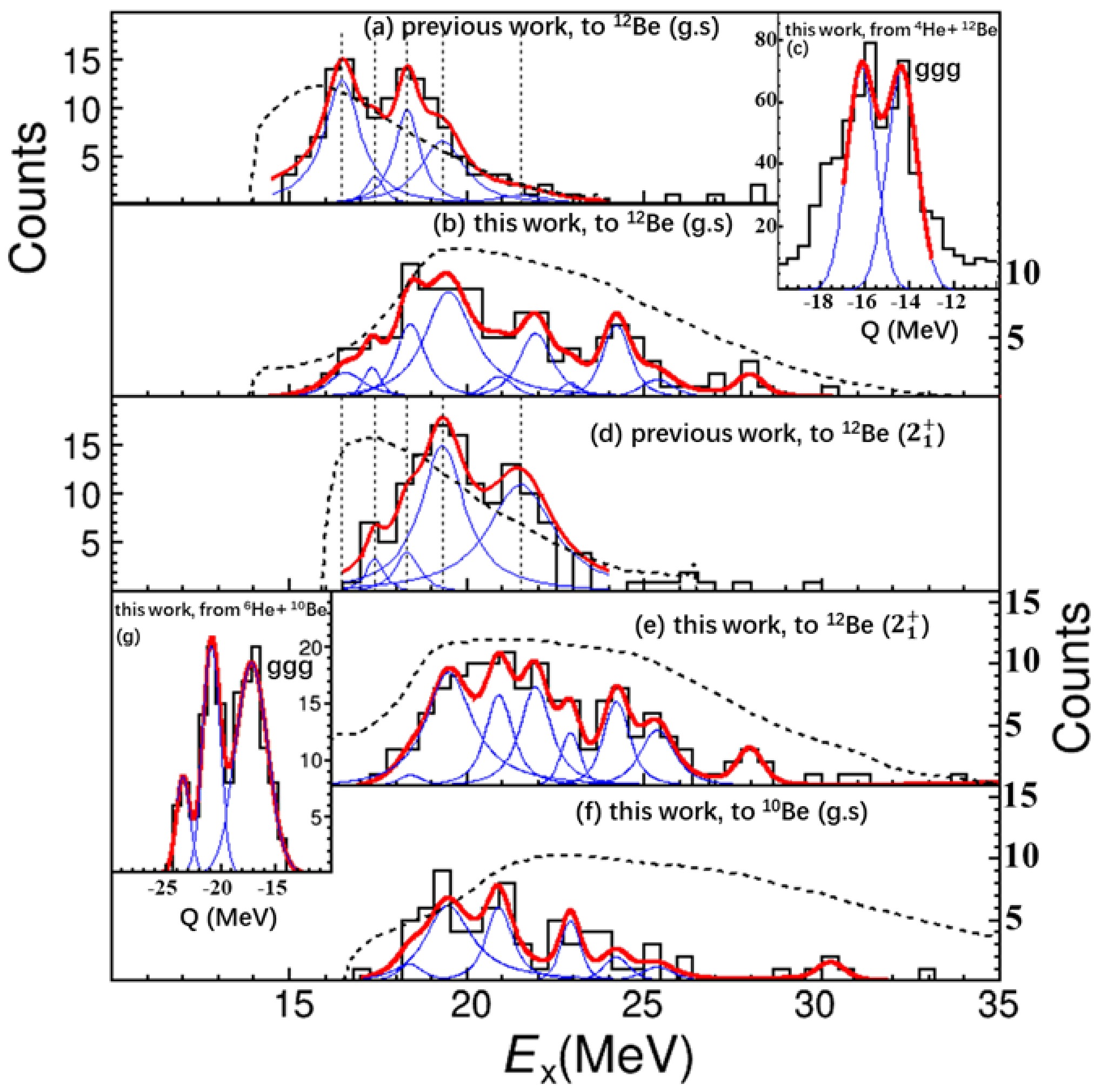

Figure 2.  (color online) Excitation energy spectra of ¹⁶C based on (a), (d) previous measurements [10] and (b), (e) present measurements. (a), (b) correspond to the decay channels of ⁴He+¹²Be(g.s.) and (d), (e) to the channels of ⁴He+¹²Be($2_1^+ $), as selected by the cuts on the associated peaks on the Q-value spectrum (c). Figure (f) is dedicated to the decay channels of ⁶He+¹⁰Be(g.s.), as selected by the cut on the Q-value spectrum in (g). The dashed curves in the figures show the corresponding detection efficiencies obtained from realistic Monte Carlo simulations.

Absolute energy calibration of the detectors was realized by comparing the experimental PID curve (energy loss $ \Delta E $ versus remaining energy E) with that calculated using energy-loss tables [45] and further checked by comparing the measured energy points corresponding to a combination of α-particle sources [32]. This method was validated using the two- and three-α coincident events to reconstruct the known $ {\rm{^8Be}} $ and ¹²C resonant states [24, 46−49].

The energy released from the reaction, the reaction Q value, is useful to identify the reaction-decay channel [7, 24]. In the present work, the Q value can be defined according to

where T is kinetic energy, $ {\rm{^2H}} $ is the recoil deuteron, and $ {\rm{^x{He}}} $ and $ {\rm{^y{Be}}} $ denote $ {\rm{^4He + ^{12}}Be} $ and $ {\rm{^6He + ^{10}}Be} $ decay pairs, respectively. Due to the large energy spread of the radioactive beam produced by the projectile fragmentation (PF) method, the Q-value resolution is generally insufficient to discriminate various decay paths. To overcome this difficulty, we may use the momentum conservation to deduce $ T_{{\rm{beam}}} $ event by event from the momenta of the three final particles [10, 32]. In this way, the Q-value resolution can be largely improved thanks to the excellent performance of the silicon detectors [10, 32, 36]. However, the Q-value resolution is also affected by the correctness of the determined reaction position on the target. Previously, the incident beam trajectory was precisely tracked by at least two of the three PPACs. In the present ¹⁶C experiment, unfortunately, only 1/3 of the PPAC information was correctly recorded by the VME DAQ system, while the other 2/3 was lost due to the accidental failure of the correspondingly connected XIA DAQ system. Therefore, we tried to determine the reaction position for these latter 2/3 events through backtracking based on the He and Be trajectories measured by the T₀-DSSDs. Obviously, the reaction position resolution obtained in this way is worse but still sufficient to meet the actual analysis goal.

As shown in Fig. 2, the Q-value spectrum for the three-fold coincidence events displays peaks corresponding to different decay channels. Although the coincident measurements incorporating the recoil deuteron are in favor of selecting the targeted reaction channels, some backgrounds still exist, as can be seen in Fig. 2(c), resulting from the breakup of the carbon contents in the target and contamination of selected ¹²Be isotopes by the much stronger ¹⁰Be isotopes. This was checked using data taken from the pure carbon target or by using the real ¹⁰Be isotopes to mimic ¹²Be. When relatively narrow cuts of approximately 1 MeV wide were applied to the relevant peaks in the Q-value spectrum, the effect of this background on the follow-up analyses of the resonant states can be neglected.

The excitation energy ($ E_x $) of ¹⁶C can be obtained by using the momenta ($ \vec{p_i} $) and energies ($ E_i $) of the two decaying fragments according to the standard IM method [10, 32, 50]:

Here, E and T denote the total energy and kinetic energy, respectively. Figure 2 shows the $ E_x $ spectra reconstructed from the decaying helium and beryllium fragments, subject to the observation of the recoil deuteron to avoid contamination from other reaction processes. In Fig. 2(a) and (b), we present the $ E_x(^{16}{\rm{C}}) $ spectra associated with the $ \alpha + ^{12}{\rm{Be}}\rm (g.s.) $ decay channel as gated on the ggg (three final particles on their g.s.) peak in the Q-value spectrum (like Fig. 2(c)) for the previous work [10] and present work, respectively. The spectra are fitted with peak functions, each being a Breit-Wigner (BW) shape convoluted with a Gaussian function representing the energy resolution obtained from the realistic simulation [10, 32, 51, 52]. A smoothly varying background function was also added to the fitting procedure but resulted in negligible contribution. The dashed curves show the detection efficiency obtained from the simulation, taking into account the realistic reaction position and detector setup and performances. Compared to the previous work (Fig. 2(a)), the detection efficiency in the present work (Fig. 2(b)) decreased at the lower $ E_x $ side due to the deuteron-detection threshold of the present thinner silicon layers in TAF. On the higher $ E_x $ side, owing to the intentionally reduced distance between the T₀ telescope and physical target as described above, the detection efficiency largely expanded, allowing the observation of the higher lying resonant states. The same situation occurred for the $ \alpha + ^{12}{\rm{Be}}(2_1^+, 2.1 \; \rm MeV) $ decay channel, as displayed in Fig. 2(d) and (e) for the previous and the present works, respectively, both gated on the left-side peak in the corresponding Q-value spectrum. During the fitting procedure, the peaks were adopted by considering the previous observations [10, 36], spectrum-shapes in both channels, and overall fitting goodness ($ \chi^2 $ value). The consistency between the two decay channels for the BW peak positions and widths was kept due to their inherent physics meaning in the mother nucleus ¹⁶C. In Fig. 2(f), we also show the $ E_x $ spectrum reconstructed from another pair of fragments, $ {\rm{^{6}}He} + {\rm{^{10}}Be(g.s.)} $, to supplement the decay information. The decays to excited ¹⁰Be are not presented due to the very low statistics.

The extracted resonant states are listed in Table 1. Among them, the states at 16.6, 17.3, 18.4, and 19.4 MeV coincide excellently with those observed previously [10, 36], demonstrating the validity of the present measurement and data analyses. In the higher excitation-energy region, the present measurement provides much more information on clustering resonant states compared with previous measurement, owing to the expanded detection acceptance, as shown in Fig. 2.

present observation				predicted[a]			previous observation[b]
$ E_{x}/{\rm{MeV}} $	$ J^{\pi} $	$ \Gamma_{{\rm{tot}}}/{\rm{keV}} $		$ E_{x} $	$ J^{\pi} $		$ E_{x}/{\rm{MeV}} $	$ J^{\pi} $	$ \Gamma_{{\rm{tot}}}/{\rm{keV}} $
16.6(1)		1225(200)		16.81	$ 0_6^+ $		16.5(1)	$ 0^+ $	1200(200)
17.3(1)		401(200)		17.51	$ 2_9^+ $		17.3(2)	$ 2^+ $	400(200)
18.4(1)		811(100)					18.3(1)		800(100)
19.4(1)		1521(160)		18.99	$ 4_{10}^+ $		19.4(1)	$ 4^+ $	1500(160)
20.9(2)		704(70)		21.49	$ 6_5^+ $		21.6(2)	$ 6^+ $	2200(200)
21.9(2)	$ (1^-) $	843(50)		22.05	$ 1_{11}^- $
22.9(2)	$ (3^-) $	302(120)		23.00	$ 3_{14}^- $
24.2(2)	$ (8^+) $	561(50)					23.5(2)[c]		680(200)
25.4(2)	$ (5^-) $	865(70)		24.76	$ 5_{15}^- $		25.5(2)[c]		1230(200)
27.9(2)	$ (7^-) $	376(50)		27.35	$ 7_6^- $
a Refer to [33–35]; b Refer to [10, 36]; c Observed only from the 6He+10 Be decay channel [10, 36].

Table 1.  Presently observed excitation energies, tentative spin parities, and total decay widths of the resonant states in ¹⁶C compared to those predicted by AMD calculation and observed in a previous experiment. The errors (standard deviation) in parentheses are mainly systematic ones for the resonance energies ($ E_{x} $) and are statistical only for the resonance widths ($ \Gamma_{{\rm{tot}}} $) [24, 32].

In our previous study, the extremely broad state at 21.6 MeV was determined with a large uncertainty due to the very low detection efficiency around that energy, as can be seen in Fig. 2(a) and (d). Now, with much higher efficiency, we see clearer structures within that energy range and the previously determined one broad resonance can fairly be split into three states at 20.9, 21.9 and 22.9 MeV, as evidenced by Fig. 2(b) and (e). Above these states, we observe several new states that decay to both the g.s. 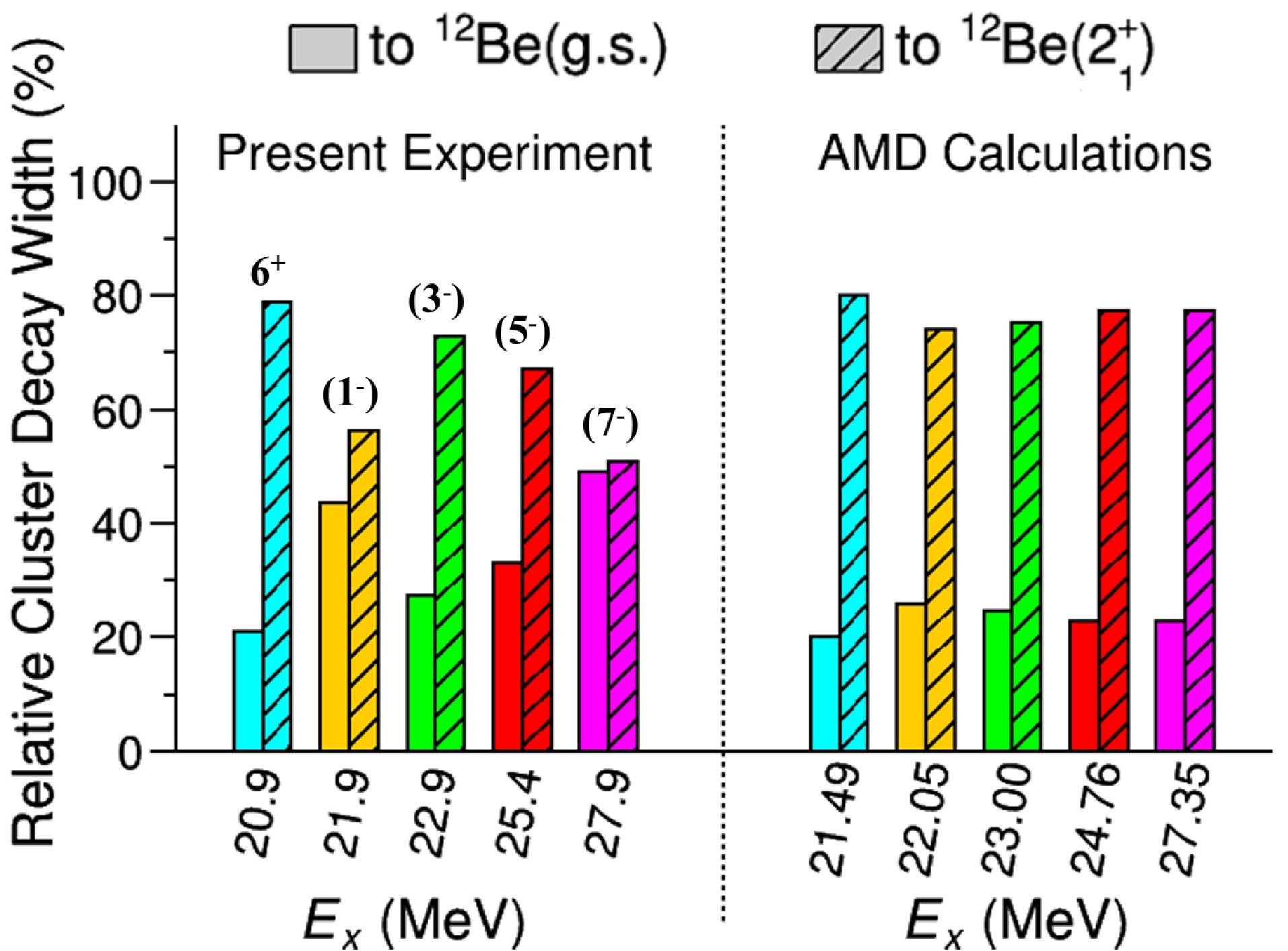and $ 2^+ $ state of ¹²Be. We deduced the relative decay widths for these states after correcting for the difference of detection efficiency and normalizing to 100% for each state, as plotted in Fig. 3 (left panel). First, the new state at 20.9 MeV may be considered as the 6⁺ member of the positive-parity linear-chain band, replacing the previously not well determined broad state around 21 MeV. Its energy position and relative decay width (see Fig. 3), in comparison with the theoretical prediction, give clear support to this assignment and do not change the conclusion of Ref. [10] for the establishment of the $ (\pi^2\sigma^2) $-bond positive-parity linear-chain molecular rotational band. In addition, considering the extension of this band (see Fig. 4), the currently observed 24.2 MeV state might serve as the $ 8^+ $ member of this band, although no theoretical calculation has been reported so far for the associated relative decay width.

Figure 3.  (color online) Relative cluster decay widths extracted from presently measured spectra in Fig. 2 (left panel) and calculated by the AMD model [33, 34] (right panel). The corresponding spin-parities of the indicated states can be found in Table 1.

Figure 4.  (color online) Excitation energy versus spin for the molecular rotational bands in ¹⁶C. Red circles show the resonant states observed in this study, which are compared with the AMD-predicted negative-parity linear-chain states (orange diamonds). Purple solid points show the resonant states observed previously [10, 36] that are related to the AMD-predicted $\pi^2 \sigma^2 $-bond positive-parity linear chain configuration, supplemented by the presently observed and tentatively assigned 24.2 MeV (8⁺) states. The horizontal dashed lines represent the indicated cluster-separation thresholds.

The predicted negative-parity linear-chain band is approximately 5 MeV above the positive-parity band [34], just in the range of our observed new resonant states (see Table 1 and Fig. 4). Meanwhile, the predicted pure σ-bond ($ (1/2_\sigma^-)^2(1/2_\sigma^+)^2 $-bond) linear-chain band appears at a much higher energy region (around 30 MeV) [35] and does not mix with the negative-parity states. Therefore, we may quite safely consider the newly observed states between 21.9 and 27.9 MeV (except the 24.2 MeV one as explained above) as the candidates for the negative-parity linear-chain band members. These assignments can further be supported by comparing the relative decay widths with the AMD calculations, as displayed in Fig. 3, which are characterized by the exotic decay primarily to the excited $ 2^+ $ state of ¹²Be. In the figure, we see good consistency between the experimental and theoretical results for the 21.9$ \leftrightarrow $22.05 MeV, 22.9$ \leftrightarrow $23.00 MeV, and 25.4$ \leftrightarrow $24.75 MeV pairs. The 27.9$ \leftrightarrow $27.35 MeV pair has a larger difference in relative decay width, which may be attributed to the low detection efficiency and hence very low counting statistics around that energy. Based on these analyses and comparisons, we may tentatively assign the presently observed states at 21.9, 22.9, 25.4, and 27.9 MeV as the predicted $ 1^- $, $ 3^- $, $ 5^- $, and $ 7^- $ members, respectively, of the negative-parity linear-chain molecular rotational band, as presented in Table 1 and Fig. 4. The results could still be regarded as tentative because direct spin analysis would require higher $ E_x $-peak resolution and statistics, as demonstrated in Ref. [32].

In Fig. 2(f), we also present the $ E_{{\rm{x}}} $ spectrum associated with the $ {\rm{^6He + ^{10}}Be(g.s.)} $ decay channel. Due to the very low statistics, this spectrum is used only to show no contradiction with the above presented results and discussion.

A new inelastic excitation and cluster-decay experiment was conducted with a ¹⁶C beam at 28 MeV/nucleon and a$ ({\rm{CD}}_2)_n $target. The two decay fragments, helium and beryllium isotopes, from highly excited states of ¹⁶C, and the recoil deuteron particle were detected in coincidence. Thanks to the excellent energy and position resolutions of the silicon-strip detectors, the beam energy can be deduced event-by-event with good energy resolution, leading to a Q-value spectrum with resolved peaks corresponding to the ground and excited states of ^10,12Be isotopes. Then, the ¹⁶C excitation-energy spectra associated with different decay paths were reconstructed using the IM method. Owing to the intentionally reconfigured detector setup, the detection acceptance was extended to a higher excitation-energy range. Several new resonant states have been observed, which are situated in between the previously reported $ \pi^2\sigma^2 $-bond positive-parity linear-chain band and predicted pure $ \sigma^4 $ band. Compared with the AMD calculations for both resonance energies and selective decay paths, the newly observed states at 21.9, 22.9, 25.4, and 27.9 MeV can be tentatively assigned as the $ 1^- $, $ 3^- $, $ 5^- $, and $ 7^- $members, respectively, of the negative-parity linear-chain molecular rotational band. These results provide additional strong evidence of the exotic chain structure in neutron-rich ¹⁶C nuclei. Of course, the present assignments of these observed resonances are based on actual knowledge from literature, which could be updated in the future when new experimental evidence and theoretical interpretations are augmented. Particularly, more experimental studies are encouraged to determine the spin of these states directly.

The authors thank the HIRFL-RIBLL staff for providing excellent technical and operational support during the experiment.