-
Baryon number violating (BNV) interactions play a crucial role in explaining the matter-antimatter asymmetry of the Universe [1], and have been predicted in various scenarios beyond the standard model (SM). The primary method to test BNV interactions is through searches of nucleon decays due to their unique experimental signature. Over the past several decades, many large-fiducial-mass experiments, including IMB [2], SNO+ [3], KamLAND [4], Kamiokande [5], and Super-Kamiokande (Super-K) [6], have conducted extensive searches for nucleon decays involving only SM particles, placing very stringent limits on their occurrence. In recent years, with the advent of next-generation neutrino experiments such as Hyper-Kamiokande [7], DUNE [8], JUNO [9], and THEIA [10], BNV nucleon decays have attracted significant attention, including in particular exotic modes involving new light invisible particles in the final state [11−20].
One such well-motivated light particle is the axion, or more generally, axion-like particles (ALP)
1 . The axion was originally proposed as a solution to the strong CP problem via the Peccei-Quinn mechanism [21−24]. By relaxing the coupling-mass relationship specific to the QCD axion, a general class of ALPs has emerged [25−28]. These particles are not necessarily tied to the strong CP problem, and thus exhibit more flexible masses and couplings. Both axions and ALPs have been widely incorporated into scenarios beyond the standard model, where they can make connections to neutrino mass generation [29, 30] and serve as viable dark matter candidates [31−35]. Especially, ALP models involving BNV interactions have been pursued recently [36−38], offering potential explanations for the long-standing neutron lifetime anomaly [15, 39, 40]. Therefore, combining BNV interactions with an ALP presents a very interesting direction to explore.Within the framework of the low energy effective field theory extended by an ALP, termed as aLEFT, Ref. [18] studied BNV nucleon and hyperon decays involving an ALP in the final state. In the aLEFT with a shift symmetry in the ALP, the relevant BNV operators first appear at dimension 8 (dim 8) [41], with a total of 20 operators without counting flavors. Under the QCD chiral symmetry
$ {\rm{SU}}(3)_{\mathtt{L}}\otimes {\rm{SU}}(3)_{\mathtt{R}} $ of the light$ u,\; d,\; s $ quarks, these dim-8 operators can be classified into three irreducible representations (irreps) and their chiral partners:$ {\bf{8}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{1}}_{ \mathtt{R}( \mathtt{L})} $ ,$ {\bf{3}}_{ \mathtt{L}( \mathtt{R})} \otimes \bar{{\bf{3}}}_{ \mathtt{R}( \mathtt{L})} $ , and$ {\bf{3}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{6}}_{ \mathtt{R}( \mathtt{L})} $ . Only 8 operators in the first two usual irreps were considered in [12], whereas the remaining 12 operators associated with the new chiral irreps$ {\bf{3}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{6}}_{ \mathtt{R}( \mathtt{L})} $ were discarded as sub-leading contributions. Recently, we have found that the operators in the new chiral irreps can contribute to nucleon decays at the same leading chiral order as the other two [42]. Moreover, processes that change isospin by 3/2 units, such as$ n\to \pi^+ e^- a $ and$ n\to \pi^+ \mu^- a $ , can only be mediated by operators belonging to the irreps$ {\bf{3}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{6}}_{ \mathtt{R}( \mathtt{L})} $ due to their unique flavor and Lorentz structures. Motivated by these considerations, in this work, we will systematically investigate the nucleon decays involving an ALP based on the complete set of all 20 BNV aLEFT operators.We begin by collecting the relevant dim-8 BNV aLEFT operators involving an ALP, a SM lepton, and three light quark fields, which are invariant under the QCD and QED symmetries
$ {\rm{SU}}(3)_{\rm{c}}\otimes {\rm{U}}(1)_{\rm{em}} $ . To calculate the hadronic matrix elements, a systematic approach is through the chiral perturbation theory (ChPT) framework [43−45] by matching the quark-level operators onto their hadronic counterparts. For all relevant nucleon decay operators in the LEFT, their leading-order chiral matching has been systematically established in [42, 46, 47] by requiring that the hadron-level operators share the same chiral and Lorentz transformation properties as their quark-level counterparts. Following these works, we decompose all aLEFT operators into irreps under the chiral group and determine the relevant spurion fields stemmed from the aLEFT interactions. By substituting these spurion fields into the matching results in [42] and expanding to the appropriate order in pseudoscalar meson fields, we obtain the desired hadron-level BNV operators. Together with the standard baryon ChPT interactions [48, 49], we calculate the amplitudes and decay widths for both octet baryon two-body decays and nucleon three-body decays involving an ALP. To extract more meaningful information from experimental data, we also analyze the momentum distributions of the final-state charged leptons and mesons in nucleon three-body decays.After establishing the theoretical framework for nucleon decays involving an ALP, we examine the experimental constraints on the relevant aLEFT interactions. Given the limited experimental search for those exotic decay modes, we constrain these channels by reanalyzing the existing data from proton decay searches conducted by the Super-K experiment [50−54]. We simulate the proton decay processes using the analytical decay distributions by accounting for the detector’s resolution and efficiency, and compare the results with Super-K data to extract lower bounds on the partial lifetime (
$ \Gamma^{-1} $ ) for certain decay modes. These lower limits are then translated into constraints on the effective scale$ \Lambda_{\mathtt{eff}} $ associated with the relevant Wilson coefficients (WCs) of the aLEFT operators. Finally, we predict new bounds on the occurrence of BNV neutron and hyperon decay modes involving an ALP. These predictions provide valuable guidance for future experimental searches.This paper is organized as follows. We first introduce the dim-8 BNV aLEFT operators and derive their hadron-level counterparts within the ChPT framework in Section 2. In Section 3, we formulate the general expressions for the decay widths of nucleon decays involving an ALP, and study the momentum distributions of the charged leptons and/or pseudoscalar mesons for the three-body decays. Section 4 is dedicated to reinterpreting the existing proton decay data to establish bounds on the corresponding modes involving an additional ALP. Subsequently, by combining these results with the available inclusive limits, we will set conservative constraints on the relevant WCs and further explore their implications for other decay modes. Finally, we summarize our results in Section 5. Additionally, Appendix A collects the relevant BNV vertices involving a spurion field and a baryon field, while Appendix B summarizes the complete expressions for the decay widths expressed in terms of the aLEFT WCs.
-
In this section, we present a detailed EFT description of the BNV interactions involving an ALP field, starting from quark-level interactions and then matching them onto hadron-level interactions based on the QCD chiral symmetry. We begin by collecting the relevant dim-8 local operators within the LEFT framework extended by an ALP (aLEFT). To perform the chiral matching, we decompose these operators into irreducible representations of the chiral group and identify the corresponding spurion fields involved in the matching. By incorporating these spurion fields into the formalism established in Ref. [42], we obtain the hadronic counterparts of the BNV aLEFT operators.
-
To investigate low energy processes, the LEFT is a good starting point. When the LEFT is extended by a light axion-like particle, we refer to it as aLEFT. In this work, we focus on two- and three-body BNV nucleon decays, whose final states contain both an ALP and a lepton, plus an additional pseudoscalar meson for three-body modes. For such
$ \Delta B = |\Delta L| = 1 $ processes, the required lowest dimensional aLEFT operators must contain three quark fields and one lepton field. We assume that the interactions preserve the shift symmetry in the axion field a, which results in the ALP field appearing only through its derivative,$ \partial_\mu a $ .2 Consequently, the relevant leading-order operators appear at dim 8 and take the form,$ lqqq\partial a $ .A complete set of those dim-8 operators was recently constructed in [41]. However, to facilitate chiral matching in the subsequent parts, we will construct a slightly modified operator basis. Denoting the SM charged lepton chiral fields as
$ e_{ \mathtt{L}, \mathtt{R}} $ , neutrinos as$ \nu_{\mathtt{L}} $ , and the up- and down-type quarks by$ u_{ \mathtt{L}, \mathtt{R}} $ and$ d_{ \mathtt{L}, \mathtt{R}} $ , respectively, the relevant dim-8 aLEFT operators adopted in our analysis are listed in the third column of Table 1. In the rightmost column, we indicate the correspondence with the operators given in [12, 41], where those highlighted in dark gray were considered in Ref. [12] to study the BNV nucleon decays, while the remaining 12 operators were neglected there. When the quark flavor is taken into account, there are totally 68 operators associated with the$ u,d,s $ quarks, among which only 22 were considered in that paper. Our operator basis exhibits a clear chirality-flip symmetry, where one half of the operators are the chirality partners of the other half under the interchange$ \mathtt{L} \leftrightarrow \mathtt{R} $ , with$ \nu_{\mathtt{L}} \leftrightarrow \nu_{\mathtt{L}}^{\mathtt{C}} $ applied in the neutrino case. This structure will simplify the chiral matching and also serve as a useful cross-check for the final results. Note that operators in the$ \Delta(B-L)=0 $ sector involve a lepton field, whereas those in the$ \Delta(B+L)=0 $ sector involve a conjugate lepton filed. This difference in global lepton number implies that they originate from distinct UV-complete scenarios, where the generation of operators in one sector may simultaneously forbid those in the other.Notation Operator Chiral Irrep. # of operators Comparison with [18] Δ(B-L)=0 $ {\cal{O}}_{\partial a e uud}^{\mathtt{VL}, \mathtt{SL}} $ 

$ \partial_\mu a (\overline{e_{\mathtt{R}}^{\mathtt{C}}}\gamma^\mu u_{\mathtt{L}}^\alpha) (\overline{u_{\mathtt{L}}^{\beta \mathtt{C}}}d_{\mathtt{L}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{8}}_{\mathtt{L}} \otimes {\bf{1}}_{\mathtt{R}} $ 

$ n_e n_u^2 n_d \,[2n_e] $ 

$ - $ 

$ {\cal{O}}^{\mathtt{VL}, \mathtt{SL}}_{\partial a eudu} $ 

$ {\cal{O}}_{\partial a e uud}^{\mathtt{SL}, \mathtt{VR}} $ 

$ \partial_\mu a (\overline{e_{\mathtt{L}}^{\mathtt{C}}} u_{\mathtt{L}}^\alpha) (\overline{u_{\mathtt{L}}^{\beta \mathtt{C}}}\gamma^\mu d_{\mathtt{R}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{6}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} $ 

$ n_e n_u^2 n_d \,[2n_e] $ 

$ - [{\cal{O}}^{\mathtt{VL}, \mathtt{SR}}_{\partial a udue}]^\dagger $ 

$ {\cal{O}}_{\partial a e udu}^{\mathtt{SL}, \mathtt{VR}} $ 

$ \partial_\mu a (\overline{e_{\mathtt{L}}^{\mathtt{C}}} u_{\mathtt{L}}^\alpha) (\overline{d_{\mathtt{L}}^{\beta \mathtt{C}}}\gamma^\mu u_{\mathtt{R}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{6}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} \oplus \bar{{\bf{3}}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} $ 

$ n_e n_u^2 n_d \,[2n_e] $ 

$ - [{\cal{O}}^{\mathtt{VL}, \mathtt{SR}}_{\partial a duue}]^\dagger $ 

$ {\cal{O}}_{\partial a e duu}^{\mathtt{SL}, \mathtt{VR}} $ 

$ \partial_\mu a (\overline{e_{\mathtt{L}}^{\mathtt{C}}} d_{\mathtt{L}}^\alpha) (\overline{u_{\mathtt{L}}^{\beta \mathtt{C}}}\gamma^\mu u_{\mathtt{R}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{6}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} \oplus \bar{{\bf{3}}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} $ 

$ n_e n_u^2 n_d \,[2n_e] $ 

$ - [{\cal{O}}^{\mathtt{VL}, \mathtt{SR}}_{\partial a uude}]^\dagger $ 

$ {\cal{O}}_{\partial a e uud}^{\mathtt{VR}, \mathtt{SR}} $ 

$ \partial_\mu a (\overline{e_{\mathtt{L}}^{\mathtt{C}}} \gamma^\mu u_{\mathtt{R}}^\alpha) (\overline{u_{\mathtt{R}}^{\beta \mathtt{C}}} d_{\mathtt{R}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{1}}_{\mathtt{L}} \otimes {\bf{8}}_{\mathtt{R}} $ 

$ n_e n_u^2 n_d \,[2n_e] $ 

$ {\cal{O}}^{\mathtt{VR}, \mathtt{SR}}_{\partial a euud} $ 

$ {\cal{O}}_{\partial a e uud}^{\mathtt{SR}, \mathtt{VL}} $ 

$ \partial_\mu a (\overline{e_{\mathtt{R}}^{\mathtt{C}}} u_{\mathtt{R}}^\alpha) (\overline{u_{\mathtt{R}}^{\beta \mathtt{C}}} \gamma^\mu d_{\mathtt{L}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{3}}_{\mathtt{L}} \otimes {\bf{6}}_{\mathtt{R}} $ 

$ n_e n_u^2 n_d \,[2n_e] $ 

$ {\cal{O}}^{\mathtt{VR}, \mathtt{SR}}_{\partial a duue} $ 

$ {\cal{O}}_{\partial a e udu}^{\mathtt{SR}, \mathtt{VL}} $ 

$ \partial_\mu a (\overline{e_{\mathtt{R}}^{\mathtt{C}}} u_{\mathtt{R}}^\alpha) (\overline{d_{\mathtt{R}}^{\beta \mathtt{C}}} \gamma^\mu u_{\mathtt{L}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{3}}_{\mathtt{L}} \otimes {\bf{6}}_{\mathtt{R}} \oplus {\bf{3}}_{\mathtt{L}} \otimes \bar{{\bf{3}}}_{\mathtt{R}} $ 

$ n_e n_u^2 n_d \,[2n_e] $ 

$ {\cal{O}}^{\mathtt{VL}, \mathtt{SR}}_{\partial a dueu} $ 

$ {\cal{O}}_{\partial a e duu}^{\mathtt{SR}, \mathtt{VL}} $ 

$ \partial_\mu a (\overline{e_{\mathtt{R}}^{\mathtt{C}}} d_{\mathtt{R}}^\alpha) (\overline{u_{\mathtt{R}}^{\beta \mathtt{C}}} \gamma^\mu u_{\mathtt{L}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{3}}_{\mathtt{L}} \otimes {\bf{6}}_{\mathtt{R}} \oplus {\bf{3}}_{\mathtt{L}} \otimes \bar{{\bf{3}}}_{\mathtt{R}} $ 

$ n_e n_u^2 n_d \,[2n_e] $ 

$ {\cal{O}}^{\mathtt{VL}, \mathtt{SR}}_{\partial a dueu} - $ 

$ {\cal{O}}^{\mathtt{VL}, \mathtt{SR}}_{\partial a eudu} $ 

$ {\cal{O}}_{\partial a \nu ddu}^{\mathtt{VR}, \mathtt{SR}} $ 

$ \partial_\mu a (\overline{\nu_{\mathtt{L}}^{\mathtt{C}}} \gamma^\mu d_{\mathtt{R}}^\alpha) (\overline{d_{\mathtt{R}}^{\beta \mathtt{C}}} u_{\mathtt{R}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{1}}_{\mathtt{L}} \otimes {\bf{8}}_{\mathtt{R}} $ 

$ n_\nu n_u n_d^2 \,[4n_\nu] $ 

$ - $ 

$ {\cal{O}}^{\mathtt{VL}, \mathtt{SR}}_{\partial a d\nu du} $ 

$ {\cal{O}}_{\partial a \nu ddu}^{\mathtt{SL}, \mathtt{VR}} $ 

$ \partial_\mu a (\overline{\nu_{\mathtt{L}}^{\mathtt{C}}} d_{\mathtt{L}}^\alpha) (\overline{d_{\mathtt{L}}^{\beta \mathtt{C}}} \gamma^\mu u_{\mathtt{R}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{6}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} \oplus \bar{{\bf{3}}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} $ 

$ n_\nu n_u n_d^2 \,[4n_\nu] $ 

$ - [{\cal{O}}^{\mathtt{VL}, \mathtt{SR}}_{\partial a dud\nu}]^\dagger $ 

$ {\cal{O}}_{\partial a \nu dud}^{\mathtt{SL}, \mathtt{VR}} $ 

$ \partial_\mu a (\overline{\nu_{\mathtt{L}}^{\mathtt{C}}} d_{\mathtt{L}}^\alpha) (\overline{u_{\mathtt{L}}^{\beta \mathtt{C}}} \gamma^\mu d_{\mathtt{R}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{6}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} \oplus \bar{{\bf{3}}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} $ 

$ n_\nu n_u n_d^2 \,[4n_\nu] $ 

$ - $ (

$ {\cal{O}}^{\mathtt{VL}, \mathtt{SL}}_{\partial a d\nu ud} $ 

$ +[{\cal{O}}^{\mathtt{VL}, \mathtt{SR}}_{\partial a dd\nu u}]^\dagger $ )

$ {\cal{O}}_{\partial a \nu udd}^{\mathtt{SL}, \mathtt{VR}} $ 

$ \partial_\mu a (\overline{\nu_{\mathtt{L}}^{\mathtt{C}}} u_{\mathtt{L}}^\alpha) (\overline{d_{\mathtt{L}}^{\beta \mathtt{C}}} \gamma^\mu d_{\mathtt{R}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{6}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} \oplus \bar{{\bf{3}}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} $ 

$ n_\nu n_u n_d^2 \,[4n_\nu] $ 

$ - [{\cal{O}}^{\mathtt{VL}, \mathtt{SR}}_{\partial a dd\nu u}]^\dagger $ 

Δ(B+L)=0 $ {\cal{O}}_{\partial a \nu ddu}^{\mathtt{VL}, \mathtt{SL}} $ 

$ \partial_\mu a (\overline{\nu_{\mathtt{L}}} \gamma^\mu d_{\mathtt{L}}^\alpha) (\overline{d_{\mathtt{L}}^{\beta \mathtt{C}}} u_{\mathtt{L}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{8}}_{\mathtt{L}} \otimes {\bf{1}}_{\mathtt{R}} $ 

$ n_\nu n_u n_d^2 \,[4n_\nu] $ 

$ {\cal{O}}^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu} $ 

$ {\cal{O}}_{\partial a \nu ddu}^{\mathtt{SR}, \mathtt{VL}} $ 

$ \partial_\mu a (\overline{\nu_{\mathtt{L}}} d_{\mathtt{R}}^\alpha) (\overline{d_{\mathtt{R}}^{\beta \mathtt{C}}} \gamma^\mu u_{\mathtt{L}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{3}}_{\mathtt{L}} \otimes {\bf{6}}_{\mathtt{R}} \oplus {\bf{3}}_{\mathtt{L}} \otimes \bar{{\bf{3}}}_{\mathtt{R}} $ 

$ n_\nu n_u n_d^2 \,[4n_\nu] $ 

$ {\cal{O}}^{\mathtt{VR}, \mathtt{SR}}_{\partial a ud\nu d} $ 

$ {\cal{O}}_{\partial a \nu dud}^{\mathtt{SR}, \mathtt{VL}} $ 

$ \partial_\mu a (\overline{\nu_{\mathtt{L}}} d_{\mathtt{R}}^\alpha) (\overline{u_{\mathtt{R}}^{\beta \mathtt{C}}} \gamma^\mu d_{\mathtt{L}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{3}}_{\mathtt{L}} \otimes {\bf{6}}_{\mathtt{R}} \oplus {\bf{3}}_{\mathtt{L}} \otimes \bar{{\bf{3}}}_{\mathtt{R}} $ 

$ n_\nu n_u n_d^2 \,[4n_\nu] $ 

$ {\cal{O}}^{\mathtt{VR}, \mathtt{SR}}_{\partial a du\nu d} $ 

$ {\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}} $ 

$ \partial_\mu a (\overline{\nu_{\mathtt{L}}} u_{\mathtt{R}}^\alpha) (\overline{d_{\mathtt{R}}^{\beta \mathtt{C}}} \gamma^\mu d_{\mathtt{L}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{3}}_{\mathtt{L}} \otimes {\bf{6}}_{\mathtt{R}} \oplus {\bf{3}}_{\mathtt{L}} \otimes \bar{{\bf{3}}}_{\mathtt{R}} $ 

$ n_\nu n_u n_d^2 \,[4n_\nu] $ 

$ {\cal{O}}^{\mathtt{VR}, \mathtt{SR}}_{\partial a dd\nu u} $ 

$ {\cal{O}}_{\partial a e ddd}^{\mathtt{VR}, \mathtt{SR}} $ 

$ \partial_\mu a (\overline{e_{\mathtt{R}}} \gamma^\mu d_{\mathtt{R}}^\alpha) (\overline{d_{\mathtt{R}}^{\beta \mathtt{C}}} d_{\mathtt{R}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{1}}_{\mathtt{L}} \otimes {\bf{8}}_{\mathtt{R}} $ 

$ {1\over 3} n_e n_d(n_d^2-1) \,[2n_e] $ 

$ {\cal{O}}^{\mathtt{VR}, \mathtt{SR}}_{\partial a eddd} $ 

$ {\cal{O}}_{\partial a e ddd}^{\mathtt{SR}, \mathtt{VL}} $ 

$ \partial_\mu a (\overline{e_{\mathtt{L}}} d_{\mathtt{R}}^\alpha) (\overline{d_{\mathtt{R}}^{\beta \mathtt{C}}} \gamma^\mu d_{\mathtt{L}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{3}}_{\mathtt{L}} \otimes {\bf{6}}_{\mathtt{R}} \oplus {\bf{3}}_{\mathtt{L}} \otimes \bar{{\bf{3}}}_{\mathtt{R}} $ 

$ n_e n_d^3 \,[8n_e] $ 

$ \tilde{ {\cal{O}}}^{\mathtt{VR}, \mathtt{SR}}_{\partial a eddd} $ 

$ {\cal{O}}_{\partial a e ddd}^{\mathtt{VL}, \mathtt{SL}} $ 

$ \partial_\mu a (\overline{e_{\mathtt{L}}} \gamma^\mu d_{\mathtt{L}}^\alpha) (\overline{d_{\mathtt{L}}^{\beta \mathtt{C}}} d_{\mathtt{L}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{8}}_{\mathtt{L}} \otimes {\bf{1}}_{\mathtt{R}} $ 

$ {1\over 3} n_e n_d(n_d^2-1)\,[2n_e] $ 

$ {\cal{O}}^{\mathtt{VL}, \mathtt{SL}}_{\partial a eddd} $ 

$ {\cal{O}}_{\partial a e ddd}^{\mathtt{SL}, \mathtt{VR}} $ 

$ \partial_\mu a (\overline{e_{\mathtt{R}}} d_{\mathtt{L}}^\alpha) (\overline{d_{\mathtt{L}}^{\beta \mathtt{C}}} \gamma^\mu d_{\mathtt{R}}^\gamma) \epsilon_{\alpha\beta\gamma} $ 

$ {\bf{6}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} \oplus \bar{{\bf{3}}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} $ 

$ n_e n_d^3 \,[8n_e] $ 

$ - [{\cal{O}}^{\mathtt{VL}, \mathtt{SR}}_{\partial a ddde}]^\dagger $ 

Table 1. The dim-8 aLEFT BNV operators involving an ALP.
$ \alpha,\beta,\gamma $ are color indices while the flavor indices are omitted for simplicity. The chiral irrep. column lists the irreducible representations under the chiral group$ {\rm{SU}}(3)_{\mathtt{L}}\otimes {\rm{SU}}(3)_{\mathtt{R}} $ for the three light quarks$ u,d,s $ . The # column counts the number of independent operators for general$ n_{e} $ charged leptons,$ n_\nu $ neutrinos, and$ n_u $ up-type and$ n_d $ down-type quarks; the number in the square bracket represents the case with only$ u,d,s $ quarks ($ n_u=1 $ and$ n_d=2 $ ). Totally, there are$ 68 n_{e,\nu} $ operators associated with the$ u,d,s $ quarks, among which only$ 22 n_{e,\nu} $ were considered in [18] and are highlighted in dark gray in the last columnTo match the aLEFT operators onto those in ChPT, one should first decompose them into irreducible representations (irreps) of the QCD chiral group
$ \rm {\rm{SU}}(3)_{\mathtt{L}}\otimes {\rm{SU}}(3)_{\mathtt{R}} $ for the$ u,d,s $ quarks in the massless limit. As can be observed from Table 1, these operators are divided into the following two structures and their chirality partners:$ \partial_\mu a (\overline{\psi_x} \gamma^\mu q_{ \mathtt{L}, y}^\alpha) (\overline{ q_{ \mathtt{L}, z}^{\beta \mathtt{C}} } q_{ \mathtt{L}, w}^\gamma )\epsilon_{\alpha \beta \gamma}, \qquad \partial_\mu a (\overline{\psi_x} q_{ \mathtt{L},y}^\alpha) (\overline{ q_{ \mathtt{L}, z}^{\beta \mathtt{C}} } \gamma^\mu q_{ \mathtt{R}, w}^\gamma ) \epsilon_{\alpha \beta \gamma}, $

(1) where
$ \psi( = e, e^{\mathtt{C}}, \nu, \nu^{\mathtt{C}}) $ stands for a lepton field, with x denoting its flavor, and$ y,z,w = 1,2,3 $ are light quark flavor indices with$ q_{1,2,3} = u, d, s $ . The triple-quark sector in the first structure,$ {\cal{N}}_{yzw}^{ \mathtt{L} \mathtt{L}}\equiv q_{ \mathtt{L}, y}^\alpha (\overline{ q_{ \mathtt{L}, z}^{\beta \mathtt{C}} } q_{ \mathtt{L}, w}^\gamma )\epsilon_{\alpha \beta \gamma} $ , already belongs to the$ {\bf{8}}_{ \mathtt{L}} \otimes {\bf{1}}_{ \mathtt{R}} $ irrep of the chiral group. However, the triple-quark component in the second structure generally does not form an irrep. As recognized in Ref. [42], the flavor symmetric and anti-symmetric combinations of the two like-chirality quark fields form the irreps$ {\bf{6}}_{ \mathtt{L}} \otimes {\bf{3}}_{ \mathtt{R}} $ and$ \bar{{\bf{3}}}_{ \mathtt{L}} \otimes {\bf{3}}_{ \mathtt{R}} $ , respectively. The antisymmetric combination can be Fierz-transformed into a similar form to$ {\cal{N}}_{yzw}^{ \mathtt{L} \mathtt{L}} $ with$ q_{ \mathtt{L},y} $ being replaced by$ q_{ \mathtt{R},y} $ . Following Ref. [42], we parametrize them as follows:$ \begin{aligned}[b]&{\cal{N}}_{yzw}^{ \mathtt{R} \mathtt{L}} \equiv q_{ \mathtt{R},y}^\alpha (\overline{ q_{ \mathtt{L}, z}^{\beta \mathtt{C}} } q_{ \mathtt{L}, w}^\gamma ) \epsilon_{\alpha \beta \gamma} \in \bar{{\bf{3}}}_{ \mathtt{L}} \otimes {\bf{3}}_{ \mathtt{R}}, \\&{\cal{N}}_{yzw}^{ \mathtt{L} \mathtt{R}, \mu} \equiv q_{ \mathtt{L},\{y}^\alpha (\overline{ q_{ \mathtt{L}, z\}}^{\beta \mathtt{C}} } \gamma^\mu q_{ \mathtt{R}, w}^\gamma ) \epsilon_{\alpha \beta \gamma} \in {\bf{6}}_{ \mathtt{L}} \otimes {\bf{3}}_{ \mathtt{R}}. \end{aligned}$

(2) The second structure in Eq. (1) then can be converted into these irreps by using the Fierz identity,
$ (\overline{\psi_x} q_{ \mathtt{L},[y}^\alpha) (\overline{ q_{ \mathtt{L}, z]}^{\beta \mathtt{C}} } \gamma^\mu q_{ \mathtt{R}, w}^\gamma ) \epsilon_{\alpha \beta \gamma} = {1 \over 2}(\overline{\psi_x}\gamma^\mu q_{ \mathtt{R},w}^\alpha) (\overline{ q_{ \mathtt{L}, z}^{\beta \mathtt{C}} } q_{ \mathtt{L}, y}^\gamma ) \epsilon_{\alpha \beta \gamma}, $

(3) leading to
$ (\overline{\psi_x} q_{ \mathtt{L},y}^\alpha) (\overline{ q_{ \mathtt{L}, z}^{\beta \mathtt{C}} } \gamma^\mu q_{ \mathtt{R}, w}^\gamma ) \epsilon_{\alpha \beta \gamma} = \overline{\psi_x} \, {\cal{N}}_{yzw}^{ \mathtt{L} \mathtt{R}, \mu} + \frac{1}{2} \overline{\psi_x}\gamma^\mu {\cal{N}}_{wzy}^{ \mathtt{R} \mathtt{L}}. $

(4) Here, the curly and square brackets denote symmetrization and antisymmetrization over the two flavor indices,
$ A_{\{y}B_{z\}} \equiv (1/2)(A_{y} B_{z} + A_{z}B_{y}) $ and$ A_{[y}B_{z]} \equiv (1/2)(A_{y} B_{z} - A_{z}B_{y}) $ , respectively. Similarly, the chirality-flipped operators with$ \mathtt{L}\leftrightarrow \mathtt{R} $ can be decomposed into$ {\bf{3}}_{ \mathtt{L}} \otimes {\bf{6}}_{ \mathtt{R}} $ and$ {\bf{3}}_{ \mathtt{L}} \otimes \bar{{\bf{3}}}_{ \mathtt{R}} $ . For instance,$ [ {\cal{O}}_{\partial a euud}^{\mathtt{SL}, \mathtt{VR}}]_{x11y} = \partial_\mu a \, \overline{e_{ \mathtt{L},x}^{\mathtt{C}}} {\cal{N}}^{ \mathtt{L} \mathtt{R},\mu}_{11y}, $

(5a) $ [ {\cal{O}}_{\partial a eudu}^{\mathtt{SL}, \mathtt{VR}}]_{x1y1} = \partial_\mu a \, \overline{e_{ \mathtt{L},x}^{\mathtt{C}}} {\cal{N}}^{ \mathtt{L} \mathtt{R},\mu}_{1y1} +\frac{1}{2} \partial_\mu a \, \overline{e_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu {\cal{N}}^{ \mathtt{R} \mathtt{L}}_{1y1}, $

(5b) $ [ {\cal{O}}_{\partial a \nu ddu}^{\mathtt{SL}, \mathtt{VR}}]_{xyz1} = \partial_\mu a \, \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} {\cal{N}}^{ \mathtt{L} \mathtt{R},\mu}_{yz1} +\frac{1}{2} \partial_\mu a \, \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu {\cal{N}}^{ \mathtt{R} \mathtt{L}}_{1zy}, $

(5c) $ [ {\cal{O}}_{\partial a eddd}^{\mathtt{SL}, \mathtt{VR}}]_{xyzw} =\partial_\mu a \, \overline{e_{ \mathtt{R},x}} {\cal{N}}^{ \mathtt{L} \mathtt{R},\mu}_{yzw} +\frac{1}{2} \partial_\mu a \, \overline{e_{ \mathtt{R},x}} \gamma^\mu {\cal{N}}^{ \mathtt{R} \mathtt{L}}_{wzy}. $

(5d) Based on the arguments outlined above, we indicate the chiral irreps of each operator under consideration in the fourth column of Table 1. It should be noted that such a chiral decomposition was neglected in [18], resulting in many operators belonging to
$ {\bf{3}}_{ \mathtt{L}( \mathtt{R})} \otimes \bar{{\bf{3}}}_{ \mathtt{R}( \mathtt{L})} $ being also omitted from their analysis.To carry out the chiral realization of the operators listed in Table 1, it is convenient to use the spurion field approach by treating the combination of the nonquark component of each operator and its corresponding WC as a spurion field
$ \cal{P} $ . Following our previous works in [42, 56], we organize the flavor components of the$ {\bf{8}}_{ \mathtt{L}} \otimes {\bf{1}}_{ \mathtt{R}} $ and$ \bar{{\bf{3}}}_{ \mathtt{L}} \otimes {\bf{3}}_{ \mathtt{R}} $ irreps in the following matrix form:$ \begin{aligned}[b]& {\cal{N}}_{{\bf{8}}_{\mathtt{L}}\otimes {\bf{1}}_{\mathtt{R}}} = \begin{pmatrix} {\cal{N}}^{ \mathtt{L} \mathtt{L}}_{uds} & {\cal{N}}^{ \mathtt{L} \mathtt{L}}_{usu} & {\cal{N}}^{ \mathtt{L} \mathtt{L}}_{uud} \\ {\cal{N}}^{ \mathtt{L} \mathtt{L}}_{dds} & {\cal{N}}^{ \mathtt{L} \mathtt{L}}_{dsu} & {\cal{N}}^{ \mathtt{L} \mathtt{L}}_{dud} \\ {\cal{N}}^{ \mathtt{L} \mathtt{L}}_{sds} & {\cal{N}}^{ \mathtt{L} \mathtt{L}}_{ssu} & {\cal{N}}^{ \mathtt{L} \mathtt{L}}_{sud} \end{pmatrix}, \\& {\cal{N}}_{\bar{{\bf{3}}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} } = \begin{pmatrix} {\cal{N}}_{uds}^{ \mathtt{R} \mathtt{L}} & {\cal{N}}_{usu}^{ \mathtt{R} \mathtt{L}} & {\cal{N}}_{uud}^{ \mathtt{R} \mathtt{L}} \\ {\cal{N}}_{dds}^{ \mathtt{R} \mathtt{L}} & {\cal{N}}_{dsu}^{ \mathtt{R} \mathtt{L}} & {\cal{N}}_{dud}^{ \mathtt{R} \mathtt{L}} \\ {\cal{N}}_{sds}^{ \mathtt{R} \mathtt{L}} & {\cal{N}}_{ssu}^{ \mathtt{R} \mathtt{L}} & {\cal{N}}_{sud}^{ \mathtt{R} \mathtt{L}} \end{pmatrix}, \end{aligned} $

(6) and similar ones for their chirality partners with
$ \mathtt{L}\leftrightarrow \mathtt{R} $ . Accordingly, we denote the corresponding spurion matrices as follows,$ \begin{aligned}[b] {\cal{P}}_{{\bf{8}}_{\mathtt{L}} \otimes {\bf{1}}_{\mathtt{R}}} = \begin{pmatrix} 0 & {\cal{P}}_{dds}^{ \mathtt{L} \mathtt{L}} & {\cal{P}}_{sds}^{ \mathtt{L} \mathtt{L}} \\ {\cal{P}}_{usu}^{ \mathtt{L} \mathtt{L}} & {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{L}} & {\cal{P}}_{ssu}^{ \mathtt{L} \mathtt{L}} \\ {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{L}} & {\cal{P}}_{dud}^{ \mathtt{L} \mathtt{L}} & {\cal{P}}_{sud}^{ \mathtt{L} \mathtt{L}} \end{pmatrix}, \\ {\cal{P}}_{{\bf{3}}_{\mathtt{L}} \otimes \bar{{\bf{3}}}_{\mathtt{R}} } = \begin{pmatrix} {\cal{P}}_{uds}^{ \mathtt{R} \mathtt{L}} & {\cal{P}}_{dds}^{ \mathtt{R} \mathtt{L}} & {\cal{P}}_{sds}^{ \mathtt{R} \mathtt{L}} \\ {\cal{P}}_{usu}^{ \mathtt{R} \mathtt{L}} & {\cal{P}}_{dsu}^{ \mathtt{R} \mathtt{L}} & {\cal{P}}_{ssu}^{ \mathtt{R} \mathtt{L}} \\ {\cal{P}}_{uud}^{ \mathtt{R} \mathtt{L}} & {\cal{P}}_{dud}^{ \mathtt{R} \mathtt{L}} & {\cal{P}}_{sud}^{ \mathtt{R} \mathtt{L}} \end{pmatrix}, \end{aligned} $

(7) and the chirality partners with
$ \mathtt{L} \leftrightarrow \mathtt{R} $ . Note that the condition$ {\rm{Tr}}{\cal{N}}_{{\bf{8}}_{\mathtt{L}}\otimes {\bf{1}}_{\mathtt{R}}}=0 $ has been used to attribute the$ (1,1) $ entry of$ {\cal{P}}_{{\bf{8}}_{\mathtt{L}}\otimes {\bf{1}}_{\mathtt{R}}} $ to its$ (2,2) $ and$ (3,3) $ entries by treating$ {\cal{N}}^{ \mathtt{L} \mathtt{L}}_{uds} $ as redundant [47]. The accompanying spurion fields of the$ {\bf{6}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ irreps$ {\cal{N}}_{yzw}^{ \mathtt{L} \mathtt{R}( \mathtt{R} \mathtt{L}), \mu} $ are denoted by$ {\cal{P}}_{yzw}^{ \mathtt{L} \mathtt{R}( \mathtt{R} \mathtt{L}),\mu} $ . With the above conventions, all aLEFT interactions in Table 1 can be compactly written as$ \begin{aligned}[b] {\cal{L}}^{\not{B}} =\; & {\rm{Tr}} \big[ {\cal{P}}_{{\bf{8}}_{\mathtt{L}} \otimes {\bf{1}}_{\mathtt{R}} } {\cal{N}}_{{\bf{8}}_{\mathtt{L}} \otimes {\bf{1}}_{\mathtt{R}} } + {\cal{P}}_{ {\bf{1}}_{\mathtt{L}} \otimes {\bf{8}}_{\mathtt{R}} } {\cal{N}}_{ {\bf{1}}_{\mathtt{L}} \otimes {\bf{8}}_{\mathtt{R}} } \big]\\& + {\rm{Tr}} \big[ {\cal{P}}_{{\bf{3}}_{\mathtt{L}} \otimes \bar{{\bf{3}}}_{\mathtt{R}} } {\cal{N}}_{\bar{{\bf{3}}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} } + {\cal{P}}_{\bar{{\bf{3}}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}} } {\cal{N}}_{{\bf{3}}_{\mathtt{L}} \otimes \bar{{\bf{3}}}_{\mathtt{R}} } \big] \\ & + \big[ {\cal{P}}_{yzw}^{ \mathtt{L} \mathtt{R},\mu} {\cal{N}}_{yzw,\mu}^{ \mathtt{L} \mathtt{R}} + {\cal{P}}_{yzw}^{ \mathtt{R} \mathtt{L},\mu} {\cal{N}}_{yzw,\mu}^{ \mathtt{R} \mathtt{L}} \big] + {\rm{H}}.{\rm{c}}., \end{aligned} $

(8) where 'Tr' denotes the trace over the flavor space as indicated in the matrix notation and the repeated indices
$ y,z,w $ are summed over the three flavors$ u,d,s $ .After decomposing all operators in Table 1 into irreps (
$ {\cal{N}}_{yzw}^{ \mathtt{L} \mathtt{L} ( \mathtt{R} \mathtt{R})} $ ,$ {\cal{N}}_{yzw}^{ \mathtt{R} \mathtt{L}( \mathtt{L} \mathtt{R})} $ , and$ {\cal{N}}_{yzw}^{ \mathtt{L} \mathtt{R}( \mathtt{R} \mathtt{L}), \mu} $ ) of the chiral group, one can immediately identify the corresponding spurion fields$ \cal{P} $ through the above conventions. Note that Eq. (11) sums both y and z over all three quark flavors, and to avoid double counting, a factor of 1/2 is included by hand for the resulting spurion fields$ {\cal{P}}_{yzw}^{ \mathtt{L} \mathtt{R}( \mathtt{R} \mathtt{L}), \mu}={\cal{P}}_{zyw}^{ \mathtt{L} \mathtt{R}( \mathtt{R} \mathtt{L}), \mu} $ when$ y\neq z $ . For example, for operators in Eq. (7) with$ yz=32 $ and$ yz=23 $ , we have$ \begin{aligned}[b]&\sum\limits_{yz=23,32}[C_{\partial a \nu ddu}^{\mathtt{SL}, \mathtt{VR}}]_{xyz1} [ {\cal{O}}_{\partial a \nu ddu}^{\mathtt{SL}, \mathtt{VR}} ]_{xyz1} \\=\;& {\cal{P}}_{uds}^{ \mathtt{R} \mathtt{L}} {\cal{N}}_{uds}^{ \mathtt{R} \mathtt{L}} + {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{R},\mu} {\cal{N}}_{dsu,\mu}^{ \mathtt{L} \mathtt{R}} + {\cal{P}}_{sdu}^{ \mathtt{L} \mathtt{R},\mu} {\cal{N}}_{sdu,\mu}^{ \mathtt{L} \mathtt{R}},\end{aligned} $

(9) leading to the spurion fields,
$ {\cal{P}}_{uds}^{ \mathtt{R} \mathtt{L}} = (1/2)( [C_{\partial a \nu ddu}^{\mathtt{SL}, \mathtt{VR}}]_{x321} - [C_{\partial a \nu ddu}^{\mathtt{SL}, \mathtt{VR}}]_{x231} ) \partial_\mu a \, \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ ,$ {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{R},\mu} ={\cal{P}}_{sdu}^{ \mathtt{L} \mathtt{R},\mu} = (1/2) ( [C_{\partial a \nu ddu}^{\mathtt{SL}, \mathtt{VR}}]_{x321} + [C_{\partial a \nu ddu}^{\mathtt{SL}, \mathtt{VR}}]_{x231}) \partial^\mu a \, \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} $ . The full expressions of the resulting spurion fields for all aLEFT operators are summarized in Table 2. Note that the absence of$ {\cal{P}}^{ \mathtt{L} \mathtt{R}( \mathtt{R} \mathtt{L}),\mu}_{uuu} $ is a consequence of electric charge conservation. It is interesting to notice that more than half of aLEFT operators contain$ {\bf{6}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ components, thereby generating non-zero$ {\cal{P}}_{yzw}^{ \mathtt{L} \mathtt{R}( \mathtt{R} \mathtt{L}), \mu} $ terms. In particular, the operators$ [{\cal{O}}_{\partial a e uud}^{\mathtt{SL}, \mathtt{VR}}]_{x11y} $ ,$ [{\cal{O}}_{\partial a\nu ddu}^{\mathtt{SL}, \mathtt{VR}}]_{xyy1} $ ,$ [{\cal{O}}_{\partial a e ddd}^{\mathtt{SL}, \mathtt{VR}}]_{xyyz} $ , and their chirality partners that contain two identical chiral quark fields belong to$ {\bf{6}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ , and therefore contribute exclusively to$ {\cal{P}}_{yzw}^{ \mathtt{L} \mathtt{R}( \mathtt{R} \mathtt{L}), \mu} $ . In the following, we will incorporate these spurion fields into the recently developed chiral framework [42] to explore their phenomenological implications, with a particular emphasis on the interactions associated with$ {\bf{6}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ irreps that were overlooked thus far [18].Irrep. Spurion Expression Spurion Expression $ {\bf{8}}_{ \mathtt{L}( \mathtt{R})}\otimes {\bf{1}}_{ \mathtt{R}( \mathtt{L})} $ 

$ {\cal{P}}_{dds}^{ \mathtt{L} \mathtt{L}} $ 

$ [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a eddd}]_{x223} (\partial_\mu a) \overline{e_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\cal{P}}_{dds}^{ \mathtt{R} \mathtt{R}} $ 

$ [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a eddd}]_{x223} (\partial_\mu a) \overline{e_{ \mathtt{R},x}} \gamma^\mu $ 

$ {\cal{P}}_{sds}^{ \mathtt{L} \mathtt{L}} $ 

$ [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a eddd}]_{x323} (\partial_\mu a) \overline{e_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\cal{P}}_{sds}^{ \mathtt{R} \mathtt{R}} $ 

$ [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a eddd}]_{x323} (\partial_\mu a) \overline{e_{ \mathtt{R},x}} \gamma^\mu $ 

$ {\cal{P}}_{usu}^{ \mathtt{L} \mathtt{L}} $ 

$ - [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a euud}]_{x113} (\partial_\mu a) \overline{e_{ \mathtt{R},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{usu}^{ \mathtt{R} \mathtt{R}} $ 

$ - [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a euud}]_{x113} (\partial_\mu a) \overline{e_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{L}} $ 

$ [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x231} (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\cal{P}}_{dsu}^{ \mathtt{R} \mathtt{R}} $ 

$ [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a \nu ddu}]_{x231} (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{ssu}^{ \mathtt{L} \mathtt{L}} $ 

$ [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x331} (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\cal{P}}_{ssu}^{ \mathtt{R} \mathtt{R}} $ 

$ [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a \nu ddu}]_{x331} (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{L}} $ 

$ [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a euud}]_{x112} (\partial_\mu a) \overline{e_{ \mathtt{R},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{uud}^{ \mathtt{R} \mathtt{R}} $ 

$ [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a euud}]_{x112} (\partial_\mu a) \overline{e_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{dud}^{ \mathtt{L} \mathtt{L}} $ 

$ - [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x221} (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\cal{P}}_{dud}^{ \mathtt{R} \mathtt{R}} $ 

$ - [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a \nu ddu}]_{x221} (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{sud}^{ \mathtt{L} \mathtt{L}} $ 

$ - [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x321} (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\cal{P}}_{sud}^{ \mathtt{R} \mathtt{R}} $ 

$ - [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a \nu ddu}]_{x321} (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\bf{3}}_{ \mathtt{L}( \mathtt{R})}\otimes \bar{{\bf{3}}}_{ \mathtt{R}( \mathtt{L})} $ 

$ {\cal{P}}_{uds}^{ \mathtt{R} \mathtt{L}} $ 

$ -[C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu ddu}]_{x231}^- (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{uds}^{ \mathtt{L} \mathtt{R}} $ 

$ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu ddu}]_{x231}^- (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\cal{P}}_{dds}^{ \mathtt{R} \mathtt{L}} $ 

$ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eddd}]_{x232}^- (\partial_\mu a) \overline{e_{ \mathtt{R},x}} \gamma^\mu $ 

$ {\cal{P}}_{dds}^{ \mathtt{L} \mathtt{R}} $ 

$ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a e ddd}]_{x232}^- (\partial_\mu a) \overline{e_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\cal{P}}_{sds}^{ \mathtt{R} \mathtt{L}} $ 

$ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eddd}]_{x233}^- (\partial_\mu a) \overline{e_{ \mathtt{R},x}} \gamma^\mu $ 

$ {\cal{P}}_{sds}^{ \mathtt{L} \mathtt{R}} $ 

$ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a e ddd}]_{x233}^- (\partial_\mu a) \overline{e_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\cal{P}}_{usu}^{ \mathtt{R} \mathtt{L}} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x131}^- (\partial_\mu a) \overline{e_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{usu}^{ \mathtt{L} \mathtt{R}} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x131}^- (\partial_\mu a) \overline{e_{ \mathtt{R},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{dsu}^{ \mathtt{R} \mathtt{L}} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x132}^- (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{R}} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x132}^- (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\cal{P}}_{ssu}^{ \mathtt{R} \mathtt{L}} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x133}^- (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{ssu}^{ \mathtt{L} \mathtt{R}} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x133}^- (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\cal{P}}_{uud}^{ \mathtt{R} \mathtt{L}} $ 

$ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x121}^- (\partial_\mu a) \overline{e_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{R}} $ 

$ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x121}^- (\partial_\mu a) \overline{e_{ \mathtt{R},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{dud}^{ \mathtt{R} \mathtt{L}} $ 

$ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x122}^- (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{dud}^{ \mathtt{L} \mathtt{R}} $ 

$ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu udd}]_{x122}^- (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\cal{P}}_{sud}^{ \mathtt{R} \mathtt{L}} $ 

$ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x123}^- (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} \gamma^\mu $ 

$ {\cal{P}}_{sud}^{ \mathtt{L} \mathtt{R}} $ 

$ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu udd}]_{x123}^- (\partial_\mu a) \overline{\nu_{ \mathtt{L},x}} \gamma^\mu $ 

$ {\bf{6}}_{ \mathtt{L}( \mathtt{R})}\otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ 

$ {\cal{P}}_{uuu}^{ \mathtt{L} \mathtt{R},\mu} $ 

— $ {\cal{P}}_{uuu}^{ \mathtt{R} \mathtt{L},\mu} $ 

— $ {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a euud}]_{x112} (\partial^\mu a) \overline{e_{ \mathtt{L},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{uud}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a euud}]_{x112} (\partial^\mu a) \overline{e_{ \mathtt{R},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{uus}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a euud}]_{x113} (\partial^\mu a) \overline{e_{ \mathtt{L},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{uus}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a euud}]_{x113} (\partial^\mu a) \overline{e_{ \mathtt{R},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{udu}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x121}^+ (\partial^\mu a) \overline{e_{ \mathtt{L},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{udu}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x121}^+ (\partial^\mu a) \overline{e_{ \mathtt{R},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{udd}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x122}^+ (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{udd}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x122}^+ (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}} $ 

$ {\cal{P}}_{uds}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x123}^+ (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{uds}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x123}^+ (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}} $ 

$ {\cal{P}}_{usu}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x131}^+ (\partial^\mu a) \overline{e_{ \mathtt{L},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{usu}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x131}^+ (\partial^\mu a) \overline{e_{ \mathtt{R},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{usd}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x132}^+ (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{usd}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x132}^+ (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}} $ 

$ {\cal{P}}_{uss}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x133}^+ (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{uss}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x133}^+ (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}} $ 

$ {\cal{P}}_{ddu}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu ddu}]_{x221} (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{ddu}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu ddu}]_{x221} (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}} $ 

$ {\cal{P}}_{ddd}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eddd}]_{x222} (\partial^\mu a) \overline{e_{ \mathtt{R},x}} $ 

$ {\cal{P}}_{ddd}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a e ddd}]_{x222} (\partial^\mu a) \overline{e_{ \mathtt{L},x}} $ 

$ {\cal{P}}_{dds}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eddd}]_{x223} (\partial^\mu a) \overline{e_{ \mathtt{R},x}} $ 

$ {\cal{P}}_{dds}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a e ddd}]_{x223} (\partial^\mu a) \overline{e_{ \mathtt{L},x}} $ 

$ {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu ddu}]_{x231}^+ (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{dsu}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu ddu}]_{x231}^+ (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}} $ 

$ {\cal{P}}_{dsd}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eddd}]_{x232}^+ (\partial^\mu a) \overline{e_{ \mathtt{R},x}} $ 

$ {\cal{P}}_{dsd}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a e ddd}]_{x232}^+ (\partial^\mu a) \overline{e_{ \mathtt{L},x}} $ 

$ {\cal{P}}_{dss}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eddd}]_{x233}^+ (\partial^\mu a) \overline{e_{ \mathtt{R},x}} $ 

$ {\cal{P}}_{dss}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a e ddd}]_{x233}^+ (\partial^\mu a) \overline{e_{ \mathtt{L},x}} $ 

$ {\cal{P}}_{ssu}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu ddu}]_{x331} (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}^{\mathtt{C}}} $ 

$ {\cal{P}}_{ssu}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu ddu}]_{x331} (\partial^\mu a) \overline{\nu_{ \mathtt{L},x}} $ 

$ {\cal{P}}_{ssd}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eddd}]_{x332} (\partial^\mu a) \overline{e_{ \mathtt{R},x}} $ 

$ {\cal{P}}_{ssd}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a e ddd}]_{x332} (\partial^\mu a) \overline{e_{ \mathtt{L},x}} $ 

$ {\cal{P}}_{sss}^{ \mathtt{L} \mathtt{R},\mu} $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eddd}]_{x333} (\partial^\mu a) \overline{e_{ \mathtt{R},x}} $ 

$ {\cal{P}}_{sss}^{ \mathtt{R} \mathtt{L},\mu} $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a e ddd}]_{x333} (\partial^\mu a) \overline{e_{ \mathtt{L},x}} $ 

Table 2. Expressions of the spurion fields from the dim-8 aLEFT interactions. The white and gray cells correspond to the
$ \Delta(B-L)=0 $ and$ \Delta(B+L)=0 $ interactions, respectively. The subscripts 1, 2, 3 stand for u, d, and s, x serves as a lepton flavor index. For the WCs related to representations$ {\bf{3}}_{ \mathtt{L}( \mathtt{R})}\otimes \bar{{\bf{3}}}_{ \mathtt{R}( \mathtt{L})} $ and$ {\bf{6}}_{ \mathtt{L}( \mathtt{R})}\otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ , the following abbreviations are used:$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a e ddq}]_{xyzw}^\pm \equiv (1/2)([C^{\mathtt{SL}, \mathtt{VR}}_{\partial a e ddq}]_{xyzw} \pm [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a e ddq}]_{xzyw} ) $ and$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a e udq}]_{x1zw}^\pm \equiv (1/2)([C^{\mathtt{SL}, \mathtt{VR}}_{\partial a e udq}]_{x1zw)} \pm [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a e duq}]_{xz1w}) $ , where$ q=d,u $ . Similar abbreviations are used for those of parity partner operators with superscript '$\mathtt{SR}, \mathtt{VL}$ ' and in the neutrino case. -
All aLEFT operators under consideration contain three light quarks without being acted upon by a derivative. For this class of operators, their chiral matching has been systematically investigated in [42] for the pure pseudoscalar meson case and in [47] for those also involving a vector meson. In this work, we focus on the pseudoscalar meson sector and utilize the chiral results in [42] for the subsequent analysis. We define the octet pseudoscalar field by
$ \Sigma(x) = \xi^2(x) = \exp[i\sqrt{2}\Pi(x)/F_0] $ and baryon field by$ B(x) $ , with$ \begin{aligned}[b]& \Pi(x) = \begin{pmatrix} \dfrac{\pi^0}{\sqrt{2}}+\dfrac{\eta}{\sqrt{6}} & \pi^+ & K^+ \\ \pi^- & -\dfrac{\pi^0}{\sqrt{2}}+\dfrac{\eta}{\sqrt{6}} & K^0 \\ K^- & \bar{K}^0 & -\sqrt{\dfrac{2}{3}}\eta \end{pmatrix}, \\& B(x) = \begin{pmatrix} {\dfrac{\Sigma^{0}}{\sqrt{2}}}+{\dfrac{\Lambda^0 }{\sqrt{6}}} & \Sigma^+ & p \\ \Sigma^- & -{\dfrac{\Sigma^{0}}{ \sqrt{2}}}+{\dfrac{\Lambda^0} {\sqrt{6}}} & n \\ \Xi^- & \Xi^0 & - \sqrt{\dfrac{2}{3}}\Lambda^0 \end{pmatrix}, \end{aligned} $

(10) where
$ F_0=f_{\pi}/\sqrt{2} $ is the pion decay constant in the chiral limit with$ f_{\pi}=130.41(20)\; \rm MeV $ [57].For the three spurion fields associated with the chiral irreps
$ \bar{{\bf{3}}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ ,$ {\bf{8}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{1}}_{ \mathtt{R}( \mathtt{L})} $ , and$ {\bf{6}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ , the leading-order chiral Lagrangian involving the octet baryon and pseudoscalar meson takes the form [42]:$ \begin{aligned}[b] {\cal{L}}_{B}^{\not{B}} =\;& c_1 {\rm{Tr}}\big[ {\cal{P}}_{ \bar{{\bf{3}}}_{\mathtt{L}} \otimes {\bf{3}}_{\mathtt{R}}} \xi B_{\mathtt{L}} \xi - {\cal{P}}_{{\bf{3}}_{\mathtt{L}} \otimes \bar{{\bf{3}}}_{\mathtt{R}}} \xi^\dagger B_{\mathtt{R}} \xi^\dagger \big] \\&+ c_2 {\rm{Tr}}\big[ {\cal{P}}_{{\bf{8}}_{\mathtt{L}} \otimes {\bf{1}}_{\mathtt{R}}}\xi B_{\mathtt{L}} \xi^\dagger - {\cal{P}}_{ {\bf{1}}_{\mathtt{L}} \otimes {\bf{8}}_{\mathtt{R}}} \xi^\dagger B_{\mathtt{R}} \xi \big] \\ & + {c_3 \over \Lambda_\chi} \big[ {\cal{P}}_{yzi}^{ \mathtt{L} \mathtt{R},\mu} {\Gamma}_{\mu\nu}^\mathtt{L} (\xi i D^\nu B_{\mathtt{L}} \xi)_{yj} \Sigma_{zk} \epsilon_{ijk} \\&- {\cal{P}}_{yzi}^{ \mathtt{R} \mathtt{L},\mu} {\Gamma}_{\mu\nu}^\mathtt{R} (\xi^\dagger i D^\nu B_{\mathtt{R}} \xi^\dagger)_{yj} \Sigma^*_{kz} \epsilon_{ijk} \big] + {\rm{H}}.{\rm{c}}.. \end{aligned} $

(11) where all indices
$ y,z $ and$ i,j,k $ are summed over the three flavors$ u,d,s $ , and$ B_{ \mathtt{L}( \mathtt{R})}\equiv P_{ \mathtt{L}( \mathtt{R})}B $ represent the chiral baryon fields.$ \Gamma_{\mu\nu}^{ \mathtt{L}, \mathtt{R}}\equiv (g_{\mu\nu}-\gamma_\mu\gamma_\nu/4)P_{ \mathtt{L}, \mathtt{R}} $ are the vector-spinor projectors with$ P_{ \mathtt{L}, \mathtt{R}}\equiv (1\mp\gamma_5)/2 $ .3 The low energy constants (LECs)$ c_{1,2} $ are the α and β parameters used in the literature, with recent lattice QCD calculations yielding$ c_1 = \alpha = -0.01257(111)\,{\rm{GeV}}^3 $ and$ c_2 = \beta = 0.01269(107)\,{\rm{GeV}}^3 $ [58], respectively. However, there is no available LQCD computation for$ c_3 $ , so we use the naive dimension analysis estimation$ c_3 \sim 0.011\,{\rm{GeV}}^3 $ [42] for the numerical analysis.By expanding the Lagrangian in Eq. (14) to the proper order in the pseudoscalar meson fields, we obtain interaction vertices involving spurion fields, the octet baryon and meson fields. For our purpose, the relevant vertices include the
$ {\cal{P}}-B $ terms without mesons and the$ {\cal{P}}-{\mathtt{N}}-M $ terms containing one pseudoscalar meson field, which are summarized in Appendix A for reference. By substituting the spurion fields$ \cal{P} $ in these terms with the corresponding results from Table 2, we obtain the desired BNV vertices containing a single ALP field, which are displayed in Tables 3 and 4.$ B\to l+a $ 

$ C^{1 \mathtt{L}}_{B \to l} $ (upper cell) and

$ C^{1 \mathtt{R}}_{B \to l} $ (lower cell)

$ C^{3 \mathtt{L}}_{B \to l} $ (upper cell) and

$ C^{3 \mathtt{R}}_{B \to l} $ (lower cell)

$ p \to \ell_x^+ $ 

$ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x121}^- + \kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a euud}]_{x112} $ 

$ - \kappa_3 \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x121}^+ -[C^{\mathtt{SL}, \mathtt{VR}}_{\partial a euud}]_{x112} \big) $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial aeudu}]_{x121}^- - \kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a euud}]_{x112} $ 

$ \kappa_3 \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial aeudu}]_{x121}^+ -[C^{\mathtt{SR}, \mathtt{VL}}_{\partial aeuud}]_{x112} \big) $ 

$ \Sigma^+ \to \ell_x^+ $ 

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x131}^- - \kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a euud}]_{x113} $ 

$ \kappa_3 \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x131}^+ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a euud}]_{x113} \big) $ 

$ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial aeudu}]_{x131}^- + \kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a euud}]_{x113} $ 

$ - \kappa_3 \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x131}^+ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a euud}]_{x113}\big) $ 

$ n\to \bar{\nu}_x$ 

($n\to \nu_x$ )

$ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu udd}]_{x122}^- -\kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x221} $ 

$ \kappa_3\big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a\nu udd}]_{x122}^+ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a\nu ddu}]_{x221} \big) $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a\nu udd}]_{x122}^- + \kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a\nu ddu}]_{x221} $ 

$ -\kappa_3 \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu udd}]_{x122}^+ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu ddu}]_{x221} \big) $ 

$ \Lambda^0 \to \bar{\nu}_x$ 

($\Lambda^0\to \nu_x$ )

$ {1 \over \sqrt{6}} \big( 2[C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x123}^- + [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x132}^- - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu ddu}]_{x231}^- \big) $ 

$ - \sqrt{3 \over 2} \kappa_3 \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x132}^+ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu ddu}]_{x231}^+ \big) $ 

$ +{\kappa_2\over\sqrt{6}} \big( [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x231} +2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x321} \big) $ 

$ - {1\over \sqrt{6}} \big( 2[C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x123}^- + [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x132}^- -[C^{\mathtt{SL}, \mathtt{VR}}_{\partial a\nu ddu}]_{x231}^- \big) $ 

$ \sqrt{3\over 2} \kappa_3 \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x132}^+ -[C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu ddu}]_{x231}^+ \big) $ 

$ - {\kappa_2 \over \sqrt{6}} \big( [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a \nu ddu}]_{x231} +2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a \nu ddu}]_{x321}\big) $ 

$ \Sigma^0 \to \bar{\nu}_x$ 

($\Sigma^0\to \nu_x$ )

$ - {1 \over \sqrt{2}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu udd}]_{x132}^- + [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu ddu}]_{x231}^- \big) - {\kappa_2 \over \sqrt{2}} [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x231} $ 

$ {\kappa_3 \over \sqrt{2}} \big( 2 [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x123}^+ -[C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x132}^+ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu ddu}]_{x231}^+ \big) $ 

$ {1\over \sqrt{2}}\big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x132}^- +[C^{\mathtt{SL}, \mathtt{VR}}_{\partial a\nu ddu}]_{x231}^- \big) + {\kappa_2\over \sqrt{2}} [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a\nu ddu}]_{x231} $ 

$ - {\kappa_3\over \sqrt{2}} \big( 2 [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu udd}]_{x123}^+ -[C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu udd}]_{x132}^+ -[C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu ddu}]_{x231}^+ \big) $ 

$ \Xi^0 \to \bar{\nu}_x$ 

($\Xi^0 \to \nu_x$ )

$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu udd}]_{x133}^- + \kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a\nu ddu}]_{x331} $ 

$ - \kappa_3 \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a\nu udd}]_{x133}^+ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a\nu ddu}]_{x331} \big) $ 

$ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a\nu udd}]_{x133}^- - \kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a\nu ddu}]_{x331} $ 

$ \kappa_3\big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu udd}]_{x133}^+ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a\nu ddu}]_{x331} \big) $ 

$ \Sigma^- \to \ell_x^- $ 

$ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial aeddd}]_{x232}^- + \kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial aeddd}]_{x223} $ 

$ - \kappa_3 \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial aeddd}]_{x232}^+ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial aeddd}]_{x223} \big) $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial aeddd}]_{x232}^- - \kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial aeddd}]_{x223} $ 

$ \kappa_3 \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial aeddd}]_{x232}^+ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial aeddd}]_{x223} \big) $ 

$ \Xi^- \to \ell_x^- $ 

$ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial aeddd}]_{x233}^- + \kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial aeddd}]_{x323} $ 

$ \kappa_3 \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial aeddd}]_{x233}^+ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial aeddd}]_{x332} \big) $ 

$ [C^{\mathtt{SL}, \mathtt{VR}}_{\partial aeddd}]_{x233}^- - \kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial aeddd}]_{x323} $ 

$ - \kappa_3 \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial aeddd}]_{x233}^+ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial aeddd}]_{x332} \big) $ 

Table 3. The specific expressions of the coefficients
$ C_{B\to l}^{1(3) \mathtt{L}/ \mathtt{R}} $ for each transition mode.$ \mathtt{N}\to lM+a $ 

$ C^{1 \mathtt{L}}_{\mathtt{N} \to lM} $ (upper cell) and

$ C^{1 \mathtt{R}}_{\mathtt{N} \to lM} $ (lower cell)

$ C^{3 \mathtt{L}}_{\mathtt{N} \to lM} $ (upper cell) and

$ C^{3 \mathtt{R}}_{\mathtt{N} \to lM} $ (lower cell)

$ p \to \ell_x^+ \pi^0 $ 

$ - {1\over 2} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x121}^- -\kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a euud}]_{x112} \big) $ 

$ {\kappa_3 \over 2} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x121}^+ + 3 [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a euud}]_{x112} \big) $ 

$ - {1 \over 2} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x121}^- - \kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a euud}]_{x112} \big) $ 

$ {\kappa_3 \over 2} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x121}^+ + 3 [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a euud}]_{x112} \big) $ 

$ p \to \ell_x^+ \eta $ 

$ {1\over 2\sqrt{3}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x121}^- + 3\kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a euud}]_{x112} \big) $ 

$ - {\kappa_3 \over 2\sqrt{3}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x121}^+ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a euud}]_{x112} \big) $ 

$ { 1\over 2\sqrt{3}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x121}^- + 3\kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a euud}]_{x112} \big) $ 

$ - {\kappa_3 \over 2\sqrt{3}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x121}^+ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a euud}]_{x112} \big) $ 

$ p \to \ell_x^+ K^0 $ 

$ {1\over \sqrt{2}}\big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x131} ^- + \kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a euud}]_{x113} \big) $ 

$ - {\kappa_3 \over \sqrt{2}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x131}^+ + [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a euud}]_{x113} \big) $ 

$ {1\over \sqrt{2}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x131}^- +\kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a euud}]_{x113} \big) $ 

$ - {\kappa_3 \over \sqrt{2}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x131}^+ + [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a euud}]_{x113} \big) $ 

$ n \to \ell_x^+ \pi^- $ 

$ - { 1\over \sqrt{2}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x121}^- -\kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a euud}]_{x112} \big) $ 

$ - {\kappa_3 \over \sqrt{2}} \big( 3 [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x121}^+ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a euud}]_{x112} \big) $ 

$ - {1 \over \sqrt{2}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eudu}]_{x121}^- - \kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a euud}]_{x112}\big) $ 

$ - {\kappa_3 \over \sqrt{2}} \big( 3 [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x121}^+ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a euud}]_{x112} \big) $ 

$ p \to \bar{\nu}_x \pi^+$ 

($p \to \nu_x \pi^+$ )

$ - {1\over \sqrt{2}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x122}^- + \kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x221}\big) $ 

$ {\kappa_3 \over \sqrt{2}} \big( 3 [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x122}^+ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu ddu}]_{x221}\big) $ 

$ - {1 \over \sqrt{2}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x122}^- + \kappa_2[C^{\mathtt{VR}, \mathtt{SR}}_{\partial a \nu ddu}]_{x221}\big) $ 

$ {\kappa_3 \over \sqrt{2}} \big( 3 [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x122}^+ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu ddu}]_{x221}\big) $ 

$ p \to \bar{\nu}_x K^+$ 

($p \to \nu_x K^+$ )

$ - {1\over \sqrt{2}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x123}^- +[C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu ddu}]_{x231}^- + \kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x321} \big) $ 

$ {\kappa_3 \over \sqrt{2}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x123}^+ + 2[C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x132}^+ -[C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu ddu}]_{x231}^+ \big) $ 

$ - {1\over \sqrt{2}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x123}^- +[C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu ddu}]_{x231}^- +\kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a \nu ddu}]_{x321} \big) $ 

$ {\kappa_3 \over \sqrt{2}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x123}^+ + 2[C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x132}^+ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu ddu}]_{x231}^+ \big) $ 

$ n \to \bar{\nu}_x \pi^0$ 

($n \to \nu_x \pi^0$ )

$ {1\over 2} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x122}^- +\kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x221} \big) $ 

$ {\kappa_3 \over 2} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x122}^+ + 3 [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu ddu}]_{x221} \big) $ 

$ {1\over 2} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x122}^- + \kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a \nu ddu}]_{x221}\big) $ 

$ {\kappa_3 \over 2} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x122}^+ + 3 [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu ddu}]_{x221}\big) $ 

$ n \to \bar{\nu}_x \eta$ 

($n \to \nu_x \eta$ )

$ {1 \over 2\sqrt{3}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x122}^- - 3 \kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x221} \big) $ 

$ {\kappa_3 \over 2\sqrt{3}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x122}^+ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu ddu}]_{x221} \big) $ 

$ {1\over 2\sqrt{3}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x122}^- -3 \kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a \nu ddu}]_{x221} \big) $ 

$ {\kappa_3\over 2\sqrt{3}}\big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x122}^+ -[C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu ddu}]_{x221} \big) $ 

$ n \to \bar{\nu}_x K^0$ 

($n \to \nu_x K^0$ )

$ - {1\over \sqrt{2}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x123}^- - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x132}^- \big) $ 

$ - {\kappa_3 \over \sqrt{2}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x123}^+ - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x132}^+ + 2 [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu ddu}]_{x231}^+ \big) $ 

$ -{\kappa_2 \over \sqrt{2}} \big( [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x231} + [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x321} \big) $ 

$ - {1 \over \sqrt{2}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x123}^- - [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a \nu udd}]_{x132}^-\big) $ 

$ - {\kappa_3 \over \sqrt{2}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x123}^+ - [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]_{x132}^+ + 2 [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu ddu}]_{x231}^+\big) $ 

$ -{\kappa_2 \over \sqrt{2}} \big( [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a \nu ddu}]_{x231} + [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a \nu ddu}]_{x321} \big) $ 

$ n \to \ell_x^- \pi^+ $ 

— $ \sqrt{2} \kappa_3 [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eddd}]_{x222} $ 

— $ \sqrt{2} \kappa_3 [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eddd}]_{x222} $ 

$ n \to \ell_x^- K^+ $ 

$ - {1\over \sqrt{2}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eddd}]_{x232}^- + \kappa_2 [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a eddd}]_{x223}\big) $ 

$ {\kappa_3 \over \sqrt{2}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eddd}]_{x232}^+ + [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eddd}]_{x223} \big) $ 

$ - {1 \over \sqrt{2}} \big( [C^{\mathtt{SL}, \mathtt{VR}}_{\partial a eddd}]_{x232}^- + \kappa_2 [C^{\mathtt{VR}, \mathtt{SR}}_{\partial a eddd}]_{x223} \big) $ 

$ {\kappa_3 \over \sqrt{2}} \big( [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eddd}]_{x232}^+ + [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eddd}]_{x223} \big) $ 

Table 4. The specific expressions of the coefficients
$ C_{\mathtt{N} \to lM}^{1(3) \mathtt{L}/ \mathtt{R}} $ for each transition mode. -
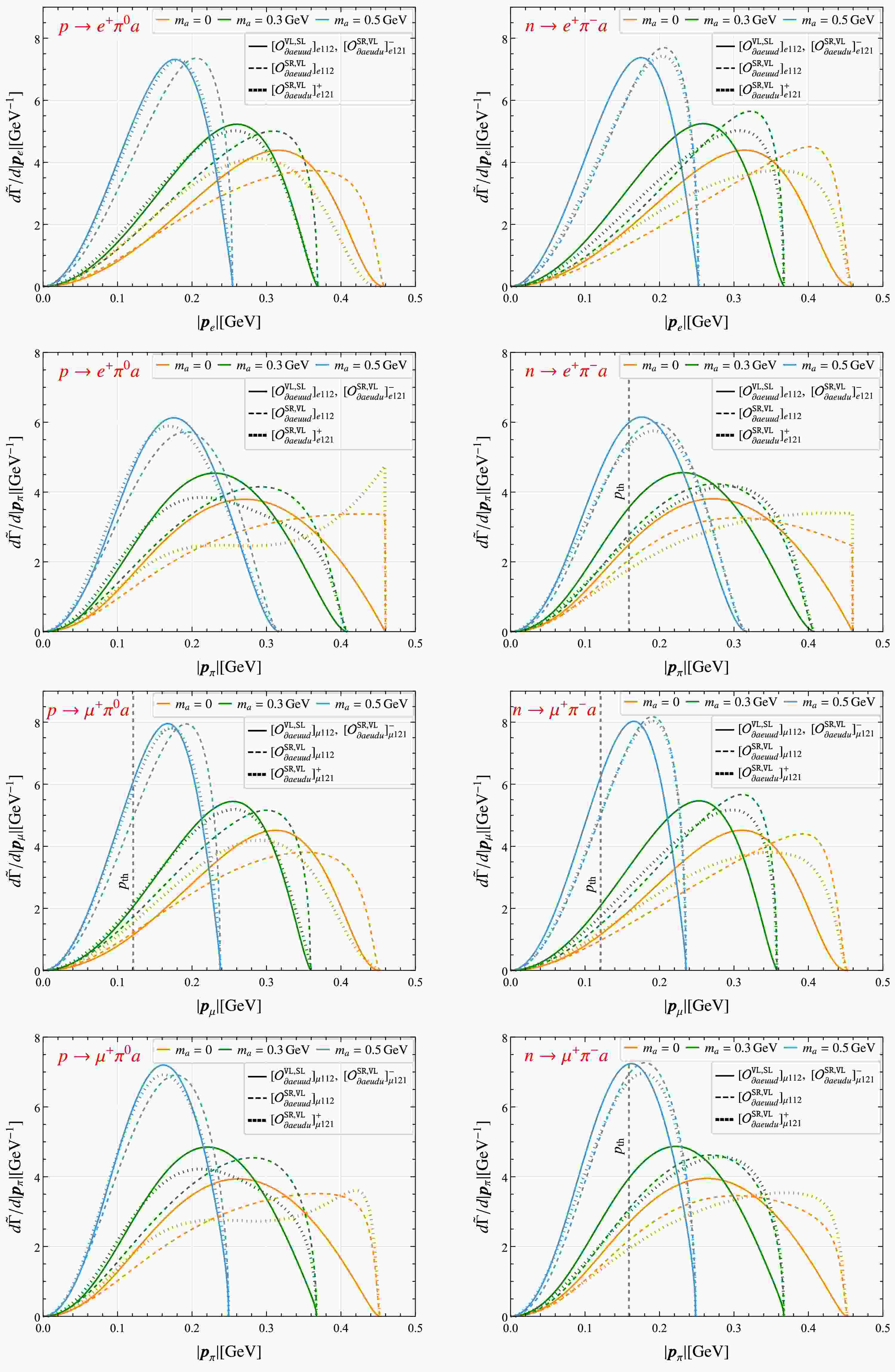
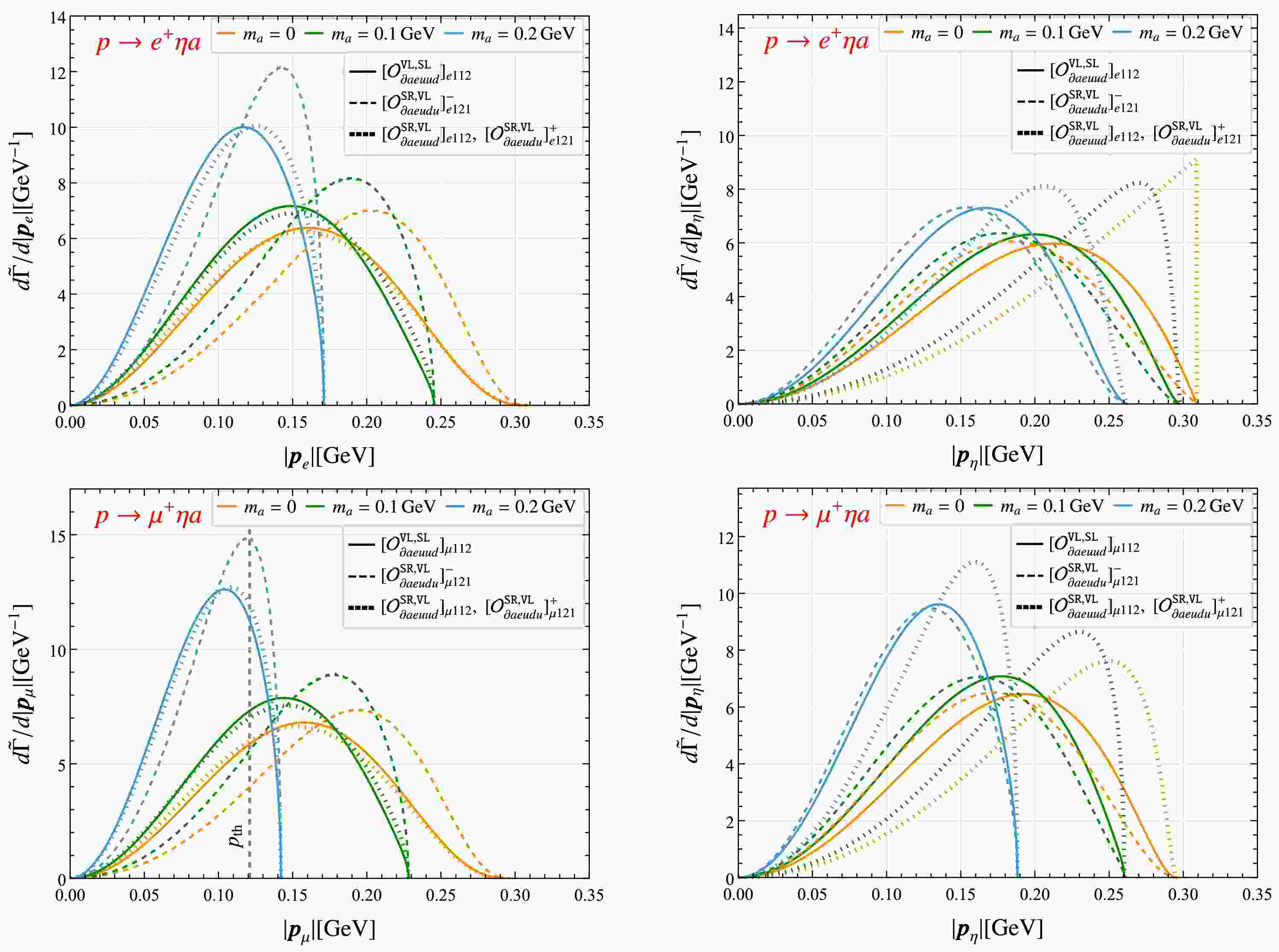
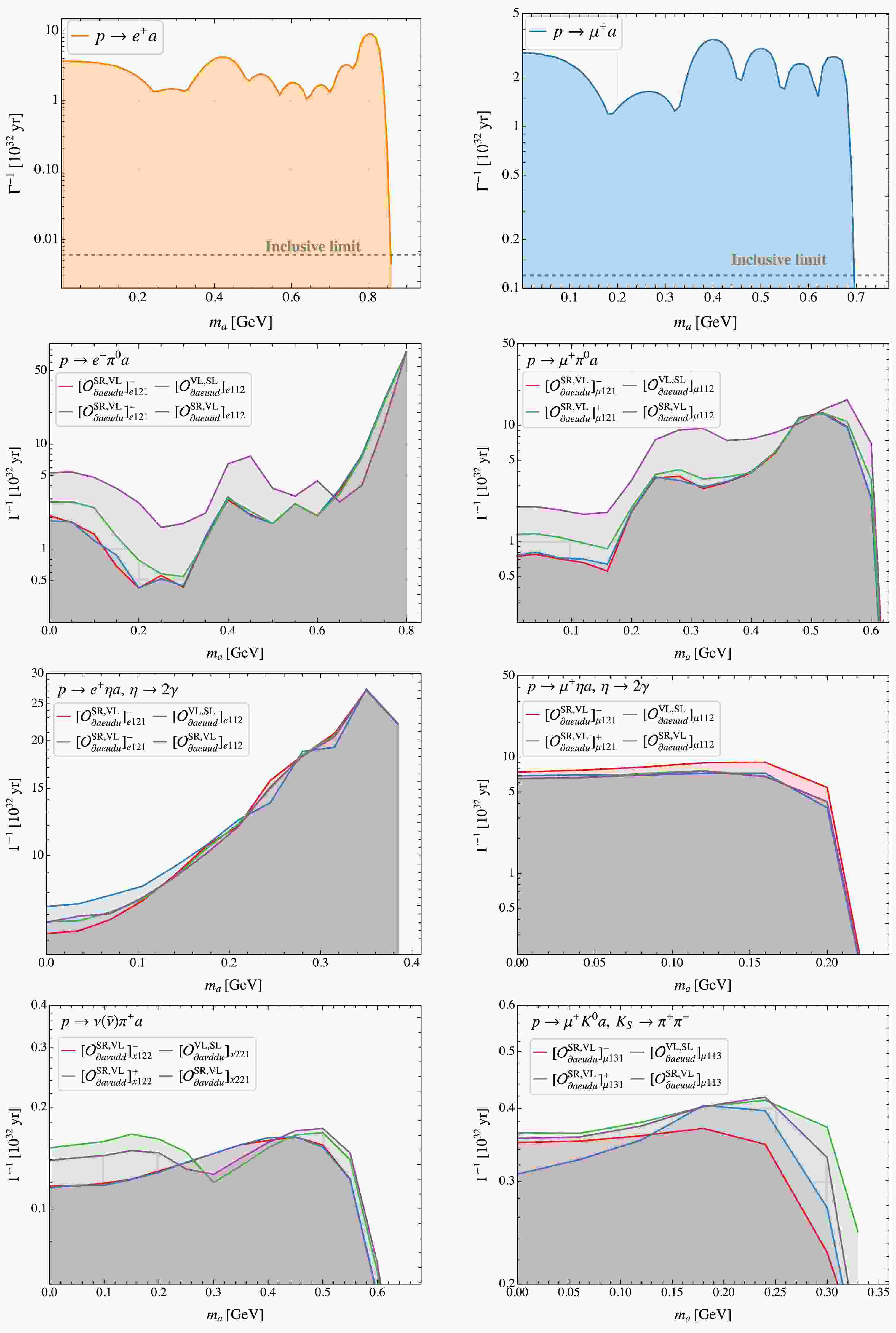
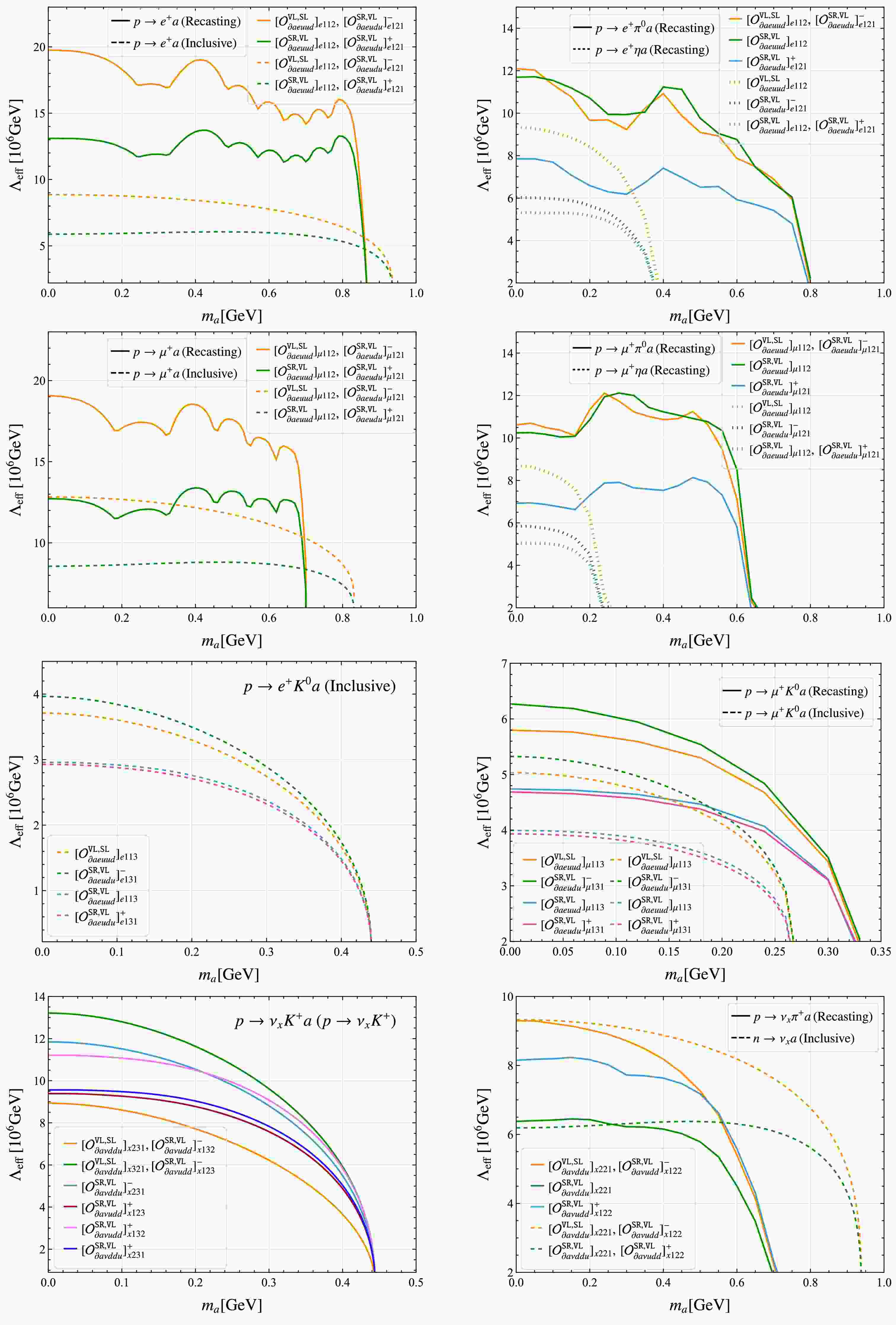
In this work, we consider BNV two-body decays of octet baryons and three-body decays of nucleons involving an ALP, with the leading-order Feynman diagrams shown in Fig. 1. We first derive the general expressions for the amplitude squared and the resulting decay width by exploiting the BNV hadronic interactions obtained in the preceding section along with the usual baryon ChPT interactions. These results provide the necessary input for the subsequent phenomenological analysis. Next, we study the differential distribution with respect to the momenta of final-state particles, which is crucial both for disentangling the operator structures and for deriving constraints on the interactions from experimental data.
-
For the octet baryon two-body decays
$ B\to l a $ involving an ALP and a lepton in the final state, the single three-point vertex$ B-l-a $ shown in Fig. 1a can be obtained by replacing the spurion fields$ {\cal{P}} $ in the$ {\cal{P}}-B $ terms of Eq. (30) with the corresponding results from Table 2. For each decay mode, it is convenient to organize the relevant terms in the following general form,$ \begin{aligned}[b] {\cal{L}}_{B \to l a} =\;& c_1 \partial^\mu a \Bigg[ C^{1 \mathtt{L}}_{B \to l}\big(\overline{l_{ \mathtt{L}}} \gamma_\mu B_{ \mathtt{L}} \big) +C^{1 \mathtt{R}}_{B \to l}\big(\overline{l_{ \mathtt{R}}} \gamma_\mu B_{ \mathtt{R}} \big) \\&+{C^{3 \mathtt{L}}_{B \to l} \over \Lambda_\chi} \big(\overline{l_{ \mathtt{R}}} i\tilde\partial_\mu B_{ \mathtt{L}} \big) +{ C^{3 \mathtt{R}}_{B \to l} \over \Lambda_\chi } \big(\overline{l_{ \mathtt{L}}} i\tilde\partial_\mu B_{ \mathtt{R}} \big) \Bigg], \end{aligned} $

(12) where l denotes a lepton field (
$ \ell^\pm, \nu, \bar{\nu} $ ) and$ \tilde\partial_\mu \equiv \partial_\mu -\gamma_\mu\not{\partial}/4 $ . Specifically, for a negatively (positively) charged lepton$ \ell^- (\ell^+) $ ,$ l_{ \mathtt{L}, \mathtt{R}} = \ell_{ \mathtt{L}, \mathtt{R}} (\ell_{ \mathtt{R}, \mathtt{L}}^{\mathtt{C}}) $ , and for a neutrino (an antineutrino) field,$ l_{ \mathtt{L}}(l_{\mathtt{R}})=\nu_{\mathtt{L}}(\nu_{\mathtt{L}}^{\mathtt{C}}) $ . The first two terms in Eq. (15) are associated with the usual$ {\bf{8}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{1}}_{ \mathtt{R}( \mathtt{L})} $ and$ {\bf{3}}_{ \mathtt{L}( \mathtt{R})} \otimes \bar{{\bf{3}}}_{ \mathtt{R}( \mathtt{L})} $ irreps, while the last two terms are relevant to the$ {\bf{6}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ representations. In terms of the above parametrization, the coefficients$ C_{B\to l}^{1(3) \mathtt{L}/ \mathtt{R}} $ for each transition can be extracted from the chiral Lagrangian and are summarized in Table 3. In the table, we have defined two ratios of LECs$ \kappa_2\equiv c_2/ c_1, \kappa_3\equiv c_3/c_1 $ . From the above Lagrangian, the two-body decay amplitude can be written as$ {\cal{M}}_{B\to l a} = i \overline{u_l}\left[ D_{B\to l}^{ \mathtt{L}} P_{\mathtt{L}} + D_{B\to l}^{ \mathtt{R}} P_{\mathtt{R}} \right] u_{B}. $

(13) with
$ \begin{aligned}[b] D_{B\to l}^{ \mathtt{L}( \mathtt{R})} \equiv\;& c_1 m_B \Bigg(C_{B\to l}^{1 \mathtt{R}( \mathtt{L})} -{ m_l \over m_B} C_{B\to l}^{1 \mathtt{L}( \mathtt{R})} + {m_B^2 - 2 m_l^2 + 2 m_a^2\over 4 m_B \Lambda_\chi } C_{B\to l}^{3 \mathtt{L}( \mathtt{R})}\\& + {m_l \over 4 \Lambda_\chi} C_{B\to l}^{3 \mathtt{R}( \mathtt{L})} \Bigg), \end{aligned} $

(14) where
$ m_B $ ,$ m_l $ ,$ m_a $ denote the masses of the baryon, lepton, and ALP, respectively. The spin-averaged and -summed matrix element squared is$\begin{aligned}[b] \overline{|{\cal{M}}_{B\to l+a}|^2} =\;& {1\over 2}(m_B^2 + m_l^2- m_a^2) \left( |D_{B\to l}^{ \mathtt{L}}|^2 + |D_{B\to l}^{ \mathtt{R}}|^2\right) \\&+ 2 m_B m_l \, \Re\left(D_{B\to l}^{ \mathtt{L}}D_{B\to l}^{ \mathtt{R}\,*} \right).\end{aligned} $

(15) Note that the
$ \overline{u_l} $ in Eq. (16) denotes the lepton's spinor, which should be rewritten as$ \overline{v_l^{\mathtt{C}}} $ when the final-state lepton is an antiparticle. Since u and$ v^{\mathtt{C}} $ share identical Dirac properties (the equation of motion and completeness relation), all the above results remain valid for antiparticles. Finally, the decay width becomes,$ \begin{aligned} \Gamma_{B \to l a} &= { \overline{|{\cal{M}}_{B\to l+a}|^2} \over 16\pi m_B}\lambda^{1/2}(1,x_l, x_a), \end{aligned} $

(16) where
$ \lambda(x,y,z)\equiv x^2+y^2+z^2-2xy-2yz-2zx $ is the triangle function, and$ x_l \equiv m_l^2/m_B^2 $ ,$ x_a\equiv m_a^2/m_B^2 $ . In Appendix B, We show the complete decay widths for the massless ALP case. The numerical constraints on the relevant WCs will be studied in the next section. -
By inserting the explicit expressions of the spurion fields from Table 2 into the
$ {\cal{P}}-{\mathtt{N}}-M $ terms in Eq. (31), we obtain effective BNV four-point interactions containing a baryon, a meson, a lepton and an ALP. These interactions yield the contact contribution to the three-body decays, shown in the second diagram of Fig. 1b. All these local vertices can be written in the following general form$ \begin{aligned}[b] {\cal{L}}_{\mathtt{N} \to l M a} =\;& c_1 \frac{i\partial^\mu a}{F_0} \Bigg[ C^{1 \mathtt{L}}_{\mathtt{N} \to lM}\,\overline{l_{ \mathtt{L}}} \gamma_\mu \mathtt{N}_{ \mathtt{L}} +C^{1 \mathtt{R}}_{\mathtt{N} \to lM}\,\overline{l_{ \mathtt{R}}} \gamma_\mu \mathtt{N}_{ \mathtt{R}}\\&+{ C^{3 \mathtt{L}}_{\mathtt{N} \to lM} \over \Lambda_\chi} \overline{l_{ \mathtt{R}}} i\tilde\partial_\mu \mathtt{N}_{ \mathtt{L}} +{ C^{3 \mathtt{R}}_{\mathtt{N} \to lM} \over \Lambda_\chi} \overline{l_{ \mathtt{L}}} i\tilde\partial_\mu \mathtt{N}_{ \mathtt{R}} \Bigg] \bar{M}, \end{aligned} $

(17) where again the first two terms are related to the irreps
$ {\bf{8}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{1}}_{ \mathtt{R}( \mathtt{L})} $ and$ {\bf{3}}_{ \mathtt{L}( \mathtt{R})} \otimes \bar{{\bf{3}}}_{ \mathtt{R}( \mathtt{L})} $ , while the last two terms are associated with$ {\bf{6}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ . The coefficients$ C_{\mathtt{N} \to lM}^{1(3) \mathtt{L}/ \mathtt{R}} $ for all relevant vertices are summarized in Table 4.In addition to the BNV interactions given above, the standard leading-order chiral interactions involving baryons are also needed. These enter into the non-contact diagram in Fig. 1b via the three-point vertices involving an octet baryon (B), a nucleon (
$ \mathtt{N} $ ), and a meson (M). They are given by [48, 49]$ \begin{aligned}[b] {\cal{L}}_\mathtt{ChPT}^B =\;& {\rm{Tr}}[\bar{B} (i \not{D} -M) B] + \frac{D}{2} {\rm{Tr}}(\bar{B} \gamma^\mu \gamma_5\{u_\mu,B\}) \\&+ \frac{F}{2} {\rm{Tr}}(\bar{B} \gamma^\mu \gamma_5 [u_\mu,B]), \end{aligned} $

(18) where
$ u_{\mu}=i\left[\xi(\partial_{\mu}-ir_{\mu})\xi^{\dagger} -\xi^{\dagger}(\partial_{\mu}-il_{\mu})\xi\right]= - i \xi^\dagger (D_\mu\Sigma )\xi^\dagger $ .4 The covariant derivatives of the meson and baryon octets are given by$ D_\mu \Sigma = \partial_\mu \Sigma - i l_\mu \Sigma +i\Sigma r_\mu $ and$ D_\mu B = \partial_\mu B + [\Gamma_\mu,B]-i v_\mu^{(s)}B $ , respectively. Here$ \Gamma_\mu $ is the chiral connection,$ \Gamma_{\mu}=\frac{1}{2} \left[\xi(\partial_{\mu}-ir_{\mu})\xi^{\dagger}+\xi^{\dagger}(\partial_{\mu}-il_{\mu})\xi\right] $ , and$ v_\mu^{(s)} $ ,$ l_{\mu} $ and$ r_{\mu} $ are external sources, which can be omitted in our case. We will use the LECs$ D=0.730(11) $ and$ F=0.447^{6}_{7} $ from the recent lattice calculation [60]. By expanding the pseudoscalar meson matrices in 21 to the linear order, we obtain$ \begin{aligned}[b] {\cal{L}}_{\bar{B}\mathtt{N}M} \supset\;& \frac{D-F}{2F_0} \Big[ \overline{\Sigma^0} \gamma^\mu \gamma_5 p \, \partial_\mu K^- - \overline{\Sigma^0} \gamma^\mu \gamma_5 n\, \partial_\mu \bar K^0 \\&+ \sqrt{2}\big(\overline{\Sigma^+}\gamma^\mu \gamma_5 p \, \partial_\mu \bar K^0 + \overline{\Sigma^-} \gamma^\mu \gamma_5 n \, \partial_\mu K^- \big) \Big] \\ & + \frac{3F-D}{2\sqrt{3}F_0} \big( \overline{p} \gamma^\mu \gamma_5 p \, \partial_\mu \eta + \overline{n} \gamma^\mu \gamma_5 n \, \partial_\mu \eta \big) \\&-\frac{D+3F}{2\sqrt{3}F_0} \left[ \overline{\Lambda^0} \gamma^\mu \gamma_5 p \, \partial_\mu K^- + \overline{\Lambda^0} \gamma^\mu \gamma_5 n \, \partial_\mu \bar K^0 \right] \\ & +\frac{D+F}{2F_0} \Big[ \overline{p} \gamma^\mu \gamma_5 p\, \partial_\mu \pi^0 - \overline{n} \gamma^\mu \gamma_5 n\, \partial_\mu \pi^0\\& + \sqrt{2} \big(\overline{n} \gamma^\mu \gamma_5 p \, \partial_\mu \pi^- + \overline{p} \gamma^\mu \gamma_5 n \, \partial_\mu \pi^+ \big) \Big]. \end{aligned} $

(19) Generally, each term has the following form:
$ {\cal{L}}_{\mathtt{N}\to B M} = { C_{\mathtt{N}\to BM}\over F_0 } \overline{B}\gamma_\mu \gamma_5 \mathtt{N} \, \partial^\mu \bar M, $

(20) where the dimensionless coefficient
$ C_{\mathtt{N}\to BM} $ can be easily read off from Eq. (22) for a given configuration of field combinations. Combining Eq. Eqs. (15) and (23) will yield the non-contact contribution to the three-body decays shown in the first diagram of Fig. 1b.After taking into account both contact and non-contact contributions, the amplitude for a general mode can be parametrized as,
$\begin{aligned}[b] {\cal{M}}_{\mathtt{N}\to l M a} =\;& \overline{u_l}\Big[ D_{\mathtt{N}\to lM}^{\mathtt{S}, \mathtt{L}} P_{\mathtt{L}} + D_{\mathtt{N}\to lM}^{\mathtt{S}, \mathtt{R}} P_{\mathtt{R}} + D_{\mathtt{N}\to lM}^{\mathtt{V}, \mathtt{L}} m_\mathtt{N}^{-1} \not{p}_B P_{\mathtt{L}}\\& + D_{\mathtt{N}\to lM}^{\mathtt{V}, \mathtt{R}} m_\mathtt{N}^{-1} \not{p}_B P_{\mathtt{R}} \Big]u_\mathtt{N}, \end{aligned}$

(21) where B denotes the baryon in the intermediate state of momentum
$ p_B $ and mass$ m_B $ . The expressions for$ D_{\mathtt{N}\to lM}^{\mathtt{S}, \mathtt{L}( \mathtt{R})} $ and$ D_{\mathtt{N}\to lM}^{\mathtt{V}, \mathtt{L}( \mathtt{R})} $ are given by$ \begin{aligned}[b] { D_{\mathtt{N}\to lM}^{{\mathtt{S}}, \mathtt{L}( \mathtt{R})}\over c_1 F_0^{-1}} =\;& m_l C^{1 \mathtt{L}( \mathtt{R})}_{\mathtt{N} \to lM} \pm \Bigg[ (m_\mathtt{N} m_B + s ) \Big( 4 m_l C^{1 \mathtt{L}( \mathtt{R})}_{B \to l} \\&- { s - 2 m_l^2 + 2m_a^2 \over \Lambda_\chi} C^{3 \mathtt{L}( \mathtt{R})}_{B \to l} \Big) \\ & - (m_\mathtt{N} + m_B) s \Big( 4 C^{1 \mathtt{R}( \mathtt{L})}_{B \to l} + { m_l\over \Lambda_\chi} C^{3 \mathtt{R}( \mathtt{L})}_{B \to l} \Big) \Bigg]{C_{\mathtt{N}\to BM} \over 4(m_B^2 - s)} \\ & - {s+t -m_M^2 - m_l^2 \over 2\Lambda_\chi} C^{3 \mathtt{L}( \mathtt{R})}_{\mathtt{N} \to lM} -{m_\mathtt{N} m_l \over 4 \Lambda_\chi}C^{3 \mathtt{R}( \mathtt{L})}_{\mathtt{N} \to lM}, \end{aligned} $

(22) $ \begin{aligned}[b] {D_{\mathtt{N}\to lM}^{{\mathtt{V}}, \mathtt{L}( \mathtt{R})}\over c_1 F_0^{-1} m_\mathtt{N}} = - C^{1 \mathtt{L}( \mathtt{R})}_{\mathtt{N} \to lM} \pm \Big[ (m_\mathtt{N} + m_B) \Big( 4 m_l C^{1 \mathtt{R}( \mathtt{L})}_{B \to l} \end{aligned} $

$ \begin{aligned}[b] &- {s-2 m_l^2 + 2 m_a^2 \over \Lambda_\chi} C^{3 \mathtt{R}( \mathtt{L})}_{B \to l} \Big) - ( m_\mathtt{N} m_B + s)\\ & \Big( 4 C^{1 \mathtt{L}( \mathtt{R})}_{B \to l} + {m_l\over \Lambda_\chi} C^{3 \mathtt{L}( \mathtt{R})}_{B \to l} \Big) \Big]{C_{\mathtt{N}\to BM} \over 4(m_B^2 - s)} + {m_\mathtt{N} \over 4 \Lambda_\chi} C^{3 \mathtt{R}( \mathtt{L})}_{\mathtt{N} \to lM}, \end{aligned} $

(23) where
$ m_\mathtt{N} $ is the nucleon mass, and$ s\equiv p_B^2 = (p_l + p_a)^2 $ ,$ t \equiv (p-p_l)^2 = (p_M +p_a)^2 $ . In the above equations, a summation over the virtual baryon B is implied. From Eq. (22), it is clear that only the decay modes$ p \to \nu_x(\bar{\nu}_x) K^+ a $ and$ n \to \nu_x(\bar{\nu}_x) K^0 a $ receive non-contact contributions from both the$ \Sigma^0 $ and$ \Lambda^0 $ intermediate states, as these baryons share the same quark content. For all other decay modes$ \mathtt{N} \to M+l+a $ , the contributing virtual baryon B is uniquely determined by the vertices$ C_{\mathtt{N} \to B M} $ in Eq. (22). It should be noticed that the process$ n \to \ell^- \pi^+ a $ changes isospin by 3/2 units, so that the required local vertex has to contain three down quarks. This flavor condition is uniquely satisfied by the operators$ {\cal{O}}_{\partial a eddd}^{\mathtt{SL}, \mathtt{VR}(SR,VL)} $ in the irreps$ {\bf{6}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ , thereby only$ C_{\mathtt{N} \to lM}^{3 \mathtt{L}/ \mathtt{R}} $ are nonzero. Meanwhile, the non-contact contribution is absent due to the lack of a$ C_{n\to B \pi^-} $ vertex from Eq. (22).Based on Eq. (24), the spin-averaged and -summed matrix element squared can be expressed compactly as
$ \begin{aligned}[b] \overline{|{\cal{M}}_{\mathtt{N}\to lMa}|^2} =\;& {1\over 2}(m_\mathtt{N}^2 + m_l^2 - t) \left(|D_{\mathtt{N}\to lM}^{{\mathtt{S}}, \mathtt{L}}|^2 + |D_{\mathtt{N}\to lM}^{{\mathtt{S}}, \mathtt{R}}|^2\right) \\ & + {1\over 2 m_\mathtt{N}^2} \Big[(m_\mathtt{N}^2 - m_M^2)(m_l^2 - m_a^2) \\&+ s (s+t - m_M^2 - m_a^2) \Big] \left(|D_{\mathtt{N}\to lM}^{{\mathtt{V}}, \mathtt{L}}|^2 + |D_{\mathtt{N}\to lM}^{{\mathtt{V}}, \mathtt{R}}|^2\right) \\ & + 2 m_l m_\mathtt{N} \, \Re\left( D_{\mathtt{N}\to lM}^{{\mathtt{S}}, \mathtt{L}}D_{\mathtt{N}\to lM}^{{\mathtt{S}}, \mathtt{R}\,*} \right) \\&+ 2 { m_l \over m_\mathtt{N} } s \, \Re \left( D_{\mathtt{N}\to lM}^{{\mathtt{V}}, \mathtt{L}}D_{\mathtt{N}\to lM}^{{\mathtt{V}}, \mathtt{R}\,*} \right) \\ & + { m_l \over m_\mathtt{N} } (s + m_\mathtt{N}^2 - m_M^2)\,\Re\Big( D_{\mathtt{N}\to lM}^{{\mathtt{S}}, \mathtt{L}}D_{\mathtt{N}\to lM}^{{\mathtt{V}}, \mathtt{L}\,*} \\&+ D_{\mathtt{N}\to lM}^{{\mathtt{S}}, \mathtt{R}}D_{\mathtt{N}\to lM}^{{\mathtt{V}}, \mathtt{R}\,*} \Big) + (s+ m_l^2 - m_a^2) \\ &\Re\left( D_{\mathtt{N}\to lM}^{{\mathtt{S}}, \mathtt{L}}D_{\mathtt{N}\to lM}^{{\mathtt{V}}, \mathtt{R}\,*} + D_{\mathtt{N}\to lM}^{{\mathtt{S}}, \mathtt{R}} D_{\mathtt{N}\to lM}^{{\mathtt{V}}, \mathtt{L}\,*} \right). \end{aligned} $

(24) Finally, the decay width is
$ \Gamma_{\mathtt{N}\to lMa}=\frac{1}{256\pi^3 m_{\mathtt{N}}^3} \int d s\int_{t_-}^{t_+} d t \overline{|{\cal{M}}_{\mathtt{N}\to lMa}|^2}, $

(25) where the integration domains are
$ \begin{aligned} & (m_l +m_a)^2 \leq s \leq (m_{\mathtt{N}} - m_M)^2, \\ & t_\pm = (E_2^* + E_3^*)^2 - \Big(\sqrt{E_2^{*2} - m_a^2} \mp \sqrt{E_3^{*2} - m_M^2} \Big)^2, \\ & E_2^* \equiv \frac{s - m_l^2 + m_a^2}{2\sqrt{s} },\, E_3^* \equiv \frac{ m_{\mathtt{N}}^2 - s - m_M^2}{2\sqrt{s}}. \end{aligned} $

(26) Using the above formalism, each decay width can be parametrized in terms of the aLEFT WCs after performing the full phase space integration for a given ALP mass. In Appendix B, we present the complete numerical results for all considered baryon and nucleon BNV decay modes with an ALP, assuming the ALP mass is negligible.
-
Experimentally, the event numbers are usually binned against some kinetic variables such as momentum, missing energy, invariant mass, etc. These distributions encode rich information about the underlying dynamics and kinematic properties of involved particles. To extract information from these distributions, we analyze the momentum distribution of the three-body nucleon decays.
For each mode, we define the normalized differential decay width against the momentum of either the charged lepton or the octet meson via
$ \frac{d\tilde \Gamma}{d |{\boldsymbol{p}}_\ell|} \equiv \frac{1}{\Gamma} \frac{d\Gamma}{d |{\boldsymbol{p}}_\ell|}, \quad \frac{d\tilde \Gamma}{d |{\boldsymbol{p}}_M|} \equiv \frac{1}{\Gamma} \frac{d\Gamma}{d |{\boldsymbol{p}}_M|}, $

(27) where
$ {\boldsymbol{p}}_\ell $ and$ {\boldsymbol{p}}_M $ denote the three-momenta of the charged lepton and the octet meson in the final state, respectively. Since both the neutrino and the ALP are invisible to the detector, their momentum distributions are not considered. For illustration, we focus on proton and neutron decay modes that involve both a charged lepton ($ e,\mu $ ) and a pion, as well as the proton decay modes involving the η meson; all of these are related to operators containing two up quarks and one down quark. We assume only one WC is nonzero at a time and consider only half of the operators with "$\mathtt{VL}, \mathtt{SL}$ " and "$\mathtt{SR}, \mathtt{VL}$ " chiral structures, since the other chirality-flipped counterparts ("$\mathtt{VR}, \mathtt{SR}$ " and "$\mathtt{SL}, \mathtt{VR}$ ") yield the same distributions.Fig. 2 shows the normalized differential distributions for the processes
$ p \to \ell^+ \pi^0a $ (left panels) and$ n \to \ell^+ \pi^- a $ (right panels) from insertion of various operators. Given that the mass of the ALP spans a wide range, we consider three benchmark points with$ m_a=\{0,\; 0.3,\; 0.5\} $ GeV. In the plots, the solid curves represent contributions from the usual chiral irrep operators$ [{\cal{O}}^{\mathtt{VL}, \mathtt{SL}}_{\partial a euud}]_{x112}\in {\bf{8}}_{ \mathtt{L}} \otimes {\bf{1}}_{ \mathtt{R}} $ and$ [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]^-_{x121} \in {\bf{3}}_{ \mathtt{L}} \otimes \bar{{\bf{3}}}_{ \mathtt{R}} $ , while the dashed and dotted curves correspond to contributions from the operators$ [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a euud}]_{x112} $ and$ [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]^+_{x121} $ , respectively, belonging to the new chiral irrep$ {\bf{3}}_{ \mathtt{L}} \otimes {\bf{6}}_{ \mathtt{R}} $ . As shown in Fig. 2, for each ALP mass scenario, the operators$ [{\cal{O}}^{\mathtt{VL}, \mathtt{SL}}_{\partial a euud}]_{x112} $ and$ [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]^-_{x121} $ lead to the same lepton/pion-momentum distributions. Moreover, since these operators have a definite isospin change of$ \Delta I=1/2 $ , they yield approximately the same distributions for the decay modes$ p \to \ell^+ \pi^0 a $ and$ n \to \ell^+ \pi^- a $ in each case. In contrast, the operators belonging to the new chiral irrep$ {\bf{3}}_{ \mathtt{L}} \otimes {\bf{6}}_{ \mathtt{R}} $ exhibit markedly different$ |{\boldsymbol{p}}_i| $ -distributions across each ALP mass point and between the two decay modes, due to the presence of both$ \Delta I=1/2 $ and$ \Delta I=3/2 $ isospin components in these operators. In each$ |{\boldsymbol{p}}_\pi| $ -distribution panel, the distributions from the two$ {\bf{3}}_{ \mathtt{L}} \otimes {\bf{6}}_{ \mathtt{R}} $ operators tend to be concentrated at higher$ |{\boldsymbol{p}}_\pi| $ values compared to those of the two usual operators. These distinct patterns in the distributions may help disentangle the operator structures and determine the ALP mass in future experimental searches.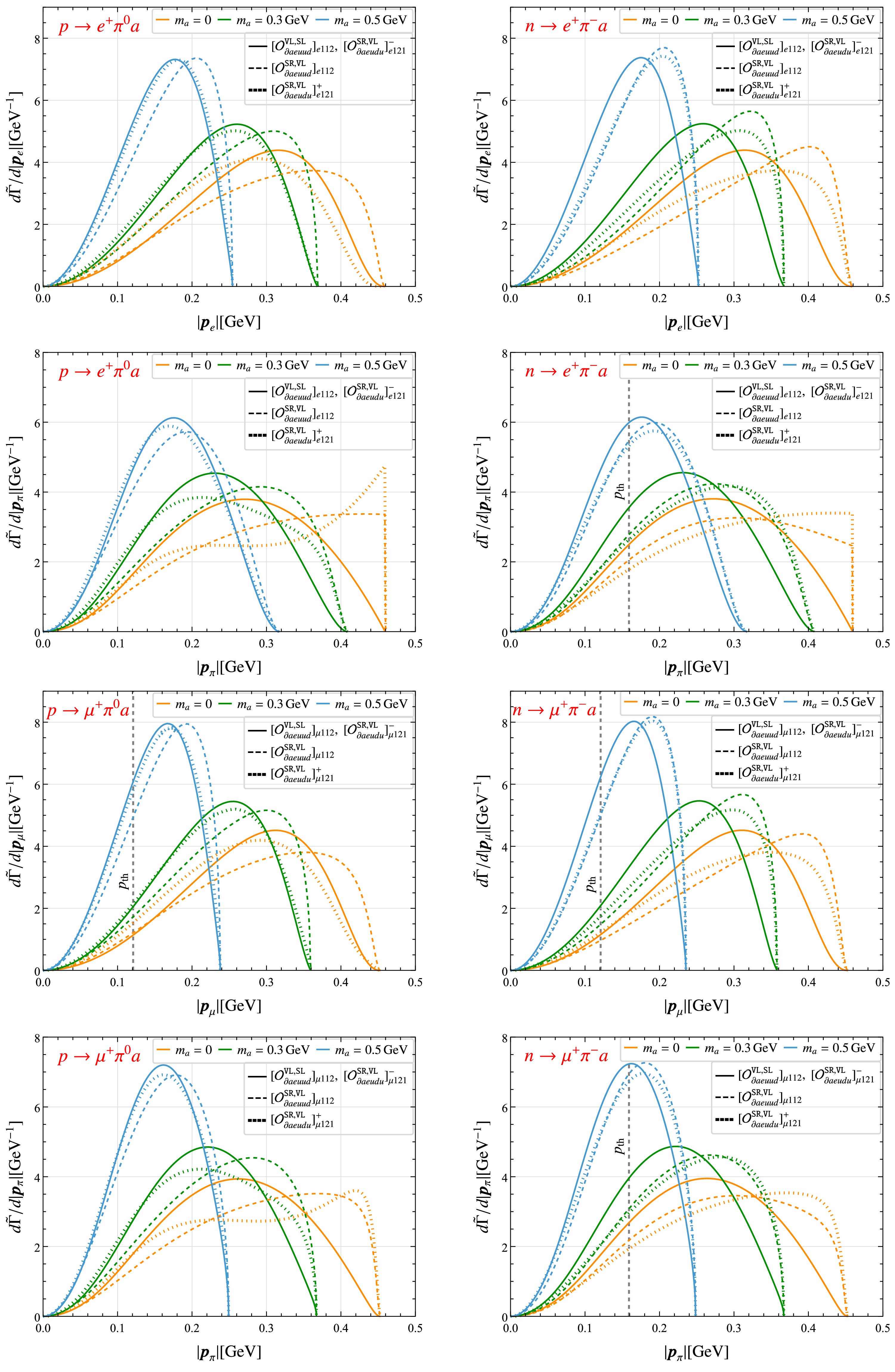
Figure 2. (color online) The normalized momentum distributions for
$ p \to \ell^+ \pi^0 a $ and$ n \to \ell^+ \pi^- a $ from insertion of various operators. All distributions are evaluated for three benchmark ALP masses:$ m_a=\{0,\; 0.3,\; 0.5\}\,{\rm{GeV}} $ . The vertical gray dashed lines indicate the Cherenkov thresholds:$ 121 \, {\rm{MeV}} $ for$ \mu^+ $ and$ 159 \, {\rm{MeV}} $ for$ \pi^- $ [61].$ [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x1y1}^\pm \equiv [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x1y1} \pm [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a eduu}]_{xy11} $ correspond to the operators associated with the WCs$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x1y1}^\pm $ , defined through the relations$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x1y1}^+ [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x1y1}^+ + [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x1y1}^- [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x1y1}^- = [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x1y1} [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]_{x1y1} + $ $[C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eduu}]_{xy11} [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a eduu}]_{xy11} $ .Fig. 3 shows the
$ |{\boldsymbol{p}}_i| $ -distributions for the decay mode$ p\to \ell^+ \eta a $ , which involves the same set of operators as the pion modes discussed above. Unlike the previous cases, the distributions from the two usual irrep operators$ [{\cal{O}}^{\mathtt{VL}, \mathtt{SL}}_{\partial a euud}]_{x112} $ (solid) and$ [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]^-_{x121} $ (dashed) exhibit clear differences across all three ALP mass values and lepton/eta-momentum scenarios. However, the two operators$ [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a euud}]_{x112} $ and$ [{\cal{O}}^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]^+_{x121} $ in the new chiral irrep share the same behavior in all cases, in contrast to the situation in the process$ p\to \ell^+ \pi^0a $ . This distribution characteristic can also be understood from isospin considerations. For the decay$ p\to \ell^+ \eta a $ , only the$ \Delta I=1/2 $ components of the two operators contribute, resulting in the coefficients of$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a euud}]_{x112} $ and$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a eudu}]^+_{x121} $ sharing the same relative ratio in both the contact ($ C_{p \to \ell \eta}^{3 \mathtt{R}} $ ) and the non-contact ($ C_{p\to \ell}^{3 \mathtt{R}} $ ) contributions. For each operator, the behavior of the$ |{\boldsymbol{p}}_\eta| $ -distribution differs from that of$ {\boldsymbol{p}}_{e,\mu} $ -distribution. In particular, the$ |{\boldsymbol{p}}_\eta| $ -distributions from the two new irrep operators are enhanced at higher$ |{\boldsymbol{p}}_\eta| $ values, whereas the two usual operators peak at intermediate$ |{\boldsymbol{p}}_\eta| $ values. Complementary to the pion modes, these new features can be further employed to distinguish among various scenarios in future experimental searches.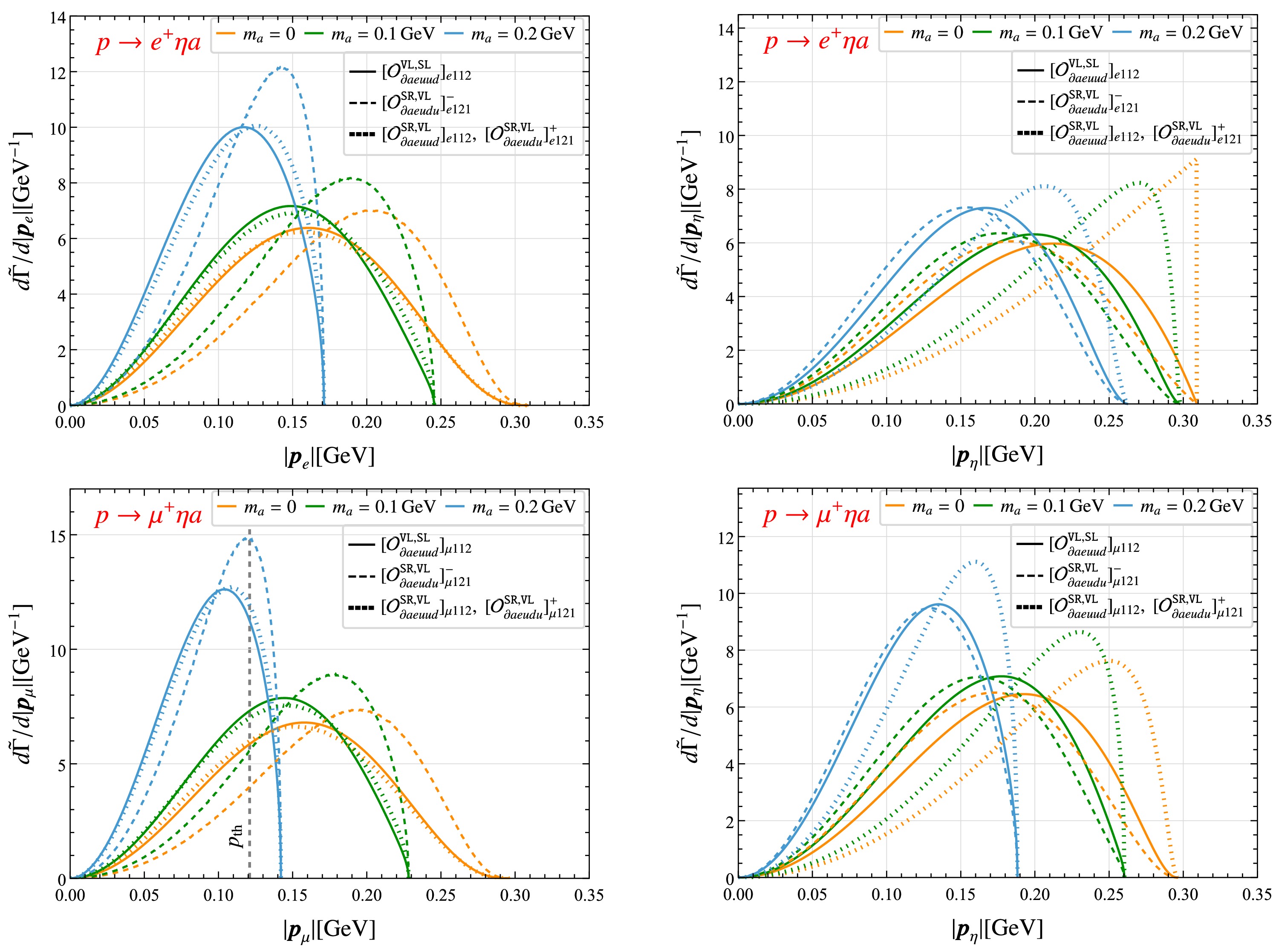
Figure 3. (color online) Same as Fig. 2 but for the decay mode
$ p \to \ell^+ \eta a $ with$ m_a=\{0,\; 0.1,\; 0.2\}\, {\rm{GeV}} $ .Similar distributions can be studied for the other three-body decay modes. For example, the
$ |{\boldsymbol{p}}_\pi| $ -distributions in the process$ p\to \nu_x(\bar{\nu}_x)\pi^+ a $ closely resemble those of$ n\to e^+\pi^- a $ for the corresponding operators with the simultaneous exchange of$ u\leftrightarrow d $ and$ e\leftrightarrow \nu(\nu^{\mathtt{C}}) $ . This is physically understandable; on the one hand, the nucleon-to-pion matrix elements are connected with each other through the exchange of$ u \leftrightarrow d $ , and on the other hand, the masses of both the neutrino and electron are negligible. All of these results can be understood analytically. Given the amplitude formulas in Eqs. (24) and (25) and neglecting the lepton masses in both processes, a direct comparison of their corresponding coefficients ($ C_{B\to l}^{1(3) \mathtt{L}/ \mathtt{R}} $ ,$ C_{\mathtt{N} \to lM}^{1(3) \mathtt{L}/ \mathtt{R}} $ ,$ C_{\mathtt{N}\to BM} $ ) suffices to determine the relationship between their amplitudes and further their distributions. Accordingly, such similarity in distributions is also anticipated between$ p \to e^+ \pi^0 (\eta) a $ and$ n \to \nu_x (\bar{\nu}_x) \pi^0 (\eta) a $ ,$ p \to \nu_x (\bar{\nu}_x) K^+ a $ and$ n \to \nu_x (\bar{\nu}_x) K^0 a $ , as well as$ p \to \ell^+ K^0 a $ and$ n \to \ell^- K^+ a $ for the corresponding operators with the simultaneous exchange of$ u\leftrightarrow d $ and the involved leptons. -
After establishing the theoretical framework for nucleon decay with an ALP in the final state, we investigate constraints on the relevant WCs from available experimental data. Exotic nucleon decays involving new light invisible particles have been largely overlooked in the past experimental searches, resulting in a lack of direct constraints on their occurrence. The only exceptions are the two-body proton decay modes
$ p\to e^+X $ and$ \mu^+X $ , and Super-K experiment has set stringent lower bounds on their inverse decay widths in the limit of$ m_X\to 0 $ :$ \Gamma^{-1}({p \to e^+ + X}) > 7.9 \times 10^{32} $ yr and$ \Gamma^{-1}(p \to \mu^+ + X)> 4.1 \times 10^{32} $ yr [50]. Nevertheless, given the non-observation of any BNV nucleon decays, existing experimental data from searches for decay modes involving only SM final states can also be used to constrain exotic modes involving new light particles. In the following, we first discuss how to reinterpret the existing experimental data into bounds on these new channels, and then use all these bounds to set limits on the WCs of the effective operators. -
First, the bounds on several inclusive decay modes can be directly applied to analogous processes involving an invisible ALP. These include the neutron invisible decay (
$ n\to{\rm{invisible}} $ ) and proton or neutron decays into a charged$ e^+ $ or$ \mu^+ $ plus any other particles ($ N\to e^+/\mu^++{\rm{anything}} $ , where$ N=p,n $ ). Due to the invisible nature of the ALP, the constraint on$ n\to{\rm{invisible}} $ is directly applicable to the two-body modes$ n\to\bar{\nu}(\nu) a $ . For the decay$ n\to{\rm{invisible}} $ , we adopt the most recent partial lifetime bound reported by the SNO$ + $ experiment,$ \Gamma^{-1}(n\to{\rm{invisible}})> 9.0\times 10^{29}\,{\rm{yr}} $ [62].5 This limit is expected to be further improved by two orders of magnitude in the JUNO experiment [64]. For the nucleon decays involving a positively charged lepton, the inclusive searches around 1980s also provide partial lifetime limits with$ \Gamma^{-1}(N\to e^+ + {\rm{anything}})>0.6\times 10^{30} $ yr [65] and$ \Gamma^{-1}(N\to \mu^+ + {\rm{anything}})>12\times 10^{30} $ yr [66], based on detecting both prompt and secondary charged leptons. These limits are expected to be broadly applicable to the decay channels involving the same charged leptons in the final state considered in this work, provided Cherenkov threshold effects are properly accounted for.Although no dedicated searches for nucleon decays involving new light particles exist, besides the aforementioned
$ p \to e^+(\mu^+) X $ channels with a massless X, existing experimental data and background information from conventional channels can be reinterpreted to constrain such processes. Here, we focus on the Super-K experiment, a water-Cherenkov detector, for our analysis, as it provides the most stringent bound. Charged particles traversing the detector produce Cherenkov radiation, forming characteristic rings that are classified as either showering$ (e^\pm,\gamma) $ or non-showing$ (\mu^\pm,\pi^\pm) $ types based on their topological features. Each molecule (H2O) contains two free protons (from hydrogen atoms) and eight bound protons (from the oxygen nucleus). In this preliminary attempt, we consider free proton decays in the hydrogen atom in our simulation to derive conservative bounds on the relevant modes. A more complete treatment of bound nucleon decays would require accounting for nuclear effects such as Fermi motion, nucleon correlations, and meson-nucleon interactions. Consequently, we restrict ourselves to the analysis of proton decay channels in this study, deferring the detailed investigations of these bound nucleon decays to our future work.The simulated channels include the two-body modes
$ p\to\ell^+a $ and the three-body modes$ p\to\nu(\bar{\nu})\pi^+ a $ ,$ p\to\ell^+\pi^0 a $ ,$ p\to\ell^+\eta a $ , and$ p\to \mu^+ K^0 a $ , with$ \ell=e,\mu $ . For$ p\to\ell^+a $ , we recast the spectral search results for$ p\rightarrow e^+X $ and$ p\rightarrow \mu^+X $ with a massless X, as reported in [50]. We employ the reconstructed momentum distributions of the charged lepton,$ \ell^+ $ , shown in Fig. 1 of that reference to obtain the bounds on$ p\to \ell^+ a $ . Similarly, for the channels$ p\to\nu(\bar{\nu})\pi^+ a $ , in which only the charged pion is visible in the final state, we derive constraints using the reconstructed momentum distributions of the$ \pi^+ $ , as provided in Fig. 3 of [53]. For$ p\to\ell^+\pi^0 a $ and$ p\to\ell^+\eta a $ , we make use of the reconstructed invariant mass distributions of the charged lepton and the neutral meson. The$ \pi^0 $ predominantly decays into two photons ($ {\rm{Br}}\simeq 98.8 $ %), thus producing Cherenkov rings. The η meson is reconstructed through the two-photon decay mode$ \eta\to 2 \gamma $ ($ {\rm{Br}}\simeq39 $ %), while reconstruction through$ \eta\to3\pi^0 $ is less effective due to the ring-counting algorithm’s limitation of identifying at most five Cherenkov rings. For the$ p\to \mu^+ K^0 a $ channel, we utilize the dominant decay channel of$ K^0_S\to\pi^+\pi^- $ ($ {\rm{Br}}\simeq69 $ %) to reconstruct the$ K^0 $ meson. We simulate the aforementioned proton decay processes using the analytical expressions and momentum distributions presented in the previous sections, considering one operator at a time, and use$\mathtt{Pythia8}$ [67, 68] to model the subsequent decays of the mesons. The detector's momentum resolution is implemented according to$ \sigma_e=(0.6+2.6/\sqrt{p_e [{{\rm{GeV}}}]}) $ % and$ \sigma_\mu=(1.7+0.7/ $ $\sqrt{p_\mu [{{\rm{GeV}}}]}) $ % [69]. To constrain the lower limits on the partial lifetime$ \Gamma^{-1} $ , we require that the expected signal do not exceed the observed number of events by more than$ 2\sigma $ in any bin, i.e.,$ N_s^i+N_b^i < N_o^i+2 \sigma^i $ , where$ N_s^i $ ,$ N_b^i $ , and$ N_o^i $ are the numbers of signal, background, and observed events in the i-th bin, respectively, and$ \sigma^i $ is the corresponding error bar. Note that we have neglected the angular resolution effects in our analysis, which were estimated to be$ 3.0^{\circ} $ for single-ring e-like events and$ 1.8^{\circ} $ for μ-like events [69], respectively.The recasting results for various proton decay channels are presented in Fig. 4. Due to the fixed kinematics in two-body decays, the obtained limits on the modes
$ p\to e^+(\mu^+) a $ are independent of the underlying interaction structures. In contrast, the momentum distributions in three-body decays strongly depend on the interaction structures; therefore, the limits for all three-body modes are presented on an operator-by-operator basis. It can be seen from the plots that the recasting constraints on modes containing a charged lepton are stronger than the corresponding inclusive limits by one to four orders of magnitude, with the exact improvement depending on the decay mode and the ALP mass. For the two-body channels$ p\to\ell^+a $ , the inclusive limits cover a slightly larger ALP mass range compared to the recasting bounds due to experimental cuts of$ |{\boldsymbol{p}}_e|>100 $ MeV and$ |{\boldsymbol{p}}_\mu|>200 $ MeV in the search [50]. Stronger bounds for heavier ALPs arise in$ e^+ $ -related channels because a sharper and more localized signal peak appears at lower reconstructed invariant masses, which improves the single bin sensitivity. However, this effect is diminished by the reduced detection efficiency for low-momentum$ \mu^+ $ or$ \pi^+ $ produced in association with heavier ALPs, causing the bounds on channels involving$ \mu^+ $ or$ \pi^+ $ to weaken as the ALP approaches the threshold.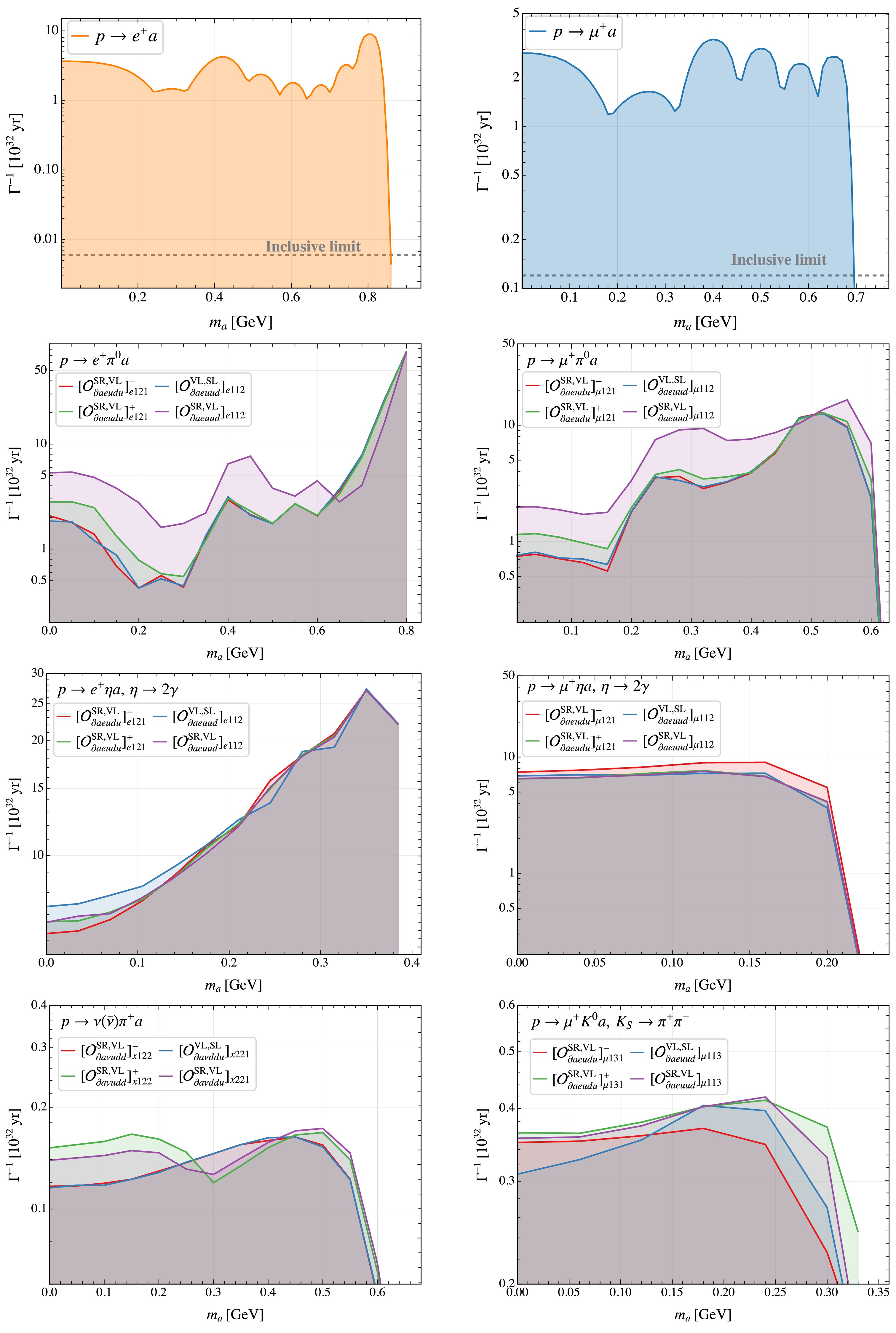
Figure 4. (color online) The new constraints on various proton decay channels as a function of the ALP mass
$ m_a $ , obtained from our simulation based on the Super-K experimental data. The plots for$ p\to \ell^+ a $ are obtained by recasting the analysis in [50]. The plots for$ p\to \ell^+\pi^0 a $ are based the data provided in Fig. 4 of [51]. The plots for$ p\to \ell^+\eta a $ are based on the data provided in Fig. 5 of [52], where the η meson is reconstructed by the decay channel$ \eta\to 2 \gamma $ . The results for$ p\to \nu(\bar{\nu})\pi^+ a $ and$ p \to \mu^+ K^0 a $ are obtained by reanalyzing the data provided in Fig. 3 of [53] and Fig. 6 of [54], respectively. Note that the results are the same for the chirality-flipped operators with$ \mathtt{L}\leftrightarrow \mathtt{R} $ . The peaks or fluctuations observed in the resulting constraints arise from the simplified statistical analysis and the neglect of nuclear effects.We did not perform a similar analysis for the
$ p\to e^+ K^0 a $ channel, as the most recent search for$ p\to e^+ K^0 $ by Super-K [70] does not provide the required kinematic distributions. Therefore, we adopt the inclusive limit to set$ \Gamma^{-1}(p\to e^+ K^0 a)>0.6\times 10^{30} $ yr. For the channels with the positively charged kaon,$ p\to \bar{\nu}(\nu) K^+ a $ , the$ K^+ $ typically carries momentum below its Cherenkov threshold (563 MeV) and thus cannot be directly detected in water Cherenkov detectors. Instead,$ K^+ $ is identified via its decay products. Due to its low momentum and short lifetime, the$ K^+ $ usually decays at rest. The Super-K experiment utilizes the dominant two-body decay modes$ K\to\mu^+\nu_\mu$ (64%) and$ K\to\pi^+\pi^0$ (21%) for its detection. Moreover, for nucleon decays occurring within the oxygen nucleus, the residual nucleus may be left in an excited state, which can promptly de-excite via gamma-ray emission, offering an additional signal. Given the similarity in final-state signatures, existing searches for$ p\to\nu K^+ $ can be directly reinterpreted as constraints on$ p\to \bar{\nu}(\nu) K^+ a $ . Consequently, we adopt the current Super-K limit [71] to set$ \Gamma^{-1}(p \to \bar{\nu}(\nu) K^+ a) > 5.9 \times 10^{33} $ yr.Although we have focused on the current Super-K experiment, we anticipate that the constraints will be further improved in the upcoming Hyper-K experiment, which will have a fiducial mass approximately eight times that of the Super-K. Additionally, the JUNO and DUNE experiments, which will utilize tracking detectors, will offer enhanced capabilities for probing ALP's mass near the threshold of nucleon decays, owing to their excellent low-energy thresholds.
-
With the bounds on the inverse decay widths for decay modes summarized in the previous subsection, we now constrain the aLEFT WCs. For the WC
$ C_i $ of an aLEFT operator$ {\cal{O}}_i $ , we define an associated effective scale$ \Lambda_\mathtt{eff} $ via$ \Lambda_\mathtt{eff}\equiv |C_i^{-1/4}| $ , and study the constraint on$ \Lambda_\mathtt{eff} $ as a function of the ALP mass$ m_a $ . To establish the bound, we operate one operator at a time and require that the theoretical decay width be less than the limit given in the previous subsection.Our final results are presented in Fig. 5. Only half of the operators with "
$\mathtt{VL}, \mathtt{SL}$ " and "${\mathtt{SR}, \mathtt{VL}}$ " chiral structures are presented since their chirality-flipped counterparts ("${\mathtt{VR}, \mathtt{SR}}$ " and "${\mathtt{SL}, \mathtt{VR}}$ ") receive identical constraints. For each operator, besides the constraint derived from our recast analysis (solid or dotted curves), we also present the limit from inclusive searches (dashed curves) in some channels for comparison. Note that operators with$ ddd $ ,$ dds $ ,$ uss $ ,$ dss $ , and$ sss $ quark configurations cannot be constrained due to the lack of corresponding experimental data, and we have neglected them in this work. Both panels in the top row of Fig. 5 feature the same set of operators with the$ a-e-u-u-d $ field content. The left panel shows the constraints from the two-body mode$ p\to e^+ a $ based on both the recasting and inclusive results, while the right panel presents only the recasting results from the three-body modes$ p\to e^+ \pi^0(\eta)a $ . It is evident that the two-body mode, based on the recasting results, provides the most stringent constraints over a wide range of ALP masses. The similar behavior is observed in the muonic case with the$ a-\mu-u-u-d $ field content, as shown in both panels of the second row. The results for the operators with the$ u-u-s $ quark content are shown in the third row, with only inclusive limits provided for the$ e^+ $ -related operators due to the lack of experimental distribution data. The last row presents results for operators with the$ u-d-s $ quark content in the left panel and the$ u-d-d $ quark content in the right panel. For$ u-d-d $ -type operators, unlike other cases, the inclusive bounds are stronger than the recasting ones for several operators across a wide range of ALP masses. In summary, these inclusive searches combined with the recasting analysis of available experimental data enable us to constrain a broader set of operators and explore a larger ALP mass range.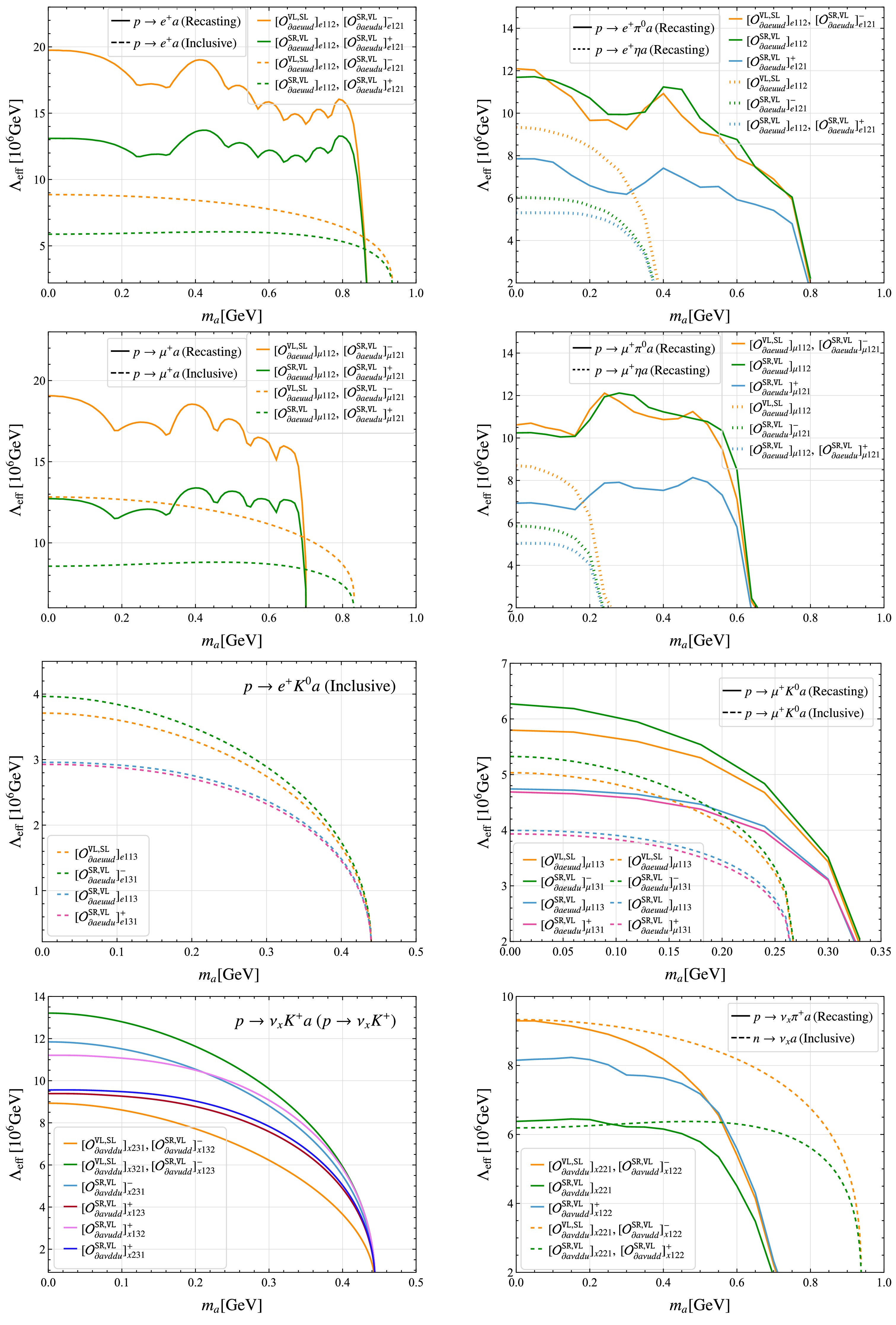
Figure 5. (color online) Constraints on the effective new physics scale associated with the dim-8 aLEFT operators as a function of the ALP mass
$ m_a $ . We have set$ \kappa_3=1 $ in the numerical analysis, and the results for the operators belonging to the irreps$ {\bf{3}}_{{\mathtt{L}}({\mathtt{R}})}\otimes {\bf{6}}_{{\mathtt{R}}({\mathtt{L}})} $ can be easily rescaled if$ \kappa_3 $ is found to differ from 1. The peaks observed in certain solid curves originate from the corresponding peaks in the recasting bounds presented in Fig. 4.To compare with the results in [18], Table 5 presents the lower bound on
$ \Lambda_\mathtt{eff} $ when$ m_a\to 0 $ . The WCs highlighted in dark gray correspond to those also considered in that paper. The last column shows the experimental lower bounds on the inverse decay widths used to reach the constraints on the WCs listed in the front cells, including the recasting bounds obtained in Fig. 4. All WCs in the fourth and fifth columns (except for the last one in the fourth column) correspond to operators belonging to the new chiral irrep$ {\bf{3}}_{ \mathtt{L}} \otimes {\bf{6}}_{ \mathtt{R}} $ . The derived energy scales associated with these operators are essentially of the same order as those for operators in the usual chiral irreps$ {\bf{3}}_{ \mathtt{L}} \otimes \bar{{\bf{3}}}_{ \mathtt{R}} $ and$ {\bf{8}}_{ \mathtt{L}} \otimes {\bf{1}}_{ \mathtt{R}} $ . The most stringent constraints for$ uud $ -type operators arise from the search for nucleon decays$ N \to \ell^+ X $ in Super-K experiment [50], and are consistent with those obtained in [12]. For the effective scales associated with operators containing$ u-d-s $ quarks, our results are five-to-six orders of magnitude stronger than those obtained in that paper based on the$ \Lambda^0 $ -hyperon invisible search performed by BESIII [72]. The derived bounds on$ \Lambda_\mathtt{eff} $ associated with$ [C^{\mathtt{VL}, \mathtt{SL}}_{\partial a \nu ddu}]_{x221} $ and$ [C^{\mathtt{SR}, \mathtt{VL}}_{\partial a \nu udd}]^-_{x122} $ are also slightly stronger.WCs/Process Derived bound on the effective scale $ \Lambda_\mathtt{eff}\equiv [C_i]^{-\frac{1}{4}} ({\rm{GeV}}) $ 

Exp. lower bound on $\Gamma^{-1} (10^{30} {\rm{yr}})$ 

WCs $ [C_{\partial a euud}^{\mathtt{VL}, \mathtt{SL}}]_{e112} $ 

$ [C_{\partial a eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e121}^- $ 

$ [C_{\partial a eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e121}^+ $ 

$ [C_{\partial a euud}^{\mathtt{SR}, \mathtt{VL}}]_{e112} $ 

$ p \to e^+ a $ 

$ 2.2 \times 10^7 $ 

$ 2.2 \times 10^7 $ 

$ 1.4 \times 10^7 $ 

$ 1.4 \times 10^7 $ 

790 (Exclusive) [50] $ p \to e^+ a $ 

$ 2.0 \times 10^7 $ 

$ 2.0 \times 10^7 $ 

$ 1.3 \times 10^7 $ 

$ 1.3 \times 10^7 $ 

364 $ p \to e^+ \pi^0 a $ 

$ 1.2 \times 10^7 $ 

$ 1.2 \times 10^7 $ 

$ 7.8 \times 10^6 $ 

$ 1.1 \times 10^7 $ 

$ 184 \big| 208 \big| 281 \big| 532 $ 

$ p \to e^+ \eta a $ 

$ 9.3 \times 10^6 $ 

$ 6.0 \times 10^6 $ 

$ 5.3 \times 10^6 $ 

$ 5.3 \times 10^6 $ 

$ 735 \big| 624 \big| 670 \big| 668 $ 

$ n \to e^+ \pi^- a $ 

$ 6.4 \times 10^6 $ 

$ 6.4 \times 10^6 $ 

$ 5.4 \times 10^6 $ 

$ 4.3 \times 10^6 $ 

0.6 (Inclusive) [57] WCs $ [C_{\partial a euud}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 112} $ 

$ [C_{\partial a eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 121}^- $ 

$ [C_{\partial a eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 121}^+ $ 

$ [C_{\partial a euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 112} $ 

$ p \to \mu^+ a $ 

$ 2.0 \times 10^7 $ 

$ 2.0 \times 10^7 $ 

$ 1.3 \times 10^7 $ 

$ 1.3 \times 10^7 $ 

410 (Exclusive) [50] $ p \to \mu^+ a $ 

$ 1.9 \times 10^7 $ 

$ 1.9 \times 10^7 $ 

$ 1.3 \times 10^7 $ 

$ 1.3 \times 10^7 $ 

285 $ p \to \mu^+ \pi^0 a $ 

$ 1.1 \times 10^7 $ 

$ 1.1 \times 10^7 $ 

$ 6.9 \times 10^6 $ 

$ 1.0 \times 10^7 $ 

$ 75 \big| 74 \big| 114 \big| 198 $ 

$ p \to \mu^+ \eta a $ 

$ 8.7 \times 10^6 $ 

$ 5.8 \times 10^6 $ 

$ 5.0 \times 10^6 $ 

$ 5.0 \times 10^6 $ 

$ 688 \big| 743 \big| 650 \big| 654 $ 

$ n \to \mu^+ \pi^- a $ 

$ 9.2 \times 10^6 $ 

$ 9.2 \times 10^6 $ 

$ 7.8 \times 10^6 $ 

$ 6.2 \times 10^6 $ 

12 (Inclusive) [57] WCs $ [C_{\partial a euud}^{\mathtt{VL}, \mathtt{SL}}]_{e113} $ 

$ [C_{\partial a eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e131}^- $ 

$ [C_{\partial a eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e131}^+ $ 

$ [C_{\partial a euud}^{\mathtt{SR}, \mathtt{VL}}]_{e113} $ 

$ p \to e^+ K^0 a $ 

$ 3.7 \times 10^6 $ 

$ 4.0 \times 10^6 $ 

$ 3.0 \times 10^6 $ 

$ 3.0 \times 10^6 $ 

0.6 (Inclusive) [57] WCs $ [C_{\partial a euud}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 113} $ 

$ [C_{\partial a eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 131}^- $ 

$ [C_{\partial a eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 131}^+ $ 

$ [C_{\partial a euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 113} $ 

$ p \to \mu^+ K^0 a $ 

$ 5.8 \times 10^6 $ 

$ 6.3 \times 10^6 $ 

$ 4.7 \times 10^6 $ 

$ 4.7 \times 10^6 $ 

$ 31 \big| 35 \big| 36 \big| 36 $ 

WCs $ [C_{\partial a \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221} $ 

$ [C_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x122}^- $ 

$ [C_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x122}^+ $ 

$ [C_{\partial a \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221} $ 

$ p \to \nu_x \pi^+ a $ 

$ 9.3 \times 10^6 $ 

$ 9.3 \times 10^6 $ 

$ 8.1 \times 10^6 $ 

$ 6.4 \times 10^6 $ 

$ 12 \big| 12 \big| 15 \big| 14 $ 

WCs $ [C_{\partial a \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321} $ 

$ [C_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^- $ 

$ [C_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^+ $ 

$ [C_{\partial a \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^+ $ 

5900 ( $ p \to \nu_x K^+ $ ) [71]

$ p \to \nu_x K^+ a $ 

$ 1.3 \times 10^7 $ 

$ 8.5 \times 10^6 $ 

$ 1.1 \times 10^7 $ 

$ 9.3 \times 10^6 $ 

WCs $ [C_{\partial a \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231} $ 

$ [C_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^- $ 

$ [C_{\partial a \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^- $ 

$ [C_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^+ $ 

$ p \to \nu_x K^+ a $ 

$ 8.5 \times 10^6 $ 

$ 1.3 \times 10^7 $ 

$ 1.2 \times 10^7 $ 

$ 9.3 \times 10^6 $ 

Table 5. Lower bounds on the effective scale of the relevant dim-8 aLEFT operators in the massless ALP limit. The limits are identical for the corresponding chirality-flipped operators with
$ \mathtt{L} \leftrightarrow \mathtt{R} $ and are therefore omitted for brevity. The experimental lower bounds without a reference in the last column correspond to the recasting bounds shown in Fig. 4 in the limit of$ m_a\to0 $ .Last, we utilize the constraints in Table 5 to derive new bounds on several hyperon and neutron BNV decay modes. In Table 6, we present the derived bounds along with the corresponding operators whose constraints were used to obtain them. As shown in the table, the constraints obtained in Table 5 impose very stringent limits on the occurrence of these hyperon decay modes. However, the bounds on neutron decay modes are comparable to those for similar modes with the SM final states, making them promising targets for future experiments.
Mode Derived bounds on branching ratios Mode Derived bounds on inverse decay widths Br aLEFT operator $ \Gamma^{-1} ({\rm{yr}}) $ 

aLEFT operator $ \Sigma^+ \to e^+ a $ 

$ 9.3\times 10^{-45} $ 

$ [{\cal{O}}_{\partial a euud}^{\mathtt{VL}, \mathtt{SL}}]_{e113} $ 

$ n \to \nu_x \pi^0 a $ 

$ 2.2\times 10^{31} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221}, \, [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122} $ 

$ 4.9\times 10^{-45} $ 

$ [{\cal{O}}_{\partial a eudu}^{\mathtt{SR}, \mathtt{VL}}]^-_{e131} $ 

$ 4.2\times 10^{30} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221} $ 

$ 3.0\times 10^{-45} $ 

$ [{\cal{O}}_{\partial a eudu}^{\mathtt{SR}, \mathtt{VL}}]^+_{e131}, \, [{\cal{O}}_{\partial a euud}^{\mathtt{SR}, \mathtt{VL}}]_{e113} $ 

$ 3.5\times 10^{32} $ 

$ [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122} $ 

$ \Sigma^+ \to \mu^+ a $ 

$ 2.5\times 10^{-46} $ 

$ [{\cal{O}}_{\partial a euud}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 113} $ 

$ n \to \nu_x \eta a $ 

$ 6.9\times 10^{32} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221} $ 

$ 1.3\times 10^{-46} $ 

$ [{\cal{O}}_{\partial a eudu}^{\mathtt{SR}, \mathtt{VL}}]^-_{\mu 131} $ 

$ 1.9\times 10^{34} $ 

$ [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122}, \, [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122} $ 

$ 8.2\times 10^{-47} $ 

$ [{\cal{O}}_{\partial a eudu}^{\mathtt{SR}, \mathtt{VL}}]^+_{\mu 131}, \, [{\cal{O}}_{\partial a euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 113} $ 

$ 2.9\times 10^{33} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221} $ 

$ \Lambda^0 \to \nu_x a $ 

$ 6.9\times 10^{-49} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321},\, [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} $ 

$ n \to \nu_x K^0 a $ 

$ 5.3\times 10^{33} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321},\, [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} $ 

$ 5.6\times 10^{-48} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231},\, [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} $ 

$ 2.7\times 10^{32} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231} $ 

$ 3.5\times 10^{-49} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} $ 

$ 4.4\times 10^{32} $ 

$ [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} $ 

$ 1.3\times 10^{-48} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} $ 

$ 9.0\times 10^{34} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} $ 

$ 3.3\times 10^{-49} $ 

$ [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} $ 

$ 1.3\times 10^{33} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} $ 

$ \Sigma^0 \to \nu_x a $ 

$ 5.6\times 10^{-57} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231},\, [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} $ 

$ 2.2\times 10^{34} $ 

$ [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} $ 

$ 3.5\times 10^{-58} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} $ 

$ 5.8\times 10^{33} $ 

$ [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x123} $ 

$ 1.7\times 10^{-58} $ 

$ [{\cal{O}}_{\partial a \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} $ 

$ 6.7\times 10^{-58} $ 

$ [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x123} $ 

$ 4.3\times 10^{-59} $ 

$ [{\cal{O}}_{\partial a \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} $ 

Table 6. Derived bounds on the hyperon two-body decay modes and neutron three-body decay modes involving a neutrino and a massless ALP based on the constraints provided in Table 5.
-
In this work, we have systematically studied two- and three-body BNV nucleon decays involving an invisible ALP. These decays are described within the framework of aLEFT, i.e., the LEFT framework extended by an ALP. By imposing shift symmetry on the ALP field, we identified the relevant BNV aLEFT operators, which first appear at dimension 8 at leading order. We then performed a chiral decomposition of these aLEFT operators under the QCD chiral group
$ {\rm{SU}}(3)_{\mathtt{L}}\otimes {\rm{SU}}_{\mathtt{R}} $ and identified the corresponding spurion fields that enter the recently developed chiral perturbation theory for nucleon decays. With these spurion fields at hand, we carried out the chiral matching for these BNV ALP interactions and derived the general expressions for the nucleon decays involving an ALP in terms of the associated Wilson coefficients and hadronic parameters in the chiral framework. Compared to the previous study in the literature, we have considered the complete set of aLEFT BNV operators involving light$ u,\; d,\; s $ quarks. In particular, we found that the 12 aLEFT operators belonging to the new chiral irreps$ {\bf{6}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ contribute at the same chiral order as operators in the usual irreps$ {\bf{8}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{1}}_{ \mathtt{R}( \mathtt{L})} $ and$ \bar{{\bf{3}}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{3}}_{ \mathtt{R}( \mathtt{L})} $ . Especially, processes that change isospin by 3/2 units, such as$ n\to\pi^+\ell^- a $ , can only be induced by operators in the new irreps. Furthermore, we analyzed the momentum distributions of the charged lepton and mesons in three-body decay modes. Our results indicate that the distinct distribution behavior may help distinguish the underlying operator structures and potentially determine the ALP mass in future experimental searches.Based on this comprehensive theoretical framework, we have simulated proton decay processes involving an ALP and recast existing Super-K data to set bounds on the inverse decay widths of these exotic modes. Although our treatment of the experimental recasts is simplified and conservative, we still obtain meaningful results thanks to the huge number of protons in the experiment. These results are complementary to current searches for nucleon decay modes involving only SM final states. The bounds we have derived not only significantly improve upon inclusive limits set by experiments nearly four decades ago, but also extend across a broad range of ALP masses. From these results, we established conservative lower limits on the effective scales
$ \Lambda_\mathtt{eff} $ associated with the relevant Wilson coefficients. We found that the lower bounds on$ \Lambda_\mathtt{eff} $ for operators corresponding to the new chiral irreps are of the same order as those for operators in the usual irreps. Last, by employing these limits on$ \Lambda_\mathtt{eff} $ in the massless ALP limit, we further predict new bounds on the occurrence of some BNV neutron and hyperon decay modes. Our results impose very stringent limits on the branching ratios of exotic hyperon decay modes, while the projected bounds on neutron decays are within reach of future neutrino experiments such as JUNO and DUNE. -
By expanding the pseudoscalar matrix in Eq. (14) to the zeroth order in the meson fields, we obtain the following general vertices involving a baryon without any pseudoscalar mesons:
$ \begin{aligned}[b] {\cal{L}}_{{\cal{P}}B} =\;& \Big\{ \big[ c_1 {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{R}} + c_2 {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{L}} + c_3 \Lambda_\chi^{-1} ( {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{R},\mu} - {\cal{P}}_{udu}^{ \mathtt{L} \mathtt{R},\mu} ) i\tilde{\partial}_\mu \big]p_{\mathtt{L}} + \big[ c_1 {\cal{P}}_{dud}^{ \mathtt{L} \mathtt{R}} + c_2 {\cal{P}}_{dud}^{ \mathtt{L} \mathtt{L}} - c_3 \Lambda_\chi^{-1} ({\cal{P}}_{ddu}^{ \mathtt{L} \mathtt{R},\mu} -{\cal{P}}_{udd}^{ \mathtt{L} \mathtt{R},\mu} ) i\tilde{\partial}_\mu \big] n_{\mathtt{L}} \\ &+ {1\over \sqrt{6} } \big[ c_1 ( {\cal{P}}_{uds}^{ \mathtt{L} \mathtt{R}} + {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{R}}-2{\cal{P}}_{sud}^{ \mathtt{L} \mathtt{R}}) + c_2 ({\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{L}} - 2 {\cal{P}}_{sud}^{ \mathtt{L} \mathtt{L}}) - 3 c_3 \Lambda_\chi^{-1} ({\cal{P}}_{usd}^{ \mathtt{L} \mathtt{R},\mu} - {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{R},\mu}) i \tilde{\partial}_\mu \big] \Lambda^0_{\mathtt{L}} +{1\over \sqrt{2}} \big[ c_1 ( {\cal{P}}_{uds}^{ \mathtt{L} \mathtt{R}} - {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{R}}) - c_2 {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{L}}\\ & + c_3 \Lambda_\chi^{-1} ( 2 {\cal{P}}_{uds}^{ \mathtt{L} \mathtt{R},\mu} - {\cal{P}}_{usd}^{ \mathtt{L} \mathtt{R},\mu}- {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{R},\mu} ) i\tilde{\partial}_\mu \big] \Sigma^0_{\mathtt{L}} + \big[ c_1 {\cal{P}}_{usu}^{ \mathtt{L} \mathtt{R}} + c_2 {\cal{P}}_{usu}^{ \mathtt{L} \mathtt{L}} - c_3 \Lambda_\chi^{-1} ( {\cal{P}}_{uus}^{ \mathtt{L} \mathtt{R},\mu} - {\cal{P}}_{usu}^{ \mathtt{L} \mathtt{R},\mu} ) i\tilde{\partial}_\mu \big] \Sigma^+_{\mathtt{L}} \\ & + \big[ c_1 {\cal{P}}_{dds}^{ \mathtt{L} \mathtt{R}} + c_2 {\cal{P}}_{dds}^{ \mathtt{L} \mathtt{L}} + c_3 \Lambda_\chi^{-1} ({\cal{P}}_{dds}^{ \mathtt{L} \mathtt{R},\mu}-{\cal{P}}_{dsd}^{ \mathtt{L} \mathtt{R},\mu}) i\tilde{\partial}_\mu \big] \Sigma^-_{\mathtt{L}} +\big[ c_1 {\cal{P}}_{ssu}^{ \mathtt{L} \mathtt{R}} + c_2 {\cal{P}}_{ssu}^{ \mathtt{L} \mathtt{L}} + c_3 \Lambda_\chi^{-1} ( {\cal{P}}_{ssu}^{ \mathtt{L} \mathtt{R},\mu} - {\cal{P}}_{uss}^{ \mathtt{L} \mathtt{R},\mu} ) i\tilde{\partial}_\mu \big]\Xi^0_{\mathtt{L}} \\ & + \big[ c_1 {\cal{P}}_{sds}^{ \mathtt{L} \mathtt{R}} + c_2 {\cal{P}}_{sds}^{ \mathtt{L} \mathtt{L}} - c_3 \Lambda_\chi^{-1} ( {\cal{P}}_{ssd}^{ \mathtt{L} \mathtt{R},\mu} - {\cal{P}}_{dss}^{ \mathtt{L} \mathtt{R},\mu} ) i\tilde{\partial}_\mu \big] \Xi^-_{\mathtt{L}} \Big\} - \mathtt{L} \leftrightarrow \mathtt{R}. \end{aligned} $

(A1) Similarly, expanding the pseudoscalar matrix in Eq. (14) to the first order in the meson fields yields the following vertices containing a nucleon and a meson:
$ \begin{aligned}[b] {\cal{L}}_{{\cal{P}}^{\mathtt{N}}M} =\;& {i \over F_0}\Big\{ - \sqrt{2} \pi^+ c_3 \Lambda_\chi^{-1} {\cal{P}}_{uuu}^{ \mathtt{L} \mathtt{R},\mu} i \tilde{\partial}_\mu p_{\mathtt{L}} + \sqrt{2} \pi^- c_3 \Lambda_\chi^{-1} {\cal{P}}_{ddd}^{ \mathtt{L} \mathtt{R},\mu} i \tilde{\partial}_\mu n_{\mathtt{L}} + \frac{1}{\sqrt{2}} \pi^- \big[ c_1 {\cal{P}}_{dud}^{ \mathtt{L} \mathtt{R}} + c_2 {\cal{P}}_{dud}^{ \mathtt{L} \mathtt{L}} - c_3 \Lambda_\chi^{-1} ({\cal{P}}_{ddu}^{ \mathtt{L} \mathtt{R},\mu}-3{\cal{P}}_{udd}^{ \mathtt{L} \mathtt{R},\mu})i\tilde{\partial}_\mu \big] p_{\mathtt{L}} \\ &+ \frac{1}{\sqrt{2}} \pi^+ \big[ c_1 {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{R}} + c_2 {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{L}} + c_3 \Lambda_\chi^{-1} ({\cal{P}}_{uud}^{ \mathtt{L} \mathtt{R},\mu}-3{\cal{P}}_{udu}^{ \mathtt{L} \mathtt{R},\mu})i\tilde{\partial}_\mu \big] n_{\mathtt{L}} + \frac{1}{2} \pi^0 \big[ c_1 {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{R}} + c_2 {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{L}} + c_3 \Lambda_\chi^{-1} ({\cal{P}}_{udu}^{ \mathtt{L} \mathtt{R},\mu} + 3 {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{R},\mu})i\tilde{\partial}_\mu \big] p_{\mathtt{L}} \\ & - \frac{1}{2} \pi^0 \big[ c_1 {\cal{P}}_{dud}^{ \mathtt{L} \mathtt{R}} + c_2 {\cal{P}}_{dud}^{ \mathtt{L} \mathtt{L}} - c_3 \Lambda_\chi^{-1} (3{\cal{P}}_{ddu}^{ \mathtt{L} \mathtt{R},\mu} + {\cal{P}}_{udd}^{ \mathtt{L} \mathtt{R},\mu})i\tilde{\partial}_\mu \big]n_{\mathtt{L}} - \frac{1}{2\sqrt{3}} \eta \big[ c_1 {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{R}} -3 c_2 {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{L}} + c_3 \Lambda_\chi^{-1} ({\cal{P}}_{udu}^{ \mathtt{L} \mathtt{R},\mu} - {\cal{P}}_{uud}^{ \mathtt{L} \mathtt{R},\mu}) i \tilde{\partial}_\mu \big]p_{\mathtt{L}} \\ &- \frac{1}{2\sqrt{3}} \eta \big[ c_1 {\cal{P}}_{dud}^{ \mathtt{L} \mathtt{R}} -3 c_2 {\cal{P}}_{dud}^{ \mathtt{L} \mathtt{L}} + c_3 \Lambda_\chi^{-1} ({\cal{P}}_{ddu}^{ \mathtt{L} \mathtt{R},\mu} - {\cal{P}}_{udd}^{ \mathtt{L} \mathtt{R},\mu}) i \tilde{\partial}_\mu \big] n_{\mathtt{L}} + \frac{1}{\sqrt{2}} \bar{K}^0 \big[ c_1 {\cal{P}}_{usu}^{ \mathtt{L} \mathtt{R}} - c_2 {\cal{P}}_{usu}^{ \mathtt{L} \mathtt{L}} - c_3 \Lambda_\chi^{-1}({\cal{P}}_{usu}^{ \mathtt{L} \mathtt{R},\mu} + {\cal{P}}_{uus}^{ \mathtt{L} \mathtt{R},\mu})i\tilde{\partial}_\mu \big]p_{\mathtt{L}} \\ & + \frac{1}{\sqrt{2}} K^- \big[ c_1 {\cal{P}}_{dds}^{ \mathtt{L} \mathtt{R}} - c_2 {\cal{P}}_{dds}^{ \mathtt{L} \mathtt{L}} + c_3 \Lambda_\chi^{-1}({\cal{P}}_{dds}^{ \mathtt{L} \mathtt{R},\mu} + {\cal{P}}_{dsd}^{ \mathtt{L} \mathtt{R},\mu})i\tilde{\partial}_\mu \big]n_{\mathtt{L}} + \frac{1}{\sqrt{2}} K^- \big[ c_1 ( {\cal{P}}_{sud}^{ \mathtt{L} \mathtt{R}} + {\cal{P}}_{uds}^{ \mathtt{L} \mathtt{R}}) + c_2 {\cal{P}}_{sud}^{ \mathtt{L} \mathtt{L}} \\ &- c_3 \Lambda_\chi^{-1} ( {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{R},\mu}-{\cal{P}}_{uds}^{ \mathtt{L} \mathtt{R},\mu} -2{\cal{P}}_{usd}^{ \mathtt{L} \mathtt{R},\mu}) i \tilde{\partial}_\mu \big] p_{\mathtt{L}} + \frac{ 1}{\sqrt{2}} \bar{K}^0 \big[ c_1 ( {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{R}} + {\cal{P}}_{sud}^{ \mathtt{L} \mathtt{R}} ) + c_2 ( {\cal{P}}_{sud}^{ \mathtt{L} \mathtt{L}} - {\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{L}} ) \\ &- c_3 \Lambda_\chi^{-1} (2{\cal{P}}_{dsu}^{ \mathtt{L} \mathtt{R},\mu} + {\cal{P}}_{uds}^{ \mathtt{L} \mathtt{R},\mu} - {\cal{P}}_{usd}^{ \mathtt{L} \mathtt{R},\mu} ) i \tilde{\partial}_\mu \big]n_{\mathtt{L}} \Big\} + \mathtt{L} \leftrightarrow \mathtt{R}. \end{aligned} $

(A2) Note that the absence of
$ K^+\mathtt{N} $ and$ K^0\mathtt{N} $ terms is because an anti-strange quark is needed. -
In this Appendix, we summarize our complete numerical results for the decay widths which are expressed in terms of the WCs in the aLEFT. We denote the specific flavors in each WC by subscripts, with the first letter (
$ e,\; \mu,\; \tau $ ) indicating the lepton flavors and the other three numbers for the quark flavors (1, 2, 3 stand for$ u,\; d,\; s $ , respectively). For modes involving a neutrino, the subscript x can be either e, or μ, or τ. We neglect the ALP mass and numerically integrate all phase space factors associated with each WC squared. Since$ c_3 $ remains undetermined now, we retain its explicit dependence through$ \kappa_3(\equiv c_3/c_1) $ in these results. To present the results more compactly, we have removed the prefix "$ \partial a $ " from the subscripts of all relevant WCs.For the two-body decay processes, the complete results are
$ \begin{aligned}[b] {\Gamma_{p\to e^+ a} \over (0.1{\rm{GeV}})^9} =\;& 1300 |[C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{e112}|^2 + 1300 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121}|^2 + 50 \kappa_3^2 \big( |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121}|^2 + |[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112}|^2 \big) +2600 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121} [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112}^* \big)\\ & -510 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121} -[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112} ) [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112}^* \big) - 510 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121} -[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e121}^{-*} \big) \\ &-99 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121} [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112}^* \big) - 0.6 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112} -[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e121}^+ ) [C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{e112}^{*} \big)\\ & + 0.2 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e121}^+ [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e112}^{*} \big) - 0.5 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112} -[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e121}^+ ) [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e121}^{-*} \big) \\ & - 0.1 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e121}^+ [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e121}^{+*}\big) - 0.1 \kappa_3^2 \Re\big( [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e112}^{*}\big)+ \mathtt{L} \leftrightarrow \mathtt{R}, \end{aligned} $

(B1) $ \begin{aligned} {\Gamma_{p\to \mu^+ a} \over (0.1{\rm{GeV}})^9} =\;& 1300 |[C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 112}|^2 + 1200 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121}|^2 + 50 \kappa_3^2 \big( |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121}|^2 + |[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112}|^2 \big) + 2500 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121} [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112}^* \big) \\ & - 490 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121} -[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112} ) [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112}^* \big) - 490 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121} -[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 121}^{-*} \big) \\ &-100 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121} [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu112}^* \big) - 110 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112} -[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121} ) [C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 112}^{*} \big) \\ & + 43 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 121}^+ [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 112}^{*} \big) - 110 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112} -[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 121}^+ ) [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 121}^{-*} \big) \\ &- 22 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 121}^+ [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 121}^{+*} \big) - 22 \kappa_3^2 \Re\big( [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 112}^{*} \big) + \mathtt{L} \leftrightarrow \mathtt{R}, \end{aligned} $

(B2) $ \begin{aligned} {\Gamma_{\Sigma^+ \to e^+ a} \over (0.1{\rm{GeV}})^9} =\;& 2700 |[C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{e113}|^2 + 2600 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e131}|^2 + 160 \kappa_3^2 \big( |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e131}|^2 + |[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e113}|^2 \big) + 5300 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e131} [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e113}^* \big) \\ &- 1300 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e131} -[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e113} ) [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e113}^* \big) - 1300 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e131} -[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e113} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e131}^{-*} \big)\\ &-330 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e131} [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e113}^* \big) - 1.1 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e113} -[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e131}^+ ) ([C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e131}^{-*} + [C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{e113}^{*} ) \big) \\ &+ 0.6 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e131}^+ [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e113}^{*} \big) - 0.3 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e131}^+ [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e131}^{+*}\big) \\ &- 0.3 \kappa_3^2 \Re\big([C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e113} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e113}^{*} \big) + \mathtt{L} \leftrightarrow \mathtt{R}, \end{aligned} $

(B3) $ \begin{aligned}[b] {\Gamma_{\Sigma^+ \to \mu^+ a} \over (0.1{\rm{GeV}})^9} =\;& 2600 |[C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 113}|^2 + 2600 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 131}|^2 + 160 \kappa_3^2 \big( |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 131}|^2 + |[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 113}|^2 \big) \\ &+ 5200 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 131} [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 113}^* \big) - 1300 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 131} -[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 113} ) [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 113}^* \big) \\ &- 1300 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 131} -[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 113} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 131}^{-*} \big) - 330 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 131} [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 113}^* \big) \\ &- 230 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 113} -[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 131}^+ ) [C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 113}^{*} \big) + 110 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 131}^+ [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 113}^{*} \big) \\ &- 230 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 113} -[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 131}^+ ) [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 131}^{-*} \big) - 56 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 131}^+ [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 131}^{+*}\big) \\ & - 56 \kappa_3^2 \Re\big( [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 113} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 113}^{*} \big) + \mathtt{L} \leftrightarrow \mathtt{R}, \end{aligned} $

(B4) $ \begin{aligned}[b] {\Gamma_{n \to \nu_x a} \over (0.1{\rm{GeV}})^9} =\;& 1300 |[C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221}|^2 + 1300 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122}|^2 + 50 \kappa_3^2 \big( |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221}|^2 + |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122}|^2 \big) \\ &- 2600 \Re\big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x122}^- [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221}^{*} \big) - 520 \kappa_3 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122} -[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221} ) [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221}^{*} \big) \\ &- 510 \kappa_3 \Re\big( ([C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221} -[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x122}^{-*} \big) - 100 \kappa_3^2 \Re\big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x122}^+ [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221}^{*} \big), \end{aligned}$

(B5) $ \begin{aligned}[b] {\Gamma_{\Lambda^0 \to \nu_x a} \over (0.1{\rm{GeV}})^9} =\;& 1500 |[C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321}|^2 + 1500 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123}|^2 + 370 |[C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}|^2 + 360 \big( |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231}|^2 + |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132}|^2 \big) \\ & + 180 \kappa_3^2 \big( |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231}|^2 + |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132}|^2 \big) - 2900 \Re\big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^- [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321}^{*} \big) + 1500 \Re\big( [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321}^{*} \big) \\ &+ 1500 \Re\big( ([C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} -[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} ) [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321}^{*} \big) - 1500 \Re\big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^{*} \big) \\ &+ 1500 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} -[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^{-*} \big) - 1000 \kappa_3 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} -[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} ) [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321}^{*} \big) \\ &- 1000 \kappa_3 \Re\big( ([C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} -[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^{-*} \big) + 730 \Re\big( ([C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} -[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} ) [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^{*} \big) \\ &- 730 \Re\big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{-*} \big) - 510 \kappa_3 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} -[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} ) [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^{*} \big) \\ &- 350 \kappa_3^2 \Re\big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^+ [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{+*} \big)- 510 \kappa_3 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} -[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} ) ([C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^{-*} -[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{-*} ) \big), \end{aligned} $

(B6) $ \begin{aligned}[b] {\Gamma_{\Sigma^0 \to \nu_x a} \over (0.1{\rm{GeV}})^9} =\;& 1400 |[C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}|^2 + 1300 \big( |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231}|^2 + |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132}|^2 \big) + 300 \kappa_3^2 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^+|^2 \\ & + 82 \kappa_3^2 \big( |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231}|^2 + |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132}|^2 \big) - 2700 \Re\big( ([C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} +[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} ) [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^{*} \big) \\ & + 2700 \Re\big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{-*} \big) - 1300 \kappa_3 \Re\big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x123} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^{*} \big) \\ & + 1300 \kappa_3 \Re\big( ([C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} +[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^{+*} \big) + 670 \kappa_3 \Re\big( ([C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} +[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} ) [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^{*} \big) \\ &+ 160 \kappa_3^2 \Re\big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^+ [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{+*} \big) - 660 \kappa_3 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} +[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} ) ([C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^{-*} +[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{-*} ) \big) \\ &- 330 \kappa_3^2 \Re\big( ([C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} +[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^{+*} \big), \end{aligned} $

(B7) $ \begin{aligned}[b] {\Gamma_{\Xi^0 \to \nu_x a} \over (0.1{\rm{GeV}})^9} =\;& 3600 |[C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x331}|^2 + 3600 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x133}|^2 + 270 \kappa_3^2 \big( |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x331}|^2 + |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x133}|^2 \big) \\ &- 7200 \Re\big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x133}^- [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x331}^{*} \big) - 2000 \kappa_3 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x133} -[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x331} ) [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x331}^{*} \big) \\ &- 2000 \kappa_3 \Re\big( ([C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x331} -[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x133} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x133}^{-*} \big) - 540 \kappa_3^2 \Re\big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x133}^+ [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x331}^{*} \big), \end{aligned} $

(B8) $ \begin{aligned}[b] {\Gamma_{\Sigma^- \to e^- a} \over (0.1{\rm{GeV}})^9} =\;& 2800 |[C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{e223}|^2 + 2700 |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^-_{e232}|^2 + 170 \kappa_3^2 \big( |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e232}|^2 + |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223}|^2 \big) \\ &+ 5400 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^-_{e232} [C_{ eddd}^{\mathtt{VR}, \mathtt{SR}}]_{e223}^* \big) - 1400 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e232} -[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223} ) [C_{ eddd}^{\mathtt{VR}, \mathtt{SR}}]_{e223}^* \big) \\ &- 1300 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e232} -[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223} ) [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e232}^{-*} \big) - 340 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e232} [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223}^* \big) \\ &- 1.2 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223} -[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e232}^+ ) [C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{e223}^{*} \big) + 0.6 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e232}^{+*} \big) \\ &- 1.1 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223} -[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e232}^+ ) [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e232}^{-*} \big) - 0.3 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e223}^{*}\big) \\ &- 0.3 \kappa_3^2 \Re\big([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e232}^+ [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e232}^{+*} \big)+ \mathtt{L} \leftrightarrow \mathtt{R} , \end{aligned} $

(B9) $ \begin{aligned}[b] {\Gamma_{\Sigma^- \to \mu^- a} \over (0.1{\rm{GeV}})^9} =\;& 2700 |[C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 223}|^2 + 2600 |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 232}|^2 + 170 \kappa_3^2 \big( |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 232}|^2 + |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223}|^2 \big) \\ &+ 5300 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 232} [C_{ eddd}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 223}^* \big) - 1300 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 232} -[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223} ) [C_{ eddd}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 223}^* \big) \\ &- 1300 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 232} -[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223} ) [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 232}^{-*} \big) - 340 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 232} [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223}^* \big) \\ &- 230 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223} -[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 232}^+ ) [C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 223}^{*} \big) + 120 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 232}^{+*} \big) \\ &- 230 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223} -[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 232}^+ ) [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 232}^{-*} \big) - 58 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 223}^{*}\big) \\ &- 58 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 232}^+ [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 232}^{+*} \big) + \mathtt{L} \leftrightarrow \mathtt{R} , \end{aligned}$

(B10) $ \begin{aligned}[b] {\Gamma_{\Xi^- \to e^- a} \over (0.1{\rm{GeV}})^9} =\;& 3700 |[C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{e323}|^2 + 3600 |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^-_{e233}|^2 + 270 \kappa_3^2 \big( |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e233}|^2 + |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e332}|^2 \big) \\ &+7300 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^-_{e233} [C_{ eddd}^{\mathtt{VR}, \mathtt{SR}}]_{e323}^* \big) - 2000 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e332} - [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e233} ) [C_{ eddd}^{\mathtt{VR}, \mathtt{SR}}]_{e323}^* \big) \\ &- 2000 \kappa_3 \Re\big( ( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e332} - [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e233} ) [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e233}^{-*} \big) - 550 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e233} [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e332}^* \big) \\ &- 1.6 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e233}^+ - [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e332} ) [C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{e323}^{*} \big) + 0.8 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e332} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e233}^{+*} \big) \\ &- 1.5 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e233}^+ - [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e332} ) [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e233}^{-*} \big) - 0.4 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e332} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e332}^{*}\big) \\ &- 0.4 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e233}^+ [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e233}^{+*} \big)+ \mathtt{L} \leftrightarrow \mathtt{R} , \end{aligned} $

(B11) $ \begin{aligned}[b] {\Gamma_{\Xi^- \to \mu^- a} \over (0.1{\rm{GeV}})^9} =\;& 3600 |[C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 323}|^2 + 3600 |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 233}|^2 + 280 \kappa_3^2 \big( |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 233}|^2 + |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 332}|^2 \big) \\ &+ 7200 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 233} [C_{ eddd}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 323}^* \big) - 2000 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 332} - [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 233} ) [C_{ eddd}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 323}^* \big) \\ &- 2000 \kappa_3 \Re\big( ( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 332} - [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 233} ) [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 233}^{-*} \big) - 550 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 233} [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 332}^* \big)\\ &- 320 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 233}^+ - [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 332} ) [C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 323}^{*} \big) + 170 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 332} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 233}^{+*} \big) \\ &- 310 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 233}^+ - [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 332} ) [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 233}^{-*} \big) - 86 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 332} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 332}^{*}\big) \\ &- 86 \kappa_3^2 \Re\big([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 233}^+ [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 233}^{+*} \big) + \mathtt{L} \leftrightarrow \mathtt{R}. \end{aligned} $

(B12) For processes with an antineutrino in the final state, their decay widths can be obtained simply by exchanging the chiral labels
$ \mathtt{L} $ and$ \mathtt{R} $ in the WCs of the corresponding neutrino cases.For the three-body nucleon decay processes, the final results are summarized as follows:
$ \begin{aligned}[b] {\Gamma_{p\to e^+ \pi^0 a} \over (0.1{\rm{GeV}})^9} =\;& 52 |[C_{euud}^{\mathtt{VL}, \mathtt{SL}}]_{e112}|^2 + 51 |[C_{eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121}|^2 + 14 \kappa_3^2 |[C_{euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112}|^2 + \kappa_3^2 |[C_{eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121}|^2 \\ &+ 102 \Re\big( [C_{eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121} [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112}^* \big) - 14 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112} +[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121} ) [C_{euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112}^* \big) \\ &- 9.6 \kappa_3 \Re\big( ([C_{euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112} +[C_{eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e121}^{+*} \big) + 6.3 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121} [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112}^* \big) \\ &- 0.1 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{e112} +[C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e121}^- ) [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112}^* \big) + 0.03 \kappa_3^2 \Re \big( [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e112}^* \big) \\ & -0.02 \kappa_3 \Re\big( ([C_{euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112} +[C_{eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121} ) [C_{eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e121}^{+*} \big) + 0.02 \kappa_3^2 \Re \big( [C_{eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121} [C_{euud}^{\mathtt{SR}, \mathtt{VL}}]_{e112}^* \big)\\ & + 0.003 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e121}^+ [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e121}^{+*} \big)+ \mathtt{L} \leftrightarrow \mathtt{R}, \end{aligned} $

(B13) $ \begin{aligned}[b] {\Gamma_{p\to \mu^+ \pi^0 a} \over (0.1{\rm{GeV}})^9} =\;& 45 |[C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 112}|^2 + 44 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121}|^2 + 13 \kappa_3^2 |[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112}|^2 + \kappa_3^2 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121}|^2 \\ &+ 89 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121} [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112}^* \big) - 16 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112} +[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121} ) [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 112}^* \big) \\ &- 13 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112} +[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121} ) [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112}^{*} \big) + 5.7 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121} [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112}^* \big) \\ &- 8.6 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112} +[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 121}^{+*} \big) + 4.6 \kappa_3^2 \Re \big( [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 112}^* \big) \\ & -2.6 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112} +[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121} ) [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 121}^{+*} \big) + 3.6 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 112}^* \big) \\ &+ 0.45 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 121}^+ [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 121}^{+*} \big)+ \mathtt{L} \leftrightarrow \mathtt{R} , \end{aligned} $

(B14) $ \begin{aligned}[b] {\Gamma_{p\to e^+ \eta a} \over (0.1{\rm{GeV}})^9} =\;& 1.6 |[C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{e112}|^2 + 0.06 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121}|^2 + 0.02 \kappa_3^2 \big( |[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112}|^2 + |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121}|^2\big) \\ &- 0.6 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121} [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112}^* \big) + 0.2 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121} - [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112} ) [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112}^* \big) \\ &+ 0.05 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112} - [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e121}^{-*} \big) - 0.04 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121} [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112}^* \big) \\ &+ 10^{-3} \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]^+_{e121} - [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e112} ) [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112}^* \big) - 10^{-4} \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e112}^* \big) \\ &+ 2\cdot10^{-4} \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e112} - [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]^+_{e121} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e121}^{-*} \big) \\ &+ 5\cdot10^{-5} \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e121}^+ [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e121}^{+*} + [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e112}^* \big) + \mathtt{L} \leftrightarrow \mathtt{R}, \end{aligned}$

(B15) $ \begin{aligned}[b] {\Gamma_{p\to \mu^+ \eta a} \over (0.1{\rm{GeV}})^9} =\;& |[C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 112}|^2 + 0.04 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121}|^2 + 0.01 \kappa_3^2 \big( |[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112}|^2 + |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121}|^2 \big) \\ & - 0.4 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121} [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112}^* \big) + 0.1 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]^+_{\mu 121} - [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 112} ) [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112}^* \big) \\ &+ 0.1 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121} - [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112} ) [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112}^* \big) - 0.03 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121} [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112}^* \big) \\ &+ 0.03 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112} - [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 121}^{-*} \big) - 0.01 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 112}^* \big) \\ &+ 0.02 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 112} - [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]^+_{\mu 121} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 121}^{-*} \big) \\ &+ 0.005 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 121}^+ [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 121}^{+*} + [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 112}^* \big) + \mathtt{L} \leftrightarrow \mathtt{R} , \end{aligned} $

(B16) $ \begin{aligned}[b] {\Gamma_{p\to e^+ K^0 a} \over (0.1{\rm{GeV}})^9} =\;& 2.1 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e131}|^2 + 1.2 |[C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{e113}|^2 + 0.2 \kappa_3^2 \big( |[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e113}|^2 + |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e131}|^2\big) \\ &- 3.2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e131} [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e113}^* \big) - 0.7 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e113} + [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e131} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e131}^{-*} \big) \\ &+ 0.6 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e131} + [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e113} ) [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e113}^* \big) + 0.4 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e131} [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e113}^* \big) \\ &- 0.004 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e113} + [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]^+_{e131} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e131}^{-*} \big) + 0.001 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e131} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e113}^* \big) \\ &+ 0.003 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]^+_{e131} + [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e113} ) [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e113}^* \big) \\ &+ 5\cdot10^{-4} \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e131}^+ [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e131}^{+*} + [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e113} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e113}^* \big) + \mathtt{L} \leftrightarrow \mathtt{R}, \end{aligned} $

(B17) $ \begin{aligned}[b] {\Gamma_{p\to \mu^+ K^0 a} \over (0.1{\rm{GeV}})^9} =\;& 1.4 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 131}|^2 + 0.9 |[C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 113}|^2 + 0.1 \kappa_3^2 \big( |[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 113}|^2 + |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 131}|^2 \big) \\ & - 2.2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 131} [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 113}^* \big) - 0.5 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 113} + [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 131} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 131}^{-*} \big) \\ &- 0.4 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 113} + [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]^+_{\mu 131} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 131}^{-*} \big) + 0.3 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 131} [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 113}^* \big) \\ &+ 0.4 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 131} + [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 113} ) [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 113}^* \big) + 0.1 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 131} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 113}^* \big) \\ &+ 0.3 \kappa_3 \Re\big( ([C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]^+_{\mu 131} + [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 113} ) [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 113}^* \big) \\ &+ 0.05 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 131}^+ [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 131}^{+*} + [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 113} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 113}^* \big)+ \mathtt{L} \leftrightarrow \mathtt{R} , \end{aligned} $

(B18) $ \begin{aligned}[b] {\Gamma_{n \to e^+ \pi^- a} \over (0.1{\rm{GeV}})^9} =\;& 102 |[C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{e112}|^2 + 100|[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121}|^2 + 27 \kappa_3^2 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121}|^2 + 4.2 \kappa_3^2 |[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112}|^2 \\ &+ 202 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121} [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112}^* \big) + 29 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112} +[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e121}^{+*} \big) \\ & - 5 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112} +[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121} ) [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112}^* \big) - 21 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121} [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112}^* \big) \\ &+ 0.2 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{e112} +[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{e121} ) [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e121}^{+*} \big) - 0.03 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{e121} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e112}^* \big) \\ &- 0.08 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{e112} +[C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e121}^- ) [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112}^* \big) + 0.05 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{e121}^+ [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{e121}^{+*} \big) \\ &+ 0.005 \kappa_3^2 \Re \big( [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{e112} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{e112}^* \big)+ \mathtt{L} \leftrightarrow \mathtt{R}, \end{aligned} $

(B19) $ \begin{aligned}[b] {\Gamma_{n \to \mu^+ \pi^- a} \over (0.1{\rm{GeV}})^9} =\;& 89 |[C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 112}|^2 + 87 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121}|^2 + 25 \kappa_3^2 |[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121}|^2 + 4 \kappa_3^2 |[C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112}|^2 \\ &+ 176 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121} [C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112}^* \big) + 31 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112} +[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121} ) [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 121}^{+*} \big) \\ &+ 26 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112} +[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121} ) [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 121}^{+*} \big) - 20 \kappa_3^2 \Re\big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121} [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112}^* \big) \\ &- 13 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 112} +[C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 121}^- ) [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112}^* \big) - 5.5 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 121} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 112}^* \big) \\ &- 4.4 \kappa_3 \Re\big( ([C_{ euud}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 112} +[C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 121} ) [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112}^* \big) + 9 \kappa_3^2 \Re \big( [C_{ eudu}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 121}^+ [C_{ eudu}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 121}^{+*} \big) \\ & + 0.7 \kappa_3^2 \Re \big( [C_{ euud}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 112} [C_{ euud}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 112}^* \big)+ \mathtt{L} \leftrightarrow \mathtt{R}, \end{aligned} $

(B20) $ \begin{aligned}[b] {\Gamma_{p \to \nu_x \pi^+ a} \over (0.1{\rm{GeV}})^9} =\;& 101 |[C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221}|^2 + 99 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122}|^2 + 27 \kappa_3^2 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122}|^2 + 4.1 \kappa_3^2 |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221}|^2 \\ &- 199 \Re \big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221}^* \big) + 29 \kappa_3 \Re\big( ([C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x122}^{+*} \big) \\ &- 21 \kappa_3^2 \Re\big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122} [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221}^* \big) + 5.1 \kappa_3 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122} - [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221} ) [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221}^* \big), \end{aligned} $

(B21) $ \begin{aligned}[b] {\Gamma_{p \to \nu_x K^+ a} \over (0.1{\rm{GeV}})^9} =\;& 3.3 |[C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321}|^2 + 3.2 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123}|^2 +1.4 |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231}|^2 +0.9 \kappa_3^2 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132}|^2 \\ &+ 0.2 \kappa_3^2 \big( |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231}|^2 + |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x123}|^2 \big) +0.1 \big( |[C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}|^2 + |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132}|^2 \big) \\ &- 6.5 \Re \big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321}^* \big) + 4.1 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} - [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321} ) [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^{-*} \big) \\ &+ 1.6 \kappa_3 \Re\big( ( [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{+*} \big) - 1.3 \kappa_3 \Re \big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{+*} \big) \\ &+ 1.2 \Re\big( ( [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} ) ([C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^{*} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{-*} ) \big) \\ &+ 0.9 \kappa_3^2 \Re\big( ( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x123} -[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{+*} \big) + 0.7 \kappa_3 \Re \big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^- [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^{+*} \big)\\ &+ 0.8 \kappa_3 \Re\big( ( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} - [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321} ) [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^{+*} \big) - 0.7 \kappa_3 \Re \big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^- [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^{+*} \big) \\ &+ 0.8 \kappa_3 \Re\big( ( [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^{+*} \big) - 0.5 \kappa_3^2 \Re \big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^+ [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^{+*} \big) \\ &+ 0.7 \Re\big( ( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} - [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231} ) [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^{-*} \big) - 0.3 \Re \big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^- [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^* \big)\\ &+ 0.1 \kappa_3 \Re\big( ( [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{+*} \big) \\ &+ 0.07 \kappa_3 \Re\big( ( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x123} - [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} ) ([C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^{*} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{-*} ) \big), \end{aligned} $

(B22) $ \begin{aligned}[b] {\Gamma_{n \to \nu_x \pi^0 a} \over (0.1{\rm{GeV}})^9} =\;& 52 |[C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221}|^2 + 51 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122}|^2 + 14 \kappa_3^2 |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221}|^2 + 1.1 \kappa_3^2 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122}|^2 \\ &- 103 \Re \big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221}^* \big) + 15 \kappa_3 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122} - [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221} ) [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221}^* \big) \\ &+ 9.7 \kappa_3 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122} - [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x122}^{+*} \big) + 6.4 \kappa_3^2 \Re\big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122} [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221}^* \big), \end{aligned} $

(B23) $ \begin{aligned}[b] {\Gamma_{n \to \nu_x \eta a} \over (0.1{\rm{GeV}})^9} =\;& 1.7 |[C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221}|^2 + 0.06 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122}|^2 + 0.02 \kappa_3^2 \big( |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221}|^2 + |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122}|^2 \big) \\ &+ 0.6 \Re \big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x122} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221}^* \big) + 0.2 \kappa_3 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122} - [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221} ) [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x221}^* \big) \\ &+ 0.05 \kappa_3 \Re\big( ([C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122} - [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x122}^{-*} \big) - 0.04 \kappa_3^2 \Re\big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x122} [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x221}^* \big), \end{aligned} $

(B24) $ \begin{aligned}[b] {\Gamma_{n \to \nu_x K^0 a} \over (0.1{\rm{GeV}})^9} =\;& 3.2 |[C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321}|^2 + 3.1 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123}|^2 + 2.1 |[C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}|^2 + 1.3 |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132}|^2 \\ &+ 0.9 \kappa_3^2 |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231}|^2 + 0.2 \kappa_3^2 \big( |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132}|^2 + |[C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x123}|^2 \big) + 0.1 |[C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231}|^2 \\ &- 6.3 \Re \big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321}^* \big) + 5.1 \Re\big( ( [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} ) [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^{*} \big) \\ &+ 3.9 \Re\big( ( [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} ) [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{-*} \big) + 3.3 \Re \big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^* \big) \\ &+ 1.6 \kappa_3 \Re\big( ( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} - [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321} ) [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^{+*} \big) - 1.4 \kappa_3 \Re \big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^* \big) \\ &- 1.3 \kappa_3 \Re \big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^+_{x231} [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{-*} \big) + 1.2 \Re\big( ( [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x123} ) [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^{-*} \big) \\ &+ 0.9 \Re \big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^* \big) + 0.9 \kappa_3^2 \Re\big( ( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x123} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} ) [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^{+*} \big) \\ &+ 0.8 \kappa_3 \Re\big( ( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x123} ) ([C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x321}^{*} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^{-*} ) \big) \\ &+ 0.8 \kappa_3 \Re \big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^* \big) - 0.7 \kappa_3 \Re \big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x123} [C_{ \nu ddu}^{\mathtt{VL}, \mathtt{SL}}]_{x231}^* \big) \\ &+ 0.7 \Re \big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{-*} \big) + 0.7 \kappa_3 \Re \big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{+*} \big) \\ &- 0.6 \kappa_3 \Re \big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^-_{x132} [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x123}^{+*} \big) - 0.4 \kappa_3^2 \Re \big( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x123} [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]_{x132}^{+*} \big) \\ &- 0.1 \kappa_3 \Re \big( [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]^-_{x231} [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^{+*} \big) + 0.07 \kappa_3 \Re\big( ( [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x132} - [C_{ \nu udd}^{\mathtt{SR}, \mathtt{VL}}]^+_{x123} ) [C_{ \nu ddu}^{\mathtt{SR}, \mathtt{VL}}]_{x231}^{-*} \big), \end{aligned} $

(B25) $ \begin{aligned}[b] {\Gamma_{n \to e^- \pi^+ a} \over (0.1{\rm{GeV}})^9} =\;& 10 \kappa_3^2 \big( |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e222}|^2 + |[C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e222}|^2 \big) + 0.05 \kappa_3^2 \Re \big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e222} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e222}^* \big), \end{aligned} $

(B26) $ \begin{aligned}[b] {\Gamma_{n \to \mu^- \pi^+ a} \over (0.1{\rm{GeV}})^9} =\;& 9.7 \kappa_3^2 \big( |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 222}|^2 + |[C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 222}|^2 \big) + 8.5 \kappa_3^2 \Re \big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 222} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 222}^* \big), \end{aligned} $

(B27) $ \begin{aligned}[b] {\Gamma_{n \to e^- K^+ a} \over (0.1{\rm{GeV}})^9} =\;& 2.3 |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^-_{e232}|^2 + 1.3 |[C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{e223}|^2 + 0.2 \kappa_3^2 \big( |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223}|^2 + |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e232}|^2 \big) \\ & - 3.4 \Re\big( [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]^-_{e232} [C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{e223}^* \big) - 0.7 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223} + [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e232} ) [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e232}^{-*} \big) \\ &+ 0.6 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223} + [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e232} ) [C_{ eddd}^{\mathtt{VR}, \mathtt{SR}}]_{e223}^* \big) + 0.4 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e232} [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223}^* \big) \\ &- 0.004 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223} + [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e232} ) [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e232}^{-*} \big) + 0.003 \kappa_3 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223} [C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{e223}^* \big) \\ &+ 0.003 \kappa_3 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e232} [C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{e223}^* \big) + 0.001 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e232} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e223}^* \big) \\ &+5\cdot10^{-4} \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{e223} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e223}^* + [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{e232} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{e232}^{+*} \big) + \mathtt{L} \leftrightarrow \mathtt{R}, \end{aligned} $

(B28) $ \begin{aligned}[b] {\Gamma_{n \to \mu^- K^+ a} \over (0.1{\rm{GeV}})^9} =\;& 1.5|[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 232}|^2 + 0.9 |[C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 223}|^2 + 0.2 \kappa_3^2 |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223}|^2 + 0.1 \kappa_3^2 |[C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 232}|^2 \\ & - 2.4 \Re\big( [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]^-_{\mu 232} [C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 223}^* \big) - 0.5 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223} + [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 232} ) [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 232}^{-*} \big) \\ &- 0.5 \kappa_3 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 232}^{-*} \big) + 0.5 \kappa_3 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223} [C_{ eddd}^{\mathtt{VR}, \mathtt{SR}}]_{\mu 223}^* \big) \\ &+ 0.4 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 223} - [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^-_{\mu 232} ) [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 232}^{+*} \big) + 0.3 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 232} [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223}^* \big) \\ &+ 0.3 \kappa_3 \Re\big( ([C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223} + [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 232} ) [C_{ eddd}^{\mathtt{VL}, \mathtt{SL}}]_{\mu 223}^* \big) + 0.2 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 232} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 223}^* \big) \\ &+ 0.1 \kappa_3^2 \Re\big( [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]_{\mu 223} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 223}^* + [C_{ eddd}^{\mathtt{SL}, \mathtt{VR}}]^+_{\mu 232} [C_{ eddd}^{\mathtt{SR}, \mathtt{VL}}]_{\mu 232}^{+*} \big) + \mathtt{L} \leftrightarrow \mathtt{R}. \end{aligned} $

(B29) Similarly, we explicitly show only processes with neutrinos in the final state. The decay widths for the antineutrino counterparts can be obtained simply through
$ \mathtt{L} \leftrightarrow \mathtt{R} $ . When restricted to the WCs associated with the$ {\bf{8}}_{ \mathtt{L}( \mathtt{R})} \otimes {\bf{1}}_{ \mathtt{R}( \mathtt{L})} $ irreps, our above results agree with those given in [12].
Comprehensive investigation on baryon number violating nucleon decays involving an axion-like particle
- Received Date: 2025-10-15
- Available Online: 2026-03-01
Abstract: In this work, we systematically investigate baryon number violating (BNV) nucleon decays into an axion-like particle (ALP), within a low energy effective field theory extended with an ALP, named as aLEFT. Unlike previous studies in the literature, we consider contributions to nucleon decays from a complete set of dimension-eight BNV aLEFT operators involving light u, d, s quarks. We perform the chiral irreducible representation (irrep) decomposition of all those interactions under the QCD chiral group






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: