Constraining Symmetry Energy from Pygmy Dipole Resonances in ⁶⁸Ni and ¹³²Sn

The properties of strong interaction matter, such as nuclear systems, are of both the experimental and theoretical interest. Its thermodynamic properties are governed by the nuclear equation of state, which is a function of the density, the temperature, and the isospin asymmetry. Asymmetric nuclear matter refers to the nuclear systems with different ratios of neutrons to protons. The study on equation of state of asymmetric nuclear matter is a fundamental and crucial research topic in the field of nuclear physics and astrophysics, which holds significant implications for the areas such as nuclear structures, nuclear reactions, and properties of neutron stars[1, 2]. Over the past few decades, extensive efforts have been made to understand the equation of state for asymmetric nuclear matter. However, there remains considerable debate, particularly concerning the equation of state for asymmetric nuclear matter, specifically for its isospin dependent component, known as the symmetry energy. Therefore, current research on the equation of state of asymmetric nuclear matter predominantly focuses on the study of the density dependence of symmetry energy.

Information on the symmetry energy can be obtained from various observables, such as neutron skins, charge radii of mirror-pair nuclei, binding energies of finite nuclei, isospin diffusions and isotopic distributions in Heavy-ion collisions and neutron star properties[3−12], none of them being so far conclusive by itself. The isovector electric or change-exchange giant resonances are much sensitive to the density dependence of symmetry energy. Hence the properties of giant resonances have ever been used to evaluate the nuclear symmetry energy. In Refs.[13−16], it is found that the value of the symmetry energy is strongly correlated with the centroid energy of the IVGDR in spherical nuclei. The electric dipole polarizabilities have recently been measured in $ ^{208} {\rm{Pb}}$, $ ^{68} {\rm{Ni}}$, $ ^{48} {\rm{Ca}}$, and Sn isotopes, and many studies try to constrain symmetry energy using electric dipole polarizabilities [17−24]. The isovector giant quadrupole resonance has also been used to get information of symmetry energy[25]. The properties of charge-exchange giant resonances, such as isobaric analog state, Gamow–Teller, spin-dipole, and anti-analog giant dipole resonances can be used to constrain the equation of states of asymmetry nuclear matter[26−30]. In the review paper by Xavier[2], more details can be found about the symmetry energy and giant resonances as well as their relationship. As we know that pygmy dipole resonance (PDR) appears in the strength distribution of isovector dipole resonances in exotic nuclei[31−33]. The PDR in neutron-rich nucleus is usually explained as a vibration in which the excess neutrons oscillate against a proton–neutron saturated core. The PDR has been measured experimentally in $ ^{130,132} {\rm{Sn}}$, $ ^{26} {\rm{Ne}}$ and $ ^{68} {\rm{Ni}}$[34−36]. It is found that the PDR of exotic nucleus is highly sensitive to the density dependence of symmetry energy. So the measured strength of the PDR can be employed to constrain the symmetry energy parameters, such as the value of symmetry energy and its slope parameter at saturation density[37, 38].

In Ref.[38], the measured percentages of energy-weighted sum rules (EWSR) exhausted by the pygmy dipole resonances in $ ^{68} {\rm{Ni}}$ and $ ^{132} {\rm{Sn}}$ are used to constrain the symmetry energy and its slope parameter at saturation density. The calculations are performed by using a representative set of Skyrme effective forces and relativistic meson-exchange effective Lagrangians. In this work, we will investigate again the correlation between the percentage of EWSR and the slope parameter of symmetry energy by considering three new features that containing more physical information. Firstly, we employ a family of effective Skyrme interactions in the calculations to get more clean correlation between the percentage of EWSR and the density dependence of symmetry energy. The interactions are named as SAMi-J interactions[39], they are built by fitting the parameters to some properties of finite nuclei. At the same time, the symmetry energy remains fixed value (≈22 MeV) at $ \rho\simeq $ 0.1 ${\rm{fm}} ^{-3} $ as a constraint, in such way the interactions are characterized by different values of the symmetry energies and slope parameters at saturation density. In the fitting procedure, all isoscalar observables remain unchanged, e.g., the incompressibility coefficient almost equals to 245 MeV. Secondly, some research works suggest that observables from finite nuclei usually provide more precise constraints on symmetry energy and its slope parameter at subsaturation density rather than at saturation density[14, 40−42], so we will constrain the density dependence of symmetry energy not only at saturation density, but it is also quite interesting to constrain the symmetry energy at subsaturation density in this work. Pairing correlation might affect the distribution of PDR in $ ^{68} {\rm{Ni}}$, which is often ignored in previous research works. Consequently it may also result in slightly different values of symmetry energy and its slope parameter. This shall be discussed in this study.

The paper is organized as follows. A brief report on the Skyrme HF and RPA (or HF+BCS and QRPA) methods is presented in Section II. In Section III we show the results and discussions. Finally, a summary and some remarks are given in Section IV.

The standard form of the Skyrme interaction and its energy density functional can be found in Ref. [45]. Within the Skyrme HF+BCS approximation, the quasiparticle wave functions and their quasiparticle energies are obtained from the self-consistent equation,

Where $ U_{b}({\bf{r}}) = V_{c}^{b}({\bf{r}})+\delta_{b,proton}V_{coul}({\bf{r}}) -iV_{so}^{b}({\bf{r}})\cdot({\boldsymbol{\nabla}}\times{\boldsymbol{\sigma}})+ V_{pair}^{b} $, $ V_{c}^{b}({\bf{r}}) $ is the central potential field for nucleons, $ V_{coul}({\bf{r}}) $ is the Coulomb potential, $ V_{so}^{b}({\bf{r}}) $ is the spin-orbit potential, and $ V_{pair}^{b} $ is the pairing potential. For the Skyrme HF calculations, the pairing potential is blocked.

We employ a density dependent zero range pairing force in our calculations, which is expressed as,

where $ \rho({\bf{r}}) $ is the nucleon density, $ \rho_{0} $ is the saturation density of nucleons (with a numerical value of 0.16 ${\rm{fm}} ^{-3} $), and η can take values of 1.0, 0.5, and 0.0, corresponding to surface, mixed, and volume pairing correlations[46, 47], respectively. Since the mixed type pairing interaction has the advantages of surface and volume pairing interactions, so we adopt it as the pairing interaction in our calculations. By fitting the experimental neutron pairing gap (1.39 MeV) of $ ^{68} {\rm{Ni}}$ calculated through a five-point formula, the strength $ V_{0} $ of the pairing force can be determined, the values of $ V_{0} $ are -561.8, -563.3, -579.5, -588.7, and -589.3 MeV $ \cdot $ ${\rm{fm}} ^3 $ for SAMi-27 to SAMi-35, respectively.

The isovector giant dipole resonance states can be obtained from the RPA or quasiparticle RPA[48]. The well-known RPA (QRPA) method in matrix form is given by,

where $ E_{\nu} $ is the excitation energy of the $ {\nu}-{\rm{th}} $ excited state, and $ {\rm{X}}^{\nu} $, $ {\rm{Y}}^{\nu} $ are amplitudes for forward and backward transitions, respectively.

The reduced transition matrix strength can be expressed as,

where $ \hat{F}_{J} $ is the external field transition operator. For the isovector giant dipole resonance, the external field operator is,

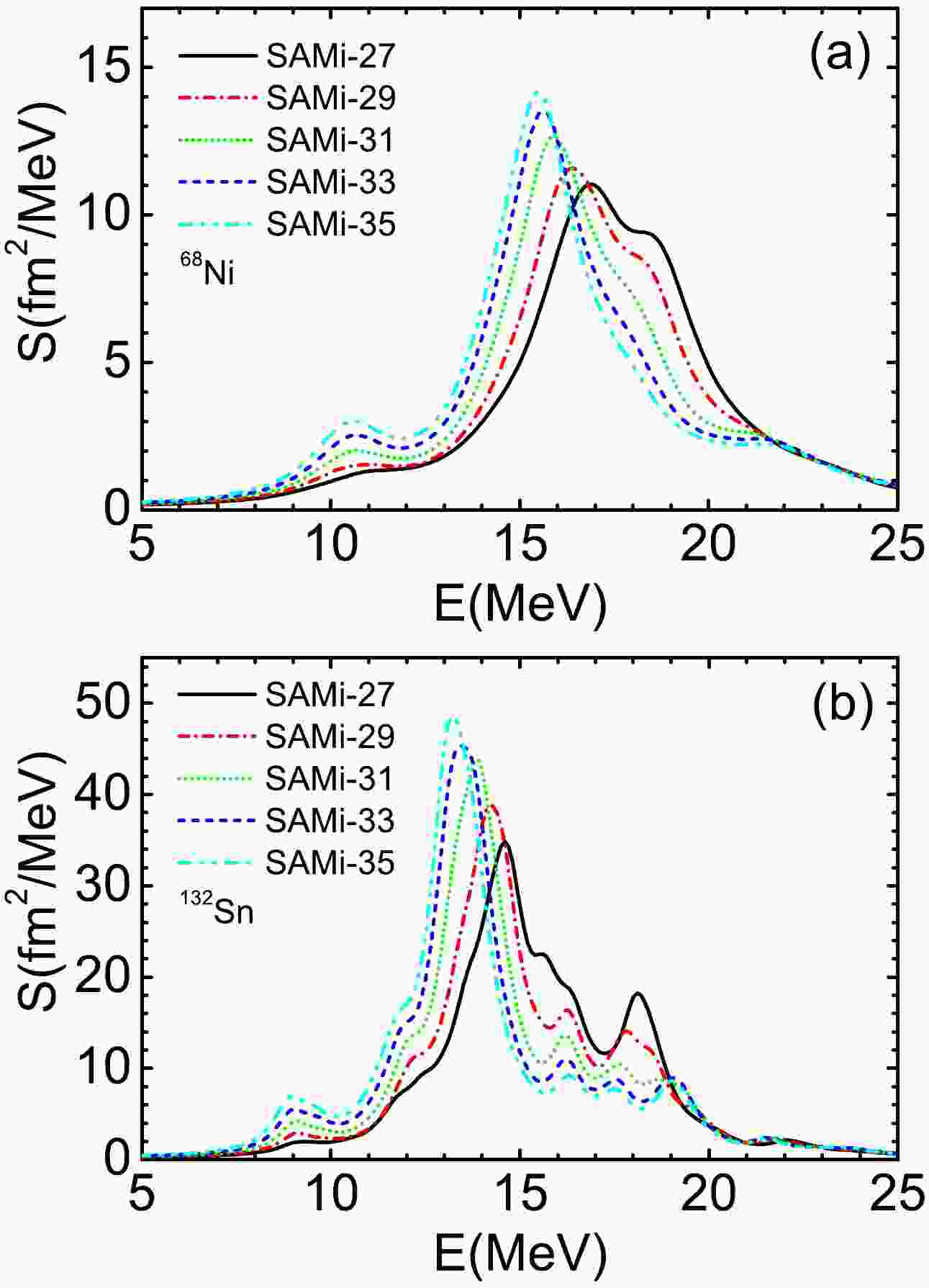
Firstly we employe the Skyrme HF plus RPA methods to compute the ground-state properties, excited states of $ ^{68} {\rm{Ni}}$ and $ ^{132} {\rm{Sn}}$ as well as the constraints on the density dependence of symmetry energy. The effect of pairing on the results will be discussed in the last paragraph of this scetion. The dipole strength distributions of $ ^{68} {\rm{Ni}}$ and $ ^{132} {\rm{Sn}}$ are shown in Fig. 1, the results are calculated by using SMAi-J Skyrme interactions. One can see that the pygmy dipole resonances are located at energy around 11 MeV for $ ^{68} {\rm{Ni}}$ (9 MeV for $ ^{132} {\rm{Sn}}$), while the giant dipole resonances are located at energy around 16 MeV for $ ^{68} {\rm{Ni}}$ (14 MeV for $ ^{132} {\rm{Sn}}$). As shown in the figures, the dipole strength distributions for two nuclei are much sensitive to density dependence of the symmetry energy, not only for the giant dipole resonances, but also for the pygmy dipole resonances. For the interaction with larger symmetry energy, it gives a stronger response strength, and a lower peak energy for giant dipole resonance, this happens both for the strength distributions of $ ^{68} {\rm{Ni}}$ and $ ^{132} {\rm{Sn}}$. This could be explained as the following: in general, there is an inverse correlation between the particle-hole configuration energies and their contribution to the giant resonance states in RPA calculations. If the configuration energies decrease (increase), their partial reduced transition amplitudes increase (decrease). The properties mentioned above are usually used to constrain the equation of state of asymmetric nuclear matter[14, 37, 38, 42].

Figure 1.  (color online) The dipole strength distributions of $ ^{68} {\rm{Ni}}$ (a) and $ ^{132} {\rm{Sn}}$ (b), the results are calculated by SAMi-J interactions.

In Ref. [38], the properties of pygmy dipole resonances of $ ^{68} {\rm{Ni}}$ and $ ^{132} {\rm{Sn}}$ have been suggested to obtain the information of symmetry energy at saturation density. Several representative relativistic and non-relativistic effective interactions are adopted in the calculations. In this work, we will use the pygmy dipole states given by SAMi-J Skyrme interactions to constrain the properties of symmetry energy. For such interactions, the symmetry energies at $ \rho\simeq $ 0.1 ${\rm{fm}} ^{-3} $ are kept unchanged. So they could have different behaviours at the densities of 0.11 ${\rm{fm}} ^{-3} $ and 0.16 ${\rm{fm}} ^{-3} $, respectively. Also the incompressibility coefficients of these interactions are kept as 245 MeV. Such features may give a smaller uncertainty on the constrained results. For the convenience of readers, we show the calculated symmetry energies and its slope parameters at density of 0.11 (0.16) ${\rm{fm}} ^{-3} $ for the SAMi-J Skyrme interactions in Table I. Experimentally the percentage of energy-weighted sum rule exhausted by the pygmy dipole resonances in $ ^{132} {\rm{Sn}}$ has been measured with the LAND-FRS facility at GSI, Darmstadt in 2005. The measured value of the EWSR percentage for $ ^{132} {\rm{Sn}}$ is 2.6% ± 1.6%[34]. Later, the EWSR percentage exhausted by the $ ^{68} {\rm{Ni}}$ pygmy dipole resonances has been measured by using the RISING setup at the fragment separator of GSI in 2009. The measured EWSR percentage for $ ^{68} {\rm{Ni}}$ is 5.0% ± 1.5%[36]. In Fig. 2 (a), the EWSR percentages exhausted by pygmy dipole resonances in $ ^{68} {\rm{Ni}}$ and $ ^{132} {\rm{Sn}}$ are plotted as function of symmetry energy slope parameters at nuclear saturation density. The solid circles (blue) and squares (green) are the results calculated by using SAMi-J Skyrme effective interactions for $ ^{68} {\rm{Ni}}$ and $ ^{132} {\rm{Sn}}$, the blue and green lines are the fitted results. It is seen that the calculated EWSR percentages show very good linear function of the slope parameters at nuclear saturation density. It means that the EWSR percentage is very sensitive to the density dependence of symmetry energy. The shaded areas with blue and green colors are the experimental results for $ ^{68} {\rm{Ni}}$ and $ ^{132} {\rm{Sn}}$, respectively. The constrained slope parameter L is to be in the interval 46.8–97.4 MeV for $ ^{68} {\rm{Ni}}$ and 34.0–93.2 MeV for $ ^{132} {\rm{Sn}}$. Considering the overlapped area constrained from two nuclei yields the final constraints: the slope parameter L at saturation density is in the range of 46.8–93.2 MeV, which overlaps with the value in Ref. [38]. In Fig. 2 (b), the good linear correlation of symmetry energies J and its slope parameters L of SAMi-J interactions at nuclear saturation density is shown. We can deduce the value of symmetry energy from the obtained range of slope parameter. J is in the range of 28.5–32.9 MeV, it is a little bit smaller than the value in Ref. [38], where J is 31.0–33.6 MeV.

Figure 2.  (color online) Panel (a), the percentage of EWSR exhausted by the PDR in $ ^{68} {\rm{Ni}}$ and $ ^{132} {\rm{Sn}}$ as function of symmetry energy slope parameter L at density of 0.16 ${\rm{fm}} ^{-3} $. The solid circles (for $ ^{68} {\rm{Ni}}$) and squares (for $ ^{132} {\rm{Sn}}$) are the results calculated by SAMi-J interactions. The straight lines correspond to the results of the fits. The shaded areas with blue and green colors present the experimental data for $ ^{68} {\rm{Ni}}$ and $ ^{132} {\rm{Sn}}$, respectively. Panel (b), correlation between the symmetry energy J and the slope parameter L at density of 0.16 ${\rm{fm}} ^{-3} $ given by SAMi-J interactions, the shaded area is the constrained result for symmetry energy and slope parameter.

It is well known that the average density of finite nuclei is less than the saturation density. For example, the average density of $ ^{208} {\rm{Pb}}$ is about 0.11 ${\rm{fm}} ^{-3} $. And thus the properties of heavy nuclei most effectively probe the properties of nuclear matter around 0.11 ${\rm{fm}} ^{-3} $ rather than at saturation density. It has been shown that the neutron skin thickness of heavy nuclei is uniquely fixed by the symmetry energy slope L($ \rho_c $) at a subsaturation cross density $ \rho_c $ = 0.11 ${\rm{fm}} ^{-3} $[41, 42]. In Refs.[49, 50], the monopole resonance energies of heavy nuclei have been shown to be well constrained by the equation of states of nuclear matter at $ \rho_c $ = 0.11 ${\rm{fm}} ^{-3} $ rather than at saturation density. So this paragraph is devoted to constrain the density dependence of symmetry energy at density of $ \rho_c $ = 0.11 ${\rm{fm}} ^{-3} $. In Fig. 3, the similar results are presented as in Fig. 2, but the slope parameters and the values of symmetry energy are calculated at $ \rho_c $ = 0.11 ${\rm{fm}} ^{-3} $. It can be seen from Fig. 3 (a) that the calculated EWSR percentages also show very good linear function of the slope parameters calculated at 0.11 ${\rm{fm}} ^{-3} $. It means that the EWSR percentage is also very sensitive to the density dependence of symmetry energy at 0.11 ${\rm{fm}} ^{-3} $. Together with the experimental data, the constrained slope parameter L is to be in the interval 41.6–67.8 MeV for $ ^{68} {\rm{Ni}}$ and 35.8–66.2 MeV for $ ^{132} {\rm{Sn}}$. From the overlapped area, one get the slope parameter L($ \rho_c $) at 0.11 ${\rm{fm}} ^{-3} $ is in the range of 41.6–66.2 MeV. In Fig. 3 (b), the good linear correlation of symmetry energies J($ \rho_c $) and its slope parameters L($ \rho_c $) of SAMi-J interactions at nuclear subsaturation density is shown. We can deduce the value of symmetry energy from the obtained range of slope parameter, it is in the range of 23.1–23.9 MeV.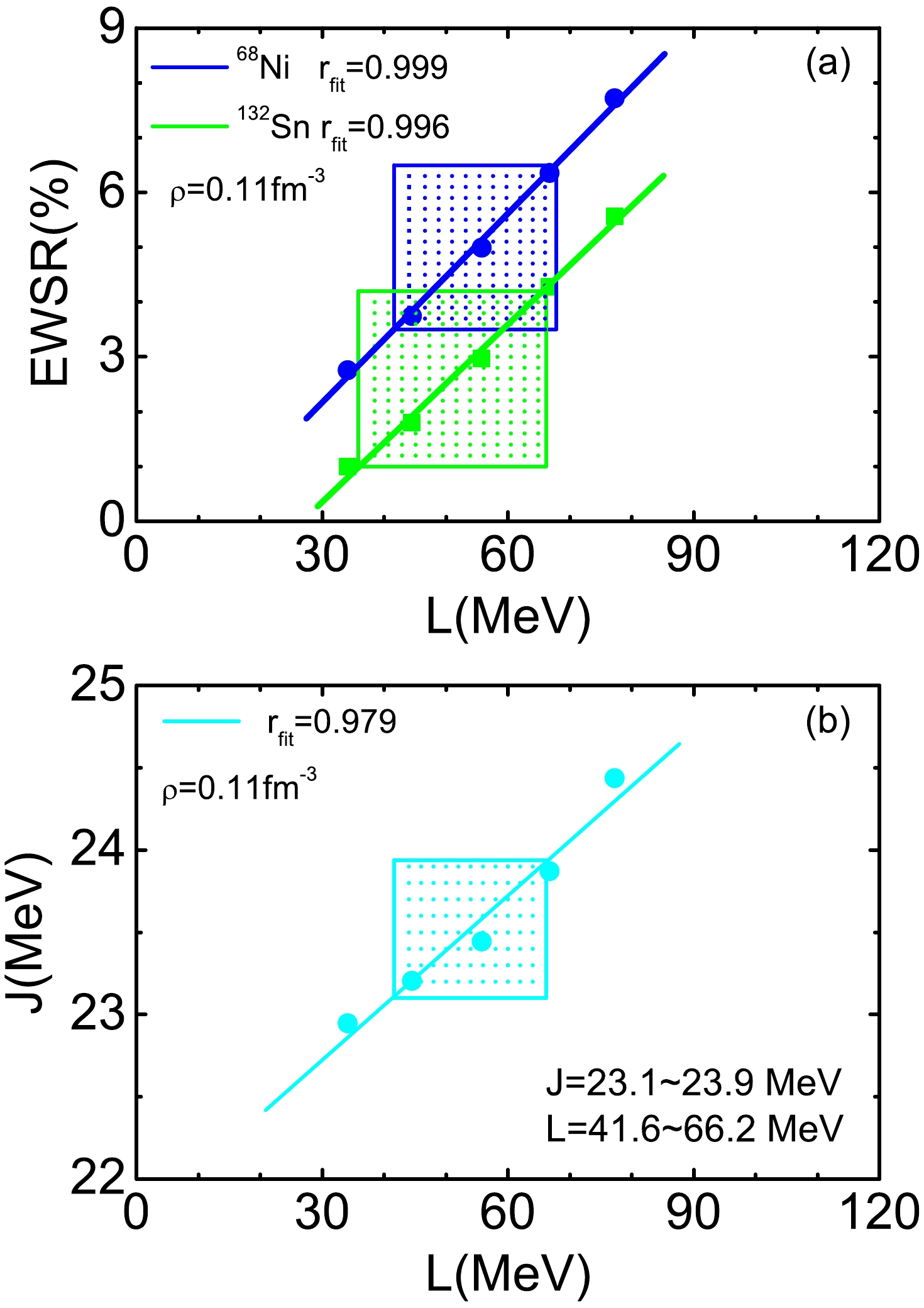

Figure 3.  (color online) The same as in Fig. 2, but for the density of 0.11 ${\rm{fm}} ^{-3} $.

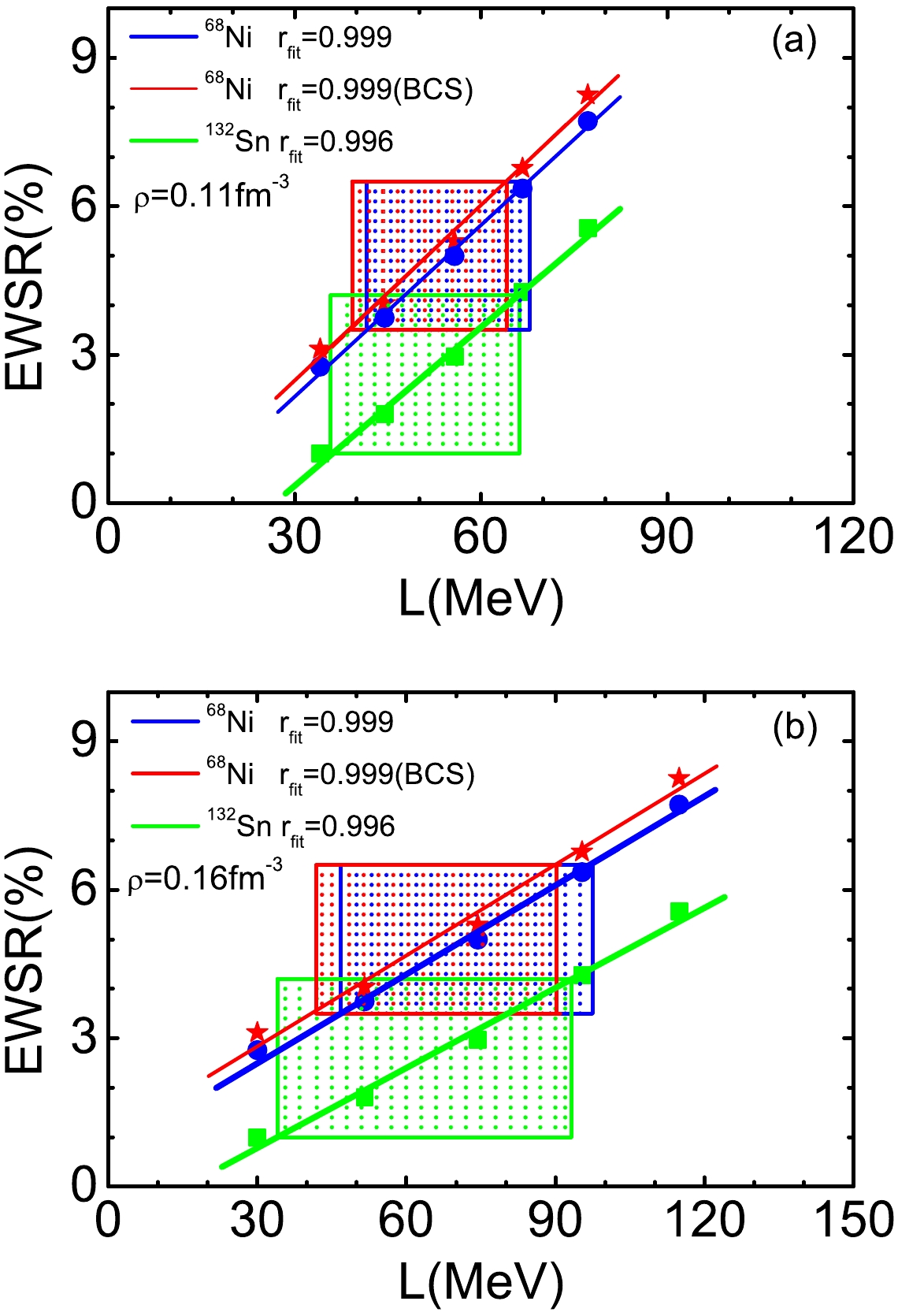
Effect of pairing correlation on the strength distribution of $ ^{68} {\rm{Ni}}$ is ignored in previous study, we shall discuss the effect of pairing correlation on the results of $ ^{68} {\rm{Ni}}$. It shall give some changes in final results of the density dependence of symmetry energy. As discussed in Refs. [52, 53], the pairing correlation enhances the low energy dipole strength in neutron-rich nucleus $ ^{22} {\rm{O}}$ compared to the results of no pairing calculations. For $ ^{68} {\rm{Ni}}$, we get similar results for pygmy dipole states. The pygmy dipole strength is slightly enhanced by including pairing correlations for all SAMi-J interactions. The calculated percentages of energy-weighted sum rules for each interactions are slightly larger that the values of no pairing. This features are depicted in Fig. 4, Fig. 4 (a) and (b) are the results for densities 0.11 ${\rm{fm}} ^{-3} $ and 0.16 ${\rm{fm}} ^{-3} $, respectively. The blue (green) symbols and lines have the same meaning as in Fig. 2 and Fig. 3, the red symbols and lines are the results for considering pairing. Together with the results given by considering pairing, we can see that the extracted slope parameter is shifted down slightly. The value is in between of 39.3-64.1 MeV (41.8-90.2 MeV) for density 0.11 (0.16) ${\rm{fm}} ^{-3} $. The corresponding symmetry energy is in 23.0-23.8 MeV (28.0-32.5 MeV) for density 0.11 (0.16) ${\rm{fm}} ^{-3} $.

Figure 4.  (color online) The same as in Fig. 2 (a) and Fig. 3 (a), the results with pairing for $ ^{68} {\rm{Ni}}$ are also shown in the figures.

This study provides a comprehensive investigation on the density dependence of symmetry energy by using the properties of pygmy dipole of the neutron-rich nuclei $ ^{68} {\rm{Ni}}$ and $ ^{132} {\rm{Sn}}$. We utilize the Skyrme-HF (or HF+BCS) and RPA (or QRPA) to calculate the ground-state and excited state properties with SAMi-J Skyrme interactions. The strength distributions indicate that the PDR in the response function is highly sensitive to the density dependence of symmetry energy. It gives the chance to constrain the density dependence behavior. Meanwhile we also discuss the effect of pairing correlation on the results. By comparing the measured and calculated percentages of EWSR associated with the PDR in $ ^{68} {\rm{Ni}}$ and $ ^{132} {\rm{Sn}}$, the ranges of the symmetry energy parameters L and J at saturation density and subsaturation density are constrained. The deduced slope parameter L and symmetry energy J at saturation density are 41.8-90.2 MeV and 28.0-32.5 MeV, which are consistent with the currently accepted limits (L = [30.6,86.8] MeV, J = [28.5, 34.9] MeV)[51]. The slope parameter L($ \rho_c $) and symmetry energy J($ \rho_c $) at subsaturation density are 39.3-64.1 MeV and 23.0-23.8 MeV. The slope parameter L($ \rho_c $) we obtained is consistent with the data from nuclear mass differences (L($ \rho_c $) = 49.6± 6.2 MeV)[8] and the data from electric dipole polarizability in $ ^{208} {\rm{Pb}}$ (L($ \rho_c $) = 47.3± 7.8 MeV)[42]. The symmetry energy J($ \rho_c $) at subsaturation density we obtained is slightly smaller than the data in Refs. [8, 42], they get J($ \rho_c $)$ \approx $ 26.0 MeV.