-
The charmonium-like and bottomonium-like states are good subjects for studying exotic states and understanding strong interactions. If they are genuine tetraquark states, there are two heavy valence quarks and two light valence quarks; therefore, the dynamics is complex compared with that of tetraquark configurations, which consist of four heavy valence quarks. The attractive interactions between the two heavy quarks (or antiquarks) should dominate over short distances and favor the formation of genuine diquark-antidiquark-type tetraquark states, rather than the loosely bound tetraquark molecular states, because the light mesons cannot be exchanged between the two heavy quarkonia to provide attraction at the leading order. In recent years, the full-heavy tetraquark states have attracted much attention and have been studied extensively [1-21].
Recently, the LHCb collaboration reported their preliminary results on the observations of
$ cc\bar{c}\bar{c} $ tetraquark candidates in the di-$ J/\psi $ invariant mass spectrum at$ p_T> 5.2\,{\rm{GeV}} $ [22, 23]. They observed a broad structure above the threshold ranging from 6.2 to 6.8 GeV and a narrow structure at approximately 6.9 GeV with a significance of greater than$ 5\sigma $ ; they also observed some vague structures near 7.2 GeV. The masses of the full-heavy tetraquark states from the phenomenological quark models lie either above or below the di-$ J/\psi $ or di-$ \Upsilon $ threshold, and vary over a large range [1-21]. This is the first time that clear structures in the di-$ J/\psi $ mass spectrum have been observed experimentally and may be evidence for genuine$ cc\bar{c}\bar{c} $ tetraquark states. The observation of evidence for the$ cc\bar{c}\bar{c} $ tetraquark states provides important experimental constraints on the theoretical models, sheds light on the nature of the exotic states, and plays an important role in establishing the tetraquark states.In Refs. [7, 8], we study the mass spectrum of the ground states of the scalar, axialvector, vector, and tensor full-heavy diquark-antidiquark-type tetraquark states with the QCD sum rules, showing that the predicted tetraquark masses lie blow the di-
$ J/\psi $ or di-$ \Upsilon $ threshold. In the present work, we extend our previous work to study the mass spectrum of the first radial excited states of the scalar, axialvector, vector, and tensor diquark-antidiquark-type$ cc\bar{c}\bar{c} $ tetraquark states with the QCD sum rules; then, we take the masses of the ground states and the first radial excited states as the input parameters, resort to the Regge trajectories to obtain the masses of the second radial excited states, and make possible assignments of LHCb's new structures.The article is arranged as follows: we derive the QCD sum rules for the masses and pole residues of the first radial excited states of the
$ cc\bar{c}\bar{c} $ tetraquark states in Sec. 2; in Sec. 3, we present the numerical results and use the Regge trajectories to obtain the masses of the second radial excited states; Sec. 4 is reserved for our conclusions. -
Let us first write down the two-point correlation functions
$ \Pi (p) $ and$ \Pi_{\mu\nu\alpha\beta}(p) $ in the QCD sum rules,$ \begin{split} & \Pi(p) = {\rm i}\int {\rm d}^4x {\rm e}^{{\rm i}p \cdot x} \langle0|T\left\{J(x)J^{\dagger}(0)\right\}|0\rangle \, ,\\ & \Pi_{\mu\nu\alpha\beta}(p)= {\rm i}\int {\rm d}^4x {\rm e}^{{\rm i}p \cdot x} \langle0|T\left\{J_{\mu\nu}(x)J_{\alpha\beta}^{\dagger}(0)\right\}|0\rangle \, , \end{split} $

(1) where
$ J_{\mu\nu}(x) = J^1_{\mu\nu}(x) $ ,$ J^2_{\mu\nu}(x) $ ,$ \begin{split} J(x) & = \varepsilon^{ijk}\varepsilon^{imn}c^{Tj}(x)C\gamma_\mu c^k(x) \bar{c}^m(x)\gamma^\mu C \bar{c}^{Tn}(x) \, , \\ J^1_{\mu\nu}(x) & = \varepsilon^{ijk}\varepsilon^{imn}\Big\{c^{Tj}(x)C\gamma_\mu c^k(x) \bar{c}^m(x) \gamma_\nu C \bar{c}^{Tn}(x)-c^{Tj}(x)C\gamma_\nu c^k(x) \bar{c}^m(x)\gamma_\mu C \bar{c}^{Tn}(x) \Big\} \, , \\ J^2_{\mu\nu}(x) & = \frac{\varepsilon^{ijk}\varepsilon^{imn}}{\sqrt{2}}\Big\{c^{Tj}(x)C\gamma_\mu c^k(x) \bar{c}^m(x) \gamma_\nu C \bar{c}^{Tn}(x)+c^{Tj}(x)C\gamma_\nu c^k(x) \bar{c}^m(x)\gamma_\mu C \bar{c}^{Tn}(x) \Big\} \, , \end{split} $

(2) i, j, k, m, and n are color indexes, and C is the charge conjunction matrix. We choose the currents
$ J(x) $ ,$ J^1_{\mu\nu}(x) $ , and$ J^2_{\mu\nu}(x) $ to interpolate the$ J^{PC} = 0^{++} $ ,$ 1^{+-} $ ,$ 1^{--} $ , and$ 2^{++} $ diquark-antidiquark-type$ cc\bar{c}\bar{c} $ tetraquark states, respectively, as the current$ J^1_{\mu\nu}(x) $ , where the Lorentz indexes$ \mu $ and$ \nu $ are antisymmetric, has both spin-parity$ J^P = 1^+ $ and$ 1^- $ components.On the hadron side, we insert a complete set of intermediate hadronic states with the same quantum numbers as the current operators
$ J(x) $ ,$ J^1_{\mu\nu}(x) $ , and$ J^2_{\mu\nu}(x) $ into the correlation functions$ \Pi(p) $ and$ \Pi_{\mu\nu\alpha\beta}(p) $ to obtain the hadronic representation [24-26]. After isolating the ground state contributions of the scalar, axialvector, vector, and tensor$ cc\bar{c}\bar{c} $ tetraquark states, we obtain the results$ \Pi (p) = \frac{\lambda_X^2}{M^2_X-p^2} +\cdots \, \, , = \Pi_S(p^2)\, , $

(3) $ \begin{split} \Pi^1_{\mu\nu\alpha\beta}(p) = & \frac{\lambda_{ Y^+}^2}{M_{Y^+}^2\left(M_{Y^+}^2-p^2\right)}\left(p^2g_{\mu\alpha}g_{\nu\beta} -p^2g_{\mu\beta}g_{\nu\alpha} -g_{\mu\alpha}p_{\nu}p_{\beta}-g_{\nu\beta}p_{\mu}p_{\alpha}+g_{\mu\beta}p_{\nu}p_{\alpha}+g_{\nu\alpha}p_{\mu}p_{\beta}\right) \\ & +\frac{\lambda_{ Y^-}^2}{M_{Y^-}^2\left(M_{Y^-}^2-p^2\right)}\left( -g_{\mu\alpha}p_{\nu}p_{\beta}-g_{\nu\beta}p_{\mu}p_{\alpha}+g_{\mu\beta}p_{\nu}p_{\alpha}+g_{\nu\alpha}p_{\mu}p_{\beta}\right) +\cdots \, \, ,\\ =& \Pi_{A}(p^2)\left(p^2g_{\mu\alpha}g_{\nu\beta} -p^2g_{\mu\beta}g_{\nu\alpha} -g_{\mu\alpha}p_{\nu}p_{\beta}-g_{\nu\beta}p_{\mu}p_{\alpha}+g_{\mu\beta}p_{\nu}p_{\alpha}+g_{\nu\alpha}p_{\mu}p_{\beta}\right) \\ &+\Pi_{V}(p^2)\left( -g_{\mu\alpha}p_{\nu}p_{\beta}-g_{\nu\beta}p_{\mu}p_{\alpha}+g_{\mu\beta}p_{\nu}p_{\alpha}+g_{\nu\alpha}p_{\mu}p_{\beta}\right) \, . \end{split} $

(4) $ \begin{split} \Pi^2_{\mu\nu\alpha\beta} (p) = & \frac{\lambda_X^2}{M_X^2-p^2}\left( \frac{\widetilde{g}_{\mu\alpha}\widetilde{g}_{\nu\beta}+\widetilde{g}_{\mu\beta}\widetilde{g}_{\nu\alpha}}{2}-\frac{\widetilde{g}_{\mu\nu}\widetilde{g}_{\alpha\beta}}{3}\right) +\cdots \, \, , \\ = &\Pi_{T}(p^2)\left( \frac{\widetilde{g}_{\mu\alpha}\widetilde{g}_{\nu\beta}+\widetilde{g}_{\mu\beta}\widetilde{g}_{\nu\alpha}}{2}-\frac{\widetilde{g}_{\mu\nu}\widetilde{g}_{\alpha\beta}}{3}\right) +\cdots \, \, , \end{split} $

(5) where
$ \widetilde{g}_{\mu\nu} = g_{\mu\nu}-\frac{p_{\mu}p_{\nu}}{p^2} $ . The pole residues$ \lambda_{X} $ and$ \lambda_{Y} $ are defined by$ \begin{split} \langle 0|J (0)|X (p)\rangle &= \lambda_{X} \, , \\ \langle 0|J^1_{\mu\nu}(0)|Y^+(p)\rangle &= \frac{\lambda_{Y^+}}{M_{Y^+}} \, \varepsilon_{\mu\nu\alpha\beta} \, \varepsilon^{\alpha}p^{\beta}\, , \\ \langle 0|J^1_{\mu\nu}(0)|Y^-(p)\rangle &= \frac{\lambda_{Y^-}}{M_{Y^-}} \left(\varepsilon_{\mu}p_{\nu}-\varepsilon_{\nu}p_{\mu} \right)\, ,\\ \langle 0|J^2_{\mu\nu}(0)|X (p)\rangle &= \lambda_{X} \, \varepsilon_{\mu\nu} \, , \end{split} $

(6) where
$ \varepsilon_{\mu} $ and$ \varepsilon_{\mu\nu} $ are the polarization vectors of the axialvector, vector, and tensor tetraquark states, respectively.If we take into account (or isolate) the first radial excited states, we obtain
$ \begin{split} \Pi_{S/T}(p^2) = & \frac{\lambda_X^2}{M^2_X-p^2} +\frac{\lambda_{X^\prime}^2}{M^2_{X^\prime}-p^2}+\cdots \, , \\ \Pi_{A/V}(p^2) = &\frac{\lambda_{ Y^\pm}^2}{M_{Y^\pm}^2\left(M_{Y^\pm}^2-p^2\right)}+\frac{\lambda_{ Y^{\prime\pm}}^2}{M_{Y^{\prime\pm}}^2\left(M_{Y^{\prime\pm}}^2-p^2\right)}+\cdots\, . \end{split} $

(7) We project out the axialvector and vector components
$ \Pi_{A}(p^2) $ and$ \Pi_{V}(p^2) $ by introducing the operators$ P_{A}^{\mu\nu\alpha\beta} $ and$ P_{V}^{\mu\nu\alpha\beta} $ , respectively,$ \begin{split} \widetilde{\Pi}_{A}(p^2) = p^2\Pi_{A}(p^2) = & P_{A}^{\mu\nu\alpha\beta}\Pi_{\mu\nu\alpha\beta}(p) \, , \\ \widetilde{\Pi}_{V}(p^2) = p^2\Pi_{V}(p^2) = & P_{V}^{\mu\nu\alpha\beta}\Pi_{\mu\nu\alpha\beta}(p) \, , \end{split} $

(8) where
$ \begin{split} P_{A}^{\mu\nu\alpha\beta} = & \frac{1}{6}\left( g^{\mu\alpha}-\frac{p^\mu p^\alpha}{p^2}\right)\left( g^{\nu\beta}-\frac{p^\nu p^\beta}{p^2}\right)\, , \\ P_{V}^{\mu\nu\alpha\beta} = & \frac{1}{6}\left( g^{\mu\alpha}-\frac{p^\mu p^\alpha}{p^2}\right)\left( g^{\nu\beta}-\frac{p^\nu p^\beta}{p^2}\right)-\frac{1}{6}g^{\mu\alpha}g^{\nu\beta}\, . \end{split} $

(9) It is straightforward but tedious to carry out the operator product expansion in the deep Euclidean space
$ P^2 = -p^2 \to \infty $ or$\gg \Lambda_{\rm QCD}^2$ , after which we obtain the QCD spectral densities through the dispersion relation [7, 8],$ \begin{split} \Pi_{S/T}(p^2) = & \int_{16m_c^2}^{\infty}{\rm d}s \frac{\rho_{S/T}(s)}{s-p^2}\, ,\\ \widetilde{\Pi}_{A/V}(p^2) = & \int_{16m_c^2}^{\infty}{\rm d}s \frac{\rho_{A/V}(s)}{s-p^2}\, , \end{split} $

(10) where
$ \begin{split} \rho_{S/T}(s) = & \frac{{\rm{Im}}\Pi_{S/T}(s)}{\pi}\, , \\ \rho_{A/V}(s) = & \frac{{\rm{Im}}\widetilde{\Pi}_{A/V}(s)}{\pi}\, . \end{split} $

(11) We take the quark-hadron duality below the continuum thresholds
$ s_0 $ and$ s_0^\prime $ , respectively, and perform a Borel transform with respect to the variable$ P^2 = -p^2 $ to obtain the QCD sum rules:$ \begin{array}{l} \lambda^2_{X/Y}\, \exp\left(-\dfrac{M^2_{X/Y}}{T^2}\right) = \displaystyle\int_{16m_c^2}^{s_0} {\rm d}s \displaystyle\int_{z_i}^{z_f}{\rm d}z \displaystyle\int_{t_i}^{t_f}{\rm d}t \int_{r_i}^{r_f}{\rm d}r\, \rho(s,z,t,r) \exp\left(-\dfrac{s}{T^2}\right) \, , \end{array} $

(12) $ \begin{array}{l} \lambda^2_{X/Y}\, \exp\left(-\dfrac{M^2_{X/Y}}{T^2}\right)+\lambda^2_{X^\prime/Y^\prime}\, \exp\left(-\dfrac{M^2_{X^\prime/Y^\prime}}{T^2}\right) = \displaystyle\int_{16m_c^2}^{s^\prime_0} {\rm d}s \int_{z_i}^{z_f}{\rm d}z \displaystyle\int_{t_i}^{t_f}{\rm d}t \int_{r_i}^{r_f}{\rm d}r\, \rho(s,z,t,r)\exp\left(-\frac{s}{T^2}\right) \, , \end{array} $

(13) where the QCD spectral densities
$ \rho(s,z,t,r) = \rho_S(s,z,t,r) $ ,$ \rho_A(s,z,t,r) $ ,$ \rho_V(s,z,t,r) $ , and$ \rho_T(s,z,t,r) $ are$ \begin{split} \rho_S(s,z,t,r) = & \frac{3m_c^4}{8\pi^6}\left( s-\overline{m}_c^2\right)^2+\frac{t z m_c^2}{8\pi^6}\left( s-\overline{m}_c^2\right)^2\left( 5s-2\overline{m}_c^2\right) +\frac{rtz(1-r-t-z)}{1-t-z} \frac{1}{32\pi^6}\left( s-\overline{m}_c^2\right)^3\left( 3s-\overline{m}_c^2\right) +\frac{rtz(1-r-t-z)}{1-z}\\ &\times \frac{1}{32\pi^6}\left( s-\overline{m}_c^2\right)^3\left( 3s-\overline{m}_c^2\right)\left[5-\frac{t}{1-t-z} \right] -\frac{rtz^2(1-r-t-z)}{1-z} \frac{3}{16\pi^6}\left( s-\overline{m}_c^2\right)^4 +rtz(1-r-t-z) \frac{3s}{8\pi^6}\left( s-\overline{m}_c^2\right)^2\\ &\times\left[ 2s-\overline{m}_c^2-\frac{z}{1-z}\left( s-\overline{m}_c^2\right)\right] +m_c^2\langle \frac{\alpha_sGG}{\pi}\rangle \left\{-\frac{1}{r^3} \frac{m_c^4}{6\pi^4}\delta\left( s-\overline{m}_c^2\right) -\frac{1-r-t-z}{r^2} \frac{m_c^2}{12\pi^4}\left[2+s\,\delta\left( s-\overline{m}_c^2\right)\right]\right. \\ & -\frac{tz}{r^3} \frac{m_c^2}{12\pi^4}\left[2+s\,\delta\left( s-\overline{m}_c^2\right)\right] -\frac{tz(1-r-t-z)}{r^2(1-t-z)} \frac{1}{12\pi^6}\left( 3s-2\overline{m}_c^2\right) -\frac{tz(1-r-t-z)}{r^2(1-z)} \frac{1}{12\pi^4}\left( 3s-2\overline{m}_c^2\right) \left[5-\frac{t}{1-t-z} \right]\\ & +\frac{tz^2(1-r-t-z)}{r^2(1-z)} \frac{1}{\pi^4}\left( s-\overline{m}_c^2\right) -\frac{tz(1-r-t-z)}{r^2} \frac{1}{2\pi^4}\left[s+\frac{s^2}{3}\delta\left( s-\overline{m}_c^2\right)-\frac{z}{1-z}s\right] \\ & \left.+\frac{1}{r^2} \frac{m_c^2}{2\pi^4} +\frac{tz}{r^2} \frac{1}{4\pi^4}\left( 3s-2\overline{m}_c^2\right)- \frac{1}{16\pi^4}\left( 3s-2\overline{m}_c^2\right) \right\} +\langle \frac{\alpha_sGG}{\pi}\rangle \left\{\frac{1}{rz} \frac{m_c^4}{6\pi^4} +\frac{t}{r} \frac{m_c^2}{6\pi^4}\left( 3s-2\overline{m}_c^2\right)\right. \\ & +\frac{t(1-r-t-z)}{(1-t-z)} \frac{1}{12\pi^4}\left( s-\overline{m}_c^2\right) \left( 2s-\overline{m}_c^2\right) +\frac{t(1-r-t-z)}{(1-z)} \frac{1}{12\pi^4}\left( s-\overline{m}_c^2\right) \left( 2s-\overline{m}_c^2\right) \left[2-\frac{t}{1-t-z} \right] \\ & -\frac{tz(1-r-t-z)}{(1-z)} \frac{1}{4\pi^4}\left( s-\overline{m}_c^2\right)^2 \left.+t(1-r-t-z) \frac{1}{12\pi^4}s\left[ 4s-3\overline{m}_c^2-\frac{z}{1-z}3\left( s-\overline{m}_c^2\right)\right]\right\}\, , \end{split} $

(14) $ \begin{split} \rho_T(s,z,t,r) =& \frac{3m_c^4}{16\pi^6}\left( s-\overline{m}_c^2\right)^2+\frac{t z m_c^2}{8\pi^6}\left( s-\overline{m}_c^2\right)^2\left( 4s-\overline{m}_c^2\right) +\frac{rtz(1-r-t-z)}{1-t-z} \frac{1}{320\pi^6}\left( s-\overline{m}_c^2\right)^3\left( 17s-5\overline{m}_c^2\right) \\ &+\frac{rtz(1-r-t-z)}{1-z} \frac{1}{320\pi^6}\left( s-\overline{m}_c^2\right)^3\left[\left( 21s-5\overline{m}_c^2\right)-\frac{t}{1-t-z}\left( 17s-5\overline{m}_c^2\right) \right] \\ &-\frac{rtz^2(1-r-t-z)}{1-z} \frac{1}{32\pi^6}\left( s-\overline{m}_c^2\right)^4 +rtz(1-r-t-z) \frac{s}{80\pi^6}\left( s-\overline{m}_c^2\right)^2\left[ 28s-13\overline{m}_c^2-\frac{z}{1-z}7\left( s-\overline{m}_c^2\right)\right] \\ &+m_c^2\langle \frac{\alpha_sGG}{\pi}\rangle \left\{-\frac{1}{r^3} \frac{m_c^4}{12\pi^4}\delta\left( s-\overline{m}_c^2\right) -\frac{1-r-t-z}{r^2} \frac{m_c^2}{12\pi^4}\left[1+s\,\delta\left( s-\overline{m}_c^2\right)\right]\right. -\frac{tz}{r^3} \frac{m_c^2}{12\pi^4}\left[1+s\,\delta\left( s-\overline{m}_c^2\right)\right]\\ & -\frac{tz(1-r-t-z)}{r^2(1-t-z)} \frac{1}{12\pi^6}\left( 2s-\overline{m}_c^2\right) -\frac{tz(1-r-t-z)}{r^2(1-z)} \frac{1}{12\pi^4}\left( 2s-\overline{m}_c^2\right) \left[1-\frac{t}{1-t-z} \right]\\ &+\frac{tz^2(1-r-t-z)}{r^2(1-z)} \frac{1}{6\pi^4}\left( s-\overline{m}_c^2\right) -\frac{tz(1-r-t-z)}{r^2} \frac{1}{6\pi^4}\left[s+\frac{s^2}{2}\delta\left( s-\overline{m}_c^2\right)-\frac{z}{1-z}s\right]\\&\left.+\frac{1}{r^2} \frac{m_c^2}{4\pi^4} +\frac{tz}{r^2} \frac{1}{4\pi^4}\left( 2s-\overline{m}_c^2\right) \right\}+\langle \frac{\alpha_sGG}{\pi}\rangle \left\{- \frac{m_c^2}{48\pi^4}\left( 4s-3\overline{m}_c^2\right)\right. -\frac{r(1-r-t-z)}{1-t-z}\frac{1}{32\pi^4} \left( s-\overline{m}_c^2\right)\left( 3s-\overline{m}_c^2\right) \end{split} $

$ \begin{split} \quad\quad\quad\quad\quad &-\frac{r(1-r-t-z)}{1-z}\frac{1}{480\pi^4} \left( s-\overline{m}_c^2\right)\left[\left( 17s-5\overline{m}_c^2\right)-\frac{t}{1-t-z}15\left( 3s-\overline{m}_c^2\right)\right]+\frac{rz(1-r-t-z)}{1-z}\frac{1}{24\pi^4} \left( s-\overline{m}_c^2\right)^2 \\&-r(1-r-t-z)\frac{1}{240\pi^4} s\left[\left( 14s-9\overline{m}_c^2\right)-\frac{z}{1-z}21\left( s-\overline{m}_c^2\right)\right]-\frac{1}{rz} \frac{m_c^4}{36\pi^4} -\frac{t}{r} \frac{m_c^2}{18\pi^4}\left( 2s-\overline{m}_c^2\right)\\ &-\frac{t(1-r-t-z)}{(1-t-z)} \frac{1}{72\pi^4}\left( s-\overline{m}_c^2\right) \left( 4s-\overline{m}_c^2\right) -\frac{t(1-r-t-z)}{(1-z)} \frac{1}{72\pi^4}\left( s-\overline{m}_c^2\right) \left[2\left( 2s-\overline{m}_c^2\right)-\frac{t}{1-t-z}\left( 4s-\overline{m}_c^2\right) \right] \\ &+\frac{tz(1-r-t-z)}{(1-z)} \frac{1}{24\pi^4}\left( s-\overline{m}_c^2\right)^2\left.-t(1-r-t-z) \frac{1}{72\pi^4}s\left[ 7s-5\overline{m}_c^2-\frac{z}{1-z}5\left( s-\overline{m}_c^2\right)\right]\right\}\, , \end{split} $

(15) $ \begin{split} \rho_A(s,z,t,r) =& \frac{3m_c^4}{16\pi^6}\left( s-\overline{m}_c^2\right)^2+\frac{t z m_c^2}{8\pi^6}\left( s-\overline{m}_c^2\right)^2\left( 4s-\overline{m}_c^2\right) +rtz(1-r-t-z) \frac{s}{16\pi^6}\left( s-\overline{m}_c^2\right)^2\left( 7s-4\overline{m}_c^2\right) \\ &+m_c^2\langle \frac{\alpha_sGG}{\pi}\rangle \left\{-\frac{1}{r^3} \frac{m_c^4}{12\pi^4}\delta\left( s-\overline{m}_c^2\right) -\frac{1-r-t-z}{r^2} \frac{m_c^2}{12\pi^4}\left[1+s\,\delta\left( s-\overline{m}_c^2\right)\right]\right. \\ &-\frac{tz}{r^3} \frac{m_c^2}{12\pi^4}\left[1+s\,\delta\left( s-\overline{m}_c^2\right)\right] -\frac{tz(1-r-t-z)}{r^2} \frac{1}{12\pi^4}\left[4s+s^2\delta\left( s-\overline{m}_c^2\right)\right] \\ &\left.+\frac{1}{r^2} \frac{m_c^2}{4\pi^4} +\frac{tz}{r^2} \frac{1}{4\pi^4}\left( 2s-\overline{m}_c^2\right) \right\} +\langle \frac{\alpha_sGG}{\pi}\rangle \left\{-\frac{m_c^2}{48\pi^4}\left( 4s-3\overline{m}_c^2\right)- \frac{r(1-r-t-z)}{16\pi^4}\left( s-\overline{m}_c^2\right)^2\right. \\ &- \frac{r(1-r-t-z)}{48\pi^4}s\left( 7s-6\overline{m}_c^2\right)+\frac{1}{rz} \frac{m_c^4}{48\pi^4} +\frac{t}{r} \frac{m_c^2}{24\pi^4}\left( 2s-\overline{m}_c^2\right)\\ &\left.+ \frac{t(1-r-t-z)}{32\pi^4}\left( s-\overline{m}_c^2\right)^2+ \frac{t(1-r-t-z)}{48\pi^4}s\left( 6s-5\overline{m}_c^2\right)\right\}\, , \end{split} $

(16) $ \begin{split} \rho_V(s,z,t,r) =& -\frac{3m_c^4}{16\pi^6}\left( s-\overline{m}_c^2\right)^2-\frac{t z m_c^2}{8\pi^6}\left( s-\overline{m}_c^2\right)^3 +rtz(1-r-t-z) \frac{s}{16\pi^6}\left( s-\overline{m}_c^2\right)^2\left( 7s-4\overline{m}_c^2\right) +m_c^2\langle \frac{\alpha_sGG}{\pi}\rangle \left\{\frac{1}{r^3} \frac{m_c^4}{12\pi^4}\delta\left( s-\overline{m}_c^2\right)\right.\\ &\left.+\frac{1-r-t-z}{r^2} \frac{m_c^2}{12\pi^4}\right. +\frac{tz}{r^3} \frac{m_c^2}{12\pi^4} -\frac{tz(1-r-t-z)}{r^2} \frac{1}{12\pi^4}\left[4s+s^2\delta\left( s-\overline{m}_c^2\right)\right] \left.-\frac{1}{r^2} \frac{m_c^2}{4\pi^4} -\frac{tz}{r^2} \frac{1}{4\pi^4}\left( s-\overline{m}_c^2\right) \right\} \\ &+\langle \frac{\alpha_sGG}{\pi}\rangle \left\{\frac{m_c^2}{48\pi^4}\left( 5s-3\overline{m}_c^2\right)+ \frac{r(1-r-t-z)}{16\pi^4}\left( s-\overline{m}_c^2\right)^2\right. + \frac{r(1-r-t-z)}{48\pi^4}s\left( 7s-6\overline{m}_c^2\right)-\frac{1}{rz} \frac{m_c^4}{48\pi^4} -\frac{t}{r} \frac{m_c^2}{24\pi^4}\left( s-\overline{m}_c^2\right)\\ &\left.- \frac{t(1-r-t-z)}{32\pi^4}\left( s-\overline{m}_c^2\right)^2- \frac{t(1-r-t-z)}{48\pi^4}s\left( s-\overline{m}_c^2\right)\right\}\, , \end{split} $

(17) and
$ \overline{m}_c^2 = \frac{m_c^2}{r}+\frac{m_c^2}{t}+\frac{m_c^2}{z}+\frac{m_c^2}{1-r-t-z}\, , $

$ \begin{split} r_{f/i} =& \frac{1}{2}\left\{1-z-t \pm \sqrt{(1-z-t)^2-4\frac{1-z-t}{\hat{s}-\frac{1}{z}-\frac{1}{t}}}\right\} \, ,\\ t_{f/i} =& \frac{1}{2\left( \hat{s}-\dfrac{1}{z}\right)}\left\{ (1-z)\left( \hat{s}-\frac{1}{z}\right)\right.\\& \left. -3\pm \sqrt{ \left[ (1-z)\left( \hat{s}-\frac{1}{z}\right)-3\right]^2-4 (1-z)\left( \hat{s}-\frac{1}{z}\right) }\right\}\, ,\\ z_{f/i} =& \frac{1}{2\hat{s}}\left\{ \hat{s}-8 \pm \sqrt{\left(\hat{s}-8\right)^2-4\hat{s} }\right\}\, , \end{split} $

(18) where
$ \hat{s} = \displaystyle\frac{s}{m_c^2} $ . We introduce the notations$ \tau = \displaystyle\frac{1}{T^2} $ ,$D^n = \left( -\displaystyle\frac{\rm d}{{\rm d}\tau}\right)^n$ , and use the subscripts 1 and 2 to representthe ground states X, Y and the first radially excited states$ X^\prime $ ,$ Y^\prime $ respectively, for simplicity. We rewrite the two QCD sum rules in Eqs. (12)-(13) as$ \lambda_1^2\exp\left(-\tau M_1^2 \right) = \Pi_{\rm QCD}(\tau) \, , $

(19) $ \lambda_1^2\exp\left(-\tau M_1^2 \right)+\lambda_2^2\exp\left(-\tau M_2^2 \right) = \Pi^{\prime}_{\rm QCD}(\tau) \, , $

(20) where we introduce the subscript
${\rm QCD}$ to represent the QCD representation of the correlation functions$ \Pi_{S/A/V/T}(p^2) $ below the continuum thresholds. We derive the QCD sum rules in Eq. (19) with respect to$ \tau $ to obtain the masses of the ground states,$ M_1^2 = \frac{D\Pi_{\rm QCD}(\tau)}{\Pi_{\rm QCD}(\tau)}\, . $

(21) We obtain the masses and pole residues of the ground states of the scalar, axialvector, vector, and tensor
$ cc\bar{c}\bar{c} $ tetraquark states with the two coupled QCD sum rules shown in Eq. (19) and Eq. (21) [7, 8].Next, we study the masses and pole residues of the first radial excited states. First, let us derive the QCD sum rules in Eq. (20) with respect to
$ \tau $ to obtain$ \lambda_1^2M_1^2\exp\left(-\tau M_1^2 \right)+\lambda_2^2M_2^2\exp\left(-\tau M_2^2 \right) = D\Pi^{\prime}_{\rm QCD}(\tau) \, . $

(22) From Eq. (20) and Eq. (22), we can obtain the QCD sum rules,
$ \lambda_i^2\exp\left(-\tau M_i^2 \right) = \frac{\left(D-M_j^2\right)\Pi^{\prime}_{\rm QCD}(\tau)}{M_i^2-M_j^2} \, , $

(23) where the indexes
$ i \neq j $ . Then, we can derive the QCD sum rules in Eq. (23) with respect to$ \tau $ to obtain$ \begin{split} M_i^2 = & \frac{\left(D^2-M_j^2D\right)\Pi_{\rm QCD}^{\prime}(\tau)}{\left(D-M_j^2\right)\Pi_{\rm QCD}^{\prime}(\tau)} \, , \\ M_i^4 = & \frac{\left(D^3-M_j^2D^2\right)\Pi_{\rm QCD}^{\prime}(\tau)}{\left(D-M_j^2\right)\Pi_{\rm QCD}^{\prime}(\tau)}\, . \end{split} $

(24) The squared masses
$ M_i^2 $ satisfy the equation,$ M_i^4-b M_i^2+c = 0\, , $

(25) where
$ \begin{split} b = & \frac{D^3\otimes D^0-D^2\otimes D}{D^2\otimes D^0-D\otimes D}\, , \\ c = & \frac{D^3\otimes D-D^2\otimes D^2}{D^2\otimes D^0-D\otimes D}\, , \\ D^j \otimes D^k = & D^j\Pi^{\prime}_{\rm QCD}(\tau) \, D^k\Pi^{\prime}_{\rm QCD}(\tau)\, , \end{split} $

(26) and the indexes
$ i = 1,2 $ and$ j,k = 0,1,2,3 $ . Finally we solve the equation analytically to obtain two solutions [27-29],$ M_1^2 = \frac{b-\sqrt{b^2-4c} }{2} \, , $

(27) $ M_2^2 = \frac{b+\sqrt{b^2-4c} }{2} \, .$

(28) From the QCD sum rules in Eqs. (27)-(28), we can obtain the masses of both the ground states and the first radial excited states. Both the QCD sum rules in Eq. (21) and Eq. (27) have one continuum threshold parameter, and both the continuum parameters
$ s_0 $ and$ s_0^\prime $ have uncertainties. From this aspect, the ground state masses from the QCD sum rules in Eq. (21) are not superior to those from Eq. (27). However, the ground state masses from the QCD sum rules in Eq. (27) suffer from additional uncertainties from the first radial excited states. In calculations, we observe that ground states masses from the QCD sum rules in Eq. (27) underestimate the experimental values [27-29]; therefore, we neglect the QCD sum rules in Eq. (27). -
We take the standard value of the gluon condensate [24-26, 30], and use the
$ \overline{MS} $ mass$m_{c}(m_c) = (1.275\pm $ $ 0.025)\,{\rm{GeV}}$ from the Particle Data Group [31]. We take into account the energy-scale dependence of the$ \overline{MS} $ mass from the renormalization group equation,$ \begin{split} m_c(\mu) = & m_c(m_c)\left[\frac{\alpha_{s}(\mu)}{\alpha_{s}(m_c)}\right]^{\frac{12}{25}} \, ,\\ \alpha_s(\mu) = & \frac{1}{b_0t}\left[1-\frac{b_1}{b_0^2}\frac{\log t}{t} +\frac{b_1^2(\log^2{t}-\log{t}-1)+b_0b_2}{b_0^4t^2}\right]\, , \end{split} $

(29) where
$ \begin{split}&t = \log \displaystyle\frac{\mu^2}{\Lambda^2},\quad b_0 = \displaystyle\frac{33-2n_f}{12\pi},\\&b_1 = \displaystyle\displaystyle\frac{153-19n_f}{24\pi^2},\quad b_2 = \displaystyle\frac{2857-\displaystyle\frac{5033}{9}n_f+\displaystyle\frac{325}{27}n_f^2}{128\pi^3},\end{split} $

$ \Lambda = 213\,{\rm{MeV}} $ ,$ 296\,{\rm{MeV}} $ , and$ 339\,{\rm{MeV}} $ for the flavors$ n_f = 5 $ ,$ 4 $ , and$ 3 $ , respectively [31]. In this article, we choose flavor number$ n_f = 4 $ , as we study the four-charm-quark states.We should choose suitable continuum threshold parameters
$ s^\prime_0 $ to avoid contamination from the second radial excited states and borrow some ideas from the conventional charmonium states. The masses of the ground state, the first radial excited state, and the second excited state are$ m_{J/\psi} = 3.0969\,{\rm{GeV}} $ ,$ m_{\psi^\prime} = 3.686097\,{\rm{GeV}} $ , and$ m_{\psi^{\prime\prime}} = 4.039\,{\rm{GeV}} $ , respectively, from the Particle Data Group [31]. The energy gaps are$ m_{\psi^\prime}-m_{J/\psi} = 0.59\,{\rm{GeV}} $ ,$ m_{\psi^{\prime\prime}}-m_{J/\psi} = 0.94\,{\rm{GeV}} $ , and we can choose the continuum threshold parameters$ \sqrt{s_0^\prime}\leqslant M_{X/Y}+0.95\,{\rm{GeV}} $ tentatively and vary the continuum threshold parameters, energy scales of the QCD spectral densities, and Borel parameters to satisfy the following three criteria:1. The ground state plus the first radial excited state makes a dominant contribution at the hadron side;
2. The operator product expansion is convergent below the continuum thresholds;
3. The Borel platforms appear both for the tetraquark masses and pole residues.
In Refs. [7, 8], we obtain the ground state masses of the scalar, axialvector, vector, and tensor diquark-antidiquark-type full-heavy tetraquark states with the QCD sum rules. In the present work, we take the ground state masses as a benchmark and study the masses of the excited states. After trial and error, we reach acceptable continuum threshold parameters, energy scales of the QCD spectral densities, and Borel windows, which are shown in Table 1. From the Table, we can see that the pole dominance on the hadron side is well satisfied. In the Borel windows, the dominant contributions come from the perturbative terms, and the operator product expansion converges well.
$ J^{PC} $ 

$ T^2/{\rm GeV}^2 $ 

$ \sqrt{s_0^\prime}/{\rm GeV} $ 

$ \mu/{\rm GeV} $ 

pole (%) $ M_{X/Y}/{\rm GeV} $ 

$ \lambda_{X/Y}/(10^{-1} {\rm GeV}^5) $ 

$0^{++}({{2S} })$ 

$ 4.4-4.8 $ 

$ 6.80\pm0.10 $ 

$ 2.5 $ 

$ 65-79 $ 

$ 6.48\pm0.08 $ 

$ 7.41\pm1.12 $ 

$1^{+-}({{2S} })$ 

$ 4.4-4.8 $ 

$ 6.85\pm0.10 $ 

$ 2.5 $ 

$ 69-82 $ 

$ 6.52\pm0.08 $ 

$ 5.56\pm0.80 $ 

$2^{++}({{2S} })$ 

$ 4.9-5.3 $ 

$ 6.90\pm0.10 $ 

$ 2.5 $ 

$ 63-76 $ 

$ 6.56\pm0.08 $ 

$ 5.92\pm0.83 $ 

$1^{--}({ {2P} })$ 

$ 4.5-4.9 $ 

$ 6.90\pm0.10 $ 

$ 2.2 $ 

$ 57-73 $ 

$ 6.58\pm0.09 $ 

$ 3.46\pm0.58 $ 

Table 1. Borel parameters, continuum threshold parameters, energy scales, pole contributions, masses, and pole residues of the
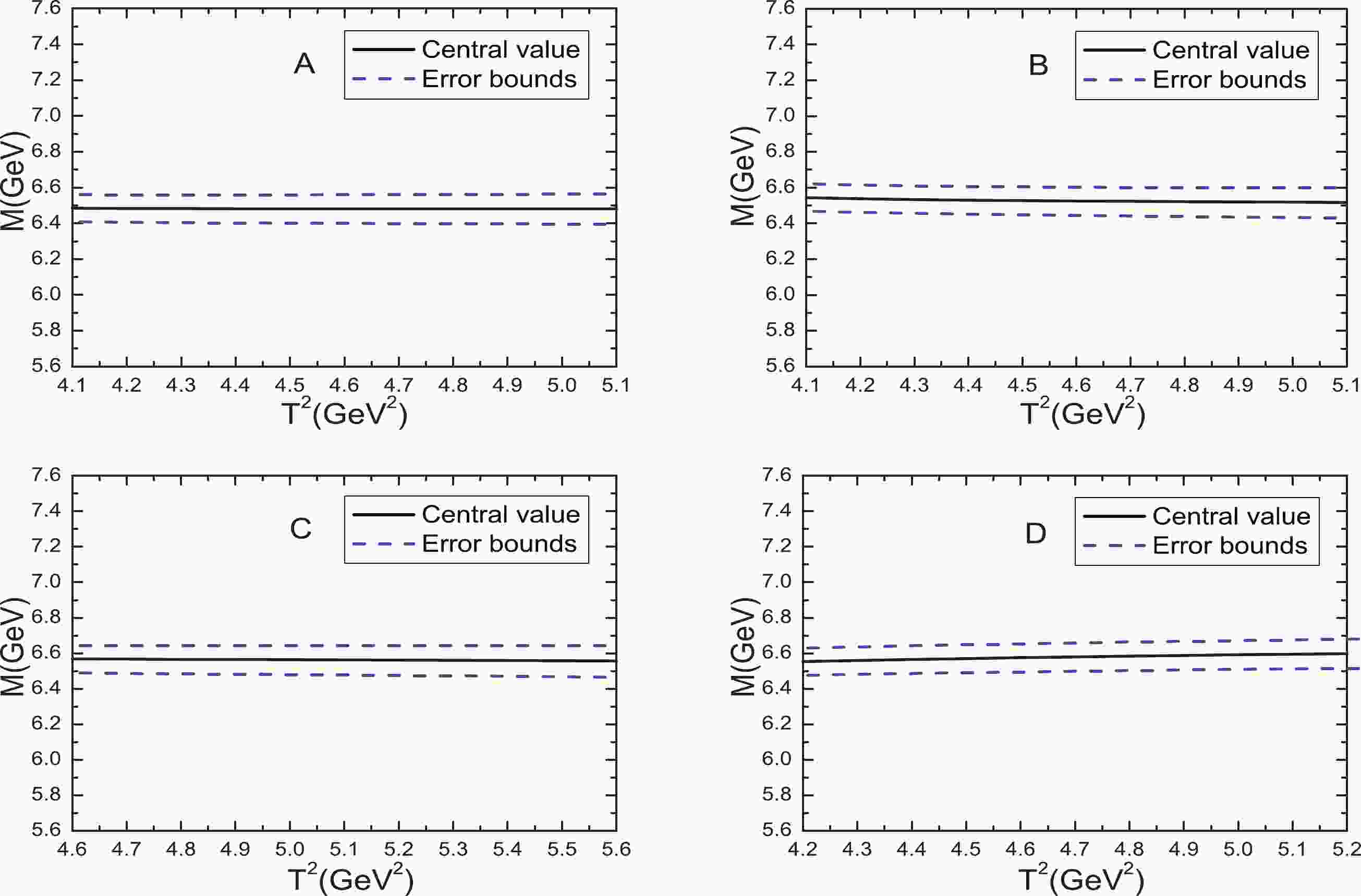
$ cc\bar{c}\bar{c} $ tetraquark states.Now, let us take into account all uncertainties of the input parameters, and obtain the values of the masses and pole residues of the first radial excited states, which are also shown explicitly in Table 1 and Fig. 1. The predicted masses and pole residues are rather stable with variation of the Borel parameters; the uncertainties that originate from the Borel parameters in the Borel windows are very small, in other words, Borel platforms appear. Now that the three criteria are all satisfied, we expect to make reliable or sensible predictions.

Figure 1. (color online) Masses of the first radial excited states of the tetraquark states with variations of the Borel parameters
$ T^2 $ , where A, B, C, and D denote the scalar, axialvector, vector, and tensor tetraquark states, respectively.In Table 2, we present the masses of the ground states and the first radial excited states from the QCD sum rules [7, 8]. The masses of the ground states, the first radial excited states, the third radial excited states, etc., satisfy the Regge trajectories,
$ J^{PC} $ 

$M_{1}/{\rm{GeV} }$ [7, 8]

$M_{2}/{\rm{GeV} }$ 

$M_{3}/{\rm{GeV} }$ 

$M_{ 4}/{\rm{GeV} }$ 

$ 0^{++} $ 

$ 5.99\pm0.08 $ 

$ 6.48\pm0.08 $ 

$ 6.94\pm0.08 $ 

$ 7.36\pm0.08 $ 

$ 1^{+-} $ 

$ 6.05\pm0.08 $ 

$ 6.52\pm0.08 $ 

$ 6.96\pm0.08 $ 

$ 6.37\pm0.08 $ 

$ 2^{++} $ 

$ 6.09\pm0.08 $ 

$ 6.56\pm0.08 $ 

$ 7.00\pm0.08 $ 

$ 7.41\pm0.08 $ 

$1^{--}$ 

$ 6.11\pm0.08 $ 

$ 6.58\pm0.09 $ 

$ 7.02\pm0.09 $ 

$ 7.43\pm0.09 $ 

Table 2. Masses of the
$ cc\bar{c}\bar{c} $ tetraquark states with the radial quantum numbers$ n = 1 $ ,$ 2 $ ,$ 3 $ , and$ 4 $ .$ M_n^2 = \alpha (n-1)+\alpha_0\, , $

(30) where
$ \alpha $ and$ \alpha_0 $ are constants. We take the masses of the ground states and the first radial excited states shown in Table 2 as input parameters to fit the parameters$ \alpha $ and$ \alpha_0 $ , and obtain the masses of the second radial excited states, which are also shown in Table 2. From the Table, we can see that the mass gap$ M_3-M_1 = 0.91\sim0.95\,{\rm{GeV}} $ , which is consistent with the mass gap$ m_{\psi^{\prime\prime}}-m_{J/\psi} = $ 0.94 GeV. Furthermore, from Table 1, we can see that the continuum threshold parameters$ \sqrt{s_0^\prime}\leqslant \overline{M}_3 $ , where$ \overline{M}_3 $ represents the central values of the masses of the second radial excited states.From Table 2, we can see that the predicted masses
$ M = 6.48\pm0.08\,{\rm{GeV}} $ ,$ 6.52\pm0.08\,{\rm{GeV}} $ ,$ 6.56\pm0.08\,{\rm{GeV}} $ , and$ 6.58\pm0.09\,{\rm{GeV}} $ for the first radial excited states of the scalar, axialvector, vector, and tensor$ cc\bar{c}\bar{c} $ tetraquark states are consistent with the broad structure above the threshold ranging from 6.2 to 6.8 GeV in the di-$ J/\psi $ mass spectrum [22, 23], while the predicted masses$ M = 6.94\pm0.08\,{\rm{GeV}} $ and$ 6.96\pm0.08\,{\rm{GeV}} $ for the second radial excited states of the scalar and axialvector$ cc\bar{c}\bar{c} $ tetraquark states are consistent with the narrow structure at approximately 6.9 GeV in the di-$ J/\psi $ mass spectrum [22, 23]. The present predictions support assigning the broad structure from 6.2 to 6.8 GeV in the di-$ J/\psi $ mass spectrum to be the first radial excited state of the scalar, axialvector, vector, or tensor$ cc\bar{c}\bar{c} $ tetraquark state, and assigning the narrow structure at approximately 6.9 GeV in the di-$ J/\psi $ mass spectrum to be the second radial excited state of the scalar or axialvector$ cc\bar{c}\bar{c} $ tetraquark state.In Table 2, we also present the third radial excited states of the
$ cc\bar{c}\bar{c} $ tetraquark states. From the Table, we can see that they lie above the vague structures near 7.2 GeV in the LHCb data [22, 23]. -
In this article, we construct the scalar and tensor currents to study the first radial excited states of the scalar, axialvector, vector, and tensor diquark-antidiquark-type
$ cc\bar{c}\bar{c} $ tetraquark states with the QCD sum rules and obtain the masses and pole residues. Then, we use the Regge trajectories to obtain the masses of the second radial excited states. The present predictions support assigning the broad structure from 6.2 to 6.8 GeV in the di-$ J/\psi $ mass spectrum to be the first radial excited state of the scalar, axialvector, vector, or tensor$ cc\bar{c}\bar{c} $ tetraquark state, and assigning the narrow structure at approximately 6.9 GeV in the di-$ J/\psi $ mass spectrum to be the second radial excited state of the scalar or axialvector$ cc\bar{c}\bar{c} $ tetraquark state.
Tetraquark candidates in LHCb's di-J/ψ mass spectrum
- Received Date: 2020-06-24
- Available Online: 2020-11-01
Abstract: In this article, we study the first radial excited states of the scalar, axialvector, vector, and tensor diquark-antidiquark-type





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: