-
According to the fact of accelerated expansion of the universe, Buchdahl proposed the
$ f(R) $ theory as a type of modified gravity [1], and further, the theory has been applied to explain the accelerated-inflation problem without dark matter or dark energy [2-4]. The$ f(R) $ gravity generalizes general relativity, and the generalization certainly arises in the description of the background around the gravitational sources. The universe evolves with decreasing temperature. In the process of the vacuum phase transition in the early stage of the universe, several types of topological defects such as domain walls, cosmic strings, and monopoles might have arisen [5, 6]. These topological defects were formed in favor of a breakdown of local or global gauge symmetries [7]. For example, a global monopole as a spherically symmetric topological defect appears in the phase transition of a system composed of a self-coupling triplet of a scalar field whose original global$ O(3) $ symmetry is spontaneously broken to$ U(1) $ [6, 7]. It was shown that the structure of the metric outside a monopole has a solid angle leading all light rays to be deflected at the same angle [8]. In the case of a massive source involving a global monopole in the universe with accelerated expansion, its metric with terms associated with the monopole and$ f(R) $ issue is necessary [9, 10]. The nonvanishing modified parameter$ \psi_{0} $ from the$ f(R) $ theory belonging to the metric components introduces a cosmological horizon as a boundary of the universe to the spacetime limited by the$ f(R) $ global monopole [9]. More efforts have been contributed to the model. It was found that the parameter subject to the modification of gravity provides stable circular orbits for massive test particles in the gravitational field of an$ f(R) $ global monopole [9, 10]. The quasinormal modes for this type of black holes were calculated with the WKB approximation [11-13]. The thermodynamics of the black hole with a global monopole within the frame of$ f(R) $ gravity was investigated [14, 15]. The strong gravitational lensing for the same models was discussed analytically [16]. The corrections from the global monopole and the gravity modification in the$ f(R) $ theory to the dominant term in the scattering absorption cross section were computed with regard to low frequencies and small angles [17].In the research on black holes, more significant measurements and theoretical predictions have been recently reported. One key experiment involves the Event Horizon Telescope (EHT) [18]. The EHT data show the gravitational physics at the event horizon, from where no light escapes, which opens a window to probe the details of the black hole core. The regions surrounding black holes are known as the black hole shadows [18]. The black holes can be fundamentally quantum objects regardless of their size; therefore, the quantum gravity effects cannot be neglected for the physics of microscopic black holes such as their evaporation profile and singularity removal [19]. The quantum characteristics relate to the horizon of the black hole, such as the metric fluctuations [20-23] and quantum structures around the black hole [24-26]. It should be pointed out that the quantum effects are related to the Uncertainty Relation [24-26]. It is impossible to omit the gravitational influence; therefore, the terms with the Newtonian constant would appear in the Heisenberg uncertainty principle [27-33]. These terms can be functions of the momentum difference or distance interval. The General Uncertainty Principle (GUP) with a series of terms based on the momentum difference is shown as a quantum gravitational correction to the standard Heisenberg relation [28, 34]. One of its simple forms is chosen as
$ \Delta x\Delta p\geqslant 1+\beta l_{pl}^{2}\Delta p^{2} , $

(1) where
$ \beta $ is a constant of order unit, and the natural units$ \hbar = c = 1 $ are utilized [28, 34]. Within the tiny region, the momentum difference is large; therefore, the deviations are obvious according to the inequality (1). The GUP is used to study the quantum gravity phenomenology of black holes and to curb the divergence from states density near the black hole horizon while relating the entropy of the black hole to a minimal length as the quantum gravity scale [35-38]. The GUP also modifies the black hole horizon and further changes the black hole entropy [35-38]. In an anti-de Sitter spacetime, the Heisenberg uncertainty principle should be deformed with a suitably chosen parameterization [39-42]. The Extended Uncertainty Principle (EUP) is shown as a position-uncertainty correction to the Heisenberg inequality [28, 39-42]. We can select [28, 39-42]$ \Delta x\Delta p\geqslant 1+\alpha\frac{\Delta x^{2}}{L_{\ast}^{2}} , $

(2) where
$ \alpha $ is a constant of order unit, and$ L_{\ast} $ is considered as a large fundamental distance scale. The additional terms involve the ratio of distance difference and distance scale according to Eq. (2). It is evident that the EUP introduces the quantum effects over macroscopic distances [28, 39-42]. The EUP will redefine the horizon to revise the entropy [19].Although black holes are perceived as perfect absorbers classically, their evolutions include the tunneling radiation and fragmentation depending on quantum mechanics and thermodynamics, respectively [43-50]. The tunneling formalism for black holes subject to the imaginary part of action for the classically forbidden region of emission across the horizon is of great concern [51-57]. With the help of the semi-classical tunneling proposed by Kraus et al., much effort has been spent on Hawking radiation of many types of objects such as BTZ black holes [58-61], Taub-NUT black holes [62], Kerr-Newman black holes [63-65], and Godel black holes [66]. The fragmentation of black holes as a type of evolution has also attracted considerable attention [50]. This thermodynamic instability was discussed under non-perturbation [50]. The fragmentation issue was used to probe the final fates of a series of black holes such as the rotating anti-de Sitter black holes [67], black holes with a Gauss-Bonnet term [68], and charged anti-de Sitter black holes [69]. It should be pointed out that the black hole tunneling radiation and fragmentation are both related to their entropy associated with their horizons [43-45]. The standard Heisenberg uncertainty principle governs the horizons [27-34, 39-42]. As mentioned above that the generalizations of the principle undoubtedly modify the horizons and further the entropy, the GUP has influence over the tunneling radiation and fragmentation of black holes [28, 34-36, 39-42]. In the context of the GUP modifying quantum mechanics [27-34, 70-75], the authors of Refs. [35, 36] derived and estimated the relation between the Hawking tunneling radiation of black holes and a minimal length as the quantum gravity scale in the higher dimensional spacetime by means of the tunneling formalism. Under the GUP, we calculated the Parikh-Kraus-Wilczeck tunneling radiation of black holes involving an
$ f(R) $ global monopole to show that the square of the momentum difference term advances the emission of this type of black holes, while the global monopole and the revision of general relativity both hinder the black hole from emitting photons [76]. We also discovered that the same black hole remains stable instead of splitting without the GUP corrections [77]. Having researched the fragmentation of the black holes with the$ f(R) $ global monopole in virtue of the second law of thermodynamics, we showed that the influence from the GUP leads the black hole to break into two parts with larger mass and smaller ones, respectively [77].It is necessary to consider the tunneling radiation and fragmentation of a Schwarzschild black hole with the global monopole under the EUP within the frame of the
$ f(R) $ scheme. As a type of generalization of Heisenberg uncertainty principle, the EUP is significant and its quantum effects can appear at an extremely large scale [19, 28, 29]. The EUP revises the relation between the horizon and the mass of black hole to correct the matter orbits and innermost stable circular orbits (ISCO), the size of the photosphere [19]. The contribution of the EUP corresponds to the dark matter effects because the EUP correction fits the Milky Way's rotation curve [19]. The thermodynamic properties of the Schwarzschild black hole and the modified Unruh effect governed by the EUP were discussed [78]. There must exist massive objects containing global monopoles in spacetime with the description of$ f(R) $ gravity as mentioned above. The EUP brings about the effects on the tunneling radiation and fragmentation of black holes through the EUP-corrected horizon [28, 34-36, 39-42]. During our research on the evolution of the black holes, we should not omit the corrections from the EUP. To the best of our knowledge, few efforts have been made to investigate the EUP influence on the black hole stability due to the radiation and the fragmentation. Under the EUP, we are going to derive and calculate the entropy of a black hole swallowing the$ f(R) $ global monopole to discuss the possibility of the black hole radiating and breaking into two sections, with the help of the techniques in Refs. [46-49] and Ref. [50], respectively. We investigate how the EUP affects the possibilities. We list our results and compare the results with those under the GUP finally. -
We are going to investigate the entropy of a black hole with a global monopole in the
$ f(R) $ theory. Under the corrections from the$ f(R) $ statement, the spherically symmetric solution to the gravitational field equation coupled to the matter field with a spontaneously broken$ O(3) $ symmetry was found [9, 10, 15]:$ {\rm d}s^{2} = A(r){\rm d}t^{2}-B(r){\rm d}r^{2}-r^{2}({\rm d}\theta^{2}+\sin^{2}\theta {\rm d}\varphi^{2}), $

(3) where
$ A(r) = B^{-1}(r) = 1-8\pi G\eta^{2}-\frac{2GM}{r}-\psi_{0}r $

(4) and
$ G $ is the Newton constant. As a monopole parameter in a typical grand unified theory,$ \eta $ is of the order$10^{18}\;{\rm GeV}$ to lead$ 8\pi G\eta^{2}\approx10^{-5} $ [6, 8].$ M $ is the mass parameter. The factor$ \psi_{0} $ represents the extension of the standard general relativity. The roots of the equation$ A(r) = 0 $ from metric (3) are [9, 10, 15]$ r_{\pm} = \frac{1-8\pi G\eta^{2}\pm\sqrt{(1-8\pi G\eta^{2})^{2}-8GM\psi_{0}}}{\psi_{0}} . $

(5) Here
$ r_{+} $ and$ r_{-} $ stand for the outer and inner radii, respectively. It is obvious that the outer horizon will disappear if the modified parameter$ \psi_{0} $ vanishes.The entropy of a black hole is related to the horizon [43-46]. The corrected horizon radius certainly generalizes the expression of the entropy [19, 35, 36, 77, 78]. According to the scheme of Ref. [19], the distance interval can be estimated as
$ \Delta x' = \frac{\Delta x}{1+\dfrac{\alpha}{L_{\ast}^{2}}\Delta x^{2}} , $

(6) where
$ \Delta x $ is the original size of the black hole. If the influence from the EUP disappears as$ \alpha = 0 $ , the distance difference$ \Delta x' $ will be reverted to the original ones. The$ \alpha $ -term from the EUP shortens the black hole size according to Eq. (6). Based on the approaches of Refs. [43-45], the Hawking temperature for the black hole with the descriptions (3) and (4) is a function of variables such as$ \eta $ and$ \psi_{0} $ ,$ T_{H} = \frac{1}{2\pi}\left(\frac{1-8\pi G\eta^{2}}{\Delta x}-\psi_{0}\right). $

(7) Here, the interval is set as
$ \Delta x = 2r_{H} $ , and$ r_{H} = r_{-} $ is the black hole horizon without the extension of Heisenberg's relation. The Bekenstein-Hawking entropy may be obtained from the Hawking temperature (7) with the help of the following thermodynamic relation [43-45, 49]:$ T_{H} = \frac{{\rm d}E}{{\rm d}S}\approx\frac{{\rm d}M}{{\rm d}S} . $

(8) In the emission process [49], the comparison between the initial and the final values of the entropy of the black hole with the solid deficit angle and
$ f(R) $ correction can be approximated as$\begin{aligned}[b] \Delta S\approx &-\frac{4\pi G}{(1-8\pi G\eta^{2})^{2}}[M^{2}-(M-\hbar\omega)^{2}]\\&-\frac{16\pi G^{2}\psi_{0}}{(1-8\pi G\eta^{2})^{4}}[M^{3}-(M-\hbar\omega)^{3}], \end{aligned} $

(9) where
$ \omega $ is a shell of energy moving along the geodesics towards the black hole with metric (3) [49, 59]. We substitute the Hawking temperature (7) into the thermodynamic relation (8) to perform the integral for the change in entropy while we take$ \Delta x = 2r_{-} $ with the help of the horizon (5). The difference in entropy of the black hole with the$ f(R) $ global monopole is denoted as$ \Delta S' $ and can be obtained in the process where the black hole emits a photon such as$ \hbar\omega $ . The black hole's tunneling probability can be expressed as [49, 56]$ \Gamma\sim {\rm e}^{\Delta S} . $

(10) From Eq. (9), the higher order of the typical grand unified theory such as that for increasing
$ 8\pi G\eta^{2} $ will lead to a larger absolute value of negative entropy difference, so will the farther away from Einstein's general relativity like increasing the magnitude of$ \psi_{0} $ . It can be argued that the existence of the global monopole in the black hole or the deviation from general relativity damps the emission of the black hole. The same topics were considered under the GUP as in Eq. (1). The emission of this type of black hole is promoted in favor of the greater parameter$ \beta $ as a coefficient of a quadratic term in the momentum difference [76, 77].It is significant to wonder how the EUP affects the entropy difference associated with the tunneling probability of the black hole described by the
$ f(R) $ global monopole metric. Following the procedure of Refs. [43-45, 77, 79], we choose the distance interval in the temperature (7) as$ \Delta x' $ , as expressed in Eq. (6), to obtain the EUP-corrected Hawking temperature,$ \begin{aligned}[b] T'_{H} =& \frac{1}{2\pi}\left(\frac{1-8\pi G\eta^{2}}{\Delta x'}-\psi_{0}\right)\\ =& T_{H}+\frac{\alpha}{\pi L_{\ast}^{2}}(1-8\pi G\eta^{2})r_{H} , \end{aligned} $

(11) while we also let
$ \Delta x = 2r_{H} $ as above. The corrections from the EUP increase the Hawking temperature. By means of the thermodynamic relation (8) [43-45, 49], we derive the corrected entropy difference of the radiating black hole involving the$ f(R) $ global monopole as follows:$ \begin{aligned}[b] \Delta S' =& \Delta S'(\eta, \psi_{0}, \alpha) \quad \\ =& \frac{2\pi}{G}\int_{r_{H}}^{r'_{H}}\frac{-2\psi_{0}r_{H}^{2}+(1-8\pi G\eta^{2})r_{H}}{\dfrac{4\alpha}{L_{\ast}^{2}}(1-8\pi G\eta^{2})r_{H}^{2}-2\psi_{0}r_{H}+(1-8\pi G\eta^{2})}{\rm d} r_{H} . \end{aligned} $

(12) Here,
$ r_{H} = r_{-} $ and$ r'_{H} = r_{-}|_{M\longrightarrow M-\hbar\omega} $ . We discuss the integral (12) in the cases of$ \alpha = 0 $ and$ \alpha\neq0 $ , respectively, because the parameter$ \alpha $ appears as the coefficient of the quadratic term of$ r_{H} $ in the integrand function. Whether the variable$ \alpha $ is equal to zero leads the entropy difference of the radiating black hole to be totally different. It can be checked whether before the performance of the integral,$ \Delta S' $ (12) recovers to$ \Delta S $ , as specified by Eq. (9), if$ \alpha = 0 $ [49]. Having performed the integral under$ \alpha\neq0 $ , we can show the change in entropy$ \Delta S' $ in the unit of the difference for a Schwarzschild black hole as$ \Delta S_{0}\approx-8\pi GM\hbar\omega $ [49],$ \begin{aligned}[b] \frac{\Delta S'}{\Delta S_{0}} \approx&\frac{\psi_{0}(r_{H}-r'_{H})}{\dfrac{2\alpha}{L_{*}^{2}}(1-8\pi G\eta^{2})} -\frac{1}{\dfrac{8\alpha}{L_{*}^{2}}}\left[\frac{\psi_{0}^{2}}{\dfrac{\alpha}{L_{*}^{2}}(1-8\pi G\eta^{2})^{2}}-1\right] \\& \times\ln\frac{\dfrac{4\alpha}{L_{*}^{2}}(1-8\pi G\eta^{2})(r')_{H}^{2}-2\psi_{0}r'_{H}+(1-8\pi G\eta^{2})}{\dfrac{4\alpha}{L_{*}^{2}}(1-8\pi G\eta^{2})r_{H}^{2}-2\psi_{0}r_{H}+(1-8\pi G\eta^{2})} -\frac{\psi_{0}^{3}-\dfrac{3\alpha\psi_{0}}{L_{*}^{2}}(1-8\pi G\eta^{2})^{2}}{\dfrac{4\alpha^{2}}{L_{*}^{2}}(1-8\pi G\eta^{2})^{2}} \\& \times\frac{1}{\sqrt{\Delta}}\ln\frac{\left(\dfrac{8\alpha}{L_{*}^{2}}r'_{H}-2\psi_{0}-\sqrt{\Delta}\right) \left(\dfrac{8\alpha}{L_{*}^{2}}r_{H}-2\psi_{0}+\sqrt{\Delta}\right)}{\left(\dfrac{8\alpha}{L_{*}^{2}}r'_{H} -2\psi_{0}+\sqrt{\Delta}\right)\left(\dfrac{8\alpha}{L_{*}^{2}}r_{H}-2\psi_{0}-\sqrt{\Delta}\right)} \approx-\frac{1}{\dfrac{\alpha}{L_{\ast}^{2}}}\frac{\psi_{0}}{4GM(1-8\pi G\eta^{2})}\frac{1}{\sqrt{(1-8\pi G\eta^{2})^{2}-8GM\psi_{0}}} .\quad \end{aligned} $ 
(13) In the case of the EUP, the tunneling probability of the black hole in Eq. (10) should be revised as
$\Gamma'\sim {\rm e}^{\Delta S'}$ [49]. The dependence of the entropy difference formulated for the black hole including the$ f(R) $ global monopole in Eq. (12) on the variables$ \alpha $ and$ \psi_{0} $ corresponding to the EUP correction and the deviation of standard gravity, respectively, is plotted in Fig. 1. The entropy change$ \Delta S' $ is a decreasing function of$ \alpha $ for$ \psi_{0} $ with a series of definite values. The stronger influence from EUP leads the value of$ \Delta S' $ to be smaller, which retards the radiation of the black hole, which is opposite to the case of the GUP appearing in Eq. (1). The considerable correction on the general relativity also causes the black hole to be unstable due to the tunnel process. -
The fragmentation probability of a Schwarzschild black hole whose spacetime has a solid deficit angle owing to a global monopole dominated by
$ f(R) $ gravity should be discussed under the EUP. We can investigate the entropy of black hole to explore the its fate. In view of Refs. [44, 80, 81], the Bekenstein-Hawking entropy of black hole is proportional to the horizon area:$ S = \frac{1}{4}A_{H} , $

(14) where
$ A_{H} = 4\pi r_{H}^{2} . $

(15) According to the second law of thermodynamics, the thermodynamic argument for the fragmentation of a black hole claimed that the black hole entropy must increase during its evolution [50]. Here, we assume that the black hole with
$ f(R) $ global monopole breaks into two parts involving the same type of monopole. In the process of fragmentation, the original black hole can be considered to have an initial state and a final state consisting of two black holes under the conservation of mass. Subject to the second law of thermodynamics, we can compare the two entropies for the initial and final states, respectively, to investigate whether fragmentation can happen. It was shown that the nature of the entropy difference for the$ f(R) $ global monopole black hole limited by the Heisenberg inequality remains negative regardless of whether the general relativity has been generalized. The division of this type of isolated black holes cannot occur spontaneously [82]. When the GUP is introduced, the black hole containing the$ f(R) $ global monopole will split into two parts [82]. The stronger influence from the GUP can lead the difference of the masses for the two fragmented black holes to be smaller [82]. As mentioned above, the EUP is also a generalization of the Heisenberg uncertainty principle. We should study the influence from the EUP on the fragmentation instability of the black hole swallowing a global monopole governed by the$ f(R) $ theory. In the initial case, the entropy of the isolated black hole can be obtained from Eq. (14):$ S_{i} = \pi r_{H}^{2}(M, \eta^{2}, \psi_{0}) , $

(16) where
$ r_{H}(M, \eta^{2}, \psi_{0}) = r_{-} $ , as shown in Eq. (5). We estimate the black hole horizon amended by the EUP with the original horizon as$ \Delta x = 2r_{H}(M, \eta^{2}, \psi_{0}) $ from Eq. (6) [19]:$ r'_{H}(M, \eta^{2}, \psi_{0}) = \frac{r_{H}(M, \eta^{2}, \psi_{0})}{1+\dfrac{4\alpha}{L_{\ast}^{2}}r_{H}^{2}(M, \eta^{2}, \psi_{0})} . $

(17) The correction will disappear with
$ \alpha = 0 $ . Under the EUP, the corrected horizons of black holes lead to the corrected entropy difference,$ \Delta S' = S'_{f}-S'_{i} , $

(18) where
$ S'_{i} = \pi r'^{2}_{H}(M, \eta^{2}, \psi_{0}) , $

(19) $ S'_{f} = \pi r'^{2}_{H}(\varepsilon_{M}M, \eta^{2}, \psi_{0})+\pi r'^{2}_{H}((1-\varepsilon_{M})M, \eta^{2}, \psi_{0}) . $

(20) By means of Eq. (17), we obtain the corrected radii
$ r'_{H}(\varepsilon_{M}M, \eta^{2}, \psi_{0}) $ and$ r'_{H}((1-\varepsilon_{M})M, \eta^{2}, \psi_{0}) $ as follows:$ r'_{H}(\varepsilon_{M}M, \eta^{2}, \psi_{0}) = r'_{H}(M, \eta^{2}, \psi_{0})|_{M\longrightarrow\varepsilon_{M}M} , $

(21) $ r'_{H}((1-\varepsilon_{M})M, \eta^{2}, \psi_{0}) = r'_{H}(M, \eta^{2}, \psi_{0})|_{M\longrightarrow(1-\varepsilon_{M})M} . $

(22) It should be pointed out that
$ r'_{H}(M, \eta^{2}, \psi_{0}) $ stands for the EUP-limited horizon of the initial black hole swallowing the$ f(R) $ global monopole. Under the EUP,$ r'_{H}(\varepsilon_{M}M, \eta^{2}, \psi_{0}) $ and$ r'_{H}((1-\varepsilon_{M})M, \eta^{2}, \psi_{0}) $ are the horizon radii of the separated black holes belonging to the final state with masses$ \varepsilon_{M}M $ and$ (1-\varepsilon_{M})M $ , respectively. Following the same procedure as in Ref. [69], we define the mass distribution and its region$ 0\leqslant\varepsilon_{M}\leqslant 1 $ .It is fundamental to explore the fragmentation possibility of an
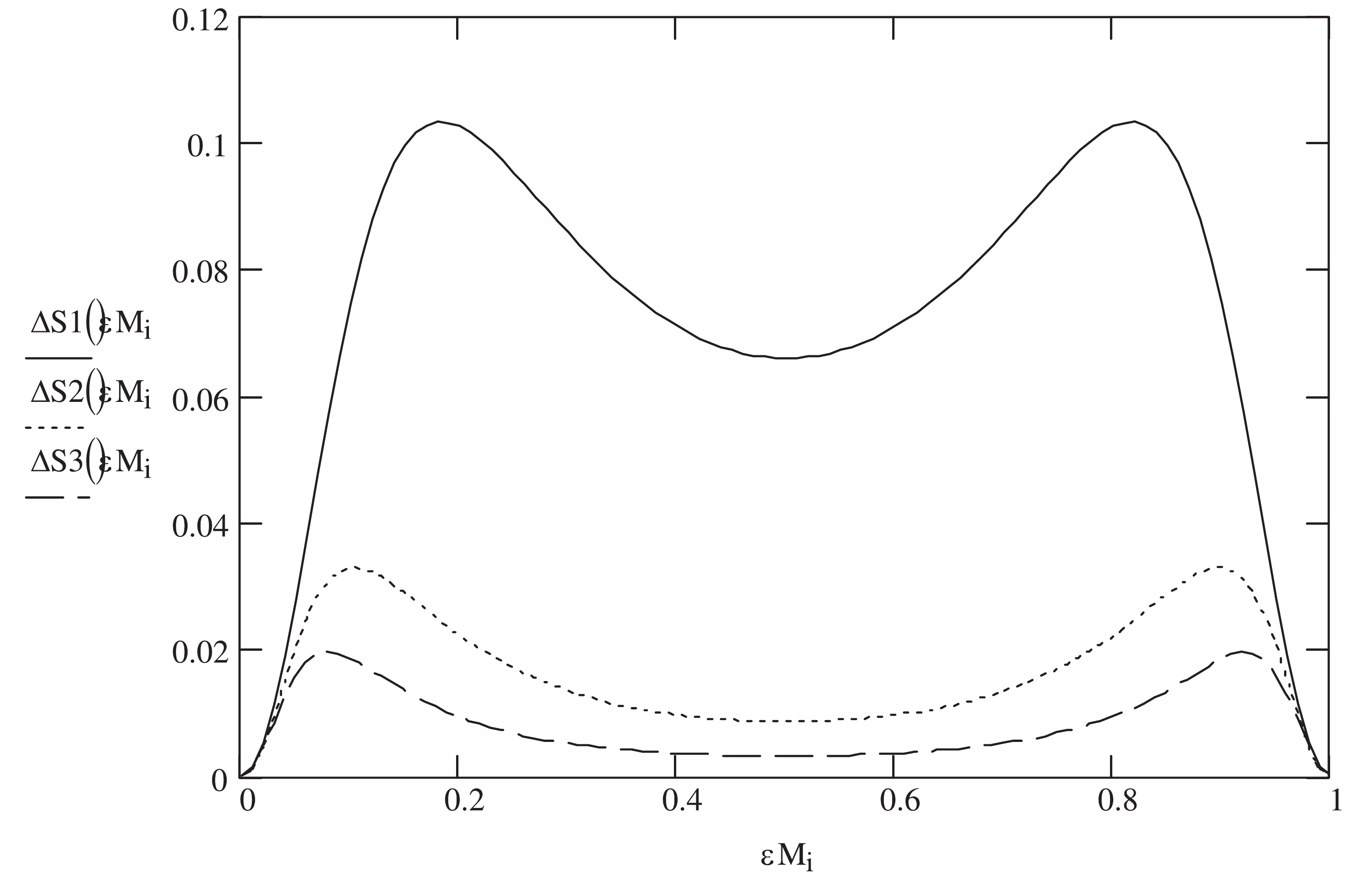
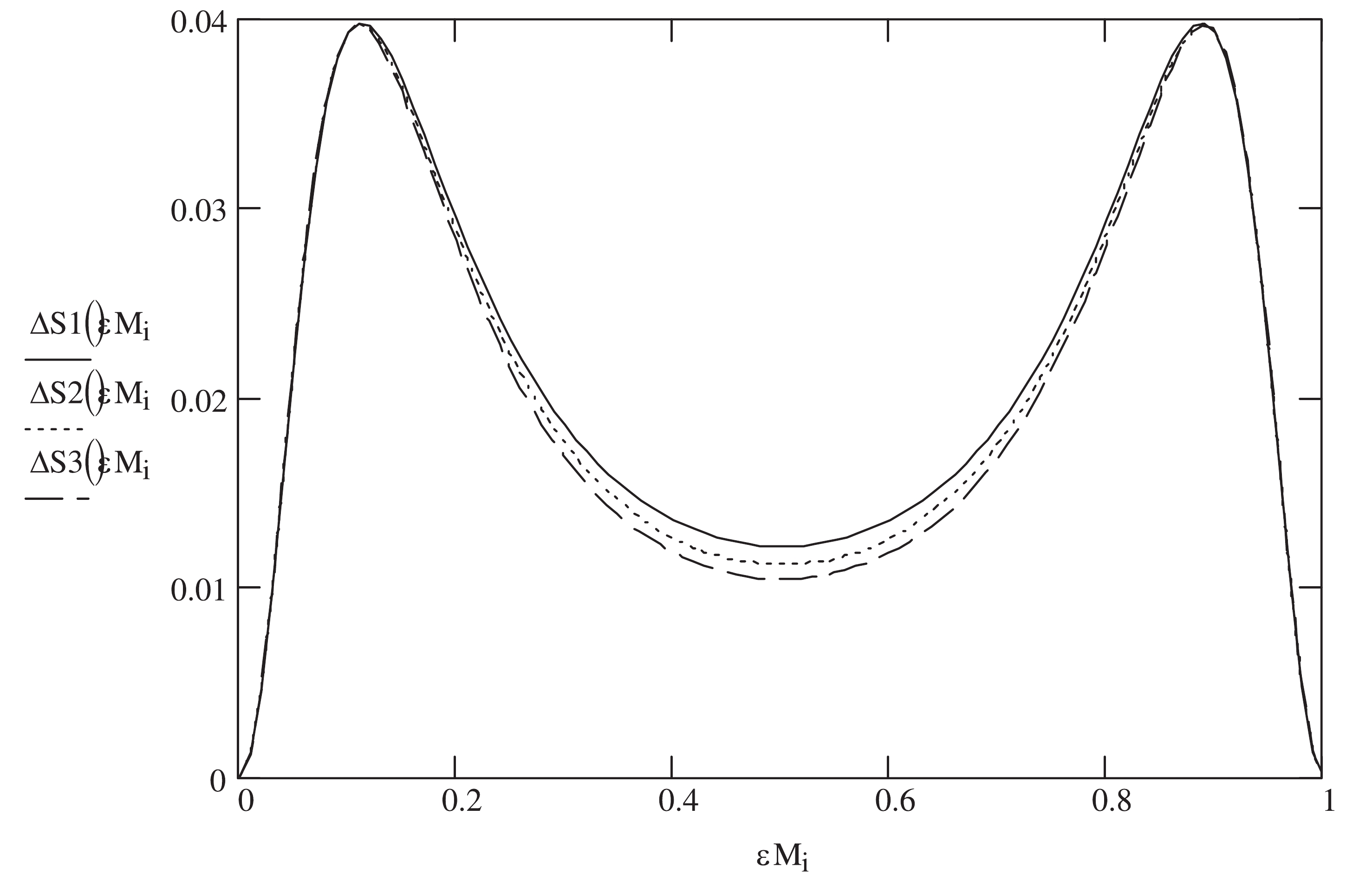
$ f(R) $ global monopole black hole under the EUP. The sign of the entropy difference during the evolution of the black hole helps us to determine whether the black hole can split because the entropy of a stable system cannot decrease in any spontaneous process [50, 83]. We ignore the generalization of the general relativity and show the entropy difference in Eq. (18) as a function of the ratio$ \varepsilon_{M} $ graphically under the EUP labeled as$ \alpha $ in Fig. 2. We find that the entropy increases during the process where the black hole becomes two new ones with$ 0\leqslant \varepsilon_{M}\leqslant 1 $ and the existence of EUP. The coefficient$ \alpha $ can adjust the curves of entropy difference, but it cannot change the natures of the difference. The entropy difference remains positive. The entropy of the$ f(R) $ global monopole black holes increases during their evolution, and this type of black holes under the EUP can break into two parts. Fig. 3 indicates that the deviation from the general relativity can also adjust the entropy difference slightly, but it cannot let the sign of the difference be negative. The entropy difference of the$ f(R) $ global monopole black holes due to EUP remains positive. The fragmentation of the EUP-influenced black holes can happen within the frame of the$ f(R) $ gravity theory. The EUP encourages the global monopole black hole under$ f(R) $ -generalized gravity to break into two parts spontaneously, with no limit to the distribution of the mass of the black hole. The GUP also impels the same black hole to break up, but the weaker influence of the generalized principle will cause the two new black holes to possess different sizes, one larger and the other smaller. -
We derive and compute the entropy difference of a black hole with a
$ f(R) $ global monopole under the Extended Uncertainty Principle to investigate the black hole evolution such as the Parikh-Kraus-Wilczeck tunneling radiation and fragmentation. The EUP adds a position-uncertainty term to the Heisenberg uncertainty principle to reflect the quantum corrections to gravity in the large scale [28, 39-42]. The EUP corrects the horizon of the black hole to change the black hole entropy. In favor of the entropy difference modified by the EUP in the process of emitting photons, the stronger influence from the EUP weakens the tunneling radiation of the black hole with the description of$ f(R) $ gravity while the global monopole exists in the compact object, which is different from the case of the GUP. Under the Heisenberg inequality, the$ f(R) $ global monopole black hole remains stable instead of splitting. In the case of black hole fragmentation, the appearance of modification from the EUP will cause the black hole to divide into two objects with arbitrary distributions of black hole mass, contrary to the case under the GUP.
Instability of a black hole with f (R) global monopole under extended uncertainty principle
- Received Date: 2021-01-13
- Available Online: 2021-10-15
Abstract: We consider the evolution of a black hole involving an f(R) global monopole based on the Extended Uncertainty Principle (EUP). The black hole evolutions refer to the instability due to the Parikh-Kraus-Wilczeck tunneling radiation or fragmentation. It is found that the EUP corrections make the entropy difference larger to encourage the black hole to radiate more significantly. We also show that the appearance of the EUP effects results in the black hole's division. The influence from the global monopole and the revision of general relativity can also adjust the black hole evolution simultaneously but cannot change the final result that the black hole will not be stable because of the EUP's effects.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: