Correlations and fluctuations in a magnetized PNJL model with and without the inverse magnetic catalysis effect

Motivated by the strong magnetic field in the core of compact stars and in the initial stage of relativistic heavy ion collisions, scholars have become increasingly attracted to the study of Quantum Chromodynamics (QCD) phase structures under external electromagnetic fields [1−44].

Lattice QCD (LQCD) simulations [7−13] have observed the inverse magnetic catalysis (IMC) phenomena of u and d quarks, the decreasing chiral condensates near the pseudocritical temperature $ T^c_{pc} $ of chiral restoration phase transition with increasing magnetic field, and the decrease in $ T^c_{pc} $under external magnetic fields. Meanwhile, studies show that the renormalized Polyakov loop increases with the magnetic field, and the transition temperature of deconfinement decreases as the magnetic field increases [7−11]. From an analytical perspective, in the presence of a uniform external magnetic field ${\boldsymbol B} =B{\it {{\boldsymbol e}_z}}$, the energy dispersion of quarks takes form $ E= \sqrt{p_z^2+2|Q_qB|l+m^2} $ with momentum $ p_z $ along the direction of the magnetic field and Landau level $l=0,1,2,\cdots$ [45]. Owing to this decrease in the fermion dimension, almost all model calculations at the mean field level exhibit the magnetic catalysis (MC) effect, the enhancement of chiral condensates in the entire temperature region and increase in pseudocritical temperatures for chiral restoration and deconfinement phase transitions under external magnetic fields; see reviews [1−5] and the references therein. Questions that remain are the explanation of the IMC phenomena of chiral condensates and the decrease in pseudocritical temperatures for chiral restoration and deconfinement phase transitions. Many scenarios have been proposed [9, 15−44], such as the magnetic inhibition of mesons, sphalerons, gluon screening effect, weakening of strong coupling, and an anomalous magnetic moment. In this paper, the IMC (MC) generally refers to the decreasing (increasing) behavior of physical quantities under an external magnetic field.

In addition to the QCD phase diagram, the thermodynamical properties of QCD matter are influenced by an external magnetic field. Among the thermodynamic quantities, the correlations and fluctuations of conserved charges are accessible in both theoretical calculations and experimental measurements and serve as useful probes for studying QCD phase transitions, such as identifying the critical end point (CEP) of the QCD phase diagram in the temperature-baryon chemical potential plane [46−52]. However, they are much less explored at the chiral restoration phase transition (crossover) with finite temperature and vanishing chemical potential under external magnetic fields. The analytical investigations at a vanishing chemical potential, finite temperature, and magnetic field [53−57] have been conducted under the hadron resonance gas model, Polyakov loop extended Nambu-Jona-Lasinio model (PNJL), and Polyakov loop extended chiral quark model. Researchers suggest the use of the correlation and/or fluctuation as the magnetometer of QCD [53, 58−60]. Note that the peak structure of quadratic fluctuations around $ T^c_{pc} $ in LQCD calculations [58] cannot be achieved in these analytical calculations. Meanwhile, the IMC effect has not been adequately considered in previous analytical studies [53−57].

In this paper, correlation $ \chi^{BQ}_{11} $ and quadratic fluctuations $ \chi^B_2,\ \chi^Q_2,\ \chi^T_2 $ of baryon number B, electric charge Q, and temperature T are investigated in a two-flavor PNJL model at finite temperature and magnetic field. The IMC effect is introduced through two methods, the magnetic-field-dependent coupling between quarks $ G(eB) $ and magnetic-field-dependent interaction between quarks and Polyakov loop $ T_0(eB) $, respectively. The results in the cases with and without the IMC effect are compared.

The remainder of this paper is organized as follows. Section II introduces the two-flavor magnetized PNJL model and the definitions of correlation $ \chi^{BQ}_{11} $ and fluctuations $ \chi^B_2,\ \chi^Q_2,\ \chi^T_2 $. Section III discusses the numerical results of the correlation and quadratic fluctuations at finite temperature and magnetic field in the cases with and without the IMC effect. Finally, we present the summary in Sec. IV.

The two-flavor PNJL model under an external magnetic field is defined through the Lagrangian density [61−69]:

Covariant derivative $D^\mu=\partial^\mu+ {\rm i} Q_f A^\mu-\mathrm{i} {\cal A}^\mu$ couples quarks to the two external fields, magnetic field ${\boldsymbol B}=\nabla\times{\boldsymbol A}$ and temporal gluon field $ {\cal A}^\mu=\delta^\mu_0 {\cal A}^0 $ with ${\cal A}^0=g{\cal A}^0_a \lambda_a/ 2= -\mathrm{i}{\cal A}_4$ in Euclidean space. Gauge coupling g is combined with the SU(3) gauge field $ {\cal A}^0_a(x) $ to define $ {\cal A}^\mu(x) $, and $ \lambda_a $ denotes the Gell-Mann matrices in color space. In this work, we consider the magnetic field ${\boldsymbol B}=(0, 0, B)$ along the z axis by setting $A_\mu= (0,0,x B,0)$ in Landau gauge, which couples with quarks of electric charge $Q_f={\rm diag}(Q_u, Q_d)= {\rm diag} (2e/3,-e/3)$. $\hat{m}_0= \; {\rm diag}(m^u_0, m^d_0)= {\rm diag}(m_0, m_0){\rm diag}(m_0, m_0)$ is the current quark mass matrix in flavor space, which controls the explicit breaking of chiral symmetry. For the chiral section in the Lagrangian, G is the coupling constant between quarks in the scalar and pseudoscalar channels, which determines the spontaneous breaking of chiral symmetry. The Polyakov potential describing deconfinement at finite temperature is expressed as

where Φ is the trace of the Polyakov loop $ \Phi=\left({\text {Tr}}_c L \right)/N_c $, with $L({\boldsymbol x})={\cal P} \text {exp}[\mathrm{i} \int^\beta_0 {\mathrm{d}}\tau {\cal A}_4({\boldsymbol x},\tau)]= \text {exp}[\mathrm{i} \beta {\cal A}_4 ]$ and $ \beta= $ 1/T, coefficient $ b_2(t)=a_0+a_1 t+a_2 t^2+a_3 t^3 $ with $ t=T_0/T $ is temperature dependent, and other coefficients $ b_3 $ and $ b_4 $ are constants.

The order parameter to describe chiral restoration phase transition is the chiral condensate $ \sigma=\langle\bar\psi\psi\rangle $ [70−74]. Φ is considered as the order parameter to describe the deconfinement phase transition, which satisfies $ \Phi \rightarrow 0 $ in a confined phase at low temperatures and $ \Phi \rightarrow 1 $ in a deconfined phase at high temperatures [61−69]. In mean field approximation, the thermodynamic potential at the finite temperature, quark chemical potential, and magnetic field contains the mean field and quark parts:

where n indicates Landau levels, $ f=u,d $ quark flavors, and $ \alpha_n=2-\delta_{n0} $ the spin factor; $ E_f^\pm=E_f \pm \mu_f $ contains quark energy $ E_f=\sqrt{p^2_z+2 n |Q_f B|+m^2} $ with dynamical quark mass $ m=m_0-G \sigma $ and quark chemical potential $\mu_u=\dfrac{\mu_B}{3}+\dfrac{2\mu_Q}{3}$, $\mu_d=\dfrac{\mu_B}{3}-\dfrac{\mu_Q}{3}$ with the baryon (electric) chemical potential $ \mu_B\ (\mu_Q) $ corresponding to the conserved baryon number (electric charge) $ B\ (Q) $.

The ground state at the finite temperature, quark chemical potential, and magnetic field is determined by minimizing the thermodynamic potential,

which leads to three coupled gap equations for order parameters σ, Φ, and $ {\bar \Phi} $. At vanishing quark chemical potential and finite temperature, the chiral symmetry restoration and deconfinement process are smooth crossover. Pseudocritical temperatures $ T_{pc}^c $ and $ T_{pc}^d $ for chiral restoration and deconfinement phase transitions are determined by the maximum changes in the order parameters $ \dfrac{\partial^2 \sigma}{\partial T^2}=0 $ and $ \dfrac{\partial^2 \Phi}{\partial T^2}=0 $, respectively [75, 76].

The quadratic fluctuations and correlations of baryon number B and electric charge Q can be obtained by taking the derivatives of thermodynamic potential Ω with respect to chemical potentials $ \hat{\mu}_X=\mu_X/T,\ (X=B,\ Q) $ evaluated at zero chemical potential:

and the quadratic fluctuation of temperature T is defined as

In this work, we focus on correlation $ \chi^{BQ}_{11} $ and fluctuations $ \chi^B_2,\ \chi^Q_2,\ \chi^T_2 $ at finite temperature, magnetic field, and vanishing chemical potential.

Because of the contact interaction among quarks, NJL models are nonrenormalizable, and we must introduce a regularization scheme to remove the ultraviolet divergence in momentum integrations. In this work, we take a Pauli-Villars regularization [16], which is gauge invariant and can guarantee the law of causality in a finite magnetic field. The three parameters in the two-flavor NJL model, namely, the current quark mass $ m_0=5 $ MeV, coupling constant $ G=7.79 $ GeV$ ^{-2} $, and mass parameter $ \Lambda=1127 $ MeV, are fixed by fitting chiral condensate $ \langle \bar \psi \psi \rangle =(-250\ \text{MeV})^3 $, pion mass $ m_{\pi}=134 $ MeV, and pion decay constant $ f_\pi=93 $ MeV in a vacuum $(T=\mu=0, eB=0)$. Note that in the parameter fitting process, we fix the current quark mass at $ m_0=5 $ MeV and use the chiral condensate and pion decay constant to determine parameters $ G,\ \Lambda $. The pion mass is calculated through the Gell-Mann-Oakes-Renner relation [77]. For the Polyakov potential, its temperature dependence is fitted from LQCD simulations, and the parameters are chosen as [62, 68, 69] $ a_0=6.75 $, $ a_1=-1.95 $, $ a_2=2.625 $, $ a_3=-7.44 $, $ b_3=0.75 $, $ b_4=7.5 $, and $ T_0=210 $ MeV.

The typical results of the PNJL model with the original parameters determined from the vacuum properties exhibit the MC effect. The chiral condensates and Polyakov loop increase with the magnetic field in the entire temperature region, and the pseudocritical temperatures for chiral restoration and deconfinement phase transitions also increase with the magnetic field [29, 56].

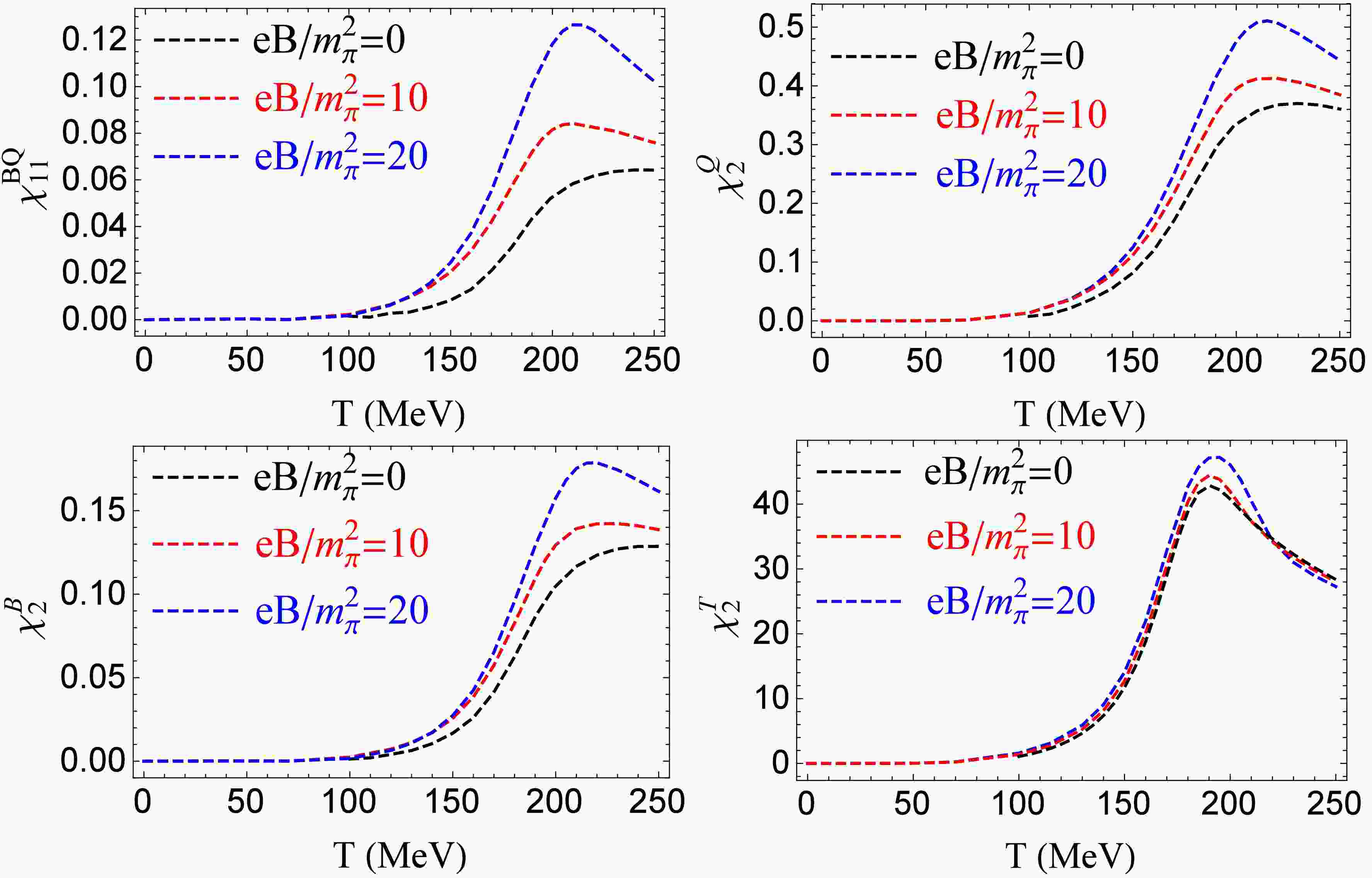
Figure 1 plots correlation $ \chi^{BQ}_{11} $ and quadratic fluctuations $ \chi^B_2,\ \chi^Q_2,\ \chi^T_2 $ as functions of temperature for a fixed magnetic field, $ eB/m^2_{\pi}=0,\ 10,\ 20 $. $ \chi^{BQ}_{11},\ \chi^B_2 $, and $ \chi^Q_2 $ have similar properties. At a vanishing magnetic field, they increase with temperature. When the magnetic field is turned on, they have higher values, and the peak structure becomes more pronounced. These properties are qualitatively consistent with LQCD simulations [58]. Compared with the results of $ \chi^{BQ}_{11},\ \chi^B_2,\ \chi^Q_2 $ in Ref. [56], where a peak structure is observed only in $ \chi^{BQ}_{11} $, the difference is due to the different regularization schemes, where the regularization is operated in the vacuum term $ (T=\mu=0) $ of the thermodynamical potential in Ref. [56], but the regularization is applied in both the vacuum and medium term of the thermodynamical potential in this work. $ \chi^T_2 $ exhibits a peak structure at vanishing and nonvanishing magnetic fields. The value of $ \chi^T_2 $ increases with the magnetic field in the region of low temperature and around the peak but decreases with the magnetic field at a sufficiently high temperature. When the external magnetic field is turned on, the strength of the phase transition increases [7, 8, 31, 37, 56], and this will enhance the correlation and fluctuations around the phase transition.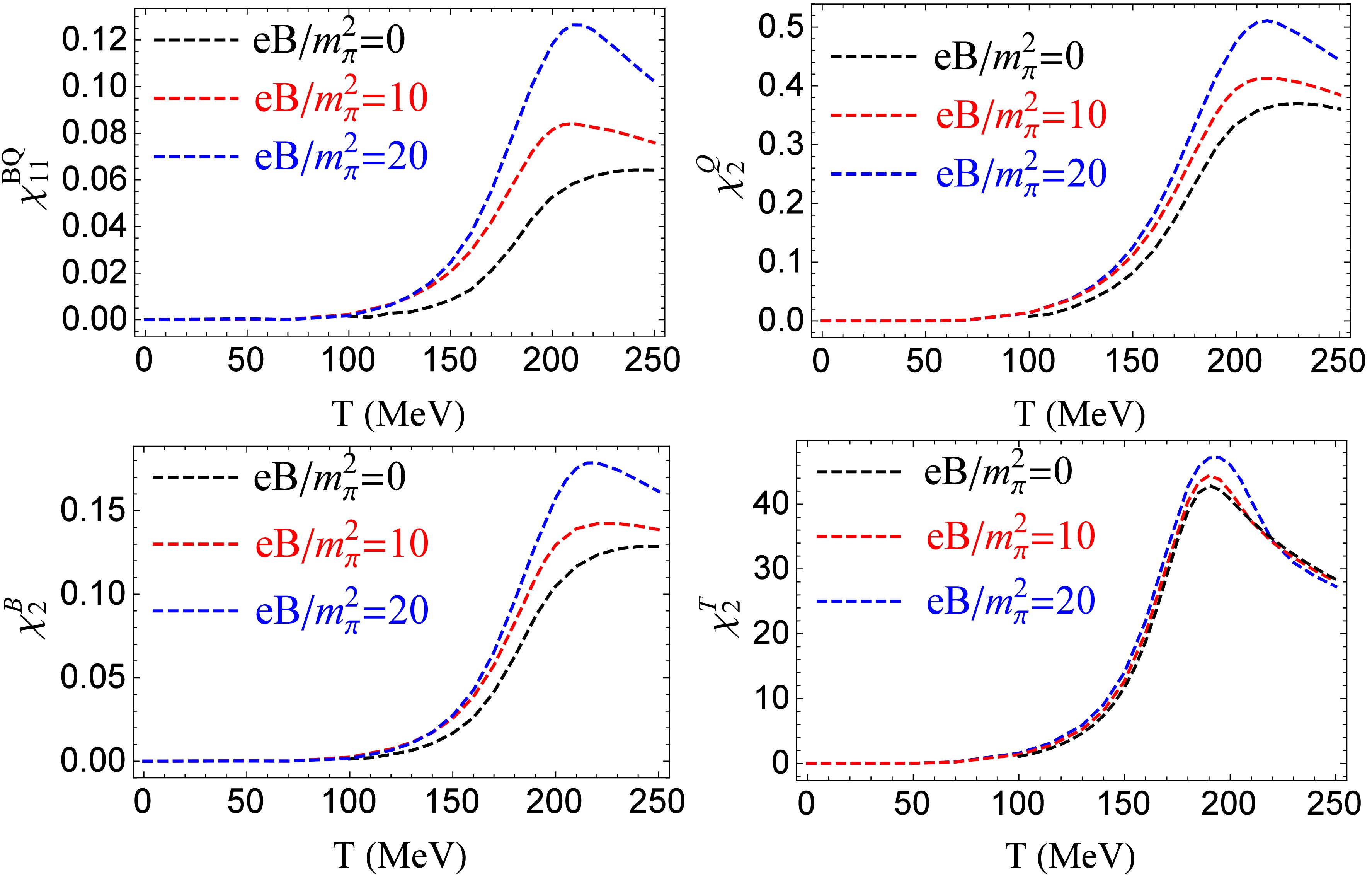

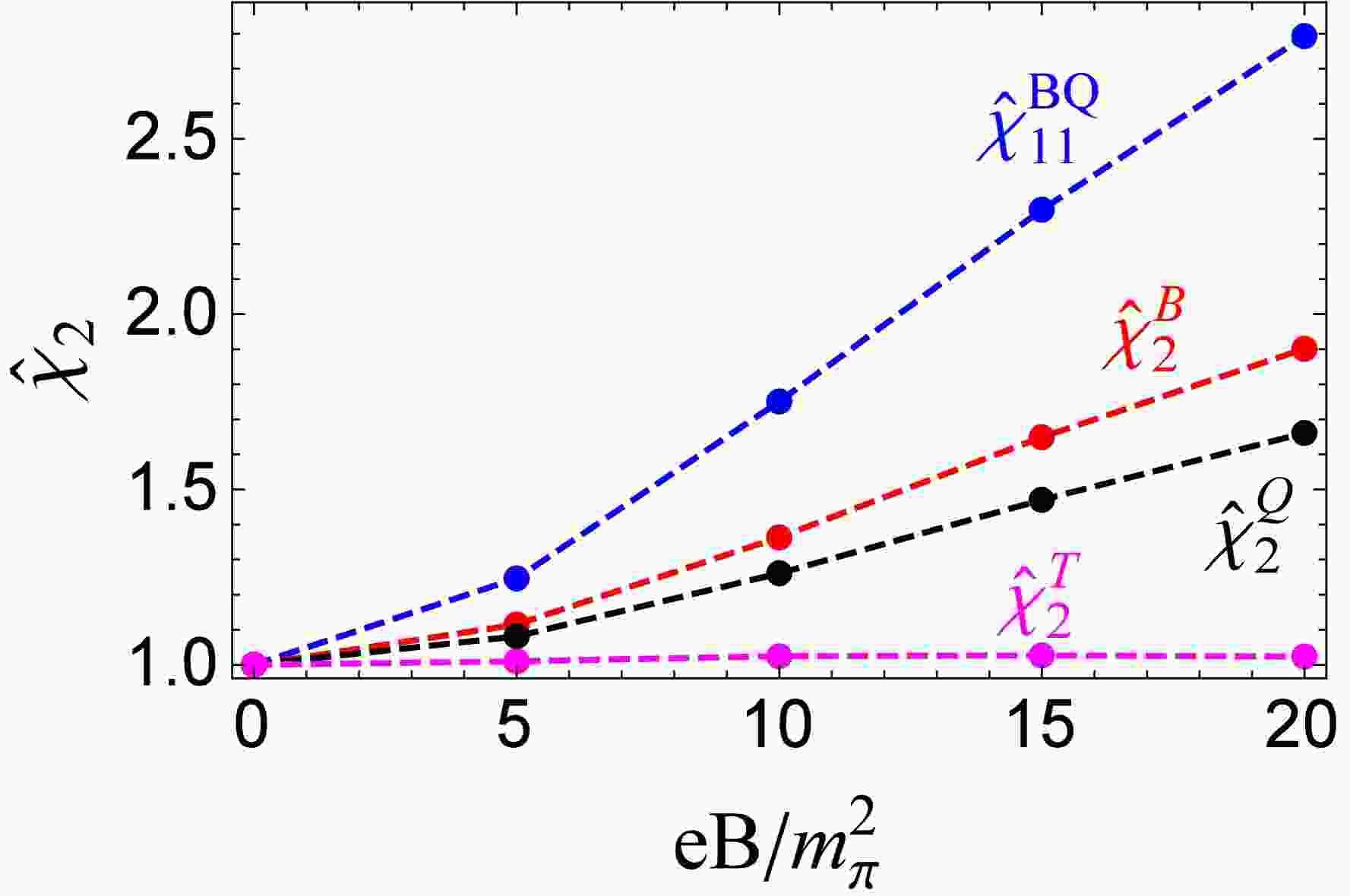
Figure 1.  (color online) Correlation $ \chi^{BQ}_{11} $ and quadratic fluctuations $ \chi^B_2,\ \chi^Q_2,\ \chi^T_2 $ as functions of temperature under fixed magnetic field $ eB/m^2_{\pi}=0,\ 10,\ 20 $.

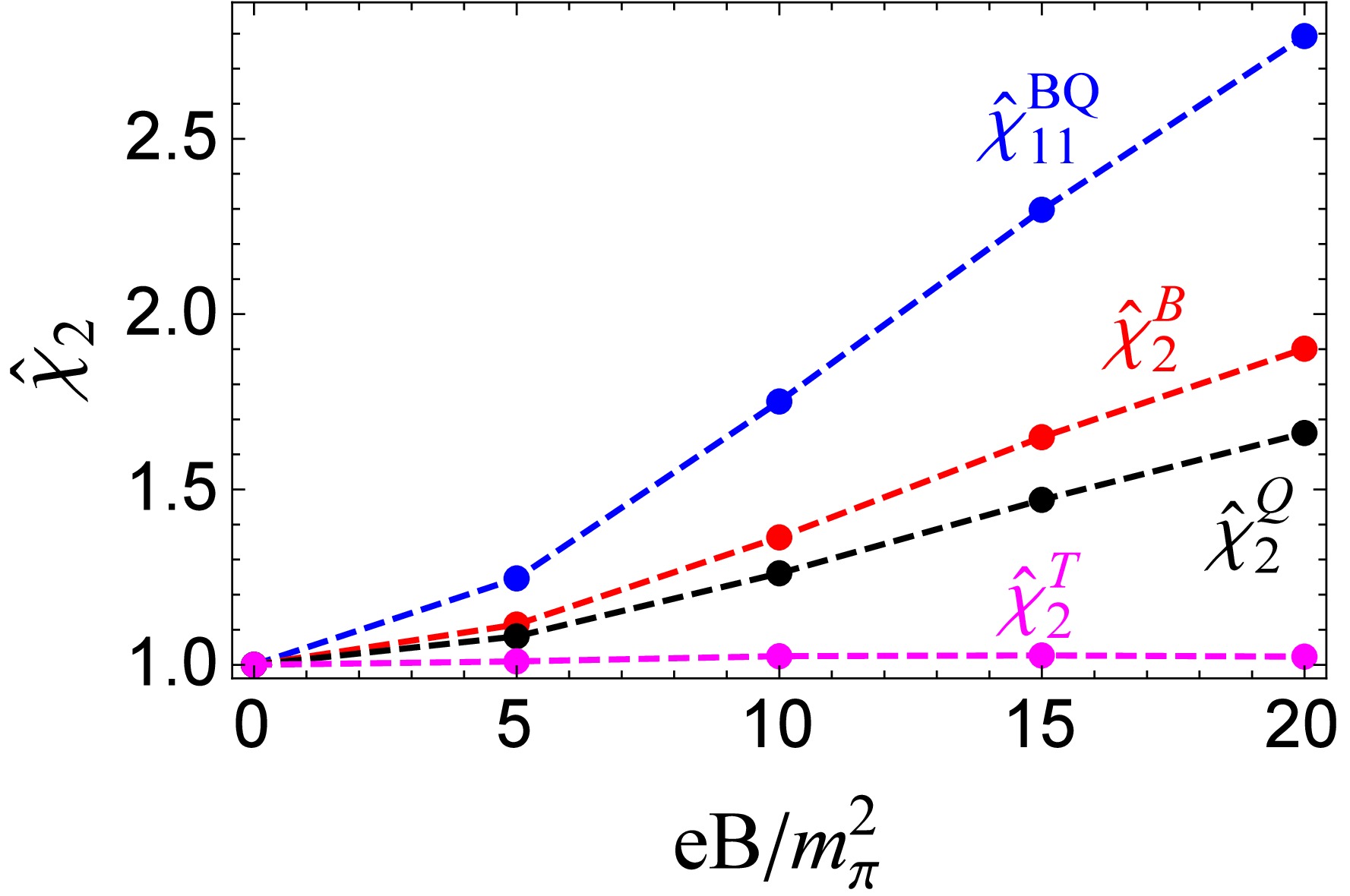
What is the property of correlation $ \chi^{BQ}_{11} $ and fluctuations $ \chi^B_2,\ \chi^Q_2,\ \chi^T_2 $ along the phase transition line under an external magnetic field? As shown in Fig. 2, scaled correlation $ {\hat {\chi}}_{11}^{BQ}=\dfrac{\chi_{11}^{BQ}(eB,T_{pc}^c(eB))}{\chi_{11}^{BQ}(eB=0,T_{pc}^c(eB=0))} $ and scaled quadratic fluctuations $ {\hat {\chi}}_2^{B}=\dfrac{\chi_2^{B}(eB,T_{pc}^c(eB))}{\chi_2^{B}(eB=0,T_{pc}^c(eB=0))} $, ${\hat {\chi}}_2^{Q}= \dfrac{\chi_2^{Q}(eB,T_{pc}^c(eB))}{\chi_2^{Q}(eB=0,T_{pc}^c(eB=0))}$, and $ {\hat {\chi}}_2^{T}=\dfrac{\chi_2^{T}(eB,T_{pc}^c(eB))}{\chi_2^{T}(eB=0,T_{pc}^c(eB=0))} $ at $ T_{pc}^c $ of chiral restoration phase transition are plotted as functions of the magnetic field. $ {\hat {\chi}}^{BQ}_{11} $ increases the fastest and it reaches a value of $ 1.75 $ at $eB=10\, m^2_{\pi}$. LQCD [60] reports $ {\hat {\chi}}^{BQ}_{11} \simeq 2.4 $ at $eB=8\,m^2_{\pi}$, which is higher than our PNJL result. $ {\hat {\chi}}^{B}_{2} $ monotonically increases with the magnetic field and approaches the value of $ 1.36 $ at $ eB=10m^2_{\pi} $, which undershoots the LQCD result [60]. $ {\hat {\chi}}^{Q}_{2} $ monotonically increases with the magnetic field and approaches the value of $ 1.26 $ at $ eB=10m^2_{\pi} $, which overshoots the LQCD result [60]. The increasing behaviors of $ {\hat {\chi}}^{BQ}_{11},\ {\hat {\chi}}^B_2,\ {\hat {\chi}}^Q_2 $ under an external magnetic field in our Fig. 2 are consistent with those in Ref. [56] and are not dependent on the regularization schemes. In contrast to $ {\hat {\chi}}^{BQ}_{11},\ {\hat {\chi}}^B_2 $, and $ {\hat {\chi}}^Q_2 $, $ {\hat {\chi}}^{T}_{2} $ is not sensitive to the magnetic field. It increases slightly and then decreases slightly with the magnetic field.

Figure 2.  (color online) Scaled correlation $ {\hat {\chi}}_{11}^{BQ} $ and scaled quadratic fluctuations $ {\hat {\chi}}_2^{B},\ {\hat {\chi}}_2^{Q},\ {\hat {\chi}}_2^{T} $ at the pseudocritical temperature of chiral restoration phase transition as functions of the magnetic field.

From LQCD simulations [7−13], the IMC phenomenon of chiral symmetry restoration of u and d quarks can be characterized either by the chiral condensates (order parameters) or pseudocritical temperature of chiral restoration phase transition. To include the IMC effect in the effect model, one approach is fitting the LQCD results of chiral condensates [78−81], and another approach is fitting the LQCD results of the pseudocritical temperature [25, 26, 44, 78, 82, 83]. The two methods provide results consistent with each other. In our current calculations, by fitting the LQCD reported decreasing pseudocritical temperature of chiral symmetry restoration $T_{pc}^c(eB)/ T_{pc}^c(eB=0)$ under an external magnetic field [7], we introduce the IMC effect in the two-flavor PNJL model through magnetic-field-dependent parameters$ G(eB) $ and $ T_0(eB) $, respectively, which represents the influence of an external magnetic field on the quark-gluon interaction.

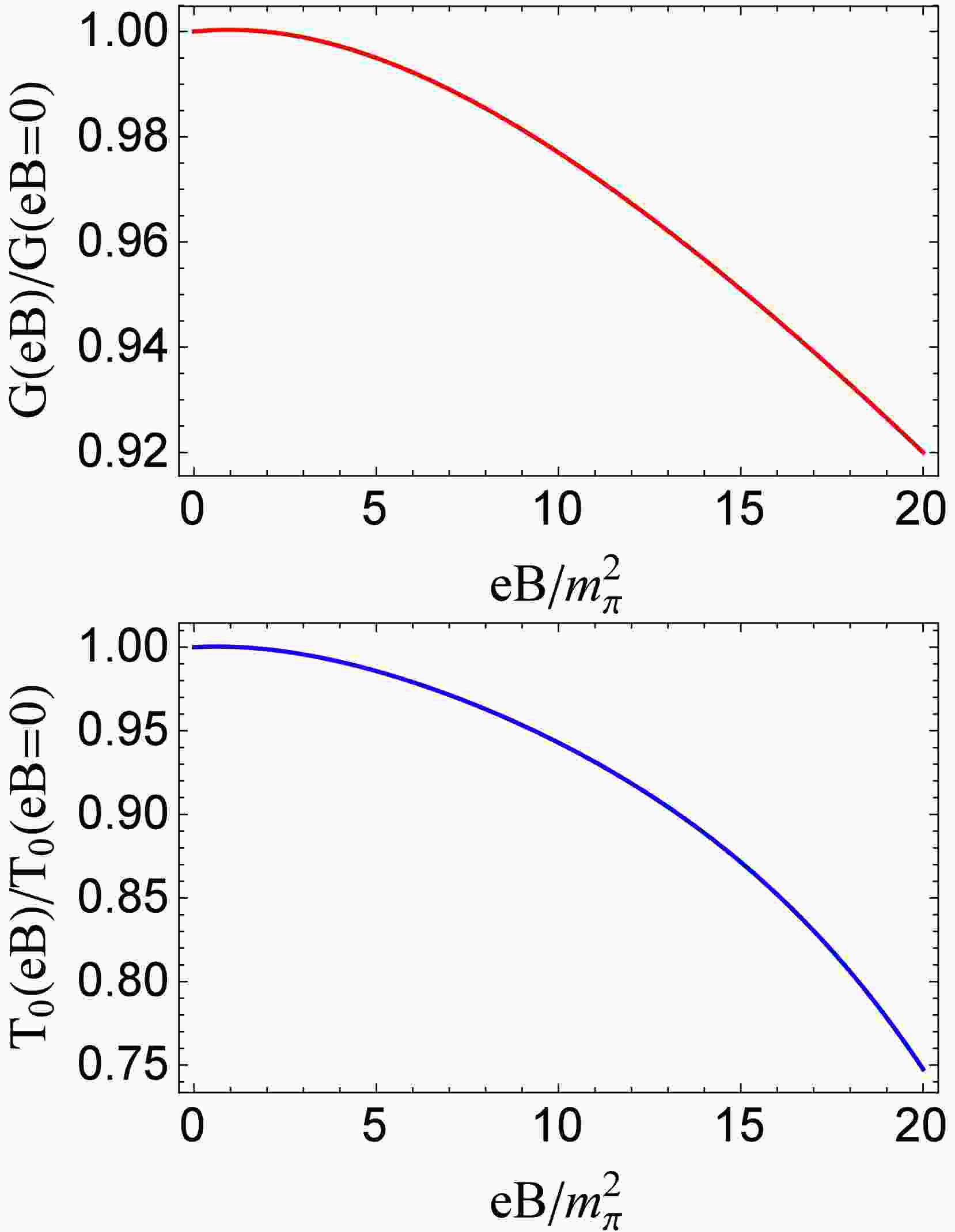
On one hand, the coupling between quarks plays a significant role in determining the spontaneous breaking and restoration of chiral symmetry. Because of the direct interaction between quarks and external magnetic fields, magnetic-field-dependent coupling $ G(eB) $ [25, 26, 78, 82, 83] is introduced into the PNJL model. To mimic the decrease in the pseudocritical temperature of chiral restoration phase transition under an external magnetic field in LQCD calculations [7], $ G(eB)/G(eB=0) $ is a monotonically decreasing function of the magnetic field, as plotted in the upper panel of Fig. 3. On the other hand, according to the LQCD analysis [9], the interaction between the Polyakov loop and sea quarks may be important for the IMC mechanism. A magnetic-field-dependent Polyakov loop scale parameter$ T_0(eB) $ is considered in the PNJL model to mimic the reaction of the gluon sector to the presence of magnetic fields [35, 38, 44]. As shown in the lower panel of Fig. 3, $ T_0(eB) $, which is determined by fitting the decrease in the pseudocritical temperature of chiral restoration phase transition in LQCD calculations [7], is also a monotonically decreasing function of the magnetic field. We have checked that, with our fitted parameter $ G(eB) $ or $ T_0(eB) $, the increase (decrease) in chiral condensates under magnetic fields at the low (high) temperatures, the increase in the Polyakov loop under magnetic fields in the entire temperature region, and the decrease in the pseudocritical temperature of the deconfinement phase transition under magnetic fields can be achieved.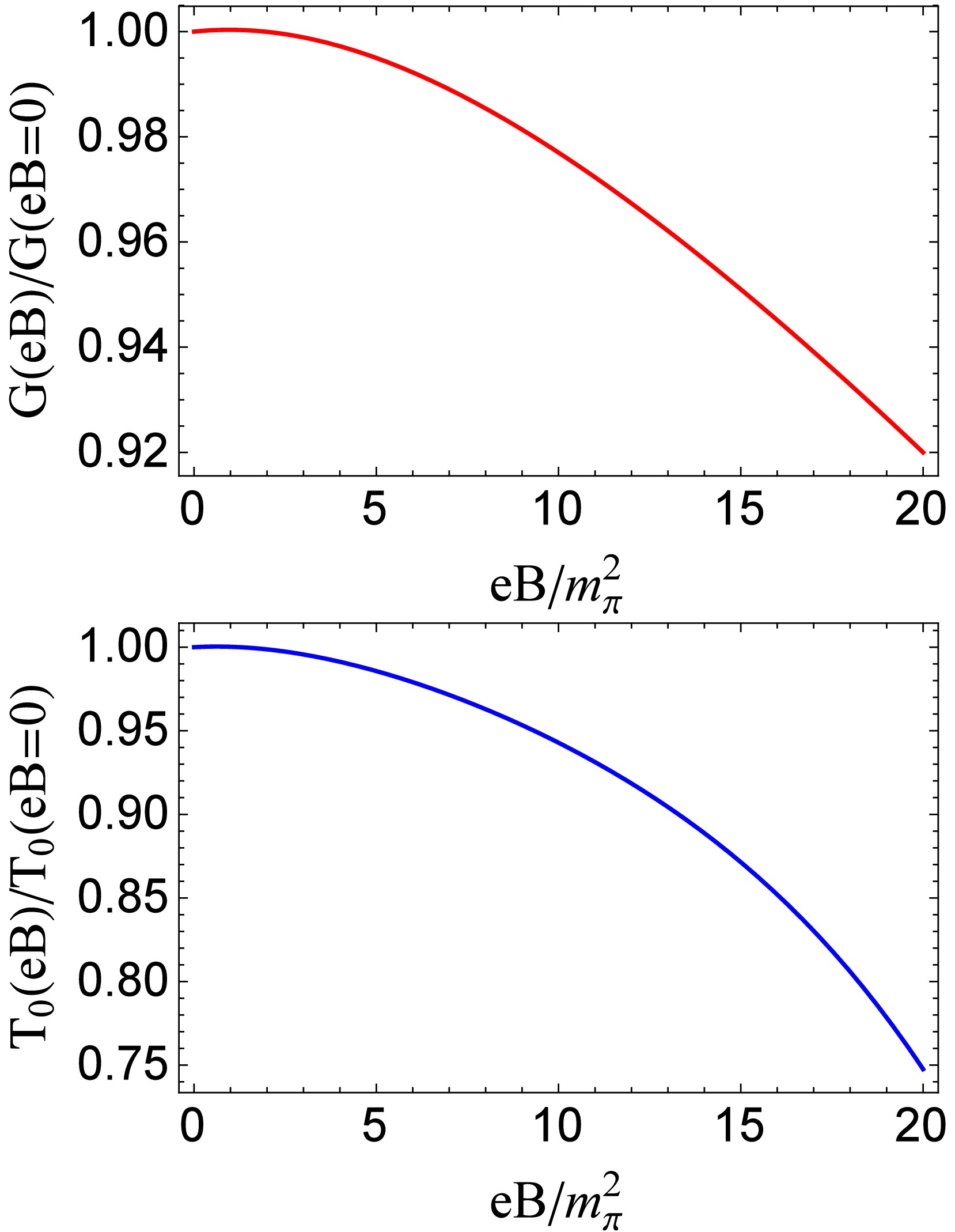

Figure 3.  (color online) Magnetic-field-dependent parameters $ G(eB) $ (upper panel) and $ T_0(eB) $ (lower panel) fitted from LQCD reported decreasing pseudocritical temperature of chiral restoration phase transition $ T_{pc}^c(eB)/T_{pc}^c(eB=0) $ [7].

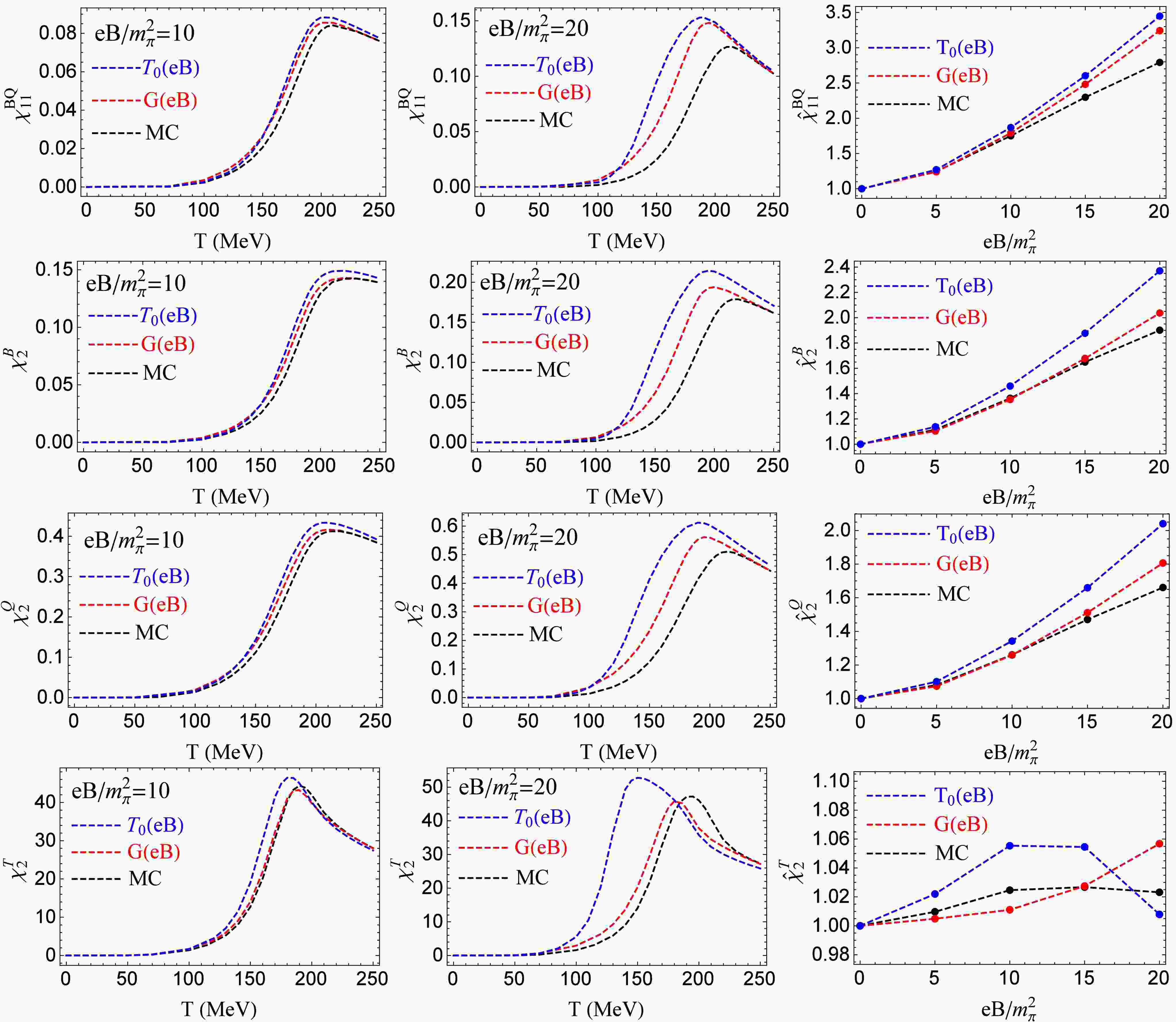
In the following calculations, we use the two schemes, $ G(eB) $ and $ T_0(eB) $, to consider the IMC effect, respectively, and compare the results with and without the IMC effect.

Figure 4 (first three rows) depicts the results of correlation $ \chi^{BQ}_{11} $ and quadratic fluctuations $ \chi^B_2,\ \chi^Q_2 $with the IMC effect (blue and red lines) and without the IMC effect (black line). Under fixed magnetic fields $ eB/m^2_\pi=10,\ 20 $, when considering the IMC effect with $ G(eB) $ and $ T_0(eB) $ schemes, $ \chi^{BQ}_{11},\ \chi^B_2 $, and $ \chi^Q_2 $ increase with temperature and have the peak around the pseudocritical temperatures of chiral restoration and deconfinement phase transitions, which are similar to the case without the IMC effect (left and middle panels). Additionally, the values of $ \chi^{BQ}_{11},\ \chi^B_2,\ \chi^Q_2 $with the IMC effect are larger than those without the IMC effect in the entire temperature region although the locations of their peaks are shifted to lower temperatures by the IMC effect. In the right panels, we plot scaled correlation ${\hat {\chi}}_{11}^{BQ}= \dfrac{\chi_{11}^{BQ}(eB,T_{pc}^c(eB))}{\chi_{11}^{BQ}(eB=0,T_{pc}^c(eB=0))}$ and scaled quadratic fluctuations $ {\hat {\chi}}_2^{B}=\dfrac{\chi_2^{B}(eB,T_{pc}^c(eB))}{\chi_2^{B}(eB=0,T_{pc}^c(eB=0))} $, $ {\hat {\chi}}_2^{Q}=\dfrac{\chi_2^{Q}(eB,T_{pc}^c(eB))}{\chi_2^{Q}(eB=0,T_{pc}^c(eB=0))} $ at the pseudocritical temperature of chiral restoration phase transition as functions of the magnetic field with the IMC effect (blue and red lines) and without the IMC effect (black line). With the IMC effect, $ {\hat {\chi}}^{BQ}_{11},\ {\hat {\chi}}^B_2 $, and $ {\hat {\chi}}^Q_2 $ increase faster. The results of $ {\hat {\chi}}^{BQ}_{11} $ and $ {\hat {\chi}}^B_2 $ have better quantitative consistency with the LQCD results [60], but the results of $ {\hat {\chi}}^Q_2 $ have larger deviations from the LQCD results [60]. Different methods to consider the IMC effect do not lead to qualitative differences in the results and only cause some quantitative changes.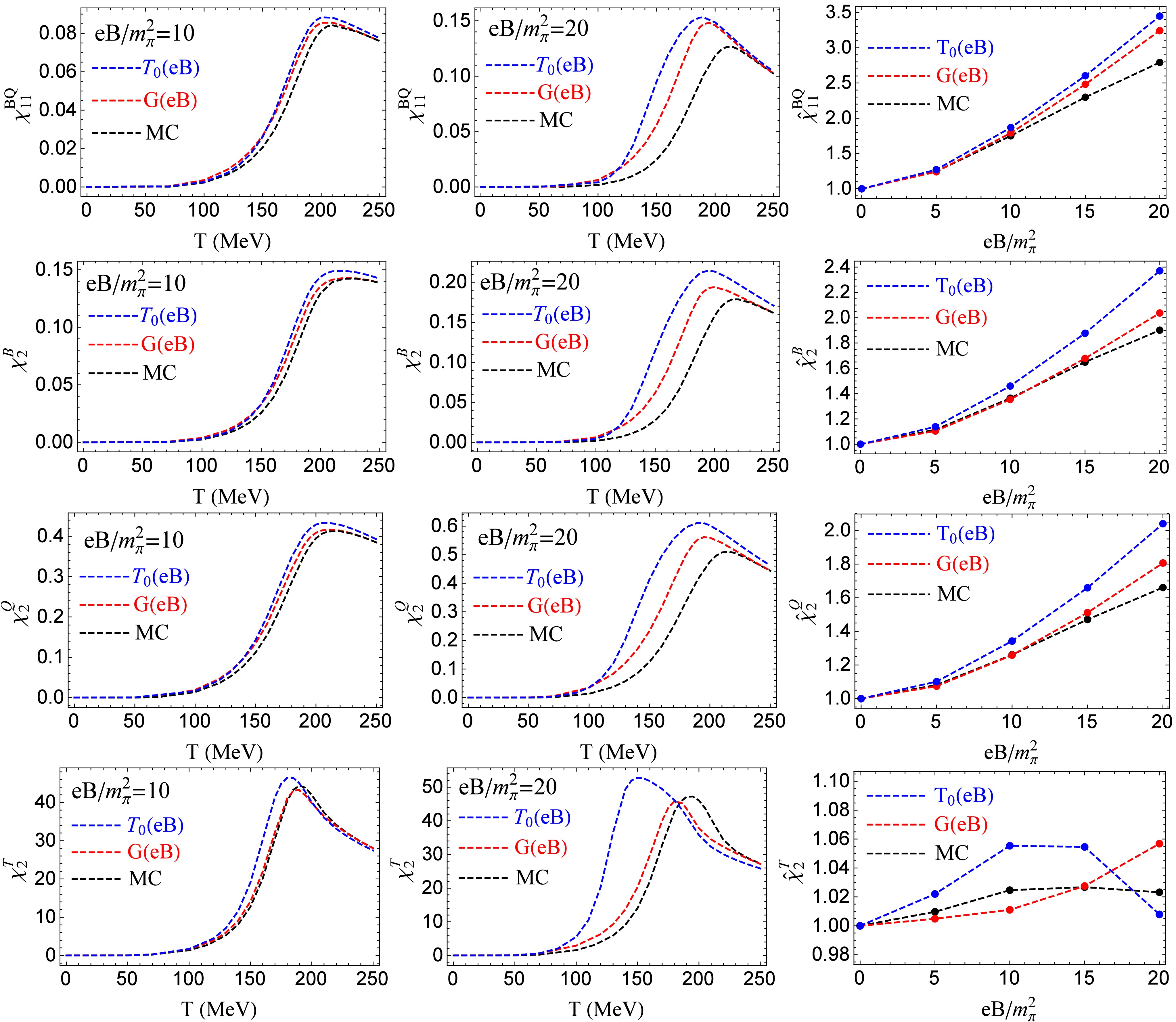

Figure 4.  (color online) (First row) Correlation $ \chi^{BQ}_{11} $ as a function of temperature under fixed magnetic field $ eB=10m^2_\pi $ (left panel) and $ eB=20m^2_\pi $ (middle panel), and scaled correlation $ {\hat{\chi}}^{BQ}_{11} $ (right panel) at $ T=T_{pc}^c $ as a function of the magnetic field. (Second row) Fluctuation $ \chi^{B}_{2} $ as a function of the temperature under fixed magnetic field $ eB=10m^2_\pi $ (left panel) and $ eB=20m^2_\pi $ (middle panel), and scaled fluctuation $ {\hat{\chi}}^{B}_{2} $ (right panel) at $ T=T_{pc}^c $ as a function of the magnetic field. (Third row) Fluctuation $ \chi^{Q}_{2} $ as a function of temperature under fixed magnetic field $ eB=10m^2_\pi $ (left panel) and $ eB=20m^2_\pi $ (middle panel), and scaled fluctuation $ {\hat{\chi}}^{Q}_{2} $ (right panel) at $ T=T_{pc}^c $ as a function of magnetic field. (Forth row) Fluctuation $ \chi^{T}_{2} $ as a function of temperature under fixed magnetic field $ eB=10m^2_\pi $ (left panel) and $ eB=20m^2_\pi $ (middle panel), and scaled fluctuation $ {\hat{\chi}}^{T}_{2} $ (right panel) at $ T=T_{pc}^c $ as a function of magnetic field. Here, the blue and red lines correspond to the case with the IMC effect using the $ T_0(eB) $ and $ G(eB) $ schemes, respectively, and the black lines correspond to the case without the IMC effect.

Figure 4 (bottom row) shows the results of fluctuation $ \chi^T_2 $ with the IMC effect (blue and red lines) and without the IMC effect (black line), where the left and middle panels plot $ \chi^T_2 $ under fixed magnetic fields $ eB/m^2_\pi=10,\ 20 $ as a function of temperature, and the right panel plots scaled fluctuation ${\hat {\chi}}^T_2= \dfrac{\chi^T_2(eB,T_{pc}^c(eB))}{\chi^T_2(eB=0,T_{pc}^c(eB=0))}$ at the pseudocritical temperature of chiral restoration phase transition as a function of magnetic field. Under fixed magnetic fields, the inclusion of the IMC effect shifts the location of the peak of $ \chi^T_2 $ to a lower temperature. However, the value of $ \chi^T_2 $ around the peak is enhanced (reduced) when we consider the IMC effect using the $ T_0(eB) $ ($ G(eB) $) method. Scaled fluctuation $ {\hat {\chi}}^T_2 $ increases slightly and then decreases as the external magnetic field increases without the IMC effect (black line). When considering the IMC effect using the $ G(eB) $ scheme, $ {\hat {\chi}}^T_2 $ monotonically increases with the magnetic field (red line), but with the $ T_0(eB) $ scheme, $ {\hat {\chi}}^T_2 $ is a nonmonotonic function of the magnetic field (blue line). The introduction of the IMC effect causes some qualitative changes in $ {\hat {\chi}}^T_2 $, which is different from the scenarios of $ {\hat {\chi}}^{BQ}_{11},\ {\hat {\chi}}^B_2 $, and $ {\hat {\chi}}^Q_2 $.

Before the end of this section, we make some comments. The LQCD calculation in Ref. [60] reports a constant pseudocritical temperature for chiral restoration phase transition under an external magnetic field $ (eB<10m^2_\pi) $. Such a result can be achieved by introducing magnetic-field-dependent parameter $ G(eB) $ or $ T_0(eB) $, which will be different from the results in Fig. 3. According to our numerical calculations, this only causes a minimal difference in scaled correlation $ {\hat \chi}^{BQ}_{11} $ and scaled fluctuations $ {\hat \chi}^B_2,\ {\hat \chi}^Q_2,\ {\hat \chi}^T_2 $ at the phase transition.

Correlation $ \chi^{BQ}_{11} $ and fluctuations $ \chi^B_2,\ \chi^Q_2,\ \chi^T_2 $ at finite temperature and magnetic field are investigated under a two-flavor PNJL model. The IMC effect is introduced into the PNJL model using two methods, the magnetic-field-dependent coupling between quarks $ G(eB) $ and magnetic-field-dependent interaction between quarks and Polyakov loop $ T_0(eB) $. We compare the results in cases with and without the IMC effect.

$ \chi^{BQ}_{11},\ \chi^B_2 $, and $ \chi^Q_2 $ exhibit similar properties at finite temperature and magnetic field. Under a vanishing magnetic field, correlation $ \chi^{BQ}_{11} $ and fluctuations $ \chi^B_2,\ \chi^Q_2 $ increase with temperature, and under a nonvanishing magnetic field, they exhibit a peak around the pseudocritical temperatures of chiral restoration and deconfinement phase transitions. These properties are consistent with LQCD results. To demonstrate $ \chi^{BQ}_{11},\ \chi^B_2 $, and $ \chi^Q_2 $ along the phase transition line under the external magnetic field, we calculate scaled correlation $ {\hat \chi}^{BQ}_{11} $ and scaled fluctuations $ {\hat \chi}^B_2,\ {\hat \chi}^Q_2 $ at $ T_{pc}^c $ of chiral restoration phase transition and they increase with the magnetic field. The results of $ {\hat \chi}^{BQ}_{11} $ and $ {\hat \chi}^B_2 $ are qualitatively consistent with LQCD results, but $ {\hat \chi}^Q_2 $ deviates from the LQCD results. The inclusion of the IMC effect in the PNJL model does not lead to qualitative difference in the results and only causes some quantitative modifications.

Fluctuation $ \chi^T_2 $ exhibits different properties from $ \chi^{BQ}_{11},\ \chi^B_2 $, and $ \chi^Q_2 $. Under vanishing and nonvanishing magnetic fields, fluctuation $ \chi^T_2 $ exhibits a peak around the pseudocritical temperatures of chiral restoration and deconfinement phase transitions, which is not altered qualitatively by the IMC effect. However, scaled fluctuation $ {\hat \chi}^T_2 $ at $ T=T_{pc}^c $ is modified by the IMC effect. Without the IMC effect, $ {\hat \chi}^T_2 $ increases slightly and then decreases slightly with the magnetic field. Considering the IMC effect using $ G(eB) $, $ {\hat \chi}^T_2 $ monotonically increases with the magnetic field, and using $ T_0(eB) $, it is a nonmonotonic function of the magnetic field.

As we know, parameter $ T_0=270 $ MeV in the Polyakov potential is the critical temperature of deconfinement phase transition in the pure gauge model [62]. The inclusion of dynamical quarks leads to a decrease in $ T_0 $ [68, 69]. In the two-flavor case, $ T_0=210 $ MeV is widely used. Note that different choices of parameter $ T_0 $ will change the pseudocritical temperatures of chiral restoration and deconfinement phase transitions, but as we have checked, it scarcely influences the results of the scaled correlations and fluctuations at the phase transition.

Readers may wonder why we calculate correlation $ \chi^{BQ}_{11} $ and fluctuations $ \chi^{B,Q,T}_2 $ in a two-flavor PNJL model, which lacks the component of strangeness. In the temperature region of interest here ($ 100 \leq T \leq 250 $ MeV), the strange quark is much heavier than up and down quarks [84, 85], and its contribution to the thermodynamical potential and $ \chi^{BQ}_{11},\ \chi^{B,Q,T}_2 $ can be neglected when compared with the up and down quarks. Therefore, the two-flavor PNJL model describes the thermodynamics of chiral restoration and deconfinement phase transitions well, and it is reliable for making a comparison between our results $ (\chi^{BQ}_{11},\ \chi^{B,Q,T}_2 ) $ and three-flavor LQCD results. Note that when investigating the correlation and fluctuations related with the strangeness number, we have to apply the three-flavor PNJL model, which is under progress and will be reported in the near future.

In our current work, we separately introduce the $ G(eB) $ and $ T_0(eB) $ schemes to consider the IMC effect, which plays a similar role for correlation $ \chi^{BQ}_{11} $ and fluctuations $ \chi^B_2,\ \chi^Q_2 $ at finite temperature and magnetic field but leads to different results for $ \chi^T_2 $. Considering both $ G(eB) $ and $ T_0(eB) $ simultaneously is an interesting endeavor, which is under progress and will be reported in the near future. Additionally, the market has other factors that can cause the IMC effect. The impact of the IMC effect on the correlation and fluctuations requires further investigation.