Exploring chiral rotation in A ≈ 60 nuclei: Role of residual interactions

Nuclear chirality is an exotic phenomenon of spontaneous symmetry breaking, which exists in rapidly rotating nuclei with a triaxial shape and high-j valence particle(s) and hole(s) [1]. In the intrinsic frame of such a system, the angular momenta of valence particle(s) and valence hole(s) are aligned along the short and long axis, respectively, and the angular momentum of the core is aligned with the intermediate axis, which can have the largest moment of inertia to maintain the energy of the system lowest. This topology forms left- and right-handed systems (transformed into each other by the chiral operator $ \chi=\mathscr{T} \mathscr{R}(\pi) $) and results in the spontaneous chiral symmetry breaking in the intrinsic frame. In the laboratory frame, the broken chiral symmetry would be restored and give rise to pairs of $ \Delta I = 1 $ rotational bands called chiral doublet bands, with the same parity and near-degeneracy in energy due to the effect of quantum tunneling. Since the chirality in nuclei was predicted by Frauendorf and Meng in 1997, chiral doublet bands have attracted a lot of attention regarding both theoretical and experimental aspects.

Theoretically, various approaches have been applied to describe chiral doublet bands. For example, the particle rotor model (PRM) [1−16] and its approximation solution based on time-dependent variation principle [17−19], the titled axis cranking (TAC) approach [20−24], the interacting boson-fermion-fermion model (IBFFM) [25−27], the TAC plus random phase approximation (RPA) [28, 29], the TAC plus collective Hamiltonian method [30−32], the angular momentum projection (AMP) method [33−38], as well as the time dependent covariant density functional theory [39, 40]. Among them, PRM describes a system in the laboratory reference frame and provides a good quantum number for total angular momentum. The energy splitting (band splitting) and quantum tunneling between the doublet bands (the tunneling between different quantum states) can be explained successfully.

Experimentally, more than $ 60 $ chiral doublet bands have been observed in many nuclei in a few mass regions of the nuclear chart. For more details, see reviews [41−56] and references therein. It can be found that all of the observations of chiral doublet bands concentrate on the $ A \geqslant 80 $ mass regions, so finding candidate chiral doublet bands in lighter mass regions is naturally an exciting and challenging task.

So far, the possibility of chiral doublet bands of the $ \rm Co $ isopotes [57] and $ \rm ^{60}Ni $ [12] in the $ A\approx 60 $ mass region has been investigated using the covariant density functional theory (CDFT) and PRM, respectively. The high-j particle-hole configuration $ \pi f_{7/2}^{-1} \otimes \nu \left[g_{9/2}^{1}(fp)^{n}\right] $ is suitable to establish chiral doublet bands and the basic microscopic inputs for PRM have been obtained from the CDFT calculations in Ref. [57].

To further explore the evidence of the existence of chiral doublet bands in the $ A\approx 60 $ mass region, the configuration $ \pi f_{7/2}^{-1} \otimes \nu g_{9/2}^{1} $ will be systematically studied by a quantal triaxial PRM with one-particle-one-hole coupled to a triaxial core in this work. Here, the $ (fp) $ shell is neglected due to its low contribution to the angular momentum of valence nucleons. In addition, the residual proton-neutron interaction will be also taken into account in PRM and applied to chiral doublet bands. This interaction is generally thought of as the residual force (between valence nucleons) not accounted for by the mean field in which nucleons move and has some effects on the energy staggering in the bands [58]. The effect of such interaction on nuclear chirality is rarely investigated.

The paper is organized as follows. The PRM model with the residual interaction is introduced in Sec. II. The numerical details are presented in Sec. III. The obtained energy spectra, electromagnetic transition probabilities $ B(M1) $ and $ B(E2) $, the energy splitting $ \Delta E $, the energy staggering $ S(I) $, analysis of angular momentum geometry based on the probability of the total angular momentum along the principal axes (K distribution) and the orientation with respective to the intrinsic frame $ \mathscr{P}(\theta,\varphi) $ are presented and discussed in detail in Sec. IV. Finally, a summary is given in Sec. V.

As a quantum model consisting of the collective rotation and the intrinsic single-particle motions, the particle rotor model (PRM) [59, 60] has been extensively used in the investigation of nuclear chirality. In Refs. [1−4, 61], the PRM has been applied to discuss the structure of doublet bands with a one-particle-one-hole configuration. With the inclusion of the residual interaction between the valence proton and neutron, the Hamiltonian of PRM can be written as

Here, $ \hat{H}_{\text{coll}} $ represents Hamiltonian of the collective rotor

where the indices $ k=1,2,3 $ refer to the three principle axes of the body-fixed frame, $ \hat{R}_{k} $, $ \hat{I}_{k} $, and $ \hat{J}_{k} $ respectively denote the angular momentum operators for the core, the total nucleus, and the valence nucleons. The moments of inertia for irrotational flow are adopted, i.e., $ \mathscr{J}_{k}=\mathscr{J} \sin ^{2}(\gamma-2 \pi k / 3) $, where $ \mathscr{J} $ depends on the mass parameter A and the quadrupole deformation β [62]. In this work, $ \mathscr{J} $ is used as an input parameter in the program.

The $ \hat{H}_{\text{intr}} $ describes the intrinsic Hamiltonian of a single valence nucleon in a high-j shell,

where the plus sign refers to a particle and the minus to a hole. The angle γ is the triaxial deformation parameter and the coupling parameter C is

proportional to the quadrupole deformation β [63].

The general form of the residual proton-neutron interaction is [64]

where each line respectively represents the central, tensor, and spin-orbit forces. The radial dependence $ V(r) $ takes the Gaussian form

due to the short-range nuclear force. In the case of zero-range force and the Gaussian radial shape, $ V_{p n} $ can be simplified in the following form [65]

The strength parameters $ u_0 $ and $ u_1 $ are used as input parameters in this work.

To discuss the nuclear phenomena using the PRM, the total wave function of the PRM Hamiltonian is usually expanded into a strong coupling basis, which considers the strong interaction between the intrinsic motion of valence nucleons and the collective motion of the nucleus. So the total wave function can be written as [12]

with

where $ |I M K\rangle $ are the Wigner D-functions $ \sqrt{\dfrac{2I+1}{8\pi^2}}D^{I}_{MK} $ which describes the rotational motion of the nucleus by quantum numbers I, M, K, and $ |\phi\rangle $ is an intrinsic wave function that describes the motion of valence nucleons, and the coefficients $ C_{K \phi} $ are the amplitudes of the basis states. The I is the total angular momentum quantum number of the nucleus and the projections of the total angular momentum vector I on the z axis in the laboratory frame and the z axis (3-axis) in the body-fixed frame are respectively denoted by M and K.

The reduced transition probabilities $ B(M1) $ and $ B(E2) $, as fingerprints of nuclear chirality, can be calculated from the total wave function of PRM [4].

The probability distribution for the projection K of total angular momentum vector I on the three principle axes (K-plot) is [5, 12]

The profile for the orientation of the angular momentum in the intrinsic reference frame (azimuthal plot) can also be calculated from the total wave function [12, 32, 34, 66],

with the expectation value $ M=I $ in the intrinsic frame.

As mentioned in the Introduction part Sec. I, the one-particle-one-hole configuration $ \pi f_{7/2}^{-1} \otimes \nu g_{9/2}^{1} $ is adopted in the PRM calculations. In Ref. [57], the configuration $ \pi f_{7/2}^{-1} \otimes \nu g_{9/2}^{1} $ favorable for nuclear chirality appears at quadrupole deformation parameter $ \beta \approx 0.25 $. According to the results for $ ^{60}\rm{Ni} $ presented in Refs. [12, 67, 68], the range of the moment of inertia $ \mathscr{J} $ can be estimated using the relationship between energy and moment of inertia given by the formula $ E_I=I(I+1)\hbar^2/2\mathscr{J} $. The estimated range for $ \mathscr{J} $ is from $ 5 $ to $ 13\; \hbar^2/ \rm MeV $. Additionally, the energy difference $ \Delta E $ is not sensitive to β and $ \mathscr{J} $ according to PRM calculations. Therefore, β is initially set to 0.25 and $ \mathscr{J} $ to the approximate middle value $ 10\hbar^2/ \rm MeV $. The triaxial deformation parameter γ is then varied to identify its optimal value to ultimately derive the optimal set of input parameter values about γ, β, and $ \mathscr{J} $. In the calculation of the electromagnetic transitions, the empirical intrinsic quadrupole moment $ Q_{0}=(3/\sqrt{5\pi}) R_{0}^{2}Z\beta $ is set at 1.28 eb. The gyromagnetic ratios for rotor $ g_{R}=Z/A=0.48 $, $ g_{p}=1+(g_s-1)/ (2l+1)= 1.336 $, and $ g_{n}=g_s/(2l+1)=-0.255 $ (where $ g_s $ is $ 0.6g_s^{\text{free}} $ [60]) have been adopted following the $ A\approx 60 $ mass region.

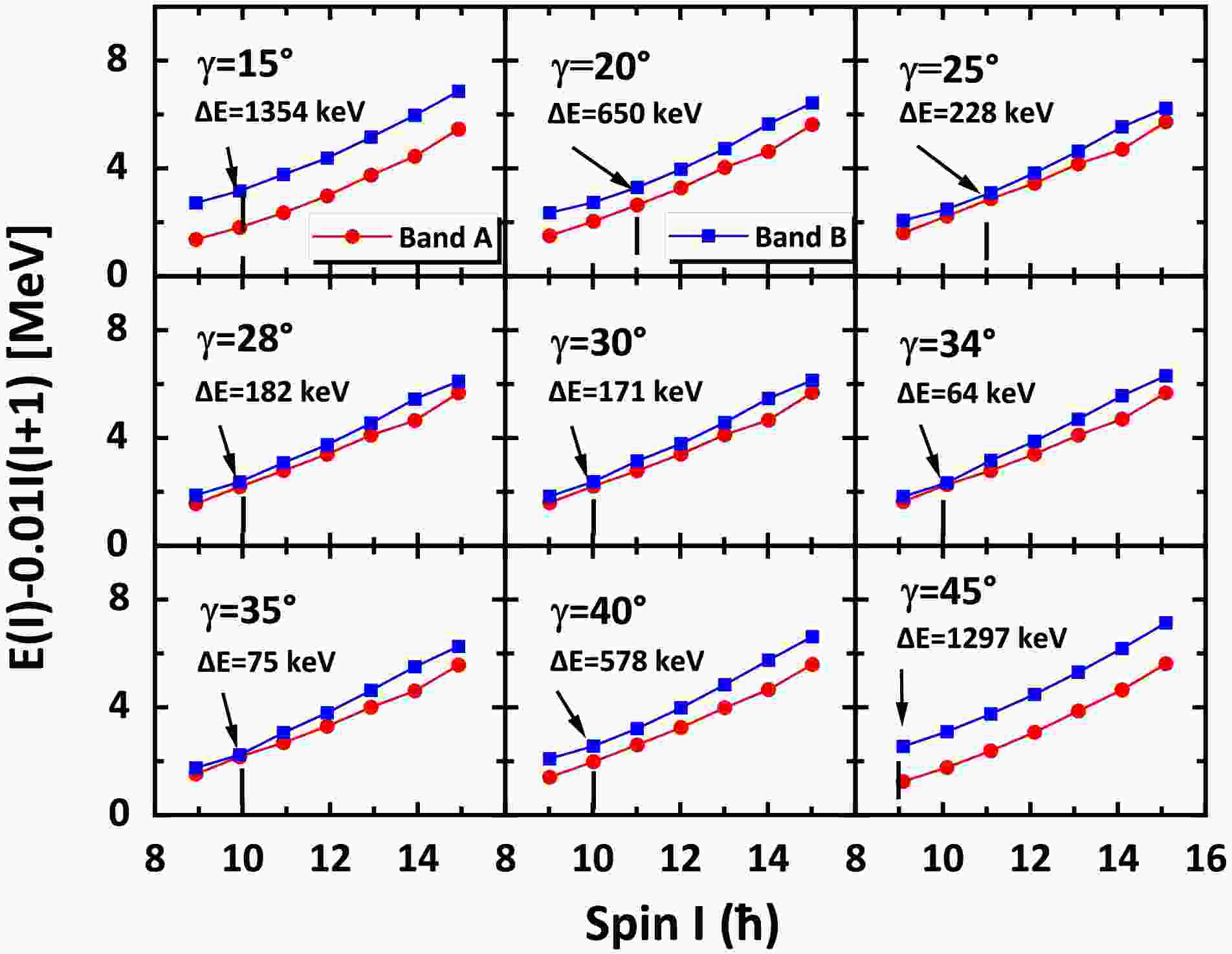
The energy spectra of the two lowest bands A and B are respectively presented as red and blue lines in Fig. 1, calculated by PRM when the triaxial deformation parameter γ varies from 15° to 45°. For the appearance of the chiral doublet bands with the smallest difference in energy, it is known that the best condition is the maximum triaxiality $ \gamma=30^{\circ} $ when the configuration is symmetrical [2]. But in Fig. 1, the best condition deviates the maximum triaxiality to $ \gamma \sim 34^{\circ} $ due to the asymmetrical configuration $ \pi f_{7/2}^{-1} \otimes \nu g_{9/2}^{1} $. For $ \gamma=30^{\circ} $, the energy of bands A and B similarly increase from $ I=9 $ to $ 15\hbar $, and the energy difference between the two bands A and B shows a trend that decreases firstly from $ I=9 $ to $ 10\hbar $ and then increases up to $ I=15\hbar $. The minimum energy splitting $ \Delta E $ is small ($ 171\; \rm keV $) but not the smallest. When γ increases from 15° to 45°, $ \Delta E $ decreases firstly and then increases, which reaches the smallest value ($ 64\; \mathrm{keV} $) for $ \gamma=34^{\circ} $ concerning the best degeneracy. The energy of bands A and B are nearly identical at $ I=9 $ and $ 10\hbar $, corresponding to the ideal chirality. As γ deviates further from 34°, the difference between the doublet bands in energy becomes more pronounced, which means the degeneracy is gradually removed. Hence, the best possible triaxial deformation condition is $ \gamma=34^{\circ} $ in this research about the chiral doublets.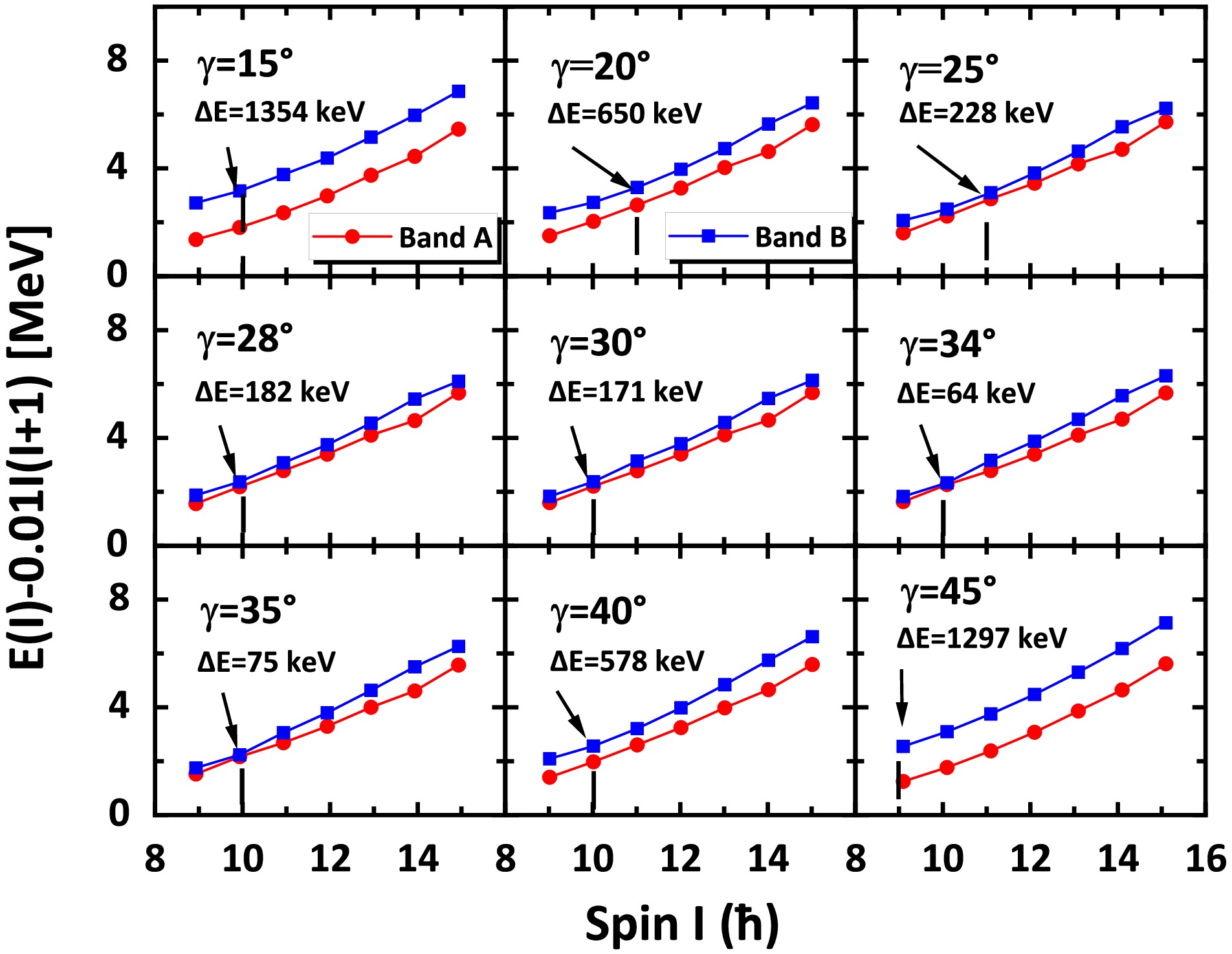

Figure 1.  (color online) The energy spectra of the yrast (labeled as band A) and yrare (labeled as band B) bands calculated by PRM at different γ deformations for the $ \pi f_{7/2}^{-1} \otimes \nu g_{9/2}^{1} $ configuration. A rigid rotor reference has been subtracted from the energies. The minimum energy splitting is marked as $ \Delta E $ in each panel.

The calculated intraband reduced magnetic dipole transition probabilities $ B(M1) $ of the two bands A and B with different triaxiality parameters γ are shown in Fig. 2. The central panel of Fig. 2 shows the calculated $ B(M1) $ of doublet bands with $ \gamma=30^{\circ} $. For $ I \leqslant 11\hbar $, the intraband $ B(M1) $ decreases gradually with spin. For $ I > 11\hbar $, a strong odd-even staggering of $ B(M1) $ can be seen clearly with the intraband $ B(M1) $ transitions enhanced from spin odd to even and forbidden from spin even to odd, implying the static chirality [69]. The staggering for band B is slightly weaker than that for band A with a similar tendency. The $ B(M1) $ staggering coincides with the odd-even staggering of intraband $ B(M1)/B(E2) $ ratios for the ideal chiral doublets [70]. However, as γ deviates from the best triaxial deformation 30°, shown in other panels of Fig. 2, the pronounced $ B(M1) $ staggering at $ \gamma=30^{\circ} $ becomes weaker and weaker and moves to the high spin region gradually. At $ \gamma=15^{\circ} $ and 45°, the $ B(M1) $ staggering completely disappears in band B and only a very weak staggering still exists in band A from $ I=13 $ to $ 16\hbar $. This suggests the $ B(M1) $ staggering will gradually disappear for $ I > 11\hbar $ when γ deviates from 30°, indicating a transition from static chirality to chiral vibration [69]. Thus γ taken as 34° near 30° is reasonable.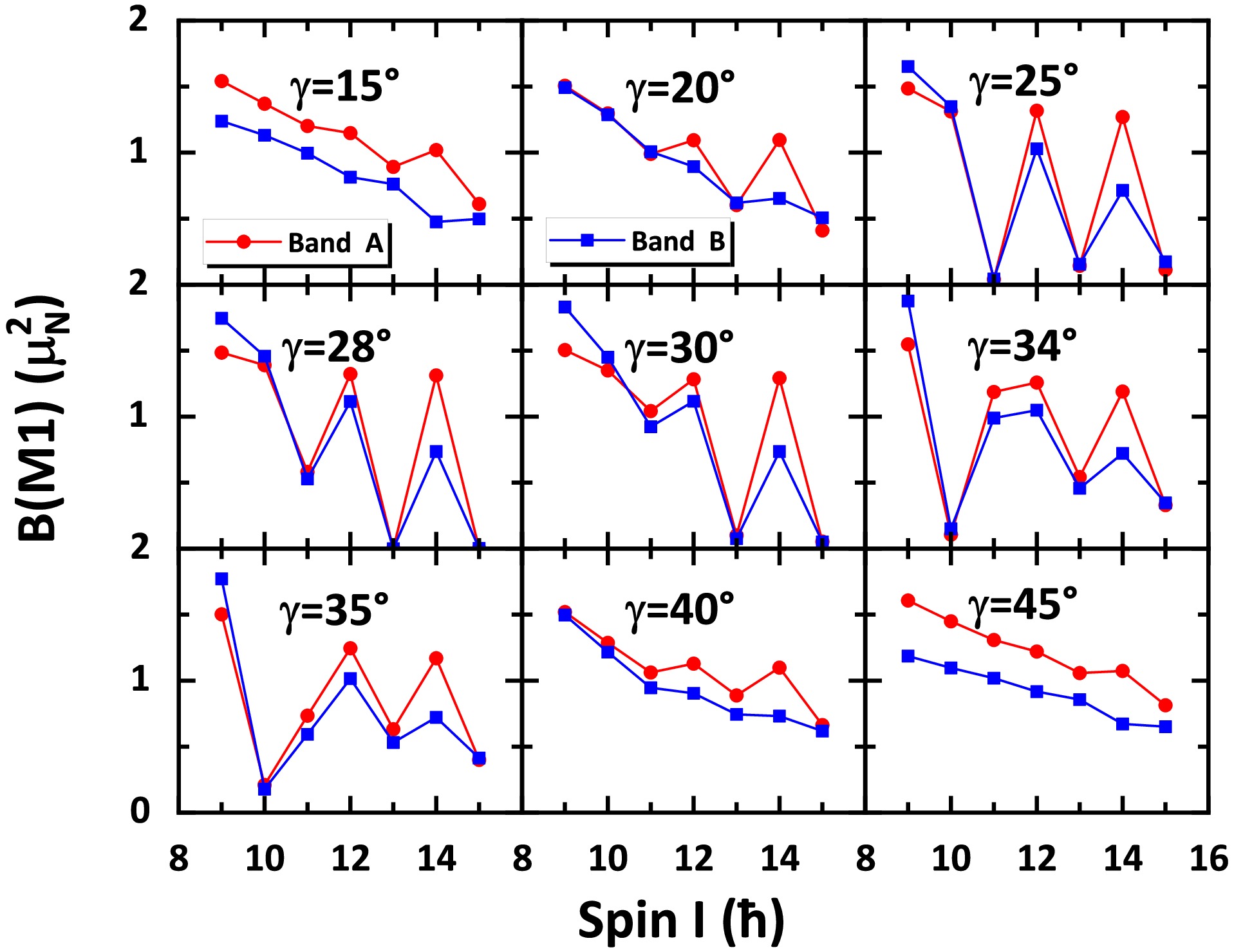

Figure 2.  (color online) Same as Fig. 1, but for the intraband $ B(M1) $ values.

The calculated intraband reduced electric quadrupole transition probabilities $ B(E2) $ as functions of spin of the two bands A and B with different triaxiality parameters γ are plotted in Fig. 3. The central panel of Fig. 3 shows the calculated $ B(E2) $ of doublet bands with $ \gamma=30^{\circ} $. For $ I \leqslant 11\hbar $, the intraband E2 transitions are forbidden. For $ I > 11\hbar $, the intraband $ B(E2) $ increases with spin. It can be found that the intraband $ B(E2) $ of the two bands are nearly identical, as excepted in ideal chiral doublet bands [71]. The other panels of Fig. 3 show the calculated $ B(E2) $ of the two bands with γ deviating 30°. The forbidden E2 transitions with $ I \leqslant 11\hbar $ are allowed gradually. For $ I > 11\hbar $, the intraband $ B(E2) $ values are not sensitive to the triaxiality parameter γ. Besides, $ B(E2) $ between the partner bands are very similar with γ changing from 15° to 45°.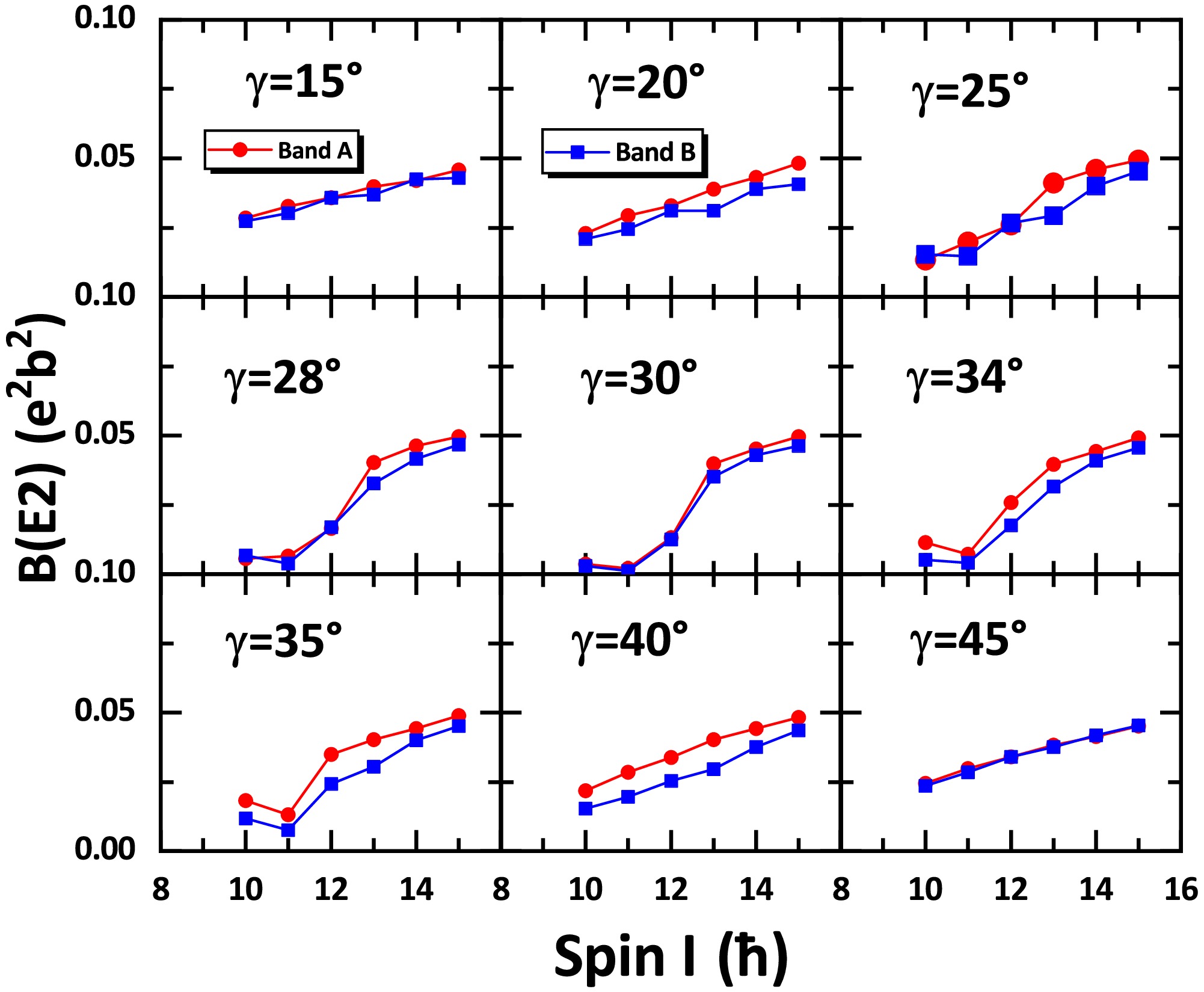

Figure 3.  (color online) Same as Fig. 1, but for the intraband $ B(E2) $ values.

Summarizing the above discussions, the parameters for the ideal chirality with the configuration $ \pi f_{7/2}^{-1} \otimes \nu g_{9/2}^{1} $ in the $ A\approx 60 $ mass region are $ \beta=0.25 $, $ \gamma=34^{\circ} $, and $ \mathscr{J}=10\; \hbar^2/\rm MeV $.

In the following, the focus is placed on investigating the effects on the chiral doublet bands caused by the residual proton-neutron interaction ($ V_{p n} $). The strength parameters $ u_0 $ and $ u_1 $ in the residual interaction, which has a standard delta function form (7), are introduced and the above ideal parameters are adopted. The other parameters remain unchanged.

The energy splitting $ \Delta E(I) $ from PRM calculations with and without $ V_{pn} $ and for different values of spin-spin strength parameter $ u_1 $ and relative strength ratio $ u_0:u_1 $ are shown in Fig. 4. For $ u_1=-0.2\rm MeV $ and $ u_0:u_1=3:1 $, the splitting $ \Delta E $ is nearly identical to the result without $ V_{p n} $. When $ u_1 $ remains constant, $ \Delta E $ with $ V_{p n} $ tends to increase in the high spin region as the ratio $ u_0:u_1 $ increases. Moreover, when the absolute value of $ u_1 $ increases, the growth trend of $ \Delta E $ becomes pronounced. The two $ \Delta E $ with and without $ V_{p n} $ are more different, especially in the high spin region. It indicates that the energy splitting between the doublet bands is significantly influenced by the presence of $ V_{p n} $, which is not conducive to the appearance of chirality. Therefore, the $ V_{p n} $ has a negative impact on the nuclear chirality.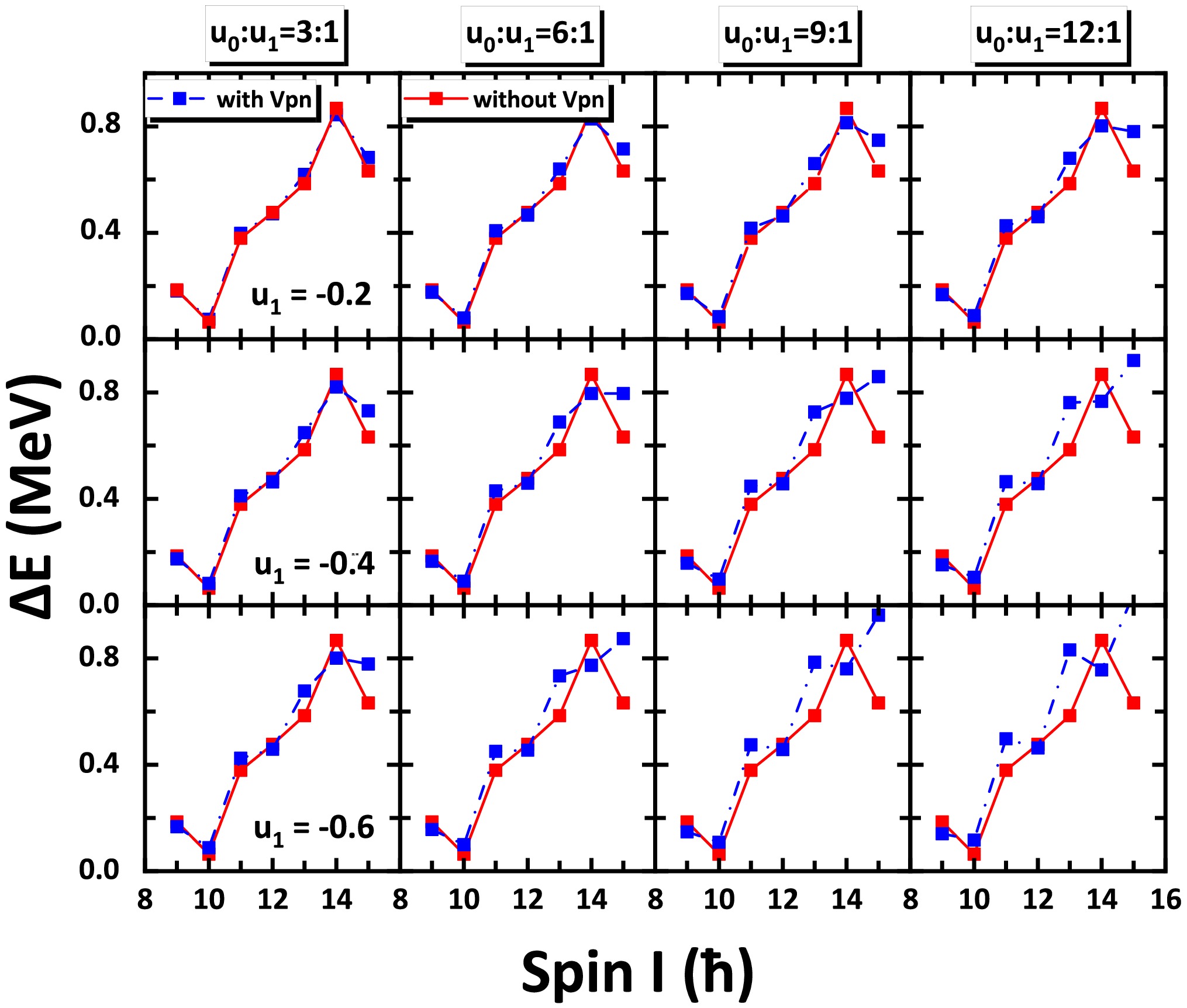

Figure 4.  (color online) The energy difference $ \Delta E (I) $ between the doublet bands calculated by PRM without and with $ V_{p n} $ at different strength parameters $ u_1= -0.2 $, $ -0.4 $, $ -0.6\; \rm MeV $ and $ u_0 : u_1= 3:1 $, $ 6:1 $, $ 9:1 $, $ 12:1 $.

As a fingerprint of nuclear chirality, the energy staggering parameter $ S(I)=\left[E(I)-E(I-1)\right]/2I $ should possess a smooth dependence with spin I in the chiral region since the particle and hole orbital angular momenta are both approximately perpendicular to the core rotation [70]. In Fig. 5 the results of quantity $ S(I) $ are illustrated as functions of spin. In the absence of $ V_{pn} $, the $ S(I) $ of doublet bands have small odd-even staggering amplitudes corresponding to the above property smoothly dependent with spin. Additionally, both bands have the same phase, with band A in the $ 11 $ to $ 13\hbar $ spin region and band B in the $ 12 $ to $ 14\hbar $ spin region. In contrast, $ S(I) $ of doublet bands have strong odd-even staggering and opposite phases to each other in the other spin region. Attention is then transferred to the results including the residual interaction. When the ratio $ u_0:u_1=3:1 $ and $ u_1=-0.2\; \rm MeV $, the $ S(I) $ results are nearly identical to those without $ V_{pn} $. But the $ S(I) $ in bands A and B have two apparent changes when the absolute value of $ u_1 $ and the ratio $ u_0 : u_1 $ are enhanced. The first one is that the $ S(I) $ of the two bands have opposite phases to each other in the whole spin region. The other one is that the odd-even staggering becomes large and changes phases as spin increases compared to those results without $ V_{p n} $. The inverted phase observed at high spins, along with the opposing phases of the double bands, arises from the signature inversion induced by the introduction of $ V_{pn} $ under the condition of triaxiality [58]. Therefore, considering the $ V_{pn} $, it is reasonable for nuclear chirality to take small values for the $ |u_1| $ and the ratio $ u_0 : u_1 $, which corresponds to the spin smooth dependence of $ S(I) $.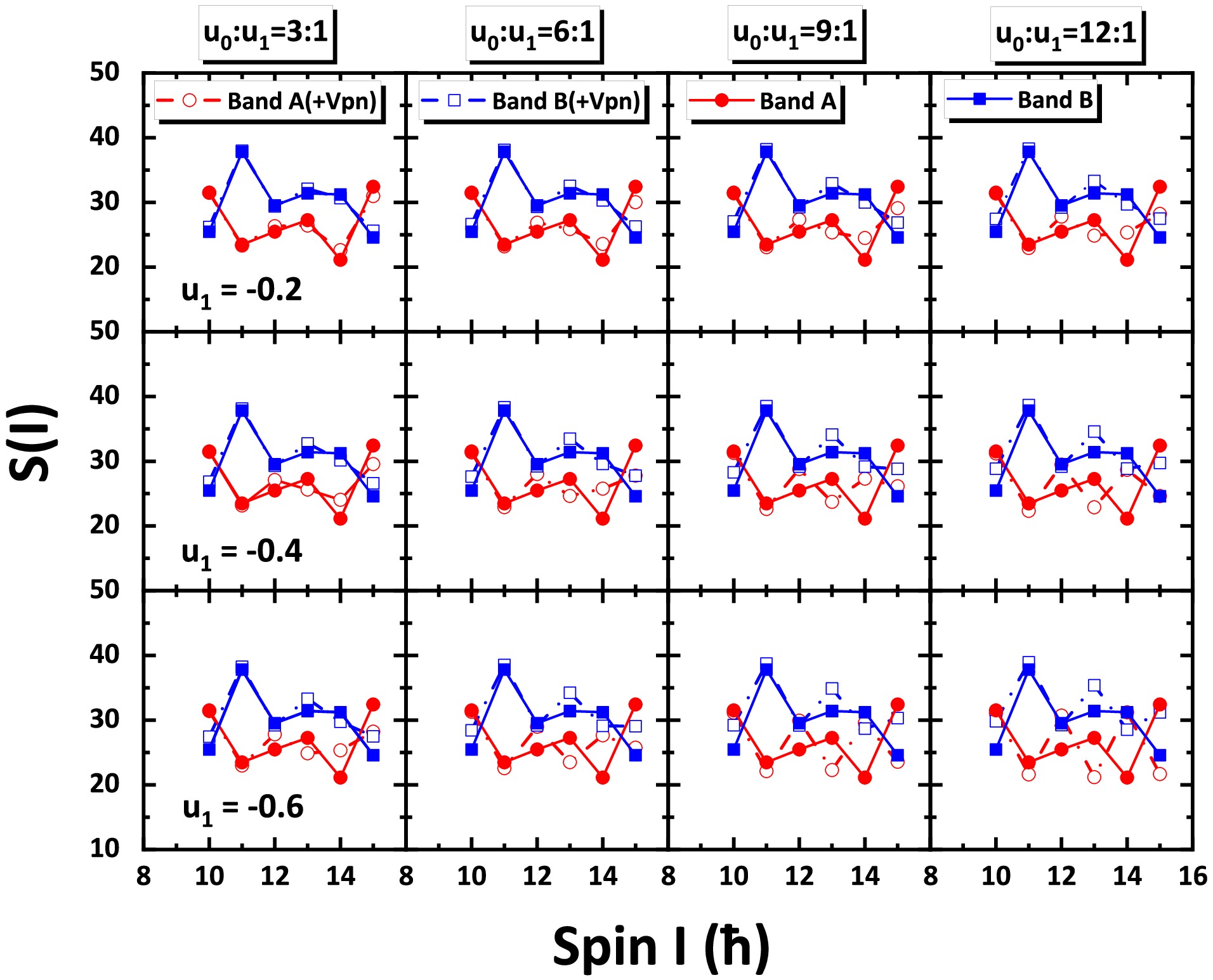

Figure 5.  (color online) Same as Fig. 4, but for the staggering parameter $ S(I)=[E(I)-E(I-1)]/2I $.

The calculated values of $ B(E2) $ and $ B(M1) $ in the doublet bands with and without $ V_{pn} $ are presented in Figs. 6 and 7, respectively. In Fig. 6, it can be shown that $ V_{pn} $ does not apparently influence the $ B(E2) $ values of bands A and B, indicating a negligible effect of $ V_{p n} $ on the collective rotation. As shown in Fig. 7, when $ u_1 $ is $ -0.2\; \rm MeV $ and $ u_0 : u_1 $ is $ 3:1 $, the $ B(M1) $ of the two bands are nearly identical to the middle-right panel of Fig. 2, whether $ V_{p n} $ is considered or not. When the absolute value of $ u_1 $ and the ratio $ u_0 : u_1 $ increase, the $ B(M1) $ odd-even staggering amplitudes are only slightly enhanced at high spins, which suggests the weak effect of $ V_{p n} $ on $ B(M1) $. In general, the $ V_{pn} $ exhibits no discernible impact on the electromagnetic transition probabilities used as fingerprints for the chiral doublet bands in this work.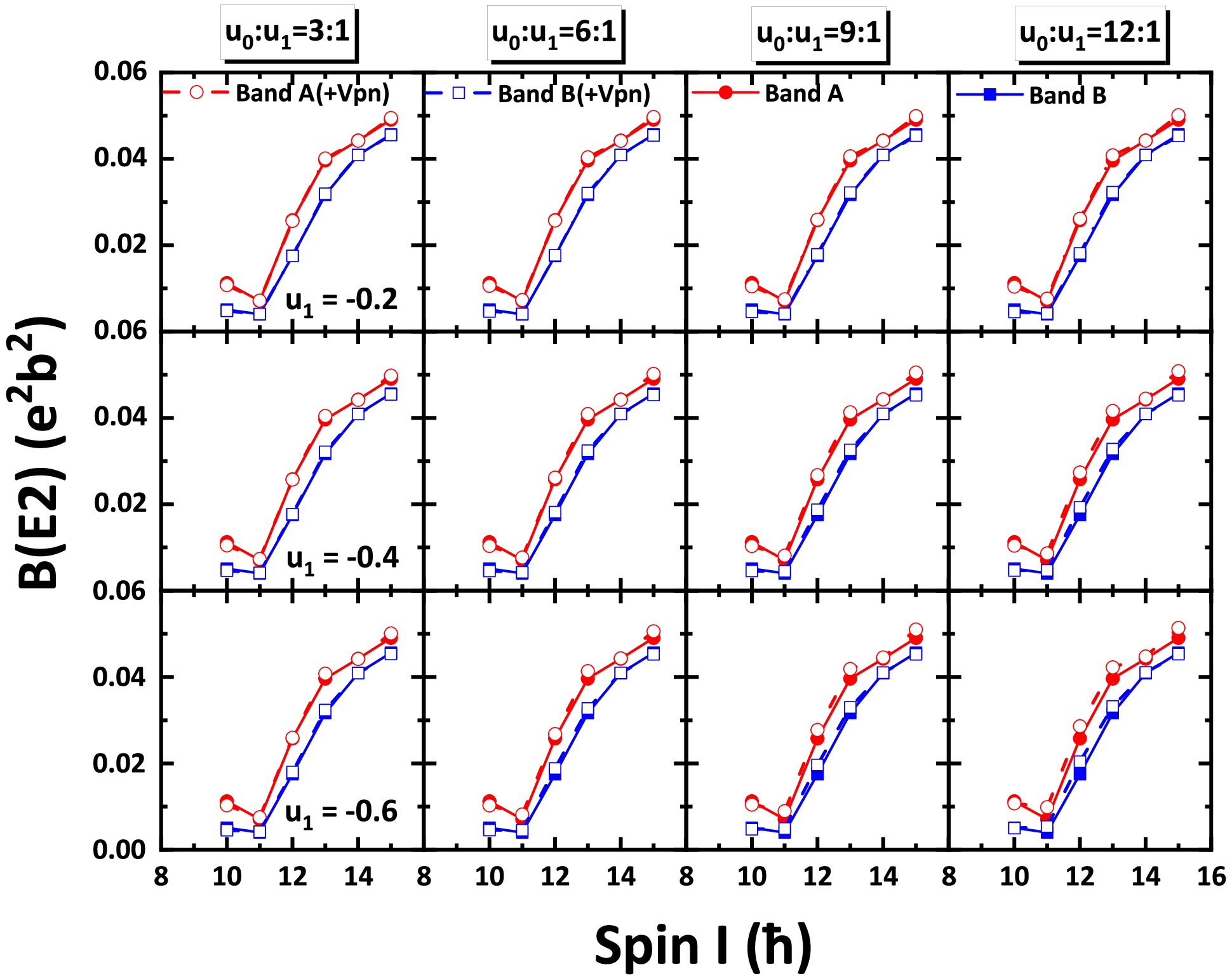

Figure 6.  (color online) Same as Fig. 4, but for the intraband $ B(E2) $ values.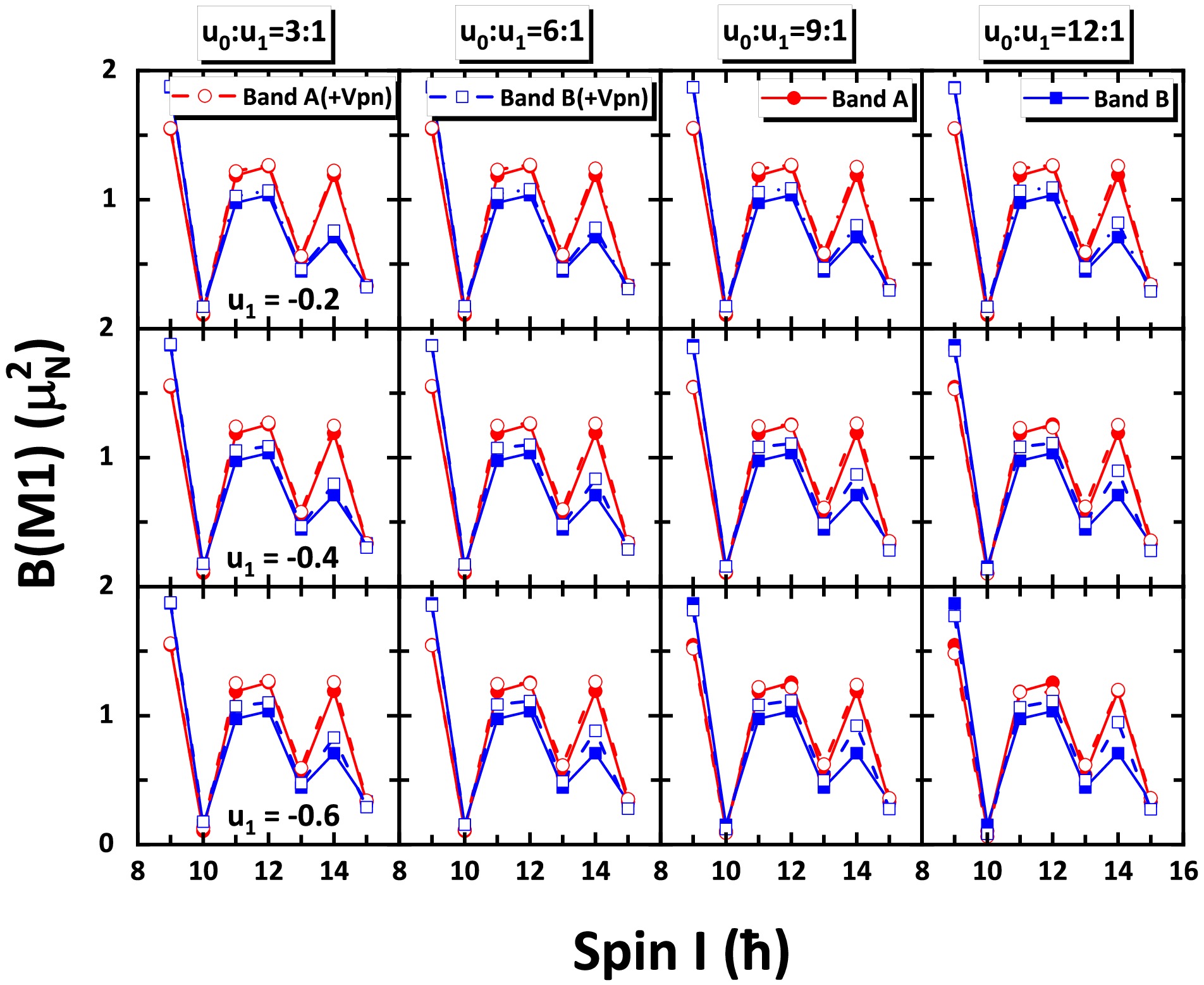

Figure 7.  (color online) Same as Fig. 4, but for the intraband $ B(M1) $ values.

Further understand the evolution of the chirality with spin I, the K distribution of total angular momentum $ K_l $, $ K_i $, and $ K_s $ on the three principle axes for bands A and B in PRM with and without $ V_{pn} $ are displayed in Fig. 8 for $ I=9 $, 10, $ 11\hbar $, corresponding to the spin region for the good energy degeneracy in Fig. 4. As seen the results without $ V_{pn} $, for $ I=9\hbar $, the K distributions for bands A and B are somewhat different. The peaks of $ K_i $ distributions locate at $ K_i=1\hbar $ for band A (symmetric zero-phonon state), while at $ K_i=6\hbar $ for band B (antisymmetric one-phonon state) [5, 69]. The peaks of $ K_l $ and $ K_s $ distributions both locate at $ 6\hbar $ for band A, while at $ 4\hbar $ and $ 8\hbar $ respectively for band B. The K distributions suggest typically a chiral vibration with an oscillation of the collective core angular momentum $ \mathit{\boldsymbol{R}} $ through the sl-plane. For $ I=10 $ and $ 11\hbar $, the $ K_i $ distributions between bands A and B are similar. The $ K_l $ distribution of band A has a bump at lower $ K_l $, while it has a similar bump at higher $ K_l $ for band B. These indicate that bands A and B have the characteristics of static chirality.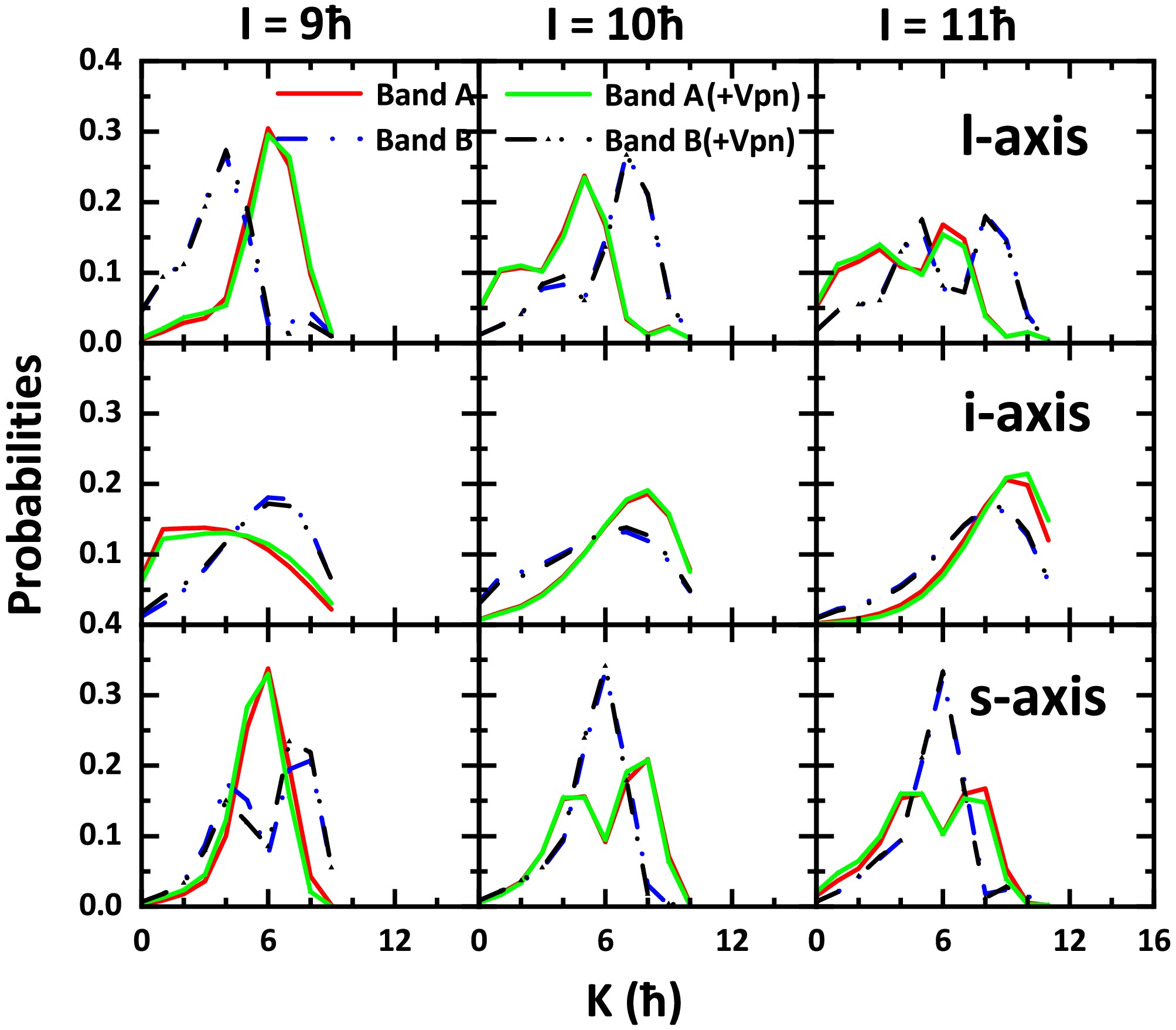

Figure 8.  (color online) Probability distributions for projections K of total angular momentum I on the long (l), intermediate (i), and short (s) axes for bands A and B in PRM with and without $ V_{p n} $ for maximum strength parameters $ u_0=-7.2\; \rm MeV $, $ u_1=-0.6\; \rm MeV $ at $ I=9 $, 10, $ 11\hbar $.

Reexamining the middle-right panel of Fig. 2, it can be found that the pronounced $ B(M1) $ staggering for $ I=10 $, $ 11\hbar $ is in accordance with the above static chirality spin region of K distributions. Now considering the $ V_{pn} $, Fig. 8 shows that the results with and without $ V_{pn} $ are similar, suggesting the slight effect of $ V_{pn} $ on characteristics of chirality with K distributions.

In order to investigate the angular momentum geometry of the nuclear system in detail, azimuthal plots [12, 32, 34, 66] (also called as spin coherent state maps [72]), i.e., profiles $ \mathscr{P}(\theta, \varphi) $ of the doublet bands on $ (\theta, \varphi) $ plane calculated by PRM with $ V_{p n} $ with maximum strength parameters $ u_{0}=-7.2\; \rm MeV $, $ u_{1}=-0.6\; \rm MeV $ at $ I=8 $-$ 12 \hbar $ are shown in Fig. 9. Here, θ is the angle between the total angular momentum I and the l axis, and φ is the angle between the projection of I onto the $ si $ plane and the s-axis. Note that the azimuthal plots are symmetric with respect to $ \varphi=0^{\circ} $ for the sake of the $ \rm{D}_2 $ symmetry.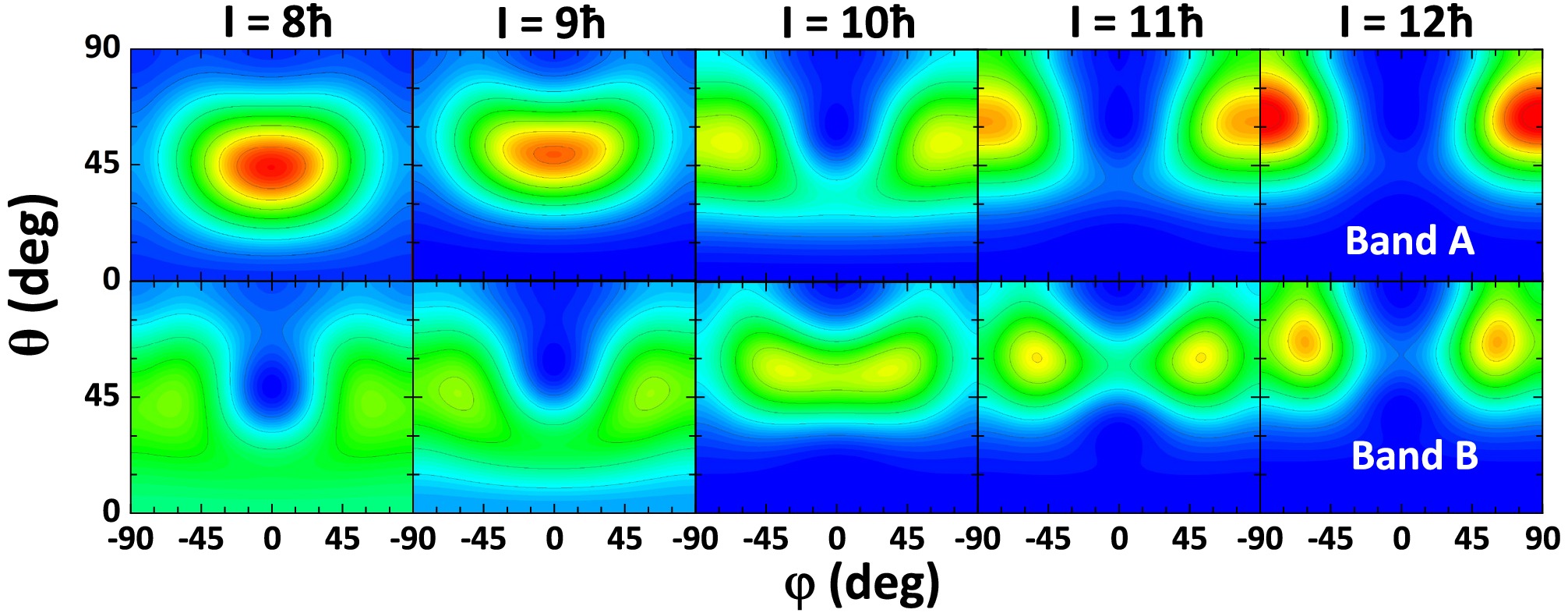

Figure 9.  (color online) Azimuthal plots (i.e., profiles for the orientation of the angular momentum) on $ (\theta, \varphi) $ plane calculated by PRM with $ V_{p n} $ with maximum strength parameters $ u_{0}=-7.2\; \rm MeV $, $ u_{1}=-0.6\; \rm MeV $ at $ I=8 $-$ 12 \hbar $, respectively.

For $ I=8 $ and $ 9\hbar $, the angular momentum for band A mainly orientates at ($ \theta\sim 45^{\circ}, \varphi=0^{\circ} $), corresponding to a planar rotation within the sl plane. The angular momentum for band B orientates equally at ($ \theta\sim 45^{\circ}, \varphi \sim \pm 60^{\circ} $), and the maximum of $ \mathscr{P}(\theta, \varphi) $ is apparently smaller than that of band A, understood as a realization of chiral vibration along the θ direction (i.e., with respect to the sl plane). This is consistent with the different K distributions between the doublet bands at $ I=9\hbar $ in Fig. 8, that i component of the rotator angular momentum for band B is larger than that for band A.

For $ I=10\hbar $, the angular momentum orientates equally at two aplanar directions, i.e., ($ \theta \sim 55^{\circ}, \varphi \sim \pm 70^{\circ} $) for band A, while ($ \theta \sim 55^{\circ}, \varphi \sim \pm 30^{\circ} $) for band B. These features demonstrate the occurrence of static chirality that accounts for the similar K distributions between the doublet bands in Fig. 8 and hence give the lowest $ \Delta E $ at $ 10 \hbar $ as shown in the bottom-right panel of Fig. 4.

For $ I=11\hbar $, the angular momentum orientates equally at ($ \theta\sim 60^{\circ}, \varphi \sim \pm 85^{\circ} $) for band A, while ($ \theta \sim 60^{\circ}, \varphi \sim \pm 50^{\circ} $) for band B. At this critical spin, the rotational mode of band A changes from an aplanar rotation back to a nearly planar rotation within the $ li $ plane, which weakens the feature of static chirality.

For $ I=12\hbar $, the static chirality disappears. The angular momentum for band A orientates at ($ \theta\sim 65^{\circ}, \varphi \sim \pm 90^{\circ} $), namely in the $ li $ plane and close to the i axis. The angular momentum for band B orientates equally at ($ \theta\sim 65^{\circ}, \varphi \sim \pm 60^{\circ} $), corresponding to an aplanar rotation. At this spin, a new type of chiral vibration appears within the $ li $ plane [12], which is consistent with the vanishing $ B(M1) $ staggering from $ I=11 $ to $ 12\hbar $ as shown in the bottom-right panel of Fig. 7.

From Figs. 8 and 9, as spin increases from $ 8 $ to $ 12\hbar $, the transition of chirality from a chiral vibration to a static chirality and then to another type of chiral vibration is illustrated.

For $ \rm Co $ isopotes with the configuration $ \pi f_{7/2}^{-1} \otimes \nu g_{9/2}^{1} $ in the $ A\approx 60 $ mass region, optimal parameter values for the ideal chiral bands have been determined through assessments of chiral features, i.e., the energy degeneracy of doublets, the staggering of $ B(M1) $, and the similarity of $ B(E2) $. These parameters are found to be $ \gamma=34^{\circ} $, $ \beta=0.25 $, and $ \mathscr{J}=10\; \hbar^2 / \rm MeV $ according to the PRM calculations.

With the inclusion of the residual proton-neutron interaction $ V_{pn} $ in the PRM adopting the above optimal parameters, the chirality of the nuclear system is discussed in detail. The electromagnetic transition probabilities are slightly affected by the presence of $ V_{pn} $. Nevertheless, The energy splitting $ \Delta E(I) $ and the energy staggering parameter $ S(I) $ illustrate that lower values of the strength parameter $ |u_0| $ and relative strength ratio $ u_0:u_1 $ are more favorable for the existence of chiral doublet bands. In addition, the evolution of the chirality is suggested based on the K-plots and the azimuthal plots $ \mathscr{P}(\theta,\varphi) $, namely, a chiral vibration appears at $ I=8\hbar $, then changes to static chirality at $ I=10\hbar $, and finally evolves to another type of chiral vibration at $ I=12\hbar $.

The present results identify optimal conditions for chiral doublet bands in the $ A\approx 60 $ mass region using the PRM and explore the residual proton-neutron interaction $ V_{pn} $ as an effect factor. It is hoped that the PRM containing $ V_{p n} $ can be applied in future studies of nuclear chiral features (especially the energy staggering $ S(I) $) in different mass regions. Furthermore, it is noted that in the current study, the core is a rigid rotor. It will be interesting to consider the effect of residual proton-neutron interaction $ V_{pn} $ in a soft core, e.g., using the IBFFM [25−27, 73]. Additionally, an experimental opportunity is presented for the observation of chiral doublet bands in the $ A\approx 60 $ mass region.