Proton separation energy predictions for proton-rich nuclei with the radial basis function approach and mirror symmetry

The proton separation energy comprises two fundamental components: the one-proton separation energy, representing the energy required to remove one proton from a nucleus in its ground state, and the two-proton separation energy, denoting the energy needed for simultaneous removal of two protons from the nuclear ground state. On the one hand, proton separation energy plays a dual role in nuclear physics research: (ⅰ) as a key parameter for investigating pairing gaps [1] in atomic nuclei and validating proton magic numbers [2, 3]; (ⅱ) as an essential diagnostic tool for identifying proton halo nuclei [4] and proton decay nuclei near the proton drip line. On the other hand, the proton separation energy is an important input parameter in the study of rapid proton capture process in nuclear astrophysics [5].

The proton separation energy is conventionally determined through nuclear mass (binding energy) differences between adjacent nuclides. Despite experimental measurements of nuclear masses for over 2,500 nuclides [6], theoretical models indicate a substantial number of nuclear mass values remain unverified. Several advanced global nuclear mass models, such as the finite-range droplet model (FRDM12) [7], Koura-Tachibana-Uno-Yamada (KTUY) model [8], Bhagwat model [9], Weizsäcker-Skyrme (WS) model [10−13], Duflo-Zuker (DZ) model [14, 15], the Hartree-Fock-Bogoliubov (HFB) model [16−18], the relativistic-mean-field (RMF) model [19], and the relativistic-continuum-Hartree-Bogoliubov (RCHB) model [20], can predict the mass of all atomic nuclei on the nuclear chart and thereby calculate the nucleon separation energy. Recent investigations [21] have revealed a robust linear correlation between the deviations of proton separation energies in atomic nuclei and their mirror counterparts' neutron separation energy deviations. This empirical relationship, validated through comparative analysis of theoretical predictions and experimental data, demonstrates a systematic interdependence between proton separation energies and neutron separation energy deviations across isotopic mirrors. The observed linearity suggests that mirror nuclei act as natural calibration benchmarks for nuclear mass models. The predictive accuracy of existing mass models, particularly for proton-rich nuclei, can be significantly enhanced by incorporating this symmetry constraint. This refinement strategy capitalizes on the intrinsic isospin symmetry of the nuclear force, offering a computationally efficient pathway to improve proton separation energy predictions without requiring fundamental model modifications.

To enhance the predictive performance of nuclear mass models, contemporary research has integrated advanced machine learning techniques including radial basis function (RBF) [22−27], Bayesian neural networks (BNNs) [28−33], kernel ridge regression (KRR) [34−38], and other machine learning [39−46] approaches. These data-driven approaches offer complementary advantages to traditional theoretical frameworks by capturing non-linear correlations within nuclear data, thereby improving the accuracy of mass predictions across the nuclide chart. Among them, the RBF approach is one of the earlier machine learning approaches applied to the prediction of nuclear masses. The RBF approach utilizes inherently linear basis functions with no computational parameters requiring optimization. In 2011, Wang et al. [22] employed the RBF approach to achieve an impressive root-mean-square (rms) deviation of merely 0.2 MeV when describing 2,149 experimental nuclear mass data from AME2003 [47]. The RBF approach not only improves the accuracy of the model's description nuclear mass, but also further enhances the accuracy of describing the two-proton separation energy and two-neutron separation energy. However, when it comes to describing the one-proton separation energy and one-neutron separation energy, the results it provides are worse than those directly given by the nuclear mass model. Niu et al. subsequently introduced a significant refinement by incorporating odd-even staggering effects during the training phase, which further reduced the rms deviation to approximately 0.135 MeV [25], and the descriptions of the one-proton separation energy and one-neutron separation energy have also improved. However, the RBF approach that takes into account the odd-even effect has a poorer description of the two-proton separation energy and two-neutron separation energy. Therefore, it is an interesting research question whether there is a way to enable the RBF approach to simultaneously improve the prediction accuracy of the nuclear mass model for the one and two nucleons separation energies.

In this work, the mirror symmetry and RBF approach will be combined to predict the proton separation energies of proton-rich nuclei (with proton number $ 8\leq Z \leq38 $, neutron number $ N \geq8 $). The methodological details of the RBF approach combine with mirror symmetry are presented in Section Ⅱ. Section Ⅲ provides the results and discussions, and the main conclusions are given in the final section.

The conventional method to improving the predictive capability of theoretical models using RBF approach involves directly training the deviation between experimental data and theoretical predictions to obtain a reconstruction function. By incorporating the numerical values of this reconstruction function into the model's original predictions, an enhanced prediction result can be derived. As demonstrated in Ref. [21], a pronounced linear correlation exists between the one-proton separation energy deviation of an atomic nucleus and the one-neutron separation energy deviation of its mirror nucleus. This relationship can be quantitatively expressed by the following equation

where $ \Delta S_{\rm{p}}(Z,N)=S_{\rm{p}}^{\rm{exp}}(Z,N)-S_{\rm{p}}^{\rm{th}}(Z,N) $, $ S_{\rm{p}}^{\rm{exp}}(Z,N) $ represents the one-proton separation energy derived from the binding energy data obtained through experimental measurements, $ S_{\rm{p}}^{\rm{th}}(Z,N) $ represents the one-proton separation energy derived from the theoretical predicted binding energy data. Similarly, one-neutron separation energy deviation of its mirror nucleus $ \Delta S_{\rm{n}}(Z^{'},N^{'})=S_{\rm{n}}^{\rm{exp}}(Z^{'},N^{'})- S_{\rm{n}}^{\rm{th}}(Z^{'},N^{'}) $. For a pair of mirror nuclei, $ Z=N^{'} $ and $ N=Z^{'} $. $ k_{1} $ and $ b_{1} $ represent the slope and intercept respectively, and they can be obtained through linear fitting. By demonstrating that this mirror symmetry correction substantially enhances the theoretical model's predictive accuracy for proton separation energies, we have further extended this symmetry relationship to integrate with the RBF approach.

The RBF approach considering mirror symmetry (RBFms) is to train the residual $ \delta (Z,N)=\Delta S_{\rm{p}}(Z,N)- \Delta S_{\rm{n}}(Z^{'},N^{'}) $, and thereby obtain the new reconstruction function $ S^{\rm{ms}}(Z,N) $. The new revised one-proton separation energy of nucleus $ (Z,N) $ is given by

The calculation details for $ S^{\rm{ms}}(Z,N) $ are similar to those of the traditional RBF approach and can be found in the Refs. [22−27]. For the theoretical models, we take the DZ31 [15], FRDM12 [7], KTUY [8], and WS4 [13] models. For convenience, the model improved by the RBFms approach is denoted with the "model+RBFms". To evaluate the predictive power of theoretical model combine with the RBFms approach, the rms deviation

is employed, where $ S_{\rm{p}}^{\rm{exp}}(Z,N) $ and $ S_{\rm{p}}^{\rm{th}}(Z,N) $ are the experimental and theoretical one-proton separation energy, respectively, and n is the number of nuclei contained in a given set. The RBFms approach can also be applied to the prediction of the two-proton separation energy, and its calculation process is similar to the aforementioned numerical description.

To verify the effectiveness of the RBFms approach, we selected 143 nuclei from AME2012 [48] as the learning set for one-proton separation energy, while the test set includes 43 nuclei from AME2020 [6] and 50 newly measured masses in Refs. [4, 5, 49−74] (AME2020 + NM50) which lie just outside the AME2012. Figure 1 illustrates the rms deviations of the learning and test sets for one-proton separation energy obtained using four nuclear mass models (DZ31, FRDM12, KTUY, and WS4) in conjunction with two machine learning approaches (RBF and RBFms) and mirror correction (MC) was proposed in Ref. [21]. As demonstrated in Fig. 1, for the learning and test sets, the results obtained by the traditional RBF approach (training 2353 nuclear masses from AME2012) are worse than those of the models themselves. We find that even when training the one-proton separation directly, the results obtained are basically comparable to those obtained from training the nuclear mass. However, for the learning and test sets, both the mirror correction method and the RBFms approach can significantly improve the prediction results of the four mass models. Both the RBFms approach and the mirror correction method demonstrate comparable performance between the DZ31 and KTUY models. The results of the RBFms approach are better than those of the mirror correction method for the WS4 model. The results of the RBFms approach are worse than those of the mirror correction method for the FRDM12 model. It is worth noting that the KTUY model combined with the RBFms approach achieved a rms deviation of 0.113 MeV in describing the one-proton separation energies of 143 nuclei for the learning set.

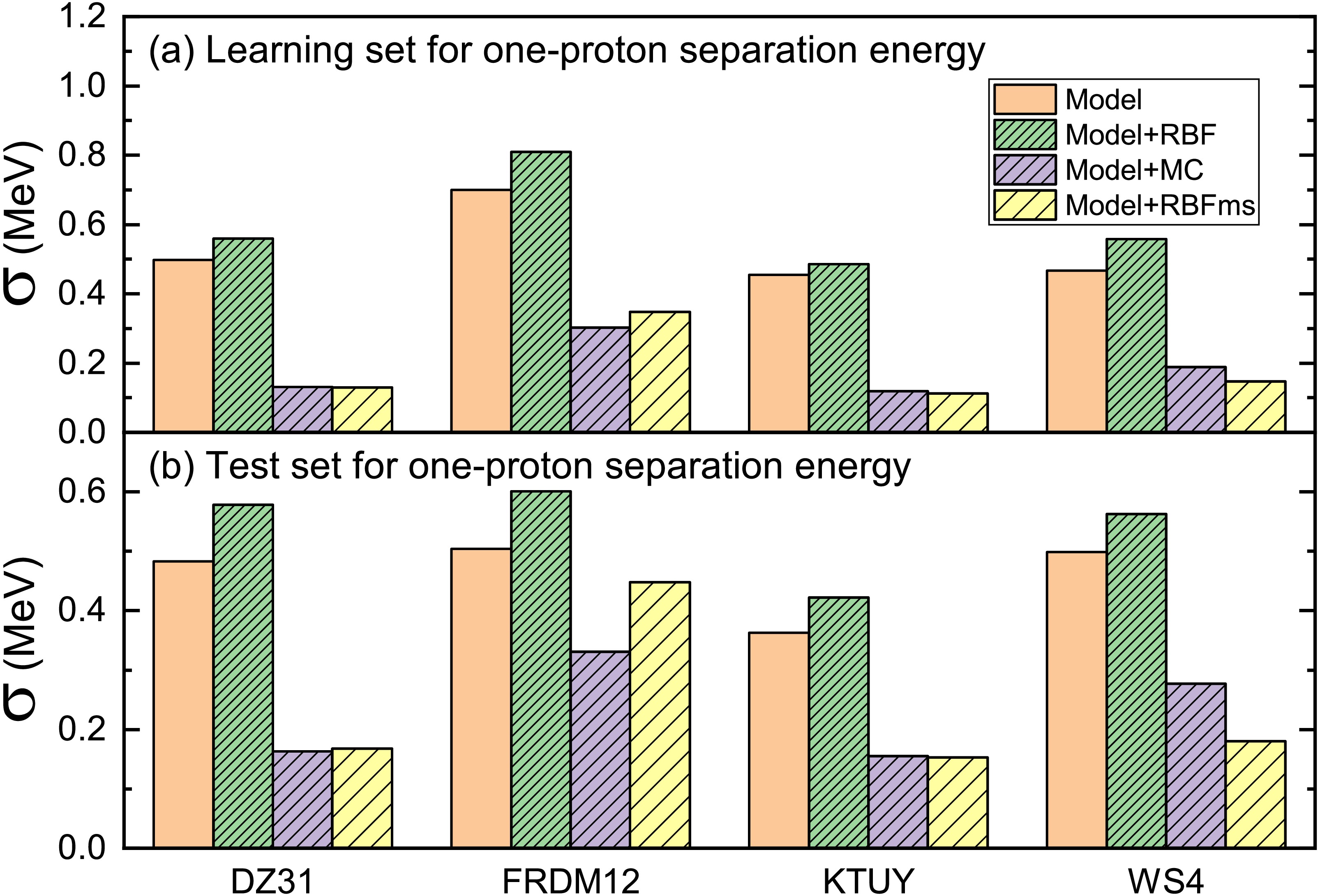
Figure 1.  (color online) (a) Root-mean-square (rms) deviation of the learning set for one-proton separation energy obtained using four nuclear mass models (DZ31, FRDM12, KTUY, and WS4) in conjunction with two machine learning approaches (RBF and RBFms) and mirror correction (MC). The unpatterned columns represent the results of the mass models. The dense, medium-dense and sparse patterned columns represent the results of the mass models combine with RBF, RBFms, and MC approaches, respectively. (b) As with (a), but for test set for one-proton separation energy.

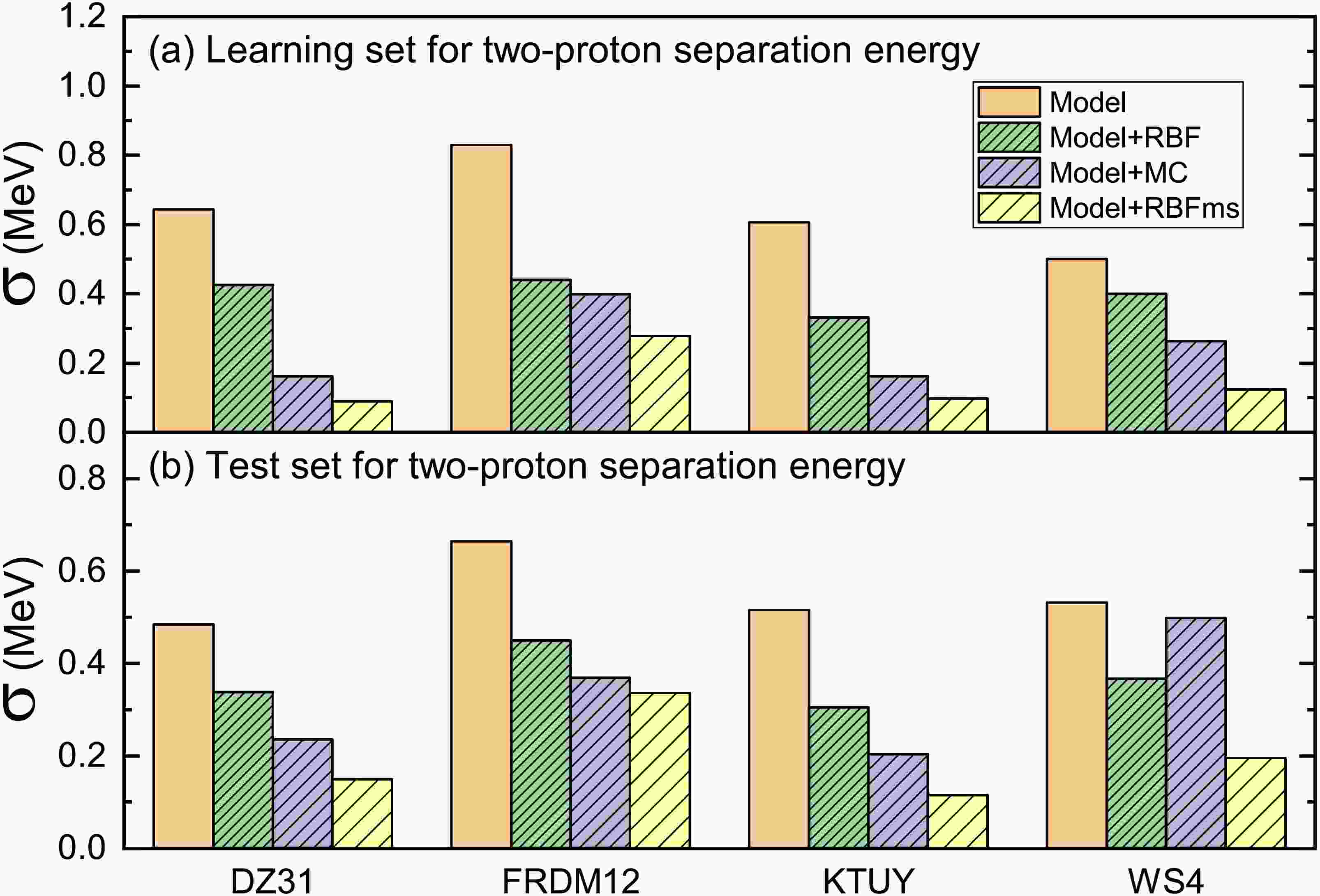
Similarly, we selected 115 nuclei from AME2012 [48] as the learning set for two-proton separation energy, while the test set includes 40 nuclei from AME2020 + NM50 which lie just outside the AME2012. Figure 2 illustrates the rms deviations of the learning and test sets for two-proton separation energy obtained using four nuclear mass models in conjunction with two machine learning approaches and MC method. As can be seen from Fig. 2, for the description of the learning and test sets of the two-proton separation energy, the RBF, MC, and RBFms methods all can improve the results of the nuclear mass model. Among all evaluated methods, the RBFms approach demonstrated the most substantial enhancement in prediction accuracy. Specifically, when applied to the DZ31 model, RBFms approach achieved a learning set rms deviation of 0.089 MeV for two-proton separation energy predictions. The RBFms approach exhibits significantly enhanced predictive accuracy for two-proton separation energy compared to the MC method. This performance advantage, however, is not observed in one-proton separation energy predictions. The observed performance discrepancy may stem from the RBF method's inherent limitations in capturing nuclear odd-even effect induced oscillation patterns, particularly in one-proton separation energy predictions.

Figure 2.  (color online) (a) Root-mean-square (rms) deviation of the learning set for two-proton separation energy obtained using four nuclear mass models (DZ31, FRDM12, KTUY, and WS4) in conjunction with two machine learning approaches (RBF and RBFms) and mirror correction (MC). The unpatterned columns represent the results of the mass models. The dense, medium-dense and sparse patterned columns represent the results of the mass models combine with RBF, RBFms, and MC approaches, respectively. (b) As with (a), but for test set for two-proton separation energy.

Accurate determination of nuclear drip line positions remains a critical research frontier in both experimental and theoretical nuclear physics. So, we systematically predicted proton drip line positions for nuclei with proton numbers $ Z=14-38 $ through an integrated method combining DZ31, FRDM12, KTUY, and WS4 mass models with the RBFms approach. This learning set used for prediction also incorporates the test set data mentioned above. The proton drip line positions in isotope chains are determined by distinct criteria for odd-Z and even-Z nuclei. For odd-Z nuclei, the outermost nucleus with positive one-proton separation energy ($ S_{\rm{p}} > 0 $) defines the drip line boundary. For even-Z nuclei, the criterion involves two-proton separation energy ($ S_{\rm{2p}} > 0 $), where the outermost nucleus satisfying this condition marks the drip line position. Figure 3 illustrates the proton drip line positions for nuclei with $ Z=14-38 $ predicted by the DZ31, FRDM12, KTUY, and WS4 models, including results predicted by their combined with the RBFms approach. Figure 3 demonstrates that while the DZ31, FRDM12, KTUY, and WS4 models yield quantitatively similar predictions, observable discrepancies persist. However, upon integration with the RBFms approach, the results from these models exhibit significantly improved consistency across most cases. This further demonstrates the effectiveness of the RBFms approach. Finally, Table 1 presents the predicted average values of one-proton and two-proton separation energies for a small number of atomic nuclei (possibly the ground-state two-proton decay nuclei). These average values are calculated by combining the prediction results of the DZ31, FRDM12, KTUY and WS4 models with the RBFms approach.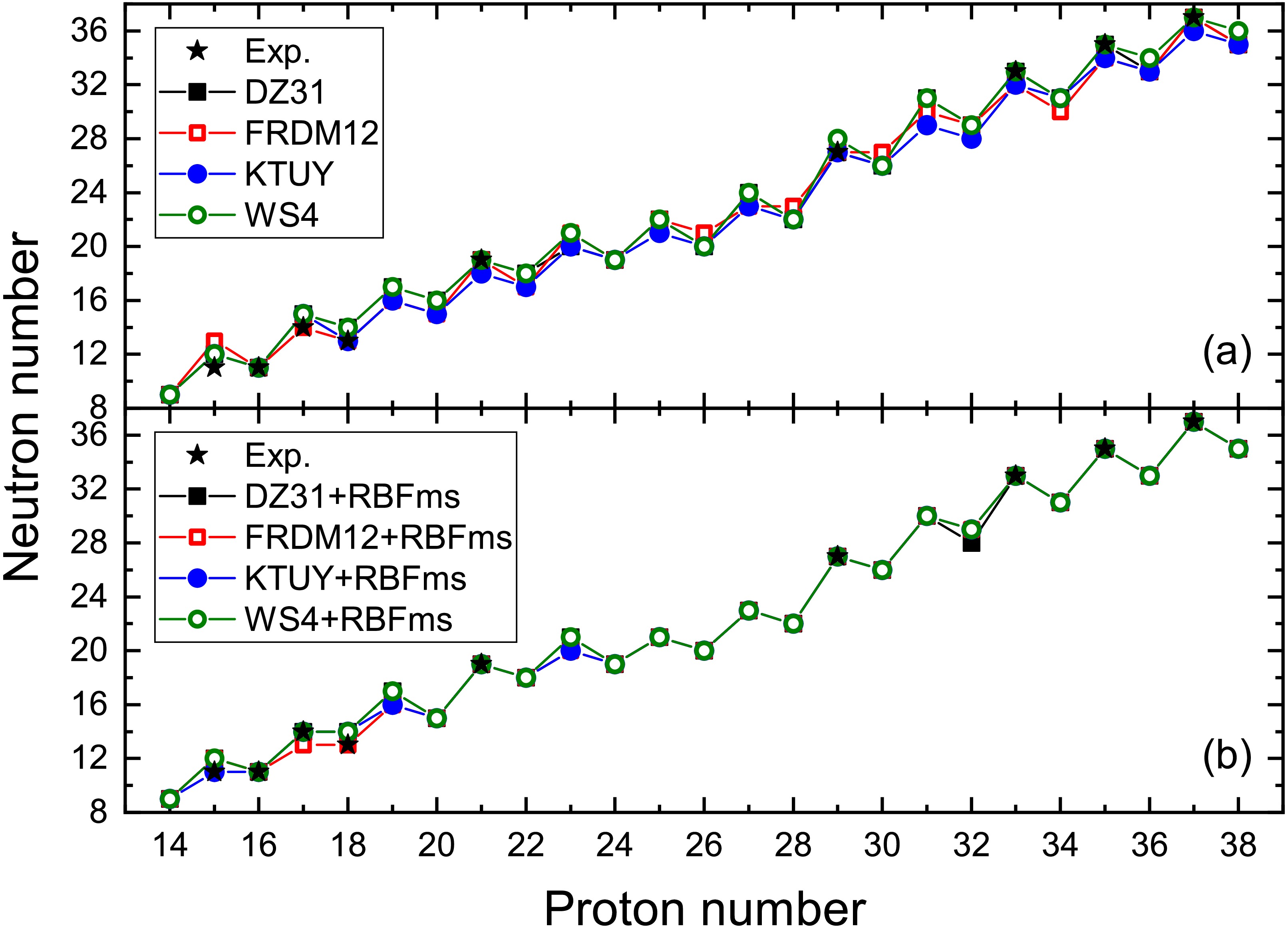

Figure 3.  (color online) (a) Predicted proton drip line by DZ31, FRDM12, KTUY, and WS4 mass models. (b) Predicted proton drip line by DZ31, FRDM12, KTUY, and WS4 mass models combine with RBFms approach. The five-pointed star indicates the proton drip line position as determined by the experiment, and the data is from reference [4, 6].

N	Z	$ \overline{S_{\rm{p}}} $ (MeV)	$ \overline{S_{\rm{2p}}} $ (MeV)
14	20	0.401	−1.987
16	22	0.369	−2.742
17	22	0.252	−0.935
18	24	1.016	−0.734
19	26	−0.065	−1.251
20	28	0.441	−1.328
24	30	−0.053	−1.752
27	32	0.243	−1.334
29	34	0.035	−2.389
30	34	0.428	−1.199
31	36	−0.002	−1.829
33	38	0.021	−2.250

Table 1.  The predicted average values of one-proton and two-proton separation energies for a small number of atomic nuclei. These average values are calculated by combining the prediction results of the DZ31, FRDM12, KTUY and WS4 models with the RBFms approach.

An innovative RBFms approach incorporating mirror symmetry has been proposed, significantly improving the prediction accuracy of one-proton and two-proton separation energies. The traditional RBF approach constructs the reconstruction function by directly fitting the deviation between experimental and theoretical data, while the RBFms approach incorporates the principle of mirror symmetry, jointly training the one/two-proton separation energy deviations of atomic nuclei with one/two-proton separation energy deviations of their mirror nuclei. This design effectively utilizes the mirror symmetry in nuclear physics, especially for the proton-rich nuclei far from the β stability line. By establishing the mirror symmetry correlation between proton and neutron separation energies, it simultaneously optimizes the residuals of both sets of physical quantities during the training process, thus breaking through the limitations of traditional methods that rely solely on a single type of data. The research results show that this method demonstrates significant improvements in both the KTUY and DZ31 models: for the prediction of one-proton separation energies of 143 atomic nuclei, the rms deviation of the KTUY model after combining RBFms is reduced to 0.113 MeV; while for the prediction of two-proton separation energies of 115 atomic nuclei using the DZ31 model, the rms deviation is further optimized to 0.089 MeV. This result verifies the effectiveness of the mirror symmetry constraint in nuclear mass models. For the nuclear region with proton number $ Z = 14-38 $, the DZ31, FRDM12, KTUY, and WS4 models combined with RBFms approach predicted the proton drip line position and some candidate nuclei for two-proton decay.