-
The phase diagram of quark matter is among the most interesting topics in high-energy nuclear physics. At high temperature and/or high baryon density, the state of the quark-gluon plasma (QGP) has been predicted and widely studied both in theory [1-7] and in experiments [8-12]. Numerous synchrotrons and colliders are built for heavy-ion collisions to generate QGP. However, it is difficult to measure the temperature of the fireball directly, especially at its very early stage, because of its small size and short lifetime. Using the statistical model [13], one can extract the temperature from the spectrum or the yield of light hadrons. Strange particles seemingly freeze-out earlier than pions [14], indicating that they carry information of the fireball at an earlier time. Heavy quarkonia may even survive the QGP owing to their large binding energies and carry information from the early stage of the fireball. However, they can hardly be thermalized, either in kinetics or in chemistry. The anomalous suppression of
$ J/\psi $ was suggested as a signal of the very early formation of QGP [15], which involves different processes, such as color screening [16], gluon scattering [17-20], and quasi-free scattering from quarks [20, 21]. It is found that the inverse process, which is the regeneration of$ J/\psi $ from charm quarks in QGP, also plays an important role in relativistic heavy collisions at RHIC and higher colliding energies [21-24], making the narrative more complicated.Although it is difficult to measure the temperature of the fireball at an early time from the momentum distribution of heavy quarkonia, the sequential dissociation model [16] offers another approach to apply heavy quarkonia as thermometers of the fireball, which assumes that a heavy quarkonium survives if and only if the temperature of the fireball is above the dissociation temperature
$ T_d $ of the quarkonium. Most other dynamic studies focus on the dissociation rate (or the width) of a heavy quarkonium at a certain temperature T [21-23, 25-30]. Indeed, the sequential dissociation model can also be regarded as a special case of the dynamic models, with a dissociation rate that is infinitely large above$ T_d $ and zero below$ T_d $ .However, even if the dissociation rate of a heavy quarkonium vanishes at finite temperature, quarkonium suppression can still occur in heavy-ion collisions because of the fast heating process at the very early stage of the bulk medium, which is the main effect we discuss in this paper. In relativistic heavy ion collisions, the fireball reaches its highest temperature within
$ 1 $ fm/c, and cools down for a significantly longer time to finally freeze-out. For simplicity, we treat the initial heating process as a rapid process and the cooling process as a very slow process. According to the adiabatic theorem, the yield of heavy quarkonia is maintained constant during the cooling process if the width of the quarkonia is negligible. Therefore, the suppression is mainly due to the transition from initial heavy quarkonia to heavy quarkonia in the hot medium. In this case, we can directly map the nuclear modification factor of heavy quarkonia to the temperature of the fireball after the fast heating process. As discussed above,$ J/\psi $ at RHIC and at colliders with higher beam energies does not fit such a model, as both the scattering dissociation and the regeneration are very important. Therefore, we consider$ \Upsilon(1S) $ instead in the following discussion and calculations, as both its dissociation rate and regeneration rate in medium are small at RHIC energy [31, 32]. -
The evolution of the wave function
$ \psi({ r},t) $ of$ \Upsilon(1S) $ at time t and the relative radius$ { r} $ between the bottom quark and the anti-bottom quark can be described by the Schroedinger equation$ {\rm i}\partial_t \psi({ r},t) = \left[-\frac{1}{m_b}\nabla^2+V(r,T(t))-{\rm i}\Gamma({ r}, T)\right]\psi({ r},t), $

(1) where
$ m_b $ is the mass of a bottom quark, and we take$ \hbar = 1 $ . In the above, thermal fluctuation [33] is neglected. The corresponding stationary radial Schroedinger equation for a given temperature T is$ \left[-\frac{1}{m_br}\frac{ \rm{d}^2}{ \rm{d} r^2}r+\frac{l(l+1)}{m_br^2}+V(r,T)-{\rm i}\Gamma(r,T)\right]\psi_r(r) = E\psi_r(r),$

(2) where
$ \psi_r(r) $ is the radial wave function of$ \Upsilon(1S) $ , and E is the eigen energy of$ \Upsilon(1S) $ . For$ \Upsilon(1S) $ , the azimuthal quantum number is$ l = 0 $ . To focus on the novel mechanism, we neglect the particle scattering process and consider that the in-medium width$ \Gamma = 0 $ . The potential V is taken in the form of a screened Cornell potential [34]$ V(r)= -\frac{\alpha}{r}{\rm e}^{-\mu r}-\frac{\sigma}{2^{3/4}\Gamma(3/4)}\left(\frac{r}{\mu}\right)^{1/2}K_{1/4}[(\mu r)^2], $

(3) where
$ \alpha = \frac{\pi}{12} $ and$ \sigma = 0.2 $ GeV$ ^2 $ [34]. Further,$ \Gamma $ and K are the gamma function and the modified Bessel function, respectively. For simplicity, we neglect the constant term that does not vanish at infinity in$ V(r) $ . The dependence on temperature T arises from the screening mass$ \mu $ . We fit the free energy of heavy quarks by the lattice QCD [34, 35], and parameterize the screening mass$ \mu $ (scaled by$ \sqrt{\sigma} $ ) as$ \frac{\mu(\bar{T})}{\sqrt{\sigma}} = s\bar{T}+a\sigma_t\sqrt{\frac{\pi}{2}}\left[ {\rm erf}\left(\frac{b}{\sqrt{2}\sigma_t}\right)- {\rm erf}\left(\frac{b-\bar{T}}{\sqrt{2}\sigma_t}\right)\right], $

(4) with
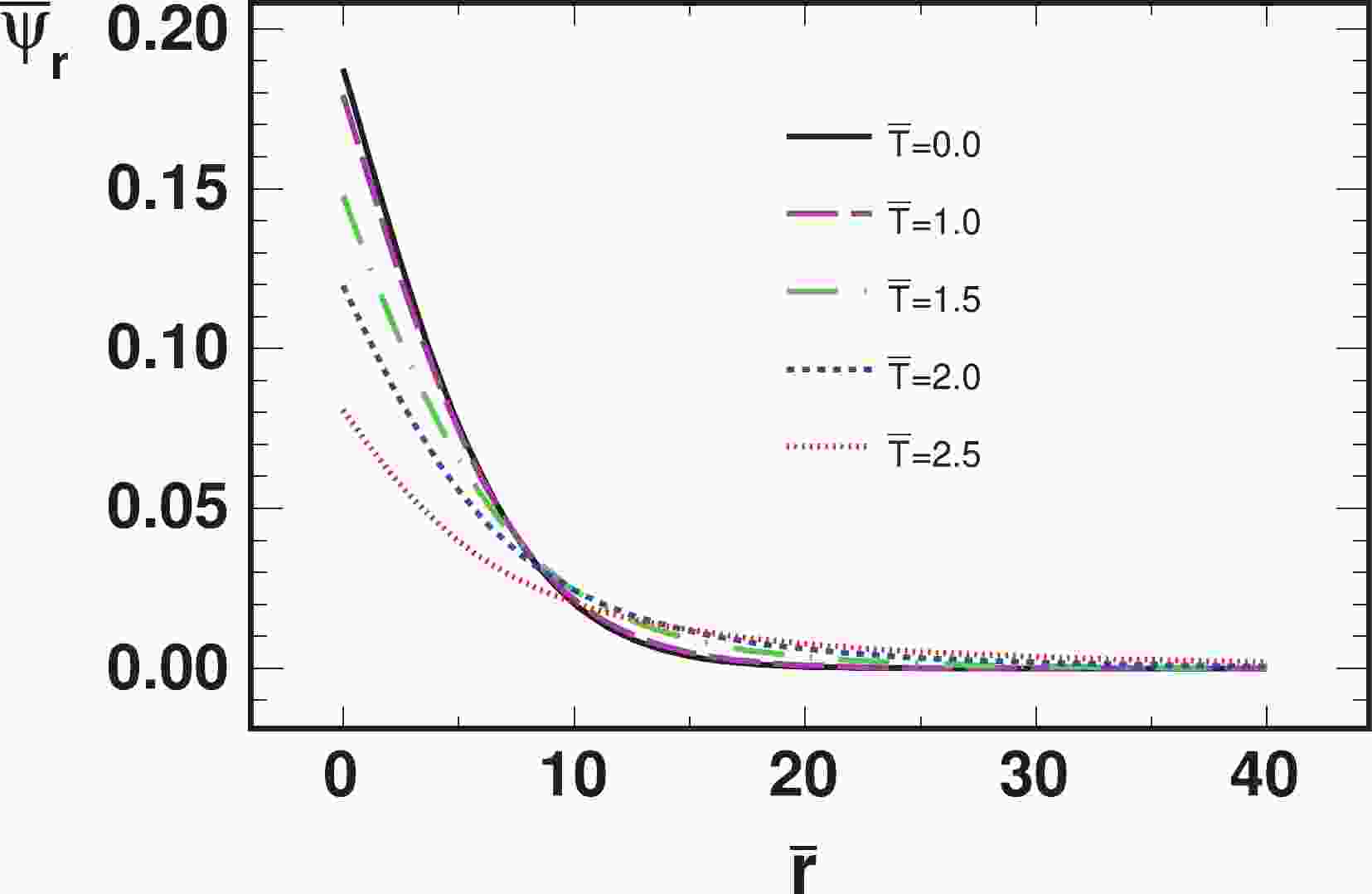
$ \bar{T} = T/T_c $ ,$ s = 0.587 $ ,$ a = 2.150 $ ,$ b = 1.054 $ ,$ \sigma_t = $ 0.07379, and the error function${\rm erf}(z) = \frac{2}{\sqrt{\pi}}\int_0^{z} {\rm e}^{-x^2} {\rm d} x$ . Here,$ T_c $ is the critical temperature of the phase transition.The radial eigen wave function is shown in Fig. 1. To be dimensionless, we scaled the radius and the wave function as
$ \bar{r} = m_b r $ and$ \bar{\psi}_r = m_b^{-3/2}\psi_r $ , respectively, resulting in$\int \left|\bar{\psi}_r\right|^2 \bar{r}^2 {\rm d} \bar{r} = 1$ . The wave function of$ \Upsilon(1S) $ at$ T = T_c $ is similar to that at$ T = 0 $ , while it becomes increasingly broad with increasing temperature. The dissociation temperature is$ T_d\approx3T_c $ .
Figure 1. (color online) Scaled radial wave functions
$\bar{\psi}_r = m_b^{-\frac{3}{2}}\psi$ of$ \Upsilon(1S) $ as a function of scaled radius$ \bar{r} = m_b r $ , at different scaled temperature$ \bar{T} = T/T_c $ .The transition probability from a
$ \Upsilon(1S) $ at zero temperature to that at T is$ P(\bar{T}) = \left|\left\langle \psi(T)|\psi(0)\right\rangle\right|^2,$

(5) which is shown as a function of
$ \bar{T} = T/T_c $ in Fig. 2. It decreases monotonically with$ \bar{T} $ , as the overlap between the wave function at finite temperature and that at zero temperature becomes small when$ \bar{T} $ increases. It is very close to unity at$ \bar{T} = 1 $ , as already indicated by Fig. 1, and it vanishes at$ T_d\approx3T_c $ . Note that excited states of$ \Upsilon(2S) $ and$ \Upsilon(3S) $ at temperature T can also be generated from$ \Upsilon(1S) $ in vacuum if T is below their dissociation temperatures$ T_d $ , and they can finally feed down to$ \Upsilon(1S) $ . This effect is not included in our current calculation.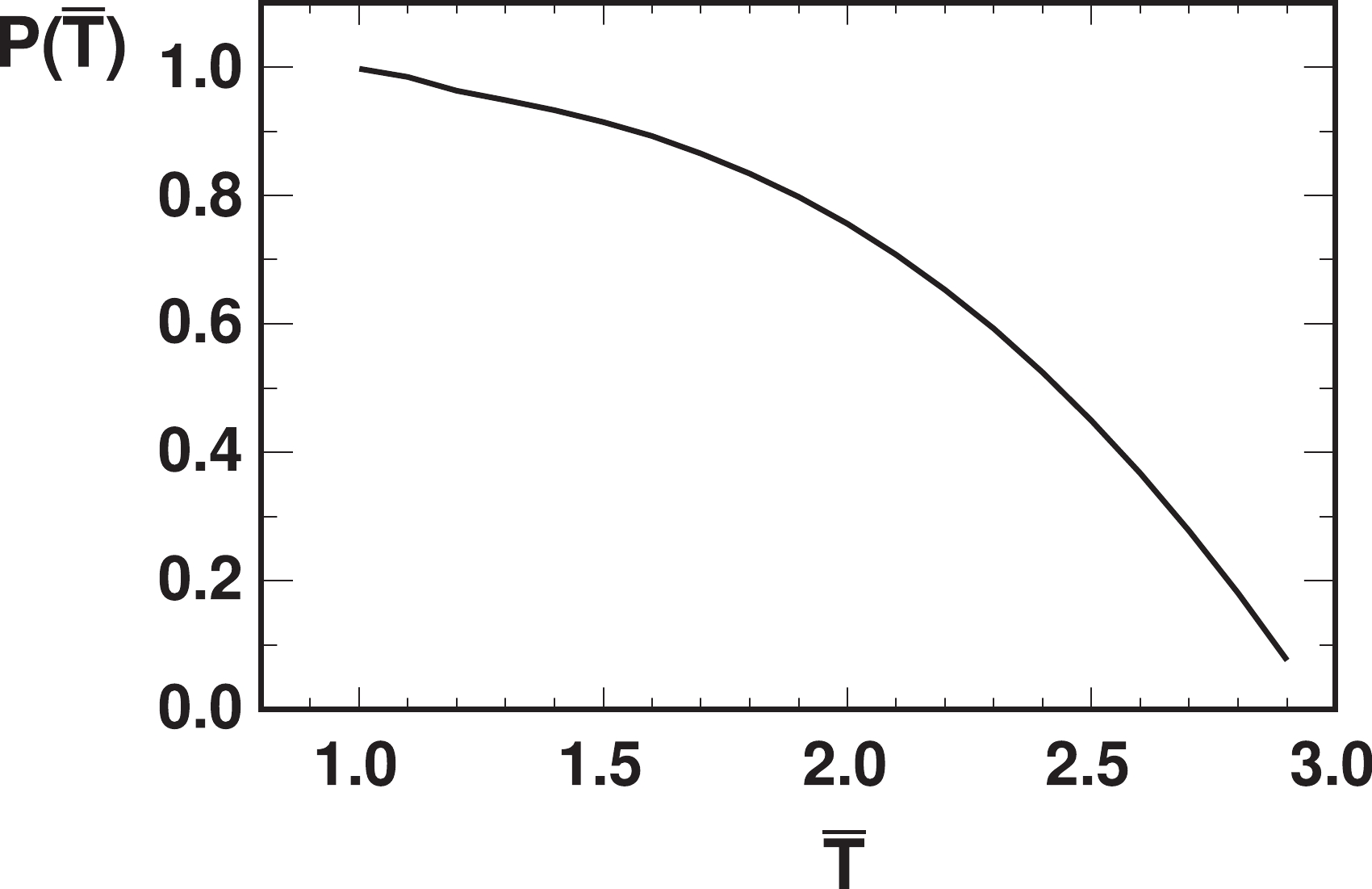
Figure 2. Transition probability P [defined in Eq. (5)] of a
$ \Upsilon(1S) $ from temperature$ 0 $ to temperature T as a function of scaled temperature$ \bar{T} = T/T_c $ .Subsequently, we verify the adiabatic approximation. At RHIC energy, the highest temperature of the fireball is around
$ 2T_c $ when the system reaches local thermal equilibrium. We suppose that the temperature decreases with time linearly from$ 2T_c $ to$ T_c $ , and evolve the wave function$ \psi({ r},t) $ of a$ \Upsilon(1S) $ by Eq. (1) with its initial condition as an eigenstate$ \Upsilon(1S) $ at$ 2T_c $ . The survival probability as a function of time is shown in Fig. 3. The typical time for the fireball to cool down to$ T_c $ is$ 5\sim10 $ fm/c. As shown in the figure, the survival probability is approximately$ 0.98 $ when the evolution time is$ 10 $ fm/c, which implies that the adiabatic approximation is very good in this case. Even if we take a lower value of$ 5 $ fm/c, the survival probability$ 0.93 $ is obviously larger than$ P(2.0) = 0.76 $ , as shown in Fig. 2. This result is qualitatively consistent with the result in Ref. [36], where the adiabatic approximation is examined for$ \Upsilon(1S) $ at LHC energy with a finite dissociation rate.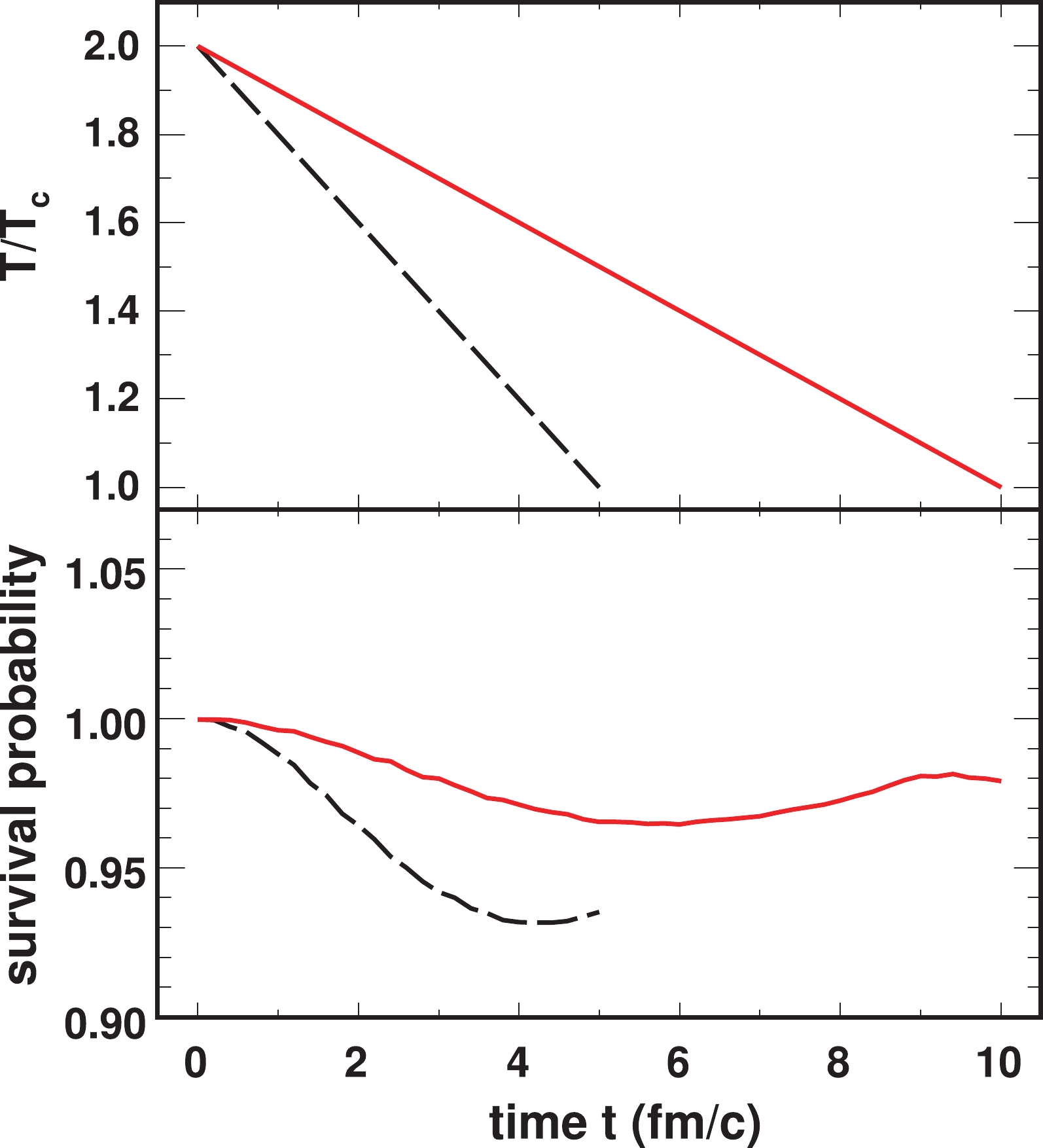
Figure 3. (color online) Upper panel: Different cooling systems with medium temperature decreasing linearly with time. Lower panel: Time evolution of survival probability of
$ \Upsilon(1S) $ at different cooling speeds calculated using Schroedinger equation with an initial$ \Upsilon(1S) $ at its eigenstate at the initial temperature.Here, we include the spatial distribution of temperature. In practice, the temperature is not uniform in space. The temperature is high in the center of the fireball, whereas it is low in peripheral regions. Therefore, the survival probability for
$ \Upsilon(1S) $ is an average of all generated$ \Upsilon(1S) $ s. Because the production of$ \Upsilon(1S) $ is a hard process, we assume that the density of generated$ \Upsilon(1S) $ is proportional to the number density of binary collisions$ n_c({ x}_T) $ at transverse coordinate$ { x}_T $ . Therefore, we have$R_{AA} = \frac{\displaystyle\int P(\bar{T}({ x}_T)) {\rm d} N_{\Upsilon(1S)}}{\displaystyle\int {\rm d} N_{\Upsilon(1S)}} = \frac{\displaystyle\int P(\bar{T}({ x}_T))n_c({ x}_T) {\rm d} { x}_T}{\displaystyle\int n_c({ x}_T) {\rm d} { x}_T}. $

(6) We assume that the entropy density s is proportional to the density of the number of participants
$ n_p $ , and we regard the hot medium as an ideal gas, such that the entropy density is likewise proportional to$ T^3 $ . Consequently, the spatial distribution of temperature is$ \bar{T}({ x}_T)= \bar{T}({\bf 0})\left(\frac{n_p({ x}_T)}{n_p({\bf 0})}\right)^{1/3}, $

(7) where
$ \bar{T}({ x}_T) $ is the scaled local temperature$ T/T_c $ at$ { x}_T $ , and$ \bar{T}({\bf 0}) $ is the scaled local temperature at$ { x}_T = {\bf 0} $ . In central collisions, the number density of participants$ n_p $ and number density of binary collisions$ n_c $ are$ n_p({ x}_T) =2{\cal T}(x_T)\left[1-{\rm e}^{-\sigma_{NN}{\cal T}(x_T)}\right], $

(8) $ n_c({ x}_T) = \sigma_{NN}{\cal T}^2(x_T), $

(9) where
$ \sigma_{NN} $ is the inelastic cross-section of nucleons, and$ {\cal T}(x_T) $ is the thickness function of a gold nucleus. For simplicity, we take a sharp-cut-off thickness function$ {\cal T}(x_T)= \frac{3A\sqrt{R^2-x_T^2}}{2\pi R^3}, $

(10) where R and A are the radius and mass number of the nucleus, respectively. By substituting Eqs. (7)-(10) to Eq. (6), we obtain the nuclear modification factor in central collisions
$ R_{AA} = 4\int_0^1P\left(\bar{T}(0)\sqrt[\root{3}3]{x\frac{1-{\rm e}^{-N_mx}}{1-{\rm e}^{-N_m}}}\right)x^3 {\rm d} x, $

(11) with
$ N_m = \sigma_{NN}{\cal T}(x_T = 0) = 3\sigma_{NN}A/(2\pi R^2) $ , and$ \begin{array}{l} P(\bar{T}) = \left\{\begin{array}{ll}0,&\bar{T}>T_d/T_c,\\ \left|\langle \psi(T)|\psi(0)\rangle\right|^2,&1<\bar{T}<T_d/T_c,\\ 1,&\bar{T}<1.\end{array}\right. \end{array} $

(12) where we take
$ P = 1 $ below$ T_c $ as an approximation. We take$ R = 6.38 $ fm and$ A = 197 $ for gold [37], and$ \sigma_{NN} = 41 $ mb at RHIC energy [25].$ R_{AA} $ as a function of$ \bar{T}({\bf 0}) $ is shown in Fig. 4. The$ R_{AA} $ is above$ 0.9 $ if the central temperature$ T({\bf 0}) $ is lower than$ 1.6T_c $ , while it is below$ 0.8 $ when$ T({\bf 0}) $ is higher than$ 2.1T_c $ . We can expect that this effect is not negligible at the RHIC, and that it is considerable at the LHC. The factor$ x^3 $ in Eq. (11) arises from two facts: 1) more$ \Upsilon(1S) $ s are generated at the center of the fireball, and 2) the thickness changes slowly with the radius at the center of the fireball. Consequently,$ R_{AA} $ relies more on the survival probability P at the center of the fireball, i.e., at$ x_T = 0 $ . Therefore, the qualitative behavior of$ R_{AA} $ in Fig. 4 is similar to P in Fig. 2, and they are quantitatively similar when$ P(\bar{T}({\bf 0})) $ is large. From the hydrodynamics simulation, the initial maximum temperature is approximately$ 350 $ MeV at proper time$ \tau_0 = 0.6 $ fm/c, and it becomes$ 250 $ MeV at$ \tau = 2 $ fm/c, while the critical temperature in the same calculation is approximately$ 164 $ MeV [38]. We estimate that$ T({\bf 0}) $ is between these two values, and the corresponding$ \bar{T}({\bf 0}) $ is between$ 1.5 $ and$ 2.1 $ .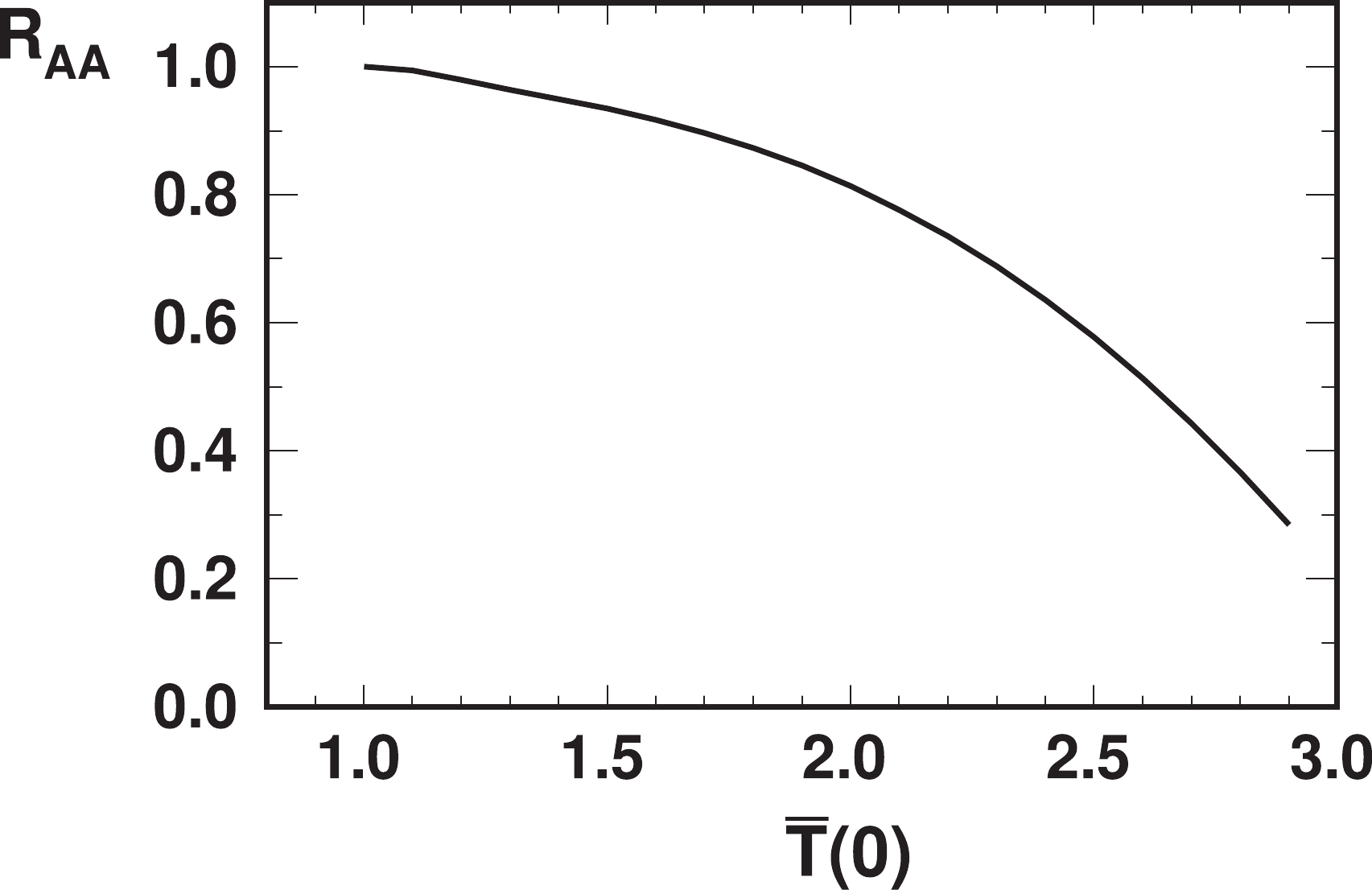
Figure 4. Nuclear modification factor
$ R_{AA} $ in central Au+Au collisions due to heating dissociation effect as a function of scaled temperature$ \bar{T}({\bf 0}) $ at center of fireball.We provide three remarks concerning this result. 1) Even if the width (or dissociation rate)
$ \Gamma $ vanishes at finite temperature, there is a fast heating dissociation effect for$ \Upsilon(1S) $ suppression, which was not carefully considered before. 2) If the width of$ \Upsilon(1S) $ is negligible as in some calculations, then the heating dissociation of$ \Upsilon(1S) $ can be used as a thermometer to detect the temperature of the fireball at an early time, and it is not sensitive to the temperature later on. It is necessary to clarify that such a temperature measured via$ \Upsilon(1S) $ should never be interpreted as the highest temperature of the fireball, but rather as the temperature felt by a$ \Upsilon(1S) $ . As a matter of fact, the highest temperature at a very early time is not well defined, and the change in the temperature at this time occurs so rapidly that the adiabatic theorem becomes invalid [39], which means that$ \Upsilon(1S) $ may not feel the temperature before it drops relatively slowly. Indeed, the most interesting temperature is not the high and short-lived temperature at the very beginning, but the temperature that can be felt by particles. In this sense, the$ \Upsilon(1S) $ -felt temperature of the medium is more meaningful. 3) The transverse momentum dependence of$ R_{AA} $ is trivial in the current model of this study. We leave further development to future studies. Some qualitative results can be expected. Because the screening is a response of the medium to color charges inside a quarkonium, it takes time to form a screening cloud. For a fast-moving quarkonium, the screening cloud can never fully catch up with the quarkonium, and the screening is weakened [40]. Fast heavy qurakonia also have a higher chance to move to a region with lower temperature or even outside the fireball, which is known as the leakage effect [41]. Consequently, we expect a weaker suppression for fast-moving quarkonia. -
In summary, we discussed a new mechanism concerning
$ \Upsilon(1S) $ dissociation, which is due to the fast heating process at the early stage of the fireball instead of a non-zero width in a steady hot medium. Because of such a fast heating dissocation, the suppression of$ \Upsilon(1S) $ is observable at RHIC energy even if the width of$ \Upsilon(1S) $ at a finite temperature is zero, and this mechanism may be used as a measure of the temperature of the fireball at early times.
Fast heating dissociation of ${ \Upsilon(1S) }$ in heavy ion collisions at RHIC
- Received Date: 2020-07-13
- Available Online: 2020-12-01
Abstract: By adopting the adiabatic assumption in the cooling process, we discuss a novel mechanism of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: