-
The color
$ SU(3) $ symmetry was initially introduced as a global symmetry to solve the spin-statistics problem of baryon wave functions but caused a new problem, namely, mesons should have color octet partners, which contradicts experiments. Furthermore, free quarks have never been observed in experiments. This motivates the color confinement conjecture that quarks can exist only in color singlet systems, namely, color singlet hadrons. After the global$ SU(3) $ color symmetry is gauged, the$ SU(3) $ gauge field theory is obtained – the quantum chromodynamics (QCD), which is very successful in explaining high energy processes and is believed to be the fundamental theory for the strong interaction. Unfortunately, confinement has not been directly derived from the first principles of QCD since QCD was established in the 1970s. There may be some important aspects that are ignored in the conventional treatment of QCD.Let us write the expression for the Lagrangian density of QCD of one flavor quark with mass
$ m $ $ {\cal{L}}_{\rm{QCD}} = -\frac{1}{2}{\rm{Tr}} F_{\mu\nu} F^{\mu\nu}+\bar{\psi}({\rm i} \not\!\!\! D -m)\psi, $

(1) where
$\not\!\!\! D$ means$ \gamma^\mu D_\mu $ ,$D_\mu = \partial_\mu-{\rm i}gA_\mu$ is the covariant derivative in the presence of gauge field$ A_\mu = A_\mu^a t^a $ , with$ g $ being the strong coupling, and$ F_{\mu\nu} = F_{\mu\nu}^a t^a $ is the strength tensor of the gauge field with$ F_{\mu\nu}^a = \partial_\mu A_\nu^a-\partial_\nu A_\mu^a+ gf^{abc}A^b_\mu A^c_\nu $ ($ f^{abc} $ denotes the structure constants of the$ SU(3) $ group; they are totally antisymmetric with respect to the interchange of color indexes$ a,b,c $ ). Evidently,$ {\cal{L}}_{\rm{QCD}} $ is invariant under the following global transformation:$ A\to UAU^\dagger, F\to UFU^\dagger, \psi\to U\psi, \bar{\psi}\to \bar{\psi}U^\dagger, $

(2) where
$ U\in SU(3) $ is an element of$ SU(3) $ . In other words, the global$ SU(3) $ symmetry does exist for QCD. According to Nöther's theorem, this continuous global symmetry should result in a conservation law$ \partial_\mu j^{a,\mu} = 0 $ , where$ j^{a,\mu} $ is the corresponding Nöther current:$ j^{a,\mu} = f^{abc}F^{b,\mu\nu}A^{c}_\nu+j_M^{a,\mu} $

(3) with
$ j_M^{a,\mu} = \bar{\psi}t^a\gamma^\mu\psi $ being the matter current of quarks. In fact, the current conservation relation is equivalent to the equation of motion of the gauge fields:$ ([D_\mu, F^{\mu\nu}])^a\equiv \partial_\mu F^{a,\mu\nu}+gf^{abc}F^{b,\nu\mu}A_\mu^c = -gj^{a,\nu}_M. $

(4) One can observe this by applying
$ \partial_\nu $ on the two sides of the above equation. These are well-known results. Conventionally, the Nöther current and its physical consequence have been rarely discussed in formal terms given that$ j^{a,\mu} $ depends explicitly on gauge field$ A_\mu^a $ , which is gauge dependent.However, this is not the whole story because the non-Abelian characteristic of
$ SU(3) $ depicted by the antisymmetric structure constants,$ f^{abc} $ , has more implications. Imagine that a quark current of$ a_0 $ type, namely$ j_M^{a_0,\mu} $ , is put into the vacuum. If the color field it generates through the field equation expressed by Eq. (4) has the following property:$ A_\mu^a(x;j^{a_0}_M) = V_\mu(x)\delta^a_{a_0}, $

(5) then the first term of the total Nöther current in Eq. (3) vanishes owing to the asymmetric
$ f^{abc} $ , resulting in$ j^{a,\mu} = j^{a_0,\mu}_M \delta^a_{a_0} $ , which is free from gauge dependence. Under this condition, it is easy to prove that the corresponding Nöther charge,$Q^a = \int {\rm d}^3 {\bf{x}}j^{a,0} = \delta^a_{a_0}\int {\rm d}^3{\bf{x}}j^{a_0,0}_M$ , is conserved, namely,$ \frac{{\rm d}}{{\rm d}t}Q^a = -\int {\rm d}^3{\bf{x}}\nabla\cdot {\bf{j}}^{a} = -\delta^a_{a_0}\int {\rm d}^3{\bf{x}}\nabla\cdot {\bf{j}}_M^{a_0} = 0, $

(6) if the boundary condition
$ \psi({\bf{x}} = \infty,t) = 0 $ is assumed. Alternatively, we can treat the condition expressed by Eq. (5) as an implicit constraint so that the Nöther current is physically meaningful. The direct consequence of this constraint is that the color current of matter fields,$ j_M^{a,\mu} $ , is conserved.With the constraint expressed by Eq. (5), the equation of motion given by Eq. (4) can be simplified as
$ \partial_\mu f^{\mu\nu} = -gj_M^{a_0,\nu}, $

(7) where
$ f_{\mu\nu} = \partial_\mu V_\nu-\partial_\nu V_\mu $ . The Bianchi identity also gives$ \partial_\mu \tilde{f}_{\mu\nu} = 0 $ with$ \tilde{f}_{\mu\nu} = \dfrac{1}{2}\epsilon_{\mu\nu\rho\delta}f^{\rho\delta} $ . These equations are very similar to Maxwell's equations of QED. The solution of Eq. (7) can be written as$ f_{\mu\nu} = f_{1,\mu\nu}+f_{0,\mu\nu}, $

(8) where
$ f_{1,\mu\nu} $ is a special solution of Eq. (4), and$ f_{0,\mu\nu} $ is the general solution of the homogeneous equation$ \partial_\mu f^{\mu\nu} = 0 $ . If we are constricted to the static case, then$ f_{0,\mu\nu} $ can take the following form:$ f_{0,\mu\nu}\propto g\sigma (n_{1,\mu} n_{2,\nu}-n_{2,\mu} n_{1,\nu}), $

(9) where
$ \sigma $ is a constant of dimension two,$ n_1^\mu $ and$ n_2^\nu $ are two constant Lorentz unit vectors, and the gauge coupling appearing here is just a convention. Given that we do not know how the color charge is quantified at present, we use the proportional sign in the above and following relations. Consequently, the scalar product of$ f_{0,\mu\nu} $ can be expressed in terms of$ n_{1,2} $ as$ f_{0,\mu\nu}f_0^{\mu\nu}\propto 2g^2\sigma^2\left[n_1^2 n_2^2-(n_1\cdot n_2)^2 \right]. $

(10) When
$ n_1^\mu $ and$ n_2^\mu $ are light-like, for instance,$ n_1^2 = n_2^2 = 0 $ , and satisfy$ n_1\cdot n_2 = 1 $ , we have$ f_{0,\mu\nu}f_0^{\mu\nu}\propto - 2g^2\sigma^2 $ .To determine the solution of Eq. (9), we would like to consider the proper boundary conditions. Evidently, the discussion above also applies to QED. In the static case, the electromagnetic field strength,
$ F^{\mu\nu}_{\rm{QED}}({\bf{x}}) $ behaves as$ F_{\mu\nu}({\bf{x}}) \sim 1/|{\bf{x}}|^2 $ when$ |{\bf{x}}|\to \infty $ , such that it is natural to set$ \sigma = 0 $ for QED. However, for a non-Abelian gauge field theory such as QCD, the vacuum is highly nontrivial and there is no ab initio requirement that$ F_{\mu\nu}({\bf{x}}) $ vanishes at an infinite point. Therefore,$ \sigma $ can take a non-zero value. In fact, the highly nontrivial QCD vacuum is reflected by the topology, the trace anomaly, and the non-zero condensates of quarks and gluons; an example of this is the gluon condensate$ \langle \alpha_s F_{\mu\nu}^a F^{a,\mu\nu}\rangle \ne 0 $ , which permits the possibility of a non-zero$ \sigma $ .By contrast, one can find that
$ F_{\mu\nu}\propto f_{0,\mu\nu}\sum\limits_a t^a $ is a non-trivial solution of the vacuum field equation$ [D_\mu,F_{\mu\nu}] = 0 $ and is uniform in both the space-time and the color space. The vacuum expectation value of the scalar product of this field is$ \langle {\rm{Tr}} F^2\rangle \propto -8 g^2 \sigma^2 $ , which means that$ \sigma $ has a direct connection with the gluon condensate. Thus, field$ f_{0,\mu\nu} $ , generated by color current$ j_M^{a_0,\mu} $ , can be considered to be vacuum field$ F_{\mu\nu} $ uniformly polarized to the$ a_0 $ type through$ f_{0,\mu\nu}\propto 2 {\rm{Tr}} F_{\mu\nu}t^{a_0} $ .Now, let us consider the free energy of a color charge. In the rest frame of a color charge of type
$ a_0 $ ,$ n_1^\mu $ and$ n_2^\mu $ can be chosen to be$ n_1 = (1,{\bf{e}}_1) $ and$ n_2 = (1,{\bf{e}}_2) $ , respectively, where$ {\bf{e}}_{1,2} $ are arbitrary spatial unit vectors with$ {\bf{e}}_1\perp {\bf{e}}_2 $ . According to Eq. (9), we have the corresponding uniform chromo-electric and chromo-magnetic field strengths:$ {\bf{E}}^{a_0}_0 \propto g\sigma({\bf{e}}_1-{\bf{e}}_2),\; \; \; {\bf{B}}^{a_0}_0\propto g\sigma({\bf{e}}_2\times {\bf{e}}_1), $

(11) which obey the normal parity transformation property and satisfy
$ {\bf{E}}^{a_0}_0\cdot{\bf{B}}_0^{a_0} = 0 $ (no$ CP $ violation). Their distribution is illustrated in Fig. 1. These expressions are in exact agreement with the conservation of color charge in that for an arbitrary closed spatial surface$ \Gamma $ surrounding the color charge, the total flux of the polarized vacuum field outward is zero. We use$ {\bf{E}}^{a_0}_1 $ and$ {\bf{B}}^{a_0}_1 $ to denote the field strength given by the solution$ f_{1,\mu\nu} $ in Eq. (8). Thus, the energy of the color field generated by the color charge is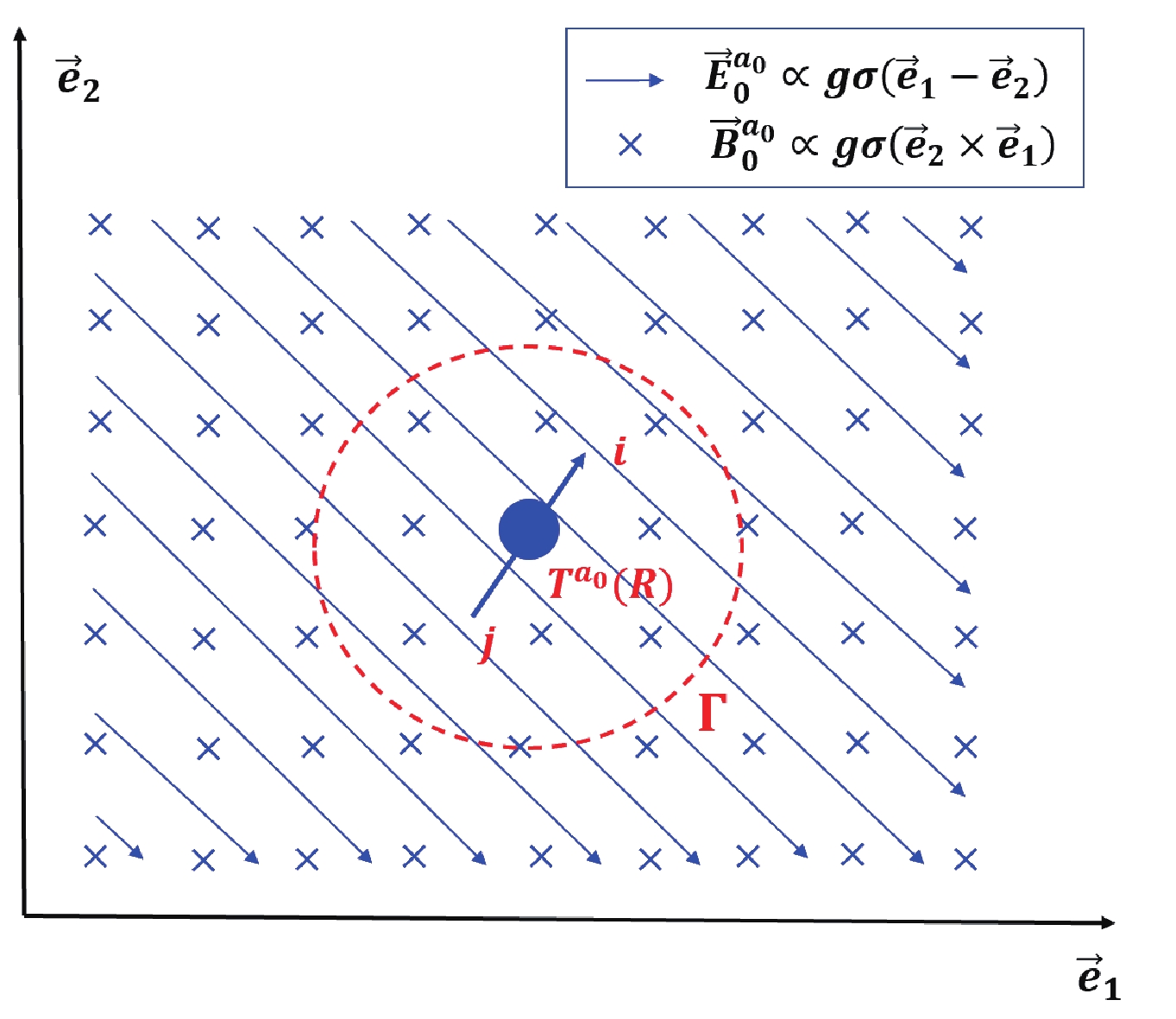
Figure 1. (color online) Schematic plot of the distribution of uniform color fields
$ {\bf{E}}^{a_0}_0 $ and$ {\bf{B}}^{a_0}_0 $ generated by charge$ T^{a_0}(R) $ . The arrowed straight lines illustrate the uniform$ {\bf{E}}^{a_0}_0 $ oriented in the$ {\bf{e}}_1-{\bf{e}}_2 $ direction, whereas the '$ \times $ 's denote the uniform$ {\bf{B}}^{a_0}_0 $ oriented in the$ {\bf{e}}_2\times{\bf{e}}_1 $ direction. Indexes$ i,j $ stand for the components of the color charge in the$ R $ representation. The dashed circle$ \Gamma $ illustrates an arbitrary closed surface surrounding the charge. It is easy to see that the total field flux outward from$ \Gamma $ vanishes.$ E_f\propto\int {\rm d}^3{\bf{x}} \frac{1}{2}\left[ ({\bf{E}}^{a_0}_0+{\bf{E}}^{a_0}_1)^2+ ({\bf{B}}^{a_0}_0+{\bf{B}}^{a_0}_1)^2\right], $

(12) which is, by definition, the free energy of the color charge. Note that
$ {\bf{E}}^{a_0}_1 $ and$ {\bf{B}}^{a_0}_1 $ behave as$ O(1/|{\bf{x}}|^2) $ when$ |{\bf{x}}|\to \infty $ . The leading term of$ E_f $ is$ \dfrac{3}{2} g^2\sigma^2 V $ , where$ V\to \infty $ is the total spatial volume (It is understood that$ {\bf{E}}_1^{a_0} $ and$ {\bf{B}}_1^{a_0} $ are properly regularized in the ultraviolet region.). In other words, the free energy of an isolated color charge is infinitely large. Lattice QCD confirms this through the observation that the vacuum expectation value of the Polyakov loop,$ L $ , is zero in the confinement phase, that is,$ \langle L\rangle \sim e^{-E_fT} = 0 $ , where$ T $ is the temporal extension of the lattice. Therefore, isolated color charges, such as quarks and color octet mesons, do not exist. This is exactly the color confinement argument. The above discussion can be simply extended to the color field generated by current$ j^{a,\mu}t^a $ , whose strength is$ F_{\mu\nu}\propto (f_{1,\mu\nu}+f_{0,\mu\nu})\sum\limits_a t^a $ .Next, we elaborate on the discussion presented above. First, the color charge providing color current
$ j^{a,\mu}_M $ can be point-like or be a spatially extended object composed of several subsystems of irreducible representations (irreps)$ R_1, R_2,\ldots $ . According to the representation theory of the$ SU(3) $ group,$ R_1\otimes R_2\otimes \cdots \to R_1'\oplus R_2' \oplus R_3'\oplus \cdots, $

(13) and the representation of the color charge can be any one of the irreps
$ R'_i $ . The global color symmetry and the conservation law expressed by Eq. (6) require that the whole system keep its color state of$ R'_i $ , regardless of how complicated the microscopic internal structure is. Except for the color singlet, the vacuum will be polarized with respect to the current of$ R'_i $ such that the free energy of the color charge becomes infinite. Second, a color singlet system does not provide a color current and, therefore, does not interact with the vacuum color field. It can move freely in the unpolarized color vacuum.Given that color charges exist only in color singlets, we now consider the simplest case for a color singlet system, that is, to be composed of a color charge in the
$ R $ representation and an anti-color charge in conjugate representation$ R^* $ of$ R $ , with the dimension of the representation denoted by$ d_R $ . We can treat this system as the$ R^* $ charge scatters against$ R $ charge through the color field generated by the$ R $ charge, as shown in Fig. 2. If the initial and final states of the$ R $ charge have color indexes$ i,j $ , respectively, with$ i,j = 1,2,\ldots, d_R $ , then the color charge of$ R $ is$ g\sum\limits_a (T_R^{a})_{ji} $ , where$ T_R^{a} $ is the representation matrix of the generators of$ SU(3) $ in the$ R $ irreps. Similarly, the color charge of$ R^* $ is$ g\sum\limits_b (T_{R^*}^{b})_{nm} $ , with$ m,n = 1, 2,\ldots, d_R $ being the indexes of the initial and final states of the$ R^* $ charge. Withrespect to the relation$ T_{R^*}^a = -(T_R^a)^* $ and$ T^{a}_R = T^{a,\dagger}_R $ , the color singlet requires that their interaction should be proportional to
Figure 2. (color online) Interaction of the color charges of representations
$ R $ and$ R^* $ in a color singlet. Imagine that$ R $ and$ R^* $ are produced at origin$ O $ ; then,$ R^* $ moves to$ {\bf{r}} $ . The initial and final color states of$ R(R^*) $ are labeled as$ i,j (m,n) $ , respectively. Thus, the color wave functions of the initial and final states of singlet$ RR^* $ are$\dfrac{\delta_{im}}{\sqrt{d(R)} }$ and$\dfrac{\delta_{jn}}{\sqrt{d(R)} }$ , respectively. If we choose$ {\bf{e}}_1 = {\bf{e}}_r $ and$ {\bf{e}}_2 = {\bf{e}}_\theta $ , then the uniform chromo-electric field does work,$ \Delta E = -C_2(R)g^2\sigma r $ , regardless of the path,$ C $ , along which$ R^* $ moves from$ O $ to$ {\bf{r}} $ .$ \sum\limits_{a,b} (T_R^a)_{ji}(T_{R^*}^b)_{nm}\frac{\delta_{im}}{\sqrt{d_R}}\frac{\delta_{jn}}{\sqrt{d_R}} = -\frac{1}{d_R}\sum\limits_{a}(T_R^a)_{ji}(T_{R}^{a})_{ij} = -C_2(R), $

(14) where
$ C_2(R) $ is the eigenvalue of the second order Casimir operator of the$ SU(3) $ group in the$ R $ irreps, and the minus sign implies that the interaction between the$ R $ and$ R^* $ charges is attractive. In QED, the equation of motion of an electric charge$ q $ in an external field$ F^{\mu\nu}_{\rm{QED}} $ is$\dfrac{{\rm d}p^\mu}{{\rm d}\tau} = qF^{\mu\nu}_{\rm{QED}}u_\nu$ , where$ p^\mu = (E,{\bf{p}}_{\rm{kin}}) $ is the energy- momentum vector of the charge,$ {\bf{p}}_{\rm{kin}} $ is the kinetic momentum, and$u^\mu = \dfrac{{\rm d}x^\mu}{{\rm d}\tau}$ is its velocity vector. Similarly, the motion of equation of the$ R^* $ charge in the field of the$ R $ charge can be written as$ {{\rm d}p^\mu}\propto -g C_2(R) (f_{1}^{\mu\nu}+f_0^{\mu\nu}){\rm d}x_\nu. $

(15) In the rest frame of the
$ R $ charge with the$ R $ charge located at the origin, we can take$ u^\mu = (1,{\bf{v}}) $ . If we ignore$ f_1^{\mu\nu} $ temporarily, according to Eqs. (9) and (11), we obtain$ {\rm d}E = -C_2(R)g^2\sigma({\bf{e}}_1-{\bf{e}}_2)\cdot {\rm d}{\bf{r}}. $

(16) Based on the discussion above,
$ {\bf{e}}_1 $ and$ {\bf{e}}_2 $ are originally arbitrary spatial unit vectors. As shown in Fig. 2, if we imagine that the$ R^* $ charge moves from the origin to point$ {\bf{r}} $ , then$ {\bf{e}}_r $ is a special direction. Thus, we can choose$ {\bf{e}}_1 = {\bf{e}}_r $ and$ {\bf{e}}_2 = {\bf{e}}_\theta $ , with$ {\bf{e}}_\theta \perp {\bf{e}}_r $ . If$ R^* $ moves from origin$ O $ to$ {\bf{r}} $ through an arbitrary path$ C $ , then the energy change is$ \Delta E = -C_2(R)g^2\sigma \int\limits_{{\bf{0}},C}^{{\bf{r}}}{\rm d}{\bf{r}}'\cdot({\bf{e}}_r-{\bf{e}}_\theta) = -C_2(R)g^2\sigma r, $

(17) where
$ r = |{\bf{r}}| $ , and the proportional relation is replaced by the equal relation, with$ \sigma>0 $ being a parameter to be determined. This means that the chromo-electric field does negative work. The conservation of energy requires that the (kinetic) energy loss be reserved in other types of energy. Given that$ \Delta E $ is independent of path$ C $ , we can interpret this energy type as potential energy$ V(r) $ . Now, taking into account the Coulomb potential energy generated by the point-like color charge$ R $ , the total potential is$ V(r) = V_0-C_2(R) \frac{\alpha_s}{r}+C_2(R)g^2\sigma r, $

(18) where
$ \alpha_s = \dfrac{g^2}{4\pi} $ . This is exactly the Cornell potential. It is very interesting to observe that the potential has a property of 'Casimir scaling' wherein the coefficients of the Coulomb part and the linear part are proportional to$ C_2(R) $ . The Cornell potential and the Casimir scaling have been observed for a long time in lattice QCD calculations [1]. Here, we report their first decent derivation.The effect of the chromo-magnetic field on color charge
$ R^* $ is very similar to a uniform magnetic field on an electric charge. According to Eq. (11), the chromo-magnetic field is oriented perpendicularly to the$ ({\bf{e}}_r,{\bf{e}}_\theta) $ plane such that it does not do work to charge$ R^* $ . With the presence of the chromo-magnetic field, kinetic momentum$ {\bf{p}}_{{\rm{kin}}} $ is related to canonical momentum$ {\bf{p}} $ and the vector potential as$ {\bf{p}}_{{\rm{kin}}} = {\bf{p}}+g C_2(R){\bf{V}}, $

(19) where
$ {\bf{V}} $ is the spatial component of$ V_\mu $ . According to Eq. (9) and$ f_{\mu\nu} = \partial_\mu V_\nu-\partial_\nu V_\mu $ , we obtain$ V_{\mu} = \frac{1}{2}g\sigma\left[n_1\cdot (x-x_0) n_{2,\mu}-n_2\cdot (x-x_0) n_{1,\mu}\right]. $

(20) If charge
$ R^* $ is at$ {\bf{r}} $ , where$ x^\mu = (0,{\bf{r}}) $ and$ x_0^\mu = (0,{\bf{0}}) $ , we obtain$ {\bf{V}} = \frac{1}{2}g\sigma y {\bf{e}}_x-\frac{1}{2}g\sigma x {\bf{e}}_y , $

(21) where
$ {\bf{e}}_x $ and$ {\bf{e}}_y $ are the orientation vectors of the$ x $ -axis and$ y $ -axis in the$ ({\bf{e}}_r,{\bf{e}}_\theta) $ plane, respectively. Thus, the$ p_{{\rm{kin}},x,y} $ and$ p_{x,y} $ are related as$ \begin{aligned}[b] &p_{{\rm{kin}},x} = p_x+\dfrac{1}{2}g^2C_2(R)\sigma y\\ &p_{{\rm{kin}},y} = p_y-\dfrac{1}{2}g^2C_2(R)\sigma x .\end{aligned} $

(22) Considering the quantum effects, the momentum and the coordinate are operators and satisfy the canonical commutation relation
$ [x_i,p_i] = i $ . When the kinetic momentum is much smaller than the potential in magnitudes, that is,$ |{\bf{p}}_{{\rm{kin}}}|\ll |gC_2(R){\bf{V}}| $ , we have$ [x,y] = -i\frac{2}{C_2(R)g^2\sigma}, $

(23) which means that the coordinates in the
$ ({\bf{e}}_r,{\bf{e}}_\theta) $ plane are non-commutative and have the following uncertainty relation:$ \Delta x \Delta y\sim \frac{2}{C_2(R)g^2\sigma}. $

(24) The uncertainty relation implies that a hadron has a minimal projected area of
$ \dfrac{2}{C_2(R)g^2\sigma} $ in the$ ({\bf{e}}_r,{\bf{e}}_\theta) $ plane and, therefore, presents a minimal size. According to lattice QCD and phenomenological results of the string tension of the$ Q\bar{Q} $ system,$ \sigma_{\rm Q\bar{Q}} = \frac{4}{3}g^2 \sigma \sim 0.2 ({\rm{GeV}})^2, $

(25) and the minimal size of a hadron can be estimated as
$ r_{\rm{h}}\sim \sqrt{(\Delta x)^2 +(\Delta y)^2}\geqslant\sqrt{2\Delta x \Delta y}\sim\frac{2}{\sqrt{\sigma_{Q\bar{Q}}}}\sim 0.89\; {\rm{fm}}. $

(26) This minimal size subsequently yields an estimate of the minimal energy of a hadron. Considering a color singlet
$ q\bar{q} $ system of a spatial volume$ V $ and referring to Eq. (18), the mean charge of the (anti) quark can be taken as$ \sqrt{C_2(F)} $ , where$ C_2(F) = 4/3 $ . If the Coulomb part is ignored again, the color field strength around the (anti) quark is$ {\bf{E}}_0 = g\frac{2}{\sqrt{3}}\sigma({\bf{e}}_1-{\bf{e}}_2),\; \; \; {\bf{B}}_0 = g\frac{2}{\sqrt{3}}\sigma({\bf{e}}_2\times {\bf{e}}_1), $

(27) such that the minimal energy in the volume is
$ E_{\min} = \int\limits_V {\rm d}^3 {\bf{x}} \frac{1}{2}({\bf{E}}_0^2+{\bf{B}}_0^2)\sim \frac{3\sqrt{\sigma_{Q\bar{Q}}}}{8\alpha_s} , $

(28) which gives
$ E_{\min}\sim 550 $ MeV if$ \alpha_s \sim 0.3 $ . This is a very rough but somewhat reasonable estimate.The global
$ SU(3) $ color symmetry has further implications. As isolated color charges do not exist, it is reasonable to assume that the whole universe is in a color singlet. Therefore, when an objective color charge of irrep$ R $ is considered, one must keep in mind that it is not isolated but coexists with a system, namely, the residual world of conjugate irrep$ R^* $ . This is somewhat a type of color interference or color entanglement. The global symmetry requires that however complicated the residual world may be, its effects on objective charge$ R $ are equivalent to that of charge$ R^* $ . The logic is illustrated in Fig. 3. The fundamental degrees of freedom of QCD are quarks, antiquarks, and gluons, which are the$ {\bf{3}} $ ,$ {\bf{3}}^* $ , and$ {\bf{8}} $ irreps of the color$ SU(3) $ group, respectively, as expressed by the Young diagrams in the first row of Fig. 3. For a color singlet$ q\bar{q}q\bar{q} $ system (diagram$ (a) $ in the second row), the remaining part of the system (red blocks), except for an objective quark (blue block), acts as a$ {\bf{3}}^* $ charge composed of an antiquark and a singlet$ q\bar{q} $ block, as described by diagram ($ b $ ). Diagram ($ c $ ) shows that the color singlet$ q\bar{q} $ can escape from the system freely, and the residual$ q $ and$ \bar{q} $ compose a color singlet$ q\bar{q} $ meson. This discussion can be extended to any color singlet system made up of many colored objects that can be reduced iteratively following the above logic. In this sense, the possible irreducible color singlet configurations are$ q\bar{q} $ (meson),$ qqq $ (baryon),$ \bar{q}\bar{q}\bar{q} $ (anti-baryon),$ q\bar{q}g $ (hybrid meson),$ qqqg $ (hybrid baryon),$ gg $ ,$ ggg $ (glueballs), etc., as shown in the third row of Fig. 3. If we treat the components of the above list of irreducible color singlets as constituent (anti) quarks and gluons, then their number might be good quantum numbers in the picture of the global color symmetry. Overall, if there are no other mechanisms, compact multiquark configurations are disfavored, except for hadronic molecules bound by the residual strong interaction between color singlet objects.
Figure 3. (color online) First row: Young diagrams for a quark
$ q({\bf{3}}) $ , an antiquark$ \bar{q}({\bf{3}}^*) $ , and a gluon$ g({\bf{8}}) $ . Second row: diagram ($ a $ ) represents a$ q\bar{q}q\bar{q} $ color singlet system. Diagram ($ b $ ) implies that for an objective quark (the blue block), the remaining parts act as a$ {\bf{3}}^* $ charge composed of an antiquark and a color singlet$ q\bar{s} $ . Diagram$ (c) $ shows that the color singlet$ q\bar{q} $ escapes from the system such that the objective quark feels only the field generated by the antiquark and results in a$ q\bar{q} $ meson. The third row shows some of the minimal irreducible color singlets composed of (anti)quarks and gluons according to the meaning of the global$ SU(3) $ color symmetry.To summarize, the global
$ SU(3) $ color symmetry has physical significance. If the color field generated by a color current of type$ a_0 $ satisfies$ A_\mu^a = V_\mu\delta_{a_0}^a $ , then the Nöther current is gauge independent and is actually governed by the matter current of this charge, which is conserved in the conventional meaning. There does exist a solution to the equation of motion of the color field under this constraint, whose strength has a uniform part owing to the nontrivial QCD vacuum and the nonzero gluon condensate. Consequently, a system with a net color charge has an infinitely large free energy and, therefore, cannot exist freely, as required by the color confinement argument. Following this logic, the potential between a static color charge and an anti color charge is derived to be exactly the Cornell type and satisfies the Casimir scaling observed by lattice QCD. For a color singlet system, such as a hadron, the uniform chromo-magnetic field also implies that the system has a minimal size and minimal energy. Furthermore, as quarks and gluons are fundamental degrees of freedom of QCD, the global$ SU(3) $ color symmetry requires that the possible irreducible color singlet systems can only be$ q\bar{q} $ ,$ qqq $ ,$ gg $ ,$ ggg $ ,$ q\bar{q}g $ ,$ qqqg $ , etc., such that a bound multi-quark system beyond the above configurations can only exist as a hadron molecule if there are no other binding mechanisms.
HTML
-
The author also acknowledges the support of the CAS Center for Excellence in Particle Physics (CCEPP).






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: