-
Leptonic decays of charmed mesons offer a clean and direct approach to understand weak decays of the
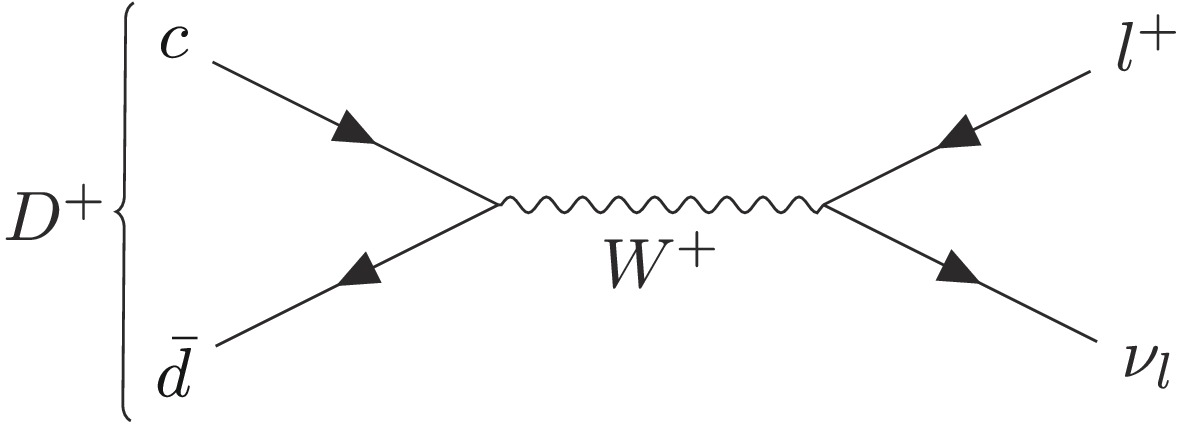
$ c $ quark (see, e.g., [1] for a recent review). The leptonic decays$ D^+\to \ell^+\nu_\ell $ ($ \ell=e $ ,$ \mu $ , or$ \tau $ ) occur via the annihilation of the$ c $ and$ \bar{d} $ quarks into an$ \ell^+\nu_\ell $ mediated by a virtual$ W^+ $ boson, as depicted in Fig. 1. The weak and strong interaction effects factorize, which leads to a simple expression for the partial decay width of$ D^+ \to \ell^+\nu_\ell $ at the lowest order in the Standard Model (SM). It is proportional to the product of the decay constant$ f_{D^+} $ , which characterizes the strong-interaction effects between the initial-state quarks, and magnitude of the Cabibbo-Kobayashi-Maskawa (CKM) matrix element$ |V_{cd}| $ , representing the$ c\to d $ flavor-changing interaction. In the SM, the decay width can be written as [2]$ \Gamma_{D^+\to\ell^+\nu_\ell}=\frac{G_{\rm F}^2}{8\pi}|V_{cd}|^2 f^2_{D^+} m_\ell^2 m_{D^+} \left (1-\frac{m_\ell^2}{m_{D^+}^2} \right )^2, $

(1) where
$G_{\rm F}$ is the Fermi coupling constant,$ m_\ell $ is the lepton mass, and$ m_{D^+} $ is the$ D^+ $ mass. Thus, the ratio of branching fractions between different lepton channels depends only on the lepton masses and is accurately predicted to be$ e^+\nu_{e}:\mu^+\nu_{\mu}:\tau^+\nu_{\tau} = 2.35\times10^{-5}:1:2.67, $

(2) with negligible uncertainty. Any observation of violation of this relation indicates new physics beyond the SM.
The
$ D^+\to e^+\nu_e $ decay, with an expected branching fraction lower than$ 10^{-8} $ , has not yet been observed experimentally. The CLEO Collaboration searched for$ D^+\to e^+\nu_e $ [3] and reported an upper limit of the branching fraction of$ 8.8\times10^{-6} $ at the 90% confidence level using 818 pb$ ^{-1} $ of the$ \psi(3770) $ data. In this study, we search for$ D^+\to e^+\nu_e $ by using 20.3 fb$ ^{-1} $ of$ e^+e^- $ collision data [4, 5], approximately 25 times larger than that of the CLEO measurement, collected with the BESIII detector at the center-of-mass energy of 3.773 GeV. Charge-conjugate modes are always implied throughout the text. -
The BESIII detector [6] records symmetric
$ e^+e^- $ collisions provided by the BEPCII storage ring [7] operating in the center-of-mass energy ($ \sqrt{s} $ ) range of 1.84 to 4.95 GeV, with a peak luminosity of$ 1.1 \times 10^{33}\;\text{cm}^{-2}\text{s}^{-1} $ achieved at$ \sqrt{s} = 3.773\;\text{GeV} $ . BESIII has collected large data samples in this energy region [8−10]. The cylindrical core of the BESIII detector covers 93% of the full solid angle and consists of a helium-based multilayer drift chamber (MDC), plastic scintillator time-of-flight system (TOF), and CsI (Tl) electromagnetic calorimeter (EMC), which are enclosed in a superconducting solenoidal magnet providing a magnetic field of 1.0 T. The solenoid is supported by an octagonal flux-return yoke with resistive plate counter muon identification modules interleaved with steel. The charged-particle momentum resolution at$ 1\; {\rm{GeV}}/c $ is 0.5%, while the$ {\rm{d}}E/{\rm{d}}x $ resolution is 6% for electrons from Bhabha scattering. The EMC measures photon energies with a resolution of 2.5% (5%) at$ 1 $ GeV in the barrel (end-cap) region. The time resolution in the TOF barrel region is 68 ps, while that in the end-cap region is 110 ps. The end-cap TOF system was upgraded in 2015 using a multigap resistive plate chamber technology, providing a time resolution of 60 ps [11−13]. Approximately 85% of the data used here benefit from this upgrade. -
Monte Carlo (MC) simulated data samples produced with the GEANT4-based [14] software package, which includes the geometric description of the BESIII detector and detector response, are used to determine detection efficiencies and estimate backgrounds. The simulation models the beam energy spread and initial state radiation (ISR) in the
$ e^+e^- $ annihilations with the generator KKMC [15]. The inclusive MC sample includes the production of$ D\bar{D} $ pairs (and treats quantum coherence for the neutral$ D $ channels), non-$ D\bar{D} $ decays of the$ \psi(3770) $ , ISR production of the$ J/\psi $ and$ \psi(3686) $ states, and continuum processes incorporated in KKMC [15, 16]. All particle decays are modelled with EVTGEN [17, 18] using branching fractions either obtained from the Particle Data Group (PDG) [19] when available, or otherwise estimated with LUNDCHARM [20]. Final state radiation (FSR) from charged final state particles is incorporated using PHOTOS [21]. The leptonic decay$ D^{+}\to e^{+}\nu_{e} $ is simulated with the SLN model [22]. A signal MC sample comprising 5 million simulated signal events is used to determine the selection efficiencies and model the signal shape. -
The process
$ e^{+}e^{-} \to \psi\; (3770) \to D^{+}D^{-} $ , without accompanying hadrons, allows studies on$ D^+ $ decays with a double tag technique [1, 23]. There are two types of samples used in this technique: single tag (ST) and double tag (DT). In the ST sample, a$ D^- $ meson is reconstructed via the six hadronic decay modes of$ D^-\to K^{+}\pi^{-}\pi^{-} $ ,$ K^0_{S}\pi^{-} $ ,$ K^{+}\pi^{-}\pi^{-}\pi^{0} $ ,$ K^0_{S}\pi^{-}\pi^{0} $ ,$ K^0_{S}\pi^{+}\pi^{-}\pi^{-} $ , and$ K^{+}K^{-}\pi^{-} $ . In the DT sample, both charged$ D $ mesons in the event are reconstructed: a ST$ D^- $ and signal$ D^+ \to e^+ \nu_e $ decay reconstructed with the remaining tracks.The branching fraction of the
$ D^+\to e^+\nu_{e} $ decay is determined by$ {\mathcal B}_{D^+\to e^+\nu_{e}} = \frac{N_{\rm{DT}}}{N^{\rm{tot}}_{\rm{ST}} \bar \epsilon_{\rm{sig}}}, $

(3) where
$ N_{\rm{ST}}^{\rm{tot}} $ is the total yield of ST$ D^- $ mesons,$ N_{\rm{DT}} $ is the DT yield, and$ \bar \epsilon_{\rm{sig}} $ is the averaged signal efficiency weighted by the ST yields of the$i^{\rm th}$ tag mode in the data. This efficiency is calculated as$ { \bar{{\mathcal \epsilon}}_{\rm{sig}} = \frac{\sum_i (N^i_{\rm{ST}} \, \epsilon^i_{\rm{DT}}/\epsilon^i_{\rm{ST}})}{N^{\rm{tot}}_{\rm{ST}}},} $

(4) where
$ N^i_{\rm{ST}} $ is the number of ST$ D^- $ mesons for the$ i^{\rm th} $ tag mode in the data,$ \epsilon^i_{\rm{ST}} $ is the efficiency of reconstruction of the ST mode$ i $ , and$ \epsilon^i_{ \rm DT} $ is the efficiency of finding the tag mode$ i $ and$ D^+\to e^+\nu_{e} $ decay simultaneously. -
All charged tracks detected in the MDC must satisfy
$ |\cos\theta|<0.93 $ , where$ \theta $ is the polar angle with respect to the$ z $ -axis, which is the symmetry axis of the MDC. For charged tracks not originating from$ K_S^0 $ decays, the distance of closest approach to the interaction point (IP) is required to be smaller than 1 cm in the transverse plane, and smaller than 10 cm along the$ z $ -axis. Particle identification (PID) for charged tracks combines the$ {\rm{d}}E/{\rm{d}}x $ measurement in the MDC with the time of flight measurement of the TOF to define the likelihood function$\mathcal{L}(h)\; (h= K,\pi, e)$ for each particle ($ h $ ) hypothesis. Charged kaons and pions are identified by requiring$ \mathcal{L}(K)>\mathcal{L}(\pi) $ and$ \mathcal{L}(\pi)>\mathcal{L}(K) $ , respectively, while positron candidates must satisfy$ \mathcal{L}(e)>0.001 $ and$ \mathcal{L}(e) $ /($ \mathcal{L}(e)+\mathcal{L}(K)+\mathcal{L}(\pi) $ )$ > $ 0.8. To further reduce misidentifications between positrons and hadrons, we require$ E/p>0.8 $ , where$ E $ is the energy deposit in the EMC from the track and$ p $ is its momentum reconstructed in the MDC. To partially recover the energy loss due to FSR and bremsstrahlung, the four-momenta of photon(s) within 5° of the initial positron direction are added to the positron candidate's four-momentum.The
$ K_{S}^0 $ candidates are reconstructed from pairs of oppositely charged tracks, each with a distance of closest approach to the IP smaller than 20 cm along the$ z $ -axis. The tracks are assigned as$ \pi^+\pi^- $ without imposing any PID criteria. They are constrained to originate from a common vertex and are required to have an invariant mass within$ (0.487,0.511) $ GeV/$ c^2 $ . The decay length of the$ K^0_S $ candidate is required to be larger than twice the vertex resolution away from the IP. The quality of both primary and secondary vertex fits is ensured by requiring$ \chi^2 $ $ < $ 100. The fitted$ K_S^0 $ four-vectors are used for later kinematic calculations.The photon candidates are reconstructed from isolated EMC showers. The deposited energy of each shower in the end-cap region (
$ 0.86 <| \cos \theta|< 0.92 $ ) and in the barrel region ($ | \cos \theta|< 0.80 $ ) must be larger than 50 MeV and$ 25 $ MeV, respectively. To exclude showers that originate from charged tracks, the angle subtended by the EMC shower and position of the closest charged track at the EMC must be larger than$ 10^\circ $ as measured from the IP. The difference between the EMC time and event start time is required to be within [0, 700] ns to suppress electronic noise and showers unrelated to the event.The
$ \pi^0 $ candidates are reconstructed from photon pairs with a$ \gamma\gamma $ invariant mass within$ (0.115,0.150) $ GeV$ /c^{2} $ . A mass-constrained (1C) fit is imposed constraining the$ \gamma\gamma $ invariant mass to the$ \pi^{0} $ nominal mass [19] to improve the momentum resolution.$ \chi^2 $ must be smaller than 50. The four-momentum of the$ \pi^0 $ candidate updated by the fit is used for further analysis. -
To separate ST
$ D^- $ mesons from combinatorial backgrounds, we utilize two kinematic observables, the energy difference$ \Delta E\equiv E_{D^-}-E_{\mathrm{beam}} $ and beam-constrained mass$ M_{\rm{BC}}\equiv\sqrt{E_{\mathrm{beam}}^{2}/c^{4}-|\vec{p}_{D^-}|^{2}/c^{2}} $ , where$ E_{\mathrm{beam}} $ is the beam energy and$ E_{D^-} $ and$ \vec{p}_{D^-} $ are the energy and momentum of the ST$ \bar D $ meson in the$ e^+e^- $ center-of-mass frame, respectively. If there is more than one$ D^- $ candidate in a given ST mode, that with the smallest$ |\Delta E| $ is kept for further analysis. The$ \Delta E $ requirements on the different tag modes are summarized in Table 1.Tag mode $ \Delta E $ /MeV

$ N^{i}_{\rm{ST}} (\times 10^3) $ 

$ \epsilon^i_{\rm{ST}} $ (%)

$ \epsilon^i_{\rm{DT}} $ (%)

$ K^+\pi^-\pi^- $ 

$ [-25,24] $ 

$ 5567.2\pm2.5 $ 

$ 51.08 $ 

$ 33.92 $ 

$ K^{0}_{S}\pi^{-} $ 

$ [-25,26] $ 

$ 656.5\pm0.8 $ 

$ 51.42 $ 

$ 35.00 $ 

$ K^{+}\pi^{-}\pi^{-}\pi^{0} $ 

$ [-57,46] $ 

$ 1740.2\pm1.9 $ 

$ 24.53 $ 

$ 17.86 $ 

$ K^{+}K^{-}\pi^{-} $ 

$ [-24,23] $ 

$ 481.4 \pm0.9 $ 

$ 40.91 $ 

$ 25.46 $ 

$ K^{0}_{S}\pi^{-}\pi^{0} $ 

$ [-62,49] $ 

$ 1442.4\pm1.5 $ 

$ 26.45 $ 

$ 20.12 $ 

$ K^{0}_{S}\pi^{-}\pi^{-}\pi^{+} $ 

$ [-28,27] $ 

$ 790.2\pm1.1 $ 

$ 29.68 $ 

$ 20.08 $ 

Table 1. Requirements on
$ \Delta E $ , ST$ D^- $ yields ($ N^i_{\rm{ST}} $ ) in the data, ST efficiencies ($ \epsilon_{\rm{ST}}^{i} $ ), and DT efficiencies ($ \epsilon^i_{\rm{DT}} $ ). The uncertainties on$ N^i_{\rm{ST}} $ are only statistical.For each tag mode, the yield of the ST
$ D^- $ meson is extracted by fitting the corresponding$ M_{\rm{BC}} $ distribution. In the fit, the signal shape is described by the MC-simulated signal shape convolved with a double-Gaussian function to account for the data-MC resolution difference. The background shape is described by an ARGUS function [24], with the endpoint fixed at$ E_{\rm{beam}} $ = 1.8865 GeV. Figure 2 shows the fit results for the tag modes in the data. The ST efficiencies are obtained by analyzing the inclusive MC sample. The candidates with$ M_{\rm{BC}} $ within (1.863,$ 1.877) $ GeV/$ c^2 $ are kept for further analysis. The ST yields and efficiencies are summarized in Table 1.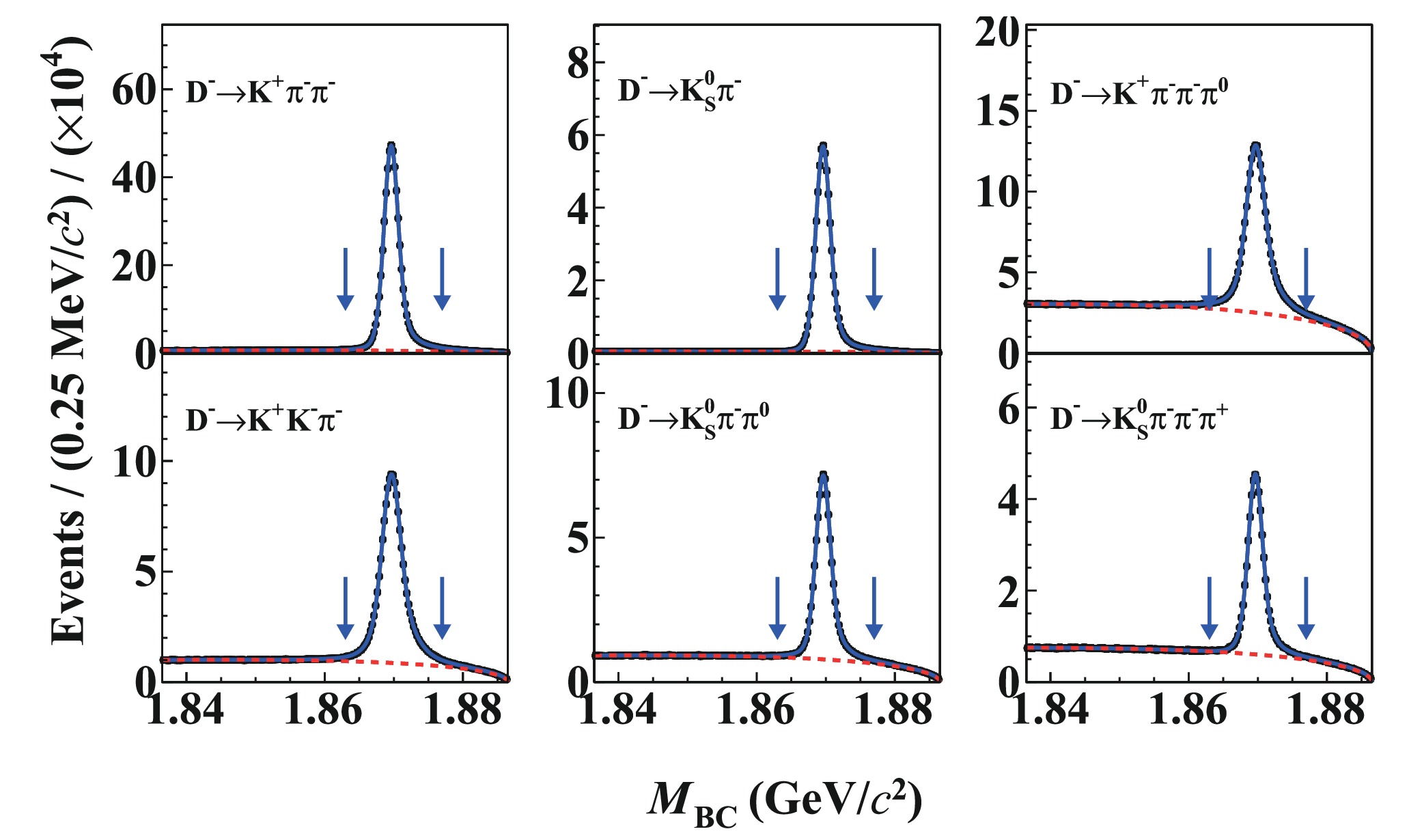
Figure 2. (color online) Fits to the
$ M_{\rm{BC}} $ distributions of the ST$ D^{-} $ candidates. The dots with error bars are data, the solid blue lines are the total fit, and the red dashed curves describe the fitted combinatorial background shapes. The pairs of blue arrows indicate the$ M_{\rm{BC}} $ signal window. -
For the signal side of
$ D^{+} \to e^+\nu_e $ , only the one positron can be reconstructed. The neutrino carries away energy and momentum that are not directly detectable, but may be inferred from four-momentum conservation. The recoiling positron and$ D^{-} $ tag are combined with the known initial-state four-momentum to achieve this and help select signal events. A kinematic fit is performed, constraining the total four-momentum to the four-momentum of the initial state and constraining the invariant masses of the$ D^- $ tag and$ D^+ $ signal to the known$ D^\pm $ mass. The four-momentum of the missing neutrino is determined by the fit.$ \chi^2 $ of this kinematic fit is required to be smaller than 50. To further suppress backgrounds, it is required that there are no extra$ \pi^{0} $ ($ N^{\text{extra}}_{\pi^0}=0 $ ) or good tracks ($ N^{\text{extra}}_{\text{char}}=0 $ ) that are not used in the DT reconstruction. The maximum energy of any extra photon ($ E_{\rm{max,\gamma}}^{\rm{extra}} $ ) is also required to be smaller than 0.2 GeV. This is optimized by maximizing$ \dfrac{\epsilon}{1.5+\sqrt{B}} $ [25], where$ \epsilon $ is the signal efficiency and$ B $ is the background yield estimated by the inclusive MC sample. The signal yield is determined from a fit to the missing-mass squared,$ M_{\rm{miss}}^2 $ , defined as$ M_{\rm{miss}}^2 = (E_{\rm{beam}}-E_{e^+})^2-(-\vec{p}_{D^-}-\vec{p}_{e^+})^2, $

(5) where
$ E_{e^+} $ ($ \vec{p}_{{e^+}} $ ) is the energy (momentum) of the candidate positron.We fit the
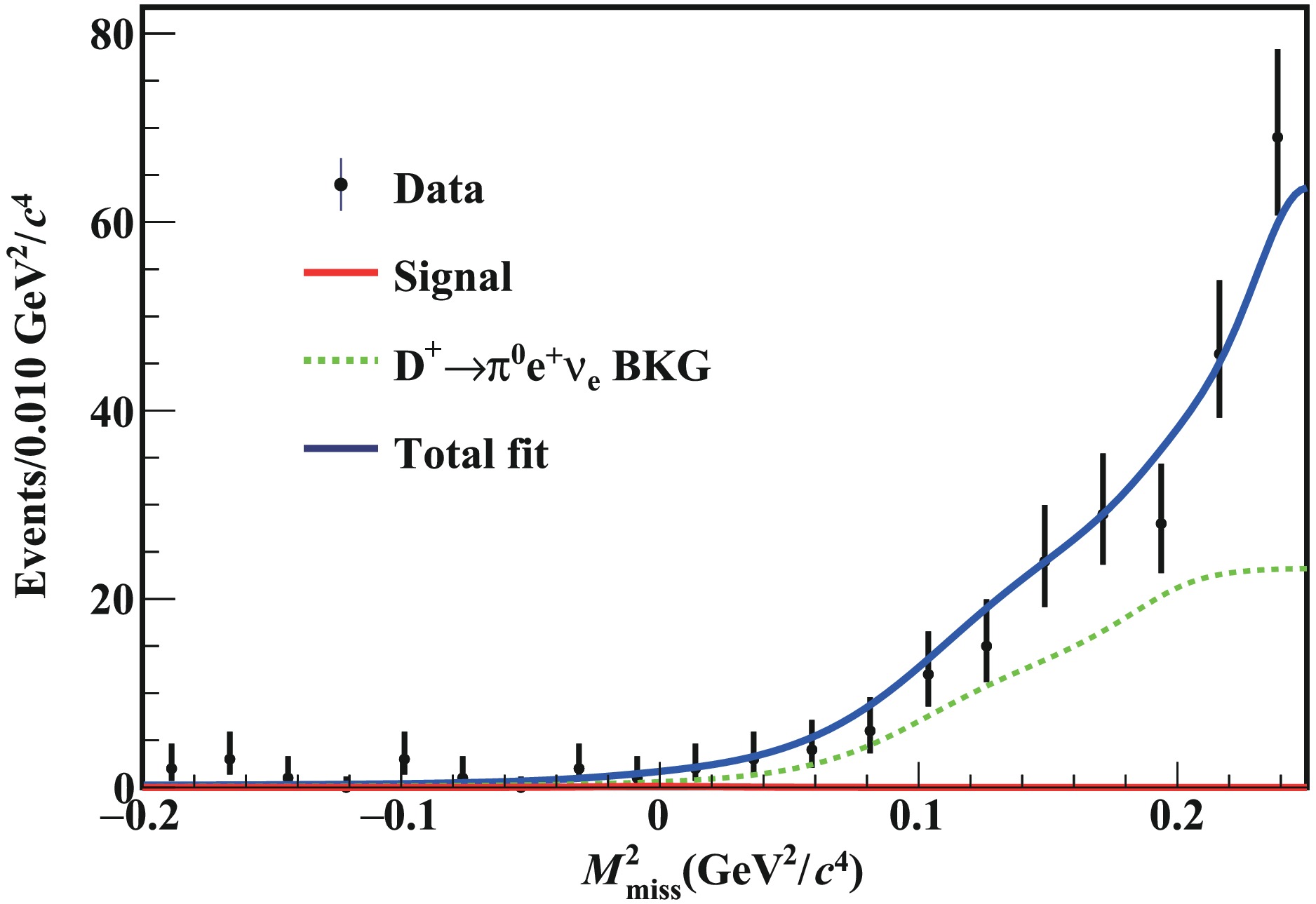
$ M_{\rm{miss}}^2 $ distribution in the data to obtain the yield of$ D^+\to e^+\nu_e $ . The signal shape is derived from the signal MC sample. The background shape is derived from the inclusive MC sample, smoothed with the tool RooKeysPDF [26]. The decay$ D^+ \to \pi^0 e^+ \nu_e $ is the main background, which is well modeled in the MC simulation. The fit result is shown in Fig. 3; the yield of$ D^+\to e^+\nu_e $ is$ N_{\rm{DT}}=0.3^{+2.9}_{-3.4} $ (stat). -
Most systematic uncertainties related to the efficiency of reconstruction of the
$ D^{-} $ mesons on the tag side are canceled due to the DT method. The multiplicative systematic uncertainty on the number of single tags,$ N_{\rm{ST}}^{\rm{tot}} $ , is estimated by varying the signal and background shapes, and allowing the parameters of the Gaussian to vary in the fit. It is assigned to be 0.1%. The$ e^+ $ tracking and PID efficiencies are studied by using a control sample of$ e^+ e^- \to \gamma e^+ e^- $ . The differences of the efficiencies between data and MC are$ 1.002 \pm 0.005 $ for$ e^+ $ tracking and$ 0.972 \pm 0.005 $ for PID. After correction for the data/MC discrepancy, we assign 0.5% and 0.5% as multiplicative systematic uncertainties for the$ e^{+} $ tracking and PID, respectively. The efficiency for the combined requirements on$ E^{\text{extra}}_{\text{max},\gamma},N^{\text{extra}}_{\text{char}} $ , and$ N^{\text{extra}}_{\pi^0} $ is studied with a control sample of DT hadronic events where both$ D^+ $ and$ D^- $ decay to one of the six ST hadronic final states. The efficiency difference between data and MC simulation, 1.3%, is used as the multiplicative systematic uncertainty. We adjust the fit range to (–0.25, 0.25) GeV$ ^2/c^4 $ for$ M_{\rm{miss}}^2 $ , with maximum upper limit and minimum values set as 1.0$ \times10^{-6} $ and 9.7$ \times10^{-7} $ , respectively, and thus consider 3% as an additive systematic uncertainty. All systematic uncertainties are summarized in Table 2. Their addition in quadrature results in a total systematic uncertainty of 4.3%.Multiplicative uncertainty Uncertainty (%) $ N_{\rm{ST}}^{\rm{tot}} $ 

0.1 $ e^+ $ tracking

0.5 $ e^+ $ PID

0.5 $ E^{\text{extra}}_{\text{max},\gamma}, N^{\text{extra}}_{\text{char}}, N^{\text{extra}}_{\pi^0} $ 

3.0 Additive Uncertainty Uncertainty (%) $ M_{\rm{miss}}^2 $ fit region

3.0 Total 4.3 Table 2. Systematic uncertainties on the branching fraction measurement.
-
As no significant signal is found, an upper limit on the branching fraction of
$ D^+\to e^+\nu_e $ is estimated using the Bayesian approach. The sources of systematic uncertainties on the upper limit measurements are classified into two types: additive and multiplicative ($ \sigma_s $ ). To incorporate the multiplicative systematic uncertainty in the calculation of the upper limit, the likelihood distribution is smeared by a Gaussian function with a mean of zero and width equal to$ \sigma_{s} $ , as described below [27],$ L(\mathcal{B}) \propto { {{\int}^{1}_{0}} { L \left( \frac{\epsilon_S}{\epsilon_{\hat{S}}}\mathcal{B} \right) {\rm e}^{ \left[ - \frac{\left(\epsilon_S - \epsilon_{\hat{S}}\right)^2}{2 {\sigma}^2_{S}} \right]} {\rm d} S }}, $

(6) where we associate
$ \epsilon_{\hat{S}} $ with the nominal efficiency,$ \epsilon_{S} $ with the expected efficiency, and$ L(\mathcal{B}) $ is the likelihood distribution obtained from a fit to the likelihood of$ \mathcal{B} $ (branching fraction) and parameterized as a Gaussian. The only significant additive uncertainty originates from the normalization of the$ D^+ \to \pi^0 e^+ \nu_e $ branching fraction. We repeat the maximum-likelihood fit, varying this BF by the PDG uncertainty and choose the most conservative upper limit among these results. The distribution of the likelihood versus the assumed branching fraction is shown in Fig. 4. Finally, the upper limit on the branching fraction of$ D^+\to e^+\nu_e $ at the 90% confidence level is set at 9.7$ \times 10^{-7} $ .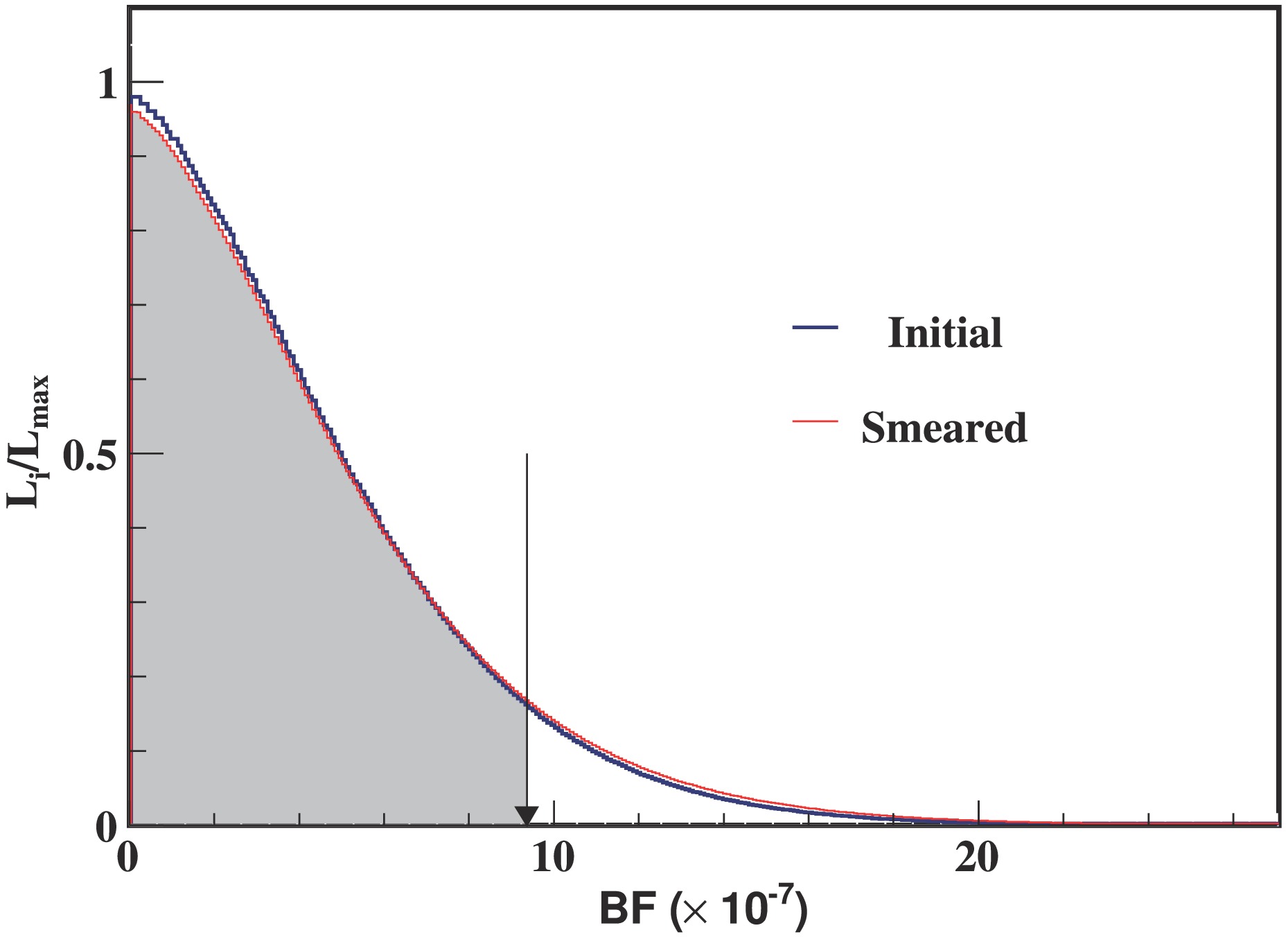
Figure 4. (color online) Distribution of likelihood versus the branching fraction of
$ D^{+} \to e^+ \nu_{e} $ . The likelihood in each bin is denoted as$ L $ . The maximum of the likelihood is$ L_{\text{max}} $ . The results obtained with and without incorporation of the systematic uncertainties are shown by the red and blue curves, respectively. The black arrow shows the upper limit corresponding to the 90% confidence level. -
By analyzing 20.3 fb
$ ^{-1} $ of$ e^+e^- $ collision data collected at$ \sqrt s=3.773 $ GeV with the BESIII detector, we search for the leptonic decay$ D^+\to e^+\nu_{e} $ . Significant signal is not observed, and an upper limit on the branching fraction of$ D^+\to e^+\nu_e $ is set at$ 9.7\times10^{-7} $ at the 90% confidence level. The sensitivity is improved by an order of magnitude compared to the CLEO measurement. -
The BESIII Collaboration thanks the staff of BEPCII and IHEP Computing Center for their strong support.
Search for the leptonic decay ${\boldsymbol D^{\bf +}{\bf\to}{\boldsymbol e}^{\bf +}\boldsymbol\nu_{\boldsymbol e}}$
- Received Date: 2025-01-11
- Available Online: 2025-06-15
Abstract: We search for the leptonic decay







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: