Nuclear matter and neutron star properties constrained by CREX results and astrophysical constraints: A covariance study

Neutron stars, strange stars, and hybrid stars provide unique opportunities to study dense matter and its interactions at levels comparable to terrestrial laboratories. These complicated astrophysical sources have resulted in advanced findings in nuclear and subnuclear physics, quantum chromodynamics, the general theory of relativity, and high-energy physics. Neutron stars (NS) play a significant role in physics and astronomy. Their density ranges from a few g cm^-3 at their surface to over 10¹⁵ g cm^-3 in the center, with pressure exceeding 10³⁶ dyne cm^-2. The very dense core of a compact star provides an opportunity to study nuclear matter beyond saturation density. At such high densities, it is not possible to know exactly the composition of the matter to date, Equation of state (EOS) can determine the thermodynamic state of matter. To understand neutron star properties, it is necessary to know the pressure and energy density (EoS) in the high-density domain. Astrophysical investigations exploring neutron stars' mass, radius, and tidal deformability have revealed restrictions on EoS. The LIGO and VIRGO collaborations [1, 2], as well as NICER mass-radius measurements [3, 4], have made significant contributions to understanding the dynamics of EoS from low to high-density regimes. The CREX has recently provided $ \Delta r_{\text{np}} $ ($ ^{48} {\rm{Ca}}$) = 0.121 ± 0.026 fm [5] that favors a smaller value of L. PREX-II has provided a neutron skin $ \Delta r_{\text{np}} $ ($ ^{208} {\rm{Pb}}$) = 0.283 ± 0.071 fm [6].

As discussed in [7−9], it is challenging to explain parity-violating asymmetry across these nuclei. The origin of the $ \Delta r_{\text{np}} $ reported by the CREX and PREX collaborations as thin for $ ^{48} {\rm{Ca}}$ and thick for $ ^{208} {\rm{Pb}}$, remains a puzzle. CREX results build on the the accomplishment of the Pb Radius Experiment (PREX) [6, 10], which tried to restrict the EoS of asymmetric dense matter near $ \rho_{0} $ by estimating neutron skin of $ ^{208} {\rm{Pb}}$. Symmetry energy is the energy necessary to turn symmetric nuclear matter (SNM) (N = Z) into highly asymmetric dense matter, also known as pure neutron matter (PNM), indicating a strong relationship between finite nuclei and compact stars. Relativistic mean-field (RMF) models have become a standard technique for precisely describing the finite nuclei and neutron star structure. These models remain crucial for understanding high-energy phenomena and dense nuclear matter, as it is essential to tackle the nuclear EoS in a relativistic approach [11]. The study of neutron stars exposes their complicated interior structures. Exotic matter may appear in the interior or core of a neutron star. Neutron star observables, such as maximum mass ($ M_{\text{max}} $), radius (R), and tidal deformability (Λ), can be well characterized by the interaction between nucleons and mesons using a Lagrangian or energy density functional. This imparts an EoS, which is used for the computation of the observables of a neutron star.

Recent advancements in the RMF models have significantly enhanced our understanding of nuclear and neutron star properties. In recent decades several nuclear energy density functional models have been employed to study finite nuclei and dense matter with diverse compositions and establish nuclear equation of state. These models include various non linear self-interactions, and mixed interactions of σ, $ \omega_{\mu} $, $ \rho_{\mu} $, and δ mesons and align well with astrophysical observations. There are many nuclear theories or model parameter sets like NL3 [12], TM1 [13], FSUGold [14], FSUGold2 [15], BigApple [16], HPU's [17], DOPS's [18], OMEG's [19], DINO's [20], HPD's [21] for nonlinear relativistic mean field model (NL-RMF), which have been widely used for studying the various neutron star properties like maximum mass, radius and tidal deformability corresponding to a canonical mass neutron star as observed from various astrophysical observations, gravitational wave events and the various bulk nuclear matter parameters along with finite nuclear properties.

The contributions from the σ - ω cross-couplings and self-coupling of ω mesons play important roles in varying the high-density behavior of the EOSs. The mixed interaction terms involving the ρ - meson field contribute to the isovector part of the effective Lagrangian density along with the usual linear couplings of the ρ to the nucleons. The σ- ρ and ω- ρ cross-coupling terms enable one to constrain the linear density dependence of the symmetry energy and the neutron-skin thickness in heavy nuclei over a wide range without affecting the other properties of finite nuclei [22].

Effective Field Theory (EFT) requires that coupling parameters within the energy density functional exhibit ``naturalness", meaning these parameters should be of similar order of magnitudes (around unity) when expressed as dimensionless ratios. This naturalness condition allows for a reasonable estimation of contributions to the energy density functional and aids in determining a suitable truncation scheme. The RMF model incorporates all possible self and mixed interaction terms for σ, ω, and ρ mesons while ensuring adjusted coupling parameters align with experimental nuclear observables [23]. Studies indicate that RMF models with terms up to order $ \nu = 4 $ effectively describe finite nuclei, while higher-order terms only marginally improve fits [24]. The primary influence on the EoS for neutron matter arises from quartic self-interaction of the ω meson, and including mixed interaction terms is crucial for maintaining the naturalness of coupling parameters, as specified by EFT [23−25]. Improvements in naturalness can be further achieved by incorporating higher-order terms involving field gradients [23].

The RMF formalism provides a computationally efficient alternative to complex nuclear many-body calculations [23] by utilizing meson-exchange interactions in a mean-field approximation, rather than direct nucleon-nucleon interactions. Conventional methods like Brueckner-Hartree-Fock are computationally intensive and limited in their scope due to the challenges of solving intricate many-body equations. RMF simplifies these interactions through phenomenological coupling constants that reflect nucleon correlations while adhering to naturalness behavior to maintain predictive accuracy. Extensions of RMF enhance the model's effectiveness in predicting properties of neutron-rich matter and neutron stars, capturing essential many-body physics without the full complexity of explicit calculation. The RMF models are based on many-body field theory. In principle, the so-called four-, six-, higher order many-body interactions have been included naively through Dyson's equation. In non-relativistic cases, the three-body force is required even to reproduce the saturation mechanism of nuclear matter. But, it still has a large ambiguity, and such calculations face the problem of causality. This is also true for chiral EFT. So, we can at least insist that the relativistic calculations are suitable to describe nuclei and neutron stars compared with those calculations.

The previous studies have extensively investigated nuclear matter properties, such as symmetry energy and maximum mass of neutron stars, but significant gaps remain in understanding how these factors collectively influence neutron star observables. Specifically, the role of the slope of symmetry energy (L) in determining neutron skin thickness and its impact on the softness or stiffness of EoS in a high-density regime remains uncertain. While most of the studies have concentrated on constraining EoS using PREX-II data, the complementary CREX results, which provide valuable insights into the neutron skin of heavy nuclei, have often been overlooked. In Ref. [26] the authors have investigated the implications of PREX-II on the equation of state of neutron-rich matter. The study discussed in Refs. [19] incorporated the δ - N coupling and mixing terms of σ - δ mesons within the Lagrangian of RMF model to study the combined analysis of PREX-II and CREX results. However, they were unable to simultaneously reproduce the empirical values of $ \Delta r_{\text{np}} $ for $ ^{208} {\rm{Pb}}$ and $ ^{48} {\rm{Ca}}$. Furthermore, as mentioned in Refs. [19, 27, 28], comprehending the results from CREX and PREX-II remains challenging, even when the mixing terms of δ - N and σ - δ mesons are included in the RMF model. In Ref. [29], effective interactions based on a relativistic energy density functional (EDF) with density-dependent point couplings were developed to study the implications of CREX and PREX-II results on the properties of finite nuclei and nuclear matter. The data from CREX and PREX-II have been directly utilized to constrain the relativistic EDFs. However the $ \Delta r_{\text{np}} $ calculated from these EDFs do not seem consistent and they concluded that no consistent conclusion from the theoretical side could be obtained when using CREX and PREX-II results. Recently, as reported in [20, 21], energy density functionals have been calibrated to accurately reproduce the binding energies and charge radii of spherical nuclei while accommodating the constraints set by CREX and PREX-II results. These models give a plausible solution to the PREX-II–CREX dilemma; however, despite their consistency with the properties of finite nuclei, their large values for $ K_{\text{sym}} $ result in significant stiffening of the EoS at high densities relevant to neutron stars. This stiffening leads to larger neutron star radii and results in an increased tidal deformability which is inconsistent with data from LIGO-Virgo and NICER missions.

The motivation of the present work is to investigate the impact of Calcium Radius Experiment (CREX) results measured at Jefferson Laboratory on neutron skin thickness ($ \Delta r_{\text{np}} $) of $ ^{48} {\rm{Ca}}$ [5] on finite nuclear properties (binding energies and charge rms radii), neutron skin thickness of $ ^{208} {\rm{Pb}}$ and neutron star observables satisfying the astrophysical constraints. CREX does not directly measure $ \Delta r_{\text{np}} $ but instead determines the parity-violating asymmetry (${\rm{A}} _{\text{PV}} $) in elastic electron scattering, which is sensitive to the weak charge distribution and thus provides an indirect probe of the neutron density profile. By comparing the measured ${\rm{A}} _{\text{PV}} $ with nuclear structure models, $ \Delta r_{\text{np}} $ is inferred. To aim this, we construct a new set of effective interactions for the Lagrangian density of the RMF model which includes different non-linear self and mixed interactions among isoscalar-scalar σ, isoscalar-vector ω, and isovector-vector ρ mesons up to the quartic order. In this work, the new effective interaction is searched in view of CREX result ($ \Delta r_{\text{np}} $ for $ ^{48} {\rm{Ca}}$) which is used to constrain the linear density dependence of symmetry energy, finite nuclear properties (binding energies and charge rms radii) and in the context of the prediction of maximum neutron star mass around $ \approx $ $ 2M_{\odot} $ recently observed with LIGO and Virgo of GW170817 event [30, 31] of binary neutron stars merger. discovery of neutron star with masses around $ \approx $ 2$ M_{\odot} $ [1−4, 32−36], and the limits of dimensionless tidal deformability of a canonical neutron star as observed by GW170817 event [1]. We also perform statistical analysis to quantify theoretical errors in parameters and physical observables, as well as identify correlation coefficients.

The study takes a methodical approach, with a brief outline of the RMF model Lagrangian, equations of motion of nucleon, mesons, and EoS of infinite nuclear matter in Section 2. Section 3 provides a detailed explanation of our findings and comments. We summarized the findings in Section 4.

The RMF model's effective Lagrangian depicts the interactions of nucleons with σ, $ \omega_{\mu} $, and $ \rho_{\mu} $ mesons. The inclusion of mixed interaction terms introduces variability in the linear density dependence of the symmetry energy coefficient and the neutron skin thickness of heavier nuclei. Importantly, the self-interaction of $ \omega_{\mu} $-meson significantly affects the high-density behavior (soft or stiff) of EoS and the structural properties of neutron stars. The impact of incorporating the self-interaction coupling ξ of $ \rho_{\mu} $-mesons is smaller and its effect is found to be appreciable in stars made up of pure neutron matter at high densities; the maximum masses of stars computed with β - equilibrated matter show little change when this coupling is varied within the bounds imposed by naturalness [37] and in the current work, we have not considered the contribution from coupling ξ. The σ and ω mesons are included to take into account the attractive and repulsive contributions of the nucleon-nucleon potential and are represented by isoscalar Lorentz scalar and Lorentz vector field σ and $ \omega_{\mu} $. As we propose an effective interaction for the RMF model that describes both finite nuclei and asymmetric nuclear matter, we also include the ρ meson to model the isospin dependence of the interaction. Although it does not contribute to infinite symmetric nuclear matter, it has an important role when the isospin asymmetry is introduced, as well as for the accurate description of finite nuclei properties such as binding energies and neutron skin. It is denoted by isovector Lorentz vector $ \rho_{\mu} $.

The Lagrangian density for the RMF model having σ, $ \omega_{\mu} $, and $ \rho_{\mu} $ mesons and nucleons (N = n,p) upto the quartic order [18, 25] is

Here, $ F_{\mu\nu} $ = $ \partial_{\mu} $ $ A_{\nu} $ $ - \partial_{\nu} $ $ A_{\mu} $ and A is photon field. The $ M_{N} $, $ m_\sigma $, $ m_\omega $, and $ m_\rho $ indicate the nucleon and respective meson masses. The parameters $ g_{\sigma N} $, $ g_{\omega N} $, $ g_{\rho N } $ quantify the couplings that represent the interaction of nucleons with the corresponding mesons. $ \overline{\kappa} $, $ \overline{\lambda} $ represent self-interactions of sigma meson, while ζ denotes the fourth-order self-interaction term of omega meson. In the Lagrangian density, coupling terms such as $ \Lambda_v $, ($ a_1 $, $ a_2 $), ($ b_1 $, $ b_2 $) represent cross interactions between ($ \omega_{\mu} - \rho_{\mu} $), ($ \sigma - \omega_{\mu} $) and ($ \sigma - \rho_{\mu} $) mesons respectively. In Eq. 1, summation is taken over nucleon (N = p, n) and leptons ($ \ell $ = e, μ). In the present study, only the neutron and proton have been considered for the calculation of finite nuclear matter and neutron star properties. The electromagnetic interaction is also included through the photon field A, where $ F_{\mu\nu} $ is the electromagnetic field tensor.

The cubic and quartic self-interaction terms ($ {\overline{\kappa}} $, $ \overline{\lambda} $) of the σ - meson plays a crucial role in RMF models, significantly improving the nuclear matter EoS beyond the original Walecka model [38]. The introduction of these self-interactions in the Lagrangian of RMF model softens the scalar potential, leading to improved nuclear saturation properties and helps in reducing the nuclear matter incompressibility (K) to more reasonable values (200 - 300 MeV) and providing a density-dependent effective mass for nucleons [39, 40]. The absence of these couplings predicts an excessively stiff EOS with an unrealistically high value of $ K \approx $ 500 MeV as in the Walecka model, [38]. The ω meson self-interaction term ζ plays a very important role in determining the soft and stiff behavior of EoS at high densities without affecting the bulk nuclear matter properties. The neutron star mass has a strong dependence on coupling ζ [16, 25, 37, 41]. The σ -ω mixed interactions improve the description of isoscalar nuclear interactions while the σ -ρ terms are critical for accurately modeling isovector interactions such as symmetry energy. The σ- ρ and ω- ρ cross-coupling terms along with $ g_{\rho N} $ account for the isovector part of the Lagrangian density and plays a significant role in constraining the linear density dependence of the symmetry energy and the neutron-skin thickness of finite nuclei without affecting the other properties of finite nuclei [22]. The contribution from the mixed interaction terms of σ - ω, σ - ρ and ω - ρ mesons in the Lagrangian of the RMF model has to be incorporated into the Lagrangian to accommodate the naturalness behavior of coupling parameters as imposed by effective field theory [17, 23, 24]. Other higher-order terms such as those involving higher powers of meson fields or more complex meson mixing, would introduce excessive parameters and lead to unphysically large or small values, violating the naturalness criterion. These selected terms allow for a balance between the richness of interaction and simplicity of the model, ensuring that the theory remains predictive without introducing artificial complexities.

The equation of motion for nucleons and respective mesons can be calculated by using the conventional Euler-Lagrange approach [25, 42] as follows:

We can calculate energy-momentum ($ { {\cal{T}}^{\mu\nu}} $) tensor from the Lagrangian density, which in turn can employed to determine energy density ($ {\cal{E}} $) as well as pressure ($ {\cal{P}} $). The third component of energy-momentum tensor $ \left\langle {{\cal{T}}^{jj}} \right\rangle $ gives pressure and zeroth component $ \left\langle {{\cal{T}}^{00}} \right\rangle $ computes the energy of the system.

The equation of motion for nucleons, mesons, and photons can be derived from the Lagrangian density defined in Eq.(1). In mean-field approximation, the meson and photon fields are replaced by their respective mean-field values: σ, $ \omega^{0} $, $ \rho^{0} $ and ${\rm{A}} ^{0} $ as,

where $ \alpha^{i} = \gamma^{0} \gamma^{i} $ ($ i = 1, 2, 3 $) and $ \beta = \gamma^{0} $. The Euler-Lagrange equations for the ground-state expectation values of the mesons fields are

The baryon vector density $ \rho_N $, scalar density $ \rho_{sN} $ and charge density $ \rho_{p} $ are, respectively,

with γ the spin-isospin degeneracy. The Dirac effective mass for the nucleon (N = n, p) can be written as

The energy density of the uniform matter within the framework of the RMF model is given by;

The pressure of the uniform matter is given by

Here, the sum is taken over nucleons and leptons.

The total binding energy of finite nuclei is given by the various individual contributions

where $ E_{\text{part}} $ signifies the sum of the single-particle energies of the nucleons. The terms $ E_{\sigma L} $, $ E_{\sigma NL} $, $ E_{\omega L} $, $ E_{\omega NL} $, $ E_{\rho} $, and $ E_{c} $ represent the contributions attributed to the corresponding meson fields including linear and nonlinear parts and Coulomb fields respectively. The terms $ E_{\sigma\omega} $, $ E_{\sigma\rho} $ and $ E_{\omega\rho} $ represent the contributions arising from the mixed interaction terms involving σ, ω and ρ mesons. additionally the effects of the pairing contribution $ E_{\text{pair}} $ and center of mass correction $ E_{\text{CM}} $ have also been taken into account.

Here, the occupation numbers $ n_{i} $ are introduced to account for the effects of pairing which is important for open-shell nuclei. In the absence of pairing interactions, they have value one (zero) for the levels below (above) the Fermi surface. When pairing is taken into account, the occupancy values ($ n_{i} $) are determined within the framework of the constant gap approximation (BCS) by the relation [43]:

The pairing correlation has a significant role in open-shell nuclei [44]. The influence of pairing correlation is considerably seen with the increase in the mass number of nuclei. We have incorporated pairing for the open shell nuclei by employing the BCS formalism with constant pairing gaps (Δ) that have been taken from the particle separation energies of neighboring nuclei [44−46]. In the calculation of pairing energy, we use a pairing window, i.e. sum over i in Eq. (28) is only extended up to the level where $ \epsilon_{i} $ - λ $ \leq $2 $ \hbar \omega^{0} $. The center-of-mass correction to the total binding energy ${\rm{E}} _{\text{CM}} $ is calculated within the harmonic oscillator approximation which yields $ E_{\text{CM}} $ = $ - \frac{3}{4}\hbar\omega^{0} $ and we take $ \hbar\omega^{0} $ = $ 45A^{-1/3 } - 25 A^{-2/3} $ MeV [47, 48].

The charge radius is calculated by using the relation [43]

The factor 0.64 included in Eq. (31) accounts for the finite size effect of the proton. The excess number of neutrons in a finite nucleus gives rise to important finite nuclear observables called neutron skin thickness.

where $ R_{n} $ and $ R_{p} $ are the rms radii for neutron and proton distribution.

We use simulated annealing technique [49, 50] to optimize the model coupling parameters ($ {\bf{p}} $) occurring in Eq. (1) by observing $ \chi^{2} $ minimization which is represented as,

where $ N_{\text{data}} $ and $ N_{\text{par}} $ indicate the number of experimental data points and parameters to be fitted, respectively. The $ {\cal{O}}_i^{\text{th}} $ and $ {\cal{O}}_i^{\text{exp}} $ denote the theoretical and experimental values, of a nuclear observable and $ {\Delta {\cal{O}}_{i}} $ indicates the value of adopted errors on the nuclear observables [51−53]. The optimal model parameters $ \bf{p}_{0} $ are those that minimize the $ {{\chi}}^{2} $ function. After searching the optimized model parameters, we use statistical/covariance analysis to estimate theoretical uncertainty in coupling parameters and nuclear observables. The statistical analysis provides insights into the sensitivity of parameters and physical quantities, as well as their interrelation [51, 52, 54, 55]. The behavior of the $ \chi^2 $ function near its minimum is characterized by the curvature matrix $ M_{\alpha\beta} $. Mathematically, this is expressed as:

where J is Jacobian matrix defined as

The covariance of two physical quantities A and B is expressed as:

Here, $ C_{\alpha\beta} = \chi^{2}(p_{0}) M_{\alpha\beta}^{-1} = \chi^{2}(p_{0}) (J^{T}J)^{-1} $ is covariance matrix. We can compute the standard deviation,$ \sqrt{\overline{\Delta{A}^2}} $, in A from Eq. (36) by putting B = A. Finally, the correlation coefficient between any two physical quantities (parameter or observable) A and B is given by [51, 52, 55−57]

We propose an effective interaction HPU4 for RMF relativistic energy density functional that provides neutron star features within astrophysical limitations, with finite nuclear and bulk nuclear matter at saturation density, in agreement with experimental data. The resulting parameterset, henceforth referred to as HPU4, is listed in Table 2. The model parameters are optimized using experimental values of binding energy (B.E.) and charge rms radii $ r_{\text{ch}} $ for sixteen spherical closed/open-shell nuclei (deformation β = 0) such as $ ^{16,24} {\rm{O}}$, $ ^{40,48,54} {\rm{Ca}}$, $ ^{56,68,78} {\rm{Ni}}$,$ ^{88} {\rm{Sr}}$,$ ^{90} {\rm{Zr}}$,$ ^{100,116,132,138} {\rm{Sn}}$, and $ ^{144} $Sm, $ ^{208} {\rm{Pb}}$ [46, 59, 60] in the fitting technique.

Parameters	HPU4	NL3	FSUGold	FSUGold2
$ g_{\sigma N} $	10.41443	10.21743	10.59265	10.39532
	(0.05179)
$ g_{\omega N} $	13.21616	12.86762	14.30241	13.55413
	(0.06147)
$ g_{\rho N} $	15.19767	8.94800	11.76733	8.97026
	(5.12104)
$ \overline{\kappa} $	2.22789	1.95734	0.71961	1.52185
	(0.09490)
$ \overline{\lambda} $	−0.03173	−1.59136	2.37646	−0.05362
	(0.21931)
$ a_{1} $	0.14718	−	−	−
	(0.00757)
$ a_{2} $	0.03293	−	−	−
	(0.04967)
$ b_{1} $	0.54871	−	−	−
	(1.41277)
$ b_{2} $	0.03254	−	−	−
	(1.27634)
$ \Lambda_{v} $	0.12590	−	0.06000	0.00165
	(0.11553)
ζ	0.01968	−	0.06000	0.02560
	(0.00412)
$ m_{\sigma} $	507.445	508.194	491.500	497.479
	(2.367)
$ m_{\omega} $	782.500	782.501	782.500	782.500
$ m_{\rho} $	770.000	763.000	763.000	763.000
$ M_{N} $	939.000	939.000	939.000	939.000

Table 2.  The model parameters for the newly optimized HPU4 Model along with accurately calibrated RMF models: NL3 [12], FSUGold [14] and FSUGold2 [15]. Theoretical uncertainties are also given in the parenthesis. The parameters $ g_{\sigma N} $, $ g_{\omega N} $, $ g_{\rho N} $, $ \overline{\lambda} $, $ a_{2} $, $ b_{2} $, ζ and $ \Lambda_{v} $ are dimensionless. The couplings $ \overline{\kappa} $, $ a_{1} $, and $ b_{1} $ are represented in units of fm$ ^{-1} $. The nucleon and meson masses $ M_{N,} $ $ m_{\sigma} $, $ m_{\omega} $, $ m_{\rho} $ are all given in MeV. The coupling parameters $ \overline{\kappa} $, $ \overline{\lambda} $, $ a_{1} $, $ a_{2} $, $ b_{1} $ and $ b_{2} $, are expressed in ($ \times10^{-2} $).

In Table 1 we have listed the experimental data for binding energies, charge radii, neutron skin thickness of $ ^{48} {\rm{Ca}}$ and maximum mass of neutron star of astrophysical interest along with adopted errors ($ {\Delta {\cal{O}}_{i}} $) that have been used in the fitting protocol for the optimizations of coupling parameters. The recent precise parity-violating electron scattering experiments for $ ^{48} {\rm{Ca}}$ (CREX) [5] and $ ^{208} {\rm{Pb}}$ (PREX-II) [6] provide a deep understanding of the $ \Delta r_{\text{np}} $. The CREX result has given $ \Delta r_{\text{np}} $ ($ ^{48} {\rm{Ca}}$) = 0.121 ± 0.026 fm [5] while PREX-II measured $ \Delta r_{\text{np}} $ ($ ^{208} {\rm{Pb}}$) = 0.283 ± 0.071 fm [6]. The larger value of $ \Delta r_{\text{np}} $ for $ ^{208} {\rm{Pb}}$ favors a stiffer value of $ L_{0} $ around $ \rho_{0} $ and suggests a stiff EoS. This leads to a higher value of $ R_{1.4} $ and $ \Lambda_{1.4} $ corresponding to a 1.4$ M_{\odot} $ neutron star [26] whereas CREX results are favored by a somewhat smaller value of $ L_{0} $ and suggest much softer EoS.

Nucleus	Data used in fitting protocol
	Observables	Expt. Value	$ {\Delta {\cal{O}}_{i}} $
	$ BE $	−127.62	4.0
$ ^{16} {\rm{O}}$	$ r_{\text{ch}} $	2.699	0.04
$ ^{24} {\rm{O}}$	$ BE $	−168.96	2.0
	$ BE $	−342.04	4.0
$ ^{40} {\rm{Ca}}$	$ r_{\text{ch}} $	3.478	0.042
	$ BE $	−415.96	1.0
$ ^{48} {\rm{Ca}}$	$ r_{\text{ch}} $	3.477	0.04
	$ \Delta r_{\text{np}} $	0.121	0.026
$ ^{54} {\rm{Ca}}$	$ BE $	−445.365	3.0
$ ^{56} {\rm{Ni}}$	$ BE $	−484.00	5.0
$ ^{68} {\rm{Ni}}$	$ BE $	−590.40	2.0
$ ^{78} {\rm{Ni}}$	$ BE $	−642.56	3.0
	$ BE $	−768.41	3.0
$ ^{88} {\rm{Sr}}$	$ r_{\text{ch}} $	4.224	0.02
	$ BE $	−783.81	2.0
$ ^{90} {\rm{Zr}}$	$ r_{\text{ch}} $	4.269	0.04
$ ^{100} {\rm{Sn}}$	$ BE $	−825.10	3.0
	$ BE $	−988.66	3.0
$ ^{116} {\rm{Sn}}$	$ r_{\text{ch}} $	4.625	0.02
	$ BE $	−1102.22	2.0
$ ^{132} {\rm{Sn}}$	$ r_{\text{ch}} $	4.709	0.04
$ ^{138} {\rm{Sn}}$	$ BE $	−1120.28	2.0
	$ BE $	−1195.77	2.0
$ ^{144} {\rm{Sm}}$	$ r_{\text{ch}} $	4.952	0.04
	$ BE $	−1636.33	1.0
$ ^{208} {\rm{Pb}}$	$ r_{\text{ch}} $	5.501	0.04
Neutron star mass	$ M_{\text{max}} $	2.08	0.07

Table 1.  Data used in fitting protocol i.e. experimental nuclear data on total binding energies ($ BE $) [46], charge radii ($ r_{\text{ch}} $) [58], and neutron skin, $ \Delta r_{\text{np}} $ for $ ^{48} {\rm{Ca}}$ nucleus [5], and maximum mass of neutron star, $ M_{\text{max}} $ (in $ M_{\odot} $) [36]. The adopted errors ($ {\Delta {\cal{O}}_{i}} $) [51−53] used for the model optimization in the fitting data. The $ BE $ is given in MeV while the $ r_{\text{ch}} $, and $ \Delta r_{\text{np}} $ are in fm.

In Table 2, we depict the proposed relativistic interaction for the HPU4 model. The theoretical uncertainties are also displayed in the parenthesis. For the comparison, we have also shown the coupling parameters for other accurately calibrated RMF models NL3 [12], FSUGold [14] and FSUGold2 [15], which are consistent with finite nuclear properties but NL3 and FSUGold2 do not support astrophysical constraints on $ \Lambda_{1.4} $ from GW170817 event while FSUGold model underestimate the neutron star maximum mass constraints of $ \approx $ 2 $ M_{\odot} $. Also as mentioned in Refs. [8, 19, 26, 28, 29, 42] it is difficult to reproduce the $ \Delta r_{\text{np}} $ as observed from CREX and PREX-II altogether within RMF approach. The CREX results favor a smaller value of $ L_{0} $, while its larger value is suggested by PREX-II.

In the present manuscript, we propose HPU4 relativistic interaction to study how the CREX results affect atomic nuclei, infinite nuclear matter, and compact star structure. So, we have incorporated CREX data $ \Delta r_{\text{np}} $ = 0.121 ± 0.026 fm [5] in our fitting protocol during the model optimization to restrict the value of $ L_{0} $, and to observe its implications on $ \Delta r_{\text{np}} $ of $ ^{208} {\rm{Pb}}$, $ R_{1.4} $ and $ \Lambda_{1.4} $ of 1.4$ M_{\odot} $ neutron star. We use the $ M_{\text{max}} $ = 2.08$ \pm0.07 $ $ M_{\odot} $ of neutron star [36] in fit data to constrain the EoS in high-density regimes. According to Refs. [17, 25, 37, 61], the fourth order self-interaction of the ω meson, measured by coupling ζ, plays a key role in calculating the soft and stiff behavior of EoS in high-density regimes. An increase in coupling ζ [17, 25, 37, 61], gives a decrease in neutron-star mass. So, by taking into account the $ M_{\text{max}} $ of the compact star in the fitting data during the model optimization, the ζ and hence the softness and stiffness of EoS at a high-density regime can be constrained. The value of $ \chi^{2} $ obtained after optimizing the HPU4 model parameters following Eq. (33) in minimization procedure, comes out to be 1.04. For the sake of comparison, the $ \chi^{2} $ values obtained for other models considered in the present work like NL3, FSUGold, FSUGold2, BigApple, DOPS3, and HPUC are 6.08, 6.25, 2.69, 13.43, 1.44, and 1.14, respectively by following the similar process and using experimental data with adopted errors as given in Table 1.

In Table 3, we summarize the theoretical prediction for ground state properties such as $ B/A $, $ r_{\text{ch}} $, and $ \Delta r_{\text{np}} $ for some finite nuclei obtained with newly proposed HPU4 interaction. For the sake of comparison, the results calculated for various parameter sets NL3 [12], FSUGold [14], FSUGold2 [15], DOPS3 [18], BigApple [16] and HPUC [62] also displayed. It can be seen from the table that the theoretical predictions of $ B/A $ and $ r_{\text{ch}} $ agree well with their experimental counterparts. The rms error in total binding energy and charge radii for all nuclei in our fitting data is 2.43 MeV and 0.03 fm, respectively. For HPU4 parametrization, the values of $ \Delta r_{\text{np}} $ for $ ^{48} {\rm{Ca}}$ = 0.146±0.019 fm and meets the CREX results [5] within the error bar. The HPU4 gives $ \Delta r_{\text{np}} $ for $ ^{208} {\rm{Pb}}$ = 0.120±0.025 fm and significantly underestimates the value of $ \Delta r_{\text{np}} $ for $ ^{208} {\rm{Pb}}$ as reported recently by PREX II [6]. The value obtained for Δr$ _{\text{np}} (^{208} {\rm{Pb}}$) = 0.120$ \pm 0.025 $ fm for the HPU4 model is close as reported in Refs. [8, 19, 28, 53] and is also in good agreement with the result reported for $ \Delta r_{\text{np}} $ = 0.18$ \pm $ 0.07 fm for $ ^{208} {\rm{Pb}}$ obtained by dispersive optical model analysis of the Washington University group [63]. This investigation suggests that by including $ \Delta r_{\text{np}} (^{48} {\rm{Ca}}$) = 0.121$ \pm 0.026 $ from CREX data [5] in our fitting data to constrain the $ L_{0} $, a smaller value of ($ \Delta r_{\text{np}} (^{208} {\rm{Pb}}$) = 0.120$ \pm 0.025 $ fm) for $ ^{208} {\rm{Pb}}$ is obtained for HPU4 model and underestimate the PREX-II results significantly [6]. This might be because the PREX-II results favor a larger value of $ J_{0} $ and $ L_{0} $ suggesting a stiffer EoS whereas CREX results suggest a somewhat smaller value of $ L_{0} $ and a much softer EoS as also discussed in [8, 19, 28, 29, 53].

Nucleus	Observable	Experiment	HPU4	NL3	FSUGold	FSUGold2	HPUC
$ ^{16} {\rm{O}}$	$ B/A $	7.98	8.16	7.94	7.87	7.89	8.13
	$ r_{\text{ch}} $	2.699	2.676	2.728	2.686	2.707	2.696
	$ \Delta r_{\text{np}} $	−	−0.029	−0.028	−0.028	−0.028	−0.029
$ ^{24} {\rm{O}}$	$ B/A $	7.04	7.01	7.10	6.88	7.09	6.96
	$ r_{\text{ch}} $	−	2.748	2.737	2.732	2.718	2.762
	$ \Delta r_{\text{np}} $	−	0.535	0.636	0.627	0.649	0.540
$ ^{40} {\rm{Ca}}$	$ B/A $	8.55	8.62	8.53	8.52	8.52	8.62
	$ r_{\text{ch}} $	3.478	3.424	3.470	3.434	3.448	3.445
	$ \Delta r_{\text{np}} $	$ 0.08^{+0.05}_{-1.0} $	−0.052	−0.048	−0.051	−0.049	−0.051
$ ^{48} {\rm{Ca}}$	$ B/A $	8.67	8.67	8.63	8.57	8.62	8.66
	$ r_{\text{ch}} $	3.477	3.462	3.471	3.460	3.449	3.478
	$ \Delta r_{\text{np}} $	0.121± 0.026	0.146	0.226	0.197	0.232	0.147
$ ^{54} {\rm{Ca}}$	$ B/A $	8.25	8.19	8.21	8.12	8.22	8.16
	$ r_{\text{ch}} $	−	3.553	3.537	3.533	3.512	3.570
	$ \Delta r_{\text{np}} $	−	0.442	0.571	0.539	0.587	0.455
$ ^{56} {\rm{Ni}}$	$ B/A $	8.64	8.58	8.60	8.52	8.58	8.60
	$ r_{\text{ch}} $	−	3.698	3.716	3.724	3.702	3.708
	$ \Delta r_{\text{np}} $	$ 0.03^{+0.08}_{-0.11} $	−0.038	−0.034	−0.038	−0.035	−0.037
$ ^{68} {\rm{Ni}}$	$ B/A $	8.68	8.71	8.69	8.67	8.69	8.72
	$ r_{\text{ch}} $	−	3.871	3.862	3.864	3.841	3.889
	$ \Delta r_{\text{np}} $	−	0.223	0.333	0.287	0.339	0.227
$ ^{78} {\rm{Ni}}$	$ B/A $	8.24	8.24	8.24	8.15	8.22	8.22
	$ r_{\text{ch}} $	−	3.965	3.942	3.957	3.925	3.980
	$ \Delta r_{\text{np}} $	−	0.382	0.554	0.495	0.566	0.390
$ ^{88} {\rm{Sr}}$	$ B/A $	8.73	8.72	8.71	8.70	8.71	8.72
	$ r_{\text{ch}} $	4.224	4.225	4.225	4.220	4.203	4.238
	$ \Delta r_{\text{np}} $	−	0.063	0.148	0.113	0.152	0.068
$ ^{90} {\rm{Zr}}$	$ B/A $	8.71	8.69	8.69	8.68	8.69	8.70
	$ r_{\text{ch}} $	4.269	4.270	4.280	4.274	4.258	4.289
	$ \Delta r_{\text{np}} $	0.090± 0.020	0.033	0.097	0.069	0.099	0.033
$ ^{100} {\rm{Sn}}$	$ B/A $	8.25	8.22	8.29	8.24	8.28	8.24
	$ r_{\text{ch}} $	−	4.502	4.511	4.519	4.495	4.516
	$ \Delta r_{\text{np}} $	−	−0.136	−0.117	−0.127	−0.120	−0.133
$ ^{116} {\rm{Sn}}$	$ B/A $	8.52	8.50	8.50	8.51	8.51	8.51
	$ r_{\text{ch}} $	4.625	4.612	4.610	4.611	4.588	4.634
	$ \Delta r_{\text{np}} $	0.100± 0.030	0.087	0.183	0.142	0.188	0.088
$ ^{132} {\rm{Sn}}$	$ B/A $	8.36	8.36	8.37	8.34	8.36	8.36
	$ r_{\text{ch}} $	4.710	4.729	4.711	4.725	4.692	4.749
	$ \Delta r_{\text{np}} $	−	0.215	0.383	0.310	0.391	0.217
Continued on next page

Table 3.  The theoretical results for ground state properties (binding energy per nucleon $ B/A $ (in MeV), charge radii $ r_{\text{ch}} $ (in fm) and neutron skin $ \Delta r_{\text{np}} $ (in fm) obtained with HPU4, NL3, FSUGold, FSUGold2 and HPUC models are displayed. Available experimental values of $ B/A $ [46] and $ r_{\text{ch}} $ [58], and $ \Delta r_{\text{np}} $ [5, 6, 63, 68] for the nuclei are shown.

The theoretical results of $ \Delta r_{\text{np}} $ for $ ^{48} {\rm{Ca}}$ and $ ^{208} {\rm{Pb}}$ obtained for HPU4 model satisfy the experimental results ($ ^{48} {\rm{Ca}}$ (RCNP) = 0.14-0.20 fm [64], $ ^{208} {\rm{Pb}}$ = $ 0.156^{+0.025}_{-0.021} $ fm [65], $ ^{208} {\rm{Pb}}$ (MAMI) = 0.15±0.03(sat.)$ ^{+0.01}_{-0.03} $(sys.)fm [66]). $ \Delta r_{\text{np}} $ for $ ^{208}{\rm Pb} $ calculated by HPU4 model is also well consistent with the value Δr$ _{\text{np}} = (0.18\pm 0.07) $ fm for $ ^{208} {\rm{Pb}}$ obtained by Washington University group as reflected in [63]. The $ \Delta r_{\text{np}} $ predicted by the HPU4 model underestimates the PREX-II results and tension for reproducing simultaneously PREX-II and CREX results continues as also discussed in Ref. [8, 19, 28, 29]. According to Refs. [8, 19], reproducing the CREX and PREX-II results for $ \Delta r_{\text{np}} $ altogether using RMF models is challenging. CREX results suggest a smaller value of $ L_{0} $ whereas PREX-II results favor a stiffer value as illustrated in detail in the above references. Other models considered in the present calculation also do not satisfy simultaneously these results for $ \Delta r_{\text{np}} $ for the $ ^{208} {\rm{Pb}}$ and $ ^{48} {\rm{Ca}}$. Recent studies on non-relativistic and RMF models have observed similar characteristics, highlighting the need for more experimental investigations. [8, 29, 67].

Table 4, depicts nuclear matter parameters such as binding energy per nucleon ($ E/A $), incompressibility coefficient (K), the effective mass ratio ($ M^*/M $) at saturation density ($ \rho_{0} $), symmetry energy ($ J_{0} $), the slope of symmetry energy ($ L_{0} $) and curvature of J, i.e. $ K_{\text{sym}} $ along with the theoretical errors. We have also displayed the $ \Delta r_{\text{np}} $ for $ ^{48} {\rm{Ca}}$ and $ ^{208} {\rm{Pb}}$. Nuclear matter characteristics significantly influence asymmetric nuclear dense matter EoS. It is found that for the proposed HPU4 model, the isoscalar nuclear matter parameters are constrained well (at the uncertainty $ \leq $ 3.4%). The error on $ L_{0} $ are relatively larger ($ \approx $ 33 %). As reported in [69−71] the $ K_{\text{sym}} $ is poorly determined and the available finite nuclear experimental data is not sufficient to restrict the value of $ K_{\text{sym}} $. We can constrain the $ K_{\text{sym}} $ in tighter limits only if we have precise knowledge of J at higher densities i.e $ \rho > 2\rho_0 $. It is noticeable that the value of $ K_{\text{sym}} $ for the HPU4 model overlaps with the theoretical analysis within the error bar, $ K_{\text{sym}} $ = -107±88 MeV [72]. The HPU4 model shows an $ E/A $ value of -15.94 MeV. $ J_{0} $ and $ L_{0} $ calculated for HPU4 model are in well agreement with $ J_{0} $ = 30.2$ ^{+4.1}_{-3.0} $ MeV and $ L_{0} $ = 15.3$ ^{+46.8}_{-41.5} $ MeV inferred by Zhang et. al., [28] and $ L_{0} $ = 50±12 MeV [73]. The value of $ K = 228.67 \pm 7.88 $ MeV for the HPU4 parameter set is satisfies $ K = 240 \pm 20 $ MeV as reported in [74, 75].

Properties	HPU4	NL3	FSUGold	FSUGold2	DOPS3	BigApple	HPUC
$ \rho_{0} $ (fm−3)	0.1506 (0.004)	0.1481	0.1484	0.1504	0.1480	0.1550	0.1490
$ E/A $(MeV)	−15.94 (0.04)	−16.23	−16.23	−16.28	−16.04	−16.34	−15.98
K(MeV)	228.67 (7.88)	271.45	230.04	237.86	227.65	227.09	220.19
$ M^{*}/M $	0.619 (0.008)	0.595	0.610	0.593	0.605	0.608	0.610
$ J_{0} $(MeV)	27.92 (1.31)	37.26	32.59	37.58	31.77	31.41	28.37
$ L_{0} $(MeV)	42.86 (14.26)	118.15	60.55	112.70	66.69	40.33	41.64
$ K_{\text{sym}} $(MeV)	55.13 (73.12)	100.96	−51.30	25.39	−0.62	89.59	81.12
$ \Delta r_{\text{np}} $($ ^{48} {\rm{Ca}}$)(fm)	0.146 (0.019)	0.226	0.197	0.232	0.184	0.168	0.147
$ \Delta r_{\text{np}} $($ ^{208} {\rm{Pb}}$)(fm)	0.120 (0.025)	0.279	0.207	0.286	0.188	0.151	0.119

Table 4.  The bulk nuclear matter properties at saturation density along with theoretical uncertainties (within the parenthesis) obtained for the HPU4 model. Here $ \rho_{0} $, $ E/A $, K, $ M^{*}/M $, $ J_{0} $, $ L_{0} $ and $ K_{\text{sym}} $ denotes the saturation density, binding energy per nucleon, nuclear matter incompressibility, the ratio of effective nucleon mass to the nucleon mass, symmetry energy, linear density dependence of symmetry energy, and the curvature of symmetry energy respectively. The $ \Delta r_{\text{np}} $ for $ ^{48} {\rm{Ca}}$ and $ ^{208} {\rm{Pb}}$ are also shown. The results obtained with various accurately calibrated RMFs are also shown for the sake of comparison.

Fig. 1, depicts the coefficients of correlation (in graphical form) for the HPU4 model parametrization occurring in Equation (1). The isoscalar coupling $ g_{\sigma N} $ is found to show a moderate to strong correlation with the model parameters $ g_{\omega N} $, $ \overline{\kappa} $, $ a_{1} $, $ a_{2} $ and $ m_{\sigma} $. Isoscalar coupling parameter $ g_{\omega N} $ also shows dependence on $ a_{1} $, $ a_{2} $. A good correlation also exists between pair of model parameters $ a_{1} $ - $ \overline{\kappa} $, $ a_{1} $ - $ m_{\sigma} $. We also notice a strong correlation for isovector coupling $ g_{\rho N} $ with $ \Lambda_{v} $ and $ b_{1} $. The parameter $ \Lambda_{v} $ also shows strong dependence on $ b_{1} $ as observed from their coefficient of correlation. If two model parameters exhibit a strong coefficient of correlation then this implies that parameters are strongly interdependent. The parameter ζ also shows strong dependence on $ a_{2} $. It can be noticed that a very strong correlation observed between isoscalar couplings $ g_{\sigma N} $ and $ g_{\omega N} $ as reported in [42, 55] becomes somewhat smaller for the HPU4 model. This might be due to the reason that in this model these couplings also show good correlations with the mixed interaction terms $ a_{1} $ ($ \sigma-\omega^{2} $) and $ a_{2} $ ($ \sigma^{2}-\omega^{2} $) included in the Lagrangian of HPU4 model. The strong dependence of isovector coupling $ g_{\rho} $ on cross interaction parameters $ b_{1} $ ($ \sigma-\rho^{2} $) and $ \Lambda_{v} $ ($ \omega^{2}-\rho^{2} $) is also observed.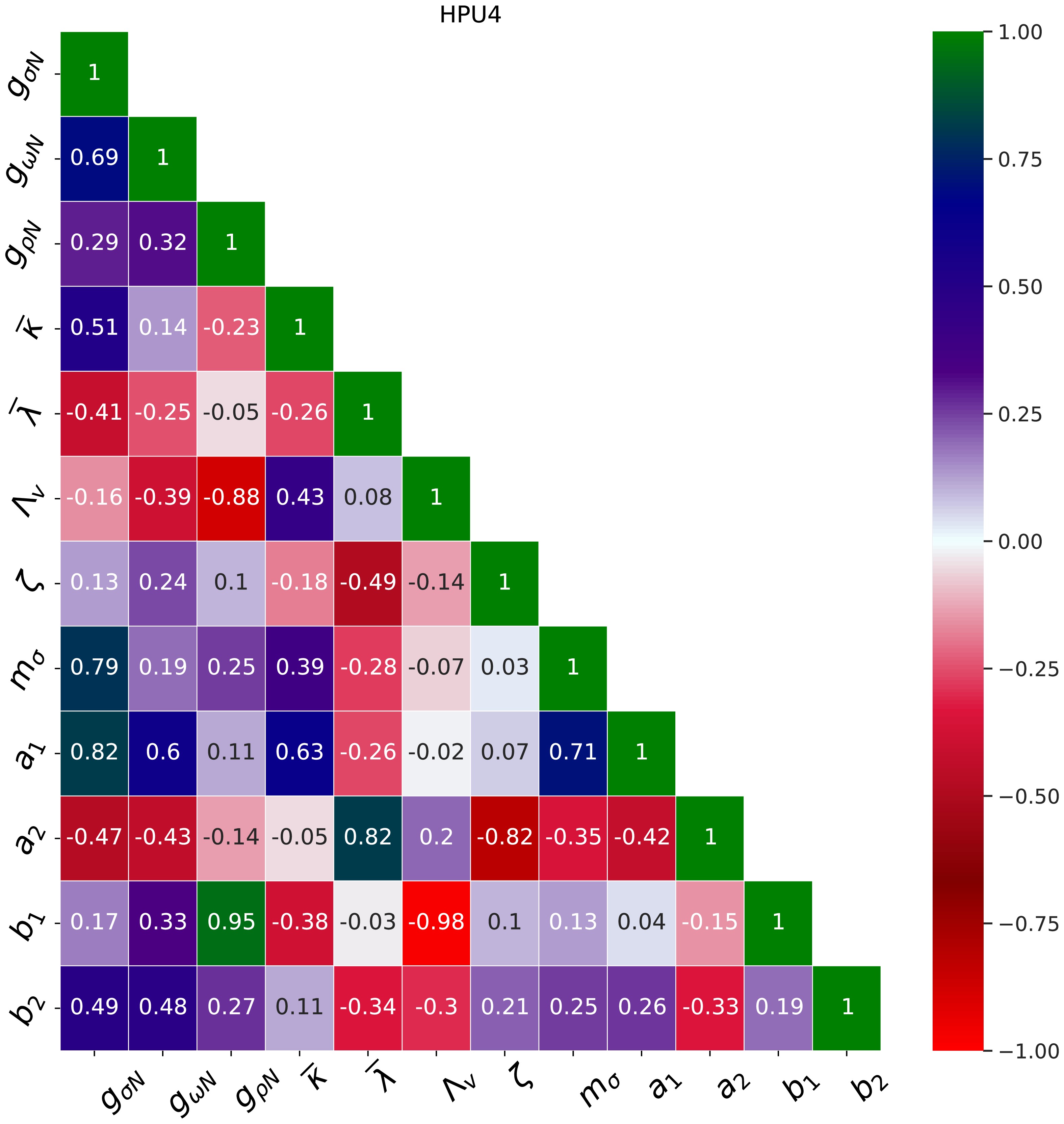

Figure 1.  (Color online) A graphical representation of coefficients of correlation between coupling terms for HPU4 model.

The Fig. 2, depicts a plot J versus (ρ/$ \rho_{0} $) for the HPU4 parametrization. For the sake of comparison, results for various parameter sets NL3 [12], FSUGold [14], FSUGold2 [15], DOPS3 [18], BigApple [16] and HPUC [62] are taken into account in the present work. The various constraints imposed on J as reported in Refs. [76, 77] are also displayed by shaded regions. It can be noticed that the value of J is found to increase with ρ for parameter sets considered and satisfies the constraints as mentioned [76, 77]. The J at 2$ \rho_{0} $ for the HPU model is found to be J (2$ \rho_{0} $) = 45.06 MeV. It is well consistent with J(2$ \rho_{0} $) = 51 ± 13 MeV [72] and also J(2$ \rho_{0} $) = 40.2 ± 12.8 MeV as reported in [54]. For the HPU4 model, we obtain the softest J around $ \rho_{0} $. This is because we obtain a larger value of coupling parameter $ \Lambda_{v} $ during the HPU4 model optimization and $ \Lambda_{v} $ is observed to have a significant contribution to constrain J and L.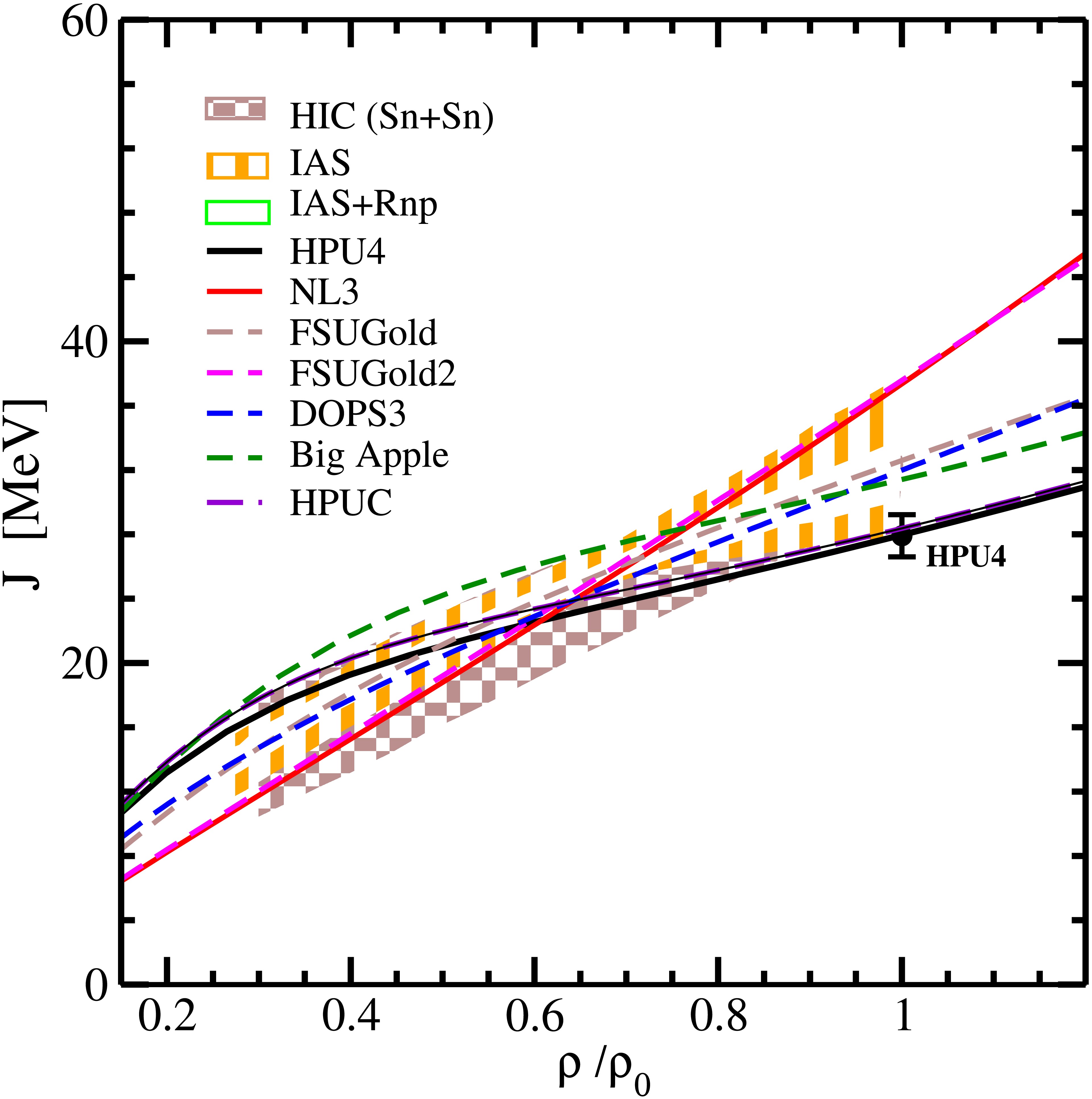

Figure 2.  (color online) Plot showing the dependence of J on $ \rho /\rho_{0} $ for HPU4 model and other RMF models. The theoretical uncertainty for J at saturation density calculated for the HPU4 model is also shown.

To calculate the mass and radius of a non-rotating compact star, we solve the Tolman-Oppenheimer-Volkoff (TOV) equations, which are Einstein's equations for static and spherically symmetric stars [78, 79]:

The mass of a compact star $ m(r) $ enclosed in a sphere of radius r is related to its energy density using the relation.

for a given EoS $ P(\epsilon $) differential Eq.(38) and Eq. (39) can be solved simultaneously. The total mass of a compact star is

When estimating neutron star parameters, it is crucial to account for the EoS of the crust, which governs the low-density regime. The radius of a 1.4$ M_{\odot} $ neutron star is particularly sensitive to the crust EoS. In this work, we employ the Baym-Pethick-Sutherland (BPS) EoS [80] for the crust region.

Fig. 3, displays the relationship of mass-radius for static stars using the HPU4 model. We also show the computed results for various models. The $ M_{\text{max}} $ of a non-rotating neutron star in the HPU4 model is found to be 2.03 ± 0.04 $ M_{\odot} $, which satisfies the mass constraints reported in [3, 4, 32, 35, 81]. The $ R_{1.4} $ of canonical mass neutron star including BPS crust [80] is 12.80 ± 0.28 Km, which is well consistent with the constraints from NICER on $ R_{1.4} $. The computed mass-radius of a neutron star with HPU4 parameterization aligns with NICER measurements [3, 4] as shown in shaded regions in Fig. 3. The $ R_{1.4} $ also aligns with radius limits from NICER measurements [3, 4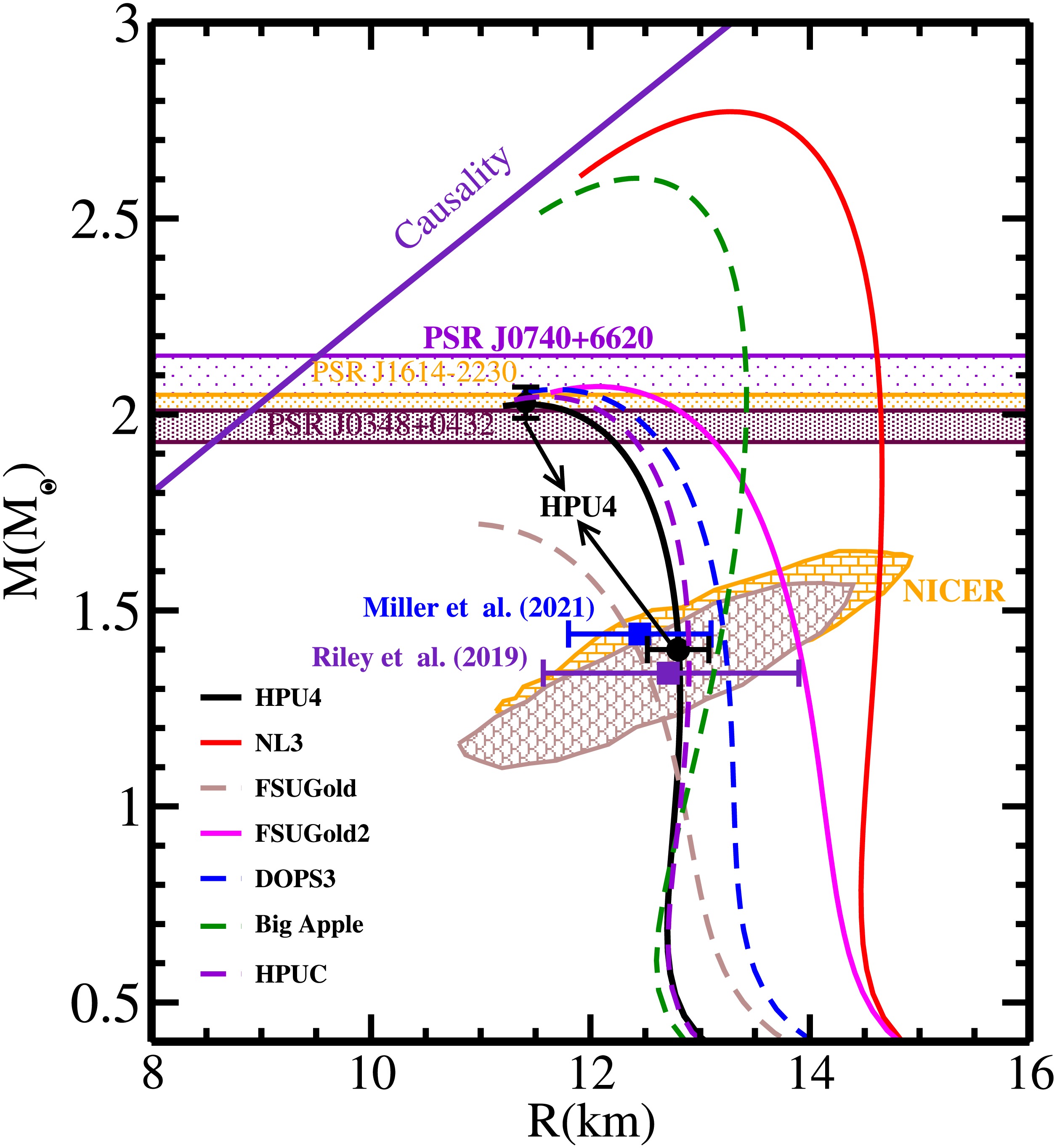, 82].

Figure 3.  (color online) Neutron star mass-radius relationship for various parametrizations considered in the current work. Mass constraints of PSR J1614-2230, PSR J0348+0432, and PSR J0740+6620 [32, 35, 36] have been shown by horizontal bands. Constraints from NICER measurements [3, 30] are also displayed. The theoretical uncertainties on $ M_{\text{max}} $ and $ R_{1.4} $ calculated for the HPU4 model are also shown.

Fig. 4 shows how the dimensionless tidal deformability $ \Lambda_{1.4} $ [84−86] varies with $ R_{1.4} $ for HPU4 and other models considered in the present study. It is noteworthy that the value of $ \Lambda_{1.4} $ calculated for HPU4 interaction is 556.60 ± 33.67 that satisfies the $ \Lambda_{1.4} \leq 580 $ for GW170817 event with 90% confidence level [1] and also consistent with the findings from [87]. This might be due to the inclusion of CREX results in our fitting protocol during the model optimization that results in soft symmetry energy with its value of linear density dependence $ L_{0} $ = 42.85±14.26 MeV. $ \Lambda_{1.4} $ strongly interelates with $ R_{1.4} $. It can be noticed that observed $ \Lambda_{1.4} $ from GW170817 favors small value of $ R_{1.4} $ and hence smaller value of $ L_{0} $.

Figure 4.  (color online) Correlation between $ \Lambda_{1.4} $ and $ R_{1.4} $. The solid line indicates the fitting line given by $ \Lambda_{1.4} = 2.088\times 10^{-4} $ ($ R_{1.4} $/km)$ ^{5.81} $. The constraints on $ \Lambda_{1.4} $ from GW170817 ($ \Lambda_{1.4} = 190^{+390}_{-120}) $ [1] and GW190814 ($ \Lambda_{1.4} = 616^{+273}_{-158}) $ [83] are also displayed. The theoretical uncertainty on $ \Lambda_{1.4} $ calculated with the HPU4 model is also shown.

Table 5, summarizes HPU4 model results for several characteristics of non-rotating neutron stars. The theoretical uncertainties on the neutron star observables are calculated by using Eqs. (37 and 36) are also listed. We have also shown the results with other models. It can be observed from Table 5 that very small theoretical uncertainties on $ M_{\text{max}} $ (1.97 %), $ R_{\text{max}} $ (0.96 %) and $ R_{1.4} $ (2.18 %) of neutron star are obtained for HPU4 model. The small uncertainties may be because $ M_{\text{max}} $ has been included in the fitting data during the optimization to constrain the EoS in the high-density regime which in turn constrains the coupling ζ. The increased error ($ \approx $ 6 %) for $ \Lambda_{1.4} $ may be because $ \Lambda \propto $ $ R^5 $, showing that accurate Λ measurement can constrain the radius of a compact star within narrower boundaries. To date, it is assumed that no terrestrial experiments can accurately constrain dense matter mass-radius [26].

Properties	HPU4	NL3	FSUGold	FSUGold2	DOPS3	BigApple	HPUC
$ M_{\text{max}} $ ($ M_{\odot} $)	2.03 (0.04)	2.77	1.72	2.07	2.07	2.60	2.04
$ R_{\text{max}} $ (km)	11.41 (0.11)	12.74	10.98	11.87	11.61	12.15	11.57
$ R_{1.4} $ (km)	12.80 (0.28)	14.60	12.45	13.91	13.30	13.12	12.90
$ \Lambda_{1.4} $	556.60 (33.67)	1228.38	401.99	848.97	672.07	715.96	590.83

Table 5.  The properties of nonrotating neutron stars calculated for the HPU4 parameter set. Theoretical uncertainties are also shown within the parenthesis. The results obtained with other RMF models are also displayed.

Fig. 5 shows a graphical representation of the correlation between observables of nuclear matter, and neutron stars with HPU4 model parameters. It can be noticed from Fig. 5 that observables like $ M^{*}/M $, $ E/A $, and K shows moderate to strong correlations with coupling terms $ \overline{\lambda} $, $ \overline{\kappa} $, $ \Lambda_{v} $, $ a_{1} $, $ a_{2} $ and $ b_{1} $. It can be noticed that a weak correlations between $ M^{*}/M $, $ E/A $ and K, and isoscalar parameters $ g_{\sigma N} $, $ g_{\omega N} $ and $ g_{\rho N} $ is observed when mixed interaction terms $ a_{1} $, $ a_{2} $, $ b_{1} $, $ b_{2} $ and $ \Lambda_{v} $ are included in the Lagrangian of HPU4 model. It can also be observed that the values of $ J_{0} $, $ L_{0} $ and $ K_{\text{sym}} $ can be constrained well by the couplings $ \Lambda_{v} $, $ b_{1} $ and $ g_{\rho N} $ as indicated by their correlations. The parameters $ \Lambda_{v} $ and $ b_{1} $ can be used to constrain the $ \Delta r_{\text{np}} $ for $ ^{208} {\rm{Pb}}$ and $ ^{48} {\rm{Ca}}$ nuclei very well as they possess strong correlations between each other. The HPU4 model shows a significant negative correlation of $ M_{\text{max}} $ with ω-meson self-coupling ζ, as expected. $ R_{1.4} $ and $ \Lambda_{1.4} $ are strongly correlated with $ g_{\rho} $ and mixed coupling terms $ \Lambda_{v} $, $ b_{1} $ and $ b_{2} $ incorporated in HPU4 model. It is observed that the correlations of nuclear matter properties in the isovector sector such as $ J_{0} $, $ L_{0} $, $ K_{\text{sym}} $, neutron star observables $ R_{1.4} $, $ \Lambda_{1.4} $ and neutron skin of $ ^{48} {\rm{Ca}}$ and $ ^{208} {\rm{Pb}}$ with couplings $ g_{\rho N} $ and $ \Lambda_{v} $ gets somewhat weaken in HPU4 model as compared to HPUC model [62]. This might be because in the case of the HPU4 model mixed interaction of σ - ρ mesons in addition to $ g_{\rho N} $ and $ \Lambda_{v} $ are incorporated that also constrain the J, L, $ \Delta r_{\text{np}} $, and behavior of EoS in the high-density regime. The dependence of these nuclear matter and neutron star observables on mixed interactions of σ - ρ mesons is also evident from their coefficients of correlation with $ b_{1} $ (σ - $ \rho^{2} $) and $ b_{2} $ ($ \sigma^{2} $ - $ \rho^{2} $).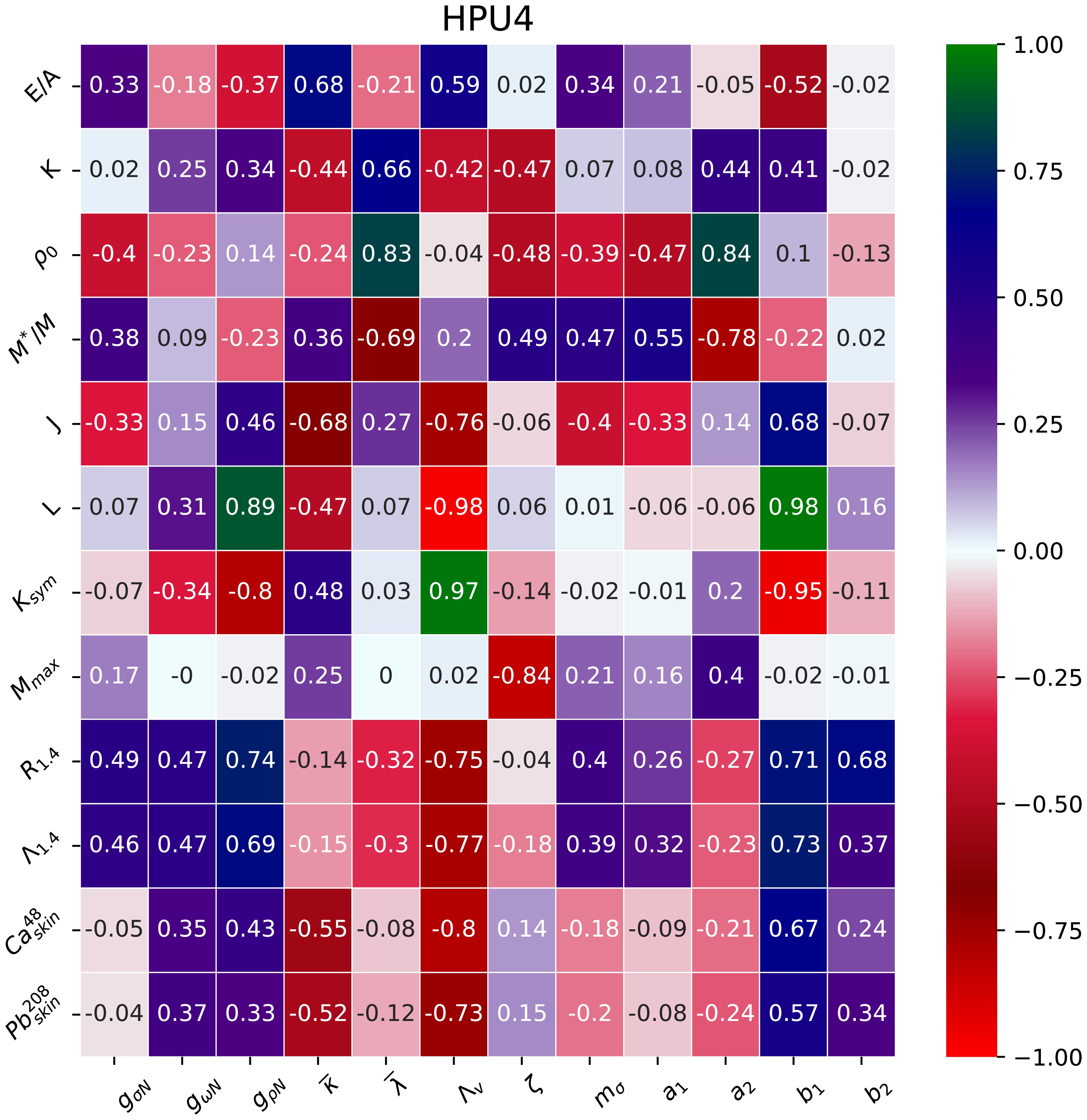

Figure 5.  (Color online) Graphical view of coefficients of correlation between the nuclear observables and parameters of the HPU4 model.

In Fig. 6 we depict the graphical view of coefficients of correlation amongst nuclear matter parameters, neutron star observables, and neutron skin thickness, $ \Delta r_{\text{np}} $ of $ ^{208} {\rm{Pb}}$ and $ ^{48} {\rm{Ca}}$ nuclei. $ \Delta r_{\text{np}} $ of $ ^{208} {\rm{Pb}}$ and $ ^{48} {\rm{Ca}}$ show a strong correlation to each other and show a strong dependence on $ J_{0} $, $ L_{0} $, $ K_{\text{sym}} $ as can be noticed from their correlations. The $ R_{1.4} $ and $ \Lambda_{1.4} $ are strongly intercorrelated (see Fig. 4 also). It can be noticed that the radius $ R_{1.4} $ shows a strong dependence on $ L_{0} $ and $ K_{\text{sym}} $. These results are in close agreement with those in Ref. [54, 55]. $ K_{\text{sym}} $ is also strongly correlated with $ R_{1.4} $ and $ \Lambda_{1.4} $.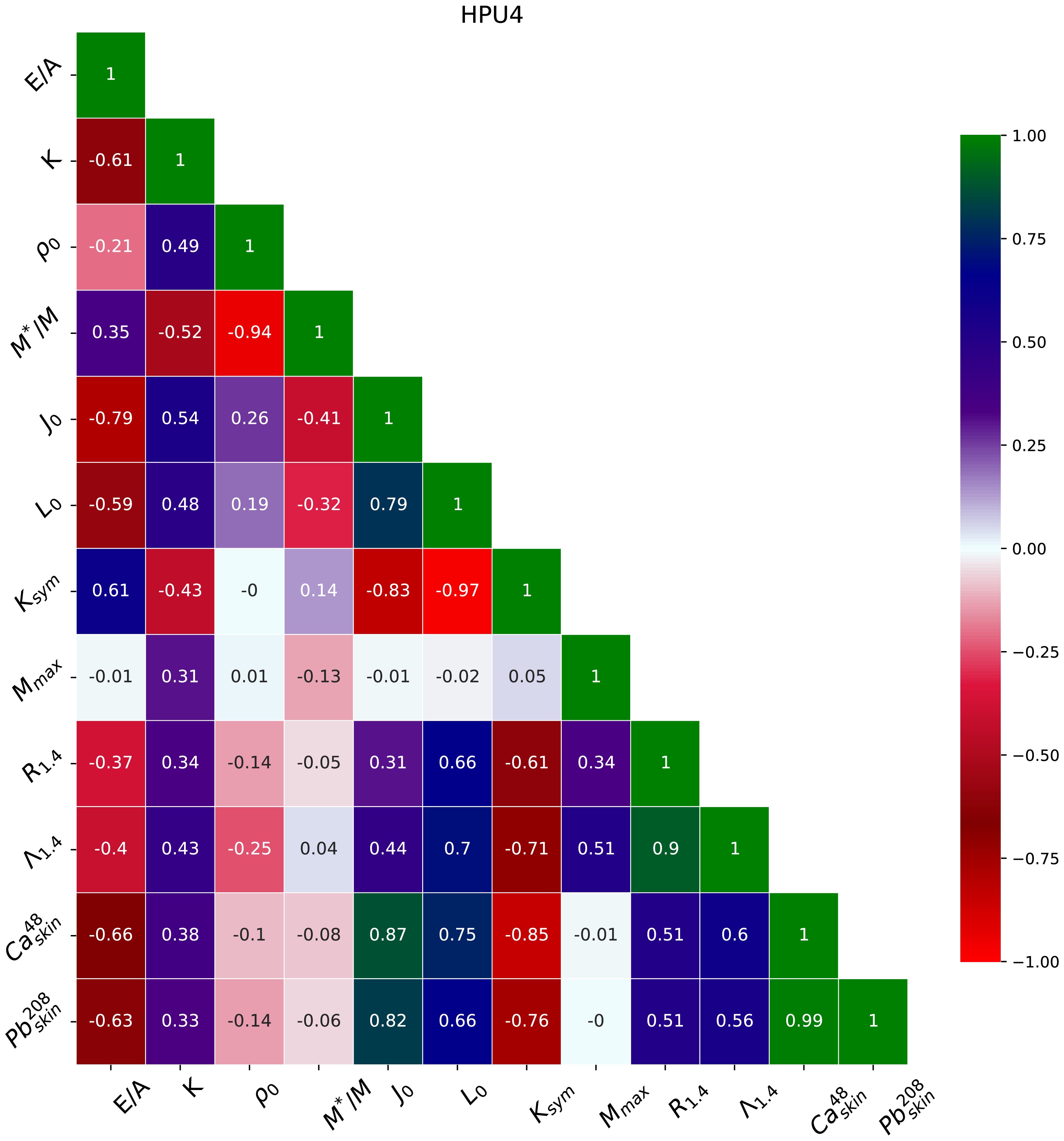

Figure 6.  (Color online) Graphical view of coefficients of correlation amongst nuclear observables for the HPU4 model.

It is noteworthy to mention that in this work, PREX-II results have not been taken into account in the fitting protocol for model optimization. The $ \Delta r_{\text{np}} $ = 0.283 ± 0.071 fm for $ ^{208} {\rm{Pb}}$ as reported from PREX-II favors a stiffer value of L around $ \rho_{0} $ and suggests a stiff EoS that generally leads to a larger value of $ R_{1.4} $ and $ \Lambda_{1.4} $ and does not satisfy the revised limit $ \Lambda_{1.4} $ $ \leq $ 580 for GW170817 event [1]. The contribution from the nucleon -δ meson interaction in the Lagrangian affects the properties of asymmetric nuclear dense matter and plays an important role in understanding the astrophysical observations of neutron stars. The nucleon -δ meson coupling stiffens the nuclear EoS above the saturation density [19, 53]. In this study, we focused on cross-couplings of σ, ω, and ρ mesons to constrain $ J_{0} $ and $ L_{0} $ values and soften EoSs, rather than the nucleon- δ meson interaction (coupling term g$ _{\delta} $) in the Lagrangian. It has been observed that in absence of contribution from δ meson in the Lagrangian, comparatively a larger value of mixed interaction term of $ \omega ^2 $ - $ \rho ^2 $ quantified by the coupling $ \Lambda_{v} $ is required to constrain the values of $ J_{0} $ and $ L_{0} $ when the CREX results are incorporated in the fitting protocol for the model optimizations.

It is also observed that the $ R_{1.4} $ shows good dependence on mixed interaction terms $ b_{1} $ (σ - $ \rho ^2 $) and $ b_{2} $ ($ \sigma^2 $ - $ \rho ^2 $). Here, we have coupling terms $ g_{\rho N} $, $ b_{1} $, $ b_{2} $ and $ \Lambda_{v} $ to constrain $ J_{0} $ and $ L_{0} $. The Cross-coupling terms of mesons are important to reconcile model parameter's naturalness behavior with EFT [24]. Furthermore, it is noticed that the inclusion of the cross-interaction couplings in the Lagrangian has significant effects on the values of L and provides comparatively softer EoSs in medium density regime (required for canonical neutron star mass) and satisfies the revised limit $ \Lambda_{1.4} $ $ \leq $ 580 inferred from GW170817 event as reported in [1].

We have constructed HPU4 interaction using the RMF model with various nucleon-meson couplings by taking the binding energies, charge rms radii of finite nuclei and neutron skin of $ ^{48} {\rm{Ca}}$ from CREX collaborations, the observed mass of astrophysical objects of interest in the fitting technique. The effective interaction illustrates the implications of the CREX results on the finite, symmetric, and asymmetric dense matter. The ground state properties calculated with the HPU4 model, such as binding energies and charge radii, correspond well with experimental results. The rms error of total binding energies (B.E.) and charge radii ($ r_{\text{ch}} $) for finite nuclei used in the fitting process are 2.43 MeV and 0.03 fm, respectively.

We have also performed the covariance analysis in the present work, which helps in estimating the statistical errors on the coupling parameters and physical observables, as well as correlations among them. The value $ \Delta r_{\text{np}} $ for $ ^{208} {\rm{Pb}}$ and $ ^{48} {\rm{Ca}}$ are strongly correlated to each other and show a strong dependence on isovector nuclear parameters $ J_{0} $, $ L_{0} $, and $ K_{\text{sym}} $ as can be noticed from their correlation coefficients. We obtain $ \Delta r_{\text{np}} $ = 0.146 ± 0.019 fm for $ ^{48} {\rm{Ca}}$ with soft symmetry energy ($ J_{0} $ = 27.91 ± 1.31 MeV) and its corresponding linear density dependence ($ L_{0} $ = 42.85 ± 14.26 MeV) at saturation density which is well consistent with the CREX results. We obtain the $ \Delta r_{\text{np}} $ = 0.120 ± 0.025 fm for $ ^{208} {\rm{Pb}}$ which is significantly underestimated from the PREX-II values and is in agreement with the findings reported in [8, 19, 28, 53]. For the HPU4 model, the value of neutron star's $ M_{\text{max}} $ and $ R_{1.4} $ are 2.03(0.04) $ M_{\odot} $ and 12.80 (0.28) km, respectively. Value of $ \Lambda_{1.4} $ equal to 556.60 ± 33.67 for HPU4 parameterization also overlaps with the revised constraint ($ \Lambda_{1.4}\leq $ 580) from GW170817 event [1]. From the present study it is observed that although the mixed interaction terms of σ, ω, and ρ mesons influence the asymmetric nuclear dense matter, they have less impact on finite nuclear properties, once the appropriate calibration of coupling parameters is obtained. A strong correlation of $ R_{1.4} $ with ρ-N coupling g$ _{\rho} $, and mixed interaction terms, $ \sigma\rho_{\mu}\rho^{\mu} $ and $ \sigma^{2}\rho_{\mu}\rho^{\mu} $ is also observed.

Author(s) are highly thankful to Himachal Pradesh University (HPU) for giving access to the computational facilities.