-
Pairing phenomena are observed in a wide range of quantum many-body systems and scales, from finite nuclei to neutron stars [1]. The pairing correlation in the nucleus is originated from the short-range and attractive nuclear interaction between like nucleons; in this case, two nucleons have large spatial overlaps and achieve a low energy. Such two nucleons are called a nucleon pair. This correlation plays an important role in low-lying states, particularly of semi-magic nuclei.
The theoretical formulation of pairing correlation can be traced back to the seniority scheme in a single-j shell [2-4], as suggested by Racah approximately 80 years ago. In 1957, Bardeen, Cooper, and Schrieffer proposed the BCS theory of superconductivity in metal conductors at low temperatures [5, 6]. This approach was introduced to nuclear physics to describe the pairing correlation in Refs. [7-9]. Approximately 50 years ago, Talmi generalized the seniority scheme for semi-magic nuclei with many-j shells [10, 11]. Richardson provided an exact numerical solution to the simplified pairing model, which was applied to various strongly correlated many-body systems owing to its intimate link to several solvable pair models [12]. As an extension of the BCS and generalized seniority scheme, in studies of the low-energy states of semi-magic nuclei, the broke-pair approximation [13] adopts collective-S (spin-zero) nucleon pairs and a very few broken (spin non-zero) nucleon pairs. In the 1970s, Arima and Iachello proposed the interacting boson model (IBM) [14] in which the building blocks,
$ sd $ bosons, are mappings of$ SD $ (spin zero and two) nucleon pairs [15]. Motivated by the IBM, Ginocchio proposed a fermionic model in which$ SD $ nucleon pairs follow dynamical symmetries [16, 17], and this Ginocchio model, called the fermion dynamical symmetry model (FDSM), was further developed by Wu and collaborators [18].In the 1990s, Chen proposed the Wick theorem for coupled fermion pairs [19, 20], and based on this novel technique, Chen established the nucleon-pair shell model (NPSM) [21], which is also called the nucleon-pair approximation (NPA) [22]. This approach was refined to treat both even and odd nuclei in a more sagacious manner [23]. In recent years, the isospin symmetry and particle-hole configuration were considered in the NPA [24, 25]. However, computations become heavy if the valence proton number and/or valence neutron pair number is larger than eight. Therefore, studies on rotational motion for heavy nuclei are prohibitively challenging in these NPA approaches.
During the last two decades, the m-scheme shell model calculations have become increasingly more affordable than the j-scheme shell-model calculations, with a rapid development of computer memory. In Ref. [26], Higashiyama and Yoshinaga expanded the NPA basis states in terms of the m-scheme basis states and conducted NPA calculations using an m-scheme shell model code. Quite recently, He and his collaborators conducted NPA calculations in terms of collective nucleon pairs but without angular-momentum coupling between pairs [27] and called their approach a nucleon-pair shell model in the m scheme. Because the approach in Ref. [27] does not resort to the angular-momentum couplings of nucleon pairs, it is more realizable than the transitional NPA calculations in Refs. [21, 22, 26]; however, the commutators between nucleon pair operators and one-body (or two-body) operators remain to be the same as in the NPA approach in Refs. [21, 22] and thus still suffer from sophisticated angular-momentum couplings and re-couplings.
In this paper, we propose an NPA approach, in which one resorts neither to angular-momentum couplings and re-couplings in the evaluation of commutators between collective nucleon pairs, nor to the couplings and re-couplings of “new” nucleon pairs in the basis states. Namely, angular-momentum couplings and re-couplings are avoided from the beginning to the end of the computation.
Toward this goal, we adopt the uncoupled representation of collective nucleon pairs. An uncoupled representation was developed many years ago by Silvestre-Brac and Piepenbring in studies on multi-phonon states [28-30]. In addition, Ginocchio and Johnson derived a similar formalism based on generating functions [31], and Mizusaki and Otsuka adopted an uncoupled representation in studies of the shell-model foundation of the IBM [32]. Otsuka
$ et.\; al. $ also used it to formulate a pair truncation of the Monte Carlo shell model [33].In this study, we developed this uncoupled representation for collective nucleon pairs and derived commutators, overlaps of the NPA m-scheme basis states, and matrix elements of the shell-model Hamiltonian under such basis. The NPA with and without isospin symmetry, for even-even nuclei and odd-mass nuclei, is presented in the unified formulation. By using this version of the NPA, numerical calculations of the rotational states for heavy nuclei are now readily realizable.
This paper is organized as follows. In Sec. II, we define the uncoupled representation of collective nucleon pairs as well as one- and two-body operators and present commutators between nucleon pairs and/or operators. In this section, we also clarify how to utilize this representation to describe the concept of a “conventional” NPA [21, 22]. In Sec. III, we derive overlaps and the matrix elements of the shell model Hamiltonian for both even and odd systems. In Sec. IV, we demonstrate the computation power of our new approach. In Sec. V, we describe the sources of such remarkable computation power. Finally, in Sec. VI, we provide some concluding remarks regarding this study.
-
In this section, we describe an uncoupled representation of collective nucleon pairs, one-body and two-body operators, and unpaired particles in the NPA framework, as well as commutators between them.
-
We define collective nucleon-pair creation and annihilation operators as follows:
$ \begin{aligned}[b] \hat{P}^{\dagger} =& \frac{1}{2}\sum\limits_{\alpha \beta} p(\alpha \beta) \hat{c}^{\dagger}_\alpha \hat{c}^{\dagger}_\beta,\\ \hat P = & (\hat P^{\dagger})^{\dagger} = -\frac{1}{2}\sum\limits_{\alpha \beta} p(\alpha \beta) \hat{c}_\alpha \hat{c}_\beta, \end{aligned} $

(1) where
$ \alpha $ and$ \beta $ denote the orthonormal single-particle basis, and$ \hat{c}^{\dagger} \; (\hat{c}) $ is a fermion creation (annihilation) operator. For example, in a spherical basis,$ \alpha / \beta $ corresponds to the$ \{nljm\} $ quantum numbers or$ \{nljm\tau\} $ with an extra isospin projection,$ \tau $ .$ p(\alpha \beta) $ are a pair of structural coefficients, with anti-symmetry$ p(\alpha \beta) = - p(\beta \alpha) $ ; here,$ p(\alpha \beta) $ are treated as matrix elements of matrix p.Conventionally, a collective nucleon pair operator in the NPA is defined as
$ \begin{aligned}[b] A^{r\dagger}_m =& \sum\limits_{a b} y(abr)A^{r\dagger}_m (ab),\\ A^{r\dagger}_m(ab) =& \left( \hat c^{\dagger}_a \times \hat c^{\dagger}_b \right)^{r}_m, \\ A^{r}_m =& \sum\limits_{a b} y(abr) A^{r}_m (ab),\\ A^{r}_m(ab) =& \left(A^{r\dagger}_m(ab)\right)^{\dagger} = -\left(\hat c_a \times \hat c_b \right)^{r}_m, \end{aligned} $

(2) where r and m are the angular momentum of the pair and its projection to the principal axis, respectively; a and b represent the quantum numbers of a spherical single-particle basis, {
$ nlj $ }; the symbol$ \times $ corresponds to angular-momentum couplings; and$ y(abr) $ is the structural coefficient of the collective pair. In addition,$ y(abr) $ has an anti-symmetric property as$ y(abr) = -(-)^{r-j_a-j_b}y(bar) $ . Eq. (2) seems to differ from Eq. (1). However, we can specialize the structural matrix as$ p(am_a,bm_b) = 2y(abr)\langle j_am_aj_bm_b|rm\rangle, $

(3) where
$ \alpha\equiv am_a $ and$ \beta\equiv bm_b $ . In addition,$ m_a $ and$ m_b $ are the projections of$ j_a $ and$ j_b $ onto principal axis, and$ \langle j_am_aj_bm_b|rm\rangle $ is the Clebsch-Gorden coefficient. One can easily see that$ p(am_a,bm_b) = - p(bm_b, am_a) $ , given$ y(abr) = -(-)^{r-j_a-j_b}y (bar) $ , corresponding to the anti-symmetry of the structural matrix. The collective pair with such defined structural matrix is$ \hat P^{\dagger}=\sum\limits_{am_a,bm_b}p(am_a,bm_b)\hat c^{\dagger}_{am_a}c^{\dagger}_{bm_b} \equiv A^{r\dagger}\;. $

For the NPA with isospin, the collective nucleon pair is
$ \begin{aligned}[b] A^{r{\mathbbm t}\dagger}_{m\tau} =& \sum\limits_{a b} y(abr{\mathbbm t})A^{r{\mathbbm t}\dagger}_{m\tau} (ab),\\ A^{r{\mathbbm t}\dagger}_{m\tau}(ab) = &\left( \hat c^{\dagger}_a \times \hat c^{\dagger}_b \right)^{r{\mathbbm t}}_{m\tau}, \\ A^{r{\mathbbm t}}_{m\tau} =& \sum\limits_{a b} y(abr{\mathbbm t}) A^{r{\mathbbm t}}_{m\tau} (ab),\\ A^{r{\mathbbm t}}_{m\tau}(ab) =& \left(A^{r{\mathbbm t}\dagger}_{m\tau}(ab)\right)^{\dagger} = -\left(\hat c_a \times \hat c_b \right)^{r{\mathbbm t}}_{m\tau}, \end{aligned} $

(4) where
$ {\mathbbm t} $ and$ \tau $ is the isospin and its projection to the principal axis, and the structural coefficients$ y(abr{\mathbbm t}) $ have an anti-symmetry of$ y(bar{\mathbbm t}) = (-)^{r-j_a-j_b+{\mathbbm t}}y(abr\mathbb) $ . Similarly, we define our collective pair as$ \hat P^{\dagger} = \sum\limits_{am_a\tau_a;bm_b\tau_b}p(am_a\tau_a,am_b\tau_b)\hat c^{\dagger}_{am_a\tau_a}\hat c^{\dagger}_{bm_b\tau_b} $

(5) with
$ \begin{aligned}[b] p(am_a\tau_a,bm_b\tau_b) =& 2y(abr{\mathbbm t})\left\langle j_am_aj_bm_b|rm\right\rangle \\ &\times\left\langle\frac{1}{2}\tau_a\frac{1}{2}\tau_b|{\mathbbm t}\tau\right\rangle, \end{aligned} $

(6) where
$ \alpha\equiv am_a\tau_a $ ,$ \beta\equiv bm_b\tau_b $ , and$ \tau_a $ and$ \tau_b $ are the single-particle isospin projections. The structural coefficients$ p(am_a\tau_a,bm_b\tau_b) $ satisfy the requirement$ p(bm_b\tau_b,am_a\tau_a) = - p(am_a\tau_a, b m_b\tau_b) \;, $

given
$ y(bar{\mathbbm t}) = (-)^{r-j_a-j_b+{\mathbbm t}}y(abr\mathbb) $ , and the collective nucleon-pair operator such defined is equivalent to$ A^{r{\mathbbm t}\dagger} $ .A general one-body operator in an uncoupled representation is defined as
$ \hat{Q} = \sum\limits_{\alpha \beta} q(\alpha \beta) \hat{c}^{\dagger}_\alpha \hat{c}_{\beta}, $

(7) where the coefficients
$ q(\alpha \beta) $ also construct a matrix q. Accordingly, the conjugate operator of$ \hat Q $ , i.e.,$ \hat Q^{\dagger} $ , has its structural matrix as$ q^\top $ , i.e., the transpose matrix of q.A conventional one-body operator in the NPA is in following form:
$ Q^k_{\kappa} = \sum\limits_{ab}{q}(abk)(c^{\dagger}_a\times \tilde c_b)^k_{\kappa},\;\; Q^{k{\mathbbm t}}_{\kappa\tau} = \sum\limits_{ab}{q}(abk{\mathbbm t})(c^{\dagger}_a\times \tilde c_b)^{k{\mathbbm t}}_{\kappa\tau}, $

(8) where
$ q(abk) $ and$ q(abk{\mathbbm t}) $ correspond to structural coefficients of the one-body operator in the NPA with and without isospin, respectively. In addition,$ \tilde c_{b} $ is the time-reversal operator of$ c_{b} $ with$ \tilde c_{j_bm_b} = (-)^{j_b-m_b}c_{j_b-m_b} $ and$ \tilde c_{j_bm_b\tau_b} = (-)^{j_b-m_b+1/2-\tau_b} $ $ c_{j_b-m_b-\tau_b} $ . The one-body operator is readily rewritten in the form of Eq. (7) as follows:$ \begin{aligned}[b] Q^k_{\kappa}& = \sum\limits_{am_a,bm_b}q(am_a,bm_b)\hat c^{\dagger}_{am_a}\hat c_{bm_b},\\ Q^{k{\mathbbm t}}_{\kappa\tau}& = \sum\limits_{am_a\tau_a,bm_b\tau_b}q(am_a\tau_a,bm_b\tau_b)\hat c^{\dagger}_{am_a\tau_a}\hat c_{bm_b\tau_b},\\ \end{aligned} $

(9) with
$ \begin{aligned} & q(am_a,bm_b) = (-)^{j_b+m_b} q(abk) \left\langle j_am_aj_b-m_b|k\kappa\right\rangle\;, \\ &q(am_a\tau_a,bm_b\tau_b) = (-)^{j_b+m_b+\frac{1}{2}+\tau_b} q(abk{\mathbbm t}) \\ & \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \left\langle j_am_aj_b-m_b|k\kappa\right\rangle \left\langle \frac{1}{2}\tau_a\frac{1}{2}-\tau_b|{\mathbbm t}\tau\right\rangle\;. \end{aligned} $

In most cases, one-body operators in the NPA are hermitian or anti-hermitian, corresponding to
$ \begin{aligned}[b] \left(Q^k_{\kappa}\right)^{\dagger} = &\pm (-)^{k-\kappa}Q^k_{-\kappa},\\ \left(Q^{k{\mathbbm t}}_{\kappa\tau}\right)^{\dagger} = &\pm (-)^{k-\kappa+{\mathbbm t} -\tau}Q^{k{\mathbbm t}}_{-\kappa-\tau},\\ \end{aligned} $

(10) and
$ \begin{aligned}[b] q^k_{\kappa}(am_a,bm_b) = &\pm q^k_{-\kappa}(bm_b,am_a),\\ q^{k\mathbbm t}_{\kappa\tau}(am_a\tau_a,bm_b\tau_b) = &\pm q^{k\mathbbm t}_{-\kappa-\tau}(bm_b\tau_b,am_a\tau_a), \end{aligned} $

(11) respectively.
In an odd-nucleon system, an unpaired nucleon is represented using a linear combination of a single-particle basis state:
$ \hat{a}^\dagger | 0 \rangle = \sum\limits_\alpha a_\alpha \hat{c}^\dagger_\alpha | 0 \rangle, $

(12) where
$ a_\alpha $ are structural coefficients of$ \hat{a}^\dagger $ ; in addition, when the unpaired nucleon occupies a given single-particle level$ \alpha $ ,$ a_\alpha = 1 $ and$ a_{\alpha'} = 0 $ $ (\alpha' \neq \alpha) $ . Similarly, the coefficients$ a_\alpha $ construct a column vector$ \vec{a} $ .Our nucleon-pair basis states of uncoupled representation is given by the following:
$ \left.\left.\hat{P}^{\dagger}_0 \hat{P}^{\dagger}_1 \hat{P}^{\dagger}_2 \cdots \hat{P}^{\dagger}_N \right|0\right\rangle $

(13) with
$ \hat P_0^\dagger = \left\{ {\begin{array}{*{20}{c}} 1&{\;{\rm{in}}\;{\rm{even}}\;{\rm{system}}}\\ {{{\hat a}^\dagger }}&{\;{\rm{in}}\;{\rm{odd}}\;{\rm{system}}} \end{array}} \right.. $

Alternatively, we can also rewrite the above basis in a conventional NPA style,
$ \left.\left.A^{\dagger}_0A^{r_1({\mathbbm t}_1)\dagger}_{m_1(\tau_1)}A^{r_2({\mathbbm t}_2)\dagger}_{m_2(\tau_2)}\cdots A^{r_N({\mathbbm t}_N)\dagger}_{m_N(\tau_N)}\right|0\right\rangle\\ $

(14) with
$ \hat A_0^\dagger = \left\{ {\begin{array}{*{20}{c}} 1&{\;{\rm{for}}\;{\rm{an}}\;{\rm{even - even}}\;{\rm{nucleus}}}\\ {\hat c_{jm(\tau )}^\dagger }&{\;{\rm{for}}\;{\rm{an}}\;{\rm{odd}}\;{\rm{mass}}\;{\rm{nucleus}}} \end{array}} \right., $

where the parentheses of
$ {\mathbbm t} $ and$ \tau $ indicate again that the isospin degree of freedom might be suppressed. The above m-scheme basis states do not have given angular momentum, but a diagonalization of the shell model Hamiltonian yields the same wave functions and eigen-energies as the NPA calculations once the configuration space in the form of the above basis states is complete. The dimensions of the above basis states are also equal to those of the NPA configuration space, as pointed out in Ref. [27].By using notations of Eqs. (3) and (9), the shell-model Hamiltonian of like nucleons are as follows:
$ \begin{aligned}[b] H_{\rm{like}} =& \sum\limits_a\varepsilon_a \sum\limits_{m_a\tau_a}c^{\dagger}_{j_am_a(\tau_a)}c_{j_am_a(\tau_a)}\\ &+\sum\limits_{L({{\mathbbm t}}),i}G^i_{L({{\mathbbm t}})}\sum\limits_{m(\tau)}A^{L({{\mathbbm t}})\dagger}_{m(\tau)}(y_i)A^{L({{\mathbbm t}})}_{m(\tau)}(y_i)\\ &+\sum\limits_{ k({{\mathbbm t}}),i}F^i_{k({{\mathbbm t}})}\sum\limits_{\kappa\tau}Q^{k({{\mathbbm t}})}_{\kappa(\tau)}( q_i)Q^{k({{\mathbbm t}})\dagger}_{\kappa(\tau)}(q_i), \end{aligned} $

(15) where the parentheses of
$ {\mathbbm t} $ and$ \tau $ indicate that the isospin degree of freedom can be suppressed for interactions between like valence nucleons. The three terms in this Hamiltonian corresponds to a one-body term, multipole pairing interaction, and multipole-multipole interaction, respectively, where$ \varepsilon_{a} $ , G, and F are the single-particle energy and interaction strengths of multipole pairing and multipole-multipole interaction. We distinguish$ A^{L({{\mathbbm t}})\dagger}_{m(\tau)}A^{L({{\mathbbm t}})}_{m(\tau)} $ (and$ Q^{k({{\mathbbm t}})}_{\kappa(\tau)}Q^{k({{\mathbbm t}})\dagger}_{\kappa(\tau)} $ terms) with different$ y_i $ (or$ q_i $ ) matrices but the same$ L({{\mathbbm t}}) $ (or$ k({{\mathbbm t}}) $ ) quantum number(s). The one-body single-particle term can be rewritten in the form of Eq. (7) as$ \sum\limits_a\varepsilon_a \sum\limits_{m_a\tau_a}c^{\dagger}_{j_am_a(\tau_a)}c_{j_am_a(\tau_a)} = \sum\limits_{\alpha \beta} q(\alpha \beta) \hat{c}^{\dagger}_{\alpha} \hat{c}_{\beta} \;, $

where
$\begin{aligned}& q(\alpha \beta) \equiv q\left(am_a(\tau_a),bm_b(\tau_b)\right) \\& = \delta_{ab}\delta_{m_am_b}(\delta_{\tau_a\tau_b})\varepsilon_{a} \;. \end{aligned}$

The proton-neutron interaction in the particle-hole channel is written as follows:
$ H_{\pi\nu} = \sum\limits_{k,i}F^i_{k}\sum\limits_{\kappa}Q^{k}_{\kappa}(q_{\pi,i})(-)^{\kappa}Q^{k}_{-\kappa}(q_{\nu,i}), $

(16) where
$ \pi $ and$ \nu $ correspond to proton and neutron degrees of freedom, respectively, and label i is introduced to distinguish$ Q^{k}_{\kappa}(q_{\pi})(-)^{\kappa}Q^{k}_{-\kappa}(q_{\nu}) $ interactions with the same k but different$ q_{\pi,i} $ and$ q_{\nu,i} $ matrices of structural coefficients.From the description in this subsection, we showed that the collective pair in the NPA as well as one-body and two-body interactions of the nuclear shell model can be formulated with the uncoupled representation. The formulas in the following sections are applicable to the NPA calculation, with the basis states written in the form of Eqs. (13) or (14). We can see clearly that the uncoupled representation of the NPA is formulated in a unified way, for both even-even nuclei and odd-mass nuclei, and both with and without isospin symmetry.
-
In this subsection, we present key commutators between one nucleon-pair operator and one-body operator in a decoupled form, as defined in the last subsection.
The commutator between a nucleon-pair annihilation operator and nucleon-pair creation operator is easily obtained as follows:
$ \left[ \hat{P}_1, \hat{P}^{\dagger}_2 \right] = - \frac{1}{2} {\rm{tr}}\left( p_2 p_1 \right) + \hat{\cal Q}. $

(17) where
$ p_1, p_2 $ are structure matrices of$ \hat{P}_1, \hat{P}_2 $ ,$ {\rm{tr}}( p_2 p_1 ) $ indicates the trace of matrix product$ p_2 p_1 $ , and$ \hat{\cal Q} $ is a one-body operator$ \hat{\cal Q} = \sum\limits_{\alpha \beta} {\cal q}(\alpha \beta) \hat{c}^{\dagger}_\alpha \hat{c}_{\beta}\;, $

with structural matrix
$ {\cal q} = p_2 p_1\;. $

Similarly, the commutator between nucleon-pair annihilation operator,
$ \hat{P}_3 $ , and one-body operator,$ \hat{Q} $ , yields another nucleon-pair annihilation operator$ \hat P_4 $ ,$ {\hat P_4} = [{\hat P_3},\hat Q]\;,\;\;\;{\rm{with}}\;\;\;{p_4} = {p_3}q + {q^ \top }{p_3}\;,$

(18) where
$ p_3 $ and$ p_4 $ are structural coefficient matrices of$ \hat{P}_3 $ and$ \hat P_4 $ , respectively. In some cases, Eq. (18) can be further simplified. For example, if the Q operator is from the commutator between$ \hat P_3 $ and another arbitrary pair creation operator$ \hat P^\dagger_5 $ , i.e.,$ q = p_5p_3 $ according to Eq. (17), the two parts of the right-hand side of Eq. (18) become equivalent according to the anti-symmetry of$ p_3 $ and$ p_5 $ , and this equation then is reduced to$ p_4 = 2p_3p_5p_3 $ . We frequently observe such a reduction in usual NPA calculations.The single-particle operators follow the following relation:
$ \hat{a} \hat{b}^\dagger = \left\{ \hat{a}, \hat{b}^\dagger \right\} - \hat{b}^{\dagger} \hat{a} = \vec{a} \cdot \vec{b} - \hat{\mathbb{Q}}, $

(19) where
$ \vec{a} \cdot \vec{b} $ is the inner product of vectors$ \vec{a} $ and$ \vec{b} $ , and$ \hat{\mathbb{ Q}} $ is a one-body operator with structural matrix$ \mathbbm{q} = \vec{b} \vec{a}^\top $ .The commutator between single-particle annihilation operator,
$ \hat{a} $ , and one-body operator,$ \hat{Q} $ , yields another single-particle annihilation operator,$ \hat{d} $ ,$\begin{aligned}[b]& \hat d = [\hat a,\hat Q] = \sum\limits_\alpha {{d_\alpha }} {\hat c_\alpha }\;,\;\;\;{\rm{with}}\\& \vec d = {q^ \top }\vec a\;,\end{aligned} $

(20) where vector
$ \vec d $ represents the structural coefficient$ \hat{d} $ operator.The commutator between single-particle annihilation operator,
$ \hat{a} $ , and pair creation operator,$ \hat P^{\dagger} $ , produces a single-particle creation operator,$ \hat{d}^{\dagger} $ ,$\begin{aligned}[b] & \hat{d}^{\dagger} = [ \hat{a}, \hat P^{\dagger}] = \sum\limits_{\alpha} d_{\alpha} \hat{c}^{\dagger}_{\alpha} \;, \; \;\; {\rm{with}}\\& \vec d = -p \vec a\;, \end{aligned} $

(21) where, again,
$ \vec d $ represents structural coefficient$ \hat{d}^{\dagger} $ operator. -
By using Eqs. (17) through (21), one easily derives the commutator between N nucleon-pair annihilation operator and one-body operator,
$ \left[\hat P_0\hat P_1\right.\left.\cdots \hat P_N,\hat Q\right] = \sum\limits_{k = 0}^N \hat P_0\cdots \hat P_{k-1}\left[P_k,\hat Q\right]\hat P_{k+1}\cdots \hat P_N, $

(22) where
$ \left[\hat P_k,\hat Q\right] = \left\{ \begin{array}{llll} {\hat{\cal P}}_k&{\rm{with}}& {\cal{p}_k} = p_kq+q^{\top}p_k&k\neq 0 \;, \\ \hat d&{\rm{with}}&\hat P_0 = \hat a \;{\rm{and}}\; \vec d = q^\top \vec a&k = 0 \;. \end{array} \right. $

(23) Similarly, one derives commutators between N nucleon-pair annihilation operators and one nucleon-pair creation operator,
$ \begin{aligned}[b] \left[\hat P_0\hat P_1\cdots \hat P_N,\hat{\mathbb{ P}}^{\dagger} \right] =& \sum\limits_{k = 0}^N \hat P_0\cdots \hat P_{k-1}\left[P_k,\hat{ \mathbb {P}}^{\dagger}\right]\hat P_{k+1}\cdots \hat P_N\\ & = \sum\limits_{k = 1}^N -\frac{1}{2}{\rm{tr}}(\mathbbm { p} p_k)\hat P_0\cdots \hat P_{k-1}\hat P_{k+1}\cdots \hat P_N\\ &+\sum\limits_{k = 1}^N \hat P_0\cdots \hat P_{k-1}\hat{\cal Q}_k\hat P_{k+1}\cdots \hat P_N\\&+\left.\hat h^{\dagger}\hat P_1\cdots \hat P_N\right|_{{\rm{in}}\;{\rm{odd}}\;{\rm{system}}}, \end{aligned} $

(24) where the one-body operator
$ \hat{\cal{Q}}_k $ has a structural matrix$ {\cal q}_k = \mathbbm { p}p_k $ , and the single-particle creation operator$ \hat h^{\dagger} $ has structural coefficients represented by$ \vec{h} = - \mathbbm{p} \vec{a} $ . The$ \hat P_0\cdots \hat P_{k-1}\hat{\cal Q}_k $ term in the second term of the right-hand side of the above equation is re-organized as follows,$\begin{aligned}[b] \hat P_0\cdots \hat P_{k-1}\hat{\cal Q}_k =& \left[\hat P_0\cdots \hat P_{k-1},\hat{\cal Q}_k\right]+\hat{\cal Q}_k\hat P_0\cdots \hat P_{k-1} \\=& \sum\limits_{i = 0}^{k-1}\hat P_0\cdots \hat P_{i-1}\left[\hat P_i,\hat{\cal Q}_k\right]P_{i+1}\cdots \hat P_{k-1}\\&+\hat{\cal Q}_k\hat P_0\cdots \hat P_{k-1},\end{aligned} $

(25) where
$ \left[\hat P_i,\hat{\cal Q}_k\right] = \left\{ \begin{array}{llll} \hat{\cal P}_{i,k}&{\rm{with}}&{\cal p}_{i,k} = p_i \mathbbm {p} p_k+p_k \mathbbm {p} p_i&i\neq 0 \;,\\ \hat e_k&{\rm{with}}&\hat P_0 = \hat a\;{\rm{and}}\;\vec e_k = p_k \mathbbm {p} \vec a&i = 0 \;. \end{array} \right. $

(26) From Eqs. (24) and (25), we have the following:
$ \begin{aligned}[b] \left[\hat P_0\hat P_1\cdots \hat P_N,\hat{ \mathbb {P}}^{\dagger} \right] =& \sum\limits_{k = 1}^N -\frac{1}{2}{\rm{tr}}( {\mathbbm p} p_k)\hat P_0\cdots \hat P_{k-1}\hat P_{k+1}\cdots \hat P_N\\&+\sum\limits_{k = 2}^N\sum\limits_{i = 1}^{k-1}\hat P_0\cdots\hat P_{i-1}\hat{{\cal P}_{i,k}}\hat P_{i+1}\cdots\hat P_{k-1}\hat P_{k+1}\cdots\hat P_N \\ &+\left.\sum\limits_{k = 1}^N \hat e_k\cdots \hat P_{k-1}\hat P_{k+1}\cdots \hat P_N\right|_{{\rm{odd}}\;{\rm{system}}}\\ &+\sum\limits_{k = 1}^N\hat{\cal Q}_k \hat P_0\cdots \hat P_{k-1}\hat P_{k+1}\cdots \hat P_N\\&+\left.\hat d^{\dagger}\hat P_1\cdots \hat P_N\right|_{{\rm{odd}}\;{\rm{system}}}, \end{aligned} $

(27) where
$ {\cal p}_{i,k} $ and$ \vec e_k $ are as given in Eq. (26).The two-body interaction operator are written in the form of
$ \hat A^\dagger \hat B $ , where$ \hat A $ is a collective nucleon-pair creation operator with structural matrix$ p_A $ , and B is a collective nucleon-pair annihilation operator. From Eq. (27), we have$ \begin{aligned}[b] \left[\hat P_0\hat P_1\cdots \hat P_N,\hat{A}^{\dagger}\hat B \right] =& \sum\limits_{k = 1}^N -\frac{1}{2}{\rm{tr}}(p_A p_k)\hat P_0\cdots \hat P_{k-1}\hat B\hat P_{k+1}\cdots \hat P_N+\sum\limits_{k = 2}^N\sum\limits_{i = 1}^{k-1}\hat P_0\cdots \hat P_{i-1}\hat{{\cal P}_{i,k}}\hat P_{i+1}\cdots\hat P_{k-1}\hat B\hat P_{k+1}\cdots \hat P_N\\ &+\left.\sum\limits_{k = 1}^N \hat e_k\cdots \hat P_{k-1}\hat B\hat P_{k+1}\cdots \hat P_N\right|_{{\rm{in}}\;{\rm{odd}}\;{\rm{system}}}+\sum\limits_{k = 1}^N\hat{\cal Q}_k \hat P_0\cdots \hat P_{k-1}\hat B\hat P_{k+1}\cdots \hat P_N+\left.\hat d^{\dagger}\hat P_1\cdots \hat P_N\right|_{{\rm{odd}}\;{\rm{system}}}, \end{aligned} $

(28) where the structural coefficients of operators
$ \hat{{\cal P}_{i,k}} $ ,$ \hat e_k $ , and$ \hat{\cal Q}_k $ are the same as in Eq. (26), with the replacement of$ \mathbbm {p} $ when using$ p_A $ .The two-body operator in a particle-hole channel is written in the form of
$ \hat Q \hat Q^{\dagger} $ . We then readily have$ \begin{aligned}[b] \left[\hat P_0\hat P_1\cdots \hat P_N,\hat Q \hat Q^{\dagger}\right]& = \left[\hat P_0\hat P_1\cdots \hat P_N,\hat Q \right]\hat Q^{\dagger}+\hat Q \left[\hat P_0\hat P_1\cdots \hat P_N,\hat Q^{\dagger} \right]\\ & = \left[\left[\hat P_0\hat P_1\cdots \hat P_N,\hat Q \right],\hat Q^{\dagger}\right]+\hat Q^{\dagger}\left[\hat P_0\hat P_1\cdots \hat P_N,\hat Q \right]+\hat Q \left[\hat P_0\hat P_1\cdots \hat P_N,\hat Q^{\dagger} \right]. \end{aligned} $

(29) The iterative application of Eq. (22) to the above commutator yields
$ \begin{aligned}[b] \left[\left[\hat P_0\hat P_1\cdots \hat P_N,\hat Q \right],\hat Q^{\dagger}\right]=& \left[\sum\limits_{k = 0}^{N}\hat P_0\cdots \hat P_{k-1}\left[\hat P_{k+1},\hat Q\right]\hat P_{k+1}\cdots \hat P_N,\hat Q^{\dagger}\right]\\ =& \sum\limits_{k,i = 0}^{N,k\neq i}\hat P_0 \cdots \left\{ \begin{array}{cc} \hat{P}_{i-1} \left[\hat P_i,\hat Q^{\dagger }\right] \hat{P}_{i+1} \cdots \hat{P}_{k-1} \left[\hat P_k,\hat Q\right] \hat{P}_{k+1}&i<k\\ \hat{P}_{k-1} \left[\hat P_k,\hat Q\right] \hat{P}_{k+1}\cdots \hat{P}_{i-1}\left[\hat P_i,\hat Q^{\dagger }\right] \hat{P}_{i+1} &k<i\\ \end{array} \right\} \cdots \hat P_N\\ &+\sum\limits_{k = i = 0}^N \hat P_0 \cdots \hat{P}_{k-1} \left[\left[\hat P_k,\hat Q\right],\hat Q^{\dagger}\right] \hat{P}_{k+1}\cdots \hat P_N, \end{aligned} $

(30) where
$ \begin{aligned}[b] &\left[\hat P_k,\hat Q \right] = \left\{ \begin{array}{llll} \hat{\cal P}_k&{\rm{with}}&{\cal p}_k = p_kq+q^\top p_k&k\neq 0\\ \hat e&{\rm{with}}&\hat P_0 = \hat a \;{\rm{and}}\;\vec e = q^\top \vec a&k = 0\\ \end{array} \right.,\; \left[\hat P_i,\hat Q^{\dagger} \right] = \left\{ \begin{array}{llll} \hat{\cal{P}}_i&{\rm{with}}& {\cal{p}}_i = p_iq^\top+q p_i&i\neq 0\\ \hat f&{\rm{with}}&\hat P_0 = \hat a \;{\rm{and}}\;\vec f = q^\top \vec a&i = 0\\ \end{array} \right.,\\ &\left[\left[\hat P_k,\hat Q \right],\hat Q^{\dagger}\right] = \left\{ \begin{array}{llll} \hat{\mathfrak P}_k&{\rm{with}}&\mathfrak p_k = p_k q q^\top + q^\top p_k q^\top + q p_k q + q q^\top p_k&k\neq 0\\ \hat g&{\rm{with}}&\hat P_0 = \hat a \;{\rm{and}}\;\vec g = qq^\top \vec a&k = 0\\ \end{array} \right.. \end{aligned} $

(31) Substituting this result into Eq. (29), we have the following:
$ \begin{aligned}[b] \left[\hat P_0\hat P_1\cdots \hat P_N,\hat Q \hat Q^{\dagger}\right] =& \sum\limits_{k,i = 1}^{N,k\neq i}\hat P_0 \cdots \left\{ \begin{array}{cc} \hat{P}_{i-1} \hat{\cal P}_i \hat{P}_{i+1} \cdots \hat{P}_{k-1} \hat{\cal P}_k \hat{P}_{k+1}&i<k\\ \hat{P}_{k-1} \hat{\cal P}_k \hat{P}_{k+1}\cdots \hat{P}_{i-1}\hat{\cal P}_i \hat{P}_{i+1} &k<i\\ \end{array} \right\} \cdots \hat P_N\\ &+\sum\limits_{k = i = 1}^N \hat P_0\cdots\hat{P}_{k-1} \hat{\mathfrak P}_k \hat{P}_{k+1}\cdots \hat P_N\\ &\left.+\left\{\sum\limits_{i = 1}^{N}\hat e \hat{P}_{k-1} \hat{\cal P}_k \hat{P}_{k+1}\cdots \hat P_N+\sum\limits_{k = 1}^{N}\hat f \hat{P}_{i-1} \hat{\cal P}_i \hat{P}_{i+1}\cdots \hat P_N+\hat g\cdots \hat P_N\right\}\right|_{{\rm{odd}}\;{\rm{system}}}\\ &+\hat Q^{\dagger}\left[\hat P_0\hat P_1\cdots \hat P_N,\hat Q \right]+\hat Q \left[\hat P_0\hat P_1\cdots \hat P_N,\hat Q^{\dagger} \right]. \end{aligned} $

(32) -
In this section, we present general formulas for overlaps of the basis states and the matrix elements of the Hamiltonian matrix elements. Some formulas are in a similar form as those in Refs. [29, 30]; the essential difference is that, in Refs. [29,30], the phonon states were treated with quasi-particle pairs, whereas herein we adopt the m-scheme NPA basis states constructed from valence-nucleon pairs. As in the previous NPA formulation [21, 23-25], in this section, we first discuss the overlaps of the basis states for systems without an unpaired nucleon. The overlaps for an odd-mass nucleus is then presented in terms of matrix elements of one-body operators in the basis states of its even-even neighboring nucleus, and the matrix elements of the shell-model Hamiltonian for an odd-mass nucleus are written in terms of overlaps of basis states for this odd-mass nucleus. Therefore, the evaluation of the overlaps for the basis states without an unpaired nucleon is the key computation, as in the previous versions of the NPA in Refs. [21, 23-25, 27].
-
Let us first consider the overlap
$ \left\langle 0\left|\hat{P}_1 \cdots \hat{P}_N \left| \hat{\mathbb P}^\dagger_1 \cdots \hat{\mathbb P}^\dagger_N\right.\right |0\right\rangle $ . By using Eq. (27), we have$ \begin{aligned}[b] \left\langle 0\left|\hat{P}_1 \cdots \hat{P}_N \left| \hat{\mathbb P}^\dagger_1 \cdots \hat{\mathbb P}^\dagger_N\right.\right| 0\right\rangle =& - \mathop \sum \limits_{k = 1}^N \frac{1}{2} {\rm{tr}}( \mathbbm {p}_N p_k )\left\langle 0\left|\hat{P}_1 \cdots \hat{P}_{k-1} \hat{P}_{k+1} \cdots \hat{P}_{N} \left| \hat{\mathbb P}^\dagger_1 \cdots \hat{\mathbb P}^\dagger_{N-1} \right.\right|0\right\rangle\\ & + \mathop \sum \limits_{k = 1}^N \mathop \sum \limits_{i = 1}^{k - 1} \left\langle 0\left|\hat{P}_1 \cdots\hat{P}_{i-1} \hat{ {\cal P} }_{i,k} \hat{P}_{i+1} \cdots \hat{P}_{k-1} \hat{P}_{k+1}\cdots \hat{P}_{N} \left| \hat{ \mathbb P}^\dagger_1 \cdots \hat{ \mathbb P }^\dagger_{N-1} \right.\right|0\right\rangle, \end{aligned} $ 
(33) where
$ \hat{\cal P}_{i,k} $ is given in Eq. (26). The above formula of an N-pair overlap can be used recursively, and thus is reduced to a sum of the overlaps for$ N = 1 $ ,$ \left\langle 0\left|\hat P\left|\hat {\mathbb P}^\dagger\right.\right|0\right\rangle = \left\langle0\left|\left[\hat P,\hat {\mathbb P}^\dagger\right]\right|0\right \rangle = - \frac{1}{2}{\rm{tr}}(\mathbbm {p} p)\;, $

where p and
$ \mathbbm {p} $ are structural matrices of$ \hat P $ and$ \hat {\mathbb P}^\dagger $ , respectively.By using Eq. (22), one obtains the matrix element of the one-body operator,
$ \hat Q $ , in the nucleon-pair basis,$ \begin{aligned}[b]& \left\langle 0\left| \hat{P}_1 \cdots \hat{P}_N \left| \hat{Q} \right| \hat{\mathbb {P}}^\dagger_1 \cdots \hat{\mathbb {P}}^{\dagger}_N \right|0\right\rangle = \left\langle 0\left| \left[\hat{P}_1 \cdots \hat{P}_N,\hat{Q}\right] \hat{\mathbb {P}}^\dagger_1 \cdots \hat{\mathbb {P}}^{\dagger}_N \right|0\right\rangle\\ &\quad = \sum\limits_{k = 1}^{N}\left \langle 0\left| \hat{P}_1 \cdots \hat{P}_{k-1} \hat{\cal{P}}_k \hat{P}_{k+1} \cdots \hat{P}_N\left | \hat{ \mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_N \right.\right|0\right\rangle, \end{aligned} $

(34) where
$ \hat{\cal P}_k $ is as given in Eq. (23).From Eq. (28), one obtains the matrix element of a two-body interaction operator in the particle-particle channel,
$ \hat{A}^\dagger \hat{B} $ ,$ \begin{aligned}[b] \left\langle 0\left|\hat{P}_1 \cdots \hat{P}_N \left| \hat{A}^\dagger \hat{B} \right| \hat{\mathbb {P}}^\dagger_1 \cdots \hat{\mathbb {P}}^{\dagger}_N\right|0\right\rangle =& \left\langle 0\left|\left[\hat{P}_1 \cdots \hat{P}_N, \hat{A}^\dagger \hat{B} \right]\hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_N\right|0\right\rangle\\ =& - \sum\limits_{k = 1}^N \frac{1}{2}{\rm{tr}}(p_{A} p_k) \left\langle0 \left|\hat{P}_1 \cdots \hat{P}_{k-1} \hat{B} \hat{P}_{k+1}\cdots \hat{P}_N \left| \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_N\right.\right |0\right\rangle\\ & + \sum\limits_{k = 2}^N \sum\limits_{i = 1}^k \left\langle 0\left|\hat P_1 \cdots\hat{P}_{i-1} \hat{\cal P}_{i,k} \hat{P}_{i+1} \cdots \hat{P}_{k-1} \hat{B} P_{k+1} \cdots\hat{P}_N \left| \hat{\mathbb {P}}^\dagger_1 \cdots \hat{\mathbb {P}}^\dagger_N\right. \right|0\right\rangle. \end{aligned} $ 
(35) Similarly, from Eq. (32), one obtains a matrix element of particle-hole interaction,
$ \hat{Q} \hat{Q}^\dagger $ ,$ \begin{aligned}[b] \left\langle 0\left|\hat{P}_1 \cdots \right.\right.\hat{P}_N \left.\left.\left| \hat{Q} \hat{Q}^\dagger \right| \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{ \mathbb {P}}^{\dagger}_N\right|0\right\rangle =& \left\langle 0\left|\left[\hat{P}_1 \cdots \hat{P}_N, \hat{Q} \hat{Q}^\dagger \right] \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{ \mathbb {P}}^{\dagger}_N\right|0\right\rangle\\ = & \sum\limits_{k,i = 1}^{N,k\neq i} \left\langle 0\left|\hat P_1 \cdots \right.\right. \left\{ \begin{array}{cc} \hat{P}_{i-1} \hat{\cal P}_i \hat{P}_{i+1} \cdots \hat{P}_{k-1} \hat{\cal P}_k \hat{P}_{k+1}&i<k\\ \hat{P}_{k-1} \hat{\cal P}_k \hat{P}_{k+1}\cdots \hat{P}_{i-1} \hat{\cal P}_i \hat{P}_{i+1} &k<i\\ \end{array} \right\} \left.\left. \cdots \hat P_N \left|\hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_N\right.\right|0\right\rangle\\ & +\sum\limits_{k = 1}^{N} \left\langle 0\left| \hat{P}_1 \cdots \hat{P}_{k-1} \hat{\mathfrak{P}}_k \hat{P}_{k+1} \cdots \hat{P}_N \left| \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_N\right.\right|0\right\rangle, \end{aligned} $

(36) where
$ \hat{\cal P}_i $ ,$ \hat{\cal P}_k $ , and$ \hat{\mathfrak{P}}_k $ are as given in Eq. (31). -
As discussed above, once the overlaps and matrix elements of one- and two-body operators for even-nucleon systems are obtained, the results for odd-mass systems are readily obtained in terms of those of even-nucleon systems. From Eq. (19), one obtains an overlap of an odd-mass nucleus in nucleon-pair basis states as follows:
$\begin{aligned}[b] \left\langle0 \left|\hat{a} \hat{P}_1\cdots \hat{P}_N \left| \hat{b}^\dagger \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_N\right.\right|0\right\rangle =& (\vec{a} \cdot \vec{b}) \left\langle 0\left| \hat{P}_1 \cdots \hat{P}_N \left| \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_{N} \right.\right|0\right\rangle\\&- \left\langle 0\left| \hat{P}_1 \cdots \hat{P}_N \left| \hat{\mathbb{Q}}\right | \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_{N} \right|0\right\rangle, \end{aligned} $

(37) where
$ \hat{\mathbb{Q}} $ has a structural matrix$ \mathbb{Q} = \vec{b} \vec{a}^\top $ . On the right hand side of the above equation, the formula of the first term is given in Eq. (33), and the formula of the second term is given in Eq. (34). For the case of$ N = 0 $ ,$ \left\langle \hat a\left|\hat b^\dagger\right.\right\rangle = \vec a^{\top}\vec b\;. $

Similarly, we preset the matrix elements of
$ \hat Q $ ,$ \hat A^{\dagger} \hat{B} $ , and$ \hat Q\hat Q^{\dagger} $ for an odd-nucleon system, in terms of overlaps of Eq. (37). By using Eq. (22), one obtains the$ \hat Q $ matrix element of an odd-nucleon system as follows:$ \begin{aligned}[b] \left\langle 0\left|\hat{a} \hat{P}_1 \cdots \hat{P}_N \left| \hat{Q} \right| \hat{b}^{\dagger} \hat{\mathbb {P}}^{\dagger}_1\right.\right. \cdots \left.\left.\hat{\mathbb {P}}^{\dagger}_N \right|0\right\rangle =& \left\langle 0\left|\left[\hat{a} \hat{P}_1 \cdots \hat{P}_N, \hat{Q} \right] \hat{b}^{\dagger} \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_N \right|0\right\rangle\\ =& \left\langle 0\left| \hat d \hat{P}_1 \cdots \hat{P}_N \left| \hat{b}^\dagger \hat{\mathbb {P}}^{\dagger}_1\cdots\mathbb {P}^{\dagger}_{N} \right.\right|0\right\rangle+\sum\limits_{k = 1}^N\left\langle 0\left|\hat{a} \cdots \hat{P}_{k-1} \hat{\cal P}_k \hat{P}_{k+1} \cdots \hat{P}_N \left| \hat{b}^{\dagger} \cdots \hat{\mathbb {P}}^{\dagger}_{N}\right.\right|0\right\rangle, \end{aligned} $ 
(38) where
$ \hat d $ and$ \hat{\cal P}_k $ are as given in Eq. (23). By using Eq. (28), one obtains the matrix elements of$ \hat A^\dagger \hat{B} $ as follows.$ \begin{aligned}[b] \left\langle 0\left|\hat{a} \hat{P}_1 \cdots \right.\right.\hat{P}_N \left.\left.\left| \hat{A}^\dagger \hat{B} \right| \hat{b}^\dagger \hat{\mathbb {P}}^\dagger_1 \cdots \hat{\mathbb {P}}^{\dagger}_N\right|0\right\rangle =& \left\langle 0\left|\left[\hat{a} \hat{P}_1 \cdots \hat{P}_N,\hat{A}^\dagger \hat{B} \right] \hat{b}^\dagger \hat{\mathbb {P}}^\dagger_1 \cdots \hat{\mathbb {P}}^{\dagger}_N\right|0\right\rangle\\ =& - \sum\limits_{k = 1}^N \frac{1}{2}{\rm{tr}}(p_{A} p_k) \left\langle 0\left| \hat{a} \hat{P}_1 \cdots \hat{P}_{k-1} \hat{B} \hat{P}_{k+1} \cdots \hat{P}_N \left| \hat{b}^\dagger \hat{\mathbb {P}}^{\dagger}_1 \hat{\mathbb {P}}^{\dagger}_2 \cdots \hat{\mathbb {P}}^{\dagger}_N \right.\right|0\right\rangle\\ &+ \sum\limits_{k = 2}^N \sum\limits_{i = 1}^k \left\langle 0\left| \hat{a} \hat P_1\cdots \hat{P}_{i-1} \hat{\cal P}_{i,k}\hat{P}_{i+1} \cdots \hat{P}_{k-1} \hat{B} P_{k+1}\cdots \hat{P}_N \left| \hat{b}^\dagger \hat{\mathbb {P}}^\dagger_1 \cdots \hat{\mathbb {P}}^\dagger_N \right.\right|0\right\rangle\\ & + \sum\limits_{k = 1}^N \left\langle 0\left|\hat{e}_k\hat P_1 \cdots \hat{P}_{k-1} \hat{B} P_{k+1} \cdots \hat{P}_N\left | \hat{b}^\dagger \hat{\mathbb {P}}^\dagger_1 \hat{\mathbb {P}}^\dagger_2 \cdots \hat{\mathbb {P}}^\dagger_N \right.\right|0\right\rangle, \end{aligned} $

(39) where
$ \hat{\cal P}_{i,k} $ and$ \vec{e}_k $ are given in Eq. (26). By using Eq. (32), one obtains the matrix elements of$ \hat Q\hat Q^\dagger $ as follows.$ \begin{aligned}[b] \left\langle 0\left| \hat{a} \hat{P}_1 \cdots \hat{P}_N \left| \hat{Q}\hat{Q}^\dagger \right|\hat{b}^{\dagger} \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_N\right| \right\rangle =& \left\langle 0\left|\left[ \hat{a} \hat{P}_1 \cdots \hat{P}_N, \hat{Q}\hat{Q}^\dagger \right]\hat{b}^{\dagger} \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_N\right| \right\rangle\\ =& \left\langle 0\left| \hat g \hat{P}_1 \cdots \hat{P}_N \left| \hat{b}^\dagger \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_{N}\right.\right|0\right\rangle+\sum\limits_{k = 1}^N\left\langle 0\left| \hat e \hat{P}_1 \cdots \hat{P}_{k-1} {\cal P}_k \hat{P}_{k+1}\cdots \hat{P}_N \left|\hat{b}^\dagger \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_{N}\right.\right|0\right\rangle\\& +\sum\limits_{i = 1}^N\left\langle 0\left|\hat f \hat{P}_1 \cdots \hat{P}_{k-1} {\cal P}_i \hat{P}_{k+1}\cdots \hat{P}_N \left| \hat{b}^\dagger \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_{N}\right.\right|0\right\rangle\\&+\sum\limits_{k = 1}^N\left\langle 0\left| \hat{a} \hat{P}_1 \cdots \hat{P}_{k-1} \hat{\mathfrak{P}}_k \hat{P}_{k+1} \cdots \hat{P}_N \left| \hat{b}^\dagger \hat{\mathbb {P}}^{\dagger}_1 \cdots \hat{\mathbb {P}}^{\dagger}_{N}\right.\right|0\right\rangle\\ &+\sum\limits_{k,i = 1}^{N,k\neq i} \left\langle 0\left|\hat{a}\hat P_1\cdots \right.\right. \left\{ \begin{array}{cc} \hat{P}_{i-1} {\cal P}_i \hat P_{i+1} \cdots \hat{P}_{k-1} {\cal P}_k \hat{P}_{k+1}&i<k\\ \hat{P}_{k-1} {\cal P}_k \hat{P}_{k+1}\cdots\hat{P}_{i-1} {\cal P}_i\hat P_{i+1} &k<i\\ \end{array} \right\} \left.\left. \cdots \hat P_N\left| \hat{b}^\dagger \cdots \hat{\mathbb {P}}^{\dagger}_{N}\right.\right|0\right\rangle, \end{aligned} $

(40) where
$ {\cal P}_k $ ,$ {\cal P}_i $ ,$ \hat{\mathfrak{P}}_k $ ,$ \hat e $ ,$ \hat f $ , and$ \hat g $ are as given in Eq. (31), -
In this section, we demonstrate the computational efficiency of the matrix-represented NPA from three aspects: overlap computation, overall timing for the whole NPA procedure, and
$ ^{156} {\rm{Sm}}$ calculation. -
The computation of overlaps between the basis states is a key part of all approaches of the NPA. In this subsection, we discuss the computational advantage of our matrix-represented NPA in the calculations of the overlaps between the basis states, in comparison with those for the NPA described in Refs. [21,23] and Ref. [27]. This comparison is exemplified by calculations for a semi-magic Ca isotope chain using
$ SD $ -pair approximation of the$ pf $ shell.In Fig. 1, we plot the evolution of the average computational time of one overlap with nucleon-pair number N. According to Fig. 1, the overlap-computation time for the NPA of Refs. [21, 23] is the smallest when
$ N = 1 $ and is almost the same for three approaches in Refs. [21, 23], Ref. [27], and for the present NPA with an uncoupled representation when$ N = 2 $ . For$ N \geqslant 3 $ , the overlap-computation time with an uncoupled representation is substantially superior to that for the NPA of Refs. [21, 23] and Ref. [27]. For instance, for$ N = 5 $ , the overlap-computation time using the approaches of Refs. [21,23] is larger by approximately 2 orders than that of Ref. [27] and by approximately 4 orders than that of the NPA with the uncoupled representation suggested in this study.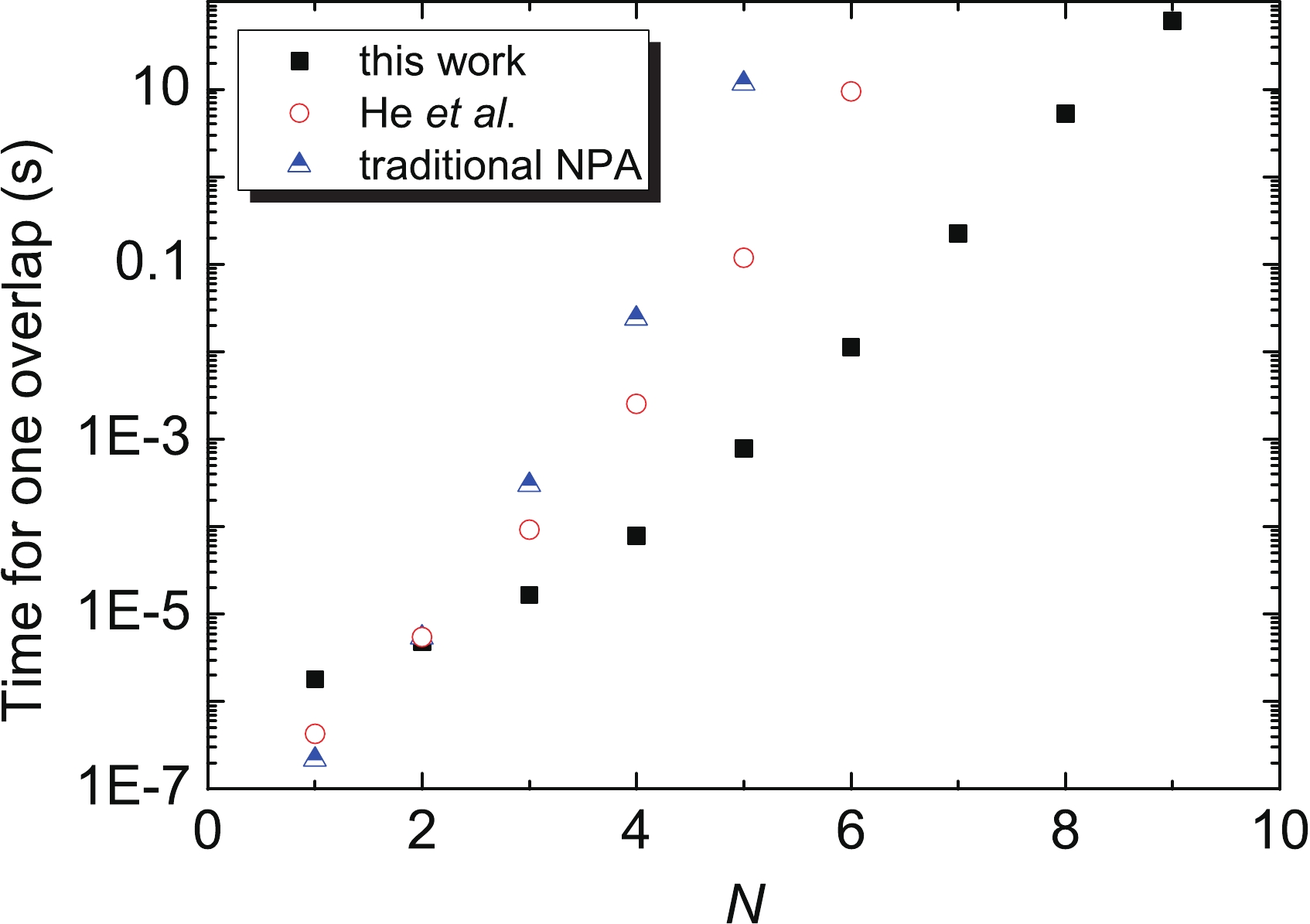
Figure 1. (color online) Average computational time of one overlap versus nucleon-pair number N, for three approaches of the NPA, exemplified by the calculations for Ca isotope chain using
$ SD $ -pair space in the$ pf $ shell. In addition, “traditional NPA” corresponds to the NPA of Refs. [21, 23], “He$ et\; al. $ ” corresponds to the NPA of Ref. [27], and “this work” corresponds to the NPA with an uncoupled representation. The calculations are carried out on a PC platform with a CPU frequency of 4.9 GHz.It is worth understanding the reason why the overlap-computation time of an uncoupled representation is larger than the other two for the case of
$ N = 1 $ . In the case of$ N = 1 $ , the NPA of Refs. [21,23] or Ref. [27] calculates the overlaps using an extremely compact formula,$\langle r_1, J_1 | s_1, J_1 \rangle = 2 \delta_{r_1 s_1} \delta_{r_1 J_1} \delta_{s_1 J_1} \sum\limits_{ab} y(abr_1)y(abs_1) \;,$

which corresponds to the inner product of the two structural y matrices of the bra and ket. On the other hand, with the uncoupled representation, the
$ N = 1 $ overlap is described with Eq. (34), an inner product of two structural matrices of p and$ \mathbbm p $ . Because in previous NPA approaches, for the angular-momentum-projection, the degree of freedom of the collective pairs is degenerative and thus frozen, its structural y matrix has a smaller dimension than the p and$ \mathbbm p $ matrices used in our approach. As a result, the$ N = 1 $ overlap of previous approach requires less time. -
Although the efficiency improvement of our approach is obvious regarding the overlap calculation, because of the introduction of the m-scheme basis, the model space is enlarged. This leads to more calculations of the Hamiltonian matrix elements. It is worth verifying whether this model space enlargement diminishes the efficiency improvement in the overlap calculation.
To achieve this, we finish a series of NPA calculations with three different approaches. Similar to the overlap computation test described in Sec. IVA, these calculations are specified for the Ca isotope chain in the
$ pf $ shell with$ SD $ pairs. Each calculation covers all of the necessary procedures to obtain the yrast level scheme of quantum many-body systems, from the basis construction to the Hamiltonian matrix element calculation, and finally to the diagonalization of the Hamiltonian. The overall time of such a calculation can comprehensively demonstrate the efficiency improvement of our approach in a general and realistic calculation regarding the nuclear structure.The overall times of these calculations are presented in Fig. 2. Regardless of how many valence nucleon pairs are introduced, our approach always requires the minimal time to finish the entire process of the NPA calculation. Thus, the enlargement of the model space brought by the m-scheme basis is tolerable in our approach. Furthermore, with the extra calculations of the Hamiltonian matrix elements, we do not observe the superiority of the traditional NPA approach and the approach in Ref. [27] for the
$ N = 1 $ case, which was seen in the overlap computation, as shown in Fig. 1. This is because the calculations of the Hamiltonian matrix elements in these two approaches can no longer be reduced to a simple and compact inner product of small y matrices and thus require a longer CPU time.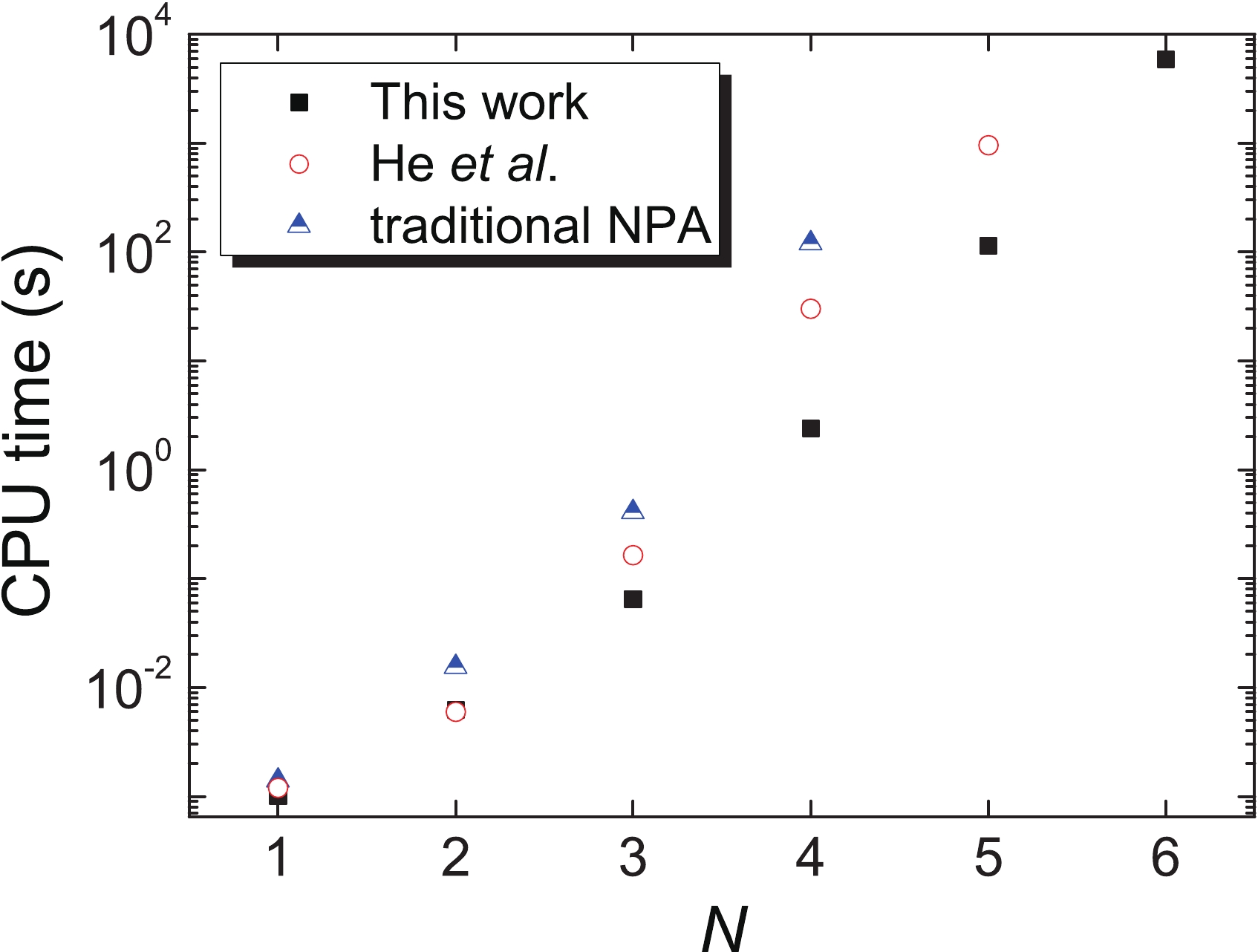
Figure 2. (color online) The same as in Fig. 1, except for the overall computational time of the whole NPA calculation.
-
Figure 2 lets us realize the possibility of NPA calculations with 6 identical valence nucleon pair on a usual PC. Therefore, we attempt to perform an NPA calculation for
$ ^{156} {\rm{Sm}}$ , which has 12 (6 pairs of) valence protons and 12 (6 pairs of) valence neutrons in 50-82 and 82-126 shells, respectively. This nucleus is impossible to manage with previous NPA approaches. Therefore, such a calculation pushes the potential capability of the uncoupled representation to its limit and can best demonstrate the power of our approach.In the
$ ^{156} {\rm{Sm}}$ calculation, we adopt the same Hamiltonian and model space as those used for$ ^{150} $ Nd calculation in Ref. [27], except for a slight tunning of the two-body interaction strengths to fit the experimental level scheme. The Hamiltonian parameters are listed in Table 1.$ \varepsilon_{\pi} $ 

$ s_{1/2} $ 

$ d_{3/2} $ 

$ d_{5/2} $ 

$ g_{7/2} $ 

$ h_{11/2} $ 

2.990 2.44 0.962 0.000 2.793 $ \varepsilon_{\nu} $ 

$ p_{1/2} $ 

$ p_{3/2} $ 

$ f_{5/2} $ 

$ f_{7/2} $ 

$ g_{9/2} $ 

$ i_{13/2} $ 

1.363 0.8537 2.0046 0.000 1.5609 2.690 two-body $ G_{0\pi} $ 

$ G_{2\pi} $ 

$ G_{0\nu} $ 

$ G_{2\nu} $ 

$ \kappa_{\pi\nu} $ 

0.140 0.063 0.120 0.019 0.251 After
$ \sim $ 36-h serial computing on a PC platform with a CPU frequency of 4.9 GHz, we obtain the low-lying spectrum of$ ^{156} {\rm{Sm}}$ and compare it with the experimental spectrum in Fig. 3. A reasonable agreement is achieved.This serial calculation for
$ ^{156} {\rm{Sm}}$ suggests that the NPA with an uncoupled representation is feasible for all nuclei with the valence-pair number$ \leqslant 6 $ . By contrast, to the best of our knowledge, a traditional NPA can only manage a valence-pair number$ \leqslant 4 $ . That means that the uncoupled representation extends the NPA-applicable region by$ \sim $ 100%, as shown in Fig. 4.
Figure 4. (color online) NPA-applicable nuclear region in
$ Z = 52-82 $ and$ N = 82-126 $ major shells. The slash shadow area is for the j scheme with$ ^{148} {\rm{Ce}}$ as the heaviest nucleus, which has four pairs of valence protons and four pairs of valence neutrons. The gray area is for an uncoupled representation with$ ^{156} {\rm{Sm}}$ as the heaviest nucleus. -
We noted the dramatic efficiency improvement of the uncoupled representation. In this section, we try to explain the reason from two aspects, i.e., the commutation efficiency and recursion number.
-
In a traditional NPA or the newly proposed approach in Ref. [27], the commutations of collective pairs and one-body operators involve a three-folded summation over a gigantic amount of 6j-symbol calculations [for example, see Eqs. (2.10a) and (4.5a) of Ref. [23], or Eqs. (16) and (17) of Ref. [27]], which are extremely time-consuming.
Represented using matrices, the commutations are simply and straightforwardly expressed, without angular-momentum coupling. Furthermore, a modern computing architecture has been developed to adapt to the instruction set of Single Instruction Multiple Data, which provides data-level parallelism on multiple data points as opposed to executing multiple instructions [36]. Such a technique favors a matrix-product operation. Thus, a matrix-represented commutation on the current generation of the processors is expected to be more efficient.
To demonstrate the commutation efficiency, we apply a commutation between a pair annihilation and creation operators with different formulas on the same PC platform with a CPU frequency of 4.9 GHz. The actual computational time for each commutation is presented in Table 2. With the matrix multiplication of Eq. (2.17), the computational time is ~10−6 s for an arbitrary commutation
$[\hat P_1,\,\hat P_2^ \dagger]$ between two collective pairs$\hat P_1 $ and$\hat P_2^ \dagger$ . By contrast, with the traditional formalism as described with Eqs. (2.10a) and (2.10b) of Ref. [23], coupled commutations with a definite t quantum number usually take$ \sim 5\times 10^{-6} $ s or more. This observation agrees with the analysis in this subsection.Commutation time (10−6 s) Commutation time (10−6 s) $ \left[\hat P_1,\hat P^{\dagger}_2\right] \quad $ 

0.926 $ \left[\hat S,\hat S^{\dagger}\right]^{t=0} $ 

4.077 $ \left[\hat D,\hat D^{\dagger}\right]^{t=1} $ 

6.320 $ \left[\hat S,\hat D^{\dagger}\right]^{t=2} $ 

4.787 $ \left[\hat D,\hat D^{\dagger}\right]^{t=2} $ 

7.637 $ \left[\hat D,\hat S^{\dagger}\right]^{t=2} $ 

8.475 $ \left[\hat D,\hat D^{\dagger}\right]^{t=3} $ 

8.010 $ \left[\hat D,\hat D^{\dagger}\right]^{t=0} $ 

4.928 $ \left[\hat D,\hat D^{\dagger}\right]^{t=4} $ 

6.374 Table 2. Computational times for one commutation in unit of
$ 10^{-6} $ s. The single-particle space is in the$ pf $ major shell. Here,$ \left[\hat P_1,\hat P^{\dagger}_2\right] $ corresponds to any arbitrary commutation of the pair creation and annihilation operators in an uncoupled representation without an angular-momentum coupling, as described in Eq. (17). The$ \hat S $ and$ \hat D $ pairs correspond to the collective pairs with$ J^{\pi}=0^+,\; 2+ $ , respectively. Their commutations with definite final angular momentums (t number) are carried out with Eqs. (2.10a) and (2.10b) of Ref. [23]. -
All NPA calculations are performed recursively. Therefore, smaller numbers of recursion are favorable in the NPA calculations. Below we enumerate the number of recursions involved in an overlap calculation for N nucleon-pair basis in terms of the
$ (N-1) $ -pair overlap number required in such a calculation.In Fig. 5 we plot such overlap numbers with
$ (N-1) $ nucleon pairs, versus nucleon-pair number N, for the NPA approach of Refs. [21,23] and Ref. [27] and the uncoupled representation suggested in this paper. One can see that the number of overlaps with$ (N-1) $ nucleon pairs involved in an overlap of N nucleon pairs for the matrix represented NPA is the smallest. In particular, in cases of nucleon pairs with larger spins, the advantage of the matrix representing the NPA is even more striking.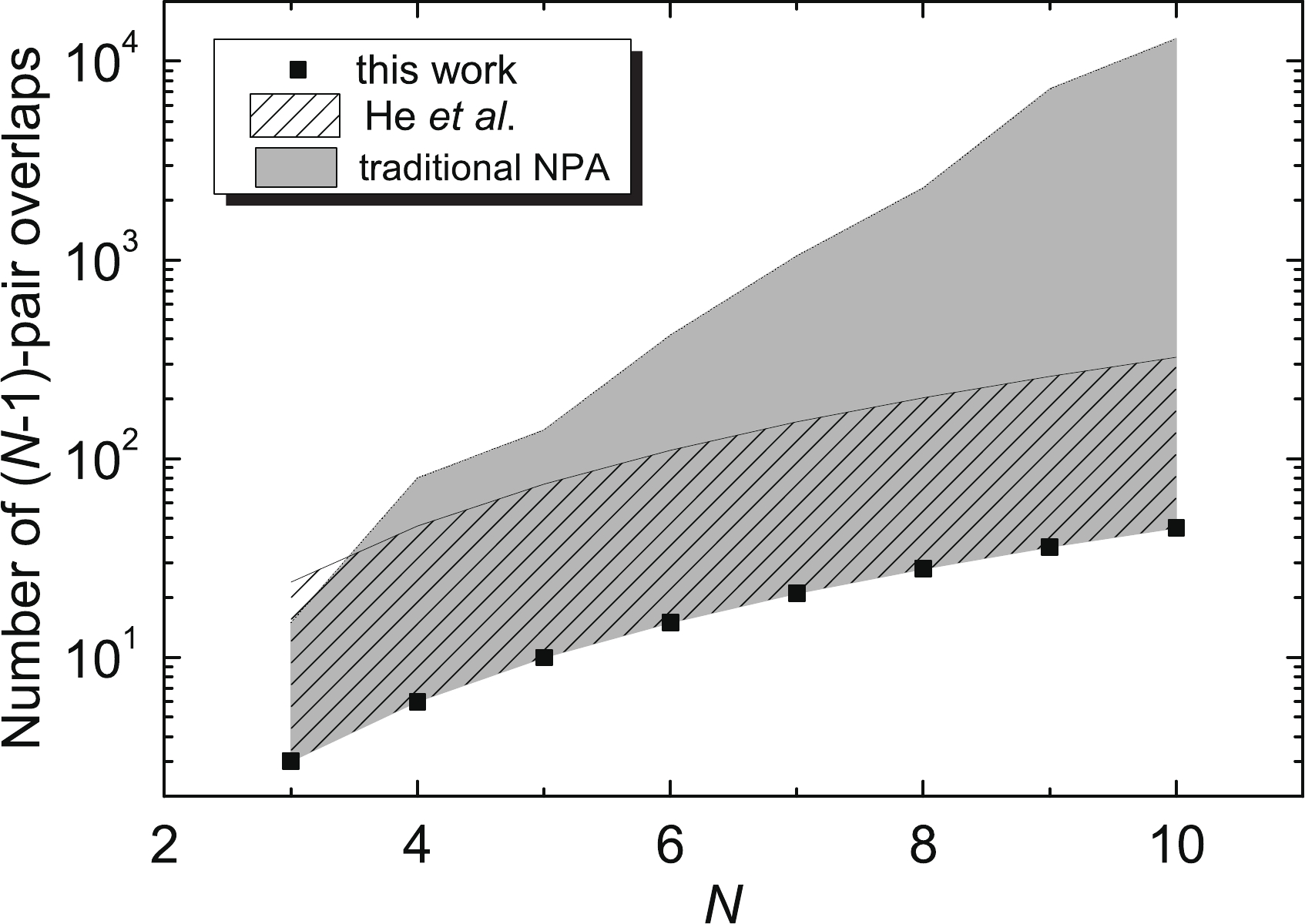
Figure 5. (color online) Number of overlaps with
$ (N-1) $ nucleon pairs required in an overlap calculation with N nucleon pairs, with the NPA approaches of Refs. [21,23] (shadow in grey, labeled as “traditional NPA”), that of Ref. [27] (stripes, labeled as “He et al.”), and the present formulation (solid squares in black, labeled as “this work”). See the text for details.Let us first take a close look at the approaches of Refs. [21,23]. In this approach, new intermediate quantum numbers arise from angular-momentum recouplings of the basis states and nucleon-pairs, i.e., the L quantum numbers therein [21, 23]. In this case, it is difficult to enumerate the number of overlaps with
$ (N-1) $ nucleon pairs analytically; herein, we apply this enumeration using our computer code and plot the numbers versus pair number N in Fig. 5, denoted using shadows in grey, for an$ SD $ -pair configuration in the$ pf $ shell. According to our enumeration, as plotted in Fig. 5 for an overlap with$ N = 6 $ , for example, one has to calculate up to a few hundred overlaps of the basis states with$ N = 5 $ .The NPA approach of Ref. [27] involves of a smaller number of recursions of overlaps with
$ N-1 $ nucleon pairs than the approaches of Refs. [21,23] in the overlaps of N nucleon pairs. In the overlap$ \left\langle 0\Big| D_{1}D_2\cdots D_i \cdots $ $ D_{N}\Big|D^\dagger_{1}D^\dagger_2\cdots \right. \left.D^{\dagger}_j \cdots D^\dagger_{N} \Big|0\right\rangle $ of Ref. [27], each$ \{i,k\} $ combination includes seven overlaps of a$ (N-1) $ -pair system, with seven possible intermediate pairs of$ A^{r^{\prime}_i = 0\sim 6} $ . In total, there are$ N(7N-5)/2 $ overlaps with$ (N-1) $ nucleon pairs involved in the calculations of overlaps with N nucleon pairs. The numbers of overlaps with$ (N-1) $ nucleon pairs for various nucleon-pair basis states are plotted using stripes in Fig. 5, with their maxima$ N(7N-5)/2 $ .In the NPA with an uncoupled representation described in this paper, all nucleon pairs including those given by a double commutation, as shown in Eq. (26), are represented by matrices, and there is no multiplicity of angular momentum arising from a commutation. There are
$ N(N-1)/2 $ overlaps of$ (N-1) $ nucleon pairs with a new pair of$ \hat {\cal P}_{i,k} $ given in Eq. (26) and N overlaps of$ (N-1) $ nucleon pairs without new pairs. In total, one N-pair overlap involves$ N(N+1)/2 $ overlaps of$ (N-1) $ nucleon pairs, as denoted by the solid squares in black. This number is in general smaller than that in the NPA approach of Ref. [27].Note that the reduction of the recursive number in our approach can be attributed to the flexibility of our formalism presented in Sec. III. Such formalism does not require a definite angular momentum for all pair and particle-hole operators. Thus, when an intermediate pair or particle-hole operator is created during the calculation, to adapt to our formalism, we do not need to decouple it into several operators with a definite angular momentum. However, this operator decoupling is required by the formalism in Ref. [27], which introduces extra overlap callings and recursions.
In a word, the boost of the commutation computing and the decrease in the recursive number are the two components of the efficiency improvement brought about by an uncoupled representation. According to the analysis in this section, these two elements are strongly related to the complete removal of angular-momentum couplings and recouplings throughout the computation.
-
To summarize, in this paper, we revisited the NPA formulation with an uncoupled representation. The nucleon-pair structural coefficients in this formulation are represented in terms of anti-symmetrized matrices. The overlaps, matrix elements of one-body operators, and a shell model Hamiltonian are calculated recursively as in previous approaches [21, 23-25, 27].
This formalism presented in Secs. IIB, IIC, and III does not necessarily require a definite angular momentum and its projection for all pairs and particle-hole operators. Such flexibility leads to fewer recursions in the overlap calculation, as presented in Fig. 5, which contributes significantly to an improvement in the computational efficiency. Furthermore, within this formalism, the NPA calculations with and without isospin symmetry and for odd and even nucleons are formulated on the same footing. This enables easy extensibility of the NPA computation.
The implementation of this formalism presents a significant improvement in the computational efficiency according to the overlap calculations, the whole-procedure NPA calculations, and perhaps the heaviest NPA calculation ever for a realistic
$ ^{156} {\rm{Sm}}$ , which only requires$ \sim $ 36 h on a typical PC. This efficiency improvement of the present approach is finally traced back to the removal of angular-momentum couplings and recouplings throughout the computation.As shown with the
$ ^{156} {\rm{Sm}}$ calculation, the uncoupled representation enables studies of the rotational motion of heavy nuclei within the framework of the nucleon-pair approximation of the nuclear shell model. -
We thank B. C. He for discussions and communications and C. W. Johnson for constructive suggestions.
Nucleon-pair approximation with uncoupled representation
- Received Date: 2020-11-19
- Available Online: 2021-05-15
Abstract: In this paper, we propose an approach to nucleon-pair approximation (NPA) with m-scheme bases, in which the collective nucleon pairs are represented in terms of antisymmetric matrices, and commutations between nucleon pairs are given using a matrix multiplication that avoids angular-momentum couplings and recouplings. Therefore the present approach significantly simplifies the NPA computation. Furthermore, it is formulated on the same footing with and without isospin.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: