-
The pion, the lightest hadron made of a first-generation quark and antiquark, plays a fundamental role in particle and nuclear physics, as the long-range nuclear force carrier which binds the nucleons together into a nucleus [1]. In theory, it is a good approximation of the Nambu-Goldstone boson [2, 3] from spontaneous chiral symmetry breaking. However, the emergence of its small mass (much smaller than that of the proton) is not yet understood quantitatively and experimentally [4-7]. Recent progress from the Dyson-Schwinger equations (DSE), which is a nonperturbative quantum chromodynamics (QCD) approach, show that the dressed quark mass which comes from dynamical chiral symmetry breaking [8-10] is largely cancelled by the attraction interaction between the quark and the antiquark [4, 5, 11]. Understanding the properties of the simplest hadron from its structure would be a remarkable advancement in revealing the strong interaction.
Along with the emergence of the pion mass, DSE predicts a broadening parton distribution amplitude (PDA) [12-14], compared to the asymptotic form of the PDA obtained from perturbative QCD [15-17]. The pion quark distribution also becomes wider at the hadronic scale
$ Q_0^2 $ (a very low scale where sea quarks and gluons disappear). Using a renormalization-group-invariant process-independent strong coupling, the initial quark distributions at$ Q_0^2 $ are connected to the extracted parton distribution functions (PDF) at high$ Q^2 $ in experiments [18-24]. Moreover the predicted valence quark distribution from dynamical chiral symmetry breaking has a similar large-x ($ x\rightarrow 1 $ ) behavior of the perturbative QCD predictions [25-27]. Measuring the pion structure over the full range of x and a broad range of$ Q^2 $ provides a promising window to see dynamical chiral symmetry breaking, which is one of the prominent features of QCD theory, and to uncover the related emergent phenomena of the strong interaction.Experimentally, the collinear parton distributions of nucleons have been measured very precisely with the help of high energy accelerator facilities worldwide. However, we have far less experimental data about the parton distributions of the pion. Measuring the pionic structure is not easy, since there is no pion target available for experiments, as it decays quickly. All the data on pion valence quark distributions are from measurements of the Drell-Yan reaction induced by the pion beam [28-31], in experiments performed more than thirty years ago. Recently, by exploiting the “pion cloud” around the proton, the pion structure function at small
$ x_{{\rm{\pi}}} $ ($ \lesssim 0.01 $ ) has been analyzed from the leading neutron (LN) tagged deep inelastic scattering (DIS) data at the HERA collider [32, 33]. Therefore, to fill the data gap in the range$ 0.01\lesssim x_{{\rm{\pi}}} \lesssim 0.2 $ is of particular interest on the experimental side. More data over the full x range and at different$ Q^2 $ are still scarce. Furthermore, measuring the pion valence quark distributions at large x using the LN-DIS technique, and comparing it with that from the Drell-Yan process, will reinforce our understanding of perturbative QCD theory with respect to the dynamics when$ x_{\rm{\pi}} $ approaches one. Lastly, experimental data from the sea quark region to the valence quark region will definitely provide an opportunity to test various theoretical approaches, such as DSE [6, 24], lattice QCD [34-37], holographic QCD [38], light-front quantization [39], the chiral quark model [40-42], the constituent quark model [43-45], QCD sum rules [46], and the dynamical parton model prediction with a naive nonperturbative input [47, 48].Recently the JAM Collaboration [49] and xFitter Collaboration [50] performed global analyses of the pionic parton distribution functions from the Drell-Yan data and the LN-DIS data. The JAM analysis shows that the addition of the LN-DIS data constrains the gluon distribution better. However, compared to the fit with only the Drell-Yan data, the valence quark, sea quark and gluon distributions change significantly [49]. Therefore, more measurements on the LN-DIS process are necessary for future global fit studies. The xFitter Collaboration finds that the current experimental data are not enough to unambiguously determine the sea quark and gluon distributions of the pion. Moreover, the xFitter Collaboration studied the model uncertainties related to the variations of the factorization and renormalization scales and the flexibility of the chosen parametrization. They estimate that these model uncertainties are significant [50]. Hence, more experimental data on the pion structure are critical to constrain the sea quark and gluon distributions of the pion and to understand the model uncertainties in the global fit.
There are ongoing discussions on building a low energy electron-ion collider in China (EicC), by upgrading the high-intensity heavy ion accelerator facility (HIAF) which is currently under construction [51, 52]. By using the same method verified at HERA, EicC with a center-of-mass (c.m.) energy of about 20 GeV would provide a competitive opportunity to acquire pionic structure data in the range
$ 0.01\lesssim x_{\rm{\pi}} \lesssim 1 $ . Hence, in this work, we investigate the feasibility and the kinematical distributions of interest, providing some guidance for detecting the final-state particles. Then we focus on the anticipated statistical errors of pionic structure function for a suggested LN-DIS experiment at EicC.The organization of the paper is as follows. The formulae of the LN-DIS process to study the structure of the pion are discussed in Sec. II. The PDFs of the pion from the JAM18 global analysis used in this simulation and the dynamical PDF model of the pion are introduced in Sec. III. The commonly used invariant kinematical distributions of the reaction and the angular distributions of the final-state particles are given in Sec. IV, for the proposed experiment at EicC. Then the statistical error projections of the pionic structure function
$ F_2 $ are shown for an assumed experimental run of 50 fb$ ^{-1} $ integrated luminosity in Sec. V. Finally, we give some discussion and a concise summary in Sec. VI. -
To explore the structure of the pion in e-p scattering, the key idea is to take advantage of the abundant “pion cloud” around the proton. The
$ \pi^+ $ in the n-$ {\rm{\pi}}^+ $ Fock state of proton dissociation [53] is abundant because of the large$ \pi-N-N $ coupling. Figure 1 shows a schematic diagram of LN-DIS, where the exchanged pion of the Sullivan process [54] is probed and broke up by the virtual photon. In the case of e-$ {\rm{\pi}}^+ $ DIS, the neutron spectator carries a large fraction of the momentum of the incoming proton and a small transverse momentum$ P_{T,n} $ . The final neutron in this case has a large longitudinal momentum and rapidity. It is called the leading neutron and is quite distinguishable from the neutron fragment from normal DIS [32, 33]. More theoretical calculations indicate that the structure of the virtual pion at low virtuality ($ |t = m_{\pi}^2|<0.6 $ GeV$ ^2 $ ) can be effectively extrapolated to the on-shell pion, based on an analysis of the Bethe-Salpeter amplitude [55].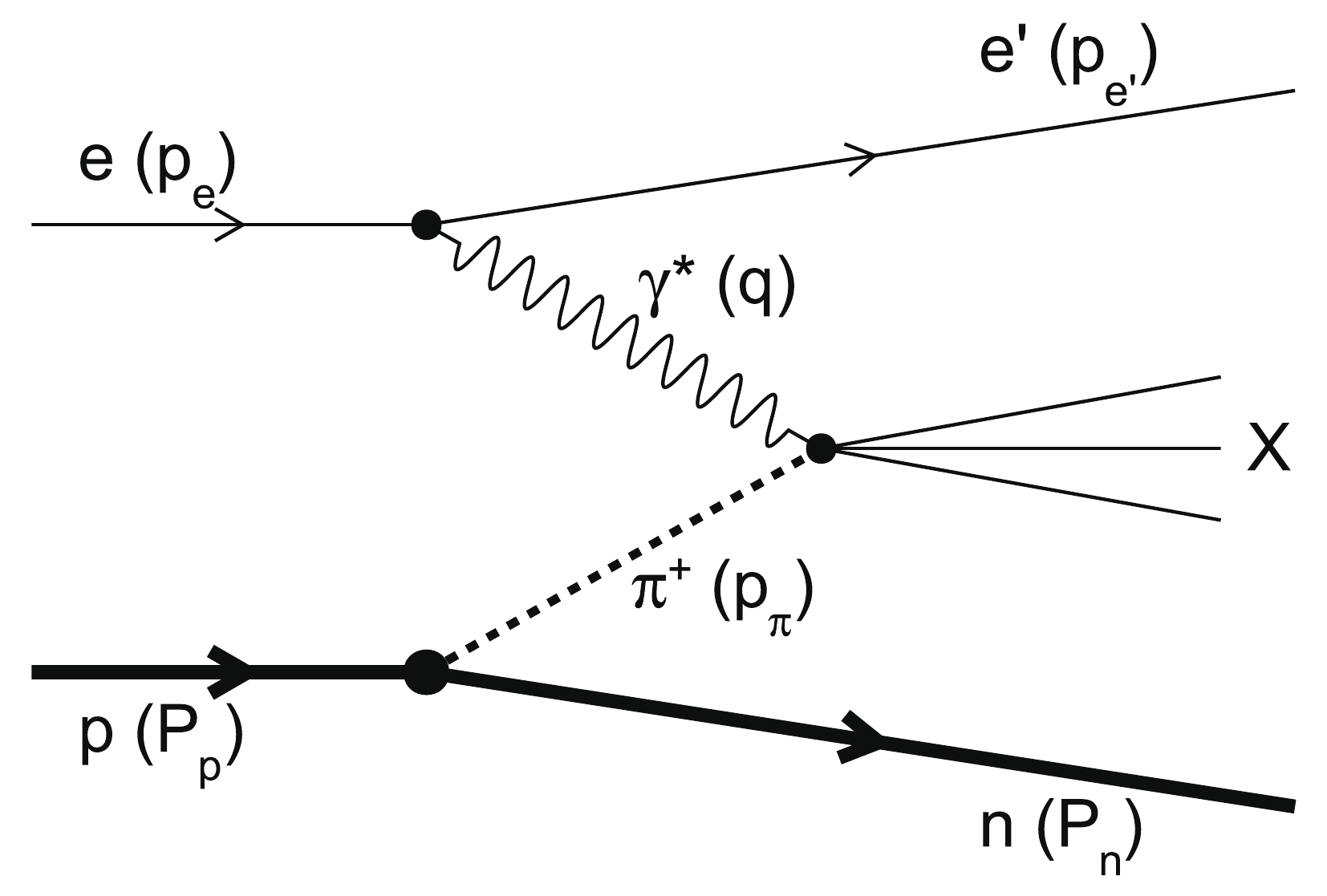
Figure 1. The Sullivan process [54] for leading-neutron deep inelastic scattering, where the one-pion exchange process dominates.
According to the momenta labeled in Fig. 1, the commonly used virtuality of the photon probe
$ Q^2 $ , the Bjorken variable$ x_B $ , and the inelasticity y of the DIS process are defined as:$ Q^2 \equiv -q^2, \;\;\; x_{\rm{B}} \equiv \frac{Q^{2}}{2P_{{p}} \cdot q}, \;\;\; y \equiv \frac{P_{{p}} \cdot q}{P_{{p}} \cdot P_{{e}}}. $

(1) Other kinematical variables related to the final-state neutron are the longitudinal momentum fraction
$ x_{\rm L} $ and the square of the momentum transfer to the virtual pion, t:$ x_{\rm{L}} \equiv \frac{P_{{n}}\cdot q}{P_{{p}}\cdot q}, \; t \equiv (P_{{p}} - P_{{n}})^2 = p_{{\rm{\pi}}^{*}}^2. $

(2) $ x_{\rm{L}} $ is the longitudinal momentum fraction (approximately, energy fraction) of the final neutron to the incoming proton. In experiment, the LN-DIS process dominates in the large-$ x_{\rm L} $ region ($ \gtrsim 0.5 $ ) [33]. Hence, a proper cut on the$ x_{\rm L} $ variable is an efficient way to select events that are sensitive to the pion structure. Viewing the virtual pion as the effective target, similar to the definition of the normal Bjorken variable, the momentum fraction of the parton inside the pion is given by$ x_{{\rm{\pi}}} \equiv \frac{Q^2}{2p_{{\rm{\pi}}}\cdot q} = \frac{x_{\rm{B}}}{1-x_{\rm{L}}}. $

(3) From the above definition, we see that the smallest momentum fraction of the parton in the pion measured in LN-DIS is larger than the smallest momentum fraction of the parton in the proton measured in DIS, for e-p collisions with the same c.m. energy.
To estimate the statistics of LN-DIS events and the distributions of the kinematical observables at EicC, we need to calculate the differential cross-section of the channel. Integrating the azimuthal angles, the four-fold differential cross-section of the LN-DIS process is expressed with the semi-inclusive structure function
$ F_2^{{\rm{LN}}(4)}(Q^2, x_{\rm{B}}, x_{\rm{L}}, t) $ [32, 33, 53]:$ \begin{aligned}[b] \frac{{\rm d}^4\sigma({{ep}}\rightarrow {{enX}})}{{\rm d}x_{\rm{B}}{\rm d}Q^2{\rm d}x_{\rm{L}}{\rm d}t} =& \frac{4\pi\alpha^2}{x_{\rm{B}}Q^4}\left(1-y+\frac{y^2}{2}\right)F_2^{{\rm{LN}}(4)}(Q^2, x_{\rm{B}}, x_{\rm{L}}, t)\\ =&\frac{4\pi\alpha^2}{x_{\rm{B}}Q^4}\left(1-y+\frac{y^2}{2}\right) F_2^{{\rm{\pi}}}\left(\frac{x_{\rm{B}}}{1-x_{\rm{L}}},Q^2\right)f_{{\rm{\pi}}^+/{{p}}}(x_{\rm{L}},t). \end{aligned} $

(4) In the above formula, the leading-neutron structure function
$ F_2^{{\rm{LN}}(4)} $ is then factorized into the pionic structure function$ F_2^{{\rm{\pi}}} $ and the pion flux around the proton$ f_{{\rm{\pi}}^+/{{p}}} $ . The pion flux is usually evaluated to be a pion pole in effective field theory [32, 33, 53],$ \begin{aligned}[b] f_{{\rm{\pi}}^+/{{p}}}(x_{\rm{L}},t) = \frac{1}{2\pi}\frac{g^2_{{pn\pi}}}{4\pi}(1-x_{\rm{L}})\frac{-t}{(m_{\pi}^2-t)^2}{\rm{exp}}\left(R^2_{{n\pi}}\frac{t-m_{\pi}^2}{1-x_{\rm{L}}}\right), \end{aligned} $

(5) where
$ g^2_{{pn\pi}}/4\pi = 13.6 $ is the$ {{\rm{\pi}}}-N-N $ effective coupling, and$ R_{{n\pi}} = 0.93 $ GeV$ ^{-1} $ is an adjustable parameter describing the radius of the n-$ {{\rm{\pi}}} $ Fock state [53]. By integrating over the t variable, the three-fold LN structure function is also often used. It is written as$ F_2^{{\rm{LN}}(3)}(Q^2, x_{\rm{B}}, x_{\rm{L}}) = \int_{t_1}^{t_0} F_2^{{\rm{LN}}(4)}(Q^2, x_{\rm{B}}, x_{\rm{L}}, t) {\rm d}t. $

(6) For now, the theoretical framework for the pion structure function measurement in the e-p process is mature and has been tested with the pioneering experiments at the HERA facility. The shape of the structure function of the pion is encoded in the LN structure function. So to complete the quantitative calculation of the cross-section, the last thing left is to seek a valid structure function model of the pion over a wide kinematical range of
$ x_{\pi} $ and$ Q^2 $ . -
In this simulation, we take the pion PDF of the recent JAM18 global analysis as the input for the cross section model. To check the JAM18 PDF of the pion and see the status of our understanding of pionic structure, the JAM18 global fit result is compared with the experimental data and the dynamical parton model [48, 56]. The pionic PDF based on the dynamical parton model is called piIMParton for the convenience of discussion and reference [48, 56]. The salient argument of the dynamical parton model is that the nonperturbative input consists of only the valence quark distributions at extremely low
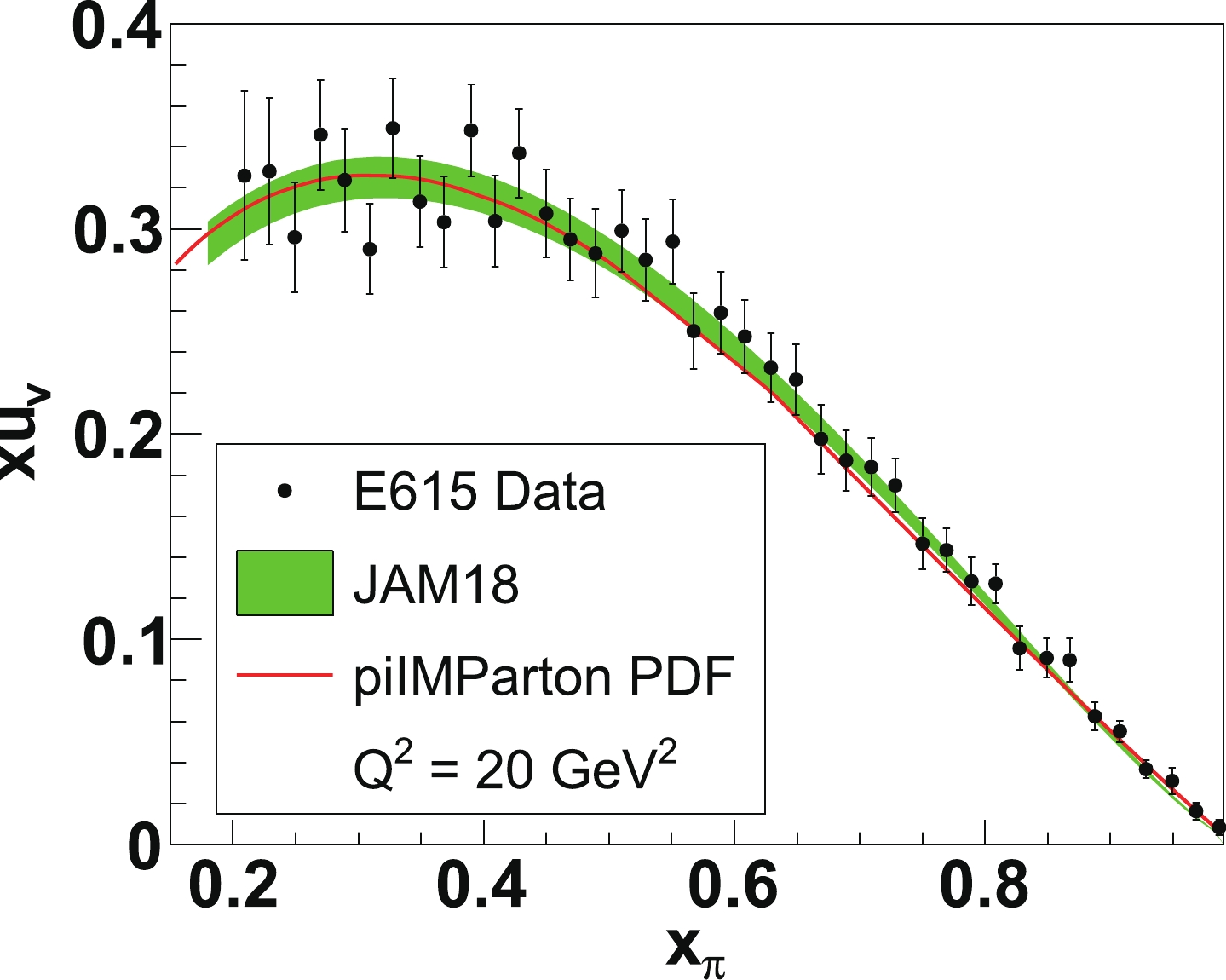
$ Q_0^2 $ scale. The low$ Q_0^2 $ scale is estimated to be around 0.1 GeV$ ^2 $ , which is also called the hadronic scale, since at this scale only the minimum components (valence) of the hadron can be resolved. In this dynamical parton model, all the sea quarks and gluons are produced from the parton splitting processes governed by the DGLAP equations [57]. The dynamical parton model is also called the radiative parton model, as all the sea quarks and gluons are given by QCD radiations. Hence it is very interesting to compare the JAM18 PDF with the piIMParton PDF.Figure 2 shows the valence quark distribution of the pion from JAM18 global analysis and piIMParton [48, 56], compared with that extracted from the
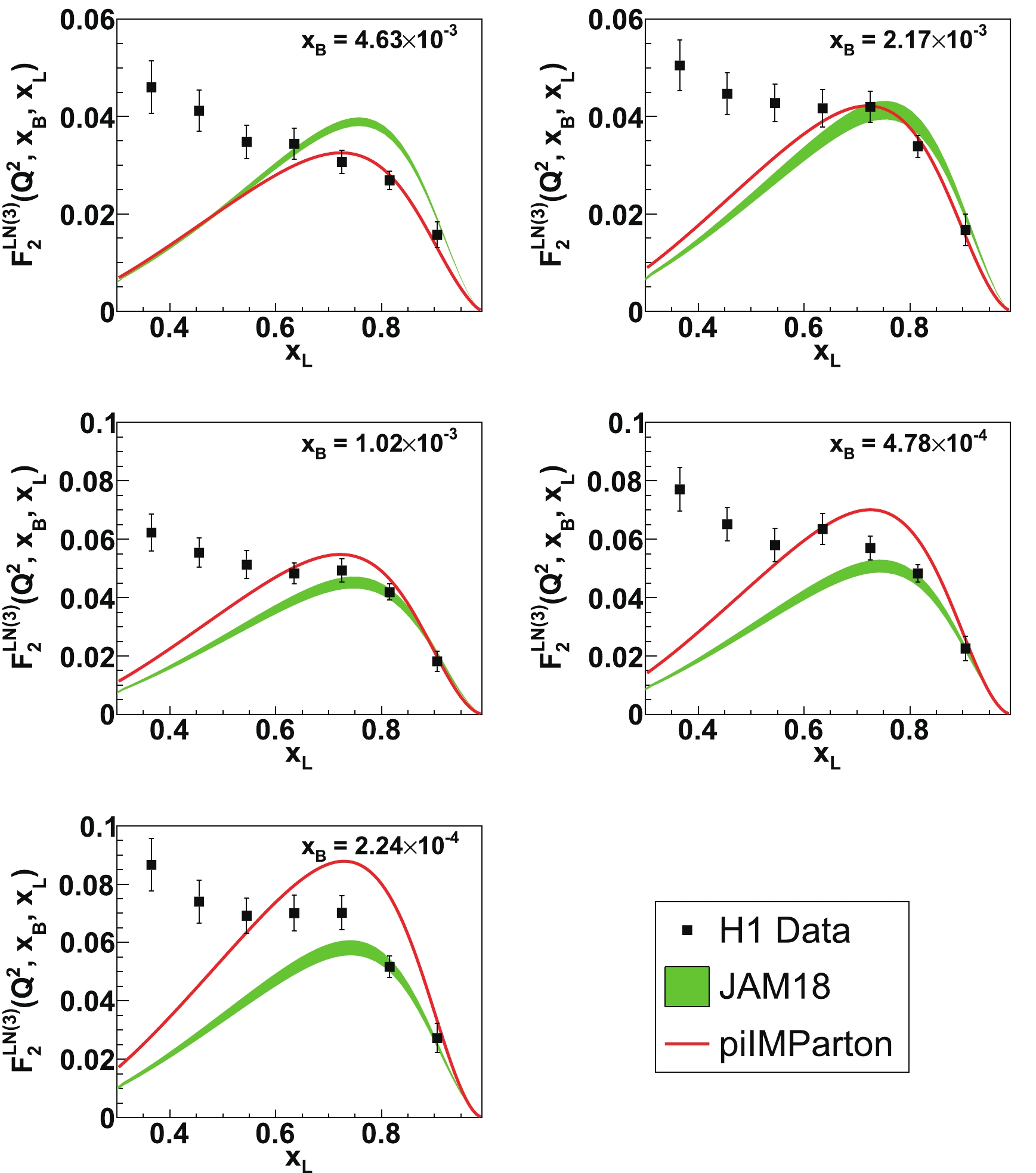
$ {{\rm{\pi}}} $ -nucleus Drell-Yan data by the E615 Collaboration [31]. We can see excellent agreements among the JAM18 global fit, the dynamical parton model calculation (piIMParton), and the experimental data in the range$ 0.2<x_{{\rm{\pi}}}<1 $ . We also notice that in the region$ x_{\rm{\pi}} \lesssim 0.6 $ the experimental data exhibit big uncertainties. So the aim of future experiments is to collect more data and to greatly reduce the uncertainties in the small-$ x_{{\rm{\pi}}} $ region. In the small-$ x_{{\rm{\pi}}} $ region ($ x_{{\rm{\pi}}}\lesssim 0.01 $ ), there are a few experimental data for the pion structure function, obtained from the H1 and ZEUS experiments at HERA [32, 33]. Figure 3 shows comparisons of the structure function prediction from the JAM18 PDF, the piIMParton model prediction, and the structure function data from H1. Note that in the model calculation of the structure function$ F_2^{{\rm{\pi}}} $ , only u, d, and s quark contributions are taken into account. Amazingly, the calculations at small$ x_{{\rm{\pi}}} $ of both the JAM18 pionic PDF and the dynamical sea quark distributions are consistent with the up-to-date experimental measurements of pion structure. Some differences are found between the JAM18 prediction and the piIMParton prediction. Therefore, future experimental measurements are important to clearly distinguish the models.
Figure 3. (color online) Comparisons of the global fit by JAM18 (green bands), the predictions from the piIMParton PDF of the pion (red solid curves), and the experimental data of the pionic structure function measured by the H1 Collaboration (black squares). The green bands show the 1
$\sigma$ uncertainties of the JAM18 global analysis. The pionic structure function extracted by H1 is from an analysis of the LN-DIS data in the kinematical region of$x_{\rm{L}}$ around 0.73 [33].To carefully check the pionic PDF of JAM18 and the dynamical parton distributions of piIMParton, we have calculated more experimental observables and compare them to the recent H1 experiment [33]. Figure 4 shows the comparisons of the calculated three-fold leading-neutron structure functions
$ F_2^{{\rm{LN}}(3)} $ and the H1 data. In the large-$ x_{\rm{L}} $ region ($ x_{\rm{L}}\gtrsim 0.6 $ ), the model calculations are consistent with the experimental data. This is because the e-$ {{\rm{\pi}}^{*}} $ DIS process plays an important role in the regime of large$ x_{\rm{L}} $ . In the small-$ x_{\rm{L}} $ region, if the contribution from the normal e-p DIS process is added to the model calculation, then the experimental data is well explained and described. Nevertheless, the focus of this simulation is on the region of$ x_{\rm{L}}>0.75 $ . We also calculate the differential cross-section as a function of$ x_{\rm{L}} $ , which is shown in Fig. 5 compared to the H1 data. In the leading-neutron production region, the predictions of both JAM18 PDF and the dynamical parton model agree well with the H1 experiment at HERA. The validity of our LN-DIS cross-section has been verified with an independent calculation using RAPGAP software. In the literature [33], it is shown that the H1 data in the small-$ x_{\rm{L}} $ region is explained well by the normal DIS process on the proton. The combination of the LN-DIS process and the normal DIS process with a neutron fragment reproduces the experimental data over the whole range of$ x_{\rm{L}} $ [33].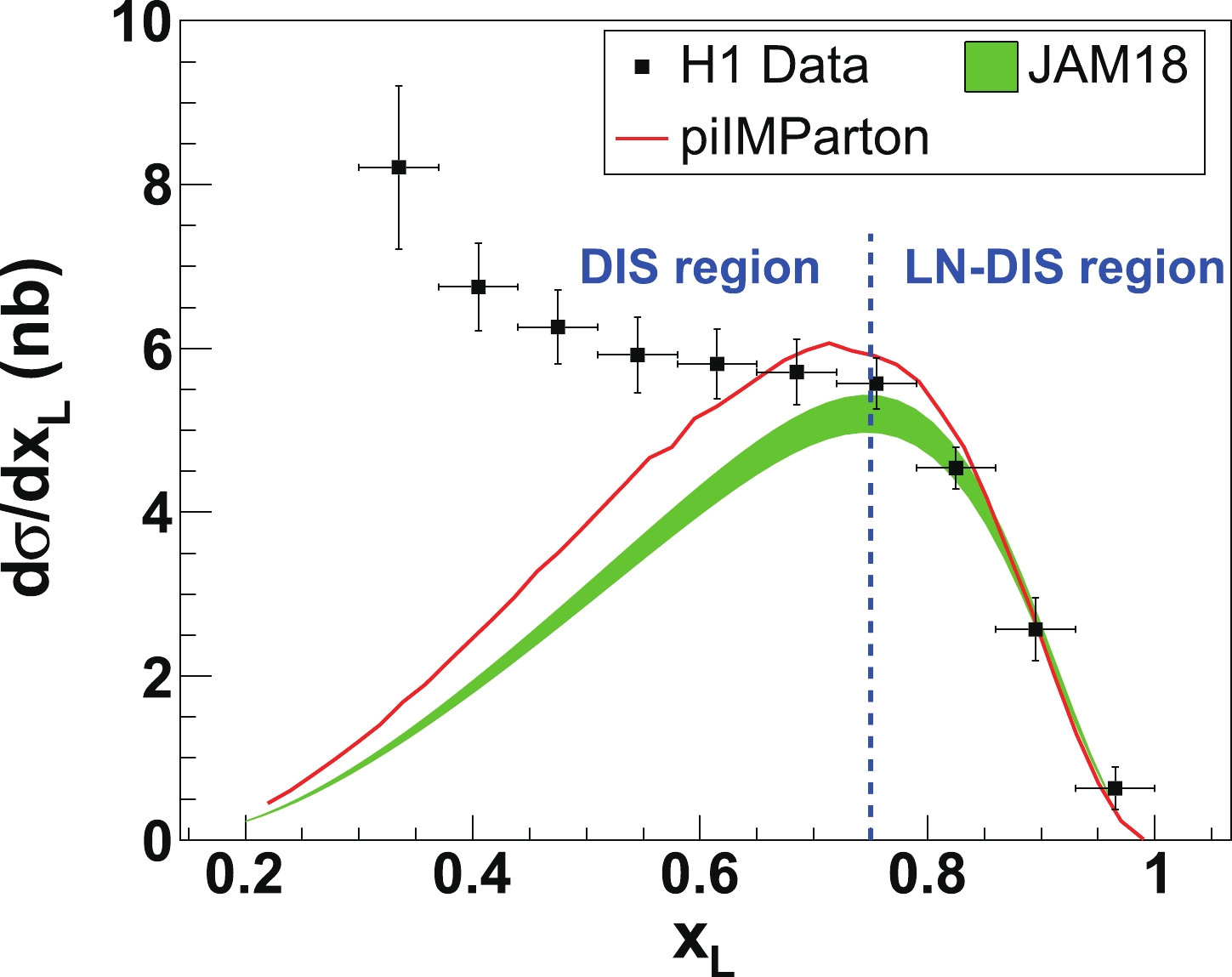
Figure 5. (color online) Comparison of the predictions of one-fold differential cross-section from the JAM18 PDF, the predictions from the piIMParton model [56], and the H1 data [33], integrated over the kinematical range of
$6<Q^2<100$ GeV$^2$ ,$1.5\times 10^{-4} <x_{\rm{B}} <3\times 10^{-2}$ , and$P_{{T}}^{{n}}<0.2$ GeV/c. The green band shows the 1$\sigma$ uncertainty of the JAM18 global analysis. In the LN-DIS dominant region (i.e.$x_{\rm{\pi}}>0.75$ ), the cross-section can be explained with the e-${{\rm{\pi}}}$ DIS formula and the dynamical parton distribution functions of the pion.Figure 6 shows comparisons of the pionic parton distributions from the recent global analyses of the current experimental data [49, 50] and the dynamical parton distributions of piIMParton. We can see that there are some differences among the different PDF sets. Nonetheless, the parton distributions of the pion from JAM18 [49] are consistent with the xFitter global fit [50] and the dynamical parton distributions of the pion [48, 56]. The purely dynamical sea quark distribution of piIMParton is lower than that from the phenomenological studies of global analyses, since in the dynamical parton model there are no intrinsic sea quark distributions at
$ Q_0^2 $ of an arbitrary parametrization. So far the pion PDFs from the global analyses exhibit big uncertainties due to the inadequate experimental data at small$ x_{{\rm{\pi}}} $ . Moreover, there are model uncertainties from varying the factorization or renormalization scales and the flexibility of parametrization of the input parton distributions. Therefore there is no significant difference between different models for the pionic parton distribution functions.
Figure 6. (color online) Comparisons of the global analysis by the JAM Collaboration [49], the global analysis by the xFitter Collaboration [50], and piIMParton PDFs from the dynamical parton model. The green bands show the 1
$\sigma$ uncertainties of the JAM18 global analysis. The red bands show the 1$\sigma$ uncertainties of the xFitter global analysis. The PDF data of the global analyses (JAM18 and xFitter) are taken from LHAPDF [58].Right now there is no measurement of LN-DIS at EicC energy. Therefore we use the JAM18 PDF of the pion and the one-pion exchange model to give projections of a possible EicC experiment. Every Monte-Carlo simulation has some model uncertainties. From the above demonstrations, we see that the pion PDFs from JAM18 [49] are acceptable for reproducing the E615 data and H1 data at very high energies. Convincingly, the cross-section model and the pionic parton distributions used in this simulation lead to controlled uncertainties for the projections of a suggested LN-DIS experiment at EicC.
-
Following the theoretical framework described in Sec. II and Sec. III, we developed a Monte Carlo (MC) simulation program, which generates the LN-DIS events very efficiently. In the simulation, the electron beam energy is 3.5 GeV and the proton beam energy is 20 GeV, which is a typical collision energy for the future EicC [51, 52]. Inside the phase space of the LN-DIS process, we apply the following kinematical ranges for the MC sampling:
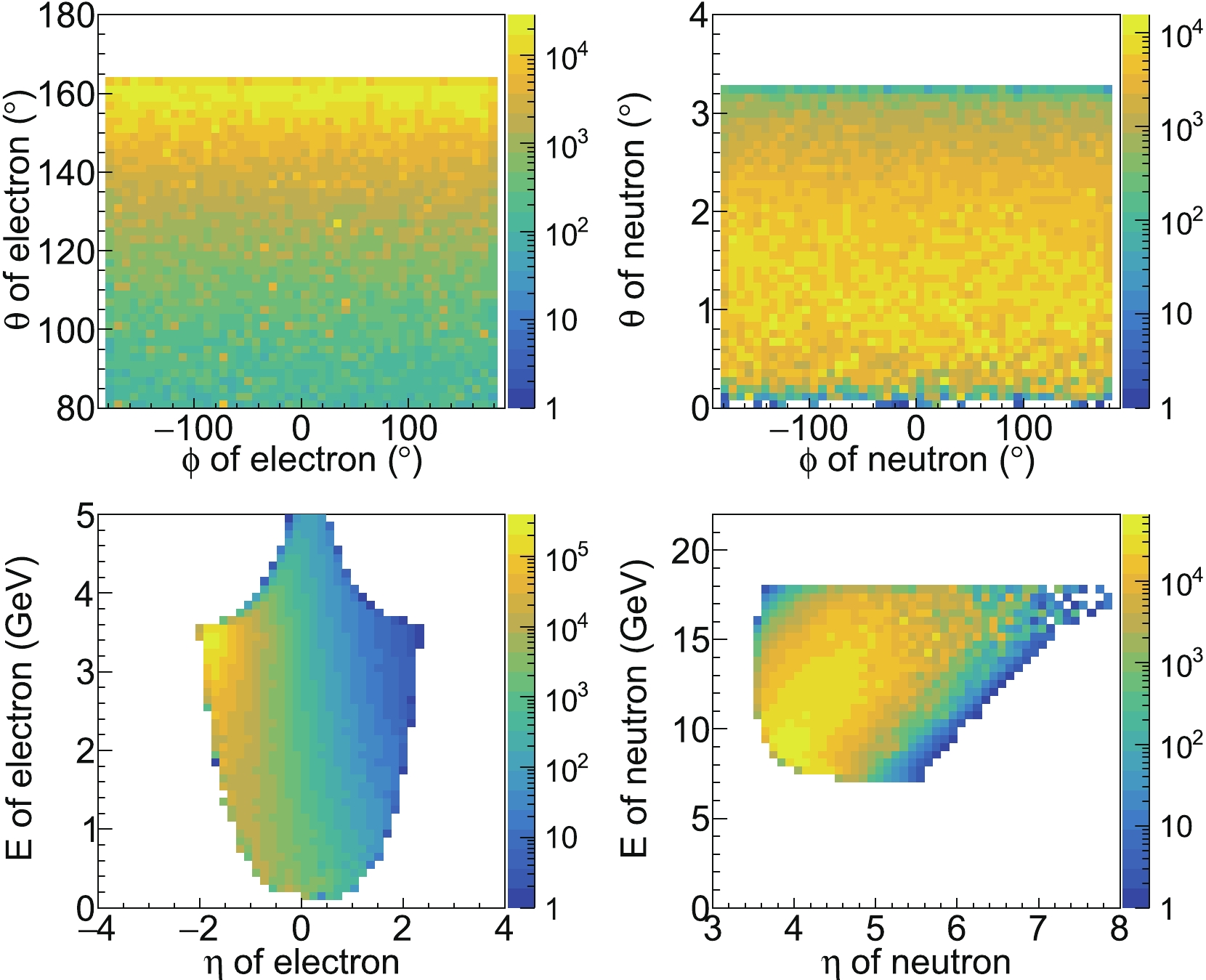
$ 0.01 $ GeV$ ^2 $ $ <-t<1 $ GeV$ ^2 $ ,$ 0.5<x_{\rm{L}}<1 $ ,$ x_{{\rm{B}},{\rm{min}}}<x_{\rm{B}}<1 $ , 1 GeV$ ^2 $ $ <Q^2< $ 50 GeV$ ^2 $ , and$ W^2>4 $ GeV$ ^2 $ , to focus on the kinematical regions of interest.Figure 7 shows the distributions of
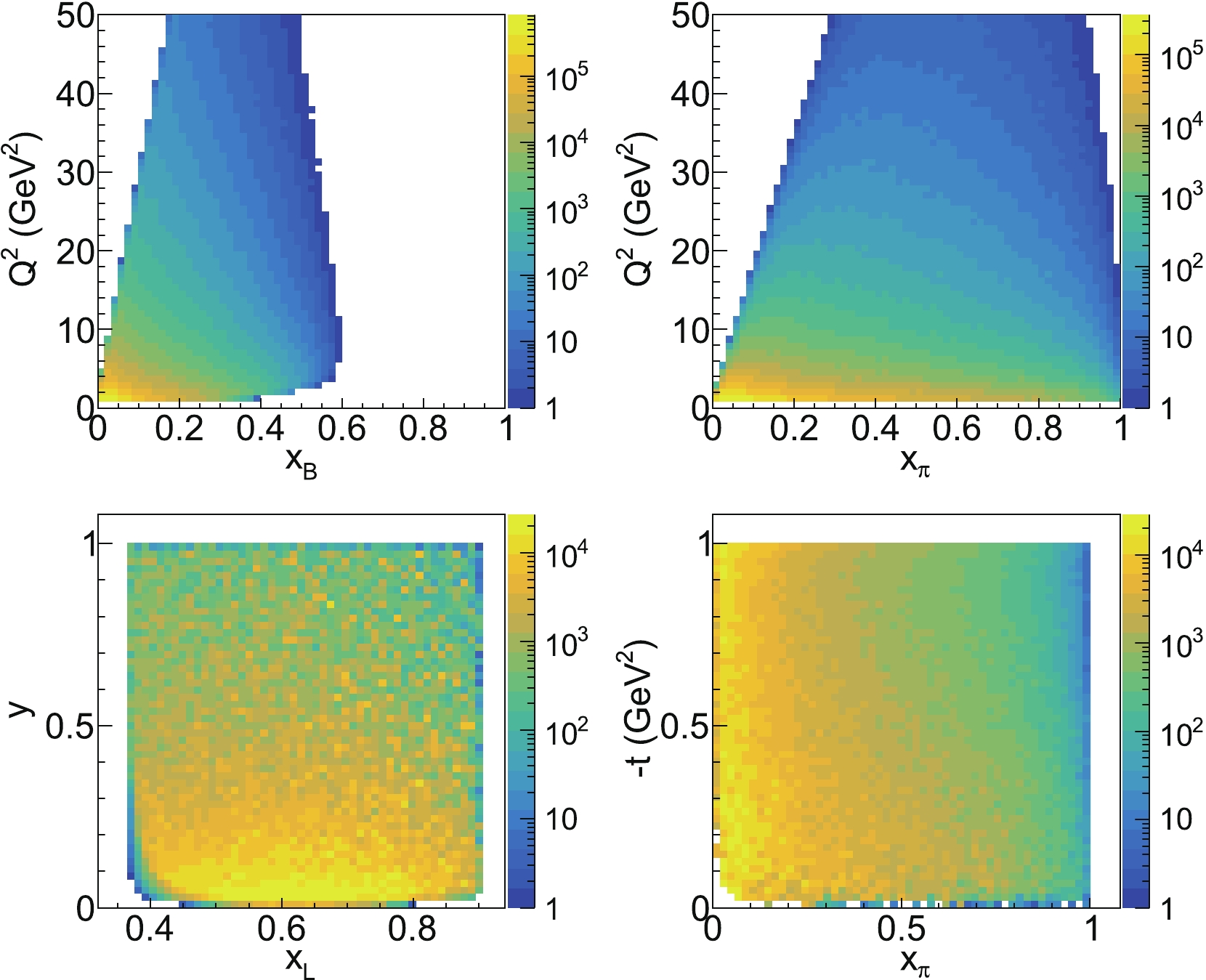
$ \theta $ angle,$ \phi $ angle, energy, and pseudorapidity of the final-state electron and neutron. Note that in the simulation the z direction is defined as the momentum of the incoming proton beam. All the scattered electrons go to the central region of the spectrometer ($ |\eta|<3 $ ), and they are precisely and efficiently measured with the central tracker and electromagnetic calorimeter [52]. The final neutrons go to very small angles, with the pseudorapidity around 5. It is suggested that they be detected with a far-forward neutron calorimeter, the so-called zero-degree calorimeter (ZDC). Figure 8 shows the cross-section weighted distributions of the invariant kinematics of interest. We see that most of the events are distributed in the low$ Q^2 $ , small$ x_{\rm{\pi}} $ , small y and small t region. The small-$ x_{\pi} $ region is a unique region where EicC can provide precise data, filling the gap in the current data acquired from the facilities of decades ago. The broad$ x_{\rm{\pi}} $ range from 0.01 to 1 and the high luminosity of EicC will provide a great opportunity to cross-check the large-x behavior of the pion parton distribution, when$ x_{\rm{\pi}} \rightarrow 1 $ , with the Drell-Yan measurements of decades ago. -
The statistical uncertainty of the measured experimental observable is directly related to the number of events collected during an experiment. Given the calculation of the cross-section in the above discussion, now we only need to know the accumulated luminosity to estimate the number of events. We assume the integrated luminosity of an EicC experiment to be 50 fb
$ ^{-1} $ , which corresponds to a run of one to two years. To study the pionic structure function, we have applied the following conditions for the event selection:$ x_{\rm{L}}>0.75 $ ,$ P_{{T}}^{{n}}<0.5 $ GeV,$ M_{{X}} = (p_{{e}}+P_{{p}}-p_{{e'}}-P_{{n}})^2>0.5 $ GeV,$ W>2 $ GeV.$ x_{\rm{L}}>0.75 $ and$ P_{{T}}^{{n}}<0.5 $ GeV makes sure the final neutron is a spectator in the e-$ {{{\pi}}} $ DIS process, where the neutron is from the Fock-state dissociation of the proton, having a large fraction of the longitudinal momentum of the incoming proton and a small transverse momentum.$ M_{{X}}>0.5 $ GeV requirement is to get rid of the contamination of the e-$ {{{\pi}}} $ elastic scattering process, and makes sure the struck pion is broken up so as to study the partons inside the pion.$ W>2 $ GeV is a common criterion of DIS.With the above event selection, the LN-DIS events then are divided into different kinematical bins. Figure 9 shows the binning scheme of
$ x_{{\rm{\pi}}} $ and$ -t $ , for the low$ Q^2 $ ($ \sim 4 $ GeV$ ^2 $ ) MC data. The number of events in each bin is calculated with the following formula,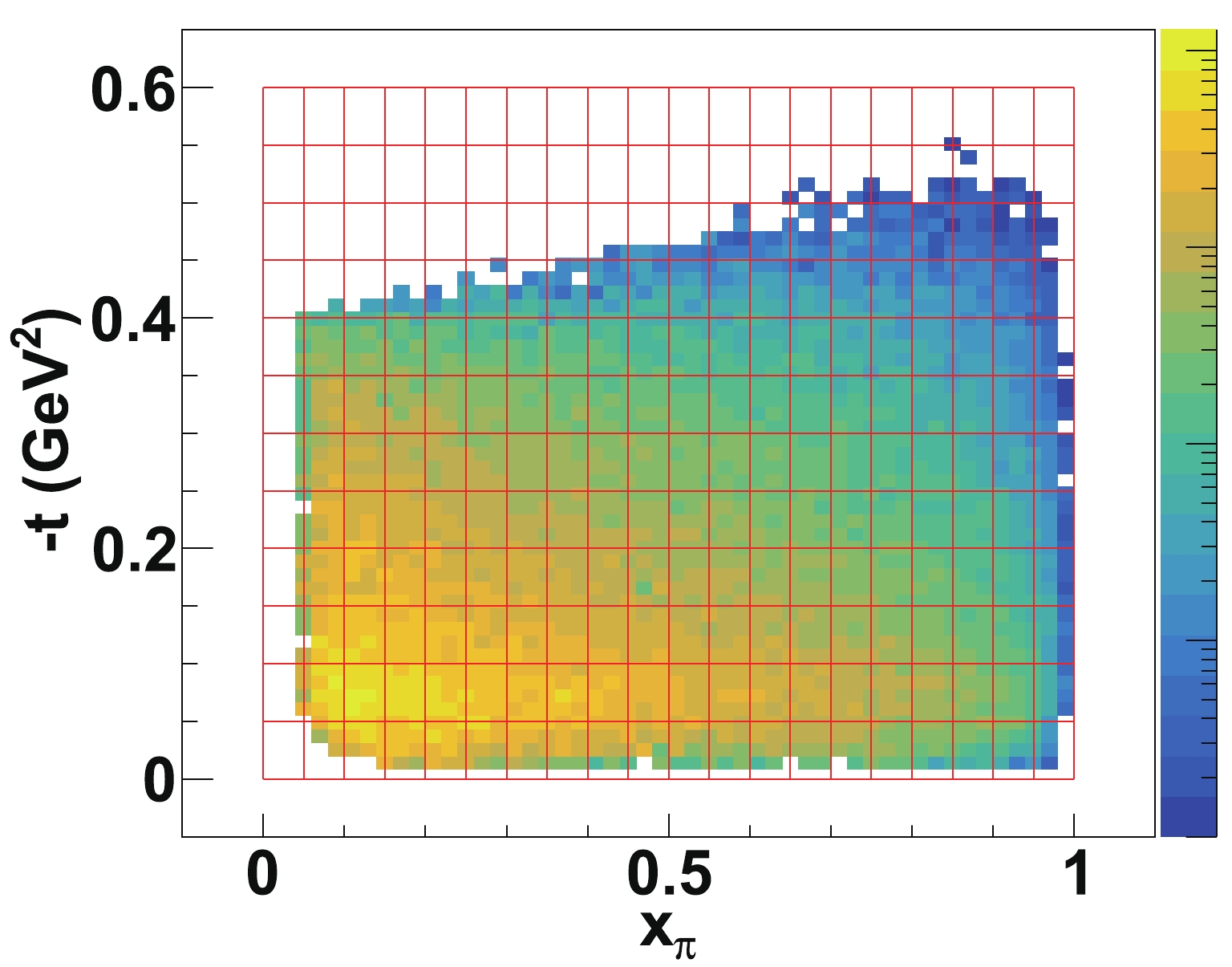
Figure 9. (color online) The binning scheme in the
$x_{\rm{\pi}}$ vs.$-t$ plane, for 3 GeV$^2$ $<Q^2<$ 5 GeV$^2$ ,$x_{\rm{L}}>0.75$ ,$P_{{T}}^{{n}}<0.5$ GeV,$M_{{x}}>0.5$ GeV, and$W^2>4$ GeV$^2$ .$ N_{{i}} = \epsilon L\overline{\sigma}_{{i}} \Delta x_{\rm{\pi}} \Delta Q^2 \Delta x_{\rm{L}} \Delta t (1-x_{\rm{L}}), $

(7) in which
$ \epsilon $ is the detector efficiency, L is the integrated luminosity,$ \overline{\sigma}_{{i}} $ is the mean differential cross-section in bin i, and the rest denotes the sizes of the kinematical bins. The factor$ (1-x_{\rm{L}}) $ is the Jacobian coefficient, which comes from the transform from integration over$ x_{\rm{B}} $ into integration over$ x_{{\rm{\pi}}} $ . According to the dimensions and performance of a conceptual design in the far-forward region, the detector efficiency for neutrons can be high. In this simulation, an efficiency of 50% is assumed for collecting both the final electron and neutron. With the number of events in each bin simulated, then the relative statistical error is estimated to be$ 1/\sqrt{N_{{i}}} $ .Figure 10 shows the statistical error projections in a low
$ Q^2 $ bin between 3 and 5 GeV$ ^2 $ , for an EicC experiment. The statistical errors are all less than 3%, starting from$ x_{{\rm{\pi}}}\sim 0.05 $ to$ x_{{\rm{\pi}}}\sim 1 $ at different t bins. For about half of the data ($ x_{\rm{\pi}}<0.45 $ ), the precisions are very high ($ <0.5 $ %). Recalling the uncertainties of pionic parton distributions from the current global analyses shown in Fig. 6, it is very clear that the precision of the EicC measurement at small$ x_{\rm{\pi}} $ will improve the current analysis tremendously. The measurement of t is important to know the virtuality of the pion and to extrapolate the structure function of the real pion. If we analyze the data at$ x_{\rm{L}} $ around 0.5, we can provide the data of$ x_{{\rm{\pi}}} $ close to 0.01. Focusing on the large-x behavior, it is quite exciting to point out that we could measure precisely the pion structure function of$ x_{{\rm{\pi}}} $ approaching 0.9. The error projections of the measurements at high$ Q^2 $ ($ >20 $ GeV$ ^2 $ ) are also projected and shown in Fig. 11 and Fig. 12. With fewer bins, the data at high$ Q^2 $ still have good precision. These precise measurements in different$ Q^2 $ bins over a broad range of$ x_{{\rm{\pi}}} $ will give a test of the QCD evolution equations and a better understanding of the gluon distribution of the pion.
Figure 10. (color online) Statistical error projections of the pionic structure function at
$Q^2 \sim 4$ GeV$^2$ , for a suggested EicC experiment with an integrated luminosity of 50 fb$^{-1}$ . The left and bottom axes indicate where the bin center of the data point is. The right axis shows how large the statistical error is.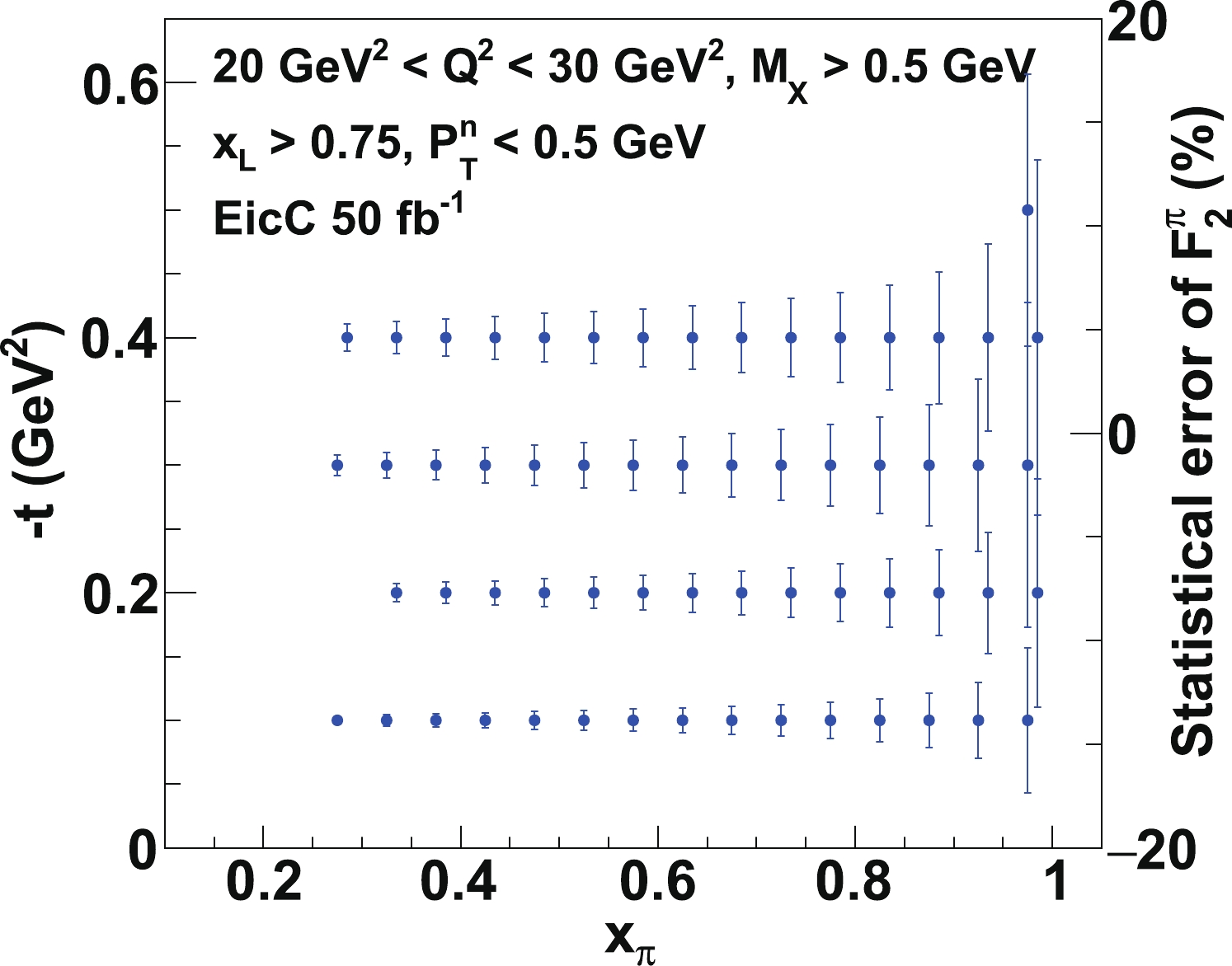
Figure 11. (color online) Statistical error projections of the pionic structure function at
$Q^2 \sim 25$ GeV$^2$ , for a suggested EicC experiment with an integrated luminosity of 50 fb$^{-1}$ . The left and bottom axes indicate where the bin center of the data point is. The right axis shows how large the statistical error is.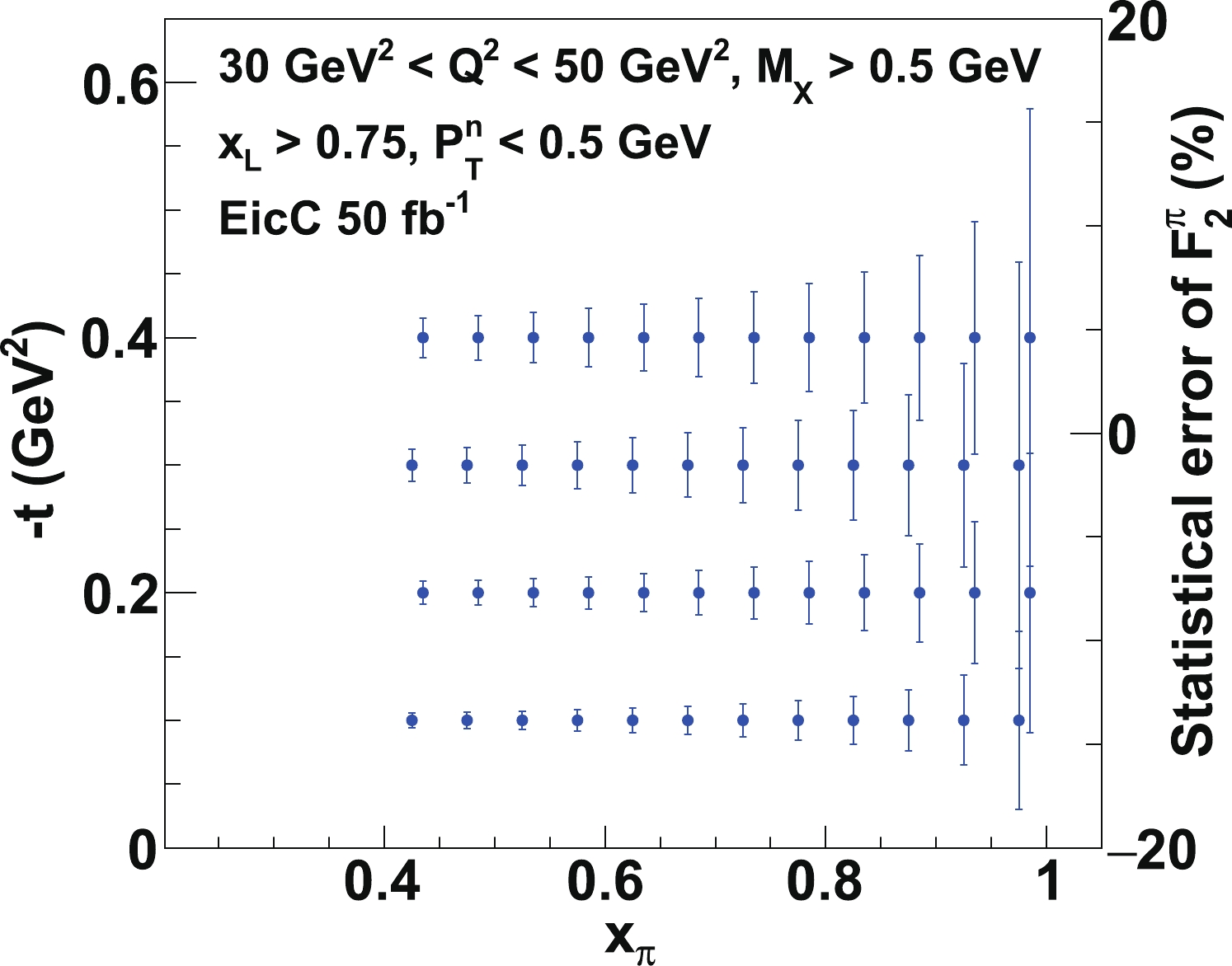
Figure 12. (color online) Statistical error projections of the pionic structure function at
$Q^2 \sim 40$ GeV$^2$ , for a suggested EicC experiment with an integrated luminosity of 50 fb$^{-1}$ . The left and bottom axes indicate where the bin center of the data point is. The right axis shows how large the statistical error is. -
The excellent agreement of the predictions of the JAM18 pionic PDFs, the dynamical parton model predictions [48, 56], and the H1 data at HERA [33] implies that the LN-DIS process can be used to study the pion structure. The LN-DIS process can be understood as the scattering between the electron and the abundant virtual pions around the proton at small momentum transfer t. Pion structure measurement at an electron-ion collider is feasible by tagging the spectator neutron.
Following the pioneering work by H1 and ZEUS, we simulate a LN-DIS experiment at EicC to investigate the pionic structure function over a wide kinematical range. The simulation indicates that the EicC machine could provide a precise measurement of the pionic structure over a range of
$ x_{\rm{\pi}} $ from 0.01 to 0.9, and of$ Q^2 $ from 1 to 50 GeV$ ^2 $ . Since the neutron is not charged, the very forward neutrons can be separated from the proton beam with a dipole magnet. Hence, measuring the neutrons at very small angles is not difficult, as long as the space of the tunnel for the accelerator is long enough to install a neutron calorimeter. In the simulation, we choose a conservative neutron efficiency of 50% to model the performance of the neutron detector. The low energy EicC, with its high luminosity, would give us a good opportunity to see precisely the one-dimensional structure of the meson.The pion structure experiment is also proposed at a high energy electron-ion collider in the US [59]. The expected precision of the pion structure data at US-EIC is argued to be around the same order-of-magnitude in statistics as the HERA proton data. The anticipated error is smaller than 2% at
$ x_{\rm{\pi}}\sim 0.01 $ and$ Q^2\sim 10 $ GeV$ ^2 $ , from a simple extraction of the pionic parton distributions [59]. The detector capabilities at EicC and US-EIC will be very similar. The US-EIC will run at a much higher energy and the high statistical data will be mainly in the small-$ x_{{\rm{\pi}}} $ region ($ \lesssim 0.3 $ ). In the large-$ x_{{\rm{\pi}}} $ region ([0.3, 0.9]), EicC would have pion structure data with competitive quality. Therefore, EicC will play an important and complementary role in exploring the meson structure.The precise measurement of the pionic structure function in a broad kinematical domain will undoubtedly deepen our understanding of the strong interaction. The systematic study of the LN-DIS reaction and the precise extraction of the pionic structure from the sea quark region to the valence quark region at EicC will be a crucial input for the database of hadron PDFs. The PDFs on the experimental side will differentiate the various current models on hadron structure. Most importantly, the LN-DIS experiment at EicC would have great potential to reveal pion parton distributions with a lot of detail, leading to a better understanding of many nonperturbative approaches, dynamical symmetry breaking, and why the pion mass is so small compared to the proton mass.
-
We are sincerely grateful to Dr. Jixie ZHANG for so much friendly help, and for the cross-checks of the simulation results with his independent estimation. We are very grateful for Craig ROBERTS' suggestions on studying the pionic structure at EicC and his efforts in promoting the project. R. WANG expresses his gratitude to Tanja HORN for her professional and constructive questions on the experimental side. We thank the EicC working group for their suggestions and fruitful discussions.
Simulation of neutron-tagged deep inelastic scattering at EicC
- Received Date: 2020-09-17
- Available Online: 2021-05-15
Abstract: Measuring the pionic structure function is of high interest, as it provides a new area for understanding the strong interaction among quarks and testing QCD predictions. To this end, we investigate the feasibility and expected impact of a possible experiment at EicC (Electron-ion collider in China). We show the simulation results on the statistical precision of an EicC measurement, based on the model of leading neutron tagged DIS process and the parton distribution functions of the pion from JAM18 global analysis. The simulation shows that at EicC, the kinematics cover the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: