-
The fine-tuning problem, known as the strong CP problem, is one of the open issues of the Standard Model (SM). It can be solved by introducing a spontaneously broken Peccei-Quinn symmetry [1, 2], which involves a light pseudoscalar particle, i.e., the QCD axion [3, 4]. This axion couples to the gluon field strength. Its phenomenology is determined by its low mass and very weak interactions. In particular, it could i) affect cosmology, ii) affect stellar evolution, iii) mediate new long-range forces, and iv) be produced in a terrestrial laboratory. At present, the QCD axion is regarded as a main component of the dark matter [5-7]. The solar axion [8, 9] was proposed to explain the excess in the low-energy electron recoil observed by the XENON1T Collaboration [10], given that its energy spectrum matches the excess.
An axion-like particle (ALP) is a particle having interactions similar to the axion. The origin of ALPs is expected to be similar but without the relationship between its coupling constant and mass. It means that the ALP mass can be treated independently of its couplings to the SM fields. The ALPs emerge in string theory scenarios [11-17], in theories with spontaneously broken symmetries [18, 19], or in the GUT [20]. All these models predict an ALP-photon coupling and, therefore, the electromagnetic decay of the ALPs in two photons. Experimental searches are mainly directed to ALPs to relax the coupling parameter [21].
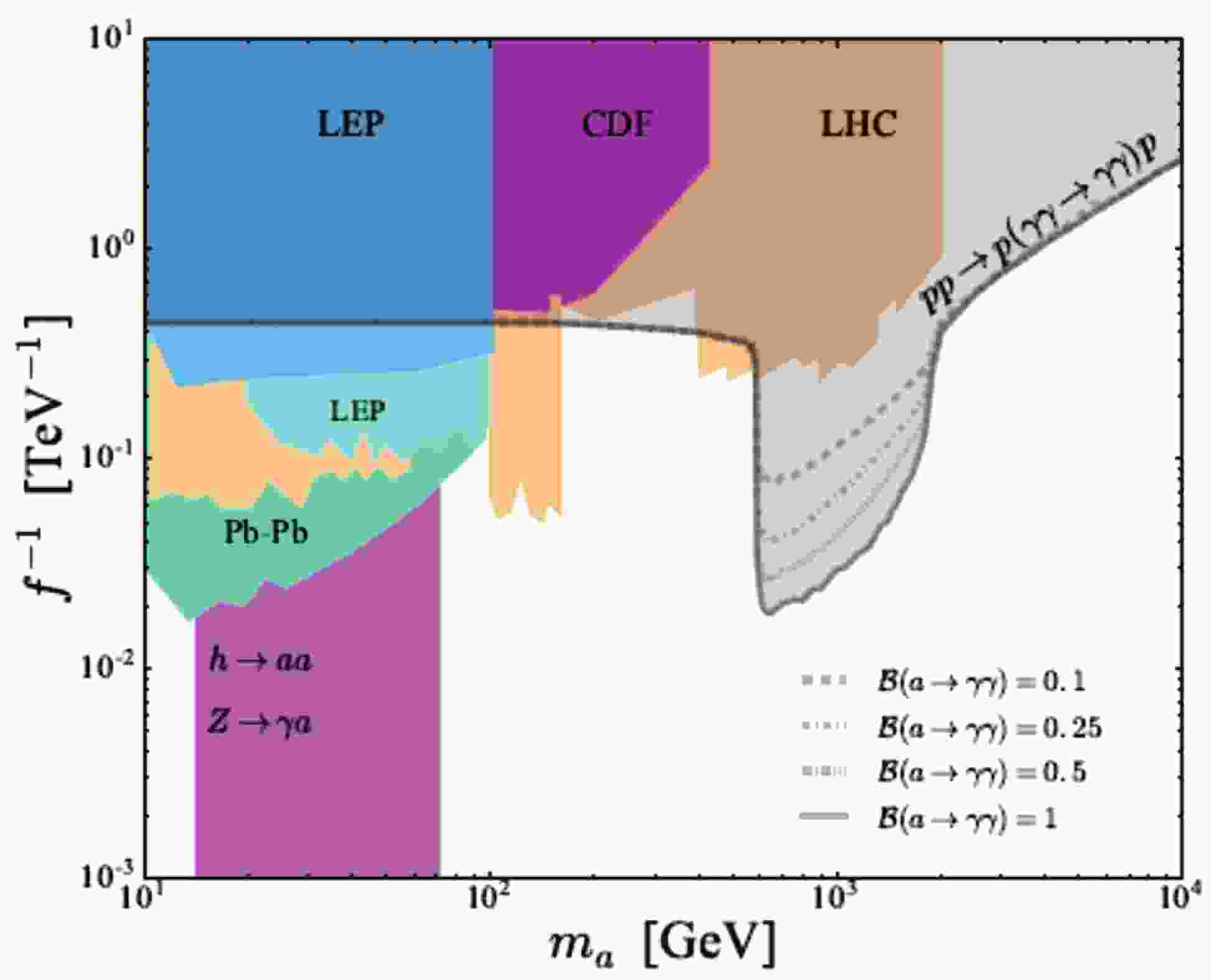
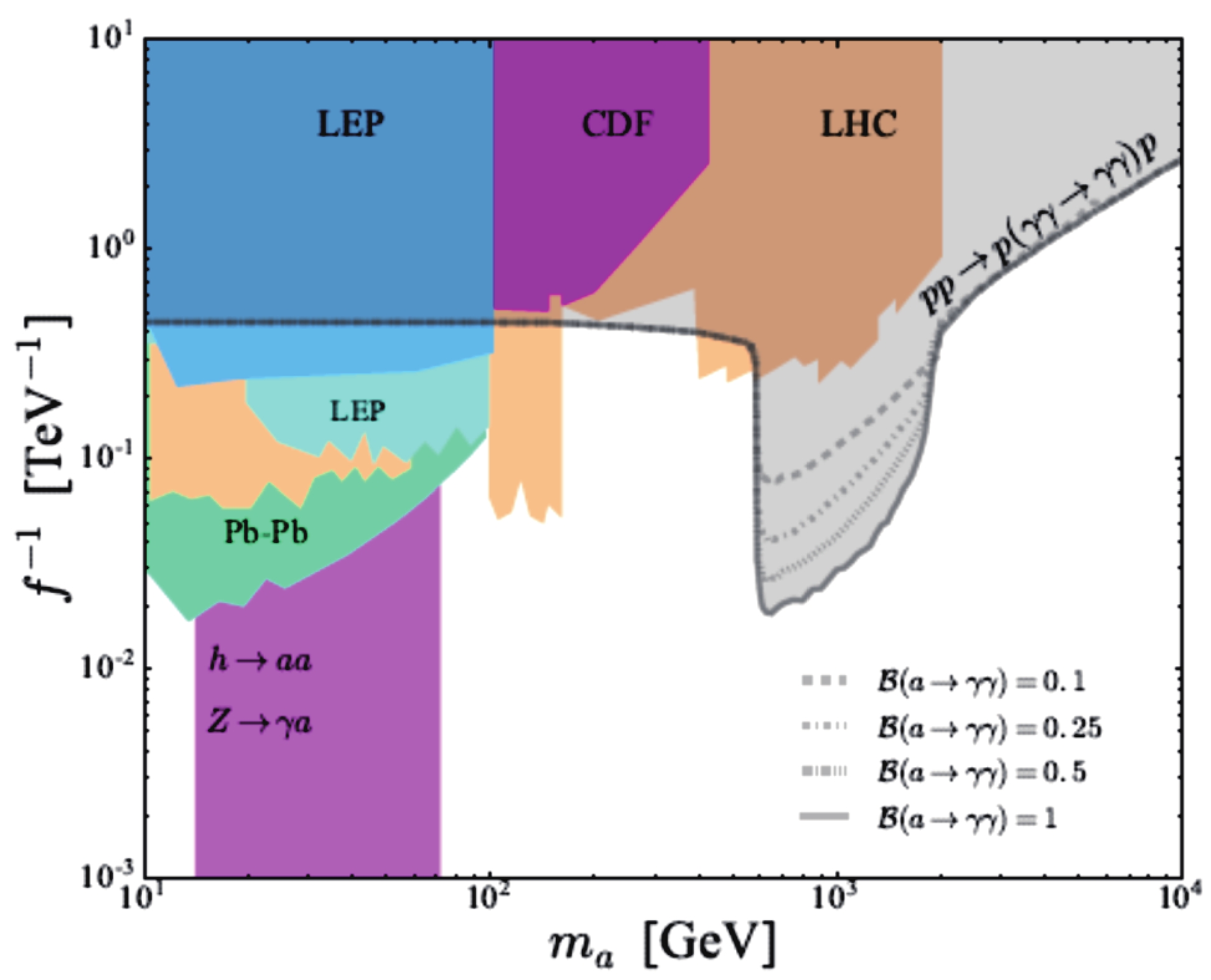
Heavy ALPs can be detected at colliders in a light-by-light (LBL) scattering [22-27]. It was shown that LHC searches employing the proton tagging technique constrain the ALP masses in the region 0.5 – 2 TeV [25-28]. The current exclusion regions for the axion and ALP searches are shown in Fig. 1. The first evidence of the subprocess
$ \gamma\gamma \rightarrow \gamma\gamma $ was observed by ATLAS Colloboration [29, 30] and CMS Colloboration [31] in high-energy ultra-peripheral PbPb collisions. The phenomenological analysis of the exclusive and diffractive$ \gamma\gamma $ production in PbPb scattering at the LHC and FCC was done in [32, 33]. The photon-induced process$ pp \rightarrow p\gamma\gamma p \rightarrow p'\gamma\gamma p' $ at the LHC was studied in [34-36].We recently investigated the virtual production of ALPs in LBL scattering at the compact linear collider (CLIC) [37, 38] with the initial unpolarized Compton backscattered (CB) photons [39]. The 95% C.L. exclusion regions for the ALP mass
$ m_a $ and ALP-photon coupling f have been calculated. It turned out that our CLIC bounds on$ m_a $ and f are stronger than the bounds for the LBL production of the ALP at the LHC presented in Fig. 1. Thus, the ALP search at the CLIC has a great physics potential to search for the ALPs, especially in the mass region 1 – 2.4 TeV [39].The CLIC is planned to accelerate and collide electrons and positrons at a maximum of 3 TeV center-of-mass energy. Three energy states of the CLIC with
$ \sqrt{s} = 380 $ GeV,$ \sqrt{s} = 1500 $ GeV, and$ \sqrt{s} = 3000 $ GeV are considered. The expected integrated luminosities are$ L = 1000 $ fb$ ^{-1} $ ,$ L = 2500 $ fb$ ^{-1} $ , and$ L = 5000 $ fb$ ^{-1} $ , respectively. The first two stages will be enable studying the gauge sector, Higgs, and top physics with high precision. The third stage will enable the most accurate investigation of the SM, as well as new physics [40-42].At the CLIC, it is possible to study not only
$ e^+e^- $ scattering but also$ \gamma\gamma $ collisions with real photons. These photon beams are given by the Compton backscattering of laser photons off linear electron beams. The physics potential of a linear collider is greatly enhanced with polarized beams [43]. The SM backgrounds may be reduced by a factor of five if the electron beam has a polarization of 80%. Searches for new physics can also be enhanced with the use of polarization beams. The conceptual design of the CLIC accelerator includes a source to produce a polarized electron beam and all the elements to transport the beam to the IP without loss of polarization. An electron beam polarization of 80% is expected for the baseline CLIC experimental programme.In a recent study of ours [39], the axion induced LBL scattering of the unpolarized CB photons was investigated. In the present paper, we aimed to study the same process with ingoing polarized CB photon beams. A summation over outgoing photons was assumed. The main goal was to demonstrate that the CLIC bounds on the ALP parameters can be improved if the polarized LBL scattering is considered.
-
As was already mentioned above,
$ \gamma\gamma $ -interactions with real photons can be examined at the CLIC. Real photon beams are obtained by the Compton backscattering of laser photons off linear electron beams. Most of these real scattered photons have high energy, and the$ \gamma\gamma $ luminosity turns out to be of the same order as the one for$ e^+e^- $ collisions [44, 45]. This is why a large cross section is obtained as a result of LBL scattering of real photons.The spectrum of backscattered photons is given by helicities of the initial laser photon and electron beam as follows
$ \begin{aligned}[b] f_{\gamma/e}(y) = &{{1}\over{g(\zeta)}} \Biggr[ 1-y + {{1}\over{1-y}} -{{4y}\over{\zeta(1-y)}}+{{4y^{2}}\over {\zeta^{2}(1-y)^{2}}} \\ &+ \lambda_{0}\lambda_{e} r\zeta (1-2r)(2-y) \Biggr] , \end{aligned} $

(1) where
$ g(\zeta) = g_{1}(\zeta)+ \lambda_{0}\lambda_{e} \,g_{2}(\zeta) \;, $

(2) $ g_{1}(\zeta) =\left( 1-{{4}\over{\zeta}}-{{8}\over{\zeta^{2}}} \right) \ln{(\zeta+1)}+{{1}\over{2}}+{{8}\over{\zeta}}-{{1}\over{2(\zeta+1)^{2}}} \;, $

(3) $ g_{2}(\zeta) = \left( 1 + {{2}\over{\zeta}} \right) \ln{(\zeta+1)} - {{5}\over{2}}+{{1}\over{\zeta+1}} - {{1}\over{2(\zeta+1)^{2}}} \;, $

(4) and
$ \zeta = \frac{4E_{e}E_{0}}{M_{e}^{2}} \;, \quad y = \frac{E_{\gamma}}{E_{e}} \;, \quad r = \frac{y}{\zeta(1-y)} \;. $

(5) Here,
$ E_\gamma $ is the scattered photon energy,$ E_0 $ and$ \lambda_0 $ are the energy and helicity of the initial laser photon beam, respectively, and$ E_e $ and$ \lambda_e $ are the energy and helicity of the initial electron beam before CB. Note that the variable y reaches a maximum value of 0.83 when$ \zeta = 4.8 $ . The helicity of the CB photons,$ \xi(E_{\gamma},\lambda_{0}) = {{\lambda_{0}(1-2r) (1-y+1/(1-y))+\lambda_{e} r\zeta[1+(1-y)(1-2r)^{2}]} \over{1-y+1/(1-y)-4r(1-r)-\lambda_{e}\lambda_{0}r\zeta (2r-1)(2-y)}} \;, $

(6) reaches its highest value when
$ y \simeq 0.83 $ . In what follows, we will consider two cases:$ \begin{aligned}[b] & (\lambda_0^{(1)}, \lambda_e^{(1)}; \lambda_0^{(2)}, \lambda_e^{(2)}) = (1, -0.8; 1,-0.8) \;, \\ &(\lambda_0^{(1)}, \lambda_e^{(1)}; \lambda_0^{(2)}, \lambda_e^{(2)}) = (1, +0.8; 1,+0.8) \;, \end{aligned} $

(7) where the superscripts 1 and 2 enumerate the beams. The integrated luminosities for the baseline CLIC energy stages were extracted from Ref. [46] (see Table 1).
Unpolarized $\lambda_e = -0.8$ 

$\lambda_e = +0.8$ 

Stage $\sqrt{s}$ /GeV

${\cal{L}}$ /fb

$^{-1}$ 

${\cal{L}}$ /fb

$^{-1}$ 

${\cal{L}}$ /fb

$^{-1}$ 

1 380 1000 500 500 2 1500 2500 2000 500 3 3000 5000 4000 1000 Table 1. CLIC energy stages and integrated luminosities for the unpolarized and polarized electron beams.
Note from Table 1 that the luminosities for the polarized electron beams are significantly smaller than those for the unpolarized beams, especially for the first two energy stages and
$ \lambda_e = 0.8 $ .Numerical estimates showed that for
$ \sqrt{s} = 380 $ GeV, the total cross sections almost coincide with the SM cross sections [39]. This is why we performed our calculations for collision energies$ \sqrt{s} = 1500 $ GeV (2nd stage of the CLIC) and$ \sqrt{s} = 3000 $ GeV (3rd stage of the CLIC). -
We considered a Lagrangian with CP-even coupling of the pseudoscalar ALP (in what follows, denoted as a) to photons, and ALP coupling to fermions,
$ {\cal{L}}_a = \frac{1}{2}\,\partial_\mu a \,\partial^{\,\mu}a - \frac{1}{2} m_a^2 a^2 + \frac{a}{f} \,F_{\mu\nu} \tilde{F}^{\mu\nu} + \frac{\partial_\mu a}{2f} \sum\limits_{\psi} c_\psi \bar{\psi} \gamma^\mu \psi \;, $

(8) where
$ F_{\mu\nu} $ is the electromagnetic tensor,$ \tilde{F}_{\mu\nu} = (1/2) \varepsilon_{\mu\nu\rho\sigma} F^{\rho\sigma} $ is its dual, and$ c_\psi $ is a dimensionless constant. Note that, in contrast to the QCD axion, the ALP does not couple to the gluon anomaly. The ALP-photon coupling f defines the ALP decay width into two photons$ \Gamma(a\rightarrow\gamma\gamma) = \frac{m_a^3}{4\pi f^2} \;, $

(9) and the decay rate of the ALP to fermions,
$ \Gamma(a \rightarrow \bar{\psi} \psi) = \frac{m_a m_\psi^2}{8\pi} \left( \frac{c_\psi}{f} \right)^{2} \sqrt{1 - \frac{4m_\psi^2}{m_a^2}} \;, $

(10) where
$ m_\psi $ is the fermion mass. Note from Eqs. (9) and (10) that, for$ m_a \gg m_\psi $ and$c_\psi = { {O}}(1)$ , the full width of the ALP will be mainly defined by its decay into two photons. In general, the ALP branching$ {\rm{Br}}(a\rightarrow\gamma\gamma) $ can be less than 1.The differential cross section of the diphoton production with initial polarized CB photons is defined by [47]
$ \begin{aligned}[b] \frac{{\rm d}\sigma}{{\rm d}\cos \theta} = &\frac{1}{128\pi s} \int\limits_{x_{1 \min}}^{0.83}\frac{{\rm d}x_1}{x_1} \,f_{\gamma/e}(x_1) \int\limits_{x_{2 \min}}^{0.83}\frac{{\rm d}x_2}{x_2} \,f_{\gamma/e}(x_2) \\ &\times \Big\{ \left[ 1 + \xi \left( E_{\gamma}^{(1)},\lambda_{0}^{(1)} \right) \xi \left( E_{\gamma}^{(2)},\lambda_{0}^{(2)} \right) \right] |M_{++}|^2 \\ &+ \left[ 1 -\xi \left( E_{\gamma}^{(1)},\lambda_{0}^{(1)} \right) \xi \left( E_{\gamma}^{(2)},\lambda_{0}^{(2)} \right) \right] |M_{+-}|^2 \Big\} , \end{aligned} $

(11) where
$ x_i = E_{\gamma}^{(i)}/E_e $ ($ i = 1,2 $ ) are the energy fractions of the CB photon beams,$ x_{1 \min} = p_\bot^2/E_e^2 $ ,$ x_{2 \min} = p_\bot^2/(x_{1} E_e^2) $ , and$ p_{\bot} $ is the transverse momentum of the final photons. Here$ \sqrt{s} $ is the center of mass energy of the$ e^+e^- $ collider, while$ \sqrt{s x_1 x_2} $ is the center of mass energy of the backscattered photons. The amplitudes$ |M_{++}| $ and$ |M_{+-}| $ are obtained by summations over the helicities of the outgoing photons in the helicity amplitudes,$ \begin{aligned}[b] & |M_{++}|^2 = |M_{++++}|^2 + |M_{++--}|^2 \;, \\ &|M_{+-}|^2 = |M_{+-+-}|^2 + |M_{+--+}|^2 \;. \end{aligned} $

(12) We applied P-, T-, and Bose symmetries. Each of the amplitudes is a sum of the ALP and SM terms,
$ M = M_a + M_{\rm{SM}} \;. $

(13) As the main SM background, both W-loop and fermion-loop contributions must be taken into account,
$ M_{\rm{SM}} = M_f + M_W \;. $

(14) The explicit analytical expressions for SM helicity amplitudes in the right-hand side of Eq. (12), both for the fermion and W-boson terms, are too long. This is why we do not present them here. They can be found in [39] (see also [25, 26]). To reduce the SM background, we will impose the cut on a rapidity of the final state photons, i.e.,
$ |\eta_{\gamma\gamma}| < 2.5 $ . Finally, a possible background with fake photons from decays of$ \pi^0 $ ,$ \eta $ , and$ \eta' $ is negligible in the signal region.Figs. 2 and 3 show the total cross sections for the process
$ \gamma\gamma \rightarrow \gamma\gamma $ with unpolarized and polarized CB initial photons as functions of the minimal transverse momenta of the final photons$ p_{t,\min} $ . In Fig. 2, the invariant energy is set to be$ \sqrt{s} = 1500 $ GeV, and the ALP mass$ m_a $ and its coupling f are chosen to be equal to 1200 GeV and 10 TeV, respectively. To reduce the SM background, we imposed the cut on the invariant energy of the final photons, i.e.,$ W = m_{\gamma\gamma} > 200 $ GeV. The cross sections are presented for two values of the ALP branching$ {\rm{Br}} = {\rm{Br}}(a \rightarrow \gamma\gamma) $ . The curves on the left, middle, and right panels correspond to the helicity of the initial electron beam before CB with$ \lambda_{e} = 0 $ (unpolarized case),$ \lambda_{e} = -0.8 $ , and$ \lambda_{e} = 0.8 $ , respectively. The SM predictions are also presented. The total cross sections for$ \sqrt{s} = 3000 $ GeV are shown in Fig. 3. Note that the deviation from the SM increases as$ p_{t,\min} $ increases, especially for$ \lambda_{e} = 0.8 \ (-0.8) $ , if$ \sqrt{s} = 1500 \ (3000) $ GeV. Note that for$ \sqrt{s} = 1500 $ GeV and$ \lambda_{e} = -0.8 $ , the total cross section for the polarized beams is even less that the unpolarized total cross section. The same is true for$ \sqrt{s} = 3000 $ GeV and$ \lambda_{e} = 0.8 $ .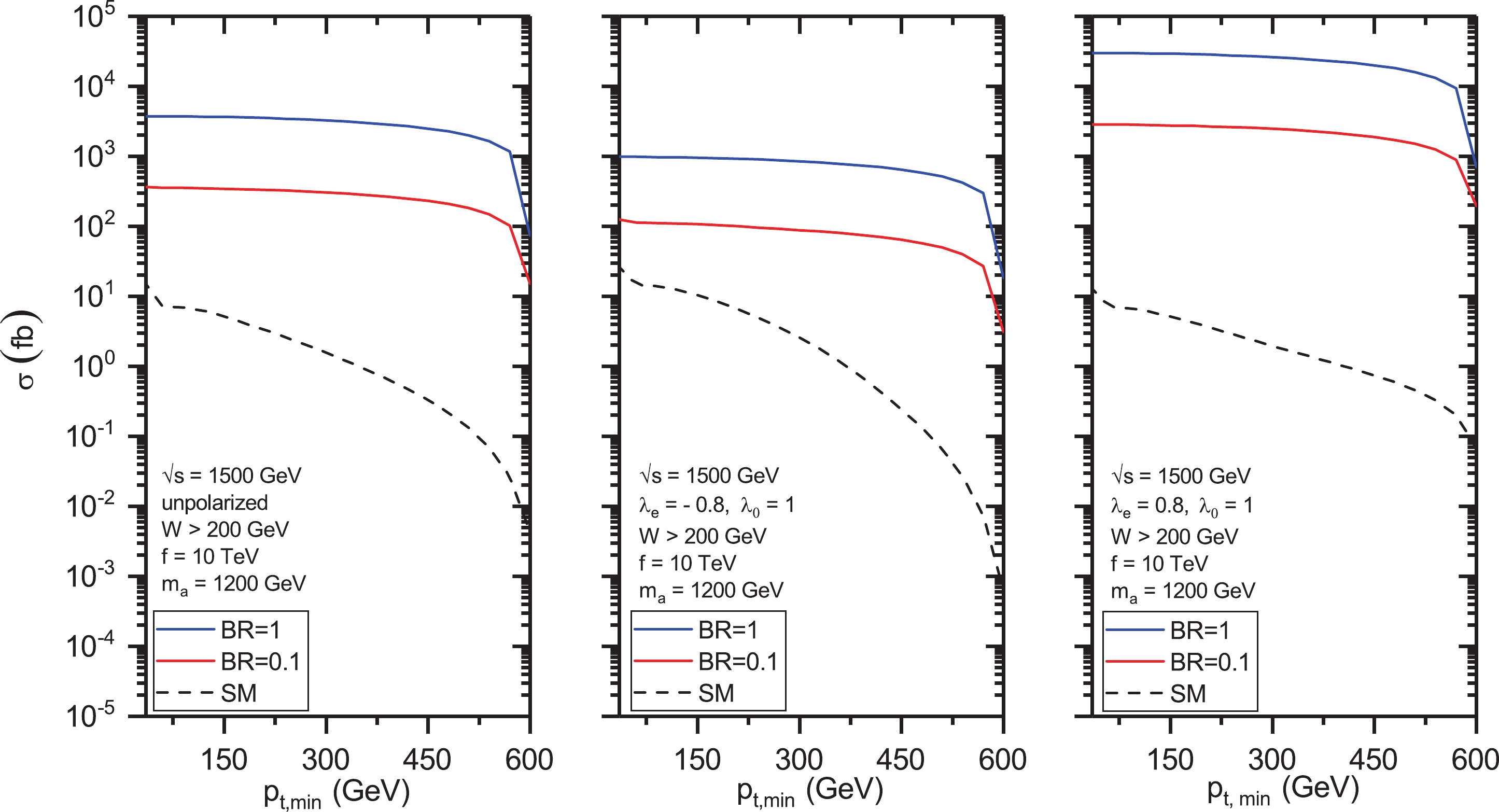
Figure 2. (color online) Total cross sections for the process
$ \gamma\gamma \rightarrow \gamma\gamma $ at the CLIC as functions of the transverse momenta cutoff$ p_{\rm{t,min}} $ of the final photons for invariant energy$ \sqrt{s} = 1500 $ GeV. Left panel: unpolarized case. Middle panel: the helicity of the electron beam is$ \lambda_e = -0.8 $ . Right panel: the helicity of the electron beam is$ \lambda_e = 0.8 $ .
Figure 3. (color online) Total cross sections for the process
$ \gamma\gamma \rightarrow \gamma\gamma $ at the CLIC as functions of the transverse momenta cutoff$ p_{\rm{t,min}} $ of the final photons for invariant energy$ \sqrt{s} = 3000 $ GeV. Left panel: unpolarized case. Middle panel: the helicity of the electron beam is$ \lambda_e = -0.8 $ . Right panel: the helicity of the electron beam is$ \lambda_e = 0.8 $ .Figures 4 and 5 demonstrate the dependence of the total cross sections on the ALP mass both for unpolarized and polarized electron beams for
$ \sqrt{s} = 1500 $ GeV, two values of the coupling constant f, and two values of the ALP branching$ {\rm{Br}}({\rm{a}} \rightarrow \gamma\gamma) $ . The total cross sections for$ \sqrt{s} = 3000 $ GeV are shown in Figs. 6 and 7. All the curves have sharp peaks near the point$ m_a = 1200 $ GeV. As mentioned above after Eq. (5), the maximum value of the ratio$ E_\gamma/E_e $ is equal to 0.83. This is why a bump around$ 0.83 \times 1500 $ GeV = 1245 GeV is expected, in agreement with Figs. 4, 5. Note that for$ \sqrt{s} = 1500 $ GeV, the polarized cross sections exceed the unpolarized cross sections by an order of magnitude. Unfortunately, owing to the relatively small integrated luminosity for the second CLIC stage (see Table 1), expected bounds on$ m_a $ and f appear to be even less stronger than the corresponding bounds for the unpolarized case. Thus, we addressed the third energy stage of the CLIC. For$ \sqrt{s} = 3000 $ GeV, the ratio of the polarized cross section to unpolarized one is approximately equal to 2.5.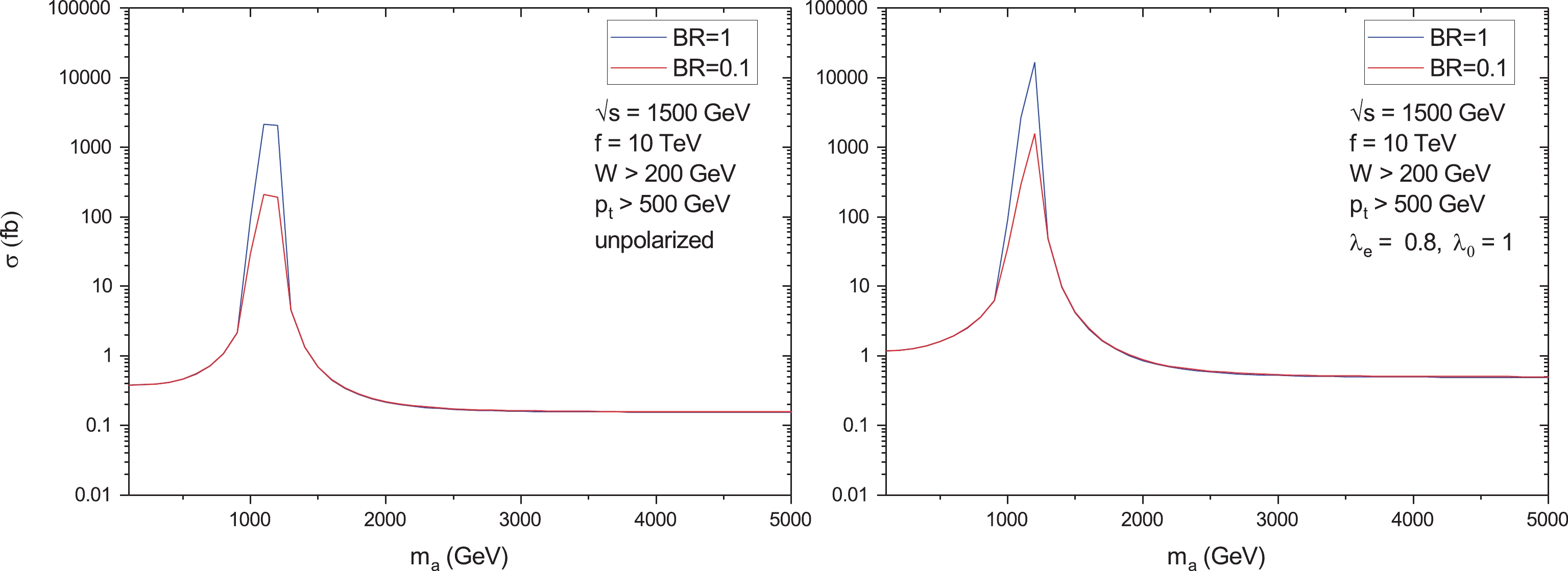
Figure 4. (color online) Total cross sections for the process
$ \gamma\gamma \rightarrow \gamma\gamma $ at the CLIC for the CB initial photons as functions of the ALP mass$ m_a $ for$ \sqrt{s} = 1500 $ GeV and$ f = 10 $ TeV. Left panel: unpolarized case. Right panel: polarized case, the helicity of the electron beam is equal to$ \lambda_e = 0.8 $ .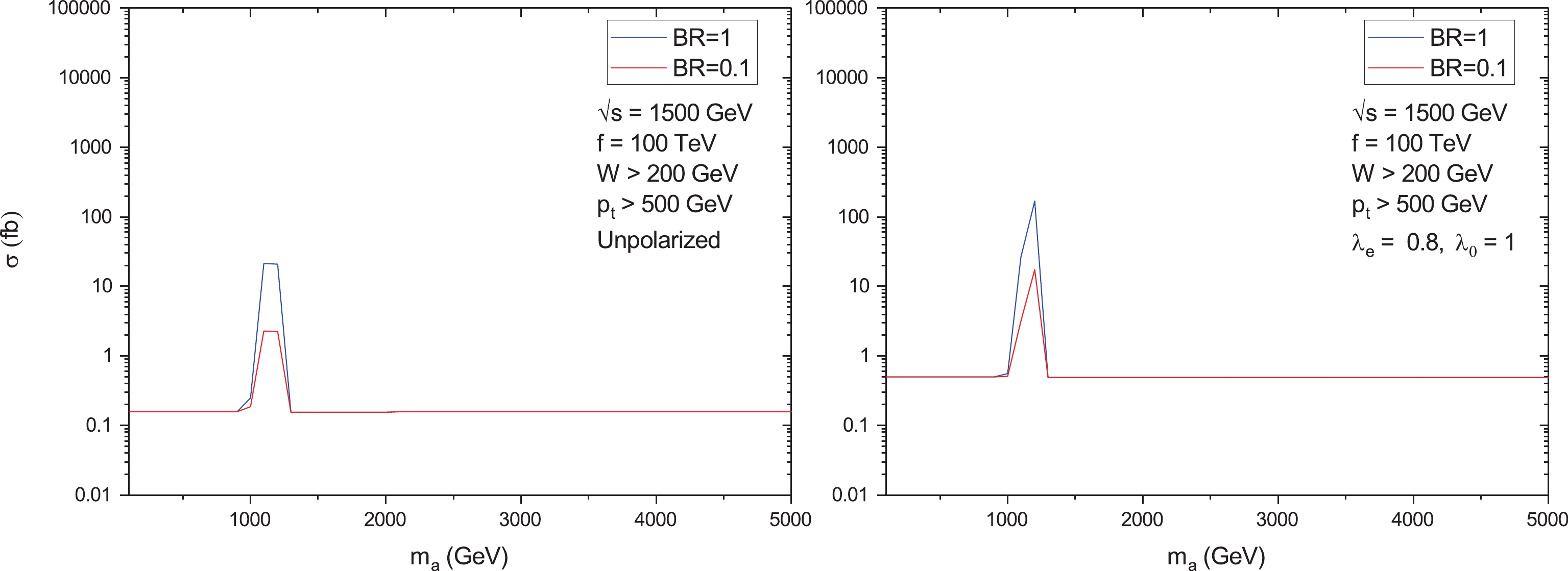
Figure 5. (color online) The same as in Fig. 4, but for
$ f = 100 $ TeV.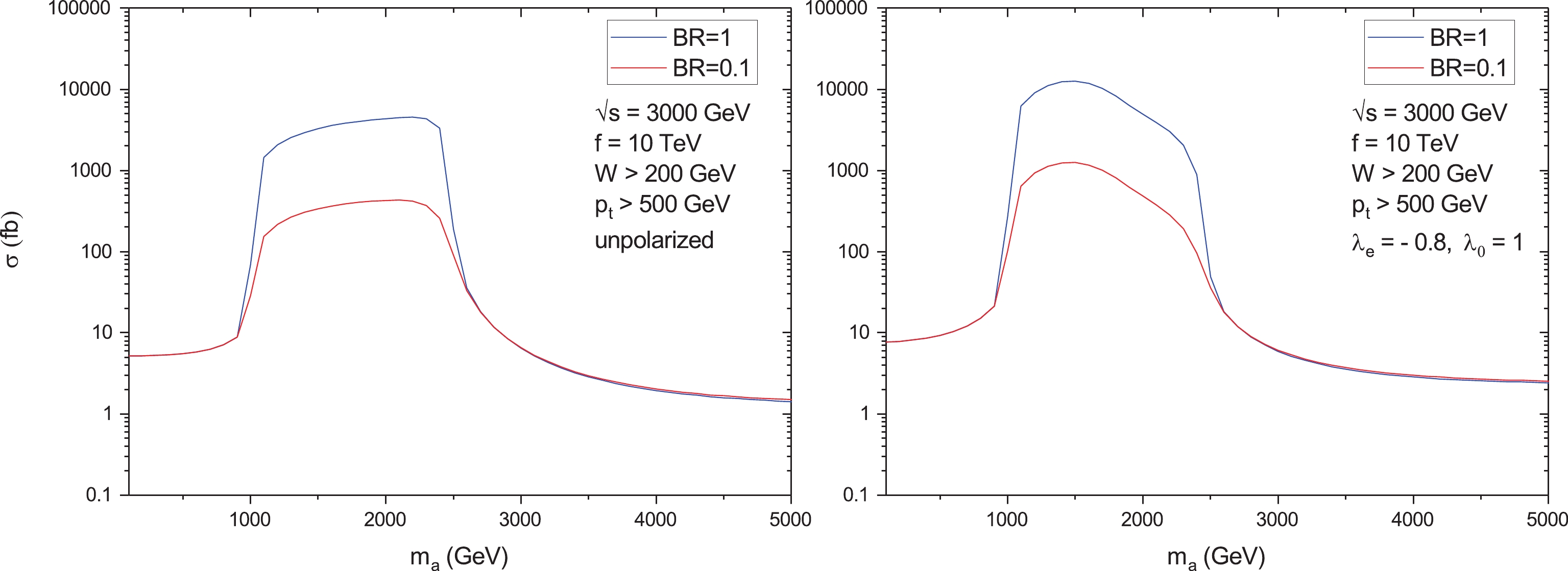
Figure 6. (color online) Total cross sections for the process
$ \gamma\gamma \rightarrow \gamma\gamma $ at the CLIC for the CB initial photons as functions of the ALP mass$ m_a $ for$ \sqrt{s} = 3000 $ GeV and$ f = 10 $ TeV. Left panel: unpolarized case. Right panel: polarized case, the helicity of the electron beam is$ \lambda_e = - 0.8 $ .
Figure 7. (color online) The same as in Fig. 6, but for
$ f = 100 $ TeV.Note that the cross sections in Figs. 6, 7 are very sensitive to the parameter
$ m_a $ in the interval$ m_a = 1000-2500 $ GeV, which is approximately two orders of magnitude greater than for$ m_a $ outside this mass region. An approximate formula for the cross section with the CB initial photons can be obtained; this formula explains a non-trivial dependence of the cross section on the ALP mass$ m_a $ , its coupling constant f, and$ {\rm{Br}}(a\rightarrow\gamma\gamma) $ in the mass region$ 1000-2500 $ GeV. The point is that a dominant contribution to the cross section comes from s-channel terms in the matrix element M. To illustrate this point, let us consider the following expression:$ M = \frac{4}{f^2} \frac{s^2}{s - m_a^2 + {\rm i} m_a\Gamma_a} \;. $

(15) The calculations show that the most important energy region is a resonance region
$ s \sim m_a^2 $ in which$ |M|^2 \big|_{s \sim m_a^2} \sim \frac{m_a^6}{f^4 \Gamma_a^2} \;. $

(16) Since our matrix element (15) depends only on s, the cross section of the subprocess
$ \gamma\gamma\rightarrow\gamma\gamma $ is given by the integral$ \sigma = \frac{1}{4E_e^2}\int {\rm d}s \,\frac{1}{16\pi s} \,|M|^2 \;. $

(17) Let us estimate the contribution to
$ \sigma $ from the resonance region$ m_a^2 - C m_a \Gamma_a \leqslant s \leqslant m_a^2 + C m_a \Gamma_a \;, $

(18) where C is a constant of order
${O}(1)$ . Then, we obtain$ \sigma = \frac{1}{f^2} \,\frac{m_a^2}{E_e^2} \,{\rm{Br}}(a\rightarrow\gamma\gamma)\int_{-C}^{C} {\rm d}x \,\frac{1}{x^2 + 1} \;. $

(19) As a result, for
$ C = 1 $ , we find that$ \sigma \simeq 0.6 \left( \frac{{\rm{TeV}}}{f} \right)^{2} \left( \frac{m_a}{E_e}\right)^{2} {\rm{Br}}(a\rightarrow\gamma\gamma) \ {\rm{fb}} \;. $

(20) This formula gives a correct dependence of the cross section on the parameters f,
$ m_a $ , and$ {\rm{Br}}(a\rightarrow\gamma\gamma) $ in the mass region$ 1100-2500 $ GeV (see Figs. 6 and 7). Note that$ \sigma $ is proportional to$ 1/f^2 $ (20), while simple dimensional arguments would give us$ 1/f^4 $ dependence. Let us underline that the above considerations are not applicable outside the mass region$ 1100-2500 $ GeV.As already mentioned above, the cross sections are very sensitive to the parameter
$ m_a $ in the interval$ m_a = 1000-2500 $ GeV, which is approximately two orders of magnitude greater than for$ m_a $ outside this mass region (see Figs. 6, 7). Therefore, it is not surprising that this is the region where the value of the ALP coupling constant f is mostly restricted by the polarized LBL process. The exclusion region is presented in the left panel of Fig. 8 in comparison with the unpolarized case shown in the right panel of this figure. We used the following formula to calculate the statistical significance ($ SS $ ) [48]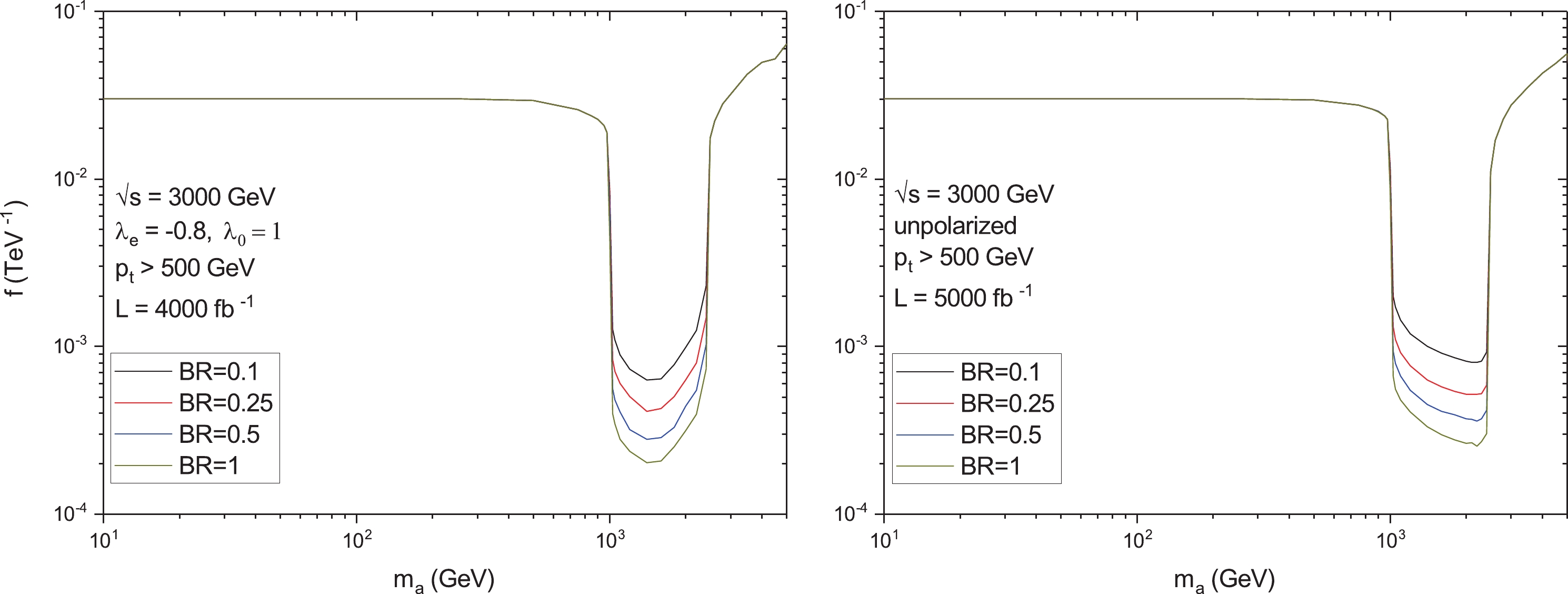
Figure 8. (color online) The 95% C.L. CLIC exclusion region for the process
$\gamma\gamma \rightarrow \gamma\gamma$ with the CB ingoing photons and invariant energy$\sqrt{s} = 3000$ GeV. Left panel: polarized electron beams with helicity$\lambda_e = -0.8$ and integrated luminosity$L = 4000$ fb$^{-1}$ . Right panel: unpolarized electron beams and integrated luminosity$L = 5000$ fb$^{-1}$ [39].$ SS = \sqrt{2[(S+B) \,\ln(1 + S/B) - S]} \;, $

(21) where S and B are the numbers of the signal and background events, respectively. It was assumed that the uncertainty of the background is negligible. To suppress the SM background, we applied the cut
$ p_t > 500 $ GeV on the momenta of the final photons.As it follows from Fig. 8, the best bounds for the LBL scattering at the CLIC are achieved for
$ {\rm{Br}}({\rm{a}} \rightarrow \gamma\gamma) = 1 $ . Herewith, we have:● For the mass region
$ 10 \ {\rm{GeV}} < m_a < 500 $ GeV, the polarized and unpolarized upper bounds on f are almost the same,$ f^{-1} = 3.0 \times 10^{-2} $ TeV$ ^{-1} $ .● In the interval
$ 500 \ {\rm{GeV}} < m_a < 1000 $ GeV, the polarized bounds are approximately 1.1 times better than the unpolarized ones. For example, for$ m_a = 850 $ GeV, we obtained$ f^{-1} = 2.65 \times 10^{-2} $ TeV$ ^{-1} $ for the unpolarized case and$ f^{-1} = 2.40 \times 10^{-2} $ TeV$ ^{-1} $ for the polarized case.● The region
$ 1000 \ {\rm{GeV}} < m_a < 2000 $ GeV is the best region in which the polarized bounds are on average 1.5 times stronger. For example, for$ m_a = 1400 $ GeV,$ f^{-1} = 3.35 \times 10^{-4} $ TeV$ ^{-1} $ for the unpolarized beams, and$ f^{-1} = 2.05 \times 10^{-4} $ TeV$ ^{-1} $ for the polarized beams.● In the mass interval
$ 2000 \ {\rm{GeV}} < m_a < 2500 $ GeV, the unpolarized bounds are 2 times better on average. For instance, for$ m_a = 2400 $ GeV, we obtained$ f^{-1} = 3.05 \times 10^{-4} $ TeV$ ^{-1} $ and$ f^{-1} = 7.35 \times 10^{-4} $ TeV$ ^{-1} $ for the unpolarized and polarized beams, respectively.● Finally, for
$ 2500 \ {\rm{GeV}} < m_a < 5000 $ GeV the unpolarized bounds are 1.2 times better on average. In particular, for$ m_a = 3500 $ GeV, we obatined$ f^{-1} = 3.35 \times 10^{-2} $ TeV$ ^{-1} $ for the unpolarized beams and$ f^{-1} = 4.20 \times 10^{-2} $ TeV$ ^{-1} $ for the polarized beams. -
In the present study, light-by-light scattering with ingoing polarized Compton backscattered photons at the CLIC induced by axion-like particles was investigated. The total cross sections were calculated for
$ e^+e^- $ collider energies of 1500 GeV and 3000 GeV. The cross sections are presented as functions of the ALP mass$ m_a $ , its coupling constant f, and ALP branching into two photons$ {\rm{Br}}(a \rightarrow \gamma\gamma) $ . By combining the results obtained in this study with those on unpolarized light-by-light scattering recently derived in Ref. [39], we drew the following conclusions:1. First energy stage of the CLIC (
$ \sqrt{s} = 380 $ GeV):The SM contribution completely dominates the axion induced contribution for
$ f = 10 $ TeV in the mass interval$ m_a = 10 - 5000 $ GeV. Any search of the ALPs is thus meaningless in this mass region.2. Second energy stage of the CLIC (
$ \sqrt{s} = 1500 $ GeV):The axion contribution dominates the SM for both the unpolarized and polarized ingoing CB photons. For electron beam helicity
$ \lambda_e = -0.8 $ , the cross section is even smaller than the unpolarized cross section, as can be seen by comparing the middle and left panels in Fig. 2. However, for$ \lambda_e = 0.8 $ , the polarized cross section exceeds the unpolarized one by one order of magnitude, as can be seen in the right panel in Fig. 2. Nevertheless, owing to the relatively small value of the expected integrated luminosity in such a case (500 fb$ ^{-1} $ , as compared with 2500 fb$ ^{-1} $ for the unpolarized electron beams), the bounds on$ m_a $ and f are weaker than the analogous bounds for the unpolarized LBL collision. Thus, there are no advantages in using the polarized electron beams in searching for heavy ALPs at this energy.3. Third energy stage of the CLIC (
$ \sqrt{s} = 3000 $ GeV):For electron beam helicity
$ \lambda_e = 0.8 $ (right panel in Fig. 3), the cross section is smaller than the unpolarized cross section (left panel in Fig. 3). However, for$ \lambda_e = -0.8 $ , the polarized cross section exceeds the unpolarized cross section by a factor of 2.5, as can be seen by comparing the middle and left panels in this figure. Figure 8 demonstrates that the bounds on$ m_a $ and f are better than recently obtained limits for the unpolarized LBL collision in the mass region$ m_a = 500 \ {\rm{GeV}} - 2000 $ GeV. Especially, this is the case in the interval$ m_a = 1000 \ {\rm{GeV}} - 2000 $ GeV, in which the bounds on f for the polarized beams are on average 1.5 times stronger than the bounds obtained for unpolarized beams.Our main results are presented in Fig. 9 along with the current exclusion regions. Note that for the wide region of the ALP mass,
$ m_a = 10 \ {\rm{GeV}} - 5000 $ GeV, our CLIC bounds are much stronger than the bounds for the ALP production in the LBL scattering at the LHC. They are also stronger than all current exclusion regions for$ m_a > 80 $ GeV, except for a very small area in between$ m_a = 600 $ GeV and$ m_a = 900 $ GeV (see Fig. 9). By comparing our results on polarized LBL scattering with the unpolarized case, we can conclude that the third energy stage of the CLIC with polarized electron beams has a greater physical potential to search for heavy ALPs, especially in the ALP mass region 1000 GeV – 2000 GeV.
Figure 9. (color online) Our prediction for the 95% C.L. exclusion region for energy
$\sqrt{s} = 3000$ GeV, electron beam polarization$\lambda_e = -0.8$ , and different values of the ALP branching${\rm{Br}}(a \rightarrow \gamma\gamma)$ (green area), in comparison with other current exclusion regions.
Polarized light-by-light scattering at the CLIC induced by axion-like particles
- Received Date: 2020-11-17
- Available Online: 2021-04-15
Abstract: In this study, light-by-light (LBL) scattering with initial polarized Compton backscattered photons at the CLIC, induced by axion-like particles (ALPs), is investigated. The total cross sections are calculated assuming CP-even coupling of the pseudoscalar ALP to photons. The 95% C.L. exclusion region for the ALP mass






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: