Iso-scalar liquid drop model fitting experimental binding energies within the macro-micro approach

Mass is the most fundamental property of atomic nuclei owing to its relevance in understanding not only the nuclear structure and the complex interaction in nuclei but also the path of the synthesis of heavy nuclei in astrophysics [1]. In the super heavy region, mass data are also essential in synthesizing super-heavy nuclides in terrestrial laboratories. Experimentally, the cooling store ring and ion trap both provide precise measurement of nuclear mass in the modern age [2−6]. Thus far, approximately 3000−4000 nuclides have been measured, whereas more than 9000 nuclides are believed to exist according to theoretical model calculations [7]. Descriptions and predictions of nuclear masses are of high theoretical interest and significance in the calculation of reaction networks in stellar environments, including the r-process [8]. Many models have been developed for this purpose. Generally, the models are classified in three groups: i) macro-micro models, including the finite range droplet model (FRDM) [9] and Weizsäcker-Skyrme (WS) models [10−12], ii) pure micro models, including Hartree-Fock-Bogoliubov (HFB) models [13], covariant density-functional theory (CDFT) [14], and relativistic Hartree-Bogoliubov theory [15, 16], and iii) local mass models, which predict the atomic nucleus mass through the relationship of the masses of neighboring nuclides by considering different physical constraints [17, 18], such as Garvey-Kelson (GK) relations [19, 20] and the isobaric multiplet mass equation (IMME) [21]. Meanwhile, many studies have been undertaken to evaluate and compare the predictive power of the models [22]. With the applications of modern machine learning or neural network techniques, the predictive power of the models have been improved further [23−28]. To date, the residues of the nucleus mass reach to about 200 keV or higher.

Among the macro-micro models, the liquid-drop (LD) model is one of the oldest nuclear theories. Von Weizsaecker first proposed it [29] in 1935, and it was generalized in 1936 by Bethe and Bacher [30]. This spherical LD model reproduced all measured atomic masses at that time with a reasonable accuracy. Four years later, Meitner and Frisch [31] added deformation degrees of freedom to the LD model to explain the fission phenomenon discovered by Hahn and Strassmann when bombarding metallic uranium with neutrons [32]. In 1939, Bohr and Wheeler proposed this new phenomenon's first theory by expanding the deformed nuclear LD surface in a series of Legendre polynomials [33].

The modern version of the LD model was proposed in 1966 by Myers and Świa̧tecki [34]. They showed that the LD energy enriched by the shell and pairing effects can adequately describe the binding energies and quadrupole moments of known nuclei and provide a reasonable description of the fission-barrier height of heavy nuclei (see also [35]). However, neither the Myers and Świa̧tecki LD formula nor its refined version, called the droplet model, could adequately reproduce the barrier heights of medium-heavy and lighter nuclei [36]. In addition, von Groote and Hilf [37] showed that a further correction to the LD model, namely the curvature term, did not change significantly it in this respect. Owing to these results, further development of the nuclear LD model was stopped in practice for more than three decades. Other much more complicated models such as the droplet, Yukawa-folded (YF), Yukawa-plus-Exponential (YpE), or Finite-Range Droplet Models (FRDM) have been used to obtain within the so-called macro-micro approximation [34] of the binding energies and the fission barrier heights (for an overview, see, e.g., Ref. [38]). A more detailed historical review of the LD models is available, e.g., in Ref. [39].

Twenty years ago, Ref. [40] showed that the original model of Myers and Świa̧tecki with an additional term containing the curvature energy could simultaneously describe the experimental binding energies of all known isotopes and fission barrier heights at that time. Note that this Lublin-Strasbourg-Drop (LSD) model has reproduced the data with better or comparable accuracy to other more advanced theories containing a larger number of adjustable parameters (e.g., Refs. [9, 41]). In the following years, some other parametrizations of the nuclear LD formula were studied (see, e.g., [42−46]). However, the fission-barrier heights estimated using these models differ significantly from experimental or estimated ones [47].

In this paper, we follow the concept of Bohr and Mottelsson [48] and Refs. [44−46] to use the quadratic in the isospin ($ T=|N-Z|/2 $) dependence of the nuclear part of the binding energy in the LD formula. Here, as in Ref. [45], we allow for a different isospin-square dependence of the volume and surface terms. In addition, the Coulomb exchange energy [49, 29] is considered in the present mass formula. Such an extension concerning version (i) of the Moretto et al. LD model [46] enables us to reproduce much better the experimental masses from the last mass-table [50]. Similar to Refs. [41, 40, 46], we have added to the LD energy the microscopic energy correction evaluated by Möller et al. [51] when fitting the LD parameters to the experimental masses. Note that the isospin-square LD model of Duflo and Zuker [44, 45] was later successfully used in several applications (see, e.g., Refs. [52−54]. Therefore, we have developed a modern version of the iso-scalar LD model with the parameters adjusted to the atomic masses known at present [50].

A typical nuclear LD formula consists of volume, surface, and Coulomb energy terms:

Only the first term is deformation-independent because we assume that the volume of the nucleus is conserved, whereas the other terms change with deformation. We must evaluate their variance assuming some parametrization of the shape of the deformed nuclei. The geometrical, deformation-dependent factors $ B_{\rm sur} $ and $ B_{\rm Coul} $ must be evaluated for a given shape parametrization of the deformed nucleus (see, e.g., [55]).

We assume the following iso-scalar liquid-drop (ISLD) formula for the energy of a spherical nucleus (see also Ref. [46]):

where Z and A are a nucleus's charge and mass numbers, respectively, and $ e^2=1.43996518\, $MeV$ \cdot $fm is the square of the elementary charge. Here, the volume and the surface part of the binding energies are dependent on the expectation value of the isospin square operator $ T(T+1) $, which is equal to $ T=|T_z|= |N-Z|/2 $, where $ N=A-Z $ is the neutron number. We can easily show that

whereas in a typical LD model, the $ |N-Z|^2 $ term is present. Odd-even energy $ E_{\rm odd} $ is assumed in the following form:

The last term in Eq. (2) describes the Coulomb exchange energy [29, 49].

Note that the linear in isospin term in the ISLD model (2) corresponds to the Wigner (or congruence) energy present in typical LD-like models (refer to, e.g., [34, 41]). In addition, in the ISLD model, the deformation dependence of this linear in $ |N-Z| $ is well defined, whereas, as in Ref. [41], we must include an additional phenomenological deformation dependence to obtain a doubling of the congruence at the scission point, when two fission fragment nuclei are born. The only free, i.e., adjustable, parameters of the ISLD model are $ a_{\rm vol},\,\kappa_{\rm vol},\,a_{\rm sur},\,\kappa_{\rm sur},\,r_0 $, and $ {\cal D} $.

The following equation gives the mass of an atomic nucleus in the ground state (g.s.):

where $ M_{\rm H} $= 7.289034 MeV and $ M_{\rm n} $= 8.071431 MeV are the hydrogen and neutron masses, respectively, measured with respect to the mass unit. The last term approximates the shell energy of electrons.

The microscopic energy correction $ E_{\rm mic} $ originates from the shell, pairing, and deformation effects,

and it is equal to the difference between the ground-state energy of the nucleus and the spherical macroscopic energy. The ground state microscopic energy corrections, taken from tables in [51], were evaluated using the FRDM macroscopic deformation energy, the YF single particle potential, and the monopole pairing force.

Using the above microscopic energy correction from the tables in [51], we make an approximation. In other words, we assume that the stiffness of the macroscopic deformation energy evaluated within the FRDM is close to that obtained using the ISLD model. A detailed calculation shows that the above approximation may lead to an approximately 50 keV inaccuracy of our mass estimates, which is about ten times smaller than the root mean square (r.m.s.) deviation of the fitted masses shown in Table 1. In addition, a similar method of evaluating the nuclear binding energies was used in Refs. [41, 40, 46].

The Fourier-over-Spheroid (FoS) shape parametrization [56, 57] is used to describe the shape of fissioning nuclei:

where the function $ f(u) $ with $ u\in [-1,1] $ is defined as follows:

Here, $ \rho_s(z) $ is the distance of a surface point to the z-axis, and $ z_0=c R_0 $, with $ R_0 $ being the sphere's radius, is the half-length of the deformed nucleus. The first two terms in $ f(u) $ describe a spheroid, whereas the others describe the deviation in the nucleus surface from the spheroidal form. Shift parameter $z_{\rm sh}= -3/(4\pi)\,z_0(a_3-a_5/2+ \cdots)$ ensures that the origin of the coordinate system is located at the center of mass of the nucleus. The volume conservation condition implies $a_2=a_4/3-a_6/5+\cdots$. The expansion coefficients $ a_i $ are treated as the deformation parameters. The parameter c determines the elongation of the nucleus, keeping its volume fixed, whereas $ a_3 $ and $ a_4 $ are the deformation parameters essentially responsible for the reflection asymmetry and neck formation of the deformed shape, respectively.

The FoS parametrization reproduces nuclear shapes very close to the optimal shapes obtained using the Strutinsky variational procedure [58] and enables us to evaluate precisely the LD energy at the saddle point. Knowing this energy, we can estimate the fission barrier height ($ V_{\rm sadd} $) with the aid of the Myers and Świa̧tecki topographical theorem [41]:

where $ M_{\rm mac}({\rm sadd}) $ is the macroscopic mass at the saddle point, and $ M_{\rm exp}({\rm g.s.}) $ is the ground-state experimental mass. The argument of Świa̧tecki in favor of Eq. (8) was that the shell, or better to say microscopic energy corrections at the saddle-point, are small as the fissioning system, attempts to avoid hills and valleys on its way to fission. Of course, such argumentation is only valid when we discuss the energy of the highest saddle point, not the deformation of the nucleus at the saddle point. Ref. [59] showed that the above approximation reproduces the experimental fission barrier heights fairly well.

The last issue of the atomics mass table [50] contains 2259 measured and 906 estimated masses of isotopes with $ Z,N\ge 20 $ having an experimental error smaller than 1.5 MeV. All these masses are taken to determine the best set of six adjustable parameters in the marcroscopic part of our ISLD model (2). The mean square deviation of theoretical estimates and the experimental masses is minimized to obtain the best set of parameters. The microscopic energy $ E_{\rm micr} $ from the Möller et al. mass table [51] were used when evaluating the masses of isotopes using Eq. (4). Two parameter sets are found: one (a) corresponding to 2259 measured masses and the second one (b) obtained using 3165 measured and estimated masses denoted by the hash sign in the mass-table [50]. The r.m.s. deviation, which is a measure of the fit quality, is taken in the following form:

where i runs over all considered isotopes. We have also evaluated σ for three traditional models: Thomas-Fermi (TF) model of Myers and Świa̧tecki [41], LSD model of Pomorski and Dudek [40], and FRDM of Möller et al. [51]. The results are presented in Table 1.

The ISLD model with only six adjustable parameters fitted to the experimental data for 2259 isotopes (a) reproduces the isotope masses with even better quality than the FRDM from which the microscopic energy corrections are obtained. Of course, the r.m.s. deviation of the theoretical and measured masses increases when we make the fit to all 3165 experimental and estimated masses. Therefore, an additional fit (b) of the ISLD parameters was performed when all 3165 isotope masses were considered. Both sets, (a) and (b), of the ISLD parameters are listed in Table 2. Surprisingly, the 28-year-old TF model predicts these 906 additional masses better than the FRDM. Additionally, the LSD model developed in 2003 describes both experimental data and all experimental and estimated data very well, proving its predictive power. The last row in Table 1 shows the number of adjustable parameters of each model. The TF model [41] has eight free parameters plus four additional parameters for the congruence (Wigner) and odd-even energy taken from Ref. [9]. The LSD model is based on the congruence and odd-even energy (four parameters) developed in Ref. [9] and has eight adjustable constants. The FRDM has nine plus four fitted parameters corresponding the the macroscopic part of energy, whereas the present ISLD model is based on six adjustable parameters only.

Parameter	Units	ISLD (a)	ISLD (b)
$ a_{\rm vol} $	MeV	−15.381912	−15.499610
$ \kappa_{\rm vol} $	−	1.87161	1.88029
$ a_{\rm sur} $	MeV	17.27931	17.64004
$ \kappa_{\rm sur} $	−	2.3022	2.2727
$ r_0 $	fm	1.229286	1.214608
$ {\cal D} $	MeV	4.305	4.234

Table 2.  Parameter set of the ISLD model (Eq. (2)) fitted to the experimental (a) and experimental plus estimated (b) atomic masses.

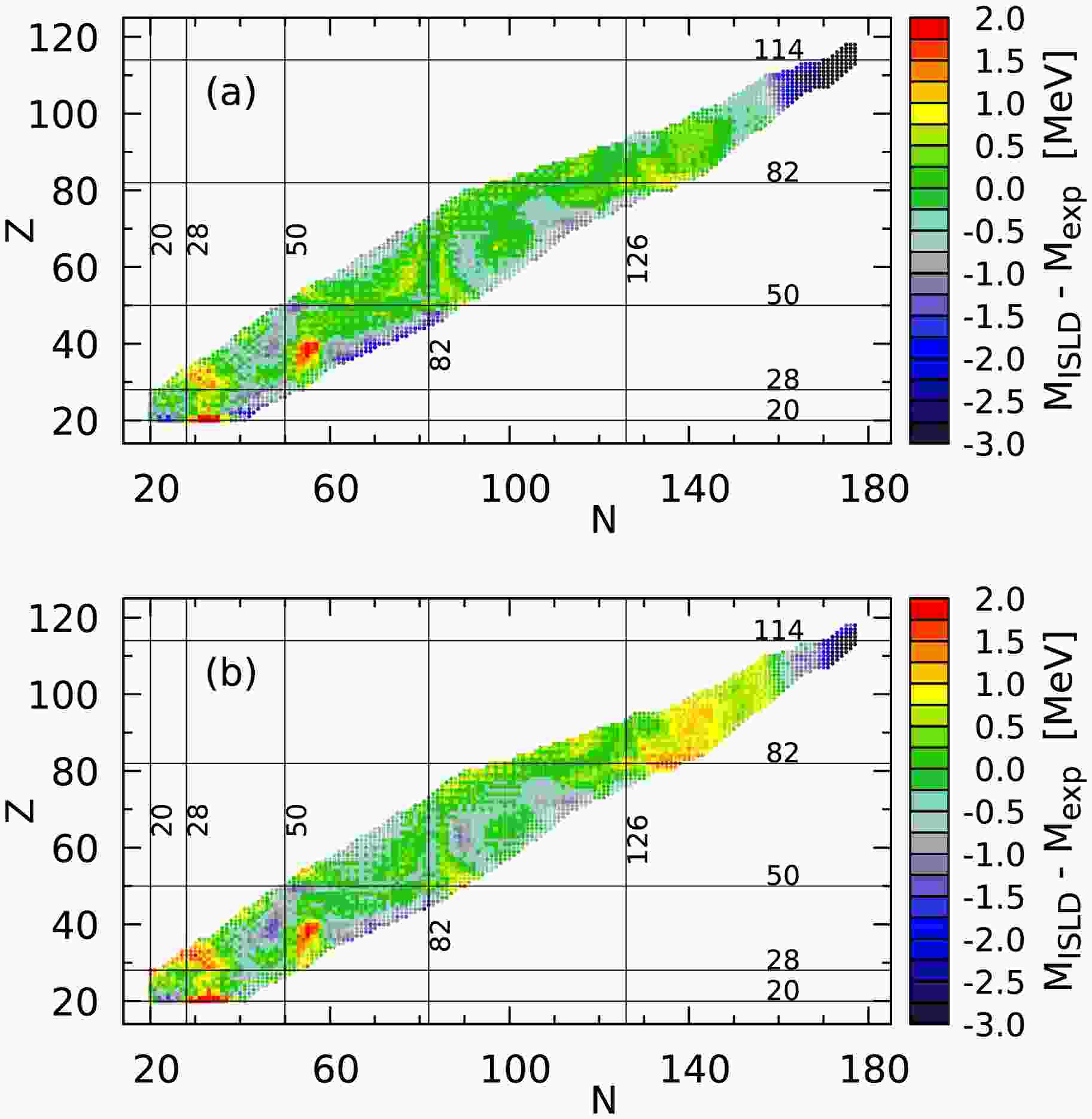
The deviations between the experimental (squares) and the estimated (circles) masses are shown in Fig. 1 for ISLD parameter sets (a) (top) and (b) (bottom). We observe that significant discrepancies appear for neutron-rich or proton-rich nuclei and superheavy nuclei (SHN), where the majority of masses are estimated (circles). In addition, some discrepancies originating probably from poorly reproduced shell effects are visible. The largest ones are in the vicinity of magic numbers $ Z=20 $ and 28 and around ⁹⁴Zr.

Figure 1.  (color online) Deviation in the atomic mass estimates obtained using ISLD(a) (top) and ISLD(b) (bottom) from experimental data (squares). Circles mark the deviations from the estimated data.

A question arises: which set of the ISLD parameters should be used: the one fitted to the experimental masses only (a) or that adjusted to all experimental and estimated masses (b)? Note that more than half of the isotopic masses of heavy nuclei with mass-number $ A\ge 220 $ listed in the mass table [50] correspond to the estimated, not measured, data. In addition, the pure experimental masses are only less than 10% of the SHN data with $ Z\ge 104 $. Therefore, set (b) of the ISLD parameters is recommended when describing the properties of the heaviest nuclei. In the following section, we shall use and refer to set (b), and we will simply call it the ISLD set of parameters.

We must mention here that we have also performed mass fits using a formula similar to the LD formula (2) but with the curvature term proportional to $ A^{1/3} $ and with the Coulomb redistribution energy ($ \sim Z^2/A $). However, adding such two terms to the ISLD formula did not significantly change the r.m.s. deviation from the data; therefore, they are not considered in our model.

It is well known that the nuclear masses predictions for nuclei close to the β-stability line obtained within different macroscopic models closely correspond with each other. Significant differences between the models may appear as we go toward the proton or neutron drip lines. This effect is illustrated in Fig. 2, where the differences between the ISLD(b) and LSD mass estimates are shown as a function of neutron (N) and proton (Z) numbers. The differences do not exceed the range (–0.5,+0.5) MeV for isotopes with $ A \le 220 $ lying between the two-proton drip and β-stability lines. Additionally, both estimates closely match for neutron reach isotopes close to the β-stability line. In the region of SHN and for isotopes close to the two-neutron drip line, the ISLD masses are 1.5 MeV larger than the LSD ones. Such differences in the mass estimates may be significant for predicting the astrophysical r-process or the stability and decays of the SHN.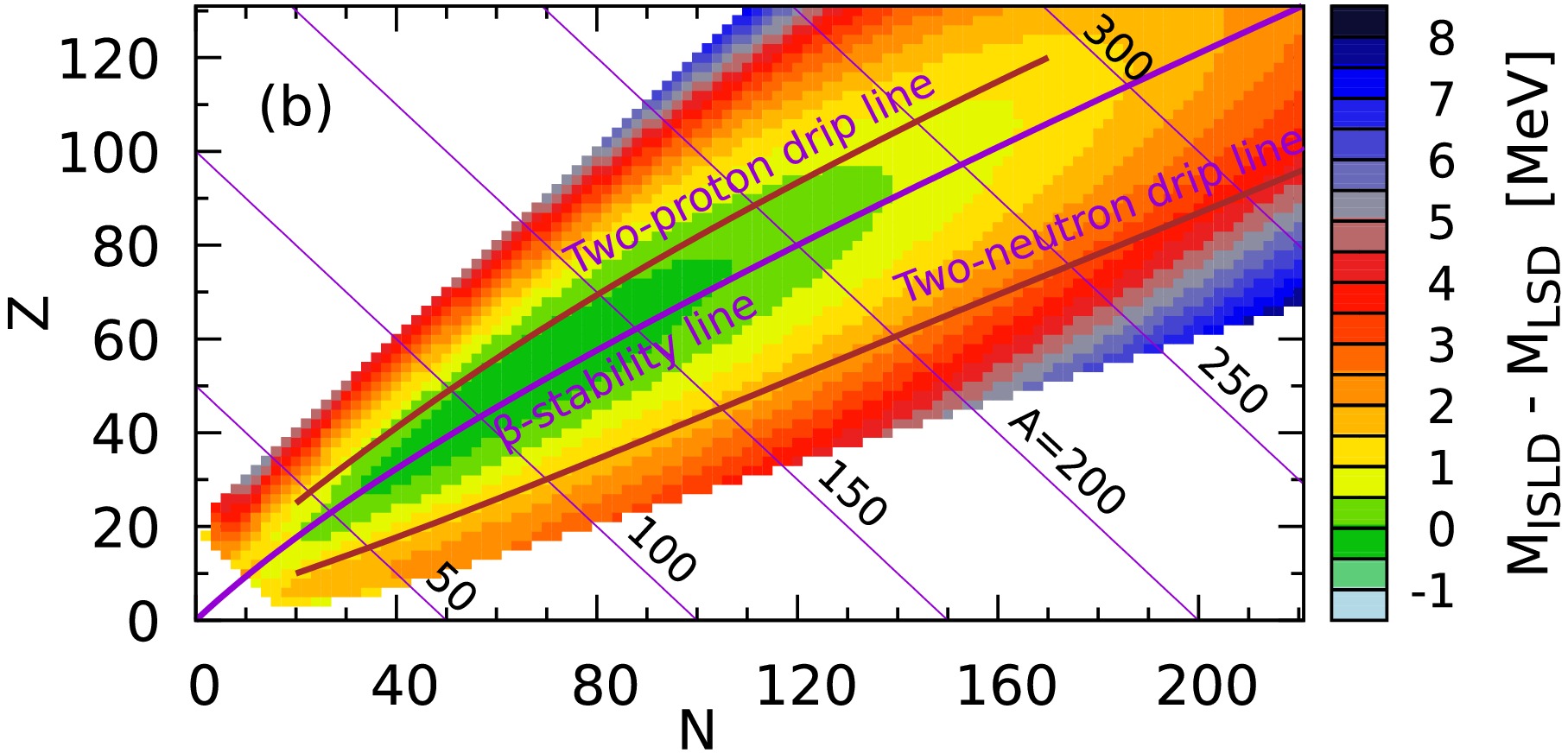

Figure 2.  (color online) Differences in the atomic mass estimates obtained using the ISLD(b) and the LSD [40] models.

The LSD and ISLD macroscopic energy surfaces of ²⁵⁰Cf are compared in Fig. 3. Here, we have used the FoS shape parametrization [57]. We have also assumed that the macroscopic energy of a spherical nucleus ($c=1, a_4=0$) is zero. The surfaces obtained in both models are close to each other, and only small differences can be noticed. That is, the ISLD fission valley (top row) is slightly deeper and corresponds to more elongated shapes than the LSD one. The exit of the LSD valley around the scission configuration (bottom raw) is located at the elongation $ c=2.62 $. It lies approximately 4 MeV above the ISLD exit, which appears at $ c=2.70 $. Such differences in energy and elongation of the nucleus in the macroscopic scission point may have some influence on the total kinetic energy (TKE) of the fission fragments. In contrast, the stiffnesses of LSD and ISLD potentials with respect to the fission fragment mass asymmetry ($ A_h $) (see the maps in the bottom raw) are very close to each other. The saddle points in both ($ c,\,a_4 $) maps correspond to almost the same energy ($ E_{\rm sadd}\approx 1.3 $ MeV) and are located around the deformation $ c\approx 1.35 $ and $ a_4\approx 0.06 $.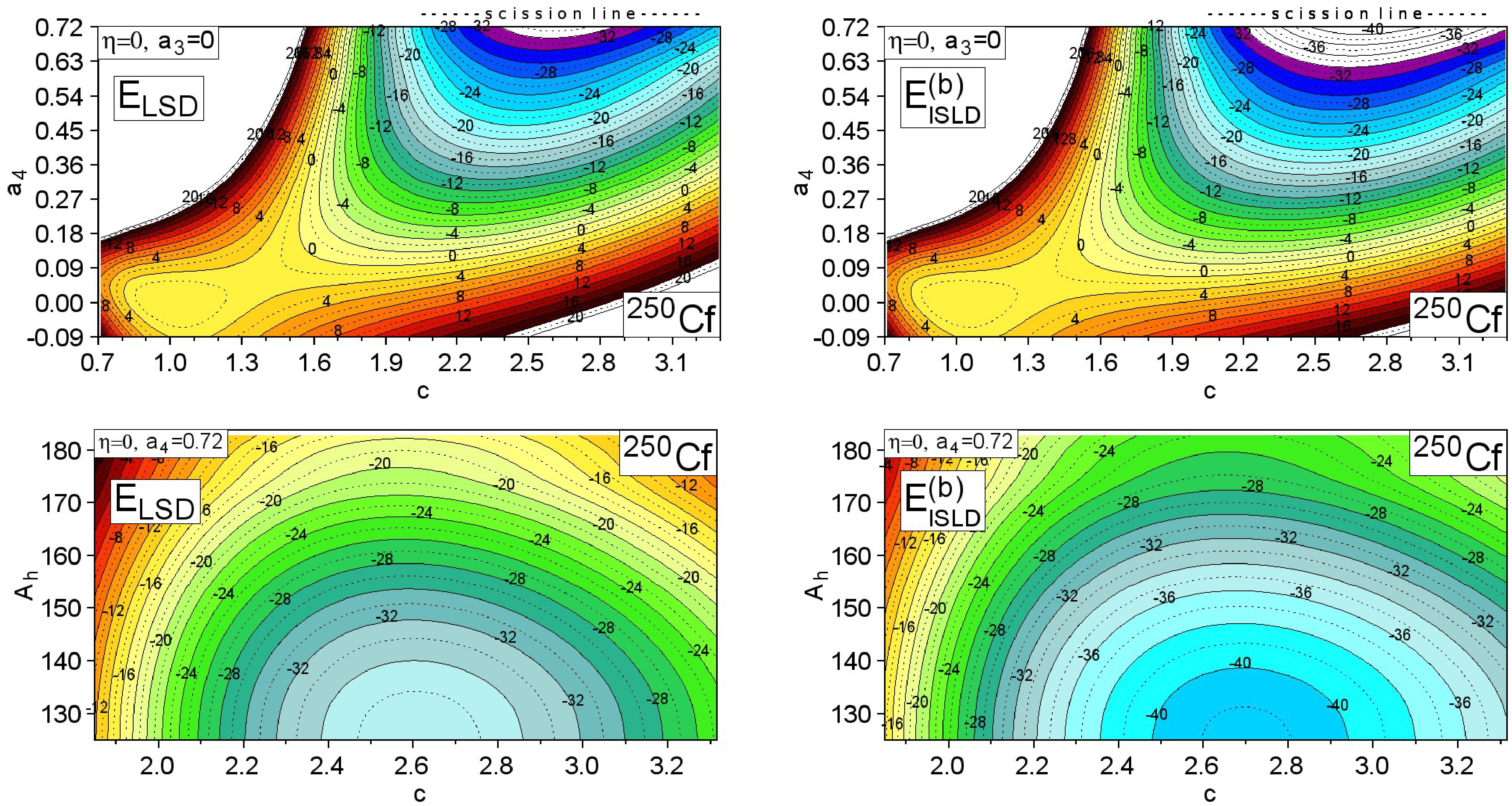

Figure 3.  (color online) Macroscopic energy surfaces of ²⁵⁰Cf on the ($ c,a_4 $) plane (top) and around the scission configuration (bottom) are evaluated using the LSD (l.h.s) c and ISLD(b) (r.h.s.) formulas. Here, c is the elongation of the nucleus, $ a_4 $ is related to the neck size, and $ {\rm A_h} $ is the heavy fission fragment mass number [57].

Such macroscopic saddle-point energies will be used in the following to estimate the fission barrier heights of the actinide nuclei using the topographical theorem of Myers and Świa̧tecki (8).

The fission barrier heights estimated using Eq. (8) and the ISLD(a) (crosses) and (b) (circles) and the LSD (open circles) formulas are compared in Fig. 4 with the experimental data taken from Refs. [60] (triangles) and [61] (stars). In addition, the theoretical estimates of the highest fission barrier obtained in Ref. [62] are marked by squares. The experimental, or better to say empirical, fission barrier heights are obtained primarily from analysis of the fission cross-section energy dependence and fissionability of nuclei. They are supplemented by data obtained from analysis of the excitation functions of spontaneously fissioning isomers and the group of strong resonances in the sub-barrier fission cross-section [60, 61]. The theoretical barrier heights tabulated in Ref. [62] were evaluated within the 7D macro-micro model with the YpE macroscopic energy part and the microscopic energy evaluated using the Woods-Saxon (WS) single-particle potential.

Figure 4.  (color online) Fission barrier heights evaluated using the Myers and Świa̧tecki topographical theorem (see Eq. 8) with the ISLD(a) (crosses), ISLD(b) (points), and LSD (open circles) sets of parameters are compared with the empirical/experimental data taken from Ref. [60] (triangles) and [61] (stars) and with the theoretical values (squares) obtained within the macro-micro model in Ref. [62].

As we can observe, the fission barrier heights obtained using the Myers and Świa̧tecki topographical theorem and the LSD and ISLD models underestimate, in most cases, the experimental barrier heights, whereas those of Ref. [62] are, as a rule, larger than the experimental values. The ISLD barriers obtained with the set (b) parameters are very close to the LSD ones, whereas those computed with set (a) are, on average, smaller by 1 MeV. We can expect that the fission barriers evaluated in a similar manner as in Ref. [62] but with the ISLD macroscopic part of the energy will be closer to the data as the topographical theorem estimates the barrier heights from below [41].

We have shown that the new liquid drop mass formula with the charge asymmetry term proportional to the isospin square (ISLD) describes the presently known experimental and estimated from systematic atomic masses well. Note that the ISLD formula for the macroscopic energy contains only six adjustable parameters. The other models contain more free parameters, e.g., the twenty-one year old LSD mass formula [40], which reproduces the binding energies even better than the FRDM theory [51], has eight directly fitted parameters and four others (in the congruence/Wigner and odd-even terms) taken from the adjustments made in Ref. [9]. Here, note that microscopic models, typically having up to 14 interaction parameters, can reproduce 2149 experimental masses with the r.m.s. deviation equal to 0.798 MeV [63].

We found that all experimentally estimated masses of SHN with a neutron number larger than 160 have up to 3 MeV larger masses than the predicted ones. What is the origin of these discrepancies: inaccuracies in evaluating the microscopic energy, wrong asymptotic behavior of our macroscopic models, or inaccurate evaluation of the atomic masses from the systematics? More detailed calculations to answer this question are necessary.

We also show that both ISLD(b) and LSD models describe the fission barrier heights of the heavy nuclei well. The ISLD model predicts slightly larger atomic masses than the LSD model in the superheavy region of nuclei and for neutron-rich isotopes close to the neutron drip line. This difference in the mass estimates can be significant for SHN physics, and it can influence the nuclear r-process probabilities, which is very important in astrophysical theories. Additionally, the ISLD model predicts a more elongated shape of fissioning nuclei at the scission configuration than the LSD formula. This effect can influence estimates of the fission fragment TKE and their charge equilibration (refer to Ref. [64]).

We plan to perform extended dynamical calculations such as those in Refs. [57, 64−67] but with the use of the new ISLD formula when evaluating the potential energy surfaces of fissioning nuclei. The well-defined deformation dependence of the macroscopic energy term linear in $ \vert N-Z\vert $ may also influence the isotopic yields of the fission fragments (refer to Ref. [64]).

The author thanks Kai Neergård for his helpful remarks.