-
As is taught in virtually every quantum field theory textbook, a generic tree-level quantum electrodynamics (QED) process with emission of a low-energy photon exhibits simplifying feature [1]. In the soft limit, the full QED amplitude can be factorized into the product of the simpler one with removed external photon times a universal eikonal factor. The universal pattern governing the emission of a soft photon can be readily carried over to the case of emission of a soft graviton [2], and can also be extended through the next-to-leading order (NLO) in the small k expansion (where
$ k^\mu $ denotes the four-momentum of the emitted photon or graviton), which is generically referred to as Low-Burnett-Kroll (LBK) theorem [3−5]. Recently, there has been an attempt to reproduce the LBK theorem entailing soft graviton emission from the perspective of the soft-collinear effective theory [6].The LBK theorem applies only to the case of on-shell photon/graviton emitted from the external legs, in which the matter fields correspond to structureless point-like particles. Nevertheless, it also attracts theoretical curiosity about the soft pattern of the processes involving composite particles and soft photon/graviton emerging in the internal line, in which the LBK theorem is not applicable. On the physical ground, it is anticipated that, in a process entailing a heavy composite particle, the soft limit implicates that the very long wavelength of the (real or virtual) photon/graviton is unable to resolve the detailed internal structure of the composite particle, and thus its properties can be simply summarized in terms of a few low-order multipoles. Correspondingly, the expanded cross sections might exhibit some simple textures. A classical example is the soft limit of the Compton scattering, with the leading contribution represented by the Thomson cross section, depending only on the total electric charge of the composite target, while the NLO contribution in
$ 1/M $ expansion becomes sensitive to its magnetic dipole [7, 8]. Another illuminating example is the Rutherford scattering process, where a low-energy projectile bombards a static, heavy, composite target particle bearing arbitrary spin, mediated by a t-channel photon exchange. Recently, the soft limit of the electromagnetic Rutherford scattering process has been comprehensively investigated, and some simple patterns about the target spin dependence have been identified upon heavy target mass expansion [10].The central aim of this study is to extend the preceding analysis in an electromagnetic case [10] to the gravitational Rutherford scattering process: i.e., a structureless point-like projectile bombs on a static, heavy, composite target particle bearing arbitrary spins, now with the graviton being the force carrier. We consider two types of benchmark gravitational Rutherford scattering processes, a low-energy massless structureless projectile hits a static massive composite particle with a spin up to
$ 2 $ , and nonrelativistic light projectile bombs on a heavy static composite target. The major observation of this study is similar to that in its electromagnetic counterpart [10]. The unpolarized cross sections in the first type are universal (independent on the target spin) at the first two orders in$ 1/M $ expansion, yet differ at the next-to-next-to-leading order (NNLO), though some terms at this order still remain universal or depend on the target spin in a definite manner. The unpolarized cross sections in the second type are universal at the lowest order in projectile velocity expansion and through all orders in$ 1/M $ , insensitive to both projectile and target's spin. The universality partially breaks down at relative order -$ v^2/M^2 $ , though some terms at this order are still universal or depend on the target spin in a recognizable manner.The rest of the paper is organized as follows. In Sec. II, we present the expression of the tree-level amplitude for a gravitational Rutherford scattering process involving a heavy composite spinning target particle, and specify the parametrization of the gravitational form factor of a massive target particle carrying varying spin. In Sec. III, we consider the low-energy massless point-like projectile with a spin of 0,
${1/ 2}$ , and$ 1 $ , striking on a heavy composite target particle with a spin ranging from 0 to 2. We organize the unpolarized cross section in the heavy target mass expansion up to NNLO, and identify some universal pattern about the target spin dependence. In Sec. IV, we consider another type of gravitational Rutherford scattering process, where the projectile is replaced by a slowly moving light structureless particle with a spin ranging from 0 to 1. We identify some universal pattern of the cross section in the double expansion of the projectile velocity and$ 1/M $ . We summarize the conclusions in Sec. V. In Appendix A, we present the spin sum formula for the target particles with varying spin. In Appendix B, we address the gravitational Rutherford scattering based on the heavy black hole effective theory (HBET), with the massless spinless projectile and heavy spinless target particle as an example. The reason responsible for the NLO amplitude vanishment is elucidated from the perspective of effective field theory. -
As is taught in virtually every quantum field theory textbook, a generic tree-level quantum electrodynamics (QED) process with emission of a low-energy photon exhibits simplifying feature [1]. In the soft limit, the full QED amplitude can be factorized into the product of the simpler one with removed external photon times a universal eikonal factor. The universal pattern governing the emission of a soft photon can be readily carried over to the case of emission of a soft graviton [2], and can also be extended through the next-to-leading order (NLO) in the small k expansion (where
$ k^\mu $ denotes the four-momentum of the emitted photon or graviton), which is generically referred to as Low-Burnett-Kroll (LBK) theorem [3−5]. Recently, there has been an attempt to reproduce the LBK theorem entailing soft graviton emission from the perspective of the soft-collinear effective theory [6].The LBK theorem applies only to the case of on-shell photon/graviton emitted from the external legs, in which the matter fields correspond to structureless point-like particles. Nevertheless, it also attracts theoretical curiosity about the soft pattern of the processes involving composite particles and soft photon/graviton emerging in the internal line, in which the LBK theorem is not applicable. On the physical ground, it is anticipated that, in a process entailing a heavy composite particle, the soft limit implicates that the very long wavelength of the (real or virtual) photon/graviton is unable to resolve the detailed internal structure of the composite particle, and thus its properties can be simply summarized in terms of a few low-order multipoles. Correspondingly, the expanded cross sections might exhibit some simple textures. A classical example is the soft limit of the Compton scattering, with the leading contribution represented by the Thomson cross section, depending only on the total electric charge of the composite target, while the NLO contribution in
$ 1/M $ expansion becomes sensitive to its magnetic dipole [7, 8]. Another illuminating example is the Rutherford scattering process, where a low-energy projectile bombards a static, heavy, composite target particle bearing arbitrary spin, mediated by a t-channel photon exchange. Recently, the soft limit of the electromagnetic Rutherford scattering process has been comprehensively investigated, and some simple patterns about the target spin dependence have been identified upon heavy target mass expansion [10].The central aim of this study is to extend the preceding analysis in an electromagnetic case [10] to the gravitational Rutherford scattering process: i.e., a structureless point-like projectile bombs on a static, heavy, composite target particle bearing arbitrary spins, now with the graviton being the force carrier. We consider two types of benchmark gravitational Rutherford scattering processes, a low-energy massless structureless projectile hits a static massive composite particle with a spin up to
$ 2 $ , and nonrelativistic light projectile bombs on a heavy static composite target. The major observation of this study is similar to that in its electromagnetic counterpart [10]. The unpolarized cross sections in the first type are universal (independent on the target spin) at the first two orders in$ 1/M $ expansion, yet differ at the next-to-next-to-leading order (NNLO), though some terms at this order still remain universal or depend on the target spin in a definite manner. The unpolarized cross sections in the second type are universal at the lowest order in projectile velocity expansion and through all orders in$ 1/M $ , insensitive to both projectile and target's spin. The universality partially breaks down at relative order -$ v^2/M^2 $ , though some terms at this order are still universal or depend on the target spin in a recognizable manner.The rest of the paper is organized as follows. In Sec. II, we present the expression of the tree-level amplitude for a gravitational Rutherford scattering process involving a heavy composite spinning target particle, and specify the parametrization of the gravitational form factor of a massive target particle carrying varying spin. In Sec. III, we consider the low-energy massless point-like projectile with a spin of 0,
${1/ 2}$ , and$ 1 $ , striking on a heavy composite target particle with a spin ranging from 0 to 2. We organize the unpolarized cross section in the heavy target mass expansion up to NNLO, and identify some universal pattern about the target spin dependence. In Sec. IV, we consider another type of gravitational Rutherford scattering process, where the projectile is replaced by a slowly moving light structureless particle with a spin ranging from 0 to 1. We identify some universal pattern of the cross section in the double expansion of the projectile velocity and$ 1/M $ . We summarize the conclusions in Sec. V. In Appendix A, we present the spin sum formula for the target particles with varying spin. In Appendix B, we address the gravitational Rutherford scattering based on the heavy black hole effective theory (HBET), with the massless spinless projectile and heavy spinless target particle as an example. The reason responsible for the NLO amplitude vanishment is elucidated from the perspective of effective field theory. -
As is taught in virtually every quantum field theory textbook, a generic tree-level quantum electrodynamics (QED) process with emission of a low-energy photon exhibits simplifying feature [1]. In the soft limit, the full QED amplitude can be factorized into the product of the simpler one with removed external photon times a universal eikonal factor. The universal pattern governing the emission of a soft photon can be readily carried over to the case of emission of a soft graviton [2], and can also be extended through the next-to-leading order (NLO) in the small k expansion (where
$ k^\mu $ denotes the four-momentum of the emitted photon or graviton), which is generically referred to as Low-Burnett-Kroll (LBK) theorem [3−5]. Recently, there has been an attempt to reproduce the LBK theorem entailing soft graviton emission from the perspective of the soft-collinear effective theory [6].The LBK theorem applies only to the case of on-shell photon/graviton emitted from the external legs, in which the matter fields correspond to structureless point-like particles. Nevertheless, it also attracts theoretical curiosity about the soft pattern of the processes involving composite particles and soft photon/graviton emerging in the internal line, in which the LBK theorem is not applicable. On the physical ground, it is anticipated that, in a process entailing a heavy composite particle, the soft limit implicates that the very long wavelength of the (real or virtual) photon/graviton is unable to resolve the detailed internal structure of the composite particle, and thus its properties can be simply summarized in terms of a few low-order multipoles. Correspondingly, the expanded cross sections might exhibit some simple textures. A classical example is the soft limit of the Compton scattering, with the leading contribution represented by the Thomson cross section, depending only on the total electric charge of the composite target, while the NLO contribution in
$ 1/M $ expansion becomes sensitive to its magnetic dipole [7, 8]. Another illuminating example is the Rutherford scattering process, where a low-energy projectile bombards a static, heavy, composite target particle bearing arbitrary spin, mediated by a t-channel photon exchange. Recently, the soft limit of the electromagnetic Rutherford scattering process has been comprehensively investigated, and some simple patterns about the target spin dependence have been identified upon heavy target mass expansion [10].The central aim of this study is to extend the preceding analysis in an electromagnetic case [10] to the gravitational Rutherford scattering process: i.e., a structureless point-like projectile bombs on a static, heavy, composite target particle bearing arbitrary spins, now with the graviton being the force carrier. We consider two types of benchmark gravitational Rutherford scattering processes, a low-energy massless structureless projectile hits a static massive composite particle with a spin up to
$ 2 $ , and nonrelativistic light projectile bombs on a heavy static composite target. The major observation of this study is similar to that in its electromagnetic counterpart [10]. The unpolarized cross sections in the first type are universal (independent on the target spin) at the first two orders in$ 1/M $ expansion, yet differ at the next-to-next-to-leading order (NNLO), though some terms at this order still remain universal or depend on the target spin in a definite manner. The unpolarized cross sections in the second type are universal at the lowest order in projectile velocity expansion and through all orders in$ 1/M $ , insensitive to both projectile and target's spin. The universality partially breaks down at relative order -$ v^2/M^2 $ , though some terms at this order are still universal or depend on the target spin in a recognizable manner.The rest of the paper is organized as follows. In Sec. II, we present the expression of the tree-level amplitude for a gravitational Rutherford scattering process involving a heavy composite spinning target particle, and specify the parametrization of the gravitational form factor of a massive target particle carrying varying spin. In Sec. III, we consider the low-energy massless point-like projectile with a spin of 0,
${1/ 2}$ , and$ 1 $ , striking on a heavy composite target particle with a spin ranging from 0 to 2. We organize the unpolarized cross section in the heavy target mass expansion up to NNLO, and identify some universal pattern about the target spin dependence. In Sec. IV, we consider another type of gravitational Rutherford scattering process, where the projectile is replaced by a slowly moving light structureless particle with a spin ranging from 0 to 1. We identify some universal pattern of the cross section in the double expansion of the projectile velocity and$ 1/M $ . We summarize the conclusions in Sec. V. In Appendix A, we present the spin sum formula for the target particles with varying spin. In Appendix B, we address the gravitational Rutherford scattering based on the heavy black hole effective theory (HBET), with the massless spinless projectile and heavy spinless target particle as an example. The reason responsible for the NLO amplitude vanishment is elucidated from the perspective of effective field theory. -
As is taught in virtually every quantum field theory textbook, a generic tree-level quantum electrodynamics (QED) process with emission of a low-energy photon exhibits simplifying feature [1]. In the soft limit, the full QED amplitude can be factorized into the product of the simpler one with removed external photon times a universal eikonal factor. The universal pattern governing the emission of a soft photon can be readily carried over to the case of emission of a soft graviton [2], and can also be extended through the next-to-leading order (NLO) in the small k expansion (where
$ k^\mu $ denotes the four-momentum of the emitted photon or graviton), which is generically referred to as Low-Burnett-Kroll (LBK) theorem [3−5]. Recently, there has been an attempt to reproduce the LBK theorem entailing soft graviton emission from the perspective of the soft-collinear effective theory [6].The LBK theorem applies only to the case of on-shell photon/graviton emitted from the external legs, in which the matter fields correspond to structureless point-like particles. Nevertheless, it also attracts theoretical curiosity about the soft pattern of the processes involving composite particles and soft photon/graviton emerging in the internal line, in which the LBK theorem is not applicable. On the physical ground, it is anticipated that, in a process entailing a heavy composite particle, the soft limit implicates that the very long wavelength of the (real or virtual) photon/graviton is unable to resolve the detailed internal structure of the composite particle, and thus its properties can be simply summarized in terms of a few low-order multipoles. Correspondingly, the expanded cross sections might exhibit some simple textures. A classical example is the soft limit of the Compton scattering, with the leading contribution represented by the Thomson cross section, depending only on the total electric charge of the composite target, while the NLO contribution in
$ 1/M $ expansion becomes sensitive to its magnetic dipole [7, 8]. Another illuminating example is the Rutherford scattering process, where a low-energy projectile bombards a static, heavy, composite target particle bearing arbitrary spin, mediated by a t-channel photon exchange. Recently, the soft limit of the electromagnetic Rutherford scattering process has been comprehensively investigated, and some simple patterns about the target spin dependence have been identified upon heavy target mass expansion [10].The central aim of this study is to extend the preceding analysis in an electromagnetic case [10] to the gravitational Rutherford scattering process: i.e., a structureless point-like projectile bombs on a static, heavy, composite target particle bearing arbitrary spins, now with the graviton being the force carrier. We consider two types of benchmark gravitational Rutherford scattering processes, a low-energy massless structureless projectile hits a static massive composite particle with a spin up to
$ 2 $ , and nonrelativistic light projectile bombs on a heavy static composite target. The major observation of this study is similar to that in its electromagnetic counterpart [10]. The unpolarized cross sections in the first type are universal (independent on the target spin) at the first two orders in$ 1/M $ expansion, yet differ at the next-to-next-to-leading order (NNLO), though some terms at this order still remain universal or depend on the target spin in a definite manner. The unpolarized cross sections in the second type are universal at the lowest order in projectile velocity expansion and through all orders in$ 1/M $ , insensitive to both projectile and target's spin. The universality partially breaks down at relative order -$ v^2/M^2 $ , though some terms at this order are still universal or depend on the target spin in a recognizable manner.The rest of the paper is organized as follows. In Sec. II, we present the expression of the tree-level amplitude for a gravitational Rutherford scattering process involving a heavy composite spinning target particle, and specify the parametrization of the gravitational form factor of a massive target particle carrying varying spin. In Sec. III, we consider the low-energy massless point-like projectile with a spin of 0,
${1/ 2}$ , and$ 1 $ , striking on a heavy composite target particle with a spin ranging from 0 to 2. We organize the unpolarized cross section in the heavy target mass expansion up to NNLO, and identify some universal pattern about the target spin dependence. In Sec. IV, we consider another type of gravitational Rutherford scattering process, where the projectile is replaced by a slowly moving light structureless particle with a spin ranging from 0 to 1. We identify some universal pattern of the cross section in the double expansion of the projectile velocity and$ 1/M $ . We summarize the conclusions in Sec. V. In Appendix A, we present the spin sum formula for the target particles with varying spin. In Appendix B, we address the gravitational Rutherford scattering based on the heavy black hole effective theory (HBET), with the massless spinless projectile and heavy spinless target particle as an example. The reason responsible for the NLO amplitude vanishment is elucidated from the perspective of effective field theory. -
In general relativity, the energy-momentum tensor of the matter field has the role of gravitational sources. The symmetric Belinfante-Rosenfeld energy-momentum tensor is defined as
$ T_{\mu \nu } = \frac{2}{\sqrt{-g}} \frac{\delta S}{ \delta g^{\mu \nu }}, $

(1) where S denotes the gravitational action of the matter field and
$ g^{\mu\nu}(x) $ denotes the spacetime metric field. In the weak gravity case, we approximate$ g_{\mu\nu}(x) = \eta_{\mu\nu}+\kappa h_{\mu\nu}(x) $ with$ \eta_{\mu\nu} = {\rm{diag}}(1,-1,-1,-1) $ being the Minkowski metric. Here,$ \kappa = \sqrt{32\pi G_N} $ , with the Newton's constant$G_\text{N} = 6.709\times 10^{-39}\;\mathrm{GeV}^{-2}$ . In the linearized approximation, the matter field couples with the graviton simply through the interaction${\cal{L}}_{\rm int} = \dfrac{\kappa}{2} h_{\mu \nu}T^{\mu \nu}$ .In this study, we focus on the gravitational Rutherford scattering process
$ I(k) N(p)\to I(k^\prime) N(p^\prime) $ , where I and N represent a point-like projectile and heavy composite target particle, respectively. We use the laboratory frame where the target particle is at rest, so that the four-momentum of the target particle in the initial state becomes$ p^\mu = (M,{\bf{0}}) $ . As depicted in Fig. 1, the tree-level gravitational Rutherford scattering process is induced by the t-channel graviton exchange, and the corresponding amplitude reads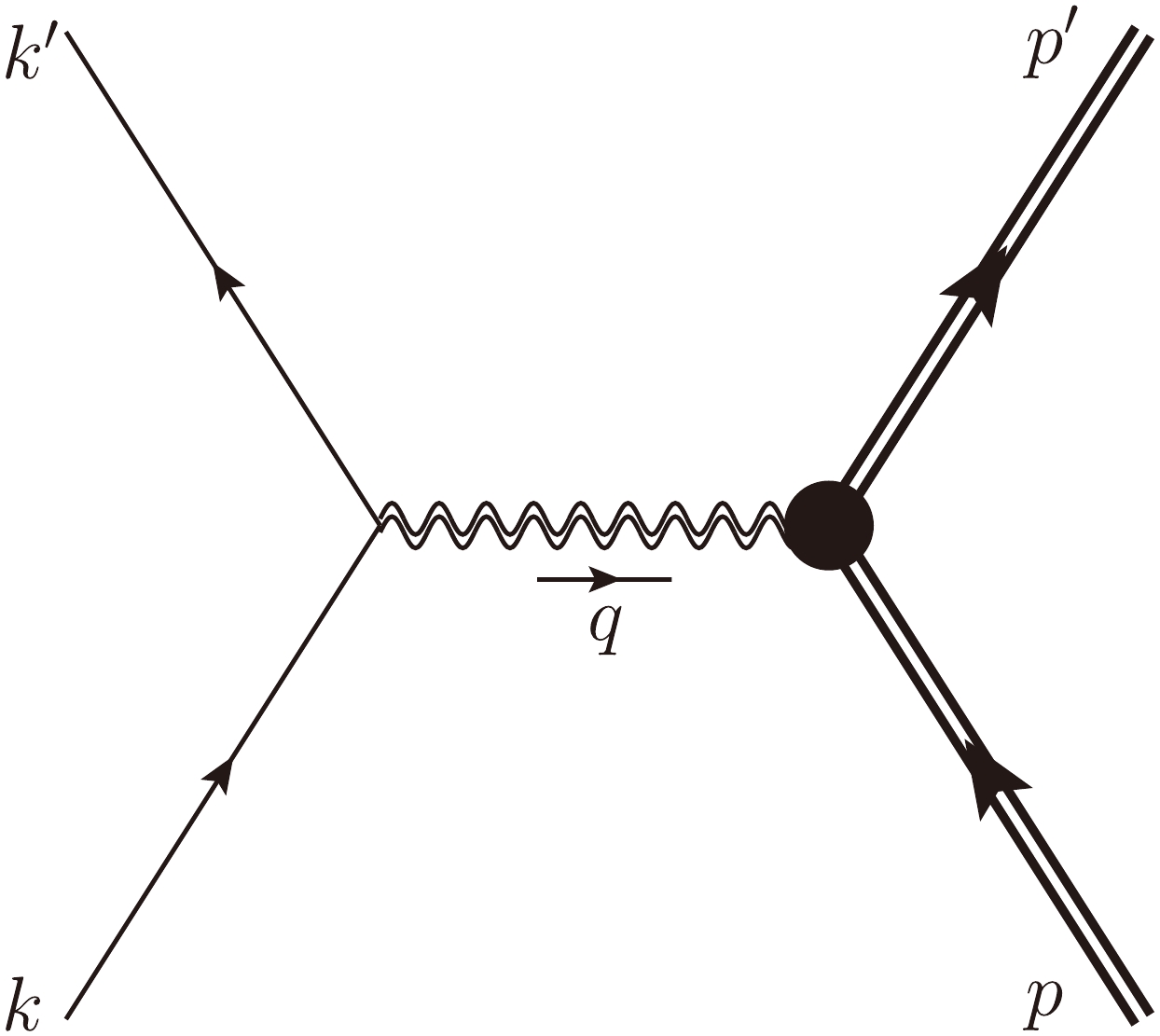
Figure 1. Tree-level Feynman diagram for a gravitational Rutherford scattering process
$ I N\to I N$ . The double wavy line represents the graviton propagator. The thick double line represents the heavy target particle. The heavy dot denotes the gravitational vertex expressed in (5).$ {\cal{M}} = \frac{\kappa^{2}{\cal{P}}_{\mu\nu\rho\sigma}}{4q^2}\langle I\left(k'\right) \vert T^{\mu \nu} \vert I\left(k\right)\rangle\langle N\left(p',\lambda'\right)|T^{\rho \sigma} |N\left(p,\lambda\right)\rangle, $

(2) with
$ {\cal{P}}_{\mu\nu\rho\sigma}\equiv \eta_{\mu\rho}\eta_{\nu\sigma}+\eta_{\mu\sigma}\eta_{\nu\rho}-\eta_{\mu\nu}\eta_{\rho\sigma} $ corresponding to the harmonic gauge.$ q = k-k' $ represents the momentum carried by the virtual graviton.$ \lambda,\lambda' $ denote the polarization indices for the massive spinning target particle. For simplicity, we suppressed the spin indices of the projectile particle.We consider three different types of projectile particles, spin-
$ 0,1/2,1 $ point-like particles. With the mass denoted by m, the corresponding energy-momentum tensors read$ T^{\mu \nu } = \partial^{\mu }\phi \partial^{\nu}\phi-\frac{\eta^{\mu \nu}}{2}\left(\partial^{\rho}\phi\partial_{\rho}\phi-m^2\phi^2\right) , \quad \text{spin-}0 $

(3a) $ T^{\mu \nu } = \frac{\rm i}{4}\bar{\psi}\left[\gamma^{\mu}\left(\partial^{\nu}-\overset{\leftarrow}{\partial^{\nu}} \right)+\gamma^{\nu}\left(\partial^{\mu}-\overset{\leftarrow}{\partial^{\mu}} \right)\right]\psi, \quad \text{spin-} \frac{1}{2} $

(3b) $\begin{aligned}[b]& T^{\mu \nu } = -F^{\mu \lambda}F^{\nu}\,_{\lambda} +\frac{1}{4} \eta^{\mu \nu }F^{\rho \sigma}F_{\rho \sigma}-\frac{1}{2}m^2 \eta^{\mu \nu }A^{\lambda}A_{\lambda}+m^2A^{\mu}A^{\nu}. \\& \text{spin-}1\end{aligned} $

(3c) The corresponding gravitational matrix elements involving the projectile particles can be readily obtained:
$ \langle I(k')\vert T^{\mu \nu}\vert I(k)\rangle = k^\mu k'^\nu+k^\nu k'^\mu- \eta^{\mu\nu}(k \cdot k'-m^2),\quad \text{spin-}0 $

(4a) $\begin{aligned}[b] \langle I(k')\vert T^{\mu \nu} \vert I(k)\rangle =\;& \frac{1}{4}\bar{u}(k')(\gamma^{\mu}(k'^{\nu}+k^{\nu}) +\gamma^{\nu}(k'^{\mu}+k^{\mu}))u(k), \end{aligned} $

$\begin{aligned}[b] \qquad \text{spin-} \frac{1}{2}\end{aligned} $

(4b) $ \begin{aligned}[b] \langle I(k')\vert T^{\mu \nu}\vert I(k)\rangle =\;& \varepsilon^*_{\sigma}(k')[P^{\mu\nu\rho\sigma}(k\cdot k'-m^2) + \eta^{\mu\nu}k^\sigma k'^{\rho}\\&+ \eta^{\rho\sigma}\left(k^\mu k'^{\nu}+k^\nu k'^{\mu}\right) - \eta^{\nu\rho}k^\sigma k'^{\mu}-\eta^{\mu\rho}k^\sigma k'^{\nu}\\&-\eta^{\nu\sigma}k^\mu k'^{\rho}-\eta^{\mu\sigma}k^\nu k'^{\rho}]\varepsilon_{\rho}(k). \qquad\quad \text{spin-}1 \end{aligned}$

(4c) The gravitational matrix elements involving the composite target particles in (2) are, in general, nonperturbative objects, which vary with target species. In the literature, they are usually referred to as gravitational form factors (GFFs) [11, 12]. As the GFFs encode some essential mechanical properties of a hadron such as mass, spin, and shear force distributions [14−16], the interest toward hadron's GFFs has revived in recent years. Although it is unfeasible to detect the gravitational Rutherford scattering in the foreseeable future, it is of high priority for the current and forthcoming
$ ep $ facilities such as$ {\mathrm{Jlab}}$ ,$ {\mathrm{EIC}} $ and$ {\mathrm{EicC}}$ to extract nucleon' GFFs in an indirect manner [17]1 . Recently, the GFFs of the proton and pion at small momentum transfer have been investigated by a lattice quantum chromodynamics (QCD) simulation [18, 19].In this study, we consider five types of composite target particles of mass M, with spin varying from 0 to 2. In line with the Lorentz group representation, the corresponding gravitational matrix elements involving various target particles can be decomposed into the linear combination of different GFFs [20]
2 :$ \langle N\left(p',\lambda'\right)|T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = 0} = 2P^\mu P^\nu\,F_{10}\left( \frac{q^2}{M^2}\right) +2\left(q^\mu q^\nu-\eta^{\mu\nu}q^2\right)F_{20}\left( \frac{q^2}{M^2}\right), $

(5a) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)|T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = \frac{1}{2}} = \overline u(p',\lambda')\Big[ 2P^\mu P^\nu\,F_{10}\left( \frac{q^2}{M^2}\right) +2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)F_{20}\left( \frac{q^2}{M^2}\right) +P^{\{\mu}\tfrac{i}{2}\sigma^{\nu\}\rho} q_\rho F_{40}\left( \frac{q^2}{M^2}\right) \Big]u(p,\lambda), \end{aligned}$

(5b) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)|T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = 1} =\;& -\varepsilon^*_{\alpha'}(p',\lambda')\Bigg[ 2P^ \mu P^\nu \left(\eta^{\alpha'\alpha}\,F_{10}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{11}\left( \frac{q^2}{M^2}\right)\right) +2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)\Bigg(\eta^{\alpha'\alpha}\,F_{20}\left( \frac{q^2}{M^2}\right)\\&-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{21}\left( \frac{q^2}{M^2}\right)\Bigg) -2M^2\eta^{\mu\nu}\left(\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{31}\left( \frac{q^2}{M^2}\right) \right)-P^{\{\mu}\eta^{\nu\}[\alpha'} q^{\alpha]}F_{40}\left( \frac{q^2}{M^2}\right) \\&-\left( q^{\{\mu}\eta^{\nu\}\{\alpha'} q^{\alpha\}}-\eta^{\mu\nu} q^{\alpha'} q^{\alpha}-\eta^{\alpha'\{\mu}\eta^{\nu\}\alpha} q^2\right)F_{50}\left( \frac{q^2}{M^2}\right)\Bigg]\varepsilon_{\alpha}(p,\lambda), \end{aligned}$

(5c) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)\vert T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = \frac{3}{2}} =\;& -\overline u_{\alpha'}(p',\lambda')\Bigg[ 2P^ \mu P^\nu \left(\eta^{\alpha'\alpha}\,F_{10}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{11}\left( \frac{q^2}{M^2}\right)\right) +2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)\Bigg(\eta^{\alpha'\alpha}\,F_{20}\left( \frac{q^2}{M^2}\right)\\&-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{21}\left( \frac{q^2}{M^2}\right)\Bigg) -2M^2\eta^{\mu\nu}\left(\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{31}\left( \frac{q^2}{M^2}\right) \right) +P^{\{\mu}\tfrac{i}{2}\sigma^{\nu\}\rho} q_\rho \Bigg(\eta^{\alpha'\alpha}\,F_{40}\left( \frac{q^2}{M^2}\right)\\ &-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{41}\left( \frac{q^2}{M^2}\right)\Bigg) -\left( q^{\{\mu}\eta^{\nu\}\{\alpha'} q^{\alpha\}}-\eta^{\mu\nu} q^{\alpha'} q^{\alpha}-\eta^{\alpha'\{\mu}\eta^{\nu\}\alpha} q^2\right)F_{50}\left( \frac{q^2}{M^2}\right)\Bigg]u_{\alpha}(p,\lambda), \end{aligned} $

(5d) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)| T^{\mu \nu} |N\left(p,\lambda\right)\rangle_{s = 2} =\;& \varepsilon^*_{\alpha'_1\alpha'_2}(p',\lambda')\bigg[ 2P^\mu P^\nu\left(\eta^{\alpha'_1\alpha_1}\eta^{\alpha'_2\alpha_2}\,F_{10}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\eta^{\alpha'_2\alpha_2}\,F_{11}\left( \frac{q^2}{M^2}\right)\right.\left.+\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\frac{ q^{\alpha'_2} q^{\alpha_2}}{2M^2}\,F_{12}\left( \frac{q^2}{M^2}\right)\right) \\ &+2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)\left(\eta^{\alpha'_1\alpha_1}\eta^{\alpha'_2\alpha_2}\,F_{20}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\eta^{\alpha'_2\alpha_2}\,F_{21}\left( \frac{q^2}{M^2}\right)\right.\left.+\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\frac{ q^{\alpha'_2} q^{\alpha_2}}{2M^2}\,F_{22}\left( \frac{q^2}{M^2}\right)\right) \\ &-2M^2\eta^{\mu\nu}\left(\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\eta^{\alpha'_2\alpha_2}\,F_{31}\left( \frac{q^2}{M^2}\right) - \frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\frac{ q^{\alpha'_2} q^{\alpha_2}}{2M^2}\,F_{32}\left( \frac{q^2}{M^2}\right)\right) \\ &-P^{\{\mu}\eta^{\nu\}[\alpha'_2} q^{\alpha_2]}\left(\eta^{\alpha'_1\alpha_1}F_{40}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}F_{41}\left( \frac{q^2}{M^2}\right)\right)-\left( q^{\{\mu}\eta^{\nu\}\{\alpha'_2} q^{\alpha_2\}}-\eta^{\mu\nu} q^{\alpha'_2} q^{\alpha_2}-\eta^{\alpha'_2\{\mu}\eta^{\nu\}\alpha_2} q^2\right) \\ &\times \left(\eta^{\alpha'_1\alpha_1}F_{50}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}F_{51}\left( \frac{q^2}{M^2}\right)\right)+ q^{[\alpha'_2}\eta^{\alpha_2]\{\mu}\eta^{\nu\}[\alpha'_{1}} q^{\alpha_{1}]}F_{70}\left( \frac{q^2}{M^2}\right)\bigg]\varepsilon_{\alpha_1\alpha_2}(p,\lambda), \end{aligned}$

(5e) where
$ P\equiv (p+p')/2 $ is the average momentum of the target particle between the initial and final states and$ q \equiv p'-p $ denotes the transfer momentum.$ a^{\{ \mu} b^{\nu \} }\equiv a^{\mu}b^{\nu}+ a^{\nu}b^{\mu} $ ,$ a^{[ \mu} b^{\nu ] } \equiv a^{\mu}b^{\nu}-a^{\nu}b^{\mu} $ , and$ \sigma^{\mu \nu} = \dfrac{\rm i}{2}[\gamma^{\mu},\gamma^{\nu}] $ . u,$ \varepsilon^\mu $ ,$ u^\mu $ , and$ \varepsilon^{\alpha\beta} $ signify the wave functions of the spin-$ {1/2} $ , 1,$ {3/2} $ , and 2 particles, respectively. Various GFFs are normalized to be dimensionless Lorentz scalars that solely depend on the ratio$ q^2/M^2 $ . Note that we, we suppressed terms that are forbidden by the current conservation.According to (5), for a target particle with spin s, the number of independent GFFs is
$2(s+1)+ 3\lfloor s\rfloor-\Theta(s-1)$ [20]3 . Analogous to electromagnetic form factors, various GFFs with zero momentum transfer encapsulate the properties of the gravitational multipoles of the composite target particles. For the target particle carrying arbitrary spin s,$ F_{10} $ and$ F_{40} $ have absolute normalization at zero momentum transfer,$ F_{10}(0) = 1 $ and$ F_{40}(0) = s $ , as dictated by the energy-momentum and angular momentum conservation, respectively. The$ F'_{10}(0) $ 4 ,$ F_{11}(0) $ ,$ F_{20}(0) $ and$ F_{50}(0) $ terms are related to the angular momentum [13, 14], pressure, and shear force [14−16] of the target particle. The mass radius of the target particle can also be obtained from the linear combination of these form factors with zero momentum transfer. -
In general relativity, the energy-momentum tensor of the matter field has the role of gravitational sources. The symmetric Belinfante-Rosenfeld energy-momentum tensor is defined as
$ T_{\mu \nu } = \frac{2}{\sqrt{-g}} \frac{\delta S}{ \delta g^{\mu \nu }}, $
(1) where S denotes the gravitational action of the matter field and
$ g^{\mu\nu}(x) $ denotes the spacetime metric field. In the weak gravity case, we approximate$ g_{\mu\nu}(x) = \eta_{\mu\nu}+\kappa h_{\mu\nu}(x) $ with$ \eta_{\mu\nu} = {\rm{diag}}(1,-1,-1,-1) $ being the Minkowski metric. Here,$ \kappa = \sqrt{32\pi G_N} $ , with the Newton's constant$G_\text{N} = 6.709\times 10^{-39}\;\mathrm{GeV}^{-2}$ . In the linearized approximation, the matter field couples with the graviton simply through the interaction${\cal{L}}_{\rm int} = \dfrac{\kappa}{2} h_{\mu \nu}T^{\mu \nu}$ .In this study, we focus on the gravitational Rutherford scattering process
$ I(k) N(p)\to I(k^\prime) N(p^\prime) $ , where I and N represent a point-like projectile and heavy composite target particle, respectively. We use the laboratory frame where the target particle is at rest, so that the four-momentum of the target particle in the initial state becomes$ p^\mu = (M,{\bf{0}}) $ . As depicted in Fig. 1, the tree-level gravitational Rutherford scattering process is induced by the t-channel graviton exchange, and the corresponding amplitude reads
Figure 1. Tree-level Feynman diagram for a gravitational Rutherford scattering process
$ I N\to I N$ . The double wavy line represents the graviton propagator. The thick double line represents the heavy target particle. The heavy dot denotes the gravitational vertex expressed in (5).$ {\cal{M}} = \frac{\kappa^{2}{\cal{P}}_{\mu\nu\rho\sigma}}{4q^2}\langle I\left(k'\right) \vert T^{\mu \nu} \vert I\left(k\right)\rangle\langle N\left(p',\lambda'\right)|T^{\rho \sigma} |N\left(p,\lambda\right)\rangle, $
(2) with
$ {\cal{P}}_{\mu\nu\rho\sigma}\equiv \eta_{\mu\rho}\eta_{\nu\sigma}+\eta_{\mu\sigma}\eta_{\nu\rho}-\eta_{\mu\nu}\eta_{\rho\sigma} $ corresponding to the harmonic gauge.$ q = k-k' $ represents the momentum carried by the virtual graviton.$ \lambda,\lambda' $ denote the polarization indices for the massive spinning target particle. For simplicity, we suppressed the spin indices of the projectile particle.We consider three different types of projectile particles, spin-
$ 0,1/2,1 $ point-like particles. With the mass denoted by m, the corresponding energy-momentum tensors read$ T^{\mu \nu } = \partial^{\mu }\phi \partial^{\nu}\phi-\frac{\eta^{\mu \nu}}{2}\left(\partial^{\rho}\phi\partial_{\rho}\phi-m^2\phi^2\right) , \quad \text{spin-}0 $
(3a) $ T^{\mu \nu } = \frac{\rm i}{4}\bar{\psi}\left[\gamma^{\mu}\left(\partial^{\nu}-\overset{\leftarrow}{\partial^{\nu}} \right)+\gamma^{\nu}\left(\partial^{\mu}-\overset{\leftarrow}{\partial^{\mu}} \right)\right]\psi, \quad \text{spin-} \frac{1}{2} $
(3b) $\begin{aligned}[b]& T^{\mu \nu } = -F^{\mu \lambda}F^{\nu}\,_{\lambda} +\frac{1}{4} \eta^{\mu \nu }F^{\rho \sigma}F_{\rho \sigma}-\frac{1}{2}m^2 \eta^{\mu \nu }A^{\lambda}A_{\lambda}+m^2A^{\mu}A^{\nu}. \\& \text{spin-}1\end{aligned} $
(3c) The corresponding gravitational matrix elements involving the projectile particles can be readily obtained:
$ \langle I(k')\vert T^{\mu \nu}\vert I(k)\rangle = k^\mu k'^\nu+k^\nu k'^\mu- \eta^{\mu\nu}(k \cdot k'-m^2),\quad \text{spin-}0 $
(4a) $\begin{aligned}[b] \langle I(k')\vert T^{\mu \nu} \vert I(k)\rangle =\;& \frac{1}{4}\bar{u}(k')(\gamma^{\mu}(k'^{\nu}+k^{\nu}) +\gamma^{\nu}(k'^{\mu}+k^{\mu}))u(k), \end{aligned} $
$\begin{aligned}[b] \qquad \text{spin-} \frac{1}{2}\end{aligned} $
(4b) $ \begin{aligned}[b] \langle I(k')\vert T^{\mu \nu}\vert I(k)\rangle =\;& \varepsilon^*_{\sigma}(k')[P^{\mu\nu\rho\sigma}(k\cdot k'-m^2) + \eta^{\mu\nu}k^\sigma k'^{\rho}\\&+ \eta^{\rho\sigma}\left(k^\mu k'^{\nu}+k^\nu k'^{\mu}\right) - \eta^{\nu\rho}k^\sigma k'^{\mu}-\eta^{\mu\rho}k^\sigma k'^{\nu}\\&-\eta^{\nu\sigma}k^\mu k'^{\rho}-\eta^{\mu\sigma}k^\nu k'^{\rho}]\varepsilon_{\rho}(k). \qquad\quad \text{spin-}1 \end{aligned}$
(4c) The gravitational matrix elements involving the composite target particles in (2) are, in general, nonperturbative objects, which vary with target species. In the literature, they are usually referred to as gravitational form factors (GFFs) [11, 12]. As the GFFs encode some essential mechanical properties of a hadron such as mass, spin, and shear force distributions [14−16], the interest toward hadron's GFFs has revived in recent years. Although it is unfeasible to detect the gravitational Rutherford scattering in the foreseeable future, it is of high priority for the current and forthcoming
$ ep $ facilities such as$ {\mathrm{Jlab}}$ ,$ {\mathrm{EIC}} $ and$ {\mathrm{EicC}}$ to extract nucleon' GFFs in an indirect manner [17]1 . Recently, the GFFs of the proton and pion at small momentum transfer have been investigated by a lattice quantum chromodynamics (QCD) simulation [18, 19].In this study, we consider five types of composite target particles of mass M, with spin varying from 0 to 2. In line with the Lorentz group representation, the corresponding gravitational matrix elements involving various target particles can be decomposed into the linear combination of different GFFs [20]
2 :$ \langle N\left(p',\lambda'\right)|T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = 0} = 2P^\mu P^\nu\,F_{10}\left( \frac{q^2}{M^2}\right) +2\left(q^\mu q^\nu-\eta^{\mu\nu}q^2\right)F_{20}\left( \frac{q^2}{M^2}\right), $
(5a) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)|T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = \frac{1}{2}} = \overline u(p',\lambda')\Big[ 2P^\mu P^\nu\,F_{10}\left( \frac{q^2}{M^2}\right) +2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)F_{20}\left( \frac{q^2}{M^2}\right) +P^{\{\mu}\tfrac{i}{2}\sigma^{\nu\}\rho} q_\rho F_{40}\left( \frac{q^2}{M^2}\right) \Big]u(p,\lambda), \end{aligned}$
(5b) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)|T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = 1} =\;& -\varepsilon^*_{\alpha'}(p',\lambda')\Bigg[ 2P^ \mu P^\nu \left(\eta^{\alpha'\alpha}\,F_{10}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{11}\left( \frac{q^2}{M^2}\right)\right) +2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)\Bigg(\eta^{\alpha'\alpha}\,F_{20}\left( \frac{q^2}{M^2}\right)\\&-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{21}\left( \frac{q^2}{M^2}\right)\Bigg) -2M^2\eta^{\mu\nu}\left(\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{31}\left( \frac{q^2}{M^2}\right) \right)-P^{\{\mu}\eta^{\nu\}[\alpha'} q^{\alpha]}F_{40}\left( \frac{q^2}{M^2}\right) \\&-\left( q^{\{\mu}\eta^{\nu\}\{\alpha'} q^{\alpha\}}-\eta^{\mu\nu} q^{\alpha'} q^{\alpha}-\eta^{\alpha'\{\mu}\eta^{\nu\}\alpha} q^2\right)F_{50}\left( \frac{q^2}{M^2}\right)\Bigg]\varepsilon_{\alpha}(p,\lambda), \end{aligned}$
(5c) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)\vert T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = \frac{3}{2}} =\;& -\overline u_{\alpha'}(p',\lambda')\Bigg[ 2P^ \mu P^\nu \left(\eta^{\alpha'\alpha}\,F_{10}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{11}\left( \frac{q^2}{M^2}\right)\right) +2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)\Bigg(\eta^{\alpha'\alpha}\,F_{20}\left( \frac{q^2}{M^2}\right)\\&-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{21}\left( \frac{q^2}{M^2}\right)\Bigg) -2M^2\eta^{\mu\nu}\left(\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{31}\left( \frac{q^2}{M^2}\right) \right) +P^{\{\mu}\tfrac{i}{2}\sigma^{\nu\}\rho} q_\rho \Bigg(\eta^{\alpha'\alpha}\,F_{40}\left( \frac{q^2}{M^2}\right)\\ &-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{41}\left( \frac{q^2}{M^2}\right)\Bigg) -\left( q^{\{\mu}\eta^{\nu\}\{\alpha'} q^{\alpha\}}-\eta^{\mu\nu} q^{\alpha'} q^{\alpha}-\eta^{\alpha'\{\mu}\eta^{\nu\}\alpha} q^2\right)F_{50}\left( \frac{q^2}{M^2}\right)\Bigg]u_{\alpha}(p,\lambda), \end{aligned} $
(5d) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)| T^{\mu \nu} |N\left(p,\lambda\right)\rangle_{s = 2} =\;& \varepsilon^*_{\alpha'_1\alpha'_2}(p',\lambda')\bigg[ 2P^\mu P^\nu\left(\eta^{\alpha'_1\alpha_1}\eta^{\alpha'_2\alpha_2}\,F_{10}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\eta^{\alpha'_2\alpha_2}\,F_{11}\left( \frac{q^2}{M^2}\right)\right.\left.+\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\frac{ q^{\alpha'_2} q^{\alpha_2}}{2M^2}\,F_{12}\left( \frac{q^2}{M^2}\right)\right) \\ &+2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)\left(\eta^{\alpha'_1\alpha_1}\eta^{\alpha'_2\alpha_2}\,F_{20}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\eta^{\alpha'_2\alpha_2}\,F_{21}\left( \frac{q^2}{M^2}\right)\right.\left.+\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\frac{ q^{\alpha'_2} q^{\alpha_2}}{2M^2}\,F_{22}\left( \frac{q^2}{M^2}\right)\right) \\ &-2M^2\eta^{\mu\nu}\left(\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\eta^{\alpha'_2\alpha_2}\,F_{31}\left( \frac{q^2}{M^2}\right) - \frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\frac{ q^{\alpha'_2} q^{\alpha_2}}{2M^2}\,F_{32}\left( \frac{q^2}{M^2}\right)\right) \\ &-P^{\{\mu}\eta^{\nu\}[\alpha'_2} q^{\alpha_2]}\left(\eta^{\alpha'_1\alpha_1}F_{40}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}F_{41}\left( \frac{q^2}{M^2}\right)\right)-\left( q^{\{\mu}\eta^{\nu\}\{\alpha'_2} q^{\alpha_2\}}-\eta^{\mu\nu} q^{\alpha'_2} q^{\alpha_2}-\eta^{\alpha'_2\{\mu}\eta^{\nu\}\alpha_2} q^2\right) \\ &\times \left(\eta^{\alpha'_1\alpha_1}F_{50}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}F_{51}\left( \frac{q^2}{M^2}\right)\right)+ q^{[\alpha'_2}\eta^{\alpha_2]\{\mu}\eta^{\nu\}[\alpha'_{1}} q^{\alpha_{1}]}F_{70}\left( \frac{q^2}{M^2}\right)\bigg]\varepsilon_{\alpha_1\alpha_2}(p,\lambda), \end{aligned}$
(5e) where
$ P\equiv (p+p')/2 $ is the average momentum of the target particle between the initial and final states and$ q \equiv p'-p $ denotes the transfer momentum.$ a^{\{ \mu} b^{\nu \} }\equiv a^{\mu}b^{\nu}+ a^{\nu}b^{\mu} $ ,$ a^{[ \mu} b^{\nu ] } \equiv a^{\mu}b^{\nu}-a^{\nu}b^{\mu} $ , and$ \sigma^{\mu \nu} = \dfrac{\rm i}{2}[\gamma^{\mu},\gamma^{\nu}] $ . u,$ \varepsilon^\mu $ ,$ u^\mu $ , and$ \varepsilon^{\alpha\beta} $ signify the wave functions of the spin-$ {1/2} $ , 1,$ {3/2} $ , and 2 particles, respectively. Various GFFs are normalized to be dimensionless Lorentz scalars that solely depend on the ratio$ q^2/M^2 $ . Note that we, we suppressed terms that are forbidden by the current conservation.According to (5), for a target particle with spin s, the number of independent GFFs is
$2(s+1)+ 3\lfloor s\rfloor-\Theta(s-1)$ [20]3 . Analogous to electromagnetic form factors, various GFFs with zero momentum transfer encapsulate the properties of the gravitational multipoles of the composite target particles. For the target particle carrying arbitrary spin s,$ F_{10} $ and$ F_{40} $ have absolute normalization at zero momentum transfer,$ F_{10}(0) = 1 $ and$ F_{40}(0) = s $ , as dictated by the energy-momentum and angular momentum conservation, respectively. The$ F'_{10}(0) $ 4 ,$ F_{11}(0) $ ,$ F_{20}(0) $ and$ F_{50}(0) $ terms are related to the angular momentum [13, 14], pressure, and shear force [14−16] of the target particle. The mass radius of the target particle can also be obtained from the linear combination of these form factors with zero momentum transfer. -
In general relativity, the energy-momentum tensor of the matter field has the role of gravitational sources. The symmetric Belinfante-Rosenfeld energy-momentum tensor is defined as
$ T_{\mu \nu } = \frac{2}{\sqrt{-g}} \frac{\delta S}{ \delta g^{\mu \nu }}, $

(1) where S denotes the gravitational action of the matter field and
$ g^{\mu\nu}(x) $ denotes the spacetime metric field. In the weak gravity case, we approximate$ g_{\mu\nu}(x) = \eta_{\mu\nu}+\kappa h_{\mu\nu}(x) $ with$ \eta_{\mu\nu} = {\rm{diag}}(1,-1,-1,-1) $ being the Minkowski metric. Here,$ \kappa = \sqrt{32\pi G_N} $ , with the Newton's constant$G_\text{N} = 6.709\times 10^{-39}\;\mathrm{GeV}^{-2}$ . In the linearized approximation, the matter field couples with the graviton simply through the interaction${\cal{L}}_{\rm int} = \dfrac{\kappa}{2} h_{\mu \nu}T^{\mu \nu}$ .In this study, we focus on the gravitational Rutherford scattering process
$ I(k) N(p)\to I(k^\prime) N(p^\prime) $ , where I and N represent a point-like projectile and heavy composite target particle, respectively. We use the laboratory frame where the target particle is at rest, so that the four-momentum of the target particle in the initial state becomes$ p^\mu = (M,{\bf{0}}) $ . As depicted in Fig. 1, the tree-level gravitational Rutherford scattering process is induced by the t-channel graviton exchange, and the corresponding amplitude reads
Figure 1. Tree-level Feynman diagram for a gravitational Rutherford scattering process
$ I N\to I N$ . The double wavy line represents the graviton propagator. The thick double line represents the heavy target particle. The heavy dot denotes the gravitational vertex expressed in (5).$ {\cal{M}} = \frac{\kappa^{2}{\cal{P}}_{\mu\nu\rho\sigma}}{4q^2}\langle I\left(k'\right) \vert T^{\mu \nu} \vert I\left(k\right)\rangle\langle N\left(p',\lambda'\right)|T^{\rho \sigma} |N\left(p,\lambda\right)\rangle, $

(2) with
$ {\cal{P}}_{\mu\nu\rho\sigma}\equiv \eta_{\mu\rho}\eta_{\nu\sigma}+\eta_{\mu\sigma}\eta_{\nu\rho}-\eta_{\mu\nu}\eta_{\rho\sigma} $ corresponding to the harmonic gauge.$ q = k-k' $ represents the momentum carried by the virtual graviton.$ \lambda,\lambda' $ denote the polarization indices for the massive spinning target particle. For simplicity, we suppressed the spin indices of the projectile particle.We consider three different types of projectile particles, spin-
$ 0,1/2,1 $ point-like particles. With the mass denoted by m, the corresponding energy-momentum tensors read$ T^{\mu \nu } = \partial^{\mu }\phi \partial^{\nu}\phi-\frac{\eta^{\mu \nu}}{2}\left(\partial^{\rho}\phi\partial_{\rho}\phi-m^2\phi^2\right) , \quad \text{spin-}0 $

(3a) $ T^{\mu \nu } = \frac{\rm i}{4}\bar{\psi}\left[\gamma^{\mu}\left(\partial^{\nu}-\overset{\leftarrow}{\partial^{\nu}} \right)+\gamma^{\nu}\left(\partial^{\mu}-\overset{\leftarrow}{\partial^{\mu}} \right)\right]\psi, \quad \text{spin-} \frac{1}{2} $

(3b) $\begin{aligned}[b]& T^{\mu \nu } = -F^{\mu \lambda}F^{\nu}\,_{\lambda} +\frac{1}{4} \eta^{\mu \nu }F^{\rho \sigma}F_{\rho \sigma}-\frac{1}{2}m^2 \eta^{\mu \nu }A^{\lambda}A_{\lambda}+m^2A^{\mu}A^{\nu}. \\& \text{spin-}1\end{aligned} $

(3c) The corresponding gravitational matrix elements involving the projectile particles can be readily obtained:
$ \langle I(k')\vert T^{\mu \nu}\vert I(k)\rangle = k^\mu k'^\nu+k^\nu k'^\mu- \eta^{\mu\nu}(k \cdot k'-m^2),\quad \text{spin-}0 $

(4a) $\begin{aligned}[b] \langle I(k')\vert T^{\mu \nu} \vert I(k)\rangle =\;& \frac{1}{4}\bar{u}(k')(\gamma^{\mu}(k'^{\nu}+k^{\nu}) +\gamma^{\nu}(k'^{\mu}+k^{\mu}))u(k), \end{aligned} $

$\begin{aligned}[b] \qquad \text{spin-} \frac{1}{2}\end{aligned} $

(4b) $ \begin{aligned}[b] \langle I(k')\vert T^{\mu \nu}\vert I(k)\rangle =\;& \varepsilon^*_{\sigma}(k')[P^{\mu\nu\rho\sigma}(k\cdot k'-m^2) + \eta^{\mu\nu}k^\sigma k'^{\rho}\\&+ \eta^{\rho\sigma}\left(k^\mu k'^{\nu}+k^\nu k'^{\mu}\right) - \eta^{\nu\rho}k^\sigma k'^{\mu}-\eta^{\mu\rho}k^\sigma k'^{\nu}\\&-\eta^{\nu\sigma}k^\mu k'^{\rho}-\eta^{\mu\sigma}k^\nu k'^{\rho}]\varepsilon_{\rho}(k). \qquad\quad \text{spin-}1 \end{aligned}$

(4c) The gravitational matrix elements involving the composite target particles in (2) are, in general, nonperturbative objects, which vary with target species. In the literature, they are usually referred to as gravitational form factors (GFFs) [11, 12]. As the GFFs encode some essential mechanical properties of a hadron such as mass, spin, and shear force distributions [14−16], the interest toward hadron's GFFs has revived in recent years. Although it is unfeasible to detect the gravitational Rutherford scattering in the foreseeable future, it is of high priority for the current and forthcoming
$ ep $ facilities such as$ {\mathrm{Jlab}}$ ,$ {\mathrm{EIC}} $ and$ {\mathrm{EicC}}$ to extract nucleon' GFFs in an indirect manner [17]1 . Recently, the GFFs of the proton and pion at small momentum transfer have been investigated by a lattice quantum chromodynamics (QCD) simulation [18, 19].In this study, we consider five types of composite target particles of mass M, with spin varying from 0 to 2. In line with the Lorentz group representation, the corresponding gravitational matrix elements involving various target particles can be decomposed into the linear combination of different GFFs [20]
2 :$ \langle N\left(p',\lambda'\right)|T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = 0} = 2P^\mu P^\nu\,F_{10}\left( \frac{q^2}{M^2}\right) +2\left(q^\mu q^\nu-\eta^{\mu\nu}q^2\right)F_{20}\left( \frac{q^2}{M^2}\right), $

(5a) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)|T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = \frac{1}{2}} = \overline u(p',\lambda')\Big[ 2P^\mu P^\nu\,F_{10}\left( \frac{q^2}{M^2}\right) +2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)F_{20}\left( \frac{q^2}{M^2}\right) +P^{\{\mu}\tfrac{i}{2}\sigma^{\nu\}\rho} q_\rho F_{40}\left( \frac{q^2}{M^2}\right) \Big]u(p,\lambda), \end{aligned}$

(5b) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)|T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = 1} =\;& -\varepsilon^*_{\alpha'}(p',\lambda')\Bigg[ 2P^ \mu P^\nu \left(\eta^{\alpha'\alpha}\,F_{10}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{11}\left( \frac{q^2}{M^2}\right)\right) +2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)\Bigg(\eta^{\alpha'\alpha}\,F_{20}\left( \frac{q^2}{M^2}\right)\\&-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{21}\left( \frac{q^2}{M^2}\right)\Bigg) -2M^2\eta^{\mu\nu}\left(\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{31}\left( \frac{q^2}{M^2}\right) \right)-P^{\{\mu}\eta^{\nu\}[\alpha'} q^{\alpha]}F_{40}\left( \frac{q^2}{M^2}\right) \\&-\left( q^{\{\mu}\eta^{\nu\}\{\alpha'} q^{\alpha\}}-\eta^{\mu\nu} q^{\alpha'} q^{\alpha}-\eta^{\alpha'\{\mu}\eta^{\nu\}\alpha} q^2\right)F_{50}\left( \frac{q^2}{M^2}\right)\Bigg]\varepsilon_{\alpha}(p,\lambda), \end{aligned}$

(5c) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)\vert T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = \frac{3}{2}} =\;& -\overline u_{\alpha'}(p',\lambda')\Bigg[ 2P^ \mu P^\nu \left(\eta^{\alpha'\alpha}\,F_{10}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{11}\left( \frac{q^2}{M^2}\right)\right) +2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)\Bigg(\eta^{\alpha'\alpha}\,F_{20}\left( \frac{q^2}{M^2}\right)\\&-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{21}\left( \frac{q^2}{M^2}\right)\Bigg) -2M^2\eta^{\mu\nu}\left(\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{31}\left( \frac{q^2}{M^2}\right) \right) +P^{\{\mu}\tfrac{i}{2}\sigma^{\nu\}\rho} q_\rho \Bigg(\eta^{\alpha'\alpha}\,F_{40}\left( \frac{q^2}{M^2}\right)\\ &-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{41}\left( \frac{q^2}{M^2}\right)\Bigg) -\left( q^{\{\mu}\eta^{\nu\}\{\alpha'} q^{\alpha\}}-\eta^{\mu\nu} q^{\alpha'} q^{\alpha}-\eta^{\alpha'\{\mu}\eta^{\nu\}\alpha} q^2\right)F_{50}\left( \frac{q^2}{M^2}\right)\Bigg]u_{\alpha}(p,\lambda), \end{aligned} $

(5d) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)| T^{\mu \nu} |N\left(p,\lambda\right)\rangle_{s = 2} =\;& \varepsilon^*_{\alpha'_1\alpha'_2}(p',\lambda')\bigg[ 2P^\mu P^\nu\left(\eta^{\alpha'_1\alpha_1}\eta^{\alpha'_2\alpha_2}\,F_{10}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\eta^{\alpha'_2\alpha_2}\,F_{11}\left( \frac{q^2}{M^2}\right)\right.\left.+\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\frac{ q^{\alpha'_2} q^{\alpha_2}}{2M^2}\,F_{12}\left( \frac{q^2}{M^2}\right)\right) \\ &+2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)\left(\eta^{\alpha'_1\alpha_1}\eta^{\alpha'_2\alpha_2}\,F_{20}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\eta^{\alpha'_2\alpha_2}\,F_{21}\left( \frac{q^2}{M^2}\right)\right.\left.+\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\frac{ q^{\alpha'_2} q^{\alpha_2}}{2M^2}\,F_{22}\left( \frac{q^2}{M^2}\right)\right) \\ &-2M^2\eta^{\mu\nu}\left(\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\eta^{\alpha'_2\alpha_2}\,F_{31}\left( \frac{q^2}{M^2}\right) - \frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\frac{ q^{\alpha'_2} q^{\alpha_2}}{2M^2}\,F_{32}\left( \frac{q^2}{M^2}\right)\right) \\ &-P^{\{\mu}\eta^{\nu\}[\alpha'_2} q^{\alpha_2]}\left(\eta^{\alpha'_1\alpha_1}F_{40}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}F_{41}\left( \frac{q^2}{M^2}\right)\right)-\left( q^{\{\mu}\eta^{\nu\}\{\alpha'_2} q^{\alpha_2\}}-\eta^{\mu\nu} q^{\alpha'_2} q^{\alpha_2}-\eta^{\alpha'_2\{\mu}\eta^{\nu\}\alpha_2} q^2\right) \\ &\times \left(\eta^{\alpha'_1\alpha_1}F_{50}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}F_{51}\left( \frac{q^2}{M^2}\right)\right)+ q^{[\alpha'_2}\eta^{\alpha_2]\{\mu}\eta^{\nu\}[\alpha'_{1}} q^{\alpha_{1}]}F_{70}\left( \frac{q^2}{M^2}\right)\bigg]\varepsilon_{\alpha_1\alpha_2}(p,\lambda), \end{aligned}$

(5e) where
$ P\equiv (p+p')/2 $ is the average momentum of the target particle between the initial and final states and$ q \equiv p'-p $ denotes the transfer momentum.$ a^{\{ \mu} b^{\nu \} }\equiv a^{\mu}b^{\nu}+ a^{\nu}b^{\mu} $ ,$ a^{[ \mu} b^{\nu ] } \equiv a^{\mu}b^{\nu}-a^{\nu}b^{\mu} $ , and$ \sigma^{\mu \nu} = \dfrac{\rm i}{2}[\gamma^{\mu},\gamma^{\nu}] $ . u,$ \varepsilon^\mu $ ,$ u^\mu $ , and$ \varepsilon^{\alpha\beta} $ signify the wave functions of the spin-$ {1/2} $ , 1,$ {3/2} $ , and 2 particles, respectively. Various GFFs are normalized to be dimensionless Lorentz scalars that solely depend on the ratio$ q^2/M^2 $ . Note that we, we suppressed terms that are forbidden by the current conservation.According to (5), for a target particle with spin s, the number of independent GFFs is
$2(s+1)+ 3\lfloor s\rfloor-\Theta(s-1)$ [20]3 . Analogous to electromagnetic form factors, various GFFs with zero momentum transfer encapsulate the properties of the gravitational multipoles of the composite target particles. For the target particle carrying arbitrary spin s,$ F_{10} $ and$ F_{40} $ have absolute normalization at zero momentum transfer,$ F_{10}(0) = 1 $ and$ F_{40}(0) = s $ , as dictated by the energy-momentum and angular momentum conservation, respectively. The$ F'_{10}(0) $ 4 ,$ F_{11}(0) $ ,$ F_{20}(0) $ and$ F_{50}(0) $ terms are related to the angular momentum [13, 14], pressure, and shear force [14−16] of the target particle. The mass radius of the target particle can also be obtained from the linear combination of these form factors with zero momentum transfer. -
In general relativity, the energy-momentum tensor of the matter field has the role of gravitational sources. The symmetric Belinfante-Rosenfeld energy-momentum tensor is defined as
$ T_{\mu \nu } = \frac{2}{\sqrt{-g}} \frac{\delta S}{ \delta g^{\mu \nu }}, $

(1) where S denotes the gravitational action of the matter field and
$ g^{\mu\nu}(x) $ denotes the spacetime metric field. In the weak gravity case, we approximate$ g_{\mu\nu}(x) = \eta_{\mu\nu}+\kappa h_{\mu\nu}(x) $ with$ \eta_{\mu\nu} = {\rm{diag}}(1,-1,-1,-1) $ being the Minkowski metric. Here,$ \kappa = \sqrt{32\pi G_N} $ , with the Newton's constant$G_\text{N} = 6.709\times 10^{-39}\;\mathrm{GeV}^{-2}$ . In the linearized approximation, the matter field couples with the graviton simply through the interaction${\cal{L}}_{\rm int} = \dfrac{\kappa}{2} h_{\mu \nu}T^{\mu \nu}$ .In this study, we focus on the gravitational Rutherford scattering process
$ I(k) N(p)\to I(k^\prime) N(p^\prime) $ , where I and N represent a point-like projectile and heavy composite target particle, respectively. We use the laboratory frame where the target particle is at rest, so that the four-momentum of the target particle in the initial state becomes$ p^\mu = (M,{\bf{0}}) $ . As depicted in Fig. 1, the tree-level gravitational Rutherford scattering process is induced by the t-channel graviton exchange, and the corresponding amplitude reads
Figure 1. Tree-level Feynman diagram for a gravitational Rutherford scattering process
$ I N\to I N$ . The double wavy line represents the graviton propagator. The thick double line represents the heavy target particle. The heavy dot denotes the gravitational vertex expressed in (5).$ {\cal{M}} = \frac{\kappa^{2}{\cal{P}}_{\mu\nu\rho\sigma}}{4q^2}\langle I\left(k'\right) \vert T^{\mu \nu} \vert I\left(k\right)\rangle\langle N\left(p',\lambda'\right)|T^{\rho \sigma} |N\left(p,\lambda\right)\rangle, $

(2) with
$ {\cal{P}}_{\mu\nu\rho\sigma}\equiv \eta_{\mu\rho}\eta_{\nu\sigma}+\eta_{\mu\sigma}\eta_{\nu\rho}-\eta_{\mu\nu}\eta_{\rho\sigma} $ corresponding to the harmonic gauge.$ q = k-k' $ represents the momentum carried by the virtual graviton.$ \lambda,\lambda' $ denote the polarization indices for the massive spinning target particle. For simplicity, we suppressed the spin indices of the projectile particle.We consider three different types of projectile particles, spin-
$ 0,1/2,1 $ point-like particles. With the mass denoted by m, the corresponding energy-momentum tensors read$ T^{\mu \nu } = \partial^{\mu }\phi \partial^{\nu}\phi-\frac{\eta^{\mu \nu}}{2}\left(\partial^{\rho}\phi\partial_{\rho}\phi-m^2\phi^2\right) , \quad \text{spin-}0 $

(3a) $ T^{\mu \nu } = \frac{\rm i}{4}\bar{\psi}\left[\gamma^{\mu}\left(\partial^{\nu}-\overset{\leftarrow}{\partial^{\nu}} \right)+\gamma^{\nu}\left(\partial^{\mu}-\overset{\leftarrow}{\partial^{\mu}} \right)\right]\psi, \quad \text{spin-} \frac{1}{2} $

(3b) $\begin{aligned}[b]& T^{\mu \nu } = -F^{\mu \lambda}F^{\nu}\,_{\lambda} +\frac{1}{4} \eta^{\mu \nu }F^{\rho \sigma}F_{\rho \sigma}-\frac{1}{2}m^2 \eta^{\mu \nu }A^{\lambda}A_{\lambda}+m^2A^{\mu}A^{\nu}. \\& \text{spin-}1\end{aligned} $

(3c) The corresponding gravitational matrix elements involving the projectile particles can be readily obtained:
$ \langle I(k')\vert T^{\mu \nu}\vert I(k)\rangle = k^\mu k'^\nu+k^\nu k'^\mu- \eta^{\mu\nu}(k \cdot k'-m^2),\quad \text{spin-}0 $

(4a) $\begin{aligned}[b] \langle I(k')\vert T^{\mu \nu} \vert I(k)\rangle =\;& \frac{1}{4}\bar{u}(k')(\gamma^{\mu}(k'^{\nu}+k^{\nu}) +\gamma^{\nu}(k'^{\mu}+k^{\mu}))u(k), \end{aligned} $

$\begin{aligned}[b] \qquad \text{spin-} \frac{1}{2}\end{aligned} $

(4b) $ \begin{aligned}[b] \langle I(k')\vert T^{\mu \nu}\vert I(k)\rangle =\;& \varepsilon^*_{\sigma}(k')[P^{\mu\nu\rho\sigma}(k\cdot k'-m^2) + \eta^{\mu\nu}k^\sigma k'^{\rho}\\&+ \eta^{\rho\sigma}\left(k^\mu k'^{\nu}+k^\nu k'^{\mu}\right) - \eta^{\nu\rho}k^\sigma k'^{\mu}-\eta^{\mu\rho}k^\sigma k'^{\nu}\\&-\eta^{\nu\sigma}k^\mu k'^{\rho}-\eta^{\mu\sigma}k^\nu k'^{\rho}]\varepsilon_{\rho}(k). \qquad\quad \text{spin-}1 \end{aligned}$

(4c) The gravitational matrix elements involving the composite target particles in (2) are, in general, nonperturbative objects, which vary with target species. In the literature, they are usually referred to as gravitational form factors (GFFs) [11, 12]. As the GFFs encode some essential mechanical properties of a hadron such as mass, spin, and shear force distributions [14−16], the interest toward hadron's GFFs has revived in recent years. Although it is unfeasible to detect the gravitational Rutherford scattering in the foreseeable future, it is of high priority for the current and forthcoming
$ ep $ facilities such as$ {\mathrm{Jlab}}$ ,$ {\mathrm{EIC}} $ and$ {\mathrm{EicC}}$ to extract nucleon' GFFs in an indirect manner [17]1 . Recently, the GFFs of the proton and pion at small momentum transfer have been investigated by a lattice quantum chromodynamics (QCD) simulation [18, 19].In this study, we consider five types of composite target particles of mass M, with spin varying from 0 to 2. In line with the Lorentz group representation, the corresponding gravitational matrix elements involving various target particles can be decomposed into the linear combination of different GFFs [20]
2 :$ \langle N\left(p',\lambda'\right)|T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = 0} = 2P^\mu P^\nu\,F_{10}\left( \frac{q^2}{M^2}\right) +2\left(q^\mu q^\nu-\eta^{\mu\nu}q^2\right)F_{20}\left( \frac{q^2}{M^2}\right), $

(5a) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)|T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = \frac{1}{2}} = \overline u(p',\lambda')\Big[ 2P^\mu P^\nu\,F_{10}\left( \frac{q^2}{M^2}\right) +2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)F_{20}\left( \frac{q^2}{M^2}\right) +P^{\{\mu}\tfrac{i}{2}\sigma^{\nu\}\rho} q_\rho F_{40}\left( \frac{q^2}{M^2}\right) \Big]u(p,\lambda), \end{aligned}$

(5b) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)|T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = 1} =\;& -\varepsilon^*_{\alpha'}(p',\lambda')\Bigg[ 2P^ \mu P^\nu \left(\eta^{\alpha'\alpha}\,F_{10}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{11}\left( \frac{q^2}{M^2}\right)\right) +2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)\Bigg(\eta^{\alpha'\alpha}\,F_{20}\left( \frac{q^2}{M^2}\right)\\&-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{21}\left( \frac{q^2}{M^2}\right)\Bigg) -2M^2\eta^{\mu\nu}\left(\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{31}\left( \frac{q^2}{M^2}\right) \right)-P^{\{\mu}\eta^{\nu\}[\alpha'} q^{\alpha]}F_{40}\left( \frac{q^2}{M^2}\right) \\&-\left( q^{\{\mu}\eta^{\nu\}\{\alpha'} q^{\alpha\}}-\eta^{\mu\nu} q^{\alpha'} q^{\alpha}-\eta^{\alpha'\{\mu}\eta^{\nu\}\alpha} q^2\right)F_{50}\left( \frac{q^2}{M^2}\right)\Bigg]\varepsilon_{\alpha}(p,\lambda), \end{aligned}$

(5c) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)\vert T^{\mu \nu}|N\left(p,\lambda\right)\rangle_{s = \frac{3}{2}} =\;& -\overline u_{\alpha'}(p',\lambda')\Bigg[ 2P^ \mu P^\nu \left(\eta^{\alpha'\alpha}\,F_{10}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{11}\left( \frac{q^2}{M^2}\right)\right) +2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)\Bigg(\eta^{\alpha'\alpha}\,F_{20}\left( \frac{q^2}{M^2}\right)\\&-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{21}\left( \frac{q^2}{M^2}\right)\Bigg) -2M^2\eta^{\mu\nu}\left(\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{31}\left( \frac{q^2}{M^2}\right) \right) +P^{\{\mu}\tfrac{i}{2}\sigma^{\nu\}\rho} q_\rho \Bigg(\eta^{\alpha'\alpha}\,F_{40}\left( \frac{q^2}{M^2}\right)\\ &-\frac{ q^{\alpha'} q^\alpha}{2M^2}\,F_{41}\left( \frac{q^2}{M^2}\right)\Bigg) -\left( q^{\{\mu}\eta^{\nu\}\{\alpha'} q^{\alpha\}}-\eta^{\mu\nu} q^{\alpha'} q^{\alpha}-\eta^{\alpha'\{\mu}\eta^{\nu\}\alpha} q^2\right)F_{50}\left( \frac{q^2}{M^2}\right)\Bigg]u_{\alpha}(p,\lambda), \end{aligned} $

(5d) $ \begin{aligned}[b] \langle N\left(p',\lambda'\right)| T^{\mu \nu} |N\left(p,\lambda\right)\rangle_{s = 2} =\;& \varepsilon^*_{\alpha'_1\alpha'_2}(p',\lambda')\bigg[ 2P^\mu P^\nu\left(\eta^{\alpha'_1\alpha_1}\eta^{\alpha'_2\alpha_2}\,F_{10}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\eta^{\alpha'_2\alpha_2}\,F_{11}\left( \frac{q^2}{M^2}\right)\right.\left.+\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\frac{ q^{\alpha'_2} q^{\alpha_2}}{2M^2}\,F_{12}\left( \frac{q^2}{M^2}\right)\right) \\ &+2\left( q^\mu q^\nu-\eta^{\mu\nu} q^2\right)\left(\eta^{\alpha'_1\alpha_1}\eta^{\alpha'_2\alpha_2}\,F_{20}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\eta^{\alpha'_2\alpha_2}\,F_{21}\left( \frac{q^2}{M^2}\right)\right.\left.+\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\frac{ q^{\alpha'_2} q^{\alpha_2}}{2M^2}\,F_{22}\left( \frac{q^2}{M^2}\right)\right) \\ &-2M^2\eta^{\mu\nu}\left(\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\eta^{\alpha'_2\alpha_2}\,F_{31}\left( \frac{q^2}{M^2}\right) - \frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}\,\frac{ q^{\alpha'_2} q^{\alpha_2}}{2M^2}\,F_{32}\left( \frac{q^2}{M^2}\right)\right) \\ &-P^{\{\mu}\eta^{\nu\}[\alpha'_2} q^{\alpha_2]}\left(\eta^{\alpha'_1\alpha_1}F_{40}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}F_{41}\left( \frac{q^2}{M^2}\right)\right)-\left( q^{\{\mu}\eta^{\nu\}\{\alpha'_2} q^{\alpha_2\}}-\eta^{\mu\nu} q^{\alpha'_2} q^{\alpha_2}-\eta^{\alpha'_2\{\mu}\eta^{\nu\}\alpha_2} q^2\right) \\ &\times \left(\eta^{\alpha'_1\alpha_1}F_{50}\left( \frac{q^2}{M^2}\right)-\frac{ q^{\alpha'_1} q^{\alpha_1}}{2M^2}F_{51}\left( \frac{q^2}{M^2}\right)\right)+ q^{[\alpha'_2}\eta^{\alpha_2]\{\mu}\eta^{\nu\}[\alpha'_{1}} q^{\alpha_{1}]}F_{70}\left( \frac{q^2}{M^2}\right)\bigg]\varepsilon_{\alpha_1\alpha_2}(p,\lambda), \end{aligned}$

(5e) where
$ P\equiv (p+p')/2 $ is the average momentum of the target particle between the initial and final states and$ q \equiv p'-p $ denotes the transfer momentum.$ a^{\{ \mu} b^{\nu \} }\equiv a^{\mu}b^{\nu}+ a^{\nu}b^{\mu} $ ,$ a^{[ \mu} b^{\nu ] } \equiv a^{\mu}b^{\nu}-a^{\nu}b^{\mu} $ , and$ \sigma^{\mu \nu} = \dfrac{\rm i}{2}[\gamma^{\mu},\gamma^{\nu}] $ . u,$ \varepsilon^\mu $ ,$ u^\mu $ , and$ \varepsilon^{\alpha\beta} $ signify the wave functions of the spin-$ {1/2} $ , 1,$ {3/2} $ , and 2 particles, respectively. Various GFFs are normalized to be dimensionless Lorentz scalars that solely depend on the ratio$ q^2/M^2 $ . Note that we, we suppressed terms that are forbidden by the current conservation.According to (5), for a target particle with spin s, the number of independent GFFs is
$2(s+1)+ 3\lfloor s\rfloor-\Theta(s-1)$ [20]3 . Analogous to electromagnetic form factors, various GFFs with zero momentum transfer encapsulate the properties of the gravitational multipoles of the composite target particles. For the target particle carrying arbitrary spin s,$ F_{10} $ and$ F_{40} $ have absolute normalization at zero momentum transfer,$ F_{10}(0) = 1 $ and$ F_{40}(0) = s $ , as dictated by the energy-momentum and angular momentum conservation, respectively. The$ F'_{10}(0) $ 4 ,$ F_{11}(0) $ ,$ F_{20}(0) $ and$ F_{50}(0) $ terms are related to the angular momentum [13, 14], pressure, and shear force [14−16] of the target particle. The mass radius of the target particle can also be obtained from the linear combination of these form factors with zero momentum transfer. -
First, we consider the case of a massless projectile of spin j. The corresponding differential unpolarized cross section in the laboratory frame is expressed by
$ \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta} = \frac{1}{2 |{\bf{k}}|}\cdot \frac{1}{2M}\cdot \frac{{{\bf{k}}'}^2}{8\pi|{\bf{k}}| M}\cdot {1\over 2j+1} \frac{1}{2s+1}\sum\limits_\text{spins}\left|{\cal{M}}\right|^2, $

(6) where θ denotes the polar angle between the reflected and incident projectile. The magnitude of the three-momentum of the outgoing projectile,
$ |{{\bf{k}}^\prime}| $ , can be expressed in terms of$ |{\bf{k}}| $ , M, and$ \cos\theta $ :$ |{\bf{k}}'| = \frac{|{\bf{k}}| }{ 1+\dfrac{|{\bf{k}}|}{ M}\left ( 1-\cos\theta\right)}. $

(7) By squaring the amplitude in (2), summing over the polarization in the final state, and averaging upon the polarizations in the initial state utilizing the spin sum formula in Appendix for target particles, we obtain rather lengthy and cumbersome expressions. It is difficult to identify any clear pattern about the dependence on the heavy target particle spin. Nevertheless, as we are solely concerned about the low-energy limit
$ |{\bf{k}}| \ll M $ , we can carry out the heavy target mass expansion for the unpolarized cross sections. The soft behavior of the gravitational Rutherford scattering is elucidated, and some universal patterns can be recognized. -
First, we consider the case of a massless projectile of spin j. The corresponding differential unpolarized cross section in the laboratory frame is expressed by
$ \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta} = \frac{1}{2 |{\bf{k}}|}\cdot \frac{1}{2M}\cdot \frac{{{\bf{k}}'}^2}{8\pi|{\bf{k}}| M}\cdot {1\over 2j+1} \frac{1}{2s+1}\sum\limits_\text{spins}\left|{\cal{M}}\right|^2, $

(6) where θ denotes the polar angle between the reflected and incident projectile. The magnitude of the three-momentum of the outgoing projectile,
$ |{{\bf{k}}^\prime}| $ , can be expressed in terms of$ |{\bf{k}}| $ , M, and$ \cos\theta $ :$ |{\bf{k}}'| = \frac{|{\bf{k}}| }{ 1+\dfrac{|{\bf{k}}|}{ M}\left ( 1-\cos\theta\right)}. $

(7) By squaring the amplitude in (2), summing over the polarization in the final state, and averaging upon the polarizations in the initial state utilizing the spin sum formula in Appendix for target particles, we obtain rather lengthy and cumbersome expressions. It is difficult to identify any clear pattern about the dependence on the heavy target particle spin. Nevertheless, as we are solely concerned about the low-energy limit
$ |{\bf{k}}| \ll M $ , we can carry out the heavy target mass expansion for the unpolarized cross sections. The soft behavior of the gravitational Rutherford scattering is elucidated, and some universal patterns can be recognized. -
First, we consider the case of a massless projectile of spin j. The corresponding differential unpolarized cross section in the laboratory frame is expressed by
$ \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta} = \frac{1}{2 |{\bf{k}}|}\cdot \frac{1}{2M}\cdot \frac{{{\bf{k}}'}^2}{8\pi|{\bf{k}}| M}\cdot {1\over 2j+1} \frac{1}{2s+1}\sum\limits_\text{spins}\left|{\cal{M}}\right|^2, $

(6) where θ denotes the polar angle between the reflected and incident projectile. The magnitude of the three-momentum of the outgoing projectile,
$ |{{\bf{k}}^\prime}| $ , can be expressed in terms of$ |{\bf{k}}| $ , M, and$ \cos\theta $ :$ |{\bf{k}}'| = \frac{|{\bf{k}}| }{ 1+\dfrac{|{\bf{k}}|}{ M}\left ( 1-\cos\theta\right)}. $

(7) By squaring the amplitude in (2), summing over the polarization in the final state, and averaging upon the polarizations in the initial state utilizing the spin sum formula in Appendix for target particles, we obtain rather lengthy and cumbersome expressions. It is difficult to identify any clear pattern about the dependence on the heavy target particle spin. Nevertheless, as we are solely concerned about the low-energy limit
$ |{\bf{k}}| \ll M $ , we can carry out the heavy target mass expansion for the unpolarized cross sections. The soft behavior of the gravitational Rutherford scattering is elucidated, and some universal patterns can be recognized. -
First, we consider the case of a massless projectile of spin j. The corresponding differential unpolarized cross section in the laboratory frame is expressed by
$ \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta} = \frac{1}{2 |{\bf{k}}|}\cdot \frac{1}{2M}\cdot \frac{{{\bf{k}}'}^2}{8\pi|{\bf{k}}| M}\cdot {1\over 2j+1} \frac{1}{2s+1}\sum\limits_\text{spins}\left|{\cal{M}}\right|^2, $
(6) where θ denotes the polar angle between the reflected and incident projectile. The magnitude of the three-momentum of the outgoing projectile,
$ |{{\bf{k}}^\prime}| $ , can be expressed in terms of$ |{\bf{k}}| $ , M, and$ \cos\theta $ :$ |{\bf{k}}'| = \frac{|{\bf{k}}| }{ 1+\dfrac{|{\bf{k}}|}{ M}\left ( 1-\cos\theta\right)}. $
(7) By squaring the amplitude in (2), summing over the polarization in the final state, and averaging upon the polarizations in the initial state utilizing the spin sum formula in Appendix for target particles, we obtain rather lengthy and cumbersome expressions. It is difficult to identify any clear pattern about the dependence on the heavy target particle spin. Nevertheless, as we are solely concerned about the low-energy limit
$ |{\bf{k}}| \ll M $ , we can carry out the heavy target mass expansion for the unpolarized cross sections. The soft behavior of the gravitational Rutherford scattering is elucidated, and some universal patterns can be recognized. -
The expansion of (6) in powers of
$ 1/M $ shows that the first two terms of the unpolarized cross sections are universal, e.g., independent on the target particle spin:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{LO}^{s} = {\kappa^{4} M^2 F_{10}^2 \over 512 \pi \sin^4 \dfrac{\theta}{2}}, $

(8a) $ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NLO}^{s} = -{ \kappa^4 M |{\bf{k}}| F_{10}^2\over 128\pi \sin^2 \dfrac{\theta}{2}}, $

(8b) with the occurring GFFs evaluated at zero momentum transfer. For simplicity, hereinafter, we use
$ F_n $ for$ F_n(0) $ .$ F_{10} = 1 $ for any type of composite target particles. The leading-order (LO) term is identical to the cross section obtained from the light-bending angle in classical general relativity [21, 22]. This is intuitively as expected, because, in the soft limit, the long-wavelength graviton can only feel the total mass of the composite target particle, insensitive to any further details about its internal structure. Interestingly, the next-to-leading order (NLO) term still remains universal, which originates from the expansion of the phase factor factor$ {{\bf{k}}'}^2/{\bf{k}}^2 $ to NLO in$ 1/M $ . It is instructive to understand why only a single GFF$ F_{10} $ contributes at NLO from the perspective of effective field theory. We present such analysis in Appendix B.In contrast, at the NNLO in heavy target mass expansion, the differential cross sections start to depend on the target particle spin:
$ \begin{aligned}[b] \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NNLO}^{s} =\;& -\frac{\kappa^4 {\bf{k}}^2}{64\pi \sin^2 \dfrac{\theta}{2}} \left\{{F_{10} F'_{10}}- \frac{1}{2}F_{10}F_{20}\left(1-\cos\theta\right) + \frac{1}{8}F_{10}^2\left[7\cos{\theta}- \frac{2}{3}\left( \frac{21}{2}+s+\lceil s\rceil\right)\right] \right. \\&+\Theta\left(s-\frac{1}{2}\right)\left[ \frac{(-1)^{2s}+7}{24}F_{10}F_{40} -f^{(0)}_s \,F_{40}^2(\cos{\theta}+1)\right] \\ &- \frac{1}{6}\Theta\left(s-1\right) \left[2\cos{\theta}F_{10}F_{50}+F_{10}F_{11} \right] -\left.\Theta\left(s-2\right) \frac{1}{6}F_{10}F_{70}(1+\cos{\theta})\right\}, \qquad s = 0, \frac{1}{2},1, \frac{3}{2},2 \end{aligned} $ 
(9) with
$ f^{(0)}_{\frac{1}{2}} = \frac{1}{16}, $

(10a) $ f^{(0)}_{1} = \frac{1}{6}, $

(10b) $ f^{(0)}_{\frac{3}{2}} = \frac{5}{144}, $

(10c) $ f^{(0)}_{2} = \frac{1}{8}. $

(10d) The
$ F'_{10}F_{10} $ ,$ F_{10} F_{20} $ , and$ F_{10}^2\cos{\theta} $ terms still remain universal, i.e., independent on the target spin. The$ F'_{10}F_{10} $ terms have the same origin of the LO and NLO cross sections, which correspond to a higher-order term in the Taylor expansion of$ F^2_{10}(q^2/M^2) $ in the squared LO amplitude and phase space measure. The GFFs$ F'_{10} $ ,$ F_{11} $ ,$ F_{20} $ , and$ F_{50} $ reflect the mechanical properties of the composite target particles such as the angular momentum [13, 14], pressure, and shear force [14−16]. Our results indicate that, at NNLO in heavy target mass expansion, the cross section starts to depend on the detailed three-dimensional internal structure of the target particle other than its mass. Curiously, the coefficient of the$ F_{10}F_{40} $ term seems to reflect the spin-statistic characteristic of the target particle, which alternates from 1 (fermions) to$ 4/3 $ (bosons). Although we enumerate only five different kinds of target spin, it is conceivable that the aforementioned patterns should be valid for arbitrary target spin. -
The expansion of (6) in powers of
$ 1/M $ shows that the first two terms of the unpolarized cross sections are universal, e.g., independent on the target particle spin:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{LO}^{s} = {\kappa^{4} M^2 F_{10}^2 \over 512 \pi \sin^4 \dfrac{\theta}{2}}, $

(8a) $ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NLO}^{s} = -{ \kappa^4 M |{\bf{k}}| F_{10}^2\over 128\pi \sin^2 \dfrac{\theta}{2}}, $

(8b) with the occurring GFFs evaluated at zero momentum transfer. For simplicity, hereinafter, we use
$ F_n $ for$ F_n(0) $ .$ F_{10} = 1 $ for any type of composite target particles. The leading-order (LO) term is identical to the cross section obtained from the light-bending angle in classical general relativity [21, 22]. This is intuitively as expected, because, in the soft limit, the long-wavelength graviton can only feel the total mass of the composite target particle, insensitive to any further details about its internal structure. Interestingly, the next-to-leading order (NLO) term still remains universal, which originates from the expansion of the phase factor factor$ {{\bf{k}}'}^2/{\bf{k}}^2 $ to NLO in$ 1/M $ . It is instructive to understand why only a single GFF$ F_{10} $ contributes at NLO from the perspective of effective field theory. We present such analysis in Appendix B.In contrast, at the NNLO in heavy target mass expansion, the differential cross sections start to depend on the target particle spin:
$ \begin{aligned}[b] \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NNLO}^{s} =\;& -\frac{\kappa^4 {\bf{k}}^2}{64\pi \sin^2 \dfrac{\theta}{2}} \left\{{F_{10} F'_{10}}- \frac{1}{2}F_{10}F_{20}\left(1-\cos\theta\right) + \frac{1}{8}F_{10}^2\left[7\cos{\theta}- \frac{2}{3}\left( \frac{21}{2}+s+\lceil s\rceil\right)\right] \right. \\&+\Theta\left(s-\frac{1}{2}\right)\left[ \frac{(-1)^{2s}+7}{24}F_{10}F_{40} -f^{(0)}_s \,F_{40}^2(\cos{\theta}+1)\right] \\ &- \frac{1}{6}\Theta\left(s-1\right) \left[2\cos{\theta}F_{10}F_{50}+F_{10}F_{11} \right] -\left.\Theta\left(s-2\right) \frac{1}{6}F_{10}F_{70}(1+\cos{\theta})\right\}, \qquad s = 0, \frac{1}{2},1, \frac{3}{2},2 \end{aligned} $ 
(9) with
$ f^{(0)}_{\frac{1}{2}} = \frac{1}{16}, $

(10a) $ f^{(0)}_{1} = \frac{1}{6}, $

(10b) $ f^{(0)}_{\frac{3}{2}} = \frac{5}{144}, $

(10c) $ f^{(0)}_{2} = \frac{1}{8}. $

(10d) The
$ F'_{10}F_{10} $ ,$ F_{10} F_{20} $ , and$ F_{10}^2\cos{\theta} $ terms still remain universal, i.e., independent on the target spin. The$ F'_{10}F_{10} $ terms have the same origin of the LO and NLO cross sections, which correspond to a higher-order term in the Taylor expansion of$ F^2_{10}(q^2/M^2) $ in the squared LO amplitude and phase space measure. The GFFs$ F'_{10} $ ,$ F_{11} $ ,$ F_{20} $ , and$ F_{50} $ reflect the mechanical properties of the composite target particles such as the angular momentum [13, 14], pressure, and shear force [14−16]. Our results indicate that, at NNLO in heavy target mass expansion, the cross section starts to depend on the detailed three-dimensional internal structure of the target particle other than its mass. Curiously, the coefficient of the$ F_{10}F_{40} $ term seems to reflect the spin-statistic characteristic of the target particle, which alternates from 1 (fermions) to$ 4/3 $ (bosons). Although we enumerate only five different kinds of target spin, it is conceivable that the aforementioned patterns should be valid for arbitrary target spin. -
The expansion of (6) in powers of
$ 1/M $ shows that the first two terms of the unpolarized cross sections are universal, e.g., independent on the target particle spin:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{LO}^{s} = {\kappa^{4} M^2 F_{10}^2 \over 512 \pi \sin^4 \dfrac{\theta}{2}}, $

(8a) $ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NLO}^{s} = -{ \kappa^4 M |{\bf{k}}| F_{10}^2\over 128\pi \sin^2 \dfrac{\theta}{2}}, $

(8b) with the occurring GFFs evaluated at zero momentum transfer. For simplicity, hereinafter, we use
$ F_n $ for$ F_n(0) $ .$ F_{10} = 1 $ for any type of composite target particles. The leading-order (LO) term is identical to the cross section obtained from the light-bending angle in classical general relativity [21, 22]. This is intuitively as expected, because, in the soft limit, the long-wavelength graviton can only feel the total mass of the composite target particle, insensitive to any further details about its internal structure. Interestingly, the next-to-leading order (NLO) term still remains universal, which originates from the expansion of the phase factor factor$ {{\bf{k}}'}^2/{\bf{k}}^2 $ to NLO in$ 1/M $ . It is instructive to understand why only a single GFF$ F_{10} $ contributes at NLO from the perspective of effective field theory. We present such analysis in Appendix B.In contrast, at the NNLO in heavy target mass expansion, the differential cross sections start to depend on the target particle spin:
$ \begin{aligned}[b] \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NNLO}^{s} =\;& -\frac{\kappa^4 {\bf{k}}^2}{64\pi \sin^2 \dfrac{\theta}{2}} \left\{{F_{10} F'_{10}}- \frac{1}{2}F_{10}F_{20}\left(1-\cos\theta\right) + \frac{1}{8}F_{10}^2\left[7\cos{\theta}- \frac{2}{3}\left( \frac{21}{2}+s+\lceil s\rceil\right)\right] \right. \\&+\Theta\left(s-\frac{1}{2}\right)\left[ \frac{(-1)^{2s}+7}{24}F_{10}F_{40} -f^{(0)}_s \,F_{40}^2(\cos{\theta}+1)\right] \\ &- \frac{1}{6}\Theta\left(s-1\right) \left[2\cos{\theta}F_{10}F_{50}+F_{10}F_{11} \right] -\left.\Theta\left(s-2\right) \frac{1}{6}F_{10}F_{70}(1+\cos{\theta})\right\}, \qquad s = 0, \frac{1}{2},1, \frac{3}{2},2 \end{aligned} $ 
(9) with
$ f^{(0)}_{\frac{1}{2}} = \frac{1}{16}, $

(10a) $ f^{(0)}_{1} = \frac{1}{6}, $

(10b) $ f^{(0)}_{\frac{3}{2}} = \frac{5}{144}, $

(10c) $ f^{(0)}_{2} = \frac{1}{8}. $

(10d) The
$ F'_{10}F_{10} $ ,$ F_{10} F_{20} $ , and$ F_{10}^2\cos{\theta} $ terms still remain universal, i.e., independent on the target spin. The$ F'_{10}F_{10} $ terms have the same origin of the LO and NLO cross sections, which correspond to a higher-order term in the Taylor expansion of$ F^2_{10}(q^2/M^2) $ in the squared LO amplitude and phase space measure. The GFFs$ F'_{10} $ ,$ F_{11} $ ,$ F_{20} $ , and$ F_{50} $ reflect the mechanical properties of the composite target particles such as the angular momentum [13, 14], pressure, and shear force [14−16]. Our results indicate that, at NNLO in heavy target mass expansion, the cross section starts to depend on the detailed three-dimensional internal structure of the target particle other than its mass. Curiously, the coefficient of the$ F_{10}F_{40} $ term seems to reflect the spin-statistic characteristic of the target particle, which alternates from 1 (fermions) to$ 4/3 $ (bosons). Although we enumerate only five different kinds of target spin, it is conceivable that the aforementioned patterns should be valid for arbitrary target spin. -
The expansion of (6) in powers of
$ 1/M $ shows that the first two terms of the unpolarized cross sections are universal, e.g., independent on the target particle spin:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{LO}^{s} = {\kappa^{4} M^2 F_{10}^2 \over 512 \pi \sin^4 \dfrac{\theta}{2}}, $
(8a) $ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NLO}^{s} = -{ \kappa^4 M |{\bf{k}}| F_{10}^2\over 128\pi \sin^2 \dfrac{\theta}{2}}, $
(8b) with the occurring GFFs evaluated at zero momentum transfer. For simplicity, hereinafter, we use
$ F_n $ for$ F_n(0) $ .$ F_{10} = 1 $ for any type of composite target particles. The leading-order (LO) term is identical to the cross section obtained from the light-bending angle in classical general relativity [21, 22]. This is intuitively as expected, because, in the soft limit, the long-wavelength graviton can only feel the total mass of the composite target particle, insensitive to any further details about its internal structure. Interestingly, the next-to-leading order (NLO) term still remains universal, which originates from the expansion of the phase factor factor$ {{\bf{k}}'}^2/{\bf{k}}^2 $ to NLO in$ 1/M $ . It is instructive to understand why only a single GFF$ F_{10} $ contributes at NLO from the perspective of effective field theory. We present such analysis in Appendix B.In contrast, at the NNLO in heavy target mass expansion, the differential cross sections start to depend on the target particle spin:
$ \begin{aligned}[b] \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NNLO}^{s} =\;& -\frac{\kappa^4 {\bf{k}}^2}{64\pi \sin^2 \dfrac{\theta}{2}} \left\{{F_{10} F'_{10}}- \frac{1}{2}F_{10}F_{20}\left(1-\cos\theta\right) + \frac{1}{8}F_{10}^2\left[7\cos{\theta}- \frac{2}{3}\left( \frac{21}{2}+s+\lceil s\rceil\right)\right] \right. \\&+\Theta\left(s-\frac{1}{2}\right)\left[ \frac{(-1)^{2s}+7}{24}F_{10}F_{40} -f^{(0)}_s \,F_{40}^2(\cos{\theta}+1)\right] \\ &- \frac{1}{6}\Theta\left(s-1\right) \left[2\cos{\theta}F_{10}F_{50}+F_{10}F_{11} \right] -\left.\Theta\left(s-2\right) \frac{1}{6}F_{10}F_{70}(1+\cos{\theta})\right\}, \qquad s = 0, \frac{1}{2},1, \frac{3}{2},2 \end{aligned} $ (9) with
$ f^{(0)}_{\frac{1}{2}} = \frac{1}{16}, $
(10a) $ f^{(0)}_{1} = \frac{1}{6}, $
(10b) $ f^{(0)}_{\frac{3}{2}} = \frac{5}{144}, $
(10c) $ f^{(0)}_{2} = \frac{1}{8}. $
(10d) The
$ F'_{10}F_{10} $ ,$ F_{10} F_{20} $ , and$ F_{10}^2\cos{\theta} $ terms still remain universal, i.e., independent on the target spin. The$ F'_{10}F_{10} $ terms have the same origin of the LO and NLO cross sections, which correspond to a higher-order term in the Taylor expansion of$ F^2_{10}(q^2/M^2) $ in the squared LO amplitude and phase space measure. The GFFs$ F'_{10} $ ,$ F_{11} $ ,$ F_{20} $ , and$ F_{50} $ reflect the mechanical properties of the composite target particles such as the angular momentum [13, 14], pressure, and shear force [14−16]. Our results indicate that, at NNLO in heavy target mass expansion, the cross section starts to depend on the detailed three-dimensional internal structure of the target particle other than its mass. Curiously, the coefficient of the$ F_{10}F_{40} $ term seems to reflect the spin-statistic characteristic of the target particle, which alternates from 1 (fermions) to$ 4/3 $ (bosons). Although we enumerate only five different kinds of target spin, it is conceivable that the aforementioned patterns should be valid for arbitrary target spin. -
We can repeat our investigation in Sec. III.A by replacing the projectile with a point-like massless Dirac fermion. After the heavy target mass expansion, we again observe that the unpolarized cross sections exhibit universal forms at LO and NLO in
$ 1/M $ expansion:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{LO}^{s} = {\kappa^{4} M^2 F_{10}^2 \cos^2\dfrac{\theta}{2} \over 512 \pi \sin^4 \dfrac{\theta}{2}}, $
(11a) $ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NLO}^{s} = -{\kappa^4 M |{\bf{k}}| F_{10}^2 \cos^2\dfrac{\theta}{2} \over 128\pi \sin^2 \dfrac{\theta}{2}}. $
(11b) It is worth emphasizing that, although these expressions are independent on the target spin, they are sensitive to the projectile spin. An extra factor
$ \cos^2 \dfrac{\theta}{2} $ appears in the numerators of (11) with respect to (8) in the case of a spinless projectile. In the forward limit$ \theta\approx 0 $ , the occurrence of this extra factor does not lead to a difference. Nevertheless, this extra factor brings a strong suppression of the LO and NLO cross sections around the backward scattering limit ($ \theta\approx \pi $ ) for a spin-${1/2}$ projectile with respect to the spin-0 projectile, as is evident by the comparison of (8) and (11). This feature can be readily understood as, analogous to QED, gravitational interaction also conserves the helicity of a massless matter particle. Therefore, the conservation of angular momentum along the beam direction forbids the backward scattering of a projectile, as the spin of the heavy static target particle cannot be changed by the soft gravitational scattering.As in Sec. III.A, the universality becomes partially violated at NNLO. For various composite target particles with spin ranging from
$ 0 $ to$ 2 $ , the NNLO contributions to the cross sections become$ \begin{aligned}[b] \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NNLO}^{s} =\;& \frac{\kappa^4 {\bf{k}}^2}{64\pi \sin^2 \dfrac{\theta}{2} } \left\{{-F_{10} F'_{10}}\cos^2 \frac{\theta}{2} + \frac{1}{8}F_{10}^2\cos^2\frac{\theta}{2}\left[13\sin^2\frac{\theta}{2}+ \frac{2}{3}\left(s+\lceil s\rceil\right)\right] \right. \\&-\Theta\left(s-\frac{1}{2}\right)\left[ \frac{(-1)^{2s}+7}{24}F_{10}F_{40}\cos^2\frac{\theta}{2} - f^{({1\over 2})}_{s} \, F_{40}^2\left(\cos{2\theta}+8\cos{\theta}+23\right)\right] \\ &\left.+ \frac{1}{6}\Theta\left(s-1\right) F_{10}\left(2F_{50}+F_{11}\right)\cos^2\frac{\theta}{2} +\Theta\left(s-2\right) \frac{1}{3}F_{10}F_{70}\cos^2 \frac{\theta}{2}\right\} ,\qquad s = 0, \frac{1}{2},1, \frac{3}{2},2 \end{aligned}$
(12) with
$ f^{({1\over 2})}_{\frac{1}{2}} = {1\over 256}, $
(13a) $ f^{({1\over 2})}_{1} = {1\over 96}, $
(13b) $ f^{({1\over 2})}_{\frac{3}{2}} = {5\over 2304}, $
(13c) $ f^{({1\over 2})}_{2} = {1\over 128}. $
(13d) Similar to the pattern revealed in the case of a massless spinless projectile, the coefficients of
$ F'_{10}F_{10} $ ,$ F_{10} F_{20} $ , and$ F_{10}^2\sin^2{\dfrac{\theta}{2}}\cos^2{\dfrac{\theta}{2}} $ remain independent on the target spin. The$ F'_{10}F_{10} $ term has the same origin of the LO and NLO cross sections. The coefficient of the$ F_{10}F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
We can repeat our investigation in Sec. III.A by replacing the projectile with a point-like massless Dirac fermion. After the heavy target mass expansion, we again observe that the unpolarized cross sections exhibit universal forms at LO and NLO in
$ 1/M $ expansion:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{LO}^{s} = {\kappa^{4} M^2 F_{10}^2 \cos^2\dfrac{\theta}{2} \over 512 \pi \sin^4 \dfrac{\theta}{2}}, $

(11a) $ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NLO}^{s} = -{\kappa^4 M |{\bf{k}}| F_{10}^2 \cos^2\dfrac{\theta}{2} \over 128\pi \sin^2 \dfrac{\theta}{2}}. $

(11b) It is worth emphasizing that, although these expressions are independent on the target spin, they are sensitive to the projectile spin. An extra factor
$ \cos^2 \dfrac{\theta}{2} $ appears in the numerators of (11) with respect to (8) in the case of a spinless projectile. In the forward limit$ \theta\approx 0 $ , the occurrence of this extra factor does not lead to a difference. Nevertheless, this extra factor brings a strong suppression of the LO and NLO cross sections around the backward scattering limit ($ \theta\approx \pi $ ) for a spin-${1/2}$ projectile with respect to the spin-0 projectile, as is evident by the comparison of (8) and (11). This feature can be readily understood as, analogous to QED, gravitational interaction also conserves the helicity of a massless matter particle. Therefore, the conservation of angular momentum along the beam direction forbids the backward scattering of a projectile, as the spin of the heavy static target particle cannot be changed by the soft gravitational scattering.As in Sec. III.A, the universality becomes partially violated at NNLO. For various composite target particles with spin ranging from
$ 0 $ to$ 2 $ , the NNLO contributions to the cross sections become$ \begin{aligned}[b] \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NNLO}^{s} =\;& \frac{\kappa^4 {\bf{k}}^2}{64\pi \sin^2 \dfrac{\theta}{2} } \left\{{-F_{10} F'_{10}}\cos^2 \frac{\theta}{2} + \frac{1}{8}F_{10}^2\cos^2\frac{\theta}{2}\left[13\sin^2\frac{\theta}{2}+ \frac{2}{3}\left(s+\lceil s\rceil\right)\right] \right. \\&-\Theta\left(s-\frac{1}{2}\right)\left[ \frac{(-1)^{2s}+7}{24}F_{10}F_{40}\cos^2\frac{\theta}{2} - f^{({1\over 2})}_{s} \, F_{40}^2\left(\cos{2\theta}+8\cos{\theta}+23\right)\right] \\ &\left.+ \frac{1}{6}\Theta\left(s-1\right) F_{10}\left(2F_{50}+F_{11}\right)\cos^2\frac{\theta}{2} +\Theta\left(s-2\right) \frac{1}{3}F_{10}F_{70}\cos^2 \frac{\theta}{2}\right\} ,\qquad s = 0, \frac{1}{2},1, \frac{3}{2},2 \end{aligned}$

(12) with
$ f^{({1\over 2})}_{\frac{1}{2}} = {1\over 256}, $

(13a) $ f^{({1\over 2})}_{1} = {1\over 96}, $

(13b) $ f^{({1\over 2})}_{\frac{3}{2}} = {5\over 2304}, $

(13c) $ f^{({1\over 2})}_{2} = {1\over 128}. $

(13d) Similar to the pattern revealed in the case of a massless spinless projectile, the coefficients of
$ F'_{10}F_{10} $ ,$ F_{10} F_{20} $ , and$ F_{10}^2\sin^2{\dfrac{\theta}{2}}\cos^2{\dfrac{\theta}{2}} $ remain independent on the target spin. The$ F'_{10}F_{10} $ term has the same origin of the LO and NLO cross sections. The coefficient of the$ F_{10}F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
We can repeat our investigation in Sec. III.A by replacing the projectile with a point-like massless Dirac fermion. After the heavy target mass expansion, we again observe that the unpolarized cross sections exhibit universal forms at LO and NLO in
$ 1/M $ expansion:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{LO}^{s} = {\kappa^{4} M^2 F_{10}^2 \cos^2\dfrac{\theta}{2} \over 512 \pi \sin^4 \dfrac{\theta}{2}}, $

(11a) $ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NLO}^{s} = -{\kappa^4 M |{\bf{k}}| F_{10}^2 \cos^2\dfrac{\theta}{2} \over 128\pi \sin^2 \dfrac{\theta}{2}}. $

(11b) It is worth emphasizing that, although these expressions are independent on the target spin, they are sensitive to the projectile spin. An extra factor
$ \cos^2 \dfrac{\theta}{2} $ appears in the numerators of (11) with respect to (8) in the case of a spinless projectile. In the forward limit$ \theta\approx 0 $ , the occurrence of this extra factor does not lead to a difference. Nevertheless, this extra factor brings a strong suppression of the LO and NLO cross sections around the backward scattering limit ($ \theta\approx \pi $ ) for a spin-${1/2}$ projectile with respect to the spin-0 projectile, as is evident by the comparison of (8) and (11). This feature can be readily understood as, analogous to QED, gravitational interaction also conserves the helicity of a massless matter particle. Therefore, the conservation of angular momentum along the beam direction forbids the backward scattering of a projectile, as the spin of the heavy static target particle cannot be changed by the soft gravitational scattering.As in Sec. III.A, the universality becomes partially violated at NNLO. For various composite target particles with spin ranging from
$ 0 $ to$ 2 $ , the NNLO contributions to the cross sections become$ \begin{aligned}[b] \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NNLO}^{s} =\;& \frac{\kappa^4 {\bf{k}}^2}{64\pi \sin^2 \dfrac{\theta}{2} } \left\{{-F_{10} F'_{10}}\cos^2 \frac{\theta}{2} + \frac{1}{8}F_{10}^2\cos^2\frac{\theta}{2}\left[13\sin^2\frac{\theta}{2}+ \frac{2}{3}\left(s+\lceil s\rceil\right)\right] \right. \\&-\Theta\left(s-\frac{1}{2}\right)\left[ \frac{(-1)^{2s}+7}{24}F_{10}F_{40}\cos^2\frac{\theta}{2} - f^{({1\over 2})}_{s} \, F_{40}^2\left(\cos{2\theta}+8\cos{\theta}+23\right)\right] \\ &\left.+ \frac{1}{6}\Theta\left(s-1\right) F_{10}\left(2F_{50}+F_{11}\right)\cos^2\frac{\theta}{2} +\Theta\left(s-2\right) \frac{1}{3}F_{10}F_{70}\cos^2 \frac{\theta}{2}\right\} ,\qquad s = 0, \frac{1}{2},1, \frac{3}{2},2 \end{aligned}$

(12) with
$ f^{({1\over 2})}_{\frac{1}{2}} = {1\over 256}, $

(13a) $ f^{({1\over 2})}_{1} = {1\over 96}, $

(13b) $ f^{({1\over 2})}_{\frac{3}{2}} = {5\over 2304}, $

(13c) $ f^{({1\over 2})}_{2} = {1\over 128}. $

(13d) Similar to the pattern revealed in the case of a massless spinless projectile, the coefficients of
$ F'_{10}F_{10} $ ,$ F_{10} F_{20} $ , and$ F_{10}^2\sin^2{\dfrac{\theta}{2}}\cos^2{\dfrac{\theta}{2}} $ remain independent on the target spin. The$ F'_{10}F_{10} $ term has the same origin of the LO and NLO cross sections. The coefficient of the$ F_{10}F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
We can repeat our investigation in Sec. III.A by replacing the projectile with a point-like massless Dirac fermion. After the heavy target mass expansion, we again observe that the unpolarized cross sections exhibit universal forms at LO and NLO in
$ 1/M $ expansion:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{LO}^{s} = {\kappa^{4} M^2 F_{10}^2 \cos^2\dfrac{\theta}{2} \over 512 \pi \sin^4 \dfrac{\theta}{2}}, $

(11a) $ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NLO}^{s} = -{\kappa^4 M |{\bf{k}}| F_{10}^2 \cos^2\dfrac{\theta}{2} \over 128\pi \sin^2 \dfrac{\theta}{2}}. $

(11b) It is worth emphasizing that, although these expressions are independent on the target spin, they are sensitive to the projectile spin. An extra factor
$ \cos^2 \dfrac{\theta}{2} $ appears in the numerators of (11) with respect to (8) in the case of a spinless projectile. In the forward limit$ \theta\approx 0 $ , the occurrence of this extra factor does not lead to a difference. Nevertheless, this extra factor brings a strong suppression of the LO and NLO cross sections around the backward scattering limit ($ \theta\approx \pi $ ) for a spin-${1/2}$ projectile with respect to the spin-0 projectile, as is evident by the comparison of (8) and (11). This feature can be readily understood as, analogous to QED, gravitational interaction also conserves the helicity of a massless matter particle. Therefore, the conservation of angular momentum along the beam direction forbids the backward scattering of a projectile, as the spin of the heavy static target particle cannot be changed by the soft gravitational scattering.As in Sec. III.A, the universality becomes partially violated at NNLO. For various composite target particles with spin ranging from
$ 0 $ to$ 2 $ , the NNLO contributions to the cross sections become$ \begin{aligned}[b] \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NNLO}^{s} =\;& \frac{\kappa^4 {\bf{k}}^2}{64\pi \sin^2 \dfrac{\theta}{2} } \left\{{-F_{10} F'_{10}}\cos^2 \frac{\theta}{2} + \frac{1}{8}F_{10}^2\cos^2\frac{\theta}{2}\left[13\sin^2\frac{\theta}{2}+ \frac{2}{3}\left(s+\lceil s\rceil\right)\right] \right. \\&-\Theta\left(s-\frac{1}{2}\right)\left[ \frac{(-1)^{2s}+7}{24}F_{10}F_{40}\cos^2\frac{\theta}{2} - f^{({1\over 2})}_{s} \, F_{40}^2\left(\cos{2\theta}+8\cos{\theta}+23\right)\right] \\ &\left.+ \frac{1}{6}\Theta\left(s-1\right) F_{10}\left(2F_{50}+F_{11}\right)\cos^2\frac{\theta}{2} +\Theta\left(s-2\right) \frac{1}{3}F_{10}F_{70}\cos^2 \frac{\theta}{2}\right\} ,\qquad s = 0, \frac{1}{2},1, \frac{3}{2},2 \end{aligned}$

(12) with
$ f^{({1\over 2})}_{\frac{1}{2}} = {1\over 256}, $

(13a) $ f^{({1\over 2})}_{1} = {1\over 96}, $

(13b) $ f^{({1\over 2})}_{\frac{3}{2}} = {5\over 2304}, $

(13c) $ f^{({1\over 2})}_{2} = {1\over 128}. $

(13d) Similar to the pattern revealed in the case of a massless spinless projectile, the coefficients of
$ F'_{10}F_{10} $ ,$ F_{10} F_{20} $ , and$ F_{10}^2\sin^2{\dfrac{\theta}{2}}\cos^2{\dfrac{\theta}{2}} $ remain independent on the target spin. The$ F'_{10}F_{10} $ term has the same origin of the LO and NLO cross sections. The coefficient of the$ F_{10}F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
We can repeat the preceding analysis by turning to a massless spin-
$ 1 $ projectile. Upon heavy target mass expansion, analogous to the cases of the spin-0 and spin-${1/2}$ projectiles, we observe a similar universal pattern at LO and NLO:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{LO}^{s} = {\kappa^{4} M^2 F_{10}^2 \cos^4\dfrac{\theta}{2} \over 512 \pi \sin^4 \dfrac{\theta}{2}}, $

(14a) $ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NLO}^{s} = -{\kappa^4 M |{\bf{k}}| F_{10}^2 \cos^4\dfrac{\theta}{2} \over 128\pi \sin^2 \dfrac{\theta}{2}}, $

(14b) except that there appears an extra factor
$ \cos^4 \dfrac{\theta}{2} $ in the numerators with respect to the case of a spinless projectile. In the forward limit$ \theta\approx 0 $ , the emergence of this extra factor does not lead to a difference. Similar to the case of the spin-${1/2}$ projectile, this extra factor brings a stronger suppression of the LO and NLO cross sections near the backward scattering limit ($ \theta\approx \pi $ ) for a spin-$ 1 $ projectile. The reason is the same as explained above. As the gravitational interaction preserves the helicity of a massless spin-1 matter particle (photon), the conservation of angular momentum along the beam direction forbids the backward scattering of the massless projectile.The universality becomes partially violated at NNLO. For a target particle with spin ranging from 0 to 2, the NNLO contributions to the unpolarized cross sections become
$ \begin{aligned}[b] \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NNLO}^{s} =\;& -\frac{\kappa^4 {\bf{k}}^2\cos^2\dfrac{\theta}{2}}{256\pi\sin^2\dfrac{\theta}{2}} \left\{F_{10}^2\cos^2\frac{\theta}{2} \left[3\cos\theta- \frac{1}{3}\left(9-s-\lceil s\rceil\right)\right] +4F_{10}F_{10}'\cos^2\frac{\theta}{2}\right. \\ & +\Theta\left(s-\frac{1}{2}\right)\left[ \frac{(-1)^{2s}+7}{6} F_{10}F_{40}\cos^2 \frac{\theta}{2}+ f^{(1)}_s \, F_{40}^2(\cos{\theta}-3)\right] \\ & \left.- \frac{2}{3}F_{10}\left[\Theta\left(s-1\right)\left(F_{11}+2F_{50}\right)+\Theta\left(s-2\right)2F_{70}\right]\cos^2 \frac{\theta}{2}\right\},\qquad s = 0, \frac{1}{2},1, \frac{3}{2},2 \end{aligned} $

(15) with
$ f^{(1)}_{\frac{1}{2}} = \frac{1}{4}, $

(16a) $ f^{(1)}_{1} = \frac{2}{3}, $

(16b) $ f^{(1)}_{\frac{3}{2}} = \frac{5}{36}, $

(16c) $ f^{(1)}_{2} = \frac{1}{2}. $

(16d) Similar to the projectiles of spin-0 and
${1/2}$ , the coefficients of the$ F'_{10}F_{10} $ ,$ F_{10} F_{20} $ , and$F_{10}^2\cos{\theta}\cos^2{\dfrac{\theta}{2}}$ terms are independent on the target spin. The$ F'_{10}F_{10} $ term has the same origin of the LO and NLO cross sections. Again, the coefficient of the$ F_{10}F_{40} $ term reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
We can repeat the preceding analysis by turning to a massless spin-
$ 1 $ projectile. Upon heavy target mass expansion, analogous to the cases of the spin-0 and spin-${1/2}$ projectiles, we observe a similar universal pattern at LO and NLO:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{LO}^{s} = {\kappa^{4} M^2 F_{10}^2 \cos^4\dfrac{\theta}{2} \over 512 \pi \sin^4 \dfrac{\theta}{2}}, $

(14a) $ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NLO}^{s} = -{\kappa^4 M |{\bf{k}}| F_{10}^2 \cos^4\dfrac{\theta}{2} \over 128\pi \sin^2 \dfrac{\theta}{2}}, $

(14b) except that there appears an extra factor
$ \cos^4 \dfrac{\theta}{2} $ in the numerators with respect to the case of a spinless projectile. In the forward limit$ \theta\approx 0 $ , the emergence of this extra factor does not lead to a difference. Similar to the case of the spin-${1/2}$ projectile, this extra factor brings a stronger suppression of the LO and NLO cross sections near the backward scattering limit ($ \theta\approx \pi $ ) for a spin-$ 1 $ projectile. The reason is the same as explained above. As the gravitational interaction preserves the helicity of a massless spin-1 matter particle (photon), the conservation of angular momentum along the beam direction forbids the backward scattering of the massless projectile.The universality becomes partially violated at NNLO. For a target particle with spin ranging from 0 to 2, the NNLO contributions to the unpolarized cross sections become
$ \begin{aligned}[b] \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NNLO}^{s} =\;& -\frac{\kappa^4 {\bf{k}}^2\cos^2\dfrac{\theta}{2}}{256\pi\sin^2\dfrac{\theta}{2}} \left\{F_{10}^2\cos^2\frac{\theta}{2} \left[3\cos\theta- \frac{1}{3}\left(9-s-\lceil s\rceil\right)\right] +4F_{10}F_{10}'\cos^2\frac{\theta}{2}\right. \\ & +\Theta\left(s-\frac{1}{2}\right)\left[ \frac{(-1)^{2s}+7}{6} F_{10}F_{40}\cos^2 \frac{\theta}{2}+ f^{(1)}_s \, F_{40}^2(\cos{\theta}-3)\right] \\ & \left.- \frac{2}{3}F_{10}\left[\Theta\left(s-1\right)\left(F_{11}+2F_{50}\right)+\Theta\left(s-2\right)2F_{70}\right]\cos^2 \frac{\theta}{2}\right\},\qquad s = 0, \frac{1}{2},1, \frac{3}{2},2 \end{aligned} $

(15) with
$ f^{(1)}_{\frac{1}{2}} = \frac{1}{4}, $

(16a) $ f^{(1)}_{1} = \frac{2}{3}, $

(16b) $ f^{(1)}_{\frac{3}{2}} = \frac{5}{36}, $

(16c) $ f^{(1)}_{2} = \frac{1}{2}. $

(16d) Similar to the projectiles of spin-0 and
${1/2}$ , the coefficients of the$ F'_{10}F_{10} $ ,$ F_{10} F_{20} $ , and$F_{10}^2\cos{\theta}\cos^2{\dfrac{\theta}{2}}$ terms are independent on the target spin. The$ F'_{10}F_{10} $ term has the same origin of the LO and NLO cross sections. Again, the coefficient of the$ F_{10}F_{40} $ term reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
We can repeat the preceding analysis by turning to a massless spin-
$ 1 $ projectile. Upon heavy target mass expansion, analogous to the cases of the spin-0 and spin-${1/2}$ projectiles, we observe a similar universal pattern at LO and NLO:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{LO}^{s} = {\kappa^{4} M^2 F_{10}^2 \cos^4\dfrac{\theta}{2} \over 512 \pi \sin^4 \dfrac{\theta}{2}}, $
(14a) $ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NLO}^{s} = -{\kappa^4 M |{\bf{k}}| F_{10}^2 \cos^4\dfrac{\theta}{2} \over 128\pi \sin^2 \dfrac{\theta}{2}}, $
(14b) except that there appears an extra factor
$ \cos^4 \dfrac{\theta}{2} $ in the numerators with respect to the case of a spinless projectile. In the forward limit$ \theta\approx 0 $ , the emergence of this extra factor does not lead to a difference. Similar to the case of the spin-${1/2}$ projectile, this extra factor brings a stronger suppression of the LO and NLO cross sections near the backward scattering limit ($ \theta\approx \pi $ ) for a spin-$ 1 $ projectile. The reason is the same as explained above. As the gravitational interaction preserves the helicity of a massless spin-1 matter particle (photon), the conservation of angular momentum along the beam direction forbids the backward scattering of the massless projectile.The universality becomes partially violated at NNLO. For a target particle with spin ranging from 0 to 2, the NNLO contributions to the unpolarized cross sections become
$ \begin{aligned}[b] \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NNLO}^{s} =\;& -\frac{\kappa^4 {\bf{k}}^2\cos^2\dfrac{\theta}{2}}{256\pi\sin^2\dfrac{\theta}{2}} \left\{F_{10}^2\cos^2\frac{\theta}{2} \left[3\cos\theta- \frac{1}{3}\left(9-s-\lceil s\rceil\right)\right] +4F_{10}F_{10}'\cos^2\frac{\theta}{2}\right. \\ & +\Theta\left(s-\frac{1}{2}\right)\left[ \frac{(-1)^{2s}+7}{6} F_{10}F_{40}\cos^2 \frac{\theta}{2}+ f^{(1)}_s \, F_{40}^2(\cos{\theta}-3)\right] \\ & \left.- \frac{2}{3}F_{10}\left[\Theta\left(s-1\right)\left(F_{11}+2F_{50}\right)+\Theta\left(s-2\right)2F_{70}\right]\cos^2 \frac{\theta}{2}\right\},\qquad s = 0, \frac{1}{2},1, \frac{3}{2},2 \end{aligned} $
(15) with
$ f^{(1)}_{\frac{1}{2}} = \frac{1}{4}, $
(16a) $ f^{(1)}_{1} = \frac{2}{3}, $
(16b) $ f^{(1)}_{\frac{3}{2}} = \frac{5}{36}, $
(16c) $ f^{(1)}_{2} = \frac{1}{2}. $
(16d) Similar to the projectiles of spin-0 and
${1/2}$ , the coefficients of the$ F'_{10}F_{10} $ ,$ F_{10} F_{20} $ , and$F_{10}^2\cos{\theta}\cos^2{\dfrac{\theta}{2}}$ terms are independent on the target spin. The$ F'_{10}F_{10} $ term has the same origin of the LO and NLO cross sections. Again, the coefficient of the$ F_{10}F_{40} $ term reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
We can repeat the preceding analysis by turning to a massless spin-
$ 1 $ projectile. Upon heavy target mass expansion, analogous to the cases of the spin-0 and spin-${1/2}$ projectiles, we observe a similar universal pattern at LO and NLO:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{LO}^{s} = {\kappa^{4} M^2 F_{10}^2 \cos^4\dfrac{\theta}{2} \over 512 \pi \sin^4 \dfrac{\theta}{2}}, $

(14a) $ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NLO}^{s} = -{\kappa^4 M |{\bf{k}}| F_{10}^2 \cos^4\dfrac{\theta}{2} \over 128\pi \sin^2 \dfrac{\theta}{2}}, $

(14b) except that there appears an extra factor
$ \cos^4 \dfrac{\theta}{2} $ in the numerators with respect to the case of a spinless projectile. In the forward limit$ \theta\approx 0 $ , the emergence of this extra factor does not lead to a difference. Similar to the case of the spin-${1/2}$ projectile, this extra factor brings a stronger suppression of the LO and NLO cross sections near the backward scattering limit ($ \theta\approx \pi $ ) for a spin-$ 1 $ projectile. The reason is the same as explained above. As the gravitational interaction preserves the helicity of a massless spin-1 matter particle (photon), the conservation of angular momentum along the beam direction forbids the backward scattering of the massless projectile.The universality becomes partially violated at NNLO. For a target particle with spin ranging from 0 to 2, the NNLO contributions to the unpolarized cross sections become
$ \begin{aligned}[b] \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)_\text{NNLO}^{s} =\;& -\frac{\kappa^4 {\bf{k}}^2\cos^2\dfrac{\theta}{2}}{256\pi\sin^2\dfrac{\theta}{2}} \left\{F_{10}^2\cos^2\frac{\theta}{2} \left[3\cos\theta- \frac{1}{3}\left(9-s-\lceil s\rceil\right)\right] +4F_{10}F_{10}'\cos^2\frac{\theta}{2}\right. \\ & +\Theta\left(s-\frac{1}{2}\right)\left[ \frac{(-1)^{2s}+7}{6} F_{10}F_{40}\cos^2 \frac{\theta}{2}+ f^{(1)}_s \, F_{40}^2(\cos{\theta}-3)\right] \\ & \left.- \frac{2}{3}F_{10}\left[\Theta\left(s-1\right)\left(F_{11}+2F_{50}\right)+\Theta\left(s-2\right)2F_{70}\right]\cos^2 \frac{\theta}{2}\right\},\qquad s = 0, \frac{1}{2},1, \frac{3}{2},2 \end{aligned} $

(15) with
$ f^{(1)}_{\frac{1}{2}} = \frac{1}{4}, $

(16a) $ f^{(1)}_{1} = \frac{2}{3}, $

(16b) $ f^{(1)}_{\frac{3}{2}} = \frac{5}{36}, $

(16c) $ f^{(1)}_{2} = \frac{1}{2}. $

(16d) Similar to the projectiles of spin-0 and
${1/2}$ , the coefficients of the$ F'_{10}F_{10} $ ,$ F_{10} F_{20} $ , and$F_{10}^2\cos{\theta}\cos^2{\dfrac{\theta}{2}}$ terms are independent on the target spin. The$ F'_{10}F_{10} $ term has the same origin of the LO and NLO cross sections. Again, the coefficient of the$ F_{10}F_{40} $ term reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
In this section, we turn to the original prototype of Rutherford scattering process, i.e., a slowly moving light projectile hits a heavy static target, albeit with the interaction mediated by exchanging a graviton exchange rather than exchanging a photon. We assume that the projectile is a point-like particle with mass
$ m\ll M $ .The differential cross section for the nonrelativistic Rutherford scattering in the laboratory frame is expressed by
$ \begin{aligned}[b]\frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta} =\;& \frac{1}{32\pi M}\left[{p'^0+k'^0\left(1- \frac{|{\bf{k}}|}{|{\bf{k}}'|}\cos\theta\right)}\right]^{-1}\\&\times \frac{|{\bf{k}}'|} {|{\bf{k}}|} {1\over 2j+1} \frac{1}{2s+1}\sum\limits_\text{spins}\left|{\cal{M}}\right|^2, \end{aligned}$

(17) where the projectile bears spin j, and θ denotes the polar angle between the reflected and incident projectile.
Similar to Sec. III, we consider again three different types of projectiles and five different types of targets. The resulting expressions of unpolarized cross sections are generally rather lengthy and unilluminating. As there are three widely separated scales inherent in this process,
$ {\bf{k}}\ll m \ll M $ , the appropriate manner of extracting the soft behavior is to simultaneously expand the differential cross sections in powers of$ v = |{\bf{k}}|/m $ (velocity of the projectile) and$ m/M $ . The necessity of double expansion renders this case more complex than the case of low-energy massless projectile, as discussed in Sec. III.Interestingly, at the lowest order in velocity, yet to all orders in
$ 1/M $ , the differential cross section scale is assumed to have a uniform form:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^{s}_{(v^0)} = \frac{ F_{10}^2 \kappa^4 m^4 M(M+m)^2 \left(\sqrt{M^2-m^2\sin^2\theta}+m \cos\theta\right)^2}{512\pi {\bf{k}}^4\sqrt{M^2-m^2\sin^2\theta}\left(M-\cos\theta \sqrt{M^2-m^2\sin^2\theta}+m \sin^2\theta\right)^2} = \frac{\kappa^4 M^2 m^4 F_{10}^2}{2048\pi{\bf{k}}^4\sin^4\dfrac{\theta}{2}}+ {\cal{O}}\left({m^6\over M^4 {\bf{k}}^4}\right). $

(18) It scales as
$ 1/{\bf{k}}^4 $ , exactly identical to the familiar Rutherford formula obtained from the classical mechanics with the Newtonian's gravitational law [28]. This expression is insensitive to both target and projectile's spins, as the spin degree of freedom decouples in the nonrelativistic limit. This is in contrast to the LO expressions in the case of massless projectile in heavy target mass expansion, which is insensitive to the target spin, yet depends on the projectile spin.At NLO in velocity expansion, the differential cross sections scale as
$ 1/{\bf{k}}^2 $ , whose explicit expressions are still rather complex, yet vary with different projectile and target species. Nevertheless, once the heavy target mass expansion is performed, some clear pattern starts to emerges. Below, we consider three different types of light projectiles with spin ranging from 0 to 1. -
In this section, we turn to the original prototype of Rutherford scattering process, i.e., a slowly moving light projectile hits a heavy static target, albeit with the interaction mediated by exchanging a graviton exchange rather than exchanging a photon. We assume that the projectile is a point-like particle with mass
$ m\ll M $ .The differential cross section for the nonrelativistic Rutherford scattering in the laboratory frame is expressed by
$ \begin{aligned}[b]\frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta} =\;& \frac{1}{32\pi M}\left[{p'^0+k'^0\left(1- \frac{|{\bf{k}}|}{|{\bf{k}}'|}\cos\theta\right)}\right]^{-1}\\&\times \frac{|{\bf{k}}'|} {|{\bf{k}}|} {1\over 2j+1} \frac{1}{2s+1}\sum\limits_\text{spins}\left|{\cal{M}}\right|^2, \end{aligned}$

(17) where the projectile bears spin j, and θ denotes the polar angle between the reflected and incident projectile.
Similar to Sec. III, we consider again three different types of projectiles and five different types of targets. The resulting expressions of unpolarized cross sections are generally rather lengthy and unilluminating. As there are three widely separated scales inherent in this process,
$ {\bf{k}}\ll m \ll M $ , the appropriate manner of extracting the soft behavior is to simultaneously expand the differential cross sections in powers of$ v = |{\bf{k}}|/m $ (velocity of the projectile) and$ m/M $ . The necessity of double expansion renders this case more complex than the case of low-energy massless projectile, as discussed in Sec. III.Interestingly, at the lowest order in velocity, yet to all orders in
$ 1/M $ , the differential cross section scale is assumed to have a uniform form:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^{s}_{(v^0)} = \frac{ F_{10}^2 \kappa^4 m^4 M(M+m)^2 \left(\sqrt{M^2-m^2\sin^2\theta}+m \cos\theta\right)^2}{512\pi {\bf{k}}^4\sqrt{M^2-m^2\sin^2\theta}\left(M-\cos\theta \sqrt{M^2-m^2\sin^2\theta}+m \sin^2\theta\right)^2} = \frac{\kappa^4 M^2 m^4 F_{10}^2}{2048\pi{\bf{k}}^4\sin^4\dfrac{\theta}{2}}+ {\cal{O}}\left({m^6\over M^4 {\bf{k}}^4}\right). $

(18) It scales as
$ 1/{\bf{k}}^4 $ , exactly identical to the familiar Rutherford formula obtained from the classical mechanics with the Newtonian's gravitational law [28]. This expression is insensitive to both target and projectile's spins, as the spin degree of freedom decouples in the nonrelativistic limit. This is in contrast to the LO expressions in the case of massless projectile in heavy target mass expansion, which is insensitive to the target spin, yet depends on the projectile spin.At NLO in velocity expansion, the differential cross sections scale as
$ 1/{\bf{k}}^2 $ , whose explicit expressions are still rather complex, yet vary with different projectile and target species. Nevertheless, once the heavy target mass expansion is performed, some clear pattern starts to emerges. Below, we consider three different types of light projectiles with spin ranging from 0 to 1. -
In this section, we turn to the original prototype of Rutherford scattering process, i.e., a slowly moving light projectile hits a heavy static target, albeit with the interaction mediated by exchanging a graviton exchange rather than exchanging a photon. We assume that the projectile is a point-like particle with mass
$ m\ll M $ .The differential cross section for the nonrelativistic Rutherford scattering in the laboratory frame is expressed by
$ \begin{aligned}[b]\frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta} =\;& \frac{1}{32\pi M}\left[{p'^0+k'^0\left(1- \frac{|{\bf{k}}|}{|{\bf{k}}'|}\cos\theta\right)}\right]^{-1}\\&\times \frac{|{\bf{k}}'|} {|{\bf{k}}|} {1\over 2j+1} \frac{1}{2s+1}\sum\limits_\text{spins}\left|{\cal{M}}\right|^2, \end{aligned}$

(17) where the projectile bears spin j, and θ denotes the polar angle between the reflected and incident projectile.
Similar to Sec. III, we consider again three different types of projectiles and five different types of targets. The resulting expressions of unpolarized cross sections are generally rather lengthy and unilluminating. As there are three widely separated scales inherent in this process,
$ {\bf{k}}\ll m \ll M $ , the appropriate manner of extracting the soft behavior is to simultaneously expand the differential cross sections in powers of$ v = |{\bf{k}}|/m $ (velocity of the projectile) and$ m/M $ . The necessity of double expansion renders this case more complex than the case of low-energy massless projectile, as discussed in Sec. III.Interestingly, at the lowest order in velocity, yet to all orders in
$ 1/M $ , the differential cross section scale is assumed to have a uniform form:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^{s}_{(v^0)} = \frac{ F_{10}^2 \kappa^4 m^4 M(M+m)^2 \left(\sqrt{M^2-m^2\sin^2\theta}+m \cos\theta\right)^2}{512\pi {\bf{k}}^4\sqrt{M^2-m^2\sin^2\theta}\left(M-\cos\theta \sqrt{M^2-m^2\sin^2\theta}+m \sin^2\theta\right)^2} = \frac{\kappa^4 M^2 m^4 F_{10}^2}{2048\pi{\bf{k}}^4\sin^4\dfrac{\theta}{2}}+ {\cal{O}}\left({m^6\over M^4 {\bf{k}}^4}\right). $

(18) It scales as
$ 1/{\bf{k}}^4 $ , exactly identical to the familiar Rutherford formula obtained from the classical mechanics with the Newtonian's gravitational law [28]. This expression is insensitive to both target and projectile's spins, as the spin degree of freedom decouples in the nonrelativistic limit. This is in contrast to the LO expressions in the case of massless projectile in heavy target mass expansion, which is insensitive to the target spin, yet depends on the projectile spin.At NLO in velocity expansion, the differential cross sections scale as
$ 1/{\bf{k}}^2 $ , whose explicit expressions are still rather complex, yet vary with different projectile and target species. Nevertheless, once the heavy target mass expansion is performed, some clear pattern starts to emerges. Below, we consider three different types of light projectiles with spin ranging from 0 to 1. -
In this section, we turn to the original prototype of Rutherford scattering process, i.e., a slowly moving light projectile hits a heavy static target, albeit with the interaction mediated by exchanging a graviton exchange rather than exchanging a photon. We assume that the projectile is a point-like particle with mass
$ m\ll M $ .The differential cross section for the nonrelativistic Rutherford scattering in the laboratory frame is expressed by
$ \begin{aligned}[b]\frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta} =\;& \frac{1}{32\pi M}\left[{p'^0+k'^0\left(1- \frac{|{\bf{k}}|}{|{\bf{k}}'|}\cos\theta\right)}\right]^{-1}\\&\times \frac{|{\bf{k}}'|} {|{\bf{k}}|} {1\over 2j+1} \frac{1}{2s+1}\sum\limits_\text{spins}\left|{\cal{M}}\right|^2, \end{aligned}$
(17) where the projectile bears spin j, and θ denotes the polar angle between the reflected and incident projectile.
Similar to Sec. III, we consider again three different types of projectiles and five different types of targets. The resulting expressions of unpolarized cross sections are generally rather lengthy and unilluminating. As there are three widely separated scales inherent in this process,
$ {\bf{k}}\ll m \ll M $ , the appropriate manner of extracting the soft behavior is to simultaneously expand the differential cross sections in powers of$ v = |{\bf{k}}|/m $ (velocity of the projectile) and$ m/M $ . The necessity of double expansion renders this case more complex than the case of low-energy massless projectile, as discussed in Sec. III.Interestingly, at the lowest order in velocity, yet to all orders in
$ 1/M $ , the differential cross section scale is assumed to have a uniform form:$ \left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^{s}_{(v^0)} = \frac{ F_{10}^2 \kappa^4 m^4 M(M+m)^2 \left(\sqrt{M^2-m^2\sin^2\theta}+m \cos\theta\right)^2}{512\pi {\bf{k}}^4\sqrt{M^2-m^2\sin^2\theta}\left(M-\cos\theta \sqrt{M^2-m^2\sin^2\theta}+m \sin^2\theta\right)^2} = \frac{\kappa^4 M^2 m^4 F_{10}^2}{2048\pi{\bf{k}}^4\sin^4\dfrac{\theta}{2}}+ {\cal{O}}\left({m^6\over M^4 {\bf{k}}^4}\right). $
(18) It scales as
$ 1/{\bf{k}}^4 $ , exactly identical to the familiar Rutherford formula obtained from the classical mechanics with the Newtonian's gravitational law [28]. This expression is insensitive to both target and projectile's spins, as the spin degree of freedom decouples in the nonrelativistic limit. This is in contrast to the LO expressions in the case of massless projectile in heavy target mass expansion, which is insensitive to the target spin, yet depends on the projectile spin.At NLO in velocity expansion, the differential cross sections scale as
$ 1/{\bf{k}}^2 $ , whose explicit expressions are still rather complex, yet vary with different projectile and target species. Nevertheless, once the heavy target mass expansion is performed, some clear pattern starts to emerges. Below, we consider three different types of light projectiles with spin ranging from 0 to 1. -
At relative order-
$ v^2 $ , after the heavy target mass expansion, the differential unpolarized cross section becomes particularly simple:$ \begin{aligned}[b]\left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^s_{(v^2)} =\;& {\kappa^4 M^2 m^2 F_{10} \over 256\pi {\bf{k}}^2 \sin^2\dfrac{\theta}{2}}\\&\times\left[ \frac{F_{10}}{2\sin^2\dfrac{\theta}{2}}- {m\over M} F_{10} + {m^2\over M^2} g^{(0)}_s +\cdots \right], \end{aligned}$

(19) with
$\begin{aligned}[b] g^{(0)}_s =\;& -F_{20}-F'_{10} + \frac{F_{10}}{4}\left[ \frac{1}{3}\left(3+s+\lceil s\rceil\right)-2\cos\theta\right] \\&-\Theta\left(s-\frac{1}{2}\right) \frac{1}{24}\left[(-1)^{2s}+7\right]F_{40} \\ & +\Theta\left(s-1\right)\left(\frac{1}{6}F_{11}+F_{50}\right) +\Theta\left(s-2\right) \frac{2}{3}F_{70}, \\& s = 0, \frac{1}{2},1, \frac{3}{2},2. \end{aligned} $

(20) where the
$ {\cal{O}}(v^2/M^n) $ ($ n = 0,1 $ ) terms remain independent on the target spin. At$ {\cal{O}}(v^2/M^2) $ , the universality becomes partially violated. Nevertheless, the$ F'_{10} $ ,$ F_{20} $ , and$ F_{10}\cos\theta $ terms still do not depend on the target particle spin. The coefficient of the$ F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
At relative order-
$ v^2 $ , after the heavy target mass expansion, the differential unpolarized cross section becomes particularly simple:$ \begin{aligned}[b]\left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^s_{(v^2)} =\;& {\kappa^4 M^2 m^2 F_{10} \over 256\pi {\bf{k}}^2 \sin^2\dfrac{\theta}{2}}\\&\times\left[ \frac{F_{10}}{2\sin^2\dfrac{\theta}{2}}- {m\over M} F_{10} + {m^2\over M^2} g^{(0)}_s +\cdots \right], \end{aligned}$

(19) with
$\begin{aligned}[b] g^{(0)}_s =\;& -F_{20}-F'_{10} + \frac{F_{10}}{4}\left[ \frac{1}{3}\left(3+s+\lceil s\rceil\right)-2\cos\theta\right] \\&-\Theta\left(s-\frac{1}{2}\right) \frac{1}{24}\left[(-1)^{2s}+7\right]F_{40} \\ & +\Theta\left(s-1\right)\left(\frac{1}{6}F_{11}+F_{50}\right) +\Theta\left(s-2\right) \frac{2}{3}F_{70}, \\& s = 0, \frac{1}{2},1, \frac{3}{2},2. \end{aligned} $

(20) where the
$ {\cal{O}}(v^2/M^n) $ ($ n = 0,1 $ ) terms remain independent on the target spin. At$ {\cal{O}}(v^2/M^2) $ , the universality becomes partially violated. Nevertheless, the$ F'_{10} $ ,$ F_{20} $ , and$ F_{10}\cos\theta $ terms still do not depend on the target particle spin. The coefficient of the$ F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
At relative order-
$ v^2 $ , after the heavy target mass expansion, the differential unpolarized cross section becomes particularly simple:$ \begin{aligned}[b]\left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^s_{(v^2)} =\;& {\kappa^4 M^2 m^2 F_{10} \over 256\pi {\bf{k}}^2 \sin^2\dfrac{\theta}{2}}\\&\times\left[ \frac{F_{10}}{2\sin^2\dfrac{\theta}{2}}- {m\over M} F_{10} + {m^2\over M^2} g^{(0)}_s +\cdots \right], \end{aligned}$
(19) with
$\begin{aligned}[b] g^{(0)}_s =\;& -F_{20}-F'_{10} + \frac{F_{10}}{4}\left[ \frac{1}{3}\left(3+s+\lceil s\rceil\right)-2\cos\theta\right] \\&-\Theta\left(s-\frac{1}{2}\right) \frac{1}{24}\left[(-1)^{2s}+7\right]F_{40} \\ & +\Theta\left(s-1\right)\left(\frac{1}{6}F_{11}+F_{50}\right) +\Theta\left(s-2\right) \frac{2}{3}F_{70}, \\& s = 0, \frac{1}{2},1, \frac{3}{2},2. \end{aligned} $
(20) where the
$ {\cal{O}}(v^2/M^n) $ ($ n = 0,1 $ ) terms remain independent on the target spin. At$ {\cal{O}}(v^2/M^2) $ , the universality becomes partially violated. Nevertheless, the$ F'_{10} $ ,$ F_{20} $ , and$ F_{10}\cos\theta $ terms still do not depend on the target particle spin. The coefficient of the$ F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
At relative order-
$ v^2 $ , after the heavy target mass expansion, the differential unpolarized cross section becomes particularly simple:$ \begin{aligned}[b]\left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^s_{(v^2)} =\;& {\kappa^4 M^2 m^2 F_{10} \over 256\pi {\bf{k}}^2 \sin^2\dfrac{\theta}{2}}\\&\times\left[ \frac{F_{10}}{2\sin^2\dfrac{\theta}{2}}- {m\over M} F_{10} + {m^2\over M^2} g^{(0)}_s +\cdots \right], \end{aligned}$

(19) with
$\begin{aligned}[b] g^{(0)}_s =\;& -F_{20}-F'_{10} + \frac{F_{10}}{4}\left[ \frac{1}{3}\left(3+s+\lceil s\rceil\right)-2\cos\theta\right] \\&-\Theta\left(s-\frac{1}{2}\right) \frac{1}{24}\left[(-1)^{2s}+7\right]F_{40} \\ & +\Theta\left(s-1\right)\left(\frac{1}{6}F_{11}+F_{50}\right) +\Theta\left(s-2\right) \frac{2}{3}F_{70}, \\& s = 0, \frac{1}{2},1, \frac{3}{2},2. \end{aligned} $

(20) where the
$ {\cal{O}}(v^2/M^n) $ ($ n = 0,1 $ ) terms remain independent on the target spin. At$ {\cal{O}}(v^2/M^2) $ , the universality becomes partially violated. Nevertheless, the$ F'_{10} $ ,$ F_{20} $ , and$ F_{10}\cos\theta $ terms still do not depend on the target particle spin. The coefficient of the$ F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
We can repeat our investigation by replacing the projectile with a slowly moving Dirac fermion. The
$ {\cal{O}}(v^0) $ cross section is expressed by (18), as the spin degree of freedom decouples in the nonrelativistic limit. At relative order-$ v^2 $ , after the heavy target mass expansion, the differential cross section again possesses a simple form:$ \begin{aligned}[b]\left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^{s}_{(v^2)} =\;& \frac{\kappa^4 M^2 m^2 F_{10}}{256\pi {\bf{k}}^2 \sin^2\dfrac{\theta}{2}}\Bigg[\frac{F_{10}}{16} \frac{3\cos{\theta}+5}{\sin^2\frac{\theta}{2}}\\&-\frac{m F_{10}}{8 M} (3\cos{\theta}+5)-{ m^2\over M^2 } g^{({1\over 2})}_s +\cdots \Bigg],\end{aligned} $

(21) with
$\begin{aligned}[b] g^{({1\over 2})}_s =\;& { F'_{10}}+F_{20} + \frac{1}{48}F_{10}\left[15\cos{\theta}-4\left( \frac{3}{4}+s+\lceil s\rceil\right)\right] \\&+\Theta\left(s-\frac{1}{2}\right) \frac{1}{24}\left[(-1)^{2s}+7\right]F_{40} \\ & -\Theta\left(s-1\right) \left(F_{50}+ \frac{1}{6}F_{11} \right) -\Theta\left(s-2\right) \frac{2}{3}F_{70},\\& s = 0, \frac{1}{2},1, \frac{3}{2},2. \end{aligned} $

(22) where the
$ {\cal{O}}(v^2/M^n) $ ($ n = 0,1 $ ) terms remain universal. The universality has been partially violated in the$ {\cal{O}}(v^2/M^2) $ term. However, even at this order, the$ F'_{10} $ ,$ F_{20} $ , and$ F_{10}\cos\theta $ terms still appear to be independent on the target particle spin. The coefficient of the$ F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
We can repeat our investigation by replacing the projectile with a slowly moving Dirac fermion. The
$ {\cal{O}}(v^0) $ cross section is expressed by (18), as the spin degree of freedom decouples in the nonrelativistic limit. At relative order-$ v^2 $ , after the heavy target mass expansion, the differential cross section again possesses a simple form:$ \begin{aligned}[b]\left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^{s}_{(v^2)} =\;& \frac{\kappa^4 M^2 m^2 F_{10}}{256\pi {\bf{k}}^2 \sin^2\dfrac{\theta}{2}}\Bigg[\frac{F_{10}}{16} \frac{3\cos{\theta}+5}{\sin^2\frac{\theta}{2}}\\&-\frac{m F_{10}}{8 M} (3\cos{\theta}+5)-{ m^2\over M^2 } g^{({1\over 2})}_s +\cdots \Bigg],\end{aligned} $

(21) with
$\begin{aligned}[b] g^{({1\over 2})}_s =\;& { F'_{10}}+F_{20} + \frac{1}{48}F_{10}\left[15\cos{\theta}-4\left( \frac{3}{4}+s+\lceil s\rceil\right)\right] \\&+\Theta\left(s-\frac{1}{2}\right) \frac{1}{24}\left[(-1)^{2s}+7\right]F_{40} \\ & -\Theta\left(s-1\right) \left(F_{50}+ \frac{1}{6}F_{11} \right) -\Theta\left(s-2\right) \frac{2}{3}F_{70},\\& s = 0, \frac{1}{2},1, \frac{3}{2},2. \end{aligned} $

(22) where the
$ {\cal{O}}(v^2/M^n) $ ($ n = 0,1 $ ) terms remain universal. The universality has been partially violated in the$ {\cal{O}}(v^2/M^2) $ term. However, even at this order, the$ F'_{10} $ ,$ F_{20} $ , and$ F_{10}\cos\theta $ terms still appear to be independent on the target particle spin. The coefficient of the$ F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
We can repeat our investigation by replacing the projectile with a slowly moving Dirac fermion. The
$ {\cal{O}}(v^0) $ cross section is expressed by (18), as the spin degree of freedom decouples in the nonrelativistic limit. At relative order-$ v^2 $ , after the heavy target mass expansion, the differential cross section again possesses a simple form:$ \begin{aligned}[b]\left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^{s}_{(v^2)} =\;& \frac{\kappa^4 M^2 m^2 F_{10}}{256\pi {\bf{k}}^2 \sin^2\dfrac{\theta}{2}}\Bigg[\frac{F_{10}}{16} \frac{3\cos{\theta}+5}{\sin^2\frac{\theta}{2}}\\&-\frac{m F_{10}}{8 M} (3\cos{\theta}+5)-{ m^2\over M^2 } g^{({1\over 2})}_s +\cdots \Bigg],\end{aligned} $

(21) with
$\begin{aligned}[b] g^{({1\over 2})}_s =\;& { F'_{10}}+F_{20} + \frac{1}{48}F_{10}\left[15\cos{\theta}-4\left( \frac{3}{4}+s+\lceil s\rceil\right)\right] \\&+\Theta\left(s-\frac{1}{2}\right) \frac{1}{24}\left[(-1)^{2s}+7\right]F_{40} \\ & -\Theta\left(s-1\right) \left(F_{50}+ \frac{1}{6}F_{11} \right) -\Theta\left(s-2\right) \frac{2}{3}F_{70},\\& s = 0, \frac{1}{2},1, \frac{3}{2},2. \end{aligned} $

(22) where the
$ {\cal{O}}(v^2/M^n) $ ($ n = 0,1 $ ) terms remain universal. The universality has been partially violated in the$ {\cal{O}}(v^2/M^2) $ term. However, even at this order, the$ F'_{10} $ ,$ F_{20} $ , and$ F_{10}\cos\theta $ terms still appear to be independent on the target particle spin. The coefficient of the$ F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
We can repeat our investigation by replacing the projectile with a slowly moving Dirac fermion. The
$ {\cal{O}}(v^0) $ cross section is expressed by (18), as the spin degree of freedom decouples in the nonrelativistic limit. At relative order-$ v^2 $ , after the heavy target mass expansion, the differential cross section again possesses a simple form:$ \begin{aligned}[b]\left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^{s}_{(v^2)} =\;& \frac{\kappa^4 M^2 m^2 F_{10}}{256\pi {\bf{k}}^2 \sin^2\dfrac{\theta}{2}}\Bigg[\frac{F_{10}}{16} \frac{3\cos{\theta}+5}{\sin^2\frac{\theta}{2}}\\&-\frac{m F_{10}}{8 M} (3\cos{\theta}+5)-{ m^2\over M^2 } g^{({1\over 2})}_s +\cdots \Bigg],\end{aligned} $
(21) with
$\begin{aligned}[b] g^{({1\over 2})}_s =\;& { F'_{10}}+F_{20} + \frac{1}{48}F_{10}\left[15\cos{\theta}-4\left( \frac{3}{4}+s+\lceil s\rceil\right)\right] \\&+\Theta\left(s-\frac{1}{2}\right) \frac{1}{24}\left[(-1)^{2s}+7\right]F_{40} \\ & -\Theta\left(s-1\right) \left(F_{50}+ \frac{1}{6}F_{11} \right) -\Theta\left(s-2\right) \frac{2}{3}F_{70},\\& s = 0, \frac{1}{2},1, \frac{3}{2},2. \end{aligned} $
(22) where the
$ {\cal{O}}(v^2/M^n) $ ($ n = 0,1 $ ) terms remain universal. The universality has been partially violated in the$ {\cal{O}}(v^2/M^2) $ term. However, even at this order, the$ F'_{10} $ ,$ F_{20} $ , and$ F_{10}\cos\theta $ terms still appear to be independent on the target particle spin. The coefficient of the$ F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
As a final example, we consider a slowly moving light spin-
$ 1 $ projectile. The$ {\cal{O}}(v^0) $ differential cross section is again described by (18). At relative order-$ v^2 $ , after the heavy target mass expansion, the expanded differential cross sections bear the following structure:$ \begin{aligned}[b]\left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^s_{(v^2)} =\;& \frac{\kappa^4 M^2 m^2 F_{10}}{1536\pi {\bf{k}}^2 \sin^2\dfrac{\theta}{2}} \Bigg[ \frac{F_{10}\left(2\cos\theta+1\right)}{\sin^2\dfrac{\theta}{2}}\\&-{2m\over M} \left(2\cos\theta+1\right) F_{10} -{m^2\over M^2} g^{(1)}_s +\cdots \Bigg],\end{aligned} $

(23) where
$\begin{aligned}[b] g^{(1)}_s =\;& F_{10}\left[\cos\theta+ \frac{1}{2}\left(1-s-\lceil s\rceil\right)\right]+6F_{10}'+6F_{20}\\&+\Theta\left(s-\frac{1}{2}\right) \frac{1}{4}\left[(-1)^{2s}+7\right]F_{40} \\ & -\Theta\left(s-1\right)\left(F_{11}-6F_{50}\right)-\Theta(s-2)4F_{70}, \\& s = 0, \frac{1}{2},1, \frac{3}{2},2. \end{aligned}$

(24) The
$ {\cal{O}}(v^2/M^n) $ ($ n = 0,1 $ ) terms remain universal. At$ {\cal{O}}(v^2/M^2) $ , the universality becomes partially violated, though the$ F'_{10} $ ,$ F_{20} $ , and$ F_{10}\cos\theta $ terms still do not depend on the target spin. The coefficient of the$ F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
As a final example, we consider a slowly moving light spin-
$ 1 $ projectile. The$ {\cal{O}}(v^0) $ differential cross section is again described by (18). At relative order-$ v^2 $ , after the heavy target mass expansion, the expanded differential cross sections bear the following structure:$ \begin{aligned}[b]\left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^s_{(v^2)} =\;& \frac{\kappa^4 M^2 m^2 F_{10}}{1536\pi {\bf{k}}^2 \sin^2\dfrac{\theta}{2}} \Bigg[ \frac{F_{10}\left(2\cos\theta+1\right)}{\sin^2\dfrac{\theta}{2}}\\&-{2m\over M} \left(2\cos\theta+1\right) F_{10} -{m^2\over M^2} g^{(1)}_s +\cdots \Bigg],\end{aligned} $

(23) where
$\begin{aligned}[b] g^{(1)}_s =\;& F_{10}\left[\cos\theta+ \frac{1}{2}\left(1-s-\lceil s\rceil\right)\right]+6F_{10}'+6F_{20}\\&+\Theta\left(s-\frac{1}{2}\right) \frac{1}{4}\left[(-1)^{2s}+7\right]F_{40} \\ & -\Theta\left(s-1\right)\left(F_{11}-6F_{50}\right)-\Theta(s-2)4F_{70}, \\& s = 0, \frac{1}{2},1, \frac{3}{2},2. \end{aligned}$

(24) The
$ {\cal{O}}(v^2/M^n) $ ($ n = 0,1 $ ) terms remain universal. At$ {\cal{O}}(v^2/M^2) $ , the universality becomes partially violated, though the$ F'_{10} $ ,$ F_{20} $ , and$ F_{10}\cos\theta $ terms still do not depend on the target spin. The coefficient of the$ F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
As a final example, we consider a slowly moving light spin-
$ 1 $ projectile. The$ {\cal{O}}(v^0) $ differential cross section is again described by (18). At relative order-$ v^2 $ , after the heavy target mass expansion, the expanded differential cross sections bear the following structure:$ \begin{aligned}[b]\left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^s_{(v^2)} =\;& \frac{\kappa^4 M^2 m^2 F_{10}}{1536\pi {\bf{k}}^2 \sin^2\dfrac{\theta}{2}} \Bigg[ \frac{F_{10}\left(2\cos\theta+1\right)}{\sin^2\dfrac{\theta}{2}}\\&-{2m\over M} \left(2\cos\theta+1\right) F_{10} -{m^2\over M^2} g^{(1)}_s +\cdots \Bigg],\end{aligned} $
(23) where
$\begin{aligned}[b] g^{(1)}_s =\;& F_{10}\left[\cos\theta+ \frac{1}{2}\left(1-s-\lceil s\rceil\right)\right]+6F_{10}'+6F_{20}\\&+\Theta\left(s-\frac{1}{2}\right) \frac{1}{4}\left[(-1)^{2s}+7\right]F_{40} \\ & -\Theta\left(s-1\right)\left(F_{11}-6F_{50}\right)-\Theta(s-2)4F_{70}, \\& s = 0, \frac{1}{2},1, \frac{3}{2},2. \end{aligned}$
(24) The
$ {\cal{O}}(v^2/M^n) $ ($ n = 0,1 $ ) terms remain universal. At$ {\cal{O}}(v^2/M^2) $ , the universality becomes partially violated, though the$ F'_{10} $ ,$ F_{20} $ , and$ F_{10}\cos\theta $ terms still do not depend on the target spin. The coefficient of the$ F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
As a final example, we consider a slowly moving light spin-
$ 1 $ projectile. The$ {\cal{O}}(v^0) $ differential cross section is again described by (18). At relative order-$ v^2 $ , after the heavy target mass expansion, the expanded differential cross sections bear the following structure:$ \begin{aligned}[b]\left( \frac{\mathrm{d}\sigma}{\mathrm{d}\cos\theta}\right)^s_{(v^2)} =\;& \frac{\kappa^4 M^2 m^2 F_{10}}{1536\pi {\bf{k}}^2 \sin^2\dfrac{\theta}{2}} \Bigg[ \frac{F_{10}\left(2\cos\theta+1\right)}{\sin^2\dfrac{\theta}{2}}\\&-{2m\over M} \left(2\cos\theta+1\right) F_{10} -{m^2\over M^2} g^{(1)}_s +\cdots \Bigg],\end{aligned} $

(23) where
$\begin{aligned}[b] g^{(1)}_s =\;& F_{10}\left[\cos\theta+ \frac{1}{2}\left(1-s-\lceil s\rceil\right)\right]+6F_{10}'+6F_{20}\\&+\Theta\left(s-\frac{1}{2}\right) \frac{1}{4}\left[(-1)^{2s}+7\right]F_{40} \\ & -\Theta\left(s-1\right)\left(F_{11}-6F_{50}\right)-\Theta(s-2)4F_{70}, \\& s = 0, \frac{1}{2},1, \frac{3}{2},2. \end{aligned}$

(24) The
$ {\cal{O}}(v^2/M^n) $ ($ n = 0,1 $ ) terms remain universal. At$ {\cal{O}}(v^2/M^2) $ , the universality becomes partially violated, though the$ F'_{10} $ ,$ F_{20} $ , and$ F_{10}\cos\theta $ terms still do not depend on the target spin. The coefficient of the$ F_{40} $ term again reflects the spin-statistic characteristic of the target particle, which alternates from$ 1 $ (fermions) to$ 4/3 $ (bosons). -
We conducted a comprehensive study on the soft pattern of the tree-level gravitational Rutherford scattering processes. Two classes of Rutherford scattering processes were considered: a low-energy massless projectile strikes on a static, heavy, composite target carrying spin up to 2, and slowly moving light structureless projectile bombs on a static, heavy, spinning composite target particle.
The soft limits of both classes of gravitational Rutherford scattering processes have exhibited some universal and simple patterns. For the former type, given a massless projectile with certain spin, the first two terms in the heavy target mass expansion remain universal, and the NNLO term starts to develop target spin dependence. Nevertheless, several terms at NNLO still remain universal or have some definite pattern of dependence on the target spin. For the latter, we have to carry out the double expansion in projectile velocity and
$ 1/M $ to identify a simple soft limit. At the lowest order in v, yet to all orders in$ 1/M $ , the differential cross section has a universal form, insensitive to both projectile and target spin. At the relative order-$ v^2 $ , the first two terms in$ 1/M $ expansion are still independent on the target spin. The universality starts to be partially violated in the$ {\cal{O}}(v^2/M^2) $ part, though some terms at this order still remain independent on the target spin, or bears a definite pattern of target spin dependence.It is curious that, at NNLO in heavy target mass expansion, the prefactors of the
$ F_{40} = s $ term in both types of gravitational Rutherford scattering processes encapsulate some peculiar spin-statistics characteristic, which alternate from a constant for a fermionic target to another constant for a bosonic target. It is of interest to examine whether this pattern is valid for a composite target with arbitrarily high spin. -
We conducted a comprehensive study on the soft pattern of the tree-level gravitational Rutherford scattering processes. Two classes of Rutherford scattering processes were considered: a low-energy massless projectile strikes on a static, heavy, composite target carrying spin up to 2, and slowly moving light structureless projectile bombs on a static, heavy, spinning composite target particle.
The soft limits of both classes of gravitational Rutherford scattering processes have exhibited some universal and simple patterns. For the former type, given a massless projectile with certain spin, the first two terms in the heavy target mass expansion remain universal, and the NNLO term starts to develop target spin dependence. Nevertheless, several terms at NNLO still remain universal or have some definite pattern of dependence on the target spin. For the latter, we have to carry out the double expansion in projectile velocity and
$ 1/M $ to identify a simple soft limit. At the lowest order in v, yet to all orders in$ 1/M $ , the differential cross section has a universal form, insensitive to both projectile and target spin. At the relative order-$ v^2 $ , the first two terms in$ 1/M $ expansion are still independent on the target spin. The universality starts to be partially violated in the$ {\cal{O}}(v^2/M^2) $ part, though some terms at this order still remain independent on the target spin, or bears a definite pattern of target spin dependence.It is curious that, at NNLO in heavy target mass expansion, the prefactors of the
$ F_{40} = s $ term in both types of gravitational Rutherford scattering processes encapsulate some peculiar spin-statistics characteristic, which alternate from a constant for a fermionic target to another constant for a bosonic target. It is of interest to examine whether this pattern is valid for a composite target with arbitrarily high spin. -
We conducted a comprehensive study on the soft pattern of the tree-level gravitational Rutherford scattering processes. Two classes of Rutherford scattering processes were considered: a low-energy massless projectile strikes on a static, heavy, composite target carrying spin up to 2, and slowly moving light structureless projectile bombs on a static, heavy, spinning composite target particle.
The soft limits of both classes of gravitational Rutherford scattering processes have exhibited some universal and simple patterns. For the former type, given a massless projectile with certain spin, the first two terms in the heavy target mass expansion remain universal, and the NNLO term starts to develop target spin dependence. Nevertheless, several terms at NNLO still remain universal or have some definite pattern of dependence on the target spin. For the latter, we have to carry out the double expansion in projectile velocity and
$ 1/M $ to identify a simple soft limit. At the lowest order in v, yet to all orders in$ 1/M $ , the differential cross section has a universal form, insensitive to both projectile and target spin. At the relative order-$ v^2 $ , the first two terms in$ 1/M $ expansion are still independent on the target spin. The universality starts to be partially violated in the$ {\cal{O}}(v^2/M^2) $ part, though some terms at this order still remain independent on the target spin, or bears a definite pattern of target spin dependence.It is curious that, at NNLO in heavy target mass expansion, the prefactors of the
$ F_{40} = s $ term in both types of gravitational Rutherford scattering processes encapsulate some peculiar spin-statistics characteristic, which alternate from a constant for a fermionic target to another constant for a bosonic target. It is of interest to examine whether this pattern is valid for a composite target with arbitrarily high spin. -
We conducted a comprehensive study on the soft pattern of the tree-level gravitational Rutherford scattering processes. Two classes of Rutherford scattering processes were considered: a low-energy massless projectile strikes on a static, heavy, composite target carrying spin up to 2, and slowly moving light structureless projectile bombs on a static, heavy, spinning composite target particle.
The soft limits of both classes of gravitational Rutherford scattering processes have exhibited some universal and simple patterns. For the former type, given a massless projectile with certain spin, the first two terms in the heavy target mass expansion remain universal, and the NNLO term starts to develop target spin dependence. Nevertheless, several terms at NNLO still remain universal or have some definite pattern of dependence on the target spin. For the latter, we have to carry out the double expansion in projectile velocity and
$ 1/M $ to identify a simple soft limit. At the lowest order in v, yet to all orders in$ 1/M $ , the differential cross section has a universal form, insensitive to both projectile and target spin. At the relative order-$ v^2 $ , the first two terms in$ 1/M $ expansion are still independent on the target spin. The universality starts to be partially violated in the$ {\cal{O}}(v^2/M^2) $ part, though some terms at this order still remain independent on the target spin, or bears a definite pattern of target spin dependence.It is curious that, at NNLO in heavy target mass expansion, the prefactors of the
$ F_{40} = s $ term in both types of gravitational Rutherford scattering processes encapsulate some peculiar spin-statistics characteristic, which alternate from a constant for a fermionic target to another constant for a bosonic target. It is of interest to examine whether this pattern is valid for a composite target with arbitrarily high spin. -
We thank Kangyu Chai for the participation in the early stage of this study . We are grateful to Zhewen Mo for the discussion.
-
We thank Kangyu Chai for the participation in the early stage of this study . We are grateful to Zhewen Mo for the discussion.
-
We thank Kangyu Chai for the participation in the early stage of this study . We are grateful to Zhewen Mo for the discussion.
-
We thank Kangyu Chai for the participation in the early stage of this study . We are grateful to Zhewen Mo for the discussion.
-
In the derivation of the unpolarized cross sections, the following spin sum formulas concerning massive target particles are useful:
$ \sum\limits_{\lambda}u(p,\lambda)\bar{u}(p,\lambda) = \frac{{\not { p}}+M}{2M}, $

(A1a) $ \sum\limits_{\lambda}\varepsilon_\alpha(p,\lambda)\varepsilon^*_{\alpha'}(p,\lambda) = \hat{\eta}_{\alpha\alpha'}, $

(A1b) $\begin{aligned}[b]& \sum\limits_{\lambda}u_\alpha(p,\lambda)\bar{u}_{\alpha'}(p,\lambda) = - \frac{{\not { p}}+M}{2M}\Bigg(\eta _{\alpha\alpha'}-\frac{1}{3}\gamma_\alpha\gamma_{\alpha'}\\&\quad-\frac{2p_\alpha p_{\alpha'}}{3M^2}+\frac{\gamma_{\alpha'}p_\alpha-\gamma_{\alpha'}p_{\alpha}}{3M}\Bigg),\end{aligned} $

(A1c) $\begin{aligned}[b]& \sum\limits_{\lambda}\varepsilon_{\alpha_1\alpha_2}(p,\lambda)\varepsilon^*_{\alpha'_1\alpha'_2}(p,\lambda) = \hat{\eta}_{\alpha_1\alpha'_1}\hat{\eta}_{\alpha_2\alpha'_2}\\&\quad+\hat{\eta}_{\alpha_1\alpha'_2} \hat{\eta}_{\alpha_2\alpha'_1}- \frac{2}{3}\hat{\eta}_{\alpha_1\alpha_2}\hat{\eta}_{\alpha'_1\alpha'_2},\end{aligned} $

(A1d) with
$ \hat{\eta}_{\alpha\beta} \equiv -\eta _{\alpha\beta}+ \dfrac{p_\alpha p_\beta}{M^2} $ . The Dirac spinor is normalized as$ \bar{u}(p,r) u(p,s) = \delta^{rs} $ . -
In the derivation of the unpolarized cross sections, the following spin sum formulas concerning massive target particles are useful:
$ \sum\limits_{\lambda}u(p,\lambda)\bar{u}(p,\lambda) = \frac{\not{p} +M}{2M}, $
(A1a) $ \sum\limits_{\lambda}\varepsilon_\alpha(p,\lambda)\varepsilon^*_{\alpha'}(p,\lambda) = \hat{\eta}_{\alpha\alpha'}, $
(A1b) $\begin{aligned}[b]& \sum\limits_{\lambda}u_\alpha(p,\lambda)\bar{u}_{\alpha'}(p,\lambda) = - \frac{\not{p}+M}{2M}\Bigg(\eta _{\alpha\alpha'}-\frac{1}{3}\gamma_\alpha\gamma_{\alpha'}\\&\quad-\frac{2p_\alpha p_{\alpha'}}{3M^2}+\frac{\gamma_{\alpha'}p_\alpha-\gamma_{\alpha'}p_{\alpha}}{3M}\Bigg),\end{aligned} $
(A1c) $\begin{aligned}[b]& \sum\limits_{\lambda}\varepsilon_{\alpha_1\alpha_2}(p,\lambda)\varepsilon^*_{\alpha'_1\alpha'_2}(p,\lambda) = \hat{\eta}_{\alpha_1\alpha'_1}\hat{\eta}_{\alpha_2\alpha'_2}\\&\quad+\hat{\eta}_{\alpha_1\alpha'_2} \hat{\eta}_{\alpha_2\alpha'_1}- \frac{2}{3}\hat{\eta}_{\alpha_1\alpha_2}\hat{\eta}_{\alpha'_1\alpha'_2},\end{aligned} $
(A1d) with
$ \hat{\eta}_{\alpha\beta} \equiv -\eta _{\alpha\beta}+ \dfrac{p_\alpha p_\beta}{M^2} $ . The Dirac spinor is normalized as$ \bar{u}(p,r) u(p,s) = \delta^{rs} $ . -
In the derivation of the unpolarized cross sections, the following spin sum formulas concerning massive target particles are useful:
$ \sum\limits_{\lambda}u(p,\lambda)\bar{u}(p,\lambda) = \frac{{\not { p}}+M}{2M}, $

(A1a) $ \sum\limits_{\lambda}\varepsilon_\alpha(p,\lambda)\varepsilon^*_{\alpha'}(p,\lambda) = \hat{\eta}_{\alpha\alpha'}, $

(A1b) $\begin{aligned}[b]& \sum\limits_{\lambda}u_\alpha(p,\lambda)\bar{u}_{\alpha'}(p,\lambda) = - \frac{{\not { p}}+M}{2M}\Bigg(\eta _{\alpha\alpha'}-\frac{1}{3}\gamma_\alpha\gamma_{\alpha'}\\&\quad-\frac{2p_\alpha p_{\alpha'}}{3M^2}+\frac{\gamma_{\alpha'}p_\alpha-\gamma_{\alpha'}p_{\alpha}}{3M}\Bigg),\end{aligned} $

(A1c) $\begin{aligned}[b]& \sum\limits_{\lambda}\varepsilon_{\alpha_1\alpha_2}(p,\lambda)\varepsilon^*_{\alpha'_1\alpha'_2}(p,\lambda) = \hat{\eta}_{\alpha_1\alpha'_1}\hat{\eta}_{\alpha_2\alpha'_2}\\&\quad+\hat{\eta}_{\alpha_1\alpha'_2} \hat{\eta}_{\alpha_2\alpha'_1}- \frac{2}{3}\hat{\eta}_{\alpha_1\alpha_2}\hat{\eta}_{\alpha'_1\alpha'_2},\end{aligned} $

(A1d) with
$ \hat{\eta}_{\alpha\beta} \equiv -\eta _{\alpha\beta}+ \dfrac{p_\alpha p_\beta}{M^2} $ . The Dirac spinor is normalized as$ \bar{u}(p,r) u(p,s) = \delta^{rs} $ . -
In the derivation of the unpolarized cross sections, the following spin sum formulas concerning massive target particles are useful:
$ \sum\limits_{\lambda}u(p,\lambda)\bar{u}(p,\lambda) = \frac{{\not { p}}+M}{2M}, $

(A1a) $ \sum\limits_{\lambda}\varepsilon_\alpha(p,\lambda)\varepsilon^*_{\alpha'}(p,\lambda) = \hat{\eta}_{\alpha\alpha'}, $

(A1b) $\begin{aligned}[b]& \sum\limits_{\lambda}u_\alpha(p,\lambda)\bar{u}_{\alpha'}(p,\lambda) = - \frac{{\not { p}}+M}{2M}\Bigg(\eta _{\alpha\alpha'}-\frac{1}{3}\gamma_\alpha\gamma_{\alpha'}\\&\quad-\frac{2p_\alpha p_{\alpha'}}{3M^2}+\frac{\gamma_{\alpha'}p_\alpha-\gamma_{\alpha'}p_{\alpha}}{3M}\Bigg),\end{aligned} $

(A1c) $\begin{aligned}[b]& \sum\limits_{\lambda}\varepsilon_{\alpha_1\alpha_2}(p,\lambda)\varepsilon^*_{\alpha'_1\alpha'_2}(p,\lambda) = \hat{\eta}_{\alpha_1\alpha'_1}\hat{\eta}_{\alpha_2\alpha'_2}\\&\quad+\hat{\eta}_{\alpha_1\alpha'_2} \hat{\eta}_{\alpha_2\alpha'_1}- \frac{2}{3}\hat{\eta}_{\alpha_1\alpha_2}\hat{\eta}_{\alpha'_1\alpha'_2},\end{aligned} $

(A1d) with
$ \hat{\eta}_{\alpha\beta} \equiv -\eta _{\alpha\beta}+ \dfrac{p_\alpha p_\beta}{M^2} $ . The Dirac spinor is normalized as$ \bar{u}(p,r) u(p,s) = \delta^{rs} $ . -
Since the first detection of gravitational wave (GW) by LIGO and VIRGO in 2015, precise predictions of the GW templates become an imperative task. As an efficient theoretical framework to organize the post-Newtonian and post-Minkowski expansion, the HBET has recently been developed [24, 25], which is analogous to the heavy quark effective theory (HQET) tailored for heavy quark physics. Recently, it has been applied to GW emission in the scattering of binary spinless black holes or neutron stars with arbitrary masses at next-to-leading order in the post-Minkowski expansion [26].
The original HBET Lagrangian is designed to describe a heavy structureless particle (black hole) interacting with soft gravitons, with the expansion parameter being
$ 1/M $ [24, 25]. We use this approach to explain why the NLO amplitude in$ 1/M $ expansion vanishes for gravitational Rutherford scattering.For simplicity, we consider a heavy spinless target particle, which is represented by a complex scalar field. The underlying theory describing a heavy structureless particle interacting with gravity is simply assumed to be
$ S = \int {\rm d}^4 x \sqrt{-g}\left( g^{\mu \nu} \partial_{\mu}\phi^{*} \partial_{\nu}\phi -M^2 | \phi |^2 \right). $
(B1) Mimicking the derivation of HQET from QCD, we integrate out the heavy antiparticle degree of freedom by substituting the equation of motion into (B1) and expand the Lagrangian in powers of
$ 1/M $ . The effective action in the general spacetime background reads [24, 25]$ \begin{aligned}[b] S_{\rm{HBET}} =\;& \int {\rm d}^4x \frac{\sqrt{-g}}{2} \Bigg[ M\left(v_{\mu} v_{\nu}g^{\mu \nu } -1\right)\varphi_{v}^{*}\varphi_{v} \\&+\frac{\rm i}{2}g^{\mu \nu} ( v_{\mu} (\varphi_{v}^{*} \partial_{\nu} \varphi_{v} -(\partial_{\nu} \varphi_{v}^{*})\varphi_{v})\\&+v_{\nu} (\varphi_{v}^{*} \partial_{\mu} \varphi_{v} -(\partial_{\mu} \varphi_{v}^{*})\varphi_{v}) ) \\& +\frac{\rm i}{2} (v_{\mu} v_{\nu}g^{\mu \nu}-1) \left( (v\cdot \partial \varphi_{v}^{*}) \varphi_{v}-\varphi_{v}^{*}v \cdot \partial \varphi_{v} \right) \Bigg]. \end{aligned} $
(B2) As we are interested in the Rutherford scattering in Minkowski spacetime, the weak field approximation
$ \sqrt{-g} = 1-\dfrac{\kappa}{2}\eta_{\mu \nu} h^{\mu \nu}+{\cal{O}}(h^2) $ is invoked. The subscript of φ is the velocity label of the heavy target particle, with$ v^\mu = (1,{\bf{0}}) $ in the laboratory frame. It should be cautioned that, (B2) was invented for a point-like target particle [24, 25]. To describe a heavy composite target particle, we should assign general Wilson coefficients$ c_i $ to those higher-dimensional operators, which reflect its nontrivial internal structure. Keeping the free kinetic term of the heavy scalar field, as well as organizing the$ \varphi_{v}^{*}\varphi_{v} $ -graviton interactions in powers of$ 1/M $ , we obtain$\begin{aligned}[b] {\cal{L}}_{\rm{HBET'}} =\;& \frac{\rm i}{2}\left( \varphi_{v}^{*}v \cdot \partial \varphi_{v}-(v\cdot \partial \varphi_{v}^{*}) \varphi_{v}\right)+c_{1}\frac{M\kappa}{2}h^{\mu \nu}v_{\mu}v_{\nu} \\&+ \frac{{\rm i}\kappa }{4} h^{\mu \nu} (c_{2,2} v_{\mu} v_{\nu}+c_{2,1}\eta_{\mu \nu })\left( (v\cdot \partial \varphi_{v}^{*}) \varphi_{v}-\varphi_{v}^{*}v \cdot \partial \varphi_{v} \right) \\& +c_{2,1}\frac{{\rm i}\kappa}{4}h^{\mu \nu} ( v_{\mu} (\varphi_{v}^{*} \partial_{\nu} \varphi_{v} -(\partial_{\nu} \varphi_{v}^{*})\varphi_{v})\\&+v_{\nu} (\varphi_{v}^{*} \partial_{\mu} \varphi_{v} -(\partial_{\mu} \varphi_{v}^{*})\varphi_{v}) ), \end{aligned}$
(B3) where the subscript HBET' implies that the original HBET is generalized to account for the composite heavy target particle.
From (B3), we readily read off the Feynman rules for the
$ \varphi_{v}^{*}\varphi_{v} $ -graviton vertices through NLO in$ 1/M $ :$ V^{\varphi_{v}^{*}\varphi_{v} h}_{\text{LO}} = c_{1}\frac{{\rm i} M\kappa}{2}v^{\mu}v^{\nu}, $
(B4a) $\begin{aligned}[b] V^{\varphi_{v}^{*}\varphi_{v} h}_{\text{NLO}} =\;& \frac{{\rm i} \kappa}{4}\Big[ c_{2,1}v^{\mu}(\tilde{p}^{\nu}+\tilde{p}'{}^{\nu})+c_{2,1}v^{\nu}(\tilde{p}^{\mu}+\tilde{p}'{}^{\mu}) \\&-(c_{2,2}v^{\mu} v^{\nu}+c_{2,1}\eta^{\mu \nu }) (v \cdot \tilde{p}+v \cdot \tilde{p}')\Big],\end{aligned} $
(B4b) For a point-like target particle,
$ c_{1} = c_{2,1} = c_{2,2} = 1 $ 5 . Notably,$ \tilde{p} $ and$ \tilde{p}' $ signify the residual momenta of the target particle, e.g.,$ p = Mv+\tilde{p} $ . Assuming that the projectile is a massless spinless point particle, by combining (4a) and$ \varphi_{v}^{*}\varphi_{v} h $ vertices enumerated in (B4), we obtain the HBET prediction to the gravitational Rutherford scattering amplitudes through NLO in$ 1/M $ expansion:$ {\cal{M}}_{\text{EFT}} = \frac{c_{1} \kappa^2 M}{4(\cos{\theta}-1)}+\frac{c_{2,2}\kappa^2(|{\bf{k}}|-|{\bf{k}}'| )}{16 \sin^2 \left(\frac{\theta}{2}\right)}+{\cal{O}}\left(\frac{1}{M}\right), $
(B5) However, in light of the relation between
$ |{\bf{k}}| $ and$ |{\bf{k}}'| $ as expressed in (7), the second (nominally NLO) term in (B5) is suppressed with respect to the LO term by a factor of$ 1/M^2 $ , rather than$ 1/M $ . Therefore,$ {\cal{M}}_{\text{EFT}} = \frac{c_{1} \kappa^2 M}{4(\cos{\theta}-1)}+{\cal{O}}\left(\frac{1}{M}\right). $
(B6) This EFT analysis provides a clear perspective to understand why the NLO amplitude vanishes.
The EFT prediction (B6) should be identical to the LO result in (8a), which has been derived earlier in terms of the GFFs of the composite target particle,
$ {\cal{M}} = \frac{\kappa^2 M^2 F_{10}}{2(\cos{\theta}-1)}+ {\cal{O}}\left(\frac{1}{M^0}\right). $
(B7) This criterion enforces
$ c_{1} = F_{10} = 1 $ once the$ 2M $ factor is compensated for the nonrelativistic state normalization. The requirement$ c_1 = 1 $ , irrespective of whether the heavy target particle is fundamental or composite, may be attributed to the reparametrization invariance in HBET.As the
$ {\cal{O}}(1/M) $ HBET vertex yields a vanishing contribution to the Rutherford scattering amplitude, the NLO contribution to the unpolarized cross section in (8b) arises solely from the expansion of the phase space factor. -
Since the first detection of gravitational wave (GW) by LIGO and VIRGO in 2015, precise predictions of the GW templates become an imperative task. As an efficient theoretical framework to organize the post-Newtonian and post-Minkowski expansion, the HBET has recently been developed [24, 25], which is analogous to the heavy quark effective theory (HQET) tailored for heavy quark physics. Recently, it has been applied to GW emission in the scattering of binary spinless black holes or neutron stars with arbitrary masses at next-to-leading order in the post-Minkowski expansion [26].
The original HBET Lagrangian is designed to describe a heavy structureless particle (black hole) interacting with soft gravitons, with the expansion parameter being
$ 1/M $ [24, 25]. We use this approach to explain why the NLO amplitude in$ 1/M $ expansion vanishes for gravitational Rutherford scattering.For simplicity, we consider a heavy spinless target particle, which is represented by a complex scalar field. The underlying theory describing a heavy structureless particle interacting with gravity is simply assumed to be
$ S = \int {\rm d}^4 x \sqrt{-g}\left( g^{\mu \nu} \partial_{\mu}\phi^{*} \partial_{\nu}\phi -M^2 | \phi |^2 \right). $

(B1) Mimicking the derivation of HQET from QCD, we integrate out the heavy antiparticle degree of freedom by substituting the equation of motion into (B1) and expand the Lagrangian in powers of
$ 1/M $ . The effective action in the general spacetime background reads [24, 25]$ \begin{aligned}[b] S_{\rm{HBET}} =\;& \int {\rm d}^4x \frac{\sqrt{-g}}{2} \Bigg[ M\left(v_{\mu} v_{\nu}g^{\mu \nu } -1\right)\varphi_{v}^{*}\varphi_{v} \\&+\frac{\rm i}{2}g^{\mu \nu} ( v_{\mu} (\varphi_{v}^{*} \partial_{\nu} \varphi_{v} -(\partial_{\nu} \varphi_{v}^{*})\varphi_{v})\\&+v_{\nu} (\varphi_{v}^{*} \partial_{\mu} \varphi_{v} -(\partial_{\mu} \varphi_{v}^{*})\varphi_{v}) ) \\& +\frac{\rm i}{2} (v_{\mu} v_{\nu}g^{\mu \nu}-1) \left( (v\cdot \partial \varphi_{v}^{*}) \varphi_{v}-\varphi_{v}^{*}v \cdot \partial \varphi_{v} \right) \Bigg]. \end{aligned} $

(B2) As we are interested in the Rutherford scattering in Minkowski spacetime, the weak field approximation
$ \sqrt{-g} = 1-\dfrac{\kappa}{2}\eta_{\mu \nu} h^{\mu \nu}+{\cal{O}}(h^2) $ is invoked. The subscript of φ is the velocity label of the heavy target particle, with$ v^\mu = (1,{\bf{0}}) $ in the laboratory frame. It should be cautioned that, (B2) was invented for a point-like target particle [24, 25]. To describe a heavy composite target particle, we should assign general Wilson coefficients$ c_i $ to those higher-dimensional operators, which reflect its nontrivial internal structure. Keeping the free kinetic term of the heavy scalar field, as well as organizing the$ \varphi_{v}^{*}\varphi_{v} $ -graviton interactions in powers of$ 1/M $ , we obtain$\begin{aligned}[b] {\cal{L}}_{\rm{HBET'}} =\;& \frac{\rm i}{2}\left( \varphi_{v}^{*}v \cdot \partial \varphi_{v}-(v\cdot \partial \varphi_{v}^{*}) \varphi_{v}\right)+c_{1}\frac{M\kappa}{2}h^{\mu \nu}v_{\mu}v_{\nu} \\&+ \frac{{\rm i}\kappa }{4} h^{\mu \nu} (c_{2,2} v_{\mu} v_{\nu}+c_{2,1}\eta_{\mu \nu })\left( (v\cdot \partial \varphi_{v}^{*}) \varphi_{v}-\varphi_{v}^{*}v \cdot \partial \varphi_{v} \right) \\& +c_{2,1}\frac{{\rm i}\kappa}{4}h^{\mu \nu} ( v_{\mu} (\varphi_{v}^{*} \partial_{\nu} \varphi_{v} -(\partial_{\nu} \varphi_{v}^{*})\varphi_{v})\\&+v_{\nu} (\varphi_{v}^{*} \partial_{\mu} \varphi_{v} -(\partial_{\mu} \varphi_{v}^{*})\varphi_{v}) ), \end{aligned}$

(B3) where the subscript HBET' implies that the original HBET is generalized to account for the composite heavy target particle.
From (B3), we readily read off the Feynman rules for the
$ \varphi_{v}^{*}\varphi_{v} $ -graviton vertices through NLO in$ 1/M $ :$ V^{\varphi_{v}^{*}\varphi_{v} h}_{\text{LO}} = c_{1}\frac{{\rm i} M\kappa}{2}v^{\mu}v^{\nu}, $

(B4a) $\begin{aligned}[b] V^{\varphi_{v}^{*}\varphi_{v} h}_{\text{NLO}} =\;& \frac{{\rm i} \kappa}{4}\Big[ c_{2,1}v^{\mu}(\tilde{p}^{\nu}+\tilde{p}'{}^{\nu})+c_{2,1}v^{\nu}(\tilde{p}^{\mu}+\tilde{p}'{}^{\mu}) \\&-(c_{2,2}v^{\mu} v^{\nu}+c_{2,1}\eta^{\mu \nu }) (v \cdot \tilde{p}+v \cdot \tilde{p}')\Big],\end{aligned} $

(B4b) For a point-like target particle,
$ c_{1} = c_{2,1} = c_{2,2} = 1 $ 5 . Notably,$ \tilde{p} $ and$ \tilde{p}' $ signify the residual momenta of the target particle, e.g.,$ p = Mv+\tilde{p} $ . Assuming that the projectile is a massless spinless point particle, by combining (4a) and$ \varphi_{v}^{*}\varphi_{v} h $ vertices enumerated in (B4), we obtain the HBET prediction to the gravitational Rutherford scattering amplitudes through NLO in$ 1/M $ expansion:$ {\cal{M}}_{\text{EFT}} = \frac{c_{1} \kappa^2 M}{4(\cos{\theta}-1)}+\frac{c_{2,2}\kappa^2(|{\bf{k}}|-|{\bf{k}}'| )}{16 \sin^2 \left(\frac{\theta}{2}\right)}+{\cal{O}}\left(\frac{1}{M}\right), $

(B5) However, in light of the relation between
$ |{\bf{k}}| $ and$ |{\bf{k}}'| $ as expressed in (7), the second (nominally NLO) term in (B5) is suppressed with respect to the LO term by a factor of$ 1/M^2 $ , rather than$ 1/M $ . Therefore,$ {\cal{M}}_{\text{EFT}} = \frac{c_{1} \kappa^2 M}{4(\cos{\theta}-1)}+{\cal{O}}\left(\frac{1}{M}\right). $

(B6) This EFT analysis provides a clear perspective to understand why the NLO amplitude vanishes.
The EFT prediction (B6) should be identical to the LO result in (8a), which has been derived earlier in terms of the GFFs of the composite target particle,
$ {\cal{M}} = \frac{\kappa^2 M^2 F_{10}}{2(\cos{\theta}-1)}+ {\cal{O}}\left(\frac{1}{M^0}\right). $

(B7) This criterion enforces
$ c_{1} = F_{10} = 1 $ once the$ 2M $ factor is compensated for the nonrelativistic state normalization. The requirement$ c_1 = 1 $ , irrespective of whether the heavy target particle is fundamental or composite, may be attributed to the reparametrization invariance in HBET.As the
$ {\cal{O}}(1/M) $ HBET vertex yields a vanishing contribution to the Rutherford scattering amplitude, the NLO contribution to the unpolarized cross section in (8b) arises solely from the expansion of the phase space factor. -
Since the first detection of gravitational wave (GW) by LIGO and VIRGO in 2015, precise predictions of the GW templates become an imperative task. As an efficient theoretical framework to organize the post-Newtonian and post-Minkowski expansion, the HBET has recently been developed [24, 25], which is analogous to the heavy quark effective theory (HQET) tailored for heavy quark physics. Recently, it has been applied to GW emission in the scattering of binary spinless black holes or neutron stars with arbitrary masses at next-to-leading order in the post-Minkowski expansion [26].
The original HBET Lagrangian is designed to describe a heavy structureless particle (black hole) interacting with soft gravitons, with the expansion parameter being
$ 1/M $ [24, 25]. We use this approach to explain why the NLO amplitude in$ 1/M $ expansion vanishes for gravitational Rutherford scattering.For simplicity, we consider a heavy spinless target particle, which is represented by a complex scalar field. The underlying theory describing a heavy structureless particle interacting with gravity is simply assumed to be
$ S = \int {\rm d}^4 x \sqrt{-g}\left( g^{\mu \nu} \partial_{\mu}\phi^{*} \partial_{\nu}\phi -M^2 | \phi |^2 \right). $

(B1) Mimicking the derivation of HQET from QCD, we integrate out the heavy antiparticle degree of freedom by substituting the equation of motion into (B1) and expand the Lagrangian in powers of
$ 1/M $ . The effective action in the general spacetime background reads [24, 25]$ \begin{aligned}[b] S_{\rm{HBET}} =\;& \int {\rm d}^4x \frac{\sqrt{-g}}{2} \Bigg[ M\left(v_{\mu} v_{\nu}g^{\mu \nu } -1\right)\varphi_{v}^{*}\varphi_{v} \\&+\frac{\rm i}{2}g^{\mu \nu} ( v_{\mu} (\varphi_{v}^{*} \partial_{\nu} \varphi_{v} -(\partial_{\nu} \varphi_{v}^{*})\varphi_{v})\\&+v_{\nu} (\varphi_{v}^{*} \partial_{\mu} \varphi_{v} -(\partial_{\mu} \varphi_{v}^{*})\varphi_{v}) ) \\& +\frac{\rm i}{2} (v_{\mu} v_{\nu}g^{\mu \nu}-1) \left( (v\cdot \partial \varphi_{v}^{*}) \varphi_{v}-\varphi_{v}^{*}v \cdot \partial \varphi_{v} \right) \Bigg]. \end{aligned} $

(B2) As we are interested in the Rutherford scattering in Minkowski spacetime, the weak field approximation
$ \sqrt{-g} = 1-\dfrac{\kappa}{2}\eta_{\mu \nu} h^{\mu \nu}+{\cal{O}}(h^2) $ is invoked. The subscript of φ is the velocity label of the heavy target particle, with$ v^\mu = (1,{\bf{0}}) $ in the laboratory frame. It should be cautioned that, (B2) was invented for a point-like target particle [24, 25]. To describe a heavy composite target particle, we should assign general Wilson coefficients$ c_i $ to those higher-dimensional operators, which reflect its nontrivial internal structure. Keeping the free kinetic term of the heavy scalar field, as well as organizing the$ \varphi_{v}^{*}\varphi_{v} $ -graviton interactions in powers of$ 1/M $ , we obtain$\begin{aligned}[b] {\cal{L}}_{\rm{HBET'}} =\;& \frac{\rm i}{2}\left( \varphi_{v}^{*}v \cdot \partial \varphi_{v}-(v\cdot \partial \varphi_{v}^{*}) \varphi_{v}\right)+c_{1}\frac{M\kappa}{2}h^{\mu \nu}v_{\mu}v_{\nu} \\&+ \frac{{\rm i}\kappa }{4} h^{\mu \nu} (c_{2,2} v_{\mu} v_{\nu}+c_{2,1}\eta_{\mu \nu })\left( (v\cdot \partial \varphi_{v}^{*}) \varphi_{v}-\varphi_{v}^{*}v \cdot \partial \varphi_{v} \right) \\& +c_{2,1}\frac{{\rm i}\kappa}{4}h^{\mu \nu} ( v_{\mu} (\varphi_{v}^{*} \partial_{\nu} \varphi_{v} -(\partial_{\nu} \varphi_{v}^{*})\varphi_{v})\\&+v_{\nu} (\varphi_{v}^{*} \partial_{\mu} \varphi_{v} -(\partial_{\mu} \varphi_{v}^{*})\varphi_{v}) ), \end{aligned}$

(B3) where the subscript HBET' implies that the original HBET is generalized to account for the composite heavy target particle.
From (B3), we readily read off the Feynman rules for the
$ \varphi_{v}^{*}\varphi_{v} $ -graviton vertices through NLO in$ 1/M $ :$ V^{\varphi_{v}^{*}\varphi_{v} h}_{\text{LO}} = c_{1}\frac{{\rm i} M\kappa}{2}v^{\mu}v^{\nu}, $

(B4a) $\begin{aligned}[b] V^{\varphi_{v}^{*}\varphi_{v} h}_{\text{NLO}} =\;& \frac{{\rm i} \kappa}{4}\Big[ c_{2,1}v^{\mu}(\tilde{p}^{\nu}+\tilde{p}'{}^{\nu})+c_{2,1}v^{\nu}(\tilde{p}^{\mu}+\tilde{p}'{}^{\mu}) \\&-(c_{2,2}v^{\mu} v^{\nu}+c_{2,1}\eta^{\mu \nu }) (v \cdot \tilde{p}+v \cdot \tilde{p}')\Big],\end{aligned} $

(B4b) For a point-like target particle,
$ c_{1} = c_{2,1} = c_{2,2} = 1 $ 5 . Notably,$ \tilde{p} $ and$ \tilde{p}' $ signify the residual momenta of the target particle, e.g.,$ p = Mv+\tilde{p} $ . Assuming that the projectile is a massless spinless point particle, by combining (4a) and$ \varphi_{v}^{*}\varphi_{v} h $ vertices enumerated in (B4), we obtain the HBET prediction to the gravitational Rutherford scattering amplitudes through NLO in$ 1/M $ expansion:$ {\cal{M}}_{\text{EFT}} = \frac{c_{1} \kappa^2 M}{4(\cos{\theta}-1)}+\frac{c_{2,2}\kappa^2(|{\bf{k}}|-|{\bf{k}}'| )}{16 \sin^2 \left(\frac{\theta}{2}\right)}+{\cal{O}}\left(\frac{1}{M}\right), $

(B5) However, in light of the relation between
$ |{\bf{k}}| $ and$ |{\bf{k}}'| $ as expressed in (7), the second (nominally NLO) term in (B5) is suppressed with respect to the LO term by a factor of$ 1/M^2 $ , rather than$ 1/M $ . Therefore,$ {\cal{M}}_{\text{EFT}} = \frac{c_{1} \kappa^2 M}{4(\cos{\theta}-1)}+{\cal{O}}\left(\frac{1}{M}\right). $

(B6) This EFT analysis provides a clear perspective to understand why the NLO amplitude vanishes.
The EFT prediction (B6) should be identical to the LO result in (8a), which has been derived earlier in terms of the GFFs of the composite target particle,
$ {\cal{M}} = \frac{\kappa^2 M^2 F_{10}}{2(\cos{\theta}-1)}+ {\cal{O}}\left(\frac{1}{M^0}\right). $

(B7) This criterion enforces
$ c_{1} = F_{10} = 1 $ once the$ 2M $ factor is compensated for the nonrelativistic state normalization. The requirement$ c_1 = 1 $ , irrespective of whether the heavy target particle is fundamental or composite, may be attributed to the reparametrization invariance in HBET.As the
$ {\cal{O}}(1/M) $ HBET vertex yields a vanishing contribution to the Rutherford scattering amplitude, the NLO contribution to the unpolarized cross section in (8b) arises solely from the expansion of the phase space factor. -
Since the first detection of gravitational wave (GW) by LIGO and VIRGO in 2015, precise predictions of the GW templates become an imperative task. As an efficient theoretical framework to organize the post-Newtonian and post-Minkowski expansion, the HBET has recently been developed [24, 25], which is analogous to the heavy quark effective theory (HQET) tailored for heavy quark physics. Recently, it has been applied to GW emission in the scattering of binary spinless black holes or neutron stars with arbitrary masses at next-to-leading order in the post-Minkowski expansion [26].
The original HBET Lagrangian is designed to describe a heavy structureless particle (black hole) interacting with soft gravitons, with the expansion parameter being
$ 1/M $ [24, 25]. We use this approach to explain why the NLO amplitude in$ 1/M $ expansion vanishes for gravitational Rutherford scattering.For simplicity, we consider a heavy spinless target particle, which is represented by a complex scalar field. The underlying theory describing a heavy structureless particle interacting with gravity is simply assumed to be
$ S = \int {\rm d}^4 x \sqrt{-g}\left( g^{\mu \nu} \partial_{\mu}\phi^{*} \partial_{\nu}\phi -M^2 | \phi |^2 \right). $

(B1) Mimicking the derivation of HQET from QCD, we integrate out the heavy antiparticle degree of freedom by substituting the equation of motion into (B1) and expand the Lagrangian in powers of
$ 1/M $ . The effective action in the general spacetime background reads [24, 25]$ \begin{aligned}[b] S_{\rm{HBET}} =\;& \int {\rm d}^4x \frac{\sqrt{-g}}{2} \Bigg[ M\left(v_{\mu} v_{\nu}g^{\mu \nu } -1\right)\varphi_{v}^{*}\varphi_{v} \\&+\frac{\rm i}{2}g^{\mu \nu} ( v_{\mu} (\varphi_{v}^{*} \partial_{\nu} \varphi_{v} -(\partial_{\nu} \varphi_{v}^{*})\varphi_{v})\\&+v_{\nu} (\varphi_{v}^{*} \partial_{\mu} \varphi_{v} -(\partial_{\mu} \varphi_{v}^{*})\varphi_{v}) ) \\& +\frac{\rm i}{2} (v_{\mu} v_{\nu}g^{\mu \nu}-1) \left( (v\cdot \partial \varphi_{v}^{*}) \varphi_{v}-\varphi_{v}^{*}v \cdot \partial \varphi_{v} \right) \Bigg]. \end{aligned} $

(B2) As we are interested in the Rutherford scattering in Minkowski spacetime, the weak field approximation
$ \sqrt{-g} = 1-\dfrac{\kappa}{2}\eta_{\mu \nu} h^{\mu \nu}+{\cal{O}}(h^2) $ is invoked. The subscript of φ is the velocity label of the heavy target particle, with$ v^\mu = (1,{\bf{0}}) $ in the laboratory frame. It should be cautioned that, (B2) was invented for a point-like target particle [24, 25]. To describe a heavy composite target particle, we should assign general Wilson coefficients$ c_i $ to those higher-dimensional operators, which reflect its nontrivial internal structure. Keeping the free kinetic term of the heavy scalar field, as well as organizing the$ \varphi_{v}^{*}\varphi_{v} $ -graviton interactions in powers of$ 1/M $ , we obtain$\begin{aligned}[b] {\cal{L}}_{\rm{HBET'}} =\;& \frac{\rm i}{2}\left( \varphi_{v}^{*}v \cdot \partial \varphi_{v}-(v\cdot \partial \varphi_{v}^{*}) \varphi_{v}\right)+c_{1}\frac{M\kappa}{2}h^{\mu \nu}v_{\mu}v_{\nu} \\&+ \frac{{\rm i}\kappa }{4} h^{\mu \nu} (c_{2,2} v_{\mu} v_{\nu}+c_{2,1}\eta_{\mu \nu })\left( (v\cdot \partial \varphi_{v}^{*}) \varphi_{v}-\varphi_{v}^{*}v \cdot \partial \varphi_{v} \right) \\& +c_{2,1}\frac{{\rm i}\kappa}{4}h^{\mu \nu} ( v_{\mu} (\varphi_{v}^{*} \partial_{\nu} \varphi_{v} -(\partial_{\nu} \varphi_{v}^{*})\varphi_{v})\\&+v_{\nu} (\varphi_{v}^{*} \partial_{\mu} \varphi_{v} -(\partial_{\mu} \varphi_{v}^{*})\varphi_{v}) ), \end{aligned}$

(B3) where the subscript HBET' implies that the original HBET is generalized to account for the composite heavy target particle.
From (B3), we readily read off the Feynman rules for the
$ \varphi_{v}^{*}\varphi_{v} $ -graviton vertices through NLO in$ 1/M $ :$ V^{\varphi_{v}^{*}\varphi_{v} h}_{\text{LO}} = c_{1}\frac{{\rm i} M\kappa}{2}v^{\mu}v^{\nu}, $

(B4a) $\begin{aligned}[b] V^{\varphi_{v}^{*}\varphi_{v} h}_{\text{NLO}} =\;& \frac{{\rm i} \kappa}{4}\Big[ c_{2,1}v^{\mu}(\tilde{p}^{\nu}+\tilde{p}'{}^{\nu})+c_{2,1}v^{\nu}(\tilde{p}^{\mu}+\tilde{p}'{}^{\mu}) \\&-(c_{2,2}v^{\mu} v^{\nu}+c_{2,1}\eta^{\mu \nu }) (v \cdot \tilde{p}+v \cdot \tilde{p}')\Big],\end{aligned} $

(B4b) For a point-like target particle,
$ c_{1} = c_{2,1} = c_{2,2} = 1 $ 5 . Notably,$ \tilde{p} $ and$ \tilde{p}' $ signify the residual momenta of the target particle, e.g.,$ p = Mv+\tilde{p} $ . Assuming that the projectile is a massless spinless point particle, by combining (4a) and$ \varphi_{v}^{*}\varphi_{v} h $ vertices enumerated in (B4), we obtain the HBET prediction to the gravitational Rutherford scattering amplitudes through NLO in$ 1/M $ expansion:$ {\cal{M}}_{\text{EFT}} = \frac{c_{1} \kappa^2 M}{4(\cos{\theta}-1)}+\frac{c_{2,2}\kappa^2(|{\bf{k}}|-|{\bf{k}}'| )}{16 \sin^2 \left(\frac{\theta}{2}\right)}+{\cal{O}}\left(\frac{1}{M}\right), $

(B5) However, in light of the relation between
$ |{\bf{k}}| $ and$ |{\bf{k}}'| $ as expressed in (7), the second (nominally NLO) term in (B5) is suppressed with respect to the LO term by a factor of$ 1/M^2 $ , rather than$ 1/M $ . Therefore,$ {\cal{M}}_{\text{EFT}} = \frac{c_{1} \kappa^2 M}{4(\cos{\theta}-1)}+{\cal{O}}\left(\frac{1}{M}\right). $

(B6) This EFT analysis provides a clear perspective to understand why the NLO amplitude vanishes.
The EFT prediction (B6) should be identical to the LO result in (8a), which has been derived earlier in terms of the GFFs of the composite target particle,
$ {\cal{M}} = \frac{\kappa^2 M^2 F_{10}}{2(\cos{\theta}-1)}+ {\cal{O}}\left(\frac{1}{M^0}\right). $

(B7) This criterion enforces
$ c_{1} = F_{10} = 1 $ once the$ 2M $ factor is compensated for the nonrelativistic state normalization. The requirement$ c_1 = 1 $ , irrespective of whether the heavy target particle is fundamental or composite, may be attributed to the reparametrization invariance in HBET.As the
$ {\cal{O}}(1/M) $ HBET vertex yields a vanishing contribution to the Rutherford scattering amplitude, the NLO contribution to the unpolarized cross section in (8b) arises solely from the expansion of the phase space factor.
Soft pattern of gravitational Rutherford scattering from heavy target mass expansion
- Received Date: 2024-04-30
- Available Online: 2026-01-15
Abstract: We investigate the soft behavior of the tree-level Rutherford scattering processes mediated via t-channel one-graviton exchange. We consider two types of Rutherford scattering processes: a low-energy massless structureless projectile (up to spin-1) hits a static massive composite particle carrying various spins (up to spin-2), and slowly moving light projectile hits a heavy static composite target. The unpolarized cross sections in the first type exhibit universal forms at the first two orders in $ 1/M $ expansion, yet differ at the next-to-next-to-leading order, though some terms at this order still remain universal or depend on the target spin in a definite manner. The unpolarized cross sections in the second type are universal at the lowest order in projectile velocity expansion and through all orders in $ 1/M $, independent on the spins of both projectile and target. The universality partially breaks down at relative order-$ v^2/M^2 $, albeit some terms at this order still depend on the target spin in a specific manner.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

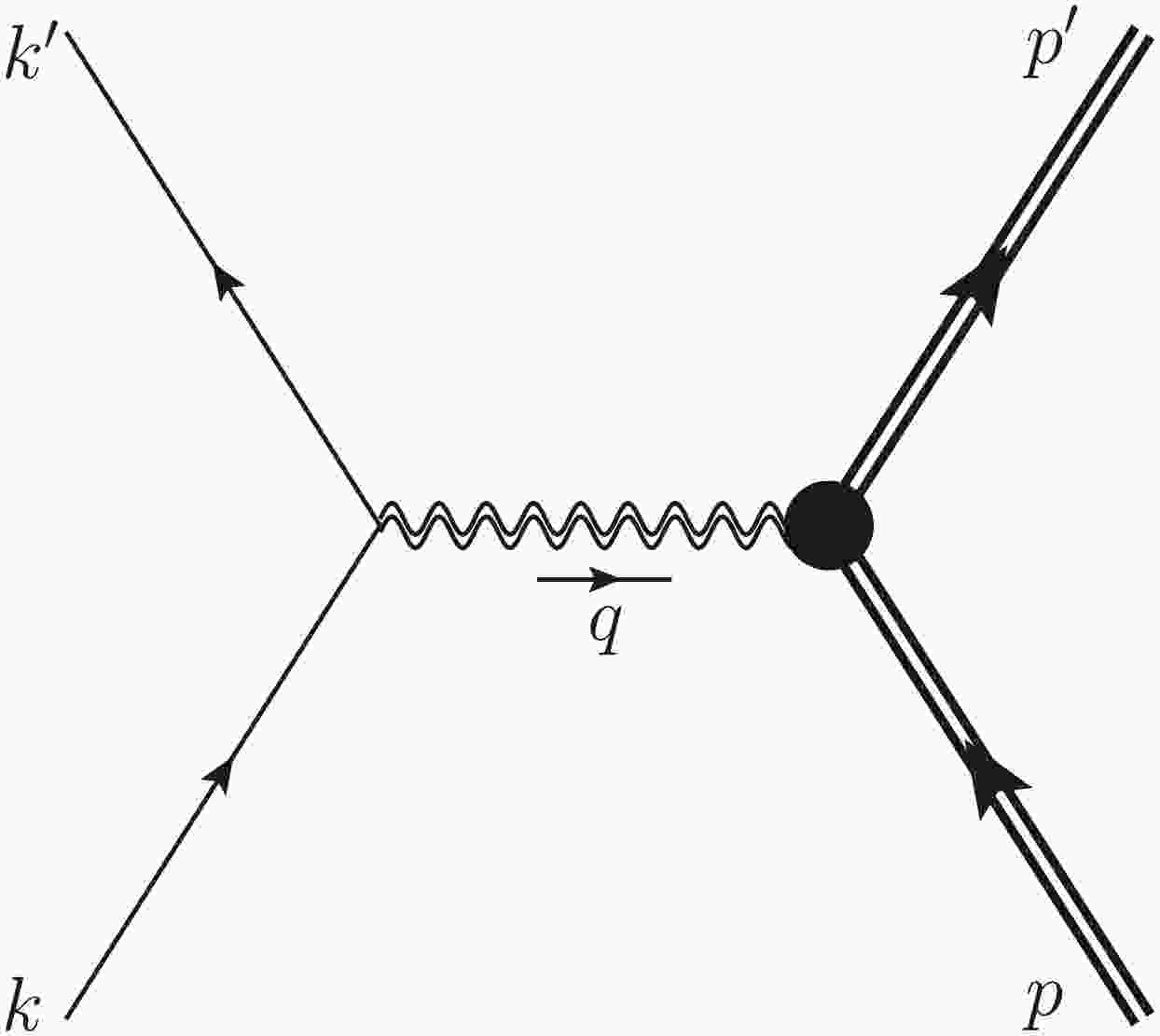













 DownLoad:
DownLoad: