Shadow cast by the Kerr MOG black hole under the influence of plasma and constraints from EHT observations

General theory of relativity $ (\mathrm{GTR}) $ is a well-established theory that successfully predicts many cosmological phenomena in the solar system and the broader universe. Notably, it predicts the existence of BHs, which are among the most astonishing astronomical phenomena. However, $ \mathrm{GTR} $does not account for the interior of BHs or certain other astronomical observations. An important example is the unusual behavior of galaxy rotation curves, discovered through studies performed by Zwicky, Rubin, and their colleagues [1, 2]. Zwicky was the first to theorize and formally introduce the concept of an unknown form of matter, later termed dark matter. Rubin's observations revealed that Einstein's theory of relativity $ (\mathrm{GTR}) $cannot fully account for the rotation curves of spiral galaxies. This observation provides a key indication of the existence of dark matter.

However, to date, dark matter has not been directly detected via experimental observation. It may be necessary to develop a theory that explains this phenomenon without relying on the concept of dark matter [3]. Firstly, modified Newtonian dynamics (MOND) was proposed by Milgrom [4], which modifies the "inverse-square" law of gravity in the scalar field framework of Newtonian gravity. MOND fits certain observations such as those within the weak-field approximation in systems like the solar system. However, it has limited ability to explain large-scale phenomena, such as the rotation curves of galaxies in the spiral region, from approximately $ \sim0.2 $ kpc to $ \sim200 $ kpc, and the velocity dispersion profiles of globular clusters [5, 6].

Moffat proposed a scalar–tensor–vector gravity (STVG) theory [7], commonly referred to as modified gravity theory (MOG). MOG was developed to address the discrepancies between $ \mathrm{GTR} $ at large scales and numerous astronomical observations, including galaxy dynamics, rotation curves, bullet clusters, the distribution of luminous matter in galaxies, and the accelerating expansion of the universe [8]. Additionally, it provides a description of structure formation, the matter power spectrum, and the acoustic power spectrum of the cosmic microwave background (CMB) [9]. This theory introduces new fields into $ \mathrm{GTR} $, strengthening the gravitational field. Its action comprises the usual Einstein-Hilbert term associated with the metric tensor $g_{\mu\nu}$, a massive vector field $\phi_{\mu}$, and three scalar fields that represent the running values of the gravitational constant G, the coupling constant Ω (which determines the strength of the coupling between matter and the vector field), and the vector field’s mass μ (which adjusts the range of the coupling) [7]. The scalar field $ G = G_N (1 + \alpha) $ represents the strength of the gravitational attraction, where $ G_N $ denotes Newton’s gravitational constant and α denotes a dimensionless parameter of the theory.

Recently, the direct observation of gravitational waves by LIGO and Virgo from binary BH and neutron star systems [10, 11] has sparked great excitement in the scientific community. These groundbreaking events have opened a new frontier for observational astronomy. As anticipated, the intrinsic properties of BHs will become increasingly clear with future detections of merging events and enhancements in signal to noise ratio. Furthermore, these observations may offer us a pathway to differentiate BHs predicted by various theories of gravity [12, 13].

There are other approaches to explore the nature of BHs, such as strong gravitational lensing and BH shadow analysis. Specifically, these effects are significantly influenced by the mass of the BH. It is widely believed that a supermassive BH exists at the center of each galaxy [14]. The immense mass of these BHs makes strong gravitational effects potentially observable. For example, the Event Horizon Telescope (EHT), with its high angular resolution, can observe the shadow cast by the supermassive BH at the center of our galaxy using advanced imaging techniques. Therefore, studying the BH shadow is highly desirable [15].

BH shadows are formed by null geodesics within the region of strong gravitational influence. Generally, photons with high angular momentum, originating from infinity, are deflected back to infinity by the BH’s gravitational potential. In contrast, photons with lower angular momentum are pulled into the BH, creating a dark region visible to an observer at infinity. Between these two behaviors, photons with critical angular momentum will orbit the BH loop by loop, delineating the boundary of the shadow [16, 17]. For a non-rotating Schwarzschild BH, this shadow was first examined by Synge and Luminet [18, 19]. The shadow cast by a rotating Kerr BH was first investigated by Bardeen [20] and was systematically introduced in [21]. These studies reveal that a non-rotating BH produces a perfectly circular shadow, whereas the shadow of a rotating BH is elongated due to the frame-dragging effect. Recent studies have examined the shadows of rotating and non-rotating BHs in the presence of plasma [22−25]

Significantly, astronomical observables are essential in connecting theoretical studies with actual astronomical observations. Thus, investigating the properties of BHs within MOG theory is of great interest. In [9, 26], the authors presented a preliminary image of the shadow cast by the MOG BH. In this study, we aim to explore the observable characteristics of the Kerr MOG BH shadow under the influence of plasma. These findings will offer detailed insights into the properties of MOG theory and provide a potential means to differentiate it from $ \mathrm{GTR} $.

The effects of plasma on light propagation have been investigated since the 1960s. In 1966, John Ston and Muhleman explored the impact of electronic plasma in the solar corona on the time delay of radio frequencies under the gravitational field of the sun using plasma and gravitational refractive indices to derive a weak-field-approximation [27]. Various analyses focusing on the solar wind and the electron density profile of the Sun's outer corona were conducted using light propagation studies from space missions such as Viking, Mariner 6 and 7, and Cassini. In 1980, Ehlers and Breuer enacted a challenging derivation of a Hamiltonian for light rays comprising magnetized plasma in a curved spacetime [28]. In literature, we can find recent studies on analyzing the influence of plasma on the propagation of light rays in different astrophysical situations [22].

The EHT group has recently succeeded in capturing polarized light around M87* and Sgr A* [29]. The orientation of light waves is evident in these polarized images and is influenced by the magnetic fields generated by the plasma revolving around the black holes (BHs). The results from these polarized images not only confirm the presence of plasma around BHs but also provide insights into the mechanisms governing their evolution and behavior [30]. This study explores the Kerr MOG BH and its implications for EHT observations of M87* and Sgr A*, focusing on how the deformation parameter α affects the BH shadow and the constraints that can be derived from EHT data in the presence of non-magnetized, pressureless plasma. By comparing the predictions of the Kerr MOG model with observed shadows, we aim to constrain α, providing a potential test for deviations from $ \mathrm{GTR} $. The shadow of M87* is consistent with the predictions of $ \mathrm{GTR} $ for a Kerr BH; however, uncertainties in spin measurements and deviations in quadrupole moments allow for potential modifications [14, 31] due to α and plasma effects. By incorporating plasma effects and the deformation parameter α, in this study, we evaluate the feasibility of distinguishing Kerr MOG BHs and constraining their parameters via EHT observations.

A key aspect of this study involves deriving the deflection angle of light near the Kerr MOG BH, considering homogeneous and nonhomogeneous plasma spacetime. Additionally, for most astronomical situations, the influence of plasma on light rays can be neglected; however, this is not the case for light rays in the radio frequency range. A well-known example is the effects of the solar corona, modeled as non-magnetized and pressureless plasma, on the time delay [27] and deflection angle when light rays propagate near the Sun [32]. Later, Perlick conducted a detailed investigation into the influence of nonhomogeneous plasma on light deflection in the Schwarzschild spacetime and within the equatorial plane of Kerr spacetime [33]. In this study, we investigate the deflection angle of light in Kerr MOG spacetime, considering a non-magnetized, pressureless plasma environment. The presence of plasma notably influences light propagation in the MOG context, making this analysis essential for understanding these effects. Our study focuses on how plasma properties and the deformation parameter α affect the deflection angle.

The organization of the paper is as follows. In Sec. II, we summarize the metric described in [9]. In Sec. II A, we review the Hamiltonian formalism for light rays in non-magnetized, pressureless plasma within a general-relativistic spacetime and specialize the relevant equations to the Kerr MOG metric. In Sec. II.B, we derive the necessary and sufficient condition on the plasma electron density that ensures the separability of the Hamilton-Jacobi $ (\mathrm{HJ}) $ equation for light rays [34], thereby guaranteeing the existence of a Carter constant. In Sec. II.C, we determine the photon region for a plasma density around a Kerr MOG BH that satisfies this separability condition. In Sec. III, we develop the general formulas needed to parameterize the contour curve of the BH shadow in pressureless, non-magnetic plasma environments adapted to the Kerr MOG metric. In Sec. III.A, we begin with considerations of BH shadows in homogeneous plasma environments, and then, we examine how the shadows and photon regions are influenced by various parameters of the BH and plasma profiles [34] in Sec. III.B and Sec. III.C. In Sec. IV, we analyze the energy emission rate and investigate the effects of the MOG parameter and plasma density on particle emission. In Sec. V, after examining Hawking radiation in Sec. IV, we explore the deviation of light in Kerr MOG spacetime surrounded by non-magnetized and pressureless plasma. Sec. VI focuses on constraining the plasma parameters by incorporating the observational data obtained from M87* and Sgr A*. We conclude with final remarks in Sec. VII. Our conventions are as follows: we employ the summation convention for Greek indices, which run over the values 0, 1, 2, and 3. Our choice of signature is $(-,+,+,+)$. We raise and lower Greek indices using the spacetime metric, and we employ the convention of setting $ G_N = c = 1 $, where $G_N$ represents the gravitational constant and c denotes the speed of light in vacuum.

Kerr MOG BH is axisymmetric solution of the gravitational field equations. The spacetime geometry of a rotating Kerr MOG BH is governed by its angular momentum a and mass M as well as a deformation parameter α, which is provided by (in Boyer Lindquist coordinates) [9]

where $G =G_{\rm N}(1+\alpha)$ is an enhanced gravitational constant with the contribution of Newton's gravitational constant $G_{\rm N}$ and deformation rate α. The Newtonian mass M and ADM mass $ {\cal{M}} $ are related with $ {\cal{M}}=(1+\alpha) M $. Furthermore, Kerr MOG metric has two horizons termed as the outer horizon $ (r_+) $ and inner horizon $ (r_-) $, similar to a Kerr BH determined by $ \Delta=0 $, namely

Furthermore, the two horizons are referred to as the event horizon and Cauchy horizon, respectively. They are provided in [3] as follows:

A Hamiltonian for light propagation in non-magnetized, pressureless plasma can be defined as [33]

where $ x =\left(x^{0}, x^{1}, x^{2}, x^{3}\right) $ denote spacetime coordinates and $ p =\left(p_{0}, p_{1}, p_{2}, p_{3}\right) $ are canonical momentum coordinates. The plasma frequency $ \omega_\text{p} $of the medium can be determined as

in which m and $ N_\text{e} $ denote the mass of the electron and electron number density, respectively, and e denotes the electric charge. In the case of a vacuum, the plasma frequency is defined as $ \omega_\text{p}(x) = 0$. A plasma is a dispersive medium with an index of refraction n given by [34]

which depends on $ \omega(x) $ (photon frequency) concerning plasma frequency. In this medium light, propagation is possible only if [35]

which assures a nonnegative and real index of refraction. With the metric coefficients defined by the Kerr MOG metric (1), the Hamiltonian in (7) takes the form

If we suppose that $ \omega_\text{p} $ only depends on r and θ, then $ \dfrac{\partial H}{\partial t}=0 $ and $ \dfrac{\partial H}{\partial \phi}=0 $, which implies that $ p_{\text{t}}= -E = -\omega_0 $ and $ p_\phi=L_\text{z} $ are constants of motion. Furthermore, $ p_\phi $ denotes angular momentum and $ \omega_0 $ denotes the frequency of photons as measured by a stationary observer at infinity [34].

According to (9), the Hamilton-Jacobi ($ \mathrm{HJ} $) equation is [34]

Using the expressions above, (10) transforms into the following:

Here, we have constants of motion $ p_t = \dfrac{\partial S}{\partial t} $ and $ p_\phi = \dfrac{\partial S}{\partial \phi} $, corresponding to the conserved energy and angular momentum of the light ray, respectively. Hence, by using separation ansatz [36]:

By substituting $ S_{\theta}^{\prime}(\theta)=\dfrac{\partial S}{\partial \theta} $ and $ S_{r}^{\prime}(r)=\dfrac{\partial S}{\partial r} $ into (11), we obtain the following:

Furthermore, the $ \mathrm{HJ} $ equation, ${\cal{ H}} = 0 $, will be separable in the variables r and θ only if the plasma distribution has the form [34]:

with some functions $ f_\text{r}(r) $ and $ f_{\theta}(\theta) $. Thus, using equation (14), we can ensure that equations of motion are fully integrable. The $ \mathrm{HJ} $equation then takes the form

where $ {\cal{C}} $ denotes the Carter constant. With $ S_{\theta}^{\prime}(\theta)= p_{\theta} $ and $ S_{r}^{\prime}(r)= p_\text{r} $, we can express the components of 4-momentum as

The insertion of equation (16) into Hamilton's equations $ \dot{x}^\mu=\dfrac{\partial H}{\partial p_\mu} $ for $ x^\mu= (t,r,\theta,\phi) $ produces the following first-order equations of motion for the photon:

The radial equation of motion (19) can be rewritten in terms of effective potential $ {\cal{R}}(r) $ as

Here, we introduced the impact parameters $\varphi=\dfrac{ {L}_z}{ {E}}$ and $\zeta=\dfrac{{\cal{C}}}{ {E}^2}$, a third conserved quantity $ {\cal{C}} $ derived by the separability of $ \mathrm{HJ} $ equation. To conclude, condition (14) is necessary and sufficient for the existence of the Carter constant, which ensures full integrability of the equations of motion.

The silhouette of a BH is determined by the unstable circular photon orbits with a fixed radial coordinate $ r= r_\text{p} $, which must satisfy conditions ${\cal{R}}(r) = 0, \; \dfrac{{\rm d}{\cal{R}}}{{\rm d}r} = 0$ [37]. Based on these two conditions, the following can be derived:

where $ \tilde{f}_\text{r} \equiv \dfrac{f_r(r)}{\omega_0^2} $, and we have introduced the photon energy $ E = \omega_0 $. Certain critical values of the parameters φ and ζ can be characterized, and under small perturbations, these critical values lead to either escape or plunge orbits for photons. In this regard, it is important to note that the outline of the shadow is primarily dependent on the critical impact parameters. Given that $ \zeta = 0 $ at the equatorial plane, the roots of (23) and (24) determine the critical orbits of photons $ r_{\text{p}} $ in Kerr MOG spacetime, respectively, at that plane. We can obtain the apparent shape of the shadow as seen by the observer by considering the celestial coordinates X and Y, which represent coordinates on the observer's sky. The general expressions for these celestial coordinates X and Y are given by [20]

With the presence of the plasma, the celestial coordinates are modified as follows [34]:

In this section, we examine various plasma distributions and their impact on the formation of BH shadow. We will analyze different plasma distributions and how they affect the formation of the BH shadow. To ensure the separability of the HJ equations, the proposed distributions must satisfy (14). Our objective here is to define functions $ f_\text{r}(r) $ and $ f_\theta(\theta) $. This will be achieved by mainly considering the plasma distributions discussed in [34].

In this case, we observe the shadow of the Kerr MOG BH in the homogeneous plasma environment. For this, we consider the plasma distribution as follows:

where $ k_0 = \dfrac{\omega_\text{p}^2}{\omega_0^2} $ represents the homogeneous plasma parameter which describes the homogeneous plasma distribution. This parameter must lie within the range (0, 1) to satisfy (8), which describes that the plasma frequency does not exceed the photon frequency. This condition is qualitatively the same as without plasma. However, it is important to note that the shadow boundaries are not defined by (26) for a homogeneous plasma profile. However, in this case, the celestial coordinates are determined by solving (25) along with the geodesic equations given by [39]

No.	$ a/\mathcal{M} $	Range of α
1	0.3	$ 0 \leq \alpha \leq 10.111 $
2	0.4	$ 0 \leq \alpha \leq 5.250 $
3	0.5	$ 0 \leq \alpha \leq 3.0 $
4	0.6	$ 0 \leq \alpha \leq 1.777 $
5	0.7	$ 0 \leq \alpha \leq 1.040 $
6	0.8	$ 0 \leq \alpha \leq 0.562 $
7	0.9	$ 0 \leq \alpha \leq 0.234 $
8	0.99	$ 0 \leq \alpha \leq 0.02 $
9	0.999	$ 0 \leq \alpha \leq 0.002 $

Table 1.  Range of deformation parameter α corresponding to different values of spin parameter a for the Kerr MOG BH. Here, we set mass parameter as $ \mathcal{M}=1 $ [38].

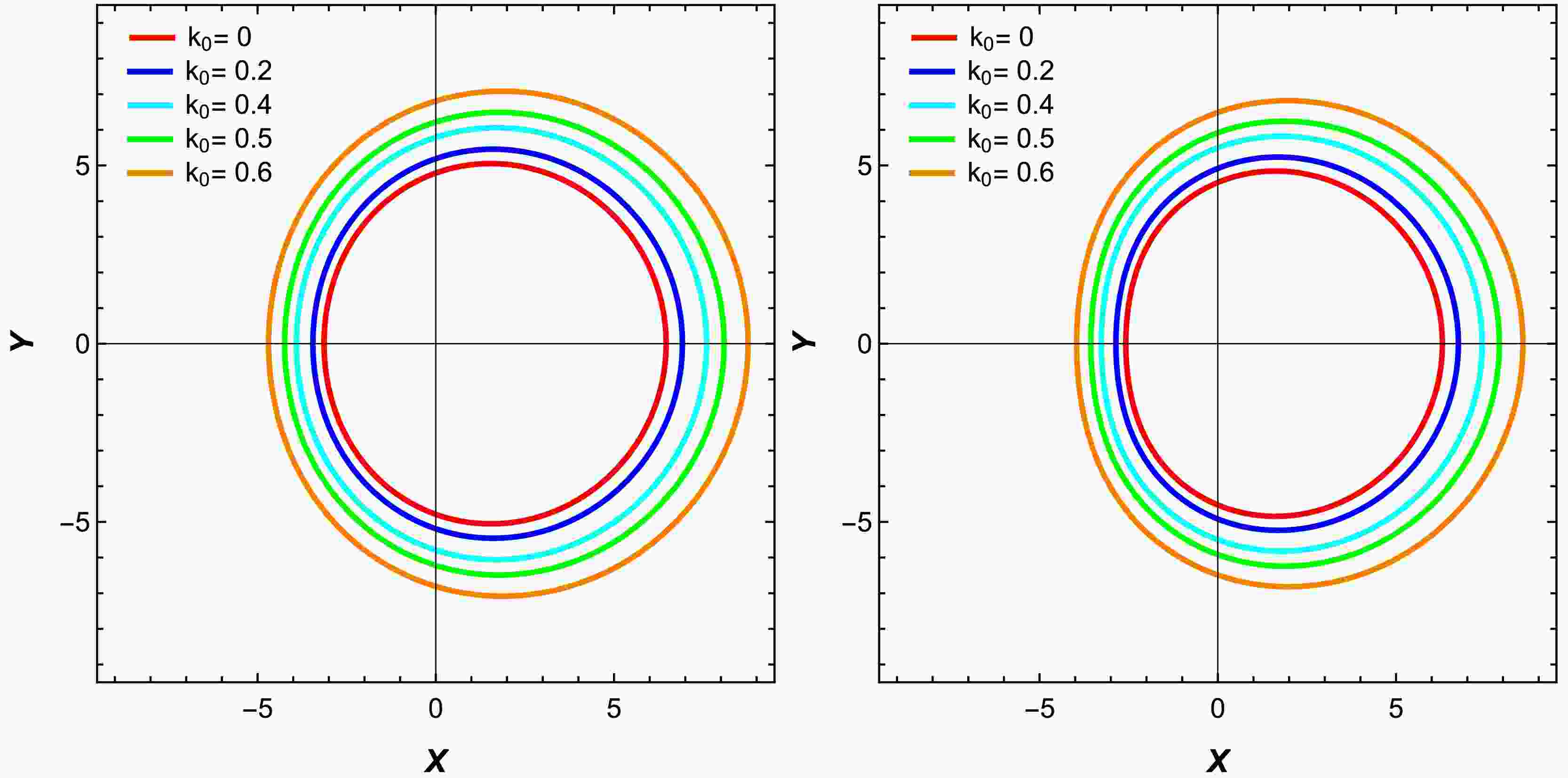
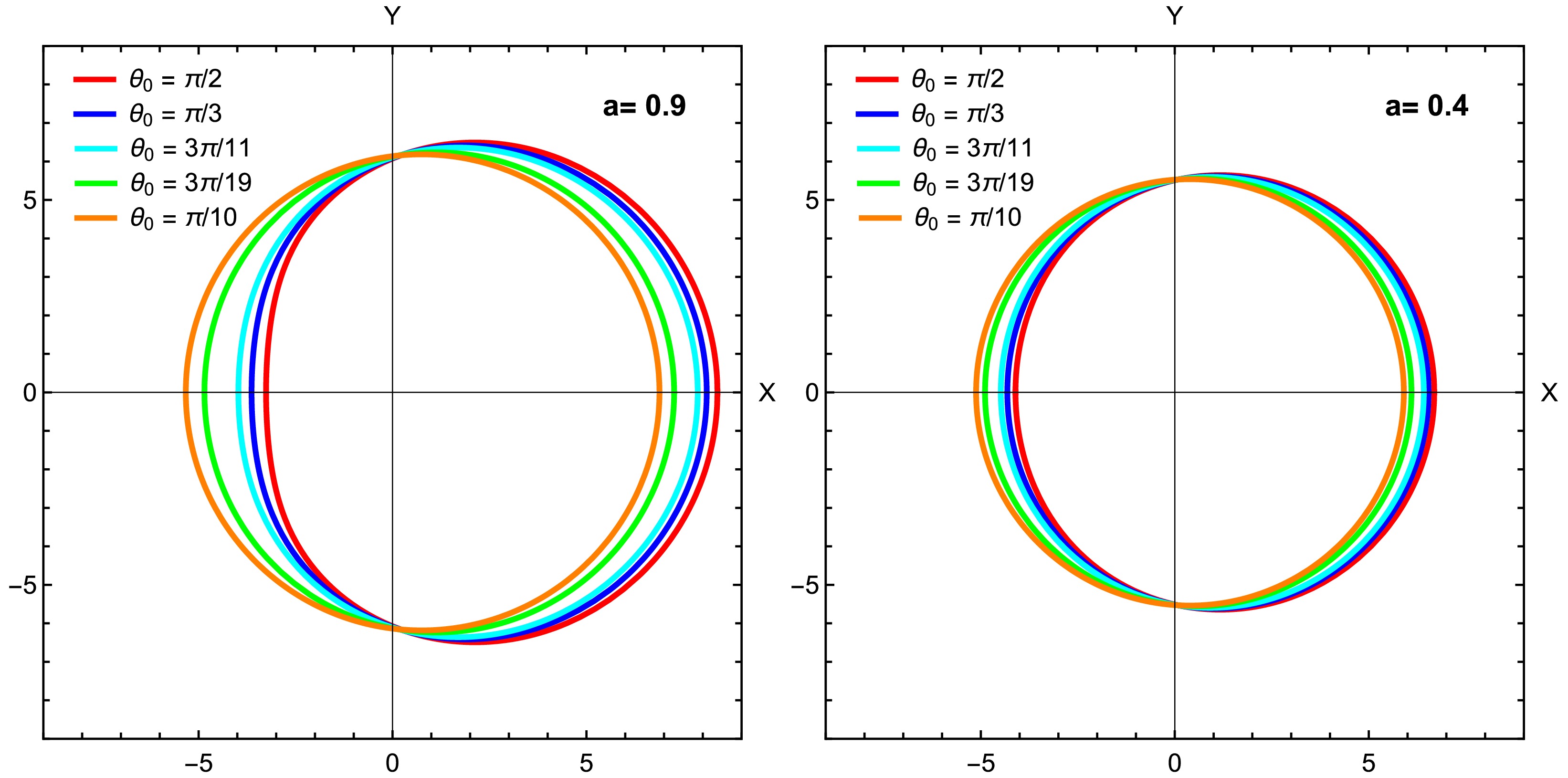
In Fig. 1, the shadow exhibits distinct shapes for different values of $ k_0 $, while the effect of α becomes apparent as its value increases within the range specified in the Table 1, causing the shadow to appear more deformed. Fig. 2 depicts the shadows of a Kerr MOG BH for different deformation parameters within the specified range and varying spin parameters, respectively. In Fig. 2 (right panel), we can observe that the spin of a BH influences its shadow in three ways. First, as the spin increases, the shadow becomes smaller in size, reducing its horizontal and vertical diameters. Second, the shadow's shape transitions from nearly circular to a distinct D-shape, with the flattened side aligned vertically due to co-rotating photon orbits. Third, the shadow shifts to the right, with this displacement becoming more pronounced at higher spin. In Fig. 2 (left panel), we can observe that as the value of α increases, with lower values of spin, the shadow becomes circular and its size decreases. Figure 3 illustrates how the angle $ \theta_0 $ between the position of the observer and rotation axis of the BH affects the shape, size, and position of the shadow. Observers near the rotation axis ($ \theta_0 \rightarrow 0 $) will see a smaller, rounder, and more centered shadow, while observers near the equatorial plane ($ \theta_0 \rightarrow \pi/2 $) will observe a displaced shadow with a larger vertical diameter and D-shaped appearance. Here, we can see how Kerr MOG spacetime affects the shape of the BH shadow as well as the role of the parameter α in this relationship. As α approaches zero, the metric converges to the standard Kerr spacetime. However, with an increase in a with deformation parameter α and $ k_o $, the shadows exhibit distinct evolution patterns that are governed by the properties of the Kerr MOG metric in the presence of homogeneous plasma.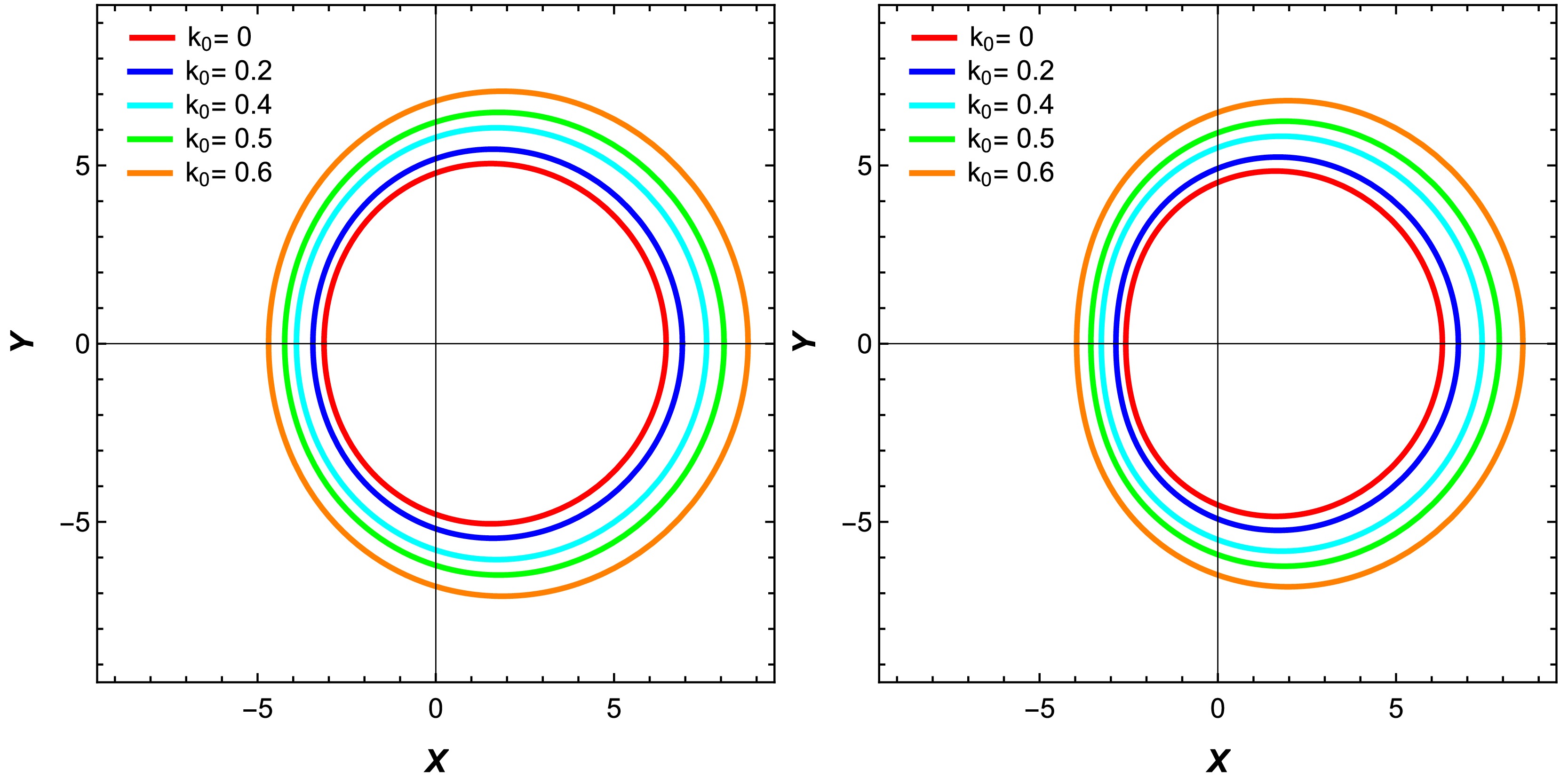

Figure 1.  (color online) Shadows of a BH for varying values of homogeneous plasma parameter $ k_0 $ and deformation parameter α. The observer's angle is fixed at $ \theta_0 = \pi/2 $, with spin $ a = 0.75 $. The left plot illustrates the shadow for $ \alpha = 0.19 $, while the right plot corresponds to $ \alpha = 0.6 $.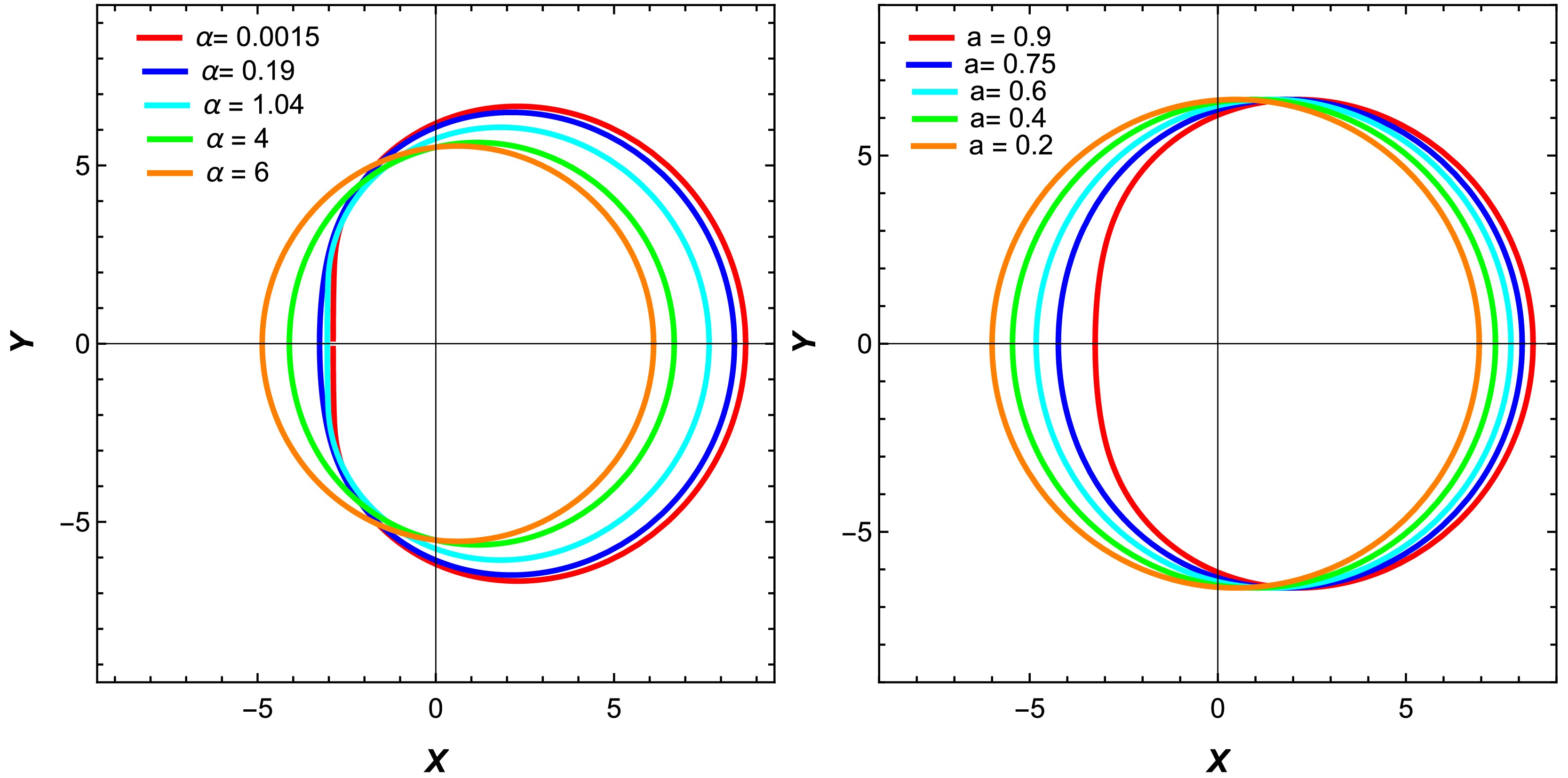

Figure 2.  (color online) Shadows of a BH for varying values of spin and deformation parameter α. In the right plot, $ \alpha = 0.19 $, while the left plot presents the shadow with different spins $ a = 0.2 $ (leftmost, orange), $ a = 0.4 $ (green), $ a = 0.7 $ (cyan), $ a = 0.9 $ (blue), and $ a=0.999 $ (red) with deformation parameter α. The observer's angle is fixed at $ \theta_0 = \pi/2 $, and the plasma parameter is set to $ k_0 = 0.5 $.

Figure 3.  (color online) Shadows for different angular positions $ \theta_0 $ of the observer. The deformation parameter is set to $ \alpha = 0.0015$ in the left plot and $ \alpha = 4$ in the right plot at $ k_0 = 0.5 $.

Now, we investigate the behavior of Kerr MOG BH shadow in an inhomogeneous plasma environment. Here, we choose $ f_\text{r}(r)=0 $ and $ f_{\theta}(\theta)=k_\theta \omega_\text{0}^2 {M}^2 (1+2 \sin ^2\theta) $; the resulting plasma density is

where $ k_\theta $ denotes the latitudinal plasma parameter.

Parameter $ k_\theta $ governs the latitude-dependent component of the plasma distribution, which remains significant near the BH. Although the overall density follows a behavior $ \sim 1/r^2 $ at large r, latitudinal variations influence the photon motion and shadow structure. The celestial coordinates for this case are provided by (26). The shadows corresponding to this plasma density are presented in Fig. 4. A forbidden region emerges around the equatorial plane, dividing the photon region into two disconnected areas. As the plasma frequency increases, this forbidden region expands until it completely encircles the BH. Low-energy photons cannot penetrate this region and are instead deflected.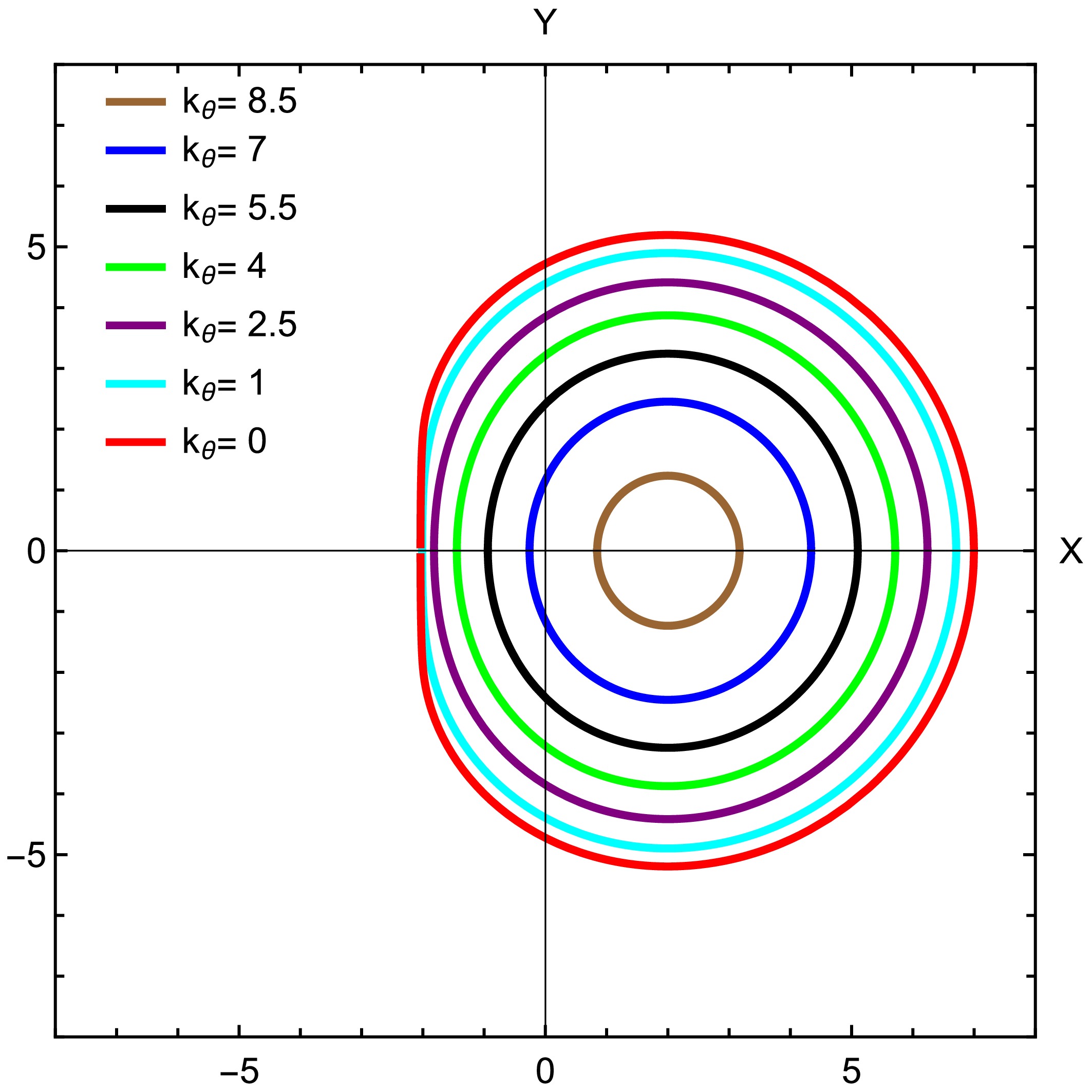

Figure 4.  (color online) This figure shows the shadow for an observer at $\theta_0= {\pi}/{2}$ with spin $ a=0.999 $ and deformation parameter $ \alpha=0.0015 $. When the forbidden region reaches the observer position, the shadow shrinks to a point and vanishes at $ k_\theta \approx 9.1 $

A forbidden region emerges around the equatorial plane, dividing the photon region into two disconnected areas. As the plasma frequency increases, this forbidden region expands until it completely encircles the BH. Low-energy photons cannot penetrate this region and are instead deflected. Consequently, observers located close to the equatorial plane ($ \theta_0 = \pi/2 $) are the first to lose sight of the shadow. The resulting view will be entirely bright for observers beyond the forbidden region and completely dark for those situated between the forbidden region and BH. In Fig. 4, the shadow becomes invisible for certain plasma frequencies, leaving a completely illuminated sky. By examining the photon region, it is observed that a specific critical frequency ratio $ \dfrac{\omega_\text{p}^2}{\omega_0^2} $ exists. Beyond this threshold, a forbidden zone appears where the propagation condition (8) is no longer met. As the plasma frequency increases, the forbidden region expands until it fully encloses the BH.

An interesting example is the case where the plasma frequency depends on r and θ, corresponding to the mass density of dust at rest at infinity. Shapiro [40] provided the analytical form of this matter distribution, even considering a non-zero pressure. When specialized to the pressureless case, the mass density is found to be independent of θ and proportional to $ r^{-3/2} $. In this scenario, the separability condition (14) is not satisfied in a Kerr MOG spacetime with $ a \neq 0 $. This implies that our calculation approach cannot be directly applied.

However, analytical formulas can still be used if we assume an additional θ dependence on the plasma frequency. The plasma density in our model retains a θ dependence due to the term $ \rho^2 = r^2 + a^2 \cos^2 \theta $ in the denominator, which naturally arises from the metric structure. This ensures compatibility with the separability of the $ \mathrm{HJ} $ equation, allowing us to proceed with our calculations. To satisfy (14), adjustments are required to the profile, resulting in

where $ k_r $ denots radial plasma distribution parameter. The celestial coordinates for this case can be represented by Equation (26) as follows [20]:

This profile approaches Rogers’ profile as the distance from the BH increases. The shadows obtained for this plasma profile are shown in Fig. 5. Here, we can observe that increasing the ratio $ \dfrac{\omega_\text{p}^2}{\omega_0^2} $ expands the forbidden region until it entirely encloses the BH at a critical value of $ \dfrac{\omega_\text{p}^2}{\omega_0^2} $. At this point, the shadow vanishes for all observers, leading to a completely bright sky, as shown in Fig. 5 at $ k_r \approx 15.25 $. The ratio $\dfrac{\omega_{\rm p}^{2}}{\omega_0^{2}}$ in this case also varies with the MOG parameter α. As the values of the spin parameter are increased within the deformation parameter α, the ratio $\dfrac{{\omega_{\rm p}^{2}}}{\omega_0^{2}}$ also increases. With the increase in plasma frequency, the effects of the plasma become more significant, counteracting gravitational effects [41]. This occurs because the plasma behaves as a repulsive medium for over-dense plasma distributions, unlike the attractive nature of the gravitational field. Consequently, the shadow shrinks as the plasma frequencies rise.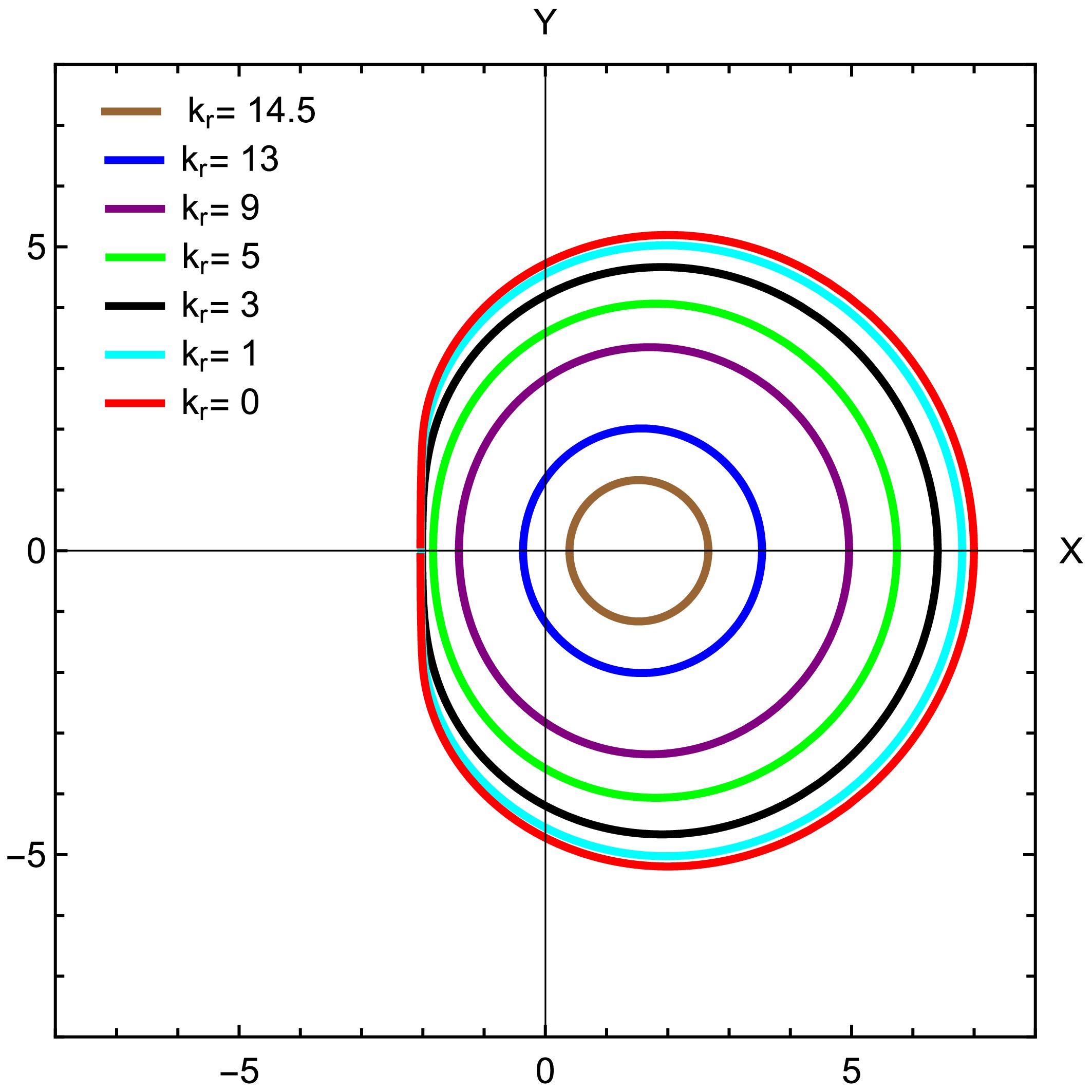

Figure 5.  (color online) Shadow for an observer at infinity with angular position $\theta_0= {\pi}/{2}$, spin $ a=0.999 $, and deformation parameter $ \alpha=0.0015 $. At $ k_r \approx 15.25 $, it vanishes.

Next, we compare the behavior of the Kerr MOG BH by considering homogeneous and inhomogeneous plasma distributions.

For a homogeneous distribution,

However, for the inhomogeneous case, we consider one of the distributions discussed in Sections B and C. The key finding in Fig. 6 is that the shadow in an inhomogeneous plasma environment is smaller than that in a homogeneous environment. We find that the shadow structures for the nonhomogeneous case almost overlap, with negligible deviation (right plot), which contrasts with the results obtained for the homogeneous case.

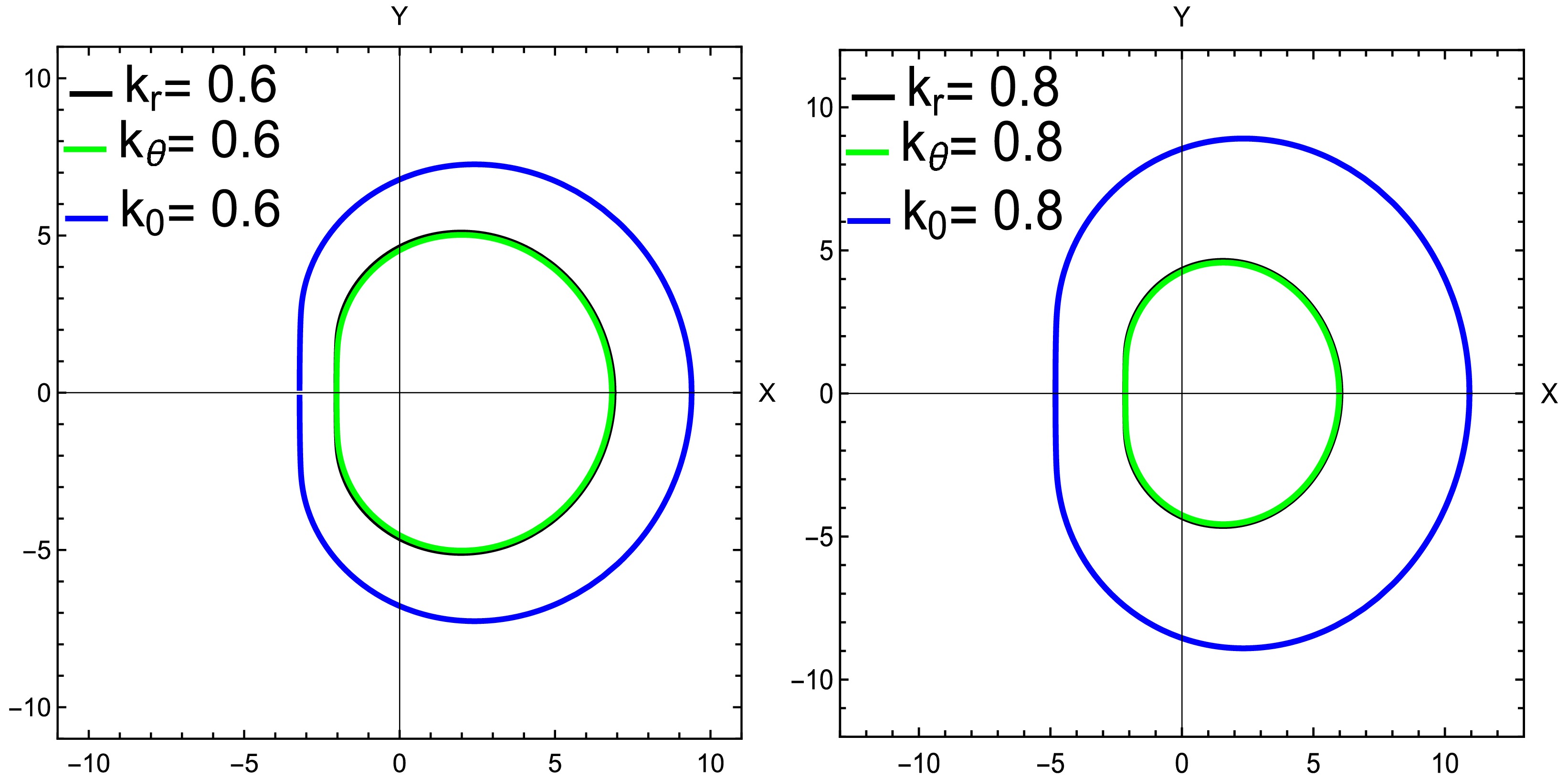
Figure 6.  (color online) Shadow of a Kerr MOG BH with homogeneous and nonhomogeneous plasma distributions. In the left plot, we consider $ a = 0.999 $ with $ \alpha = 0.0015 $, whereas in the right plot, we consider $ a = 0.7 $ with $ \alpha = 1.04 $. The shadow for the nonhomogeneous plasma environment appears smaller than the homogeneous one.

The EHT Collaboration provided the first horizon-scale image of M87* in 2019 [14]. With M87* at a distance of $ d = 16.8 \, \text{Mpc} $ and an estimated mass of $ M = (6.5 \pm 0.7) \times 10^9 M_\odot $ [14], the EHT results constrain the shadow angular diameter to $\theta_d = (42 \pm 3) \, \mu\text{as}$ and a circularity deviation $ \Delta C \leq 0.1 $. The shadow of M87* is consistent with $ \mathrm{GTR} $ predictions for a Kerr BH; however, uncertainties in spin measurements and deviations in quadrupole moments allow for potential modifications [14, 31] due to α and plasma effects. In 2022, EHT shadow observations of Sgr A* in the Milky Way revealed an angular diameter of $d_{\text{sh}} = (48.7 \pm 7) \, {\rm{\mu}}\text{as}$ and a thick emission ring with $\theta_d = (51.8 \pm 2.3) \, {\rm{\mu}}\text{as}$. With Sgr A* having a mass of $ M = 4.0^{+1.1}_{-0.6} \times 10^6 M_\odot $ and distance of $ 8 \, \text{kpc} $, these results align with predictions of $ \mathrm{GTR} $ . Furthermore, they permit exploration of Kerr MOG BH scenarios. Following the findings of [42], we use a distance to M87* of $ D = (16.8 \pm 0.8) $ Mpc and mass of $ M = (6.5 \pm 0.7) \times 10^9 M_\odot $. Based on these values, the average diameter of the shadow can be expressed as [42]

whereas the diameter of the shadow for Sgr A* can be obtained as [42]

As we discussed above, rotating BHs produce shadows that differ significantly from those of nonrotating BHs, which are perfectly circular. When observed from non-polar directions, the shadow of a rotating BH appears displaced in the direction of rotation due to relativistic effects. For sufficiently high spin values, the shadow undergoes further distortion due to the Lense-Thirring effect [44, 45]. Traditionally, the size and distortion of the shadow have been characterized by two parameters, $ \delta_s $ and $ R_s $, introduced by [46]. Here, $ R_s $ represents the radius of a circle that approximates the shadow by passing through its top, bottom, and right edges and is expressed as [47] follows:

$ \delta_s $ quantifies the deviation of the shadow's left edge from this circular boundary [46] as $ \delta_s=\dfrac{D_{cs}}{R_s} $, where $ D_{cs} $ denotes the difference between the left endpoints of the circle and left endpoints of the shadow [48]. Hence, newer observables have been proposed [34, 49−53]. The EHT has provided valuable constraints on BH parameters such as mass, but it cannot directly measure angular momentum [14]. For instance, the EHT-derived mass of M87* aligns with estimates from stellar dynamics but deviates from measurements based on gas dynamics [54, 55]. To address the limitations of existing observables, new metrics for shadow characterization are proposed, including the shadow's area (A), circumference (C), and oblateness (D) [56]. These observables allow for a general description of the shadow's geometry without relying on assumptions of circularity or symmetry, providing a more robust framework for examining BHs across diverse theoretical contexts [57]. Observable A is defined by [58, 59]

From an observational standpoint, astronomers can measure the area, boundary length, and horizontal and vertical diameters of the shadow using precise astronomical imaging techniques. These observables uniquely characterize the shadow, enabling direct estimation of key BH parameters, such as spin and deviation from standard metrics. Recent EHT observations of the M87* BH have provided estimates of the Schwarzschild shadow deviation (δ), a parameter that quantifies the difference between the observed shadow diameter ($d_{\text{metric}}$) and Schwarzschild shadow diameter. This deviation can be defined as [43]

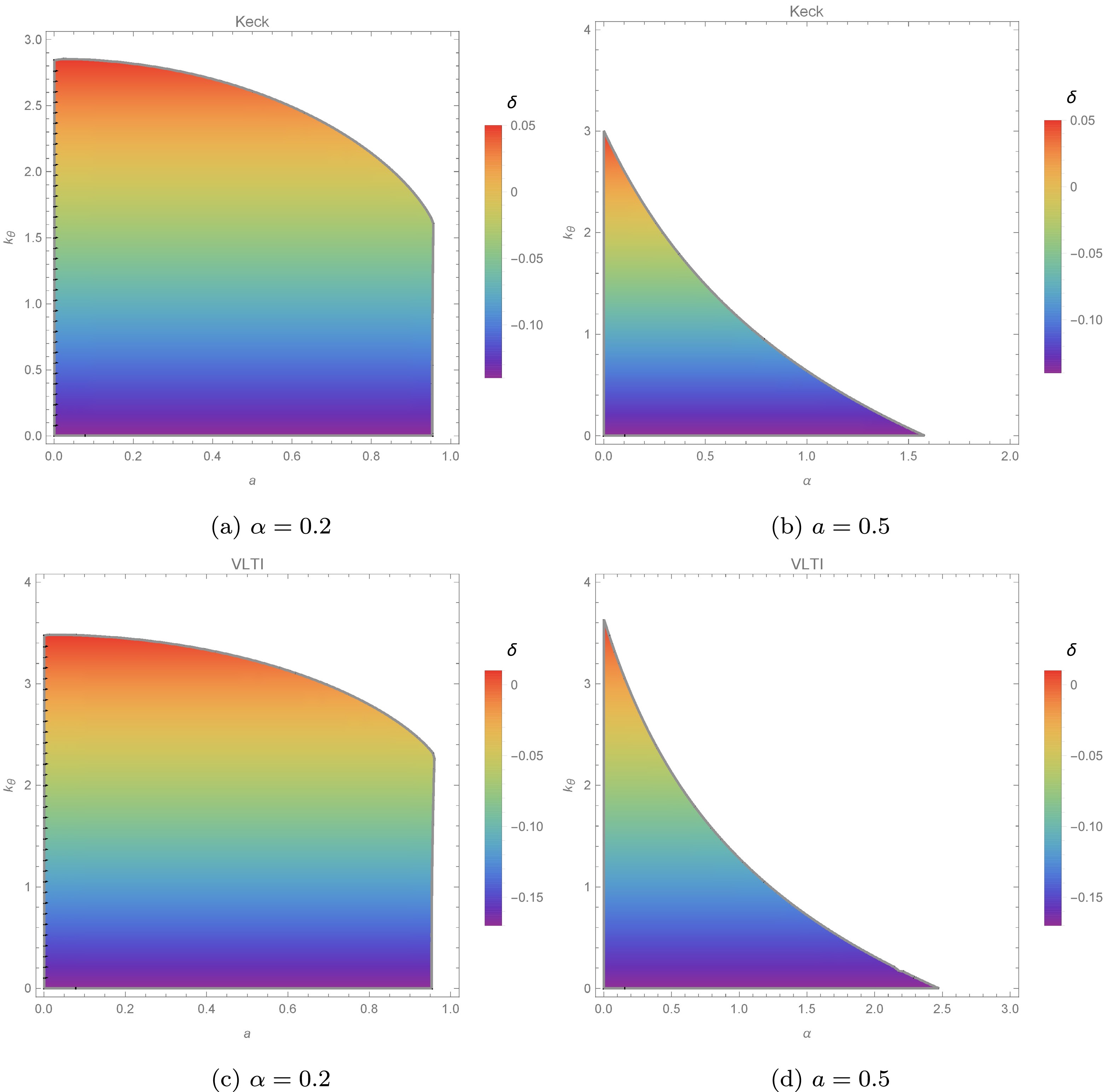
where $R_a = \sqrt{\dfrac{A}{\pi}}$, with A derived from (34). Notably, δ can assume positive or negative values, depending on whether the observed shadow size is larger or smaller than that of a Schwarzschild BH of equivalent mass [60]. According to the results reported by the EHT observations, the measured Schwarzschild deviation is bounded as $ \delta = -0.01 \pm 0.17 $ [14, 43].

The EHT utilized two distinct priors for the angular size of Sgr A*, derived from observations by Keck and the Very Large Telescope Interferometer (VLTI), to estimate the bounds on the fractional deviation observable δ, as follows [43]:

Calculating the mentioned observables, we can constrain the plasma and other parameters by the EHT for the supermassive BH M87* and Sgr A*. Table 2 shows the allowed regions of parameters that satisfy the mentioned constraint of M87* data. Evidently, in homogeneous plasma spacetime and for a small deformation parameter α, the resulting shadow is consistent with EHT data within $ 2\sigma $ uncertainty for the range $ 0 < a < 0.76 $. However, in nonhomogeneous plasma spacetime, the resulting shadow is located in the $ 1\sigma $ confidence region for the mentioned range. In another analysis, we fixed the plasma and rotation parameters and investigated the allowed range of the deformation parameter.

Observable	Homogeneous plasma distribution			Inhomogeneous plasma distribution
	$\alpha=0.2,\; k_0=0.5$			$\alpha=0.2,\; k_r=0.5$
	$ 1 \sigma $	$ 2 \sigma $		$ 1 \sigma $	$ 2 \sigma $
$ d_{sh} $	$ a \in(0.76,0.9] $	$ a \in[0,0.76] $		$ a \in[0,0.75] $	$ a \in(0.75,0.9] $
δ	–	$ a \in[0,0.9] $		$ a \in[0,0.9] $	–
Observable	$ a=0.5, k_0=0.5 $			$ a=0.5, k_r=0.5 $
	$ 1 \sigma $	$ 2 \sigma $		$ 1 \sigma $	$ 2 \sigma $
$ d_{sh} $	$ \alpha \in(0.39,3] $	$ \alpha \in[0,0.39] $		$ \alpha \in[0,0.41] $	$ \alpha \in(0.41,3] $
δ	$ \alpha \in[0.83,3] $	$ \alpha \in[0,0.83) $		$ \alpha \in[0,2.1] $	$ \alpha \in(2.1,3] $
Observable	$ a=0.5, \alpha=0.2 $			$ a=0.5, \alpha=0.2 $
	$ 1 \sigma $	$ 2 \sigma $		$ 1 \sigma $	$ 2 \sigma $
$ d_{sh} $	$ k_0 \in[0,0.47) $	$ k_0 \in[0.47,0.603] $		$ k_r \in[0,1.23] $	$ k_r \in(1.23,5.15] $
δ	$ k_0 \in[0,0.417) $	$ k_0 \in[0.417,0.589] $		$ k_r \in[0,3.9] $	$ k_r \in(3.9,7.8] $

Table 2.  Constraints on BH parameters using EHT data of M87*.

We noticed that, in homogeneous (nonhomogeneous) plasma spacetime and for intermediate values of the rotation parameter, the resulting shadow is in agreement with observations data of M87* within $ 1\sigma $ ($ 2\sigma $) uncertainty for a wide range of α. We also fixed the rotation and deformation parameters and found the allowed range of the plasma parameter. According to our findings, the probability of finding results consistent with observational data is higher in a nonhomogeneous plasma distribution than in a homogeneous distribution.

We continue our analysis by constraining parameters using EHT data of Sgr A*. The allowed range of parameters is addressed in Table 3. It can be observed that the resulting shadow is more consistent with observational data in a nonhomogeneous environment. Furthermore, this table indicates the allowable region of parameters that satisfy the Keck and VLTI bounds. In a nonhomogeneous plasma distribution, all values of the rotation parameter satisfy VLTI and Keck bounds within $ 1\sigma $ uncertainty. While in a homogeneous plasma distribution, no value of a satisfies the $ 1\sigma $ VLTI bound, and only the range $ 0.52<a<0.9 $ satisfies the $ 1\sigma $ Keck bound. For fixed rotation and plasma parameters and in both homogeneous and nonhomogeneous plasma distributions, a range of α that satisfies the $ 1\sigma $ VLTI bound is wider than a range that satisfies the $ 1\sigma $ Keck bound. Comparing Table 2 with Table 3, it can be determined that, for small plasma parameters, Sgr A* BH can be a suitable model for MOG BHs, while for intermediate values of $ k_{0}/k_{r} $, M87* BH is a suitable model for MOG BHs.

Observable	Homogeneous plasma distribution			Inhomogeneous plasma distribution
	$ \alpha=0.1, k_0=0.2 $			$ \alpha=0.1, k_r=0.2 $
	$ 1 \sigma $	$ 2 \sigma $		$ 1 \sigma $	$ 2 \sigma $
$ d_{sh} $	$ a \in(0.48,0.9] $	$ a \in[0,0.48] $		$ a \in[0,0.9] $	–
δ (VLTI)	–	$ a \in[0,0.9] $		$ a \in[0,0.9] $	–
δ (Keck)	$ a \in(0.52,0.9] $	$ a \in[0,0.52] $		$ a \in[0,0.9] $	–
Observable	$ a=0.5, k_0=0.2 $			$ a=0.5, k_r=0.2 $
	$ 1 \sigma $	$ 2 \sigma $		$ 1 \sigma $	$ 2 \sigma $
$ d_{sh} $	$ \alpha \in(0.092,3] $	$ \alpha \in[0,0.092] $		$ \alpha \in[0,3] $	–
δ (VLTI)	$ \alpha \in(0.041,3] $	$ \alpha \in[0,0.041] $		$ \alpha \in[0,2.25] $	$ \alpha \in(2.25,3] $
δ (Keck)	$ \alpha \in(0.108,3] $	$ \alpha \in[0,0.108] $		$ \alpha \in[0,1.5] $	$ \alpha \in(1.5,3] $
Observable	$ a=0.5, \alpha=0.1 $			$ a=0.5, \alpha=0.1 $
	$ 1 \sigma $	$ 2 \sigma $		$ 1 \sigma $	$ 2 \sigma $
$ d_{sh} $	$ k_0 \in[0,0.203] $	$ k_0 \in(0.203,0.427] $		$ k_r \in[0,5.6) $	$ k_r \in[5.6,9.5] $
δ (VLTI)	$ k_0 \in[0,0.103] $	$ k_0 \in(0.103,0.297] $		$ k_r \in[0,4.1] $	$ k_r \in(4.1,6.4] $
δ (Keck)	$ k_0 \in[0,0.197] $	$ k_0 \in(0.197,0.361] $		$ k_r \in(0,3.4) $	$ k_r \in[3.4,5.9] $

Table 3.  Constraints on BH parameters using the EHT data of Sgr A*.

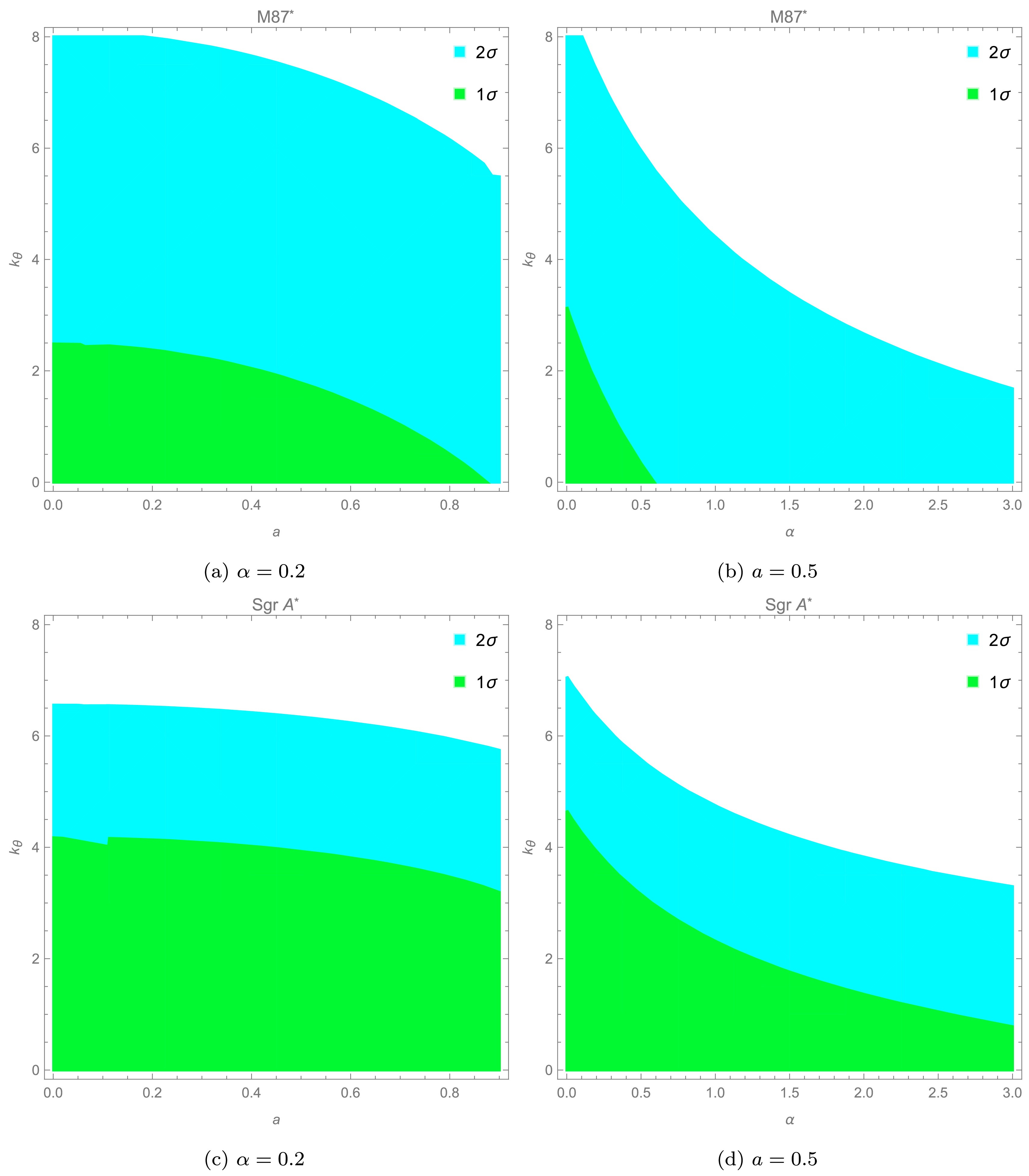
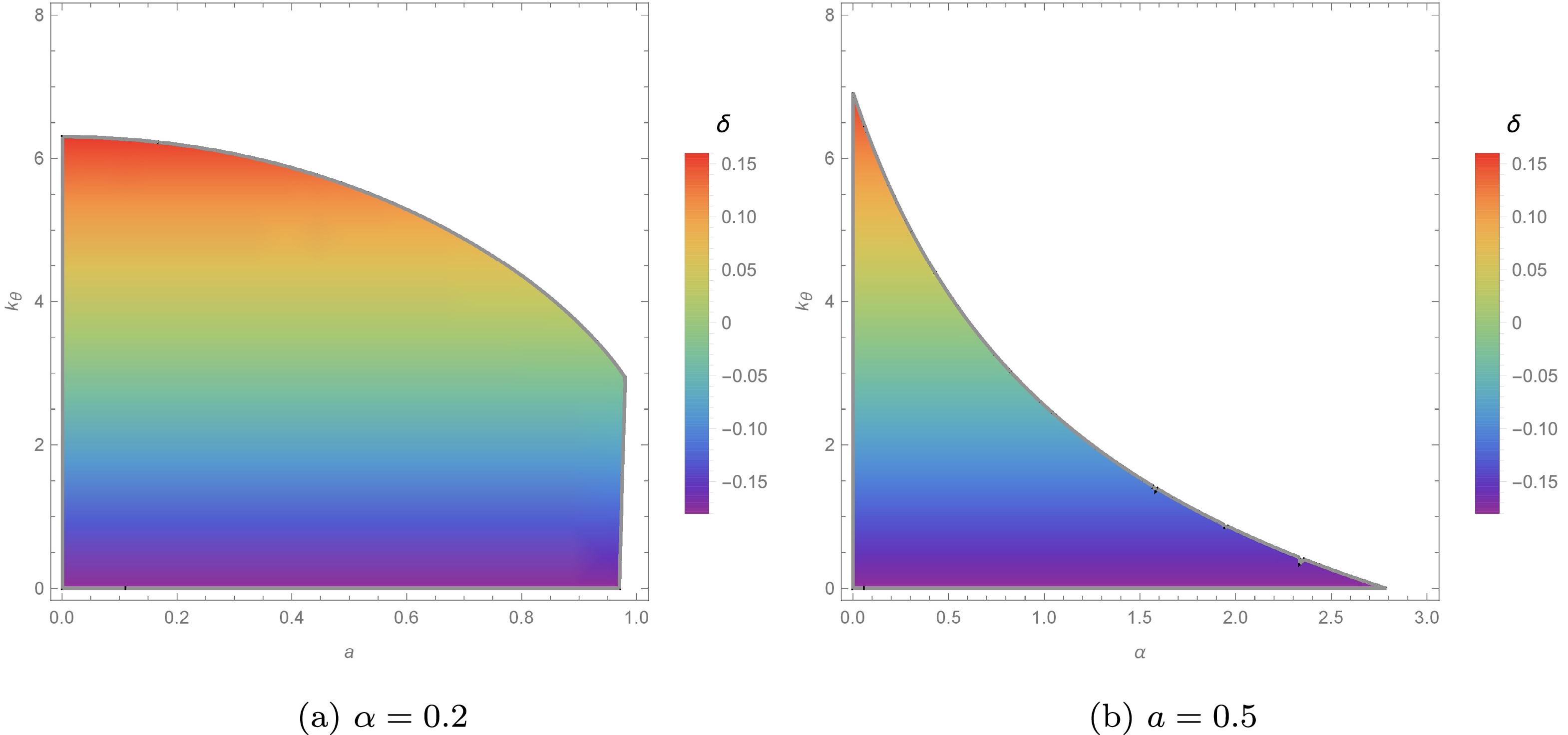
To determine the allowed region of parameters in latitudinal plasma distribution, we plotted Figs. 7−9. From Fig. 7, it can be observed that the allowed range of parameters a, α, and $ k_{\theta} $, for which $ d_{sh} $ agrees with the Sgr A* data, is wider than the range that matches M87* data. Figure 8 shows the regions of parameters that satisfy the constraint on the deviation δ using values reported by M87* measurements. As mentioned earlier, δ can be negative (positive) if the BH shadow size is smaller (greater) than the Schwarzschild BH of the same mass. From Fig. 8, it can be determined that, for a small (large) latitudinal plasma parameter, an MOG BH with the same mass as that of the Schwarzschild BH exhibits a shadow smaller (greater) than that of the Schwarzschild BH. To estimate upper and lower bounds of parameters using VLTI and Keck measurements, we plot Fig. 9. It is clear that the ranges of parameters satisfying the VLTI bound are wider than those for the Keck bound.

Figure 7.  (color online) Constraints on BH parameters with the EHT observations of M87* and Sgr A*.

Figure 9.  (color online) Shadow diameter deviation from that of a Schwarzschild BH as a function of a, α, and $ k_{\theta} $ based on Sgr A* data.

Figure 8.  (color online) Shadow diameter deviation from that of a Schwarzschild BH as a function of a, α, and $ k_{\theta} $ based on M87* data.

The energy emission rate associated with BHs, particularly through the mechanism known as Hawking radiation, is a fascinating interplay of quantum mechanics and $ \mathrm{GTR} $. This process involves the creation of virtual particle pairs near the event horizon of a BH, where one particle escapes while the other falls into the BH, effectively reducing its mass [61]. For Kerr MOG BHs, this analysis becomes more complex due to the modifications in spacetime geometry introduced by the STVG framework of the theory. These modifications influence critical parameters such as the Hawking temperature. By extending the methods of analyzing Hawking radiation to the Kerr MOG scenario, it is possible to explore how modified gravity affects BH thermodynamics and energy emission characteristics. According to [47], the energy emission rate can be expressed in its general form as

where ω denotes the frequency of photons, and $R_{s}$ denotes the radius of the shadow provided in (33). The corresponding formula of the Hawking temperature is as follows:

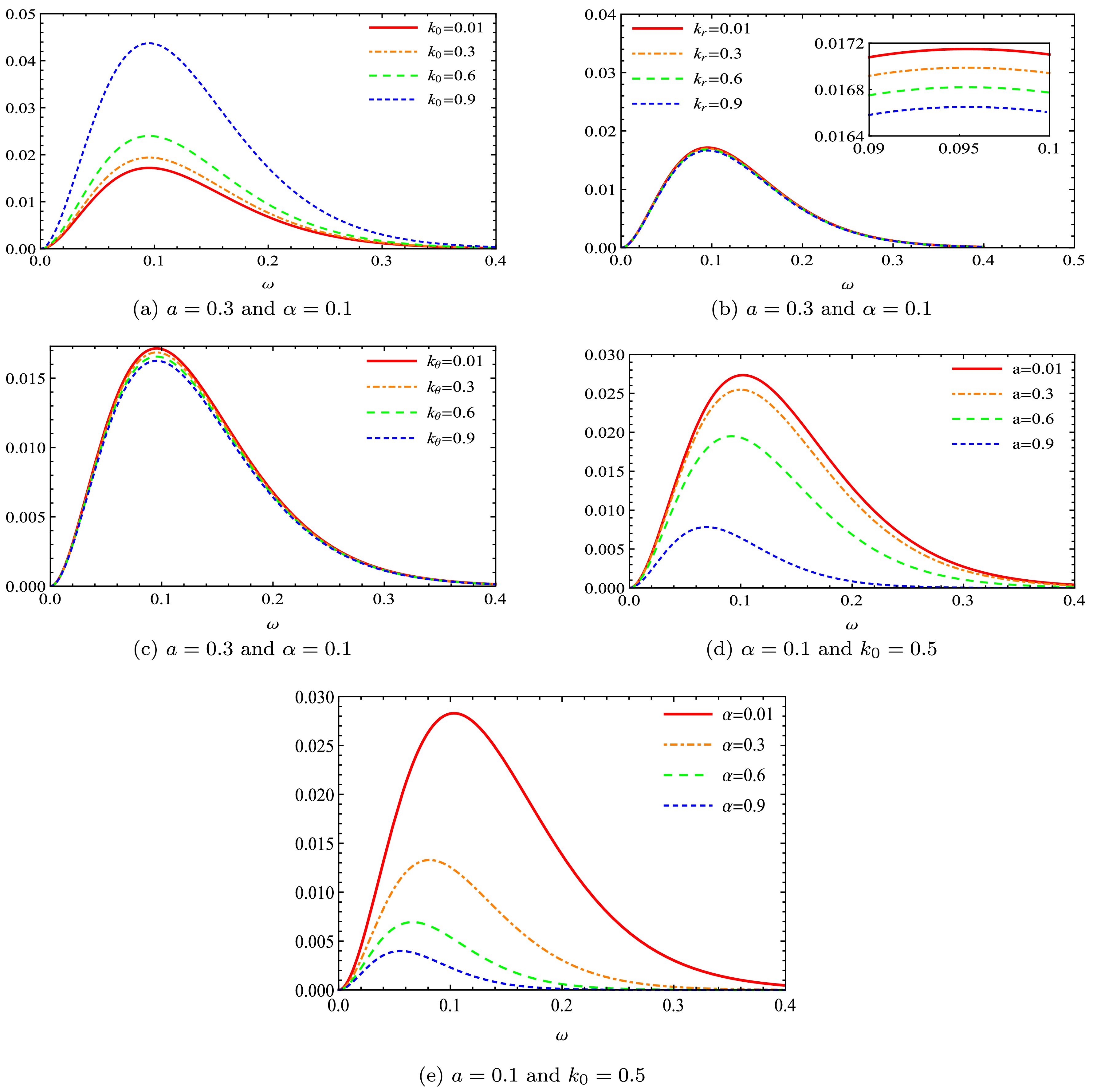
where $r_{e}$denotes the event horizon of the BH. To show how the energy emission rate is affected by the parameters of the model, we plot Fig. 10. Figure 10(a) illustrates the influence of the homogeneous plasma parameter $ k_{0} $ on the emission rate, verifying that the evaporation process can be faster for a BH located in homogeneous plasma spacetime. This implies that the BH has a shorter lifetime in a homogeneous plasma distribution. From Figs. 10(b) and 10(c), it can be observed that the effect of nonhomogeneous plasma parameters on the emission rate is opposite to $ k_{0} $ effect, implying that the BH has a longer lifetime in nonhomogeneous plasma spacetime. Comparing Fig. 10(b) and 10(c) with 10(a), it can be observed that nonhomogeneous plasma parameters have an insignificant effect on the emission rate in comparison with the homogeneous plasma parameter. Regarding the effect of the rotation parameter a and deformation parameter α on this optical quantity, Figs. 10(d) and 10(e) depict that both parameters decrease the emission rate, implying that the evaporation process can be slower for fast-rotating BHs.

Figure 10.  (color online) Energy emission rates $\dfrac{{\rm d}^2E(\omega)}{{\rm d}\omega {\rm d}t}$ plotted on the vertical axis with respect to frequency ω for different values of a, α, $ k_0 $, $ k_r $, and $ k_{\theta} $.

In this section, we investigate the influence of plasma distributions on the deflection angle within the deformation parameter. When the value of $ \dfrac {\omega_\text{p}^2}{\omega_0^2} $ increases from the critical value, a photon arriving from infinity will be reflected back to infinity after reaching a certain distance. To a distant observer, the photon's trajectory will not appear as a straight line but will be bent due to the curvature of spacetime.

Here, we aim to examine the deflection angle of a photon as it passes by the BH. Based on the equations of motion, we obtain the following:

As $ -p_t= \omega_0 $ and considering $ H=0 $, we can rewrite the aforementioned expression as [62]

where

and$ k=(k_0,k_r,k_\theta) $. At a minimum distance $R, {\rm d} r / {\rm d} \phi=0$ is satisfied, and therefore, we have

Integrating (38) with respect to r, we obtain the representation of the deflection angle of the light ray in Kerr MOG spacetime, provided by [62]

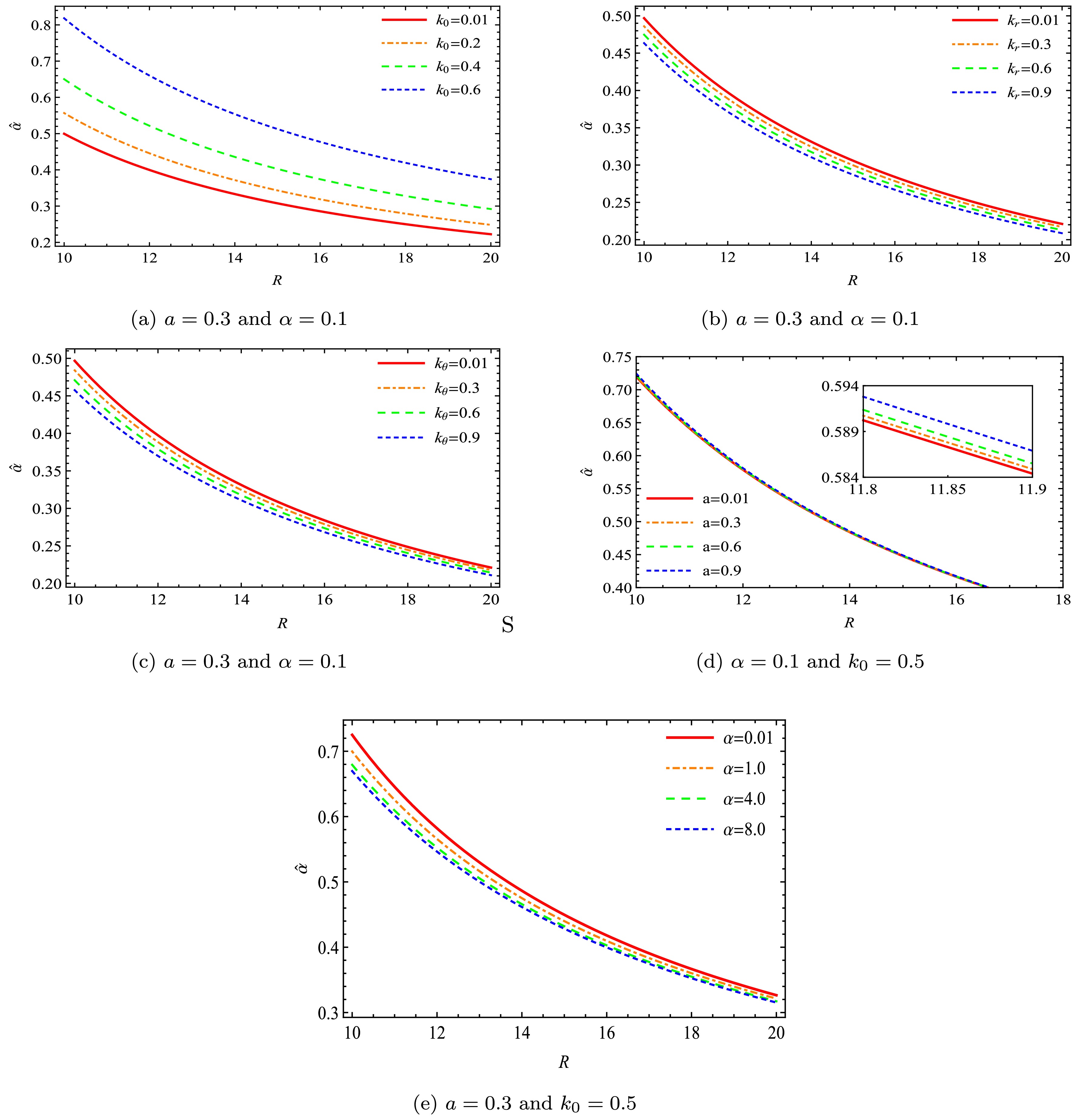
The behavior of the deflection angle of light $ \hat{\alpha} $ concerning the impact parameter b is illustrated in Fig. 11. From Fig. 11(a), it can be determined that light rays are deflected more by BHs in homogeneous plasma spacetime, whereas an opposite behavior is observed in nonhomogeneous plasma spacetime (see Figs. 11(b) and 11(c)). Fig. 11(d) displays the effect of the spin parameter on $ \hat{\alpha} $ and confirms that an increase in this parameter leads to an increase in the deflection angle. The influence of the deformation parameter on $ \hat{\alpha} $ is illustrated in Fig. 11(e), verifying that the deflection angle decreases as α increases.

Figure 11.  (color online) Deflection angle vs. distance R for different values of a, α, $ k_{0} $, $ k_{r} $, and $ k_{\theta} $.

We investigated light propagation in non-magnetized, pressureless plasma, which is a dispersive medium with a frequency-dependent refractive index in Kerr MOG spacetime. The gravitational field is determined solely by the mass, spin, and MOG parameter α of the Kerr MOG BH. The gravitational field of the plasma particles is not included in this analysis. In this model, the presence of the plasma affects only the trajectories of the light rays. We applied the Hamiltonian formalism to describe photon dynamics within the plasma environment. Here, we utilized $ \mathrm{HJ} $ equations and separated the equation by applying a specific condition on the plasma density and attained the generalized Carter constant [34]. Based on the separability condition, we identify photon regions that meet this criterion and provide an analytical formula for the boundary curve of the shadow.

It was observed that the spacetime model influenced the shape and size of the shadow in distinct ways, with the deformation parameter α playing a crucial role. If the plasma frequency is much smaller than the photon frequency, the shadow closely resembles one from the pure gravity case. However, when the plasma frequency approaches the photon frequency, the shadow’s properties change significantly depending on the plasma distribution. Notably, there exists a certain plasma frequency ratio, $\dfrac{\omega_{\rm p}^{2}}{\omega_0^{2}}$, above which the shadow becomes invisible. This threshold depends on the metric and α parameter. Consequently, the size and shape of the shadow are altered in the presence of a plasma environment around the BH, depending significantly on the ratio between the plasma frequency and photon frequency, as well as the deformation parameter α. Then, our analysis revealed that the shadow characteristics of M87* and Sgr A* are more consistent with EHT observational data in nonhomogeneous plasma spacetime than in homogeneous plasma spacetime. For a small deformation parameter α, the shadow aligns within the $ 2\sigma $ uncertainty in homogeneous plasma and within $ 1\sigma $ in nonhomogeneous plasma.

The probability of finding the results consistent with observational data is higher in a nonhomogeneous plasma distribution than in a homogeneous distribution. These findings underscore the role of plasma properties and spacetime deformations in refining models of supermassive BHs. Using EHT data of Sgr A* highlights that the resulting shadow is more consistent with observational data in a nonhomogeneous plasma environment. In a nonhomogeneous plasma distribution, all values of the rotation parameter a satisfy VLTI and Keck bounds within $ 1\sigma $ uncertainty, while in a homogeneous plasma distribution, no value of a satisfies $ 1\sigma $ VLTI bound, and only a limited range satisfies $ 1\sigma $ Keck bound. For fixed rotation and plasma parameters, the range of the deformation parameter α satisfying $ 1\sigma $ VLTI bound is broader than the range satisfying $ 1\sigma $ Keck bound. Comparing Sgr A* and M87*, we find that, for a small plasma parameter, Sgr A* serves as a more suitable model for MOG BHs, while for intermediate values of $ k_{0} $ and $ k_{r} $, M87* aligns better.

The energy emission rate of BHs is significantly affected by the plasma distribution and model parameter α. The BH undergoes a faster evaporation process in homogeneous plasma spacetime, leading to a shorter lifetime. In contrast, nonhomogeneous plasma parameters extend the lifetime of the BH and have an opposite effect on the emission rate, when compared with homogeneous plasma parameters. Furthermore, the impact of nonhomogeneous plasma parameters on the emission rate is relatively minor when compared with that of homogeneous plasma parameters. The spin parameter a and deformation parameter α also decrease the emission rate, indicating that fast-rotating BHs as well as BHs with larger deformation parameters evaporate more slowly, resulting in longer lifetimes. Finally, we determine that light rays are more strongly deflected by BHs in homogeneous plasma spacetime, while the deflection angle is reduced in nonhomogeneous plasma spacetime. The spin parameter a enhances the deflection angle, indicating that BHs with higher rotation parameters bend light more significantly. In contrast, α decreases the deflection angle, suggesting that greater deformation reduces the gravitational lensing effect of the BH.