Non-linear corrections to the derivative of nuclear reduced cross-section at small x at a future electron-ion collider

The nuclear structure can be determined through Deep Inelastic Scattering (DIS) of leptons off nuclei across a wide range of ($ x, Q^2 $). Nuclear structure functions differ from proton structure functions due to the shadowing effect at $ x{\lesssim}0.1 $, anti-shadowing at $ 0.1{\lesssim}x{\lesssim}0.3 $, the EMC effect at $ 0.3{\lesssim}x{\lesssim}0.7 $ and Fermi motion as $ x{\rightarrow }1 $. The proton structure function of the nucleus in the leading order in the QCD-improved parton model is defined by its parton distributions as [1]

The difference between the nuclear parton distribution functions (nPDFs) and the parton distribution in the free proton is determined by the ratio

The nuclear shadowing effect demonstrates that at small values of x, the gluon distribution in a nucleus is less than the gluon distribution in a nucleon. It is essential to determine the gluon distribution of nucleons within a nucleus, especially at small x values. Nuclear effects play a significant role in $ xg^{A}(x,Q^2) $, and utilizing inclusive observables can help to constrain future electron-nucleus colliders at Brookhaven National Laboratory (eRHIC) [2] and the Electron Ion Collider (EIC) [3]. The behavior of the nuclear gluon distribution can be determined using the momentum sum rule. Nuclear physics with electron-nucleus (eA) collisions can be explored at the Large Hadron electron Collider (LHeC) [4, 5] and the Future Circular electron-hadron Collider (FCC-eh) [6] as proposed in Ref.[7]. The maximum energy envisioned for electron-heavy ion runs would be achieved by colliding $ 18\; {\rm{GeV}} $ electrons with $ 110\; {\rm{GeV}} $ ions for a $ \sqrt{s}=89\; {\rm{GeV}} $ in the EIC Conceptual Design Report [8].

The standard evolution based on the Dokshitzer-Gribov-Lipatov-Altarelli-Parisi (DGLAP) linear equations provides an accurate description of QCD dynamics at moderate to large values of the momentum fractions x of the probed parton and virtualities $ Q^2{\gg}\Lambda^{2}_{QCD} $ but needs modification to include the effects of the resummation of large $ {\ln}(1/x) $. Gluon recombination processes, tame the growth of parton densities towards small x and lead to gluon saturation. Non-linear evolution becomes important when the mass number A is increased or by either decreasing x or some combination of the two [7, 9]. Non-linear modifications to DGLAP evolution equations were first proposed in Refs.[10−13] where two gluon ladders merge into a gluon or a quark-antiquark pair. The study of non-linear corrections is indeed useful for a comprehensive understanding of gluon recombination and saturation [14]. The correlative interactions between gluons become important at extremely small x at fixed $ Q^2 $, where the probability of recombining two gluons into one, in the leading twist approximation, is taken to be the product of two conventional one-gluon distributions by the following form

The region of a nucleon where gluons are distributed is characterized by $ {\cal{R}}_{N} $. The correlation length $ {\cal{R}}_{N} $ determines the magnitude of the nonlinear terms. This value is influenced by how the gluon ladders interact with the nucleon or how the gluons are dispersed within the nucleon. The $ {\cal{R}}_{N} $ is approximately equal to $ {\simeq}5\; {\rm{GeV}}^{-1} $ if the gluons are spread throughout the proton, and it is $ {\simeq}2\; {\rm{GeV}}^{-1} $ if the gluons exhibit a hotspot-like structure [15, 16].

This saturation tamed the increase of gluons by relying on a Froissart-Martin bound [17]. The evolution equations of the correction terms (without the Higher Twist (HT) terms) are given by [10−12]

and

where $ C_{A}=N=3 $ and $ K=\dfrac{9}{8} $. The nuclear target with mass number A is denoted by $ {\cal{R}}_{A} $, and is defined as $ {\cal{R}}_{A}=1.25A^{1/3}\; {\rm{fm}} $. This value is determined by the hotspot-like structure of the gluons within the nucleon. The specific value of $ 1.25\; {\rm{fm}} $ is dependent on the presence of a hotspot-like structure of the gluons. The importance of the non-linear corrections for a nuclear target ¹ (especially heavy nuclei) is visible, as the non-linear terms in Eqs.(4) and (5) scale as $ A^{4/3} $ [18].

Adding these contributions to the DGLAP equations yields the non-linear Gribov-Levin-Ryskin-Mueller-Qiu (GLR-MQ) [10, 11] evolution equations for nuclei in the following forms ²

and

where the non-linear term tames the growth of the distribution functions at small x and leads to their suppression [18−20]. Here $ xg^{A}(x,Q^2) $ is the gluon distribution function of nuclei and $ F_{2}^{A}(x,Q^2)=\sum{e_{i}^{2}}[xq_{i}^{A}(x,Q^2)+x\overline{q}_{i}^{A}(x,Q^2)] $ where $ e_{i} $ is the electric charge of the i-quark or antiquark and $ q_{i}^{A}(x,Q^2) $ is the number density of the i-quarks in the nucleus.

In this paper, we analyze the reduced cross sections for light and heavy nuclei at the center-of -mass (COM) energy of the EIC. We also investigate the recombination of the derivative of the reduced cross section into $ \ln Q^2 $ for a wide range of light and heavy nuclei.

The double differential cross section for deep inelastic scattering (DIS) of an electron-nucleus from an unpolarized nucleus in the one photon exchange approximation has the following form

Here, $ Y_{+}=1+(1-y)^2 $ and y represents the inelasticity. The nuclear reduced cross section $ \sigma_{r}^{A} $ can be standardly defined using the structure functions $ F_{2}^{A} $ and $ F_{L}^{A} $ as follows [7]

The longitudinal structure function in nuclear deep inelastic scattering (nDIS) is an observable that can be used to unfold the gluon distribution [21]. nQCD provides the Altarelli-Martinelli equation [22] in the following form

The scheme-independent coefficient functions for the longitudinal structure function can be found in Ref.[23]. The nuclear effects for the eA scattering can be defined by the ratio of distribution functions as

and

where $ xg(x,Q^2) $ and $ F_{2}(x,Q^2) $ are respectively the gluon distribution and the structure function of a free nucleon.

The expression for $ \sigma_{r}^{A} $ can be rewritten as a function of the structure function $ F^{A}_{2}(x,Q^2) $ and the gluon distribution $ xg^{A}(x,Q^2) $ of nuclei in the following form

Nuclear effects are shown in the ratio of distribution functions. Parameterizations of the nuclear parton distribution functions have been proposed by various groups in Refs.[24−28] and further developed in recent years in Refs.[9, 29−31]. The HIJING2.0 [29] parameterization combines the information on the impact parameter and the target nuclear mass number in a single collision. This parameterization, which is in good agreement with the ALICE experiment at LHC energies, provides a more stringent constraint on gluon shadowing due to the impact parameter dependence on shadowing as reported in Refs.[30, 31] for both light and heavy nuclei

and

where $ s_{q} = 0.1 $, $ s_{g}= 0.22-0.23 $. To accurately model the eA collision discussed in this study, the HIJING2.0 parameterization needs to be integrated over the entire impact parameter space. In this case, according to Refs.[30, 31], the impact parameter b is chosen as central at $ b=0 $ for light nuclei and peripheral at $ b=5\; {\rm{fm}} $ for heavy nuclei.

The non-linear correction to the derivative of the nuclear structure function divided by A (according to Eq.(6)) is defined as follows

This equation defines the magnitude of the non-linear corrections as

Non-linear corrections can be determined from the inclusive nuclear cross section in the low x and $ Q^2 $ region. This behavior can be utilized in a derivative method in an EIC based on the cross section derivative. The derivative of the reduced cross section for nuclei is expressed as ³

Gluon recombination alters the behavior of the parton densities and introduces nonlinear effects. Consequently, the derivative of the nuclear reduced cross section is adjusted due to these nonlinear effects:

where $ {\cal{O}}(\alpha_{s}^{3}) $ represents the non-linear effects to the derivative of the longitudinal structure function of nuclei as

where at moderate inelasticity we observe that the term $ {\cal{O}}(\alpha_{s}^{3}) $ is very small across a wide range of x, therefore

In conclusion, we can safely ignore this term and simplify Eq.(18) for the derivative of the reduced cross section of nuclei to the following form

which is similar to the GLR-MQ evolution equations. Indeed, the effect of the non-linear corrections to the derivative of the reduced cross section of nuclei divided by A is defined as

This is similar to the derivative of the structure functions of nuclei divided by A as

In the following, we consider the non-linear effects on the reduced cross section of nuclei divided by A, based on shadowing effects. The non-linear corrections at the initial scale $ Q_{0}^2 $ are adjusted by applying shadowing corrections [15] for $ x<x_{0}{\equiv}10^{-2} $ through the nuclear parton distribution functions as

where

with

where $ g^{A}_{{\rm{sat}}} $ is the value of the gluon that would saturate the unitarity limit in the leading shadowing approximation in nuclei (for future discussion, please refer to Appendix A). The non-linear corrections to the reduced cross sections of nuclei are defined by the following form

where

and

Therefore, we find that the derivative of the reduced cross section divided by A, due to the non-linear corrections, is defined by the following form

Instead of starting with a theoretically motivated form of the non-linear corrections in deep inelastic scattering, we begin with a parameterization of the deep inelastic distribution functions using the parameterizations of $ F_{2}(x,Q^2) $ and $ G(x,Q^2) $ by Donnachie-Landshoff(DL) [32]. This parameterization is defined for the full range of $ Q^2 $, although it has a limited range of applicability in its describing experimental data. Additionally, we utilize the methods of Block et al.,[33, 34] which apply to large and small $ Q^2 $ and small x. In the subsequent analysis, the gluon distribution and proton structure functions are defined using the Donnachie-Landshoff and Block et al., methods (refer to Appendix B for details).

The EMC [35] effect demonstrates that distribution functions measured between nucleons and nuclei differ, particularly in the lower x region where shadowing effects are significant due to the behavior of gluon density [36]. This effect, resulting from non-linear corrections, is observed in relation to the magnitude of these corrections. Therefore, the non-linear correction to the nuclear shadowing effect, which is linked to the alteration of target gluon recombination, is defined as

where $ {\pi}{\cal{R}}^{2}_{p}=1.55{\pm}0.02\; {\rm{fm}}^2 $ [37] and the parameterization of the nuclear radius ⁴ is $ {\cal{R}}_{A}=1.12A^{1/3}-0.86A^{-1/3}\; {\rm{fm}} $. This equation (i.e., Eq.(31)) predicts that the modification of magnitude appears to be solely due to the nuclear shadowing factor resulting from gluon recombination in nucleons and nuclei. This new phenomenon could be a key factor in the Color Glass Condensate (CGC) [38] theory, which is one of the main topics in hadron physics in the new accelerators at small x limit [39]. Future electron-nucleus colliders are the best candidates for discriminating between saturation models and CGC physics [5, 40, 41]. The CGC forms the initial state, which is important in itself as a new state of matter that depends on the unintegrated gluon distribution (UGD). Recently, the importance of including a finite size for the target on observables sensitive to small-x evolution within the CGC is discussed in Ref.[42].

The non-linear correction to shadowing in nuclei (i.e., Eq.(31)) is explored by comparing the non-linear corrections to the structure functions per nucleon for different nuclei ⁵.

The QCD parameter Λ is determined from the running coupling $ \alpha_{s}(Q^2) $, where $ \Lambda_{{\rm{QCD}}}=0.12\; {\rm{GeV}} $ yields $ \alpha_{s}(M_{z}^2)=0.118 $ for the one-loop coupling, with the number of active flavors being $ n_{f}=4 $. The behavior of the reduced cross section and the non-linear corrections to the derivative of the nuclear reduced cross section are determined for the light nucleus of C-12 and the heavy nucleus of Pb-208 at the hot-spot point $ {\cal{R}}_{A}=1.25A^{1/3}\; {\rm{fm}} $ in Figs.1-6. The results are presented for the kinematic range relevant for the EIC ($ \sqrt{s}=89\; {\rm{GeV}} $ and y less than approximately 1), as indicated by the fact that x values are shown down to $ \; 0.65{\times}10^{-3} $ (or $ y{\simeq}0.97 $) for $ Q^2=5\; {\rm{GeV}}^2 $ ($ x=Q^2/ys $) and $ \; 0.13{\times}10^{-2} $ for $ Q^2=10\; {\rm{GeV}}^2 $.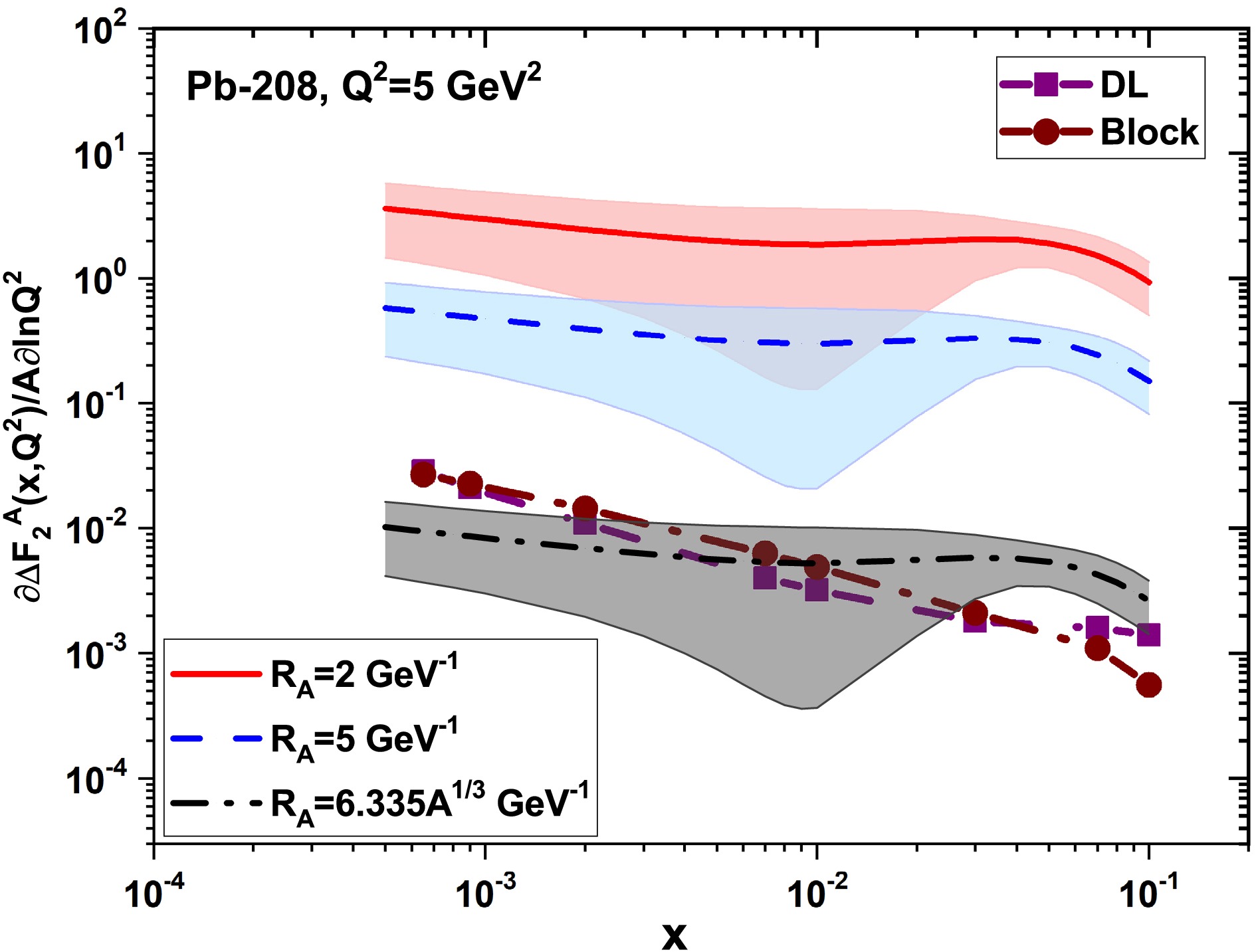

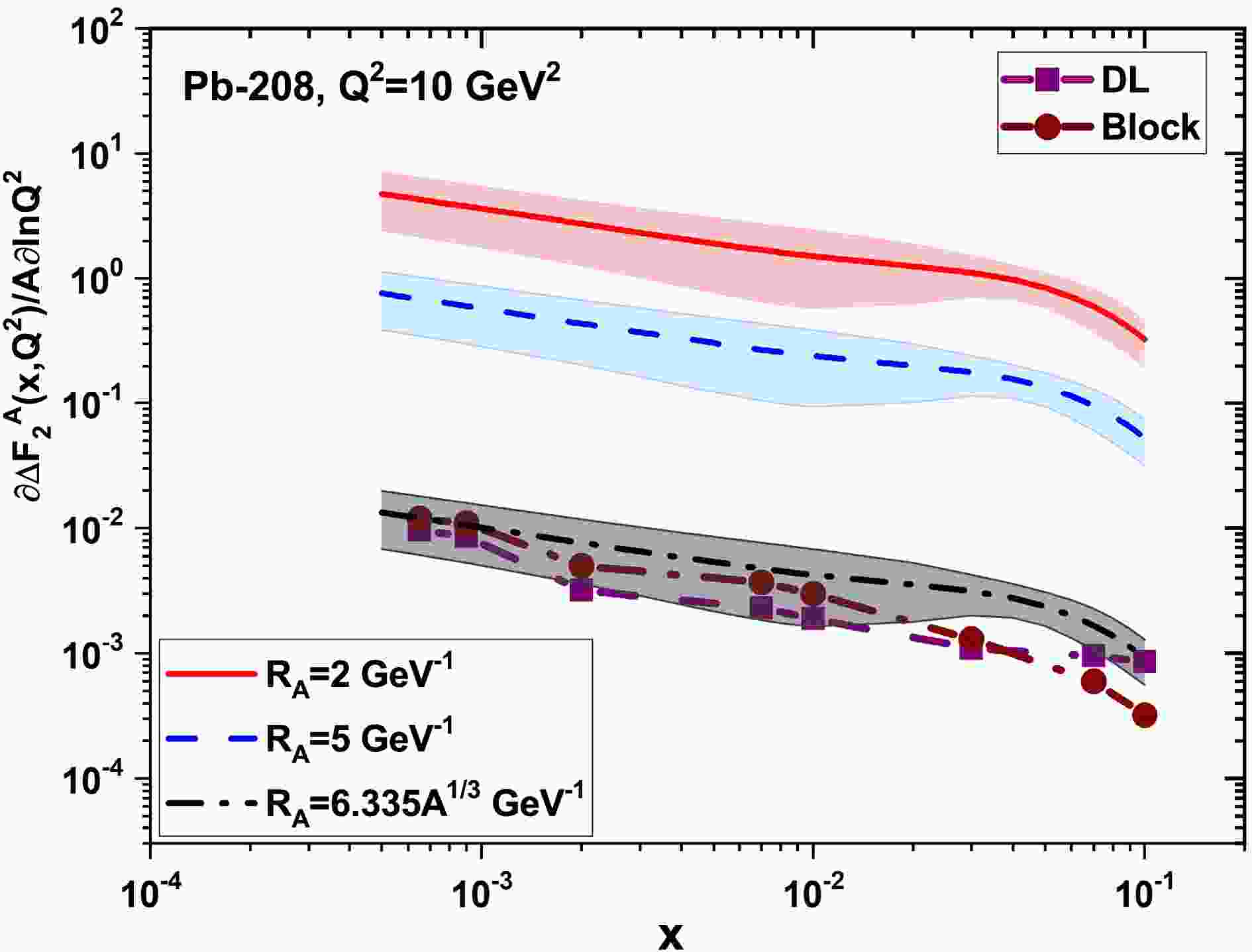
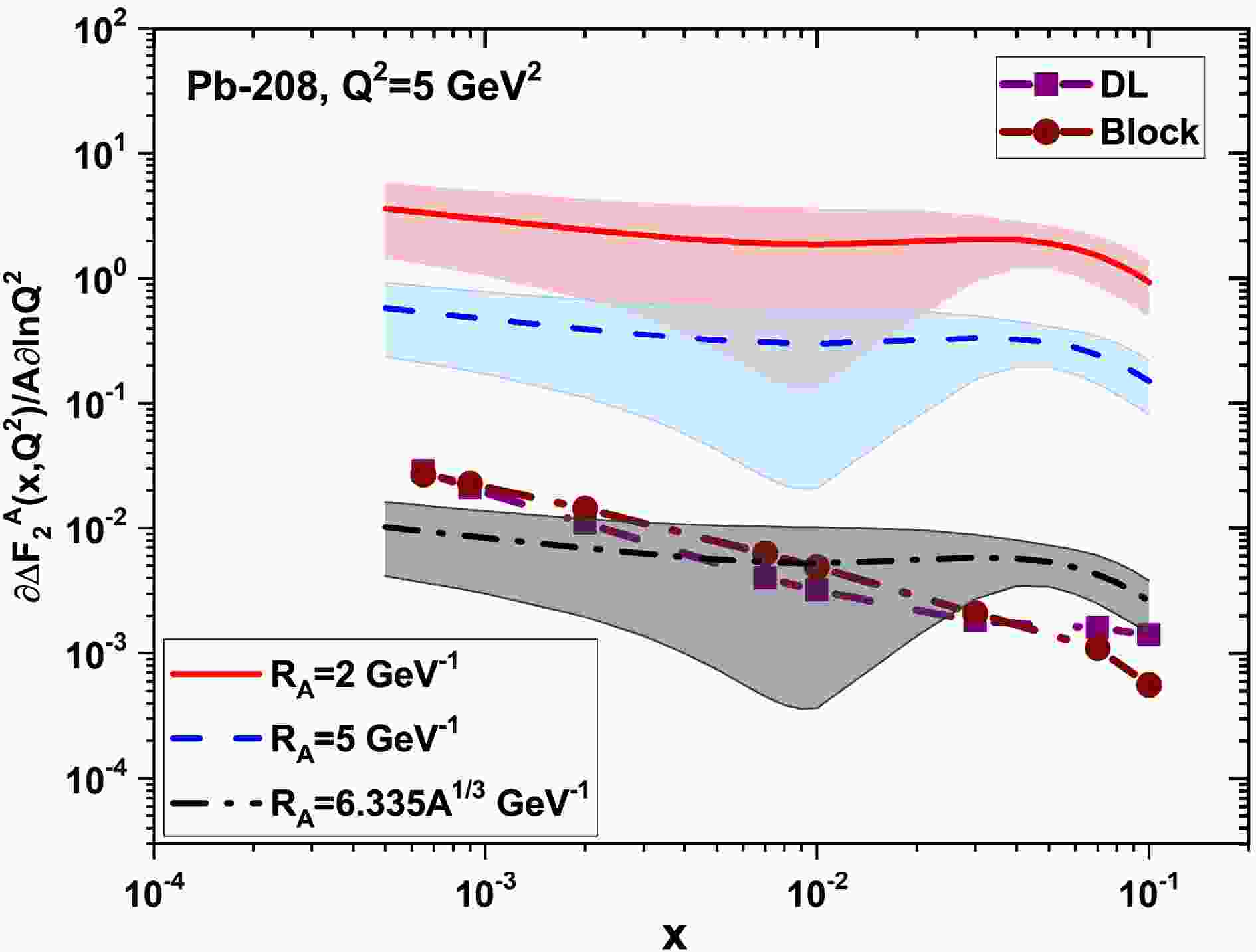
Figure 1.  (color online) The non-linear corrections to $ \frac{1}{A}\frac{\partial}{\partial{\ln}Q^2}{\Delta}F_{2}^{A}(x,Q^2) $ for the heavy nucleus of Pb-208 are shown as a function of the momentum fraction x at $ Q^2=5\; {\rm{GeV}}^2 $ at $ {\cal{R}}_{A}=1.25A^{1/3}\; {\rm{fm}} $. These results are determined by the DL (square-purple) [32] and Block et al (circle-brown) [33, 34] gluon distributions and compared with the nCETQ15 parameterization [45] results at $ {\cal{R}}_{A}=2\; {\rm{GeV}}^{-1} $ (solid curve-red), $ {\cal{R}}_{A}=5\; {\rm{GeV}}^{-1} $ (dashed curve- blue) and $ {\cal{R}}_{A}=6.335A^{1/3}\; {\rm{GeV}}^{-1} $ (dashed- dot curve- black) with uncertainties.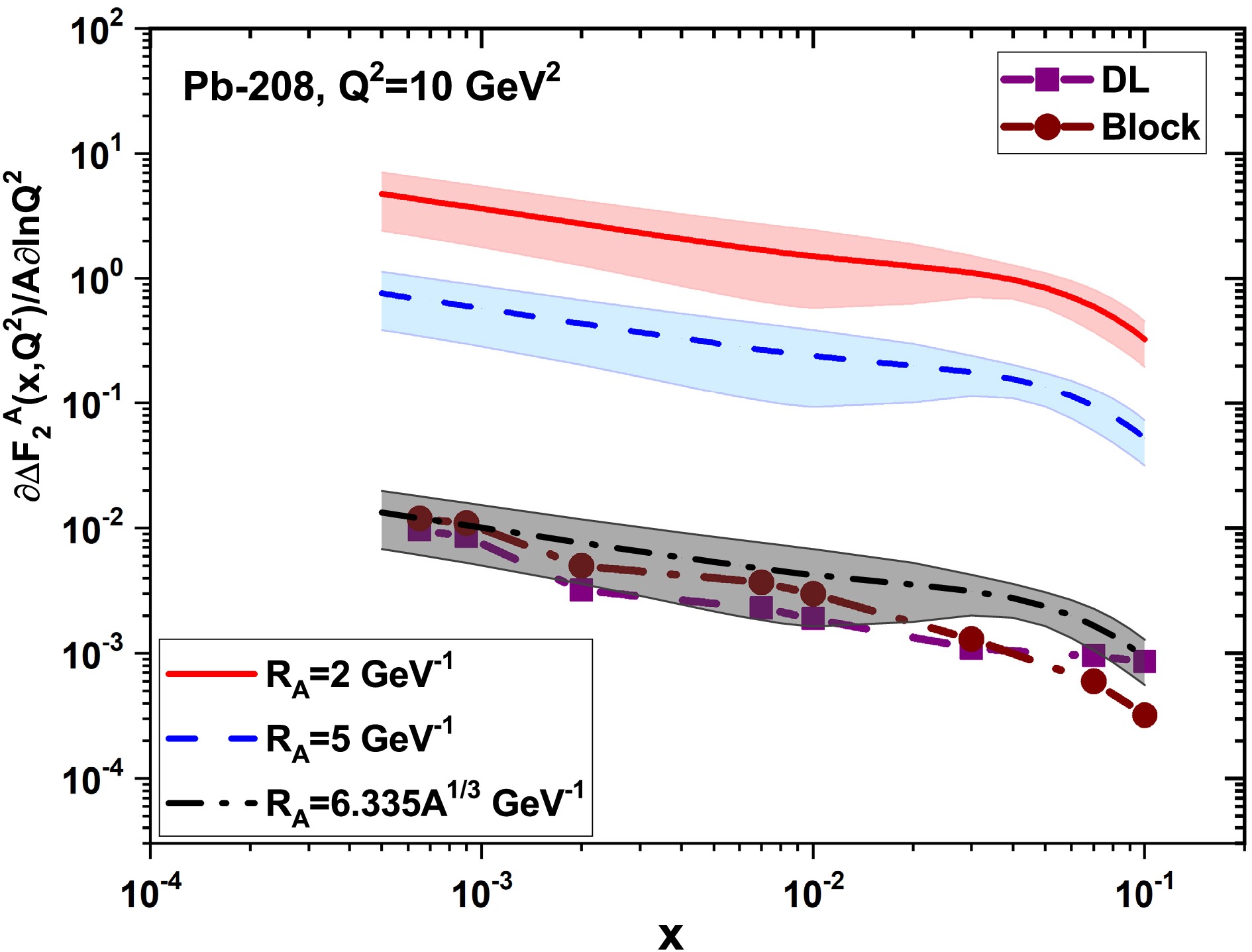

Figure 2.  (color online) The same as Fig.1 for Pb-208 at $ Q^2=10\; {\rm{GeV}}^2 $.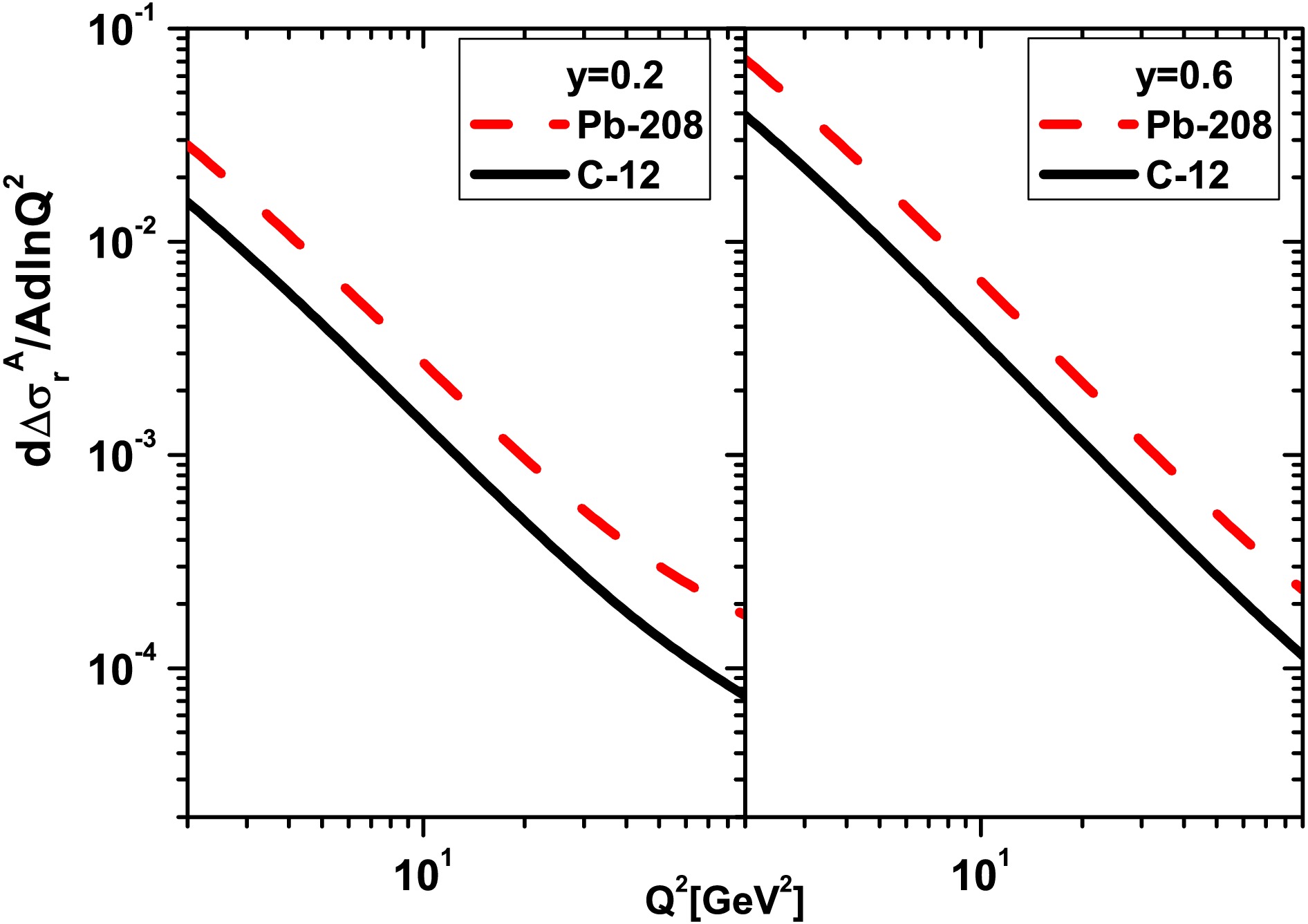

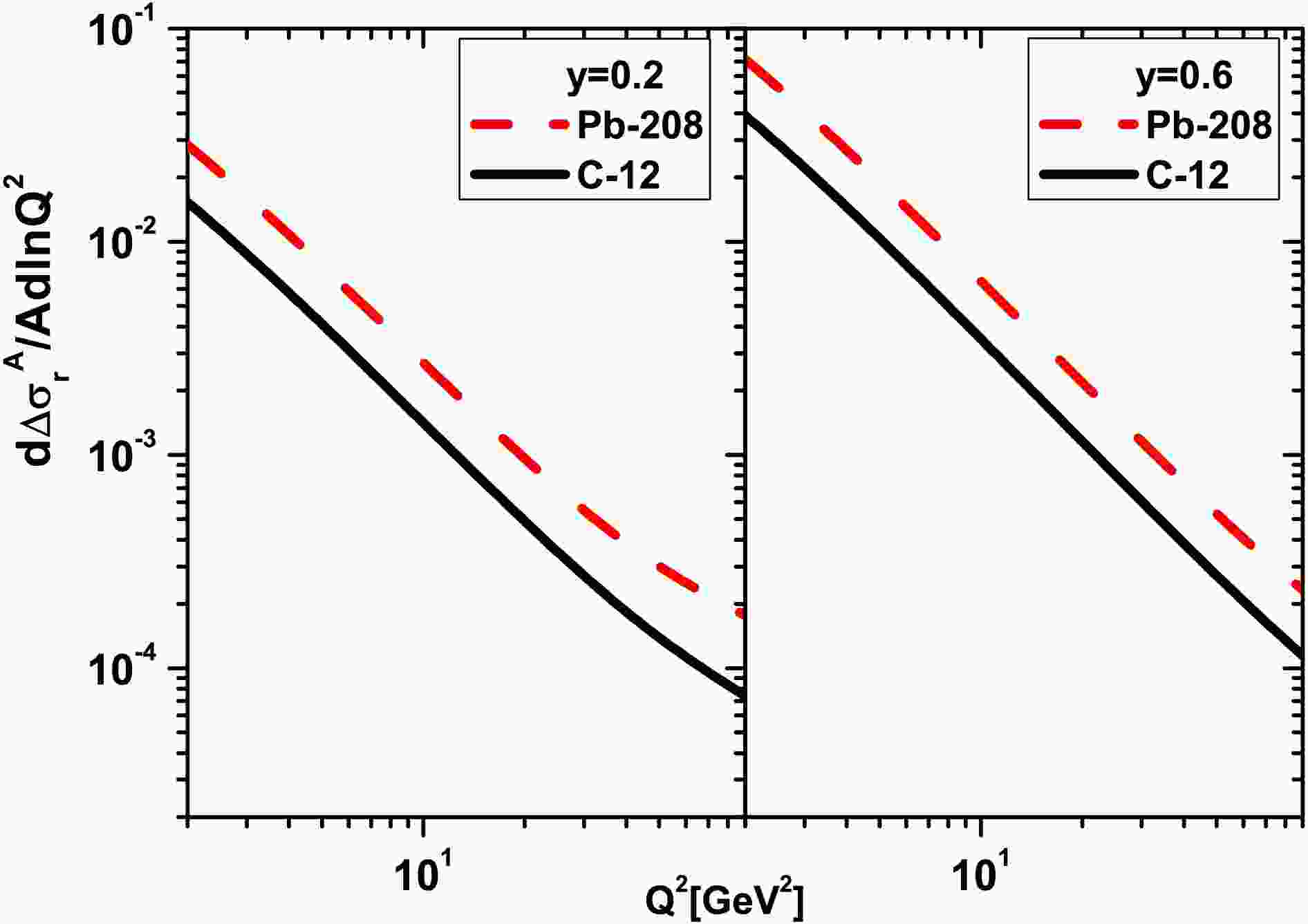
Figure 3.  (color online) Results of $ \frac{1}{A}\frac{{\partial}}{{\partial}{\ln}Q^2}\Delta\sigma_{r}^A(x,Q^2) $ are shown as a function of $ Q^2 $ at $ y=0.2 $ (left) and $ y=0.6 $ (right) for the light nucleus of C-12 (black-solid curve) and the heavy nucleus of Pb-208 (red-dashed curve) due to the DL method [32].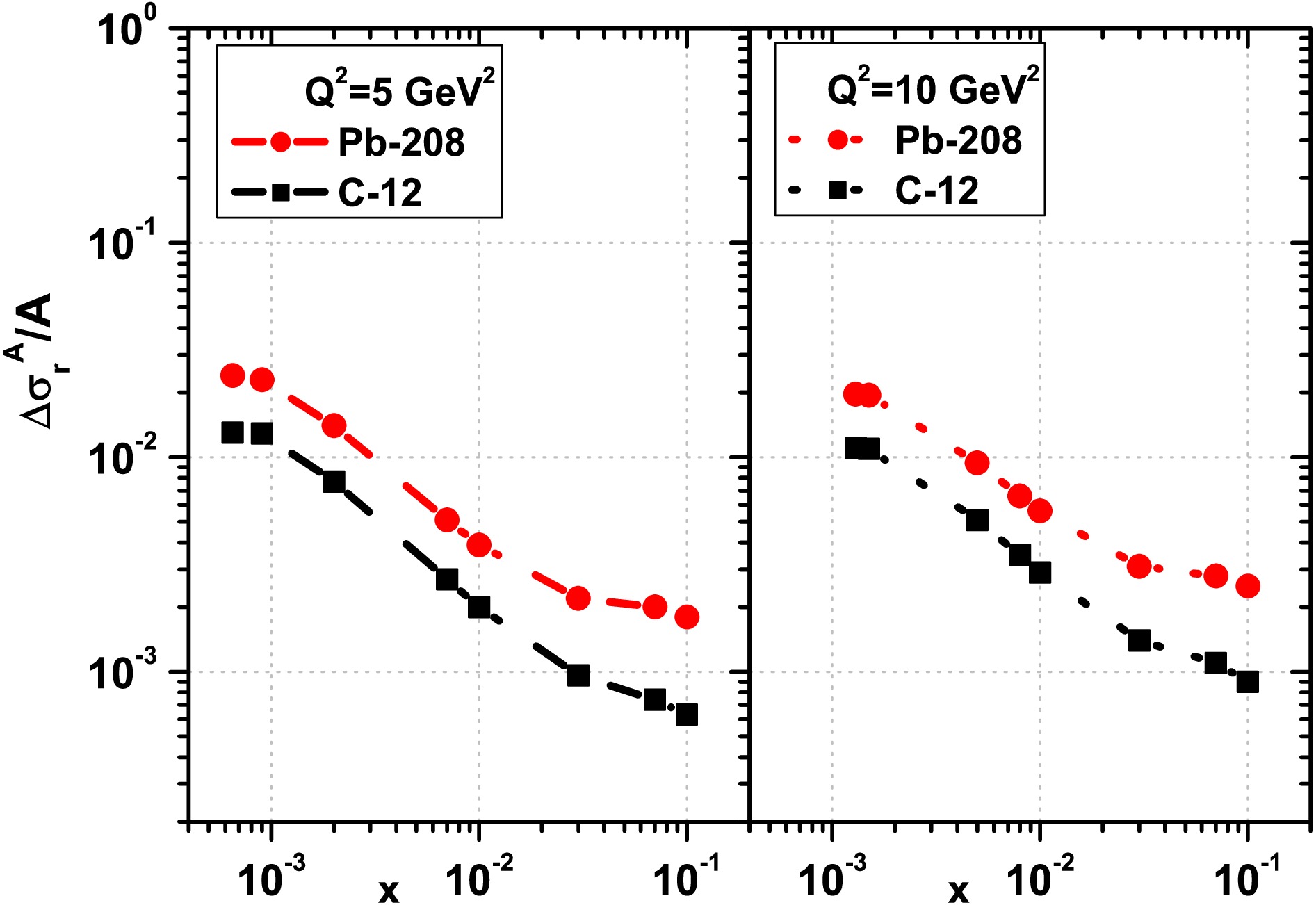

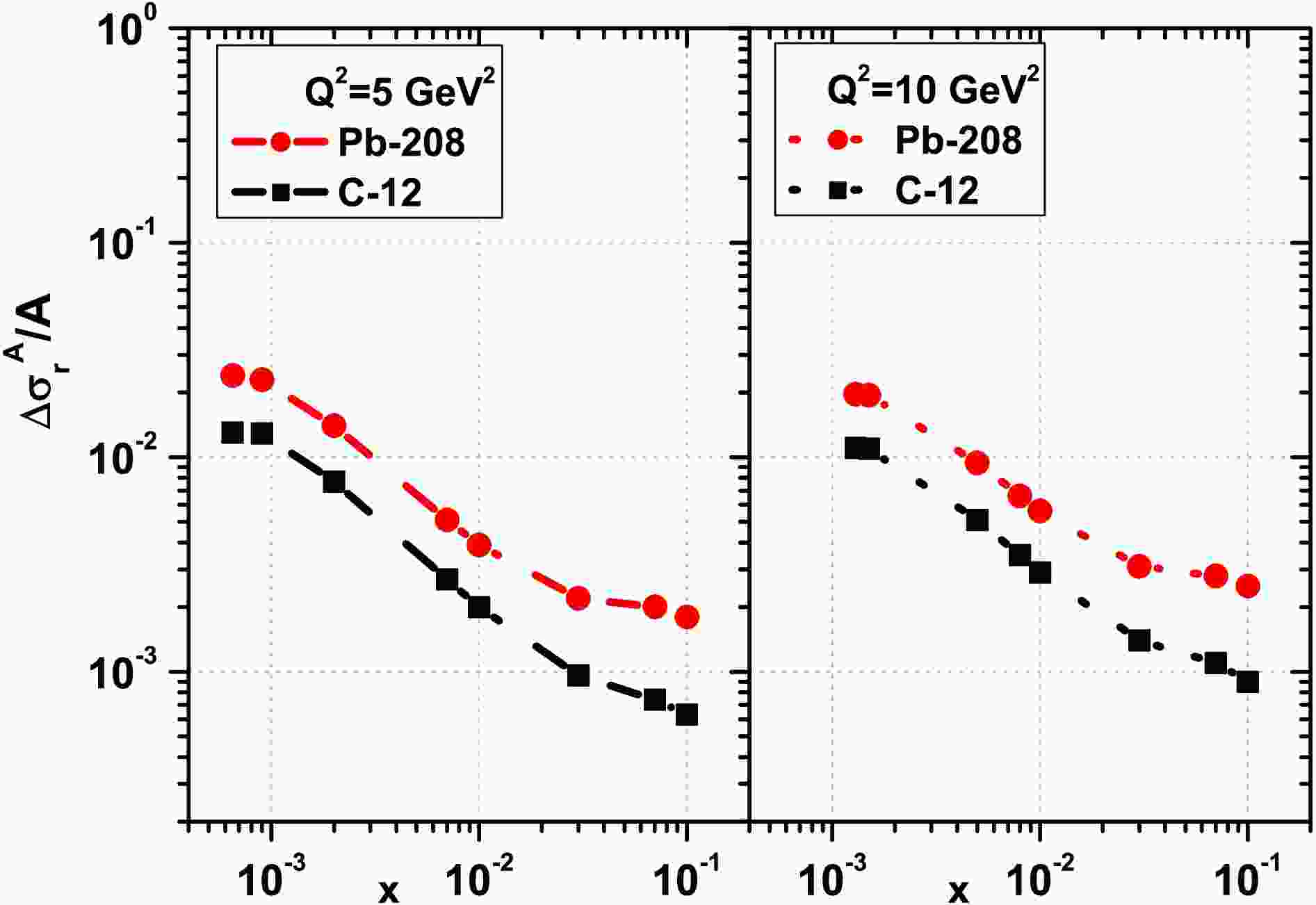
Figure 4.  (color online) The same as Fig.3 due to the Block et al., method [33, 34].

Figure 5.  (color online) Results of $ \frac{1}{A}\Delta\sigma_{r}^A(x,Q^2) $ are shown as a function of $ Q^2 $ at $ Q^2=5\; {\rm{GeV}}^2 $ (left) and $ Q^2=5\; {\rm{GeV}}^2 $ (right) for the light nucleus of C-12 (black-square points) and the heavy nucleus of Pb-208 (red-circle points) due to the DL method [32].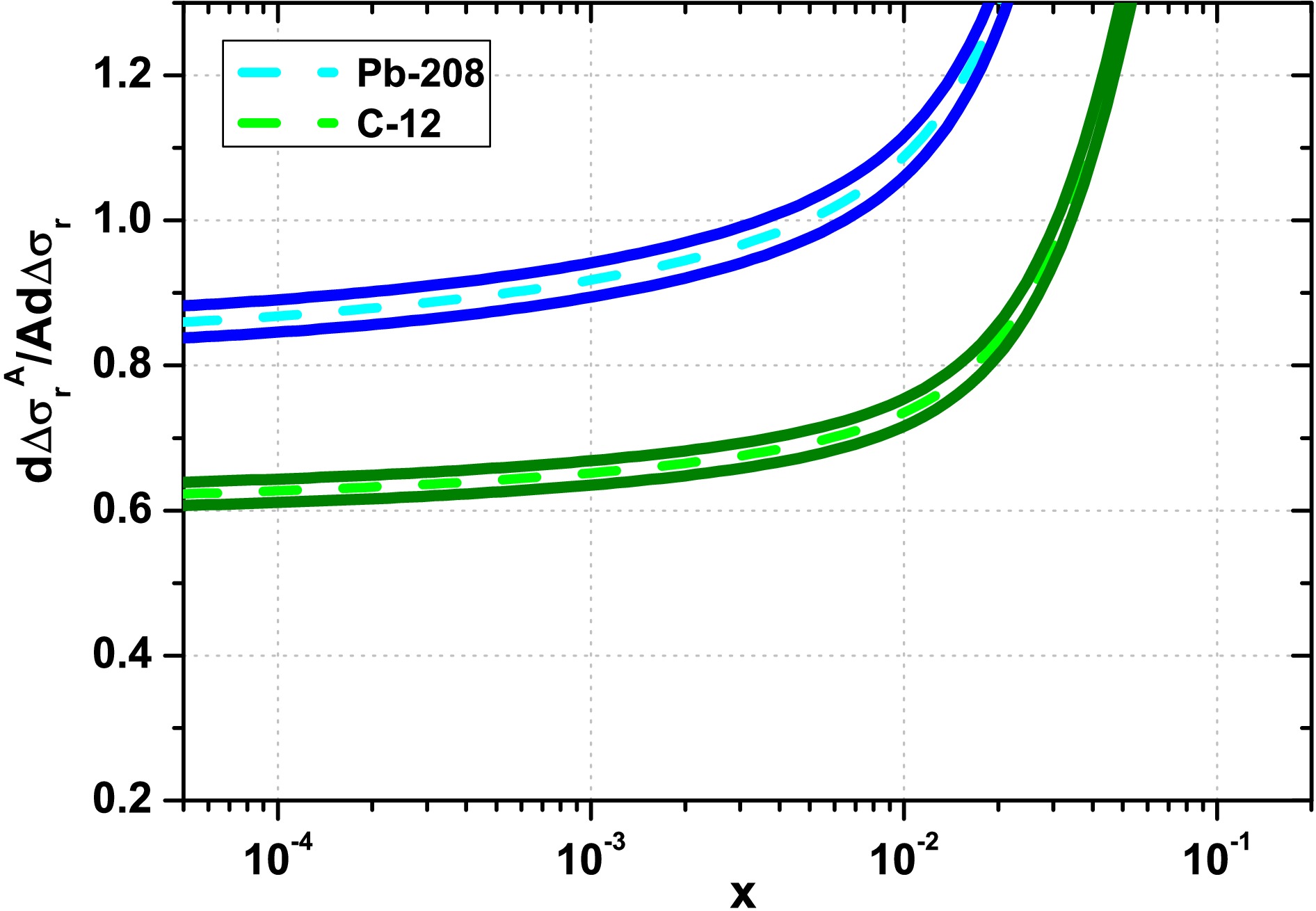

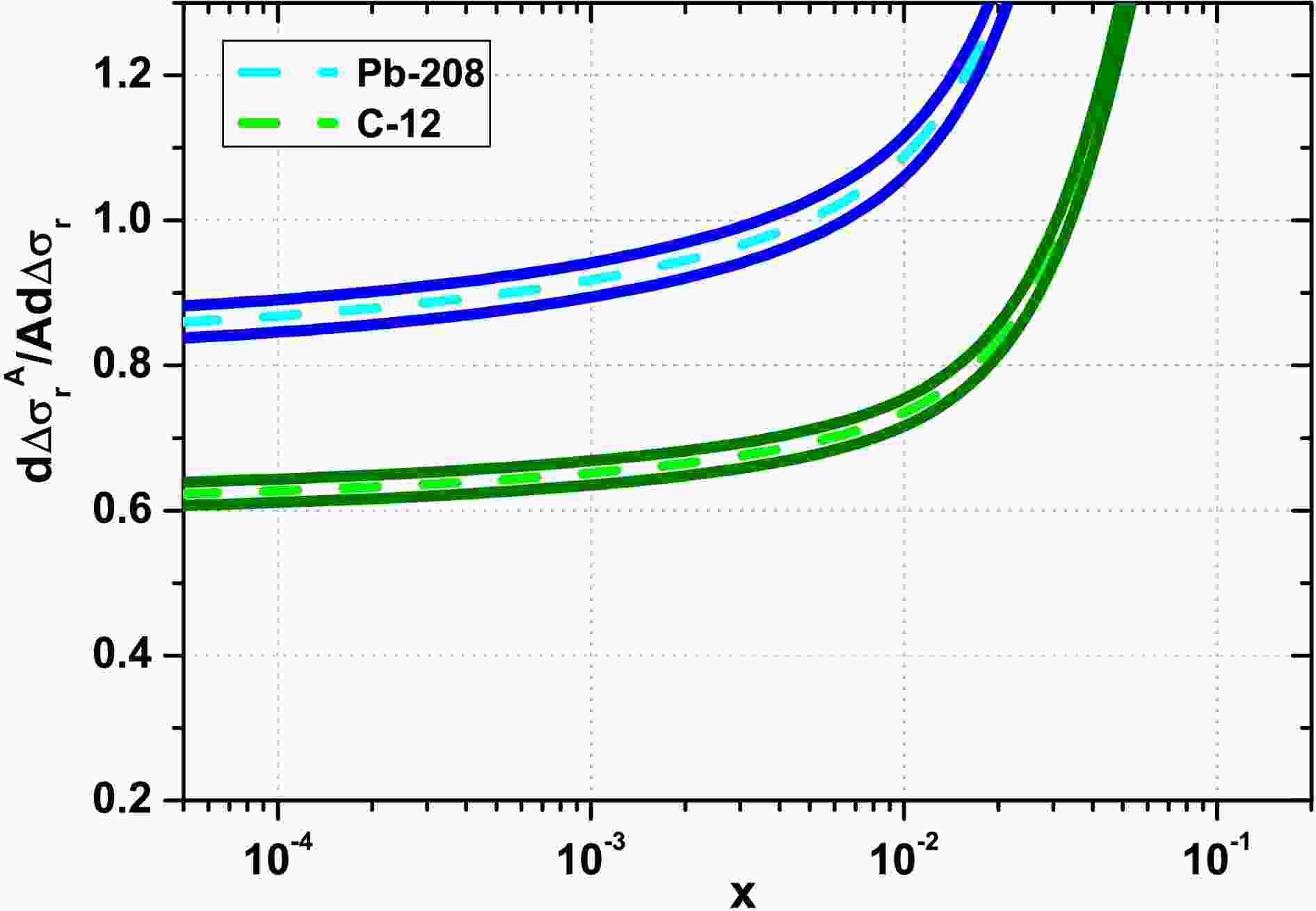
Figure 6.  (color online) Ratio $ \frac{{\partial}{\Delta}\sigma_{r}^{A}(x,Q^2)}{A{\partial}{\Delta}\sigma_{r}(x,Q^2)}|_{y=cte}{\simeq} \frac{\partial{\Delta}F_{2}^{A}(x,Q^2)}{A\partial{\Delta}F_{2}(x,Q^2)}= $$ A(R_{g}^{A})^2\frac{{\pi}{\cal{R}}^{2}_{p}}{{\pi}{\cal{R}}_{A}^2} $ as a function of Bjorken-x for the light nucleus of C-12 (green curves) and the heavy nucleus Pb-208 (blue curves) with $ {\pi}{\cal{R}}^{2}_{p}=1.55{\pm}0.02\; {\rm{fm}}^2 $ and $ {\cal{R}}_{A}=1.12A^{1/3}- $$ 0.86A^{-1/3}\; {\rm{fm}} $. $ R_{g}^{A} $ is predicted by the HIJING parameterization.

For comparison with the nCTEQ15 nPDFs [45] results, we calculate the expression $ \frac{1}{A}\frac{\partial}{\partial{\ln}Q^2}{\Delta}F_{2}^{A}(x,Q^2) $, which quantifies the effect of non-linear corrections. In Fig.1, the non-linear corrections to $ \frac{1}{A}\frac{\partial}{\partial{\ln}Q^2}{\Delta}F_{2}^{A}(x,Q^2) $ for the heavy nucleus of Pb-208 are plotted as a function of the momentum fraction x at $ Q^2=5\; {\rm{GeV}}^2 $ and $ {\cal{R}}_{A}=1.25A^{1/3}\; {\rm{fm}} $ (or $ {\cal{R}}_{A}=6.335A^{1/3}\; {\rm{GeV}}^{-1} $)). The results are determined with respect to the DL (square-purple) [32] and Block et al (circle-brown) [33, 34] methods. They are also compared to the nCTEQ15 parameterization with uncertainties at corresponding values of $ Q^2 $ represented by the solid curve (red, $ {\cal{R}}_{A}=2\; {\rm{GeV}}^{-1} $), the dashed curve (blue, $ {\cal{R}}_{A}=5\; {\rm{GeV}}^{-1} $) and the dashed-dot curve (black, $ {\cal{R}}_{A}=1.25A^{1/3}\; {\rm{fm}} $. These results are comparable to the nCTEQ15 parameterization at $ {\cal{R}}_{A}=1.25A^{1/3}\; {\rm{fm}} $. The nCTEQ15 parameterization results in a wide range of x are flat, while our results increase as x decreases. This difference is due to the behavior of the DL and Block et al gluon distribution functions. With an increase in $ Q^2 $ values, the nCTEQ15 parameterization results increase as x decreases. In Fig.2, we show this behavior for the heavy nucleus of Pb-208 at $ Q^2=10\; {\rm{GeV}}^2 $. Our results are comparable to the nCTEQ15 parameterization results accompanied by uncertainties at small x values. The difference between the results with the nCTEQ15 parameterization results at $ {\cal{R}}_{A}=1.25A^{1/3}\; {\rm{fm}} $ at moderate x values is due to the gluon dominance solely in our results. In Figs.1 and 2, we observe that the non-linear corrections to the derivative of the nuclear structure function (i.e., Eq.(16)) decrease with increasing correlation radius $ {\cal{R}}_{A} $ of the gluon hot spots (Indeed, the non-linear terms in the GLR-MQ equations are suppressed as $ 1/{\cal{R}}^{2}_{A} $). The x and $ Q^2 $ dependence in these figures (i.e., Figs.1 and 2) is also influenced by the behavior of the gluon distribution function in Eq.(16). As expected, the recombination of low-x gluons can be seen as a consequence of gluon-gluon recombination in Eq.(16) as $ [xg(x,Q^2)]^2 $.

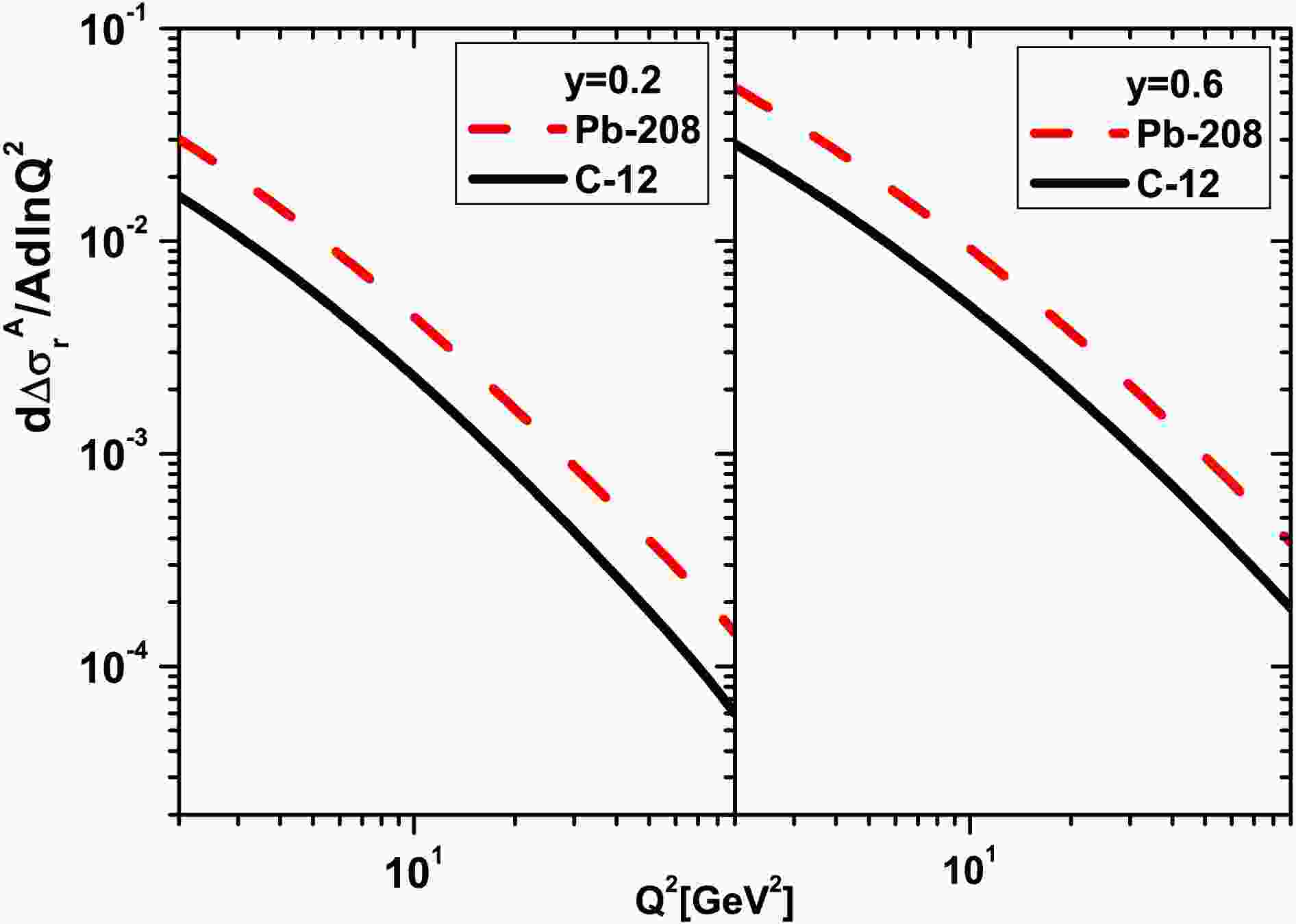
In the following, we present the non-linear corrections to the derivative of the nuclear reduced cross section into $ {\ln}Q^2 $ divided by A, $ \frac{1}{A}\frac{{\partial}}{{\partial}{\ln}Q^2}\Delta\sigma_{r}^A(x,Q^2) $ (i.e., Eq.(22)), for the light nucleus of C-12 and the heavy nucleus of Pb-208 according to the EIC COM energy at the fixed value of the inelasticity y (for $ y=0.2 $ and $ y=0.6 $). In Figs.3 and 4, these results are obtained with respect to the DL [32] and the Block et al., methods [33, 34] are presented respectively. We observe that these non-linear corrections are visible at high inelasticity and small $ Q^2 $ values for the light nucleus of C-12 and the heavy nucleus of Pb-208. We observe that the non-linear effects increase as the $ Q^2 $ values decrease and the inelasticity increases.

In Fig.5, we present the results of our numerical studies on the non-linear corrections of the nuclear reduced cross section divided by A, $ \frac{1}{A}\Delta\sigma_{r}^A(x,Q^2) $ (i.e., Eq.(30)), for the light nucleus of C-12 and the heavy nucleus of Pb-208 according to the EIC COM energy at the fixed value of $ Q^{2} $ (for $ Q^{2}=5 $ and $ 10\; {\rm{GeV}}^2 $). These results are shown with respect to the gluon distribution of the DL [32] method. We observe that these non-linear corrections are visible at low x values for both the light nucleus of C-12 and the heavy nucleus of Pb-208. Additionally, we notice that the non-linear effects increase as the values of $ Q^2 $ and x decrease.

In Fig.6, the ratio $ \frac{{\partial}{\Delta}\sigma_{r}^{A}(x,Q^2)}{A{\partial}{\Delta} \sigma_{r}(x,Q^2)}|_{y=cte} $ is shown, which is approximately equal to $ \frac{\partial{\Delta}F_{2}^{A}(x,Q^2)}{A\partial{\Delta}F_{2}(x,Q^2)}=A(R_{g}^{A})^2\frac{{\pi}{\cal{R}}^{2}_{p}}{{\pi}{\cal{R}}_{A}^2} $ (i.e., Eq.(31)). This comparison is made for the light nucleus of C-12 and the heavy nucleus Pb-208 as a function of Bjorken-x to determine the non-linear correction to the saturation effect in nuclei. It is evident that the magnitude of shadowing due to the non-linear corrections is well-defined. This indicates that shadowing effects resulting from the non-linear corrections can be readily constrained at the EIC for $ x{\lesssim}10^{-2} $, which strongly depends on the proton hot-spot point and the mass number A. Therefore, by measuring $ A(R_{g}^{A})^2\frac{{\pi}{\cal{R}}^{2}_{p}}{{\pi}{\cal{R}}_{A}^2} $, it is possible to determine the existence and magnitude of the non-linear correction to the shadowing effect in the GLR-MQ evolution equation, which is a crucial quantity for probing nuclear effects and QCD dynamics at small-x. Indeed, Fig.6 shows that the shadowing effects due to the difference in non-linear terms between nucleons and nuclei are visible at small x and depend on the mass number A. The error bounds in Fig.6 are a result of uncertainties in the proton target.

In conclusion, we have examined the non-linear corrections for various values of x and found that the shadowing effect in the GLR-MQ equations increases for heavy nuclei. We have analyzed the behavior of the logarithmic slopes of the nuclear structure function and the nuclear reduced cross section in the kinematic region of future electron-ion colliders (LHeC, FCC-eh and EIC). These results, using the HIJING parameterization, suggest a decrease in the nuclear cross section in future electron-ion colliders. The growth of the reduced cross section divided by A for the heavy nucleus Pb-208 and the light nucleus C-12 at small x is controlled at low values of $ Q^2 $ at the hot spot point $ {\cal{R}}_{A}=1.25A^{1/3}\; {\rm{fm}} $. This gluonic hot spot structure in the nucleus is significant for EIC collisions. The magnitude of $ \frac{1}{A}\frac{{\partial}}{{\partial}{\ln}Q^2}\Delta\sigma_{r}^A(x,Q^2) $ and $ \frac{1}{A}\Delta\sigma_{r}^A(x,Q^2) $ increases as x decreases and the atomic number A increases. The behavior of $ \frac{1}{A}\frac{\partial}{\partial{\ln}Q^2}{\Delta}F_{2}^{A}(x,Q^2) $ for the heavy nucleus Pb-208 is compared to the results of the nCTEQ15 parameterization at $ Q^{2}=5 $ and $ 10\; {\rm{GeV}}^2 $. Our analysis indicates that the non-linear corrections are quite significant at $ x{\sim}10^{-3} $ and high inelasticity according to the EIC COM. These results demonstrate that the inclusive observables are sensitive to the non-linear corrections. Drawing firm conclusions about the QCD dynamics from the nuclear reduced cross sections in the kinematic range of future electron-ion experiments is possible.

Additionally, the author would like to express thanks to Professor Vadim Guzey for his helpful comments and invaluable support.

To study the possible importance of non-linear corrections, we base our initial gluon and singlet distribution $ xg(x,Q_{0}^{2})|_{{\rm{Non-Linear}}} $ and $ xq_{s}(x,Q_{0}^{2})|_{{\rm{Non-Linear}}} $ by imposing nonlinear corrections on linear distribution functions. We note that at $ x{\geq}x_{0}=10^{-2} $, the non-linear corrections are negligible [46−48]. At the initial scale $ Q^2_{0} $, the low-x behavior of the nonlinear distribution functions are assumed to be [15]

where $ xg^{A}_{{\rm{sat}}}(x,Q^{2}) $ is defined in Eq.(26). The non-linear corrections to the gluon distribution are reflected in the seq-quark distributions which the seq-quark starting distribution in the region in proportion to the non-linear correction to the gluon by the following form

Therefore we find

For the reduced cross-section of nuclei, as previously mentioned, we require the nucleon distribution functions to be in terms of the variables x and $ Q^2 $. The gluon distribution function and the proton structure function are initially parameterized by Donnachie-Landshoff [32] for the deep inelastic structure function in electromagnetic scattering with protons. The structure function $ F_{2}(x,Q^{2}) $ parameterized by Donnachie-Landshoff, at large $ W=\sqrt{s} $, is expressed as

where

The proton structure function data indicates the presence of a hard pomeron, with an intercept of $ 1+\epsilon_{0} $ at small x. The fitted results to the ZEUS and H1 data in the range $ x<0.001 $ and $ 0.045{\leq}Q^2{\leq}35\; {\rm{GeV}}^2 $ are provided as follows [32]:

The charmed quark component $ F_{2}^{c} $ of $ F_{2} $ is predominantly influenced by hard pomeron exchange at small x. Therefore, a numerical fit to the solution of the DGLAP evolution for the gluon distribution at small x is defined as [32]:

The Donnachie-Landshoff parameterization of the distribution functions has a limited range of applicability. In Ref.[33], the authors have presented a parameterization of $ F_{2} $ that applies to large and small $ Q^2 $ using the proposed Froissart-bound. This parameterization provides an excellent fit to all available ZEUS and H1 data across a wide range of x and $ Q^2 $. The explicit expression for the Block et al., parameterization [34] is as follows:

with $ F_{P}=0.41 $ and $ x_{P}=0.09 $ (The other coefficients are shown in Table I). In Ref.[33], the authors have derived a second-order linear differential equation for the leading-order gluon distribution function directly from the proton structure function parameterization. The analytical solution of the gluon distribution for $ 0<x{\lesssim}x_{P} $ is defined

where $ k=-3/2 $ and $ \omega=\sqrt{7}/2 $, the function $ {\cal{G}}(\upsilon,Q^2) $ parameterized in $ \upsilon={\ln}(1/x) $ reads

The coefficients of the function are quadratic polynomials in $ \ln Q^2 $ [33].