Extracting the neutron skin thickness of ¹²⁴Sn from the ¹²C + ¹²⁴Sn elastic scattering angular distribution

Neutron stars, the remnants of massive stellar explosions, are among the most extreme and fascinating objects in the universe. Their interiors are composed of ultra-dense matter, with densities exceeding that of atomic nuclei, making them natural laboratories for studying the properties of matter under extreme conditions. Understanding the equation of state (EoS) of dense matter is crucial for interpreting neutron star observations, such as their masses, radii, and tidal deformabilities [1−3].

The EoS of neutron star matter is intimately connected to the nuclear symmetry energy, which characterizes the energy cost of deviating from equal numbers of protons and neutrons in nuclear systems. In neutron-rich nuclei, the symmetry energy plays a critical role in determining the distribution of protons and neutrons, which is governed by the isospin asymmetry $ \delta = \left(N - Z\right)/A $ of the system. The symmetry energy not only influences the structure of neutron-rich nuclei but also determines the density dependence of the EoS in neutron stars, making it a key quantity for both nuclear and astrophysical studies [4, 5].

The nuclear symmetry energy $ E_{\text{sym}}(\rho) $ is a key quantity describing the energy difference between nuclear matter composed of protons and neutrons at equal density. It can be expanded as a function of nuclear density ρ around the saturation density $ \rho_0 $:

where L is the slope parameter of the symmetry energy at $ \rho_0 $:

Although the slope parameter is typically extracted around the saturation density, this information is essential for extrapolating to both high and low densities.

Compared to the symmetry energy at saturation density, the uncertainties in the slope parameter L are even larger, and extensive research has been conducted. Among them, one approach involves determining the neutron skin thickness of atomic nuclei to extract the slope parameter of the symmetry energy. In 2009, M. Centelles et al. determined the symmetry energy slope parameter $ L = 55 \, \pm \, 25 \, \text{MeV} $ using neutron skin thickness data from 26 stable nuclei measured in antiprotonic atom experiments, combined with liquid-drop model calculations and multiple nuclear interaction models [6]. In 2010, L. W. Chen et al. derived $ L = 58 \, \pm \, 18 \, \text{MeV} $ by analyzing neutron skin thickness of $ ^{208}\text{Pb} $ through Skyrme-Hartree-Fock calculations and constraints from heavy-ion collision experiments [7]. Next year, L. W. Chen reported $ L = 52.5 \, \pm \, 20 \, \text{MeV} $ based on neutron skin measurements of tin isotopes [8]. In 2012, B.K. Agrawal et al. obtained $ L = 64 \, \pm \, 5 \, \text{MeV} $ using $ ^{208}\text{Pb} $ neutron skin data with relativistic mean-field models [9]. In 2013, Z. Zhang et al. yielding L to $ 45.2 \, \pm \, 10 \, \text{MeV} $ via Skyrme-Hartree-Fock calculations on tin isotopes [10]. Next year, P. Danielewicz and J. Lee used the neutron skin thickness of $ ^{208}\text{Pb} $, combined with isobaric analog state data and the Hohenberg-Kohn functional method, to constrain the symmetry energy slope parameter L to a range of $ 35 \, - \,70 $ MeV [11]. In 2020, J. Xu et al. employed Bayesian analysis of Sn isotope data to estimate $ L = 53.4^{+18.6}_{-29.5} \, \text{MeV} $ [12]. Although these data do not fully encompass all current theoretical predictions, it can be observed that the average value of L remains consistent across these analyses. Furthermore, by analyzing the recent experimental data on the neutron skin thickness of $ ^{208} $Pb published by the PREX-II collaboration [13], L predicted by the relativistic mean-field theory is $ 106 \, \pm \, 37 $ MeV [14]. This value differs significantly from previous results obtained based on terrestrial laboratory experiments and astrophysical observations, and it also falls outside the range of symmetry energy slope parameters inferred from GW170817 observations [15]. Building upon the PREX measurement results, subsequent studies have focused on reconciling these discrepancies: J.M. Lattimer derived $ L = 53 \, \pm \, 13 \, \text{MeV} $ by combining PREX and CREX neutron skin data with nuclear mass systematics [16]. Essick et al. obtained $ L = 53^{+14}_{-15} \, \text{MeV} $ using nonparametric EoS methods with PREX-II $ ^{208}\text{Pb} $ data and chiral effective field theory [17]. B. Hu et al. constrained L to $ 38.3 \, - \, 68.5 $ MeV via ab initio quantum many-body calculations of $ ^{208}\text{Pb} $ neutron skin [18], while Y. Lim et al. reported $ 54 \, \pm \, 8 \, \text{MeV} $ through Bayesian analysis of $ ^{208}\text{Pb} $ measurements [19].

Long isotopic chains provide an excellent opportunity to study the impact of symmetry energy on nucleon distributions at different δ. Tin isotopes (Sn), with their magic number ($ Z = 50 $) shell structure and an extended chain of stable isotopes ($ ^{112-124} $Sn), are particularly advantageous for such investigations. Several methods, including proton scattering [20−22], inelastic α-scattering [23, 24], spin-dipole resonance [25], and antiprotonic atom spectroscopy [26], have been employed to study the neutron skin.

In the present work, we first quantitatively analyzes the correlation between L and the neutron skin thickness of $ ^{112-124} $Sn. Then the neutron skin thickness of $ ^{124} $Sn is extracted from the elastic scattering angular distribution of $ ^{12} $C + $ ^{124} $Sn. Finally, the extracted neutron skin thickness is utilized to place constraints on the symmetry energy in the high-density region. The results provide valuable references for further studies on neutron stars and nuclear matter properties.

To study the correlation between the slope coefficient of the symmetry energy and the neutron skin of Sn isotopes with different δ, we employed the Skyrme-Hartree-Fock (SHF) model, which has been widely used in nuclear physics. The Skyrme-Hartree-Fock model, as described in references [27−32], employs an interaction characterized by zero range, along with dependencies on both density and momentum. The parameters of the Skyrme interaction are calibrated to reproduce the binding energies and charge radii of numerous nuclei across the periodic table. For infinite nuclear matter, the nuclear symmetry energy from the Skyrme interaction can be expressed as follows [31, 32]:

where the σ, $ t_0 $ - $ t_3 $, and $ x_0 $ - $ x_3 $ are Skyrme interaction parameters.

The neutron skin thickness of a nucleus is defined as the difference between the root-mean-square radii of the neutron and the proton distributions, i.e.,

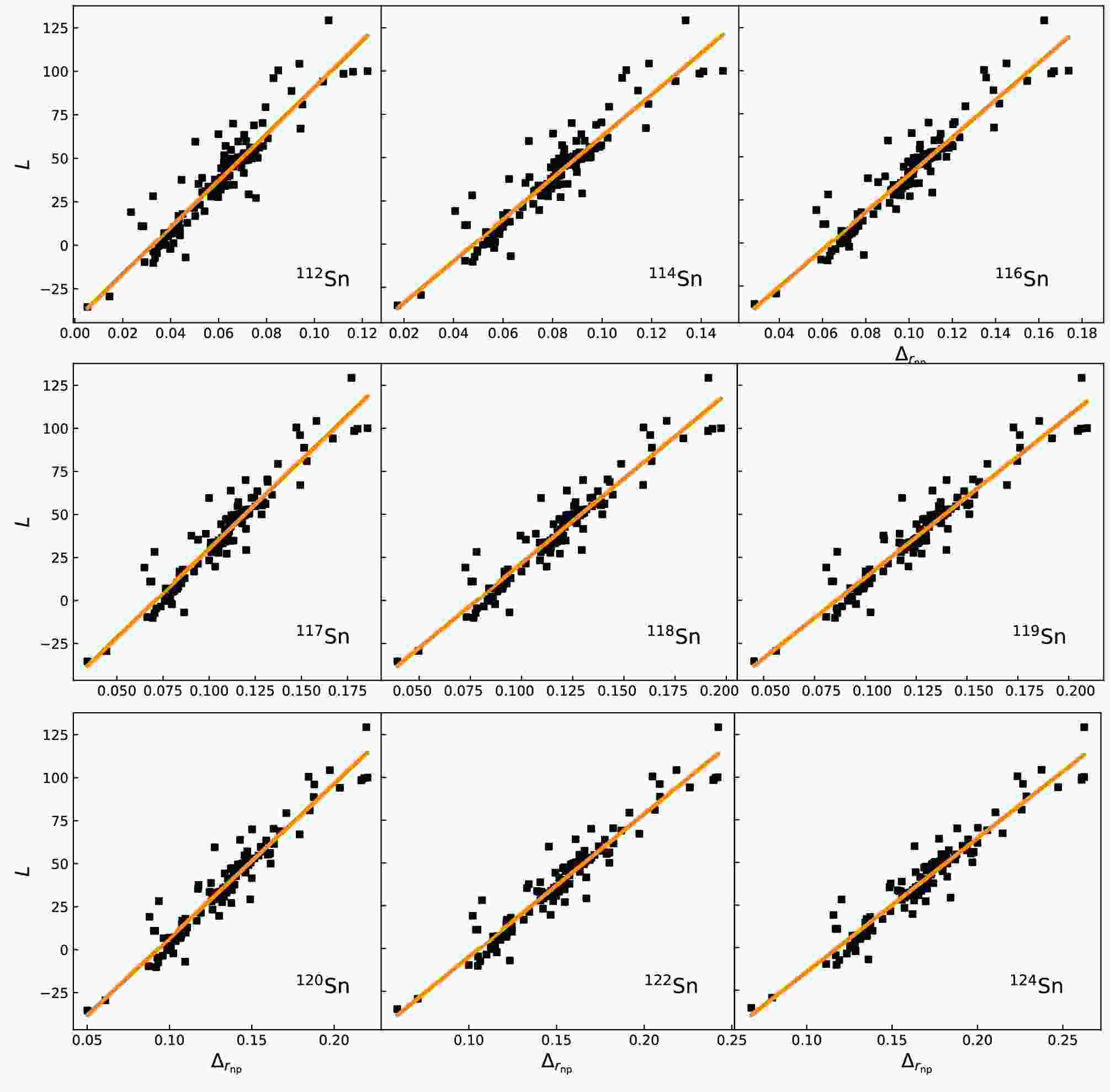
The SHF model calculates neutron skin thickness by self-consistently solving mean-field equations with selected Skyrme interactions, computing neutron and proton density distributions, and evaluating the neutron-proton root-mean-square radius difference. The neutron skin thickness is sensitive to the density dependence of the nuclear symmetry energy, particularly the slope parameter L at the normal nuclear matter density [27, 33−38]. Using 184 sets of Skyrme interaction parameters, we have evaluated the correlation between $ \Delta_{r_{\text{np}}} $ and L of $ ^{116,117,118,119,120,122,124} $Sn, which is shown in Fig. 1. The 184 sets of Skyrme interaction parameters are: BSk1, BSk2, BSk2', BSk3, BSk4, BSk5, BSk6, BSk7, BSk8, BSk9, BSk10, BSk11, BSk12, BSk13, BSk14, BSk15, BSk16, Bsk17, FPLyon, KDE, KDE0v, KDE0v1, LNS, MSk1, MSk2, MSk3, MSk4, MSk5, MSk5^*, MSk6, MSk7, MSk8, MSk9, MSkA, MSL0, NRAPR, Sefm074, Sefm081, Sefm09, Sefm1, SGI, SGII, SGOI, SI, SII, SIII, SIII^*, SIV, Skyrme1', SkI2, SkI3, SkI5, SkM, SkM^*, SkM1, SkMP, SkO', SkP, SKRA, SkS1, SkS2, SkS3, SkS4, SkSC1, SkSC2, SkSC3, SkSC4, SkSC4o, SkSC5, SkSC6, SkSC10, SkSC11, SkSC14, SkSC15, SkT, SkT1, SkT2, SkT3, SkT4, SkT5, SkT6, SkT7, SkT8, SkT9, SkT1^*, SkT3^*, SkT1a, SkT2a, SkT3a, SkT4a, SkT5a, SkT6a, SkT7a, SkT8a, SkT9a, SkTK, SKX, SKXce, SKXm, Skxs15, Skxs20, Skxs25, SKz1, SKz2, SKz3, SKz4, SLy0, SLy1, SLy2, SLy230a, SLy230b, SLy3, SLy4, SLy5, SLy6, SLy7, SLy8, SLy9, SLy10, SSk, SV, SV-bas, SV-min, SVI, SVII, SV-K218, SV-K226, SV-K241, SV-kap00, SV-kap02, SV-kap06, SV-mas07, SV-mas08, SV-mas10, SV-sym28, SV-sym32, SV-sym34, SV-tls, T, T11, T12, T13, T14, T15, T16, T21, T22, T23, T24, T25, T26, T31, T32, T33, T34, T35, T36, T41, T42, T43, T44, T45, T46, T51, T52, T53, T54, T55, T56, T61, T62, T63, T64, T65, T66, v070, v075, v080, v090, v100, v105, v110, Zs, Zs^*. The parameters of these Skyrme interactions can be found in Ref. [39]. The solid lines in the figures represent the linear fit of the correlation between $ \Delta_{r_{\text{np}}} $ and L.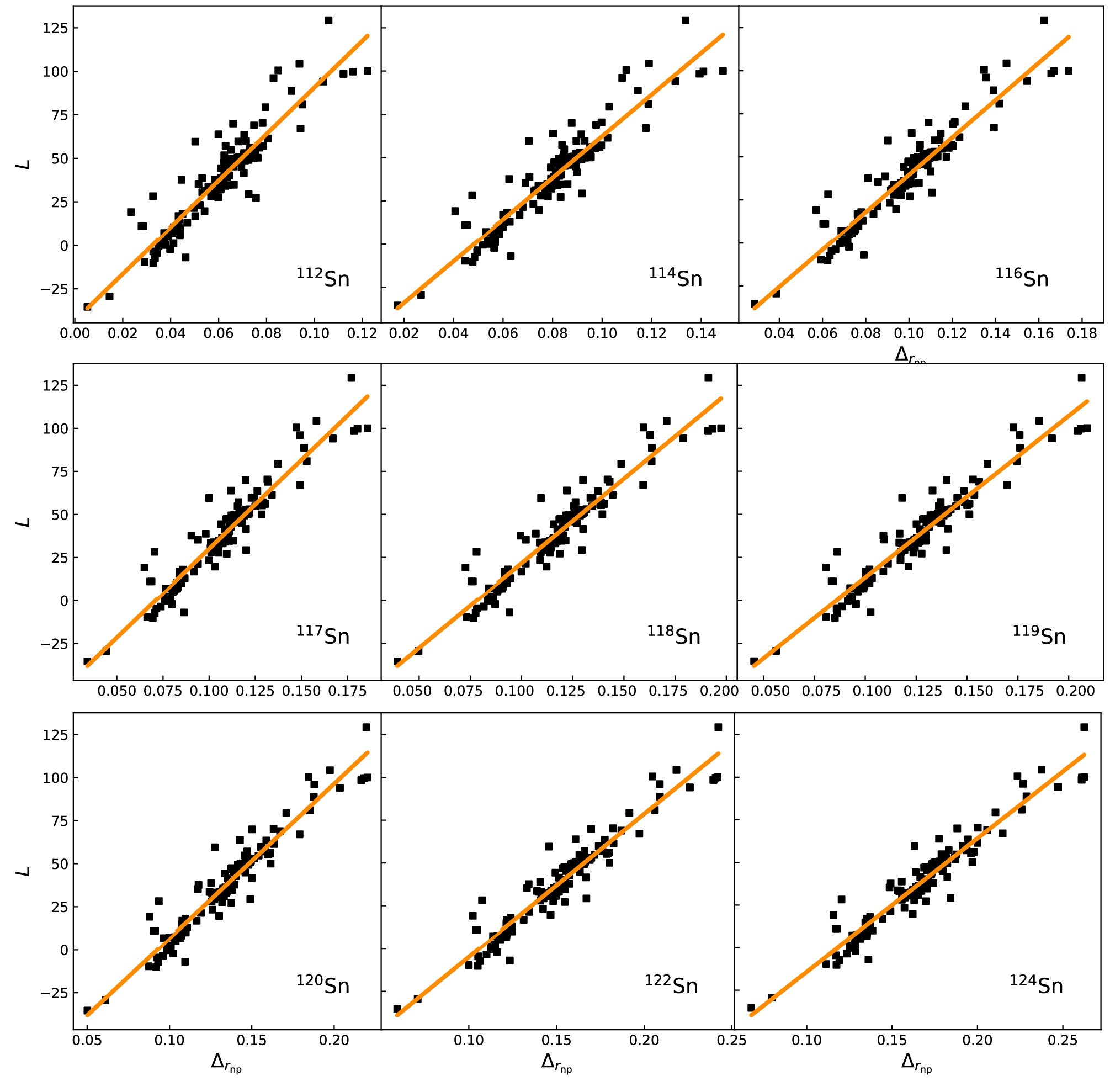

Figure 1.  (color online) L as a function of neutron skin thickness $\Delta_{r_{\text{np}}}$ for 184 sets of Skyrme interaction parameters and for stable Sn isotopes. The line is a linear fit to the data.

It can be observed in Fig. 1 that Sn isotopes exhibit an approximate linear correlation between L and $ \Delta_{r_{\text{np}}} $. To give a quantitative estimate of above correlations, we define the following linear correlation coefficient $ R^2 $:

where $ SS_{\text{res}} $ and $ SS_{\text{tot}} $ are the residual sum of squares (RSS) and the total sum of squares, respectively, i.e.,

In the above, a and b are the linear regression coefficients. The linear correlation coefficient $ R^2 $ measures the degree of linear correlation, and $ R^2 =1 $ corresponds to an ideal linear correlation. Table 1 presents the linear correlation coefficient $ R^2 $ for the correlations between L and $ \Delta_{r_{\text{np}}} $ of Tin isotopes under different Skyrme interactions, as shown in Figs. 1, as well as the slope and intercept of the linear fit. From the figure, it also can be seen that as the isospin asymmetry increases, the linear relationship between L and $ \Delta_{r_{\text{np}}} $ becomes stronger, with the strongest linearity between L and $ \Delta_{r_{\text{np}}} $ observed in $ ^{124} $Sn nucleus. Therefore, within the stable isotopic chain of Sn, the neutron skin thickness of $ ^{124} $Sn will provide the most effective constraint on L.

nuclei	a	b	$ C_l $(%)
$ ^{116} $Sn	$ -68.82 \, \pm \, 2.66 $	$ 1084.08 \, \pm \, 26.11 $	90.45
$ ^{117} $Sn	$ -73.12 \, \pm \, 2.64 $	$ 1031.54 \, \pm \, 23.72 $	91.22
$ ^{118} $Sn	$ -76.79 \, \pm \, 2.62 $	$ 983.36 \, \pm \, 21.80 $	91.79
$ ^{119} $Sn	$ -80.64 \, \pm \, 2.65 $	$ 939.13 \, \pm \, 20.41 $	92.09
$ ^{120} $Sn	$ -83.08 \, \pm \, 2.66 $	$ 897.35 \, \pm \, 19.13 $	92.36
$ ^{122} $Sn	$ -88.39 \, \pm \, 2.74 $	$ 835.08 \, \pm \, 17.64 $	92.49
$ ^{124} $Sn	$ -92.58 \, \pm \, 2.83 $	$ 783.39 \, \pm \, 16.54 $	92.50

Table 1.  Linear correlation coefficient $ R^2 $, intercept a, and slope b for the correlation between L and $ \Delta_{r_{\text{np}}} $ of Tin isotopes under different Skyrme interactions.

The fitted line for $ ^{124} $Sn is given by the following expression:

where L and $ \Delta_{r_{\text{np}}} $ are measured in units of MeV and fm, respectively. The errors are mainly due to statistical fluctuations arising from different interactions.

The angular distributions of elastic scattering for $ ^{12} $C + $ ^{124} $Sn at 66 MeV were measured using the high-precision Q3D magnetic spectrograph at the Beijing HI-13 tandem accelerator of the China Institute of Atomic Energy [40]. The isotopic abundances and thicknesses of the tin targets, as well as the experimental setup, are detailed in Ref. [41]. The measured experimental differential cross section to Rutherford cross section ratio and uncertainties are shown as black dots and error bars in the lower panel of Fig. 2.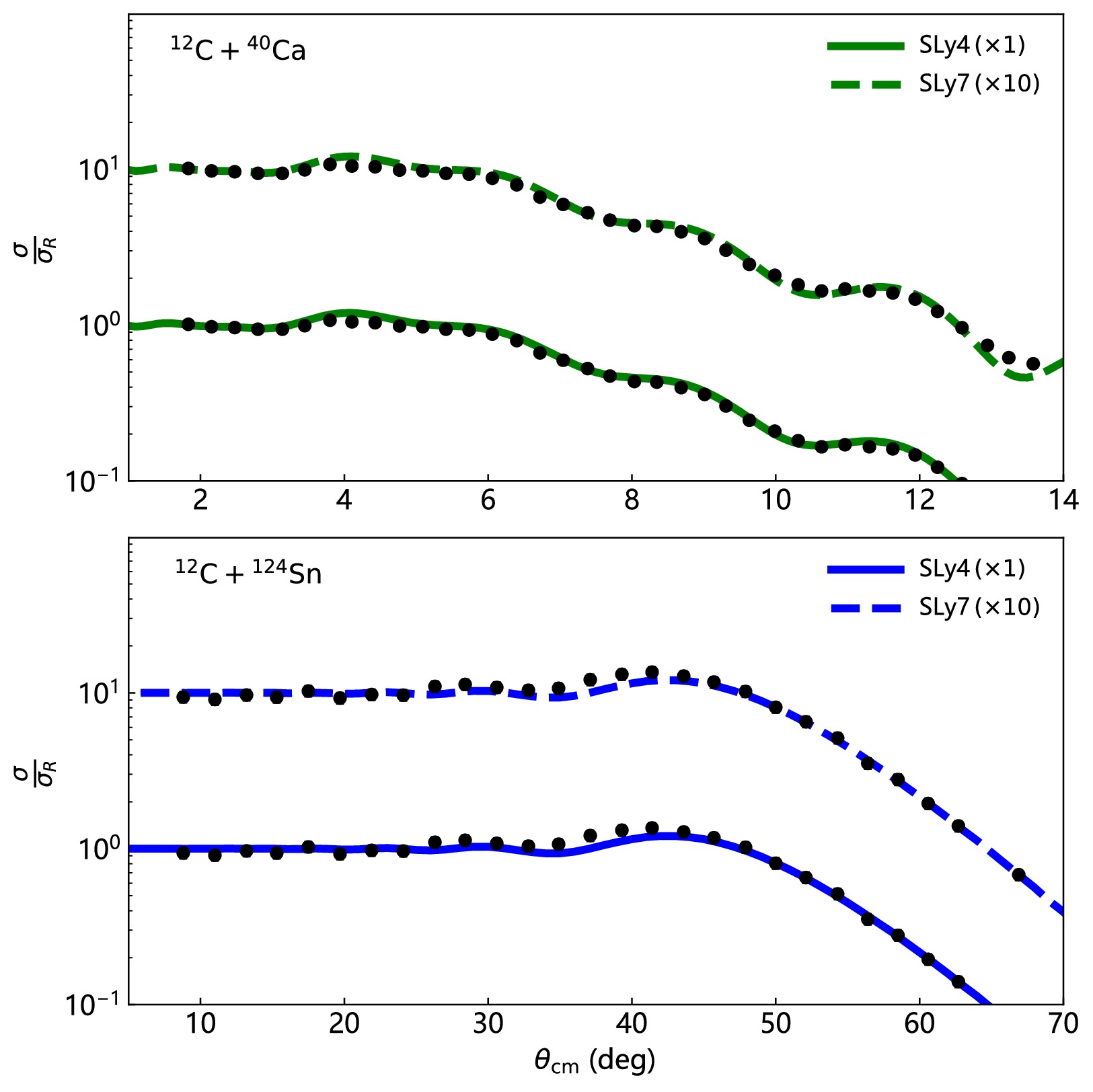

Figure 2.  (color online) The differential cross section to Rutherford cross section ratio for $^{12}$C + $^{40}$Ca at $E_{\text{c.m.}} \approx 180 \, \text{MeV}$ (upper panel) and $^{12}$C + $^{124}$Sn at $E_{\text{c.m.}} \approx 66 \, \text{MeV}$ (lower panel). The dots are the experimental values while the solid line corresponds to the DF calculations.

We use the FRESCO code [42] to analyze elastic scattering data, and the differential cross section to Rutherford cross section ratio is typically calculated. The total interaction potential can be written as the sum of three terms,

here, r is the separation distance between the interacting nuclei. The $ V_{C}(r) $ and $ V_{l}(r) $ are the Coulomb potential and the centrifugal potential, respectively. The last term in Eq. 9 denotes the short-range and attractive nuclear potential, and consists of real and imaginary potential parts, generated using fully microscopic (FM) method. The FM method calculates the nuclear potential real and imaginary parts using the double-folded optical model based on the CDM3Y6 effective NN interactions, i.e. $ V_{n}(r) = N_{\text{R}}V_{n}^{\text{DF}}(r) + iN_{\text{I}}V_{n}^{\text{DF}}(r) $, where $ V_{n}^{\text{DF}}(r) $ is the double-folded potential generated by the BiFold code [43], and $ N_{\text{R}} $ and $ N_{\text{I}} $ are the normalization factors of the real and imaginary parts respectively, which are adjusted to obtain the best fit to experimental data. This method has been successfully applied in [44−46] to the study of neutron skin or neutron halo.

The CDM3Y6 double-folded potential has two parts: the direct part $ V _ { D } $ and exchange part $ V _ { {\rm{ E x }} } $, and can be written as [47, 48],

here, $ V _ { D } $ and $ V _ { {\rm{ E x }} } $ represent the direct and exchange effective NN interactions, respectively. Using the M3Y-Paris, $ V _ { D } $ and $ V _ { {\rm{ E x }} } $ are expressed as [47, 48],

and

Both $ V _ { D } $ and $ V _ { {\rm{ E x }} } $ are scaled by a weak energy-dependent function $ g(E) $ and a density-dependent function $ F(\rho) $ [47, 48]

The energy-dependent function is expressed as [47, 48]:

where $ E _ { {\rm{ l a b }} } $ is the incident energy in MeV and $ \text{A} _ { {\rm{ p }} } $ is the mass of the projectile nucleus. Furthermore, the densitydependent function $ F ( \rho ) $ can be written as [47, 48]:

where ρ is the overlapping density of the interacting nuclei.

The matter density distribution of $ ^{12}\text{C} $ projectile nucleus is expressed by the two-parameter Fermi (2pF) model $ \rho(r)=\rho_{0} / \left[1+\exp\left(\dfrac{r-R}{a}\right)\right] $ with $ \rho_{0}=0.207 \, \text{fm}^{-3} $, $ R=2.1545 $ fm and $ a=0.425 $ fm [45]. As for $ ^\text{124}\text{Sn} $ target nucleus, we consider proton and neutron densities calculated with the SHF with the widely used SLy4 parameter set and its refined variant SLy7 as the original density $ \rho(r) $. The scaled density $ \rho_{\text{scaling}}(r) $ is determined from the original density $ \rho(r) $ as

with a scaling factor

The actual procedure to determine α (of p and n) for each case is: Firstly we scale the proton density so as to be $ R_{\text{p}} $(scaling) = $ R_{\text{p}} $(exp) [21, 49] although is a tiny adjustment, secondly we scale the neutron density so as that the theoretical angular distribution reproduces the experimental data well [24].

First, to verify the reliability of the method, we tested the results of the $ ^{40}\text{Ca} $ neutron skin thickness extracting from elastic scattering of $ ^{12}\text{C} + ^{40}\text{Ca} $. The experimental angular distribution data was digitally extracted from Fig. 3 of Ref. [50], shown as black dots and error bars in the upper panel of Fig. 2. The values of $ N_{\text{R}} $ and $ N_{\text{I}} $ that provide the best fit to the data are 0.85 and 0.6, and the scaling factors $ \alpha_\text{p} $ and $ \alpha_\text{n} $ are listed in Table 2. The results are shown and compared with the experimental data in the upper panel of Fig. 2. The errors of radii are extracted by adjusting $ \alpha_n $ such that the chi-squared $ \chi^2 $ value $ \chi^2_{\text{min}}+1 $. We determine the neutron skin thickness of $ ^{40}\text{Ca} $ as $ -0.018_{\text{−}0.015}^{+0.012} $ fm (SLy4) and $ -0.013 \pm 0.013 $ fm (SLy7), which is consistent with $ -0.010_{\text{−}0.024}^{+0.022} $fm by J. Zenihiro et al. [51] and $ -0.011 \pm 0.011 $fm by T. Wakasa et al. [52].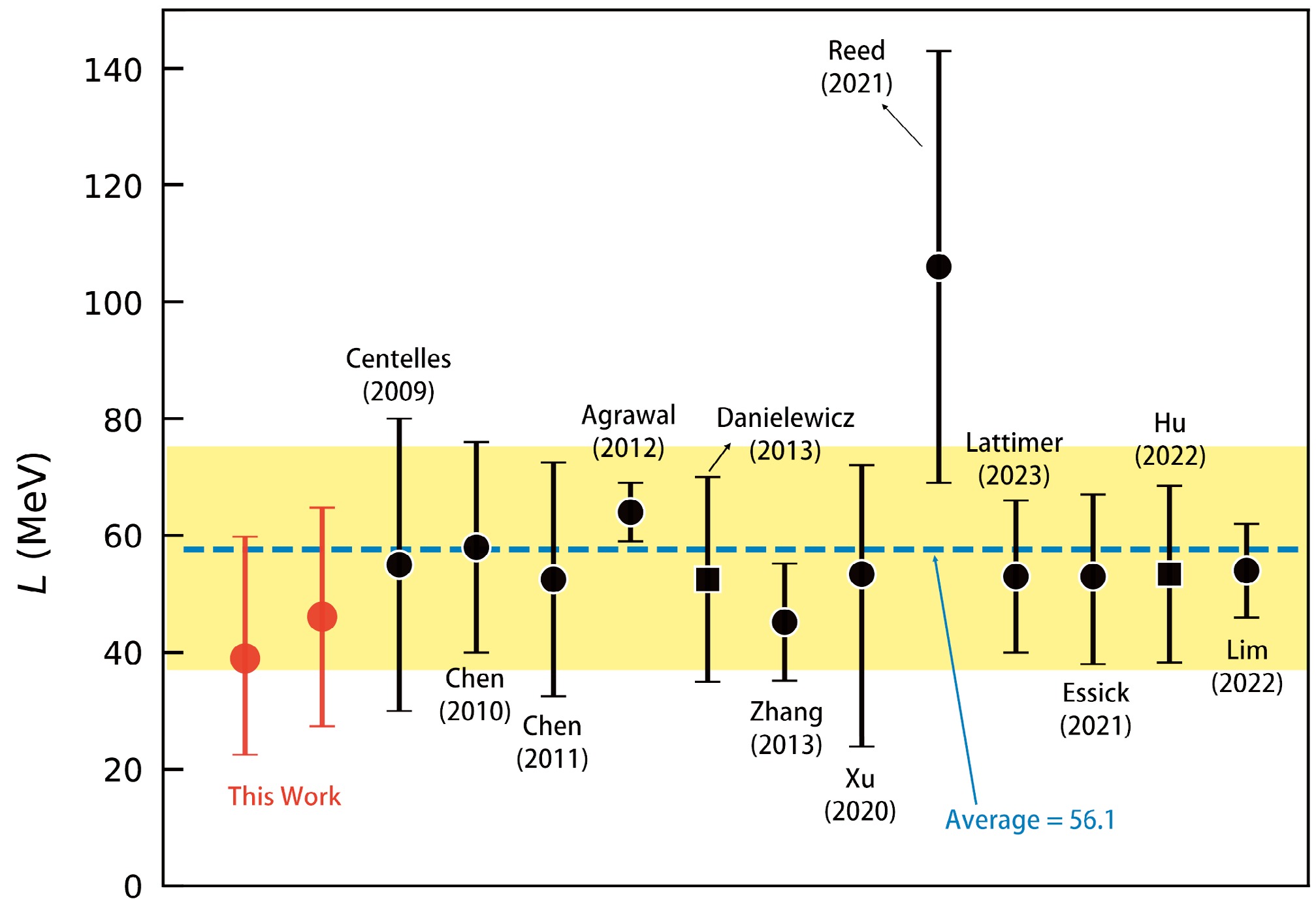

Figure 3.  (color online) Constraints on L from this work and 12 other studies. The blue dashed line represents the mean of all 14 results, and the yellow band indicates the $1 \sigma$ uncertainty of the mean. Square markers denote data with no error information.

Isotope	SLy4			SLy7
	$ \alpha_p $	$ \alpha_n $		$ \alpha_p $	$ \alpha_n $
$ ^{40}\text{Ca} $	0.9832	0.9917		0.9893	0.9969
$ ^{124}\text{Sn} $	0.9925	0.9924		0.9939	0.9960

Table 2.  Scaling factors $ \alpha_\text{p} $ and $ \alpha_\text{n} $ for neutron and proton.

Next, we applied the same methodology to $ ^{124}\text{Sn} $. The values of $ N_{\text{R}} $ and $ N_{\text{I}} $ that provide the best fit to the data are 0.7 and 0.4, and the scaling factors $ \alpha_\text{p} $ and $ \alpha_\text{n} $ are listed in Table 2. The results are shown and compared with the experimental data in the lower panel of Fig. 2. We determine the neutron skin thickness of $ ^{124}\text{Sn} $ as $ 0.168_{\text{−}0.019}^{+0.025} $ fm (SLy4) and $ 0.177 \pm 0.022 $ fm (SLy7) Table 3.

Isotope	Skyrme set	$ R_\text{n} $	$ R_\text{m} $	$ \Delta_{r_{\text{np}}} $
$ ^{40}\text{Ca} $	SLy4	$ 3.366_{\text{−}0.015}^{+0.012} $	$ 3.375 \pm 0.007 $	$ -0.018_{\text{−}0.015}^{+0.012} $
$ ^{40}\text{Ca} $	SLy7	$ 3.371 \pm 0.013 $	$ 3.378 \pm 0.007 $	$ -0.013 \pm 0.013 $
$ ^{124}\text{Sn} $	SLy4	$ 4.767_{\text{−}0.019}^{+0.025} $	$ 4.700_{\text{−}0.012}^{+0.014} $	$ 0.168_{\text{−}0.019}^{+0.025} $
$ ^{124}\text{Sn} $	SLy7	$ 4.775 \pm 0.022 $	$ 4.705 \pm 0.014 $	$ 0.177 \pm 0.022 $

Table 3.  Our results for $ R_\text{n} $, $ R_\text{m} $, and $ \Delta_{r_{\text{np}}} $. The radii are shown in units of fm.

Table 4 lists the neutron skin thickness $ \Delta_{r_{\text{np}}} $ of $ ^{124} $Sn from this work and other studies. It can be seen that the neutron skin thickness extracted in the present work is consistent with the values obtained by other methods. Substituting the neutron skin thickness into Eq. 8, we obtain a constraint on the slope parameter of the symmetry energy: $ L = 39.0_{\text{−}16.5}^{+20.8} $ MeV (SLy4) and $ L = 46.1 \, \pm \, 18.7 $ MeV (SLy4). Figure 3 presents the results of this work and other studies mentioned in the introduction. As evident from the figure, our data align with other data within the error margins.

Method	$ \Delta_{r_{\text{np}}} $ (fm)	Ref.
This Work	$ 0.168_{\text{−}0.019}^{+0.025} $	−
	$ 0.177 \pm 0.022 $	−
Proton Scattering	$ 0.25 \, \pm \, 0.05 $	[20]
Inelastic α−Scattering	$ 0.21 \, \pm \, 0.11 $	[23]
Spin-Dipole Resonance	$ 0.19 \, \pm \, 0.07 $	[25]
Proton Scattering	$ 0.185 \, \pm \, 0.017 $	[21]
$ ^4 $He Reaction Cross Sections	$ 0.180 \, \pm \, 0.142 $	[24]
Proton Scattering	$ 0.156 \, \pm \, 0.022 $	[22]

Table 4.  Neutron skin thickness $ \Delta_{r_{\text{np}}} $ of $ ^{124} $Sn from different researches.

The average of all 14 results shown in Fig. 3 yields $ L = 56.1 \, \pm \, 18.9 \, \text{MeV} $. Using the results from this work (SLy7) and the average, we derive a constraint on the symmetry energy described by $ E_{\text{sym}}(\rho) = E_{\text{sym}}(\rho_0)\left(\rho/\rho_0\right)^{L/3 E_{\text{sym}}(\rho_0)} $ [53], as indicated by the red-shaded and blue-shaded regions in Fig. 4, respectively. Among the 184 sets of Skyrme interaction parameters mentioned earlier, only 62 sets satisfy the constraints of this work (FPLyon, KDE, LNS, SkM, SKRA, SkT1, SkT2, SkT3, SkT1^*, SkT3^*, SkT1a, SkT2a, SkT3a, SLy0, SLy1, SLy2, SLy230a, SLy230b, SLy3, SLy4, SLy5, SLy6, SLy7, SLy8, SLy10, SV-sym32, T11, T12, T13, T14, T15, T16, T21, T22, T23, T24, T25, T26, T31, T32, T33, T34, T35, T36, T41, T42, T43, T44, T45, T46, T51, T52, T53, T54, T55, T56, T61, T62, T63, T64, T65, T66). When considering average constraints, this number remains 62, but with exclusions of FPLyon, KDE, SkM, and SLy10, while incorporating MSkA, NRAPR, SIV, and SkO' sets.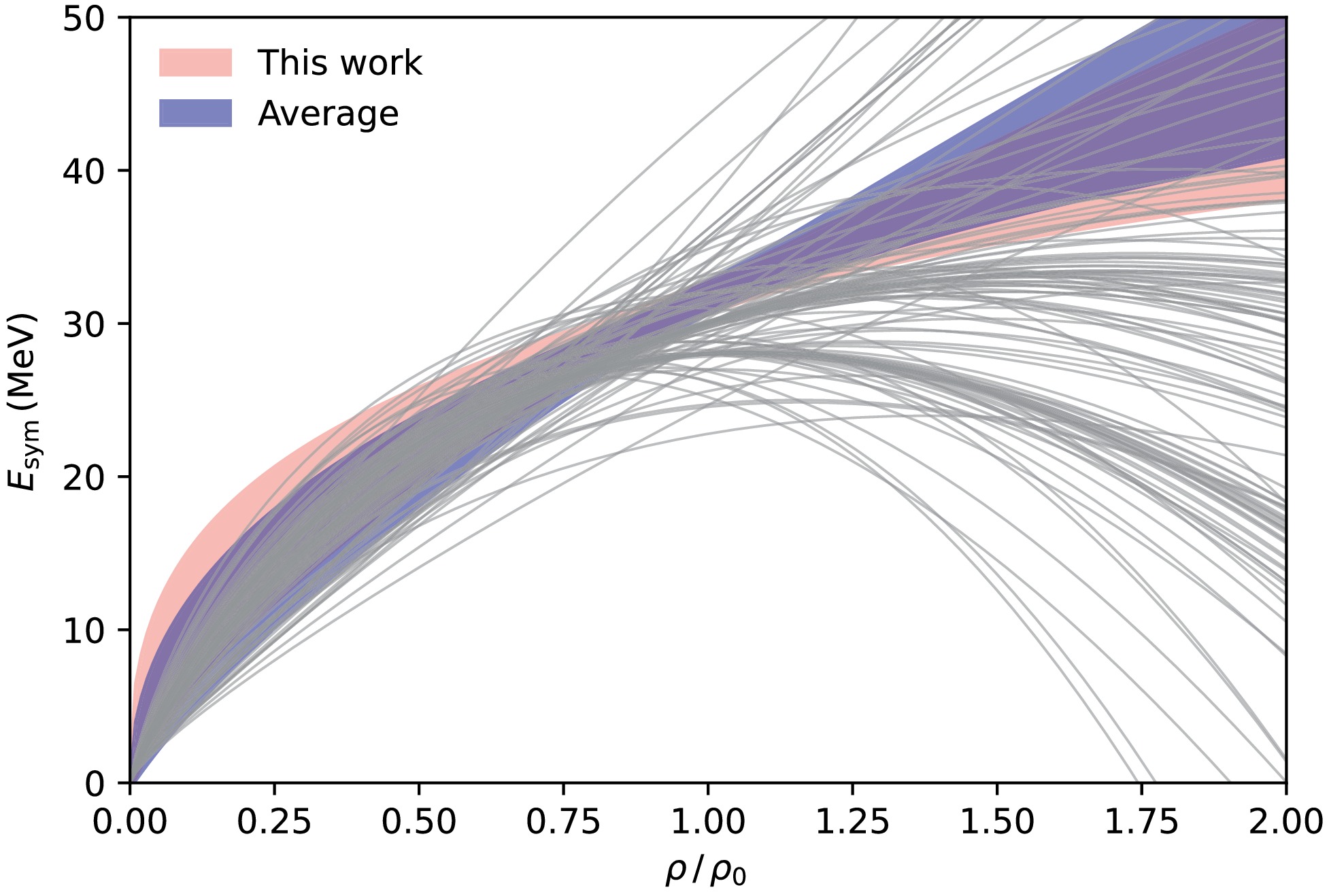

Figure 4.  (color online) Boundary of the constrained region for the symmetry energy as a function of density. The gray lines depict the density dependence of the symmetry energy with $\rho_0 = 0.16 \,\text{fm}^{-3}$ for 122 sets of Skyrme interaction parameters that do not satisfy the constraints of the average.

The study of nuclear symmetry energy is of paramount importance for understanding the properties of neutron stars, as it directly influences the EoS of dense matter, the structure of neutron stars, and their maximum mass and radius. In particular, the slope parameter L at saturation density, which characterizes the density dependence of the symmetry energy, plays a crucial role in determining the pressure of neutron-rich matter and thus the thickness of the neutron star crust and the neutron skin of heavy nuclei. However, the relatively large uncertainty in the slope parameter L remains a significant challenge in nuclear physics, making it a focal point of symmetry energy research. Using the SHF method, we investigated the relationship between L and $ \Delta_{r_{\text{np}}} $ in stable Sn isotopes. Our results reveal an approximately linear correlation between $ \Delta_{r_{\text{np}}} $ and L for Sn isotopes. This linear correlation strengthens with increasing isospin asymmetry, with the strongest linear relationship observed in the $ ^{124} $Sn nucleus. This indicates that the neutron skin thickness of $ ^{124} $Sn provides the most effective constraint on L. We can imagine that uranium isotopes with even larger isospin asymmetry would be a better choice for constraining L. Additionally, the nucleon distribution in neutron stars, which have an isospin asymmetry close to 1, would provide the best data for constraining L.

We have extracted the neutron skin thickness of $ ^{124} $Sn from the elastic scattering angular distribution of $ ^{12} $C + $ ^{124} $Sn using the CDM3Y6 double-folding potential. The extracted neutron skin thickness is $ 0.168_{\text{−}0.019}^{+0.025} $ fm (SLy4) and $ 0.177 \pm 0.022 $ fm (SLy7), which is consistent with the results obtained by other methods. Additionally, we have constrained the slope parameter L of the nuclear symmetry energy to $ L = 39.0_{\text{−}16.5}^{+20.8} $ MeV (SLy4) and $ L = 46.1 \, \pm \, 18.7 $ MeV (SLy4), which is in agreement with the average values predicted by other studies, and eliminates 122 sets of Skyrme interaction parameters out of the original 184. Furthermore, the average constraint derived from 13 works gives $ L = 56.1 \, \pm \, 18.9 $ MeV, significantly reducing the theoretical uncertainty in the behavior of high-density nuclear matter, thereby providing a theoretical foundation for understanding the properties of high-density neutron stars.

Despite good agreement, future investigations are needed to address potential systematic uncertainties. In this study, for the sake of simplicity, we considered only the elastic scattering channel in the folding potential analysis. In reality, nucleus–nucleus interactions can involve various inelastic processes and coupling effects [54]. In future studies, a coupled-channel analysis could be employed to reduce the deviations caused by inelastic scattering.