-
At sufficiently high temperatures and densities, one expects that normal nuclear matter undergoes a phase transition to quark-gluon plasma (QGP), wherein quarks and gluons become deconfined and essentially chiral. This is a topic of great interest related to the physics of heavy-ion collisions at ultrarelativistic energies as well as to the astrophysics of neutron stars [1-3]. Quantum chromodynamics (QCD), as a theory of strong interactions, is applicable for determining the properties of strongly interacting matter at high temperatures and densities. However, because of the phenomenon of asymptotic freedom, the nature of the quark-hadron phase transition remains an open question, especially when quark chemical potentials are involved in the practical calculations [2]. Therefore, we still lack the capabilities to describe the low-energy nonperturbative phenomena in the framework of QCD theory and have to resort to effective models to study the nontrivial structure of the QCD vacuum, such as the Nambu-Jona-Lasinio (NJL) model [4-9], the linear sigma model (LSM) [10], or their modernized versions, i.e., the Polyakov Nambu-Jona-Lasinio model (PNJL) [11] and the Polyakov Quark Meson Model (PQM) [12].
The nature of the QCD phase diagram in the temperature and chemical potential plane was intensively studied in past decades. Most effective models usually predict a smooth crossover transition at low chemical potential and non-zero temperature, while at high density and low temperature, there is a first-order phase transition for QCD phase transitions. At the endpoint of the first-order phase boundary, there should exist a so-called QCD critical endpoint (CEP) [13]. Finding and identifying the CEP in experiments is the main goal of the beam energy scan (BES) program at the Relativistic Heavy-Ion Collider (RHIC) [14] and Super-Proton Synchrotron (SPS) facilities [15]. On the theoretical side, a recent study based on chiral effective models showed that a vast part of the QCD phase diagram is a crossover if the quark and meson fluctuations are included via the functional renormalization group [16]. However, the possibility of a first-order phase transition at large baryon chemical potentials is not ruled out from both experimental and theoretical points of view. In reality, most descriptions of the equation of state (EoS) of neutron stars with a quark core are undertaken via a hybrid equation of state with a hadron phase connected to a quark phase through a first-order phase transition [17-19]. Moreover, the properties of hybrid stars with a strong first-order phase transition and their relevance to gravitational wave observations will enable the probing of the EoS for matter under extreme circumstances [20, 21]. Besides the quark-hadron phase transition, the first-order phase transition would also play important roles in the evolution history of the early universe, such as its possible roles in electroweak baryogenesis and dark matter [22, 23]. Recently, a strong first-order phase transition was also considered as a potential source of gravitational waves (GWs) that could be measured by future detectors [24, 25]. Specifically, the approved Laser Interferometer Space Antenna (LISA) project assigns great importance to the direct detection of the electroweak phase transition through the companion GW signals [26].
In a first-order phase transition, the initial metastable (or false) vacuum decays to the stable vacuum through the nucleation of bubbles larger than a critical size. The nucleation rate of critical bubbles can be calculated from the microphysics using semiclassical methods in the Euclidean thermal field theory [27-31]. Within this framework, an effective thermodynamic potential in the form of a Landau function with cubic interaction is an important and useful theoretical tool [1]. According to the mean-field theory of phase transitions, the free energy density of the system can be expanded in terms of the parameter near the critical point, and we can perform a general analysis without going into much detail about the underlying dynamics [32]. Therefore, at least in the mean-field approximation, the thermodynamical potential of the effective models can be parameterized in the form of a Landau expansion around the equilibrium phase with all terms up to the quartic term in the region of the first-order phase transition. This scenario was adopted to describe the dynamical mechanism of bubble nucleation in a strong first-order cosmological electroweak phase transition [33] and in a weak first-order quark-hadron phase transition [34, 35]. The benefit of this type of parameterization is that it simplifies the effective potential to facilitate the solution of the equation of motion of the critical bubble profile with both numerical and analytical methods.
For a weak first-order quark-hadron phase transition, when the temperature is slightly less than the critical temperature
$ T_{\rm c} $ , the thermodynamic potential exhibits a local minimum aside from the global minimum. As the temperature decreases to some specific value$ T_{\rm sp} $ , the local minimum gradually disappears and ends at a point of inflection known as spinodal instability. Hence, the effective potential has no potential barrier for$ T<T_{\rm sp} $ , and the shift in the coarse-grained free energy due to the appearance of the critical bubble monotonously decreases with the decrease of temperature and should eventually become zero at some specific temperature, as shown in Refs. [34, 35]. The weak first-order quark-hadron phase transition was intensively investigated in the framework of the linear sigma model coupled to quarks [20, 34, 36, 37] and the hybrid model, by combining the EoS obtained within lattice QCD for the quark phase with that of gas corresponding to resonances in the hadron phase [35]. Thus, in this study, a strong first-order quark-hadron phase transition induced by an effective potential with a zero-temperature potential barrier was considered; the Friedberg-Lee (FL) model [38-40] fulfils the requirement.The FL model was originally developed to describe the static properties of isolated hadrons and their behaviors at low energy. By taking the hadrons as the baglike soliton solutions in vacuum, the model provides a very intuitive physical explanation of the confinement in QCD theory. Recently, the model was also extended to finite temperatures and densities to study the deconfinement phase transition in Refs. [41-45]. Note that the FL model and its descendant model with chiral symmetry [46] can only predict a first-order phase transition in the phase diagram. This evidently disagrees with most predictions demonstrated in effective models and lattice QCD data [1-3]. The solution to this problem is to introduce the Polyakov loop in the models. The results in Ref. [47] show that the PQM model indeed gives a prediction of a crossover in the low-density region and a weakly first-order phase transition in the high-density region. However, most of these previous studies focused on the thermodynamic effective potential, the properties of isolated hadrons in thermal medium, and the phase diagram, while our current study focused on the dynamics of a strong first-order phase transition via bubble nucleation. Nowadays, the strong first-order phase transition is increasingly gaining attention both in the astrophysics of neutron stars and the cosmological phase transitions in the early universe, especially when GWs are relevant. Although the quantitative results in this study are model-dependent, the general and qualitative results presented can also be applied to study the bubble dynamics of the first-order phase transitions in various fields driven by cubic interaction, especially beyond the limit on the thin-wall approximation.
The paper is organized as follows. In the following section we briefly describe the Friedberg-Lee model and its effective potential at finite temperatures and densities. In Sec. III, we comprehensively describe the homogeneous nucleation and methods used for both numerical and analytic computations of the critical bubble profiles. Our results and discussions are presented in Sec. IV, while in the last section we conclude with a summary.
-
We start with the Lagrangian of the Friedberg-Lee model for a phenomenological scalar field
$ \sigma $ interacting with spin-$ \dfrac{1}{2} $ quark fields$ \psi $ of the form [38-40],$ {\cal{L}} = \overline{\psi}({\rm i}\eth -g \sigma)\psi+\frac{1}{2}\partial_{\mu}\sigma \partial^{\mu}\sigma -U(\sigma), $

(1) where the potential, which exhibits a typically first-order phase transition, is parameterized in the form of a Landau expansion with all the terms up to the quartic term, expressed as
$ U(\sigma) = \frac{1}{2!}a\sigma^2+\frac{1}{3!}b \sigma^3+\frac{1}{4!}c \sigma^4. $

(2) The model parameters a, b, and c are chosen such that
$ b^2 > 3ac $ to ensure a local minimum of$ U(\sigma) $ at$ \sigma = 0 $ and a global minimum at a relatively larger value of the$ \sigma $ field$ \sigma_v = \frac{3|b|}{2c}\left[1+\left[1-\frac{8ac}{3b^2}\right]^{\frac 1 2}\right]. $

(3) Usually, the global minimum at
$ \sigma = \sigma_v $ is interpreted as the physical or true vacuum, whereas the local minimum at$ \sigma = 0 $ represents a metastable vacuum where the condensate vanishes and quarks have zero rest mass. The difference in the potential values of the two vacuum states is defined as the quantity$ \varepsilon $ . For convenience, in the following discussions, we assume$ U(0) = 0 $ . Therefore, we have$ -\varepsilon = \frac{a}{2!}\sigma^2_v+\frac{b}{3!}\sigma^3_v+\frac{c}{4!}\sigma^4_v. $

(4) A wide range of model parameters a, b, c, and g were adopted in Refs. [42, 43, 48] to confront the basic properties of nucleons in vacuum. However, for the problem discussed here, different sets of values show similar physical results. Therefore, we consider one set of parameters,
$ a = 17.70\; {\rm{fm}}^{-2} $ ,$ b = -1457.4 \;{\rm{fm}}^{-1} $ ,$ c = 20000 $ , and$ g = 12.16 $ , widely used in previous studies.A convenient framework for studying phase transitions is thermal field theory. Within this framework, the finite temperature effective potential is an important and useful theoretical tool. Keeping only contributions to one-loop order, the effective potential of the Friedberg-Lee model can be computed exactly in closed form following the steps presented in Ref. [49]
$ V_{\rm{eff}}(\sigma;T,\mu) = U(\sigma)+V_B(\sigma;T)+V_F(\sigma;T,\mu), $

(5) where
$ V_B(\sigma;T) $ is the finite temperature contribution from the boson loop, and$ V_F(\sigma;T,\mu) $ is the finite temperature and density contribution from the fermion loop [44, 49]. These terms in turn contribute the following terms in the effective potential$ V_B(\sigma;T) = T \int \frac{{\rm d}^3 \vec{p}}{(2\pi)^3} {\rm{ln}} \left( 1-{\rm e}^{-E_{\sigma}/T} \right), $

(6) $\begin{aligned}[b] V_F(\sigma;\beta,\mu) =& -2N_f N_c T \int \frac{{\rm d}^3 \vec{p}}{(2\pi)^3} \Big[ {\rm{ln}} \left( 1+{\rm e}^{-(E_q-\mu)/T} \right)\\&+{\rm{ln}} \left( 1+{\rm e}^{-(E_q+\mu)/T} \right) \Big], \\[-10pt]\end{aligned}$

(7) in which
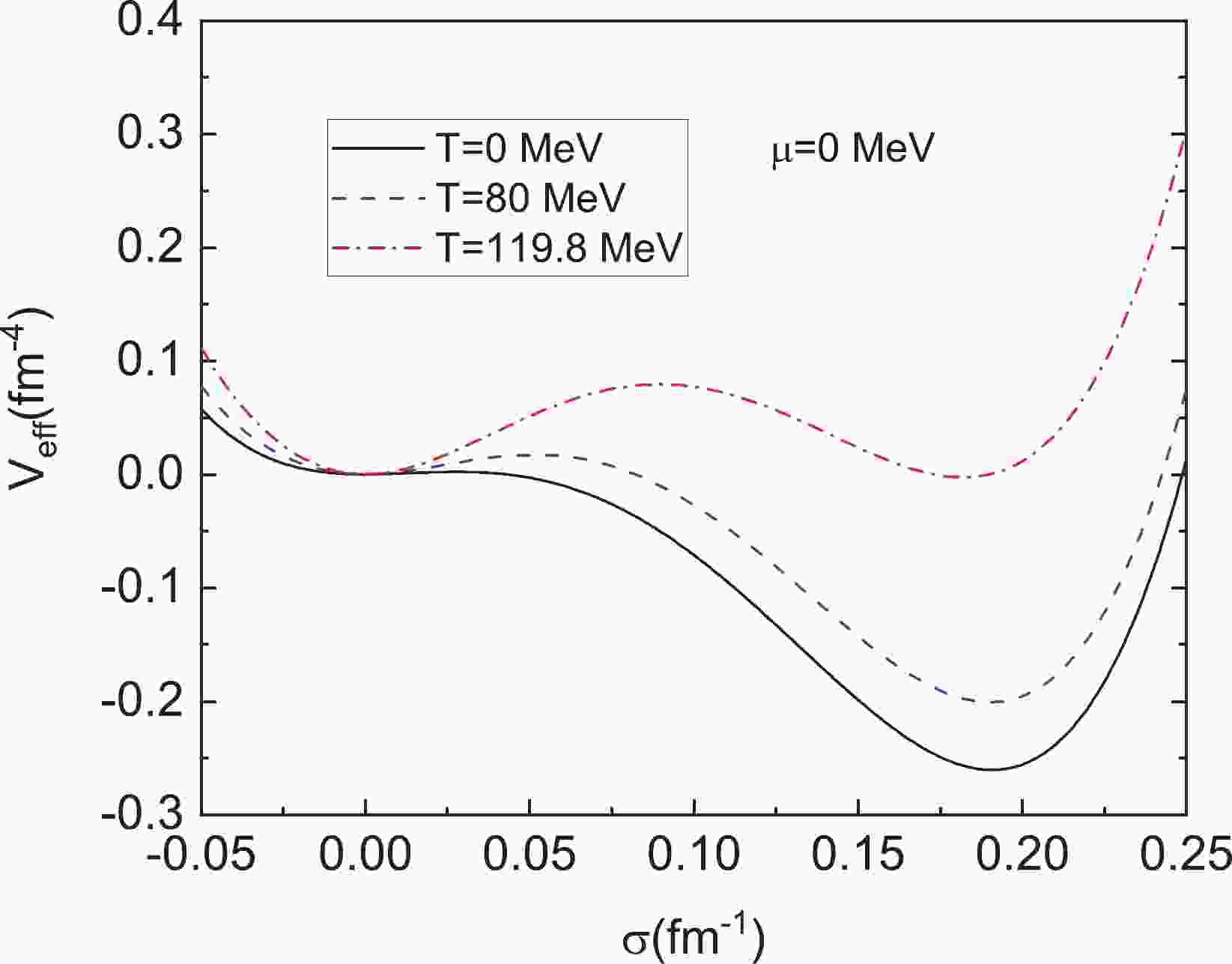
$ N_f = 2 $ and$ N_c = 3 $ .$ E_{\sigma} = \sqrt{\vec{p}^2+m_{\sigma}^2} $ and$ E_q = \sqrt{\vec{p}^2+m_q^2} $ are energies for the$ \sigma $ mesons and quarks in which the constituent quark (antiquark) mass$ m_q $ is defined as$ m_q = g \sigma $ , while the effective mass of scalar meson field is set by$ m^2_{\sigma} = a+b \sigma+\dfrac{c}{2} \sigma^2 $ . To ensure that$ m_{\sigma} $ is positive, in this study we fix it to the vacuum value.The one-loop effective potential at different temperatures in the absence of the chemical potential is plotted in Fig. 1. The shape of the potential shows that a first-order phase transition takes place as it exhibits two degenerate minima at a certain temperature
$ T_{\rm c}\simeq 119.8 $ MeV, which is usually defined as the critical temperature. Normally, apart from this critical temperature, there exists another particular temperature that occurs when one of the minima of the potential disappears as the temperature increases. Between these two particular temperatures, metastable states exist and lie close to$ \sigma_v $ , and the system can exhibit supercooling or superheating. With temperature decreasing across the critical one, the metastable and physical vacua will become flipped, and the metastable states become centered around the origin$ \sigma = 0 $ . Then, the difference between the effective potential at the metastable vacuum state and the physical vacuum state is
Figure 1. (color online) One-loop effective potential
$ V_{\rm eff} $ as a function of$ \sigma $ at$ T = 0 $ MeV,$ T = 80 $ MeV and$ T = 119.8 $ MeV when fixing the chemical potential$ \mu $ at$ 0 $ MeV. According to our choice of parameters, the two minima appear as degenerate at$ T_{\rm c}\simeq 119.8 \;{\rm{MeV}} $ , which is usually defined as the critical temperature.$ \varepsilon(T) = V_{\rm{eff}}(0;T)-V_{\rm{eff}}(\sigma_v;T). $

(8) It is easy to check that the quantity
$ \varepsilon $ will decrease with the increase of temperature, and when$ T = T_{\rm c} $ , the two vacua are equal, and$ \varepsilon $ is zero.When the temperature is fixed at
$ T = 50 $ MeV, the resulting one-loop effective potential$ V_{\rm{eff}} $ as a function of$ \sigma $ at various chemical potentials$ \mu = 0 $ MeV,$ \mu = 150 $ MeV, and$ \mu = 256.4 $ MeV is depicted in Fig. 2. According to this figure, the shapes of the potentials show similar behaviors as in Fig. 1. For$ \mu = 256.4 $ MeV, the values of the effective potentials at the two vacua are equal. At this moment, the chemical potential is defined as the critical chemical potential$ \mu_{\rm c} = 256.4 $ MeV. With the decrease of the chemical potential from$ \mu_{\rm c} $ , the global minimum of the potential moves from the position at$ \sigma = 0 $ to that at$ \sigma_v $ . The difference between the values of the effective potential at the false vacuum and at the physical vacuum as usual is defined as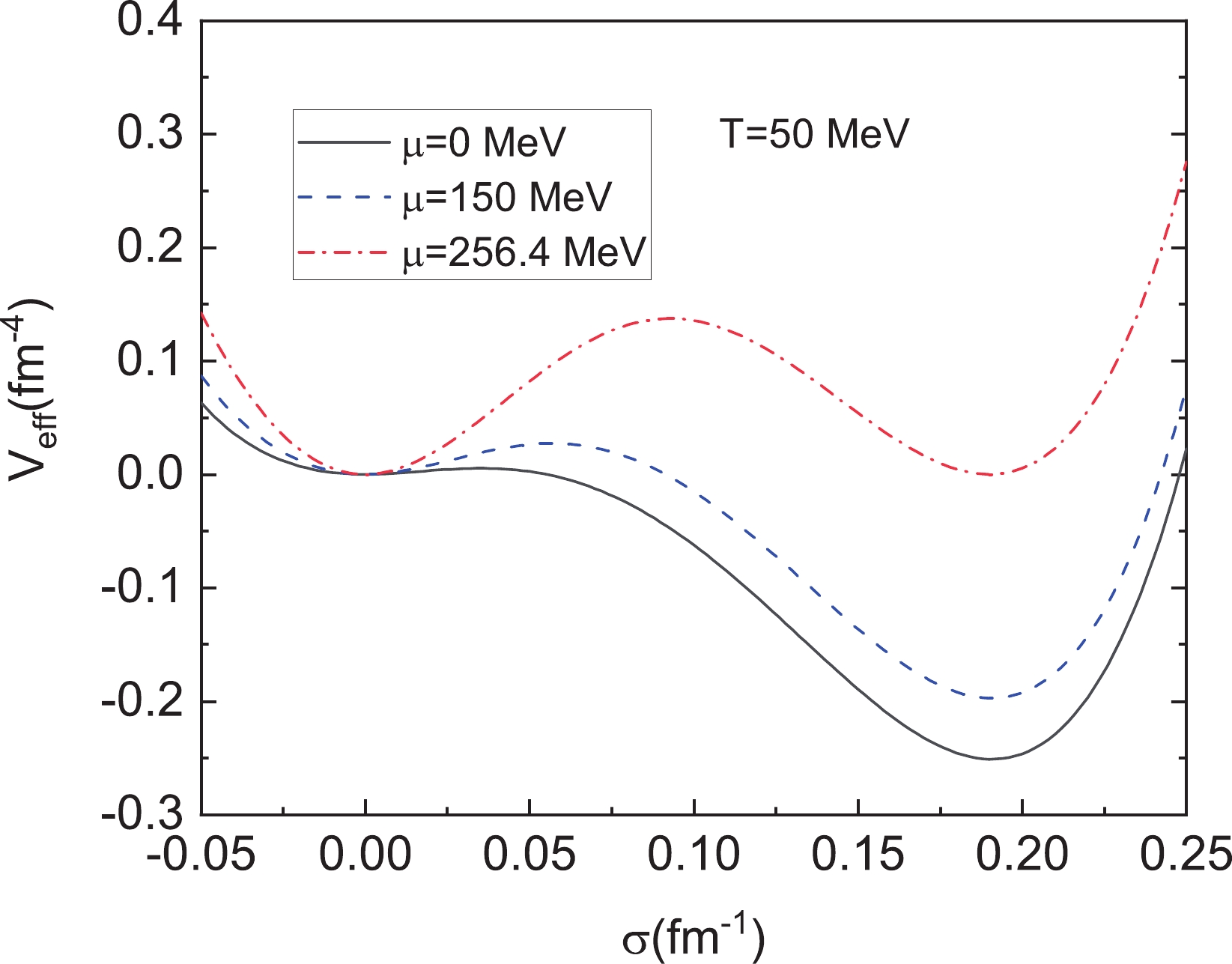
Figure 2. (color online) One-loop effective potential
$ V_{\rm eff} $ as a function of$ \sigma $ at$ \mu = 0 $ MeV,$ \mu = 150 $ MeV, and$ \mu = 256.4 $ MeV when fixing the temperature T at$ 50 $ MeV. According to our choice of parameters, the critical chemical potential is set at$ \mu_{\rm c}\simeq 256.4 $ MeV when the two minima are equal.$ \varepsilon(T,\mu) = V_{\rm{eff}}(0;T,\mu)-V_{\rm{eff}}(\sigma_v;T,\mu). $

(9) This quantity will also decrease to zero as the chemical potential increases up to its critical value.
-
For the first-order phase transition, when the temperature or chemical potential approximately reaches its critical value, the effective potential exhibits degenerate minima that are separated by a barrier. As the temperature or chemical potential is lowered, the local minimum at
$ \sigma\simeq 0 $ becomes the false vacuum, while the global minimum of the effective potential at$ \sigma\approx \sigma_v $ is taken as the stable or physical vacuum. The false vacuum would be stable classically, but quantum mechanically it is only a metastable state and can decay via the nucleation of bubbles larger than a critical size. Technically, this decay may be triggered by either quantum or thermal fluctuations, depending on what type of physics we are interested in. In this study, we were mostly concerned with the regime in which thermal fluctuations are much larger than quantum fluctuations.The dynamics of a first-order phase transition can be described by the mechanism of bubble nucleation of the stable vacuum inside the false vacuum, which is believed to be a natural consequence of the thermal and quantum fluctuations of any thermodynamic systems closely interrelated with a first-order phase transition. For
$ T<T_{\rm c} $ or$ \mu<\mu_{\rm c} $ , bubbles of the stable vacua created by thermal fluctuations may grow or shrink inside the false vacuum depending on its energy budget with regard to a homogeneous false vacuum. Given that the bulk free energy density of the false vacuum is higher than that of the stable vacuum, the phase conversion from the false vacuum to the stable vacuum decreases the bulk free energy of the whole system. However, the appearance of a spherical bubble means there is an interface that is needed to separate the stable vacuum from the exterior of the false vacuum. The creation of such an interface represents an energy cost. Therefore, the mechanism of phase conversion from the metastable phase to the stable phase proceeds by a competition between the free energy gain from the phase transition of the bulk and the energy cost from the formation of an interface. Note that the free energy shift due to the appearance of a spherical bubble of stable vacuum is proportional to$ -R^3 $ , where R is the bubble radius, and the surface tension of the interface between two phases is proportional to$ +R^2 $ . For the nucleation of small bubbles, the energy cost is higher than the energy gain, and small bubbles tend to shrink. By contrast, a bubble with a sufficiently large radius represents a large bulk energy gain. The energy gain in the system exceeds the surface energy cost of creating the bubble. Consequently, these large bubbles tend to expand even further and to coalesce completely, completing the phase conversion. Therefore, only bubbles of a very large radius play a decisive role in the theory of dynamics of a first-order phase transition.In the theory of bubble nucleation, a scalar field
$ \sigma $ is treated as the order parameter and a coarse-grained free energy functional of the system is defined as$ F(\sigma) = \int {\rm d}r^3 \left[ \frac{1}{2} \left(\nabla \sigma \right)^2+V_{\rm{eff}}(\sigma;T,\mu) \right]. $

(10) The critical bubble configuration is an extremum of the coarse-grained free energy functional
$ F(\sigma) $ with respect to the scalar field$ \sigma $ ; thus, the equation of motion to be solved now becomes a nonlinear ordinary differential equation,$ \frac{{\rm d}^2\sigma(r)}{{\rm d}r^2}+\frac{2}{r}\frac{{\rm d}\sigma(r)}{{\rm d}r} = \frac{\partial V_{\rm{eff}}(\sigma;T,\mu)}{\partial \sigma}, $

(11) with boundary conditions
$ \lim\limits_{r \to \infty }\sigma(r) = 0 $ and$ \dfrac{{\rm d}\sigma(0)}{{\rm d}r} = 0 $ . The first boundary condition is because the bubbles are embedded in the homogeneous false vacuum, outside the bubble, and the$ \sigma $ field should arrive at its false vacuum at$ \sigma \simeq 0 $ , while the second boundary condition is set by the requirement of no singularity of the solution at the origin. The solution for this equation of motion with the above proper boundary conditions is a saddle point solution$ \sigma_b $ .Once the solution
$ \sigma_b $ is found, the shift in the coarse-grained free energy due to the formation of a nucleation bubble can be calculated as$ \Delta F_b = 4 \pi \int r^2 {\rm d}r \left[ \frac{1}{2} \left( \frac{{\rm d}\sigma_b}{{\rm d}r} \right)^2+V_{\rm{eff}}(\sigma_b;T,\mu) \right]. $

(12) Note that here, and subseqeuntyl,
$ V_{\rm{eff}}(0;T,\mu) $ is well normalized to be zero for simplicity. The nucleation rate per unit volume is expressed as [30, 31]$ \Gamma = {\cal{P}}\exp\left[ -\frac{\Delta F_b}{T} \right], $

(13) where the pre-exponential factor
$ {\cal{P}} $ corresponds to the probability for a critical bubble-like field fluctuation$ \sigma_b $ to be generated and grow. Evaluation of the pre-exponential factor is a nontrivial matter. A rough estimate of their ratio can be obtained by dimensional arguments and we could approximate$ {\cal{P}} $ by$ T^4 $ for simplicity [34]. The surface tension of the nucleation bubble interface between the false and stable vacua is then defined as$ \Sigma = \int {\rm d}r \left[ \frac{1}{2} \left(\frac{{\rm d}\sigma_b}{{\rm d}r} \right)^2+V_{\rm{eff}}(\sigma_b;T,\mu) \right]. $

(14) For a generic effective potential
$ V_{\rm{eff}} $ , the equation of motion (11) with some certain boundary conditions usually cannot be solved analytically. However, when the system is very close to the critical coexistence line, e.g.,$ T\sim T_{\rm c} $ or$ \mu \sim \mu_{\rm c} $ , the problem can be essentially simplified. In such a situation, the quantity$ \varepsilon $ is much smaller than the height of the barrier separating these two vacua because of the competition between the free energy gain and the surface energy cost. In addition, the typical radius of the bubbles becomes much greater than the wall thickness, and the second term in the equation of motion (11) can be neglected. Then, the so-called thin-wall approximation is applicable and the equation of motion (11) reduces to the equation for a typical one-dimensional solution:$ \frac{{\rm d}^2 \sigma (r)}{{\rm d}r^2} = \frac{{\rm d} V_{\rm{eff}}}{{\rm d} \sigma}. $

(15) This static field equation implies that
$ \frac{{\rm d} \sigma(r)}{{\rm d}r} = \pm \sqrt{2 V_{\rm{eff}}}. $

(16) Integrating Eq. (16) yields
$ r = \int_{\sigma}^{\sigma_v} \frac{{\rm d} \sigma}{\sqrt{2 V_{\rm{eff}}}}. $

(17) In the case of an arbitrary potential
$ V_{\rm{eff}} $ with two or more degenerate global minima as in the limit$ \varepsilon\rightarrow 0 $ , the profile of the critical bubble can be estimated as follows. For a smoothly varying potential$ V_{\rm{eff}} $ , the integral on the right-hand side diverges as$ \sigma(r) $ approaches any of the global minima. Hence, as r ranges from$ 0 $ to$ \infty $ ,$ \sigma(r) $ must vary monotonically from one global minimum of$ V_{\rm{eff}} $ at$ \sigma = \sigma_v $ to an adjacent global minimum at$ \sigma = 0 $ . In this case, the approximate solution for the bubble with the critical size is given by$\sigma (r) = \left\{ {\begin{array}{*{20}{l}} {{\sigma _v}}&{0 < r < R - \Delta R,}\\ {{\sigma _{{\rm{wall}}}}(r)}&{R - \Delta R < r < R + \Delta R,}\\ 0&{r > R + \Delta R,} \end{array}} \right.$

(18) which indicates that the stable vacuum inside the bubble is separated from the metastable one outside by the bubble wall
$ \sigma_{\rm{wall}}(r) $ , solved from Eq. (17). Moreover, in the thin-wall approximation, given that there exists an energy competition between the free energy gain and the surface energy cost, the free energy$ F(R) $ , relative to the false vacuum background, of a bubble with radius R could be expressed as [31, 50]$ F(R) = 4 \pi R^2 \Sigma-\frac{4}{3}\pi R^3 \varepsilon. $

(19) Here, the first term is the contribution from the bubble wall with a surface tension
$ \Sigma $ , while the second is from the true vacuum interior. The typical radius$ R_c $ of the bubble is determined by minimization of the free energy$ F(R) $ with respect to R, which in turn requires that$ 0 = \frac{{\rm d}F}{{\rm d}R} = 8 \pi R \Sigma- 4 \pi R^2 \varepsilon. $

(20) This is solved by
$ R_c = \frac{2 \Sigma}{\varepsilon}. $

(21) As described in previous discussion, only bubbles that have a size equal to or larger than the typical radius
$ R_c $ are energetically favorable and would play an important role in the dynamical seed of the phase conversion.Finally, note that, in the absence of the quantity
$ \varepsilon $ , the one-dimensional energy or the surface tension of the bubble is$ \Sigma_{tw} = \int_{0}^{\infty} {\rm d}r \left[ \frac{1}{2} \left(\frac{{\rm d}\sigma_b}{{\rm d}r} \right)^2+V_{\rm{eff}} \right] = \int_{0}^{\sigma_v} {\rm d}\sigma \sqrt{2 V_{\rm{eff}}} . $

(22) From Eqs. (17) and (22), a saddle point field configuration
$ \sigma(r) $ and the surface tension can be directly obtained by using the effective potential$ V_{\rm{eff}} $ without solving the equation of motion in Eq. (11), which is usually difficult to be solved analytically or even numerically. This is the main advantage of the thin-wall approximation approach. Given that the thin-wall approximation is so widely adopted in previous studies [34-37, 51-54], we focused on the exact numerical computations and established limits on the reliability of the thin-wall approximation. -
Next, we numerically solve the equation of motion in Eq. (11) with some proper boundary conditions,
$ \sigma\rightarrow 0 $ as$ r\rightarrow \infty $ and$ \dfrac{{\rm d} \sigma(0)}{{\rm d}r} = 0 $ . The exact numerical solutions setting$ T = 0 $ ,$ 70 $ ,$ 109 $ ,$ 118 $ ,$ 119 $ , and$ 119.8 $ MeV in the absence of chemical potential are plotted in the left panel of Fig. 3. Note that, when the temperature decreases from$ T = T_{\rm c} $ , all curves approach zero when the radius r is large, whereas$ \sigma(r) $ at the center of the bubble changes dramatically. When the temperature is sufficiently close to the critical temperature at$ T_{\rm c} = 119.8 $ MeV, the$ \sigma $ field at the center of the bubble only slightly deviates from its stable vacuum value at$ \sigma = \sigma_v $ . However, for$ T \leqslant 109 $ MeV, the$ \sigma $ field at the center of the bubble is visibly different from its stable vacuum value. Such a deviation can be demonstrated by an "overshoot-undershoot" argument, proposed by Coleman [27]. According to this idea, the equation of motion (11) is reinterpreted as the equation for a particle moving under an "upside-down" potential energy$ -V_{\rm{eff}} $ , and the$ \sigma'(r) $ term is interpreted as a damping force. The boundary conditions require that the particle starts at rest at some initial point$ \sigma_0 $ on the true vacuum side of the potential well, and it rolls down to rest at its false vacuum$ \sigma(0) $ . For$ -V_{\rm{eff}}(\sigma_0)\leq -V_{\rm{eff}}(0) $ , because of the damping term, the particle will never have sufficient energy to reach$ \sigma_0 $ , and it undershoots. By contrast, if$ \sigma_0 $ differs only infinitesimally from$ \sigma_v $ , the particle could have nonzero kinetic energy when it reaches$ \sigma_0 $ , it will continue on and never return, and it overshoots. The desired$ \sigma_0 $ that determines the bounce is located among these two ranges. In our case, when the temperature is very close to the critical temperature$ T_{\rm c} $ , the damping force will have almost died away, and the potential has two degenerate vacua. Moreover, the field$ \sigma_0 $ starts at the top of the effective potential$ -V_{\rm{eff}} $ around$ \sigma\simeq\sigma_v $ . However, when the temperature decreases, two degenerate vacua become decoupled and the damping force takes effect. Consequently, the field$ \sigma_0 $ will increasingly deviate from its vacuum value. In other words, the thin-wall approximation is expected to be invalid, and any further extension of the thin-wall approximation to lower temperature deviation from$ T_{\rm c} $ should be checked very carefully.
Figure 3. (color online) (left panel) Critical bubble profiles for different temperatures and zero chemical potential. From left to right, the curves correspond to
$ T = 0 $ ,$ 70 $ ,$ 109 $ ,$ 118 $ ,$ 119 $ , and$ 119.8 $ MeV. (right panel) Critical bubble profiles for different chemical potentials when fixing the temperature T at$ 50 $ MeV. From left to right, the curves correspond to$ \mu = 0 $ ,$ 200 $ ,$ 230 $ ,$ 253 $ ,$ 254 $ , and$ 256.4 $ MeV.Similar discussion can be applied to the second case, when the temperature is fixed. The critical bubble profiles at different chemical potentials are depicted in the right panel of Fig. 3, where the chemical potentials are
$ \mu = 0 $ ,$ 200 $ ,$ 230 $ ,$ 253 $ ,$ 254 $ , and$ 256.4 $ MeV for a fixed temperature$ T = 50 $ MeV. The evolution of the$ \sigma(r) $ for different chemical potentials implies that the typical radius of the critical bubble should increase when the chemical potential increases, and the nontrivial behavior of the$ \sigma(r) $ in the center of the bubble can be interpreted as a limit to the applicability of the thin-wall approximation. From the right panel in Fig. 3, given that$ \sigma(0) $ reaches its maximum when$ \mu\simeq 230 $ MeV, this specific value is considered as the lower limit that keeps the thin-wall approximation valid.Once the bubble profiles have been solved, the surface tension of the nucleation bubble interface between the false and the stable vacua as a function of the temperature can be obtained, as shown in the left panel of Fig. 4 for zero chemical potential. An interesting behavior is found: with the increase of the temperature, the surface tension
$ \Sigma(T) $ starts growing quickly from$ T = 60 $ MeV, and reaches a maximum$ \Sigma(T)\simeq 7.38 $ $ \;{\rm{MeV}}/{\rm{fm}}^2 $ at$ T\simeq 109 $ MeV. This nontrivial behavior of$ \Sigma(T) $ at$ T\simeq 109 $ MeV can be analyzed by the evolution of the bubble profile with temperature. According to the left panel in Fig. 3, as T decreases from its critical temperature$ T_{\rm c} $ , the$ \sigma(r) $ field near the center of the bubble gradually departures from its thin-wall approximate solution$ \sigma_v $ in Eq. (18), and when$ T\simeq 109 $ MeV, the$ \sigma(r) $ field reaches its maximal value before it starts decreasing. This implies that the turning point of the surface tension could be treated as a landmark for the breakdown of the thin-wall approximation. For the second case presented in the right panel of Fig. 4,$ \Sigma(\mu) $ shows a similar behavior. With the increase of chemical potential,$ \Sigma(\mu) $ increases accordingly until reaching its maximum value,$ \mu\simeq 230 $ MeV. Then, it drops quickly to small values. The turning point is also treated as a generous limit to the applicability of the thin-wall approximation. Note that the non-monotonic behavior of the surface tension in the present study was also reported for a weak first-order phase transition [35], in which the evolution of the surface tension first increases to its maximum value and then decreases rapidly to zero, rather than to a small value. This is the main difference between the strong first-order phase transition and the weak ones. The reason is that, for a weak first-order phase transition, as long as the temperature is under a spinodal temperature$ T_{\rm sp} $ , a small barrier between the two minima in the potential will disappear, and there is only one minimum left in the effective potential. According to a standard criterion to guarantee the existence of the stable bounce, it is indispensable for the potential of the order parameter fields, e.g.,$ \sigma $ field in this study, to exhibit three distinct extrema [29, 47, 50, 55]. Consequently, we can only have a trivial solution to the equation of motion (11) as$ \sigma(r) = 0 $ if$ T<T_{\rm sp} $ , and the surface tension should approach zero when$ T\rightarrow T_{\rm sp} $ .
Figure 4. (left) Surface tension as a function of temperature T for
$ T\leqslant T_{\rm c} $ at zero chemical potential. (right) Surface tension as a function of chemical potential$ \mu $ for$ \mu \leqslant \mu_{\rm c} $ when fixing the temperature at$ 50 $ MeV.The typical radius of the critical bubble as a function of temperature and chemical potential is displayed in Fig. 5. As mentioned above, any bubble smaller than the critical bubble will shrink and rapidly disappear, and any larger bubble will grow and drive the phase conversion. Therefore, bubbles with radii larger than
$ R_c $ will have a decisive role and can be considered as the dynamical seed of the first-order phase conversion.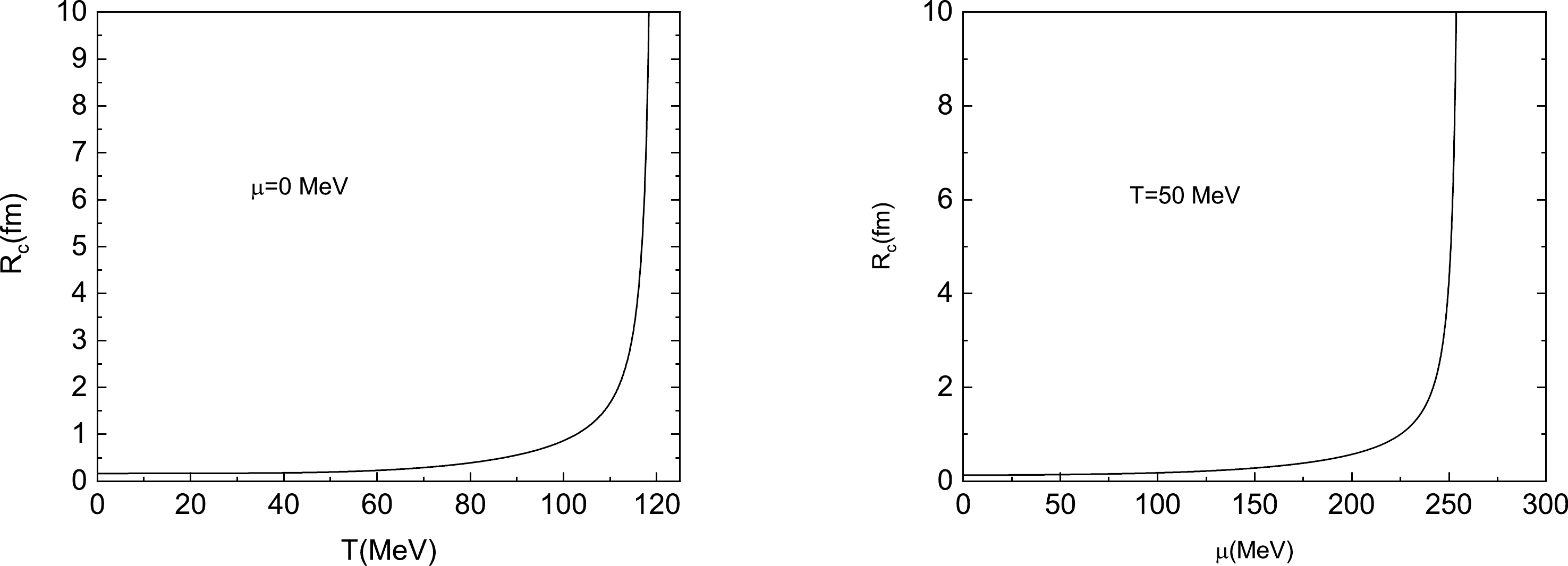
Figure 5. (left) Typical radius of the critical bubble as a function of temperature T when
$ T\leqslant T_{\rm c} $ at zero chemical potential. (right) The typical radius of the critical bubble as a function of chemical potential$ \mu $ when$ \mu \leqslant \mu_{\rm c} $ when fixing the temperature at$ 50 $ MeV.According to Fig. 5, the critical bubble swells with the increase of temperature and chemical potential. This behavior is more evident for larger variables, and diverges at
$ T = T_{\rm c} $ and$ \mu = \mu_{\rm c} $ . The divergent behaviors of$ R_c $ at$ T = T_{\rm c} $ and$ \mu = \mu_{\rm c} $ are in agreement with the definition of the typical radius in Eq. (21). Note also that$ \varepsilon\rightarrow 0 $ as$ T \rightarrow T_{\rm c} $ . For futher numerical analysis, besides the nontrivial numerical solutions presented in Fig. 3, the equation of motion in Eq. (11) can always have two trivial solutions:$ \sigma(r) = \sigma_v $ and$ \sigma(r) = 0 $ . The former trivial solution is subject to the divergence of the$ R_c $ when the system is at its critical point.The shift in the coarse-grained free energy due to the activation of a nucleation bubble
$ \Delta F_b $ can be calculated directly from Eq. (12). In this study, we focused on the relatively violent behavior of the exponential factor in Eq. (13), which is an essential ingredient for the nucleation rate per unit volume$ \Gamma $ , whereas the pre-exponential factor$ {\cal{P}} $ is approximately set to$ T^4 $ . To show the shift in the coarse-grained free energy due to the appearance of the critical bubble and its crucial role in the nucleation rate for the first-order phase transition,$ \Delta F_b/T $ is plotted as a function of the temperature T and chemical potential$ \mu $ in Fig. 6. In the absence of the chemical potential,$ \Delta F_b/T $ decreases with the increase of the temperature, reaching a minimum point. Then, it will grow very quickly and diverge near the critical temperature$ T_{\rm c} $ . For$ T\simeq114.5 $ MeV,$ \Delta F_b/T \simeq1 $ , and$ \Gamma $ will become strongly suppressed by the exponential factor. Then, the system is likely to stay in the metastable vacuum for a relatively long time. By contrast, for$ T<114.5 $ MeV, the unstable vacuum tends to decay very quickly to the true vacuum. The non-monotonic behavior of$ \Delta F_b/T $ as a function of the temperature T was also reported in a recent study on the bounce action for a strong cosmological first-order phase transition [25]. When fixing the temperature at$ 50 $ MeV, the resulting plots of$ \Delta F_b/T $ as a function of chemical potential$ \mu $ for$ \mu \leqslant \mu_{\rm c} $ are shown in the right panel in Fig. 6. In this case, when$ \mu $ is approximately$ 231 $ MeV,$ \Delta F_b/T\simeq1 $ , and the system is likely to remain in the metastable vacuum as long as the chemical potential is larger than$ 231 $ MeV.
Figure 6. (left) Bubble-activation free energy shift
$ \Delta F_b/T $ as a function of temperature T for$ T\leqslant T_{\rm c} $ at zero chemical potential. (right) Bubble activation free energy shift$ \Delta F_b/T $ as a function of chemical potential$ \mu $ for$ \mu \leqslant \mu_{\rm c} $ when fixing the temperature at$ 50 $ MeV. -
In the present study, we investigated the dynamics of a strong first-order phase transition via homogeneous bubble nucleation within the Friedberg-Lee model at finite temperatures and chemical potentials. After obtaining the effective thermodynamical potential, a saddle point solution of the equation of motion and the exact bubble profiles were numerically calculated. For zero chemical potential, the critical temperature
$ T_{\rm c} $ was approximately$ 119.8 $ MeV when the two minima of the effective potential were equal to each other. Alternatively, when taking the chemical potential as a variable, a critical chemical potential appeared at$ \mu\simeq 256.4 $ MeV; then, the temperature was fixed at$ 50 $ MeV.The evolution of surface tension in a thermal medium shows similar behaviors. It first increases to a maximum value and then decreases with the decrease of temperature or chemical potential. The maximum value of the surface tension can be considered as a limit on the reliability of the thin-wall approximation, because the bubble profile at this point represents a large distortion of that of the thin-wall approximation. Moreover, given that two minima of the classical potential in the Friedberg-Lee model are separated by a barrier, no matter how small the barrier becomes, we can always have a nontrivial bounce solution for the equation of motion of the bubble profiles. This implies that, as the temperature or the chemical potential goes to zero, the surface tension
$ \Sigma $ approaches a small value rather than zero as long as the barrier exists there. By contrast, for a weak first-order phase transition, given that the local minimum of the effective potential will gradually disappear when$ T = T_{\rm sp} $ , there only exits a trivial bounce solution for the equation of motion, and the surface tension$ \Sigma $ should subsequently become zero at this moment [35]. This is an apparent feature of the zero-temperature effective potential with and without a barrier. Furthermore, because of its important role in heavy-ion collision and in astrophysics, the surface tension has attracted much attention recently. Most effective models predict$ \Sigma\leqslant 30 $ $ {\rm{MeV/fm^2}} $ , such as the MIT bag model [56], the quark-meson model [36, 37, 54, 57], NJL model [58, 59], three-flavor PQM model [52], and the nucleon-meson model [53]. Our calculations result in rather low values. For example, we obtained approximately$ 7.38 $ $ {\rm{MeV/fm^2}} $ for zero chemical potential and$ 7.73 $ $ {\rm{MeV/fm^2}} $ when fixing the temperature at$ T = 50 $ MeV for the system at its critical point.Unlike the surface tension, the typical radius of the critical bubble exhibits a monotonic property with the increase of temperature or chemical potential. In both cases,
$ R_c $ starts from a small value and then increases slightly with the increase of the variable. When the system is close to its critical point, it sharply grows and disappears. However, for a weak first-order quark-hadron phase transition,$ R_c\rightarrow 0 $ as$ T\rightarrow T_{\rm sp} $ because there is only a trivial bounce solution as$ T\leqslant T_{\rm sp} $ .The shift in the coarse-grained free energy
$ \Delta F_b/T $ shows a very interesting behavior when the system warms up. In particular, when the temperature increases,$ \Delta F_b/T $ first decreases to a minimum value and then increases rapidly. As the temperature is close to the critical temperature$ T_{\rm c} $ , it will quickly go across unity$ 1 $ and become divergent. In comparison with previous studies based on a weak first-order quark-hadron phase transition [34, 35], we found that$ \Delta F_b/T $ as a function of temperature shows a similar behavior when the temperature is close to the critical temperature$ T_{\rm c} $ . However, when the temperature departs from$ T_{\rm c} $ , our results present a non-monotonic behavior with the decrease of the temperature, whereas for a weak first-order phase transition with spinodal instability,$ \Delta F_b/T $ will drop monotonically to zero quickly as$ T\rightarrow T_{\rm sp} $ . This is another apparent feature of the zero-temperature effective potential with and without a barrier. In the end,$ \Delta F_b/T \simeq1 $ corresponds to the moment at which the system is likely to stay in the metastable vacuum for a relatively long time. -
We thank Jinshuang Jin for valuable comments and discussions.
Bubble dynamics in a strong first-order quark-hadron transition
- Received Date: 2020-06-18
- Available Online: 2021-04-15
Abstract: We investigate the dynamics of a strong first-order quark-hadron transition driven by cubic interactions via homogeneous bubble nucleation in the Friedberg-Lee model. The one-loop effective thermodynamic potential of the model and the critical bubble profiles have been calculated at different temperatures and chemical potentials. By taking the temperature and the chemical potential as variables, the evolutions of the surface tension, the typical radius of the critical bubble, and the shift in the coarse-grained free energy in the presence of a nucleation bubble are obtained, and the limit on the reliability of the thin-wall approximation is also addressed accordingly. Our results are compared to those obtained for a weak first-order quark-hadron phase transition; in particular, the spinodal decomposition is relevant.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: