Tensor force impact on shell evolution in neutron-rich Si and Ni isotopes

The development of experimental methods with radioactive beams made it possible to significantly expand the isotope map in regions of neutron or proton excess. When moving into the region of exotic nuclei, new and often unexpected phenomena were uncovered, such as the disappearance of the "classical" magic numbers $ N=20 $ and 28 and the appearance of new $ N=14, $ 16, 32, or 34. Such profound changes in nuclear structure allow for further improvement and selection of theoretical models, motivating more studies of nuclear structure evolution using sufficiently complete chains of isotopes or isotones as an example. New problems arose in describing the changes in the splitting between certain single-particle states in the framework of the usual mean-field theory using effective nucleon-nucleon ($ NN $) forces. These issues compelled us to pay closer attention to the subtle features of the interaction. Thus, in recent decades, the role of the tensor $ NN $ interaction in the formation of some features in the structure of exotic nuclei has been actively studied [1].

The most general form of nucleon-nucleon forces involves the contribution of the tensor component contained in all meson-exchange models. One of the most important experimental evidences for the presence of off-center forces is the non-zero quadrupole moment of the deuteron. Tensor interaction leads to additional long-range spatial correlation of the wave functions of two nucleons in the triplet state and actually defines the existence of the deuteron [2]; the alignment state of the vector connecting the neutron with the proton with their spins is the most energetically favorable. A simple account of the isospin dependence of nuclear forces shows that in the case of the isovector state, the attraction arising due to tensor forces should be three times weaker than in the state with zero isospin [1].

Despite the crucial role of the tensor component in the structure of the deuteron, various models of many-particle systems based on effective interactions, such as Skyrme or Gogny forces, have not explicitly considered the contribution of the tensor interaction for a long time. On the one hand, the introduction of additional parameters complicates the computational procedure; on the other, fitting the interaction parameters to the experimental data of a large number of nuclei makes it possible to effectively consider the influence of certain interaction features. However, following the accumulation of new data in experiments with radioactive beams, the question of the influence of the tensor contribution on the calculations of the nuclear structure in many-particle models has again become relevant.

The role of tensor forces in the formation of new magic numbers and their influence on the shape of various nuclei was investigated in several studies [3−8]. In [1, 9], tensor neutron-proton interaction in nuclei was shown to lead to attraction when the nucleon spins are parallel and repulsion in the opposite case. This property affects the spin-orbit splitting and changes the energies of single-particle states. In many cases, tensor forces were shown to play a crucial role in the formation of the islands of inversion [10, 11]. The interplay between tensor interaction and pairing correlation was also reported to cause changes in the single-particle structure and nucleon density distribution with the possible formation or disappearance of bubble structures in certain nuclei [12]. Changes in nuclear structure are also of importance in various applications in astrophysics. Examples include the impact on the strength distribution of Gamow-Teller resonances affecting the weak processes occurring alongside the r-process in supernovae [13]. A detailed analysis of the role of tensor interaction in weak processes taking place in stars undergoing a gravitational collapse is also given in [14, 15].

Notably, describing the neutron-proton interaction when discussing the role of tensor forces is standard practice; the influence of tensor forces on the position of single-particle levels of nucleons of one type is considered when nucleons of another type are added to the nucleus [1]. At the same time, significantly less attention was paid to the role of the isovector tensor component, which is also responsible for the interaction of identical nucleons. Some studies on this topic include [16], where the authors study the impact of tensor forces on the shell structure and deformation of zirconium isotopes.

In this article, we discuss the influence of tensor forces on the various characteristics of even $ ^{28-42} $Si silicon isotopes and $^{56-78}$Ni nickel isotopes. All calculations are carried out using the self-consistent Skyrme-Hartree-Fock approach with forces that include the tensor interaction component. Previously, in [6], the influence of tensor forces on the splitting of proton states in silicon isotopes was considered using the SLy5 parametrization compared with the relativistic mean field theory approach. The impact of tensor forces on the deformation of silicon nuclei was also discussed in [17]. Nickel isotopes with the magic number $ Z=28 $ were studied more extensively in various approaches (see, for example, [18−21]). Our task is to compare the results for different variants of $ NN $ interaction and estimate the contribution of tensor forces to the splitting of protons and neutron single-particle levels with increasing neutron excess. We also check the interplay between the effect of pairing identical nucleons and the influence of tensor forces. Using the Bardeen-Cooper-Schrieffer approach to describe pairing makes it possible to isolate the role of pairing effects and evaluate the change in the effect when tensor forces are turned on.

The article is structured as follows: In Section II, we review the basics of the Skyrme-Hartree-Fock approach and account for tensor forces in the approximation of zero-range forces. In Section III, we discuss the impact tensor interaction has on various nuclei in silicon and nickel isotope chains. On the example of the two interactions, SLy5 and SGII, with and without forces, we demonstrate that the shell structure evolution in these isotopes can be very sensitive to both the central and tensor parts of the nucleon-nucleon interaction. Several other interactions were also employed to verify the effects of tensor forces on the splitting between various neutron and proton states in select isotopes.

All calculations were performed within the framework of the Hartree-Fock approach, with phenomenological interaction in the form of Skyrme forces. Pairing correlations were treated within the BCS model. The standard nucleon-nucleon Skyrme potential reads [22]:

Here, $ \vec{r}_1 $ and $ \vec{r}_2 $ are nucleon coordinates, $\vec{k}= (\vec{\nabla}_1-\vec{\nabla}_2)/{(2i)}$, $ \vec{k}' $ is the operator complex-conjugate to $ \vec{k} $ (the corresponding conjugate operators $ \vec{\nabla}' $ act on the wave function to the left), $ \vec{\sigma}=\vec{\sigma}_1+\vec{\sigma}_2 $, $P_\sigma = \dfrac{1}{2}(1+\vec{\sigma}_1\vec{\sigma}_2)$, $ t_0..t_3 $, $ x_0..x_3 $, and γ and $ W_0 $ are the interaction parameters.

The expression for the tensor nucleon-nucleon interaction of zero radius was proposed in the first works of Skyrme [23]. It is given as

where $ t_e $ and $ t_o $ are tensor interaction parameters. The indices e and o correspond to the parity of states: the term $ \sim t_e $ affects the states of a pair of nucleons with relative orbital momentum $ L=0 $ and $ L=2 $ (S and D wave), while the term $ \sim t_o $ affects the states with $ L=1 $ and $ L=3 $ (P and F wave). Since the nucleon-nucleon tensor interaction works only in the state of a pair of nucleons with a total spin $ S=1 $, the parts $ \sim t_e $ and $ \sim t_o $ describe tensor effects in the isoscalar and isovector channels, respectively.

Relations (1) and (2) are used to obtain an expression for the energy density functional and, subsequently, the Hartree-Fock equations. The expression for the energy density corresponding to the nucleon-nucleon potential (1) is given in [22, 24].

The contribution of tensor forces to the energy density comes in form of the so-called $ J^2 $-terms [4, 25]:

where $ \vec{J}_{p,n} $ are proton and neutron spin densities:

Here, $ \phi_i $ are single-particle wave functions, and $ m_s $ is the nucleon spin projection. Notably, $ J^2 $-terms arise from the exchange terms even without accounting for tensor forces. The inclusion of tensor interaction results in the dependence of $ \alpha, \beta $ on both the features of the central and tensor parts of the interaction [5, 18], as follows:

Indeed, only the isovector part of the tensor force is relevant for pairs of like nucleons, while both the isovector and isoscalar components contribute to $ np $-interaction.

The impact of tensor interaction on single-particle energies (SPEs) is considered in detail in the works of Otsuka et al. [1, 9]. It was shown that if the neutron level $ j' $ is filled in the given isotope chain, then the matrix elements of the tensor interaction $ V^T_{j,j'} $ between the $ j' $ neutrons and protons in $ j_>=l+1/2 $ and $ j_ <=l-1/2 $ states fulfill the following relation:

where T is the isospin of the nucleon pair. Furthermore, the filling of $ j'_< $ with neutrons increases the spin-orbit splitting between proton levels, and when $ j'_> $ is filled, this splitting, on the contrary, decreases. Otsuka's rule (4), which is commonly used to describe the tensor part of the $ np $ interaction, is also valid for identical nucleons, although there is still an ongoing debate regarding the sign of the tensor force contributions in the isovector channel. As such this is one of the questions we study extensively in this article.

The effect of tensor forces on the spin-orbit splitting can be explained by their contribution to the one-particle potential being of similar structure to the contribution from the spin-orbit interaction. The sum of these two contributions, calculated as the first derivative of the energy density with respect to the nucleon density ρ, for protons (neutrons) reads [18]:

In the $ 1d2s $-shell nuclei, the pairing of identical nucleons plays an important role. In our calculations, we used the Bardeen-Cooper-Schrieffer (BCS) [26] method, and the joint HF + BCS procedure was carried out in several iterations, each iteration including the solution of the self-consistent HF problem with subsequent application of the BCS scheme. A simple potential in the form of δ-forces was taken as the pair correlation potential. The magnitude of the pair forces for each nucleus was chosen so that the energy gap obtained during the BCS procedure for a given even nucleus was equal to

where $ S_q $ is the proton ($ q=p $) or neutron ($ q=n $) separation energy.

Notably, we used the spherical symmetry approximation. Experimental data indicate the presence of deformation in stable silicon isotopes. The value of the quadrupole deformation parameter $ ^{28} $Si is $ \beta = -0.42\pm 0.02 $ [27]. For other silicon isotopes, there is no experimental information other than estimates based on the strength of E2 transitions $ B(E2) $. The same can be said about most isotopes of nickel, although data on $ B(E2) $ points to values of $ \beta \simeq 0.1 \div 0.2 $. In such a situation, the spherical approximation is a reasonable approach for model estimates and investigation of such features of nucleon interactions as tensor forces or nucleon pairing effects.

The single-particle structure of even silicon isotopes $ ^{28-42} $Si and nickel isotopes $ ^{56-78} $Ni were calculated using the SLy5+T [5] and SGII+T [28] parametrizations. Notably, these sets of parameters were initially selected without considering the tensor interaction component. The SLy5 parametrization [24] was chosen to realistically describe the main characteristics of symmetric nuclear matter and the binding energies and root-mean-square radii of doubly magic nuclei from oxygen to lead. The SGII interaction [29] was developed to describe collective nuclear excitations better. The parameters of the tensor interaction were obtained later in both cases, while the values of the initial parameters of the central part of the interaction were retained. Such a tactic, strictly speaking, violates the consistency of the fitting procedure. However, from the point of view of analyzing the effect of tensor forces on the structure of atomic nuclei, this kind of parametrization is more convenient, allowing comparison of the results of calculations with and without the tensor component. Notably, most currently existing parametrizations of Skyrme forces involving a tensor component agree on the signs of parameters $ \alpha_T<0 $ and $ \beta_T>0 $ and typically have their absolute value ranging up to around 200 MeV$ \cdot $fm$ ^5 $. In order to get a better understanding of how the $ np $ and isovector tensor forces compare with each other, we carried out some additional calculations with several interactions, namely SLy4(+T), SAMi(+T), and SGII with different tensor forces (which we will denote as SGII+T2 in the remainder of the article to avoid confusion), exhibiting $ \alpha_T $ and $ \beta_T $ in this wide range.

Some characteristics of nuclear matter and the tensor force parameters for the mentioned interactions, are given in Table 1. The SGII+T parametrization serves as our choice of interaction with the largest contribution of tensor forces. Although this parameter set does not always adequately describe the characteristics of nuclei, it is very interesting as a test variant. Notably, in addition to tensor contributions, there are also differences for the main parts of the parameter sets: the SLy family forces give more realistic values of the symmetry energy and incompressibility of nuclear matter.

Interaction	Ref.	$\rho_0$	$E_0$	$K_{\infty}$	$a_s $	$\alpha_C $	$\beta_C$	$\alpha_T $	$\beta_T$
SGII	[29]	$0.158$	$-15.60$	$214.65$	$26.83$	$0$	$0$	$0$	$0$
SGII+T	[28]	$0.158$	$-15.60$	$214.65$	$26.83$	$-5.434$	$-53.171$	$-180$	$120$
SGII+T2	[30]	$0.158$	$-15.60$	$214.65$	$26.83$	$-5.434$	$-53.171$	$-162.5$	$4.17$
SLy5	[24]	$0.161$	$-15.98$	$229.92$	$32.01$	$80.2$	$-48.9$	$0$	$0$
SLy5+T	[5]	$0.161$	$-15.98$	$229.92$	$32.01$	$80.2$	$-48.9$	$-170$	$100$
SLy4	[24]	$0.16$	$-15.97$	$229.9$	$32$	$0$	$0$	$0$	$0$
SLy4+T	[31]	$0.16$	$-15.97$	$229.9$	$32$	$81.79$	$-47.37$	$-105$	$15$
SAMi	[32]	$0.159$	$-15.93$	$245$	$28$	$101.88$	$31.78$	$0$	$0$
SAMi+T	[33]	$0.164$	$-16.15$	$244$	$29.7$	$112.79$	$35.13$	$-39.80$	$66.65$

Table 1.  Characteristics of nuclear matter for SLy5, SGII, SLy4 and SAMi parametrizations: saturation density $\rho_0$ (fm$^{-3}$), energy per nucleon $E_0$ (MeV), incompressibility $K_{\infty}$ (MeV), symmetry energy $a_s$ (MeV), and the parameters of the central $\alpha_C$, $\beta_C$, tensor $\alpha_T$, and $\beta_T$ contributions in $J^2$-terms (MeV fm$^5$).

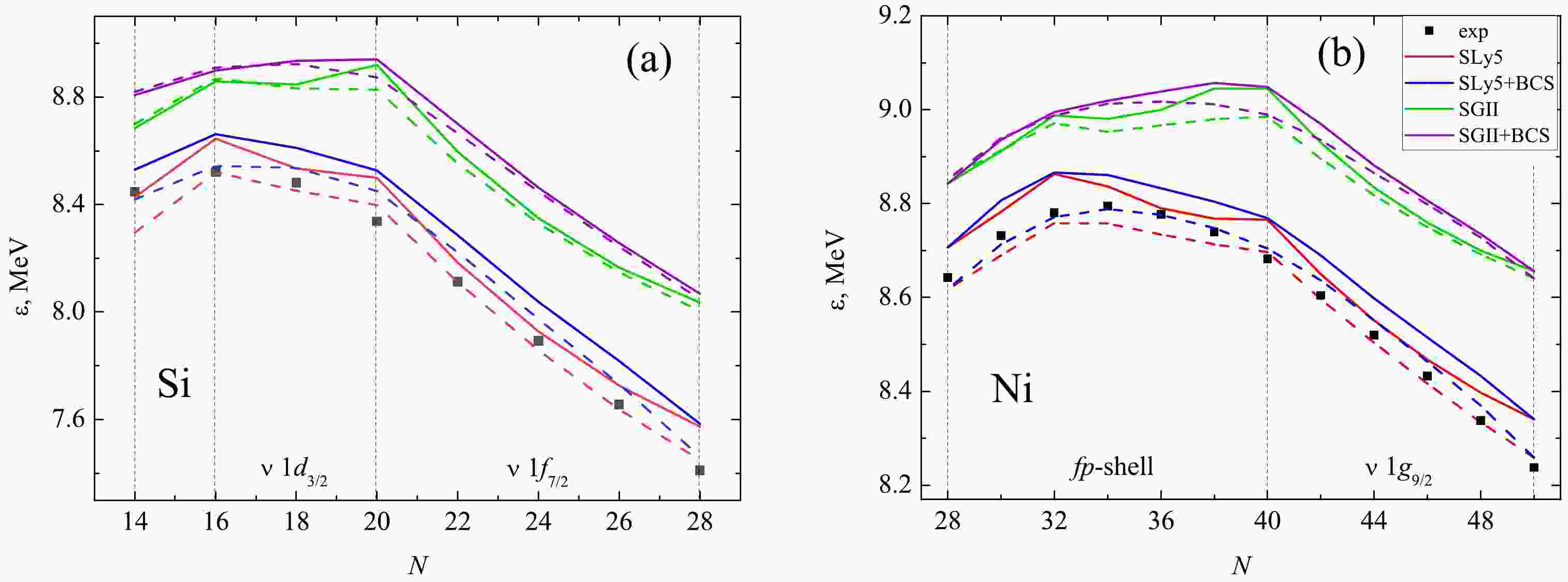
The general scale of effects associated with considering tensor forces or pair correlations in comparison with the differences due to the properties of the central parts of the interaction can be illustrated by the binding energy per nucleon $ \varepsilon = B/A $ obtained with various $ NN $-interactions (Fig. 1). We see that the parametrization SLy5 is in the best agreement with the experimental values of the binding energies of silicon isotopes (Fig. 1a) in a fairly wide range, while SGII overestimates the binding energy in all of the isotopes under consideration. The same can be said of the results for nickel isotopes (Fig. 1b). Accounting for pairing, as well as the introduction of a tensor component, leads to overestimated values for almost all isotopes as well. Notably, the introduction of pairing appears to smooth out the shell effects. Finally, it can be seen that the calculation results depend much more strongly on the choice of the central interaction; the effects of tensor forces and nucleon pairing are comparable in magnitude and have a smaller impact on the properties of the ground states of the considered nuclides.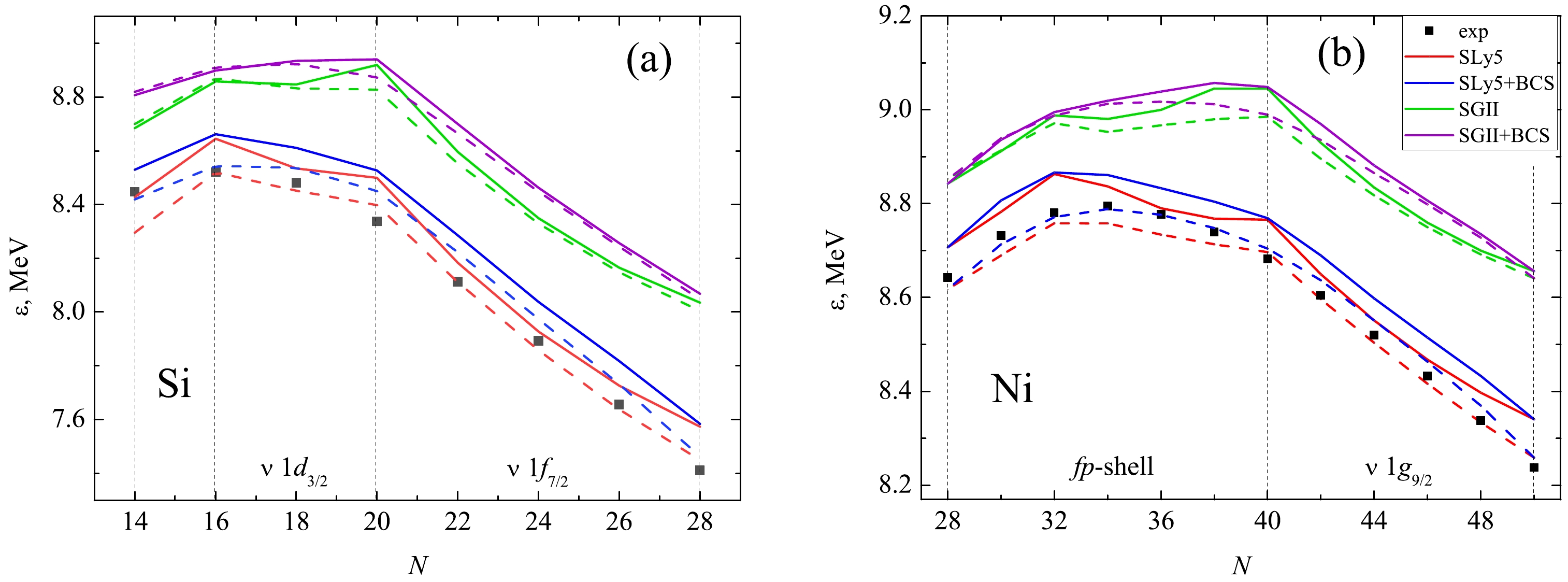

Figure 1.  (color online) Binding energy per nucleon $\varepsilon$ in even silicon (a) and nickel (b) isotopes with N neutrons, with and without considering pairing correlations. Solid (dashed) lines show calculations with tensor forces (without considering the tensor forces). Experimental data [34] are marked with dots.

Figure 2 shows the dependences of proton $ E^\pi_{nlj} $ and neutron $ E^\nu_{nlj} $ SPEs ($ nlj $ denoting the quantum numbers) on the number of neutrons N in even silicon isotopes $ ^{28-42} $Si obtained with the SLy5+T and SGII+T parametrizations. For comparison, the results of the calculations are also given without considering the tensor contribution. Here and onwards, all the shown results were obtained with pairing correlations. Additionally, we show the value of the chemical potential of nucleons of the corresponding type that was estimated using the formula:

Figure 2.  (color online) SPEs in even silicon isotopes: proton (a, b) and neutron states (c, d). Solid (dashed) lines show calculations with tensor forces (without considering the tensor forces). Experimental evaluated data [35] are marked with dots. The dashed-dotted line shows the chemical potential of protons (neutrons) in figures a and b (c and d).

Let us consider the evolution of proton states. Fig. 2(a, b) shows that for both parametrizations the calculations agree satisfactorily with the experimental data estimates [35] for the $ 1d_{5/2} $ and $ 2s_{1/2} $ states and underestimate higher states, while the SGII parametrization shows slightly better agreement in the region of neutron-rich isotopes. Including the tensor contribution does not affect the position of the $ 2s_{1/2} $ state. However, it affects the behavior of the $ 1d $ states and thus leads to some increase in the energy gap between $ 1d_{5/2} $ and $ 2s_{1/ 2} $, which, as we shall see later, affects the populations of the corresponding states. Changes in the position of the $ 1d $ and $ 1p $ states upon inclusion of the tensor component are consistent with Otsuka's rule. As $ 1d_{3/2} $ is filled with neutrons, the proton states $ 1d_{5/2} $ and $ 1p_{3/2} $ with $ j_> $ attract more strongly, while the states $ 1d_{3/2} $ and $ 1p_{1/2} $ with $ j_< $ are repelled. Further filling of the state $ \nu 1f_{7/2} $ leads to the opposite effect. In the case of the SGII+T parametrization, the changes in the spin-orbit splitting of different levels are much more pronounced than in the case of SLy5+T. Apparently, in addition to the difference in the strength of the tensor interaction (in the SGII+T parametrization, the contribution of tensor forces is greater), the differences in the characteristics of the basic parametrizations also play a certain role. The response of the core structure to additional changes is stronger with smaller $ K_{\infty} $values; in the case of SGII, the value of incompressibility is somewhat smaller.

The change in the spin-orbit splitting between proton d-states as the $ 1f_{7/2} $ shell is filled with neutrons is of great interest. Experimental data show the strongest splitting in the $ ^{34} $Si magic nucleus. However, quantitative estimates differ greatly and can reach 10 MeV. We have previously discussed this issue in detail in [35] and will use the estimates from that paper for comparison. Fig. 3a shows the results of our calculations. Both variants of interaction lead to a splitting of d-states in $ ^{34} $Si of about 9 MeV, and for other nuclei, they also overestimate the said splitting. However, in this case, the SGII+T interaction succeeds at reproducing the behavior of the dependence at a qualitative level.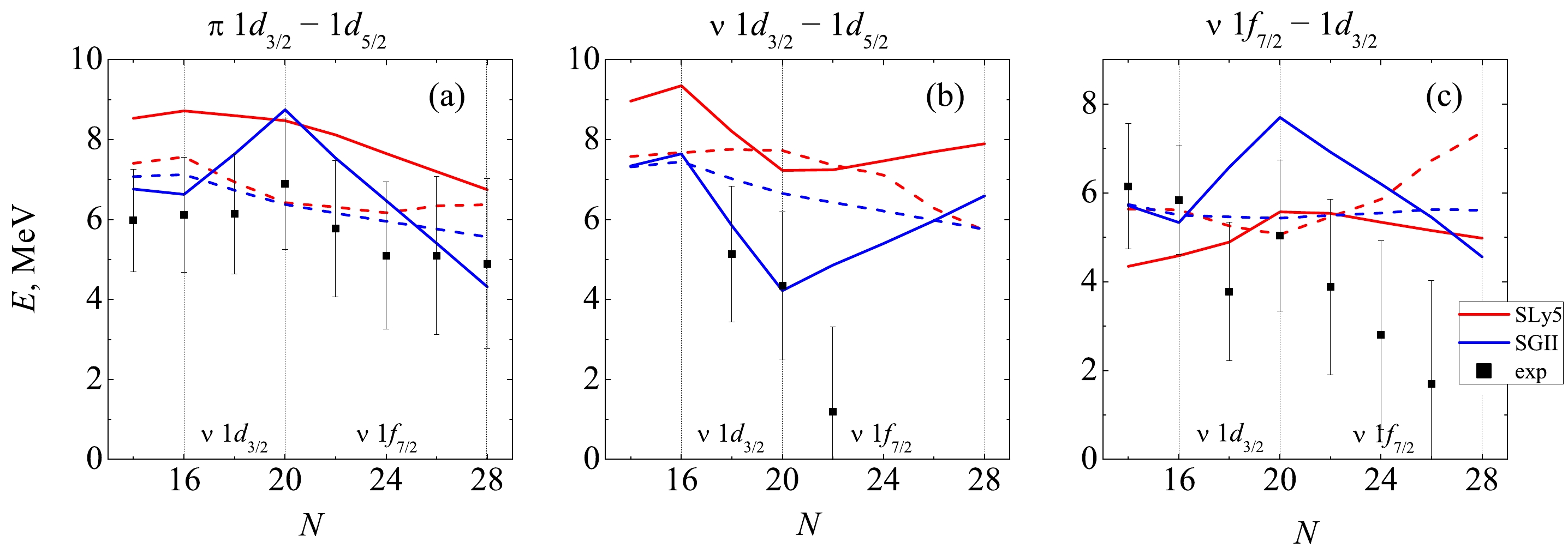

Figure 3.  (color online) Splitting of proton (a) and neutron (b) states $1d_{3/2} - 1d_{5/2}$, as well as $1f_{7/2} - 1d_{3/2}$ states in silicon isotopes. Solid (dashed) lines show calculations with tensor forces (without considering the tensor forces).

Regarding the influence of the neutron excess on the single-particle states of neutrons, the presence of tensor interaction here also leads to changes in SPEs, and the effect will be opposite compared to the case of $ np $-interaction. As seen from Fig. 2(c, d), as $ \nu 1d_{3/2} $ is filled, the neutron states with $ j_> $ are repelled, and with the filling of $ \nu 1f_{ 7/2} $, the attraction is strengthened by the shell. At the same time, the unsatisfactory description of experimental estimates for $ 1d2s $ states should be stressed. On the other hand, it should be noted that the accuracy of the experimental data based on the spectroscopy of single-nucleon transfer reactions drops dramatically for states lying much lower than the Fermi surface. Nevertheless, Fig. 3(b) shows that for the range of nuclei up to $ ^{34} $Si, including tensor forces is what makes it possible to qualitatively reproduce the dependence of the neutron spin-orbit splitting of the d-states.

For neutron single-particle states, we can also consider the splitting between $ 1d_{3/2} $ and $ 1f_{7/2} $. The experimental data demonstrate a maximum in $ ^{34} $Si related to the manifestation of the magic number $ N=20 $ and a substantial drop to very small values as $ \nu 1f_{7/2} $ is filled, which illustrates the decrease in the role of shell effects in highly neutron-rich silicon isotopes. As can be seen in Fig. 3(c), reproducing this character of the experimental dependence without including the tensor component is not possible. However, the SGII+T parametrization makes it possible to reproduce the dependence at a qualitative level. The results with SLy5+T also give a maximum in $ ^{34} $Si, and the splitting value agrees with the experimental estimates.

Notably, the scale of the effect for neutrons is comparable to that observed earlier for protons (Fig. 3a). In [9] it is shown that in the most elementary case, when $ \alpha_T=\beta_T $, the interaction of like nucleons (governed purely by the isovector component of the forces) is two times weaker than $ np $-interaction (dependent on both isoscalar and isovector components). Therefore, traditionally, when considering the effects associated with tensor interaction, one treats the influence of the neutron excess on the states of protons in isotopes, or, vice versa, the influence of the number of protons on the states of neutrons in isotones. In the case of interactions SLy5+T and SGII+T obtained by fitting the experimental data, $ |\alpha_T|>|\beta_T| $, indicating that the contribution from the isovector component of the tensor interaction may indeed be comparable to that from the $ np $ tensor interaction. This inequality holds for quite a few of the existing interactions, including SLy4+T, SkP+T, SkO+T [31], Sktxb [36], and the more recent SGII+T2 and SkO'+T interactions [30]. All of these were obtained perturbatively with the tensor terms added on top of the fixed central part. It may also be interesting to check the case when a parameter set was generated via a variational procedure, with parameters of the central part refitted altogether as tensor forces are included. An example of such a set would be SAMi [32] with its recently obtained counterpart SAMi+T [33]. Notably, for SAMi+T $ \alpha_T=-39.8 $ and $ \beta_T=66.7 $ MeV fm$ ^5 $, and the mentioned inequality does not hold. For SGII+ T2, on the other hand, $ \alpha_T=-162.5 $ and $ \beta_T=4.7 $ MeV fm$ ^5 $. As such, the isovector part responsible for the interaction of like nucleons should be dominant in this interaction.

For the sake of verifying the impact of different components of tensor forces on the single-particle structure of silicon isotopes, we performed some few additional calculations with interactions SLy4 and SLy4+T, SGII+T2, SAMi and SAMi+T in $ ^{28,34,42} $Si with filled $ \nu 1d_{5/2} $, $ sd $-shell, and $ \nu 1f_{7/2} $ respectively. The results are shown in Table 2. We note the significant effect tensor forces have on the splitting between the neutron states $ 1d_{3/2,5/2} $ and $ 1f_{7/2} $ when SLy4+T and SGII+T2 forces are used. Particularly, the $ \nu 1f_{7/2} - 1d_{3/2} $ splitting seems to be best reproduced with the SGII+T2 Skyrme forces. Indeed, the effect has an opposite sign compared to the Otsuka rules formulated for the $ np $-tensor interaction, for all the parametrizations under consideration. Notably, SAMi predicts the opposite behavior of the neutron level splittings compared to those of the other interactions (maximum in $ 1d_{3/2,5/2} $ and minimum in $ 1f_{7/2} - 1d_{3/2} $ splitting in $ ^{34} $Si), but these extrema are less pronounced when tensor forces are considered. The largest impact on the proton states is observed with SGII+T and SAMi+T interactions, the latter describing the behavior of the $ \pi 1d_{3/2} - 1d_{5/2} $ splitting the best.

Parametrization	$\pi 1d_{3/2}-1d_{5/2}$				$\nu 1d_{3/2}-1d_{5/2}$				$\nu 1f_{7/2}-1d_{3/2}$
	$^{28}$Si	$^{34}$Si	$^{42}$Si		$^{28}$Si	$^{34}$Si	$^{42}$Si		$^{28}$Si	$^{34}$Si	$^{42}$Si
SGII	7.08	6.38	5.60		7.31	6.65	5.98		5.74	5.43	5.61
SGII+T	6.77	8.74	4.32		7.34	4.22	6.59		5.71	7.70	4.56
SGII+T2	8.91	8.16	7.02		9.35	7.13	8.31		3.81	5.00	3.18
SLy5	7.41	6.42	6.37		7.58	7.73	5.73		5.63	5.07	7.36
SLy5+T	8.54	8.48	6.75		8.96	7.23	7.90		4.35	5.58	4.98
SLy4	7.60	7.03	6.27		7.87	7.30	6.47		5.36	5.51	6.55
SLy4+T	8.60	7.65	7.35		8.90	8.06	7.51		4.40	4.78	5.53
SAMi	4.86	4.84	3.91		4.94	5.56	3.55		8.59	7.62	9.61
SAMi+T	5.24	5.83	3.87		5.42	5.79	4.36		8.34	7.68	9.22
exp	6.0±1.5	6.9±1.6	4.9±2.0			4.2±1.9			5.8±1.2	5.0±1.5	1.8±2.2

Table 2.  Splitting between the proton and neutron $1d_{3/2}$ and $1d_{5/2}$ levels, as well as the neutron $1f_{7/2}$ and $1d_{3/2}$ obtained with various Skyrme force parametrizations in $^{28,34,42}$Si. Experimental values from [35] are shown at the end for comparison.

For nickel isotopes, the general tendencies for the impact of the tensor force are the same, which brings about certain additional phenomena. Before discussing the results, we will first address the current state of available experimental data on neutron-rich nickel nuclei. In this work, we compare the calculated SPEs with those obtained from consistent stripping and pickup reaction analysis [37−45]. Analysis of stripping and pickup reactions is typically very sensitive to experimental conditions, the resolution of the obtained spectra, and the measurement range. For example, the authors of [40] compared the estimated SPEs of stable even $ ^{58-64} $Ni based on the single out states assigned the largest spectroscopic factors, with the results taking into account the state fragmentation. The largest deviations amounted to 2 MeV far from the Fermi level, which may be of importance to states with small SPEs. Furthermore, while such deviations may not be critical for the localization of individual single-particle states, the estimates of the spin-orbital splitting may differ significantly on a qualitative level in various approaches.

Our calculations of SPEs in neutron-rich nickel isotopes, together with experimental data from the sources listed earlier, are shown on Fig. 4. For protons, the inversion of states $ 1d_{3/2} $ and $ 2s_{1/2} $ taking place when tensor forces are accounted for is notable. Their initial reversal as the neutron $ fp $-shell is filled, and second reversal to the original order as $ \nu 1g_{9/2} $ is filled, was predicted in [12] and recently in [10], and is reproduced here using the SGII+T parametrization. In light of recently confirmed experimental data in copper isotopes [47] obtained at RIBF, the behavior of the splitting between the $ \pi 2p_{3/2} $ and $ \pi 1f_{5/2} $ states is also of interest. The systematics of the first $ 3/2^- $ and $ 5/2^- $ states in these data suggest that the reversal of the corresponding proton orbitals takes place at around $ N=45 $. While this is not obtained with the SLy5+T or SGII+T forces, SGII+T interaction does succeed at changing the ordering at $ N=50 $. A thorough comparison of this and other approaches in reproducing the crossing between these levels in neutron-rich nickel isotopes is also given in [19].

Figure 4.  (color online) SPEs in even nickel isotopes: proton (a, b) and neutron (c, d) states. Solid (dashed) lines show calculations with tensor forces (without considering the tensor forces). The dashed-dotted line shows the chemical potential of protons (neutrons) in figures a and b (c and d). Experimental evaluated data are marked with dots. Experimental data for the proton states were taken from [42] for $^{56,78}$Ni and [37] for other isotopes. Experimental data for the neutron states were taken from [42] for $^{56,78}$Ni; $1f_{5/2}$ and $2p_{1/2, 3/2}$ states were taken from [41] for stable isotopes $^{58-64}$Ni, $1g_{9/2}$ and $1f_{7/2}$ states in these isotopes were taken from [37] and [43], respectively.

When it comes to neutron states in neutron-rich nickel isotopes, neutrons initially fill the $ fp $-shell, although the order of the filling within the shell appears to depend on the choice of the central part of the interaction, as seen in Fig. 4. Furthermore, the introduction of the strong tensor component, such as in SGII+T, may also affect the order of certain levels. We note the influence of tensor forces on the neutron $ 1f_{5/2} $ state that gets additionally attracted as the $ fp $-shell is filled, which results in it getting pushed below the $ \nu 2p_{1/2} $ and then the $ \nu 2p_{3/2} $ state. Experimental data taken from [35] show that $ \nu 2p_{1/2} $ should indeed lie above the other states of the $ fp $-shell, and SGII family interactions describe such ordering the best.

The tensor effects in nickel isotopes can be most clearly observed on the example of the magic gap between the proton or neutron $ 1f_{7/2} $ and $ 1f_{5/2} $ states (see Fig. 5a and b, respectively). Various experimental data for these splittings appear to differ by up to 2−3 MeV for various nuclides, but the general pattern described by the Otsuka rule emerges clearly. We note that including tensor forces allows for describing the local maximum and minimum in protons and neutron level splittings, respectively. The general scale of the effect is, once again, better described by the interaction SGII+T. Results of additional calculations performed with interactions SLy4(+T), SGII(+T2), and SAMi(+T) are presented in Table 3. While SAMi+T with the stronger $ np $-component does reproduce qualitatively the maximum of the $ \pi 1f_{7/2,5/2} $ splitting for $ ^{68} $Ni, it also severely underestimates said splitting on the entire chain of nickel isotopes, while SGII and SLy4 appear to give more reasonable values. Although no experimental data is currently available for the difference between the neutron $ \nu 1f_{7/2,5/2} $ SPEs in $ ^{56,68,78} $Ni, some few data in $ ^{30,32,34} $Ni indicates the decrease of the splitting towards $ ^{68} $Ni (as seen in Fig. 5), which also is reproduced with SGII+T2 and SLy4+T. We suspect this suggests the correct expectation that the isovector part of tensor forces should be prominent and that the Otsuka rule may indeed work in the opposite way for $ np $ tensor forces and tensor forces between like nucleons.

Figure 5.  (color online) Splitting of proton (a) and neutron (b) states $1f_{5/2} - 1f_{7/2}$ in nickel isotopes. Solid (dashed) lines show calculations with tensor forces (without considering the tensor forces). For protons, experimental data from [37] and [42−46] are shown with black and white circles, respectively. For neutrons, experimental data from [41] and [43] are shown with black circles.

Parametrization	$\pi 1f_{5/2}-1f_{7/2}$				$\nu 1f_{5/2}-1f_{7/2}$
	$^{56}$Ni	$^{68}$Ni	$^{78}$Ni		$^{56}$Ni	$^{68}$Ni	$^{78}$Ni
SGII	7.26	6.27	5.67		7.52	6.67	5.92
SGII+T	6.97	8.58	5.24		7.48	4.16	5.94
SGII+T2		8.16	7.21		9.74	6.82	7.98
SLy5	7.77	6.22	6.37		7.97	8.19	6.21
SLy5+T		8.72	7.16		9.58	7.16	7.95
SLy4	8.07	7.08	6.47		8.37	7.53	6.77
SLy4+T		7.65	7.51		9.57	8.22	7.79
SAMi	4.42	4.54	3.54		4.44	5.70	3.26
SAMi+T	4.75	5.90	3.60		4.92	5.80	3.85
exp	7.5±1.6	7.0±1.0	5.5±0.9

Table 3.  Splitting between the proton and neutron $1f_{5/2}$ and $1f_{7/2}$ levels obtained with various Skyrme force parametrizations in $^{56,68,78}$Si. Experimental values from [37, 42] are shown at the end for comparison.

Notably, the tensor terms in SAMi+T were fitted using the pseudodata of the neutron-proton drops coming from relativistic Brueckner-Hartree-Fock (RBHF) calculations rather than experimental data. The approach of comparing to meta-data generated within ab initio calculations allows for narrowing down the constraints on the possible nuclear density functionals, and has the benefit of avoiding the particle-vibration coupling which typically makes it harder to analyze experimental data. In recent works [48−50] employing the RBHF approach, it was shown that tensor forces in neutron and neutron-proton drops may work similarly for proton and neutron states as neutrons are added in the system. This result was indeed also obtained in [33] where interaction SAMi+T was originally proposed. As seen from Table 2 and Table 3, SAMi+T often predicts maxima for neutron-level splittings in cases when minima are obtained with other forces, and vice versa. The reasons can be traced down to the central part of the interaction, as the same behavior is obtained with SAMi without tensor terms. Evidently, these extremes in $ ^{34} $Si and $ ^{68} $Ni are smoothed out for splittings between neutron states, and become more prominent for splittings between proton states as tensor terms are considered, meaning that even here the isovector and $ np $ tensor components work in opposite directions.

Let us consider the effect of tensor forces on the occupation of single-particle states near the Fermi level. In the BCS approach, this characteristic depends on the energy of the single-particle state $ E_{nlj} $:

where λ is the chemical potential, and Δ is the energy gap. Since accounting for tensor interaction results in a change in the energies of single-particle states, these changes should be reflected in the corresponding occupation numbers $ n_{nlj} $.

The calculated single-particle occupation numbers for even silicon isotopes are presented in Fig. 6. Both parametrizations, SLy5+T and SGII+T, effectively reduce the effects of nucleon pairing. Pairing correlations of nucleons lead to smearing of the Fermi level, with states above $ \lambda_q $ getting partially filled. Accounting for the tensor interaction leads to a decrease in this effect: the population of the levels with $ E_{nlj}<\lambda $ (see Fig. 2) increases. This is most clearly manifested in calculations for the $ ^{34} $Si isotope, where in the case of the SGII+T parametrization with a large tensor component, neutron pairing actually disappears. Using proton states as an example, one can see that in silicon isotopes, the Fermi level lies between the $ \pi 1d_{5/2} $ and $ \pi 1 d_{3/2} $ levels. When the contribution of tensor forces is considered, the splitting between these states increases; accordingly, due to moving away from the Fermi level, the population of subshells with energies above $ \lambda_p $ decreases. The population of neutron states changes according to the same patterns: an increase in the splitting between the $ \nu 1f_{7/2} $ and $ \nu 1d_{3/2} $ levels, between which the Fermi level passes for nuclei near $ ^{34} $Si, effectively leads to a decrease in pairing correlations. It is important to note that the results also strongly depend on the properties of the central part of the interaction: in the case of SLy5, the neutron level $ 2p_{3/2} $ can turn out to be in the continuum for all neutron-rich isotopes (Fig. 6c), and in the case of SGII in the $ ^{38-42} $Si isotopes, it is in the potential well (Fig. 6d). Thus, in the case of SLy5(+T), the magic core $ ^{42} $Si is closed. As in the case of SPEs, theoretical calculations do not agree with experimental estimates of the populations of neutron states. This suggests that other effects must be considered in addition to tensor forces, primarily the deformation of nuclides.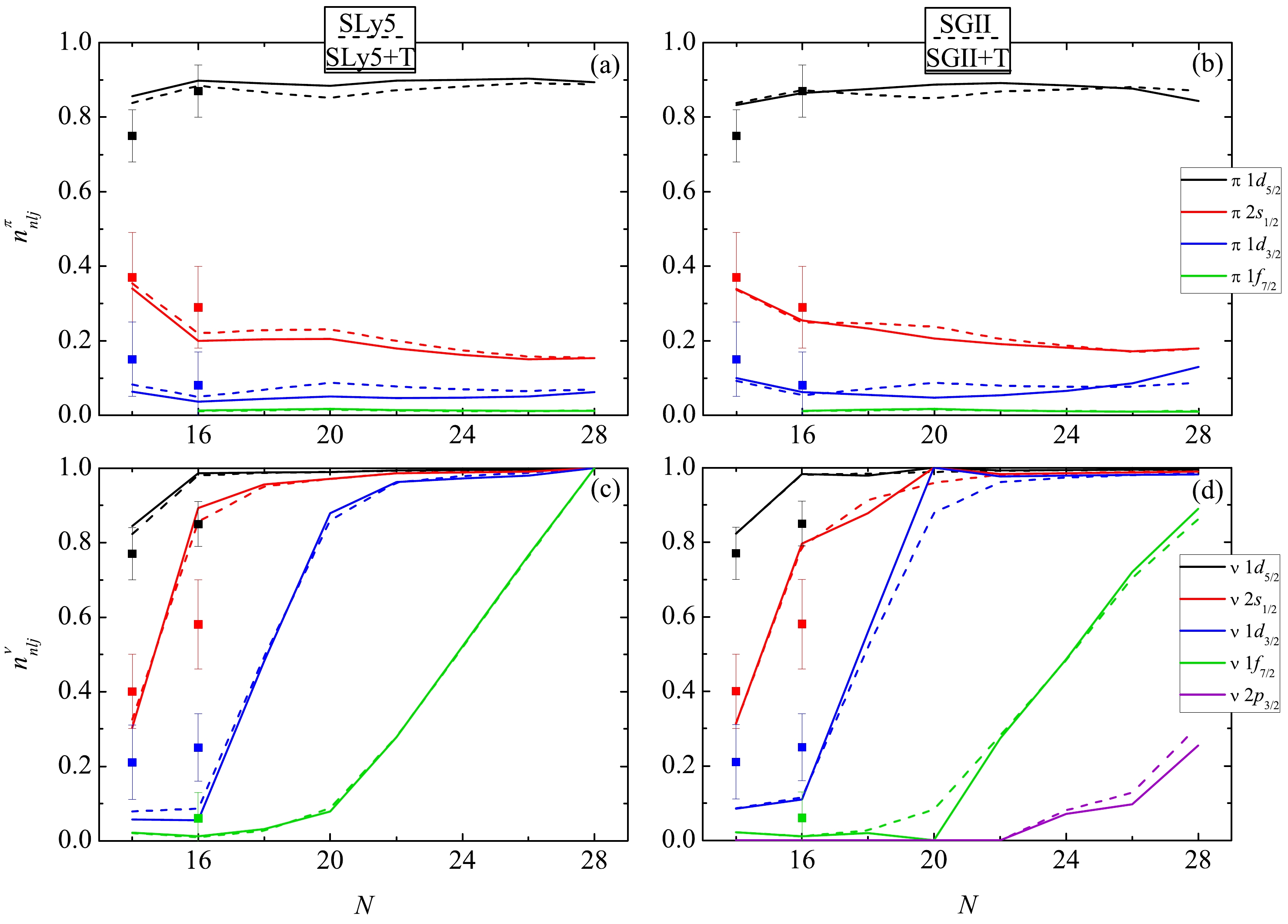

Figure 6.  (color online) Occupation numbers of (a, b) proton and (c, d) neutron single-particle levels near the Fermi surface in silicon isotopes. Solid (dashed) lines show calculations with tensor forces (without considering the tensor forces). Experimental data [35] are marked with dots.

We only considered neutron pairing for nickel isotopes, as $ Z=28 $ is a magic number. Tensor forces result in much the same phenomenon: nucleons are pushed below the Fermi level, effectively decreasing the pairing correlations, , as seen from Fig. 7. Here, once again, we notice the difference in occupation order between neutron states $ 2p_{1/2} $ and $ 1f_{5/2} $. This correlates with the order of these states in Fig. 4, and the correct reproduction of ordering from experimental data is achieved with SGII interactions. Admittedly, SGII without the tensor component appears to give better results here, which is due to inconsistencies in the fitting procedure.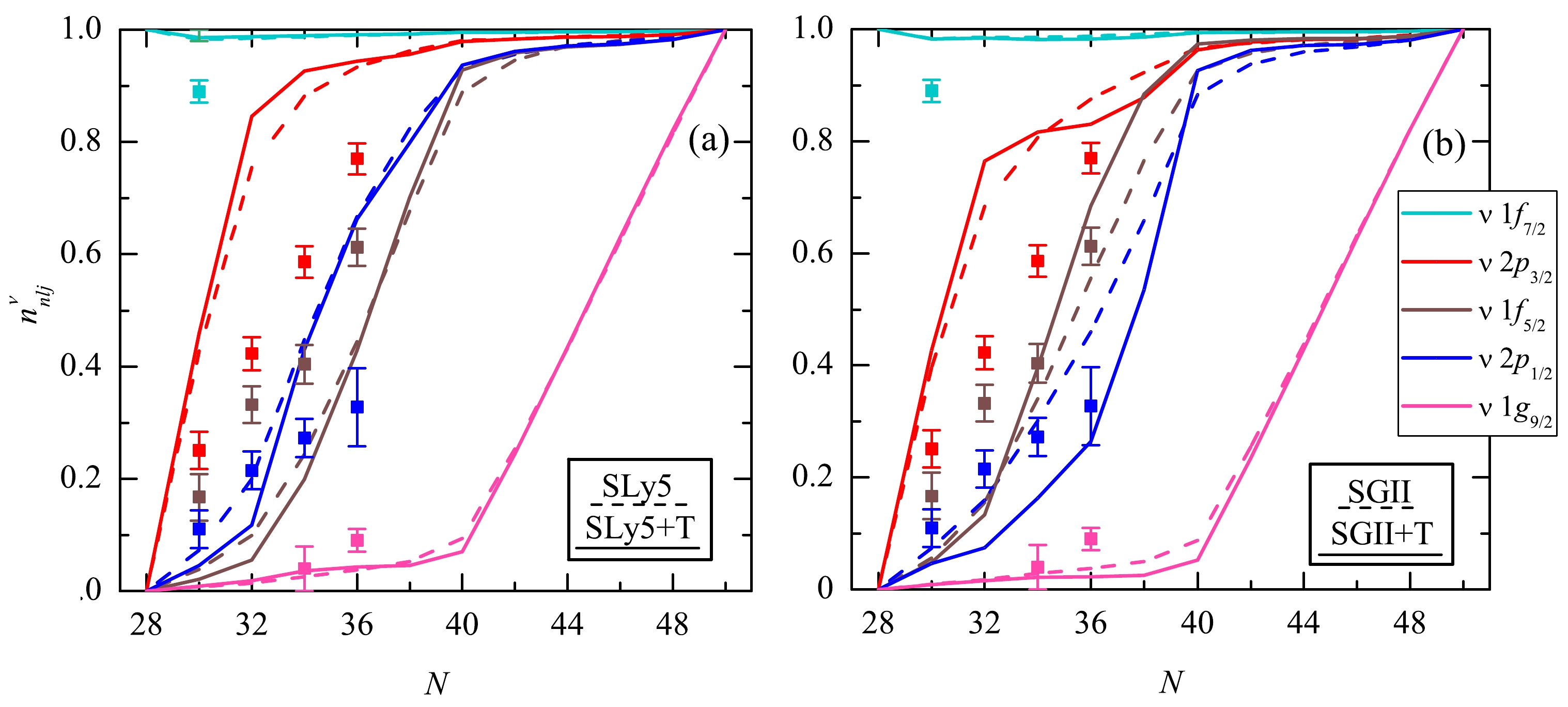

Figure 7.  (color online) Occupation numbers of neutron single-particle levels near the Fermi surface in nickel isotopes. Solid (dashed) lines show calculations with tensor forces (without considering the tensor forces). Experimental data [41] for the $1f_{5/2}$ and $2p_{1/2, 3/2}$ states and [37] for state $1g_{9/2}$ are marked with dots.

The structure of even silicon isotopes $ ^{28-42} $Si and nickel isotopes $ ^{56-78} $Ni was calculated within the framework of the self-consistent Hartree-Fock approach with the Skyrme interaction. Our task was to analyze the influence of the tensor interaction component on changes in single-particle characteristics with an increase in the excess of neutrons using the example of the SLy5+T and SGII+T parametrizations, which include tensor forces of various magnitudes. When Skyrme forces are used, tensor forces contribute to the $ J^2 $ terms, and thus, their influence leads to a change in the spin-orbit splitting of single-particle levels.

Both tensor forces and pair correlations lead to an increase in the binding energy. Consequently, considering these effects leads to an overestimation of the binding energy per nucleon of all considered silicon and nickel isotopes and the best agreement is obtained for parametrization SLy5 in the absence of additional effects. In this case, the SGII+T interaction leads to a particularly strong overbinding of nuclei, which is associated with the peculiarities of SGII fitting protocol. Thus, it should be recognized that the inclusion of the tensor contribution on top of the parametrizations previously fitted to various experimental data, strictly speaking, can only be used for test calculations. For a more accurate quantitative reproduction of the experimental estimates of the energy characteristics, it is necessary to fit the Skyrme parameters via a variational procedure affecting both the tensor and central parts.

However, accounting for the tensor forces improves the description of the splitting of various single-particle levels in neutron-rich even silicon and nickel isotopes. Changes in the energies of proton single-particle states in silicon isotopes, and, accordingly, the dependence of the spin-orbit splitting of the d-states with an increase in the number of neutrons, are in full accordance with Otsuka rules: filling the $ j'_< $ level with neutrons leads to an increase in the spin-orbit splitting between proton levels, and when $ j'_> $ is filled, this splitting, on the contrary, decreases. The results of calculations for neutron states show that the changes in the spin-orbit splitting of neutron levels are reversed, but the magnitude of the change is comparable in absolute value. In this case, the dependence of the splitting of $ d_{3/2}-d_{5/2} $ levels and $ sd $- and f-shells on the number of neutrons in silicon isotopes is qualitatively better reproduced with the SGII+T forces. For nickel, tensor forces additionally induce several changes in the ordering of various single particle states, namely, neutron and proton $ 2s_{1/2} $ and $ 1d_{3/2} $, as well as the states of the neutron $ fp $-shell. The general behavior of the splitting between the proton and neutron $ f_{5/2} - f_{7/2} $ states was reproduced with the SGII+T interaction, although the SHF approach appears to be insufficient when it comes to the energy descriptions of the individual states.

According to spectroscopic data on neutron-rich silicon and nickel isotopes, the splitting between various neutron single-particle states appears to change oppositely to the proton states along the isotopic chains. This behavior of neutron state splitting appears to be best reproduced when interactions SGII+T, SGII+T2, SLy5+T, and SLy4+T are employed. All of these parametrizations are indeed characterized by the $ np $ and isovector tensor terms of opposite signs and comparable amplitudes. Parametrization SAMi+T, on the other hand, predicts similar behavior of the proton and neutron state splittings, which is attributed to the peculiarities of its central part. While the contribution from the isovector component of tensor forces is noticeably smaller compared to the $ np $ tensor forces, these two terms still act in the opposite way, in agreement with other interactions.

Analysis of the populations of both proton and neutron levels near the Fermi surface showed that the inclusion of tensor forces effectively leads to a decrease in pairing in silicon and nickel isotopes. This effect is related to the fact that the tensor interaction additionally pushes the levels closest to $ \lambda_{n,p} $ away from the Fermi surface. Such filling is specific, however, for silicon and nickel isotopes, and in other nuclei one can expect a different kind of interplay between tensor forces and pairing correlations.