-
Studies on the QCD phase structure have attracted considerable attention in the past decade. Remarkable efforts, both from experimental and theoretical, have been involved in the promising but challenging task of searching for the critical end point (CEP) in the QCD phase diagram. The first principle lattice QCD simulations indicated that the finite-temperature QCD phase transition is a continuous analytic crossover in the low baryon chemical potential or density regime [1-6]. Although the predictive capacity of the lattice simulations is hampered by the so-called sign disaster when the baryon chemical potential is high, other complementary first principle theoretical methods, e.g., the widely used functional approaches of QCD, such as the functional renormalization group (fRG) [7-14] and Dyson-Schwinger equations (DSE) [15-20], predicted the existence of a CEP in the phase diagram spanned by the temperature and the baryon chemical potential. Note, however, that the existence of the CEP itself, and if it really exists, its location in the phase diagram are still open questions.
In the past decade, the Beam Energy Scan (BES) Program at the Relativistic Heavy Ion Collider (RHIC) has made significant progress with respect to experimental studies on the QCD phase structure. Moments of the net-proton multiplicity distributions of different orders were measured, and a non-monotonic dependence of the kurtosis of the net-proton distributions on the beam energy was found [21, 22]. Moreover, moments of the net-charge multiplicity distributions [23] and those of the net-kaon multiplicity distributions [24] were also measured; refer to [25, 26] and the references therein for further details. Recently, the measurements of the second-order off-diagonal cumulants, i.e., the correlations of the net-proton, net-charge, and net-kaon multiplicity distributions, were reported by the STAR Collaboration [27]. In response to these experimental measurements, in this study, we aimed to investigate the correlations of conserved charges, viz. the baryon number, electric charge, and strangeness, from the theoretical side. The order of the correlations is not just constrained to be quadratic but also extended to the more interesting higher-order ones up to the fourth. The dependence of various correlations on the temperature and baryon chemical potential in the strangeness neutral system, with a fixed value of the ratio between the electric charge and baryon number density, was addressed. Furthermore, we studied the evolution of these correlations with the beam energy in heavy ion collision experiments. After conducting an extensive study on all the correlations of conserved charges up to the fourth order, we selected those that demonstrated the most non-monotonic behavior. Such correlations are potentially useful in experiments.
We employed the 2+1 flavor low energy effective theory (LEFT) within the fRG approach, which has already been used and described in detail in a previous study of ours [28]. In the fRG approach, quantum fluctuations of different momentum scales are encoded successively through the evolution of the renormalization group (RG) scale from the ultraviolet (UV) to the infrared (IR) regimes [29]. Therefore, the fRG approach is extremely suitable for describing physical systems. It features a distinct hierarchy of scales and, thus, entails transformation of the effective degrees of freedom. QCD belongs to this type of systems. Significant progress in the first principle QCD studies with the fRG approach has been witnessed in recent years [9-14]. Remarkably, a phase diagram has recently been extracted from a detailed QCD calculation at nonzero temperature and density within the fRG approach, and a critical end point has been predicted in the phase diagram [14]. Moreover, the fRG has also been widely employed in low energy effective models; refer to studies such as [28,30-49] for a selective list of relevant wo-rks, and refer to [50-55] for reviews on the fRG approach.
The remainder of this paper is organized as follows. In Sec. II, we briefly introduce the 2+1 flavor low energy effective theory within the fRG approach. In Sec. III, we discuss the thermodynamics and the generalized susceptibilities at finite temperature and chemical potentials. Both constraints, i.e., the strangeness neutrality and the fixed ratio of the electric charge to baryon number density, were implemented. The resulting equilibrium strangeness and electric charge chemical potentials were investigated and expanded in powers of the baryon chemical potential, which can be compared with the relevant lattice results. Sec. IV presents the calculation of the correlations of conserved charges, viz. the baryon number, electric charge, and strangeness, at the finite temperature and density up to the fourth order. The dependence of various correlations on the collision energy is also discussed. In Sec. V, we provide a summary, including the discussions.
-
In this study, we employed the Polyakov-loop improved quark-meson theory with
$ N_f = 2+1 $ flavor quarks, which was also used in a previous study of ours [28]. Next, we provide a brief introduction. More details about the theory and our calculations can be found in the aforementioned reference. The scale dependent effective action is given by$ \begin{aligned}[b] \Gamma_{k}[\Phi] =& \int_x \bigg\{ \bar{q} [\gamma_\mu \partial_\mu-\gamma_0(\hat\mu+ig A_0)]q+h\,\bar{q} \,\Sigma_5 q\\ &+ {\rm{tr}}(\bar D_\mu \Sigma \cdot \bar D_\mu\Sigma^\dagger)+\tilde{U}_{k}(\Sigma)+V_{\rm{glue}}(L, \bar L)\bigg\}\,, \end{aligned} $

(1) with
$\int_{x}\equiv\int_0^{1/T}{\rm d} x_0 \int {\rm d}^3 x$ and$ \Phi = (q, \bar{q}, \sigma^a, \pi^a) $ ($ a = 0,1, $ $\cdots,8 $ ), where q,$ \bar{q} $ ,$ \sigma^a $ , and$ \pi^a $ are the quark, antiquark, scalar, and pseudo-scalar mesonic nonets, respectively. In fact, the mesons of other channels, for instance vector mesons [56-58], are also relevant to the analysis conducted in this study and will be taken into account in future studies. In addition,$ \hat{\mu} = {\rm{diag}}(\mu_u, \mu_d,\mu_s) $ is the matrix of the quark chemical potentials in the flavor space. The kinetics of the mesons is encoded within the trace term in Eq. (1), where the covariant derivative is$ \bar D_\mu \Sigma = \partial_\mu \Sigma +\big[\delta_{\mu 0} \hat \mu ,\Sigma\big]\,, $

(2) with
$\Sigma = T^a(\sigma^a+{\rm i} \pi^a)$ ; the mesonic fields are in the adjoint representation of$ U_{V}(3)\times U_{A}(3) $ . Here,$ T^a $ are the generators of the$ U(N_f) $ group with$ {\rm{tr}}(T^aT^b) = \delta^{ab}/2 $ . Quarks and mesons couple with each other through the Yukawa coupling with$\Sigma_5 = T^a(\sigma^a+ {\rm i} \gamma_5\pi^a)$ . The meson masses and the interactions among them are governed by the mesonic potential, which is$ \tilde{U}_{k}(\Sigma) = U_k(\rho_1,\tilde{\rho}_2)-c_A \xi-j_L\sigma_L-j_S\sigma_S\,, $

(3) with
$ \rho_1 = {\rm{tr}}(\Sigma \cdot \Sigma^\dagger)\,, $

(4) $ \tilde{\rho}_2 = {\rm{tr}}\Big(\Sigma \cdot \Sigma^\dagger-\frac{1}{3}\,\rho_1\,{1}_{3\times 3}\Big)^2 \,, $

(5) and
$ \xi = \det(\Sigma)+\det(\Sigma^\dagger)\,, $

(6) where
$ \rho_1 $ and$ \tilde{\rho}_2 $ are invariant under the transformation of$ U_{V}(3)\times U_{A}(3) $ ; the Kobayashi-Maskawa-'t Hooft determinant,$ \xi $ , breaks the$ U_{A}(1) $ symmetry and keeps the remaining ones unchanged. The effective potential in Eq. (3) is expanded as a Taylor series as follows:$ U_k(\rho_1,\tilde{\rho}_2) = \sum\limits_{m,n = 0}^{N}\frac{\lambda_{mn,k}}{m!\,n!}(\rho_1-\kappa_{1,k})^m(\tilde{\rho}_2-\kappa_{2,k})^n\,, $

(7) where
$ \lambda_{mn,k} $ 's are the k-dependent expansion coefficients,$ \kappa_{1,k} $ and$ \kappa_{2,k} $ are the expansion points, and$ N\geqslant m+2n $ is the maximal order of the expansion. In the numerical calculations, we adopted$ N = 5 $ , which is large enough to ensure that the convergence of expansion is achieved; refer to [28] for further details. The two$ j_{L/S} $ terms in Eq. (3) break the chiral symmetry explicitly and are related to the light and strange current quark mass, respectively. Here, we used the light-strange quark basis implicitly, which is related to the singlet-octet basis through a proper rotation as follows:$\left( {\begin{array}{*{20}{c}} {{\sigma _L}}\\ {{\sigma _S}} \end{array}} \right) = \frac{1}{{\sqrt 3 }}\left( {\begin{array}{*{20}{c}} 1&{\sqrt 2 }\\ { - \sqrt 2 }&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\sigma _8}}\\ {{\sigma _0}} \end{array}} \right){\mkern 1mu} .$

(8) The quark confinement and its relevant deconfinement phase transition are encoded, in statistical terms, through the temporal component of the gluon background field
$ \langle A_0 \rangle $ on the r.h.s. of Eq. (1), or the related Polyakov loops, i.e.,$L({{x}}) = \langle {\rm{Tr}}\, {\cal{P}}({{x}})\rangle/N_c$ and$\bar L ({{x}}) = \langle {\rm{Tr}}\,{\cal{P}}^{\dagger}({{x}})\rangle/N_c$ , with$ \langle\cdots \rangle $ denoting the ensemble average. Thus, we obtain$ {\cal{P}}({{x}}) = {\cal{P}}\exp\Big({\rm i}g\int_0^{\beta}{\rm d}\tau A_0({{x}},\tau)\Big)\,, $

(9) with the path ordering operator,
$ {\cal{P}} $ , on the r.h.s. For further details about the Polyakov loop and its application in the phenomenology, refer to [59-62]. The dynamics of the Polyakov loops is governed by glue potential$ V_{\rm{glue}}(L, \bar L) $ in the effective action. Note that the RG scale dependence of the glue potential was not taken into account in this study; refer to [63] for further details. In this study, we employed the parameterization of$ V_{\rm{glue}} $ with the$ SU(N_c) $ Haar measure [64], which is$ \begin{aligned}[b] \bar V_{\rm{glue}}(L,\bar L) =& -\frac{a(T)}{2} \bar L L + b(T)\ln M_H(L,\bar{L}) \\ & + \frac{c(T)}{2} (L^3+\bar L^3) + d(T) (\bar{L} L)^2\,, \end{aligned} $

(10) with the dimensionless
$ \bar V_{\rm{glue}} = V_{\rm{glue}}/T^4 $ and the Haar measure as follows:$ M_H (L, \bar{L}) = 1 -6 \bar{L}L + 4 (L^3+\bar{L}^3) - 3 (\bar{L}L)^2\,. $

(11) The temperature dependence of the coefficients in Eq. (10) is given by
$ x(T) = \frac{x_1 + x_2/(t_r+1) + x_3/(t_r+1)^2}{1 + x_4/(t_r+1) + x_5/(t_r+1)^2}\,, $

(12) for
$ x\in \{a, c, d\} $ , and$ b(T) = b_1 (t_r+1)^{-b_4}\left (1 - {\rm e}^{b_2/(t_r+1)^{b_3}} \right)\,, $

(13) where
$ t_r = (T-T_c)/T_c $ is the reduced temperature. The parameters in Eqs. (12) and (13) are fixed by fitting the thermal behaviors of the Polyakov loop, including its fluctuations, and the thermodynamics in the Yang-Mills (YM) theory at a finite temperatur; refer to [64] for their values. The back reaction of the quarks on the glue potential can be captured well through an appropriate rescaling for the reduced temperature [36]:$\begin{aligned}[b] (t_r)_{\rm{YM}} \rightarrow \alpha\,(t_r)_{\rm{glue}},\quad {\rm{with}} \quad (t_r)_{\rm{glue}} = (T-T_c^{\rm{glue}})/T_c^{\rm{glue}}\,. \end{aligned}$

(14) In a previous study of ours, we comprehensively investigated the influence of parameters
$ \alpha $ and$ T_c^{\rm{glue}} $ on the QCD thermodynamics (see Figs. 9 and 10 in [28]). In this study, we adopted$ \alpha = 0.52 $ and$ T_c^{\rm{glue}} = 270 $ MeV. These values achieved the best agreement with the lattice calculations.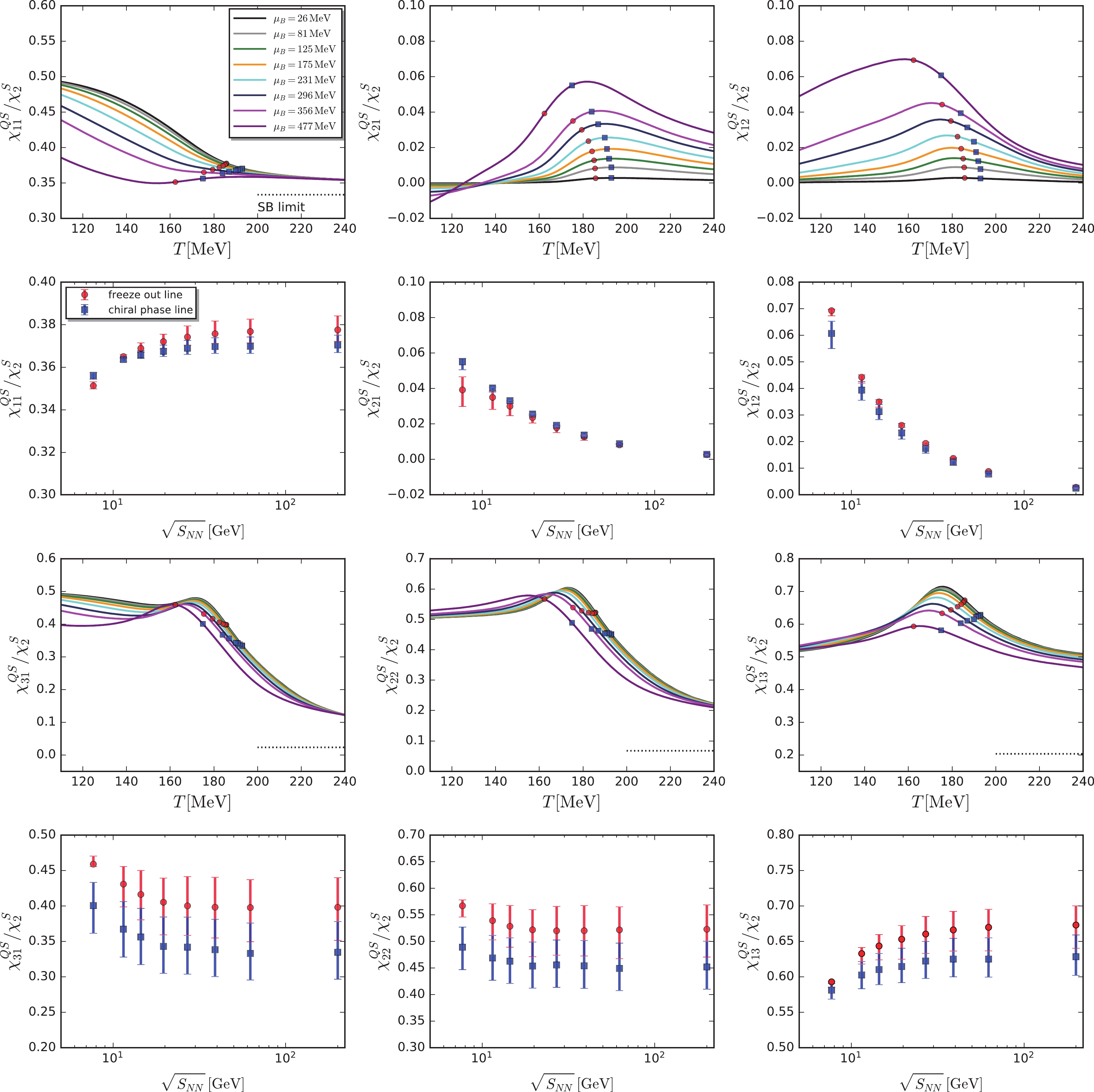
Figure 9. (color online) Correlations between the electric charge and the strangeness, from the second to the fourth orders, as functions of the temperature (subplots in the first and third rows) at the values of the chemical freeze-out baryon chemical potential,
$ {\mu_B}_{{CF}}^{{\rm{LEFT}}} $ , shown in Table 1. Two constraints were assumed: the strangeness neutrality defined by$ n_S = 0 $ and a fixed value of the ratio between the electric charge and the baryon number density,$ r = n_Q/n_B = 0.4 $ . On the different lines related to the different chemical potentials or different values of the collision energy, the red circles denote the freeze-out temperature$ T_{{CF}}^{{\rm{LEFT}}} $ , whereas the blue squares refer to the chiral pseudo-critical temperature$ {T_{c}^{\chi}}^{{\rm{LEFT}}} $ in Table 1. The two sets of points are also plotted as functions of the collision energy in a companion subplot for every plot above it. In the subplots of collision energy, we use error bars to indicate the variation of correlations at temperatures of$ T_{{CF}}^{{\rm{LEFT}}}\pm 5 $ MeV and$ {T_{c}^{\chi}}^{{\rm{LEFT}}}\pm 5 $ MeV.The evolution of the scale dependent effective action in Eq. (1) is described by the Wetterich equation [29], which is
$ \partial_{t}\Gamma_{k} = -{\rm{Tr}}\big(G^{q\bar q}_{k}\partial_{t} R^{q}_{k}\big)+\frac{1}{2}{\rm{Tr}}\big(G^{\phi\phi}_{k}\partial_{t} R^{\phi}_{k}\big)\,, $

(15) with
$ t = \ln (k/\Lambda) $ . Here,$ \Lambda $ is the ultraviolet cutoff of the effective theory, i.e., the initial evolution scale for the flow equation;$ G^{q\bar q}_{k} $ and$ G^{\phi\phi}_{k} $ are the propagators for the quarks and mesons, respectively. In this study, we used the$ 3d $ flat infrared regulators$ R^{q}_{k} $ and$ R^{\phi}_{k} $ , which are suitable for computations at finite temperature and densities. The explicit expressions of the regulators are given in Appendix A in [28]. Inserting the effective action in Eq. (1) into the flow equation in Eq. (15), we obtain the flow equation for the effective potential$ \tilde{U}_{k} $ in Eq. (1) or$ U_k $ in Eq. (3). Evidently, the effective potential is the only term that is scale dependent in Eq. (1). This type of truncation is also known as local potential approximation (LPA). Within LPA, only the flow equation of$ \tilde{U}_{k} $ remains. After the flow is evolved from the UV cutoff toward the IR limit, i.e.,$ k = 0 $ , quantum fluctuations at different scales, as well as thermal and density fluctuations, are encoded in the effective potential$ \tilde{U}_{k = 0} $ . For further details with regard to solving the flow equation and relevant numerical settings, refer to a previous study of ours [28]. Finally, we obtain the thermodynamical potential density as follows:$ \Omega = \left(\tilde{U}_{k = 0}(\sigma_L,\sigma_S)+V_{\rm{glue}}(L, \bar L)\right)\bigg|_{\rm{EoM}}\,, $

(16) where the subscript EoM denotes that
$ \sigma_L $ ,$ \sigma_S $ , L, and$ \bar L $ are on their respective equations of motion. Thus, the pressure is given by$ p = -\Omega\,, $

(17) -
The baryon number, electric charge, and strangeness are conserved charges in heavy ion collisions as they are not changed through the strong interactions of QCD. Thus, there are three relevant chemical potentials, i.e.,
$ \mu_B $ ,$ \mu_Q $ , and$ \mu_S $ , which are related to the three-flavor quark chemical potentials through the following expressions:$ \mu_u = \mu_B/3 + 2\mu_Q/3 $ ,$ \mu_d = \mu_B/3-\mu_Q/3 $ , and$ \mu_s = \mu_B/3 - \mu_Q/3 -\mu_S $ . Here,$ \mu_u $ ,$ \mu_d $ , and$ \mu_s $ are the chemical potentials for the u, d, and s quarks, respectively. When the chemical potentials are nonvanishing, thermodynamical potential density$ \Omega $ or pressure p in Eq. (17) are functions of temperature T and the chemical potentials, that is,$ p(T, \mu_B,\mu_Q,\mu_S) $ . By differentiating the pressure w.r.t the three different chemical potentials, the generalized susceptibilities are obtained:$ \chi_{ijk}^{BQS}(T, \mu_B,\mu_Q,\mu_S) = \frac{\partial^{i+j+k} (p/T^4)}{\partial \hat \mu_B^i \partial \hat \mu_Q^j \partial \hat\mu_S^k}\,, $

(18) with
$ \hat \mu_X = \mu_X/T $ ($ X = B$ , Q, S). The generalized susceptibilities in Eq. (18) are related to the cumulants of the conserved charge distributions, such as the diagonal ones:$ \chi_1^X = \frac{1}{VT^3}\big\langle N_X \big\rangle\,, $

(19) $ \chi_2^X = \frac{1}{VT^3}\big\langle(\delta N_X)^2\big\rangle\,, $

(20) $ \chi_3^X = \frac{1}{VT^3}\big\langle(\delta N_X)^3\big\rangle\,, $

(21) $ \chi_4^X = \frac{1}{VT^3}\Big(\big\langle(\delta N_X)^4\big\rangle-3\big\langle(\delta N_X)^2\big\rangle^2\Big)\,, $

(22) with
$ \delta N_X = N_X-\langle N_X\rangle $ , where the ensemble average is denoted by the symbol$ \langle \cdots\rangle $ . Here, V is the volume of the system; typically, the number density,$ n_X = \langle N_X\rangle/V $ , is employed. Similarly, one has similar relations for the off-diagonal cumulants of the conserved charge distributions, or the correlations among the conserved charges, e.g.,$ \chi_{11}^{XY} = \frac{1}{VT^3}\big\langle(\delta N_X) (\delta N_Y)\big\rangle\,, $

(23) $ \chi_{12}^{XY} = \frac{1}{VT^3}\big\langle(\delta N_X) (\delta N_Y)^2\big\rangle\,, $

(24) $ \chi_{111}^{XYZ} = \frac{1}{VT^3}\big\langle(\delta N_X) (\delta N_Y) (\delta N_Z)\big\rangle\,, $

(25) with
$ Y\,, Z \in \{B,\,Q,\,S\} $ .In the environment of heavy ion collisions, the produced matter of the quark-gluon plasma (QGP) is neutral in strangeness, which entails that the expected value of the density of strangeness is vanishing, i.e.,
$ \langle n_S\rangle = 0 $ . Furthermore, the ratio between the electric charge and the baryon number density,$ r = \langle n_Q\rangle/\langle n_B\rangle $ , is a constant on average, whose value is determined by the charge-mass ratio$ Z/A $ of the colliding nuclei. In this study, we adopted$ r = 0.4 $ , which is consistent with that of the Au- or Pb- nucleus. According to these two constraints, the following equations are obtained:$ \chi_1^S(T, \mu_B,{\mu_Q}_0,{\mu_S}_0) = 0\,, $

(26) $ \frac{\chi_1^Q(T, \mu_B,{\mu_Q}_0,{\mu_S}_0)}{\chi_1^B(T, \mu_B,{\mu_Q}_0,{\mu_S}_0)} = r\,, $

(27) where
$ {\mu_Q}_0 $ and$ {\mu_S}_0 $ are defined. They depend on T and$ \mu_B $ . Employing Eqs. (26) and (27), the following differential equations for$ {\mu_Q}_0(T,\mu_B) $ and$ {\mu_S}_0(T,\mu_B) $ w.r.t.$ \mu_B $ are obtained:$ \frac{\partial {\mu_{S}}_0(T,\mu_B)}{\partial \mu_B} = -\frac{\chi^{BS}_{11}}{\chi^S_2}-\frac{\chi^{QS}_{11}}{\chi^S_2}\frac{\partial {\mu_Q}_0}{\partial \mu_B}\,, $

(28) $ \frac{\partial {\mu_Q}_0(T,\mu_B)}{\partial \mu_B} = \frac{\chi^{BS}_{11}(\chi^{SQ}_{11}-r \chi^{BS}_{11})-\chi^S_2(\chi^{BQ}_{11}-r \chi^B_2)} {\chi^S_2(\chi^Q_2-r \chi^{BQ}_{11})-\chi^{SQ}_{11}(\chi^{SQ}_{11}-r \chi^{BS}_{11})}\,. $

(29) Equations (28) and (29) were first derived in [47]. These two differential equations, along with
${\mu_{S}}_0(T,0) = {\mu_Q}_0(T,0) = 0$ , can be employed to obtain the values of$ {\mu_{S}}_0 $ and$ {\mu_Q}_0 $ at any finite$ \mu_B $ for a fixed value of T.Fig. 1 shows the dependence of
$ {\mu_{S}}_0 $ and$ {\mu_Q}_0 $ on the baryon chemical potential under the constraints$ r = n_Q/n_B = 0.4 $ and$ n_S = 0 $ at several temperatures. Note that the magnitude of$ {\mu_Q}_0 $ is significantly smaller than that of$ {\mu_{S}}_0 $ , which is reasonable as$ {\mu_Q}_0 $ would be vanishing if the value of the ratio of the electric charge to baryon number density were set to be$ r = 0.5 $ , due to the isospin symmetry between the u and d quarks. In the environment of heavy ion collisions,$ r = 0.4 $ is not far from the symmetric case. Concentrating on the left panel of Fig. 1, note that, when the temperature is high,$ {\mu_{S}}_0 $ approaches the free quark gas limit,$ {\mu_{S}}_0 = \mu_B/3 $ , as denoted by the black dashed line. However, this is not the case when the temperature is low and the system is near or below the chiral phase transition, where the deviation is remarkable. In summary, based on the results shown in Fig. 1, the commonly adopted approximation for the strangeness neutral matter produced in heavy ion collisions, with$ \mu_Q = 0 $ and$ \mu_s = \mu_B/3-\mu_S = 0 $ , is applicable in the chiral symmetric phase, but its validity should be treated carefully with the decrease in temperature.
Figure 1. (color online) Strangeness chemical potential
$ {\mu_{S}}_0 $ (left panel) and electric charge chemical potential$ {\mu_Q}_0 $ (right panel) as functions of baryon chemical potential$ \mu_B $ , with$ r = n_Q/n_B = 0.4 $ and$ n_S = 0 $ , for different temperatures. The left panel also shows$ {\mu_{S}}_0 = \mu_B/3 $ (black dashed line).Note that the calculated
$ {\mu_{S}}_0 $ and$ {\mu_Q}_0 $ in Fig. 1 from Eqs. (28) and (29) are exact and, in principle, can be extended to the regime of any large baryon chemical potential, which is in contradiction with the lattice QCD simulations, where the calculations are usually constrained to the region of$ \mu_B/T\leqslant 2\sim3 $ due to the sign problem. For the sake of a better comparison between our results and those from the lattice QCD, we adopted the approach of Taylor expansion in [3] to calculate the strangeness and the electric charge chemical potentials with the constraints of the strangeness neutrality and the fixed ratio between the electric charge and the baryon number density. We begin with the pressure expanded around the vanishing chemical potentials, which reads$ \frac{p(T, \mu_B,\mu_Q,\mu_S)}{T^4} = \sum\limits_{i,j,k = 0}^\infty \frac{\chi_{ijk}^{BQS}(T, 0)}{ i!j!k!}\hat \mu_B^i \hat \mu_Q^j \hat\mu_S^k, $

(30) where
$ \chi_{ijk}^{BQS}(T, 0) $ denotes the generalized susceptibility in Eq. (18) with$ \mu_B = \mu_Q = \mu_S = 0 $ . Similarly,$ {\mu_{S}}_0 $ and$ {\mu_Q}_0 $ in Eqs. (28) and (29) can be expanded in a series of the baryon chemical potential as follows:$ {\hat \mu}_{S0}(T,\mu_B) = s_1(T)\hat \mu_B+s_3(T){\hat \mu_B}^3+s_5(T){\hat \mu_B}^5+..., $

(31) $ {\hat \mu}_{Q0}(T,\mu_B) = q_1(T)\hat \mu_B+q_3(T){\hat \mu_B}^3+q_5(T){\hat \mu_B}^5+..., $

(32) where coefficients
$ s_n $ 's and$ q_n $ 's can be determined order by order (refer to [3] for further details. Inserting Eqs. (31) and (32) into Eq. (30),$ \mu_S $ and$ \mu_Q $ can be eliminated on the r.h.s.; thus, the pressure is only expanded in terms of the baryon chemical potential, which reads$ \begin{aligned}[b] \frac{p(T, \mu_B)}{T^4}-\frac{p(T, 0)}{T^4} =& p_{2}(T){\hat \mu_B}^2\\&+p_{4}(T){\hat \mu_B}^4+p_{6}(T){\hat \mu_B}^6+... \end{aligned} $

(33) We present the leading order expansion coefficients
$ s_1 $ and$ q_1 $ in Eqs. (31) and (32), respectively, in Fig. 2, and the ratio of the next-leading to leading order coefficients, i.e.,$ s_3/s_1 $ and$ q_3/q_1 $ , in Fig. 3, which are also compared with the continuum extrapolated lattice results from the HotQCD Collaboration [3]. As discussed in a previous study of ours [28], the pseudo-critical temperatures at the vanishing baryon chemical potential, obtained from lattice simulations and effective models, are generally not identical due to various reasons, e.g., the different absolute scale. Accordingly, it is more appropriate to rescale the temperature for the x-axis in Figs. 2 and 3 based on their respective values for$ T_c $ at$ \mu_B = 0 $ . Note that the pseudo-critical temperature of the QCD chiral crossover at zero values for the chemical potentials is$ T_c = 156 $ MeV for the lattice calculations by the HotQCD Collaboration [5]. In our calculations, we found that$ T_c^{\chi} = 194 $ MeV for the chiral crossover, and$ T_c^{d} = 177 $ MeV for the deconfinement phase transition; refer to [28] for further details and relevant discussions about these two pseudo-critical temperatures. Thus, it is reasonable to adopt a value of$ T_c $ in-between$ T_c^{d} $ and$ T_c^{\chi} $ for the fRG calculation. In Figs. 2 and 3, we employed$ T_c = 183 $ MeV for the fRG. This was motivated by the fact that, with this choice, the lattice and fRG yield a consistent result for$ s_1 $ when the temperature is around and below$ T_c $ , as shown in the left plot of Fig. 2. However, it is evident that one cannot match the calculated$ s_1 $ from two different approaches in the entire temperature range shown in the plot just by tuning$ T_c $ . We observed that the fRG slightly undershoots$ s_1 $ as$ T\gtrsim T_c $ in comparison to the lattice result. Similarly, from Figs. 2 and 3, it is not difficult to conclude that the fRG results are in qualitative, or even quantitative for some values of T, agreement with those of the lattice, e.g., both approaches lead to the conclusion that the$ q_3/q_1 $ ratio crosses the zero line and changes its sign at a value of T larger than$ T_c $ , and that$ s_3/s_1 $ is vanishing in the high temperature regime. As mentioned previously, when the temperature is high,$ {\mu_{S}}_0 $ approaches the free quark gas limit$ {\mu_{S}}_0 = \mu_B/3 $ with the constraint of strangeness neutrality, as shown in the left panel of Fig. 1. Consequently, only the linear term in the expansion of$ {\hat \mu}_{S0} $ in the powers of$ \hat \mu_B $ on the r.h.s. of Eq. (31) is nonvanishing, and$ s_3/s_1 $ is zero in the high temperature limit. Note, however, that the discrepancies between the results obtained from the fRG and the lattice are still significant. For instance, besides leading order$ s_1 $ at high temperatures,$ |q_1| $ from fRG is also smaller than that from the lattice in the entire temperature region, as shown in the right panel of Fig. 2. Furthermore, one also finds that the next-leading to leading order ratios$ s_3/s_1 $ and$ q_3/q_1 $ obtained from the fRG are slightly smaller than those of the lattice in some regimes of temperature.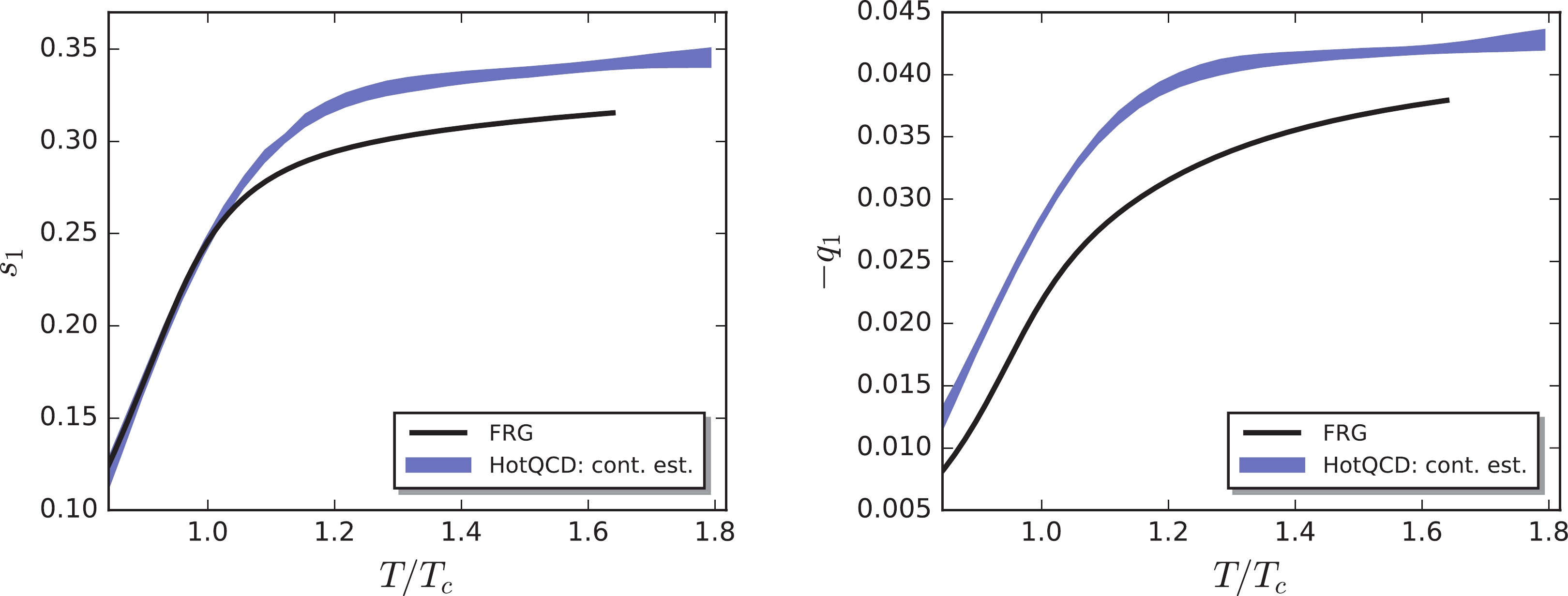
Figure 2. (color online) Leading order expansion coefficients of the strangeness and electric charge chemical potentials in powers of
$ \hat \mu_B $ , i.e.,$ s_1 $ (left panel) and$ -q_1 $ (right panel) in Eqs. (31) and (32), respectively, as functions of the temperature in units of$ T_c $ , in comparison to the relevant lattice results in [3], depicted by the blue bands. Note that$ T_c $ is the pseudo-critical temperature of the chiral crossover at vanishing chemical potentials. The constraints$ r = n_Q/n_B = 0.4 $ and$ n_S = 0 $ were implemented in the calculations.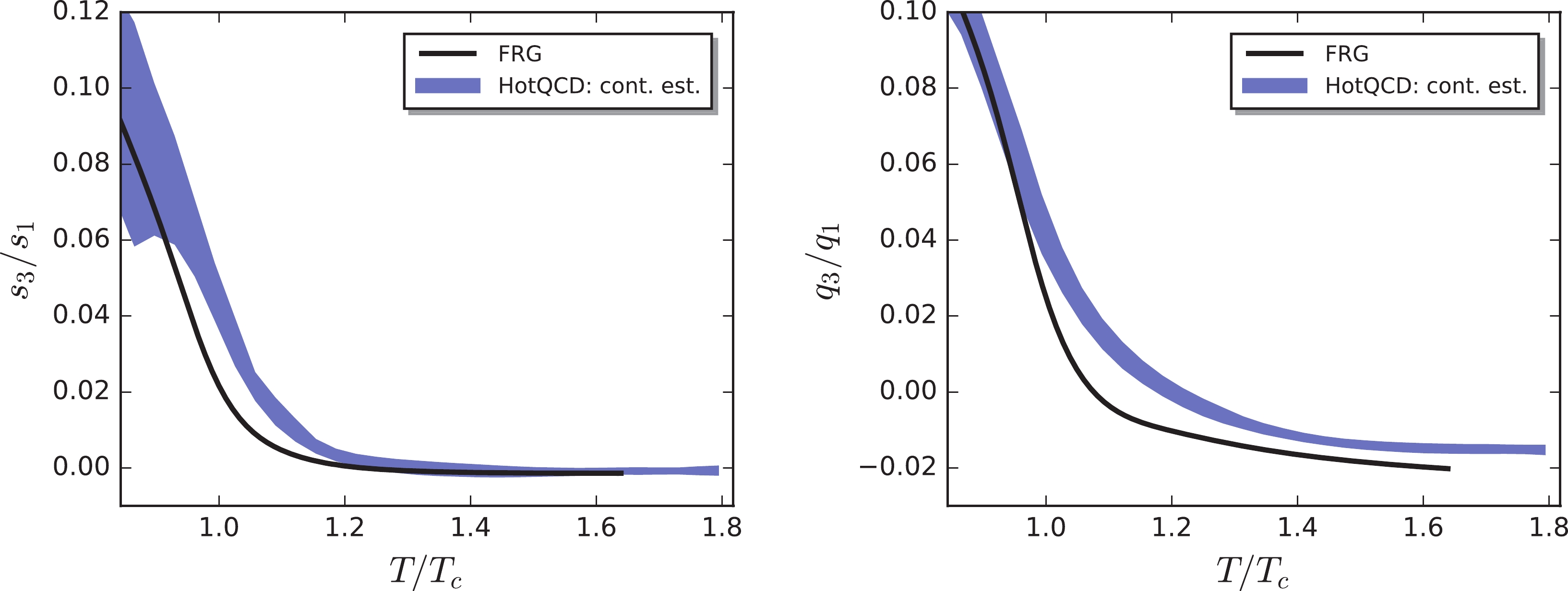
Figure 3. (color online)
$ s_3/s_1 $ (left panel) and$ q_3/q_1 $ (right panel) (see Eqs. (31) and (32)) as functions of the temperature in units of$ T_c $ , in comparison to the relevant lattice results in [3], depicted by the blue bands. Note that$ T_c $ is the pseudo-critical temperature of the chiral crossover at vanishing chemical potentials. The constraints$ r = n_Q/n_B = 0.4 $ and$ n_S = 0 $ were implemented in the calculations.As discussed previously, due to the sign problem at the finite density, the Taylor expansion is usually employed in lattice simulations; see, for instance, Eqs. (31)-(33). Therefore, it is important to investigate the convergency of the Taylor expansion in powers of
$ \mu_B/T $ . In this study, we aimed to study this convergency through the comparison between the Taylor expansion and full results. In Fig. 4, the full results of$ {\mu_{S}}_0(T,\mu_B) $ and$ {\mu_Q}_0(T,\mu_B) $ , obtained from Eqs. (28) and (29), respectively, are compared with those from the Taylor expansions in Eqs. (31) and (32), both of which are calculated within the fRG approach. Two results for the Taylor expansion are presented that correspond to the order of expansion up to$ {\cal{O}}(\mu_B^3) $ and$ {\cal{O}}(\mu_B^5) $ . They are denoted by the dashed and dotted lines, respectively, in Fig. 4. Three different temperatures were adopted. The relevant results are plotted in different colors. We found that the convergency of the Taylor expansion is observed for both the strangeness chemical potential and the electric charge chemical potential with$ \mu_B/T\lesssim 2 $ ; moreover, comparing these two chemical potentials, one can observe that the convergency property of$ {\mu_S}_0 $ is better than that of$ {\mu_Q}_0 $ , and the Taylor expansion result of$ {\mu_S}_0 $ of order$ {\cal{O}}(\mu_B^5) $ is still comparable to the full result when$ \mu_B $ is increased up to$ \sim 3T $ . Furthermore, in Fig. 4, one can observe an alternating divergence with the increase in the order for$ T = 160 $ and 180 MeV. This is not the case for$ T = 140 $ MeV. To explore the underlying mechanism, we present the lowest three coefficients of the Taylor expansion in Eqs. (31) and (32) in Fig. 5; they were rescaled appropriately for the convenience of presentation in one plot. Note that, when the temperature is low,$ s_3 $ and$ s_5 $ ($ q_3 $ and$ q_5 $ ) have the same signs, whereas with an increase in the temperature, they develop opposite signs. The oscillating behaviors stem from the fact that there is a finite convergence radius for the Taylor expansions of$ {\hat \mu}_{S0} $ and$ {\hat \mu}_{Q0} $ in Eqs. (31) and (32), respectively, as shown in Fig. 4.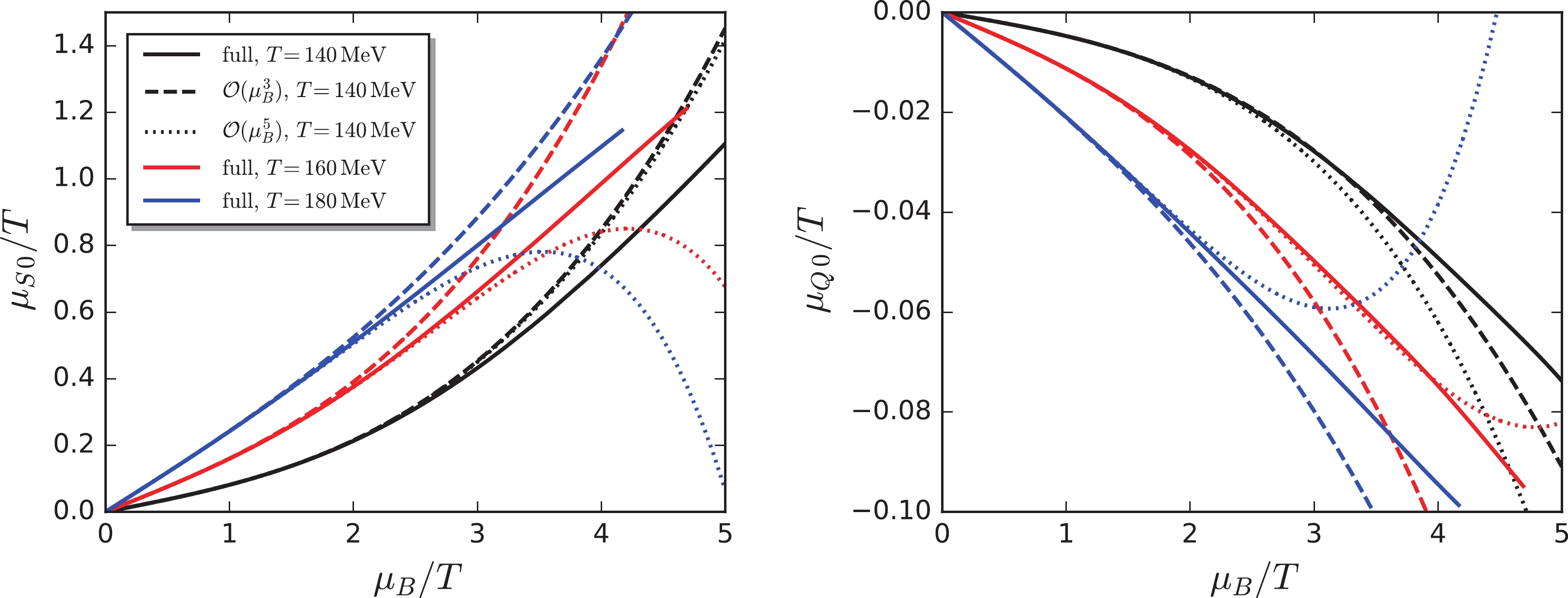
Figure 4. (color online) Strangeness chemical potential
$ {\mu_{S}}_0 $ (left panel) and electric charge chemical potential$ {\mu_Q}_0 $ (right panel) as functions of baryon chemical potential$ \mu_B $ normalized by T, with$ r = n_Q/n_B = 0.4 $ and$ n_S = 0 $ , obtained from Eqs. (28) and (29) (solid lines) in comparison to those from the Taylor expansion in Eqs. (31) and (32) up to the orders of$ {\cal{O}}(\mu_B^3) $ (dashed lines) and$ {\cal{O}}(\mu_B^5) $ (dotted lines). Different colors are employed to denote different temperatures.
Figure 5. (color online) Expansion coefficients of the strangeness chemical potential according to Eq. (31) (left panel) and electric charge chemical potential according to Eq. (32) (right panel), with
$ r = n_Q/n_B = 0.4 $ and$ n_S = 0 $ , as functions of temperature.Fig. 6 shows the dependence of the pressure on the baryon chemical potential within the constraints of the strangeness neutrality and the fixed ratio of the electric charge to the baryon number density. We also compare the full results with those from the Taylor expansion. Note that the convergency property for the pressure is better than that for the strangeness chemical potential and the electric charge chemical potential, as shown in Fig. 4, and the computation of the Taylor expansion up to the order of
$ {\cal{O}}(\mu_B^6) $ is in good agreement with the full one when the baryon chemical potential is increased to approximately four times the value of the temperature. In conclusion, the Taylor expansion of$ {\mu_{S}}_0 $ and$ {\mu_Q}_0 $ around$ \mu_B = 0 $ up to the fifth order is found to be convergent with$ \mu_B/T\lesssim 2\sim3 $ , and that of the pressure up to the sixth order is convergent with$ \mu_B/T\lesssim 4 $ .
Figure 6. (color online) Pressure subtracted by its value at
$\mu_B=0$ as a function of the baryon chemical potential$\mu_B$ , with$r=n_Q/n_B=0.4$ and$n_S=0$ . The full results (solid lines) are compared with those from the Taylor expansion in Eq. (33) up to the orders of${\cal{O}}(\mu_B^4)$ (dashed lines) and${\cal{O}}(\mu_B^6)$ (dotted lines). Different colors are used to denote different temperatures. -
In this section, we investigate the correlations of conserved charges at finite temperature and density in the context of the 2+1 flavor low energy effective theory within the fRG approach. Two constraints, i.e., the strangeness neutrality,
$ n_S = 0 $ , and a fixed value of the electric charge to baryon number density,$ r = n_Q/n_B = 0.4 $ , were implemented. We focused on the correlations between any two different conserved charges, i.e., those of form$ \chi_{n_{{X}}n_{{Y}}}^{XY} $ with$ X\,, Y \in \{B,\,Q,\,S\} $ . All the relevant correlations of orders from the quadratic to quartic, viz.,$ n_{{X}}+n_{{Y}} = $ 2, 3, and 4, were calculated. The motivations of this extensive study were as follows. In terms of the theoretical side, it is valuable to study the correlations, in particular the higher-order ones and in the case of heavy-ion collisions with strangeness neutrality and a fixed value of the electric charge to baryon number density, in the fRG approach. The relevant calculated results can easily be compared with other theoretical calculations, e.g., the lattice results [65]. With respect to the experimental side, through an extensive study, we provide useful information for researchers who are searching for the CEP. The dependence of various correlations on the temperature, baryon chemical potential, and collision energy was investigated, and several correlations that manifest the most non-monotonic behavior were selected, which could potentially be useful in future experiments.In fact, the second-order correlations between the net proton, net charge, and net kaon were measured by the STAR Collaboration [27]. Although these observables are related to the
$ \chi^{BS}_{11} $ ,$ \chi^{BQ}_{11} $ , and$ \chi^{QS}_{11} $ investigated in this study, it is still challenging to compare the experimental measurements with the theoretical calculations directly. It is of particular interest to study the relations among them; refer to [66] for related discussions.Although, to date, only the quadratic correlations have been experimentally measured, higher-order correlations and higher-order fluctuations (see e.g. [21-23]) carry more sensitive information about the critical dynamics of the chiral symmetry, for instance the non-monotonic behavior observed for the kurtosis of the net proton distribution as a function of the collision energy; refer to [25] and the references therein for further details. Therefore, it is more interesting to study the higher-order correlations in heavy ion collisions from the theoretical side, especially their dependence on the collision energy and potentially possible non-monotonic behaviors, which might provide some useful insights for the experimental measurement of higher-order correlations in the future. Nonetheless, it should be noted that our results should be carefully and cautiously considered, because many effects, such as the non-equilibrium evolution of the system [67], centrality and rapidity dependence, volume fluctuations, and resonance decays [68], were not taken into account in our studies. These effects may remarkably influence a direct confrontation of the theoretical prediction with the experimental measurements; refer to [66] for a relevant review.
To investigate the dependence of the conserved charge correlations on different values of the collision energy, we employed the chemical freeze-out (CF) temperature,
$ T_{{CF}} $ , and the baryon chemical potential,$ {\mu_B}_{{CF}} $ , reported in [69], which were obtained from the statistical hadronization approach. The parametrization for the dependence of$ T_{{CF}} $ and$ {\mu_B}_{{CF}} $ on collision energy$ \sqrt{s_{NN}} $ is$ T_{{CF}} = \frac{T_{{CF}}^{\rm lim}}{1+\exp\Big(2.60-\ln\big(\sqrt{s_{NN}}\big)/0.45\Big)}, $

(34) and
$ {\mu_B}_{{CF}} = \frac{a}{1+0.288\sqrt{s_{NN}}}, $

(35) with
$T_{{CF}}^{\rm lim} = 158.4$ MeV and$ a = 1307.5 $ MeV. Please, refer to [70] for further details about the freeze-out conditions in heavy ion collisions. Moreover, as discussed previously, the scale in the low energy effective theory is slightly different from that in the QCD, and this mismatch is taken into account for the freeze-out parameters through the rescale as follows:$ T_{{CF}}^{{\rm{LEFT}}} = \beta\,T_{{CF}},\quad {\rm{and}} \quad {\mu_B}_{{CF}}^{{\rm{LEFT}}} = \beta\,{\mu_B}_{{CF}}\,, $

(36) where the quantities with the superscript
$ {\rm{LEFT}} $ denote those in the low energy effective theory, and$ \beta $ is a rescale coefficient. We employed the pseudo-critical temperature from the lattice simulation,$ {T_c}^{{\rm{LAT}}} = 156 $ MeV, at the vanishing chemical potential, and$ {T_c}^{{\rm{LEFT}}} = 183 $ MeV in our calculations in the context of the low energy effective theory, as discussed in Sec. III, to determine rescale coefficient$ \beta $ , which yields$ \beta = \frac{{T_c}^{{\rm{LEFT}}}}{{T_c}^{{\rm{LAT}}}}\simeq 1.173\,. $

(37) Within this framework, values of the chemical freeze-out parameters in the low energy effective theory,
$ {\mu_B}_{{CF}}^{{\rm{LEFT}}} $ and$ T_{{CF}}^{{\rm{LEFT}}} $ , are presented in Table 1, corresponding to the eight values of the collision energy. Furthermore, we also investigated the dependence of the calculated results on the approach for determining rescale coefficient$ \beta $ . We used$ {T_{c}^{\chi}}^{{\rm{LEFT}}} = 194 $ MeV for the chiral crossover at the vanishing baryon chemical potential obtained in our calculations to replace$ {T_c}^{{\rm{LEFT}}} $ in Eq. (37) and found that various correlations as functions of the collision energy do not change qualitatively. To investigate the quantitative errors caused by the freeze-out temperature further, we also considered the case where the freeze-out temperature coincides with the chiral pseudo-critical temperature,$ {T_{c}^{\chi}}^{{\rm{LEFT}}} $ , for every value of$ {\mu_B}_{{CF}}^{{\rm{LEFT}}} $ , or the collision energy$ \sqrt{s_{NN}} $ . The relevant values of$ {T_{c}^{\chi}}^{{\rm{LEFT}}} $ are listed in the last row of Table 1.$\sqrt{s_{NN}}$ /GeV

200 62.4 39 27 19.6 14.5 11.5 7.7 ${\mu_B}_{{CF}}^{{\rm{LEFT}}}$ /MeV

26 81 125 175 231 296 356 477 $T_{{CF}}^{{\rm{LEFT}}}$ /MeV

186 186 185 184 183 179 175 162 ${T_{c}^{\chi}}^{{\rm{LEFT}}}$ /MeV

193 193 192 191 190 187 184 175 Table 1. Chemical freeze-out baryon chemical potential
${\mu_B}_{{CF}}^{{\rm{LEFT}}}$ and temperature$T_{{CF}}^{{\rm{LEFT}}}$ in context of the low energy effective theory for eight values of collision energy$\sqrt{s_{NN}}$ . In the last row,${T_{c}^{\chi}}^{{\rm{LEFT}}}$ is the pseudo-critical temperature of the chiral crossover at a fixed value of${\mu_B}_{{CF}}^{{\rm{LEFT}}}$ , which is determined by the peak position of$|\partial \rho_1/\partial T|$ , with$\rho_1$ given in Eq. (4).Numerical results for correlations
$ \chi^{BS}_{n_{{B}}n_{{S}}} $ ,$ \chi^{BQ}_{n_{{B}}n_{{Q}}} $ , and$ \chi^{QS}_{n_{{Q}}n_{{S}}} $ are shown in Figs. 7, 8, and 9, respectively. They are normalized by either the quadratic fluctuation of the strangeness$ \chi^{S}_{2} $ or that of the baryon number$ \chi^{B}_{2} $ . In every figure, six different correlations of the second order,$ \chi^{XY}_{11} $ , third order$ \chi^{XY}_{21} $ ,$ \chi^{XY}_{12} $ , and fourth order$ \chi^{XY}_{31} $ ,$ \chi^{XY}_{22} $ ,$ \chi^{XY}_{13} $ , are presented. They are depicted as functions of the temperature, with the different values of$ {\mu_B}_{{CF}}^{{\rm{LEFT}}} $ presented in Table 1, in the subplots of the first and third rows. We also analytically calculated the Stefan-Boltzmann (SB) limit values of the three-flavor massless free quark gas for the various correlations. To simplify the calculations of the SB limits, it must be assumed that the electric charge chemical potential is vanishing, i.e.,$ {\mu_Q}_0 = 0 $ , which is a reasonable approximation given its small value, as shown in the right panel of Fig. 1. Then, we obtain$ {\mu_{S}}_0 = \mu_B/3 $ , demanded by the strangeness neutrality. We plot the SB values for some selective correlations in Figs. 7, 8, and 9 in black dotted lines. Note that the SB values are constant and do not depend on the baryon chemical potential. Note also that for$ \chi^{QS}_{31}/\chi^{S}_{2} $ ,$ \chi^{QS}_{22}/\chi^{S}_{2} $ , and$ \chi^{QS}_{13}/\chi^{S}_{2} $ in Fig. 9, the deviation of the calculated values from their SB values in the high temperature regime grows with the increasing order of$ n_{{S}} $ from 1 to 3. This is due to the fact that the quantum fluctuations of the open strange mesons, such as kaons, still play a significant role in this region in the context of the low energy effective theory; refer to [28] for further details and discussions. Therefore, the low energy effective theory should be improved for describing the QCD (see, for instance, [14]), where the mesonic degrees of freedom are quickly decoupled once the temperature is above the pseudo-critical one.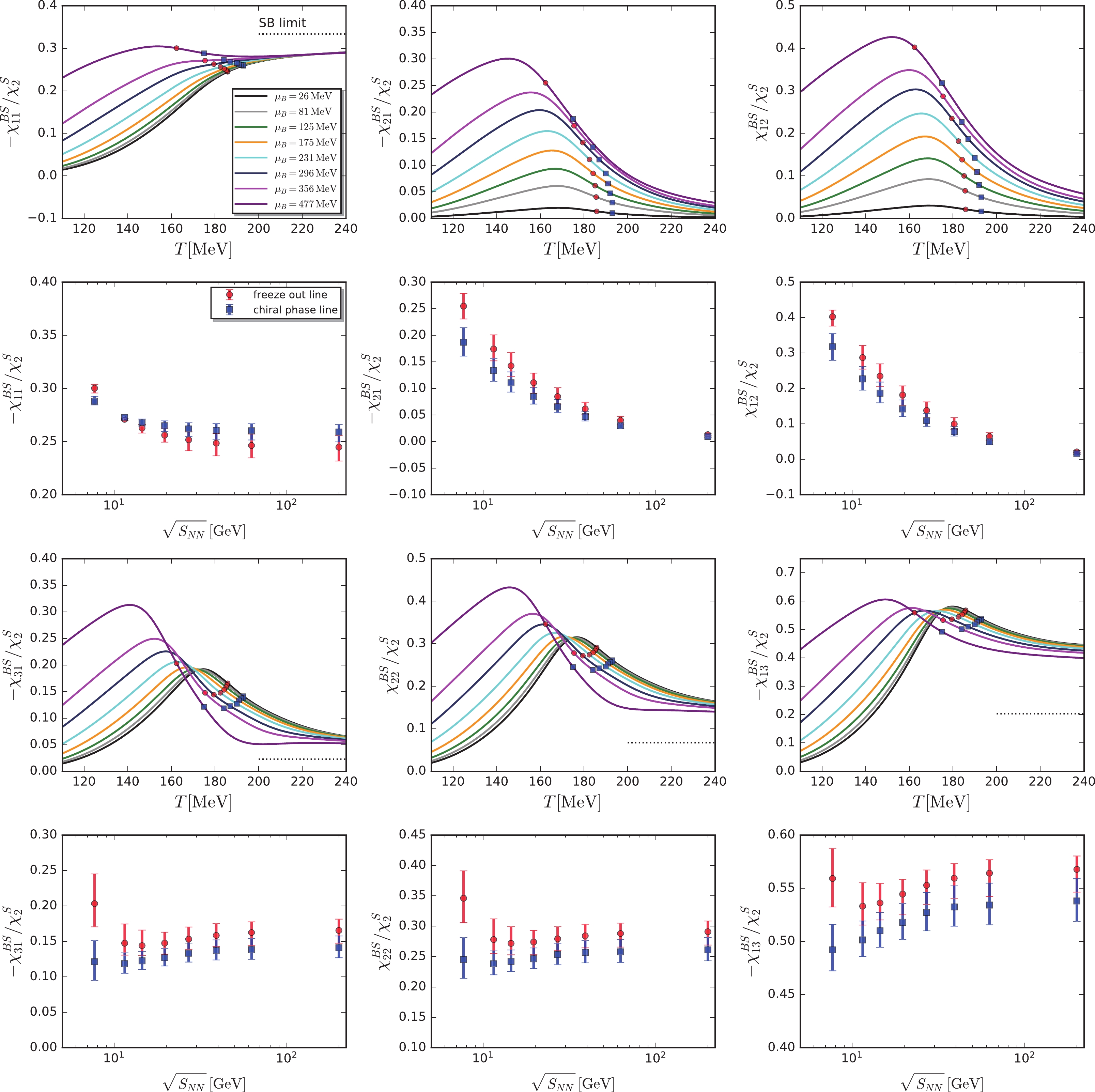
Figure 7. (color online) Correlations between the baryon number and the strangeness from the second to the fourth orders as functions of temperature (subplots in the first and third rows) at the values of the chemical freeze-out baryon chemical potential
$ {\mu_B}_{{CF}}^{{\rm{LEFT}}} $ presented in Table 1. Two constraints, i.e., the strangeness neutrality expressed as$ n_S = 0 $ and a fixed value of the ratio between the electric charge and the baryon number density,$ r = n_Q/n_B = 0.4 $ , were implemented. On the different lines related to the different chemical potentials or different values of the collision energy, we used red circles to denote the freeze-out temperature$ T_{{CF}}^{{\rm{LEFT}}} $ and blue squares to denote the chiral pseudo-critical temperature$ {T_{c}^{\chi}}^{{\rm{LEFT}}} $ in Table 1. The two sets of points are also plotted as functions of the collision energy in a companion subplot for every plot above it. In the subplots of the collision energy, we used error bars to indicate the variation of correlations at the temperatures of$ T_{{CF}}^{{\rm{LEFT}}}\pm 5 $ MeV and$ {T_{c}^{\chi}}^{{\rm{LEFT}}}\pm 5 $ MeV.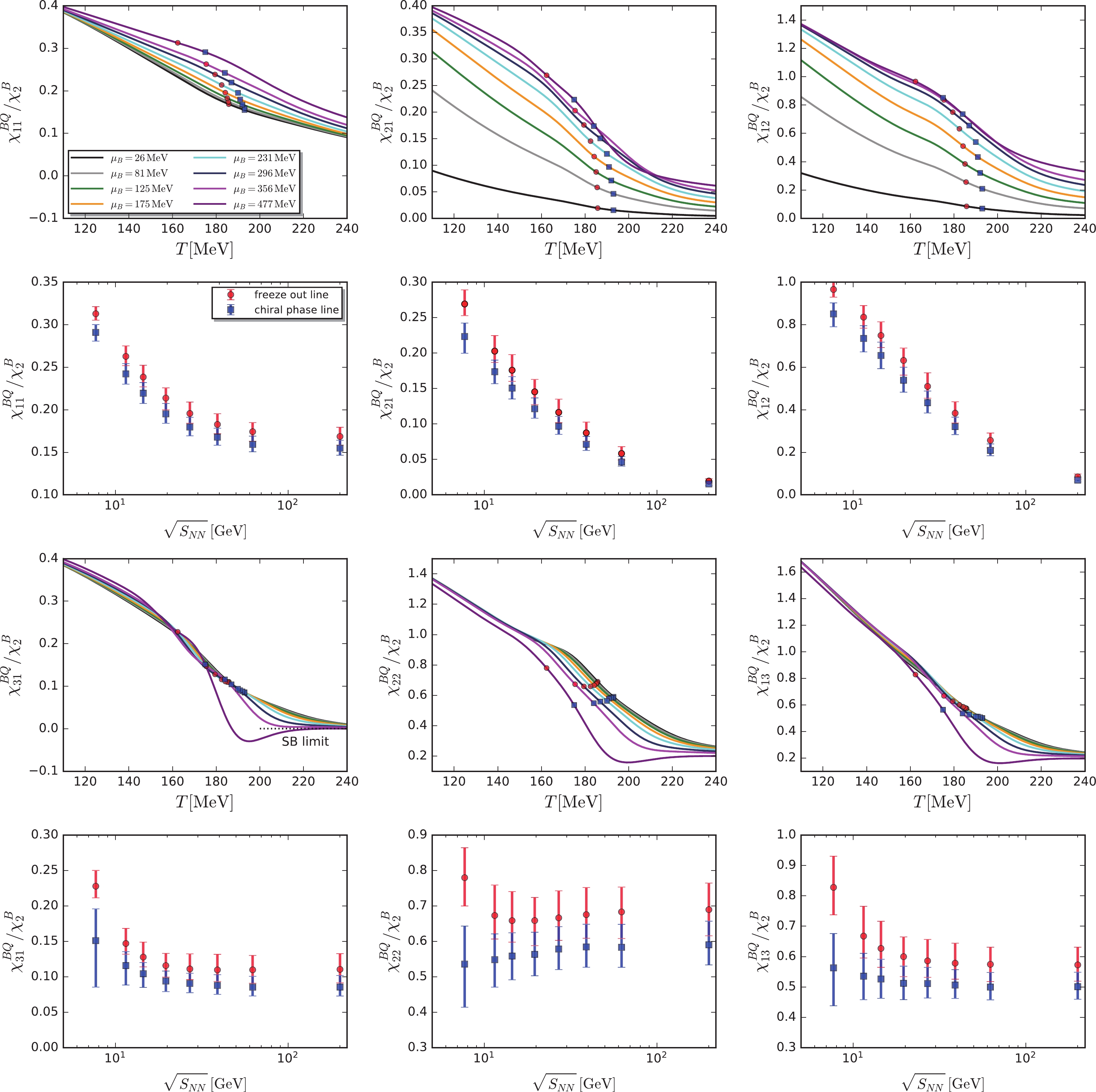
Figure 8. (color online) Correlations between the baryon number and the electric charge from the second to the fourth orders as functions of temperature (subplots in the first and third rows) at values of the chemical freeze-out baryon chemical potential
$ {\mu_B}_{{CF}}^{{\rm{LEFT}}} $ presented in Table 1. Two constraints, i.e., the strangeness neutrality expressed as$ n_S = 0 $ and a fixed value of the ratio between the electric charge and the baryon number density,$ r = n_Q/n_B = 0.4 $ , were implemented. On the different lines related to the different chemical potentials or different values of the collision energy, we used red circles to denote the freeze-out temperature$ T_{{CF}}^{{\rm{LEFT}}} $ and the blue squares to denote the chiral pseudo-critical temperature$ {T_{c}^{\chi}}^{{\rm{LEFT}}} $ in Table 1. The two sets of points are also plotted as functions of the collision energy in a companion subplot for every plot above it. In the subplots of the collision energy, we used error bars to indicate the variation of correlations at the temperatures of$ T_{{CF}}^{{\rm{LEFT}}}\pm 5 $ MeV and$ {T_{c}^{\chi}}^{{\rm{LEFT}}}\pm 5 $ MeV.Employing chemical freeze-out temperature
$ T_{{CF}}^{{\rm{LEFT}}} $ and chiral pseudo-critical temperature$ {T_{c}^{\chi}}^{{\rm{LEFT}}} $ for the eight values of the collision energy in Table 1, we plot all the correlations as functions of the collision energy in the second and fourth rows of Figs. 7, 8, 9, with each below their respective plots showing the T-dependence. The correlations determined from$ T_{{CF}}^{{\rm{LEFT}}} $ and$ {T_{c}^{\chi}}^{{\rm{LEFT}}} $ are denoted with red circles and blue squares, respectively, and their legends feature the freeze-out and chiral phase lines, respectively. Their positions are also shown in the T-subplots. Furthermore, to estimate the errors arising from the determinations of$ T_{{CF}}^{{\rm{LEFT}}} $ and$ {T_{c}^{\chi}}^{{\rm{LEFT}}} $ , we employed the error bars to represent the values of correlations at the temperatures of$ T_{{CF}}^{{\rm{LEFT}}}\pm 5 $ MeV and$ {T_{c}^{\chi}}^{{\rm{LEFT}}}\pm 5 $ MeV.Note from Figs. 7, 8, and 9 that higher-order correlations are more interesting than the second-order ones, given that the singular part, which contributes to the various correlations and is related to the critical dynamics, holds increasing importance with the increase in the order of correlations. For instance, the quadratic, cubic, and quartic cumulants of the pion or proton multiplicities were found to be proportional to powers of correlation length
$ \xi $ as$ \langle (\delta N)^2 \rangle\sim \xi^2 $ ,$ \langle (\delta N)^3 \rangle\sim \xi^{4.5} $ , and$ \langle (\delta N)^4 \rangle\sim \xi^7 $ , respectively [71]. Similar behavior was also observed in our calculations through the dependence of all the correlations on the temperature with a fixed value of the baryon chemical potential. The non-monotonic behaviors become progressively evident with the increasing order. Among all the correlations presented in Figs. 7, 8, and 9, two of the fourth-order correlations between the baryon number and the strangeness, namely$ -\chi^{BS}_{31}/\chi^{S}_{2} $ and$ \chi^{BS}_{22}/\chi^{S}_{2} $ , manifest themselves as the most non-monotonic correlations, as shown markedly in the third row of Fig. 7, where they are plotted as functions of temperature. Moreover, we found that the dependence of these two fourth-order correlations on the collision energy is non-monotonic as well, for both the freeze-out and the chiral phase lines. Note that these two correlations slightly decrease when the collision energy decreases from 200 GeV to 14.5 GeV and then, increase after the collision energy is reduced further. In summary, after an extensive study of all the correlations of conserved charges up to the fourth order, we found that two of them, i.e., the ones between the baryon number and the strangeness,$ -\chi^{BS}_{31}/\chi^{S}_{2} $ and$ \chi^{BS}_{22}/\chi^{S}_{2} $ , have the most significant non-monotonic behaviors. This could potentially be useful in the BES program at RHIC to search for the CEP. Furthermore, we also investigated the influence of rescale coefficient$ \beta $ in Eq. (37) on the calculated results, replaced$ {T_{c}}^{{\rm{LEFT}}} = 183 $ MeV with$ {T_{c}^{\chi}}^{{\rm{LEFT}}} = 194 $ MeV as well as$ {T_{c}^{d}}^{{\rm{LEFT}}} = 177 $ MeV, and repeated the calculations in Figs. 7, 8, and 9. We found that the non-monotonic behaviors for$ -\chi^{BS}_{31}/\chi^{S}_{2} $ and$ \chi^{BS}_{22}/\chi^{S}_{2} $ as functions of the collision energy do not change. -
In this study, we analyzed the correlations of conserved charges, i.e., the baryon number, electric charge, and strangeness, up to the fourth order at nonzero temperatures and chemical potentials. The computations were performed in the context of a 2+1 flavor low energy effective theory within the fRG approach, following the setup presented in a previous study of ours [28]. Employing a set of phenomenological chemical freeze-out parameters, we also studied the possible evolution behavior of the correlations with the collision energy in the beam energy scan experiments at RHIC.
The computations in this study were performed for strangeness neutral systems with a fixed ratio of the electric charge to the baryon number density. These systems mimic the environment in the heavy ion collisions. Due to these two constraints, the equilibrium strangeness and electric charge chemical potentials, denoted in this study by
$ {\mu_{S}}_0 $ and$ {\mu_Q}_0 $ , respectively, develop dependence on baryon chemical potential$ \mu_B $ , which were calculated fully in our approach. Furthermore, we also expanded$ {\mu_{S}}_0 $ and$ {\mu_Q}_0 $ in powers of$ \mu_B/T $ , and the leading and next-leading order coefficients were compared with the lattice results. We found that, although there is a small quantitative deviation, the fRG results are in qualitative agreement with those of the lattice QCD. The Taylor expansion of$ {\mu_{S}}_0 $ and$ {\mu_Q}_0 $ around$ \mu_B = 0 $ up to the fifth order was found to be convergent with$ \mu_B/T\lesssim 2\sim3 $ , and the convergency property for the pressure was better with$ \mu_B/T\lesssim 4 $ .The dependence of various correlations on the temperature and baryon chemical potential were investigated, and we found that higher-order correlations are more sensitive to critical dynamics than the quadratic ones. Among all the correlations of conserved charges up to the fourth order, we found that two of them, namely the fourth-order correlations between the baryon number and the strangeness normalized by the variance of strangeness,
$ -\chi^{BS}_{31}/\chi^{S}_{2} $ and$ \chi^{BS}_{22}/\chi^{S}_{2} $ , manifest themselves as the most non-monotonic correlations. They also have a non-monotonic dependence on the collision energy. However, we should emphasize that this result should be carefully and cautiously considered. First, as discussed previously, many effects, especially the non-equilibrium evolution of the system, were not taken into account in our calculations. These effects may play a significant role in the comparison between the theoretical prediction and the experimental measurements. Second, in the experimental measurements of correlations, the net-proton and net-kaon multiplicity distributions were used as proxies for those of the net baryon and net strangeness, respectively. However, the relations among them certainly need to be elucidated more clearly in a future study. Furthermore, detailed error analyses of calculations in the low energy effective theory are indispensable, particularly when the theoretical calculation is intended to be confronted with the corresponding experimental measurement. In this study, estimates for the errors stemming from the variation of the freeze-out temperature were made. Notably, a more careful analysis of the errors in the low energy effective theory was conducted recently [72]. In addition, the computation of LEFT was improved by resorting to the first-principle QCD calculation within the fRG approach [14]. It was also constrained significantly via a detailed comparison with the lattice QCD simulations, e.g., in [73, 74]. -
We thank the members of the fQCD collaboration [75] for their work on related projects.
Correlations of conserved charges and QCD phase structure
- Received Date: 2020-11-23
- Available Online: 2021-04-15
Abstract: Correlations of conserved charges, i.e., the baryon number, electric charge, and strangeness, are calculated at finite temperature and chemical potentials up to the fourth order. The calculations are done in a 2+1 flavor low energy effective theory, in which the quantum and thermal fluctuations are encoded through the evolution of flow equations within the functional renormalization group approach. Strangeness neutrality and a fixed ratio of the electric charge to the baryon number density are implemented throughout the computation. We find that higher-order correlations incorporate more sensitive critical dynamics than the quadratic ones. In addition, a non-monotonic dependence of the fourth-order correlations between the baryon number and strangeness, i.e.,






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: