New Z' boson of the bestest little Higgs model as a portal to signatures of Higgs bosons h₀ and H₀ at the future muon collider

Since the confirmation of the existence of the Higgs boson by the ATLAS [1] and CMS [2] Collaborations at the Large Hadron Collider (LHC), the scientific community has undertaken the task of confirming that its properties match those of the scalar boson predicted by the Standard Model (SM) [3−7]. Any deviation from the SM predictions could be valuable information about a possible extended theory. Despite the excellent predictive power of the SM, unsolved problems remain, such as the hierarchy problem, namely, quantum corrections render the Higgs potential fine-tuned. These quantum corrections result from three different sectors of the SM: the gauge, fermion, and Higgs sectors. For a theory that is not fine-tuned, new physics is required in each of these three sectors to cancel quantum corrections to the Higgs potential.

Several physics models beyond the SM have been proposed to solve the hierarchy problem. Some of the proposed extensions are the Little Higgs Models (LHM) [8−12], which employ a mechanism called collective symmetry breaking. Its main concept is to represent the SM Higgs boson as a pseudo-Nambu-Goldstone boson of an approximate global symmetry spontaneously broken at a certain scale in the teraelectronvolt (TeV) range. In these models, the collective symmetry-breaking mechanisms are implemented in three sectors: fermion, gauge, and Higgs. In each sector, new particles in the mass range of a few TeVs are predicted. These new particles play the role of partners of the top quark, gauge bosons, and Higgs boson, the effect of which is to generate radiative corrections for the mass of the Higgs boson and thus cancel the divergent corrections induced by SM particles. In constrast, the LHM [8−12] have the inconvenience of being strongly constrained by electroweak precision measurements in the gauge sector [13−15], but they also predict top partners that are much heavier than the mass of the new gauge bosons, which leads to significant fine-tuning in the Higgs potential [13, 16].

The Bestest Little Higgs Model (BLHM) [13, 17−25] overcomes the difficulties presented by LHM, achieved by incorporating two independent symmetry-breaking scales, f and F with $ F>f $. Consequently, a disassociation in the masses of the quark (T, $ T_5 $, $ T_6 $, $ T^{2/3} $, B, $ T^{5/3} $) and boson gauge ($ Z' $, $ W'^{\pm} $) partners is generated. Regarding the quarks, four of them are heavy partners of the top quark ($ +2/3 $ charge), one heavy partner of the bottom quark ($ -1/3 $ charge), and one exotic quark ($ +5/3 $ charge). The new quarks obtain masses proportional only to the f energy scale, whereas the new gauge bosons acquire masses proportional to the combination of the f and F scales, i.e., $ \sqrt{f^{2}+F^{2}} $. Because the new quarks are now lighter than the new gauge bosons, fine-tuning in the fermion sector and electroweak precision data constraints in the gauge sector are avoided. In constrast, the scalar sector of the BLHM has a rich phenomenology that generates the scalar fields: $ h_0, H_0, A_0, \phi^{0},\eta^{0}, H^{\pm}, \phi ^{\pm} $ , and $ \eta^{\pm} $. The $ h_0 $ state is assumed to be similar to the SM Higgs boson. For more information on the BLHM, the interested reader can refer to Refs. [19−25].

Because the SM Higgs boson plays essential roles in several extended model scenarios, we naturally expect that new physics beyond the SM would influence the properties of this Higgs boson, thus leading to deviations in Higgs properties from the SM predictions. Probing the extended models meaningfully beyond the direct LHC searches would require precision measurements of the Higgs boson couplings. Thus far, several couplings of the Higgs to SM fermions and vector bosons based on current LHC data still have large uncertainties, for example, the $ ZZh_0 $ coupling [26−28]. Such a precision, if achieved, will be very useful to discovering the evidence of new physics beyond the SM. In contrast, Lepton colliders have the advantage of clean signatures and high-statistics samples of the Higgs boson. Compared with the Hadron collider, a future Lepton collider may have a higher capacity in the measurement of the $ ZZh_0 $ coupling through Higgs-strahlung production $ l^{+}l^{-} \to Zh_0 $. The $ l^{+}l^{-} $ colliders could reduce the aforementioned uncertainties to few percent level.

In this paper, we explore the phenomenology of the production of Higgs bosons $ h_0 $ and $ H_0 $of the BLHM in muon collisions. Specifically, we present a comprehensive analysis of the production mechanism, $ \mu^{+}\mu^{-}\rightarrow (Z, Z') \to Zh_0 $ and $ \mu^{+}\mu^{-}\rightarrow (Z, Z') \to ZH_0 $, and its sensitivity including both the resonant and nonresonant effects at future high-energy and high-luminosity muon collider. In the BLHM scenario, Higgs-strahlung productions $ \mu^+ \mu^- \to Zh_0 $ and $ \mu^+ \mu^- \to ZH_0 $ are essential processes to study tree-level interactions: $ Z Z h_0 $, $ Z Z H_0 $, $ Z'Z h_0 $, and $ Z'Z H_0 $. Additionally, the above processes are useful for testing the consistency of the parameter space of the BLHM. Our search for the Higgs bosons is implemented in the environment of a future muon collider [29, 30], as this could provide a potential solution to the problems regarding energy, luminosity, background cleanliness, and the limited sensitivity of current and other future colliders. These features make the muon collider an ideal collider for the search for new particles, as the first evidence of new physics is expected to appear in the TeV energy range. A high-energy, high-luminosity collider such as the muon collider will enable High Energy Physics to be explored at energy frontiers beyond the reach of existing and proposed colliders. Moreover, note that in this work, we focus only on investigating Higgs-strahlung production processes $ \mu^{+}\mu^{-}\rightarrow (Z, Z') \to Zh_0, ZH_0 $. However, Higgs bosons can also be produced via vector boson fusion (VBF). Given the high collision energy capabilities of the muon collider, the cross-sections for VBF processes could become significantly more important than Higgs-strahlung processes. We are currently working on this complementary project, and it will be addressed in future work.

The remainder of this paper is outlined as follows: Sec. II presents the decay widths of the $ Z' $ boson in the BLHM. In Sec. III, we find the scattering amplitudes and cross-sections of processes $ \mu^{+}\mu^{-}\rightarrow (Z, Z') \to Zh_0, Z H_0 $. Section IV presents our numerical results. Finally, in Sec. V, we present our conclusions. The Feynman rules involved in our calculations are provided in Appendix A.

In this section, we determine the total decay width of the $ Z' $ boson, which we require to calculate the cross-section of the Higgs-strahlung processes. In the context of the BLHM, the main decay channels of the $ Z' $ gauge boson are $ Z' \to f \bar f $ ($ f = t, b, T, T_5, T_6, T^{2/3}, T^{5/3}, B $), $ Z' \to W^+W^- $, $ Z' \to Zh_0 $, and $ Z' \to ZH_0 $. Note that the BLHM has no $ Z'H^{+}H^{-} $ coupling. Thus, total decay width $ \Gamma_{Z'} $ of the $ Z' $ boson can be estimated as follows:

Below, we provide the analytical expressions for the partial decay widths of the $ Z' $ boson involved in Eq. (1):

where $ N_c $ is the color factor ($ N_c = 1 $ for leptons and $ N_c = 3 $ for quarks), $ g^{Z'ff}_V $ and $ g^{Z'ff}_A $ are the vector and axial-vector coupling constants of the $ Z' $ boson with the fermions, respectively (see Table A1 in Appendix A [31]), and $ g_{Z'Zh_0} $ and $ g_{Z'ZH_0} $ denote the effective couplings of the $ Z^{\prime} $ and Z bosons to Higgs bosons $ h_0 $ and $ H_0 $, respectively, whose explicit expressions are given in Table A2 in Appendix A. Additionally,

Particle	Couplings
$ Z \bar{e}_i e_i $	$ g_{A}^{Z \bar{e}_i e_i } = $$\dfrac{\mathrm{i} g }{4 c_{W} }$
	$ g_{V}^{Z \bar{e}_i e_i } = $$\dfrac{\mathrm{i} g }{4 c_{W} } (-1+ 4 s^{2}_{W})$
$ Z' \bar{e}_i e_i $	$ g_{A}^{Z' \bar{e}_i e_i } = $$\dfrac{\mathrm{i} g c_{g} }{8 s_{g} } \left(2+ \dfrac{(c_{g}-s_{g}) s_{g}^2 (c_{g}+s_{g}) \left(c_{W}^2-3 s_{W}^2\right) v^2}{c_{W}^2 \left(f^2+F^2\right)}\right)$
	$ g_{V}^{Z' \bar{e}_i e_i } = $$-\dfrac{\mathrm{i} g c_{g} }{8 s_{g} } \left( 2 + \dfrac{(c_{g}-s_{g}) s_{g}^2 (c_{g}+s_{g}) \left(c_{W}^2+s_{W}^2\right) v^2}{c_{W}^2 \left(f^2+F^2\right)}\right)$

Table A1.  Three-point couplings of one gauge boson to two leptons in the BLHM.

Particle	Couplings
$ Z Z h_{0} $	$ \begin{array}{l} g_{Z Z h_{0}} = \dfrac{g m_{W} \sin (\alpha +\beta )}{c^{2}_{W}} -\dfrac{s_{W}^2 v^3 \left(g^2+g_{Y}^2\right)^2 \sin (\alpha +\beta )}{6 g_{Y}^2 f^2} \\ \;\;\;\;\;\;\;\;\;\; -\dfrac{s_{W} v^3 x_{s} \left(g^2+g_{Y}^2\right) \sin (\alpha +\beta ) \left( - c_{g}^2 g g_{Y}+c_{g} s_{g} s_{W} \left(g^2+g_{Y}^2\right)+g g_{Y} s_{g}^2\right)}{2 c_{g} s_{g} g_{Y}^2 \left(f^2+F^2\right)} \end{array} $
$ Z Z' h_{0} $	$ \begin{array}{l} g_{Z Z' h_{0}} = -\dfrac{g s_{W} v \left(c_{g}^2-s_{g}^2\right) \left(g^2+g_{Y}^2\right) \sin (\alpha +\beta )}{2 c_{g} s_{g} g_{Y} }+ \dfrac{g s_{W} v^3 \left(c_{g}^2-s_{g}^2\right) \left(g^2+g_{Y}^2\right) \sin (\alpha +\beta )}{6 c_{g} s_{g} g_{Y} f^2 } \\ \;\;\;\;\;\;\;\;\;\; + \dfrac{v^3 x_{s} \sin (\alpha +\beta ) \left(c_{g}^2 g g_{Y} s_{W} \left(g^2+g_{Y}^2\right)+2 c_{g} s_{g} \left(g^4 s_{W}^2+g^2 g_{Y}^2 \left(2 s_{W}^2+1\right)+g_{Y}^4 s_{W}^2\right)-g g_{Y} s_{g}^2 s_{W} \left(g^2+g_{Y}^2\right)\right)}{2 c_{g} s_{g}g_{Y}^2 \left(f^2+F^2\right)} \end{array} $
$ Z Z H_{0} $	$ \begin{array}{l} g_{Z Z H_{0}} = \dfrac{s_{W}^2 v \left(g^2+g_{Y}^2\right)^2 \cos (\alpha +\beta )}{2 g_{Y}^2} - \dfrac{s_{W}^2 v^3 \left(g^2+g_{Y}^2\right)^2 \cos (\alpha +\beta )}{6 g_{Y}^2 f^2 } \\\;\;\;\;\;\;\;\;\;\; -\dfrac{s_{W} v^3 x_{s} \left(g^2+g_{Y}^2\right) \cos (\alpha +\beta ) \left(c_{g}^2 (-g) g_{Y}+c_{g} s_{g} s_{W} \left(g^2+g_{Y}^2\right)+g g_{Y} s_{g}^2\right)}{2 c_{g} s_{g}g_{Y}^2 \left(f^2+F^2\right)} \end{array} $
$ Z Z' H_{0} $	$ \begin{array}{l} g_{Z Z' H_{0}} = -\dfrac{g s_{W} v \left(c_{g}^2-s_{g}^2\right) \left(g^2+g_{Y}^2\right) \cos (\alpha +\beta )}{2 c_{g} s_{g} g_{Y} }+\dfrac{g s_{W} v^3 \left(c_{g}^2-s_{g}^2\right) \left(g^2+g_{Y}^2\right) \cos (\alpha +\beta )}{6 c_{g} s_{g} g_{Y} f^2 } \\ \;\;\;\;\;\;\;\;\;\; + \dfrac{v^3 x_{s} \cos (\alpha +\beta ) \left(c_{g}^2 g g_{Y} s_{W} \left(g^2+g_{Y}^2\right)+2 c_{g} s_{g} \left(g^4 s_{W}^2+g^2 g_{Y}^2 \left(2 s_{W}^2+1\right)+g_{Y}^4 s_{W}^2\right)-g g_{Y} s_{g}^2 s_{W} \left(g^2+g_{Y}^2\right)\right)}{2 c_{g} s_{g} g_{Y}^2 \left(f^2+F^2\right)} \end{array} $

Table A2.  Three-point couplings of two gauge bosons to one Higgs boson in the BLHM.

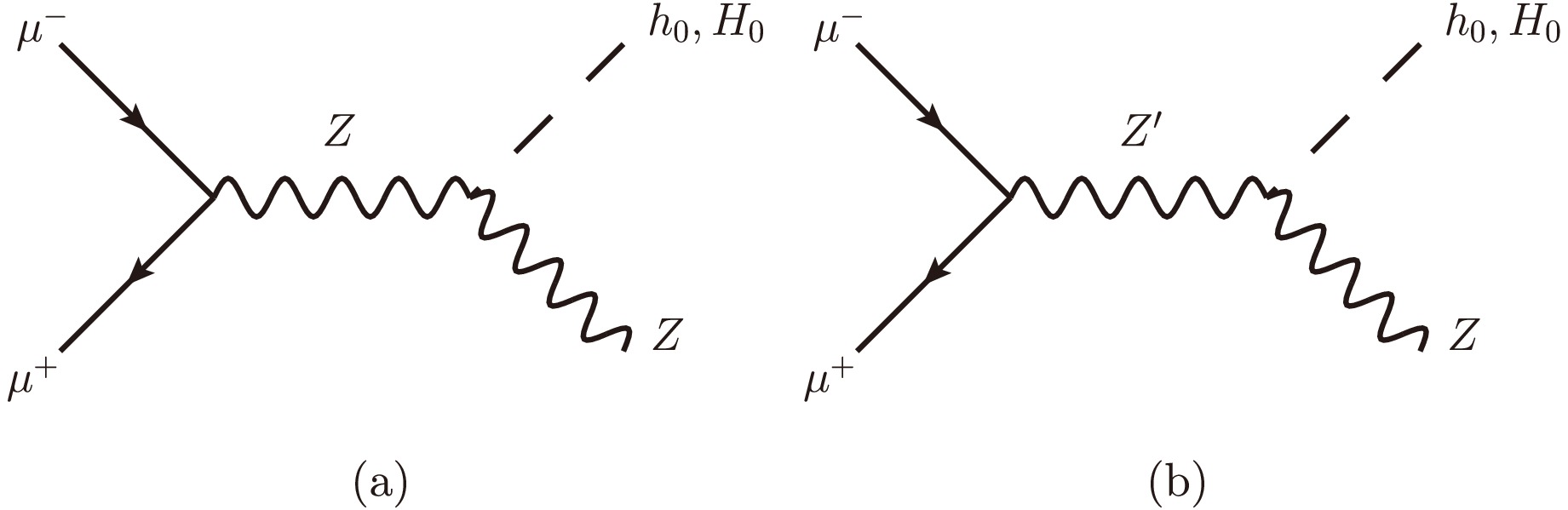
The Feynman diagrams contributing to Higgs-strahlung production processes $ \mu^+\mu^{-} \to (Z, Z') \to Zh_0 $ are shown in Fig. 1. The corresponding scattering amplitudes are represented by Eqs. (7) and (8):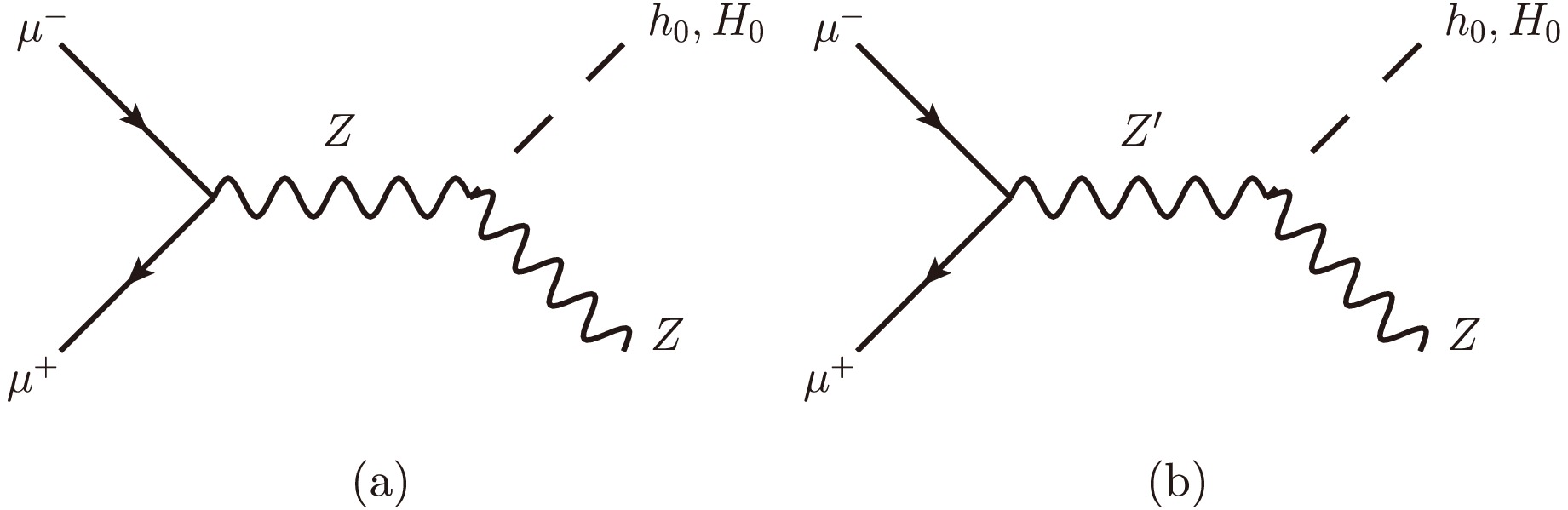

Figure 1.  Feynman diagrams for Higgs-strahlung production processes a) $ \mu^{+}\mu^{-}\to Z \to Zh_0, ZH_0 $ and b) $\mu^{+}\mu^{-}\to Z' \to $$ Zh_0, ZH_0$ in the BLHM.

where $ \epsilon^\nu_\lambda(Z) $ represents the polarization vector of the Z boson, whereas $ p_{\mu} = (p_1+ p_2)_{\mu} $ is the four-momentum of the mediator particle. The vector and vector-axial coupling constants of the Z or $ Z^{\prime} $ boson are given in Appendix A.

From the transition amplitudes, Eqs. (7) and (8), we calculate total cross-section $ \sigma^{Zh_0}_{T} $ for processes $ \mu^+ \mu^- \to (Z,Z') \to Zh_0 $:

with

where $ \sigma^{ Zh_0 }_Z $ and $ \sigma^{ Zh_0 }_{Z'} $ are the cross-sections of processes $ \mu^+ \mu^- \to Z \to Zh_0 $ and $ \mu^+ \mu^- \to Z' \to Zh_{0} $, respectively. The $ \sigma^{ Zh_0 }_{ZZ'} $ cross-section represents the interference term between the Z and $ Z' $ bosons. In Eqs. (10)−(12), $ \sqrt{s} $ is the center-of-mass energy, and λ is the usual two-particle phase space function:

We must mention that Eq. (9), which corresponds to the total cross-section in the context of the BLHM, reproduces the cross-section for process $\mu^+ \mu^- \to Z \to Zh_0$ obtained in the SM scenario [32−37]. This is reached in the decoupling limit of the new physics scales, i.e., $ (f, F) \to \infty $.

To quantify the combined effects of free parameters $ \sqrt{s} $, f, and F of the BLHM, we define the relative correction for the total cross-section as follows:

where $\sigma^{\rm SM}(\sqrt{s})$ represents the cross-section of the SM, and $ \sigma^{Z h_0}_{T} (\sqrt{s}, f, F) $ represents the cross-section in the presence of interactions of the BLHM.

We determine the scattering amplitudes and cross-sections of Higgs-strahlung production $ \mu^+\mu^- \to (Z, Z') \to ZH_0 $. The transition amplitudes are obtained from the Feynman diagrams contributing to process $ \mu^+\mu^- \to ZH_0 $ (see Fig. 1), which are given by

Using Eqs. (15) and (16), we calculate the total cross-section for process $ \mu^+ \mu^- \to (Z,Z') \to ZH_0 $, which can be expressed in the following compact form:

where

In these expressions, the two-particle phase space function is given by

In our numerical analysis of Higgs-strahlung production processes $ \mu^+\mu^- \to Zh_0 $ and $ \mu^+\mu^- \to ZH_0 $, various LHC measurements are used to constrain specific relevant parameters of the BLHM. In the following, we summarise the different input parameters, searches, and measurements used for our analysis.

Yukawa couplings $ y_i $ ($ i = 1,2,3 $) [18, 22, 24] are related to the generation of the new quark masses: T, B, $ T_5 $, $ T_6 $, $ T^{2/3} $, $ T^{5/3} $. These Yukawa couplings generate two study scenarios, which occur because in the region where $ y_2\approx y_3 $, the masses of the T and $ T_5 $ states are degenerate [18]. The two scenarios to which we refer are

● Scenario a ($ y_2 > y_3 $): $ y_1 = 0.61 $, $ y_2 = 0.84 $, and $ y_3 = 0.35 $ [22−24],

● Scenario b ($ y_2 < y_3 $): $ y_1 = 0.61 $, $ y_2 = 0.35 $, and $ y_3 = 0.84 $ [22−24].

In the first scenario ($ y_2 > y_3 $), the mass separation between new quarks $ T_5 $ and $ T_6 $ is relatively small and leads to the decays of $ T_5 $ being predominantly to SM particles. In the second scenario ($ y_2 < y_3 $), the mass separation between the $ T_5 $ and $ T_6 $ states is large, which increases the decay modes available for the $ T_5 $ quark through decay cascades to non-SM particles [18, 38]. Because of the phenomenological implications of the first scenario, in this paper, we explore Higgs-strahlung productions $ \mu^+\mu^- \to Zh_0 $ and $ \mu^+\mu^- \to ZH_0 $ in the $ y_2 > y_3 $ scenario. Other parameters involved in our calculations are discussed briefly below.

${\boldsymbol{m}}_{{\bf{A}}_{{\bf{0}}}}$: The mass of the $ A_0 $ pseudoscalar is an input parameter of the BLHM. This parameter is set to 1 000 GeV, which is consistent with current searches for new scalar bosons [39, 40].

${{\boldsymbol{m}}_{{\bf{H}}_{{\bf{0}}}}}$: The mass of Higgs boson $ H_0 $ is calculated from the mass of the $ A_0 $ pseudoscalar and values of $ \tan\, \beta $ (the ratio of the vacuum expectation values (VEVs) of the two Higgs doublets) [17]:

where

Ratio of the VEVs $ v_1 $ and $ v_2 $ ($ \tan \beta $): The authors of Refs. [13, 17, 41] set lower and upper bounds on parameter $ \tan \beta $, which occurs owing to perturbativity requirements on parameter $ \lambda_0 $. Thus, the range of values that $ \tan \beta $ could acquire is set according to the following equation:

For $m_{A_{0}} = 1\,000$ GeV, we obtain $ 1 < \tan \beta < 10.45 $. Consistently, in this work, we have selected $ \tan \beta = 3 $ and $ \tan \beta = 6 $ [22−24] to perform our numerical analysis of the production of $ Z h_0 $ and $ Z H_0 $ at a future muon collider.

Gauge couplings: Gauge couplings $ g_{A} $ and $ g_{B} $ can be parametrized in terms of mixing angle $ \theta_{g} $ and electroweak gauge coupling: $ \tan \theta_{g} = g_{A}/g_{B} $ and $ g = g_{A} g_{B}/\sqrt{g^{2}_{A}+ g^{2}_{B}} $. For our study, we assume that gauge coupling $ g_B = \frac{1}{2} g_A $ implies that $ g_A = \sqrt{5}g $. Another possible study scenario arises when $ g_{A} = g_{B} $; however, this project could be left for later work.

Symmetry breaking scales (f, F): The BLHM is characterized because it incorporates two different global symmetries that are broken into diagonal subgroups at different scales, f and F. With respect to the f scale, certain limits on this parameter occur when considering fine-tuning constraints on the masses of heavy quarks and experimental constraints on the production of quarks: $ f\in [700,3000] $ GeV [17, 18]. In constrast, energy scale F acquires sufficiently large values compared with the f scale. The objective is to ensure that the new gauge bosons are much heavier than the new quarks; thus, $F > 3\,000$ GeV [13, 17].

One of the motivations for building the BLHM is to avoid fine-tuning the Higgs potential. Thus, scenarios a and b mentioned above provide realistic values of the Yukawa couplings as they minimize the fine-tuning constraints. From Eq. (26),

we determine the measure of the fine-tuning for certain values of scale f. In Tables 1 and 2, we show a measure of the fine-tuning when energy scale f assumes values such as 1.0, 1.5, 2.0, 2.5, and 3.0 TeV. When $ \tan\, \beta = 3 $ (see Table 1), the size of the fine-tuning for $ f = 1.0 $ TeV is $ \Psi = 0.54 $, which indicates that there is no fine-tuning in the BLHM [13, 38]. The absence of fine-tuning prevails up to $ \Psi = 2.2 $, that is, for values of the f scale close to 2 TeV. The fine-tuning starts to become relevant for $ f > 2.1 $ TeV. With respect to Table 2 generated for $ \tan\, \beta = 6 $, the absence of fine-tuning only prevails for points close to $ f = 1 $ TeV, for $ f>1.2 $ TeV the model needs to be fine-tuned.

$ \tan\, \beta=3 $
f /TeV	Ψ
$ 1.0 $	$ 0.54 $
$ 1.5 $	$ 1.21 $
$ 2.0 $	$ 2.16 $
$ 2.5 $	$ 3.37 $
$ 3.0 $	$ 4.85 $

Table 1.  Measure of the fine-tuning in the BLHM for some values of the f scale. The values generated for Ψ are obtained by setting $ \tan\, \beta=3 $.

$ \tan\, \beta=6 $
f /TeV	Ψ
$ 1.0 $	$ 1.99 $
$ 1.5 $	$ 4.49 $
$ 2.0 $	$ 7.98 $
$ 2.5 $	$ 12.47 $
$ 3.0 $	$ 17.96 $

Table 2.  Measure of the fine-tuning in the BLHM for some values of the f scale. The values generated for Ψ are obtained by setting $ \tan\, \beta=6 $.

As a summary, we provide in Table 3 the values assigned to the parameters involved in our calculation.

$ {\rm{Parameter}} $	$ {\rm{Value}} $	$ {\rm{Reference}} $
$ m_{h_{0}} $	$ 125.20\ \text{GeV} $	[32]
$ m_{A_{0}} $	$1\,000\ \text{GeV}$	[39, 40]
$ \tan \beta $	$ 3, 6 $	[22−24]
$ m_{H_{0}} $	$1\,015\ \text{GeV}$
$ g_{A} $	$ \sqrt{5}\, g $
$ \Gamma_Z $	$2.495\,5\pm 0.002\,3$ GeV	[32]
f	$[1\,000, 3\,000]\ \text{GeV}$	[13, 18, 22−24]
F	$> 3\,000 \ \text{GeV}$	[13, 17, 18, 22−24]

Table 3.  Values assigned to the parameters involved in our numerical analysis at the BLHM.

Another of the essential input parameters involved in our study of Higgs-strahlung production $ \mu^+\mu^- \to (Z, Z') \to Zh_0, ZH_0 $ is the total decay width of the $ Z' $ boson ($ \Gamma_{Z^{\prime}} $), which has a dependence on the two energy scales, f and F. These represent the scales of the new physics in the BLHM. In this subsection, we analyze the different contributions that receive $ \Gamma_{Z^{\prime}} $, and we discuss the behavior of partial widths $ \Gamma(Z' \to X) $ when the f scale has values from $1\, 000$ to $3\, 000$ GeV while keeping the F scale fixed, and when F varies from $4\, 000$ to $6\, 000$ GeV while fixing f (see Fig. 2). In the left plot of Fig. 2, we show the evolution of $ \Gamma(Z' \to X) $ vs. f; these curves are generated by setting $F = 6\, 000$ GeV. In this scenario, the main partial contributions are generated by the decays $ Z^{\prime} \to T^{2/3}\bar T^{2/3} $ and $ Z^{\prime} \to T\bar T $. These provide the dominant and subdominant numerical contributions: $ \Gamma(Z' \to T^{2/3}\bar T^{2/3}) = [262.43,256.61] $ GeV and $ \Gamma(Z' \to T\bar T) = [259.70,249.83] $ GeV, respectively. This occurs while $ f\in [1000, 1650] $ GeV; outside this interval, $ \Gamma(Z' \to t\bar t) $ becomes dominant. On the opposite side, the most suppressed contribution is given by the $ Z' \to Z H_0 $ decay: $ \Gamma(Z' \to Z H_0) = [9.27 \times 10^{-3}, 1.07\times 10^{-2}] $ GeV over the entire analysis interval of the f scale. With respect to the remaining curves, $ \Gamma(Z' \to T^{5/3}\bar T^{5/3}) \approx \Gamma(Z' \to B\bar B) \approx \Gamma(Z' \to b\bar b) \in [2.60, 1.35]\times 10^{2} $ GeV, $ \Gamma(Z' \to WW) \approx \Gamma(Z' \to Z h_0) \in [6.0, 2.3] \times 10^{1} $ GeV, and $ \Gamma(Z' \to T_5\bar T_5) \approx \Gamma(Z' \to T_6\bar T_6) \in [10^{-1}, 10^{-3}] $ GeV. Furthermore, in the right-hand plot of Fig. 2, we can appreciate the behavior of $ \Gamma(Z' \to X) $ vs. F. These curves have been generated for $ f = 1000 $ GeV. In this case, the most significant contributions are given by decays $ Z' \to T^{2/3}\bar T^{2/3} $ and $ Z' \to T\bar T $: $ \Gamma(Z' \to T^{2/3}\bar T^{2/3}) = [172.99,262.43] $ GeV and $ \Gamma(Z' \to T\bar T) = [169.08, 259.70] $ GeV when the F scale obtains values in the interval from 4000 to 6000 GeV. In contrast, the minor contribution is led by process $ Z' \to Z H_0 $, $ \Gamma(Z' \to Z H_0) = [5.39,9.27]\times 10^{-3} $ GeV. The other curves approximately assumes values in the following ranges: $ \Gamma(Z' \to t\bar{t})\approx \Gamma(Z' \to T^{5/3}\bar T^{5/3}) \approx \Gamma(Z' \to B\bar{B}) \in [1.0, 2.5] \times 10^{2} $ GeV, $ \Gamma(Z' \to b\bar{b})\approx \Gamma(Z' \to W W) \approx \Gamma(Z' \to Z h_0) \in [0.9\times 10^{2}, 1.0 \times 10^{1}] $ GeV, and $ \Gamma(Z' \to T_5\bar T_5)\approx \Gamma(Z' \to T_6 \bar T_6) \sim 10^{-1} $ GeV. From the above, $ \Gamma(Z' \to X) $ shows a strong sensitivity to variations in the scales of the new physics (f and F). The dependence of $ \Gamma(Z' \to X) $ on F is more pronounced with respect to f, and all curves exhibit increasing behavior [see Fig. 2(b)]. In addition, the dominance of the fermionic decay modes of $ Z' $ ($ Z^{\prime} \to T^{2/3}\bar T^{2/3}, T\bar{T}, t \bar{t} $) leads to the assumption that the discovery channels should be related to the new QCD fermions.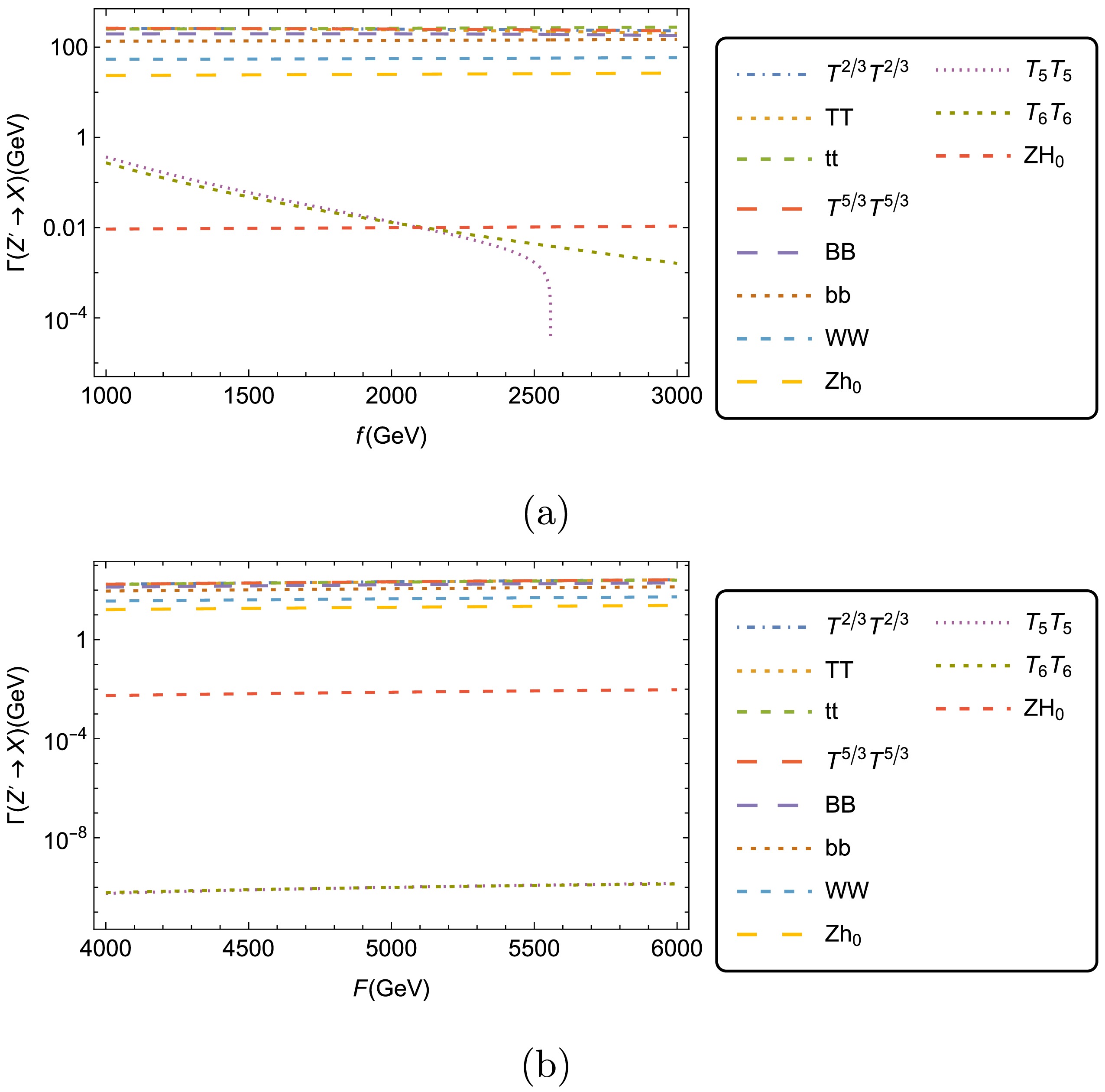

Figure 2.  (color online) Decay widths for processes $ Z' \to X $, where $ X= t\bar t, T\bar T, T_5\bar T_5, $ $ T_6\bar T_6, T^{2/3}\bar T^{2/3}, T^{5/3}\bar T^{5/3}, b\bar b, B\bar B, Z h_{0}, Z H_{0}, W W $. a) $ \Gamma(Z^{\prime} \to X) $ as a function of the f energy scale (with the fixed value of $ F=6\, 000 $ GeV). b) $ \Gamma(Z^{\prime} \to X) $ as a function of the F energy scale (with the fixed value of $ f=1\, 000 $ GeV).

We now present our results on the branching ratios of the $ Z' $ gauge boson as a function of the scales of new physics (f or F). We first discuss the behavior observed in Fig. 3(a). In this figure, we plot Br$ (Z' \to X) $ vs. the f scale while fixing the second F scale at 6000 GeV. The curve that provides the dominant contribution is given by the $ Z'\to T^{2/3}\bar{T}^{2/3} $ decay; its associated branching ratio is Br$ (Z' \to T^{2/3} \bar{T}^{2/3}) = [1.80,1.68]\times 10^{-1} $ when $ f\in [1\, 000, 3\, 000] $ GeV. On the opposite side, we find that the $ Z' \to ZH_0 $ decay provides the most suppressed contribution, Br$ (Z' \to Z H_0) = [6.35, 7.85]\times 10^{-6} $. Regarding the remaining branching ratios, these acquire values of Br$ (Z' \to T\bar{T})\sim $ Br$ (Z' \to t \bar{t})\sim $ Br$ (Z' \to T^{5/3}\bar{T}^{5/3})\sim $ Br$ (Z' \to B\bar{B})\sim 10^{-1} $, Br$ (Z' \to b\bar{b})\sim $ Br$ (Z' \to Z h_0)\sim $ Br$ (Z' \to W W)\sim 10^{-1}-10^{-2} $, and Br$ (Z' \to T_5\bar{T}_5)\sim \text{Br}(Z' \to T_6\bar{T}_6)\sim 10^{-4}- 10^{-6} $. Concerning Fig. 3(b), here we explore the behavior of Br$ (Z' \to X) $ vs. the F scale in the interval from 4 000 to 6 000 GeV, and all the curves shown in the figure have been generated with the fixed value of $ f = 1\, 000 $ GeV. In this scenario, we can appreciate that the curve that provides the slightly more significant contribution is derived from the $Z' \to T^{2/3} \bar{T}^{2/3}$ decay, Br$(Z' \to T^{2/3}\bar{T}^{2/3}) = [1.79,1.80]\times 10^{-1}$. In contrast, the smallest contribution is given by Br$ (Z' \to Z H_0) = [5.58, 6.35]\times 10^{-6} $. Decays $ Z' \to T\bar T $, $ Z' \to t\bar t $, $ Z' \to T^{5/3}\bar T^{5/3} $, and $ Z' \to B\bar B $ also generate branching ratios with values of the same order of magnitude than the main contribution although slightly smaller. Complementarily, the other branching ratios acquire values of Br$ (Z' \to b\bar b)\sim $ Br$ (Z' \to W W)\sim $ Br$ (Z' \to Z h_0)\sim 10^{-2} $, Br$ (Z' \to T_5\bar T_5)\sim 10^{-4} $, and Br$ (Z' \to T_6\bar T_6)\sim 10^{-5} $. In conclusion, the values obtained by branching ratios Br $ (Z' \to X) $ do not exhibit appreciable changes as the F scale increases to 6000 GeV, as shown in the corresponding figure. Br$ (Z' \to X) $slightly depends on the F scale compared with the f scale. The new heavy quarks and top quark of the SM are the most likely decays of new gauge boson $ Z' $.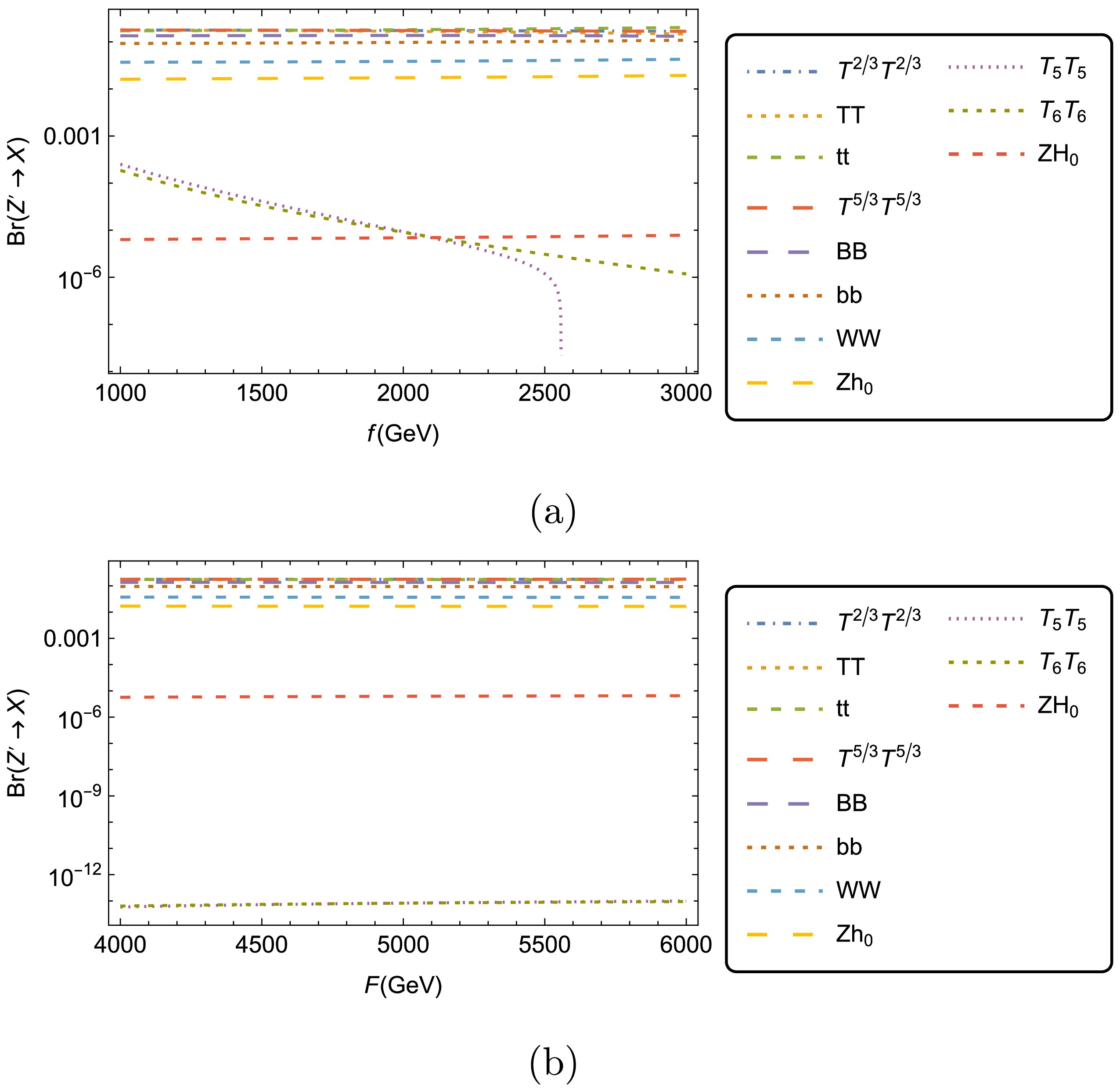

Figure 3.  (color online) Branching ratios for processes $ Z' \to X $, where $ X= t\bar t, T\bar T, T_5\bar T_5, $ $ T_6\bar T_6, T^{2/3}\bar T^{2/3}, T^{5/3}\bar T^{5/3}, b\bar b, B\bar B, Z h_{0}, Z H_{0}, W W $. a) $ \text{Br}(Z^{\prime} \to X) $ as a function of the f energy scale (with the fixed value of $ F=6\, 000 $ GeV). b) $ \text{Br}(Z^{\prime} \to X) $ as a function of the F energy scale (with the fixed value of $ f=1\, 000 $ GeV).

We investigate Higgs-strahlung production process $ \mu^{+} \mu^{-} \to Zh_0 $ at the future muon collider and calculate the BLHM predictions on the $ \sigma^{Z h_0}_{T}\left(\sqrt{s}, f, F \right) $ cross-section. We scan the BLHM parameters by considering various experimental and theoretical constraints. In Fig. 4, we present our results for total cross-section $ \sigma^{Z h_0}_{T}\left(\mu^{+} \mu^{-} \to Zh_0 \right) $, where the resonant and nonresonant effects of processes $ \mu^{+} \mu^{-}\rightarrow (Z, Z') \to Zh_0 $ are considered. We also show the different contributions received by $ \sigma^{Z h_0}_{T}\left(\mu^{+} \mu^{-} \to Zh_0 \right) $ according to Eq. (9): $ \sigma^{Z h_0}_{Z}\left(\mu^{+} \mu^{-} \to Zh_0 \right) $, $ \sigma^{Z h_0}_{Z'}\left(\mu^{+} \mu^{-} \to Zh_0 \right) $, and $\sigma^{Z h_0}_{Z Z'}\left(\mu^{+} \mu^{-} \to Zh_0 \right)$. Complementarily, in this same scenario, we plot the contribution of the SM represented by $ \sigma_{SM}\left(\mu^{+} \mu^{-} \to Zh_0 \right) $. From Fig. 4, we can appreciate that the behavior of cross-section $ \sigma_{SM}\left(\mu^{+} \mu^{-} \to Zh_0 \right) $ very closely resembles that of the curve represented by $ \sigma^{Z h_0}_{Z}\left(\mu^{+} \mu^{-} \to Zh_0 \right) $. The latter corresponds to the cross-section with the Z boson exchange in the context of the BLHM. In this particular case, the contribution of new physics is almost negligible. Concerning the other curves, $ \sigma^{Z h_0}_{Z'} $ and $ \sigma^{Z h_0}_{T} $, these obtain an increase in the cross-section for large values of the center-of-mass energy, reaching their maximum value at the resonance of the $ Z' $ gauge boson, i.e., when $ \sqrt{s}\approx 5\, 200 $ GeV: $ \sigma^{Z h_0}_{Z'}\left(\mu^{+} \mu^{-} \to Zh_0 \right) = 3.72 $ fb, and $ \sigma^{Z h_0}_{T}\left(\mu^{+} \mu^{-} \to Zh_0 \right) = 4.04 $ fb. For this benchmark, $ \sigma^{Z h_0}_{Z Z'}\left(\mu^{+} \mu^{-} \to Zh_0 \right) $, its contribution is $ 0.64 $fb. Additionally, note that in certain regions, the total cross-section of process $ \mu^{+}\mu^{-} \to (Z, Z') \to Zh_0 $ has values smaller than the sum of the individually contributing processes, i.e., $ \mu^{+}\mu^{-} \to Z \to Zh_0 $ and $ \mu^{+}\mu^{-} \to Z' \to Zh_0 $. This effect is basically due to the negative interference between channels $ \mu^{+}\mu^{-} \to Z \to Zh_0 $ and $ \mu^{+}\mu^{-} \to Z' \to Zh_0 $and the effect of effective couplings $ g_{ZZ'h_0} $ and $ g_{ZZh_0} $, which contain positive and negative terms, as shown in Table A2 in Appendix A.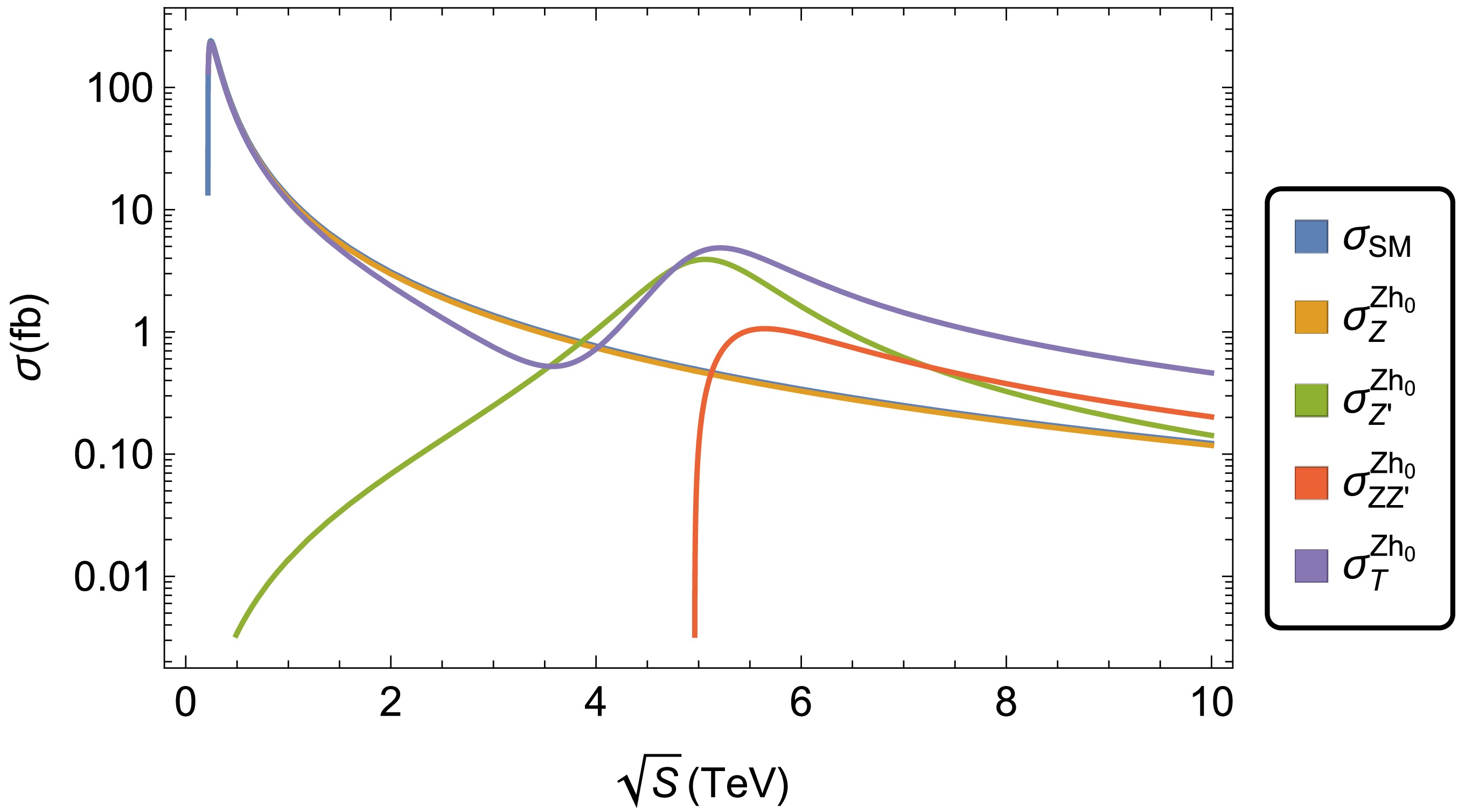

Figure 4.  (color online) Cross-section of process $ \mu^{+}\mu^{-}\to $$ (Z, Z') \to Zh_0 $ as a function of $ \sqrt{s} $. The curves are generated for $f = 1\,000$ GeV and $F=6\,000$ GeV (for $ m_{Z'} = 5\, 200 $ GeV) and correspond to $ \sigma_{SM} $, $ \sigma^{Z h_0}_Z $ [Eq. (10)], $ \sigma^{Z h_0}_{Z'} $ (Eq. (11)), $ \sigma^{Z h_0}_{ZZ'} $ [Eq. (12)], and $ \sigma^{Z h_0}_{T} $ [Eq. (9)].

Through the total cross-section, we test the effects that could be provided by the new physics scales, f and F, on $ \sigma^{Z h_0}_{T}\left(\mu^{+} \mu^{-} \to Zh_0 \right) $. Hence, in Fig. 5, we show the different curves generated for $ \sigma^{Z h_0}_{T}\left(\mu^{+} \mu^{-} \to Zh_0 \right) $ when the f and F scales take specific fixed values while center-of-mass energy $ \sqrt{s} $ varies in the interval from 0 to 10 000 GeV. In this figure, we can observe that the curves corresponding to $ \sigma^{Z h_0}_{T}\left(\mu^{+} \mu^{-} \to Zh_0 \right) $ decrease for large values of $ \sqrt{s} $. We also note that the height of the resonance peaks for the $ Z' $ boson changes depending on the value of the F scale. For the plotted curves, $ \sigma^{Z h_0}_{T}\left(\mu^{+} \mu^{-} \to Zh_0 \right) $ reaches its local maxima at the resonance of the $ Z' $ gauge boson: $ \sigma^{Z h_0}_{T}\left(\sqrt{s}, 1000 \ \text{GeV}, 4000\ \text{GeV} \right) = 10.99 $ fb, $ \sigma^{Z h_0}_{T} \left(\sqrt{s}, 1000 \ \text{GeV}, 5000\ \text{GeV} \right) = 7.02 $ fb, and $\sigma^{Z h_0}_{T}\left(\sqrt{s}, 1000 \ \text{GeV}, 6000\ \text{GeV} \right) = 4.87$ fb for $ m_{Z'} \approx 3500 $ GeV, $ m_{Z'} \approx 4300 $ GeV, and $ m_{Z'} \approx 5200 $ GeV, respectively. Note that in the context of the BLHM, the mass of the $ Z' $gauge boson depends on the scales of the new model physics, f and F. This analysis shows that total cross-section $ \sigma^{Z h_0}_{T}\left(\sqrt{s}, f, F \right) $ is sensitive to changes in the free parameters. Contributions from new physics show remarkable effects concerning the SM contribution; the region of most significant appreciation of such effects is for $ \sqrt{s}\in $ [800, 10000] GeV. Moreover, Fig. 5 has been generated by setting $ \tan\, \beta = 3 $. However, to study the possible dependence of the total cross-section on $ \tan\, \beta $, we consider another allowed parameter point, $ \tan\, \beta = 6 $. For this choice, we find that the generated curves are similar to those provided in Fig. 5. Thus, the dependence of the results on $ \tan\, \beta $ is null.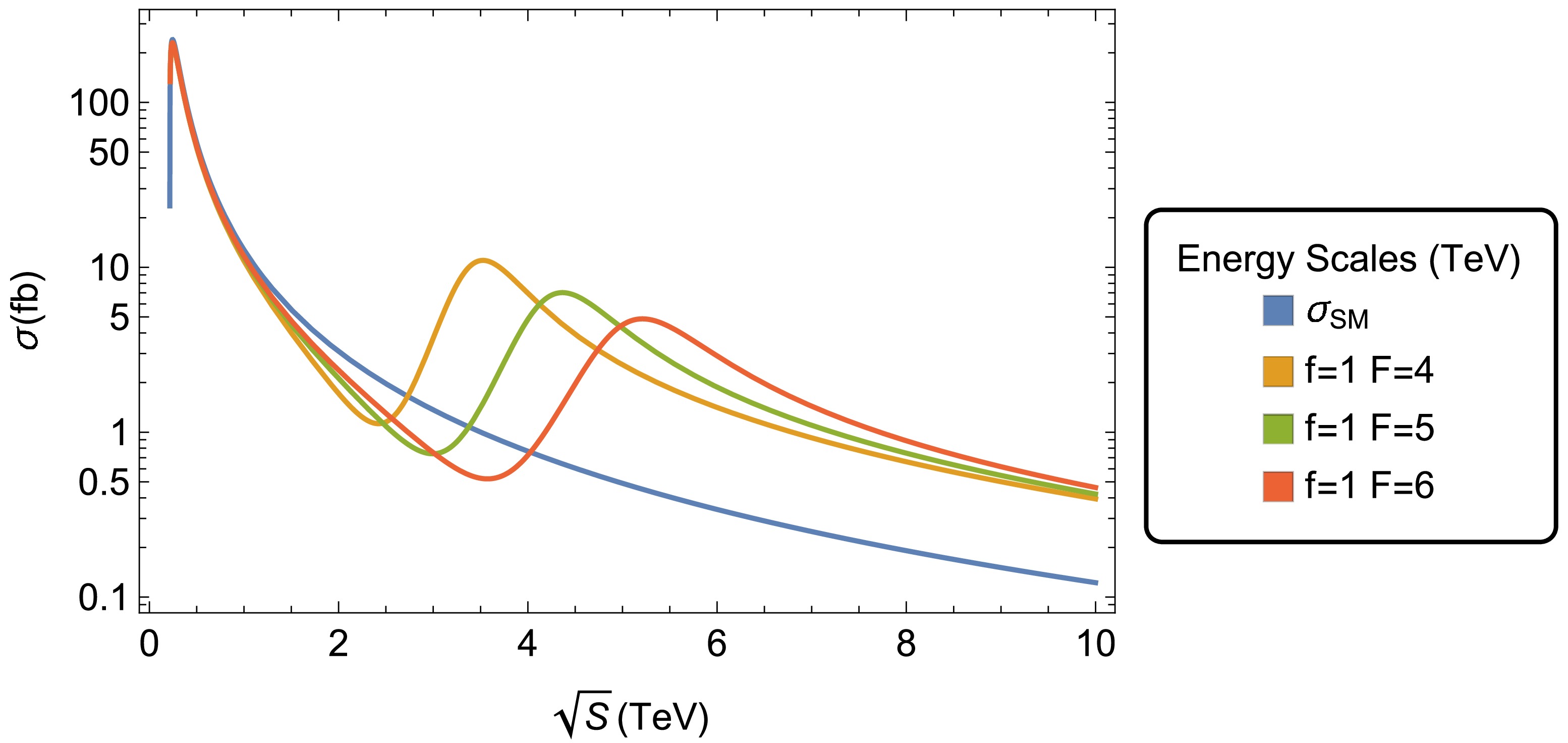

Figure 5.  (color online) Total cross-section of process $ \mu^{+}\mu^{-}\to $$ (Z, Z') \to Zh_0 $ as a function of $ \sqrt{s} $. The curves are generated for $f=1\,000$ GeV and $F=4\, 000$ GeV, $f=1\, 000$ GeV and $F=5\,000$ GeV, and $f=1\, 000$ GeV and $F=6\, 000$ GeV.

The BLHM can generate corrections to the production cross-section for process $ \mu^{+}\mu^{-} \to Zh_0 $ via modification of the tree-level $ Z Z h_0 $ coupling, as well as by new interaction vertex $ Z' Z h_0 $. The values of the relative corrections are calculated from Eq. (14). In Fig. 6, we show the relative corrections $\dfrac{\delta\sigma_{\rm BLHM}}{\sigma_{\rm SM}}$ of Higgs-strahlung process $ \mu^{+}\mu^{-} \to Zh_0 $ as a function of $ \sqrt{s} $ for $f = 1\,000$ GeV and $F = 4\, 000$ GeV, $f = 1\, 000$ GeV and $F = 5\,000$ GeV, and $f = 1\, 000$ GeV and $F = 6\, 000$ GeV. In this figure, the absolute value of the relative correction increases for smaller values of energy scale F and decouples at high scales of the $ \sqrt{s} $ parameter. The values of $|\dfrac{\delta\sigma_{\rm BLH}}{\sigma_{\rm SM}}|$ are in the ranges of 0%−10% in most of the parameter space. Our numerical results show that for reasonable values of the free parameters of the BLHM, $ \sqrt{s} $, f, and F, can generate significant contributions to the total cross-section of Higgs-strahlung process $ \mu^{+}\mu^{-} \to Zh_0 $ concerning their value in the context of the SM.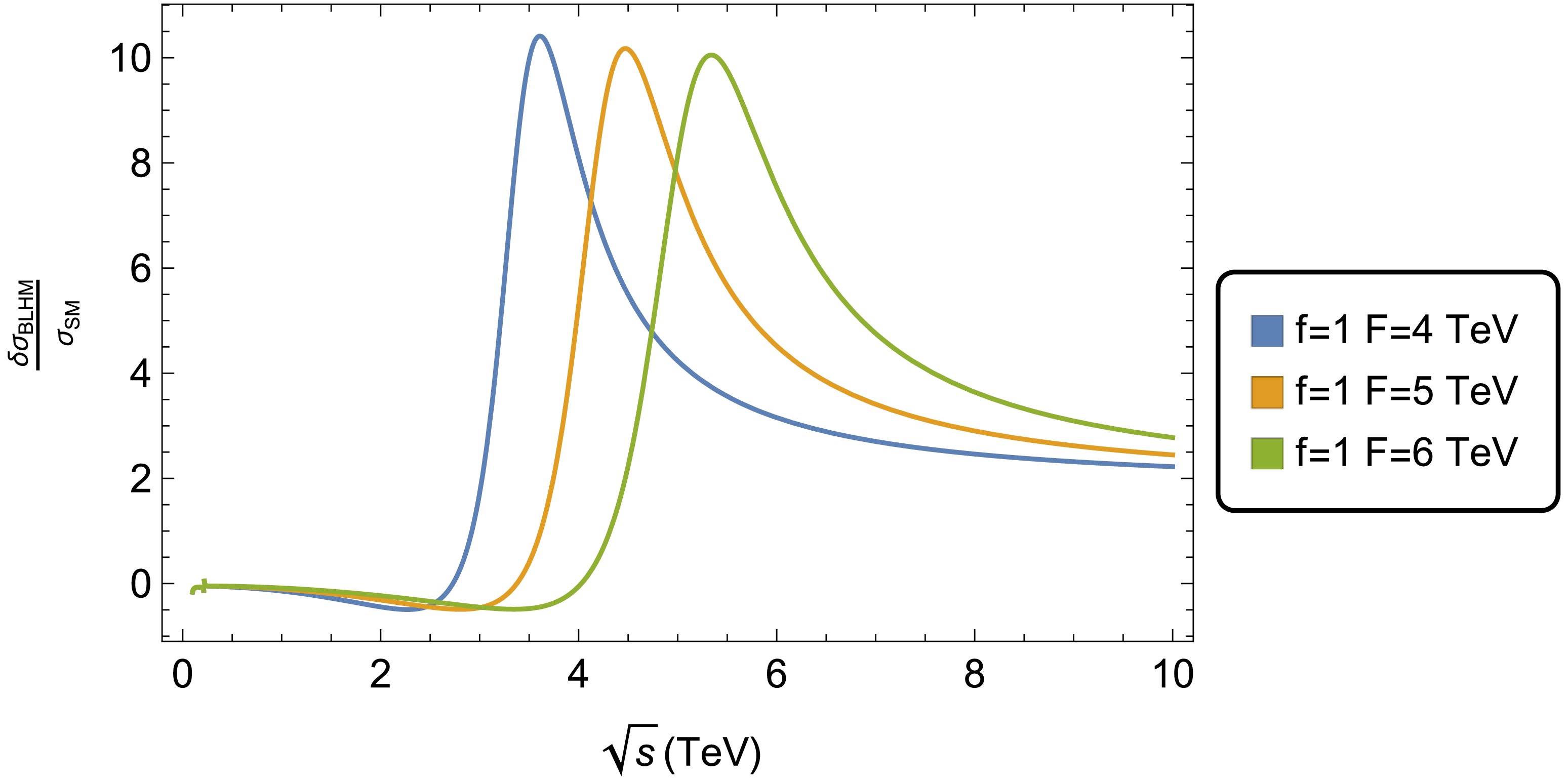

Figure 6.  (color online) Relative correction $\dfrac{\delta\sigma_{\rm BLHM}}{\sigma_{\rm SM}}$ as a function of center-of-mass energy $ \sqrt{s} $.

We also discuss the production of $ Z h_0 $ at the future muon collider, assuming design luminosities $ {\cal L} = $ 2, 4, 6, 10, 30 ab^–1 and center-of-mass energies, $ \sqrt{s} = $ 3, 4, 6, 10, 30 TeV [29, 42, 43]. In Tables 4 and 5 for $f = 1\, 000$ GeV and $F = 4\, 000$ GeV and $f = 1\, 000$ GeV and $F = 6\,000$ GeV, respectively, we present an event estimate of the production associated to $ Z h_0 $. According to the numerical results, around the resonance of the $ Z' $ gauge boson, the number of $ Z h_0 $events reaches high values. Generally, the possibility of being observed in process $ \mu^{+} \mu^{-} \to (Z, Z') \to Zh_0 $ is quite promising at the future muon collider.

$ \tan\, \beta=3 $
$f=1\, 000$ GeV, $F=4\, 000$ GeV
$ \sqrt{s} $/TeV	$ {\cal{L}} = 2 $ $\rm ab^{-1}$	$ {\cal{L}} = 4 $ $\rm ab^{-1}$	$ {\cal{L}} = 6 $ $\rm ab^{-1}$	$ {\cal{L}} = 10 $ $\rm ab^{-1}$	$ {\cal{L}} = 30 $ $\rm ab^{-1}$
3	7 405	14 810	22 215	37 026	111 079
4	13 882	27 764	41 646	69 410	208 231
6	2 822	5 645	8 468	14 113	42 341
10	787	1 575	2 363	3 938	11 861
30	79	158	237	396	1 188

Table 4.  Total production of $ Zh_0 $ at the future muon collider in the context of the BLHM when $ \tan \, \beta=3 $ with $f=1\, 000\ \text{GeV}$ and $\ F=4\,000\ \text{GeV}$ ($ m_{Z'}= 3 \, 500 $ GeV).

$ \tan\, \beta=3 $
$f=1\, 000$ GeV, $F=6\, 000$ GeV
$ \sqrt{s} $/TeV	$ {\cal{L}} = 2 $ $\rm ab^{-1}$	$ {\cal{L}} = 4 $ $\rm ab^{-1}$	$ {\cal{L}} = 6 $ $\rm ab^{-1}$	$ {\cal{L}} = 10 $ $\rm ab^{-1}$	$ {\cal{L}} = 30 $ $\rm ab^{-1}$
3	1 501	3 003	4 505	7 509	22 529
4	1 447	2 895	4 343	7 239	21 717
6	5 793	11 586	17 380	28 966	86 900
10	922	1 485	2 768	4 614	13 844
30	80	160	240	401	1 204

Table 5.  Total production of $ Zh_0 $ at the future muon collider in the context of the BLHM when $ \tan \, \beta=3 $ with $f=1\, 000\ \text{GeV}$ and $\ F=6\, 000\ \text{GeV}$ ($ m_{Z'}=5\ 200 $ GeV).

In this subsection, we present our results on the production cross-section of Higgs-strahlung process $ \mu^{+}\mu^{-}\to (Z, Z') \to ZH_0 $ and analyze the impact of the parameters of the BLHM on this process. From Fig. 1, we can observe that the total cross-section of the production process $ \mu^{+}\mu^{-} \to ZH_0 $ receives contributions from the Z and $ Z' $ gauge bosons and from the interference effects between them. Thus, cross-sections $ \sigma^{Z H_0}_{Z}\left(\mu^{+} \mu^{-} \to Z H_0 \right) $, $ \sigma^{Z H_0}_{Z'}\left(\mu^{+} \mu^{-} \to Z H_0 \right) $, and $ \sigma^{Z H_0}_{Z Z'}\left(\mu^{+} \mu^{-} \to Z H_0 \right) $ contribute to total cross-section $ \sigma^{Z H_0}_{T}\left(\mu^{+} \mu^{-} \to Z H_0 \right) $. These production cross-sections depend on the free parameters of the BLHM: f, F, and $ \sqrt{s} $. Thus, to analyze the effects of $ \sqrt{s} $ on $ \sigma^{Z H_0}_{i}\left(\mu^{+} \mu^{-} \to Z H_0 \right) $ with $ i = Z,Z',ZZ',T $, we generate the curves in Fig. 7 by setting the other input parameters to $f = 1\, 000$ GeV and $F = 6\, 000$ GeV. For these elections, new heavy gauge boson $ Z' $ obtains a mass of about $ 5\, 200 $ GeV. In this figure, we observe that the curves associated to $ \sigma^{Z H_0}_{Z'} $, $ \sigma^{Z H_0}_{ZZ'} $, and $ \sigma^{ZH_0}_{T} $ obtain large values around the resonance energy of the $ Z' $ boson; specifically, for the values of $ \sqrt{s}\approx 5\, 200, 5\, 600, 5\, 200 $ GeV generate $ \sigma^{ZH_0}_{Z'}\left(\mu^{+} \mu^{-} \to Z H_0 \right) = 1.60\times 10^{-3} $ fb, $ \sigma^{Z H_0}_{ZZ'}\left(\mu^{+} \mu^{-} \to Z H_0 \right) = 4.47\times 10^{-4} $ fb, and $ \sigma^{Z H_0}_{T}\left(\mu^{+} \mu^{-} \to Z H_0 \right) = 2.01\times 10^{-3} $ fb, respectively. Regarding the cross-section $ \sigma^{Z H_0}_{Z}\left(\mu^{+} \mu^{-} \to Z H_0 \right) $, it reaches the maximum when $ \sqrt{s}\approx 2\, 000 $ GeV; at this point, $ \sigma^{Z H_0}_{Z}\left(\mu^{+} \mu^{-} \to Z H_0 \right) = 5.84\times 10^{-4} $ fb. As discussed in Subsection IV C, in specific regions, the total cross-section of process $ \mu^+\mu^- \to (Z,Z') \to ZH_0 $ is smaller than the individual contributions. This is primarily owing to negative interference between channels $ \mu^+\mu^- \to Z \to ZH_0 $ and $ \mu^+\mu^- \to Z' \to ZH_0 $. This effect is further influenced by effective couplings $ g_{ZZ'H_0} $ and $ g_{ZZH_0} $ (see Table A2 in Appendix A).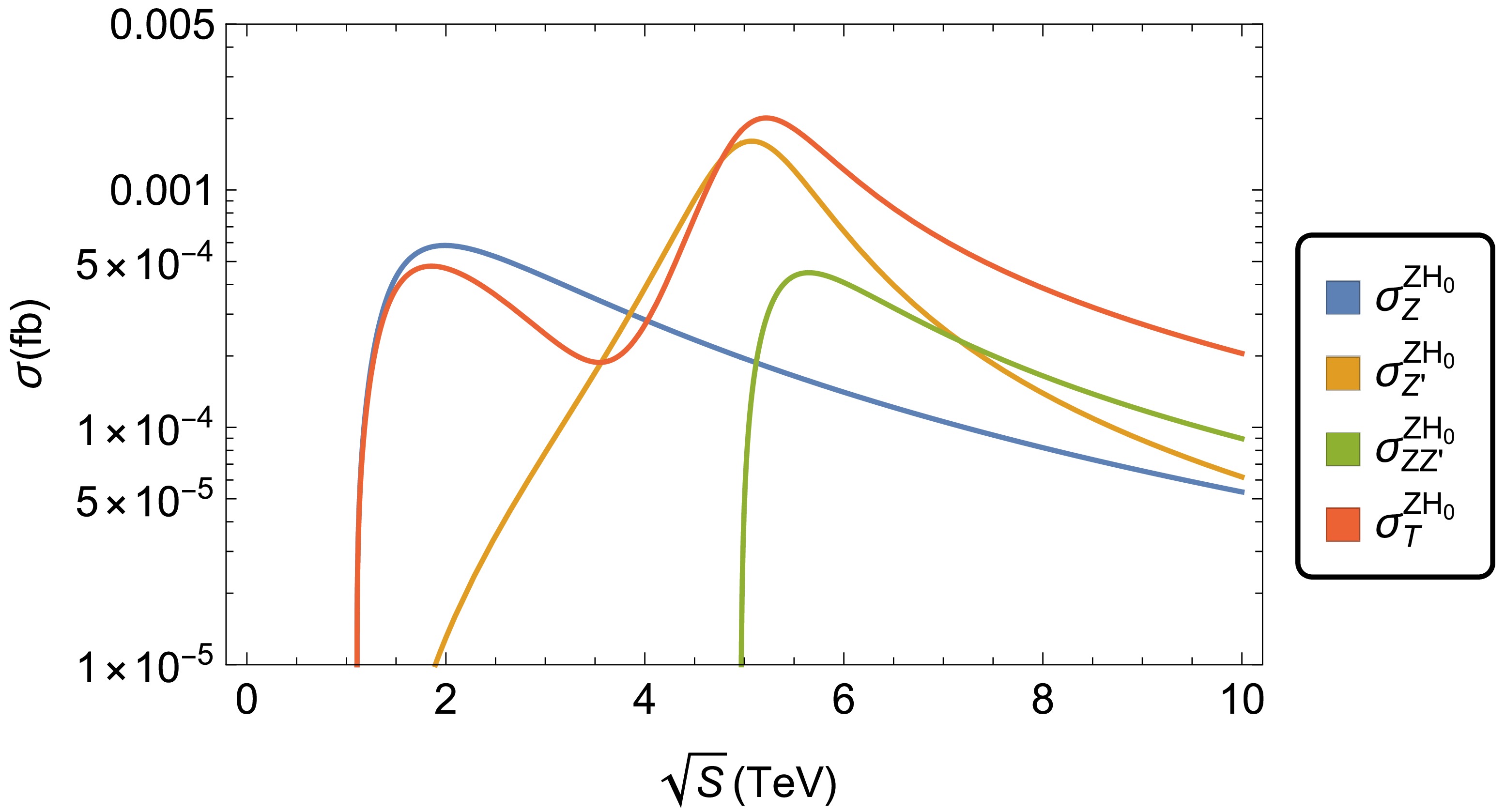

Figure 7.  (color online) Cross-section of process $ \mu^{+}\mu^{-}\to $$ (Z, Z') \to ZH_0 $ as a function of $ \sqrt{s} $. The curves are generated for $f = 1\, 000$ GeV and $F=6\, 000$ GeV (for $ m_{Z'} = 5\ 200 $ GeV) and correspond to $ \sigma^{Z H_0}_Z $ [Eq. (18)], $ \sigma^{Z H_0}_{Z'} $ [Eq. (19)], $ \sigma^{Z H_0}_{ZZ'} $ [Eq. (20)], and $ \sigma^{Z H_0}_{T} $ [Eq. (17)].

In Figs. 8 and 9, we also analyze the dependence of the production cross-section of process $ \mu^{+}\mu^{-} \to ZH_0 $ on $ \tan\, \beta $. These figures have been generated considering the parameter points, $ \tan\, \beta = 3 $ and $ \tan\, \beta = 6 $, respectively. For these cases, the total cross-section is a function of $ \sqrt{s} $, whereas the energy scales, f and F, have fixed values: $ f = 1 000 $ GeV and $ F = 4 000 $ GeV, $ f = 1 000 $ GeV and $ F = 5 000 $ GeV, and $ f = 1 000 $ GeV and $ F = 6 000 $ GeV. Regarding Fig. 8, a slight increase in total cross-section $ \sigma^{Z H_0}_{T}\left( \mu^{+}\mu^{-} \to ZH_0 \right) $is observed for small values of the F scale, whereas for large values of center-of-mass energy $ \sqrt{s} $, $ \sigma^{Z H_0}_{T}\left( \mu^{+}\mu^{-} \to ZH_0 \right) $ becomes smaller. For the plotted curves, resonant effects dominate, i.e., the maximum peaks of each curve are reached at the resonance of the $ Z' $ gauge boson: $ \sigma^{Z H_0}_{T}\left(\sqrt{s},1\, 000\ \text{GeV}, 4\, 000\ \text{GeV} \right) = 3.93 \times 10^{-3} $ fb, $ \sigma^{Z H_0}_{T}\left(\sqrt{s},1\, 000\ \text{GeV}, 5\, 000\ \text{GeV} \right) = 2.72 \times 10^{-3} $ fb, and $ \sigma^{Z H_0}_{T}\left(\sqrt{s},1\, 000\ \text{GeV}, 6\, 000\ \text{GeV} \right) = 2.01 \times 10^{-3} $ fb for the corresponding energies, $ \sqrt{s} \approx 3\, 500,\, 4\, 300,\, 5\, 200 $ GeV. With respect to Fig. 9, obtained for $ \tan\, \beta = 6 $, we can appreciate that the height of the maximum peaks of each curve is reached, again, at the resonance of the $ Z' $ gauge boson: $ \sigma^{Z H_0}_{T}\left(\sqrt{s},1\, 000\ \text{GeV}, 4\, 000\ \text{GeV} \right) = 1.82 \times 10^{-2} $ fb, $ \sigma^{Z H_0}_{T}\left(\sqrt{s},1\, 000\ \text{GeV}, 5\, 000\ \text{GeV} \right) = 1.29 \times 10^{-2} $ fb, and $ \sigma^{Z H_0}_{T}\left(\sqrt{s},1\, 000\ \text{GeV}, 6\, 000\ \text{GeV} \right) = 9.46 \times 10^{-3} $ fb when $ \sqrt{s} \approx 3\, 500,\, 4\, 300,\, 5\, 200 $ GeV, respectively. For this case, the height of the maximum peaks of the plotted curves is higher than the maximum peaks reached when $ \tan\, \beta = 3 $. This occurs because $ m_{H_0} $, a parameter involved in the calculation of total cross-section $ \sigma^{Z H_0}_{T}\left( \mu^{+}\mu^{-} \to ZH_0 \right) $, has a dependence on parameter β (see Eq. (22)). In the BLHM scenario, the fine-tuning measurement depends on the f energy scale. As discussed earlier, for values of f close to 1000 GeV, the absence of the fine-tuning prevails in the model. Therefore, our plots have been generated for $ f = 1\, 000 $ GeV while allowing the other free parameters to vary.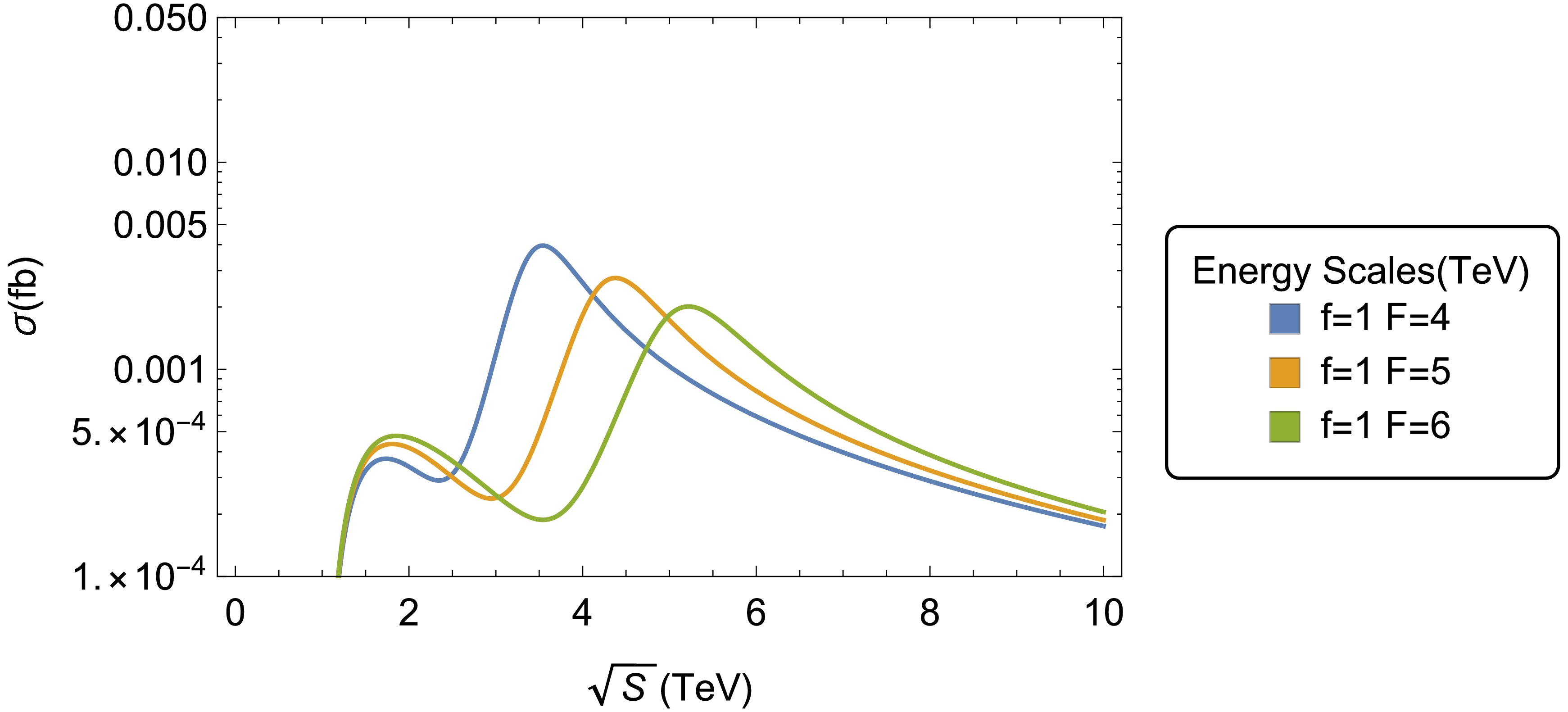

Figure 8.  (color online) Total cross-section of process $ \mu^{+}\mu^{-}\to $$ (Z, Z') \to ZH_0 $ as a function of $ \sqrt{s} $. The curves are generated for $f=1\, 000$ GeV and $F=4\, 000$ GeV, $f=1\, 000$ GeV and $F=5\, 000$ GeV, and $f=1\, 000$ GeV and $F=6\, 000$ GeV. In each case, $ \tan\, \beta=3 $ and $m_{H_{0}} \approx 1\,015\ \text{GeV}$ have been considered.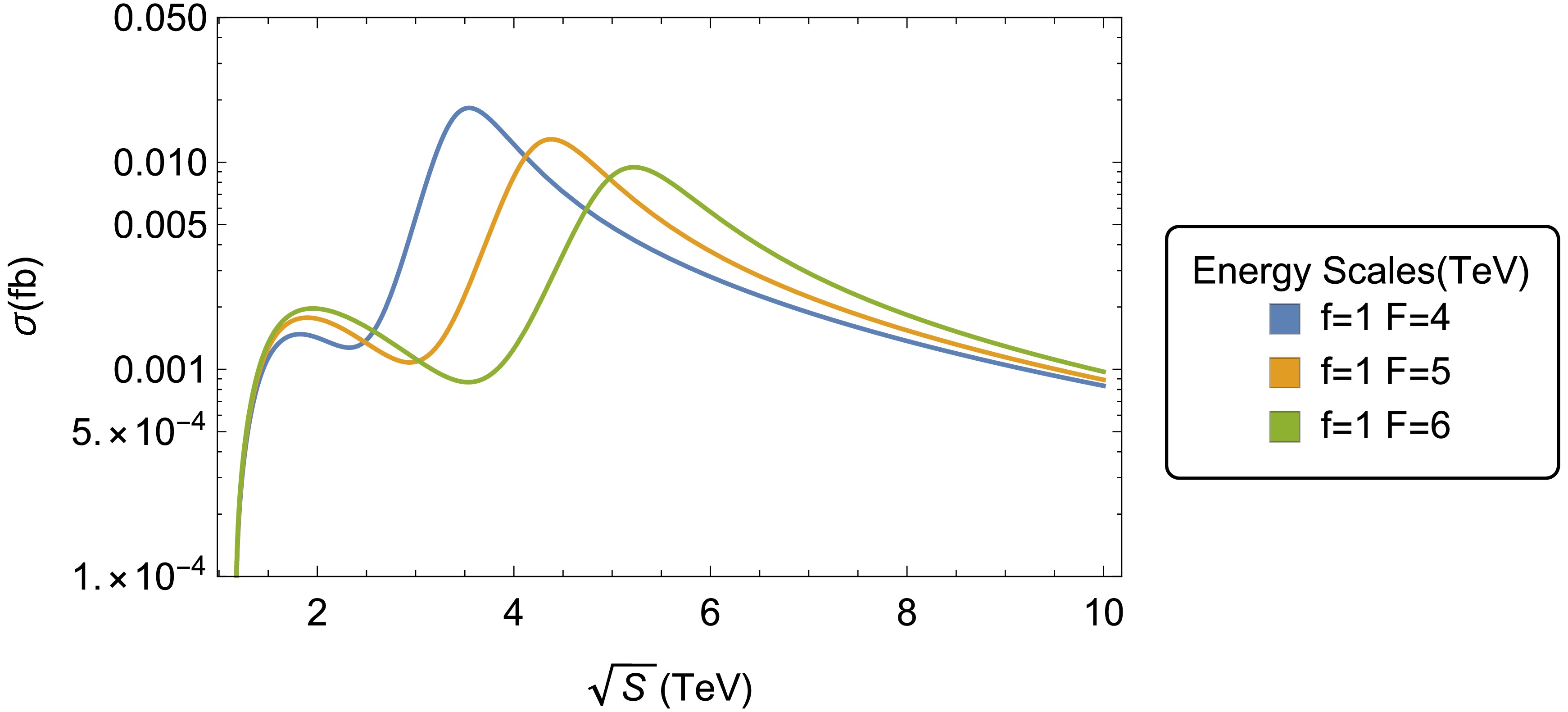

Figure 9.  (color online) Total cross-section of process $ \mu^{+}\mu^{-}\to $$ (Z, Z') \to ZH_0 $ as a function of $ \sqrt{s} $. The curves are generated for $f=1\,000$ GeV and $F=4\,000$ GeV, $f=1\, 000$ GeV and $F=5\, 000$ GeV, and $f=1\, 000$ GeV and $F=6\, 000$ GeV. In each case, $ \tan\, \beta=6 $ and $m_{H_{0}} \approx 1\,076\ \text{GeV}$ have been considered.

As part of our study, and as an indicator of the possible number of $ Z H_0 $ events to be produced in a future muon collider, we consider again center-of-mass energies $ \sqrt{s} = 3, 4, 6, 10, 30 $ TeV and integrated luminosities $ {\cal L} = 2, 4, 6, 10, 30 $ $ {\rm{ab}}^{-1} $ [29, 42, 43]. For the two scenarios discussed above, $ \tan \, \beta = 3 $ and $ \tan \, \beta = 6 $, Tables 6−9 list the numbers of $ Z H_0 $ events arising when $f = 1\,000$ GeV and $F = 4\, 000$ GeV, and $f = 1\, 000$ GeV and $F = 6\, 000$ GeV. According to our numerical data, the possibility of performing measurements for the $ Z' $ gauge boson and heavy Higgs boson $ H_0 $ at the future high-energy muon collider is modest. For these cases of interest, resonant effects dominate over nonresonant effects. Thus, total cross-section $ \sigma^{Z H_0}_{T}\left( \mu^{+}\mu^{-} \to ZH_0 \right) $ reaches its maximum value at the resonance of heavy gauge boson $ Z' $.

$ \tan\, \beta=3 $
$f=1\, 000$ GeV, $F=4\, 000$ GeV
$ \sqrt{s} $ /TeV	$ {\cal{L}} = 2 $ $\rm ab^{-1}$	$ {\cal{L}} = 4 $ $\rm ab^{-1}$	$ {\cal{L}} = 6 $ $\rm ab^{-1}$	$ {\cal{L}} = 10 $ $\rm ab^{-1}$	$ {\cal{L}} = 30 $ $\rm ab^{-1}$
3	2	4	7	11	35
4	5	10	15	26	78
6	1	2	3	5	17
10	1	1	1	2	5
30	1	1	1	1	1

Table 6.  Total production of $ ZH_0 $ at the future muon collider in the context of the BLHM when $ \tan \, \beta=3 $ with $f=1\,000\ \text{GeV}$ and $\ F=4\, 000\ \text{GeV}$ ($ m_{Z'}=3\, 500 $ GeV).

$ \tan\, \beta=3 $
$f=1\, 000$ GeV, $F=6\, 000$ GeV
$ \sqrt{s} $/TeV	$ {\cal{L}} = 2 $ $\rm ab^{-1}$	$ {\cal{L}} = 4 $ $\rm ab^{-1}$	$ {\cal{L}} = 6 $ $\rm ab^{-1}$	$ {\cal{L}} = 10 $ $\rm ab^{-1}$	$ {\cal{L}} = 30 $ $\rm ab^{-1}$
3	1	1	1	2	7
4	1	1	1	2	8
6	2	4	7	12	36
10	1	1	2	2	6
30	1	1	1	1	1

Table 7.  Total production of $ ZH_0 $ at the future muon collider in the context of the BLHM when $ \tan \, \beta=3 $ with $f=1\, 000\ \text{GeV}$ and $\ F=6\, 000\ \text{GeV}$ ($ m_{Z'}=5\, 200 $ GeV).

$ \tan\, \beta=6 $
$f=1\, 000$ GeV, $F=4\, 000$ GeV
$ \sqrt{s} $/TeV	$ {\cal{L}} = 2 $ $\rm ab^{-1}$	$ {\cal{L}} = 4 $ $\rm ab^{-1}$	$ {\cal{L}} = 6 $ $\rm ab^{-1}$	$ {\cal{L}} = 10 $ $\rm ab^{-1}$	$ {\cal{L}} = 30 $ $\rm ab^{-1}$
3	10	21	32	53	161
4	24	48	72	121	364
6	5	11	16	27	83
10	1	3	4	8	24
30	1	1	1	1	2

Table 8.  Total production of $ ZH_0 $ at the future muon collider in the context of the BLHM when $ \tan \, \beta=6 $ with $f=1\,000\ \text{GeV}$ and $\ F=4\,000\ \text{GeV}$ ($ m_{Z'}=3\, 500 $ GeV).

$ \tan\, \beta=6 $
$f=1\, 000$ GeV, $F=6\, 000$ GeV
$ \sqrt{s} $/TeV	$ {\cal{L}} = 2 $ $\rm ab^{-1}$	$ {\cal{L}} = 4 $ $\rm ab^{-1}$	$ {\cal{L}} = 6 $ $\rm ab^{-1}$	$ {\cal{L}} = 10 $ $\rm ab^{-1}$	$ {\cal{L}} = 30 $ $\rm ab^{-1}$
3	2	4	6	11	33
4	2	5	7	12	37
6	11	22	34	57	172
10	1	3	5	9	29
30	1	1	1	1	2

Table 9.  Total production of $ ZH_0 $ at the future muon collider in the context of the BLHM when $ \tan \, \beta=6 $ with $f=1\, 000\ \text{GeV}$ and $\ F=6\, 000\ \text{GeV}$ ($ m_{Z'}=5\, 200 $ GeV).

We also include an analysis of the final signal and SM background for each of the processes studied $ \mu^{+}\mu^{-} \to Zh_0 $ and $ \mu^{+}\mu^{-} \to ZH_0 $. Specifically, we provide the total cross-section and corresponding number of events when considering the most important SM background of processes $ \mu^{+}\mu^{-} \to Zh_0 $ and $ \mu^{+}\mu^{-} \to ZH_0 $. The background of the processes studied in our article are described below.

Because the Higgs boson’s decay rate to $ b\bar b $ is greater than the decay rate to other quarks and leptons, the $ b\bar b $ decay mode of Higgs $ (h_0 \to b\bar b) $ is considered. Because the cross-sections of the background processes corresponding to the leptonic decays of the Z boson are less than the background cross-sections corresponding to the other decays, the leptonic decays of the Z boson in the Higgs-strahlung process are considered. The signal process of interest is $ \mu^{+}\mu^{-} \to Zh_0 \to l^+l^- b\bar b $ ($ l^{-} = e^{-}, \mu^{-} $) with background processes $ \mu^{+}\mu^{-} \to ZZ, Z\gamma, \gamma\gamma $.

For the analysis, we start from the narrow-width approximation, which is a useful method of simplifying the calculation of complicated processes. Therefore, we apply this method to determine the total cross-section of the $ \sigma \bigl(\mu^{+}\mu^{-} \to Zh_0 \to l^+l^- b\bar b) $ signal:

An SM Higgs boson of mass 125 GeV has a 60% branching ratio to the final state $ b\bar b $, $ \text{Br}(h_0 \to b\bar b) = $ 60% [32]. Therefore, the representative cross-sections for the dominant background of the $ Zh_0 $ final state at the future muon collider are shown in Table 10.

Background cross-section /fb
$ {\rm{Process}} $	$ \sqrt{s}=3 $ TeV	$ \sqrt{s}=4 $ TeV	$ \sqrt{s}=6 $ TeV	$ \sqrt{s}=10 $ TeV	$ \sqrt{s}=30 $ TeV
$ \mu^+\mu^- \to ZZ $	10.65	14.20	21.31	35.52	106.54

Table 10.  Representative cross-sections for the background of the $ Zh_0 $ final state at the future muon collider for the center-of-mass energies of $ \sqrt{s}=3, 4, 6, 10, 30 $ TeV.

In Table 11, we present the number of events for the $ \mu^{+}\mu^{-} \to Zh_0 \to l^+l^- b\bar b $ signal and consider the dominant background. Furthermore, the $ l^+l^- b\bar b $ process can be mimicked by diboson production at the future muon collider with sizable rates (see Table 10). Thus, more complete results on the total production in the number of events are presented below in Table 11.

$ \tan\, \beta=3 $
$ f=1 000 $ GeV, $ F=4 000 $ GeV
$ \sqrt{s} $/TeV	$ {\cal{L}} = 2 $ $\rm ab^{-1}$	$ {\cal{L}} = 4 $ $\rm ab^{-1}$	$ {\cal{L}} = 6 $ $\rm ab^{-1}$	$ {\cal{L}} = 10 $ $\rm ab^{-1}$	$ {\cal{L}} = 30 $ $\rm ab^{-1}$
3	1 119	2 238	3 358	5 597	16 792
4	1 648	3 297	4 946	8 244	24 738
6	1 772	3 544	5 316	8 861	26 583
10	2 801	5 602	8 403	14 006	42 020
30	8 313	16 626	24 939	41 566	124 698

Table 11.  Total production of $ \mu^{+}\mu^{-} \to (Z, Z') \to Zh_0 \to l^+l^- b\bar b $ and dominant background $ ZZ $ at the future muon collider in the context of the BLHM when $ \tan \, \beta=3 $ with $ f=1 000\ \text{GeV} $ and $ \ F=4000\ \text{GeV} $ ($ m_{Z'}= 3 \, 500 $ GeV).

For the Higgs-strahlung process, $ \mu^{+}\mu^{-} \to ZH_0 $ (with the heavy Higgs boson $ H_0 $ predicted by the BLHM). For the final state with $ W^\pm $ bosons, the signal process is $ \mu^{+}\mu^{-} \to ZH_0 \to l^+l^- W^+W^- $ with background processes $ \mu^{+}\mu^{-} \to W^{+}W^{-}Z, W^{+}W^{-} \gamma $. In this case, we must evaluate the branching ratio for the $ H_0 \to X $ process ($ X \equiv t\bar t, WW, ZZ, h_0h_0, gg,\gamma\gamma, \gamma Z $) to analyze the final signal and SM background. Therefore, in Fig. 10, we present the $ \text{Br}(H_0\to X) $ vs. $ m_{H_0} $ plot when $ f = 1000 $ GeV and $ \tan\beta = 3 $. This figure shows that the subdominant channel of the heavy Higgs boson decay is to a pair of $ W^\pm $-bosons, followed by pairs of Z-bosons, etc.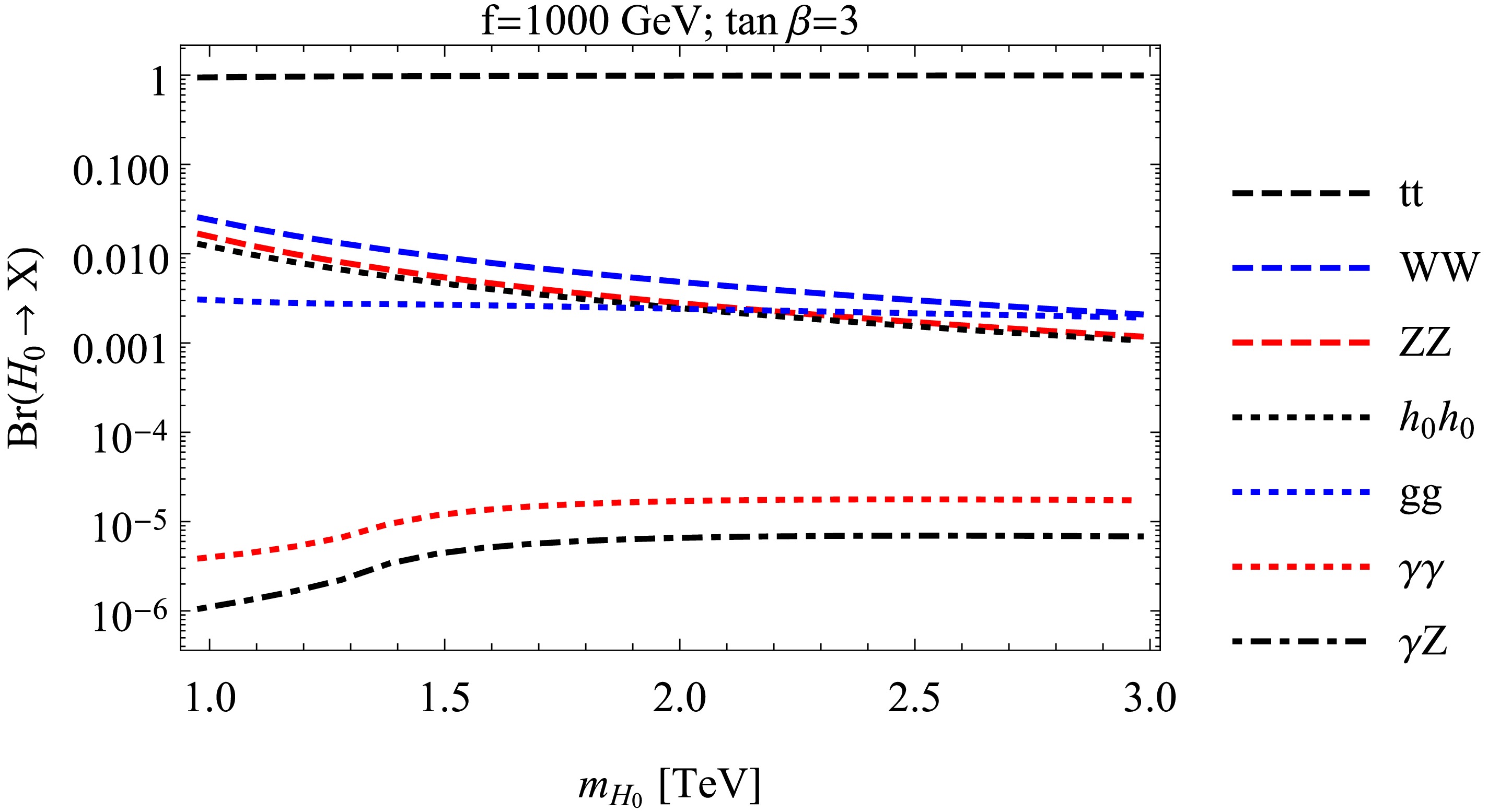

Figure 10.  (color online) Branching ratio for the $ H_0\to X $ process as a function of the $ m_{H_0} $ parameter, where $ X \equiv $ $ t\bar{t} $, $ WW $, $ ZZ $, $ h_0h_0 $, $ gg $, $ \gamma\gamma $, $ \gamma Z $.

With these elements, we apply the narrow-width approximation to determine the total cross-section of the $ \mu^{+}\mu^{-} \to ZH_0 \to l^+l^- W^+W^- $ signal:

As an illustration, we consider only the most important background for process $ \mu^{+}\mu^{-} \to ZH_0 \to l^+l^- W^+W^- $. Remember (see Fig. 10) that the heavy Higgs boson subdominantly decays into pairs of $ W^\pm $-bosons. Therefore, the cross-sections of the most important background of the $ \mu^{+}\mu^{-} \to ZH_0 \to l^+l^- W^+W^- $ signal is shown in Table 12.

Background cross-section /fb
Process	$ \sqrt{s}=3 $ TeV	$ \sqrt{s}=4 $ TeV	$ \sqrt{s}=6 $ TeV	$ \sqrt{s}=10 $ TeV	$ \sqrt{s}=30 $ TeV
$ \mu^+\mu^- \to WWZ $	31	41.3	62	103.3	310

Table 12.  Representative cross-sections for the background of the $ ZH_0 $ final state at the future muon collider for the center-of-mass energies of $ \sqrt{s}=3, 4, 6, 10, 30 $ TeV.

The total production in the number of events is presented in Table 13 for $ \sqrt{s} = 3 000, 10 000 $ GeV and $ {\cal{L}} = 3, 4, 6, 10, 30 $ $ {\rm{ab}}^{-1} $. In addition, we consider the leptonic, semi-leptonic, and hadronic channels of the $ W^\pm $ for the signal. Thus, we assume that the branching ratios for $ W^\pm $ decays are $ \text{Br}(W^\pm \to qq') = 0.454 $ for hadronic decays, $ \text{Br}(W^\pm \to qq'; W^\pm \to l\nu_{e, \mu}) = 0.143 $ for semi-leptonic decays, and $ \text{Br}(W^\pm \to l\nu_{e, \mu}) = 0.045 $ for light leptonic decays [32].

$ \tan\, \beta=3 $
${\cal L} \, ( { \rm{ab} }^{-1})$	$ \sqrt{s}=3 000 $ GeV, $ f=1 000 $ GeV, $ F=4 000 $ GeV
	Leptonic channel	Semi-leptonic channel	Hadronic channel
3	167	532	1 688
4	335	1 064	3 377
6	502	1 596	5 066
10	837	2 660	8 442
30	2 511	7 979	25 333
${\cal L} \, ( { \rm{ab} }^{-1})$	$ \sqrt{s} = 10 000 $ GeV, $ f=1 000 $ GeV, $ F=4 000 $ GeV
	Leptonic channel	Semi-leptonic channel	Hadronic channel
3	558	1 772	5 628
4	1 115	3 545	11 255
6	1 673	5 318	16 883
10	2 789	8 863	28 139
30	8 367	26 589	84 417

Table 13.  Total production of $ \mu^{+}\mu^{-} \to (Z, Z') \to ZH_0 \to l^+l^- W^+W^- $ and dominant background $ WWZ $ at the future muon collider in the context of the BLHM when $ \tan \, \beta=3 $ with $ f=1 000\ \text{GeV} $ and $ \ F=4000\ \text{GeV} $ ($ m_{Z'}= 3 \, 500 $ GeV). The leptonic, semi-leptonic, and hadronic channels of the $ W^\pm W^\mp $ in the final state are considered.

In this study, we analyze the $ Z' $ boson of the BLHM as a portal to signatures of Higgs bosons $ h_0 $ and $ H_0 $ through Higgs-strahlung production processes $ \mu^+\mu^- \to (Z,Z') \to Zh_0, ZH_0 $, including both the resonant and nonresonant effects. The new $ Z' $ boson is a hypothetical massive particle of spin 1 that is also predicted in other extensions of the SM and has been the subject of extensive phenomenological studies in recent years [44]. Experimentally, the $ Z' $ gauge boson will be searched at the LHC [32]. In the context of the BLHM, Higgs-strahlung productions $ \mu^+\mu^- \to Zh_0, ZH_0 $ are essential processes to study tree-level interactions: $ Z'Z h_0 $, $ Z'Z H_0 $, $ Z Z h_0 $, and $ Z Z H_0 $. Additionally, the mentioned processes are useful for testing the consistency of the current parameter space of the BLHM. For example, through Higgs-strahlung process $ \mu^+\mu^- \to Z \to Zh_0 $, we have found that it reproduces the SM predictions very well when the new physics scales, f and F, have large values (see Fig. 4). For this case, the effective couplings $ g^{\text{BLHM}}_{ZZh_0} \approx g^{\text{SM}}_{ZZh_0} $.

To study Higgs-strahlung process $ \mu^+\mu^- \to (Z,Z') \to Zh_0 $, we consider the BLHM contributions generated through the $ Z'Z h_0 $ and $ ZZ h_0 $ couplings. We find that the relative correction of total cross-section $ \sigma^{Z h_0}_{T} (\mu^+\mu^- \to Zh_0 ) $ from its SM prediction can vary from 0% to 10%, which result primarily from the modifications of the $ Z Z h_0 $ coupling, and also from the contribution induced through the $ Z'Z h_0 $ interaction vertex. Our numerical data show that for reasonable values of the free parameters of the BLHM, it can generate significant contributions to $ \sigma^{Z h_0}_{T} \left(\mu^+\mu^- \to Zh_0 \right) $. In most of the parameter space, the relative corrections values are positive and decoupled at high scales from the $ \sqrt{s} $ parameter.

In the BLHM, we explore the phenomenological implications of the production cross-section of processes $ \mu^+\mu^- \to Zh_0, ZH_0 $. In our analysis, we find cross-sections $ \sigma^{Z h_0}_{T} \left(\mu^+\mu^- \to Zh_0 \right) $ and $ \sigma^{Z H_0}_{T} \left(\mu^+\mu^- \to Z H_0 \right) $ reach large values at the resonance of heavy gauge boson $ Z' $ when $ \sqrt{s} = m_{Z'} $. $ \sigma^{Z h_0}_{T} \left(\mu^+\mu^- \to Zh_0 \right) $ and $ \sigma^{Z H_0}_{T} \left(\mu^+\mu^- \to Z H_0 \right) $ are also sensitive to variations in the F parameter, and the height of the resonance peaks for the $ Z' $ boson changes depending on the F scale values. Thus, cross-sections $ \sigma^{Z h_0}_{T} \left(\mu^+\mu^- \to Zh_0 \right) $ and $ \sigma^{Z H_0}_{T} \left(\mu^+\mu^- \to Z H_0 \right) $ obtain large values when F has small values. Another input parameter involved in our cross-section calculations is the f scale, which is set to 1000 GeV to ensure the absence of fine-tuning in our phenomenological predictions.

To estimate the production of Higgs bosons $ h_0 $ and $ H_0 $ at the future muon collider, we use the energies and design luminosities of the muon collider with the center-of-mass energies of $ \sqrt{s} = 3, 4, 6, 10, 30 $ TeV and integrated luminosities of $ {\cal L} = 2, 4, 6, 10, 30 $ $ {\rm{ab}}^{-1} $ [29, 42, 43]. We can observe from Tables 4−9 that the total number of expected events for $ Z h_0 $ and $ ZH_0 $ at a future muon collider increase at the resonance energy of the $ Z' $ boson. Our results show a very optimistic scenario for producing Higgs bosons $ h_0 $ and bosons Z in the future muon experiment. Regarding the production of Higgs bosons $ H_0 $ and bosons Z, these show a more conservative scenario.

Note that in our study, we have incorporated the final signal and SM background corresponding to processes $ \mu^+\mu^- \to Zh_0 \to l^{+} l^{-}b \bar{b} $ and $ \mu^+\mu^- \to ZH_0 \to l^{+} l^{-} W^{+} W^{-} $, respectively. Our results for the main background and total number of events are shown in Tables 10−13. These tables show that the incorporation of the final signal and SM background has an impact on the sensitivity of the processes. Particularly, for process $ \mu^+\mu^- \to ZH_0 \to l^{+} l^{-} W^{+} W^{-} $ (see Table 13), a significant improvement in the signal is expected.

Finally, studying the resonances is an excellent place to search for new physics. Hence, our results may be useful to the scientific community and complement other studies performed in extended models. The predictions presented in this work can be relevant for the community to prioritize future searches and experimental efforts.

J. M. Martínez-Martínez is a scholarship fellow of CONAHCyT. E. Cruz-Albaro appreciates the postdoctoral stay at the Universidad Autónoma de Zacatecas. A.G.R. and M.A.H.R. thank SNII and PROFEXCE (México).

Data Availability Statement: All data generated or analyzed during this study are included in this article.

In this Appendix, we provide the Feynman rules for the interaction vertices involved in the calculation of the Higgs-strahlung production processes $ \mu^+\mu^- \to Zh_0, ZH_0 $.