-
The existence of loosely bound states near the charm threshold, first envisaged in Ref. [1], seems to be confirmed now by the wealth of evidence concerning the
$ X(3782) $ state with a binding energy$ B_X = M_D+ M_{\bar D^*} -$ $M_X = 0.00(18) $ MeV [2], which has triggered a proliferation of the so-called X, Y, Z states (for reviews see e.g. [3, 4]). In the absence of electroweak interactions, this state has the smallest known hadronic binding energy. However, since it is unstable, all detection methods of$ X(3872) $ are based on looking at the decay channel spectra, such as$ X\to J/\psi\pi^+\pi^- $ , where the mass resolution does not exceed$ \Delta m \sim 1-2 $ MeV [5–8] (see e.g. [9] for a pictorial display of the experimental resolution). Therefore, it is in principle unclear if the mass of$ X(3872) $ can be determined with such a precision, or equivalently its binding energy if$ \Delta B_X \ll \Delta m $ , since we cannot distinguish clearly the initial state.In most analyses (see however [10]), the bound state nature is assumed rather than deduced. In fact, the molecular interpretation has attracted considerable attention, since for a loosely bound state many properties are mainly determined by its binding energy [4], and characterized by the line shape in the production processes [11]. However, we have noticed recently a clear and accurate cancellation between the would-be X(3872) bound state and the
$ D \bar D^* $ continuum, which has a sizable impact on the occupation number at finite temperature [12, 13]. This reduction stems from a cancellation of the density of states in the$ 1^{++} $ channel, and potentially blurs any detected signal where a superposition of$ 1^{++} $ states is at work. Such a situation leads to the question of the actual character of this state raised in the present letter. We proceed by analyzing the$ p_T $ distribution of$ X(3872) $ in high energy experiments and by folding the expected distribution with the actual mass distribution, corresponding to the$ 1^{++} $ spectrum, via the level density and with the achievable experimental resolution. For our argument, a qualitative and quantitative comparison with a true weakly bound state, such as the deuteron d, is most enlightening. As a matter of fact, the similarities between d and$ X(3872) $ have been inspiring [14–16]. Compared to$ X(3872) $ , the main difference is that the deuteron is detected directly by analyzing its well defined tracks and/or its stopping power. Actually, the production of loosely bound nuclei and anti-nuclei, including$d, \bar d $ ,$ ^3{\rm He}_\Lambda $ , etc. in ultra-high energy pp collisions, is a remarkable and surprising experimental result obtained in recent years [17], and so far poorly understood [18].The cancellation echoes a similar effect in the deuteron pointed out by Dashen and Kane in their discussion of the counting of states in the hadron spectrum in the coarse grained sense [19], which we review in some detail in the next section. In Section 3, we analyze the consequences in a production process. Finally, we draw our conclusions in Section 4, and provide an outlook for future work.
-
In order to illustrate the Dashen-Kane mechanism [19], we introduce the cumulative number of states with invariant CM mass
$ \sqrt{s} $ below M in a given channel with fixed$ J^{PC} $ quantum numbers. This involves the$ J^{PC} $ spectrum, which contains bound states and continuum states with threshold$ M_{\rm th} $ , and is given as$ N(M) = \displaystyle\sum\limits_i \theta(M-M_i^B) + \frac1\pi \sum\limits_{\alpha = 1}^{n} [\delta_\alpha (M)-\delta_\alpha (M_{\rm th})] \, , $

(1) where the index i runs over the
$ M_i^B $ bound states, and$ \alpha $ over the n coupled channels. Here, we have explicitly separated the bound states$ M_n^B $ from the scattering states written in terms of the eigenvalues of the S-matrix, i.e.$ S = U {\rm Diag} ({\rm e}^{2{\rm i}\delta_1}, \dots, {\rm e}^{2{\rm i}\delta_n} ) U^\dagger $ , with U a unitary transformation for n-coupled channels, and$ \delta_i(M) $ the eigenphase shift for channel i and CM invariant mass$ \sqrt{s} = M $ . This definition fulfills$ N(0) = 0 $ . In the case of a single channel and in the limit of high masses$ M \to\infty $ , one gets$ N(\infty) = n_B + \frac1{\pi} [\delta(\infty)-\delta(M_{\rm th})] = 0 $ due to Levinson's theorem. While the origin of the bound state term is quite obvious, the derivation of the continuum term is a bit more subtle but still standard, and can be found in many textbooks on statistical mechanics dealing with the quantum virial expansion (see e.g. [20, 21]). For potential scattering, it can be best deduced by confining the system in a large spherical box, which quantizes the energy and relates the energy shift due to the interaction to the phase shift, and then letting the volume of the system increase to infinity [19].In the particular case of the deuteron, which is a neutron-proton
$ 1^{++} $ state bound by$ B_d = 2.2 \;{\rm MeV} $ , the cancellation between the continuum and discrete parts of the spectrum was pointed out by Dashen and Kane long ago [19]. (see also [22, 23] for an explicit picture and further discussion within the resonance-gas model). The opening of new channels and the impact of the confining interactions was discussed in Ref. [24]. In the$ 1^{++} $ channel, the presence of the tensor force implies coupling between the$ ^3S_1 $ and$ ^3D_1 $ channels. While the partial wave analysis of the NN scattering data and the determination of the corresponding phase shifts is a well known subject [25], we note that a similar analysis of the$ D \bar D^* $ case is at present in its infancy. In our first model in Refs. [12, 13], the mixing has an influence for energies larger than considered here. Therefore, in order to illustrate how the cancellation comes about, we consider a simple model which works sufficiently well for the deuteron and$ X(3872) $ just by considering the contact (Gaussian) interaction [26] in the$ ^3S_1 $ -channel and using the effective range parameters to determine the corresponding phase shift in the d and$ X(3872) $ channels [12, 27].The result for
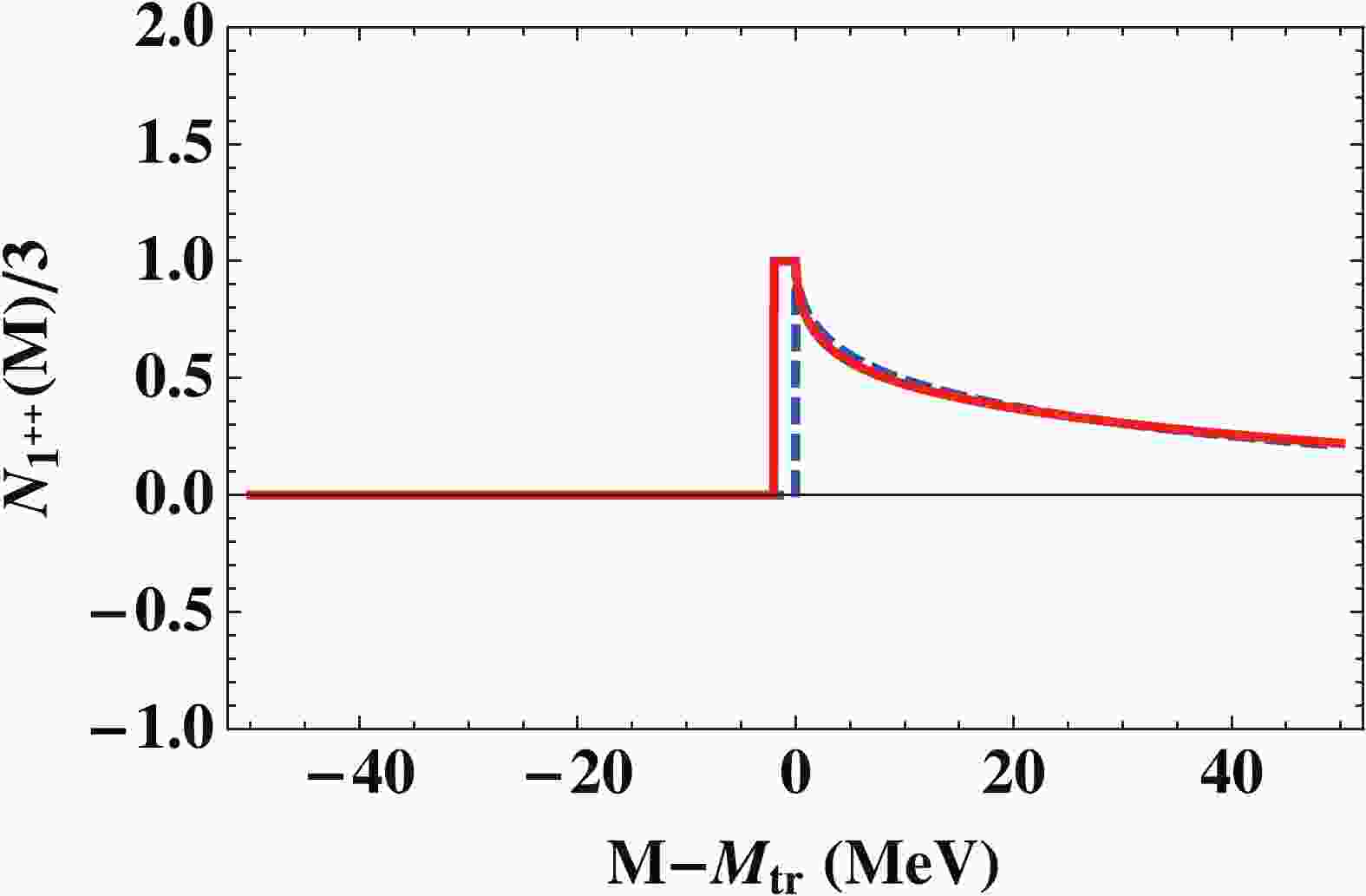
$ N(M) $ in the case of d and X is depicted in Fig. 1 , and exhibits a similar pattern for the$ np $ or$ D\bar D^* $ invariant masses. The sharp rise of the cumulative number is followed by a strong decrease generated by the phase shift. For larger invariant masses M, several effects appear, and in particular the nuclear core (see e.g. [23]) or the composite nature of$ X(3872) $ and its$ c \bar c $ content become manifest (see eg. [28]).
Figure 1. (color online) The cumulative number of states N(M) in the
$1^{++}$ channel for the deuteron (solid) and$X(3872)$ (dashed) as a function of the invariant mass M, with respect to the np and$D \bar D^{*}$ values, respectively. We divide N(M) by the spin degeneracy.An immediate consequence of this effect follows trivially from Eq. (1) for an observable depending on the invariant mass function
$ O(M) $ . The corresponding measured quantity in a bin$ (m-\Delta m/2 , m+\Delta m/2) $ becomes$ O_{\Delta m} \equiv \int_{m-\Delta m/2}^{m+\Delta m/2} {\rm d}M \rho(M) O (M) \, , $

(2) where
$ \rho(M) $ is the density of states, defined as$ \rho(M) = \frac{{\rm d} N(M)}{{\rm d}M} = \sum\limits_i \delta(M-M_i^B) + \frac1\pi \sum\limits_{\alpha = 1}^{n} \delta'_\alpha (M) \, , $

(3) where
$ \delta'_\alpha(M) $ denotes the derivative of the phase shift with respect to the mass.In the case of a single channel with phase shift
$ \delta_\alpha (M) $ , and if the resolution is much larger than the binding energy$ \Delta m \gg |B| \equiv |M_B-M_{\rm tr}| $ , one has$ O|_{M^B \pm \Delta m} = O(M^B) + \frac1\pi \int_{M_{\rm tr}}^{M_{\rm tr}+\Delta m/2} {\rm d}M \delta_\alpha ' (M) O(M)\, , $

(4) which, in view of Fig. 1 and for a smooth observable
$ O(M) $ , points to the cancellation, anticipated by Dashen and Kane [24]. The effect was explicitly seen in the$ np $ virial coefficient at astrophysical temperatures$ T \sim 1-10 $ MeV [29]. We have recently shown [12] how this cancellation can likewise be triggered for the$ X(3872) $ occupation number at quark-gluon crossover temperatures$ T \sim 100-200 $ MeV. This will be relevant in relativistic heavy ion collisions when the X-production yields are measured, because the partition function involves a Boltzmann factor$ \sim e^{-\sqrt{p^2+m^2}/T} $ in the density of states. Eq. (3) and the measured yields reproduce remarkably the predicted occupation numbers in the hadron resonance gas model [30].Therefore, given these tantalizing similarities, a comparative study of the deuteron and
$ X(3872) $ production rates at ultra-high energies in colliders provides a suitable calibration tool for the Dashen-Kane cancellation, which is due to the finite resolution$ \Delta m $ of the detectors measuring the$ X(3872) $ state via its decay products, and which hence allows to conclude on its bound state character. Here, we propose to study the effect on the observed transverse momentum ($ p_T $ ) distributions. -
While the theory behind the shape of the transverse momentum distribution is not fully developed (see e.g. Ref. [31] for an early review, and Ref. [32] for a historical presentation), we rest with a phenomenological ansatz which describes the data. On the one hand, the asymptotic
$ p_T $ -spectrum [33] provides a production rate proportional to$ 1/p_T^8 $ , based on the quark-quark scattering. Hagedorn realized that an interpolation between the power correction and the thermal Boltzmann$ p_T $ -distribution could work [34]. A thermodynamic interpretation of the rapidity distribution in non-extensive systems [35] was proposed by Tsallis [36], and first applied to high energy phenomena in Refs. [37, 38], giving the differential occupation number as$ \frac{{\rm d}^3 N}{{\rm d}^3 p} = \frac{g V}{(2\pi)^3}\left(1+(q-1)\frac{E(p)}{T}\right)^{-\frac{q}{q-1}} \xrightarrow{q\to 1} \frac{g V}{(2\pi)^3} e^{-\frac{E(p)}{T}} $

(5) where
$ E(p) = \sqrt{p^2+m^2} $ , V is the volume of the system, T the temperature and g the degrees of freedom. As indicated, this relation reduces in the limit$ q \to 1 $ to the Boltzmann distribution. We use here the form obtained by the maximum Tsallis entropy principle [39].The invariant differential production rate,
${\rm d}^3N/ ({\rm d}^2 p_T $ ${\rm d}y) \equiv E_p {\rm d}^3 N /{\rm d}^3 p $ , with the rapidity$ y = \tanh^{-1}(E_p/p_z) $ , exhibits asymptotic matching corresponding to$ q = 1.25 $ [40]. While the thermodynamic interpretation is essential to link the degrees of freedom g with the production rate [41], we note that we have checked in [42] that the Tsallis distribution describes accurately the results of the Monte Carlo particle generators such as PYTHIA [43, 44]. This distribution was also applied recently by the ALICE collaboration to the d-production in pp collisions [45].We show next that the prompt production cross-sections of
$ X(3872) $ ,$ \Psi(2S) $ and the deuteron can be described with the same Tsallis distribution:$ \frac1{2\pi p_T} \frac{{\rm d}\sigma (m)}{{\rm d}p_T} = {\cal N}\int {\rm d}y\,\, E(p_T,y) \left[1+ \frac{q-1}{T}E(p_T,y)\right]^{\frac{q}{1-q}} $

(6) with
$ E(p_T,y) = \sqrt{p_T^2+m^2} \cosh y $ , and$ {\cal N} $ a normalization factor. Obviously, a direct comparison requires similar$ p_T $ values for d,$ \Psi(2S) $ and$ X(3872) $ ; the closest come from ALICE [45] and CMS [46, 47]. The ATLAS data for$ X(3872) $ [48] confirm a power law behavior of$ p_T $ , but extend over a much wider range than the available data for d , and hence are not used in this study. The deuteron data are given by the invariant differential yields$ {\rm d}^2N/(2\pi p_T{\rm d}p_T{\rm d}y) $ . Hence, the inelastic$ pp $ cross-section at$ \sqrt{s} = 7 $ TeV,$ \sigma_{\rm inel}^{pp} = 73.2\pm1.3 $ mb, as measured by TOTEM [49] , was used to transform it into the differential cross-section.On a phenomenological level, we perform two fits: one including the d and
$ X(3872) $ data, and the other by adding the$ \Psi(2S) $ data. In both cases,$ {\cal N}_{d,X,[\Psi]} $ , q and T are fitted by minimizing the corresponding$ \chi^2 $ function with Minuit [50]. The experimental error of the x-axis is included in the$ \chi^2 $ via a Monte Carlo procedure with$ 5000 $ runs, where the$ p_T $ value of each experimental point is randomly shifted within the experimental range with a uniform distribution. Due to the scarcity of X data, we assume that the production rate is mainly driven by the deuteron. In this way, an initial minimization of q, T and$ {\cal N}_d $ is performed, and the resulting best-fit values for q and T are employed to fix$ {\cal N}_X $ and$ {\cal N}_{\Psi} $ .The results can be found in Table 1, and the final production fit in Fig. 2 , for the two fits considered, one for
$ X(3872) $ and the deuteron, and the other for$ X(3872) $ ,$ \Psi(2S) $ and the deuteron. As expected, they are compatible, since the production ratio of X to$ \Psi(2S) $ measured by CMS is almost constant [47]. The$ X/d $ production ratio is$ 0.046^{+0.016}_{-0.013} $ for the$ X+d $ fit (and practically the same for the X+$ \Psi $ +d fit), dependent on the branching fraction. Note that we do not show a pure cross-section for X, as it is multiplied by the unmeasured branching fraction, which was recently constrained in an analysis of the BESIII data by C. Li et al [51] to$ {\cal B}_X\equiv{\cal B}(X\to J/\psi\pi^+\pi^-) =$ $ 4.5^{+2.3}_{-1.2} $ %. This value is consistent with the PDG lower-$ {\cal B}_X> $ 3.2% [52] - and upper bound$ {\cal B}_X< $ 6.6% at 90% C.L. [53]. The uncertainty comes from the most recent value of${\cal B}_X\cdot(B^-\to K^- $ $ X(3872))< 2.6\times 10^{-4} $ at 90% C.L. [54]. We note that in a recent paper, Esposito et al. [55] consider a wider range$ 8.1^{+1.9}_{-3.1} $ %.$X(3872)+d$ 

$X(3872)+\Psi(2S)+d$ 

$\ln({\cal N}_X{\cal B}_X)$ 

$41.4\pm0.4$ 

$41.4\pm0.4$ 

$\ln({\cal N}_d)$ 

$40.35\pm0.09$ 

$40.35\pm0.09$ 

$\ln({\cal N}_{\Psi})$ 

− $44.3\pm0.2$ 

$q$ 

$1.122\pm0.001$ 

$1.122\pm0.001$ 

T [MeV] $7.017\pm0.07$ 

$7.018\pm0.07$ 

$N_d$ 

$(2.02\pm0.02)\cdot 10^{-4}$ 

$(2.01\pm0.02)\cdot 10^{-4}$ 

$N_X{\cal B}_X$ 

$(9\pm 3)\cdot 10^{-6}$ 

$(9\pm3)\cdot 10^{-6}$ 

$N_{\Psi}$ 

− $(2.2\pm0.3)\cdot 10^{-4}$ 

$\langle p_T \rangle_d$ 

$1.102\pm0.007$ 

$1.102\pm0.007$ 

$\langle p_T \rangle_X$ 

$2.249\pm0.015$ 

$2.249\pm0.015$ 

$\langle p_T \rangle_{\Psi}$ 

$2.142\pm0.014$ 

$2.142\pm0.014$ 

$N_X{\cal B}_X/N_d$ 

$0.046^{+0.016}_{-0.013}$ 

$0.046^{+0.015}_{-0.013}$ 

$N_{\Psi}/N_d$ 

− $1.09^{+0.16}_{-0.17}$ 

Table 1. Best fit of the parameters of the Tsallis distribution. The X data from CMS [47] are multiplied by the branching fraction
${\cal B}_X\equiv{\cal B}(X\to J/\psi\pi^+\pi^-) $ . The correlation between q and T is practically$-1$ ($r=-0.9992$ ).
Figure 2. (color online) Comparison between the prompt production cross-section of
$X(3872)$ (blue), the deuteron (green) and$\Psi(2S)$ (red) in pp collisions. The$\Psi(2S)$ data are from CMS [46]. The$X(3872)$ data from CMS [47] are multiplied by the branching fraction${\cal B}(X\to J/\psi\pi\pi)$ . The deuteron data are taken from ALICE [45]. The lines are the Tsallis distributions fitted to each data set, with the same q and T parameters. The shadowed bands represent the statistical 68% confidence level (CL) obtained from the fits.Consequently, we can study the ratio of the occupation numbers for X and d as a function of the branching fraction
$ {\cal B}_X $ . The results are shown in Fig. 3. Considering the error bars, the experimental constraints give ratios between$ 0.3 $ and$ 1.9 $ for$ N_X /N_d $ .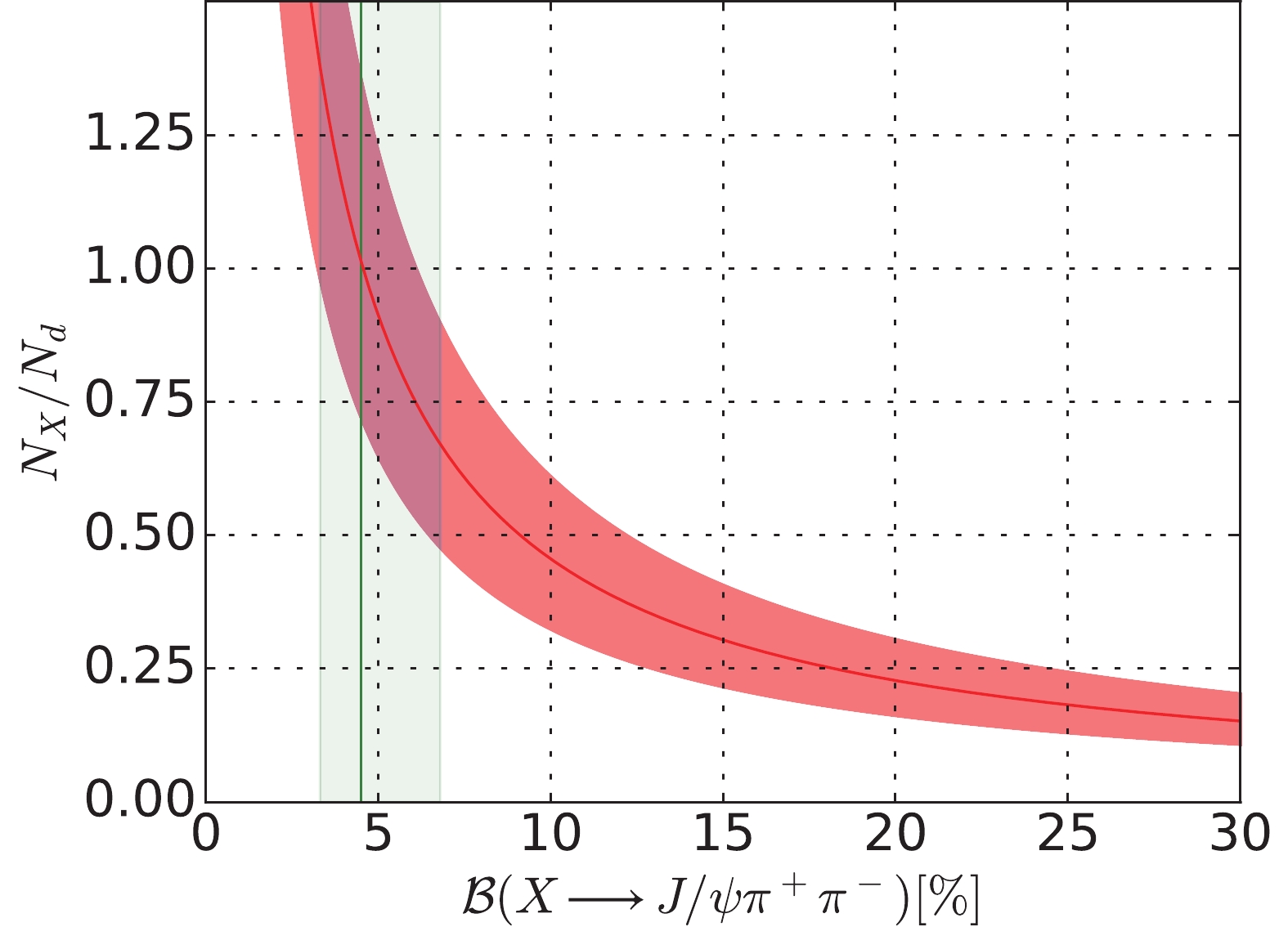
Figure 3. (color online) The ratio of the prompt production of
$X(3872)$ and the deuteron as a function of the branching fraction${\cal B}(X\to J/\psi\pi^+\pi^-)$ , fitted to the$X(3872)$ ,$\Psi(2S)$ and deuteron data. The shadowed band represents the statistical 68% confidence level (CL) obtained from the fit. The green band shows the constraints from the recent analysis of C. Li et al of the BESIII data [51]$ {\cal B}_X\equiv{\cal B}(X\to J/\psi\pi^+\pi^-)=4.5^{+2.3}_{-1.2}$ .In our fits above, we did not take into account the role of the finite resolution of the detectors
$ \Delta m $ , which we dicuss next. In Ref. [47], a$ \pm 2\sigma $ window around the$ X(3872) $ mass, with$ \sigma = 5-6 $ MeV, was used to select the$ X(3872) $ events in the$ J/\psi\pi\pi $ invariant mass spectrum. This means that the branching fraction$ {\cal B}(X\to J/\psi\pi^+\pi^-) $ , as measured by CMS, is averaged in the$ \left[M_X-2\sigma,M_X+2\sigma\right] $ energy window, which includes the continuum. As a consequence of this window, many decays can be affected, including those involving the$ \bar D^0D^{0\,*} $ channel.In fact, the distribution obtained from Eq. (5) depends on the mass, and hence its observed value satisfies Eq. (4), reflecting the finite resolution. Similarly to the case of finite temperature [12], we have checked that the Tsallis
$ p_T $ -shape is basically preserved for$ p_T \gg \Delta m $ , but the occupation number is modified for$ \Delta m \gg B $ .For definiteness, we use
$ \Delta m = 2\sigma $ , as CMS measured$ X(3872) $ in a$ \pm2\sigma $ region around the central value of the X mass. The net effect is summarized in a ratio, which we find to be practically independent of the transverse momentum$ p_T $ for the Tsallis distribution,$ \frac{\sigma_{m = M_X \pm \Delta m }}{\sigma_{M_X}} \sim \frac{{\cal N}_{\Delta m}}{{\cal N}_X} \, . $

(7) This formula allows to set the relative occupation numbers due to the finite resolution. We take
$ M_X = M_D + M_{\bar D^*} - \gamma_{X}^2/(2 \mu_{D , \bar D^*}) $ as a parameter by looking at the poles of the$ D \bar D^* $ S-matrix in the$ ^3S_1-^3D_1 $ channel [12]. Therefore, while in the limit$ \Delta m \to 0 $ we should expect the ratio$ N_X/N_d \to 1 $ ,$ 1/2 $ or$ 0 $ for a bound ($ \gamma_X > 0 $ ), half-bound ($ \gamma_X = 0 $ ) or unbound (actually virtual,$ \gamma_X < 0 $ ) state, for a finite and increasing$ \Delta m $ the ratio lies somewhat in between, and different situations can be hardly distinguished. However, as seen in Fig. 4 , the numerical value$ N_{\Delta m} /N_X \sim 0.5-0.6 $ is rather stable in a reasonable range of$ B_X $ and$ \sigma $ . If we reinterpret$ N_X $ as$ N_{X,\Delta m} $ , it falls remarkably in the center of Fig. 3 , where$ N_{X,\Delta m}/N_d \sim 0.5 $ implies$ N_{X}/N_d \sim 1 $ . Thus, contrary to expectations, we do not find that the production rate changes dramatically due to the binding energy effects related to$ \Delta m $ ; likewise, the$ p_T $ shape does not depend on this parameter (unlike the expectation in Ref. [55]). In a recent and insightful paper, Kang and Oller analyzed the character of$ X(3872) $ in terms of the bound and virtual states with simple analytical parametrization [10]. While the Dashen-Kane cancellation has not been explicitly identified, it would be interesting to see if the trends can be reproduced by a more microscopic approach.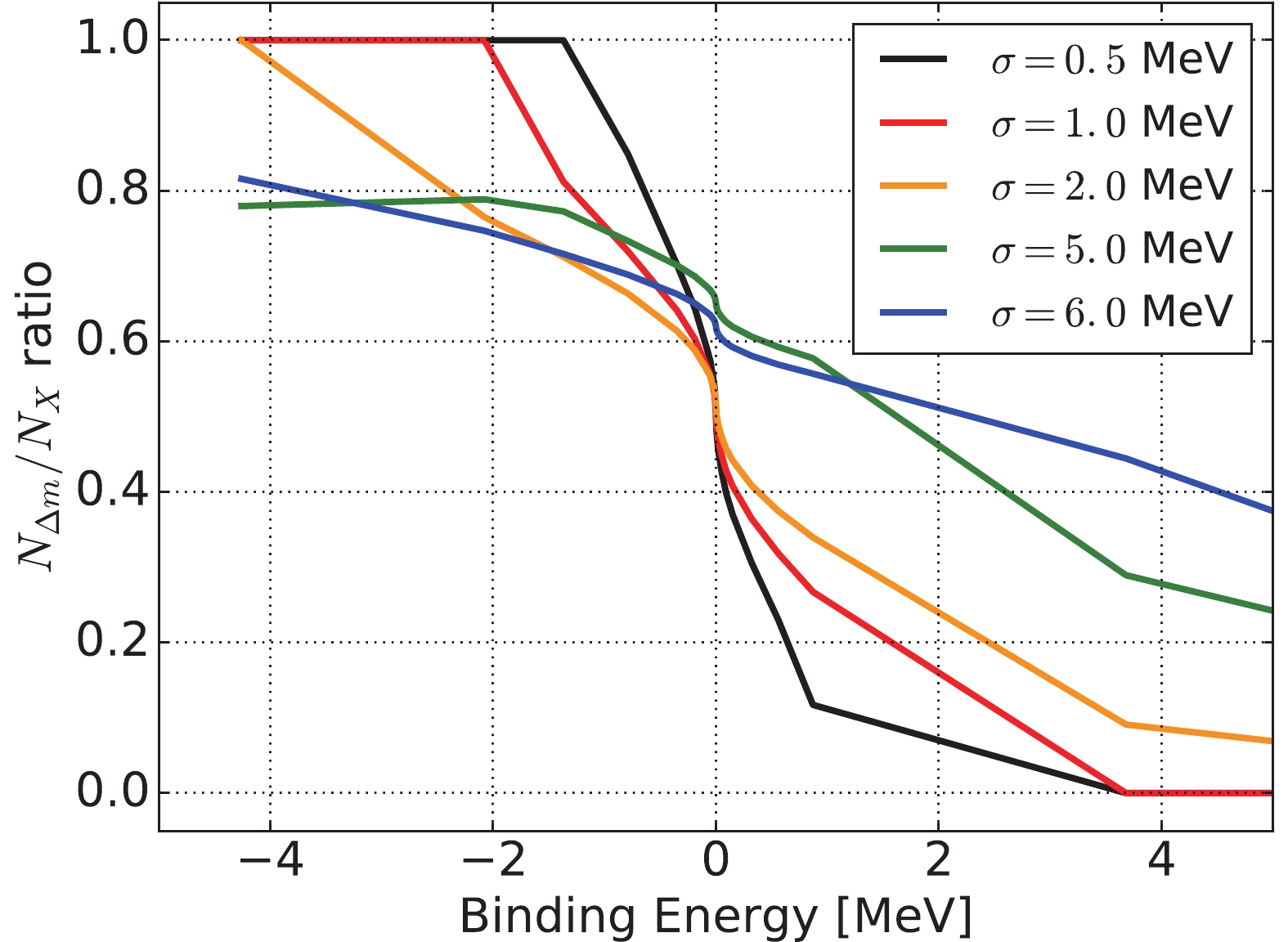
Figure 4. (color online) The relative occupation number with and without the finite resolution
$\Delta m= 2 \sigma$ as a function of the$X(3872)$ binding energy. Using$M_X = M_D + M_{\bar D^*} - $ $\gamma_{X}^2/(2 \mu_{D , \bar D^*})$ , we take the positive branch for the virtual state ($\gamma_X > 0$ ), and the negative branch for the bound state ($\gamma_X < 0$ ), for different$\sigma$ values. -
Theoretically, it is appealing to consider the scenario where
$ X(3872) $ is a half-bound state (zero binding energy) corresponding to the so-called unitarity limit, characterized by scale invariance [56]. In this case, the phase shift becomes$ \delta = \pi/2 $ around the threshold, and the occupation number is half of that of the bound state. Our analysis shows that the large production rate of$ X(3872) $ for finite$ p_T $ does not depend strongly on the details of the binding, since the experimental bin size is much larger than the binding energy. We also found striking and universal shape similarities with the$ \psi(2S) $ and deuteron production data, via a common Tsallis distribution. A more direct check of our predicted mild suppression could be undertaken if the production data were within the same$ p_T $ range. Finally, we note that in order to identify a clear fingerprint of the binding character of$ X(3872) $ , a substantial improvement of the experimental resolution for its decay products is required.One of us (E.R.A.) would like to thank Airton Deppman for discussions on Tsallis distributions.
Is X(3872) a bound state?
- Received Date: 2019-07-17
- Accepted Date: 2019-09-20
- Available Online: 2019-12-01
Abstract: All existing experimental evidence for the bound state nature of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: