-
Quantum phase transition (QPT) implies an abrupt change in the ground state properties of a system under study when a control parameter reaches a critical value [1-3]. In nuclear physics, usually, a complete chain of isotopes is studied to observe systematic variations and, eventually, abrupt changes in the ground state properties [4], where the neutron number is the control parameter. Typically, QPTs are found in transitional regions, where the structure of nuclei evolves in between two different limiting structures (symmetries), either spherical and rigidly deformed, spherical and gamma unstable, or gamma unstable and rigidly deformed. The appearance of a QPT implies, and consequently has been characterized by, peculiar changes in certain observables. Some of these observables are as follows:
● The slope of the two-neutron separation energy presents a discontinuity.
● There is a minimum in the excitation energy of certain states such as the
$ 0_2^+ $ state and an increase in the density of states.● There is a sudden decrease in the excitation energy of certain states, such as the
$ 2_1^+ $ state.● There is a rapid increase in B(E2:
$ 2_1^+\rightarrow 0_1^+ $ ), among other transition probabilities.● There is a rapid increase in the
$ 2_1^+ $ quadrupole moment.For nuclei placed at the critical point, Iachello introduced the concept of critical point symmetry [5-7], which provides parameter-free values of energy ratios and transition probabilities.
Although shape coexistence is a broad phenomenon that appears almost ubiquitously in the nuclear mass table, it is observed particularly near the proton or neutron shell closures [8, 9]. It supposes the presence of states with very different shapes or deformations, for instance vibrational-like and deformed, in a narrow excitation energy range. The existence of different configurations is associated with particle-hole (np-nh) excitations across the shell closure. Typically, vibrational-like states correspond to 0p-0h excitations, whereas the deformed states are associated with 2p-2h excitations. It may be pointed out that the shape of a given state is not an observable although it is an extensively used concept; it can be extracted from the Kumar-Cline sum rule over E2 matrix elements [10, 11]. The presence of shape coexistence has significant impact on the spectroscopic properties of a chain of nuclei.
● There is a family of states, with clear parabolic-like excitation energy systematics centered at the midshell when depicted as a function of the neutron (proton) number.
● The crossing of states belonging to different families implies sudden changes in the deformation of the states. These crosses lie before and after the midshell.
● There is a decrease in the energy of a number of
$ 0^+ $ states. In general, several$ 0^+ $ states correspond to very low energies.● When both families of states cross in the ground state, an abrupt change in the deformation, with consequences for the systematics of the two-neutron separation energy, quadrupole moment, or B(E2:
$ 2_1^+\rightarrow 0_1^+ $ ) values is experiencedAccording to the above list, QPT and shape coexistence exhibit similar systematics. In many cases, it is not easy to identify which of these two is responsible for the rapid onset of deformation. Therefore, this study is focused on investigating the two-neutron transfer intensity as an observable displaying distinct behaviors under the presence of a QPT, shape coexistence, and QPT induced by shape coexistence. This approach to explore the existence of QPTs was first used in Ref. [12], later in [13], and more recently in [14]. Moreover, the two-neutron transfer intensity has been used to analyze the possible interplay between QPT and shape coexistence in [15, 16], which indicated that some differences exist when comparing a schematic QPT with a schematic shape coexistence situation. The two-neutron transfer intensity is significantly more fragmented for QPT than for shape coexistence, although rapid changes appear in this observable in both cases. In this study, we will explore a set of realistic calculations in detail.
Several regions of the atomic mass table are of significant interest. The Zr region is characterized by rapid changes in the ground state structure. In particular, the onset of deformation when passing from
$ ^{98} $ Zr to$ ^{100} $ Zr is one of the fastest ever observed in the nuclear chart. It has been determined both experimentally and theoretically that certain excited states of Zr isotopes have shapes different than the ground state [17]. This change is associated with low-lying intruder configurations. In the Pb region, the evolution of the structure of the ground state is significantly stable, but the spectra own states with different shapes, i.e., shape coexistence is present, as in Pb, Hg, and Pt nuclei [9]. However, in the rare-earth region, the changes in the structure of the ground state have been associated with QPT [18], for instance in the Sm isotope chain [19].Although the onset of a QPT and the importance of shape coexistence for the aforementioned isotopes have been studied in detail in many publications, we present the partial spectra of Hg, Pt, Zr, and Sm isotopes in Fig. 1 for completeness. In this figure, the spectra of Hg isotopes clearly illustrate the existence of a family of intruder states with a parabolic trend, centered at the midshell,
$ N = 104 $ [20]. For Pt, the presence of intruder states is not clear, and it is believed that the shape coexistence is concealed under somewhat unclear parabolic-like energy systematics for the intruder states [21, 22], although the energy trend is still symmetric with respect to the midshell. For Zr isotopes, a sudden onset of deformation is observed, as can be deduced from the low energy of the$ 2_1^+ $ state and the yrast band, in general; this can be interpreted as the existence of a QPT [17]. Moreover, the very low energy of the$ 0_2^+ $ state and the influence of the midshell,$ N = 66 $ , on the energy systematics of the yrast band is remarkable, which suggests the presence of configuration mixing [23]. Finally, for Sm isotopes, a rapid onset of deformation is observed, with the lowering of the energy of the yrast band and the existence of a QPT [18], as well as a notable decrease in the energy of the$ 0_2^+ $ state, although not as much as that observed for the Zr case. Moreover, there are no hints pointing to the existence of shape coexistence.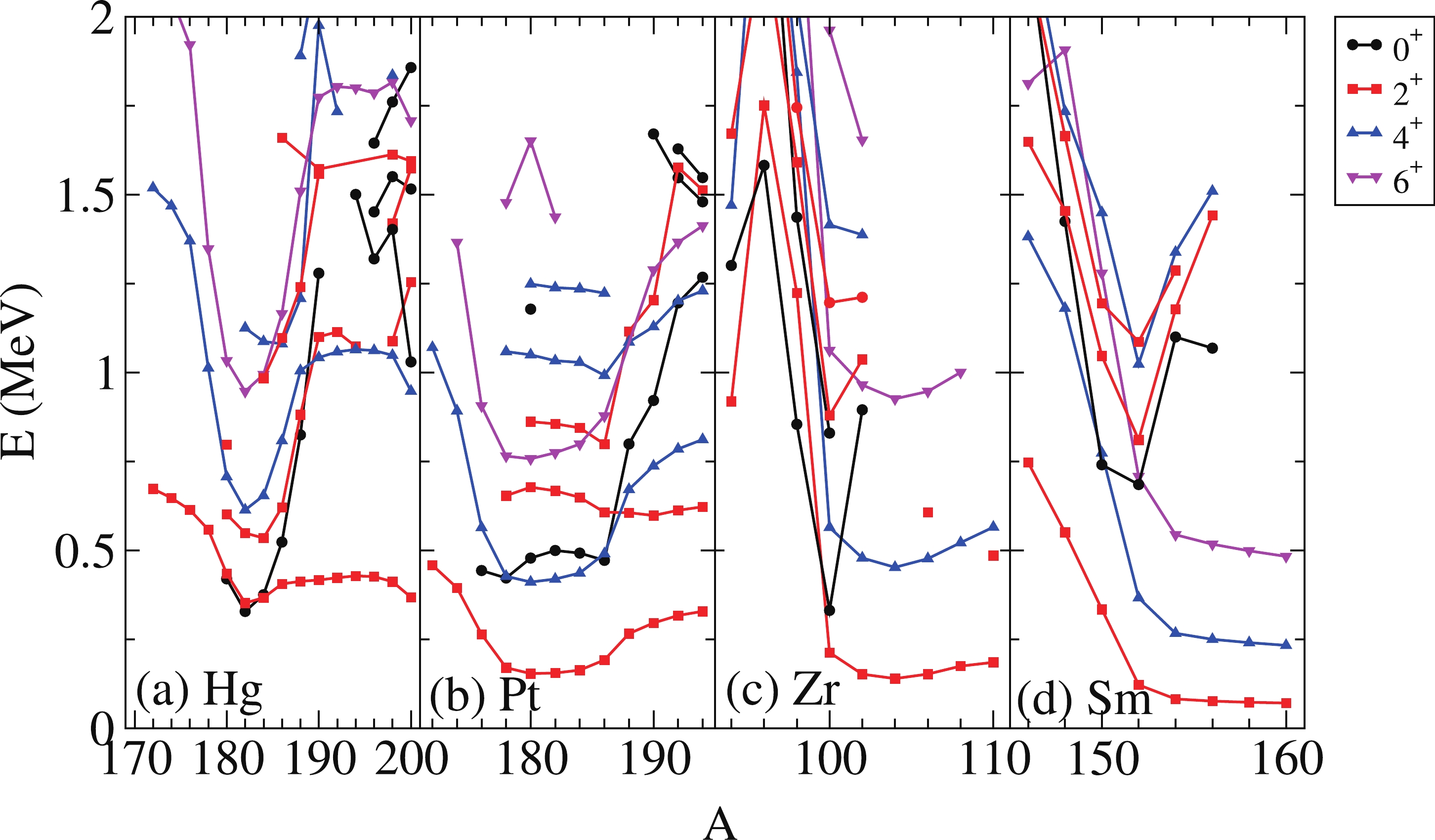
Figure 1. (color online) Partial spectra of Hg (panel (a)), Pt (panel (b)), Zr (panel (c)), and Sm isotopes (panel (d)).
The concept of QPT was also analyzed in the framework of IBM-CM, first by defining a method to construct an energy functional considering different configurations, as introduced in [24, 25], and then by constructing a schematic phase diagram of the model [26]. Subsequently, the phase diagram of the IBM-CM Hamiltonian was studied in detail in [27, 28]. The phase diagram in these cases is significantly more involved than that for a single configuration; and it is difficult to obtain a single phase diagram considering all possible parameters.
This paper is organized as follows. The formalism for calculating two-nucleon transfer intensities is discussed briefly in Section 2. In Section 3, a systematic study of the two-nucleon transfer intensities for several isotope chains is presented, first by considering configuration mixing calculations (subsection 3.1) and then using a single configuration (subsection 3.2). Finally, our main conclusions are presented in Section 4.
-
To compute two-nucleon transfer intensities, we use the IBM as the framework in this study [29]. The model is proposed as a symmetry-dictated approximation of the shell model, assuming that the relevant degrees of freedom are pairs of nucleons coupled to either angular momentum
$ L = 0 $ (S pairs) or$ L = 2 $ (D pairs), which are considered as bosons for further approximation. The number of active pairs of nucleons regardless of their particle or hole nature or proton or neutron character is denoted by N. The IBM was modified to account for particle-hole excitations, e.g., 2p-2h excitations [30, 31]. In this case, the original Hilbert space is enlarged to$ [N]\oplus[N+2] $ . The$ [N+2] $ space corresponds to considering two extra bosons that arise from the promotion of a pair of protons across the corresponding shell closure, generating an extra boson made of proton holes and another made of proton particles.For the case of the IBM without configuration mixing, a simplified Hamiltonian, called the extended consistent-Q Hamiltonian (ECQF) [32, 33], is considered. This Hamiltonian has been used to describe successfully even-even medium- and heavy-mass nuclei. The Hamiltonian can be written as
$ \hat{H}_{\rm ecqf} = \varepsilon \hat{n}_d+\kappa' \hat{L}\cdot\hat{L}+ \kappa \hat{Q}\cdot\hat{Q}, $

(1) where the operators appearing in the Hamiltonian are the d boson number, angular momentum, and quadrupole operator.
$ \varepsilon, \kappa' $ , and$ \kappa $ are parameters of the model.The considered Hamiltonian for the case of IBM-CM has been
$ \hat{H} = \hat{P}^{\dagger}_{N}\hat{H}^N_{\rm ecqf}\hat{P}_{N}+ \hat{P}^{\dagger}_{N+2}\left(\hat{H}^{N+2}_{\rm ecqf}+ \Delta^{N+2}\right)\hat{P}_{N+2}\ +\hat{V}_{\rm mix}^{N,N+2}\; , $

(2) where
$ \hat{H}^N_{\rm ecqf} $ and$ \hat{H}^{N+2}_{\rm ecqf} $ correspond to the ECQF Hamiltonians (1) for the regular and intruder sectors;$ \hat{P}_{N} $ and$ \hat{P}_{N+2} $ are projection operators onto the$ [N] $ and$ [N+2] $ boson spaces, respectively;$ \hat{V}_{\rm mix}^{N,N+2} $ describes the mixing between the$ [N] $ and the$ [N+2] $ boson subspaces; and$ \Delta^{N+2} $ accounts for energy needed to promote a pair of protons across the proton shell closure [34, 35].After the parameters of the Hamiltonian have been fixed, the wave functions are available and can be used to calculate the value of the two-neutron transfer intensities. Because we are interested only in two-neutron transfer reactions between the low-lying
$ L^\pi = 0^+ $ states, we will use the simplest possible option for the transfer operator, namely,$ \hat {\cal P}^\dagger = \hat s^\dagger $ and$ \hat {\cal P} = \hat s $ , which are the transfer intensities proportional to the square of the reduced matrix element. Therefore, we implicitly assume that the results do not depend strongly on the precise structure of the transfer operator. For IBM-CM, the intensities can be written as (note that the emission or absorption of a nucleon pair implies that the number of bosons changes in one unit)$ I(N,0_i^+\rightarrow N-1, 0_f^+) = \left|\langle N-1, L^\pi = 0^+_f||\hat{P}^{\dagger}_{N-1}\hat {\cal P} \hat{P}_{N}+ \hat{P}^{\dagger}_{N+1}\hat {\cal P} \hat{P}_{N+2}|| N, L^\pi = 0^+_i \rangle \right|^2 $

(3) for
$ (p,t) $ reactions, and as$ I(N,0_i^+\rightarrow N+1, 0_f^+) = \left|\langle N+1, L^\pi = 0^+_f||\hat{P}^{\dagger}_{N+1}\hat {\cal P^\dagger} \hat{P}_{N}+\hat{P}^{\dagger}_{N+3}\hat {\cal P^\dagger} \hat{P}_{N+2} || N, L^\pi = 0^+_i \rangle \right|^2 $

(4) for
$ (t,p) $ reactions. The structure of the two-neutron transfer operator implies that it connects only the regular (intruder) part of the wave function of the parent nucleus with the regular (intruder) part of the daughter one, which does not exist; therefore, it crosses terms connecting different sectors. Otherwise, the operator will connect states with a different number of active protons, which is not allowed because we are dealing with a two-neutron transfer operator. In the case of IBM calculations with a single configuration, only the first terms in Eqs. (3) and (4) will give a non-null contribution. Note that, in this study, we assume no scale factors in front of the operators and the same weight for the regular and intruder contributions; therefore, all the provided results are given in arbitrary units.Assume the wave function of the involved nuclei written in the U(5) basis of the IBM as
$ \begin{split}\Psi(0_k^+;N) = & \sum\limits_{n_d,\tau,n_\Delta} a^{k}_{n_d,\tau,n_\Delta}[N] \psi((sd)^{N}_{n_d,\tau,n_\Delta};0^+) \\ & + \ \sum\limits_{n_d,\tau,n_\Delta} b^{k}_{n_d,\tau,n_\Delta}[N+2]\psi((sd)^{N+2}_{n_d,\tau,n_\Delta};0^+)\; , \end{split} $

(5) where
$ n_d $ is the number of d bosons,$ \tau $ is the boson seniority,$ n_\Delta $ is the number of d boson triplets coupled to zero, k is a rank number to label the state, and [N] and [N+2] are the regular and intruder sectors, respectively. Then, the two-neutron transfer intensity for the (p,t) reaction can be expressed as$ I(N,0_i^+\rightarrow N-1, 0_f^+) = \left | \sum\limits_{n_d,\tau,n_\Delta} \sqrt{N-n_d}\; a^{i}_{n_d,\tau,n_\Delta}[N] a^{f}_{n_d,\tau,n_\Delta}[N-1] + \sum\limits_{n_d,\tau,n_\Delta} \sqrt{N+2-n_d} \;b^{i}_{n_d,\tau,n_\Delta}[N+2] b^{f}_{n_d,\tau,n_\Delta}[N+1] \right |^2, $

(6) where as for the (t,p) reaction, it is expressed as
$ I(N,0_i^+\rightarrow N+1, 0_f^+) = \left | \sum\limits_{n_d,\tau,n_\Delta} \sqrt{N+1-n_d}\; a^{i}_{n_d,\tau,n_\Delta}[N] a^{f}_{n_d,\tau,n_\Delta}[N+1] + \sum\limits_{n_d,\tau,n_\Delta} \sqrt{N+3-n_d} \;b^{i}_{n_d,\tau,n_\Delta}[N+2] b^{f}_{n_d,\tau,n_\Delta}[N+3] \right |^2. $

(7) From these expressions, it is evident that as soon as the initial and final states fully lie on a single sector, either regular or intruder, the value of the intensity will be lost (i.e., if the parent state is fully regular and the daughter state is purely intruder, or vice versa, the intensity will be lost). However, for vibrational nuclei, the intensity will be lost when the initial and final states have a different phonon composition due to the selection rules
$ \Delta n_d = 0 $ and$ \Delta\tau = 0 $ . For well-deformed nuclei, the same as that shown in [12] holds, i.e, the ground state band is hardly connected with the quasi-$ \beta $ band or not at all connected with the double-$ \gamma $ one. -
In this section, Zr, Hg, and Pt isotope chains are analyzed using the IBM-CM with the parameters obtained in previous IBM-CM calculations without any fine-tuning.
In this section, we present the theoretical IBM-CM results of (t,p) two-neutron transfer intensities, as well as the excitation energies of the unperturbed regular and intruder band heads and the regular content of the two first
$ 0^+ $ states. The results for the ground to the excited state (p,t) reactions are not presented owing to space constraints; however, the results for them are essentially the same as those for (t,p) reactions. -
We use an IBM-CM Hamiltonian, as mentioned in Section 2. The details of the calculations can be found in Ref. [23], where the systematics of the spectroscopy of the low-lying collective states for Zr isotopes was assessed using IBM-CM from
$ A = 94 $ to$ A = 110 $ . For each of the isotopes, a set of parameters was fixed to reproduce excitation energies and E2 transition probabilities. The obtained Hamiltonians also provided a rather good description of other observables such as two-neutron separation energies,$ \rho^2(E0) $ values, or isotopic shifts, which point to an accurate description of the wave functions of the nuclei under study. In particular, the rapid onset of deformation when passing from$ ^{98} $ Zr to$ ^{100} $ Zr is well reproduced. The objective of this study is to take advantage of those calculations without any extra fitting and obtain the systematic behavior of the (t,p) two-neutron transfer intensities in this isotope chain.In Fig. 2, for the Zr isotopes, we present the values obtained for the (t,p) two-neutron transfer intensities from the ground state of the parent nucleus into the first five low-lying
$ 0^+ $ states of the daughter one (panel (a)) using operator (4) and the parameters given in Ref. [23]. For clarity, the energies of the unperturbed$ 0_1^+ $ regular ([N]) and$ 0_2^+ $ intruder ([N+2]) states are presented in panel (b). In addition, the regular content (fraction of the wave function in the regular sector, [N]) of the$ 0^+_1 $ and$ 0_2^+ $ states is shown in panel (c) (see [23] for details).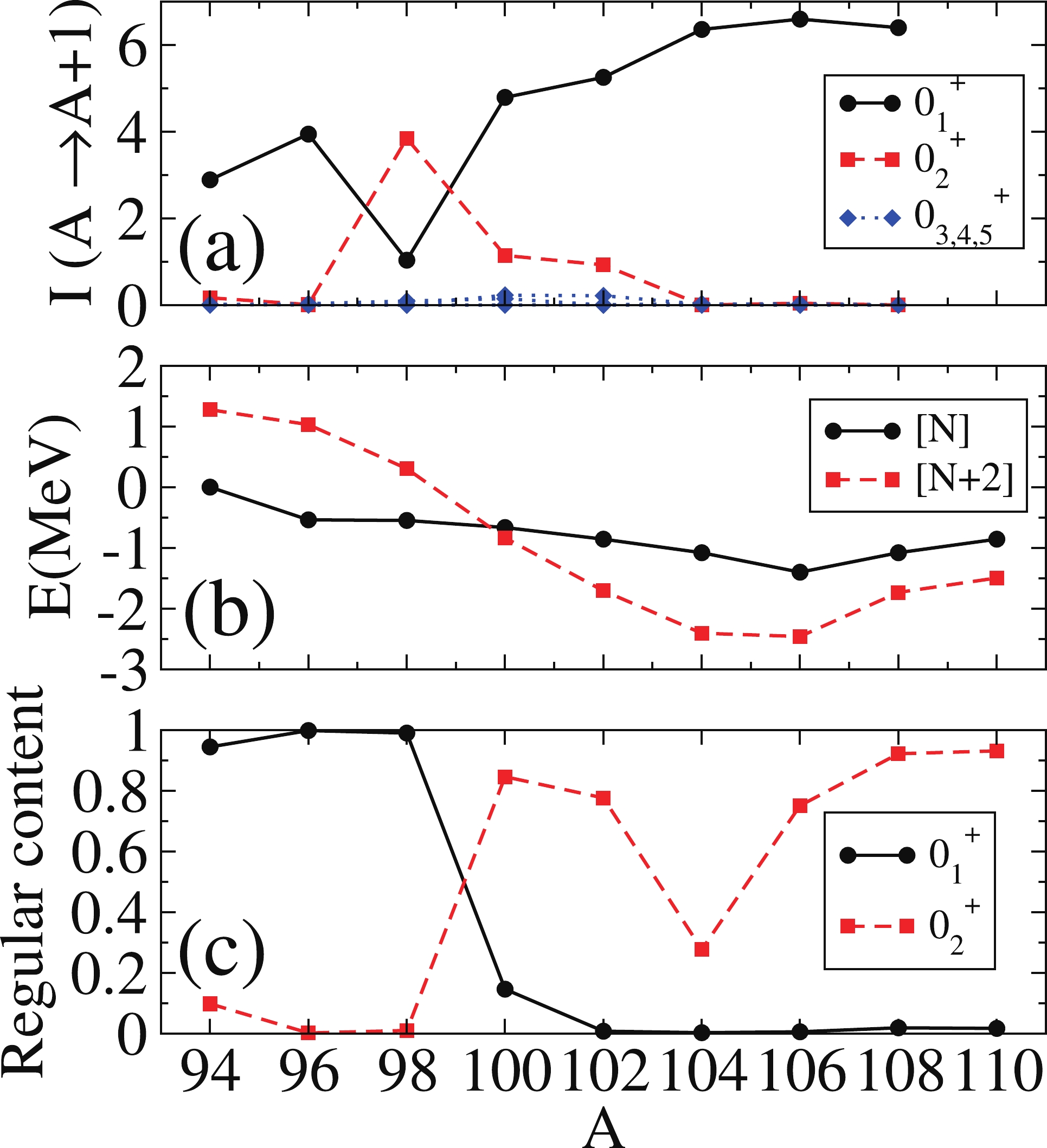
Figure 2. (color online) (t,p) transfer intensities from
$0_1^+$ in the parent nucleus to$0_i^+$ in the daughter for Zr isotopes, given in arbitrary units, using the IBM-CM Hamiltonian provided in [23]. Panel (a) depicts the value of (t,p) transfer intensity. Panel (b) depitcs the unperturbed energy of [N] and [N+2] band heads. Panel (c) depicts the regular content of states$0_1^+$ and$0_2^+$ in each isotope.Some comments in relation to Fig. 2 are in order. In panel (a), one can see that the values of the intensities of the
$ 0_1^+ $ and$ 0_2^+ $ states cross at point$ A = 98 $ , precisely where the regular and intruder configurations also cross (panel (b)). This latter fact is also manifested in the interchange of the regular content of states$ 0_1^+ $ and$ 0_2^+ $ (panel (c)). The relevant observation is that at this point (between$ A = 98 $ and$ A = 100 $ )$I(0_1^+ (A)\rightarrow 0_1^+ (A+2)) < I(0_1^+ (A)\rightarrow 0_2^+ (A+2))$ , whereas the opposite holds for the rest of the cases. This fact is linked to the use of two configurations, as will be seen in Section 3.2.1, where only a single configuration is considered. To understand why the intensity in states other than the ground state is roughly zero, we resort to the argument given at the end of Section 2, where we have seen that the intensities vanish when the structures of the involved states in parent and daughter nuclei are different (one normal and the other intruder). The cancellation of the transfer intensity occurs for states that either belong to different sectors (regular or intruder), for those with different phonon structures, e.g., different number of phonons in a vibrational nucleus, or those having phonons of different nature in a well-deformed one. In fact, the (t,p) transfer intensity is always zero for states other than$ 0_{1,2}^+ $ , i.e., intensity is barely fragmented.In Fig. 3, we depict schematically how the (t,p) two-neutron transfer operator connects states with similar structures and how they cross for
$ A = 98-100 $ , assuming that states with a similar structure (same color) are strongly connected. Fig. 2(a) simply shows the manifestation of the schematic configuration crossing represented in Fig. 3. All along the isotope chain, two configurations coexist, and they cross between$ A = 98 $ and$ A = 100 $ . Thus, the transfer is large between vibrational ground states for$ A<98 $ (blue lines) and between deformed ones for$ A>100 $ (red lines). However, at the crossing point, i.e., between$ A = 98 $ and$ A = 100 $ , the corresponding ground states have different shapes (structures): spherical in$ A = 98 $ and deformed in$ A = 100 $ . Consequently, there is a decrease in the two-nucleon transfer intensity between the ground states.
Figure 3. (color online) Schematic representation for Zr isotopes of the relative position of the two first
$0^+$ states and (t,p) transfer intensities connecting them (the width of the arrow is proportional to the value of the intensity). States with the same color that are connected with dotted lines have the same structure.Remarkably, a two-level mixing calculation is used for light Zr isotopes [36], namely,
$ ^{90-96} $ Zr, where the mixing amplitude is extracted considering two-neutron transfer intensities, concluding that mixing is moderated in$ ^{90-94} $ Zr. However, the mixing is small in$ ^{96} $ Zr, which is in agreement with the results presented here. -
The nuclear region around Pb isotopes is identified by the coexistence of low-lying states with different deformations [9]. In this region, the structure of the ground state of the isotope chains presents a rather smooth evolution; however, the structure of the states as a function of the excitation energy changes abruptly, especially around the midshell, i.e., N
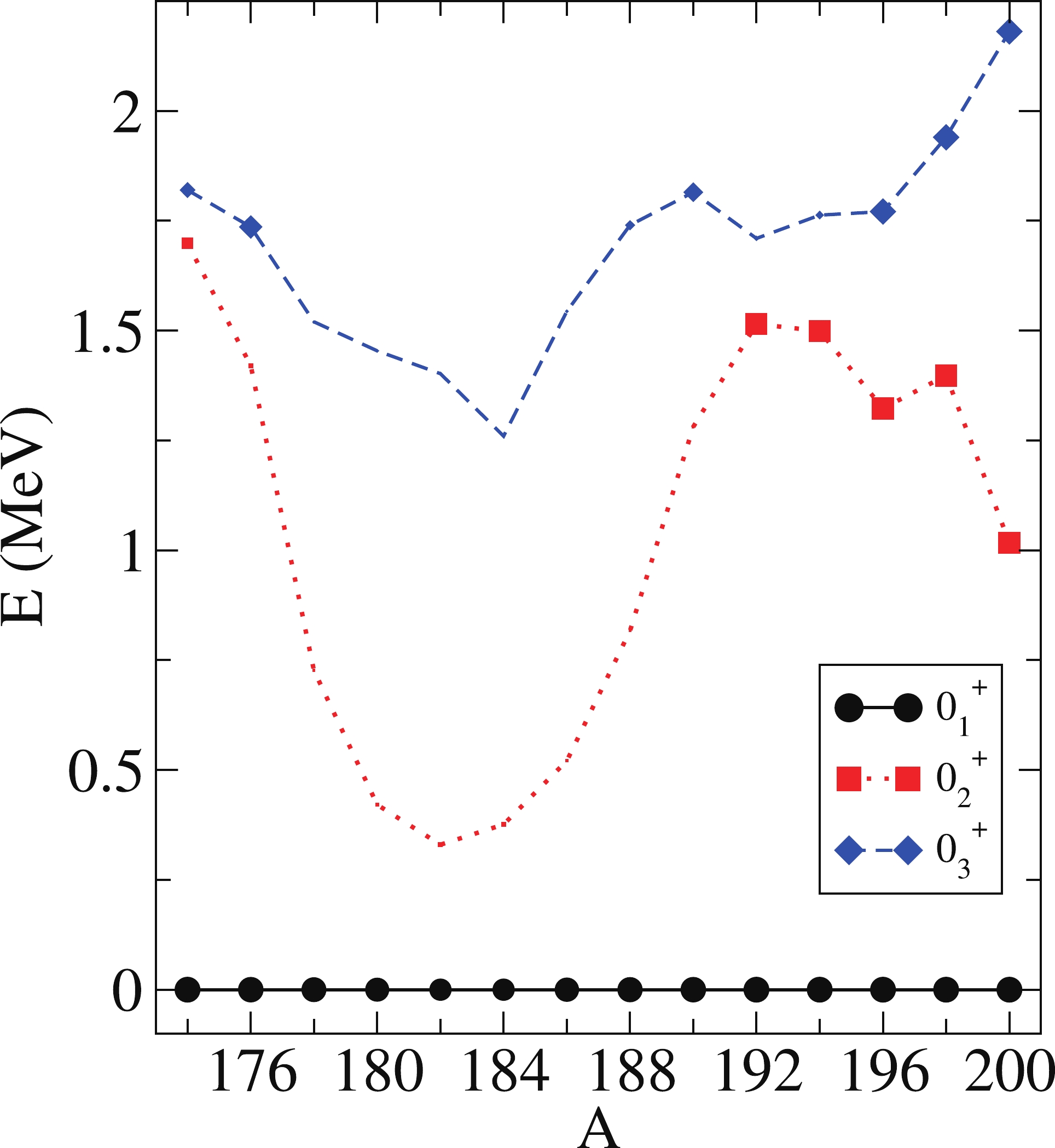
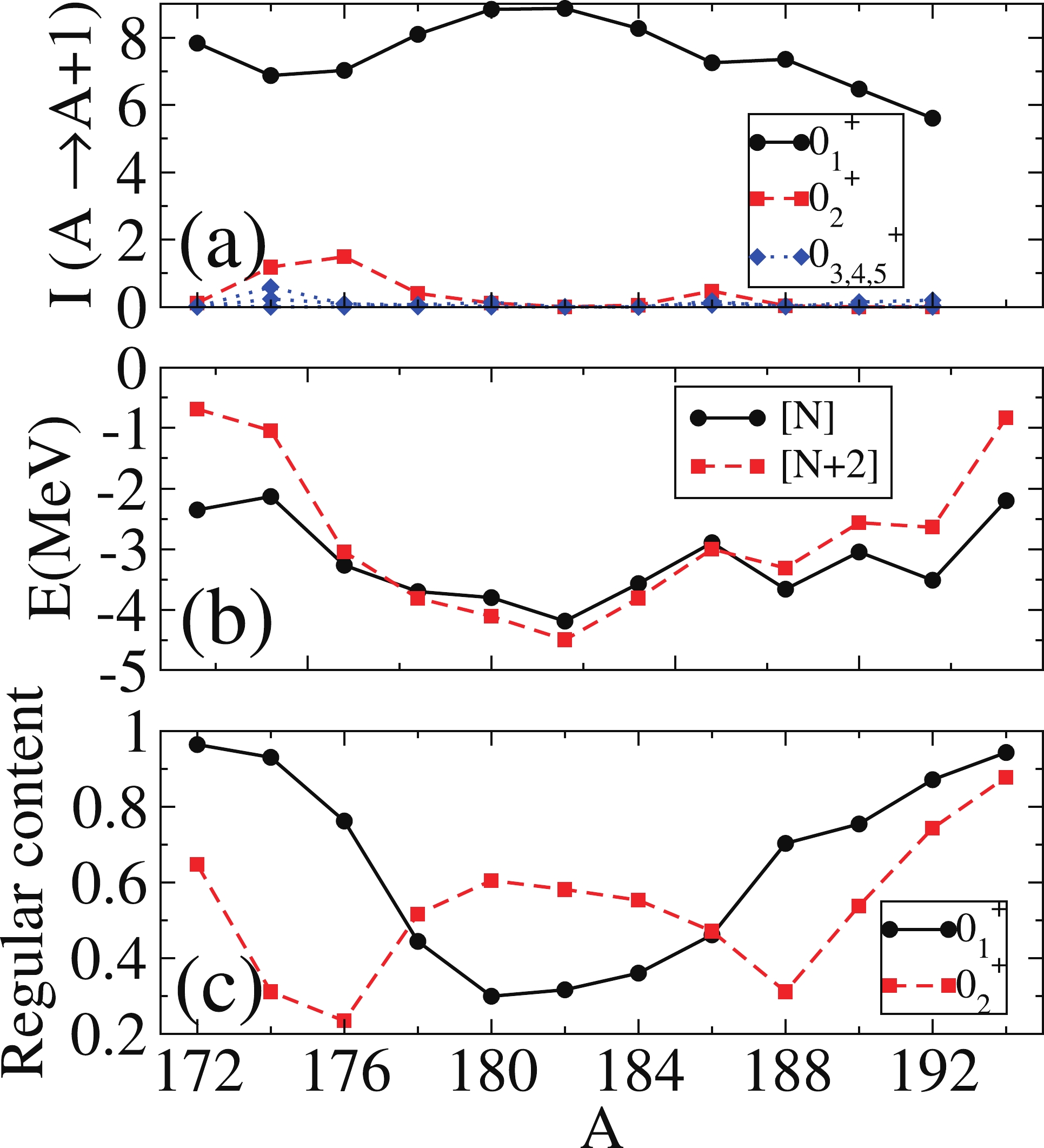
$ \approx 104 $ . This is the result of the presence of intruder states corresponding to 2p-2h or even 4p-4h excitations across the Z = 82 shell closure [37]. The Hg isotopic chain is a paradigmatic example of shape coexistence. It depicts the presence of a family of intruder low-lying states and has been studied systematically using the IBM-CM Hamiltonian in Refs. [20, 38, 39], obtaining a rather satisfactory description of excitation energies,$ B(E2) $ values, isotopic shifts, and$ \rho^2(E0) $ values. Here again, the obtained parameters from that study allow the generation of the wave functions of the different nuclei without any additional fitting.In Fig. 4, the values of the calculated (t,p) transfer intensities for the Hg isotope chain between the ground state of the parent and the first five states of the daughter nucleus are presented in panel (a). In panel (b), the behavior of the energies obtained for the unperturbed [N] and [N+2] lowest
$ 0^+ $ states is plotted. Finally, the regular content of the states$ 0^+_1 $ and$ 0_2^+ $ is depicted in panel (c) (see [20] for details).For this isotope chain, the two competing configurations never cross, as can be observed in Fig. 4(b), with the almost pure [N] configuration being always below the pure [N+2] one. Because of this, it is shown that there is little mixing between both configurations all along the isotope chain. Consequently, the dominant two-neutron transfer intensity for all the isotopes is between the ground states, i.e.,
$ I(0_1^+ (A)\rightarrow 0_1^+ (A+2)) $ . The transfer to any other low-lying$ 0^+ $ is very small for all isotopes. We conclude that no significant impact is observed in the transfer intensities of the Hg isotopes involving$ 0^+ $ states because there is almost no mixing between the regular and intruder sectors (panel (c)). It is seen that the$ 0_2^+ $ state in isotopes$ A = 172 $ and$ A = 192-200 $ is mostly the second regular$ 0^+ $ state, i.e., it belongs to the [N] configuration. From$ A = 174 $ to 190, the lowest intruder$ 0^+ $ state belonging to the$ [N+2] $ configuration comes lower than the second$ 0^+ $ of$ [N] $ . However, the intensity still vanishes because the ground and$ 0_2^+ $ states present different numbers of vibrational phonons. To help understand this better, in Fig. 5, we plot the energy systematics of the first three$ 0^+ $ states together with the value of the regular component. -
Another significant isotope in the Pb region is Pt, which presents low-lying intruder states arising from the
$ [N+2] $ configuration. The systematics of this isotope chain including configuration mixing have been studied within the IBM-CM Hamiltonian in Refs. [21, 22]. One of the main conclusions from these previous studies is that a very large degree of mixing between the intruder and the regular states exists in Pt. Furthermore, the shape coexistence is somehow concealed, with hardly any differences between the calculations with one or two configurations. The parameters obtained from these studies were used to generate the wave functions of the relevant states considered in the present study.In Fig. 6, the calculated values for (t,p) transfer intensities from the
$ 0^+_1 $ state in the parent nucleus to the$ 0^+_i $ states in the daughter one for the Pt isotope chain are plotted in panel (a). As in the case of Hg, the energies of the unperturbed$ [N] $ and$ [N+2] $ $ 0^+ $ band heads are presented in panel (b), and the regular content of the states$ 0^+_1 $ and$ 0_2^+ $ is depicted in in panel (c). Panel (a) is very similar to that in the Hg case; however, looking at panels (b) and (c), one notices significant differences. Regarding the Pt isotopes, both relevant configurations compete, cross, and are very close for most of the isotopes. In panel (c), it is evident that the$ 0_1^+ $ and$ 0_2^+ $ states are strongly mixed, around 50% in both of them for many midshell isotopes. The systematics of the two-neutron transfer intensity (panel (a)) indicates that the transfer between the ground states in neighboring isotopes dominates. However, in this case, it does not follow that the$ [N] $ configuration dominates, because it is strongly mixed thoroughly with the intruder$ [N+2] $ configuration. In this case, the intruder and regular configurations cross before and after the midshell, with the ground state around the midshell becoming the intruder configuration. Concerning the two-neutron transfer intensities, one notices some impact at the place where the states cross; however, the impact is hardly noticeable, and$ I(0_1^+ (A)\rightarrow 0_1^+ (A+2)) $ remains the dominant intensity all the way. This fact could be considered as unexpected because of the crossing of the configuration and the large mixing between them, roughly 50%, at the points where the configurations cross. Indeed, the 50% mixing in both the father and daughter isotopes allows obtaining a large fraction of intensity from both sectors. Note that the transition operator connects the regular (intruder) sector of the parent nucleus with the regular (intruder) one in the daughter nucleus; therefore, both sectors contribute either in a constructive (for$ 0^+_1 \rightarrow 0^+_1 $ ) or destructive (for$ 0^+_1 \rightarrow 0^+_2 $ ) way. The leading transition remains quite stable and only a minor lowering (a modest increase in the transfer to the$ 0_2^+ (A+2) $ state) is observed around the crossing points. Based on the results, the contributions for the transition to$ 0_1^+ $ sum up in a constructive manner, whereas these sum up in a negative manner for the transition to the$ 0_2^+ $ state, which is almost zero all the way. -
In this section, the two-neutron transfer intensities for Zr, Pt, and Sm isotopes are explored using the IBM with a single configuration. As in the preceding section, the parameters of the Hamiltonians are the same as those in previous studies. In this study, the wave functions are used without further tuning.
In this section, we present theoretical IBM results using a single configuration concerning (t,p) two-neutron transfer intensities, as well as the excitation energy of the first
$ 0^+ $ excited state and the E2 reduced transition probability between the$ 0_2^+ $ and$ 2_1^+ $ states. The two latter observables are considered as indicators for the existence of a QPT [1, 2]. -
To study the two-neutron transfer intensities based on systematic calculations within the Zr isotope chain using a single configuration, we use the IBM Hamitonian and the parameters obtained in Ref. [40] without extra fitting for the calculation of the two-neutron transfer intensity. In Ref. [40], the spectroscopic properties of even-even Zr isotopes were studied in detail with the objective of an appropriate reproduction of the two-neutron separation energy. Moreover, this study indicated the possibility of a QPT being
$ ^{100} $ Zr, the critical nucleus.In panel (a) of Fig. 7, (t,p) two-neutron transfer intensities from
$ 0^+_1 $ in the parent nucleus to$ 0^+_i $ in the daughter one for Zr isotopes, described using a single configuration calculation, are shown. As complementary observables, the excitation energy of the$ 0_2^+ $ state is plotted in panel (b), and the$ B(E2:0_2^+\rightarrow 2_1^+) $ values are presented in panel (c) . Regarding the systematics of the intensities, one notices a certain drop and an associated increase in$ I(0_1^+ (A)\rightarrow 0_1^+ (A+2)) $ and$ I(0_1^+ (A)\rightarrow 0_2^+ (A+2)) $ at$ A = 100 $ , whereas the transfer to other$ 0^+ $ states remains all the way almost at zero, which supposes little fragmentation of the strength even at$ A = 100 $ , where a QPT is supposed to exist. Concerning the$ E(0_2^+) $ excitation energy (panel (b)), a minimum for$ A = 100 $ is observed; however, the energy of the experimental one at$ A = 100 $ is significantly lower because it corresponds to a state of vibrational nature that is not considered in our IBM calculation, which uses a single configuration. In the present calculation, owing to the use of a single configuration, both ground and excited$ 0_2^+ $ states (intruder) have a deformed character. Therefore, the presented energy systematics are smoother than the experimental one. The lowering of this excitation energy with a minimum for$ ^{100} $ Zr is consistent with the presence of a critical point at$ A = 100 $ .
Figure 7. (color online) (a) (t,p) transfer intensities for Zr isotopes from
$0^+_1$ in the parent nucleus to$0^+_i$ in the daughter one, given in arbitrary units, using the IBM with a single configuration and the parameters from [40]. (b) Excitation energy of state$0_2^+$ . (c)$B(E2:0_2^+\rightarrow 2_1^+)$ values.For
$ B(E2:0_2^+\rightarrow 2_1^+) $ (panel (c)), the situation is analogous and the decrease when passing from$ A = 100 $ to$ A = 102 $ is smoother than the experimental observation. This decrease is caused by the transformation of a spherical shape, where the transition involves the change of a two-phonon state into a one-phonon state, to a deformed one, where the transition implies the connection of states belonging to different irreps (if they were in the SU(3) limit). When calculating this same observable using two configurations, instead of modifying the Hamiltonian as a function of the neutron number to generate the observed sudden change in deformation (see [40]), the onset of deformation is generated through the crossing of two families, one spherical and the other deformed (see Section 3.1.1). In general, all the analyzed quantities present a significantly faster rate of change.Note that the theoretical values of
$ B(E2:0_2^+\rightarrow 2_1^+) $ have been calculated with an effective charge$ e = 2.8 \sqrt{\rm{W.u.}} $ , which has been fixed to reproduce the experimental value of$ B(E2:2_1^+\rightarrow 0_1^+) $ [40]. This observable resembles the behavior of the order parameter of a QPT, with a null value in one of the phases and a rapid increase when passing to the other. The observed behavior is smoother than the experimental one and than that obtained using two configurations (see [23]). Clearly, the smoother trends obtained theoretically in this subsection are due to the use of a single configuration. This IBM calculation (with a single configuration) was tailored to reproduce the rapid changes observed around$ ^{100} $ Zr, such as two-neutron separation energies,$ E(2_1^+) $ , and$ E(4_1^+)/E(2_1^+) $ . However the trend for$ E(0_2^+) $ cannot be reproduced correctly, in particular for$ ^{100} $ Zr, because in this case the$ 0_2^+ $ state corresponds to a regular state whereas the ground state corresponds to the intruder one. In other words, the passing from a spherical to a deformed shape has been generated, changing appropriately the parameters of the Hamiltonian; however, when regular and intruder states are involved simultaneously in the description of a given observable, it is not possible to provide an accurate description using a single configuration.The (t,p) transfer intensity changes are smoother for single configuration calculations than for the two mixing-configuration case. Moreover, for all the isotopic chains,
$ I(0_1^+ (A)\rightarrow 0_1^+ (A+2))> I(0_1^+ (A)\rightarrow 0_2^+ (A+2)) $ in the single configuration calculation; for the configuration mixing study,$ I(0_1^+ (A = 98)\rightarrow 0_1^+ (100))<I(0_1^+ (98)\rightarrow 0_2^+ (100)) $ , reflecting the crossing of two configurations (see Fig. 2). -
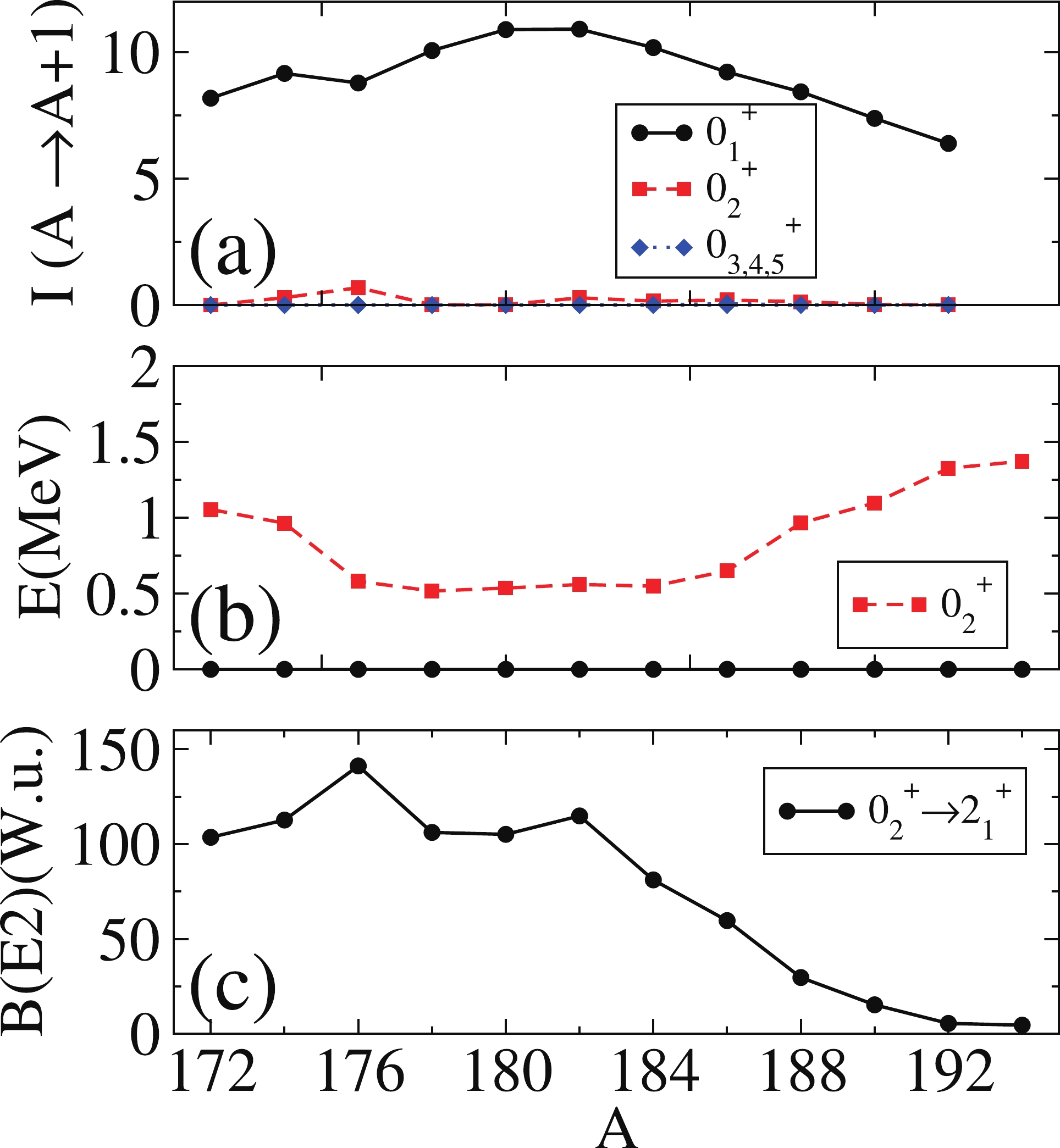
In this section, we study the systematics of the two-neutron transfer intensity of even-even Pt isotopes using the IBM Hamiltonian with a single configuration obtained in [41], wherein the excitation energy systematics and the E2 transition rates of the even-even
$ ^{172-196} $ Pt isotopes have been described adequately. We generate the wave functions and study the two-neutron transfer without any additional parameter fitting.In panel (a) of Fig. 8, (t,p) two-neutron transfer intensities in Zr isotopes obtained using a single configuration calculation are shown. As complementary observables, the excitation energy of
$ 0_2^+ $ is plotted in panel (b) and the$ B(E2:0_2^+\rightarrow 2_1^+) $ values are depicted in panel (c). Regarding the systematics of the intensities, one notices a relatively constant and large value of$ I(0_1^+ (A)\rightarrow 0_1^+ (A+2)) $ , with the rest of intensities being almost zero except for$ I(0_1^+ (A)\rightarrow 0_2^+ (A+2)) $ at$ A = 176 $ . The excitation energy of the$ 0_2^+ $ state depicted in panel (b) exhibits a rather constant value, which is not affected by the presence of the midshell at$ A = 182 $ . Although slowly, the structure of the state is evolving along the isotope chain, as can be readily seen in the continuous drop in the$ B(E2:0_2^+\rightarrow 2_1^+) $ value (panel (c)); however, there is almost no impact on the value of the (t,p) transfer intensity.The Hamiltonian obtained in [41] provides a sound and detailed description of the spectroscopic properties of the whole isotope chain, almost as good as that obtained using IBM-CM [21]. Furthermore, the values of the two-neutron intensities provided by both approaches are almost equal.
-
The Sm isotope chain is considered a clear example of a QPT from spherical to axially deformed shapes at
$ N = 90 $ . There are many indications of abrupt changes in this isotope chain: the two-neutron separation energies, B(E2) values, energy ratios, etc. In Ref. [42], systematic calculations for a large set of isotopes, including Sm, have been performed using IBM with a single configuration. In this section, we use the IBM parameters for the case of even-even Sm isotopes without any fine-tuning to generate the corresponding wave functions. With these conditions, the two-neutron transfer intensities between$ 0^+ $ states in the initial and final nuclei have been calculated. To compute B(E2) values, we considered the same effective charge for the whole chain,$ e_{\rm eff} = 2.2 \sqrt{\rm{W.u.}} $ (this value of the effective charge reproduces the experimental value$ B(E2:4_1^+\rightarrow 2_1^+) $ in$ A = 152 $ ).In Fig. 9, the values of the calculated (t,p) transfer intensities from the
$ 0^+ $ ground state into the first five low-lying$ 0^+ $ states in the daughter nucleus have been plotted in panel (a). In panel (b), the systematics of the excitation energies of the$ 0_2^+ $ states are presented. Finally, the$ B(E2:0_2^+\rightarrow 2_1^+) $ values are depicted in panel (c). Note that, in panel (b), the drop in the$ 0_2^+ $ energy is somehow similar to that in the presence of intruder states, although the minimum is not placed at midshell, but where a QPT is supposed to exist. Note that the rare-earth region is known by the interplay between quadrupole degrees of freedom and pairing vibrations, as reported recently in [43]. Considering that a phenomenological IBM Hamiltonian has been used in [42] to describe the excitation energies and B(E2) transition rates, it is expected that quadrupole and pairing degrees of freedom have been incorporated correctly. In panel (c), an abrupt change in$ B(E2:0_2^+\rightarrow 2_1^+) $ is evident, from a reasonably large value to basically zero when passing from$ A = 150 $ to$ A = 154 $ , which resembles the behavior of an order parameter in a QPT. As for the (t,p) intensity values presented in panel (a), a sudden increase in$ I(0_1^+ (A)\rightarrow 0_2^+ (A+2)) $ accompanied by a decrease in$ I(0_1^+ (A)\rightarrow 0_1^+ (A+2)) $ is observed at$ A = 150 \rightarrow 152 $ ($ N = 90 $ ). The two-neutron transfer intensities of$ 0_3^+ $ ,$ 0_4^+ $ , and$ 0_5^+ $ in the daughter nucleus are significantly small. Note that$I(0_1^+ (A) \! \rightarrow \! 0_1^+ (A+2)) \! > I(0_1^+ (A) \! \rightarrow $ $ \! 0_2^+ (A+2))$ . A previous IBM calculation reported in [44] provides almost identical results.The results of this case are similar to those observed in the IBM calculation with a single configuration for Zr, although the intensities of states
$ 0^+_{3,4,5} $ in the case of Sm are a little higher than those for Zr. Therefore, there is a certain degree of fragmentation of the (t,p) strength in Sm.Recently, a two-level mixing calculation has been reported for
$ ^{150-152} $ Sm isotopes [45]; this calculation tried to reproduce two-neutron transfer intensities and E2 transition rates. It concluded that a moderate mixing exists between two families of states. -
In this study, we calculated the values of the (t,p) two-neutron transfer intensities by taking advantage of the previous systematic studies, using the IBM with and without configuration mixing in the regions of Zr, Pb, and Sm, which provided the corresponding wave functions of the
$ 0^+ $ low-lying states in each isotope chain. Next, we calculated the value of the intensity without additional tuning. Our main objective was to confirm whether the two-neutron intensity is a reliable observable to distinguish between the existence of shape coexistence and QPT, as previously suggested in [15, 16], where the schematic calculations indicated that the two-neutron intensities suffer abrupt changes in both cases, although the intensity is significantly more fragmented in the presence of a quantum phase transition than shape coexistence.The first studied chain of isotopes was Zr. We used both approaches, IBM-CM and IBM, with a single configuration. In both cases, a rapid change in the (t,p) transfer intensity at
$ A = 100 $ was seen. The change was more abrupt in the case of shape coexistence. No fragmentation was observed in the QPT case. Evidently, the presence or absence of fragmentation in the case of a QPT depends on the precise characteristics of the used Hamiltonians, which is fragmented in the schematic calculation shown in [12, 15, 16] but not in the realistic case shown here.The second case was the Hg isotope chain, which was studied using IBM-CM alone [20] because it is not possible to describe the experimental spectroscopic systematics when using IBM with a single configuration. In this case, there was no significant impact of shape coexistence on the value of the intensities because the intruder configuration was always well above the regular one, and the two hardly mixed.
The third case corresponds to the Pt isotope chain, which has been analyzed using both the IBM-CM [21, 22] and the IBM with a single configuration [41]. The obtained systematics are somehow surprising owing to the large mixing before and after the midshell, which is expected to affect strongly the two-neutron intensities in the
$ 0_1^+ $ and$ 0_2^+ $ states of the daughter nuclei; however, the particular phases of the different components of the wave function produce a constructive impact on the$ 0_1^+ $ state and a destructive impact on the$ 0_2^+ $ state.The final case was the chain of Sm isotopes, which was studied using an IBM Hamiltonian with a single configuration [42]. Clearly, the presence of a QPT had significant impact on the two-neutron intensity, affecting the transitions in the
$ 0_1^+ $ and$ 0_2^+ $ states, but without any further fragmentation. This result is in disagreement with the conclusion reported in [12, 15, 16], where a schematic QPT was simulated and a large fragmentation was observed, which suggested that the results should be sensitive to the precise characteristic of the Hamiltonian evolution along the isotope chain.The evolution of nuclear structure is the result of the fine balance of the nuclear interaction. This can be schematically understood in terms of the competition between the quadrupole interaction, which tends to deform the nucleus, and the monopole part, which is significantly dependent on the specific orbitals around the shell closures. This tends to keep the nucleus spherical. This competition is at the origin of the appearance of deformation in the nuclear chart. In the case of Zr and Sm isotopes, where a rapid onset of deformation appears, the competition can be understood easily in terms of the impact suggested by Federman and Pittel in 1979 [46]. They emphasized the importance of the simultaneous filling of neutron and proton spin-orbit partners (
$ \pi g_{9/2} $ and$ \nu g_{7/2} $ in the case of Zr, and$ \pi h_{11/2} $ and$ \nu h_{9/2} $ in the case of Sm) to understand the appearance of deformation. In the case of Zr, the description of the spectroscopic properties needs the inclusion of an intruder configuration, which is not in the case corresponding to Sm, although there is a rapid onset of deformation in both cases and several states present significantly different degrees of deformation (see [17] for Zr and [19] for Sm). In both cases, there is a strong impact on two-neutron transitions; however, the precise trend along the chain depends on the precise details of the interaction, and it is not possible to disentangle clearly the shape coexistence from the QPT by using only the two-neutron transfer intensity.One of the authors (JEGR) thanks K. Heyde for the enlightening discussions.
Two-neutron transfer reactions as a tool to study the interplay between shape coexistence and quantum phase transitions
- Received Date: 2020-06-02
- Available Online: 2020-12-01
Abstract: The atomic mass table presents zones where the structure of the states changes rapidly as a function of the neutron or proton number. Among them, notable examples are the A ≈ 100 Zr region, the Pb region around the neutron midshell (N = 104), and the N ≈ 90 rare-earth region. The observed phenomena can be understood in terms of either shape coexistence or quantum phase transitions. The objective of this study is to find an observable that can distinguish between both shape coexistence and quantum phase transitions. As an observable to be analyzed, we selected the two-neutron transfer intensity between the 0+ states in the parent and daughter nuclei. The framework used for this study is the Interacting Boson Model (IBM), including its version with configuration mixing (IBM-CM). To generate wave functions of isotope chains of interest needed for calculating transfer intensities, previous systematic studies using IBM and IBM-CM were used without changing the parameters. The results of two-neutron transfer intensities are presented for Zr, Hg, and Pt isotopic chains using IBM-CM. Moreover, for Zr, Pt, and Sm isotopic chains, the results are presented using IBM with only a single configuration, i.e., without using configuration mixing. For Zr, the two-neutron transfer intensities between the ground states provide a clear observable, indicating that normal and intruder configurations coexist in the low-lying spectrum and cross at A = 98 → 100. This can help clarify whether shape coexistence induces a given quantum phase transition. For Pt, in which shape coexistence is present and the regular and intruder configurations cross for the ground state, there is almost no impact on the value of the two-neutron transfer intensity. Similar is the situation with Hg, where the ground state always has a regular nature. For the Sm isotope chain, which is one of the quantum phase transition paradigms, the value of the two-neutron transfer intensity is affected strongly.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: