-
Black holes are a type of compact objects with an event horizon from which all particles, including light, cannot escape. Owing to the effect of this boundary, an observer located outside the black hole is unable to detect emissions from the horizon. However, considering the quantum effects, black holes discharge a small quantity of emission called Hawking radiation [1, 2]. Accordingly, black holes can be considered as radiative objects with the Hawking temperature. They are also known to have an irreducible mass that does not decrease during any physical process [3–6]. Focusing on this irreducible nature, which is similar to the second law of thermodynamics, the entropy of black holes is found to be proportional to the surface area of the horizon [7, 8]. Hence, a black hole can be considered as a system having both Hawking temperature and Bekenstein–Hawking entropy. Based on these variables, we have identified the laws of thermodynamics applicable to black holes.
The thermodynamic properties of black holes are defined at the horizon. In this case, because of its nature, the horizon acts as the effective surface of the black hole, separating the inside of the hole from the outside. In particular, the horizon hides the curvature singularity from an outside observer. A naked singularity observed without the horizon can cause the breakdown of a causal structure; hence, the singularity is conjectured to be hidden by the horizon. This is known as the weak cosmic censorship conjecture (WCCC) [9, 10]. The WCCC was first tested in Wald's gedanken experiment for the Kerr black hole by adding a test particle [11]. Thereafter, the WCCC has been actively studied for various black holes and test channels. Based on particle addition, the WCCC has also been investigated considering several effects, such as self-force and back-reaction effects [12– 30]. Furthermore, the WCCC can be examined based on the scattering of an external field because the back-reacted black hole alters its states depending on the modes of the external field [31–45]. Although the external field affects the black hole, the changes in the hole are in agreement with the laws of thermodynamics, which ensure the validity of the WCCC [20, 36]; therefore, the laws of thermodynamics are closely associated with the WCCC.
The thermodynamics of black holes is also important in terms of the anti-de Sitter (AdS)/conformal field theory (CFT) correspondence. Here, the gravity theory described in the AdS spacetime is related to the CFT in its one-dimensional lower boundary [46–49]. According to the AdS/CFT correspondence, the properties of AdS black holes provide meaningful insights into the physics of dual CFTs. The thermodynamics of black holes is related to that of the dual CFT. Moreover, because the Hawking radiation provides the temperature of a black hole, the dual CFT associated with the AdS black hole has a finite temperature provided by the Hawking temperature that is identical to that of the AdS black hole in the bulk [50]. Furthermore, in three-dimensional AdS black holes, the generators of diffeomorphisms can be obtained such that they preserve the asymptotic boundary conditions and obey the Virasoro algebra with a specific central charge [51]
; thus, we can determine the dual CFT to AdS3. Remarkably, when AdS3 black holes are assumed to be an excitation from the zero-mass vacuum, the Cardy formula corresponds to the Bekenstein–Hawking entropy [52]. The AdS/CFT correspondence has been extended to various topics, such as quantum chromodynamics (QCD) [53–56] and condensed matter theory (CMT) [57, 58]. In particular, AdS3 black holes, which are considered in this study, are dual to holographic superconductors [59–61] in terms of the AdS/CMT correspondence. In this research, the variation tendency of CFT2 is investigated as the rotating AdS3 black hole changes because of the flux transfer caused by the scattering of a massive scalar field on the gravity side. On this side, the variables of black holes, such as mass and angular momentum, are bounded by the extremal condition. In particular, the laws of thermodynamics ensure that the extremal condition functions as a physical boundary. Notwithstanding the AdS/CFT correspondence, the dual description of the extremal condition remains unclear. The rotating AdS3 black hole is a well-studied case that is directly related to dual CFT2; hence, the implications of dual CFT2 may be determined with respect to the extremal condition while ensuring that the second and third laws of thermodynamics for black holes are satisfied. Furthermore, according to the third law, the temperature of black holes cannot be zero because of any physical processes, such as the scattering of a scalar field considered in this study. The dual description regarding the zero-temperature bound is also investigated. Therefore, the bound found in dual CFT2 is enforced by the second law. Finally, the relationship of the bounded behaviors between the rotating AdS3 black hole and dual CFT2 is obtained for the variations originating from the scattering of the massive scalar field.
The remainder of this paper is organized as follows. In Section 2, the relationship between the rotating AdS3 black hole and its dual CFT2 is briefly reviewed. In Section 3, the solution to the scattering of a massivescalar field at the horizon of the black hole is described. In Section 4, the effects of the scalar field on the black hole are described in terms of the fluxes of the scalar field. The variations in the dual CFT2 originating from the changes in the black hole caused by the scalar field are described in Section 5. The results are briefly summarized in Section 6.
-
The relationship between the rotating AdS3 black hole and its dual CFT2 is considered under the changes caused by the scattering of a scalar field. The AdS/CFT correspondence is well-constructed for the rotating AdS3 black hole. Moreover, the entropy of black holes according to the microscopic derivation is well explained in [51, 52]. Here, the derivation is briefly introduced to elucidate on the dual description for the AdS3 black hole. The three-dimensional action with a cosmological constant is
$ S = \frac{1}{16\pi G} \int {\rm d}^3x\sqrt{-g}\left(R+\frac{2}{\ell^2}\right), $

(1) where R is the curvature, and
$ \ell $ is the AdS radius. Considering dual CFT2, the AdS radius is assumed in the semiclassical limit, such as$ \ell\gg G $ . The action in Eq. (1) includes the AdS3 spacetime in an$ SL(2,R)_L\otimes SL(2,R)_R $ isometry group. To define dual CFT2 at the boundary of the AdS3 bulk, the asymptotic boundary condition is given by [52]$ \begin{aligned}[b]& g_{tt} = -\frac{r^2}{\ell^2}+{\cal{O}}(1),\quad g_{t\phi} = {\cal{O}}(1),\quad g_{tr} = {\cal{O}}(r^{-3}),\\& g_{rr} = \frac{\ell^2}{r^2}+{\cal{O}}(r^{-4}),\quad g_{r\phi} = {\cal{O}}(r^{-3}),\quad g_{\phi\phi} = r^2+{\cal{O}}(1). \end{aligned} $

(2) Diffeomorphisms can be constructed to preserve Eq. (2). The generators of diffeomorphisms are defined as
$ L_n $ and$ \bar{L}_n $ with$ -\infty < n < +\infty $ ; these also obey the Virasoro algebra with the central charge$ c = \dfrac{3\ell}{2G} $ . This implies that CFT2 with$ c = \dfrac{3\ell}{2G} $ is dual to the gravity theory on the AdS3 bulk.The rotating AdS3 black hole with mass, M, and angular momentum, J, has an AdS3 boundary that satisfies Eq. (2) [62, 63]. When the horizon is located at
$ r = r_{\rm{h}} $ , its metric is expressed as [52]$ {\rm d}s^2 = -N^2 {\rm d}t^2+\rho^2(N^\phi {\rm d}t+{\rm d}\phi)^2+\frac{r^2}{N^2 \rho^2}{\rm d}r^2, $

(3) and
$\begin{aligned}[b] &N^2 = \frac{r^2(r^2-r_{\rm{h}}^2)}{\ell^2 \rho^2},\quad N^\phi = -\frac{4GJ}{\rho^2},\quad\rho^2 = r^2+4GM\ell^2-\frac{1}{2}r^2_{\rm{h}},\\& r_{\rm{h}}^2 = 8G\ell\sqrt{M^2\ell^2-J^2}. \end{aligned}$

(4) This metric significantly differs from that of the Bañados, Teitelboim, and Zanelli (BTZ) black hole in [62, 63] because the metric in Eq. (3) is transformed to associate CFT2. The rotating velocity at the horizon is
$ \ \Omega_{\rm{h}} = \frac{4GJ}{\rho_{\rm{h}}^2},\quad \rho_{\rm{h}}^2 = \frac{1}{2}r_{\rm{h}}^2+4GM\ell^2. $

(5) The Hawking temperature and Bekenstein–Hawking entropy are expressed as
$ \ T_{\rm{H}} = \frac{4G\sqrt{M^2\ell^2-J^2}}{\pi \ell \rho_{\rm{h}}},\quad S_{\rm{BH}} = \frac{\pi \sqrt{16GM\ell^2+2r_{\rm{h}}^2}}{4G}. $

(6) The dual theory is still CFT2 with
$ c = \dfrac{3\ell}{2G} $ because the boundary condition in Eq. (3) satisfies Eq. (2). However, the metric of the AdS3 spacetime is not at$ M = J = 0 $ but at$ M = -\dfrac{1}{8G} $ . Hence, the black hole and AdS3 spacetime are locally equivalent [52]. The black hole in Eq. (3) is regarded as the finite mass excitation from the black hole with (M = 0) because of the naked singularity in$ -\dfrac{1}{8G}<M<0 $ . Thus, the mass and angular momentum are related to generators$ L_0 $ and$ \bar{L}_0 $ as follows:$ M = \frac{1}{\ell}(L_0+\bar{L}_0),\quad J = L_0-\bar{L}_0. $

(7) Therefore, the Cardy formula for the asymptotic growth of the states of dual CFT2 is
$ S_{\rm{CFT}} = 2\pi \sqrt{\frac{c n_{\rm{R}}}{6}}+2\pi \sqrt{\frac{c n_{\rm{L}}}{6}}, $

(8) where
$ n_{\rm{R}} $ and$ n_{\rm{L}} $ are the eigenvalues of$ L_0 $ and$ \bar{L}_0 $ , respectively. According to Eq. (7), the Cardy formula in Eq. (8) can be rewritten in terms of M and J of the black hole, exactly corresponding to the Bekenstein–Hawking entropy [52]:$ S_{\rm{CFT}} = \pi \sqrt{\frac{\ell(\ell M +J)}{2G}}+\pi \sqrt{\frac{\ell(M\ell-J)}{2G}} = S_{\rm{BH}}. $

(9) Therefore, the Bekenstein–Hawking entropy microscopically originates from the asymptotic growth of the states of CFT2. Considering this correspondence, the changes in the rotating AdS3 black hole caused by the scattering of a massive scalar field and the impact of these changes in terms of CFT2 are examined herein.
-
The fluxes of a massive scalar field are considered to be scattered by the rotating AdS3 black hole. Owing to the energy and angular momentum of the scalar field that are transferred to the black hole during the scattering, the black hole changes. These transferred energy and angular momentum can be estimated based on the fluxes of the scalar field at the horizon. Therefore, according to Eq. (7), the changes in the black hole can be related to those in dual CFT2. The general procedure and convention followed are those reported in [36, 42, 64]. Note that such a scalar solution has also been reported in [65] for the metric of the BTZ black hole [62, 63]. The action of the massive scalar field begins as
$ S_\Psi = -\frac{1}{2}\int {\rm d}^3 x \sqrt{-g}\left(\partial_\mu \Psi \partial^\mu \Psi^*+\mu^2 \Psi\Psi^*\right), $

(10) where the mass of the scalar field is considered as
$ \mu $ to include the null and timelike cases in terms of a particle. Consequently, the equation of motion of the scalar field is obtained as$ \frac{1}{\sqrt{-g}} \partial_\mu \left(\sqrt{-g} g^{\mu\nu} \partial _\nu \Psi\right)-\mu^2 \Psi = 0. $

(11) This is rewritten as
$\begin{split} & -\frac{1}{N^2}\partial_t^2 \Psi +\frac{2N^\phi}{N^2}\partial_t\partial_\phi\Psi+\frac{1}{r}\partial_r\left(\frac{N^2 \rho^2}{r}\partial_r \Psi\right)\\ &\quad +\left(-\frac{(N^\phi)^2}{N^2}+\frac{1}{\rho^2}\right)\partial_\phi^2 \Psi-\mu^2\Psi = 0, \end{split}$

(12) where the angular parts and time are easily separated. Thus, the solution of the scalar field is considered with the separation constants
$ \omega $ and m corresponding to its frequency and angular number, respectively:$ \Psi(t,r,\phi) = {\rm e}^{-{\rm i}\omega t}{\rm e}^{{\rm i}m\phi} R(r). $

(13) The remaining radial equation becomes
$\begin{split} &\frac{1}{R(r)}\partial_r\left(\frac{N^2 \rho^2}{r}\partial_r R(r)\right)+\left(\frac{\omega^2}{N^2}+\frac{2\omega m N^\phi}{N^2}\right.\\&\quad \left.+\left(\frac{(N^\phi)^2}{N^2}-\frac{1}{\rho^2}\right)m^2-\mu^2\right)r = 0. \end{split}$

(14) This radial equation (Eq. (14)) can be rewritten and solved in the tortoise coordinate defined as
$ \frac{{\rm d}r^*}{{\rm d}r} = \frac{r}{N^2 \rho^2}. $

(15) The interval
$ (r_{\rm{h}},+\infty) $ in the r coordinate becomes$ (-\infty,0) $ in the tortoise coordinate. The radial equation (Eq. (14)) is simplified as$ \frac{1}{R(r)}\frac{{\rm d}^2R(r)}{{\rm d}{r^*}^2}\!+\!\left(\omega^2\!+\!2\omega m N^\phi\!+\!\left((N^\phi)^2\!-\!\frac{N^2}{\rho^2}\right)m^2\!-\!\mu^2N^2\right)\rho^2 \!=\! 0, $

(16) which should be satisfied by an exact solution to the scalar field. To solve Eq. (16), two boundary conditions are necessary for the horizon and radial infinity. There is no alternative for the boundary condition at the horizon because the scalar field is ingoing into the horizon; accordingly, the reflection rate is assumed to be zero. However, the boundary condition at the radial infinity can be defined in various ways. Nevertheless, it is ensured that the two boundary conditions also satisfy Eq. (16). Here, the fluxes of the scalar field are significant to estimate the energy and angular momentum transferred from the scalar field into the black hole. Hence, the fluxes may be obtained without fixing the boundary condition at the radial infinity because they are solely the solution to the scalar field at the horizon. To obtain these fluxes, the foregoing solution should be determined. Equation (16) is reduced by setting
$ r\rightarrow r_{\rm{h}} $ . Then, at the horizon, the scalar field satisfies$ \frac{1}{R(r)}\frac{{\rm d}^2R(r)}{{\rm d}{r^*}^2}+\left(\omega-m \Omega_{\rm{h}}\right)^2\rho_{\rm{h}}^2 = 0. $

(17) The solution of the scalar field to Eq. (17) is also the exact solution to Eq. (16), because Eq. (17) is simply the reduced form of Eq. (16) at the horizon. The radial solutions to Eq. (17) at the horizon are
$ R(r) = {\rm e}^{\pm {\rm i}(\omega - m \Omega_{\rm{h}})\rho_{\rm{h}} r^*}. $

(18) The plus and minus signs in the solutions indicate the outgoing and ingoing scalar fields, respectively. Note that these radial solutions are independent of the boundary condition at the radial infinity. Therefore, Eq. (18) is invariably the solution regardless of the chosen boundary condition at the radial infinity. Here, it is assumed that the ingoing scalar field is scattered by the black hole; hence, the radial solution should describe an ingoing wave with a minus sign in Eq. (18). The solutions to the ingoing scalar field are
$\begin{split}& \Psi = {\rm e}^{-{\rm i}\omega t} {\rm e}^{{\rm i}m \phi} {\rm e}^{- {\rm i}(\omega - m \Omega_{\rm{h}})\rho_{\rm{h}}r^*} { : {\rm{ingoing}}}, \\& \Psi^* = {\rm e}^{{\rm i}\omega t} {\rm e}^{-{\rm i}m \phi} {\rm e}^{{\rm i} (\omega - m \Omega_{\rm{h}})\rho_{\rm{h}}r^*} { : {\rm{conjugate}}}. \end{split}$

(19) By applying these solutions, the energy fluxes and angular momentum flowing into the black hole are derived.
-
Based on the fluxes of the scalar field, the amount of mass and angular momentum flowing into the rotating AdS3 black hole may be estimated. Accordingly, the changes in the mass and angular momentum of the black hole can be specified for an initial condition. Furthermore, because the conserved quantities of the black hole are directly related to states
$ n_{\rm{R}} $ and$ n_{\rm{L}} $ in Eq. (7), these changes are also associated with the variations in dual CFT2 [64].The fluxes of the scalar field are defined in terms of its energy–momentum tensor expressed as
$ T_{\mu\nu} = \partial_{(\mu}\Psi \partial_{\nu)}\Psi^*-g_{\mu\nu}\left(\frac{1}{2}\partial_\mu\Psi \partial^\mu\Psi^* -\frac{1}{2}\mu^2\Psi\Psi^*\right). $

(20) The energy and angular momentum fluxes are obtained as
$\begin{split} \frac{{\rm d}E}{{\rm d}t} =& \int T_T^r \sqrt{-g} {\rm d}\Phi = 2\pi\omega(\omega-m\Omega_{\rm{h}})\rho_{\rm{h}},\\\frac{{\rm d}J}{{\rm d}t} =& -\int T^r_\phi \sqrt{-g}{\rm d}\Phi = 2\pi m(\omega-m\Omega_{\rm{h}})\rho_{\rm{h}},\quad\frac{{\rm d}J}{{\rm d}t} = \frac{\omega}{m} \frac{{\rm d}E}{{\rm d}t}. \end{split}$

(21) The energy and angular momentum of the scalar field are conserved quantities because they are added to the corresponding quantities of the black hole, i.e., mass, and angular momentum. Note that the signs of the fluxes in Eq. (21) depend on the modes of the scalar field
$ (\omega,m) $ . If$ \omega> m\Omega_{\rm{h}} $ , then the ingoing scalar field adds its energy to the black hole. However, if$ \omega< m\Omega_{\rm{h}} $ , then the energy flux is negative; thus, the scalar field becomes an outgoing wave and extracts energy from the black hole. This is called the superradiance. The analysis includes both positive and negative flux cases. According to the fluxes in Eq. (21), the exact changes in the mass and angular momentum during the infinitesimal time interval,$ {\rm d}t $ , may be explained.$ {\rm d}M = 2\pi\omega(\omega-m\Omega_{\rm{h}})\rho_{\rm{h}}{\rm d}t,\quad {\rm d}J = 2\pi m(\omega-m\Omega_{\rm{h}})\rho_{\rm{h}}{\rm d}t. $

(22) The changes in Eq. (22) above are caused by the scalar field; hence, the initial black hole of
$ (M,J) $ becomes the final black hole of$ (M+{\rm d}M,J+{\rm d}J) $ with as much energy and angular momentum transferred from the scalar field. The thermodynamic properties of the black hole depend on the mass and angular momentum, causing infinitesimal changes in the properties. In particular, the validity of Eq. (22) can be ensured because these changes agree with the laws of thermodynamics. Note that the energy scale of the scalar field is assumed to be small compared to that of the black hole. Therefore, the scattering of the scalar field still conserves geometric symmetry, and the form of the metric is retained.The black hole entropy, which is a function of mass and angular momentum, is given in Eq. (6). Hence, by the fluxes of the scalar field, the black hole undergoes changes indicated in Eq. (22). The foregoing also infinitesimally varies the entropy of the black hole from
$ S_{\rm{BH}}(M,J) $ to$ S_{\rm{BH}}(M+{\rm d}M,J+{\rm d}J) $ . The entropy change is$\begin{split} {\rm d}S_{\rm{BH}} =& S_{\rm{BH}}(M+{\rm d}M,J+{\rm d}J)-S_{\rm{BH}}(M,J) \\=& \frac{\partial S_{\rm{BH}}}{\partial M}{\rm d}M+\frac{\partial S_{\rm{BH}}}{\partial J}{\rm d}J, \end{split}$

(23) where
$ r_{\rm{h}} $ and$ \rho_{\rm{h}} $ can be written in terms of$ (M,J) $ ; thus, the independent variables are only$ (M,J) $ . Then, the change in entropy is obtained as$ {\rm d}S_{\rm{BH}} = \frac{\pi^2 \rho_{\rm{h}}^2 \ell(\omega-m \Omega_{\rm{h}})^2{\rm d}t}{4G\sqrt{M^2 \ell^2 -J^2}}>0. $

(24) The entropy for any initial state of the black hole increases for the arbitrary modes of the scalar field. This irreducible entropy is the second law of thermodynamics. Note that this is consistent with [65] for the metric of the BTZ black hole. Furthermore, by combining Eqs. (22) and (24), it is found that
$ {\rm d}M = T_{\rm{H}}{\rm d}S_{\rm{BH}}+\Omega_{\rm{h}}{\rm d}J. $

(25) which is the first law of thermodynamics. Therefore, the analysis on the scattering of the scalar field is congruent with the laws of thermodynamics and ensures that Eq. (22) is physically reasonable.
Accordingly, the variation in the eigenvalues in the dual CFT may be determined under the changes in the mass and angular momentum given in Eq. (22). The eigenvalues are related to the mass and angular momentum of the black hole, as indicated in Eq. (7). The changes between the initial and final black holes can be demonstrated by the corresponding eigenvalues in the dual CFT. Hence, the relationship between the changes in the black hole and dual CFT may be derived as follows:
$\begin{split} {\rm d} n_{\rm{R}} =& \pi (\omega -m\Omega_{\rm{h}})(\omega \ell +m)\rho_{\rm{h}}{\rm d}t,\\ {\rm d} n_{\rm{L}} = &\pi (\omega -m\Omega_{\rm{h}})(\omega \ell -m)\rho_{\rm{h}}{\rm d}t. \end{split}$

(26) Equation (26) provides the variation tendency in dual CFT2 originating from the changes in the black hole caused by the scattering of the scalar field.
-
In this section, the bounded behaviors of the rotating AdS3 black hole and their implications for dual CFT2 are discussed. Owing to the transferred energy and angular momentum, the mass and angular momentum of the black hole changes under constraints, such as the laws of thermodynamics. Hence, the changes in the black hole are related to the variations in the eigenvalues for dual CFT2 and may be analyzed.
-
The mass and angular momentum transferred by the fluxes of the scalar field alter various properties of the black hole. Among these properties, a relevant quantity for measuring the tendency of changes depending on the scalar field is the Hawking temperature. Owing to the scalar field fluxes, the temperature,
$ T_{\rm{H}}(M,J) $ , changes during the infinitesimal time interval:$ T_{\rm{H}}(M+{\rm d}M,J+{\rm d}J) = \frac{\partial T_{\rm{H}}}{\partial M}{\rm d}M+\frac{\partial T_{\rm{H}}}{\partial J}{\rm d}J, $

(27) where
$\begin{split} \frac{\partial T_{\rm{H}}}{\partial M} =& \frac{4GM\ell}{\pi \rho_{\rm{h}} \sqrt{M^2\ell^2-J^2}}-\frac{2G}{\pi \rho_{\rm{h}}},\\ \frac{\partial T_{\rm{H}}}{\partial J} =& \frac{8GJ}{\pi \rho_h^3}-\frac{4GJ}{\pi \ell \rho_{\rm{h}}\sqrt{M^2\ell^2 -J^2}}. \end{split}$

Using Eq. (22), the temperature change during the infinitesimal time interval is given by the following:
$\begin{split} {\rm d}T_{\rm{H}} = &\frac{4G\ell (4GJ^2+M\rho_{\rm{h}}^2)}{\rho_{\rm{h}}^2 \sqrt{M^2\ell^2-J^2}}(\omega-m\Omega_{\rm{h}})\\&\times\left(\omega-m\frac{J(4GM\ell^2+\rho_{\rm{h}}^2)}{\ell^2(4GJ^2+M\rho_{\rm{h}}^2)}\right){\rm d}t. \end{split}$

(28) The change in Eq. (28) depends on the initial state of the black hole and the modes of the scalar field; therefore, the temperature may either increase or decrease. However, when the initial black hole becomes extremal, the temperature change exhibits a tendency. To denote the extremality of the black hole, the following is introduced:
$ \delta\equiv M^2\ell^2-J^2. $

(29) When
$ \delta $ is zero, the black hole is extremal. The change in Eq. (28) is divergent to the extremal black hole; thus, it can be expanded under the near-extremal condition,$ \delta\ll 1 $ [42]. Equation (28) becomes$ {\rm d}T_{\rm{H}} = \frac{8GM\ell}{\sqrt{\delta}}(\omega-m\Omega_{\rm{e}})^2{\rm d}t+{\cal{O}}(\delta^0),\quad \Omega_{\rm{e}} = \frac{J}{M\ell^2}, $

(30) where
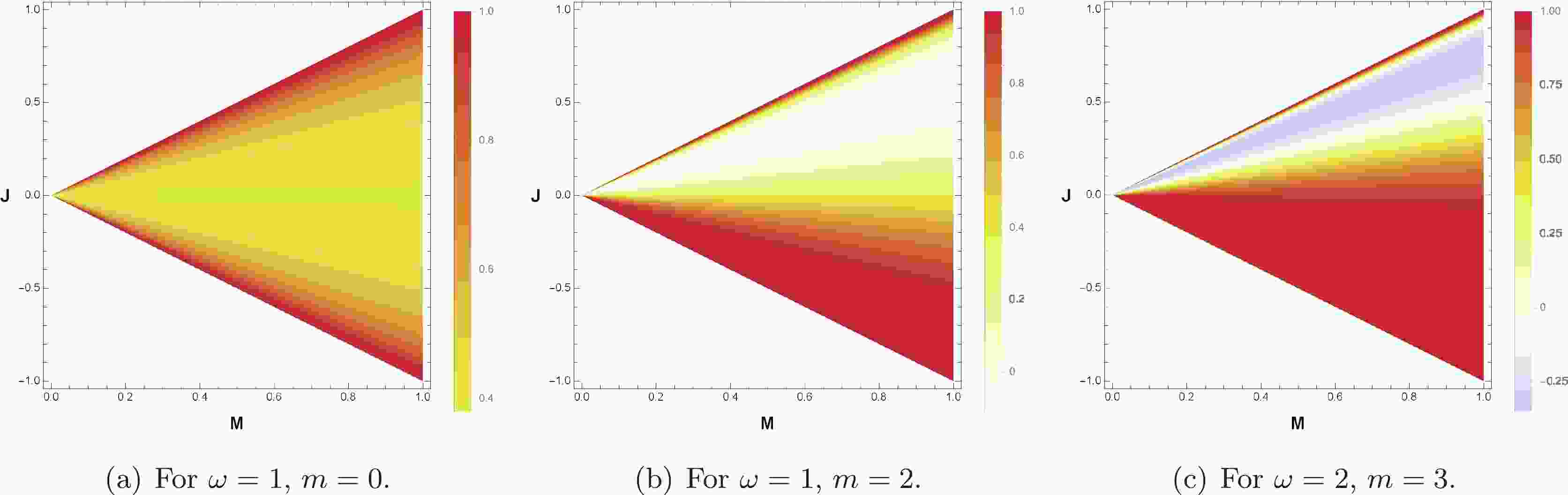
$ \Omega_{\rm{e}} $ is the angular velocity of the extremal black hole. When the black hole becomes extremal, the leading term in Eq. (30) becomes dominant and positive for all modes of the scalar field. This implies that the temperature of the near-extremal black hole invariably increases. However, the temperature of an extremal black hole is zero, indicating that a non-extremal black hole cannot evolve to an extremal black hole under this physical process. This agrees with the third law of thermodynamics presented in [66]. In other words, the black hole cannot achieve zero surface gravity via a finite physical process. Thus, we conclude that the third law of thermodynamics remains valid when the scaterring of the scalar field is used; details regarding the temperature are depicted in Fig. 1. Here, each point$ (M,J) $ represents the initial state of the black hole, and the colors represent the temperature variations for the given modes$ (\omega,m) $ is pre of the scalar field. The sign of the change is more important than the value of the change. Accordingly, the sign of temperature change is preserved using a hyperbolic tangent function. It should be noted that the denominator (i.e.,$ 300 $ ) is arbitrarily chosen. According to Fig. 1, the temperature variations may be positive or negative depending on the initial states. In particular, when the initial states approach the extremal condition, sudden and large positive changes occur, as presented in Eq. (30). Thus, based on the third law of thermodynamics, it is concluded that a black hole cannot be extremal. This implies that the extremal condition acts as a type of bound to attain the extremal condition in the parameter space$ (M,J) $ . Note that the third law has various versions. According to the Nernst theorem, in the limit of zero temperature, an isothermal reversible process can be an isentropic process, and zero temperature cannot be attained by finite processes. Among these versions, Planck's version is more definitive: the entropy of the system is an absolute constant that can be considered zero [67]. However, the third law is not as robust as the first and second laws. In particular, relative to black holes, Wald showed that the entropy cannot be zero; thus, the third law is violated in some systems [68]. Here, the focus is set on the version of Bardeen, Carter, and Hawking: the zero surface gravity cannot be attained in the finite operation of black holes [66]. In an asymptotically flat spacetime, this version of the third law was shown to be valid in [67]. The analysis of Eq. (30) may be a specific proof about the third law in the asymptotically AdS black hole in three dimensions. The significance of the bounds originating from the third law of thermodynamics in dual CFT2 according to the AdS/CFT correspondence is demonstrated.
Figure 1. (color online) Graphs of
$\tanh\left(\frac{1}{300}\frac{{\rm d}T_{\rm{H}}}{{\rm d}t}\right)$ in rotating AdS$_3$ black holes with scalar field mode$(\omega,m)$ .The third law for the black hole side acts as a bound for the eigenvalues
$ (n_{\rm{L}},n_{\rm{R}}) $ . According to the third law, the extremal condition cannot be saturated via a physical process. In terms of the eigenvalues related to the dual CFT, the extremal condition is rewritten as$ \delta = (n_{\rm{R}}+n_{\rm{L}})^2-(n_{\rm{R}}-n_{\rm{L}})^2. $

(31) To make
$ \delta $ equal to zero,$ n_{\rm{R}} $ and/or$ n_{\rm{R}} $ should be zero. However, because the third law prevents$ \delta $ from becoming zero, neither$ n_{\rm{R}} $ nor$ n_{\rm{R}} $ can be zero for a process. For the eigenvalues corresponding to the non-extremal black holes, the variation of$ \delta $ is$ \begin{split} {\rm d}\delta = \frac{\partial \delta}{\partial n_{\rm{R}}}{\rm d}n_{\rm{R}}+\frac{\partial \delta}{\partial n_{\rm{L}}}{\rm d}n_{\rm{L}} = \frac{8\pi (m(n_{\rm{L}}-n_{\rm{R}})+(n_{\rm{L}}+n_{\rm{R}})\ell \omega)\left(m(n_{\rm{L}}-n_{\rm{R}})+\left(n_{\rm{L}}+n_{\rm{R}}+2\sqrt{n_{\rm{L}}n_{\rm{R}}}\right)\ell\omega\right)}{\sqrt{\left(n_{\rm{L}}+n_{\rm{L}}+2\sqrt{n_{\rm{L}} n_{\rm{R}}}\right)\ell}}. \end{split} $

(32) This can be observed in Fig. 2, which is rescaled using the hyperbolic tangent to preserve the sign of temperature change. The eigenvalues cannot be zero under the variations because the change in
$ \delta $ is positive near$ n_{\rm{R}} = 0 $ or$ n_{\rm{L}} = 0 $ . Interestingly, this implies that the black hole cannot be an$ M = 0 $ vacuum by extracting its energy, because$ n_{\rm{R}} = n_{\rm{R}} = 0 $ cannot be achieved, as previously stated. The black hole is considered to be excited from an$ M = 0 $ vacuum [52]; hence,$ n_{\rm{R}} = n_{\rm{R}} = 0 $ also acts as a bound. Therefore, the eigenstates of the dual CFT cannot become zero via any process. -
The Cardy formula indicates that the asymptotic growth of states corresponds to the Bekenstein– Hawking entropy, as shown in Eq. (9). When the mass and angular momentum of the rotating AdS3 black hole vary because of the scalar field, dual CFT2 alters the eigenvalues
$ n_{\rm{R}} $ and$ n_{\rm{L}} $ . Consequently, this modifies the value of the asymptotic growth of states. According to the variation in this growth, the tendency of the eigenvalues and the application of the second law in the dual CFT are derived. The asymptotic growth of states varies as$ {\rm d}S_{\rm{CFT}} = \frac{\partial S_{\rm{CFT}}}{\partial n_{\rm{R}}}{\rm d}n_{\rm{R}}+\frac{\partial S_{\rm{CFT}}}{\partial n_{\rm{L}}}{\rm d}n_{\rm{L}}, $

(33) where the variations in the eigenvalues are given in Eq. (26) in terms of the parameters of the scalar field. Accordingly, the following is obtained:
$ {\rm d}S_{\rm{CFT}} = \pi^2\ell \left(\sqrt{\frac{c}{6n_{\rm{R}}}}+\sqrt{\frac{c}{6n_{\rm{L}}}}\right)(\omega-m\Omega_{\rm{h}})^2 \rho_{\rm{h}}{\rm d}t\geqslant 0. $

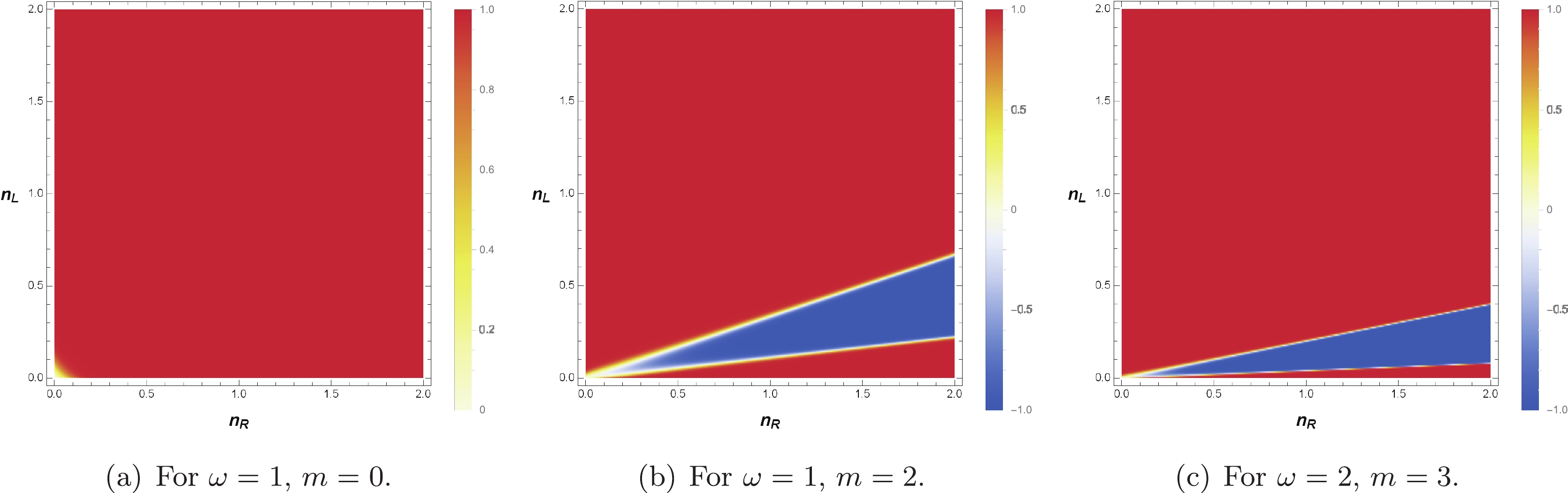
(34) The increase in the asymptotic growth of states represents the second law of thermodynamics according to Eq. (9). Moreover, because it is known that
$ n_{\rm{R}} $ and$ n_{\rm{L}} $ are non-zero values, the variation in the Cardy formula diversifies near$ n_{\rm{R}} = 0 $ or$ n_{\rm{L}} = 0 $ . The detailed behaviors in Eq. (34) are depicted in Fig. 3; here, the increase in the asymptotic growth is ensured. Furthermore, as shown in Fig. 2, the eigenvalues cannot be zero, and the asymptotic growth sharply increases similar to the bound that ensures non-zero eigenvalues. This implies that the changes in eigenvalues are also connected and constrained under physical processes in a manner similar to that applied to its dual black hole. As the changes in the black hole are clearly related to the scattering of the scalar field, the eigenvalues can only change with specific directions because the mass and angular momentum are directly related to the eigenvalues as a result of the AdS/CFT duality. According to Eq. (7),
Figure 3. (color online) Graphs of
$\tanh\left(\frac{1}{300}\frac{{\rm d}S_{\rm{CFT}}}{{\rm d}t}\right)$ in eigenvalues$(n_{\rm{R}},n_{\rm{L}})$ with scalar field mode$(\omega,m)$ .$ {\rm d}n_{\rm{R}} = \frac{1}{2}(\ell {\rm d}M +{\rm d}J),\quad {\rm d}n_{\rm{L}} = \frac{1}{2}(\ell {\rm d}M -{\rm d}J), $

(35) which is also connected to the modes of the scalar field by Eq. (26). The one-to-one correspondence in Eq. (35) makes the zero-eigenvalue states working as bounds meaningful. Again, the black holes and CFTs are dual to each other; hence, the changes in eigenvalues should be restricted because these changes also satisfy Eq. (7) on the gravity side. Then, according to the third law, the black hole cannot be extremal by a finite process. Thus, the eigenvalues cannot be zero states that are dual to the extremal condition.
Therefore, according to the laws of thermodynamics for the black hole, the eigenvalues
$ n_{\rm{R}} $ and$ n_{\rm{L}} $ cannot be zero. If one of these eigenvalues tends to zero, the asymptotic growth sharply increases, thereby increasing the eigenvalue. -
The relationships between the physical boundaries for the rotating AdS3 black hole and its dual CFT2 according to the AdS/CFT correspondence are invetigated, and the black hole is specified by its conserved quantities. The conserved quantities, such as mass and angular momentum, are clearly bounded by the extremal condition. The third law of thermodynamics ensures that extremality cannot be achieved via any physical process, and the second law implies that such a bounded behavior is naturally preferred. For the rotating AdS3 black hole satisfying this particular boundary condition, the conserved quantities can be directly related to the microstates of its dual CFT2. Moreover, the second law of thermodynamics coincides with the Cardy formula in dual CFT2. Owing to the scattering of the scalar field, we conclude that the changes in the black hole conform to the laws of thermodynamics and that the third and second laws act as bounds to the mass and angular momentum. Consequently, this particular relationship is imposed for a few black holes to rewrite the conserved quantities as eigenvalues in dual CFT2. Here, the third law implies that the eigenvalues
$ n_{\rm{R}} $ and$ n_{\rm{L}} $ cannot be zero. The variation in the eigenvalues decreases their difference; hence, the extremality becomes small under the changes caused by the scalar field. The second law ensures that the asymptotic growth of states on the CFT2 side sharply increases when one of the eigenvalues tends to zero. Therefore, such an extremely large difference between$ n_{\rm{R}} $ and$ n_{\rm{L}} $ cannot be achieved via a physical process. Even if such a large difference is considered as an initial condition, it decreases by a small perturbation. Therefore, according to the AdS/CFT correspondence, the laws of thermodynamics for the rotating AdS3 black hole are closely related to the non-zero state of the eigenvalues in CFT2.
Thermodynamics in rotating anti-de Sitter black holes with massive scalar field in three dimensions
- Received Date: 2020-06-04
- Available Online: 2020-12-01
Abstract: We investigated the tendency in the variations of CFT2 when a rotating AdS3 black hole changes because of the fluxes transferred by the scattering of a massive scalar field according to the anti-de Sitter (AdS)/conformal field theory (CFT) correspondence. The conserved quantities of the black hole are definitely constrained by the extremal condition. Moreover, the laws of thermodynamics provide a direction for the changes in the conserved quantities. Therefore, the black hole cannot be extremal under the scattering; this is naturally preferred. According to the relationship between the rotating AdS3 black hole and dual CFT2, we find that such changes in the black hole constrain the variations in the eigenstates of dual CFT2. Furthermore, the tendency in the variations is closely related to the laws of thermodynamics.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: