Fully self-consistent calculation of β-decay half-lives within Skyrme energy density functional

$ \beta $-decay has played an important role in the history of modern physics. Presently, with the development of radioactive nuclear beam facilities, $ \beta $-decay plays an important role in exploring the limits of stability in nuclear physics. In nuclear astrophysics, the $ \beta $-decay is an essential ingredient in almost all stellar processes [1-4]. Knowledge about $ \beta $-decay and neutrinoless double $ \beta $-decay is also important for physics beyond the standard model [5].

Recently, experiments conducted on the $ \beta $-decay half-lives of nuclei far from the stability line have made significant progress. Theoretical studies of $ \beta $-decay half-lives mainly fall into three categories. The first and earliest developed theory is the parametric phenomenological description, including the gross theory [6], the Kratz-Herrmann formula [7, 8], and the new exponential law of $ \beta $-decay half-lives [9-11]. The other two theories are microscopic approaches: the large basis interacting shell model [12-16] and the charge-exchange random phase approximations (RPA) [17-29]. Earlier systematic calculations of the $ \beta $-decay half-lives with charge-exchange QRPA [17] and RPA [18] models employed schematic effective NN-interactions and empirical deformed single-particle potentials. Since then, numerous versions of charge-exchange RPA (or QRPA) have become available in the literature. Some calculations violate the self-consistency, which is a critical theoretical requirement to have predictive power for nuclei far from the experimentally known regions [1]. Fully self-consistent RPA had been developed, employing the matrix formulation of RPA for the non spin-flip and spin-flip excitations within the Skyrme energy density functional [30-33]. The first attempt of self-consistent charge-exchange QRPA on top of HFB was made in Ref. [34], where the Skyrme zero-range force and a finite-range pairing interaction were used to estimate $ \beta $-decay half-lives of spherical neutron-rich r-process waiting-point nuclei. Recently, beta-decay half-lives of nuclei were also predicted by the machine learning method with very good accuracy [35].

In this work, $ \beta $-decay half-lives of magic and semi-magic nuclei were calculated in the allowed Gamow-Teller (GT) approximation; the ground and excited states were obtained in a fully self-consistent Hartree-Fock (HF) plus charge-exchange RPA. The same Skyrme interaction was adopted in both ground and excited states calculations to fulfill the requirement of self-consistency. The contribution from $ {{J}}^2 $ terms to $ \beta $-decay half-lives, which was often omitted in fitting procedures of numerous Skyrme parameter sets [33, 36], is considered in this study due to its impact on the strength function of spin-flip excitations in finite nuclei [33]. In Ref. [37], we discussed the contribution of $ J^2 $ terms to M1 and GT resonances. We found that the $ J^2 $ terms have a strong impact on the distribution of GT strength in finite nuclei, and consequently those terms affect the $ \beta $-decay half-life, because it is very sensitive to the strength in the low-energy $ \beta $-decay window. The comparison with results of other theoretical models and different density functionals is also discussed in the text.

The outline of the paper is the following. In Sec. II, the theoretical model is briefly presented, focusing in particular on the particle-hole residual interaction from the $ J^2 $ terms. In Sec. III, we present the results for the $ \beta $ decay of some selected nuclei calculated using different Skyrme interactions. In Sec. IV, we summarize the results and draw our conclusions.

The calculations are performed within the HF plus charge-exchange RPA, and the standard Skyrme interaction [36] is used as an effective two-body nucleon-nucleon interaction in the calculations. The Skyrme HF calculation is presented in Refs. [31, 36], and thus not repeated here. For the charge-exchange RPA method, its matrix form is presented in Refs. [38, 39]. We briefly summarize the formulas as follows. The RPA equation reads as

where $ E_{\nu} $ is the eigenvalue of the $ \nu $-th charge-exchange excited state, and $ {{X}}^\nu $, $ {{Y}}^\nu $ are the corresponding forward and backward amplitudes, respectively. A and B are the matrix elements of residual interaction, they are written as

where the sub-indexes $ i,j $ are the hole states; $ m,n $ are the particle states; $ V_{{\rm{res}}} $ is the residual interaction; and $ \epsilon $ is the energy of a single-particle state. The particle-hole (p-h) matrix elements are calculated based on the Skyrme energy density functional; all other terms except for the Coulomb term are included in charge exchange case. One can find the detailed expression of p-h matrix elements in Ref. [32]. We also wrote down in detail the formulas for tow-body p-h matrix elements of non spin-flip RPA [31]; some of them are common in charge-exchange and normal RPA.

With the standard Skyrme force, the Skyrme energy density functional may be obtained [36], which is a function of various densities. Among those terms, the terms due to tensor coupling with spin and gradient are usually referred to as $ {{J}}^2 $ terms in the literature. These are the functions of spin-densities $ J_q(r) $, where $ q = n(p) $ is the isospin quantum number, and $ {{J}}^2 $ terms have the following expression

with

where the index i runs over all hole states for a given q, and $ \phi_i(r) $ is the radial wavefunction. Some Skyrme energy functionals were fitted and used without including the $ {{J}}^2 $ terms in the ground state calculation. To maintain the self-consistency in the excited states calculation, the contribution to residual interaction from $ {{J}}^2 $ terms shall be switched off [31, 33]. Because those terms yield the contribution to the residual interaction in the spin and spin-isospin channels, the Landau-Migdal parameters $ G_0 $ and $ G_0^{'} $ could be changed accordingly [37, 40]. They shall also affect the distribution of strength functions of finite nuclei in spin-flip modes, such as the M1 and GT giant resonances. The half-lives of the $ \beta $-decay could be influenced if the calculations are not done self-consistently. This is one point that is addressed in the following paragraph.

After solving the RPA equation, the reduced transition strength is generally given by

The process of $ \beta $-decay happens from an initial ground or excited state in a mother nucleus to a final state in the daughter nucleus. For the allowed $ \beta $-decay transitions, the GT operator is chosen as the external operator $ \hat{F}_J $, and we do not consider the allowed Fermi transition in present calculations. The external operator is

The calculation of the $ \beta $-decay half-life was suggested using the well-known Fermi Golden Rule. A fairly extensive account of these steps is provided in Refs. [41, 42]. In general, the $ \beta $-decay half-life of a nucleus can be calculated in the allowed GT approximation using the following formula

where the constant $ D \equiv \dfrac{2\pi^3\hbar^7ln2}{g_A^2m_e^5c^4} = 6163.4\pm3.8 $ s [21], and $ g_A $ is the weak axial nucleon coupling constant. $ B(GT,E_m) $ is the GT nuclear matrix element, where the summation index m runs over all final decay states with an excitation energy $ E_m $ (referred to the ground state of daughter nucleus) that is smaller than the $ \beta $-decay energy $ Q_\beta $, and $ E_0 = Q_\beta+m_ec^2-E_m $ is the maximum energy of the$ \beta $ particle. $ f(Z,A,E_0) $ is the integrated Fermi function describing the size of phase space, which is expressed by

where relative energy of the $ \beta $ particle $ \epsilon_0 = (E_0/m_ec^2) $ and $ \epsilon = (E/m_ec^2) $, and E is the total energy of the $ \beta $ particle. $ F(Z,A,\epsilon) $ is the Fermi function, which accounts for the effects of Coulomb screening and finite-size corrections due to nuclear charge distribution [43].

The excitation energy $ E_{\nu} $ in Eq. (1) is usually referred as to the ground state of the mother nucleus, where $ E_{\nu} = E_m+\triangle B $ and $ \triangle B = \triangle_{nH}-Q_\beta $, where $ \triangle B $ denotes the binding energy difference between the mother and daughter nuclei, and $ \triangle_{nH} $ is the mass difference between the neutron and hydrogen atom. Then, $ E_m = E_{\nu}-\triangle_{nH}+ Q_\beta\leqslant Q_\beta $ and $ E_0 = \triangle_{nH}+m_ec^2-E_{\nu} $, and the $ \beta $-decay half-life formula Eq. (8) can be rewritten as

where $ E_{\nu} $ and $ B(GT,E_{\nu}) $ are the outputs of the self-consistent RPA calculation.

In this study, we pay attention to the contribution of $ {{J}}^2 $ terms to $ \beta $-decay half-lives of nuclei. $ {{J}}^2 $ terms are often omitted in the fitting procedure of some parameter sets, and we exclude those terms in the excited states calculation accordingly to maintain the self-consistency. We apply the Skyrme HF plus charge-exchange RPA approach to some typical magic and semi-magic nuclei with experimental $ \beta $-decay half-lives. In the calculations, the shape of the nuclei is assumed to be spherical, the pairing contribution is not included, and the equal filling approximation in semi-magic nuclei is employed. The ground state properties of these nuclei are calculated in the coordinate space with a box approximation, where the radius of the box is set to be 21 fm. The $ \Delta_n = 8 $ shell cut-off is adopted to build the RPA model space, which is sufficient to fulfill the Ikeda GT sum rule. We have also checked the convergence of the calculated $ \beta $-decay half-life; for example, the calculated results of ¹⁵⁰Ce are 0.7170, 0.7099, and 0.7072 s using the SKX interaction if we use the shell cut-off $ \Delta_n = 7, 8, 9 $, respectively. The results indicate that a good convergence is obtained if we use $ \Delta_n = 8 $.

First, let us discuss the self-consistency in the calculations. According to previous studies [33, 37], the inclusion of $ {{J}}^2 $ terms has a strong effect on Landau parameters $ G_0 $ and $ G_0^\prime $, as well as the distribution of GT strength function, which further has an impact on the calculated $ \beta $-decay half-lives. For example, SGII [44] is the parameter set that omits $ {{J}}^2 $ terms in ground states in the fitting procedure. The contribution of those terms shall be blocked down when the SGII parameter set is used to calculate the spin-isopsin flip GT excitations of nuclei. Fig. 1 displays relative deviations $ (T_{00}-T_{01})/T_{00} $ and $ (T_{00}-T_{11})/T_{00} $ for typical magic and semi-magic nuclei by the Skyrme HF plus RPA approach with SGII interaction. $ T_{00} $ is the $ \beta $-decay half-life obtained by excluding $ {{J}}^2 $ terms both in ground and excited states. This indicates that the calculation of $ T_{00} $ is fully self-consistent with the SGII parameter set, whereas $ T_{01} $ is calculated by excluding $ {{J}}^2 $ terms in ground states and including them in excited states; $ T_{11} $ is obtained by including $ {{J}}^2 $ terms both in ground and excited states. The latter two calculations break the self-consistency of the theoretical framework for SGII interaction. Fig. 1 shows that $ {{J}}^2 $ terms play a role in predicting $ \beta $-decay half-lives. The results obtained considering $ {{J}}^2 $ terms consistently for these nuclei are higher than the values (except for the data of $ ^{78} $Ni and $ ^{102} $Sr of $ T_{11} $) when $ {{J}}^2 $ terms are treated inconsistently. The effect is more obvious for lighter nuclei than for heavier ones; in Fig. 1, the smallest and largest relative derivations (in absolute values) are 0.07 and 0.88, respectively. The $ \beta $-decay half-lives of $ ^{22} $O and $ ^{24} $O calculated using SGII in a fully self-consistent calculation are 72.070 and 5.936 s, respectively. In the case of T$ _{01} $ (T$ _{11} $), the half-lives are 22.395 (8.696) and 2.703 s (1.788 s) for $ ^{22} $O and $ ^{24} $O, respectively, the values having changed by more than fifty percent. Further, there is a similar effect on the $ \beta $-decay half-lives of finite nuclei if we perform the same calculation using other parameter sets.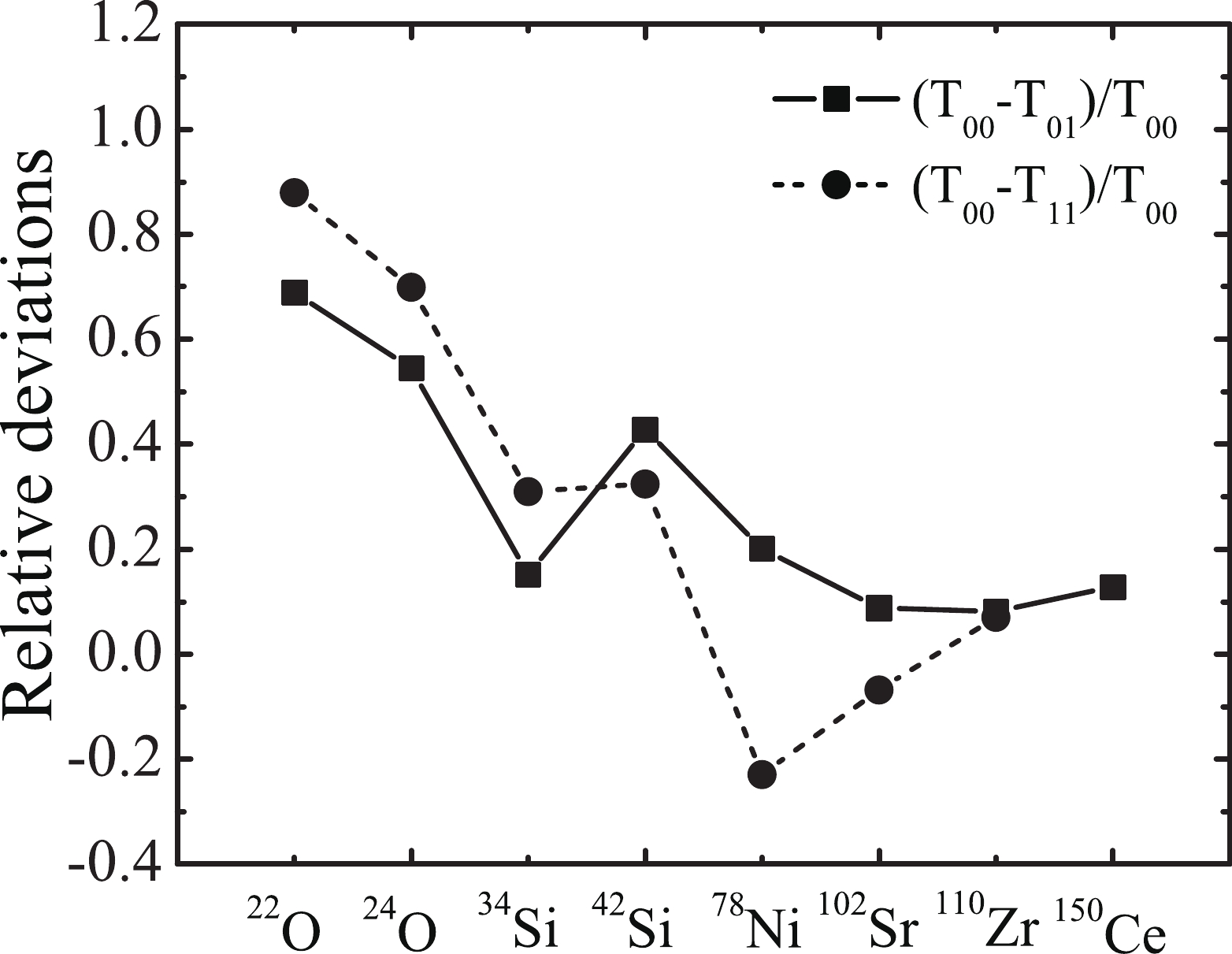

Figure 1.  Relative deviations $(T_{00}-T_{01})/T_{00}$ and $(T_{00}-T_{11})/$ $T_{00} $ for typical magic and semi-magic nuclei by Skyrme HF plus RPA approach with SGII interaction. $T_{00}(T_{11})$ is the $\beta$-decay half-life calculated by excluding (including) ${{J}}^2$ terms both in ground states and in excited states, whereas $T_{01}$ is calculated by excluding ${{J}}^2$ terms in ground states and including them in excited states.

Fully self-consistent calculated $ \beta $-decay half-lives of selected magic and semi-magic nuclei are listed in the fifth to eighth columns of Table 1. The calculations are performed within Skyrme HF plus the charge-exchange RPA approach with SGII [44], LNS [48], SKX [49], and SAMi [50] interactions. The Landau parameters $ G_0 $ and $ G_0^\prime $ were considered as constraints in the fitting procedure of the above Skyrme interactions, which are important for spin-isospin flip responses and $ \beta $-decay half-lives of nuclei. Experimental values [46] and results from other three theoretical models are also displayed, including the recently proposed pnQRPA calculation from Ni [47] with a $ \delta $-form GT residual interaction, the empirical exponential law results from Zhang [10], and the finite-range droplet model QRPA results obtained by Möller [19]. The first four columns in Table 1 denote the element symbol, mass number of parent nuclei, experimental $ \beta $-decay energy and half-life.

element	A	$ Q^{\rm{exp}}_{\beta^-} $[45]	T$_{1/2}^{\,\rm{exp} }$[46]	SGII	LNS	SKX	SAMi	Ni [47]	Zhang [10]	Möller [19]
O	22	6.490(60)	2.25(9)	72.070	0.434	0.545	0.917	0.780	0.050	8.299
	24	10.960(190)	0.072(5)	5.936	0.101	0.106	0.361	0.049	0.015	0.243
Si	34	4.592(14)	2.77(20)	447.809	28.932	15.759	535.963	6.690	0.410	20.571
	42	15.460(590)	0.0125(35)	0.941	0.060	0.023	0.397	0.0034	0.0278	0.032
Ca	52	6.180(80)	4.60(3)	−	20.765	123.572	1077.770	0.100	0.400	0.6122
Ni	68	2.103(3)	29(2)	−	1027255.637	38.289	−	−	−	−
	78	10.610(780)	0.1222(51)	15.370	0.745	0.161	37.999	0.044	0.071	0.1404
Ge	82	4.690(4)	4.56(26)	−	100729.983	18.997	−	2.820	3.410	30.0553
Sr	102	9.010(70)	0.069(6)	0.160	0.015	0.009	0.275	0.035	0.056	0.119
Zr	104	6.095(10)	0.87(6)	0.584	0.044	0.020	1.297	0.269	0.396	0.7416
	110	9.420(1030)	0.0375(20)	0.185	0.016	0.008	0.266	0.027	0.014	0.0745
Sn	132	3.089(3)	39.7(8)	−	−	40.914	−	−	3.900	27.9702
Ce	150	3.454(14)	4.0(6)	527.495	1.440	0.710	−	2.900	4.200	6.9476

Table 1.  Calculated $ \beta $-decay half-lives by Skyrme HF plus charge-exchange RPA approach with SGII, LNS, SKX, and SAMi interactions. Experimental values and results from three theoretical models are also presented. We show the experimental decay energy $ Q^{\rm{exp}}_{\beta^-} $ in this table. The unit of $ \beta $-decay half-life $ T_{1/2} $ is in second (s), and the decay energy $ Q^{\rm{exp}}_{\beta^-} $ is in MeV.

Table 1 indicates discrepancies between the results obtained by different Skyrme interactions, though they are calculated in a fully self-consistent way. For example, the experimental $ \beta $-decay half-life of nucleus $ ^{102} $Sr is 0.069 s, while predictions from SGII, LNS, SKX, and SAMi interactions are 0.160, 0.015, 0.009, and 0.275 s, respectively. All of these four interactions yield reasonable results. However, for lighter nuclei $ ^{22} $O, calculations by LNS, SKX, and SAMi interactions yield similar results, which are 0.434, 0.545, and 0.917 s, respectively. They are all in the same order of magnitude and not substantially different from the experimental value of 2.25 s, while the result of the SGII interaction is 72.070 s, about 100 times larger compared to the results of previous three Skyrme interactions. For the heavier nucleus $ ^{104} $Zr, the experimental $ \beta $-decay half-life is 0.87 s. The predicted values obtained via the SGII and SAMi interactions are 0.584 and 1.294 s, which are close to experimental values. However, predictions by LNS and SKX interactions are 0.044 and 0.020 s, deviating significantly from experimental values and results of other Skyrme interactions.

In Table 1, the symbol "-" indicates that the half-life of the nucleus cannot be calculated by the corresponding theoretical method, such as $ ^{52} $Ca, $ ^{68} $Ni, $ ^{82} $Ge, and $ ^{132} $Sn by SGII interaction, and $ ^{132} $Sn by LNS interaction. This is because there are no excited GT states appearing in the beta-decay window of that nucleus for the corresponding interaction; thus, it is a beta-stable nucleus in our model. The half-life predictions with the LNS interaction for nuclei $ ^{68} $Ni and $ ^{82} $Ge are likewise far from the experimental values. These two situations result from the same reason, namely, the low energy GT strengths in the $ \beta $-decay window for these nuclei are not strong enough for a LNS Skyrme interaction. As stated in Eq. (10), the $ \beta $-decay half-life is in inverse proportion to the reduced transition strength $ B(GT,E_{\nu}) $ and integrated fermi function $ f(Z,A,E_0) $. Furthermore, $ f(Z,A,E_0) $ entails a direct proportion upto about $ {\epsilon_0^5} $ (see estimation in Ref. [41] for details). Consequently, the $ \beta $-decay half-life is very sensitive to low energy excitations. Regarding $ ^{68} $Ni, the calculation by LNS interaction yields only one final decay state ($ \nu = 1 $ in Eq. (10)) with $ B(GT,E_{\nu}) *f(Z,A,E_0) = $$ 0.006 $, whereas the result of the SKX interaction yeilds four final decay states ($ \nu = 4 $ in Eq. (10)) with maximum $ B(GT,E_{\nu})* f(Z,A,E_0) = 159.438 $. This is because the $ \beta $-decay half-life of $ ^{68} $Ni calculated by the LNS interaction is about twenty-seven thousand times the value given by the SKX interaction.

For long-lived nuclei $ ^{68} $Ni and $ ^{132} $Sn, whose experimental $ \beta $-decay half-lives are 29 and 39.7 s, respectively, their lives are more difficult to predict. For the seven different theoretical calculations listed in Table 1, only the HF plus charge-exchange RPA method with SKX interaction can reproduce their $ \beta $-decay half-lives well, while the calculation performed by Möller can reproduce the $ \beta $-decay half-life of $ ^{132} $Sn.

To elaborate on the difference between our models and others, we display ratios of calculated $ \beta $-decay half-lives to experimental data for typical magic and semi-magic nuclei with four microscopic theoretical models in Fig. 2, including the Skyrme HF plus charge-exchange RPA approach with SKX and LNS interactions, the pnQRPA calculations of Ni, and the finite-range droplet model QRPA results of Möller. The four calculations are depicted with diamonds (SKX), squares (LNS), solid circles (Ni's data), and uptriangles (Möller's data). The dotted line in Fig. 2 indicates that the calculated results are equal to experimental values. For the results of nuclei $ ^{68} $Ni and $ ^{82} $Ge given by the LNS interaction, as shown in Table 1, the ratios are larger than twenty thousand, and we exclude those two datasets in Fig. 2 to clearly present other results. Almost all calculations of the four models give reasonable results for the nuclei in comparison to experimental values. However, the $ \beta $-decay half-lives calculated by different models exhibit different behaviors for these nuclei. The results obtained by the LNS and SKX interactions behave approximately in the same way, and they tend to overestimate $ \beta $-decay half-lives of nuclei lighter than $ A = 100 $, while their results are all lower than the experimental values for heavier nuclei. Calculations of Ni systematically underestimate the experimental data, while Möller's results systematically overestimate the experimental data of $ \beta $-decay half-lives for most nuclei.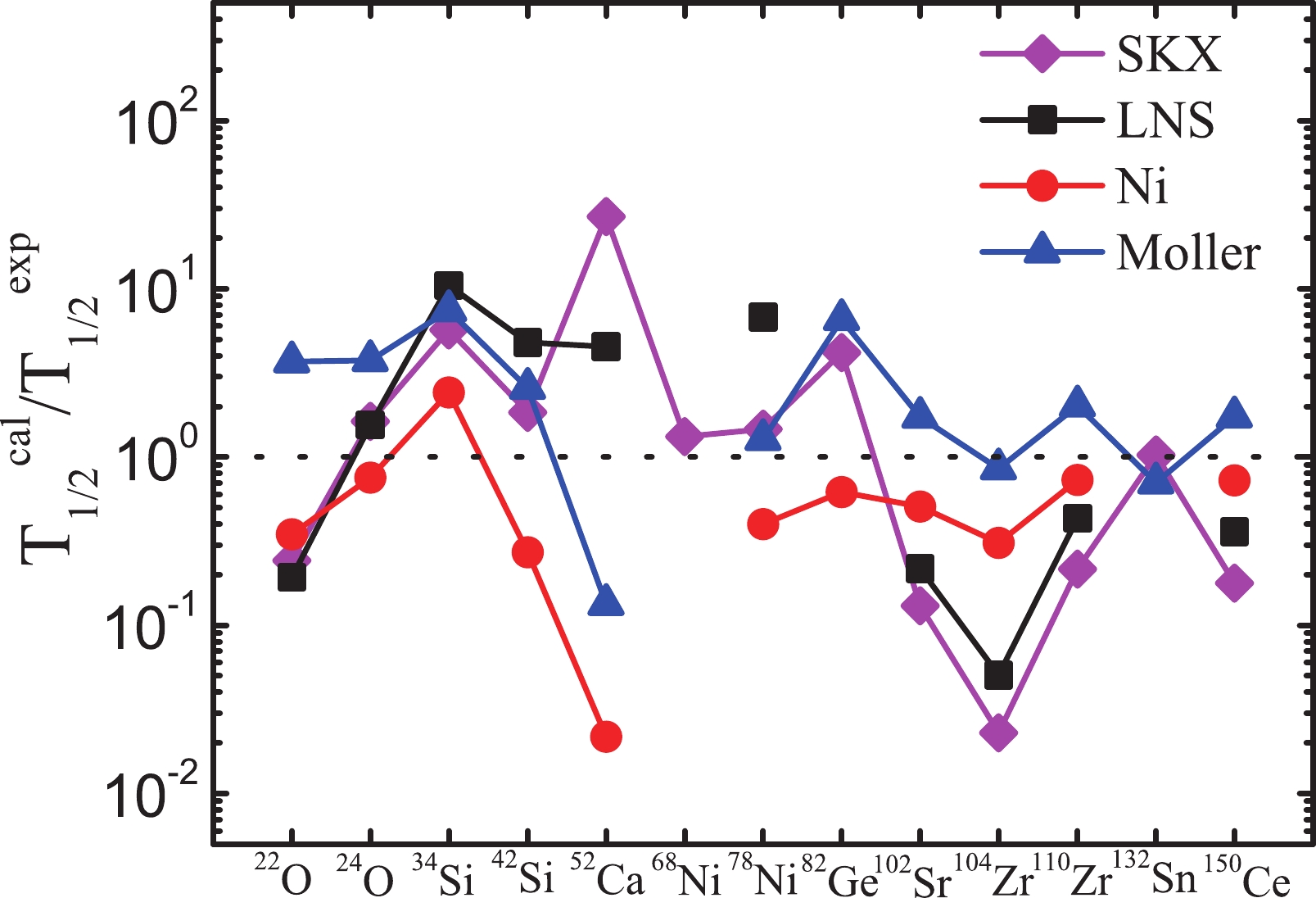

Figure 2.  (color online) Ratios of calculated $ \beta $-decay half-lives to experimental data for typical magic and semi-magic nuclei with four theoretical models, including the Skyrme HF plus charge-exchange RPA approach with SKX (diamonds) and LNS (squares) interactions, pnQRPA calculations of Ni (solid circles) and finite-range droplet model QRPA results of Möller (uptriangles).

We display $ \beta $-decay $ 1^+ $ spectra of nuclei near the stability line in Table 2, which are obtained from experiments and the corresponding Skyrme HF plus charge-exchange RPA calculations with SGII, LNS, SkX, and SAMi interactions. The last four columns in the table denote the half-life, intensity per decay, partial $ 1^+ $ excitation energy of daughter nuclei and the log$ ft $ value. Overall, the theoretical predictions of $ 1^+ $ spectra do not agree well with experimental data for most nuclei listed in the table, as there are several experimental $ \beta $-decay $ 1^+ $ spectra existing in the daughter nucleus for most nuclei (except for $ ^{98} $Zr), whereas only one state is predicted by the theoretical calculation. One experimental branch dominates in the $ \beta $-decay process for all the nuclei, as shown in the table. Although the $ \beta $-decay half-life of $ ^{20} $O and the intensity per decay of first state can be efficiently predicted by LNS, the relative errors of the predicted $ \beta $-decay level and log$ ft $ value are large. For $ ^{22} $O and $ ^{98} $Zr, none of the theoretical results can reproduce both the experimental $ 1^+ $ levels and log$ ft $ values well. The levels given by LNS and SAMi in $ ^{22} $O and the level given by SGII in $ ^{98} $Zr are close to the experimental data. For log$ ft $ values, all theoretical results are lower than the data. For $ ^{128} $Sn and $ ^{132} $Sn nuclei, only the calculation with the SKX interaction can yield a reasonable $ \beta $-decay half-life, and the partial $ 1^+ $ excitation energy of daughter nucleus and log$ ft $ value are also close to the experimental data. To solve the discrepancy mentioned above, the calculation may need to be performed beyond the mean field approximation [52-54], where the single-particle states are more fragmented. Therefore, better predictions on the $ \beta $-decay partial $ 1^+ $ spectra and the log$ ft $ values might be achieved.

nuclei	methods	T$_{1/2}$ /s	Int (%)	E$_{1^+}$/MeV	log$ft$
$^{20}$O	EXP	13.51(5)	0.027(3)	3.49	3.64(6)
			99.973(3)	1.06	3.7340(6)
	LNS	15.47	100	1.83	3.17
	SKX	21.49	100	1.76	3.38
	SAMi	23.87	100	1.92	3.28
$^{22}$O	EXP	2.25(9)	68(8)	2.57	3.8(1)
			31(5)	1.63	4.6(1)
	SGII	72.07	100	3.79	3.40
	LNS	0.43	100	2.30	3.05
	SKX	0.55	100	1.78	3.39
	SAMi	0.92	100	2.62	3.28
$^{98}$Zr	EXP	30.7(4)	100	0	4.154(10)
	SGII	4.99	100	-0.25	3.56
	LNS	0.19	100	-2.34	3.29
	SAMi	112.18	100	1.16	3.45
$^{128}$Sn	EXP	3544.2(84)	16.1(25)	0.83	4.62(8)
			84(10)	0.64	4.44(6)
	SKX	11850.98	100	0.95	3.80
$^{132}$Sn	EXP	39.7(8)	0.88(7)	2.27	4.82(4)
			99(4)	1.33	4.02(2)
			<0.19	0.48	>7.4
	SKX	40.9	100	1.48	3.87

Table 2.  Experimental $\beta$-decay $1^+$ spectra [51] (EXP) and calculated $1^+$ spectra by Skyrme HF plus charge-exchange RPA approach with SGII, LNS, SkX, and SAMi interactions. See the text for details.

In conclusion, $ \beta $-decay half-lives of nuclei have been studied in a fully self-consistent Skyrme HF plus charge-exchange RPA approach. We adopt the same Skyrme energy density functional in ground state and GT excited state calculations to satisfy the full self-consistency requirement. Typical even-even semi-magic and magic nuclei with measured experimental values are chosen for the investigation; in this case pairing effects can be neglected, and spherical approximation is employed. The calculations were performed within SGII, LNS, SKX, and SAMi Skyrme energy density functionals. The effect of $ {{J}}^2 $ terms on $ \beta $-decay half-lives is investigated for the SGII interaction, which reveals a large influence on the$ \beta $-decay half-lives of finite nuclei. We further compare the calculated $ \beta $-decay half-lives with experimental values and other theoretical models. The microscopic numerical results reveal a strong dependency on the choice of Skyrme interactions. Meanwhile, the $ \beta $-decay half-life calculation can be engaged as a benchmark to testify lower energy GT excitations. Further systematic investigations on $ \beta $-decay half-lives of finite nuclei, by incorporating the tensor force into the Skyrme energy density functional [55-57], are in progress.

Discussions with Yi-Fei Niu are gratefully acknowledged.