HTML
-
The fusion burn of Li nuclei in the
$ ^7{\rm{Li}}(n,n'\alpha)t $ and$ ^6{\rm{Li}}(n,\alpha)t $ reactions under the neutrons generated at the respective facilities as a result of the$ dt\to\alpha n $ controlled reaction is of importance in tritium self-reproduction. Decreased efficiency of the thermonuclear facility and mal-synchronization of the tritium-reproduction cycle may be attributed to inadequate understanding of how the fast ions in preheated$ dt $ plasma interact with Li nuclei within the blanket material. Among the ion induced nuclear reactions in the thermonuclear reactor walls, the most interesting are the reactions that produce additional tritium recovery. These include the$ (d,t) $ reaction in the 6Li(d,t)p$ \alpha $ , proceeding through a compound 5Li nucleus, and the 7Li(d,t)d$ \alpha $ and 7Li(d,t)6Li processes. An important feature of the deuteron induced reactions on Li nuclei is that they are mostly exothermal reactions, ranging from ($ d,\gamma $ ) radiation capture to partial fragmentation of the target nucleus into three or more clusters. The energy thus removed by the deuterons from the$ dt $ reaction site may be partially compensated by additional tritium produced in the blanket as well as by virtue of the charged particles formed through several exothermic reactions possible for Li nuclei up to the deuteron kinetic-energy level$ E_d = 20 $ MeV.Most experimental studies of deuteron-Li reactions were carried out in the last century. Tritium formation on the 6Li and 7Li isotopes in the energy region
$ E_d\le4 $ MeV was investigated in [1]. The angular distributions were not measured. More details were given in relation to the formation of charged particles – helium and hydrogen isotopes – in the course of the deuteron-Li reactions. Formation of two$ \alpha $ -particles was an active area of research in [2-6]. The total cross sections of the(d, p, or n) stripping reactions, accompanied by formation of both unstable 7Be [2, 7, 8] and 8Li [2, 9, 10] and stable 7Li [2, 3] nuclei, were measured. Currently, there are no data regarding the 7Li(d,n)8Be exothermal reaction. No evidence of the three-body break up reactions with the three particles being formed in the final state was given either. Such reactions refer to the above-mentioned studies [7, 8], focusing on the reactions to convert an initial scattering state into a two-neutron one. This also applies to [11], where total cross sections of the 6Li (d,n3He)4He and 6Li (d,p3H)4He three-body break up reactions were measured in the energy region$ E_d\leqslant 0.8 $ MeV. Although the d+Li system has always attracted much interest, there are no data on some of the d+Li reactions, such as 6Li$ (d,2d')\alpha $ , 6Li$ (d,np)^6 {\rm{Li}}$ , 7Li$ (d,2\alpha)n $ , 7Li$ (d,d')t\alpha $ , and 6Li$ (d,np)^7 {\rm{Li}}$ . There are also no data on (d,$ \gamma $ ) radiation capture for both 6Li and 7Li nuclei, although there is some evidence of the resonance structure in the 7Li$ (d,\gamma)^9 {\rm{Be}}$ process in the energy region$ E_{d} $ = 0.35-0.4 MeV [9].The theoretical treatment in this field primarily covers the refined optical models, with parameters selected to describe differential-angular distributions of deuteron elastic scattering by Li nuclei. The most detailed study of deuteron elastic scattering is given in Ref. [12] at
$ E_d $ = 3-50 MeV and in Ref. [13] at$ E_d $ = 10-50 MeV. The latter study reports on sets of optical model parameters found for the considered energy region. They are used in calculations within the continuum discretized coupled-channels (CDCC) formalism to describe the differential cross sections of deuteron elastic scattering. The optical models used in the context of the coupled-channel formalism can provide useful information on the total contribution of various inelastic channels in their total cross sections (the so called reaction cross section), as well as on the partial cross sections, but the available references do not give such predictive calculations. There are only calculated cross sections for the inclusive 7Li$ (d,Xn) $ and 7Li$ (d,Xp) $ reactions to predict the total yield of continuum neutrons and continuum protons in the dipole giant-resonance energy region$ E_d\geqslant $ 20 MeV [14], in which the main contribution to the cross-section comes through Glauber (diffraction) scattering. In addition, there are crude estimates for the s-wave cross section of deuteron induced reactions on the 7Li [15] nucleus in the energy region$ E_d $ = 0.4-1 MeV. Use of the statistical Hauser-Feshbach model with formation of a combined nucleus and its break-up, irrespective of the triggering mechanism, appears to be dubious and of limited value in Ref. [16] for a light nuclei with an open p-shell and a small number of neutron resonances. Currently, microscopic models of the deuteron-Li reactions are unavailable, and they have not yet been studied systematically. The present work focuses on addressing the lack of understanding in this area.In this work, we consider the target nucleus as a bound two-body system. This allows us to solve the scattering problem based on the integral Faddeev equations. These equations are further used to describe the nuclear-reaction cross sections. With such an approach, we avoid searching for an efficient optical potential to describe the target nucleus. At the same time, coupling of inelastic two-body channels in the d+Li reaction is equally considered while in preparation for the seed two-body interactions. In addition, the few-body microscopic approach resolves the question concerning how this or that cluster interaction contributes to the nuclear-reaction intensity.
Chapter I briefly describes the nucleus cluster model and the three-body deuteron-Li reactions in the energy region
$ E_d $ = 0.5-20 MeV. Chapter II gives classification of themost relevant deuteron-Li reactions, in terms of the input into their total cross section, along with the associated measured cross sections. The final part of the work provides a Discussion of the Results, followed by the Conclusion. -
In the cluster model, the lowest-energy state of the nucleus-target is determined by pairwise interaction of the (
$ \alpha-d $ ) clusters forming the 6Li and ($ \alpha-t $ ) clusters forming the 7Li. Thus, the cluster system is in a state wherein the quantum numbers are equivalent to the corresponding numbers of target nucleus. Let the$ \vec p $ momentum specify motion in the coupled cluster and$ \vec q $ characterize the motion of the spectator-particle with respect to the coupled pair. The prime over the variables corresponds to the momenta resulting from particle transfer. The$ \alpha,\beta,\gamma\in(1,2,3) $ indices specify the type of particular three-body cluster state, and repetitive rearrangement of Greek indices provides a set of independent values X, characterizing the probability amplitude for transition from one cluster channel to the other. Then, the integral three-body Faddeev equations, considering the adopted notations, are as follows:$\begin{aligned}[b] X_{\beta\alpha}(\vec q',\vec q,E) =& Z_{\beta\alpha}(\vec q',\vec q,E)+\sum\limits_{\substack{\gamma = 1 \\ \gamma\not = \beta}}^3\int\frac{{\rm d}^3q''}{(2\pi)^3}Z_{\beta\gamma}(\vec q',\vec q'',E)\\&\times\tau_{\gamma}(\vec q'',E)X_{\gamma\alpha}(\vec q'',\vec q,E).\end{aligned} $

(1) In Eq. (1)
$ \tau_{\gamma}(\vec q'',E) $ are two-body propagators that depend on the three-body kinetic energy E. The driving terms$ Z_{\beta\alpha} $ are the matrix elements of the free three-body Green's function$ G_0(E) $ :$ Z_{\beta\alpha}(\vec q',\vec q,E) = (1-\delta_{\beta\alpha})\langle\vec q',\beta\mid G_0(E)\mid\vec q,\alpha\rangle .$

(2) Condensed index
$ \gamma \,$ (as well as$\alpha, \beta$ ) determines the following sets of states:$\begin{aligned}[b] \mid \vec q,\vec p,\gamma\rangle_{^6{\rm{Li}}} =& \begin{cases} \mid d-(d\alpha),\vec q,\vec p\rangle,\phantom{111}\gamma = 3,\\ \mid d-(d\alpha),\vec q,\vec p\rangle,\phantom{111}\gamma = 2,\\ \mid \alpha-(dd),\vec q,\vec p\rangle,\phantom{111}\gamma = 1;\\ \end{cases} \\\mid \vec q,\vec p,\gamma\rangle_{^7{\rm{Li}}} =& \begin{cases} \mid d-(t\alpha),\vec q,\vec p\rangle,\phantom{111}\gamma = 3,\\ \mid t-(d\alpha),\vec q,\vec p\rangle,\phantom{111}\gamma = 2,\\ \mid \alpha-(dt),\vec q,\vec p\rangle,\phantom{111}\gamma = 1.\\ \end{cases} \end{aligned}$

(3) The on-shell three-body kinetic energy is determined by the two-body kinetic energy and the energy
$ E_b $ of the bound state. In general, the solution technique of Eq. (1) is similar to determining the solutions in Ref. [17] and will not be used here. It will only be noted that the first two states in Eq. (3) for 6Li can be combined. We will discuss the two-body cluster subsystems in more detail below. -
Interactions in each pair of particles are specified by the following separable potentials:
$ v_{\gamma}^{l'l} = \lambda_{\gamma}^{l'l}\xi_{\gamma}^{l'}(p')\xi_{\gamma}^{l}(p), $

(4) which are transformed as tensors in the orbital
$ (l,l') $ momenta space of the interacting pairs of clusters. In calculations, for the interacting pairs, we adopt the following states:$ \begin{cases} dd - (l,J^P) = (0,0^+),\,(0,2^+),\,(1,1^-), \\ d\alpha - (l,J^P) = (0,1^+),\,(1,0^-),\,(1,1^-), \\ dt - (l,J^P) = (1,3/2^-), \\ \alpha t - (l,J^P) = (1,3/2^-). \end{cases} $

(5) From the sets in Eq. (5), it follows that for both 6Li and 7Li nuclei, each matrix element
$ X_{\beta\alpha} $ contains p-wave scattering. This suggests that the three-body matrices have a complicated spin-angular structure. It is precisely for the simplicity of calculations that we restrict ourselves to the$ l,l'\in(0,1) $ requirement; furthermore, it will be demonstrated that it is quite sufficient for description of the typical cross-sectional properties in most of the considered reactions. In any two-body subsystem, for all states given in Eq. (5), the$ \xi(\vec p) $ form-factors have a similar functional form:$ \xi(\vec p) = \frac{c_1}{\vec p^{\,2}+\beta_1^2}+\frac{c_2\vec p^{\,2}}{(\vec p^{\,2}+\beta_2^2)^2}. $

(6) $ c_{1,2} $ and$ \beta_{1,2} $ parameters are found from the best-description condition based on the$ \delta_{l}^{J} $ phase-shift parameters and the inelasticity$ \eta_{l}^{J} $ (J-total spin) available in the literature. Additionally, it should be noted that in this work, in all the cluster states, the$ \lambda_{\gamma}^{l'l} $ interaction intensity is independent of the energy. The two-body T-matrix with respect to the inelastic channels up to the order of smallness with respect to$ \lambda $ intensity takes the following form:$ \begin{aligned}[b] T(p,p') =& \xi(p)\tau(p,p^2/2\mu)\xi(p');\\ \tau(p,p^2/2\mu) =& (\lambda^{-1}-\Sigma_{\rm el}(p)-\Sigma_{\rm inel}(p))^{-1}, \end{aligned} $

(7) wherein the energy shifts
$ \Sigma_{\rm el/inel} $ in the propagator are calculated using the form-factors in Eq. (6),$ \begin{aligned}[b] \Sigma_{\rm el}(p) =& \frac{\mu}{\pi^2}\int\limits_0^{\infty} \frac{p^{'2}{\rm d}p'\xi^2(p')}{p^2-p^{'2}+{\rm i}\varepsilon}, \\ \Sigma_{\rm inel}(p) =& \frac{\mu}{\pi^2}\int\limits_0^{\infty} \frac{p^{'2}{\rm d}p'\xi_{\rm inel}^2(p')}{p^2-p^{'2}+{\rm i}\varepsilon}, \\ \xi_{\rm inel}(p') = &\frac{c_3}{\vec p^{'\,2}+\beta_3^2}. \end{aligned} $

(8) Quantity
$ \Sigma_{\rm inel} $ , like form-factors$ \xi_{\rm inel} $ , is introduced to take into account some inelastic effects that are important in elastic nucleus-nucleus scattering. There is no doubt that this inclusion should be in coincidence with rearrangement matrix elements$ X_{\beta\alpha} $ . In this case, the eigenstate of the initial nucleus is a vector strained on elastic as well as rearrangement channels. In this work, for the sake of simplicity, we avoid direct inclusion of all of the rearrangement channels in the matrix$ X_{\beta\alpha} $ , retaining only the energy shift in two-body propagators.For the
$ \alpha d $ and$ \alpha t $ bound states with the$ E_b $ binding energy, the interaction intensity is found according to the formula$ \lambda^{-1} = \frac{\mu}{\pi^2}\int\limits_{0}^{\infty}\frac{(\xi^2(p)+\xi_{\rm inel}^2))p^2{\rm d}p}{(2\mu\mid E_b\mid +p^2)}. $

(9) Figure 1 shows results of the phase-shift parametrization, as well as the inelasticity parameters for
$ dd $ and$ d\alpha $ scattering. For$ dt $ elastic scattering, the data on the phase shifts in the pertinent energy region are unavailable. Instead, we will rely on the fact that this interaction in the considered energy region is characterized by high inelasticity related to a neutron source reaction$ dt\to\alpha n $ . The$ \eta $ inelasticity parameter characterizes the reaction cross section$ \sigma_r $ in the specified spin-orbital state (for the purpose of simplification, the corresponding indexes are omitted).
Figure 1. (color online) Real
$ \mathfrak{Re}(\delta_l^J) $ and imaginary$ \mathfrak{Im}(\delta_l^J) $ parts of phase shifts for$ dd $ scattering; data taken from [18] on the left. Real$ \mathfrak{Re}(\delta_l^J) $ and imaginary$ \mathfrak{Im}(\delta_l^J) $ parts of phase shifts for$ d\alpha $ scattering; data taken from [19] on the right.$ \sigma_r = \frac{\pi}{k^2}\sum\limits_{l = 0}^{\infty}(2l+1)(1-\eta^2). $

(10) Here, k is a wave-number of the relative motion vector for the d and t nuclei. Then, using the parametrized differential cross section
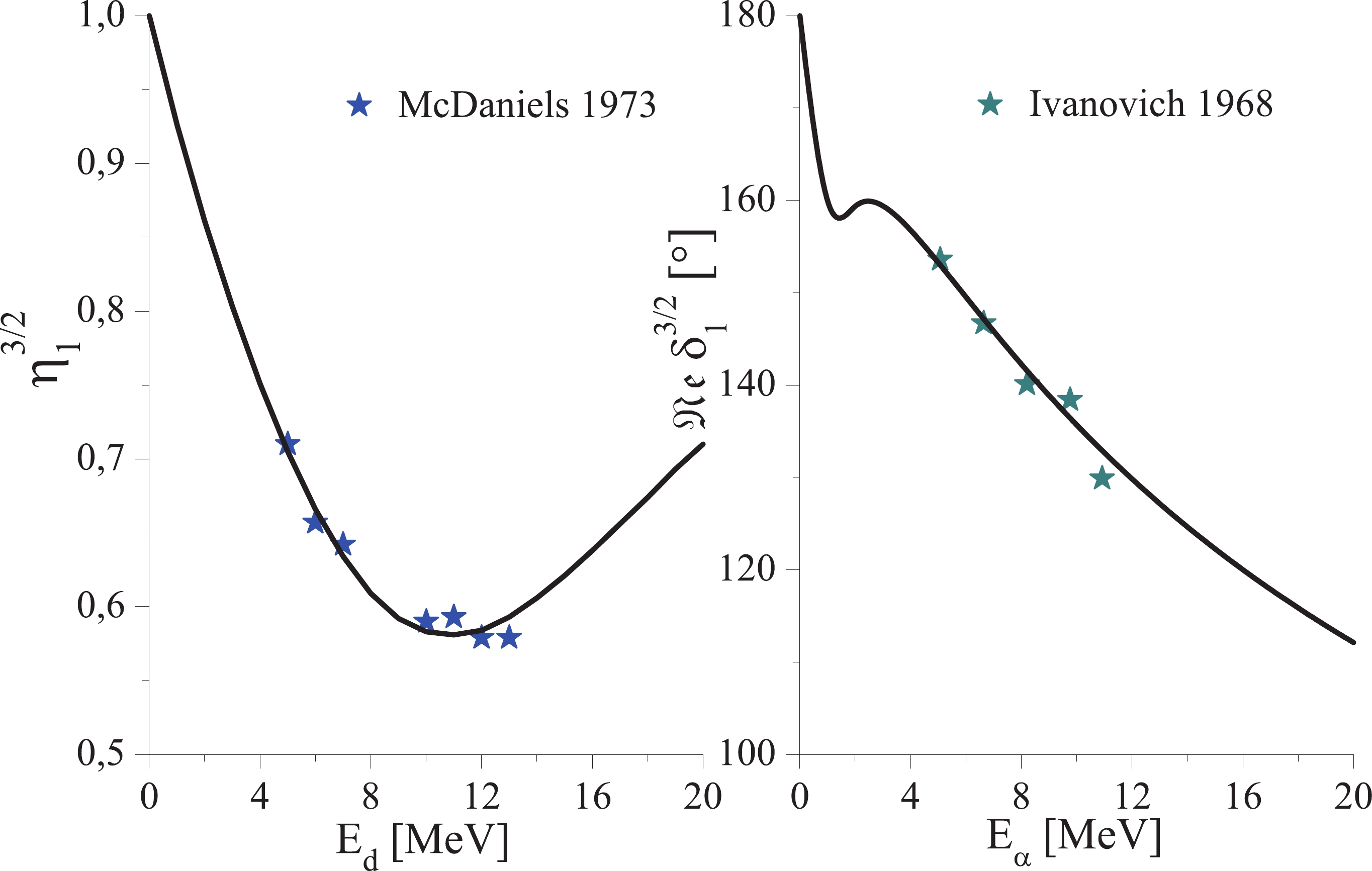
$ \sigma(\theta) $ of the neutron-source reaction reported in Ref. [20], we numerically integrate it for each l over the solid angle. The obtained partial cross sections of the reaction are substituted into equation (10) to express the inelasticity parameter$ \eta $ in the specified spin-orbital state. Figure 2 shows the inelasticity parameter$ \eta $ obtained in this manner for the$ dt $ interaction. Comparison to the data in Ref. [21] regarding the real part of the phase shift$ \mathfrak{Re}\delta_{1}^{3/2} $ for$ \alpha t $ elastic scattering is also presented here. Table 1 summarizes the two-body cluster interaction parameters.Sys. (l, $ J^P $ )

$ \lambda^{-1} $ /MeV

$ ^{-1} $ 

$ c_1 $ /MeV

$ ^{2} $ 

$ c_2 $ /MeV

$ ^{2} $ 

$ c_3 $ /MeV

$ ^{2} $ 

$ \beta_1 $ /MeV

$ \beta_2 $ /MeV

$ \beta_3 $ /MeV

$ dd $ 

(0, $ 0^+ $ )

-0.3 $ \cdot 2\pi^2 $ 

−430 345 49/ $ \lambda $ 

106 57 1 (0, $ 2^+ $ )

−7.75 $ \cdot 2\pi^2 $ 

−991 319 14/ $ \lambda $ 

300 101 5 (1, $ 1^- $ )

−1 $ \cdot 2\pi^2 $ 

−989 588 75/ $ \lambda $ 

350 156 3.6 $ d\alpha $ 

(0, $ 1^+ $ )

(12) −310 320 82/ $ \lambda $ 

140 64 24 (1, $ 0^- $ )

−40 $ \cdot 2\pi^2 $ 

−500 0 245/ $ \lambda $ 

225 − 10 (1, $ 1^- $ )

−25 $ \cdot 2\pi^2 $ 

−989 2 560/ $ \lambda $ 

490 100 17 $ dt $ 

$ (1,\dfrac{3}{2}^-) $ 

−3 $ \cdot 2\pi^2 $ 

−745 0 112/ $ \lambda $ 

674 − 30 $ \alpha t $ 

$(1, \dfrac{3}{2}^- )$ 

(12) −435 100 − 169 53 − Table 1. Intensity
$ \lambda $ of the two-body interactions and$ c, \beta $ parameters that appear in the form-factors (6) and (8). In the third column, the equation number is given in parentheses. -
In the notations adopted in Eq. (3), the T-matrix of elastic scattering corresponds to
$ X_{33} $ , and the matrix associated with the partial amplitude$ F^L(q) $ of the elastic scattering is$ F^L(q) = -\frac{\mu_{d{\rm{Li}}}}{2\pi} N X_{33}^L(q,q,E). $

(11) Here, the reduced mass of the deuteron-Li is denoted by
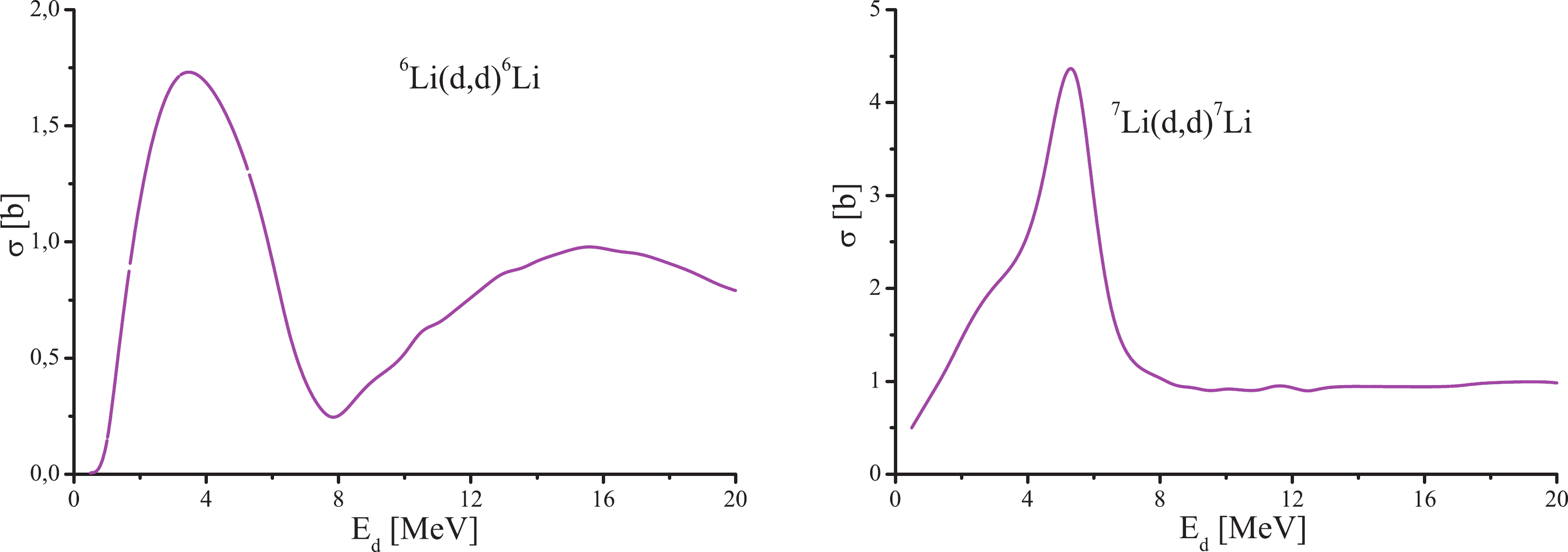
$ \mu_{d{\rm{Li}}} $ , where N is a normalization factor calculated from the binding energy of the cluster$ E_{b} $ [17]. Figure 3 shows the measured cross sections of$ d^6 {\rm{Li}}$ and$ d^7 {\rm{Li}}$ elastic scattering. The presence of resonance-like structures in the regions$ E_d\approx 4 $ MeV and$ E_d\approx 5 $ MeV is to be noted. In this paper, their formation mechanism will not be discussed in detail. The only thing to be noted here is that the full information about all the inelastic processes, possible within the adopted cluster scheme, Eq. (3), within the used parametrization, Eq. (6), has already been entered in the$ X_{13} $ ,$ X_{23} $ , and$ X_{12} $ matrices, against which the matrix$ X_{33} $ is expressed. Taking into account the fact that there are no experimental data regarding d+Li elastic scattering, the major criterion for accurate prediction is agreement with the other model approximations, specifically, with the optical-model predictions. We have found that the calibrated optical predictions based on the available differential distributions are in reasonable agreement with the data in Fig. 3 for the elastic-scattering cross sections on the level of 800-900 mb in the region$ E_d\geqslant $ 8 MeV. -
Among the considered deuteron-Li reactions in the energy region
$ E_d $ = 0.5-20 MeV, the most significant are listed below:$\begin{aligned}[b]& d+^6{\rm{Li}}\to \begin{cases} \gamma+^8{\rm{Be}},\; Q = 22.279, \\ 2\alpha, \;Q = 22.37, \\ p+^7{\rm{Li}},\; Q = 5.026, \\ n+^7{\rm{Be}},\; Q = 3.382, \\ n+p+^6{\rm{Li}}, \;Q = -2.224,\; E_{\rm th} = 2.969, \\ 2d'+\alpha, \;Q = -1.473,\; E_{\rm th} = 1.967,\\ t+p+\alpha, \;Q = 2.559, \\ ^3{\rm{He}}+n+\alpha,\; Q = 1.7951; \end{cases}\end{aligned}$

$\begin{aligned}[b]& d+^7{\rm{Li}}\to \begin{cases} \gamma+^9{\rm{Be}},\; Q = 8.623, \\ t+^6{\rm{Li}}, \;Q = -0.994,\; E_{\rm th} = 1.279, \\ p+^8{\rm{Li}},\; Q = -0.192,\; E_{\rm th} = 0.247, \\ n+^8{\rm{Be}},\; Q = 15.029, \\ n+p+^7{\rm{Li}},\; Q = -2.224, \;E_{\rm th} = 2.863,\\ \alpha+d+t,\; Q = -2.467, \;E_{\rm th} = 3.176, \\ 2n+^7{\rm{Be}},\; Q = -3.869,\; E_{\rm th} = 4.979, \\ 2\alpha+n, \;Q = 15.121. \end{cases}\end{aligned}$

(12) The masses of all nuclei were calculated using the recent values of their mass excess from [22]. In Eq. (12), the reaction energy Q and the threshold energy
$ E_{\rm th} $ are given in MeV, respectively. The amount of exothermic reactions, which (as mentioned in the introduction) might have a significant effect on the energy balance of advanced fusion facilities, is to be noted. The cross sections$ \sigma $ of the stripping reactions associated with the so called "two by two" reaction are expressed using the formula$\begin{aligned}[b] \frac{{\rm d}\sigma}{{\rm d}\Omega_c} =& \frac{E_f E_{{\rm{Li}}} \omega_d \omega_c}{(2\pi W)^2}\frac{p_f}{p_i}\frac{1}{3(2J_{{\rm{Li}}}+1)}\\&\times \sum\limits_{M_iM_f} \Big| \sum\limits_{\gamma}\xi_{\gamma}(p) X_{\gamma 3}(p_i,p_f,E) N\Big|^2. \end{aligned}$

(13) Here, W is the total system energy;
$ \omega_d $ and$ \omega_c $ are the deuteron and light particle energy reaction product, respectively;$ E_{{\rm{Li}}} $ and$ E_f $ are the Li-nucleus and heavy particle energy reaction product, respectively; and$ p_i $ ,$ p_f $ , and$ \Omega_c $ are the relative momenta of the particles before and after the reaction, as well as the solid angle of escape of light particles, respectively.Summation in Eq. (13) is taken over the complete-spin (spin-channel) projections of the initial and final nuclear system. Index
$ \gamma $ runs over the values [1, 2], and for the given stripping or rearrangement reaction, these values give the required final state.$ \xi_{\gamma}(p) $ is an additional vertex form-factor (where$ \vec p $ is the relative momentum of the neutron or proton and the removal particle; see Fig. 4) used in calculation of the stripping processes. Stripping processes, for example, 7Li(d,n)8Be or 6Li(d,p)7Li, seem to be two-step processes under the three-body approach, where the deuteron is split off on the first step and the final nucleus is formatted on the second one. Moreover, integration over the relative momentum of splitting particles is required. Instead of avoiding the inevitable numerical complexity, we neglect the propagation of splitting particles (proton, neutron, deuteron, and two neutron quasi-particle – 2n) in the nuclear medium that takes place in the stripping processes. For the stripping reactions with formation of short-lived or stable nuclei, it is typical that the interaction of the incident particle with the target nucleus seems to be of a pole type (see Fig. 4), where the pole takes the role of reduced width for only the removal proton for 6Li(d,p)7Li and 7Li(d,p)8Li or only the removal neutron for 6Li(d,n)7Be and 7Li(d,n)8Be. In this paper, for the stripping reactions, we actually use just two types of vertices. The first one is the (pn) vertex, wherein the interaction is specified by the simple rank-one separable potential [23], and the second is the (nd) vertex, achieved on the separable rank one potential with the parameters for the$ 1/2^+ $ state [17]. Here, we do not distinguish either nd or p(2n) interactions, where (2n) is the quasi-bound two neutron state. In this simplification, the integration over relative momentum of splitting particles is replaced by the vertex form-factor$ \xi_{\gamma}(p) $ multiplier calculated at the mass shell relative momentum$ \vec p $ . Another simplification has been made for the three-body nature of the residual nuclei 7Li, 8Li, 7Be, and 8Be that underlies the present stripping process calculations and should be carefully taken into account in searching for bound energies. However, we avoid the direct solution of three-body problems for n-$ \alpha $ -d, (2n)-$ \alpha $ -d, p-$ \alpha $ -d and (np)-$ \alpha $ -d interactions in the final states and relate them to the internal structures of residual nuclei 7Li, 8Li, 7Be, and 8Be. Instead of precise calculation of the three-body final states in stripping processes, we have made an attempt to reproduce stripping cross sections from a kinematic point of view, in which we explicitly have a phase space for the reactions 6Li(d,p)7Li, 7Li(d,p)8Li, 6Li(d,n)7Be, and 7Li(d,n)8Be with residual nuclei 7Li, 8Li, 7Be, and 8Be and emitted protons or neutrons.
Figure 4. Diagrammatic representation of rearrangement and stripping processes. Solid circles correspond to an additional vertex form-factor
$ \xi_{\gamma}(p) $ used in stripping processes. Propagators$ \tau $ are denoted by shaded boxes. Indexing for probability amplitudes X is determined by (3).It should be emphasized that some information about stripping processes is already partially contained in the
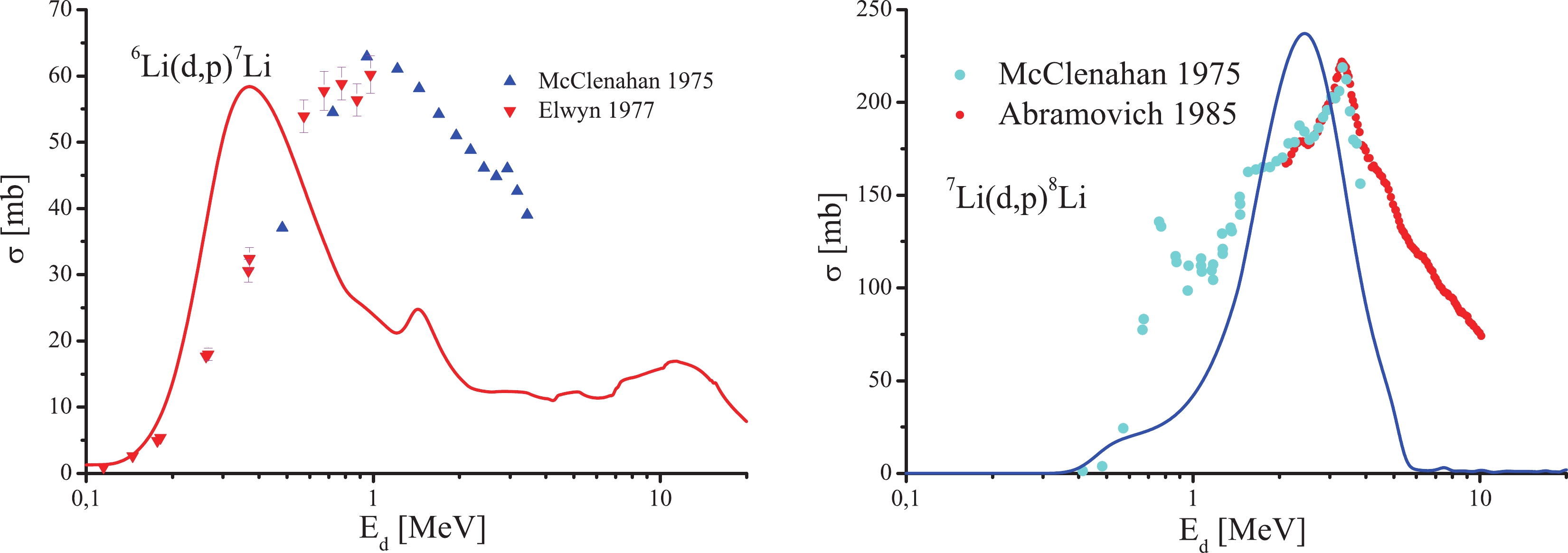
$ \Sigma_{\rm inel} $ quantities. These terms must be in coincidence with elastic nd, np, and dt scattering data needed for$ \xi_{\gamma}(p) $ search. Here, for the sake of simplicity, we restrict calculations by independent searching of$ \Sigma_{\rm inel} $ and nd, np, and dt two-body form-factors. The amplitudes for elastic pn and nd scattering are taken into account with the use of separable rank one potentials from [23] and [17], respectively. For the dt potential, as previously mentioned, we fitted an inelastic parameter$ \eta $ under the separable rank one approximation. Figures 5-7 show calculated total cross sections of the considered rearrangement and stripping reactions.
Figure 7. (color online) Total cross sections for the 6Li(d,n)7Be (on the left) and 7Li(d,n)8Be (on the right) reactions. The experimental points are taken from [3].
-
Within the considered energy region, the deuteron-induced reactions may have up to 4 different channels with the three particles in the final state on both stable Li isotopes. In this regard, the measured cross sections, which are not provided with the experimental data, are of interest. First of all, this applies to the reactions yielding the following sets of particles:
$ n+p+^6 {\rm{Li}}$ ,$ 2d'+\alpha $ ,$ 2\alpha+n $ ,$ n+p+^7 {\rm{Li}}$ , and$ \alpha+d+t $ .The total cross section of the three-particle break up reaction is calculated via integration over the following expression:
$ \begin{aligned}[b] \frac{{\rm d}\sigma}{{\rm d}\Omega_cd\omega_{12}{\rm d}\Omega_{12}} =& (2\pi)^{-5}\frac{\omega_{\rm d}E_{{\rm{Li}}}\omega_c p_c E_{1} E_{2} p_{12}}{p_i W^2} \frac{1}{3(2J_{{\rm{Li}}}+1)} \\&\times \sum\limits_{M_iM_f} \Big|\sum\limits_{\gamma = 1,2,3}\tau_{\gamma} (\vec p_{\gamma},E-\vec p^{\,2}_{\gamma}/2M_{\gamma}) \\&\times\xi_{\gamma}(p_{\gamma}) X_{\gamma 3}(p_i,p_c,E)N\Big|^2. \end{aligned}$

(14) New notations are introduced in Eq. (14) as compared with Eq. (13):
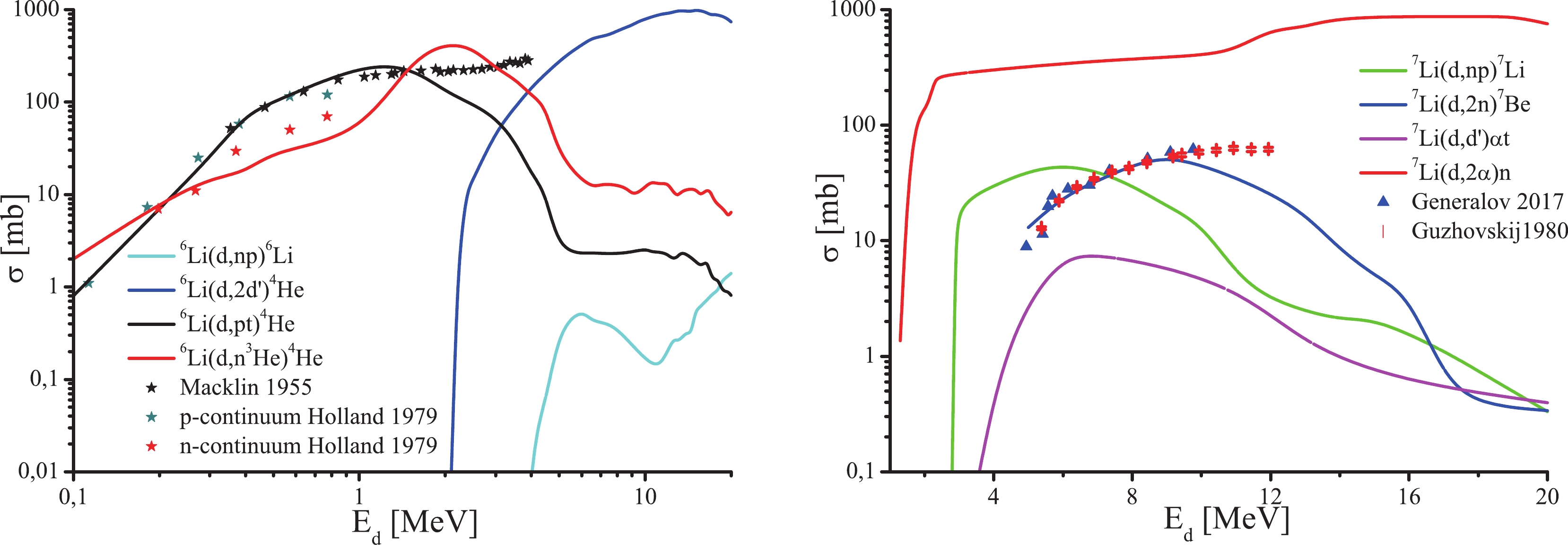
$ \omega_c $ ,$ p_c $ , and$ \Omega_c $ are the energy, momentum, and solid angle for one of the three escaping particles;$ p_{12} $ and$ \Omega_{12} $ are the relative momentum for the other pair of particles and its solid angle calculated in the center-of-mass system of the pair, respectively;$ E_1 $ and$ E_2 $ are the energies of the other two particles in the common center-of-mass system.Figure 8 shows calculated cross sections for the three-body break up reaction based on Eq. (14).
-
The radiation-capture processes in the form
$ d(\omega_i,\vec q_i)+{\rm{Li}}(E_i,-\vec q_i)\to \gamma(\omega_{\gamma},\vec k_{\gamma}) + {\rm{Be}}(E_f,\vec p_f) $

(15) reveal information about the internal structure of the Be nucleus and relate to the electromagnetic transitions between the excited discrete levels of the Be nucleus and low-lying or ground states. The cross section of the process given in Eq. (15) is expressed by the formula
$ \frac{{\rm d}\sigma}{{\rm d}\Omega_{\gamma}} = \frac{E_i E_f \omega_i \omega_{\gamma}^2}{q_i (2\pi W)^2}\frac{1}{3(2J_{{\rm{Li}}}+1)}\sum\limits_{l\mu,{\rm{EM}}} \big|T_{{\rm{Be}}\,{\rm{Li}}}(l\mu,{\rm{EM}})\big|^2. $

(16) In the longwave approximation, when the wave number of radiation
$ k_{\gamma} $ is much smaller than the spatial dimensions of the system R, i.e.,$ k_{\gamma}\cdot R\ll 1 $ , that for the special case$ \omega_{\gamma} = 10 $ MeV and$ R = 2.5 $ fm yields$ 0.13\ll 1 $ , and the probability$ T_{{\rm{Be}}\,{\rm{Li}}}(l\mu,{\rm{EM}}) $ of the electromagnetic transition of the$ {\rm{EM}}\in({\rm{E}},{\rm{M}}) $ type with multipolarity$ l\mu $ may be represented [25] by the following:$ T_{{\rm{Be}}\,{\rm{Li}}}(l\mu,{\rm{EM}}) = \frac{8\pi (l+1)k_{\gamma}^{2l+1}}{l\big((2l+1)!! \big)^2} \Big|\langle {\rm{Be}} \mid \Omega_{l\mu}({\rm{EM}}) \mid {\rm{Li}}\rangle \Big|^2, $

(17) where
$ \begin{aligned}[b] \Omega_{l\mu}({\rm{E}}) =& \sum\limits_{j = 1}^{A}\Big[e_j r_j^l Y_{l\mu}(\hat r_j) - {\rm i} \frac{e \hbar c}{M_N c^2} K_j \frac{k_{\gamma}}{l+1}(\vec\sigma_{j}\times\vec r_j)\\&\times \vec\nabla_j\big(r_j^l Y_{l\mu}(\hat r_j)\big)\Big], \\ \\ \Omega_{l\mu}({\rm{M}}) =& {\rm i}\sum\limits_{j = 1}^{A}\Big[\Big(\frac{e_j\hbar c}{2M_N c^2} \frac{2}{l+1}\vec L_j +\frac{e\hbar c}{2M_N c^2} K_j \vec\sigma_j \Big)\\&\times\vec\nabla_j\big(r_j^l Y_{l\mu}(\hat r_j)\big)\Big]. \end{aligned} $

(18) In Eq. (18), e and
$ e_j $ are the elementary charges, and$ e_j = e $ for protons and$ e_j = 0 $ for neutrons;$ r_j $ and$ K_j $ are the coordinate of the j-th nucleon and its magnetic moment, respectively;$ \vec\sigma_j $ ,$ \vec L_j $ , and$ \vec\nabla $ are spin operators of the orbital moment and gradient acting upon the j-th nucleon.Typically, radiation captures are calculated with complicated cluster systems. Each of them consists of several protons and neutrons. Therefore, it is advantageous to limit summation over j entirely by the initial nuclei with the effective charge
$ \varepsilon_l $ . Then, for the process given in Eq. (15), the effective charge is$ \varepsilon_l = \Big(\frac{A}{A+2}\Big)^l+3\Big(-\frac{2}{2+A}\Big)^l. $

(19) Here, A is the atomic number of the Li nucleus. Further summation of Eq. (18) over magnetic quantum numbers with the Wigner-Eckart formula and integration over
$ \hat r_j $ angles with the$ d- $ Wigner function are rather time-consuming and can be found elsewhere. We will dwell on calculations of the$ \langle{\rm{Be}}\mid r^{l} \mid {\rm{Li}}\rangle $ and$ \langle{\rm{Be}}\mid r^{l-1} \mid {\rm{Li}}\rangle $ radial integrals included in Eq. (17). The d+Li scattering states are roughly approximated by the s-wave only. Then, numerically solving the Schrödinger equation with the central complex potential taking into consideration the Coulomb potential screening at r = 1.5 fm yields the appropriate radial wave functions. For the central complex potential given below,$ \frac{V+{\rm i}W}{1+\exp{\Big(\dfrac{r-r_0}{a}\Big)}}, $

(20) the free parameters – the depths of the real and imaginary parts V [MeV] and W [MeV] of the potential, as well as its diffuseness a [fm] and the cutoff parameter
$ r_0 $ [fm], were adjusted based on reproduction of the previously-found phase shifts and inelasticity parameter for d+Li elastic scattering using Equation (11). Figure 9 demonstrates the phase shifts as compared with the inelasticity parameters for the s-wave scattering calculated using the Faddeev equations and the optical model with the central potential given in Eq. (20). The potential parameters were taken to be equal to V = 70(6Li), 30(7Li), W = 30(6Li), 5(7Li), a = 0.15(6Li), 0.1(7Li), and$ r_0 $ = 1.5(6Li,7Li). Figure 10 shows the calculated cross sections of the radiation captures for the transition$ 1^+\to 0^+ $ within the process 6Li$ (d,\gamma_{M1})^8 {\rm{Be}}$ , and$ \tfrac12^+\to\tfrac32^- $ within the process 7Li$ (d,\gamma_{E1})^7 {\rm{Be}}$ .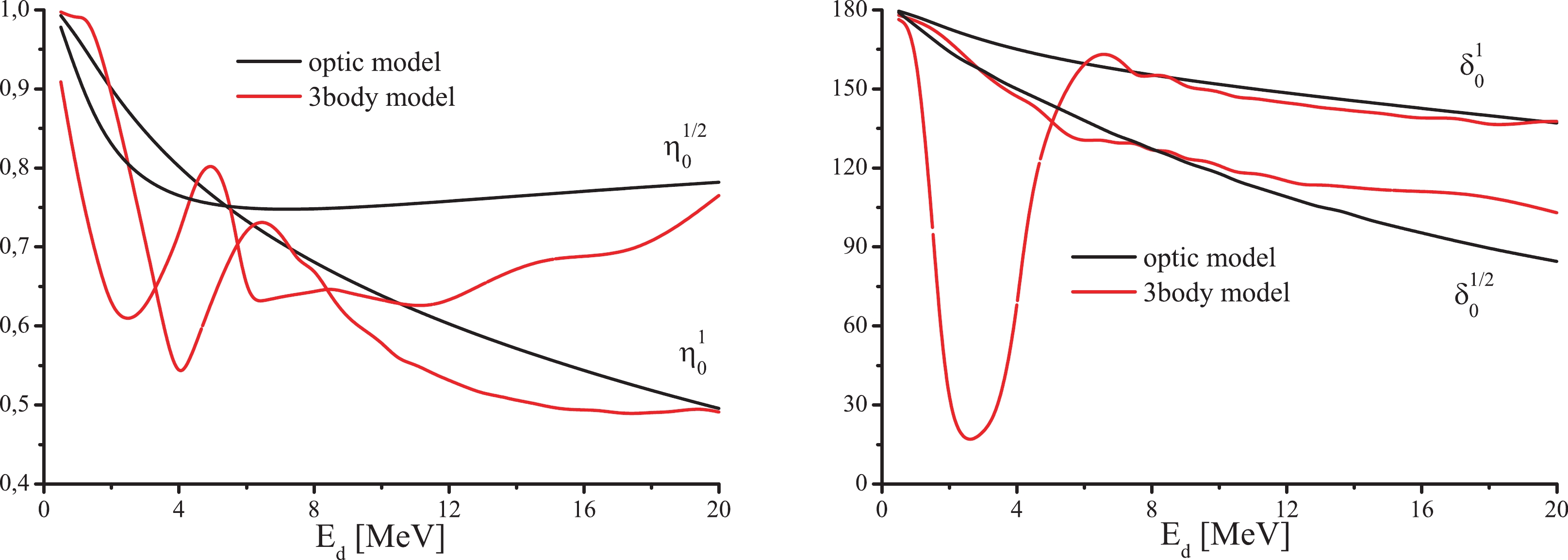
Figure 9. (color online) Results of calculations based on the simple optical model (black lines) and exact calculation (red lines) of the inelasticity parameters (on the left) and the phase shifts (on the right) in degrees. Data on d+6Li elastic scattering of
$ \eta_0^{1} $ ,$ \delta_0^1 $ and on the d+7Li elastic scattering of the$ \eta_0^{1/2} $ ,$ \delta_0^{1/2} $ are plotted. -
Structurally, the Faddeev Eq. (1) allows one to consider multiple scattering within the three-body systems. The system of Eq. (1) solved with respect to the
$ X_{33} $ elastic scattering matrix can be written in the following form,$\begin{aligned}[b] X_{33}(\vec q',\vec q, E) =& K_{31}(\vec q',\vec q'',E)X_{13}(\vec q'',\vec q,E)\\&+K_{32}(\vec q',\vec q'',E)X_{23}(\vec q'',\vec q,E), \end{aligned}$

(21) where
$ K_{31} $ and$ K_{32} $ are kernels of the integral Eq. (1). Information on inelastic interactions accompanied by transfer of the clusters from one interacting pair of particles to the other has already been added to the structure of Eq. (21). Therefore, the Faddeev equations offer an advantage in describing the processes accompanied by transformation because the amplitude obtained while constructing the elastic cross section already contains the required information for the potential inelastic processes within the system. However, the Faddeev equations cannot be simply used until, in each partial wave, the inter-particle interactions are successfully parametrized, and the potentials of pairwise interactions have to reveal all the dynamic properties typical for the processes under consideration. If parametrization of the two-particle interactions is a success and the number of these interactions approaches an actual value, the chance to reach the correctly described three-particle dynamics in the considered system increases. For the same reason, we believe that if the parametrization of two-body interactions of charged particles is a success without the introduction of the Coulomb penetration factor introduction, the Coulomb forces have been indirectly taken into account.In this work, not all of the pairwise interactions are parametrized by the phase shifts. For dt interactions, the inelasticity parameters calculated with respect to the measured cross sections for the
$ dt\to\alpha n $ reaction [20] were used. Our predictions show that the form of the$ \xi_{dt} $ form-factor determines the typical behavior of the elastic scattering in the region$ E_d<5 $ MeV. That is why the role of this interaction has been crucial for all the reactions within the$ d+^7 {\rm{Li}}$ . At the same time, Fig. 5 shows that the cross section of the 7Li(d,t)6Li reaction reproduces itself quite well in the region$ E_d<5 $ MeV, which suggests that the adopted functional relationship of the$ \xi_{dt} $ form-factor is quite comparable with the real one. Figures 6 and 7 show that although calculations of the stripping reaction cross sections have been considerably simplified, they are still reflective of the experimental cross-section features in the near-threshold energy region.The three-body break up reactions are less sensitive to details of the scattering matrix than the stripping reactions, as their phase space is larger and increases with increasing energy. That is why the peculiarities of the pairwise interactions in the three-body reactions are only noticeable in the threshold region. Our calculations of the 6Li(d,pt)4He and 6Li(d,n3He)4He cross sections are in reasonable agreement with the experimental data in the energy region
$ E_d<2 $ MeV; above this energy region, the theoretical cross section significantly underestimates the experimental one. The specified underestimation may be attributed to the d-wave contributions of the cluster interactions, which were neglected in our calculations. For the d+7Li system, only the experimental data for the 7Li(d,np)7Be reaction are available. Comparison with these data reveals agreement with the experimental value in the low-energy region$ E_d<10 $ MeV and further underestimation of the cross section with increasing energy. The remaining calculations associated with the three-body break up reaction and the radiation capture are presented in this paper for the first time.Neglect of multiple scattering in (
$ \alpha d $ ) and ($ \alpha t $ ) subsystems is equivalent to substitution in (21)$ X_{13}\to Z_{13} $ and$ X_{23}\to Z_{23} $ . Figure 11 shows the differential by the invariant mass of$ (\alpha d) $ cross section calculations of 6Li(d,2d')4He and 6Li(d,pt)4He reactions at$ E_d = 10 $ MeV and$ E_d = 1 $ MeV, respectively, versus the relative rate in the$ (\alpha d) $ pair. Here, the dashed lines indicate calculations disregarding multiple$ (\alpha d) $ scattering events. The obtained differential cross sections of the 7Li(d,d't)4He reactions at$ E_d = 5 $ MeV and the 7Li(d,2n)7Be at$ E_d = 7 $ MeV versus the relative rate within the clusters$ (dt) $ and$ (nn) $ , respectively, are also presented in Fig. 11. Calculations neglecting multiple interactions in the$ (\alpha t) $ subsystem are indicated by dashed lines and take into account multiplier 160 for the 7Li(d,d't)4He reaction and multiplier 380 for the 7Li(d,2n)7Be reaction. As can be seen, the role of multiple scattering in$ (\alpha d) $ and$ (\alpha t) $ subsystems turns out to be different. If we take the real lengths of deuteron elastic scattering on the 6Li and 7Li nuclei as a unit, the ratio of the scattering length calculated neglecting multiple scattering events in the$ (\alpha d) $ and$ (\alpha t) $ subsystems will be equal to 1.27 (or +27%) and 2.59 (or +159%), respectively, which is also in correlation with the results in Fig. 11. We believe that such divergence in properties in d+6Li and d+7Li systems depending on the interactions in the coupled$ (\alpha d) $ and$ (\alpha t) $ clusters within the adopted cluster scheme (3) reveals the significant role of inelastic dt interactions in the area surrounding the nucleus. This may be verified in the experimental investigation of dt systems or in forthcoming theoretical calculations of the partial phase shifts of dt elastic scattering.
Figure 11. (color online) Distributions, differentiated by the invariant mass, in the accurate calculation and in the calculation with neglected multiple interaction in the coupled pair of clusters versus relative rate in this pair (in speed of light unity).
$ \dfrac{{\rm d}\sigma}{{\rm d}\omega_{\alpha d}} $ for the 6Li(d,2d')4He at$ E_d $ =10 MeV and the 6Li(d,pt)4He at$ E_d $ =1 MeV on the left.$ \dfrac{{\rm d}\sigma}{{\rm d}\omega_{nn}} $ for the 6Li(d,2n')7Be at$ E_d $ =7 MeV and$ \dfrac{{\rm d}\sigma}{{\rm d}\omega_{{\rm d}t}} $ for the 6Li$ (d,d')\alpha t $ at$ E_d $ =5 MeV. -
The cross sections of most nuclear reactions in
$ d+^6 {\rm{Li}}$ and$ d+^7 {\rm{Li}}$ systems existing in the energy range$ E_d = 0.5-20 $ MeV are presented in this work. The cross sections for radiation capture and some reactions with the (n+p+6Li, 2d'+$ \alpha $ ,$ 2\alpha $ +n, n+p+7Li,$ \alpha $ +d+t) three-body break up have been calculated for the first time. In general, the adopted parametrization provides an adequate characterization of the cross sections in the near-threshold energy range, and in some cases, specifically in the$ 2n+^7 {\rm{Be}}$ channel, it is even possible to describe the experimental data up to 10 MeV. Despite the cluster behavior of both 6Li and 7Li nuclei, which is characterized by remarkable isolation of the cluster configurations, interaction in the coupled pair reveals itself in different ways for$ d+^6 {\rm{Li}}$ and$ d+^7 {\rm{Li}}$ . The next step in searching for d+Li stripping processes should carefully take into account the three-body nature of residual 7Li, 8Li, 7Li, and 8Be nuclei. Further studies are also possible in this area with the help of the d-wave interactions in the cluster subsystems and by employing some other kind of parametrization for elastic$ dt $ interactions.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: