Lorentz violation, quantum tunneling, and information conservation

Given that the observable signals of Lorentz invariance violation (LIV) can be described using effective field theory [1], the Planck-scale physics effect induced by the LIV has been extensively studied over the past few decades [2-5]. In the standard model extension (SME), Colladay and Alan Kostelecḱ observed that the spontaneous LIV occurs in the low-energy limit of a physically relevant fundamental theory [6]. In 2002, Amelino-Camelia determined that the Double Special Relativity (DSR) naturally leads to the Lorentz invariance violation of dispersion relations (LIV-DR) [7]. More importantly, it is generally believed that the introduction of gravity into quantum theory gives rise to the Planck-scale departure from Lorentz symmetry [8-13]. The potential mechanism for spontaneous breakdown of Lorentz symmetry has been detailed based on covariant string field theory [8]. The possible violations of Lorentz symmetry due to loop quantum gravity have been carefully discussed by considering the correspondence principle [9]. In Hořava's-Lifshitz theory, the violation of Lorentz invariance is also included [10]. In this respect, the results of numerous experimental observations imply that the LIV may be regarded as an effective model for exploring the effect of quantum gravity [14-19]. Using the LIV, various constraints on the assumed energy scale for quantum gravity effects $ E_{\rm QG} $ have been reported for Gamma-ray bursts (GRBs) [14-17]. In the context of the LIV-DR, the observation of $ 100-{\rm MeV} $ synchrotron radiation from the Crab nebula serves as an important constraint on theories related to quantum gravity [19]. Moreover, there are many other similar and interesting techniques that are designed to experimentally investigate the violation of Lorentz invariance [20-32], i.e., testing Lorentz-symmetry violation using atomic systems [31, 32]. These observations indicate that the concept of the LIV as a candidate for describing the effect of quantum gravity has been one of the most interesting and popular research topics in recent years.

From a phenomenological perspective, we adopt the simple framework of deformed dispersion relation to characterize the Lorentz violation in this report. Assuming the preferred frames in which dispersion relation breaks boost invariance but preserves rotation invariance, a generic approximate quantum-gravity-induced LIV-DR in the high-energy regime can be expected to have the following form (1) [12-19]:

where we only consider the leading quantum-gravity correction of the LIV in Eq. (1). For convenience, we have chosen the form (1) to work in our paper, other different forms of LIV-DR can also be found in the Standard Model Extension (SME) [6]. It should be noted that this relation can be considered only when it occurs at high energy scales, where E, m, and p are the energy, mass, and momentum of the particles, respectively. As described in our previous work [33], we have enough evidence to confirm that the parameters $ E_{\rm QG} $, $ \eta_ \pm $, and n should be properly fixed to $ E_{p} $, $ 1 $, and $ 2 $, where $ E_{p} $ is the Planck energy scale. Therefore, the LIV-DR can be usually expressed in the following form [18, 19]:

where $ {l_p} = 1/({\xi_2}^2 {M_p}^2) = \dfrac{{L_p}^2}{{\xi_2}^2} $ is related to the Plank length, and $ \xi_2 $ is a dimensionless parameter.

Black holes are intriguing entities in our universe, and are considered as test beds for a complete theory of quantum gravity. In the final stage of black hole evaporation, the effect of quantum gravity induced LIV is so large that it must be considered during black hole evolution. Considering these facts, it is evident that there is a need to study the LIV effects on black hole thermodynamics. In addition, gravity as a special interaction force, is very sensitive to the mass of a particle, i.e. the energy of the particle according to the mass-energy relation $ \omega = mc^2 $. This phenomenon is distinguished from several other interaction forces (i.e., electromagnetic interaction, strong interaction, and weak interaction). In this report, by studying the sensitivity of the LIV-DR induced Hawking temperature on the energy and charge of the emission particle, we attempt to discover phenomenological evidence for the LIV-DR as a candidate for describing the effect of quantum gravity. It should be noted that quantum tunneling is very successful as a model for describing black hole radiation. Based on this concept, one can find the exact emission spectrum for which the black hole deviates from the pure thermal spectrum, which is consistent with an underlying unitary theory. This provides a qualitative explanation for black hole information loss [34-38]. In recent studies, it has been further shown that Hawking radiation via tunneling is indeed an entropy conservation process, and no information loss occurs during the radiation [39-41]. Of course, there are many other attempts that have been made to study this issue in the past decade [42-44] and references therein. However, to the best of our knowledge, most of these interesting works on Hawking radiation via tunneling have focused on the semiclassical case, ignoring the effect of quantum gravity. As previously indicated, in such instances, the radiation process of the black hole cannot be appropriately described. In particular, the final stage of the black hole evaporation where the energy of the emission particle is very high cannot be accurately described. Therefore, the effect of quantum gravity is very important [45-65], and it should be in the description of black hole radiation^③. It is necessary to examine the previous work on Hawking radiation via tunneling with the inclusion of the effect of quantum gravity. Specifically, by using the LIV induced Dirac equation, we will study the quantum gravity effect on the Hawking radiation of charged fermions via tunneling from the R-N black hole. In addition, the modified dispersion relation (MDR) near the minimum measurable length can also be treated as a quantum gravity candidate since the minimum length is a common feature of quantum gravity theories. In recent years, numerous studies have focused on the effect of MDR [66-71]. Considering the MDR, the generation of primordial perturbation in various cosmological evolutions has been carefully addressed [68]. Based on the Friedmann-Robertson-Walker (FRW) universe, the form of the MDR for theories with extra dimensions has also been obtained [69]. In particular, we note that, in [66], a new form of MDR with the inclusion of a minimum length and maximum momentum was introduced to investigate the radiation of the R-N black hole. In the LIV and MDR, the effects of quantum gravity are shown from different perspectives; therefore, it is interesting to compare our results to those of this scenario. Furthermore, in the context of the generalized uncertainty principle (GUP) (i.e., another candidate for quantum gravity), Nozari and Saghafi studied information loss during the emission process, and obtained the non-zero correlations with the Plank-scale corrections between successive emissions. However, this is not adequate for the recovery of information [72]. In Nozari's analysis, it should be pointed out that the influence of conditional probability and the question that whether the entropy and information are conserved or not were lacking. And in previous studies [73], when one ignored the influence of conditional probability, their results are presented to be misleading in calculation of the statistical correlation. In this report, by analyzing the dynamic evolution behavior of the Dirac particle with the inclusion of the effect of quantum gravity (i.e., the effect of the LIV), we also attempt to examine whether the statistical correlations with the Planck-scale corrections between successive emissions can leak out information via radiation. We also examine whether the black hole radiation via tunneling is an entropy conservation process wherein no information loss occurs.

The remainder of this report is organized as follows. In Sec. II, by considering the effect of the LIV-DR, we rewrite the dynamic Dirac equation to obtain the Hawking radiation of charged fermions via tunneling from the R-N black hole and analyze the sensitivity of the LIV-DR induced Hawking temperature to the energy and charge of the emission particle. Based on the LIV-DR induced tunneling radiation, in Sec. III, we obtain the statistical correlations with the Planck-scale corrections between successive emissions and examine whether black hole radiation via tunneling is an entropy conservation process, in which no information loss occurs. Sec. IV presents a brief discussion and conclusion.

In this section, we will study the effect of the LIV on Hawking radiation of the charged Dirac particle via tunneling from the R-N black hole. At first, it is necessary to obtain the dynamic Dirac equation by considering the effect of the LIV. Based on the LIV-DR, the corrected Dirac equation can be rewritten as [74]

Obviously, the Lorentz symmetry is broken by the additional term ($ l_p $) under the boost transformation. In [74], Eq. (3) has been proved to be compatible with the quadratically-suppressed LIV-DR (2) when the wave function $ \Psi \left( x \right) = \Psi \left( p \right)\exp [{\rm i}\left( {\overrightarrow p \overrightarrow x - {p_0}{x_0}} \right)] $ is substituted into the corrected Dirac Eq. (3), where $ {\overline \gamma^\mu} $ is the ordinary gamma matrix, and $ \mu, j $ are the spacetime coordinates and space coordinates, respectively. The corrected Dirac equation in curved spacetime should therefore be of the form

where m is the mass of the emission particle. In the curved spacetime, $ {D_\mu } $ represents $ {D_\mu } = {\partial_\mu } + {\Omega_\mu } + ({\rm i}/\hbar) e A_\mu $, and $ \gamma^\mu $ is the gamma matrix that satisfies the relation $ \left\{ {{\gamma^\mu },{\gamma^\nu }} \right\} = {\gamma^\mu }{\gamma^\nu } + {\gamma^\nu }{\gamma^\mu } = 2{g^{\mu \nu }}I $. $ e{A_\mu } $ and $ {\Omega _\mu } $ are the charge term and spin connection, respectively. Next, considering the effect of the LIV-DR, we attempt to investigate the form of the charged fermions that undergo tunneling from the R-N black hole. For the R-N black hole, it is written as $ {\rm d}s^2 = -f(r){\rm d}t^2 + g(r)^{-1}{\rm d}r^2 +r^2 ({\rm d}\theta^2 +\sin{\theta}^2 {\rm d}\varphi^2) $ with $ f(r) = g(r) = 1- \dfrac{2M}{r} + \dfrac{Q^2}{r^2} = \dfrac{(r -r_+)(r -r_-)}{r^2} $, where $ A_\mu = (A_t,0,0,0) = (\dfrac{Q}{r},0,0,0) $ represents the electromagnetic potential, and $ r_{\pm} = M \pm \sqrt{M^2 - Q^2} $ are the outer and inner horizons of the R-N black hole. According to the standard ansatz, the wave function of the corrected Dirac equation is always written as [75]

Here, both $ \varepsilon $ and S are the functions of the coordinates $ ({t,{x^j}}) $, and S is the action of the emission fermion. Substituting the wave function (5) into the corrected Dirac Eq. (4) and separating the variables as $ S = - \omega t + W(r) + \Theta(\theta,\varphi) $ for the spherically symmetric R-N spacetime [76-80], we have

where the terms that are related to the high orders of $ \hbar $ are neglected by considering the WKB approximation, $ \hbar \Omega_\mu $ has also been ignored for high energy levels, and $ \omega $ is the energy of the emission fermion. It is well known that there are two states for the spin-1/2 particles, which correspond to the spin up-$ \varepsilon_{\uparrow}(t,r,\theta,\varphi) $ and spin down-$ \varepsilon_{\downarrow}(t,r,\theta,\varphi) $ states, respectively. Without loss of generality, it is sufficient for us to choose the spin-up state. In this case, we have

where $ \zeta_{\uparrow} = \Big( {\begin{array}{*{20}{c}} {1}\\ {0}\\ \end{array}} \Big) $ for the spin-up state. To solve Eq. (6), the choice of suitable gamma matrices is very important. There are many choices to construct the $ \gamma $ matrices, and in this paper, we employ

where, $ {\sigma^i} $ are the Pauli matrices with $ {i = 1,2,3} $. Inserting the function $ \varepsilon_{\uparrow} \left({t,r,\theta,\varphi} \right) $ and the $ \gamma $ matrices into the generalized Dirac Eq. (6), four simplified equations that are related to the functions $ (A,B) $ can be obtained, and two of them are given as

Obviously, the functions A and B are required here to obtain a non-trivial solution, which demands that the determinant of the coefficient matrix should be zero. In this case, it yields

where the high order terms of $ {l_p} $, ie., $ O\left({\geqslant l_p^2} \right) $, are so small that they have been neglected. By using the residue principle near the event horizon of the R-N black hole [75], the value of $ W( r ) $ reads as

Here, the sign $ \pm $ corresponds to the solutions of the outgoing (ingoing) particles,$ A_{t+} = \dfrac{Q}{r_+} $ is the electromagnetic potential at the event horizon, and the parameter $ \Xi $ is given by $ \Xi = \dfrac{e Q \omega (5 r_- - r_+)}{2(r_+ - r_-)^2} +\dfrac{r_+ \omega^2 (r_+ - 2r_-)}{(r_+ - r_-)^2} - \dfrac{m^2}{4} -\dfrac{e^2 Q^2}{2 r_+ (r_+ - r_-)} $. Following the WKB approximation, it is well known that the relationship between the imaginary part of the action and the tunneling probability can be expressed as $ P = \exp ({-\dfrac{2}{\hbar }{\mathop{\rm{Im}}\nolimits}S}) $ [37, 38], so the total emission rate of the Dirac particles can be written as

Evidently, there is a small correction to the semiclassical tunneling rate when the effect of the LIV-DR is included. As defined by [60, 81, 82], when the principle of “detailed balance” is used for the emission rate (13), the effective temperature of the R-N black hole is given by

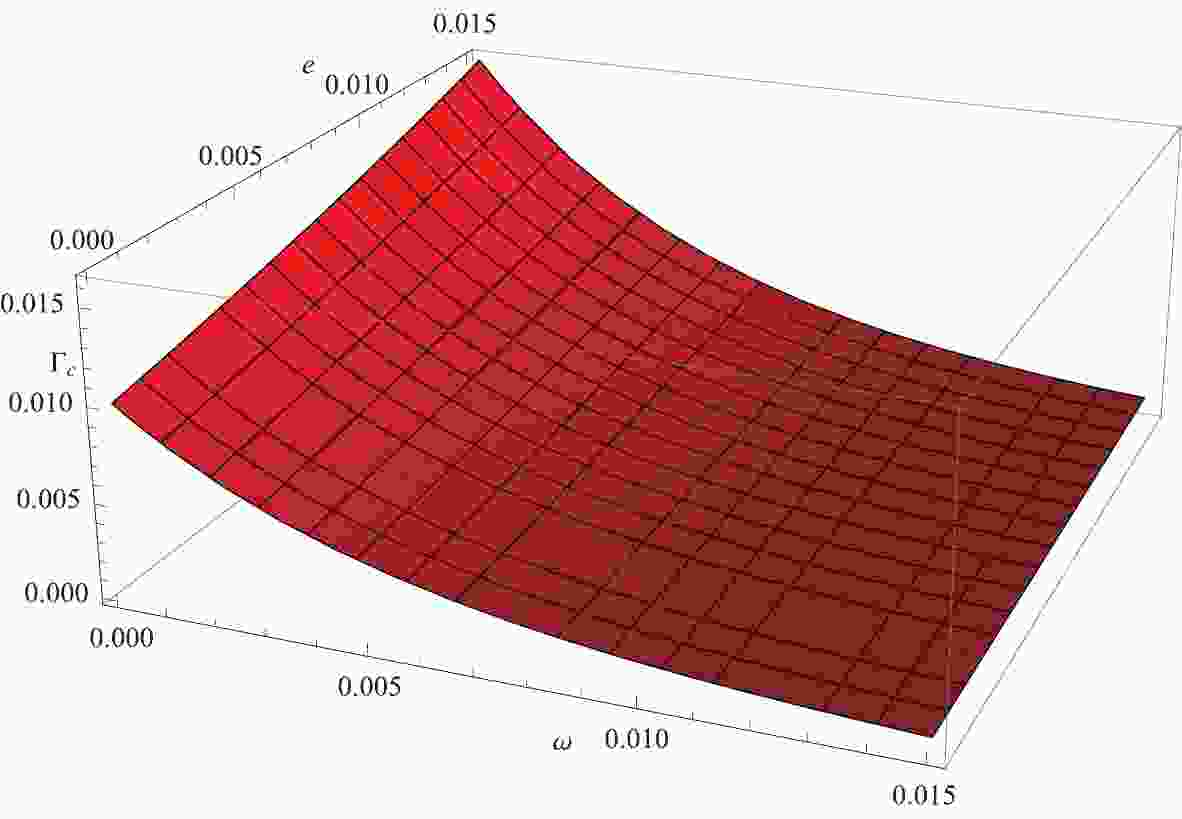
where $ {l_p} = \dfrac{1}{({\xi_2}^2 {M_p}^2)} = \dfrac{{L_p}^2}{{\xi_2}^2} $, $ T_0 = \dfrac{r_+ - r_-}{4 \pi {r_+}^2} $ is the standardHawking temperature of the R-N black hole, and theother terms originate from the corrections due to the effect of the LIV-DR. From Eq. (14), we initially determine that the black hole radiation is not only related to the black hole parameters $ (M,Q) $ but also to the energy $ (\omega) $, charge $ (e) $, and mass $ (m) $ of the emitted particle. In the GUP case, a similar result was also reported in [60, 73] and the references therein. Using equation (14), we can plot Figs. 1, 2 to visually show the LIV-DR induced corrections for the emission rate and the effective temperature of the R-N black hole versus the charge e and energy $ \omega $ of the emitted particle.

Figure 1.  (color online) The LIV-DR induced correction for the emission rate of the R-N black hole versus the charge e and energy $\omega$ of the emitted particle, i.e., $\Gamma_c = - l_p \Gamma_0 \Xi$, where $\Gamma_0$ is the original emission rate of the Dirac particles of the R-N black hole. In this case, we have utilized the acceptable parameters $M = 30,\; Q = 10,\; l_p = 0.01,\; m = 1,\;c = 1, \;k_B = 1$.

Figure 2.  (color online) The LIV-DR induced correction for the effective temperature of the R-N black hole versus the charge e and energy $\omega$ of the emitted particle, i.e., $T_c = l_p T_0 \Xi$. In this case, we have utilized the acceptable parameters $M = 30, Q = 28,\; l_p = 0.01,\; m = 1,\;c = 1,\; k_B = 1$.

In Fig. 1, it is evident that the LIV induced correction of the emission rate increases with the parameter e but decreases with the particle's energy $ \omega $. More importantly, the result also shows that the quantum gravity induced LIV correction for the emission rate is always a positive value, which implies that quantum gravity gives rise to an increase in the tunneling probability of emitted Dirac particles. Therefore, we can conclude that quantum gravity speeds up black hole evaporation.

In Fig. 2, it is evident that the LIV-DR induced correction to the effective temperature of the R-N black hole increases with the emitted particle's energy $ \omega $ but is unchanged when the emitted particle's charge e increases, in a certain energy level. Gravity as a special interaction force, is very sensitive to the mass of the particle, i.e., the energy of the particle according to the mass-energy relation $ \omega = mc^2 $. This phenomenon is distinguished from several other interactions (i.e., electromagnetic interaction, strong interaction, and weak interaction). Considering these facts, Fig. 2 provides phenomenological evidence for the LIV-DR as a candidate for describing the effect of quantum gravity.

To gain an appropriate perspective, we compared our results with earlier findings using another modified dispersion relation that requires a minimum measurable length and maximum measurable momentum (i.e., MDR) [66, 67]. In Ref. [66], if we only consider the 4-dimensional R-N black hole and keep terms up to the order of $ \alpha $, the corrected temperature is given as $ T = T_0 \big(1+{2\alpha}/ {(M + \sqrt{M^2 - Q^2}})^2\big) $. In this case, comparing the effective temperature induced by the MDR with that induced by the LIV-DR, we obtain the following plot Fig. 3, where we have replaced $ \omega $ in the Eq. (14) with the characteristic energy of the emitted particle with T, i.e. $ \omega = k_B T $ [83].

Figure 3.  (color online) The effective temperature of the R-N black hole versus its charge Q for different values of $\xi^2_2$ and $\alpha = 1$. For simplicity, the value of M has been set to 4.

In Figs. 3 and 4, we have chosen reasonable values for $ \xi_2 $ that are within a range of parameters from flaring active galactic nucleus (AGNs) for the $ n = 2 $ case $ \xi_2 \geqslant 10^{-9} $. In Figs. 3 and 4, we first find that the case $ \xi^2_2 \rightarrow \infty $ corresponds to the standard Hawking temperature of the R-N black hole. In addition, we determine that both the effects of the MDR and the LIV-DR speed up the black hole evaporation. However, the MDR-induced departure from the standard temperature is much larger than the LIV-DR induced one when the model-dependent parameter $ \xi^2_2 = \alpha $. The reason for the tracing is that the dispersion relation of the MDR is linearly suppressed by the power $ (E/E_{\rm QG}) $, yet that of the LIV-DR is quadratically suppressed by the power $ (E/E_{\rm QG})^2 $.

Figure 4.  (color online) The effective temperature of the R-N black hole versus its mass M for different values of $\xi^2_2$ and $\alpha = 1$. For simplicity, we have utilized the acceptable parameters $Q = 4, M_p = 1,\; k_B = 1,\; c = 1,\; m = 0.01, \;e = 0.01,\;\alpha = 1$.

In summary, the effective temperature (14) obtained using the semi-classical tunneling method reveals the Planck-scale correction for the original black hole temperature, which is a result of the LIV-DR effect. We also note that a similarly corrected temperature has also been presented in the context of the GUP model [60, 73, 84-87]. In the GUP model, it is determined that this temperature is an important result, which may not only exhibit intriguing properties in the final stage of black hole evaporation [60, 84-87] but also provide insight into the black hole information loss paradox [73, 84]. In our previous study [33], the effect of quantum gravity on black hole thermodynamics was carefully addressed, and some interesting results were obtained. However, in the context of the LIV-DR, the existence of intriguing properties regarding information loss is unknown. As such, it is very interesting for us to further discuss the black hole information loss problem for the inclusion of the effect of the LIV-DR.

In this section, we attempt to investigate the black hole information loss problem with the inclusion of the LIV-DR effect. For simplicity, assuming that the black hole is uncharged (i.e.,$ Q = 0 $), the R-N spacetime is naturally reduced to Schwarzschild spacetime. In this case, as described in our previous research [33], when the heat capacity of the black hole is equal to zero, it would stop a further collapse at a remnant mass, temperature, and entropy, i.e.,

Furthermore, the quantum-gravity induced black hole entropy can also be written in a familiar form,

where the coefficients $ c_j $ are functions of $ \xi_2^{-2} $. The new variable $ \widetilde{{A}} $ is defined as $ \widetilde{{A}} = 16\pi G^2 M^2- \dfrac{2}{4\pi \xi_2^{2} } G^2M_p^2 = {A}-\dfrac{2}{4\pi \xi_2^{2} } L_p^2 $, which is the reduced area, and $ {A} = 16\pi G^2 M^2 $ is the typical area of the Schwarzschild black hole horizon. It is easy to determine that Eq. (16) can be regarded as a new area theorem by considering the quantum gravity effect, which is similar to the standard modified area theorem [58, 81, 88-92]. Most importantly, we find that LIV-DR produced a Logarithmic correction to the black hole entropy, which is consistent with previously reported results [92-95]. In summary, the effect of LIV-DR on black hole thermodynamics coincides with that found in another quantum gravity candidate (i.e. the GUP model), which implies that the LIV-DR is also a good effective phenomenological model of quantum gravity. Moreover, the GUP model, which gives rise to a nonthermal spectrum for black hole radiation, has shown some statistical correlations with the Planck correction between quanta of Hawking radiation [73]. It was found that these correlations can yield a possible solution to the information loss paradox. However, they are not adequate for recovery of the information by themselves. In [73], it should be noted that the influence of conditional probability and the investigation of whether the entropy and information are conserved were not considered. As such, it is very interesting for us to examine the information loss problems in the context of the LIV-DR.

The information loss paradox during Hawking radiation is an outstanding issue in black hole physics. Several research groups have attempted to solve this paradox [39-44, 72, 73, 84, 96-109]. In particular, using the nonthermal radiation spectrum that originated from the self-gravitational effect, the interesting observation that the Hawking radiation via tunneling is an entropy conservation process has been reported. This leads naturally to the conclusion that the process of Hawking radiation is unitary, and no information loss occurs [42-44]. However, the effect of quantum gravity was not considered in resolving this paradox. To completely solve the information loss paradox, the quantum gravity effect and the self-gravitational effect should be considered. As such, before we discuss the information loss problems, it is necessary to initially reproduce the tunneling probability with inclusion of the self-gravitational effect. If the self-interaction effect is taken into account [35], the tunneling rate in the presence of the LIV-DR can be obtained with the aid of the relationship $ \Gamma \sim \exp[\Delta S] = \exp[S_{(M-\omega)}-S_{(M)}] $ [98], that is,

where, $ \widetilde{ A}_{(M-\omega)} = 16 \pi (M - \omega)^2 - \dfrac{2}{4 \pi \xi_2^2} $, and $ \widetilde{ A}_{(M)} = 16 \pi M^2 - \dfrac{2}{4 \pi \xi_2^2} $. For convenience, we used the units $ G = k_B = L_p = 1 $. The expression (17), obtained using the semi-classical tunneling method, shows a deviation from the thermal spectrum radiation, which is a result of the self-interaction and the LIV-DR. Using this expression, we will detail the information loss problems in the next step.

For a black hole with the initial mass M, if one considers a successive emission with an energy $ E_1 $, the associated probability can be expressed as [42-44]

For sequential emissions of energies $ E_1 $ and $ E_2 $, the tunneling probability for the second emission with an energy $ E_2 $ should be considered to be the conditional probability, given the occurrence of tunneling of the particle with an energy $ E_1 $. In this sense, we have

The probability for two simultaneous emissions with energies $ E_1 $ and $ E_2 $ is

Using the standard approach described in [42-44], the independent probability for the second emission is taken as the expected functional form of Eq. (17), that is,

For two emissions ($ E_1, E_2 $), it is obvious that their joint probability $ \Gamma(E_1, E_2) $^⑥ is not equal to the sum of the probability of each emission ($ \Gamma(E_1), \Gamma(E_2) $) of Hawking radiation, i.e., $ \Gamma(E_1+ E_2) \neq \Gamma(E_1) + \Gamma(E_2) $. Alternatively, one can find that the relationship $ \Gamma(E_1,E_2) = \Gamma(E_1) \cdot \Gamma(E_2 \mid E_1) = \Gamma(E_1 + E_2) $ obtained in [42-44] without including the effect of quantum gravity also holds in this case. As such, it is true that a nontrivial correlation must exist between two sequential emissions ($ E_1, E_2 $), and they are indeed dependent. To present this correlation, a quantity used to measure the correlation between sequential emissions $ E_1 $ and $ E_2 $ has been defined in Refs. [42-44]:

Using Eqs. (18), (20), and (21), the corresponding correlation function $ {\cal C}(E_1+E_2;E_1,E_2) $ between the two emitted particles is easy to obtain, which is

By comparing with the correlation functions obtained in [42-44], we found that there is a new term with quantum gravity correction, which enhances the statistical correlations in our case due to the corrected nonthermal spectra produced by the LIV-DR. This result is compatible with the finding in Ref. [73]. Moreover, we can continue to calculate the correlations between the $ n-1 $ emissions and the nth emission with energy $ E_n $. Therefore, by considering that the remnant value of the black hole is $ M_{\rm rem} $ in unit $ c = 1 $^⑦, the total correlation among a queue of Hawking radiations $ E_1,E_2,\cdots E_n $ can be summed up as follows:

where the relation $ M = \displaystyle\sum\limits^{i = n} _{i = 1} E_i + M_{\rm rem} $ is used in the preceding calculation. From Eq. (24), it is evident that when the parameter $ \xi_2 \rightarrow \infty $ , the correlation is naturally reduced to $ \displaystyle\sum\limits_{n \geqslant 2} 8\pi ({E_1 + E_2 + \cdots + E_{n-1}}){E_n} $, which isconsistent with the result obtained by B. C. Zhang [108, 109]. However, the concept of mutual information in a composite quantum system composed of sub-systems A and B is defined as $ S(A:B) = S(A) + S(B) - S(A,B) = S(A) - S(A \mid B) $, where $ S(A \mid B) $ is the conditional entropy. As described in [108, 109], this information $ S(A:B) $ can be used to measure the total correlation between any bi-partite systems. In this sense, with inclusion of the effect of quantum gravity, we find that the mutual information for sequential emission of two emissions ($ E_1 $ and $ E_2 $) is exactly equal to the correlation of Eq. (23), which allows for a reasonable interpretation of the correlation (23). However, this nontrivial correlation (24) is insufficient if one attempts to recover the black hole information. Therefore, it is necessary to carefully reexamine the entropy and information conservation in the next step.

For the first particle with an energy $ E_1 $, when it was emitted from a black hole with a mass M, the entropy carried away by the emission $ E_1 $ is given by

For sequential emissions, the conditional entropy carried away by the second emission $ E_2 $ is given by

Therefore, the total entropy carried away by the two emitted particles can be expressed as

Repeating the process until the black hole radiation ceases, we can easily find that the total entropy carried away by all emissions is [42-44]

with

where $ \Gamma(M-E_1;E_2) $ represents the probability Eq. (17) for an emission with energy $ E_2 $ by a black hole with mass $ (M-E_1) $, which has the same meaning as $ \Gamma(E_2|E_1) $. Earlier in this report, we confirmed that, when the effect of quantum gravity is included during the emission process, the black hole stops further collapse at a remnant mass and becomes an inert remnant. In this sense, black hole remnants should possess a certain amount of entropy in the final stage of black hole evaporation. Assuming that the remnant value of the black hole is $ M_{\rm rem} $ and considering the relation $ M = \displaystyle\sum\limits ^{n}_{i = 1} E_i + M_{\rm rem} $, the total entropy carried away by all emissions for thecondition that the black hole remnant is $ M_{\rm rem} $ takes the form

where $ S_{\rm ini} $ is the total entropy of an initial black hole, the form of which is given by

$ S_{\rm rem} $ is the entropy of the black hole remnants, which is gven by

and $ S_{\rm emi} $ is the entropy of all emitted particles. From Eq. (30), the total entropy ($ S_{\rm ini} $) of an initial black hole is equal to the sum of the entropy ($ S_{\rm emi} $) carried away by all the emissions and the residual entropy $ (S_{\rm rem}) $ of the black hole remnants. Therefore, we conclude that black hole radiation via tunneling is an entropy conservation process, even if the effect of quantum gravity is present. This conclusion is compatible with the findings obtained by [98, 99].

However, we note in the preceding discussions that the specific meaning of the entropy carried away by an emission remains unclear. Thus, it is necessary to continue to investigate this puzzling aspect by considering quantum gravity induced LIV effects. In Refs. [108, 109], B. C. Zhang et al. noted that entropy should be regarded as the uncertainty of the information of the precollapsed configurations of a black hole's forming matter, self-collapsed configurations, and the inter-collapsed configurations. Specifically, when the back reaction of emission is considered and the effect of quantum gravity is not the entropy carried away by a particle $ S(E) = 8 \pi E ( M- E/2) $ should be reexpressed as $ S(E) = 8 \pi E ( M- E) + (4 \pi E^2 - S_0 )+ S_0 $, where $ S_0 $, $ 4 \pi E^2 - S_0 $, and $ 8 \pi E ( M- E) $ are the inherent entropy of the radiating particle that refers to the precollapsed configuration, the entropy of the remaining black hole that refers to the self-collapsed configuration, and the correlation between the radiation and the remaining black hole that refers to the inter-collapsed configuration, respectively. According to this approach, in the context of quantum gravity, we find that the entropy carried away by an emission E should be rewritten as follows:

with

From expression (32), it can easily be determined that the original result, i.e., $ {\cal S}_{ic} = 8 \pi E (M - E),\; {\cal S}_{sc} = 4 \pi E^2 - S_0, \; {\cal S}_{pc} = S_0 $ can be recovered by setting $ \xi_2 \rightarrow \infty $. For a closed physical system, based on information theory, we know that the uncertainty of an event (an emission with an energy E) or the information we gain from this event [110] is $ I(E) = S(E) = -\ln \Gamma(E) $ on average. In this report, we have emphasized that a black hole and its radiations can constitute a closed physics system. As such, the preceding entropies $ {\cal S}_{ic},\; {\cal S}_{sc} $, and $ {\cal S}_{pc} $ that are carried away by Hawking radiation should be interpreted as the uncertainty of the information of its inter-collapsed configuration, self-collapsed configuration, and precollapsed configuration, respectively. Moreover, we can also employ expression (31) to calculate the total entropy carried away by the sequential Hawking radiation. For the first emitted particle with energy $ E_1 $, the entropy is $ {S}(E_1) = {\cal S}_{ic}(E_1:M-E_1) + {\cal S}_{sc}(E_1) + {S}_{01} $. After the first emission, the entropy of the second emitted particle with energy $ E_2 $ is $ {S}(E_2\mid E_1) = {\cal S}_{ic}(E_2:M-E_1-E_2) + {\cal S}_{sc}(E_2) + {S}_{02} $. Repeating this process until the black hole radiation ceased with the remnant mass $ M_{\rm rem} $, the total entropy carried away by black hole radiation can be determined to be the same as (30), i.e., $ S_{\rm emi} = S_{\rm ini} - S_{\rm rem} = \Delta S $. Based on information theory, the total amount of information carried away by all emissions is $ I_{\rm emi}(E_1,E_2,\cdots,E_n) = S( M ) - S( M - \sum^{n}_{i = 1}E_i) = S_{\rm ini} - S_{\rm rem} $. As such, the change in entropy denotes the loss of the information of the black hole $ (\Delta I = - \Delta S) $. Therefore, entropy and information are conserved at all times. This means that the total entropy or information of Hawking radiations can be carried away by themselves, without loss. In addition, it is true that when the effect of LIV is included, we can establish a self-consistent interpretation for the black hole entropy, which is consistent with that obtained in [108, 109]. Finally, we can conclude that in the context of quantum gravity, black hole radiation is not only an entropy and information conservation process but also a unitary process, which is consistent with previous findings [98-100].

In this paper, we applied the Lorentz-invariance-violation (LIV) class of dispersion relations (DR) suppressed by the second power $ (E/E_{\rm QG})^2 $, to carefully study the Hawking radiation of Dirac particles via tunneling from a charged R-N black hole. We determined that black hole radiation is related to not only black hole parameters $ (M,Q) $ but also the energy $ (\omega) $, charge $ (e) $, and mass $ (m) $ of the emission particle. In Fig. 2, it is evident that the LIV-DR induced correction to the effective temperature increases with the increase in the particle's energy $ (\omega) $. However, there were no observed changes for the emitted particle's charge $ (e) $ at a certain energy level. This is phenomenological evidence for the LIV-DR as a candidate for describing the effect of quantum gravity, which confirms the conclusions of [18, 19]. In addition, to place our results in a proper perspective, they were compared with the earlier findings for another deformed dispersion relation suppressed by the first power $ (E/E_{\rm QG}) $. In Figs. 3, 4, the results show that the MDR and the LIV-DR speed up the black hole evaporation. However, the MDR-induced departure from the standard temperature is much larger than the LIV-DR induced departure when the model-dependent parameter $ \xi^2_2 = \alpha $.

The standard Hawking formula predicts the complete evaporation of black holes. However, when the effect of quantum gravity is included during the emission process, we find that there is no complete evaporation in the final stage of black hole evaporation; instead, the remnant values of mass $ {M_{\rm rem}} $, temperature $ {T_{\rm rem}} $, and entropy $ S_{\rm rem} $ arise naturally. In this case, with the inclusion of the LIV-DR, we further discussed the black hole information loss problem using a standard statistical method. The results revealed that the original statistical correlation ($ {\cal C} = 8\pi E_1 E_2 $) was modified, and the quantum-gravity-induced LIV-DR produced a new term with the Planck-scale correction in the statistical correlation function. This effect cannot be neglected once the black hole mass becomes comparable to the Planck mass. Then, based on this correlation, the conditional entropy and total entropy carried away by the emitted particles are calculated, for which the existence of the residual mass is emphasized in the final stage of the black hole evolution. In addition, from Eq. (30), we determined that black hole radiation via tunneling is also an entropy conservation process. Finally, by interpreting the entropy as the uncertainty related to information, it is evident that Hawking radiation can take away information and no information loss occurs during the evaporation process. Therefore, we assert that black hole evaporation is still a unitary process, even if the effect of quantum gravity is present.

The authors would like to thank Professor Shu-Zheng Yang and Qing-Quan Jiang for their useful discussions and the anonymous reviewers for their helpful comments and suggestions, which improved the quality of this paper.