-
α decay, one of the most important decay modes of heavy and superheavy nuclei, attracts constant attention [1-4] because it can be a probe to reveal some important nuclear structure information, such as the properties of the ground state, nuclear deformation, nuclear shape coexistence, energy levels, and so on [5-13], and can be an important tool to identify the new synthesized superheavy nuclei [14-21].
Constructing a reasonable nuclear potential between an α-particle and a daughter nucleus is the most crucial issue in many α decay theoretical models, because the α decay half-life is mainly determined by the barrier penetrating probability [22]. There are many α decay models choosing different nuclear potentials between the α-particle and the daughter nucleus, such as the Coulomb and proximity potential model with proximity potential [23-26], the two-potential approach with a cosh parametrized form nuclear potential [27-29], the density-dependent cluster model with a double-folding integral of the renormalized M3Y nucleon-nucleon potential [30-34], the preformed cluster model with SLy4 Skyrme-like effective interaction [9, 35, 36], and so on.
Unlike other models, the Generalized Liquid Drop Model (GLDM) has two major advantages: introducing the quasimolecular shape mechanism [37], which can describe the complex deformation process from the parent nucleus continuous transition to the appearance of a deep and narrow neck, finally resulting in two tangential fragments, and adding the proximity energy, including an accurate radius and mass asymmetry. When a neck or a gap appears in one-body shapes or between separated fragments, proximity energy plays a key role in taking into account the effects of the nuclear forces between the close surfaces, balancing the repulsion of the Coulomb barrier, and reasonably constructing the barrier heights and positions of the nucleus in complex deformation processes [37-40]. Therefore, the GLDM can successfully deal with proton radioactivity [41], cluster radioactivity [42], fusion [43], fission [44] and the α decay process [22, 37, 40, 45-48].
The proximity energy was first proposed by Blocki et al. [49] for describing the interaction energy associated with the crevice or neck in the nuclear configuration that would be expected immediately after contact of two nuclei in heavy-ion reactions. Therefore, it was also introduced into the GLDM by Royer [37] to take account of the effects of the nucleon–nucleon force inside the neck or the gap between the nascent or separated α-particle and daughter nucleus. The proximity energies are also used to study the fusion reaction cross sections and nuclear decay (including proton radioactivity, α decay, and cluster radioactivity), because these decay modes proceed in the opposite direction of fusion between a particle or cluster and the daughter nucleus [50, 51]. The proximity energy is based on the proximity force theorem [49, 52], which is described as the product of a factor depending on the mean curvature of the interaction surface and a universal function (depending on the separation distance) and is independent of the masses of colliding nuclei [53, 54]. In the past few decades, numerous works have been devoted to improving the original proximity energy (Prox. 77) [49], by either adopting a better form of the surface energy coefficients [55-62] or introducing an improved universal function or another nuclear radius parameterization [52, 53, 63-74].
In order to obtain more precise calculations of α decay half-lives for known nuclei and to enhance the prediction ability of α decay half-lives and the island of stability for superheavy nuclei, it is very important and interesting to develop the GLDM by adopting a more suitable proximity energy for constructing a reasonable potential barrier based on available α decay experimental data. This is the purpose of the present work. We also notice that there have been some works using the GLDM with proximity energy Prox. 81 [52] or proximity energy Denisov [73] instead of the original proximity energy formalism in the GLDM to study the α decay [75-78]. The calculations can reproduce the experimental data better than those calculated by the original GLDM. However, in the present work, we find that proximity energy Prox. 81 [52] is not the most suitable substitute for the original one, and the proximity energy Denisov [73] has a different nuclear radius formalism from that of the GLDM, which is not self-consistent for calculation. In this work, for self-consistency, we choose 16 various versions of proximity energies that have the same radii forms as the GLDM and systematically study the applicability of these when applied to the GLDM. The calculations indicate that GLDM with the proximity energy Prox. 77-Set 13 gives the lowest root-mean-square (RMS) deviation in reproducing experimental α half-lives. Using GLDM with proximity energy Prox. 77-Set 13, we predict α decay half-lives of superheavy even-even nuclei with
$ Z = 112-122 $ . The predictions are compared with the ones calculated by the improved Royer formula [79] and the universal decay law (UDL) [80].This article is organized as follows. In Sec. II, theoretical framework for the α decay half-life and the GLDM are briefly presented. The detailed calculations and discussion are given in Sec. III. Sec. IV presents a brief summary.
-
The α decay half-life can be calculated with decay constant
$ \lambda $ as$ T_{1/2} = \frac{\ln{2}}{\lambda} . $

(1) In the framework of the GLDM [22, 37, 40, 45-48], the α decay constant
$ \lambda $ can be obtained by the product of α-particle preformation factor$ P_{\alpha} $ , the assault frequency$ \nu $ , and the barrier penetrating probability$ P $ :$ \lambda = P_{\alpha}{\nu}P . $

(2) The α-particle preformation factor
$ P_{\alpha} $ can be estimated by the analytic formula put forwarded in our previous work [81]. It is expressed as$ \log_{10}P_{\alpha} = a+bA^{1/6}\sqrt{Z}+c\frac{Z}{\sqrt{Q_{\alpha}}}-d\chi^{\prime}-e\rho^{\prime}+f\sqrt{l(l+1)} , $

(3) where
$ \chi^{\prime} \!=\! Z_1Z_2\sqrt{\frac{A_1A_2}{(A_1+A_2)Q_{\alpha}}} $ and$ \rho^{\prime} \!\!=\!\! \sqrt{\frac{A_1A_2}{A_1\!+\!A_2}Z_1Z_2(A_1^{1/3}\!+\!A_2^{1/3})} $ ;$ A $ ,$ Z $ represent the mass number and proton number of the α decay parent nucleus, respectively;$ l $ is the angular momentum taken away by the α-particle; and the values of adjustable parameters$ a $ ,$ b $ ,$ c $ ,$ d $ ,$ e $ , and$ f $ are fitted by the extracted α-particle preformation factor from the ratios of calculated α decay half-lives with$ P_{\alpha} = 1 $ to experimental data and are listed in Table 3.The assault frequency
$ \nu $ can be obtained by$ \nu = \frac{1}{2R_0}\sqrt{\frac{2E_{\alpha}}{M}} , $

(4) with
$ E_{\alpha} $ and$ M_{\alpha} $ being the kinetic energy and mass of the α-particle, respectively;$ R_0 $ is the radius of the α decay parent nucleus obtained by$ R_{i} = 1.28A_{i}^{1/3}-0.76+0.8A_{i}^{-1/3}(i = 0,1,2) . $

(5) The barrier penetrating probability
$ P $ can be obtained by Wentzel-Kramers-Brillouin (WKB) approximation as$ P = \exp\bigg[-\frac{2}{\hbar}{\int_{r_{{\rm{in}}}}^{r_{{\rm{out}}}} \sqrt{2B(r)(E_{r}-E({\rm{sphere}}))} {\rm d}r}\bigg] , $

(6) where
$ r $ represents the center of mass distance between the preformed α-particle and the daughter nucleus. The classical turning points$ r_{{\rm{in}}} $ and$ r_{{\rm{out}}} $ can be obtained by$ r_{{\rm{in}}} = $ $ R_1+R_2 $ and$ E(r_{{\rm{out}}}) = Q_{\alpha} $ .$ B(r) = \mu $ represents the reduced mass between the preformed α-particle and daughter nucleus.The total interaction potential
$ E $ in the GLDM is composed of five parts [37]: volume energy$ E_{\rm V} $ , surface energy$ E_{\rm S} $ , Coulomb energy$ E_{\rm C} $ , proximity energy$ E_{{\rm{Prox}}} $ , and centrifugal potential$ E_{l} $ .$ E = E_{\rm V}+E_{\rm S}+E_{\rm C}+E_{{\rm{Prox}}}+E_{l} . $

(7) For one-body shapes, the volume, surface, and Coulomb energies are expressed as
$ E_{\rm V} = -15.494(1-1.8I^2)A , $

(8) $ E_{\rm S} = 17.9439(1-2.6I^2)A^{2/3}(S/4{\pi}R_0^2) , $

(9) $ E_{\rm C} = 0.6e^2(Z^2/R_0)\times0.5\int(V(\theta)/V_0)(R(\theta)/R_0)^3\sin\theta{{\rm d}\theta} , $

(10) where
$ S $ denotes the surface of the one-body deformed nucleus,$ I $ is the relative neutron excess,$ V(\theta) $ represents the electrostatic potential at the surface, and$ V_0 $ is the surface potential of the sphere.For two separated fragments, the volume, surface, and Coulomb energies are defined as
$ E_{\rm V} = -15.494[(1-1.8I_1^2)A_1+(1-1.8I_2^2)A_2] , $

(11) $ E_{\rm S} = 17.9439[(1-2.6I_1^2)A_1^{2/3}+(1-2.6I_2^2)A_2^{2/3}] , $

(12) $ E_{\rm C} = 0.6e^2Z_1^2/R_1+0.6e^2Z_2^2/R_2+e^2Z_1Z_2/r , $

(13) with
$ A_i $ ,$ Z_i $ ,$ R_i $ , and$ I_i $ being the mass numbers, proton numbers, radii, and the relative neutron excesses of the α-particle and the daughter nucleus, respectively.The centrifugal barrier
$ E_l(r) $ can be calculated by$ E_l(r) = \frac{{\hbar}^2l(l+1)}{2{\mu}r^2} . $

(14) On the basis of the conservation laws of angular momentum and parity [82], the minimum angular momentum
$ l_{\min} $ carried by an α-particle can be obtained by$ l_{\min} = \left\{\begin{array}{llll} {\Delta}_j,&{\rm{for\;even}}\;{\Delta}_j\;{\rm{and}}\;{\pi}_p = {\pi}_d,\\ {\Delta}_j+1,&{\rm{for\;even}}\;{\Delta}_j\;{\rm{and}}\;{\pi}_p\ne{\pi}_d,\\ {\Delta}_j,&{\rm{for\;odd}}\;{\Delta}_j\;{\rm{and}}\;{\pi}_p\ne{\pi}_d,\\ {\Delta}_j+1,&{\rm{for\;odd}}\;{\Delta}_j\;{\rm{and}}\;{\pi}_p = {\pi}_d, \end{array}\right. $

(15) where
$ {\Delta}_j = |j_p-j_d| $ ,$ j_p $ ,$ \pi_p $ ,$ j_d $ ,$ \pi_d $ are the spin and parity values of the parent and daughter nuclei, respectively. -
The surface energy comes from the effects of the surface tension forces in half-space. When a neck or a gap appears in one-body shapes or between separated fragments, an additional term called the proximity energy must be added to take into account the effects of the nuclear forces between the close surfaces [37, 40]. The proximity energy is described as the product of a factor depending on the mean curvature of the interaction surface and a universal function depending on the separation distance [53, 54].
In the present work, for self-consistency, we choose 16 various versions of proximity energies that have the same radii forms as the GLDM, including proximity energy formalisms Prox. 77 [49] and its 12 modified forms on the basis of improving the surface energy coefficients [55-62], Bass 80 [69], Prox. 81 [52], and Guo 2013 [74]. Proximity energy Prox. 77 [49] and its 12 modified forms are expressed as
$ E_{\rm{Prox}}(r) = 4\pi{\gamma}b\bar{R}\phi(\xi) , $

(16) where the mean curvature radius
$ \bar{R} $ can be obtained as$ \bar{R} = \frac{C_1C_2}{C_1+C_2} , $

(17) where
$ C_1 $ and$ C_2 $ denote the matter radii of the α-particle and the daughter nucleus, respectively, which are given by$ C_i = R_i\left[1-(\frac{b}{R_i})^2\right] (i = 1,2) , $

(18) with the effective sharp radius
$ R_i $ obtained by Eq. (5).The surface energy coefficient
$ \gamma $ can be obtained by$ \gamma = \gamma_0(1-k_sA_s^2), $

(19) where
$ A_s = \dfrac{N-Z}{N+Z} $ represents neutron-proton excess. The surface energy constant$ \gamma_0 $ and the surface asymmetry constant$ k_s $ are set in various improvements asSet 1:
$ \gamma_0 = 0.9517\ ({\rm{MeV/fm}}^2) $ ,$ k_s = 1.7826 $ [49],Set 2:
$\gamma_0 = 1.01734\ ({\rm{MeV/fm}}^2)$ ,$ k_s = 1.79 $ [55],Set 3:
$\gamma_0 = 1.460734\ ({\rm{MeV/fm}}^2)$ ,$ k_s = 4.0 $ [56],Set 4:
$ \gamma_0 = 1.2402\ ({\rm{MeV/fm}}^2) $ ,$ k_s = 3.0 $ [57],Set 5:
$\gamma_0 = 1.1756\ ({\rm{MeV/fm}}^2)$ ,$ k_s = 2.2 $ [58],Set 6:
$\gamma_0 = 1.27326\ ({\rm{MeV/fm}}^2)$ ,$ k_s = 2.5 $ [58],Set 7:
$\gamma_0 = 1.2502\ ({\rm{MeV/fm}}^2)$ ,$ k_s = 2.4 $ [58],Set 8:
$\gamma_0 = 0.9517\ ({\rm{MeV/fm}}^2)$ ,$ k_s = 2.6 $ [59],Set 9:
$\gamma_0 = 1.2496\ ({\rm{MeV/fm}}^2)$ ,$ k_s = 2.3 $ [60],Set 10:
$ \gamma_0 = 1.25284\ ({\rm{Mev/fm}}^2) $ ,$ k_s = 2.345 $ [61],Set 11:
$\gamma_0 = 1.08948\ ({\rm{MeV/fm}}^2)$ ,$ k_s = 1.9830 $ [62],Set 12:
$\gamma_0 = 0.9180\ ({\rm{MeV/fm}}^2)$ ,$ k_s = 0.7546 $ [62],Set 13:
$\gamma_0 = 0.911445\ ({\rm{MeV/fm}}^2)$ ,$ k_s = 2.2938 $ [62].The universal function
$ \phi(\xi) $ is expressed as$ \phi(\xi) = \left\{\begin{array}{ll} -\dfrac{1}{2}(\xi-\xi_0)^2-0.0852(\xi-\xi_0)^3,&0<\xi\leqslant{1.2511},\\ -3.347\exp\left(\dfrac{-\xi}{0.75}\right),&\xi\geqslant{1.2511}, \end{array}\right. $

(20) where
$ \xi_0 = 2.54 $ .$ \xi = \dfrac{r-C_1-C_2}{b} $ is the distance between the near surface of the α-particle and daughter nucleus with the width parameter$ b $ taken as unity. -
The aim of the present work is to develop the GLDM for enhancing calculation accuracy and prediction ability of α decay half-lives for known and unsynthesized superheavy nuclei by chosing a more suitable proximity energy in constructing a reasonable potential barrier.
If the improved versions of the original proximity energy can be applied to the GLDM, three conditions need to be met: first, the radii formulas for the proximity energy and GLDM should be the same; second, the total GLDM energy, including the proximity energy, between the α-particle and daughter nucleus should be reasonable; and finally, the calculated α decay half-lives by the GLDM with the best selected proximity energy should give the lowest RMS deviation in reproducing experimental α half-lives. Therefore, we comparatively study the abilities of 16 various versions of proximity energies when they are applied to the GLDM for describing the α decay half-lives, in which the proximity energies have the same radii forms as the GLDM. These proximity energies include Prox. 77 [49] and its 12 modified forms on the basis of improving the surface energy coefficients [55-62], Bass 80 [69], Prox. 81 [52], and Guo 2013 [74].
In these various versions of proximity energies, we find that the proximity energy Guo 2013 [74] is not suitable for application to the GLDM because for some α decay nuclei such as 148Gd, the total nuclear potential distribution shows short-term decline, even less than zero, after the two tangent fragments have separated, which results from the proximity energy determining too strong an attractive interaction potential.
For choosing the most suitable one from the remainder of proximity energies that can be applied to the GLDM, we calculate the RMS deviation between the calculated α decay half-lives by the GLDM with various proximity energies, where the α-particle preformation factor is assumed as the constant
$ P_{\alpha} = 1 $ , and experimental data for all 535 nuclei, including 159 even-even nuclei, 295 odd-$ A $ nuclei, and 81 doubly odd nuclei using$ \sigma = \sqrt{\frac{1}{n}\sum \left({\log_{10}T_{1/2}^{{\rm{cal}}}-\log_{10}T_{1/2}^{{\rm{exp}}}}\right)^2} . $

(21) The results are listed in Table 1. In this table, we can find that the
$ \sigma $ values are all greater than 1, indicating that there are average deviations of more than one order of magnitude between the calculations and the experimental data because α-particle preformation factors are assumed as$ P_{\alpha} = 1 $ , which are overestimated. In addition, we find that the values of$ \sigma $ are different when caused by the GLDM with various proximity energies. The minimum$ \sigma = 1.459 $ and maximum$ \sigma = 1.644 $ are caused by the GLDM with proximity energies Prox. 77-Set 13 and Bass 80, respectively.GLDM with proximity energy $\sigma$ 

GLDM with proximity energy $\sigma$ 

Prox. 77-Set 1 1.472 Prox. 77-Set 2 1.488 Prox. 77-Set 3 1.579 Prox. 77-Set 4 1.534 Prox. 77-Set 5 1.525 Prox. 77-Set 6 1.546 Prox. 77-Set 7 1.541 Prox. 77-Set 8 1.467 Prox. 77-Set 9 1.542 Prox. 77-Set 10 1.543 Prox. 77-Set 11 1.505 Prox. 77-Set 12 1.471 Prox. 77-Set 13 1.459 Bass 80 1.644 Prox. 81 1.500 original one 1.605 Table 1. The RMS deviations between calculated α decay half-lives by GLDM with different versions of proximity energies and experimental data.
The experimental data and calculations of α decay half-lives for 148Gd, as an example, are listed in Table 2. From this table, one can find that the GLDM with various proximity energies calculates different α decay half-lives. Further, all calculations are an order of magnitude smaller than the experimental data, indicating that the α-particle preformation factor is on the order of
$ 10^{-1} $ . In addition, one can see that most of the calculations by the GLDM with improved proximity energies are better than the ones by the original GLDM from the aspect of reproducing experimental data. However, the GLDM with proximity energy Bass 80 gives a worse calculation than the one calculated by the original GLDM, showing that it is not appropriate for application to the GLDM. The calculation by the GLDM with proximity energy Prox. 77-Set 13 gives the closest reproduction of the experimental data. Why are calculations by the GLDM with various proximity energies different from each other? Based on our comparative analysis, we can explore what particular feature of a given potential impacts these differences between various theoretical calculations, as well as differences between theory and experiments. From Sec. II.A, we find that the α decay half-life can be obtained using the α-particle preformation factor, which is assumed as the constant$ P_{\alpha} = 1 $ in comparing proximity energies, the assault frequency$ \nu $ , which is dependent on α decay energy$ Q_{\alpha} $ , and barrier penetration probability$ P $ , which is related to the total GLDM energy. However, for an α decay nucleus,$ Q_{\alpha} $ and the assault frequency$ \nu $ are fixed. Therefore, these have different total GLDM energies, and various versions of the proximity energies cause the differences between calculated α decay half-lives. In order to verify this conclusion, taking 148Gd, for instance, we plot its 16 versions of total GLDM energy distributions, including the original proximity energy and its 15 improved versions, in Fig. 1. In this figure, we can see that the proximity energies only work in the short region from 7.8 to 12 fm. After the α-particle and daughter nuclei are separated, the proximity energies are equal to zero. Therefore, as can be seen from Section 2.1, the classic turning points$ r_{{\rm{in}}} = R_1+R_2 $ and$ E(r_{{\rm{out}}}) = Q_{\alpha} $ in the GLDM with various proximity energies are the same. In addition, we see that the proximity energies can lower the height of the potential barriers, and their attractive effect balances the Coulomb repulsion between the two fragments. Further, the peaks of potential barriers are shifted toward more external positions. Thus, the different proximity energies cause changes in the shape and height of the total GLDM energy distributions.
Figure 1. (color online) The distributions of total GLDM energies including various versions of proximity energies for 148Gd.
method α decay half-lives for 148Gd/s experimental data $2.24\times10^9$ 

GLDM with original proximity energy $4.83\times10^8$ 

GLDM with Prox. 77- Set 1 $6.93\times10^8$ 

GLDM with Prox. 77- Set 2 $6.49\times10^8$ 

GLDM with Prox. 77- Set 3 $4.31\times10^8$ 

GLDM with Prox. 77- Set 4 $5.30\times10^8$ 

GLDM with Prox. 77- Set 5 $5.56\times10^8$ 

GLDM with Prox. 77- Set 6 $5.05\times10^8$ 

GLDM with Prox. 77- Set 7 $5.16\times10^8$ 

GLDM with Prox. 77- Set 8 $7.03\times10^8$ 

GLDM with Prox. 77- Set 9 $5.15\times10^8$ 

GLDM with Prox. 77- Set 10 $5.14\times10^8$ 

GLDM with Prox. 77- Set 11 $6.05\times10^8$ 

GLDM with Prox. 77- Set 12 $7.04\times10^8$ 

GLDM with Prox. 77- Set 13 $7.28\times10^8$ 

GLDM with Bass 80 $3.90\times10^8$ 

GLDM with Prox. 81 $6.33\times10^8$ 

Table 2. The α decay half-lives of calculations by GLDM with different versions of proximity energies and experimental data for 148Gd.
The same values of
$ r_{{\rm{in}}} $ and$ r_{{\rm{out}}} $ as well as the highest height of$ E(r) $ in the GLDM with proximity energy Prox. 77-Set 13 result in the minimum barrier penetration probability$ P $ . Thus, the calculated α decay half-life is the maximum one in Table 2. Similarly, the lowest height of$ E(r) $ in the GLDM with proximity energy Bass 80 resulted in the minimum calculation. It is shown that the proximity energy is very important in the GLDM, because it affects the shape and height of the total potential barrier, which determines the possibility of barrier penetration and in turn leads to the theoretical calculation of α decay half-life. Therefore, it is interesting and important to find the most suitable proximity energy for developing the GLDM to obtain precise calculations and enhance the prediction ability of α decay half-lives. From Tables 1 and 2, it is shown that the proximity energy Prox. 77-Set 13 is the most suitable one for application to the GLDM for describing the α decay half-lives. The$ \sigma $ values indicate that, compared with the original GLDM, the calculated α decay half-lives using the GLDM with proximity energy Prox. 77-Set 13 are improved by$ \dfrac{1.605-1.459}{1.605}$ = 9.1%. Although the relative value is not large, this is a significant improvement on the GLDM because the proximity energy can affect the total interaction potential in a short region.In our previous work [81], we proposed an analytic formula for estimating the α-particle preformation factor, i.e., Eq. (3). In this work, because we choose a more suitable proximity energy in the GLDM, the parameters of Eq. (3) should be redetermined. First, we extract the α-particle preformation factor using the ratio of the calculated α decay half-life within the GLDM with proximity energy Prox. 77-Set 13 and
$ P_{\alpha} = 1 $ to the experimental data. We then use the extracted α-particle preformation factor and Eq. (3) to obtain the parameters, which are listed in Table 3.nuclei region $a$ 

$b$ 

$c$ 

$d$ 

$e$ 

$f$ 

even-even nuclei $N\le126$ 

−9.4985 −8.9005 4.0450 1.0432 −2.9731 − $N>126$ 

−2.1047 0.1230 4.2051 1.0681 0.0533 − odd-A nuclei $N\le126$ 

−24.5445 −13.2233 9.9493 2.5690 −4.5754 −0.0350 $N>126$ 

1.3626 −6.2523 −0.0252 −0.0155 −1.9616 −0.0937 doubly odd nuclei $N\le126$ 

−2.7484 −4.2572 2.2748 0.5947 −1.3917 −0.0901 $N>126$ 

−37.5320 −20.0571 23.5391 6.0638 −6.9409 −0.2030 Table 3. The parameters of Eq. (3) for estimating the α-particle preformation factor.
The calculated α decay half-lives and experimental data are listed in Tables 4-6 for even-even nuclei, odd-
$ A $ nuclei, and doubly odd nuclei, respectively. In each part of these three tables, the first four columns represent the α decay parent nucleus, the daughter nucleus, experimental α decay energy, and the minimum angular momentum taken away by the α-particle, while the spin and parity values for the α decay parent and daughter nuclei are taken from the latest evaluated nuclear properties table NUBASE2016 [83], respectively. The fifth one represents the experimental α decay half-life. The sixth one represents the calculated α decay half-life within the original GLDM with$ P_{\alpha} = 1 $ . The seventh one represents the calculated α decay half-life by GLDM with proximity energy Prox. 77-Set 13 and$ P_{\alpha} = 1 $ . The eighth one represents the obtained α-particle preformation factor from Eq. (3). The last one represents the calculated α decay half-life within the GLDM with proximity energy Prox. 77-Set 13 and estimated α-particle preformation factor from Eq. (3). From these three tables, it is seen that, compared with$ \lg T^{{\rm{cal1}}}_{1/2} $ ,$ \lg T^{{\rm{cal2}}}_{1/2} $ has a significant improvement in conformity with the experimental data. However, both$ \lg T^{{\rm{cal1}}}_{1/2} $ and$ \lg T^{{\rm{cal2}}}_{1/2} $ are smaller than experimental data by more than an order of magnitude on the whole. This is because the α preformation factor is assumed as$ P_{\alpha} = 1 $ , which is overestimated. Therefore, an α preformation factor$ P_{\alpha} $ should be introduced in the theoretical model. After considering the α-particle preformation factor calculated by Eq. (3),$ \lg T^{{\rm{cal3}}}_{1/2} $ can well reproduce the experimental data.α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

148Gd 144Sm 3.27 0 9.35 8.68 8.86 0.2841 9.41 150Gd 146Sm 2.81 0 13.75 13.17 13.17 0.3578 13.62 150Dy 146Gd 4.35 0 3.07 2.17 2.21 0.1775 2.96 152Dy 148Gd 3.73 0 6.93 6.26 6.32 0.2117 6.99 154Dy 150Gd 2.95 0 13.98 13.17 13.39 0.3075 13.9 152Er 148Dy 4.94 0 1.06 0.12 0.26 0.1635 1.05 154Er 150Dy 4.28 0 4.68 3.72 3.95 0.1845 4.69 156Er 152Dy 3.48 0 10.24 9.49 9.61 0.2389 10.23 154Yb 150Er 5.47 0 −0.35 −1.39 −1.15 0.1601 −0.36 156Yb 152Er 4.81 0 2.41 1.79 1.95 0.1725 2.71 158Yb 154Er 4.17 0 6.63 5.52 5.55 0.1917 6.27 156Hf 152Yb 6.03 0 −1.63 −2.73 −2.55 0.1609 −1.75 158Hf 154Yb 5.41 0 0.35 −0.18 −0.15 0.165 0.64 160Hf 156Yb 4.9 0 3.28 2.28 2.38 0.1672 3.15 162Hf 158Yb 4.42 0 5.69 5.07 5.2 0.1719 5.96 158W 154Hf 6.62 0 −2.9 −4.04 −3.9 0.1645 −3.12 160W 156Hf 6.07 0 −0.99 −2.05 −1.91 0.1616 −1.12 162W 158Hf 5.68 0 0.42 −0.46 −0.31 0.1549 0.5 164W 160Hf 5.28 0 2.22 1.31 1.52 0.1501 2.34 166W 162Hf 4.86 0 4.74 3.49 3.58 0.1475 4.41 168W 164Hf 4.5 0 6.2 5.57 5.71 0.1439 6.55 180W 176Hf 2.52 0 25.75 24.54 24.72 0.1572 25.52 162Os 158W 6.77 0 −2.68 −3.76 −3.58 0.1623 −2.79 166Os 162W 6.14 0 −0.53 −1.55 −1.43 0.1412 −0.58 168Os 164W 5.82 0 0.68 −0.23 −0.08 0.1327 0.79 170Os 166W 5.54 0 1.89 1.01 1.21 0.124 2.12 172Os 168W 5.22 0 3.23 2.46 2.54 0.1171 3.48 174Os 170W 4.87 0 5.25 4.35 4.53 0.1122 5.48 186Os 182W 2.82 0 22.8 21.72 21.89 0.1048 22.87 166Pt 162Os 7.29 0 −3.52 −4.73 −4.58 0.1518 −3.76 168Pt 164Os 6.99 0 −2.69 −3.78 −3.65 0.14 −2.8 172Pt 168Os 6.46 0 −1 −2.02 −1.9 0.1185 −0.98 174Pt 170Os 6.18 0 0.06 −0.95 −0.76 0.1096 0.2 176Pt 172Os 5.89 0 1.2 0.28 0.48 0.1019 1.47 178Pt 174Os 5.57 0 2.43 1.63 1.71 0.0953 2.73 180Pt 176Os 5.24 0 4.27 3.28 3.47 0.0898 4.51 182Pt 178Os 4.95 0 5.62 4.83 5.02 0.0842 6.09 184Pt 180Os 4.6 0 7.77 6.94 7.06 0.0803 8.15 190Pt 186Os 3.27 0 19.31 17.86 17.98 0.0797 19.08 172Hg 168Pt 7.53 0 −3.64 −4.79 −4.65 0.1315 −3.77 174Hg 170Pt 7.23 0 −2.7 −3.9 −3.7 0.1206 −2.78 176Hg 172Pt 6.9 0 −1.65 −2.79 −2.59 0.1114 −1.63 178Hg 174Pt 6.58 0 −0.53 −1.69 −1.59 0.1029 −0.6 180Hg 176Pt 6.26 0 0.73 −0.47 −0.28 0.0952 0.74 182Hg 178Pt 6 0 1.89 0.62 0.81 0.0876 1.87 184Hg 180Pt 5.66 0 3.44 2.12 2.23 0.0816 3.32 186Hg 182Pt 5.2 0 5.7 4.37 4.55 0.0778 5.66 178Pb 174Hg 7.79 0 −3.64 −4.94 −4.8 0.114 −3.86 180Pb 176Hg 7.42 0 −2.39 −3.81 −3.62 0.1049 −2.64 184Pb 180Hg 6.77 0 −0.21 −1.64 −1.53 0.0885 −0.48 186Pb 182Hg 6.47 0 1.07 −0.54 −0.36 0.0813 0.73 188Pb 184Hg 6.11 0 2.43 0.94 1.13 0.0752 2.25 190Pb 186Hg 5.7 0 4.24 2.81 2.93 0.0703 4.08 192Pb 188Hg 5.22 0 6.55 5.26 5.44 0.0664 6.62 186Po 182Pb 8.5 0 −4.47 −6.36 −6.16 0.086 −5.09 190Po 186Pb 7.69 0 −2.61 −4.08 −3.98 0.0724 −2.84 194Po 190Pb 6.99 0 −0.41 −1.79 −1.6 0.0608 −0.38 196Po 192Pb 6.66 0 0.75 −0.58 −0.47 0.0557 0.78 198Po 194Pb 6.31 0 2.27 0.82 1 0.0512 2.29 200Po 196Pb 5.98 0 3.79 2.26 2.44 0.047 3.76 202Po 198Pb 5.7 0 5.14 3.53 3.64 0.0431 5.01 204Po 200Pb 5.49 0 6.27 4.61 4.77 0.0393 6.18 206Po 202Pb 5.33 0 7.14 5.44 5.61 0.0357 7.06 208Po 204Pb 5.22 0 7.96 6.06 6.17 0.0323 7.66 212Po 208Pb 8.95 0 −6.53 −8 −7.81 0.1047 −6.83 214Po 210Pb 7.83 0 −3.79 −4.94 −4.75 0.1419 −3.91 216Po 212Pb 6.91 0 −0.84 −1.86 −1.69 0.1921 −0.97 218Po 214Pb 6.12 0 2.27 1.28 1.45 0.2616 2.03 194Rn 190Po 7.86 0 −3.11 −3.9 −3.72 0.0708 −2.57 196Rn 192Po 7.62 0 −2.33 −3.16 −3.08 0.0641 −1.89 200Rn 196Po 7.04 0 0.07 −1.22 −1.04 0.053 0.23 202Rn 198Po 6.77 0 1.09 −0.27 −0.16 0.0482 1.15 204Rn 200Po 6.55 0 2.01 0.61 0.78 0.0438 2.14 206Rn 202Po 6.38 0 2.74 1.27 1.45 0.0396 2.85 208Rn 204Po 6.26 0 3.37 1.79 1.91 0.0358 3.35 210Rn 206Po 6.16 0 3.95 2.16 2.32 0.0323 3.81 212Rn 208Po 6.38 0 3.16 1.15 1.31 0.0287 2.86 214Rn 210Po 9.21 0 −6.57 −7.97 −7.77 0.0891 −6.72 Continued on next page Table 4. Calculations of α decay half-lives for even-even nuclei. Experimental α decay half-lives are taken from the latest evaluated nuclear properties table NUBASE2016 [83]. The α decay energies are taken from the latest evaluated atomic mass table AME2016 [84, 85]. The α decay energies and half-lives are in units of MeV and s, respectively.
Table 4-continued from previous page α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

216Rn 212Po 8.2 0 −4.35 −5.3 −5.13 0.1146 −4.19 218Rn 214Po 7.26 0 −1.47 −2.37 −2.2 0.1515 −1.38 220Rn 216Po 6.41 0 1.75 0.92 1.09 0.206 1.78 222Rn 218Po 5.59 0 5.52 4.76 4.91 0.2943 5.44 202Ra 198Rn 7.88 0 −2.39 −3.34 −3.24 0.0557 −1.98 204Ra 200Rn 7.64 0 −1.22 −2.58 −2.41 0.0504 −1.11 208Ra 204Rn 7.27 0 0.1 −1.37 −1.26 0.0412 0.13 214Ra 210Rn 7.27 0 0.39 −1.49 −1.31 0.03 0.21 216Ra 212Rn 9.53 0 −6.74 −8.08 −7.9 0.075 −6.77 218Ra 214Rn 8.55 0 −4.6 −5.61 −5.44 0.094 −4.41 220Ra 216Rn 7.59 0 −1.75 −2.71 −2.54 0.1221 −1.63 222Ra 218Rn 6.68 0 1.53 0.65 0.81 0.1653 1.59 224Ra 220Rn 5.79 0 5.5 4.7 4.85 0.2376 5.48 226Ra 222Rn 4.87 0 10.7 10.04 10.2 0.3838 10.61 208Th 204Ra 8.2 0 −2.62 −3.65 −3.54 0.0485 −2.22 212Th 208Ra 7.96 0 −1.5 −2.98 −2.81 0.0394 −1.41 214Th 210Ra 7.83 0 −1.06 −2.58 −2.41 0.0355 −0.96 216Th 212Ra 8.07 0 −1.59 −3.41 −3.24 0.0319 −1.75 218Th 214Ra 9.85 0 −6.93 −8.21 −8.03 0.0634 −6.83 220Th 216Ra 8.95 0 −5.01 −6.04 −5.86 0.0765 −4.74 222Th 218Ra 8.13 0 −2.65 −3.69 −3.52 0.0934 −2.5 224Th 220Ra 7.3 0 0.02 −0.93 −0.76 0.1182 0.16 226Th 222Ra 6.45 0 3.27 2.46 2.62 0.1578 3.42 228Th 224Ra 5.52 0 7.78 7.04 7.15 0.2354 7.77 230Th 226Ra 4.77 0 12.38 11.74 11.89 0.3509 12.34 216U 212Th 8.53 0 −2.16 −4.05 −3.89 0.0382 −2.47 218U 214Th 8.78 0 −3.26 −4.81 −4.64 0.0344 −3.17 222U 218Th 9.48 0 −5.33 −6.74 −6.57 0.0612 −5.36 224U 220Th 8.63 0 −3.4 −4.48 −4.31 0.0736 −3.18 226U 222Th 7.7 0 −0.57 −1.56 −1.4 0.0935 −0.37 230U 226Th 5.99 0 6.24 5.48 5.63 0.1673 6.4 232U 228Th 5.41 0 9.34 8.64 8.79 0.2148 9.46 234U 230Th 4.86 0 12.89 12.22 12.37 0.2849 12.91 236U 232Th 4.57 0 14.87 14.21 14.35 0.3309 14.83 228Pu 224U 7.94 0 0.32 −1.65 −1.54 0.0785 −0.44 230Pu 226U 7.18 0 2.01 1.08 1.23 0.0971 2.24 232Pu 228U 6.72 0 4.24 2.98 3.13 0.1114 4.08 234Pu 230U 6.31 0 5.72 4.82 4.97 0.1269 5.87 236Pu 232U 5.87 0 7.96 6.98 7.12 0.1491 7.95 238Pu 234U 5.59 0 9.44 8.49 8.63 0.1647 9.41 240Pu 236U 5.26 0 11.32 10.52 10.66 0.1897 11.38 242Pu 238U 4.98 0 13.07 12.3 12.45 0.2137 13.12 244Pu 240U 4.67 0 15.4 14.6 14.73 0.2508 15.33 234Cm 230Pu 7.37 0 2.28 1.15 1.31 0.08 2.41 236Cm 232Pu 7.07 0 3.35 2.26 2.41 0.0859 3.47 238Cm 234Pu 6.67 0 5.31 3.95 4.1 0.0962 5.11 240Cm 236Pu 6.4 0 6.37 5.2 5.35 0.1037 6.33 242Cm 238Pu 6.22 0 7.15 6.08 6.23 0.1085 7.19 244Cm 240Pu 5.9 0 8.76 7.7 7.84 0.1204 8.76 246Cm 242Pu 5.48 0 11.17 10.07 10.2 0.1424 11.05 248Cm 244Pu 5.16 0 13.08 12.05 12.19 0.1621 12.98 238Cf 234Cm 8.13 0 1.02 −0.91 −0.76 0.0562 0.49 240Cf 236Cm 7.71 0 1.61 0.55 0.7 0.0616 1.91 242Cf 238Cm 7.52 0 2.42 1.26 1.41 0.0636 2.61 244Cf 240Cm 7.33 0 3.07 1.96 2.11 0.0657 3.29 246Cf 242Cm 6.86 0 5.11 3.84 3.99 0.0745 5.11 248Cf 244Cm 6.36 0 7.46 6.16 6.31 0.0869 7.37 250Cf 246Cm 6.13 0 8.62 7.33 7.46 0.0927 8.49 252Cf 248Cm 6.22 0 7.94 6.85 6.99 0.0872 8.05 254Cf 250Cm 5.93 0 9.22 8.31 8.45 0.0955 9.47 244Fm 240Cf 8.55 0 −0.11 −1.63 −1.48 0.0434 −0.12 248Fm 244Cf 8 0 1.56 0.18 0.33 0.0477 1.65 252Fm 248Cf 7.15 0 4.96 3.39 3.53 0.0578 4.77 254Fm 250Cf 7.31 0 4.07 2.67 2.81 0.0539 4.08 256Fm 252Cf 7.03 0 5.07 3.83 3.98 0.0573 5.22 254No 250Fm 8.23 0 1.75 0.03 0.17 0.0387 1.58 256No 252Fm 8.58 0 0.46 −1.18 −1.04 0.0347 0.42 258No 254Fm 8.15 0 2.08 0.24 0.37 0.0376 1.8 256Rf 252No 8.93 0 0.32 −1.55 −1.4 0.0297 0.13 258Rf 254No 9.19 0 −0.98 −2.4 −2.26 0.0275 −0.7 260Rf 256No 8.9 0 0.02 −1.53 −1.4 0.0286 0.15 260Sg 256Rf 9.9 0 −1.91 −3.77 −3.63 0.0218 −1.96 264Hs 260Sg 10.59 0 −2.97 −4.97 −4.82 0.0173 −3.06 268Hs 264Sg 9.63 0 0.15 −2.44 −2.3 0.0195 −0.59 270Hs 266Sg 9.07 0 0.95 −0.75 −0.62 0.0213 1.05 270Ds 266Hs 11.12 0 −3.69 −5.69 −5.55 0.014 −3.69 286Fl 282Cn 10.37 0 −0.46 −2.8 −2.67 0.0115 −0.73 288Fl 284Cn 10.07 0 −0.12 −1.99 −1.87 0.0118 0.05 290Lv 286Fl 11.01 0 −2.1 −3.92 −3.79 0.0094 −1.77 292Lv 288Fl 10.78 0 −1.62 −3.36 −3.23 0.0095 −1.21 294Og 290Lv 11.84 0 −2.94 −5.36 −5.23 0.0076 −3.11 α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

149Tb 145Eu 4.08 2 4.95 3.68 3.8 0.0841 4.88 151Tb 147Eu 3.5 2 8.82 7.76 7.79 0.1413 8.64 151Dy 147Gd 4.18 0 4.28 3.19 3.25 0.0986 4.25 153Dy 149Gd 3.56 0 8.39 7.54 7.67 0.1652 8.45 151Ho 147Tbm 4.64 0 2.2 1.09 1.18 0.0838 2.25 151Hom 147Tb 4.74 0 1.79 0.6 0.7 0.0774 1.81 153Hom 149Tb 4.12 0 5.47 4.14 4.27 0.1119 5.23 153Er 149Dy 4.8 0 1.84 0.78 0.91 0.0796 2 155Er 151Dy 4.12 0 6.15 4.74 4.86 0.119 5.79 153Tm 149Ho 5.25 0 0.21 −0.87 −0.75 0.076 0.37 153Tmm 149Hom 5.24 0 0.43 −0.85 −0.72 0.0763 0.39 155Tm 151Ho 4.57 0 3.38 2.55 2.69 0.1032 3.67 155Yb 151Er 5.34 0 0.3 −0.8 −0.65 0.0782 0.46 157Yb 153Er 4.62 0 3.89 2.76 2.81 0.1057 3.78 155Lu 151Tm 5.8 0 −1.12 −2.3 −2.14 0.0789 −1.04 155Lum 151Tmm 5.73 0 −0.74 −2 −1.84 0.0821 −0.76 155Lun 151Tm 7.58 8 −2.57 −4.48 −4.29 0.0181 −2.55 157Lum 153Tm 5.13 0 1.89 0.64 0.72 0.0967 1.73 157Hf 153Yb 5.89 0 −0.91 −2.22 −2.08 0.0827 −0.99 157Tan 153Lu 7.95 8 −2.77 −4.75 −4.46 0.0246 −2.85 159Ta 155Lum 5.66 0 0.48 −0.83 −0.6 0.1006 0.39 159Tam 155Lu 5.75 0 0.01 −1.19 −0.97 0.0964 0.05 159W 155Hf 6.45 0 −2 −3.46 −3.23 0.0926 −2.2 161W 157Hf 5.92 0 −0.25 −1.46 −1.31 0.0963 −0.29 163W 159Hf 5.52 0 1.27 0.24 0.4 0.0961 1.42 159Rem 155Ta 6.97 0 −3.54 −4.8 −4.56 0.1005 −3.57 161Rem 157Tam 6.43 0 −1.8 −2.97 −2.82 0.1018 −1.82 163Re 159Ta 6.01 0 0.08 −1.41 −1.24 0.0998 −0.24 163Rem 159Tam 6.07 0 −0.49 −1.63 −1.46 0.0975 −0.45 165Re 161Ta 5.69 0 1.25 −0.13 0.08 0.0949 1.1 165Rem 161Tam 5.66 0 1.12 0.02 0.22 0.0963 1.24 167Rem 163Ta 5.41 0 2.77 1.17 1.29 0.0898 2.34 169Re 165Ta 5.01 3 5.18 3.79 3.99 0.0681 5.15 169Rem 165Tam 5.16 3 3.88 3 3.19 0.0632 4.39 161Os 157W 7.07 0 −3.19 −4.74 −4.57 0.1068 −3.6 163Os 159W 6.69 0 −2.26 −3.5 −3.31 0.101 −2.32 165Os 161W 6.34 0 −1.1 −2.28 −2.08 0.0951 −1.05 167Os 163W 5.99 0 0.21 −0.93 −0.79 0.0903 0.25 169Os 165W 5.71 0 1.4 0.21 0.42 0.0837 1.49 165Irm 161Rem 6.89 0 −2.57 −3.82 −3.6 0.1031 −2.62 167Ir 163Re 6.51 0 −1.17 −2.51 −2.36 0.0971 −1.35 167Irm 163Rem 6.56 0 −1.55 −2.71 −2.56 0.0954 −1.54 169Ir 165Re 6.14 0 −0.18 −1.13 −0.92 0.0916 0.11 169Irm 165Rem 6.27 0 −0.45 −1.63 −1.42 0.0877 −0.37 171Ir 167Rem 5.87 0 1.31 −0.05 0.06 0.0842 1.14 171Irm 167Re 6.16 2 0.43 −0.94 −0.84 0.0625 0.37 173Irm 169Re 5.94 2 1.26 −0.09 0.04 0.0562 1.29 175Ir 171Re 5.43 2 3.02 2.23 2.42 0.0567 3.67 177Ir 173Re 5.08 0 4.69 3.67 3.79 0.0664 4.97 167Pt 163Os 7.16 0 −3.1 −4.33 −4.17 0.104 −3.18 171Pt 167Os 6.61 0 −1.3 −2.54 −2.43 0.0851 −1.36 173Pt 169Os 6.36 0 −0.35 −1.64 −1.5 0.0767 −0.38 175Pt 171Os 6.16 2 0.58 −0.57 −0.38 0.056 0.87 177Pt 173Os 5.64 0 2.27 1.36 1.48 0.0676 2.65 179Pt 175Os 5.41 2 3.94 2.72 2.81 0.0503 4.11 181Pt 177Os 5.15 0 4.85 3.74 3.93 0.0564 5.17 183Pt 179Os 4.82 0 6.61 5.57 5.69 0.0535 6.96 171Aum 167Irm 7.16 0 −2.76 −4.04 −3.95 0.0947 −2.93 173Au 169Ir 6.84 0 −1.53 −2.96 −2.82 0.0863 −1.75 173Aum 169Irm 6.9 0 −1.86 −3.17 −3.02 0.085 −1.95 175Au 171Ir 6.59 0 −0.64 −2.08 −1.88 0.0773 −0.77 175Aum 171Irm 6.59 0 −0.75 −2.08 −1.88 0.0773 −0.77 177Au 173Ir 6.3 0 0.56 −1 −0.89 0.0702 0.26 177Aum 173Irm 6.26 0 0.25 −0.85 −0.74 0.0709 0.41 179Au 175Ir 5.98 1 1.51 0.35 0.44 0.0575 1.68 181Au 177Ir 5.75 2 2.7 1.56 1.75 0.0475 3.07 183Au 179Ir 5.47 0 3.89 2.59 2.7 0.053 3.98 185Au 181Ir 5.18 0 4.98 4.05 4.23 0.0488 5.54 171Hg 167Pt 7.67 2 −4.15 −4.9 −4.8 0.0898 −3.75 173Hg 169Pt 7.38 2 −3.1 −4.04 −3.88 0.0804 −2.79 177Hg 173Pt 6.74 2 −0.82 −1.92 −1.82 0.0657 −0.64 179Hg 175Pt 6.36 0 0.14 −0.86 −0.76 0.0737 0.37 181Hg 177Pt 6.28 2 1.12 −0.27 −0.09 0.0519 1.2 183Hg 179Pt 6.04 0 1.9 0.42 0.53 0.0566 1.78 185Hg 181Pt 5.77 0 2.91 1.58 1.77 0.0511 3.06 177Tl 173Au 7.07 0 −1.61 −2.97 −2.88 0.0951 −1.86 177Tlm 173Aum 7.66 0 −3.44 −4.91 −4.78 0.0849 −3.71 179Tl 175Au 6.71 0 −0.36 −1.75 −1.64 0.0863 −0.57 179Tlm 175Aum 7.38 0 −2.85 −4.07 −3.93 0.0756 −2.81 181Tlm 177Aum 6.97 2 −0.46 −2.42 −2.23 0.0567 −0.99 Continued on next page Table 5. Same as Table 4, but for α decay of odd-A nuclei. Elements with superscript "m," "n," "p," or "x" indicate assignments to excited isomeric states (defined as higher states with half-lives greater than 100 ns). Elements with superscript "p" also indicate non-isomeric levels but are used in AME2016 [84, 85].
Table 5-continued from previous page α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

183Tl 179Au 5.98 0 2.54 1.16 1.28 0.072 2.42 183Tlm 179Au 6.61 3 0.54 −0.83 −0.72 0.0474 0.6 187Tlm 183Au 5.66 2 4 2.87 3.05 0.0453 4.39 179Pb 175Hg 7.6 2 −2.41 −4.06 −3.93 0.0764 −2.81 183Pbm 179Hg 7.02 3 −0.38 −1.93 −1.83 0.0555 −0.58 185Pbm 181Hgm 6.56 0 0.91 −0.82 −0.63 0.0674 0.54 187Pb 183Hg 6.39 2 2.2 0.06 0.24 0.0482 1.56 187Pbm 183Hgm 6.21 0 2.18 0.53 0.71 0.0609 1.93 189Pb 185Hg 5.92 2 3.99 2.1 2.21 0.0447 3.56 191Pbm 187Hgm 5.4 0 5.82 4.29 4.47 0.0512 5.76 187Bi 183Tl 7.78 5 −1.43 −3.24 −3.07 0.0385 −1.65 187Bim 183Tl 7.89 0 −3.43 −5.02 −4.82 0.0591 −3.59 189Bi 185Tl 7.27 5 −0.18 −1.64 −1.54 0.0351 −0.09 191Bi 187Tlm 6.45 0 1.36 −0.07 0.12 0.0522 1.4 191Bim 187Tl 7.02 0 −0.78 −2.26 −2.08 0.048 −0.76 193Bi 189Tlm 6.02 0 3.26 1.68 1.86 0.0474 3.19 193Bim 189Tl 6.61 0 0.56 −0.8 −0.61 0.0433 0.75 195Bi 191Tlm 5.54 0 5.76 4.01 4.19 0.0436 5.55 195Bim 191Tl 6.23 0 2.42 0.73 0.92 0.0389 2.33 209Bi 205Tl 3.14 5 26.8 24.29 24.43 0.0145 26.27 211Bi 207Tl 6.75 5 2.11 −0.21 −0.05 0.0287 1.49 213Bi 209Tl 5.99 5 5.12 2.96 3.12 0.031 4.63 187Po 183Pb 7.98 2 −2.85 −4.61 −4.42 0.061 −3.21 189Po 185Pb 7.69 2 −2.42 −3.78 −3.68 0.0536 −2.41 195Po 191Pb 6.75 0 0.69 −0.89 −0.71 0.0451 0.64 195Pom 191Pbm 6.84 0 0.33 −1.26 −1.07 0.0446 0.28 197Po 193Pb 6.41 0 2.08 0.43 0.61 0.04 2.01 197Pom 193Pbm 6.51 0 1.48 0.02 0.2 0.0395 1.6 199Po 195Pb 6.08 0 3.64 1.84 2.02 0.0355 3.47 199Pom 195Pbm 6.18 0 3.02 1.36 1.53 0.035 2.99 201Po 197Pb 5.8 0 4.92 3.05 3.23 0.0313 4.74 201Pom 197Pbm 5.9 0 4.34 2.55 2.73 0.0309 4.24 203Po 199Pb 5.5 2 6.29 4.86 5.02 0.0227 6.66 203Pom 199Pb 6.14 5 5.05 2.92 3.07 0.0165 4.85 205Po 201Pb 5.33 0 7.18 5.46 5.63 0.0241 7.25 207Po 203Pb 5.22 0 7.99 6.06 6.23 0.0208 7.91 209Po 205Pbm 4.98 0 9.59 7.46 7.62 0.0183 9.36 211Pom 207Pb 9.06 13 1.4 −0.66 −0.53 0.0037 1.9 213Po 209Pb 8.54 0 −5.43 −6.94 −6.75 0.0666 −5.57 215Po 211Pb 7.53 0 −2.75 −3.99 −3.84 0.0714 −2.69 219Po 215Pb 5.92 0 3.34 2.19 2.35 0.0834 3.43 191At 187Bim 7.71 0 −2.68 −3.77 −3.58 0.0701 −2.42 191Atm 187Bi 7.88 2 −2.66 −4 −3.81 0.0566 −2.56 193At 189Bim 7.39 0 −1.54 −2.76 −2.58 0.0616 −1.37 193Atm 189Bi 7.58 2 −1.68 −3.11 −2.92 0.0497 −1.62 193Atn 189Bi 7.62 3 −0.93 −2.93 −2.75 0.0456 −1.41 195At 191Bim 7.1 0 −0.54 −1.79 −1.6 0.054 −0.33 197At 193Bi 7.11 0 −0.39 −1.84 −1.66 0.0461 −0.32 197Atm 193Bim 6.84 0 0.3 −0.87 −0.69 0.0472 0.63 199At 195Bi 6.78 0 0.89 −0.64 −0.46 0.0405 0.93 199Atm 195Bi 7.02 5 1.44 −0.12 0.04 0.0255 1.64 201At 197Bi 6.47 0 2.07 0.51 0.69 0.0356 2.14 203At 199Bi 6.21 0 3.15 1.6 1.76 0.0312 3.27 205At 201Bi 6.02 0 4.3 2.45 2.62 0.0271 4.18 207At 203Bi 5.87 0 4.81 3.12 3.29 0.0235 4.92 209At 205Bi 5.76 0 5.67 3.66 3.83 0.0203 5.52 211At 207Bi 5.98 0 4.79 2.49 2.66 0.0171 4.42 213At 209Bi 9.25 0 −6.9 −8.4 −8.2 0.0623 −7 215At 211Bi 8.18 0 −4 −5.6 −5.45 0.0663 −4.27 217At 213Bi 7.2 0 −1.49 −2.52 −2.35 0.0716 −1.2 219At 215Bi 6.34 0 1.78 0.74 0.91 0.0781 2.02 193Rn 189Po 8.04 2 −2.94 −4.15 −3.96 0.0601 −2.74 195Rn 191Po 7.69 0 −2.15 −3.39 −3.2 0.0642 −2 195Rnm 191Pom 7.71 0 −2.22 −3.45 −3.26 0.0641 −2.07 197Rn 193Po 7.41 0 −1.27 −2.49 −2.31 0.056 −1.06 197Rnm 193Pom 7.51 0 −1.59 −2.82 −2.64 0.0556 −1.39 203Rn 199Po 6.63 0 1.82 0.29 0.45 0.0369 1.88 203Rnm 199Pom 6.68 0 1.55 0.08 0.24 0.0368 1.67 205Rn 201Po 6.39 2 2.84 1.57 1.74 0.0263 3.32 207Rn 203Po 6.25 0 3.42 1.84 2.02 0.0277 3.57 209Rn 205Po 6.16 0 4 2.25 2.41 0.0239 4.03 211Rn 207Po 5.97 2 5.28 3.34 3.5 0.017 5.27 213Rn 209Po 8.25 5 −1.71 −4.03 −3.86 0.0224 −2.21 215Rn 211Po 8.84 0 −5.64 −7.06 −6.9 0.0621 −5.69 217Rn 213Po 7.89 0 −3.27 −4.38 −4.21 0.0656 −3.03 219Rn 215Po 6.95 2 0.6 −0.95 −0.78 0.0419 0.59 221Rn 217Po 6.16 2 3.84 2.27 2.44 0.0455 3.78 223Rn 219Po 5.28 2 8.56 6.73 6.88 0.0526 8.16 197Fr 193Atm 7.88 0 −2.63 −3.64 −3.45 0.0677 −2.29 199Fr 195At 7.82 0 −2.18 −3.45 −3.27 0.0582 −2.03 199Frm 195Atm 7.83 0 −2.19 −3.5 −3.32 0.0581 −2.09 201Fr 197At 7.52 0 −1.2 −2.54 −2.35 0.0506 −1.06 201Frm 197Atm 7.6 0 −1.77 −2.81 −2.63 0.0504 −1.33 203Fr 199At 7.27 0 −0.26 −1.73 −1.56 0.0439 −0.2 Table 5-continued from previous page α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

203Frm 199Atm 7.39 0 −0.68 −2.14 −1.97 0.0436 −0.61 205Fr 201At 7.05 0 0.58 −0.95 −0.78 0.038 0.64 207Fr 203At 6.89 0 1.19 −0.37 −0.19 0.0328 1.29 209Fr 205At 6.78 0 1.75 0.06 0.23 0.0283 1.78 211Fr 207At 6.66 0 2.33 0.45 0.61 0.0244 2.23 213Fr 209At 6.91 0 1.54 −0.53 −0.36 0.0209 1.32 215Fr 211At 9.54 0 −7.07 −8.42 −8.26 0.0582 −7.03 219Fr 215At 7.45 0 −1.7 −2.62 −2.45 0.0667 −1.27 221Fr 217At 6.46 2 2.46 1.43 1.59 0.0439 2.95 223Fr 219At 5.56 4 7.34 6.36 6.51 0.0324 8 201Ra 197Rn 8 0 −1.7 −3.7 −3.51 0.0616 −2.3 201Ram 197Rnm 8.07 0 −2.22 −3.89 −3.71 0.0615 −2.5 203Ra 199Rn 7.74 0 −1.44 −2.89 −2.72 0.0533 −1.45 203Ram 199Rnm 7.76 0 −1.6 −2.98 −2.81 0.0533 −1.54 207Ra 203Rn 7.27 2 0.21 −1.06 −0.88 0.0327 0.6 209Ra 205Rn 7.14 0 0.67 −0.91 −0.74 0.0343 0.72 213Ra 209Rn 6.86 2 2.31 0.35 0.52 0.0209 2.2 215Ra 211Rn 8.86 5 −2.78 −5.09 −4.96 0.0199 −3.25 217Ra 213Rn 9.16 0 −5.79 −7.22 −7.04 0.0575 −5.8 219Ra 215Rn 8.14 2 −2 −4.17 −3.99 0.0361 −2.55 221Ra 217Rn 6.88 2 1.45 0.14 0.31 0.0414 1.69 223Ra 219Rn 5.98 2 5.99 4.04 4.2 0.0465 5.53 205Ac 201Frn 7.9 3 −1.1 −2.48 −2.31 0.0427 −0.94 207Ac 203Fr 7.85 0 −1.51 −2.92 −2.74 0.0486 −1.42 211Ac 207Fr 7.62 0 −0.67 −2.25 −2.08 0.0361 −0.64 215Ac 211Fr 7.75 0 −0.77 −2.73 −2.59 0.0269 −1.02 217Ac 213Fr 9.83 0 −7.16 −8.45 −8.27 0.0542 −7 217Acm 213Fr 11.84 11 −4.77 −7.07 −6.93 0.0037 −4.5 219Ac 215Fr 8.83 0 −4.93 −6.04 −5.86 0.0567 −4.61 221Ac 217Fr 7.78 0 −1.28 −2.95 −2.78 0.0612 −1.56 223Ac 219Fr 6.78 2 2.1 0.93 1.08 0.04 2.48 225Ac 221Fr 5.94 2 5.93 4.72 4.87 0.0446 6.23 227Ac 223Fr 5.04 0 10.7 9.38 9.54 0.0897 10.59 209Thm 205Ram 8.28 0 −2.51 −3.91 −3.73 0.0517 −2.45 215Th 211Ra 7.67 2 0.08 −1.79 −1.65 0.027 −0.08 217Th 213Ra 9.44 5 −3.61 −5.9 −5.74 0.0178 −3.99 219Th 215Ra 9.51 0 −5.99 −7.44 −7.26 0.0531 −5.98 221Th 217Ra 8.63 2 −2.75 −4.87 −4.7 0.0324 −3.21 223Th 219Ra 7.57 2 −0.22 −1.6 −1.44 0.0354 0.01 225Th 221Ra 6.92 2 2.77 0.78 0.94 0.0368 2.38 227Th 223Ra 6.15 2 6.21 4.08 4.24 0.0402 5.64 229Th 225Ra 5.17 2 11.4 9.4 9.54 0.0484 10.86 231Th 227Ra 4.21 2 17.36 16.34 16.48 0.063 17.68 213Pa 209Ac 8.4 0 −2.15 −3.97 −3.79 0.0476 −2.47 215Pa 211Ac 8.24 0 −1.85 −3.52 −3.37 0.0409 −1.98 217Pa 213Ac 8.49 0 −2.46 −4.31 −4.14 0.0357 −2.7 221Pa 217Ac 9.25 0 −5.23 −6.48 −6.29 0.0517 −5.01 223Pa 219Ac 8.33 0 −2.29 −3.93 −3.77 0.0543 −2.5 227Pa 223Ac 6.58 0 3.43 2.29 2.45 0.0634 3.65 229Pa 225Ac 5.84 1 7.43 5.91 6.06 0.0515 7.34 219U 215Th 9.94 5 −4.26 −6.51 −6.34 0.0161 −4.55 221U 217Th 9.89 0 −6.18 −7.68 −7.5 0.0487 −6.19 225U 221Th 8.02 2 −1.21 −2.34 −2.18 0.0317 −0.68 227U 223Th 7.23 2 1.82 0.34 0.5 0.0335 1.98 229U 225Th 6.48 0 4.24 3.18 3.33 0.0614 4.54 231U 227Th 5.58 2 9.95 7.99 8.13 0.0419 9.51 233U 229Th 4.91 0 12.7 11.87 12.02 0.0808 13.11 227Np 223Pa 7.82 2 −0.29 −1.34 −1.18 0.0309 0.33 229Np 225Pa 7.02 1 2.55 1.41 1.56 0.0414 2.95 231Np 227Pa 6.36 1 5.14 4.22 4.37 0.044 5.72 235Np 231Pa 5.19 1 12.12 10.52 10.64 0.0515 11.93 237Np 233Pa 4.96 1 13.83 12.07 12.21 0.0515 13.49 239Np 235Pa 4.6 1 16.61 14.68 14.82 0.0542 16.08 231Pu 227U 6.84 0 3.58 2.46 2.61 0.055 3.87 233Pu 229U 6.41 2 6 4.61 4.76 0.0329 6.24 235Pu 231U 5.95 0 7.72 6.55 6.67 0.0577 7.91 239Pu 235Uxm 5.24 0 11.88 10.6 10.74 0.0604 11.96 241Pu 237U 5.14 2 13.26 11.54 11.68 0.034 13.15 229Am 225Np 8.14 2 0.3 −1.67 −1.51 0.0282 0.04 233Am 229Np 7.06 1 3.62 2.07 2.22 0.0366 3.66 235Am 231Np 6.59 1 5.18 4.01 4.14 0.0374 5.57 237Am 233Np 6.2 1 7.24 5.84 5.99 0.0378 7.41 239Am 235Np 5.92 1 8.63 7.24 7.38 0.0375 8.81 241Am 237Np 5.64 1 10.14 8.8 8.95 0.0375 10.37 243Am 239Np 5.44 1 11.37 9.96 10.1 0.0368 11.53 233Cm 229Pu 7.47 0 2.13 0.78 0.94 0.0468 2.27 237Cm 233Pu 6.78 0 4.82 3.5 3.64 0.0459 4.98 241Cm 237Pu 6.19 3 8.45 6.78 6.93 0.0213 8.6 243Cm 239Pu 6.17 2 8.96 6.57 6.71 0.0246 8.32 245Cm 241Pu 5.62 2 11.42 9.46 9.59 0.0264 11.17 247Bk 243Am 5.89 2 10.64 8.43 8.56 0.0232 10.2 241Cf 237Cmp 7.46 0 2.75 1.51 1.66 0.0354 3.11 243Cf 239Cm 7.42 3 3.66 2.16 2.29 0.0156 4.1 245Cf 241Cm 7.26 0 3.87 2.18 2.32 0.0314 3.83 Table 5-continued from previous page α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

247Cf 243Cm 6.5 2 7.5 5.78 5.92 0.0203 7.61 251Cf 247Cm 6.18 5 10.45 8.38 8.51 0.0098 10.52 245Es 241Bkp 7.87 0 2.22 0.28 0.42 0.0285 1.97 247Es 243Bkp 7.44 1 3.59 1.93 2.08 0.021 3.75 249Es 245Bkp 6.9 1 6.03 4.2 4.34 0.0218 6 253Es 249Bk 6.74 0 6.25 4.77 4.91 0.0262 6.49 255Es 251Bkm 6.4 0 7.63 6.3 6.44 0.0263 8.02 243Fm 239Cf 8.7 1 −0.6 −1.98 −1.83 0.0201 −0.14 247Fm 243Cf 8.26 4 1.69 0.13 0.27 0.0095 2.29 247Fmm 243Cf 8.31 0 0.76 −0.88 −0.73 0.0248 0.87 253Fm 249Cfm 7.05 2 6.33 4.07 4.21 0.0147 6.04 257Fm 253Cf 6.86 2 6.94 4.81 4.93 0.0131 6.82 247Md 243Es 8.77 1 0.08 −1.91 −1.76 0.0172 0.004 247Mdm 243Es 9.03 3 −0.5 −2.29 −2.14 0.0106 −0.17 251Md 247Es 7.96 1 3.4 0.73 0.86 0.0169 2.64 251No 247Fm 8.76 0 −0.02 −1.65 −1.51 0.0203 0.18 251Nom 247Fmm 8.82 0 0.01 −1.84 −1.7 0.0201 −0.003 253No 249Fm 8.42 1 2.23 −0.48 −0.34 0.0146 1.5 255No 251Fmm 8.23 2 2.84 0.26 0.4 0.0112 2.35 259No 255Fm 7.85 2 3.66 1.56 1.69 0.0102 3.68 253Lr 249Md 8.93 0 −0.15 −1.84 −1.7 0.0185 0.03 253Lrm 249Mdm 8.86 0 0.17 −1.62 −1.48 0.0187 0.25 255Lr 251Mdp 8.5 0 1.49 −0.54 −0.4 0.0183 1.34 257Lr 253Md 9.08 4 0.78 −1.58 −1.45 0.0059 0.78 259Lr 255Mdp 8.58 0 0.9 −0.83 −0.7 0.0155 1.11 255Rf 251No 9.06 1 0.54 −1.86 −1.71 0.0125 0.19 257Rfm 253No 9.16 2 0.69 −2.03 −1.9 0.0091 0.14 259Rf 255Nop 9.03 0 0.46 −1.9 −1.76 0.0146 0.07 261Rf 257No 8.65 0 0.9 −0.72 −0.59 0.0144 1.26 263Rf 259No 8.26 4 3.34 1.36 1.5 0.0054 3.77 259Db 255Lrm 9.58 1 −0.29 −3.11 −2.97 0.01 −0.97 259Sg 255Rf 9.77 2 −0.38 −3.14 −3 0.0079 −0.9 259Sgm 255Rfm 9.71 2 −0.63 −2.97 −2.84 0.008 −0.74 261Sg 257Rf 9.71 2 −0.73 −3.02 −2.88 0.0074 −0.75 263Sg 259Rf 9.41 0 0.03 −2.41 −2.27 0.0121 −0.35 261Bh 257Db 10.5 3 −1.87 −4.53 −4.39 0.0054 −2.12 265Hs 261Sg 10.47 0 −2.71 −4.7 −4.56 0.0099 −2.56 269Hs 265Sg 9.35 0 1.2 −1.62 −1.48 0.0099 0.52 267Ds 263Hs 11.78 0 −5 −7.1 −6.96 0.0079 −4.85 269Ds 265Hsm 11.28 0 −3.64 −6.04 −5.9 0.0078 −3.79 271Ds 267Hs 10.88 5 −1.05 −4.01 −3.88 0.0023 −1.24 271Dsm 267Hs 10.95 2 −2.77 −5.08 −4.94 0.0044 −2.58 273Ds 269Hs 11.38 3 −3.62 −5.92 −5.79 0.0031 −3.28 277Ds 273Hs 10.83 4 −2.22 −4.39 −4.26 0.0023 −1.62 277Cn 273Dsm 11.42 0 −3.07 −5.9 −5.76 0.0057 −3.52 281Cn 277Ds 10.46 4 −0.74 −2.87 −2.75 0.0021 −0.07 289Fl 285Cn 9.97 0 0.38 −1.72 −1.6 0.0044 0.76 α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

148Eu 144Pm 2.69 0 14.98 13.77 13.95 0.0795 15.04 152Ho 148Tb 4.51 0 3.12 1.83 1.95 0.0634 3.14 152Hom 148Tbm 4.58 0 2.66 1.44 1.56 0.0635 2.76 154Ho 150Tb 4.04 0 6.56 4.65 4.88 0.0582 6.11 154Tm 150Ho 5.09 0 1.17 −0.16 0.08 0.059 1.3 154Tmm 150Hom 5.18 0 0.75 −0.54 −0.31 0.0592 0.92 156Tm 152Ho 4.35 0 5.12 3.88 4.03 0.0533 5.3 156Lum 152Tmm 5.72 0 −0.68 −1.96 −1.78 0.0558 −0.53 158Ta 154Lu 6.13 0 −1.29 −2.71 −2.62 0.0526 −1.34 158Tam 154Lum 6.21 0 −1.42 −3.01 −2.91 0.0528 −1.63 160Re 156Ta 6.7 2 −2.26 −3.6 −3.46 0.0303 −1.94 162Re 158Ta 6.25 0 −0.95 −2.32 −2.15 0.0456 −0.81 162Rem 158Tam 6.28 0 −1.07 −2.43 −2.26 0.0457 −0.92 164Rem 160Tam 5.77 0 1.46 −0.43 −0.22 0.0411 1.16 164Irm 160Rem 7.06 0 −2.78 −4.36 −4.15 0.0445 −2.8 166Ir 162Re 6.73 0 −1.95 −3.29 −3.15 0.0405 −1.76 166Irm 162Rem 6.73 0 −1.81 −3.29 −3.15 0.0405 −1.76 168Ir 164Re 6.38 0 −0.64 −2.03 −1.9 0.0368 −0.46 168Irm 164Rem 6.48 0 −0.68 −2.41 −2.27 0.0371 −0.84 170Ir 166Rep 5.96 0 1.24 −0.37 −0.17 0.0332 1.31 170Irm 166Re 6.27 2 0.35 −1.32 −1.12 0.0205 0.57 172Ir 168Re 5.99 3 2.34 0.06 0.16 0.0151 1.98 172Irm 168Re 6.13 0 1.36 −1.16 −1.04 0.0314 0.46 174Ir 170Re 5.63 2 3.17 1.31 1.5 0.0168 3.27 174Irm 170Re 5.82 2 2.29 0.44 0.63 0.0172 2.4 170Au 166Ir 7.18 0 −2.58 −4.03 −3.82 0.0362 −2.38 Continued on next page Table 6-continued from previous page α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{\exp}_{1/2}$ 

$\lg T^{{\rm{cal1}}}_{1/2}$ 

$\lg T^{{\rm{cal2}}}_{1/2}$ 

${P_{\alpha}}$ 

$\lg T^{{\rm{cal3}}}_{1/2}$ 

170Aum 166Irm 7.29 0 −2.84 −4.38 −4.17 0.0365 −2.74 176Au 172Ir 6.44 0 0.14 −1.52 −1.32 0.0277 0.24 186Au 182Ir 4.91 1 7.89 5.59 5.77 0.0122 7.69 180Tl 176Aum 6.57 3 1.23 −0.62 −0.43 0.0117 1.5 186Tlm 182Au 6.02 6 5.66 3.01 3.18 0.0048 5.5 186Bi 182Tl 7.76 1 −1.83 −4.51 −4.32 0.0162 −2.53 186Bim 182Tlm 7.88 3 −2.01 −4.38 −4.19 0.0107 −2.22 190Bi 186Tl 6.86 1 0.91 −1.56 −1.46 0.013 0.43 190Bim 186Tlm 6.97 3 0.94 −1.45 −1.35 0.0086 0.72 192Bi 188Tl 6.38 1 2.44 0.29 0.47 0.0115 2.41 192Bim 188Tlm 6.49 3 2.58 0.36 0.54 0.0076 2.66 194Bi 190Tl 5.92 1 4.31 2.25 2.43 0.0101 4.42 194Bin 190Tlm 6.02 3 4.74 2.31 2.48 0.0067 4.66 196Bi 192Tlp 5.26 0 7.42 5.46 5.57 0.0114 7.51 196Bin 192Tln 5.32 2 7.8 5.45 5.56 0.0069 7.72 212Bi 208Tl 6.21 5 4 1.99 2.15 0.0085 4.22 214Bi 210Tl 5.62 5 6.75 4.73 4.89 0.0091 6.93 192At 188Bi 7.7 0 −1.94 −3.72 −3.54 0.0175 −1.78 192Atm 188Bim 7.63 3 −1.06 −2.94 −2.76 0.0085 −0.69 194At 190Bin 7.33 0 −0.54 −2.59 −2.4 0.0158 −0.6 194Atm 190Bim 7.31 0 −0.49 −2.49 −2.3 0.0157 −0.5 200At 196Bi 6.6 0 1.92 0.06 0.24 0.0119 2.17 200Atn 196Bim 6.77 3 1.88 −0.05 0.12 0.0059 2.35 202At 198Bi 6.35 0 3.16 0.99 1.1 0.0108 3.07 202Atm 198Bim 6.26 0 3.32 1.4 1.51 0.0106 3.48 202Atn 198Bin 6.4 0 2.68 0.79 0.9 0.0109 2.86 204At 200Bi 6.07 0 4.16 2.22 2.38 0.0097 4.4 206At 202Bi 5.89 0 5.31 3.06 3.23 0.0088 5.29 208At 204Bi 5.75 0 6.02 3.7 3.82 0.0081 5.91 210At 206Bi 5.63 2 7.22 4.52 4.68 0.0045 7.03 212At 208Bi 7.82 5 −0.5 −3.1 −2.93 0.0061 −0.72 218At 214Bi 6.87 0 0.18 −1.38 −1.21 0.0501 0.09 220At 216Bim 6.05 0 3.43 2.02 2.18 0.0542 3.45 200Frm 196Atm 7.71 0 −0.72 −3.11 −2.92 0.0133 −1.05 212Fr 208At 6.53 2 3.44 1.27 1.44 0.0047 3.77 214Fr 210At 8.59 5 −2.29 −4.66 −4.49 0.0058 −2.25 218Fr 214At 8.01 0 −3 −4.43 −4.26 0.0513 −2.97 218Frm 214Atn 7.87 2 −1.66 −3.7 −3.53 0.017 −1.76 220Fr 216At 6.8 1 1.44 −0.16 0.01 0.0289 1.55 216Ac 212Fr 9.24 5 −3.36 −5.74 −5.57 0.0061 −3.36 216Acm 212Fr 9.28 5 −3.36 −5.84 −5.68 0.006 −3.46 218Ac 214Fr 9.37 0 −6 −7.43 −7.25 0.0595 −6.02 222Ac 218Fr 7.14 0 0.7 −0.72 −0.56 0.0548 0.7 226Ac 222Fr 5.51 2 9.23 6.98 7.13 0.0156 8.94 220Pa 216Ac 9.65 0 −6.11 −7.45 −7.27 0.0698 −6.11 224Pa 220Ac 7.69 2 −0.07 −1.64 −1.48 0.017 0.29 228Pa 224Ac 6.27 3 6.63 4.25 4.36 0.0078 6.47 230Pa 226Ac 5.44 2 10.67 8.27 8.41 0.011 10.37 242Amm 238Np 5.64 3 11.99 9.26 9.4 0.0018 12.15 246Es 242Bkp 7.5 0 3.66 1.65 1.79 0.0101 3.79 248Es 244Bk 7.16 2 5.76 3.24 3.38 0.0024 6 252Es 248Bk 6.79 2 7.72 4.83 4.96 0.0013 7.85 254Esm 250Bk 6.7 1 7.64 4.96 5.1 0.0016 7.9 256Mdm 252Es 7.91 3 4.7 1.27 1.41 0.0008 4.5 258Md 254Es 7.27 1 6.65 3.29 3.42 0.0014 6.27 The differences between logarithmic values of the three calculated α decay half-lives and the experimental data are denoted as black open squares, red solid squares, and blue solid circles in Figs. 2-4 for even-even nuclei, odd-
$ A $ nuclei and doubly odd nuclei, respectively. From these figures, it is seen that$ \lg T^{{\rm{cal1}}}_{1/2} $ is significantly less than the experimental value. After adopting the GLDM with proximity energy Prox. 77-Set 13, compared with$ \lg T^{{\rm{cal1}}}_{1/2} $ ,$ \lg T^{{\rm{cal2}}}_{1/2} $ is significantly improved in reproducing the experimental data. In addition, when the neutron numbers are close to the$ N = 126 $ closed shell and the superheavy nuclei region, the deviations caused by$ \lg T^{{\rm{cal1}}}_{1/2} $ and$ \lg T^{{\rm{cal2}}}_{1/2} $ have maximum values, indicating that there are important physics, such as the shell effect, which need to be considered. This also indicates that changing the proximity energy does not affect the revealing of the microscopic shell effect, which is important for predicting the island of stability for superheavy nuclei. After considering the α-particle preformation factors obtained using Eq. (3), the deviations caused by$ \lg T^{{\rm{cal3}}}_{1/2} $ are approximately zero, indicating that the accuracy of the calculations has been significantly improved. For all 535 nuclei, the RMS deviation between$ \lg T^{{\rm{cal3}}}_{1/2} $ and$ \lg T^{\exp}_{1/2} $ is$ \sigma = 0.258 $ , indicating that the calculated α decay half-lives using the GLDM with proximity energy Prox. 77-Set 13 and the α-particle preformation factor estimated by Eq. (3) can reproduce the experimental data within a factor of$ 10^{0.258} = 1.81 $ . In addition, as can be seen from Figs. 2-4,$ \lg T^{{\rm{cal2}}}_{1/2} $ is approximately 0.2 larger than$ \lg T^{{\rm{cal1}}}_{1/2} $ on the whole, indicating that the introduction of proximity energy Prox. 77-Set 13 systematically improves the calculated accuracy of the GLDM to describe the α decay half-lives. Fig. 5 shows the deviations between the calculations by the GLDM with proximity energy Prox. 77-Set 13 and that with the original one for even-even heavy and superheavy nuclei. In this figure, it is seen that the deviations are approximately 0.2 and 0.14 in the heavy and superheavy nuclei regions, respectively. This indicates that compared with the heavy nuclei, in the superheavy nuclei region, the α decay half-life is less sensitive to the proximity energy, which helps us to predict α decay half-lives of unsynthesized superheavy nuclei.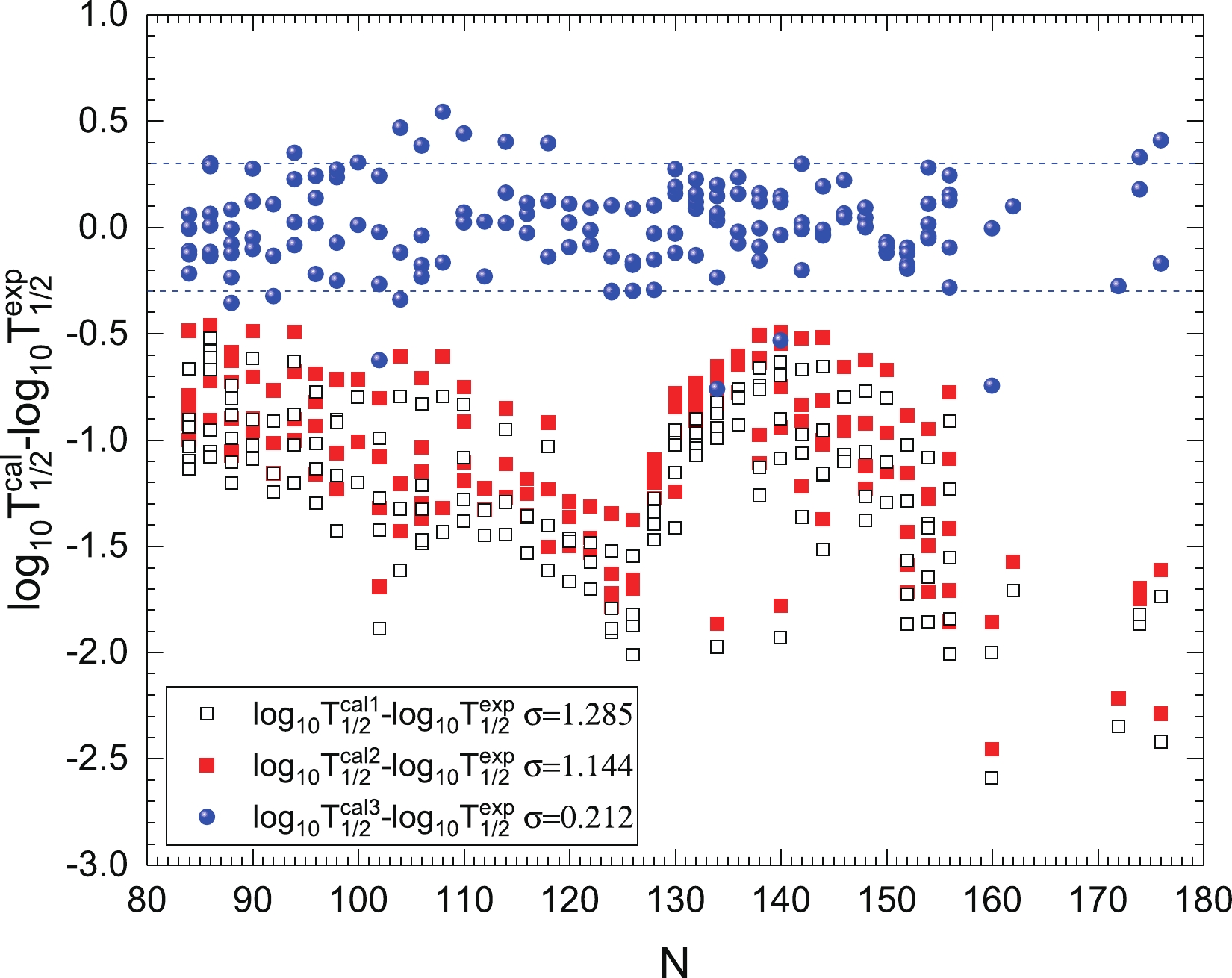
Figure 2. (color online) The logarithmic differences between three calculated
$\alpha$ decay half-lives and experimental data of even-even nuclei. The black open squares, red solid squares, and blue solid circles denote the differences caused by$\lg T^{{\rm{cal1}}}_{1/2}$ ,$\lg T^{{\rm{cal2}}}_{1/2}$ , and$\lg T^{{\rm{cal3}}}_{1/2}$ , respectively.
Figure 3. (color online) Same as Fig. 2, but depicting the logarithmic differences between three calculated α decay half-lives and experimental data of odd-A nuclei.
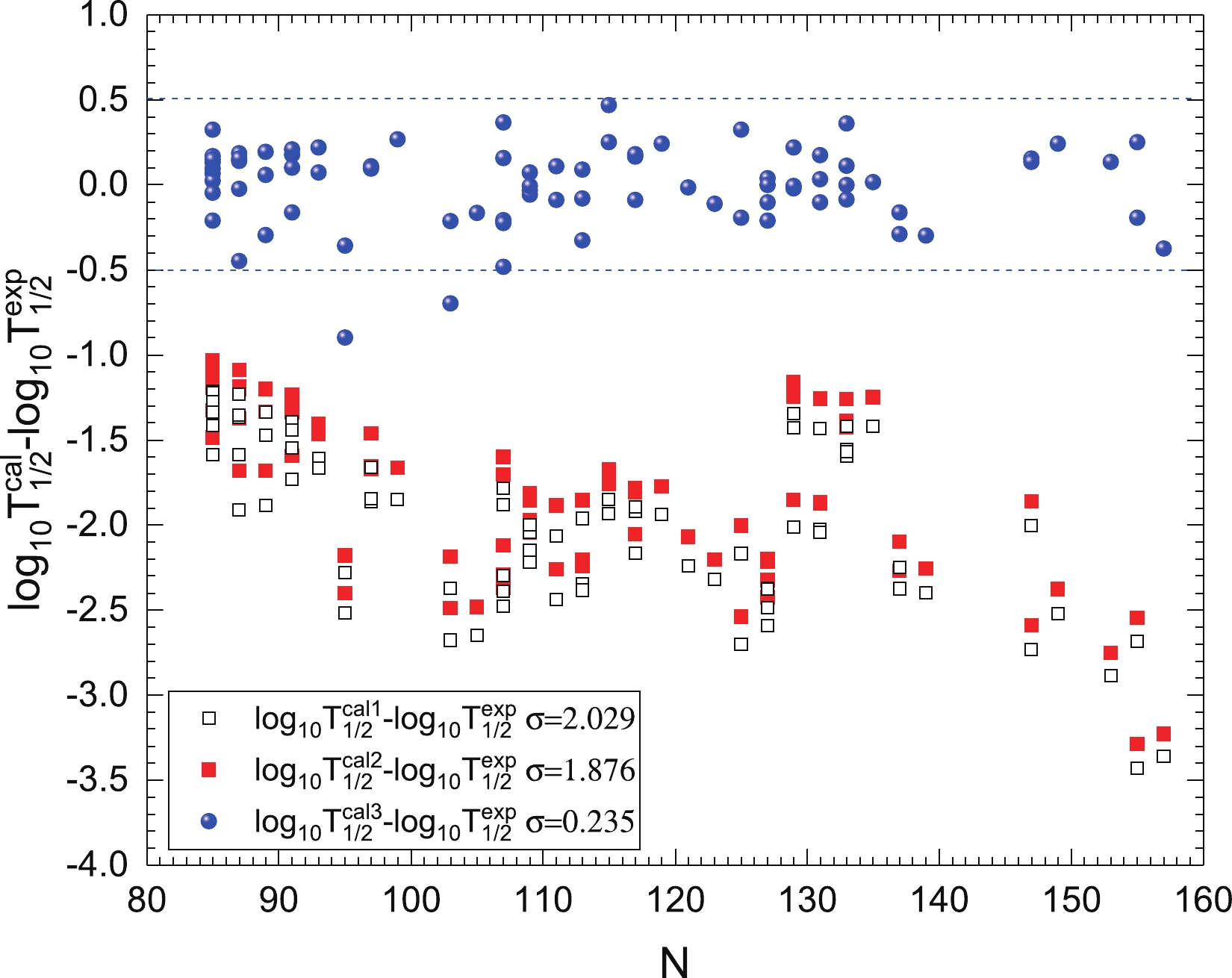
Figure 4. (color online) Same as Fig. 2, but depicting the logarithmic differences between three calculated α decay half-lives and experimental data of doubly odd nuclei.
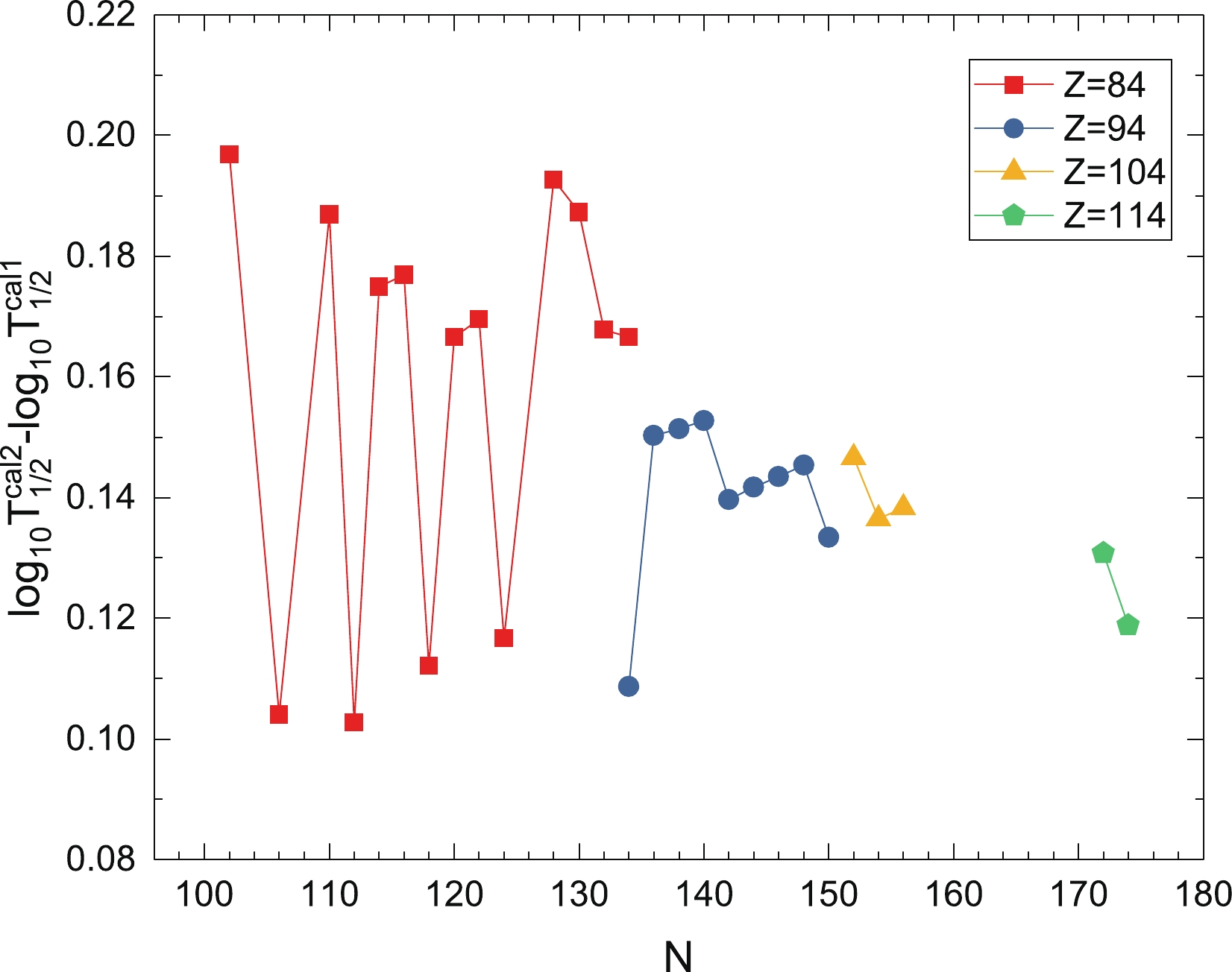
Figure 5. (color online) The differences between calculated α decay half-lives
$\lg T^{{\rm{cal2}}}_{1/2}$ and$\lg T^{{\rm{cal1}}}_{1/2}$ for even-even nuclei with Z = 84, 94, 104, and 114.Encouraged by the good precision of the calculated α decay half-lives for known nuclei, the α decay half-lives of even-even superheavy nuclei with
$ Z = 112-122 $ are predicted using the GLDM with proximity energy Prox. 77-Set 13 and α-particle preformation factors obtained from Eq. (3), the improved Royer formula [79], and the UDL [80]. The α decay energies are taken from the WS4+ mass model [86], which is the most accurate nuclear mass model at present. The predictions are listed in Table 7. In each part of this table, the first, second, and fourth columns are the same as those of Tables 4–6. The third one is the α decay energy obtained by the WS4+ mass model [86]. The last three columns are the predicted α decay half-lives by the improved Royer formula, the UDL formula, and the GLDM with proximity energy Prox. 77-Set 13 and the α-particle preformation factor obtained from Eq. (3). From this table, one can see that the three calculations are consistent with each other, and that the change trends of half-lives are consistent. Additionally, the logarithms of half-lives from the three methods are plotted in Fig. 6. In this figure, one can see that GLDM and UDL formulas give the longest and shortest predictions of α decay half-lives, respectively. The predictions by the GLDM are very close to the ones predicted by the improved Royer formula. Notably, for 286Fl, 288Fl,290Lv, 292Lv, and 294Og, the predictions can reproduce experimental data well, indicating that the predictions are reliable. In particular, one can find that when neutron numbers$ N $ cross$ N = 184 $ , the predicted α decay half-lives decrease sharply, and at$ N = 186 $ , the α decay half-lives reduce by more than two orders of magnitude. It is indicated that strong shell effects are reflected, implying that the next neutron magic number after$ N = 126 $ is$ N = 184 $ . Fig. 7 shows plots of the logarithms of half-lives for the three methods for$ N = 184 $ isotones. In this figure, one can see that when the proton number$ Z>114 $ , the predicted α decay half-lives drop dramatically by eight orders of magnitude at$ Z = 116 $ , indicating that there is a major proton shell, and the next proton magic number after$ Z = 82 $ is$ Z = 114 $ . In addition, the half-life of 296Og shows a peak, where the nucleus is the closest one to the heaviest nucleus 295Og at present and may be the next candidate for synthesizing a superheavy nucleus.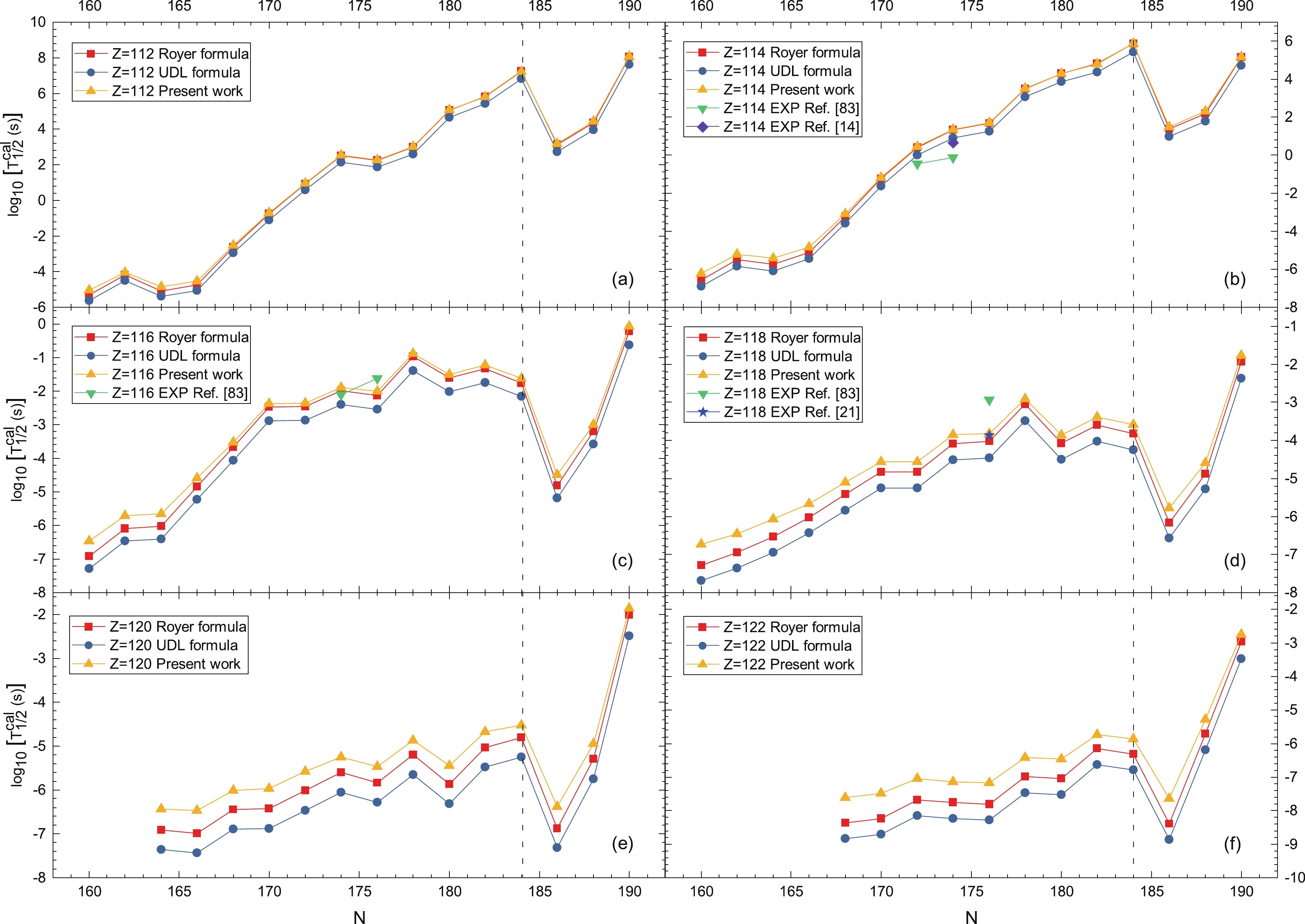
Figure 6. (color online) The predicted α decay half-lives of even-even nuclei with
$ Z = 112-122 $ using the GLDM with proximity energy Prox. 77-Set 13 and α-particle preformation factors obtained from Eq. (3), the improved Royer formula [79], and the universal decay law [80], taking$ Q_{\alpha} $ obtained from the WS4+ mass model [86]. The purple square, blue star, and green triangles denote the experimental α decay half-lives taken from Refs. [14, 21, 83].α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{{\rm{Royer}}}_{1/2}$ 

$\lg T^{{\rm{UDL}}}_{1/2}$ 

$\lg T^{{\rm{calc3}}}_{1/2}$ 

α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{{\rm{Royer}}}_{1/2}$ 

$\lg T^{{\rm{UDL}}}_{1/2}$ 

$\lg T^{{\rm{calc3}}}_{1/2}$ 

Nucsth Z = 112 272Cn 268Ds 12.05 0 −5.32 −5.62 −5.04 274Cn 270Ds 11.52 0 −4.18 −4.5 −4.04 276Cn 272Ds 11.9 0 −5.08 −5.38 −4.85 278Cn 274Ds 11.74 0 −4.75 −5.06 −4.52 280Cn 276Ds 10.83 0 −2.63 −2.96 −2.53 282Cn 278Ds 10.11 0 −0.76 −1.11 −0.69 284Cn 280Ds 9.52 0 0.94 0.57 0.97 286Cn 282Ds 9.01 0 2.51 2.13 2.53 288Cn 284Ds 9.09 0 2.24 1.86 2.27 290Cn 286Ds 8.85 0 2.98 2.59 3.01 292Cn 288Ds 8.27 0 5.06 4.65 5.08 294Cn 290Ds 8.06 0 5.83 5.41 5.81 296Cn 292Ds 7.7 0 7.24 6.81 7.21 298Cn 294Ds 8.77 0 3.12 2.73 3.18 300Cn 296Ds 8.42 0 4.36 3.96 4.42 302Cn 298Ds 7.49 0 8.05 7.61 8.08 Nuclei with Z = 114 274Fl 270Cn 12.95 0 −6.58 −6.91 −6.21 276Fl 272Cn 12.41 0 −5.5 −5.84 −5.22 278Fl 274Cn 12.51 0 −5.75 −6.09 −5.43 280Fl 276Cn 12.19 0 −5.11 −5.45 −4.84 282Fl 278Cn 11.34 0 −3.23 −3.59 −3.08 284Fl 280Cn 10.54 0 −1.24 −1.62 −1.19 286Fl 282Cn 9.94 0 0.4 −0.002 0.45 288Fl 284Cn 9.62 0 1.33 0.92 1.35 290Fl 286Cn 9.5 0 1.68 1.26 1.71 292Fl 288Cn 8.93 0 3.49 3.06 3.52 294Fl 290Cn 8.69 0 4.3 3.86 4.29 296Fl 292Cn 8.54 0 4.81 4.37 4.8 298Fl 294Cn 8.25 0 5.87 5.41 5.87 300Fl 296Cn 9.54 0 1.37 0.97 1.48 302Fl 298Cn 9.27 0 2.19 1.78 2.31 304Fl 300Cn 8.41 0 5.15 4.71 5.17 Nuclei with Z = 116 276Lv 272Fl 13.43 0 −6.92 −7.28 −6.47 278Lv 274Fl 12.99 0 −6.09 −6.47 −5.71 280Lv 276Fl 12.94 0 −6.03 −6.4 −5.66 282Lv 278Fl 12.35 0 −4.84 −5.23 −4.58 284Lv 280Fl 11.8 0 −3.67 −4.06 −3.52 286Lv 282Fl 11.28 0 −2.47 −2.88 −2.36 288Lv 284Fl 11.26 0 −2.45 −2.86 −2.36 290Lv 286Fl 11.06 0 −1.98 −2.4 −1.89 292Lv 288Fl 11.1 0 −2.13 −2.54 −2.01 294Lv 290Fl 10.64 0 −0.97 −1.39 −0.88 296Lv 292Fl 10.87 0 −1.61 −2.02 −1.51 298Lv 294Fl 10.75 0 −1.33 −1.74 −1.22 300Lv 296Fl 10.9 0 −1.76 −2.16 −1.61 302Lv 298Fl 12.17 0 −4.81 −5.18 −4.49 304Lv 300Fl 11.45 0 −3.19 −3.58 −3 306Lv 302Fl 10.29 0 −0.2 −0.62 −0.07 Nuclei with Z = 118 278Og 274Lv 13.93 0 −7.28 −7.69 −6.74 280Og 276Lv 13.73 0 −6.95 −7.35 −6.45 282Og 278Lv 13.49 0 −6.54 −6.95 −6.07 284Og 280Lv 13.21 0 −6.02 −6.44 −5.66 286Og 282Lv 12.89 0 −5.42 −5.84 −5.1 288Og 284Lv 12.59 0 −4.83 −5.25 −4.57 290Og 286Lv 12.57 0 −4.83 −5.25 −4.56 292Og 288Lv 12.21 0 −4.08 −4.51 −3.84 294Og 290Lv 12.17 0 −4.03 −4.46 −3.82 296Og 292Lv 11.73 0 −3.04 −3.48 −2.91 298Og 294Lv 12.16 0 −4.07 −4.5 −3.86 300Og 296Lv 11.93 0 −3.59 −4.02 −3.38 302Og 298Lv 12.02 0 −3.83 −4.25 −3.59 304Og 300Lv 13.1 0 −6.17 −6.57 −5.77 306Og 302Lv 12.46 0 −4.87 −5.28 −4.59 308Og 304Lv 11.18 0 −1.93 −2.37 −1.77 Nuclei with Z = 120 284120 280Og 13.99 0 −6.91 −7.35 −6.44 286120 282Og 14.01 0 −6.99 −7.43 −6.46 288120 284Og 13.71 0 −6.45 −6.9 −6.01 290120 286Og 13.68 0 −6.43 −6.88 −5.97 292120 288Og 13.44 0 −6.01 −6.46 −5.57 294120 290Og 13.22 0 −5.6 −6.05 −5.25 Continued on next page Table 7. Predicted α decay half-lives of even-even nuclei with
$Z = 112-122$ using the GLDM with proximity energy Prox. 77-Set 13, the improved Royer formula [79], and the universal decay law [80]. The α decay energies are calculated by the WS4+ mass model [86]. The α decay energies and half-lives are in units of MeV and s, respectively.Table 7-continued from previous page α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{{\rm{Royer}}}_{1/2}$ 

$\lg T^{{\rm{UDL}}}_{1/2}$ 

$\lg T^{{\rm{calc3}}}_{1/2}$ 

α transition $Q_{\alpha}$ 

$l_{\min}$ 

$\lg T^{{\rm{Royer}}}_{1/2}$ 

$\lg T^{{\rm{UDL}}}_{1/2}$ 

$\lg T^{{\rm{calc3}}}_{1/2}$ 

296120 292Og 13.32 0 −5.84 −6.29 −5.46 298120 294Og 12.98 0 −5.2 −5.65 −4.87 300120 296Og 13.29 0 −5.87 −6.31 −5.45 302120 298Og 12.87 0 −5.03 −5.48 −4.67 304120 300Og 12.74 0 −4.8 −5.25 −4.53 306120 302Og 13.77 0 −6.88 −7.31 −6.38 308120 304Og 12.95 0 −5.3 −5.75 −4.95 310120 306Og 11.48 0 −2.01 −2.49 −1.86 Nuclei with Z = 122 290122 286120 15.09 0 −8.37 −8.84 −7.62 292122 288120 14.99 0 −8.24 −8.71 −7.48 294122 290120 14.64 0 −7.68 −8.15 −7.05 296122 292120 14.67 0 −7.76 −8.23 −7.14 298122 294120 14.68 0 −7.81 −8.28 −7.17 300122 296120 14.2 0 −6.99 −7.46 −6.42 302122 298120 14.21 0 −7.05 −7.52 −6.46 304122 300120 13.71 0 −6.15 −6.63 −5.73 306122 302120 13.78 0 −6.31 −6.79 −5.87 308122 304120 14.92 0 −8.4 −8.86 −7.64 310122 306120 13.44 0 −5.71 −6.19 −5.28 312122 308120 12.14 0 −2.97 −3.48 −2.75 
Figure 7. (color online) Same as Fig. 6, but depicting predicted α decay half-lives of even-even nuclei with N = 184 isotones.
-
In summary, we systematically studied the abilities of various versions of proximity energies when they are applied to the GLDM for enhancing the calculation accuracy and prediction ability of α decay half-lives for known and unsynthesized superheavy nuclei. When a more suitable proximity energy is chosen for application to the GLDM, calculations of α half-lives exhibit systematic improvements in reproducing experimental data. In addition, the calculations indicate that changing the proximity energy will not affect the revealing of the microscopic shell effect, which is important for predicting the island of stability for superheavy nuclei. Encouraged by this, the α decay half-lives of even-even superheavy nuclei with
$ Z = 112-122 $ were predicted by the GLDM with a more suitable proximity energy. The predictions conform to the ones calculated by the improved Royer formula and the UDL. In addition, the features of the predicted α decay half-lives imply that the next double magic nucleus after 208Pb is 298Fl.
Systematic study of α decay half-lives within the Generalized Liquid Drop Model with various versions of proximity energies
- Received Date: 2020-07-30
- Available Online: 2021-02-15
Abstract: It is universally acknowledged that the Generalized Liquid Drop Model (GLDM) has two advantages over other α decay theoretical models: introduction of the quasimolecular shape mechanism and proximity energy. In the past few decades, the original proximity energy has been improved by numerous works. In the present work, the different improvements of proximity energy are examined when they are applied to the GLDM for enhancing the calculation accuracy and prediction ability of α decay half-lives for known and unsynthesized superheavy nuclei. The calculations of α half-lives have systematic improvements in reproducing experimental data after choosing a more suitable proximity energy for application to the GLDM. Encouraged by this, the α decay half-lives of even-even superheavy nuclei with Z=112-122 are predicted by the GLDM with a more suitable proximity energy. The predictions are consistent with calculations by the improved Royer formula and the universal decay law. In addition, the features of the predicted α decay half-lives imply that the next double magic nucleus after 208Pb is 298Fl.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: