-
Dated back to the early stages of nuclear physics, Geiger and Nuttall discovered an empirical relationship between the traveling range of an emitted
$ \alpha $ particle from the parent nucleus and the period of transformation [1]. Accordingly, the partial half-life$ T_{1/2} $ of the$ \alpha $ decay is related to the corresponding decay energy,$ \log_{10}T_{1/2}\; = \; A(Z)Q_{\alpha}^{-1/2}+B(Z), $

(1) where the coefficients A and B, interpreted as functions of the atomic number Z, are determined by fitting the experimental data for each isotopic chain. This simple law has been confirmed since then and still holds generally for various isotopes, despite the increasing amount of
$ \alpha $ decay data from heavy and superheavy nuclei [2-8]. Consequently, a natural question arises: what is the physical mechanism behind this simple and reliable relationship? Leveraging the foundations of quantum mechanics, the$ \alpha $ decay process was described in terms of the quantum tunneling phenomenon by Gamow [9] and independently by Condon and Gurney [10, 11] in 1928, properly explaining the linear dependence of$ Q_{\alpha}^{-1/2} $ in the above formula. This was a remarkable milestone in modern physics and the first successful application of the quantum theory to nuclear physics.Currently, the original GN law has been developed and extended to make it universal or adjust it to different external environments [12-19]. In an earlier study, Buck et al. pointed out that the emitted
$ \alpha $ particle should orbit around the core nucleus with different global quantum numbers via the GN plots of isotopic chains [12]. The effects of these quantum numbers were embedded in a new version of the GN law, successfully reproducing the$ \alpha $ decay half-lives of various isotopes across the$ N = 126 $ shell closure [14]. Based on the Thomas expression of$ \alpha $ emission, Qi et al. explored the validity of the GN law and identified its microscopic basis [15]. Very recently, the debate over the influence of a strong electromagnetic field on the$ \alpha $ decay process was also initiated from a proposed shifted GN law [16, 17]. It is well known that the$ \alpha $ decay is usually considered as a two-simultaneous-step process of preformation of$ \alpha $ cluster at the nuclear surface and its penetration through the Coulomb barrier. Given the success of the GN law, it is expected that these two physical steps respectively play an important role in this simple relationship (1). However, the GN plot has been always attributed to the penetration part since the Gamow scenario, while the$ \alpha $ preformation probability is supposed to vary smoothly in the off-shell region. Although the experimental$ \alpha $ decay half-lives can be well reproduced through this strategy, the systematic deviation between the calculated and measured half-lives still exists, not to mention the situation across the shell closure. Therefore, there must be something missing, rooted in the preformation of the$ \alpha $ cluster. The present study precisely addresses this subject in view of the GN law, which can not only lead to a novel understanding of an old rule but also provide a new perspective of$ \alpha $ clustering in heavy nuclei. -
The present challenge is how to designate the role of the two abovementioned processes that act in the GN law. Meanwhile, the fully microscopic description of the formation of the
$ \alpha $ cluster, in particular for a large range of nuclei, is an open problem [20]. Hence, a practical alternative is to present the systematics of calculated and experimental$ \alpha $ decay half-lives versus$ Q_{\alpha}^{-1/2} $ in parallel, thereby leading to the indirect description of the behavior of the$ \alpha $ preformation factor. To this end, the available$ \alpha $ -decaying nuclei are divided into three regions:(i)
$ N\leqslant 126,\ Z\leqslant 82 $ ;(ii)
$N\leqslant 126,\ Z > 82$ ;(iii)
$ N>126,\ Z>82 $ ,guided by present experimental facts. Note that the
$ N>126,\ Z\leqslant 82 $ region is not considered here, because there is only one$ \alpha $ emitter identified up to now, namely$ ^{210} $ Pb. Let us now recall the relationship between the decay half-life and the decay width in logarithm scale,$ \begin{aligned}[b] \log_{10}T_{1/2} =& \log_{10}\frac{\hbar\ln2}{P_{\alpha}\Gamma}\\ =& -\log_{10}\Gamma-\log_{10}P_{\alpha}+\log_{10}(\hbar\ln2). \end{aligned} $

(2) Evidently, the first two terms are responsible for the
$ Q^{-1/2}_{\alpha} $ dependence in the GN law of one isotopic chain. As mentioned above, the$ \Gamma $ term or related penetration probability, is indeed crucial for such an idea, based on the quantum tunneling interpretation. The$ \alpha $ preformation factor, especially in the logarithm scale of the GN law, is usually believed to vary quite limitedly as compared to the decay width or the penetrability. The GN law is therefore well understood within the tunneling explanation, while its involved coefficients are generally constant for a prescribed isotopic chain. Of physical interest is the deviation from this judgement, especially when it comes to the extreme proton-neutron ratios or various isotopes across the shell closure [8, 21, 22]. The implementation of the present objective starts from the calculation of partial decay width based on the Thomas expression [23],$ \Gamma = \frac{\hbar^2k}{\mu}\frac{R^2 \phi_{n\ell j}(R)^2}{G_{\ell}(R)^2+F_{\ell}(R)^2}, $

(3) where the wave number k =
$ \sqrt{2\mu Q_{\alpha}}/\hbar $ , and$ \mu $ is the reduced mass$ A_{d}A_{\alpha}/(A_{d}+A_{\alpha}) $ in the unit of nucleon mass. The angular momentum$ \ell $ , carried by the emitted$ \alpha $ particle, equals zero for the present case as only ground-state ($ 0^{+} $ ) to ground-state transitions of even-even$ \alpha $ emitters are considered. R is the$ \alpha $ -core relative distance, while$ \phi_{n\ell j} $ and$ G_{\ell} $ ($ F_{\ell} $ ) are respectively the radial wave function of the$ \alpha $ -core relative motion and the regular (irregular) Coulomb function. For a large enough R beyond the nuclear surface, the final$ \Gamma $ value is actually not dependent at all on the choice of R considering the asymptotic behavior of the former functions. In such an$ \alpha $ cluster model, the fundamental ingredient is the$ \alpha $ -core relative motion, which is constrained by the large global quantum number G. The internal nodes n in the above wave function are connected to this quantum number by the Wildermuth condition [12],$ G\; = \; 2n+\ell\; = \; \sum\limits_{i = 1}^{4}g_{i}, $

(4) presenting the effect of the Pauli principle;
$ g_i $ denotes here the oscillator quantum number of nucleons to form the$ \alpha $ particle, and its value is set as$ g_i = $ 4 for nuclei with$ 50\leqslant Z,\;N\leqslant 82 $ ,$ g_i = $ 5 for nuclei with$ 82< Z,\;N\leqslant 126 $ , and$ g_i = $ 6 for nuclei above the$ N = $ 126 neutron shell closure. In this sense, all the nucleons in the$ \alpha $ cluster should occupy the states above the Fermi surface of the residual daughter nucleus, and the cluster-daughter scheme is then somewhat constructed on the building blocks of the shell model. The$ \alpha $ decay width$ \Gamma $ can then be obtained by following the above procedure once the$ \alpha $ -core potential is constructed via the double-folding integral (see details in Refs. [24-26]). The$ \log_{10}\dfrac{\hbar\ln2}{\Gamma} $ in the right side of Eq. (2) is here written as$ \log_{10}T_{1/2}^{\rm calc} $ . Once the left side term in Eq. (2) is chosen as the experimental value, namely$ \log_{10}T_{1/2}^{\rm expt} $ , the$ P_{\alpha} $ term can be extracted as the deviation between the$ \log_{10}T_{1/2}^{\rm expt} $ and$ \log_{10}T_{1/2}^{\rm calc} $ , namely$ \log_{10}P_{\alpha} = \log_{10}T_{1/2}^{\rm calc}-\log_{10}T_{1/2}^{\rm expt}. $

(5) -
To analyze the contribution of the penetration part in the GN law, we calculated the
$ \alpha $ decay width of various even-even isotopes with$ N\leqslant 126 $ . These calculated$ \alpha $ decay half-lives follow the GN law with different coefficients A and B fitted for each isotopic chain, as shown in Fig. 1, including elements from hafnium to thorium. By contrast, for the next major shell above$ N = 126 $ , the global quantum number G changes from 20 to 22. This can result in a deviation from the initial linear dependence of$ \log_{10}T_{1/2}^{\rm calc} $ on$ Q_{\alpha}^{-1/2} $ to a certain extent, which is crucial in explaining the different GN plots for$ N<126 $ and$ N>126 $ [12]. To present this key factor of the$ \alpha $ -cluster model, the calculated$ \alpha $ decay half-lives are plotted as a function of$ Q_{\alpha}^{-1/2} $ for the whole Rn and Ra isotopic chains. As expected, two linear relations can be clearly distinguished for regions (ii) and (iii) in Fig. 2; note that the deviation between them is quite limited. However, the GN plots of experimental$ \alpha $ decay data are believed to change in an evident manner especially when crossing the$ N = 126 $ shell closure. Hence, one may doubt whether it is enough that the well-known GN law is entirely described in terms of the tunneling phenomenon.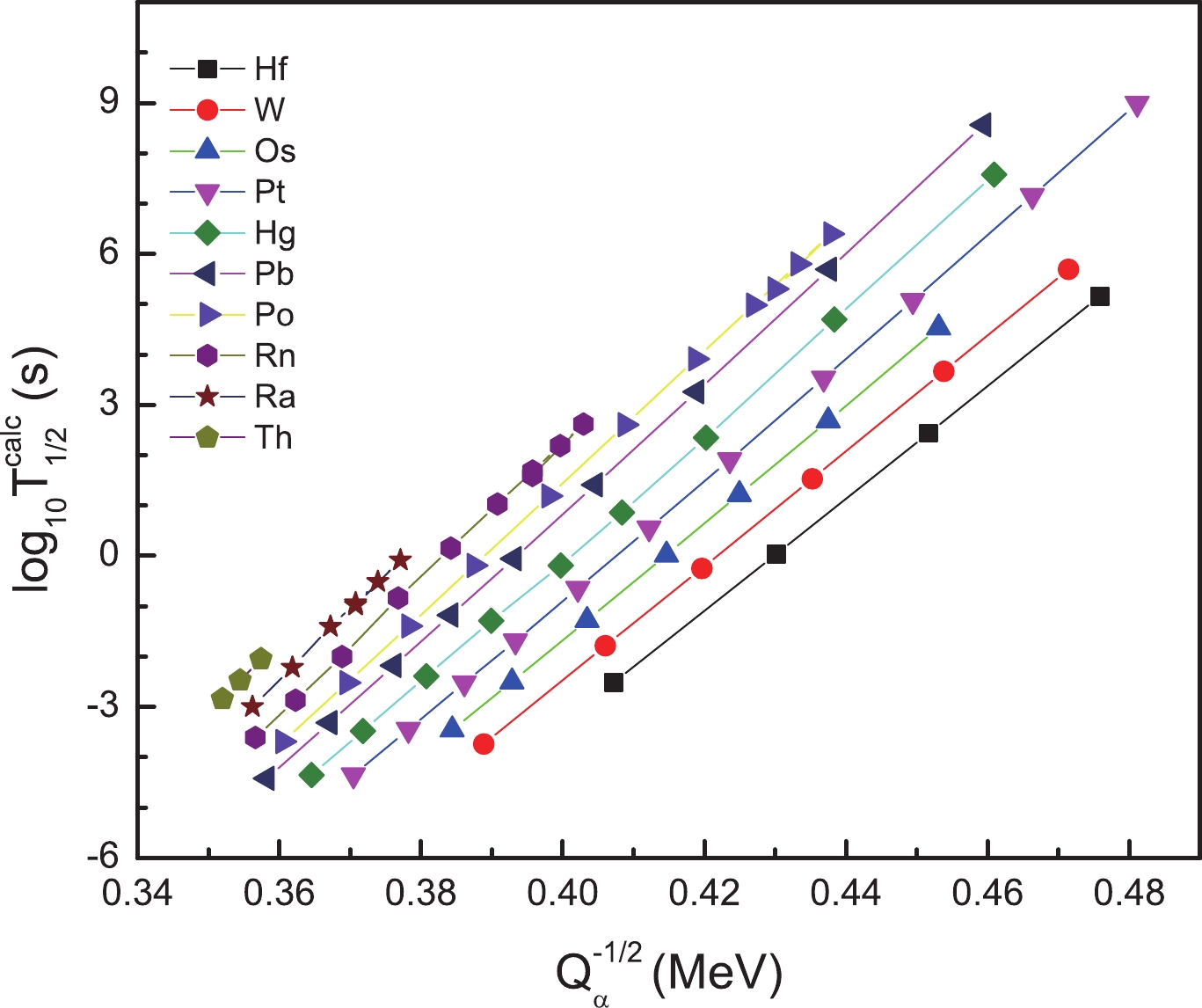
Figure 1. (color online) The logarithm of calculated
$ \alpha$ decay half-lives versus$ Q_{\alpha}^{-1/2}$ for the even-even Hf-Th isotopes, in which the preformation factor is excluded, namely$ P_{\alpha} = 1$ . Note that the straight line guides the GN law for each isotopic chain.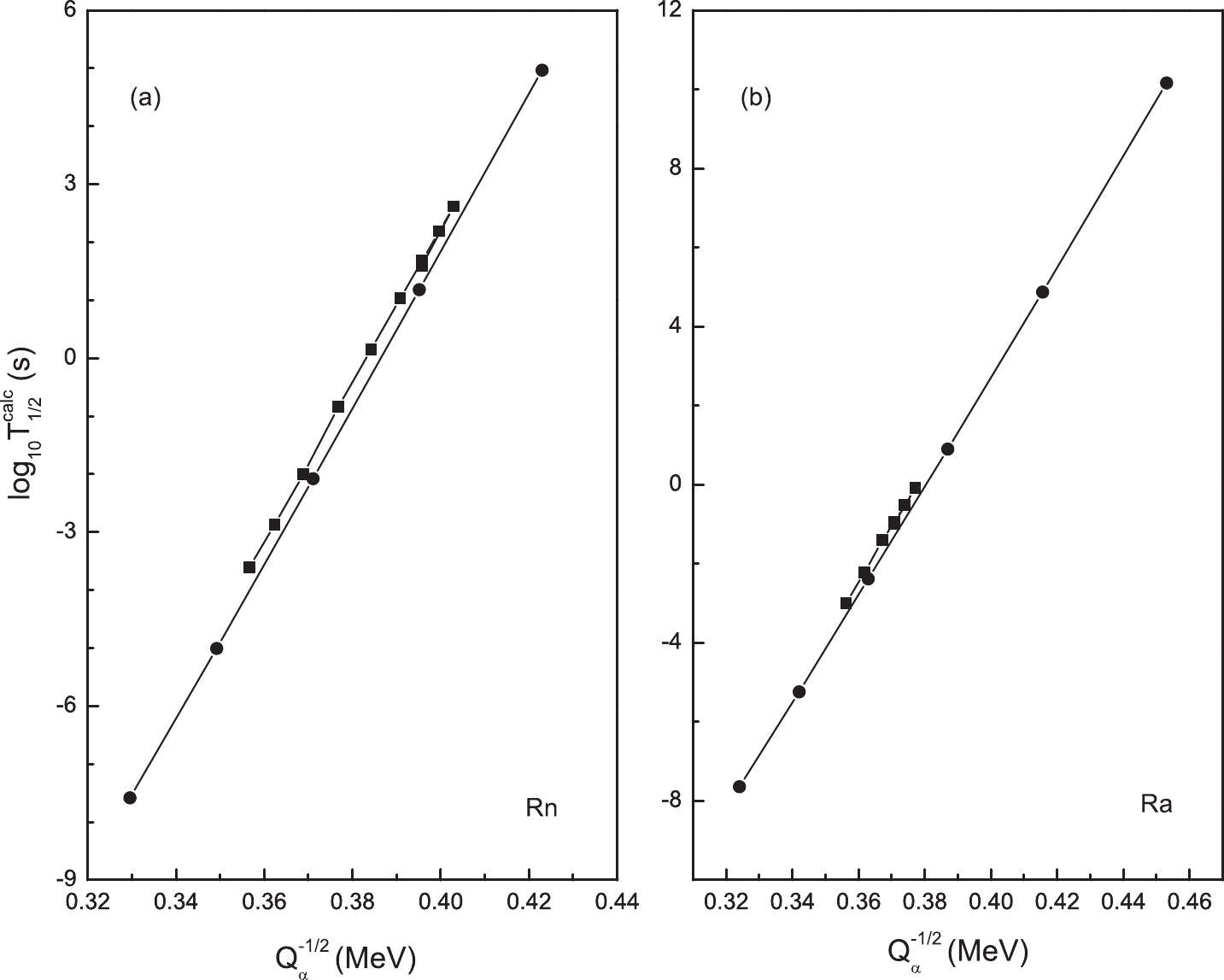
Figure 2. Same as Fig. 1 but only for the Rn and Ra nuclei including the regions with
$ N>126$ (square) and$ N\leq 126$ (circle). Note that the two straight lines correspond to these two regions with different G values.To clarify the above ambiguity, we systematically analyzed the GN relationship of
$ \log_{10}T_{1/2}^{\rm expt} $ values with the decay energy term$ Q_{\alpha}^{-1/2} $ for available even-even$ \alpha $ emitters in the three regions mentioned. Accordingly, the coefficients A and B were determined for one isotopic chain in a prescribed region. The same procedure is also valid for the$ T_{1/2}^{\rm calc} $ case. All these coefficients A and B are presented as functions of the atomic number Z of parent nuclei in Fig. 3. For convenience, the comparative analyses of experimental data$ T_{1/2}^{\rm expt} $ and calculated results$ T_{1/2}^{\rm calc} $ are respectively denoted as case I and case II. A clear point is that different sets of coefficients (divided by the vertical dotted line) in the GN plot are requested for regions (i) (with$ Z\leqslant 82 $ ) and (ii) (with$ Z>82 $ ), regardless of considering case I or II. This is expected owing to the shell effect on the$ \alpha $ decay, which is not a new phenomenon. However, the unexpected and remarkable issue is that there is an unambiguous discrepancy between the coefficients A (and B) of case I and those of case II, regardless of the region considered. We may therefore conclude that tunneling, corresponding to case II, is definitely not the whole explanation for the$ \alpha $ decay process. The only way to fill this gap should be a dependency on the$ \alpha $ preformation probability. According to Eq. (5), the$ \alpha $ preformation factor$ P_{\alpha} $ is supposed to follow an exponential law with$ Q_{\alpha}^{-1/2} $ , i.e.,
Figure 3. (color online) Coefficients A and B of even-even nuclei involved in the GN law versus the atomic number Z for regions (i) plus (ii) at the left panel and region (iii) at the right panel. The square indicates the computational case II, whereas the experimental case I is denoted by the circle. The dashed lines guide the eye for presenting the various dependences in different regions.
$ \log_{10}P_{\alpha} = {\cal{A}}(Z)Q_{\alpha}^{-1/2}+{\cal{B}}(Z). $

(6) Furthermore, by a careful analysis on the specific values of A and B for both cases I and II, one can combine two panels of this figure to illustrate the following two aspects about the preformation probability of the emitted
$ \alpha $ particle:i) The two terms on the right side of the above
$ P_{\alpha} $ expression appear to compete with each other considering their signs and absolute values. What are their microscopic basements?ii) The slope of linear relationship
$ {\cal{A}} $ or$ {\cal{B}} $ appears to be different for the three focused regions. Moreover, the values of$ {\cal{A}} $ and$ {\cal{B}} $ in region (ii) are obviously larger than those in the two other regions.To answer these questions and gain a deep understanding of clustering at the surface of heavy nuclei, we recall the formation amplitude in the conventional formalism, namely [20, 27]
$ F(R) = \int {\rm d}\hat{R}{\rm d}\xi_{\alpha}{\rm d}\xi_{d}[\Psi_{d}(\xi_{d})\phi_{\alpha}(\xi_{\alpha})Y_{l}(\hat{R})]^{*}\Psi_{p}, $

(7) where
$ \xi_{d} $ and$ \xi_{\alpha} $ are respectively the internal degrees of freedom for the daughter nucleus and the$ \alpha $ particle, and$ \Psi_{d}(\xi_{d}) $ and$ \Psi_{p}(\xi_{d},\xi_{\alpha},\hat{R}) $ denote the wave functions of the daughter and parent nuclei, respectively. The intrinsic$ \alpha $ particle wave function behaves in an$ n = l = 0 $ harmonic oscillator eigenstate [28]$ \phi_{\alpha}(\xi_{\alpha}) = \sqrt{\frac{1}{8}}\left(\frac{\nu_{\alpha}}{\pi}\right)^{9/4}\exp[-\nu_{\alpha}(r_{nn}^2+r_{pp}^2+r_{np}^2)/4]S_{\alpha}, $

(8) with the relative distances
$ r_{nn} $ ($ r_{pp} $ ) of neutron-neutron (proton-proton) pairs plus the distance$ r_{np} $ between the mass centers of the nn and pp pairs. The quantity$ \nu_{\alpha} $ is the$ \alpha $ particle harmonic oscillation parameter, and$ S_{\alpha} $ is its spin-isospin function. Very recently, given the extreme case induced by four non-interacting protons and neutrons, the particle decay unit (p.d.u.) was defined to set a simple averaged single-particle limit for the$ \alpha $ particle formation amplitude [29],$ F_{\alpha;{\rm pdu}} = \frac{\sqrt{8}\nu_{\alpha}^{-3/4}\pi^{-7/4}}{R^3}, $

(9) when the ground-state to ground-state (g.s.) transitions of even-even nuclei are considered. The collectivity involved in the
$ \alpha $ decay process is then revealed via the ratio between the extracted$ \alpha $ particle formation amplitude and the corresponding p.d.u. value. Inspired by this, we assume that the$ \alpha $ preformation probability can be written as$ P_{\alpha} = P_{\alpha}^{c}P_{\alpha}^{0}, $

(10) where
$ P_{\alpha}^{0} $ denotes the contribution of the "mean-field"-like part in terms of uncorrelated nucleons, corresponding to the$ |F_{\alpha;{\rm pdu}}|^{2} $ value. The former$ P_{\alpha}^{c} $ part corresponds to the enhancement factor due to the collectivity's degree of freedom. By contrast, as shown above,$ F_{\alpha;{\rm pdu}} $ actually relates to the nuclear volume, i.e., the mass number of the parent nuclei. With this in mind, the$ {\cal{B}}(Z) $ term in Eq. (6) is expected to present the effect of single particle pattern, while$ {\cal{A}}(Z)Q_{\alpha}^{-1/2} $ should be derived from the collective behavior of corresponding parent nuclei. The latter$ Q_{\alpha}^{-1/2} $ dependence of$ P_{\alpha} $ can be unravelled in the shell-model context. It is believed that the clustering of$ \alpha $ particles at the nuclear surface is governed by the pairing force acting among the involved neutrons and protons. For two particles in a non-degenerate system with a constant pairing strength$ {\cal{G}} $ , the corresponding two-particle wave function amplitudes$ X_{i} $ should be related to the$ {\cal{G}} $ value. By contrast, the$ \alpha $ (four-particle) formation amplitude is connected to the$ X_{i} $ values. This can also be confirmed through the multistep shell-model method (MSM), where the MSM basis consists of the tensorial product of the two-particle correlated states [30]. The g.s. energy of even-even nuclei can be presented as a function of the pairing strength$ {\cal{G}} $ , which determines the$ \alpha $ decay energy via the difference between g.s. energies of parent and daughter nuclei. As a result, a connection between$ Q_{\alpha} $ and the final$ \alpha $ preformation probability is expected, namely$ P_{\alpha}^c\sim X_{i}\sim {\cal{G}}\sim Q_{\alpha} $ . In this sense, the pairing correlations can be understood as the origin of the term$ {\cal{A}}(Z)Q_{\alpha}^{-1/2} $ in the$ P_{\alpha} $ expression, i.e., Eq. (6).In a nutshell, the interplay between the mean-field and pairing effects leads to the final clustering of two neutrons and two protons at the nuclear surface, expressing a simple but meaningful relationship similar to the GN law. After the above discussion on issue i), the second issue can be explained as follows. The valence neutrons and protons are supposed to be located in the same major shell in region (ii) with
$ 82<Z,\;N<126 $ , leading to larger overlaps of single particle radial wave functions and relative stronger pairing correlation. Hence, the absolute values of coefficients$ {\cal{A}} $ and$ {\cal{B}} $ in region (ii) are relatively larger than those in the two other regions. Moreover, despite this discrepancy, the comparable competition between these two terms in Eq. (6) causes a smooth varying trend of$ P_{\alpha} $ off the shell closure. This is the deep reason why the Geiger-Nuttal law can be successfully explained in terms of the quantum tunneling phenomenon while excluding the contribution of the$ \alpha $ preformation process. Let us mention here that the four-nucleon correlations (quartetting) may play an important role in the collective dynamics of clustering [31-33]. Considering this, we plot the coefficients$ {\cal{A}} $ and$ {\cal{B}} $ in Eq. (6), generated by the difference between the systematics of experimental data and that of the calculated results based on Eq. (5), versus the number of quartets$ N_{q} $ in Fig. 4. The$ N_{q} $ value is determined by the number of proton pairs above the closest proton magic number$ Z_{\rm mag} $ , namely$ N_{q} = (Z- Z_{\rm mag})/ 2 $ , as suggested in Ref. [33]. This figure shows that the involved coefficients in the$ P_{\alpha} $ systematics vary more evidently with the quartet numbers in region (ii) as compared to those in region (i). These$ \alpha $ decaying nuclei in region (ii) are closer to the doubly-magic nuclei, implying that the large quartetting effect is present in emitters near the shell closure. This point is consistent with other studies [32, 33], and the quartetting effect is supposed to diminish greatly due to the Pauli principle when more valence nucleons are added.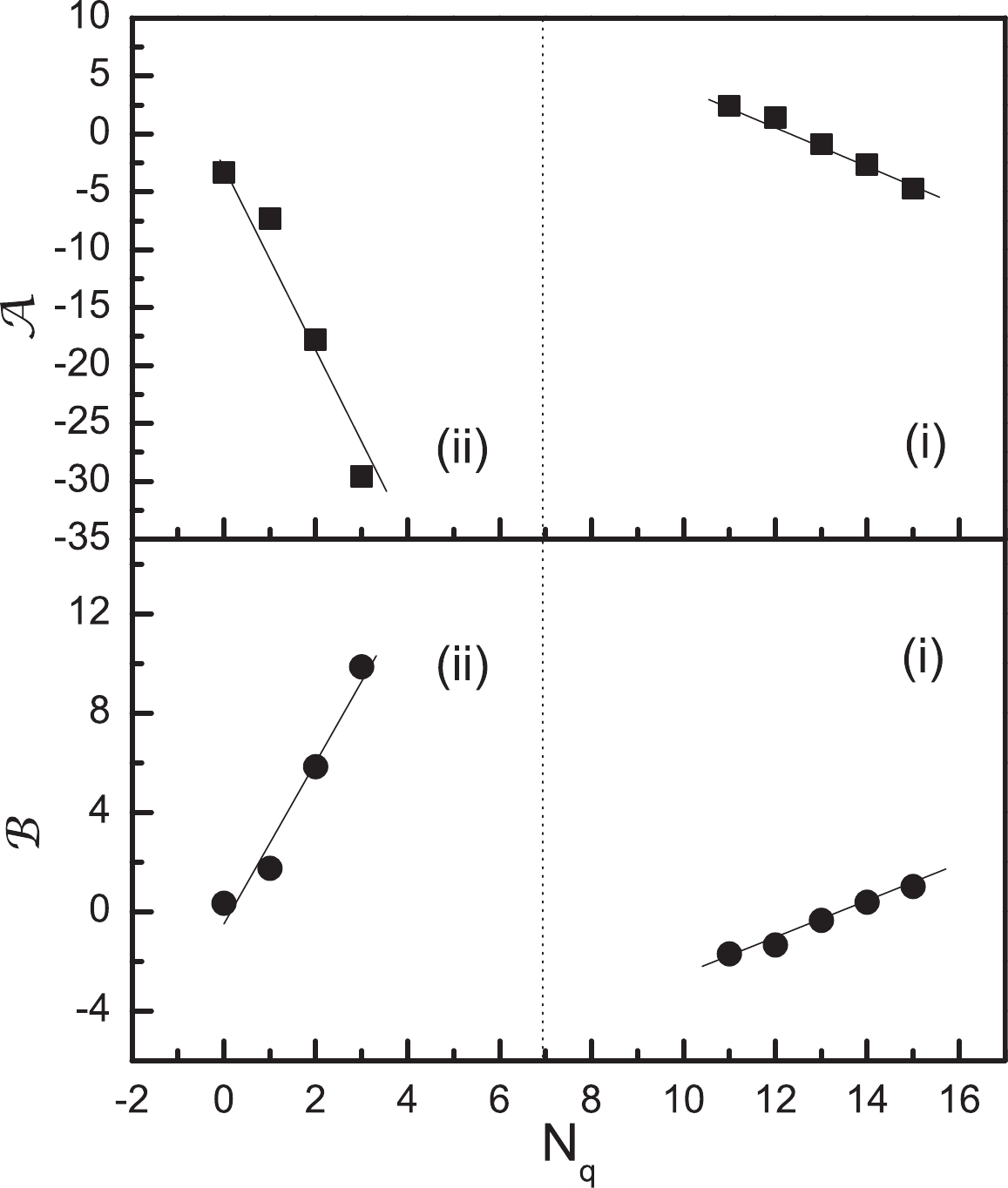
Figure 4. Coefficients
$ {\cal{A}}$ and$ {\cal{B}}$ extracted from the$ P_{\alpha}$ formula, i.e., Eq. (6), based on Eq. (5), versus the quartet number for$ \alpha$ emitters in regions (ii)$ Z>82$ and (i)$ Z\leq 82$ , respectively.Last but not least, we would like to discuss the consistency of the present conjecture about
$ P_{\alpha} $ with other theoretical studies. Recently, the cluster formation model (CFM) was proposed to evaluate the$ \alpha $ preformation probability in an effective way [34, 35]. Within the CFM, the$ \alpha $ formation amplitude is connected with the formation and decay energies, thereby supporting the above conclusion. Given the two-particle formation treatment in the BCS approach, the similarity between the neutron/proton pairing gaps and the$ \alpha $ preformation amplitude is also presented [5], supporting the present GN-like law of$ P_{\alpha} $ to some extent. Dated back to the earlier microscopic calculation on the absolute$ \alpha $ decay width in the shell model plus the cluster component [36], the g.s. energy of$ ^{212} $ Po, with respect to the four-nucleon threshold, was found to be very sensitive to the shell-model basis states, including the cluster states. This g.s. energy, after dividing the$ \alpha $ particle energy, equals the$ \alpha $ decay energy, while the$ \alpha $ formation is regulated by the components of the state vector in the standard cluster basis. Consequently, it is expected that the final$ \alpha $ preformation probability is related to the decay energy accompanied by the Z dependence. Moreover, the penetration process is well addressed regardless of whether the microscopic or semi-classical (such as the WKB approximation) approach is used, which is actually the basis for various phenomenological formulas of$ \alpha $ decay half-lives after considering some extra factors for different types of parent nuclei [13, 18, 19]. However, through the present analysis, onecan find that the missing point is the similar behavior of the$ \alpha $ preformation factor, as demonstrated here, which is another integral aspect for the success of these empirical evaluations. -
In conclusion, surface
$ \alpha $ -clustering is an important and profound phenomenon for both the cluster structure and decay properties of heavy neutron-deficient nuclei. We derived an effective relationship for the$ \alpha $ -cluster preformation probability by carefully analyzing the famous Geiger-Nuttall law of$ \alpha $ decay, thereby shedding new light on this topic. By comparably analyzing the involved coefficients of the GN law from the systematics of experimental and calculated$ \alpha $ decay half-lives, it was found that the amount of surface$ \alpha $ clustering should follow a GN-like pattern. This conjecture is requested by the full description of the well-known GN law rather than its simple description in terms of quantum tunneling. Within the shell-model context, the behavior of the$ \alpha $ preformation factor is determined by the mean-field and pairing effects, which explicitly manifest themselves via the two Z dependent terms in the GN-like formula of$ P_{\alpha} $ . Furthermore, the balance between these two components produces a relative smooth value of$ \alpha $ preformation probability, leading to the success of most of the effective approaches on$ \alpha $ decay. Moreover, the results of the present study are consistent with other available theoretical results on$ \alpha $ clustering of heavy nuclei. Encouraged by this, we hope that the present derivation can offer a novel window to understand the$ \alpha $ correlations when probing fundamental nuclear interactions.
New look at Geiger-Nuttall law and α clustering of heavy nuclei
- Received Date: 2020-10-09
- Available Online: 2021-02-15
Abstract: The Geiger-Nuttall (GN) law of α decay is commonly explained in terms of the quantum tunneling phenomenon. In this study, we show that such an explanation is actually not enough regarding the α particle clustering. Such a conclusion is drawn after exploring the involved coefficients of the GN law based on the conventional description of α decay, namely the formation of an α cluster and its subsequent penetration. The specific roles of the two former processes, in the GN law, manifest themselves via the systematical analysis of the calculated and experimental α decay half-lives versus the decay energies across the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: