-
The conventional quark model [1, 2], which inherits parts of the properties of Quantum Chromo-Dynamics (QCD), has successfully been used to understand hadrons since 2003. Quark model tells us that hadrons can be classified as either mesons made of
$ q\bar{q} $ or baryons made of three quarks. However, QCD tells us that any color neutral configuration (especially exotics) could exist upon the two configurations mentioned above. This leaves us with two questions: where to find these exotic candidates; and how to understand the underlying mechanism. The observation of the first exotic candidate,$ X(3872) $ [3], in 2003 and the remarkable sucess of experimental measurements [4, 5] partly answered the first question. Among such measurements, the observation of the first pentaquarks [6, 7], the first fully heavy quark states [8], and the first exotic candidates with four different flavors, i.e., the$ X_0(2900) $ [9, 10], were reported by the LHCb Collaboration recently, thereby setting experimental milestones. Different theoretical prescriptions have been proposed to understand the nature of these exotic candidates [11-18]. Among them, a hadronic molecule [11], as an analogy of a deuteron formed by a proton and a neutron, was proposed because it is a few MeV below the nearby S-wave threshold.However, a problem that must be addressed is that different configurations with the same quantum number can mix with each other and cannot be isolated well. For instance, although the
$ X(3872) $ was initially proposed as a hadronic molecule [19] owing to its closeness to the$ D\bar{D}^*+c.c. $ threshold, it could still become mixed with the normal charmonium$ \chi_{c1}(2P) $ [20-27]. Some other typical examples are the$ D^*_{s0}(2317) $ and$ D_{s1}(2460) $ , which are approximately$ 160\; {\rm{MeV}} $ and$ 70\; {\rm{MeV}} $ below the$ J^P = 0^+ $ and$ J^P = 1^+ $ $ c\bar{s} $ charmed-strange mesons of the Godfrey-Isgur quark model, respectively [28]. They are approximately$ 45\; {\rm{MeV}} $ below the$ DK $ and$ D^*K $ thresholds, respectively, which can be explained naturally if the systems are bound states of the$ DK $ and$ D^*K $ meson pairs [29-36]. However, because the light quark and anti-quark in the isosinglet$ D^{(*)}K $ system belong to the same flavor, the possibility of mixture with the normal$ c\bar{s} $ configurations [30, 31, 37-41] cannot be dismissed, despite previous comprehensive studies. Fortunately, the LHCb Collaboration reported a$ J^P = 0^+ $ [9, 10] narrow state$ X_0 (2900)$ with a mass of$ 2866\pm 7\; {\rm{MeV}} $ and width of$ \Gamma_0 = 57\pm 13\; {\rm{MeV}} $ , as well as another broader$ J^P = 1^- $ state with a mass of$ 2904\pm 7\; {\rm{MeV}} $ and width of$ \Gamma_1 = 110\pm 12\; {\rm{MeV}} $ in the$ \bar{D}K $ invariant mass distribution. They are the first exotic states with four different flavors, which could provide a potential ultimate solution for the problem from different perspectives.In this letter, we solve the Lippmann-Schwinger Equation (LSE) with leading order contact potentials of the
$ \bar{D}^{(*)}K^{(*)} $ system in the heavy quark limit to extract the mass position of the spin partners of the$ X_0(2900) $ . The$ X_0(2900) $ exists as a$ I(J^P) = 0(0^+) $ $ \bar{D}^*K^* $ hadronic molecule and is an input in our framework. Under that assumption, we predicted the masses of its heavy quark spin partners. Searching for those spin partners could aid in understanding the nature of the$ X_0(2900) $ . -
The heavy quark spin structure [42] can be expressed in terms of the heavy-light basis from the hadron basis. A similar example is given by the
$ Z^{(\prime)}_c $ and$ Z_b^{(\prime)} $ case with two heavy quarks in Refs. [43-48]. Likewise, the S-wave$ \bar{D}^{(*)}K^{(*)} $ system, with only one heavy quark, can be written in terms of the heavy degree of freedom,${1}/{2}$ , and light degree of freedom,$ s_l $ , as follows [49]$ \begin{aligned}[b] |{({\bar c_{{j_1}}}{q_{{j_2}}})_{{j_{12}}}}{(\bar s{q^\prime })_{{j_3}}}{\rangle _J} =& \sum\limits_{{s_l}} {{{\left( { - 1} \right)}^{{j_2} + {j_3} + {j_{12}} + {s_l}}}} \left\{ {\begin{array}{*{20}{c}} {{j_1}}&{{j_2}}&{{j_{12}}}\\ J&{{j_3}}&{{s_l}} \end{array}} \right\}\\&\times\widehat {{j_{12}}}\widehat {{s_l}}|{\bar c_{{j_1}}}{({q_{{j_2}}}{(\bar s{q^\prime })_{{j_3}}})_{{s_l}}}\rangle \end{aligned}$

(1) with
$ \hat{j} = \sqrt{2j+1} $ . Here,$ j_1 = \dfrac{1}{2} $ ,$ j_2 = \dfrac{1}{2} $ , and$ j_{12} = 0,1 $ are spins of anti-charm quark$ \bar{c} $ , light quark q, and their sum in the$ \bar{D}^{(*)} $ meson, respectively;$ j_3 = 0,1 $ and$ J = 0,1,2 $ are the spins of the$ K^{(*)} $ meson and the total spin of the$ \bar{D}^{(*)}K^{(*)} $ system, respectively; and$ s_l $ on the right hand side of Eq. (1) is the light degree of freedom of the system, which is the only relevant quantity for the dynamics in the heavy quark limit. Following Eq. (1), one can obtain the decompositions of the$ \bar{D}^{(*)}K^{(*)} $ system as$ |\bar{D}K\rangle_{0^+} = \Big|\frac{1}{2}\Big\rangle, $

(2) $ |\bar{D}^*K\rangle_{1^+} = \Big|\frac{1}{2}\Big\rangle , $

(3) $ |\bar{D}K^*\rangle_{1^+} = \frac{1}{\sqrt{3}}\Big|\frac{1}{2}\Big\rangle^*+\sqrt{\frac{2}{3}}\Big|\frac{3}{2}\Big\rangle^*, $

(4) $ |\bar{D}^*K^*\rangle_{0^+} = -\Big|\frac{1}{2}\Big\rangle^* , $

(5) $ |\bar{D}^*K^*\rangle_{1^+} = \sqrt{\frac{2}{3}}\Big|\frac{1}{2}\Big\rangle^*-\frac{1}{\sqrt{3}}\Big|\frac{3}{2}\Big\rangle^*, $

(6) $ |\bar{D}^*K^*\rangle_{2^+} = \Big|\frac{3}{2}\Big\rangle^*. $

(7) Here, the heavy degree of freedom is suppressed due to the same value, leaving only the light degrees of freedom,
$ s_l $ , in$ |\dots\rangle $ . Although K and$ K^* $ have the same quark content, the light degrees of freedoms in the first two equations and those in the last four equations can be distinguishable owing to the large scale separation of the K and$ K^* $ masses. Similar to the potentials in Ref. [50], through the contact potential, which is defined as$ C_{2l}^{(*)}\equiv^{(*)}\langle l |\hat{H}_{\rm{HQS}}|l\rangle^{(*)}, $

(8) the potentials of the
$ \bar{D}^{(*)}K $ and$ \bar{D}^{(*)}K^* $ systems are$ V_{0^+} = C_{1} , $

(9) $ V_{1^+} = C_{1} , $

(10) and
$ V^*_{0^+} = C^*_{1} , $

(11) $ V_{{1^ + }}^* = \left( {\begin{array}{*{20}{c}} {\dfrac{1}{3}C_1^* + \dfrac{2}{3}C_3^*}&{\dfrac{{\sqrt 2 }}{3}\left( {C_1^* - C_3^*} \right)}\\ {\dfrac{{\sqrt 2 }}{3}\left( {C_1^* - C_3^*} \right)}&{\dfrac{2}{3}C_1^* + \dfrac{1}{3}C_3^*} \end{array}} \right) , $

(12) $ V^*_{2^+} = C^*_{3}, $

(13) $ V_{J^+} $ and$ V^*_{J^+} $ denote the potentials of the$ \bar{D}^{(*)}K $ and$ \bar{D}^{(*)}K^* $ systems, respectively. The subindex$ J^+ $ presents the total spin and parity of the corresponding system. The transition between$ |l\rangle $ and$ |l\rangle^* $ is the higher order contribution, which is set to zero in this study ①. The above decomposition and the corresponding potentials also work for the$ D^{(*)}K^{(*)} $ systems but with different values of$ C_{2l}^{(*)} $ .With the above potentials, the LSE can be solved:
$ T = V+VGT $

(14) with V denoting the potentials for specific channels of a given quantum number. Here, the two-body non-relativistic propagator is
$ \begin{aligned}[b] G_\Lambda(M,m_1,m_2) =& \int\frac{{\rm{d}}^3q}{(2\pi)^3}\frac{1}{M-m_1-m_2-{{q}}^2/(2\mu)}\\ =& \Lambda+ {\rm i}\frac{m_1 m_2}{2\pi(m_1+m_2)}\sqrt{2\mu (M-m_1-m_2)} \end{aligned}$

with the power divergence subtraction [51] employed to regularize the ultraviolet (UV) divergence. The value of
$ \Lambda $ should be small enough to preserve the heavy quark symmetry, leaving the physics insensitive to the details of short-distance dynamics [50]. Here,$ m_1 $ ,$ m_2 $ , and$ \mu $ are the masses of the two intermediate particles and their reduced mass, respectively, and M is the total energy of the system. The expression of the second Riemann sheet,$ G^{\rm{II}}_\Lambda(M,m_1,m_2) $ , can be obtained by changing the sign of the second term of$ G_\Lambda(M,m_1,m_2) $ . -
Before presenting the numerical results, we estimate the values of the contact potential,
$ C_1 $ . The leading contact terms between heavy-light mesons and Goldstone bosons can be obtained using the following Lagrangian [52-57]:$ {\cal{L}}_{D\phi}^{(1)} = {\cal{D}}_{\mu}D{\cal{D}}^{\mu}D^{\dagger}-M_{0}^{2}DD^{\dagger}, $

(15) where
$ {\cal{D}}_{\mu}H = H\left(\overset\leftarrow{\partial}_{\mu}+\Gamma_{\mu}^{\dagger}\right),\quad{\cal{D}}_{\mu}H^{\dagger} = \left(\partial_{\mu}+\Gamma_{\mu}\right)H^{\dagger}, $

(16) with
$ H\in\left\{ D,D^{*}\right\} ,\quad D^{(*)} = \left(D^{(*)0},D^{(*)+},D_{s}^{(*)+}\right) $

(17) and chiral connection
$ \Gamma_{\mu} = \left(u^{\dagger}\partial_{\mu}u+u\partial_{\mu}u^{\dagger}\right)/2. $

(18) Here, the chiral building blocks are
$ u_{\mu} = {\rm i}\left[u^{\dagger}\partial_{\mu}u-u\partial_{\mu}u^{\dagger}\right],\quad U = u^{2},\quad\chi^{\pm} = u^{\dagger}\chi u^{\dagger}\pm u\chi^{\dagger}u. $

where
$U = \exp\left({\rm i}\sqrt{2}\phi/f_0\right)$ , with$ \phi $ denoting the Goldstone boson octet. To the leading order,$ f_0 $ is the pion decay constant. The isospin singlet$ J^P = 0^+ $ $ DK $ and$ \bar{D}K $ systems are defined as$ D_{s0}^{*+}(2317)\equiv\frac{1}{\sqrt{2}}\left(D^{0}K^{+}-D^{+}K^{0}\right), $

(19) which is associated with the
$ D_{s0}^{*+}(2317) $ and$ X^\prime_{0}\equiv\frac{1}{\sqrt{2}}\left(D^{0}\bar{K}^{0}+D^{+}K^{-}\right). $

(20) The definitions of the isospin singlet
$ J^P = 1^+ $ $ D^*K $ and$ \bar{D}^*K $ systems are similar. From Eq. (15), we obtain$ V_{D_{s0}^{*+}(2317)} = V_{D_{s1}^{+}(2460)}, $

(21) which agrees with those obtained from the heavy-light decomposition, i.e., Eqs. (9), (10), and
$ V_{D_{s0}^{*+}(2317)} = 2V_{X_0}. $

(22) As a result, the value of
$ C_1 $ for the$ \bar{D}^{(*)}K $ system is half of that for the$ D^{(*)}K $ system. Note that any parameter set, i.e.,$ (\Lambda, C_1) $ , for the existence of the$ D_{s0}^*(2317) $ and$ D_{s1}(2460) $ as$ DK $ and$ D^*K $ molecular states (both bound and virtual states) does not indicate the existence of the analogous$ \bar{D}K $ and$ \bar{D}^*K $ molecules. From this point on, we focus on the discussion of the formation of the$ \bar{D}^{(*)}K^{(*)} $ molecule instead of their isospin breaking effect. The isospin average masses, expressed as$ m_D = 1.867\; {\rm{GeV}},\quad m_{D^*} = 2.009\; {\rm{GeV}} $

(23) $ m_K = 0.496\; {\rm{GeV}},\quad m_{K^*} = 0.892\; {\rm{GeV}} $

(24) are considered in this letter.
Concerning the
$ \bar{D}^{(*)}K^* $ interaction, the$ X_0(2900) $ recently observed by the LHCb collaboration is assumed to be a$ I(J^P) = 0(0^+) $ $ \bar{D}^*K^* $ molecular state [58]. We consider two cases for the$ X_0(2900) $ ● a bound state, with the
$ X_0(2900) $ mass$ m_{X_0(2900)} $ satisfying$ 1-C_1^* G_\Lambda(m_{X_0(2900)},m_{\bar{D}^*},m_{K^*}) = 0 . $

(25) ● a virtual state, with the
$ X_0(2900) $ mass$ m_{X_0(2900)} $ satisfying$ 1-C_1^* G^{\rm{II}}_\Lambda(m_{X_0(2900)},m_{\bar{D}^*},m_{K^*}) = 0. $

(26) We consider
$ \Lambda = 0.05\; {\rm{GeV}} $ and$ \Lambda = 0.03\; {\rm{GeV}} $ to illustrate the mass positions of its heavy quark spin partners and the corresponding properties.For the bound state solution of the
$ X_0(2900) $ ,$ C_1^* = 33.56\; {\rm{GeV}}^{-2} $ and$ C_1^* = 102.09\; {\rm{GeV}}^{-2} $ correspond to$ \Lambda = 0.05\; {\rm{GeV}} $ and$ \Lambda = 0.03\; {\rm{GeV}} $ , respectively. Fig. 1 shows how the poles move with the variation of the two parameter sets. The blue triangle and green square curves show the pole trajectory of the bound state and resonance in the$ 1^+ $ channel, respectively. Note that, with$ C^*_3 $ varying between$ 40\; {\rm{GeV}}^{-2} $ and$ 170\; {\rm{GeV}}^{-2} $ , one bound state and one resonance emerge with tens of MeV below the$ \bar{D}K^* $ and$ \bar{D}^*K^* $ thresholds, respectively. The bound state in the$ 2^+ $ channel is more sensitive to parameter$ C_3^* $ . Assuming that light quark spin symmetry also works here in similar terms to that for the two$ Z_b $ states [59], i.e.,$ C^*_3 = C^*_1 $ , the pole position of the above three states are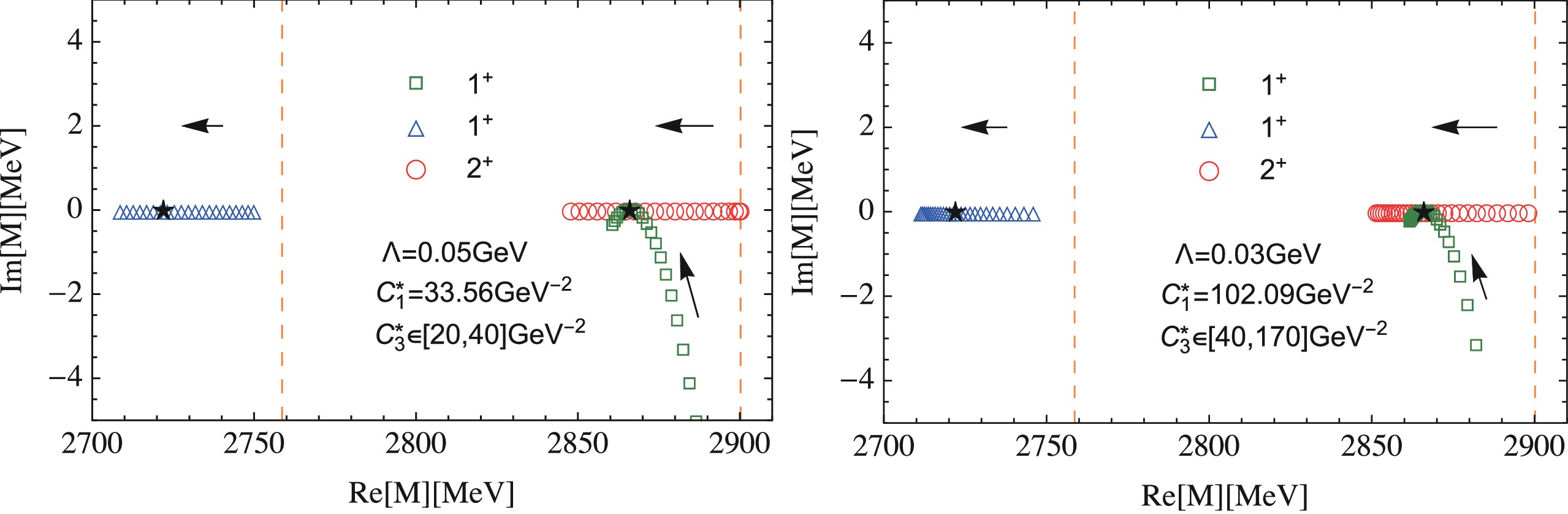
Figure 1. (color online)
$ X_0(2900) $ is assumed to be a$ I(J^P) = 0(0^+) $ $ \bar{D}^*K^* $ bound state. The values of$ C_1^* = 33.56\; {\rm{GeV}}^{-2} $ and$ C_1^* = 102.09\; {\rm{GeV}}^{-2} $ are obtained for$ \Lambda = 0.05\; {\rm{GeV}} $ and$ \Lambda = 0.03\; {\rm{GeV}} $ , respectively. The$ 2^+ $ (red circles) and the lower$ 1^+ $ (blue triangles) behave as bound states. The higher$ 1^+ $ (green squares) is a resonance between the$ \bar{D}K^* $ and$ \bar{D}^*K^* $ thresholds. The pole trajectories of these three states with the increasing$ C_3^* $ are shown in the figures. The black arrows indicate the direction of the increasing$ C_3^* $ . The black stars are the mass positions in the light quark spin symmetry.$ m_{2^+} = 2.866\; {\rm{GeV}}, $

(27) $ m_{1^+} = 2.722\; {\rm{GeV}},\quad m_{1^+} = 2.866\; {\rm{GeV}} . $

(28) The vanishing imaginary part of the higher
$ 1^+ $ state is because of the degenerance of the two$ 1^+ $ states.For the virtual state solution of the
$ X_0(2900) $ ,$ C_1^* = 14.24\; {\rm{GeV}}^{-2} $ and$ C_1^* = 19.92\; {\rm{GeV}}^{-2} $ correspond to$ \Lambda = 0.05\; {\rm{GeV}} $ and$ \Lambda = 0.03\; {\rm{GeV}} $ , respectively. Fig. 2 shows how the poles move with$ C^*_3 $ variation between$ 22\; {\rm{GeV}}^{-2} $ and$ 36\; {\rm{GeV}}^{-2} $ for the two$ \Lambda $ values. For the former case, the blue triangles and red circles show the pole trajectories of the bound states for the$ 1^+ $ and$ 2^+ $ channels, respectively. For the latter case, both of them become virtual states. Consequently, whether the higher$ 1^+ $ $ \bar{D}^*K^* $ molecule exists or not depends on the nature of the$ X_0(2900) $ , i.e., either a bound state or a virtual state, which can be studied through further detailed scanning of its line shape. Thus, searching for these heavy quark spin partners would help to reveal the nature of the$ X_0(2900) $ .
Figure 2. (color online)
$ X_0(2900) $ is assumed to be a$ I(J^P) = 0(0^+) $ $ \bar{D}^*K^* $ virtual state. The values of$ C_1^* = 14.24\; {\rm{GeV}}^{-2} $ and$ C_1^* = 19.92\; {\rm{GeV}}^{-2} $ are obtained for$ \Lambda = 0.05\; {\rm{GeV}} $ and$ \Lambda = 0.03\; {\rm{GeV}} $ , respectively. The$ 2^+ $ (red circles) and the lower$ 1^+ $ (blue triangles) behave as bound states for the former case. They behave as virtual states for the latter case. The higher$ 1^+ $ (green squares) is far away from the physical sheet and has marginal physical impact for both cases. The pole trajectories of the two states with increasing$ C_3^* $ are shown in the figures. The black arrows indicate the direction of the increasing$ C_3^* $ . -
Under the assumption that the
$ X_0(2900) $ recently reported by the LHCb Collaboration is a$ I(J^P) = 0(0^+) $ $ \bar{D}^*K^* $ hadronic molecule, we extracted the pole trajectories of its heavy quark spin partners with the variation of parameter$ C_3^* $ . Parameter$ C_1^* $ is fixed by the mass position of the$ X_0(2900) $ (either a bound state or a virtual state). For the bound state, in the light quark spin symmetry, we extract the mass positions of its heavy quark spin partners, i.e.,$ 2.722\; {\rm{GeV}} $ and$ 2.866\; {\rm{GeV}} $ for$ 1^+ $ state and$ 2.866\; {\rm{GeV}} $ for$ 2^+ $ state. For the virtual state, the higher$ 1^+ $ state is far away from the physical region and will not have significant impact on the physical observables. Searching for those states will help to shed light on the nature of the$ X_0(2900) $ .During the updation of this manuscript, several studies [60-68] were observed to have discussed some relevant topics.
-
The discussions with Tim Burns, M.L. Du, Li-Sheng Geng, Ming-Zhu Liu, Eulogio Oset, and Jun-Jun Xie are appreciated. A special acknowledgement to C. Hanhart for pointing out the relation between the
$ C_1 $ and the potential of the$ D_{s0}(2317) $ in the hadronic molecular picture to the leading order.
X0(2900) and its heavy quark spin partners in molecular picture
- Received Date: 2020-10-12
- Available Online: 2021-02-15
Abstract: The






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


























 DownLoad:
DownLoad: