-
The change in chiral symmetry is one of the most important properties of quantum chromodynamics (QCD) in a hot and dense medium, which is essential for understanding the light hadrons at finite temperature and density [1-4]. In the chiral limit, the phase transition from chiral symmetry breaking in vacuum and at low temperature to its restoration at high temperature occurs at a critical temperature
$ T_{\rm c} $ , which has been reported in a recent lattice QCD simulation to be$ T_{\rm c} \simeq 132 $ MeV [5]. In a real case with non-vanishing current quark mass, the chiral symmetry restoration is no longer a genuine phase transition but rather a smooth crossover. Because the crossover occurs in a region and not at a point, the way to describe it with a fixed temperature is not unique. Considering the maximum fluctuations around a continuous phase transition in the chiral limit, the pseudo-critical temperature$ T_{\rm pc} $ to characterize the chiral crossover in the real case is normally defined by the maximum change in the chiral condensate,$ \partial^2\langle\bar\psi\psi\rangle/\partial T_{\rm pc}^2 = 0 $ . From the lattice QCD simulation [6], this value is approximately$ T_{\rm pc}\simeq 156 $ MeV.The mechanism for a continuous phase transition is spontaneous symmetry breaking. It is possible to define an order parameter that changes from a nonzero value to zero or vice versa when the phase transition occurs. Conversely, spontaneous breaking of a global symmetry manifests itself in Goldstone's theorem [7, 8]: whenever a global symmetry is spontaneously broken, massless fields, known as Goldstone bosons, emerge. Corresponding to the spontaneous chiral symmetry breaking, the order parameter is the chiral condensate, and the Goldstone modes are pions. If we take
$ T_{\rm pc} $ defined above as the characteristic temperature of the chiral crossover, the problem is whether the chiral condensate at$ T_{\rm pc} $ is already small enough and the pseudo-Goldstone modes at$ T_{\rm pc} $ are already heavy enough to guarantee that the system is in chiral restoration phase. According to Goldstone's theorem, in the chiral breaking phase at low temperature, pions as pseudo-Goldstone modes should be in bound states, and in the chiral restoration phase at high temperature, pions should be in resonant states with nonzero width. The connection between the two states is the Mott transition at temperature$ T_m $ [9-11], where the decay process$ \pi\to q\bar q $ begins. It is clear that$ T_{\rm pc} = T_m $ in the chiral limit. In the real case, however, there is no guarantee of the coincidence of the two temperatures. In this case, Goldstone's theorem breaks down because pions may already be in resonant states with large mass at$ T<T_{\rm pc} $ or still be in bound states with small mass at$ T>T_{\rm pc} $ . To remain consistent with Goldstone's theorem, we propose to pin down the chiral crossover using the Mott transition of the pseudo-Goldstone boson. Taking into account energy conservation for the decay process, the Mott transition temperature$ T_m $ is defined through the pion mass$ m_\pi(T) $ and quark mass$ m_q(T) $ ,$ m_\pi(T_m) = 2m_q(T_m). $

(1) Because of the non-perturbative difficulty in QCD, we calculate the Mott transition temperature in an effective chiral model. One of the models that enables us to see directly how the dynamical mechanism of chiral symmetry breaking and restoration operates is the Nambu-Jona-Lasinio (NJL) model applied to quarks [12-16]. Within this model, the hadronic mass spectrum and the static properties of mesons can be obtained remarkably well. In this paper, we calculate in the model the chiral condensate in mean field approximation and the meson mass beyond mean field through random phase approximation (RPA), which has been proven to guarantee Goldstone's theorem in the chiral breaking phase.
In recent years, the investigation of chiral symmetry has been extended to include external electromagnetic fields. Considering the dimension reduction of fermions in external magnetic fields, chiral symmetry breaking in vacuum is enhanced by the background magnetic field, from both the lattice QCD simulation [17-23] and effective models [24-28]. The surprise is in the behavior of the chiral crossover temperature
$ T_{\rm pc} $ . With increasing magnetic field, it decreases, from lattice QCD simulations [17-23], which is called the inverse magnetic catalysis, but increases from effective models in mean field approximation [24-28]. Many scenarios have been proposed to understand this qualitative difference between lattice QCD and effective models [29-42]. Note that, in previous works, the chiral crossover temperature is usually defined by the variation of the chiral condensate. In this work, we point out that, when defining the crossover temperature by the Mott transition of pseudo-Goldstone bosons, an inverse magnetic catalysis effect appears with decreasing Mott temperature in magnetic fields. Throughout this paper, the increase (decrease) in characteristic temperature with magnetic fields is called the (inverse) magnetic catalysis effect.The magnetized two-flavor NJL model is defined through the Lagrangian density [12-16]
$ {\cal{L}} = \bar{\psi}\left({\rm i}\gamma_\mu D^\mu-m_0\right)\psi+\frac{G}{2}\left[\left(\bar\psi\psi\right)^2+\left(\bar\psi {\rm i}\gamma_5\tau\psi\right)^2\right], $

(2) where the covariant derivative
$ D^\mu = \partial^\mu+{\rm i}Q A^\mu $ couples quarks with electric charge$ Q = {\rm diag} (Q_u,Q_d) = {\rm diag} (2e/3, -e/3) $ to the external magnetic field$ {{B}} = B{{e}}_z $ through the potential$ A_\mu = (0,0,Bx,0) $ , G is the coupling constant in scalar and pseudo-scalar channels, and$ m_0 $ is the current quark mass characterizing the explicit chiral symmetry breaking.Using the Leung-Ritus-Wang method [43-48], the chiral condensate
$ \langle\bar\psi\psi\rangle $ or the dynamical quark mass$ m_q = m_0-G\langle\bar\psi\psi\rangle $ at mean field level is controlled by the gap equation$ m_q\left(1-GJ_1\right) = m_0 $

(3) with
$ J_1 = N_{\rm c}\sum\limits_{f,n}\alpha_n {|Q_f B|\over 2\pi} \int {{\rm d} p_z\over 2\pi}{\tanh \dfrac{E_f} {2T}\over E_f}, $

(4) where
$ N_{\rm c} = 3 $ is the number of colors, which is trivial in the NJL model;$ \alpha_n = 2-\delta_{n0} $ is the spin degeneracy; T is the temperature of the quark system; and$ E_f = \sqrt{p^2_z+2 n |Q_f B|+m_q^2} $ is the quark energy with flavor$ f = u,d $ , longitudinal momentum$ p_z $ , and Landau energy level n.Mesons in the model are treated as quantum fluctuations above the mean field and constructed through RPA [12-16]. In the chiral limit with
$ m_0 = 0 $ , the isospin triplet$ \pi_0 $ and$ \pi_\pm $ and isospin singlet$ \sigma $ are respectively the Goldstone modes and Higgs mode, corresponding to spontaneous chiral symmetry breaking with a vanishing magnetic field. Turning on the external magnetic field, only the neutral pion$ \pi_0 $ remains as the Goldstone mode.With the RPA method, the meson propagator
$ D_m $ can be expressed in terms of the meson polarization function or quark bubble$ \Pi_m $ ,$ D_m(q) = \frac{G}{1-G\Pi_m(q)}. $

(5) The meson mass
$ m_m $ is defined as the pole of the propagator at zero momentum$ {{q}} = {\bf{0}} $ ,$ 1-G\Pi_m(m_m, {\bf{0}}) = 0 $

(6) with
$ \begin{aligned}[b] \Pi_m(q_0,{\bf{0}}) =& J_1-(q_0^2-\epsilon_m^2) J_2(q_0),\\ J_2(q_0) =& -N_{\rm c}\sum\limits_{f,n}\alpha_n \frac{|Q_f B|}{2\pi} \int \frac{{\rm d} p_z}{2\pi}{\tanh \dfrac{E_f} {2T}\over E_f (4 E_f^2-q_0^2)}, \end{aligned} $

(7) $ \epsilon_{\pi_0} = 0 $ for the Goldstone mode, and$ \epsilon_\sigma = 2m_q $ for the Higgs mode. In a nonzero magnetic field, the three-dimensional quark momentum integration in the gap equation (3) and pole equation (6) becomes a one-dimensional momentum integration plus a summation over the discrete Landau levels.In the chiral limit with vanishing current quark mass, by comparing the gap equation (3) for quark mass with the pole equation (6) for meson mass, we have the analytic solutions
$ m_{\pi_0} = 0,\ \ m_\sigma = 2m_{q} $

(8) in the chiral breaking phase with
$ m_q\neq 0 $ and$ m_{\pi_0} = m_\sigma\neq 0 $

(9) in the chiral restoration phase with
$ m_q = 0 $ . A direct consequence of these solutions is that the Mott transition temperature$ T_m $ defined by$ m_{\pi_0}(T_m) = 2m_q(T_m) $ coincides with the critical temperature$ T_{\rm c} $ defined by$ m_q(T_{\rm c}) = 0 $ . The phase transition from chiral symmetry breaking to its restoration is a second order phase transition.In the physical case with nonzero current quark mass, the chiral restoration becomes a smooth crossover. At low temperature, spontaneous chiral symmetry breaking dominates the system. Considering the fact that the explicit chiral symmetry breaking is slight, we can use
$ m_0 $ expansion to solve the gap equation for quark mass and pole equation for meson mass. With the notations$ m_q = m^{cl}_q+\delta_q $ and$ m_{\pi_0} = m^{cl}_{\pi_0}+\delta_{\pi_0} $ , where$ m_q^{cl} $ and$ m_{\pi_0}^{cl} = 0 $ are the quark and neutral pion masses in the chiral limit, respectively, and keeping only the linear term in$ \delta_q $ and quadratic term in$ \delta_{\pi_0} $ in the gap and pole equations, we have$ \begin{aligned}[b] \delta_q = & -\frac{m_0}{m^{cl}_q} \frac{1}{G \dfrac{\partial J_1}{\partial m_q}{\big |}_{{{c}}l}},\\ \delta_{\pi_0}^2 =& -\frac{m_0}{m^{cl}_q+\delta_q}\frac{1}{G J_2{\big |}_{{{{c}}l}}}. \end{aligned} $

(10) It is obvious that, in the chiral limit with
$ m_0 = 0 $ , we have$ \delta_q = 0 $ and$ \delta_{\pi_0} = 0 $ . The explicit chiral symmetry breaking with$ m_0 \neq 0 $ modifies the dynamical quark mass, and the Goldstone mode in the chiral limit becomes a pseudo-Goldstone mode with nonzero mass.At high temperature, the quark dimension reduction under an external magnetic field causes an infrared (
$ p_z\to 0 $ ) singularity of the quark bubble$ \Pi_m(m_m,{\bf{0}}) $ [49-51]. For the pseudo-Goldstone mode$ \pi_0 $ , the infrared singularity of$ \Pi_{\pi_0}(m_{\pi_0},{\bf{0}}) $ occurs at the Mott transition temperature$ T_m $ , where the mass$ m_{\pi_0} $ jumps up from$ m_{\pi_0}<2m_q $ to$ m_{\pi_0}>2m_q $ . This indicates a sudden transition from a bound state to a resonant state [49, 51].We next perform numerical calculations on the Mott transition temperature in both the chiral limit and real case. Because of the four-fermion interaction, the NJL model is not a renormalizable theory and requires regularization. To guarantee the law of causality in magnetic fields, we apply the Pauli-Villars regularization scheme, as explained in detail in Ref. [42]. The three parameters in the NJL model, namely the current quark mass
$ m_0 $ , coupling constant G, and Pauli-Villars mass parameter$ \Lambda $ , are listed in Table 1 by fitting the chiral condensate$ \langle\bar\psi\psi\rangle $ , pion mass$ m_\pi $ , and pion decay constant$ f_\pi $ in a vacuum at$ T = B = 0 $ . We take the current quark mass to be$ m_0 = 0 $ in the chiral limit and$ 6.4 $ MeV in the real world.$ m_0 $ /MeV

G/GeV $ ^{-2} $ 

$ \Lambda $ /MeV

$ \langle\bar\psi\psi\rangle $ /MeV3

$ m_\pi $ /MeV

$ f_\pi $ /MeV

0 5.03 977.3 −2303 0 93 6.4 4.9 977.3 −2303 134 93 Table 1. NJL parameters in Pauli-Villars regularization.
We first discuss the temperature behavior of the phase structure for chiral symmetry at
$ B = 0 $ . Fig. 1 shows the quark mass and pion mass as functions of temperature in the chiral limit and the real world. For a vanishing magnetic field, the three pions are all Goldstone or pseudo-Goldstone modes. To clearly see the Mott transition temperature$ T_m $ and its difference from the pseudo-critical temperature$ T_{\rm pc} $ , we plot$ 2m_q $ instead of$ m_q $ itself. In the chiral limit, the quark mass, which is proportional to the order parameter$ \langle\bar\psi\psi\rangle $ , continuously decreases at low temperature, reaches zero at the critical temperature$ T_{\rm c} = 163 $ MeV, and remains zero at higher temperature. This denotes a second order chiral phase transition. Correspondingly, the Goldstone modes$ \pi $ remain massless in the chiral breaking phase and begin to have mass at$ T_{\rm c} $ . It is clear that the Mott transition temperature defined by the threshold condition (1) is exactly the critical temperature$ T_m = T_{\rm c} = 163 $ MeV. Note that the critical temperature obtained here in the NJL model is higher by$ 20-30 $ MeV than the results of recent lattice QCD [5] and other effective models [52, 53]. In the real world, the quark mass continuously decreases, and the pion mass continuously increases throughout the entire temperature region. In this case, the chiral phase transition becomes a smooth crossover, and there is no strict definition for the crossover temperature. Generalizing the idea of maximum fluctuations around the second order phase transition in the chiral limit, the maximum change in the chiral condensate or dynamical quark mass is commonly used to identify the crossover, referring to the corresponding temperature as the pseudo-critical temperature$ T_{\rm pc} $ of the chiral crossover. From the definition$ \partial^2m_q/\partial T_{\rm pc}^2 = 0 $ , we numerically have$ T_{\rm pc} = 162 $ MeV, which is close to the lattice QCD result of$ 156 $ MeV [6]. From the definition$ m_\pi(T_m) = 2m_q(T_m) $ , denoted by the crossing point of the two dashed lines in Fig. 1, the Mott transition temperature is different from the pseudo-critical temperature:$ T_m = 174 $ MeV$ >T_{\rm pc} = 162 $ MeV. Therefore, pions as pseudo-Goldstone modes can still survive as bound states after the chiral crossover. This means that the definition of$ T_{\rm pc} $ explicitly violates Goldstone's theorem.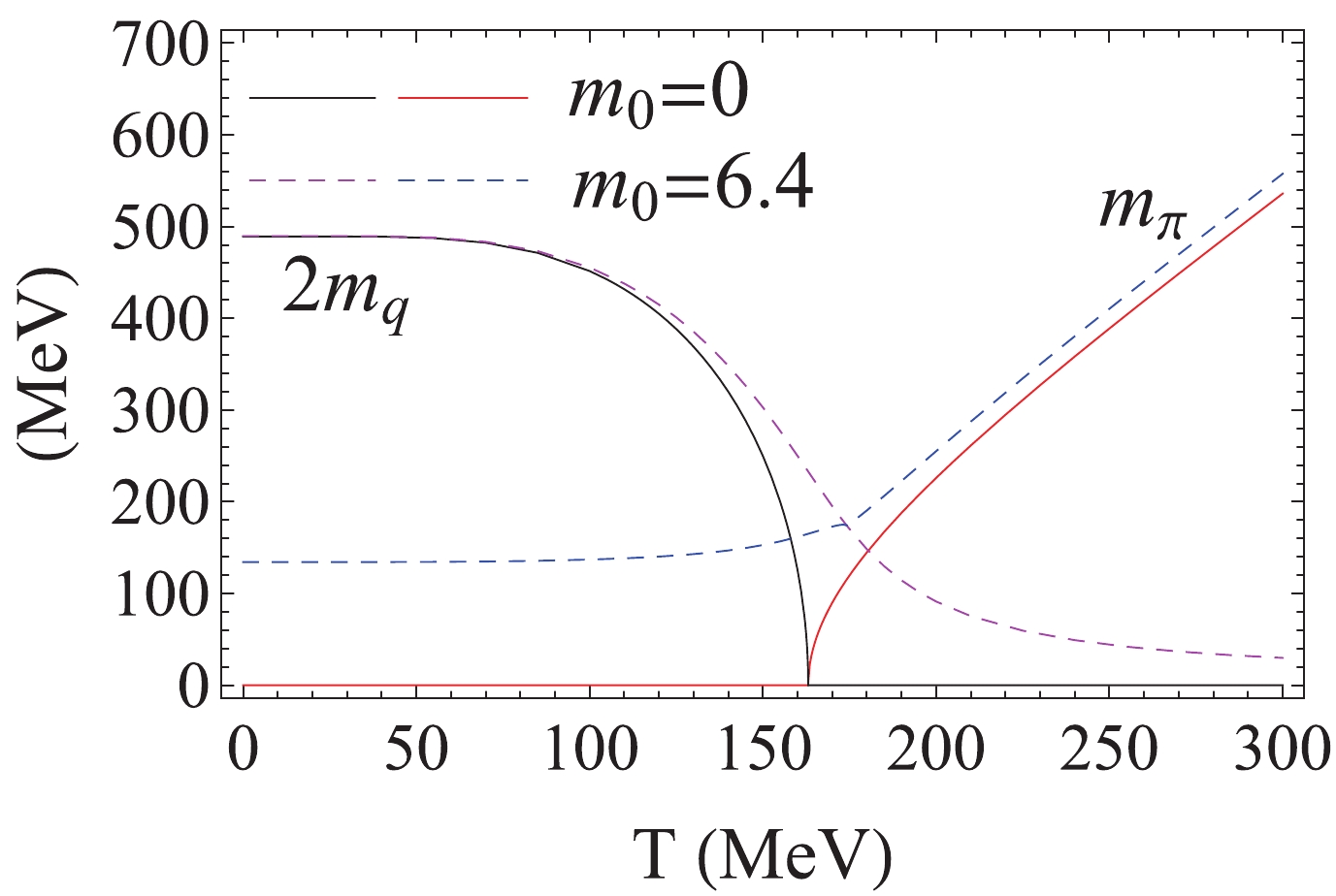
Figure 1. (color online) Dynamical quark mass
$ m_q $ and pion mass$ m_\pi $ as functions of temperature in the chiral limit (solid lines) with current quark mass$ m_0 = 0 $ and real world (dashed lines) with$ m_0 = 6.4 $ MeV.In the chiral limit, chiral restoration is a genuine phase transition, and the phase transition temperature is unique from either the order parameter or Goldstone's theorem, with
$ T_{\rm c} = T_m $ . In the physical world, which is the focus of this paper, chiral restoration is a smooth crossover. The characteristic temperature$ T_{\rm pc} $ from the maximum change in order parameter and$ T_m $ from the Mott transition of pseudo-Goldstone bosons will not coincide with each other:$ T_{\rm pc} \neq T_m $ . To guarantee Goldstone's theorem, we propose to define the crossover temperature as$ T_m $ .Because charged pions interact with the magnetic field, they are no longer pseudo-Goldstone modes, and only the neutral pion is the pseudo-Goldstone boson corresponding to spontaneous chiral symmetry breaking. Fig. 2 shows the pseudo-critical temperature
$ T_{\rm pc} $ and Mott transition temperature$ T_m $ for the pseudo-Goldstone mode as functions of the magnetic field. While$ T_{\rm pc} $ is controlled by the magnetic catalysis, i.e., it increases with increasing magnetic field, the Mott transition temperature$ T_m $ clearly shows the inverse magnetic catalysis effect, decreasing throughout the entire magnetic field region. The physics to explain this difference is as follows:$ T_{\rm pc} $ is controlled by quarks, which are calculated at mean field level, but$ T_m $ is governed by mesons, which are treated as quantum fluctuations beyond mean field. It is the quantum fluctuation that changes the magnetic catalysis to inverse magnetic catalysis. This is consistent with the scenario of fluctuation induced inverse magnetic catalysis discussed in Refs. [30, 40-42]. When we consider the feedback effect from mesons to quarks by including the meson contribution to the thermodynamics of the system,$ \Omega = \Omega_{mf}+\Omega_M $ , the suppressed chiral condensate at high temperature and decreasing pseudo-critical temperature$ T_{\rm pc} $ have been observed.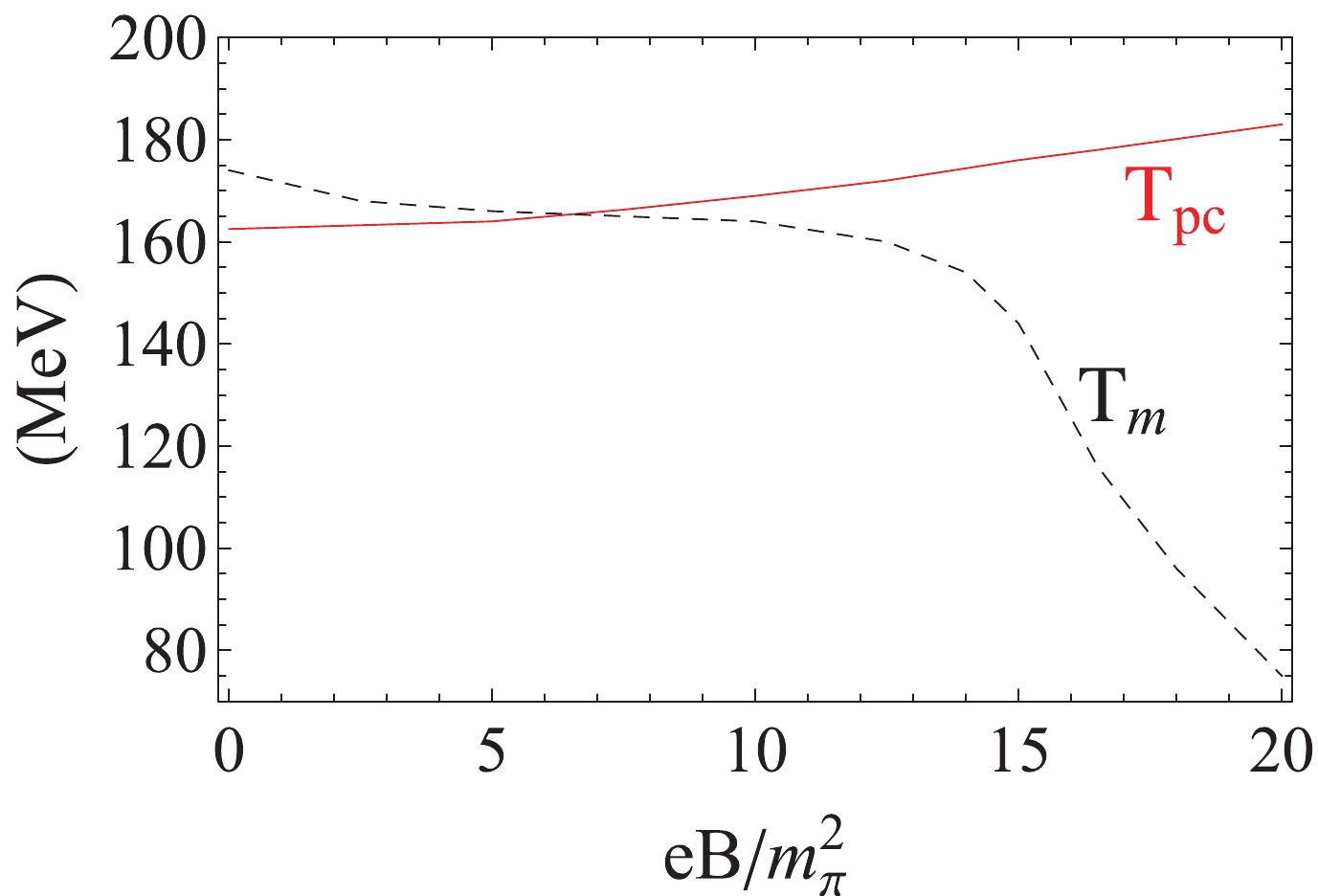
Figure 2. (color online) Pseudo-critical temperature
$ T_{\rm pc} $ (solid line) and Mott transition temperature$ T_m $ (dashed line) for the pseudo-Goldstone mode as functions of magnetic field in the physical case with$ m_0 = 6.4 $ MeV.Again, the result of
$ T_{\rm pc}\neq T_m $ violates Goldstone's theorem in any magnetic field. In a weak magnetic field, with$ eB/m_\pi^2<7 $ , where$ m_\pi $ is the pion mass in a vacuum at$ T = B = 0 $ ,$ T_m>T_{\rm pc} $ , which leads to the survival of the neutral pion as a bound state in the chiral restoration phase. Conversely, in a strong magnetic field with$ eB/m_\pi^2 > 7 $ ,$ T_m < T_{\rm pc} $ , which results in the disappearance of the neutral pion in the chiral breaking phase. In either case, Goldstone's theorem is significantly broken.We investigate in this paper the chiral crossover at finite temperature and in external magnetic fields. In the physical world, chiral restoration is a smooth crossover because of the explicit chiral symmetry breaking. Different from the commonly used maximum change in chiral condensate, we propose defining the crossover temperature by the Mott transition of pseudo-Goldstone bosons. This, by definition, guarantees Goldstone's theorem for chiral symmetry. As an analytical example, we calculate the order parameter (dynamical quark mass) in mean field and Goldstone mode (pion mass) beyond mean field in the frame of a Pauli-Villars regularized NJL model. If we take the maximum change in chiral condensate to describe the chiral crossover, the pseudo-Goldstone mode will survive in the chiral restoration phase with weak magnetic fields and disappear in the chiral breaking phase with strong magnetic fields.
While we believe that the idea of choosing the Mott transition temperature
$ T_m $ to characterize the chiral crossover is correct, the values of the temperatures$ T_m, T_{\rm pc} $ , and$ T_{\rm c} $ we obtained here are model dependent. To precisely fix the Mott transition temperature, we need to use the direct result from lattice QCD simulations.
HTML
-
I am grateful for the hospitality of Professor Dirk H. Rischke of Frankfurt University. Part of this work was done while I was visiting his group as an EMMI visiting professor.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: