-
Since the pioneering work of Bekenstein [1, 2] and Hawking [3, 4], black hole thermodynamics has become a fundamental topic in general relativity. Temperature and entropy in normal thermodynamical systems are related to the horizon of a black hole. To date, numerous methods have been reported to derive the temperature and entropy of black holes [5-11]. It was found that the temperature T of a black hole is related to the surface gravity
$ \kappa $ at the horizon, i.e.,$ T = \kappa/(2 \pi) $ , and that the entropy is proportional to the area of the horizon. The horizon is important not only for the thermodynamics but also for the causality of spacetime. If there is no horizon, the singularity will be naked for an infinity observer; this causes the causality to break down. However, according to Penrose [12], all singularities arising from gravitational collapse must be hidden by black hole horizons. This is the so-called “weak cosmic censorship conjecture”.The laws of thermodynamics and the weak cosmic censorship conjecture can be tested from a charged particle absorption by a black hole. It was demonstrated that, as a particle drops into a black hole, the first and second laws of black hole thermodynamics still hold [13, 14]. Concerning the weak cosmic censorship conjecture, there are still some debates. Wald first proposed a gedanken experiment to check this conjecture in the extremal Kerr-Newman black hole, proving that no violations occur as a particle is thrown into the black hole [15]. Nevertheless, the conjecture would be violated in the near-extremal Reissner-Nordstrom [16] black hole and near-extremal Kerr black hole [17]. Later, it was found that when the backreaction and self-force effects are taken into account, particles may escape from black holes, and naked singularities can be avoided [18]. Many studies addressed the validity of weak cosmic censorship conjecture in various black hole backgrounds under absorption of charged or spinning particles [19-29]. Now, we know that, when including the self-force effect or backreaction, both extremal and near-extremal black holes cannot be overcharged. This result was recently confirmed by considering second-order corrections to mass [30-33]. Note that there is also a counterexample to the weak cosmic censorship conjecture in four-dimensional anti de Sitter (AdS) space-time [34], in which the curvature grows without bound in the future, leaving regions of spacetime with arbitrarily large curvatures naked to infinite boundary observers.
Thermodynamics in AdS space now prevails. One possible reason is the application of the AdS/CFT correspondence [35-39], which relates the gravity theory in D-dimensional AdS spacetime to the conformal field theory in
$ (D-1) $ -dimension. Under this duality, the temperature of black holes is dual to the temperature of the conformal field theory. Currently, there are various applications of AdS/CFT duality, such as holographic superconductors [40, 41], holographic Fermi/non-Fermi liquids [42-44], and others [45-55]. Another possible reason for the popularity of the AdS space is that the phase structures of the AdS spacetime are more abundant, such as the Hawking-Page [56] and Van der Waals-like [57, 58] phase transitions. The Van der Waals-like phase transition exists in the extended phase space, where the negative cosmological constant is treated as the pressure while its conjugate acts as the thermodynamical volume in the Einstein gravity. When imposing the cosmological constant as a dynamical variable, the mass of a black hole corresponds to the enthalpy of the black hole system. The Smarr relation and the first law of thermodynamics will hold in this case [59].In this study, we investigated the laws of thermodynamics and the weak cosmic censorship conjecture in the extended phase space of the Born-Infeld-anti-de Sitter spacetime. The first law and phase transition of Born-Infeld-anti-de Sitter black holes were extensively investigated in previous studies. Fernando discussed their thermodynamics and stability in the grand canonical ensemble [60]. Myung investigated their phase transition shortly after [61]. The thermodynamics and phase transition were also investigated from the point of view of geometry [62]. Recently, many studies addressed the thermodynamics of Born-Infeld-anti-de Sitter black holes in the extended phase space, because in this spacetime, there are abundant phases, such as Van der Waals [63] and reentrant [64, 65] phase transitions. However, to date, there is still lack of studies on the second law of thermodynamics of Born-Infeld-anti-de Sitter black holes in the extended phase space. For Einstein gravity with a negative cosmological constant, a D-dimensional charged AdS black hole with consideration of pressure and volume was investigated [66]. It was found that the first law of thermodynamics holds, while the second law is violated for extremal and near-extremal black holes. The weak cosmic censorship conjecture was also analyzed. It was found that extremal and near-extremal black holes do not change their configurations; therefore, the weak cosmic censorship conjecture is valid. In this study, we investigated the first and second laws of thermodynamics as well as the weak cosmic censorship conjecture of Born-Infeld-anti-de Sitter black holes in the extended phase space.
Our motivation was two-folded. On the one hand, we wanted to explore the effect of other extensive quantities on the laws of thermodynamics and the weak cosmic censorship conjecture, in addition to pressure and volume. In [63], it was found that, to satisfy the Smarr relation in Born-Infeld-anti-de Sitter black holes, the Born-Infeld parameter should be treated as a dynamical variable with a conjugate quantity, called Born-Infeld vacuum polarization. In this case, the first law of thermodynamics is modified owing to the contribution of the vacuum polarization energy. We also wanted to explore whether the Born-Infeld parameter affects the laws of thermodynamics and the weak cosmic censorship conjecture. We found that the first law and weak cosmic censorship conjecture are not affected. However, the second law of thermodynamics is affected: it is violated for double horizon black holes and part of single horizon black holes. On the other hand, in [66], some approximations were applied to investigate the weak cosmic censorship conjecture. The author found that extremal and near-extremal black holes do not change their configurations under the absorption of a charge particle. This differs from the normal phase space, in which extremal black holes deform into non-extremal black holes [13, 14]. In this study, we aimed at finding an analytical method with no approximation to study the configurations of black holes under a charged particle absorption. We describe a general approach to check whether the phase space will affect the configurations of black holes when a charged particle is absorbed. Our results show that configurations of black holes will be changed in both the normal and extended phase spaces under a charged particle absorption. In particular, in both cases, extremal black holes will change into non-extremal black holes.
This paper is organized as follows. In Sec. II, Born- Infeld-anti-de Sitter black holes are introduced, and the motion of a charged particle around the black hole is investigated. In Sec. IV, we establish the first law of thermodynamics under charged particle absorption in the extended phase space and further discuss the second law of thermodynamics as well as the weak cosmic censorship conjecture. The second law is violated for double horizon black holes and part of single horizon black holes, and the weak cosmic censorship conjecture is valid for all black holes. In Sec. III, we elaborate on the first and second laws and the weak cosmic censorship conjecture in the normal phase space. We found that, for all black holes, the first and second laws of thermodynamics hold, and the weak cosmic censorship conjecture is not violated. Throughout this paper, we set the gravitational constant G and the light velocity c to one.
-
The Einstein-Born-Infeld theory in AdS is described by the action [67]
$ S = \int {\rm d}^4 x \sqrt{-g}\left[\frac{R-2 \Lambda }{16 \pi G} +\frac{b^2}{4 \pi G}\left(1-\sqrt{1+\frac{2F}{b^2}}\right)\right], $

(1) in which
$ F = \dfrac{1}{4}F_{\mu\nu}F^{\mu\nu} $ , R is scalar curvature, G is the gravitational constant,$ \Lambda $ is the cosmological constant with$ \Lambda = -3/l^2 $ , where l is the AdS radius, and b is the Born-Infeld parameter, which relates to the string tension$ \alpha $ through the relation$ b = 1/(2 \pi \alpha) $ . The solution of the Born-Infeld AdS black hole can be written as [68-70]$ {\rm d}s^{2} = -f(r){\rm d}t^{2}+f^{-1}(r){\rm d}r^{2}+r^{2}({\rm d}\theta^2+\sin^2\theta {\rm d}\phi^2), $

(2) where
$\begin{aligned}[b] f(r) =& \frac{4 Q^2 \, _2F_1\left(\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r^4}\right)}{3 r^2}\\&+\frac{ 2 b^2 r^2}{3} \left(1-\sqrt{\frac{Q^2}{b^2 r^4}+1}\right)+\frac{r^2}{l^2}-\frac{2 M}{r}+1, \end{aligned}$

(3) in which M represents the ADM mass and Q the electric charge, and
$ _2F_1 $ is the hypergeometric function. From Eq. (3), we know that, in the limit$ b \rightarrow \infty $ ,$ Q\neq0 $ , the solution reduces to the Reissner-Nordström-AdS black hole, and in the limit$ Q\rightarrow 0 $ , it reduces to the Schwarzschild AdS black hole. The nonvanishing component of the vector potential is$ A_t = -\frac{Q_2F_1\left(\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r^4}\right)}{r}, $

(4) which reminds us that the chemical potential depends on the Born-Infeld parameter.
In [61, 71], the author computed the horizon of extremal black holes as
$\begin{aligned}[b] r_{\rm e}^2 = \frac{l^2}{6}\left(\frac{1 + \dfrac{3}{2b^2 l^2}}{1 + \dfrac{4}{4b^2 l^2}}\right)\times \left[- 1 + \sqrt{ 1 + \frac{12\left(1 + \dfrac{3}{4b^2 l^2}\right)}{b^2l^2\left(1 + \dfrac{3}{2b^2 l^2} \right)^2} \left(b^2Q^2 -\frac{1}{4} \right)}\; \right]. \end{aligned}$

(5) They claimed that
$ b Q \geqslant 0.5 $ should be satisfied to have a real root for$ r^2_{\rm e} $ . In particular, they stressed that$ 0 \leqslant b Q < 0.5 $ is a forbidden region because in this region there is no black hole solution. However, it was later found that there is a single horizon black hole solution in the region$ 0 \leqslant b Q < 0.5 $ [72]. The action growth of the Wheeler-DeWitt patch for single horizon black holes was calculated, and it was found that the Lloyd bound is satisfied. In fact, a single horizon black hole exists not only in the region$ 0 \leqslant b Q < 0.5 $ but also in$ b Q \geqslant 0.5 $ ; please refer to Fig. 3 or Fig. 4. Black holes with two horizons exist only in a narrow region of the value of M. In [63], the author obtained a marginal mass$ M_{m} = \frac{1}{6}\sqrt{\frac{b}{\pi}}Q^{3/2}\Gamma\left(\frac{1}{4}\right)^2. $

(6) If the black hole mass is larger than the marginal mass, there are only single horizon black holes.
-
In this subsection, we analyze the dynamics of a charged particle as it is absorbed by a Born-Infeld-anti-de Sitter black hole. We focus mainly on the relations between conserved quantities, such as energy and momentum.
The Hamilton-Jacobi equation for the vector potential
$ A_\mu $ is$ g^{\mu\nu}(P_\mu-e A_\mu)(P_\nu-e A_\nu)+u^2 = 0, $

(7) in which u is the rest mass, e is the electric charge, and
$ P_\mu $ is the momentum of the particle defined as$ P_\mu = \partial_\mu {\cal I}, $

(8) where
$ {\cal I} $ is the Hamilton-Jacobi action. Considering the symmetry of the black hole, the action can be written as$ {\cal I} = - E t +{\cal I}_r(r) + {\cal I}_\theta(\theta) +L \phi, $

(9) where E and L are the energy and angular momentum of the particle, respectively. They are conserved quantities with respect to t and
$ \phi $ . From Eq. (2), the inverse of the metric is$ g^{\mu\nu}\partial_\mu\partial_\nu = -f(r)^{-1}(\partial_t)^2+f(r)(\partial_r)^2 + r^{-2} (\partial_\theta ^2 + \sin^{-2}\theta \partial_\phi^2). $

(10) Therefore, the Hamilton-Jacobi equation can be re-expressed as
$\begin{aligned}[b] u^2 & -f(r)^{-1}(-E-eA_t)^2+f(r)(\partial_r {\cal I}_r(r))^2 \\&+ r^{-2} ((\partial_\theta {\cal I}_\theta)^2 + \sin^{-2}\theta L^2) = 0. \end{aligned}$

(11) One can readily separate the angular part from Eq. (11) and define it as
$ K = (\partial_\theta {\cal I}_\theta)^2 +\frac{1}{ \sin^2\theta}L^2, $

(12) in which K can be solved from the radial part in Eq. (11) as
$ K = - u^2 r^2 +\frac{ r^2}{f(r)}(-E-eA_t)^2 -r^2f(r)(\partial_r {\cal I}_r(r))^2. $

(13) Therefore, Eq. (9) can be rewritten as
$ {\cal I} = -Et +\int {\rm d}r \sqrt{R} + \int {\rm d}\theta \sqrt{\Theta} +L\phi, $

(14) with
$ \begin{aligned}[b]& {\cal I}_r \equiv \int {\rm d}r \sqrt{R},\\& {\cal I}_\theta \equiv \int {\rm d}\theta \sqrt{\Theta},\\&\Theta = K-\frac{1}{\sin^2\theta}L^2, \\& R = \frac{1}{ r^2 f(r)}\left(-K- u^2 r^2\right)+\frac{1}{ r^2 f(r)}\left(\frac{ r^2}{f(r)}(-E-eA_t)^2\right). \end{aligned} $

(15) Hence, from Eq. (14), the radial momentum
$ P^r $ and angular momentum$ P^\theta $ can be written as$ P^r = f(r) \sqrt{ -\frac{K+u^2 r^2}{ r^2 f(r)} +\frac{1}{f^2(r)}(-E-eA_t)^2}, $

(16) $ P^\theta = \frac{1}{r^2 } \sqrt{K -\frac{1}{ \sin^2\theta}L^2}. $

(17) We studied how the black hole thermodynamics changes as a charged particle is absorbed by the black hole. Specifically, we focused on the relation between the momentum and energy. In principle, as K is eliminated, we can obtain such a relation at any location. Our goal was to investigate the thermodynamics on the event horizon. Thus, we mainly paid attention to the near horizon behavior of the particle. In this case, Eq. (16) can be simplified as
$ E = \frac{Q_2F_1\left(\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right)}{r_+}e+|P^r_+|. $

(18) Note that a positive sign should be added in front of the
$ |P^r_+| $ term. This ensures that the signs in front of E and$ |P^r_+| $ are the same and positive throughout the positive flow of time [73]. According to Eq. (18), the energy depends on the electric potential as well. However, the potential is independent of the flow of time and only related to the interaction between the particle and black hole. Thus, the total value of the energy under the sum of the potential is not important, and we simply set a positive sign in front of$ |P^r_+| $ . -
In this section, we examine whether the first and second laws of thermodynamics and the weak cosmic cosponsorship conjecture are valid in the normal phase space of Born-Infeld-anti-de Sitter spacetime. Our discussions are mainly based on the relation between the energy and momentum of the absorbed particle in Eq. (18).
-
In the Born-Infeld-anti-de Sitter black hole, the electrostatic potential difference between the black hole horizon and the infinity is
$ \Phi = \frac{Q_2F_1\left(\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right)}{r_+}, $

(19) in which
$ r_+ $ is the event horizon of the black hole, which is determined from$ f(r_+) = 0 $ . The Hawking temperature, defined by$ T = \dfrac{f^{\prime}(r)}{4\pi}\mid_{r_+} $ , can be written as$ T = \frac{-2 l^2 Q^2 \, _2F_1\left(\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right)+r_+^4 \left(3-2 b^2 l^2 \left(\sqrt{\dfrac{Q^2}{b^2 r_+^4}+1}-1\right)\right)+3 l^2 M r_+}{6 \pi l^2 r_+^3},$

(20) In addition, according to the Bekenstein-Hawking entropy area relation, we can obtain the black hole entropy
$ S = \pi r_+^2. $

(21) At the horizon, the mass M can be expressed as
$ M = \frac{4 l^2 Q^2_2F_1 \left[\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right]+3 l^2 r_+^2+3 r_+^4+2 b^2 l^2 r_+^4-2 b^2 l^2 \sqrt{1+\dfrac{Q^2}{b^2 r_+^4}} r_+^4}{6 l^2 r_+}. $

(22) With Eqs. (19)-(22), we can obtain the first law of thermodynamics.
In the normal phase space, the cosmological parameter is a constant, and the mass M is the internal energy of the black hole. According to energy and charge conservation, when a charged particle is absorbed by the black hole, the variations of the internal energy and charge satisfy
$ E = {\rm d}M, \;\;\;\; e = {\rm d}Q, $

(23) and Eq. (18) can be written as
$ {\rm d}M = \frac{Q_2F_1\left(\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right)}{r_+}{\rm d}Q+|P^r_+|. $

(24) In addition, when the charged particle is absorbed by the black hole, the variation of the entropy can be written as
$ {\rm d}S = 2 \pi r_{+} {\rm d}r_{+}, $

(25) where we have used Eq. (21). To obtain the last result describing the variation of the entropy, we must find
$ {\rm d}r_+ $ firstly.The absorbed particle leads to a variation in the event horizon of the black hole, which further leads to the change in
$ f(r) $ . The variation in$ f(r) $ , labeled by$ {\rm d}f_\text{+} $ , satisfies$ {\rm d}f_\text{+} = \frac{\partial f_\text{+}}{\partial M}{\rm d}M+\frac{\partial f_\text{+}}{\partial Q}{\rm d}Q+\frac{\partial f_\text{+}}{\partial r_\text{+}}{\rm d}r_\text{+} = 0. $

(26) Substituting Eq. (24) into Eq. (26), we can obtain
$ {\rm d}r_{+} $ directly as$ {\rm d}r_{+} = \frac{-3 l^2 |P^r_+| r_+^2}{2 l^2 Q^2_2F_1\left[\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right]-3r_+^4-3 M l^2 r_++2 b^2 l^2 \left(-1+\sqrt{1+\dfrac{Q^2}{b^2 r_+^4}}\right) r_+^4}. $

(27) With Eq. (25), the variation in entropy can be expressed as
$ {\rm d}S = \frac{-6\pi l^2 |P^r_+| r_+^3}{2 l^2 Q^2_2F_1\left[\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right]-3r_+^4-3 M l^2 r_++2 b^2 l^2 \left(-1+\sqrt{1+\dfrac{Q^2}{b^2 r_+^4}}\right) r_+^4}. $

(28) Combining Eqs. (20) and (28), we obtain
$ T {\rm d}S = |P^r_+| $ . Therefore, the internal energy in Eq. (24) can be rewritten as$ {\rm d}M = T{\rm d}S+\Phi {\rm d}Q, $

(29) which is the first law of black hole thermodynamics in the normal phase space.
Next, we study the second law of thermodynamics, which states that the entropy of the black hole never decreases with the arrow of time. As the charged particle is absorbed by the black hole, the entropy of the black hole increases according to the second law of black hole thermodynamics. We employ Eq. (28) to check whether this is true in the normal phase space.
We first discuss an extremal black hole, for which the inner and outer horizons coincide and the temperature vanishes at the horizon. With Eq. (20), we can obtain the mass of the extremal black hole
$ M_{\rm e} = \frac{2 l^2 Q^2 \, _2F_1\left(\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right)+2 b^2 l^2 r_+^4 \sqrt{\dfrac{Q^2}{b^2 r_+^4}+1}-2 b^2 l^2 r_+^4-3 r_+^4}{3 l^2 r_+}. $

(30) Substituting Eq. (30) into Eq. (28), we obtain
$ {\rm d}S_{\rm extreme} = \infty. $

(31) The divergency of the variation of the entropy means that it is meaningless to investigate the second law of thermodynamics for extremal black holes. Therefore, we mainly focused on non-extremal black holes thereafter.
As the charge Q and the Born-Infeld parameter b are given, we can find the extremal black hole mass
$ M_{\rm e} $ via the asymptotic evaluation method①. With the extremal mass, we can also obtain the extremal radius via Eq. (30). Then, we can provide any mass, which should be larger than the critical mass, to find the corresponding horizon and variation of the entropy of the non-extremal black hole. Throughout this study, we set$ l = P^r_+ = 1 $ . For the case$ Q = 1, b = 0.8 $ , we obtain that the extremal black hole mass is$ M_{\rm e} = 1.0302893 $ . For extremal and non-extremal black holes, the variations in entropy and horizon$ r_{\rm h} $ are listed in Table 1. Note that, for all the black holes, the variations in entropy are positive. That is to say, the second law of black hole thermodynamics always holds as a charged particle is absorbed by the black hole in the normal phase space.M $r_{+}$ 

dS 1.0302893 0.377831 7951.91 1.06 0.559903 10.1647 1.09 0.630175 7.75712 1.12 0.682279 6.67212 1.15 0.725166 6.01545 1.18 0.762249 5.56131 1.21 0.795261 5.22208 1.23 0.815527 4.95557 1.26 0.843831 4.80642 1.29 0.870061 4.61436 1.32 0.894579 4.45151 1.35 0.917657 4.31095 Table 1. Numerical results of the variation in entropy in the normal phase space for the case
$Q = 1, \;b = 0.8$ .Substituting Eq. (22) into Eq. (28), the variation in entropy can be rewritten as
$ {\rm d}S = -\frac{4 l^2 \pi r_+}{-3 r_+^2+l^2 \left(-1+2 b^2 \left(-1+\sqrt{1+\dfrac{Q^2}{b^2 r_+^4}}\right) r_+^2\right)}. $

(32) On the basis of Eq. (32), we can plot the relation between the variation in entropy and the horizon, which is shown in Fig. 1. Note that the variation in entropy is positive for all black holes, which is consistent with the results in Table 1.
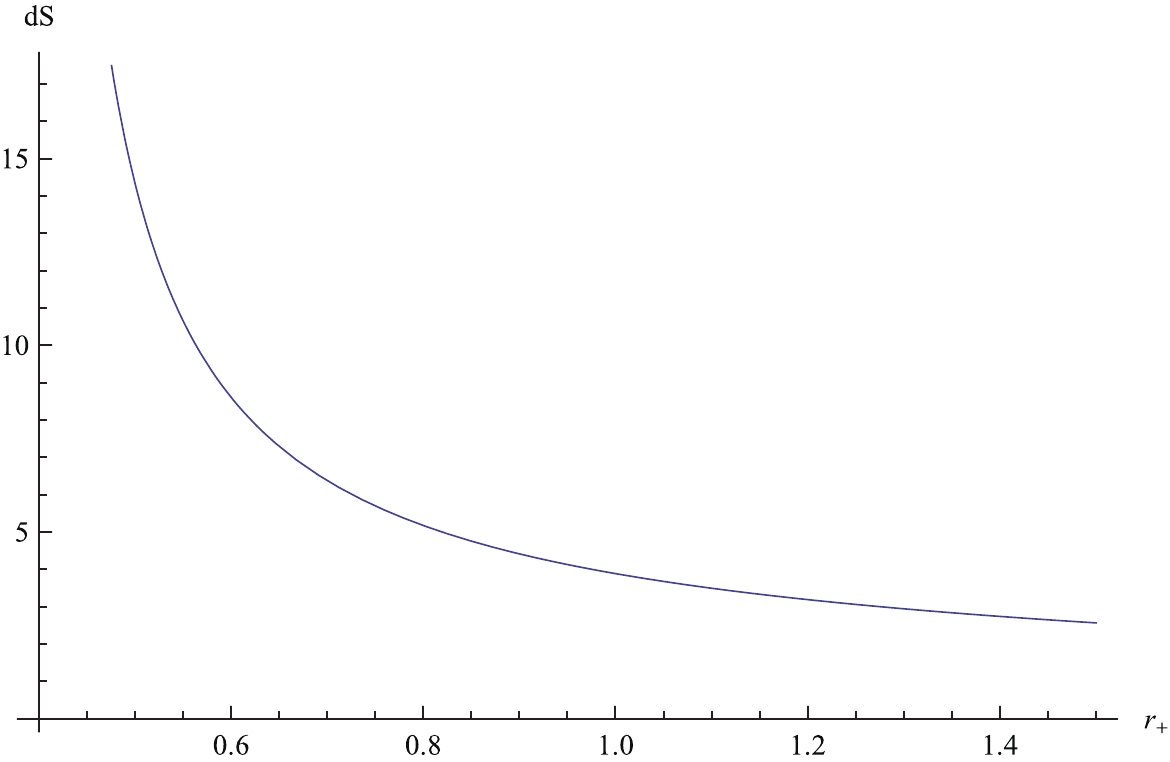
Figure 1. (color online) Relation between dS and
$ r_+ $ for the case of$ Q = 1,\; b = 0.8 $ in the normal phase space.To confirm that this conclusion is independent of Q and b, we can set other values to such parameters. For the case of
$ Q = 0.8,\; b = 0.8 $ , the extremal mass of the black hole is 0.7671287. For extremal and non-extremal black holes, the variations in entropy are listed in Table 2, and the relation between the variations in entropy and horizons is plotted in Fig. 2. Note that the variation in entropy is positive as well. In other words, the second law of black hole thermodynamics is satisfied in the normal phase space for Born-Infeld-anti-de Sitter black holes, which is independent of the charge and Born-Infeld parameter.M $r_{+}$ 

dS 0.7671287 0.257154 13834.3 0.77 0.327056 24.1034 0.78 0.399628 12.9661 0.79 0.443068 10.392 0.80 0.476571 9.08111 0.81 0.504592 8.24664 0.82 0.529029 7.6531 0.83 0.550894 7.20171 0.84 0.570803 6.84265 0.85 0.589163 6.5477 Table 2. Numerical results of the variation in entropy in the normal phase space for the case
$Q = 0.8,\; b = 0.8$ .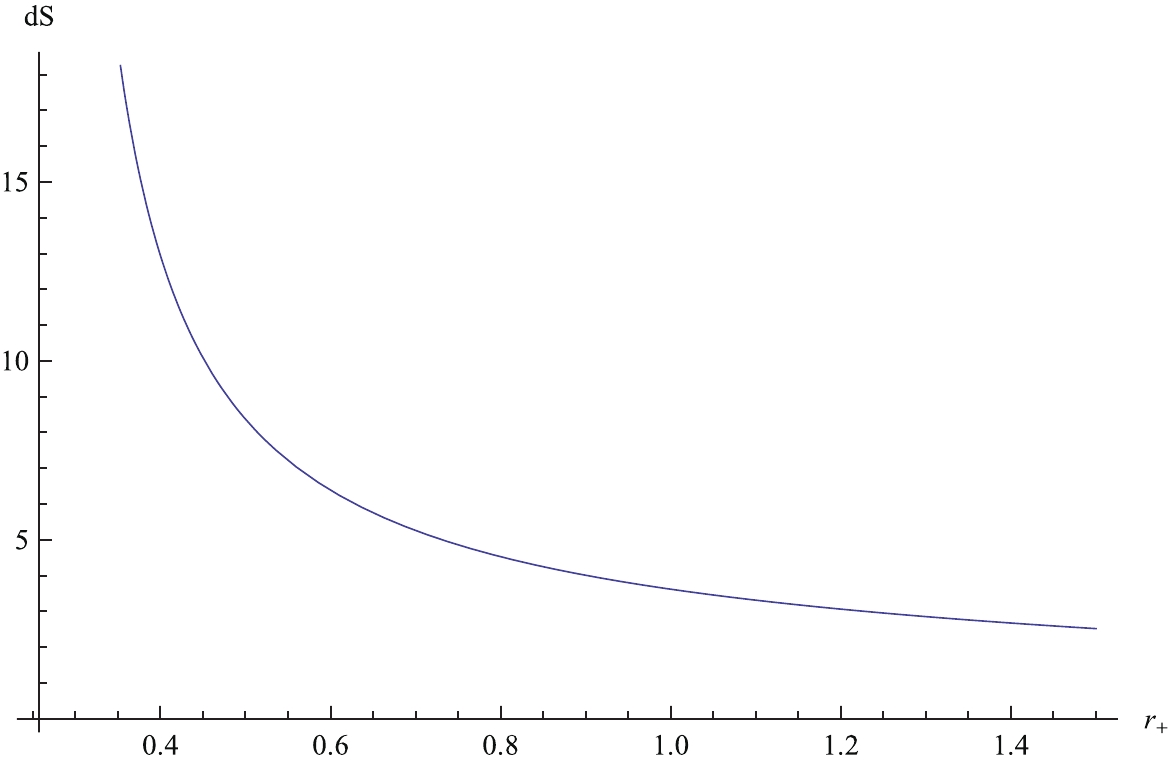
Figure 2. (color online) Relation between dS and r for the case
$ Q = 0.8, b = 0.8 $ in the normal phase space.In addition, from Eq. (6), we know that, as the mass of the black hole becomes larger than the critical mass
$ M_m $ , the black hole becomes a single horizon black hole. For the cases$Q = 1, \;b = 0.8$ and$ Q = 0.8, \;b = 0.8 $ , the critical masses are$ M_m = 1.10556 $ and$ M_m = 0.791072 $ , respectively. Tables 1 and 2 show that the second law is satisfied in the normal phase space not only for double horizon black holes but also for single horizon black holes. -
The weak cosmic censorship conjecture asserts that there are no singularities visible from future null infinity. In other words, singularities need to be hidden from an observer at infinity by the event horizon of a black hole. Consequently, an event horizon must exist to ensure the validity of the weak cosmic censorship conjecture. We checked whether an event horizon exists when a charged particle is absorbed by the black hole. For single horizon black holes in the Born-Infeld theory, the horizons will not be broken, while they may be broken for double horizon black holes, as can be seen in Fig. 3. Thus, the weak cosmic censorship conjecture is always valid for single horizon black holes, and we only studied double horizon black holes thereafter.

Figure 3. (color online) Relation between
$ f(r) $ and r for the case$ Q = 1, \;b = 0.8 $ . Curves from top to bottom correspond to M varying from 1.03 to 1.35 with step 0.03.For a double event horizon black hole, there is a minimum value for
$ f(r) $ , and the corresponding radial coordinate is labeled as$ r_{m} $ . At$ r_{m} $ , we found that there always exist the following relations:$ \begin{aligned}[b] f|_{r = r_{m}}\equiv & f_{m} = \delta\leqslant 0, \\ \partial_{r}f|_{r = r_{m}}\equiv & f'_{m} = 0, \\ (\partial_{r})^2 f|_{r = r_{m}}\equiv & f^{\prime\prime}_{m}>0. \end{aligned} $

(33) For extremal black holes,
$ \delta = 0 $ , and for near extremal black holes,$ \delta $ is a small quantity. For extremal and near-extremal black holes, as a charged particle is absorbed by the black hole,$ f_{m} $ may move upward or downward, which correspond to the non-existence or existence of horizon, respectively. Next, we analyze how$ f_{m} $ moves in the normal phase space.The absorption of a charged particle will lead to variations in the mass and charge of the black hole. Correspondingly, the locations of the minimum value and event horizon will change as
$ r_{m}\rightarrow r_{m}+{\rm d}r_{m} $ ,$ r_{+}\rightarrow r_{+}+{\rm d}r_{+} $ . The variation in$ f(r) $ , defined by$ {\rm d}f_{m} $ , can be expressed as$ {\rm d}f_{m} = \left(\frac{\partial f_{m}}{\partial M}{\rm d}M+\frac{\partial f_{m}}{\partial Q}{\rm d}Q\right), $

(34) where we have used
$ f'_{m} = 0 $ . In addition, at the new minimum point, there is also the relation$ \partial_{r} f|_{r = r_m+{\rm d}r_m} = f'_{m}+{\rm d}f'_{m} = 0, $

(35) which implies
$ {\rm d}f'_{m} = \frac{\partial f'_{m}}{\partial M}{\rm d}M+\frac{\partial f'_{m}}{\partial Q}{\rm d}Q+\frac{\partial f'_{m}}{\partial r_{m}}{\rm d}r_{m} = 0. $

(36) With the condition
$ f'_{m} = 0 $ , we can obtain M and further dM, which is$ \begin{aligned}[b] {\rm d}M = r_m^2 \left(\frac{2 b^4 {\rm d}r \sqrt{1+\dfrac{Q^2}{b^2 r_m^4}} r_m^4}{Q^2+b^2 r_m^4}+b^2 \left(-2 {\rm d}r+\frac{{\rm d}Q Q \sqrt{1+\dfrac{Q^2}{b^2 r_m^4}} r_m}{Q^2+b^2 r_m^4}\right)\right)-r_m^2 \dfrac{3 {\rm d}r }{l^2} +\dfrac{{\rm d}Q Q _2F_1\left[\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_m^4}\right]}{r_m}. \end{aligned} $

(37) We are interested in extremal black holes, for which Eq. (24) is valid at
$ r_m $ . Inserting Eq. (37) into Eq. (24), we obtain$ {\rm d}r_{m} = \frac{l^2 \left(|P^r_+| \left(b^2 r_m^4+Q^2\right)-b^2 {\rm d}Q Q r_m^3 \sqrt{\dfrac{Q^2}{b^2 r_m^4}+1}\right)}{r_m^2 \left(b^2 r_m^4 \left(2 b^2 l^2 \left(\sqrt{\dfrac{Q^2}{b^2 r_m^4}+1}-1\right)-3\right)+Q^2 \left(-2 b^2 l^2-3\right)\right)}. $

(38) In addition, substituting Eq. (37) into Eq. (36),
${\rm d}r_{m} = 0$ will be produced, which means$ {\rm d}Q = \frac{|P^r_+| r_m \sqrt{\dfrac{Q^2}{b^2 r_m^4}+1}}{Q}. $

(39) Similarly, substituting Eq. (37) into Eq. (34),
$ {\rm d}f_{m} $ can be expressed as a function with respect to$ {\rm d}Q, {\rm d}r_{m} $ . From Eq. (39), Eq. (34) can be simplified as$ {\rm d}f_{m} = -\frac{2 |P^r_+|}{r_{m}}, $

(40) which shows that there is a shift of
$ f_m $ in the negative direction as a charged particle is absorbed by the black hole. In other words, the weak cosmic censorship conjecture holds in the normal phase space given that there always exist horizons to ensure that the singularity of the spacetime is hidden. -
In this section, we examine the thermodynamics and weak cosmic censorship conjecture in the extended phase space of Born-Infeld-anti-de Sitter spacetime under a charged particle absorption with Eq. (18).
-
In the extended phase space, the cosmological constant is treated as the pressure Y and the corresponding conjugate quantity is treated as the volume V. In this case, to satisfy the Smarr relation, the Born-Infeld parameter b must also be treated as an extensive quantity. The Smarr relation for the Born-Infeld-anti-de Sitter black hole is [63]
$ M = 2(T S-V Y)+\Phi Q-Bb, $

(41) in which
$ \begin{aligned}[b] Y =& -\frac{\Lambda}{8 \pi} = \frac{3}{8 \pi l^2}, \\ V =& \frac{4}{3} \pi r_+^3, \\ B =& \frac{Q^2 _2F_1\left[\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right]-2 b^2 \left(-1+\sqrt{1+\dfrac{Q^2}{b^2 r_+^4}}\right) r_+^4}{3 b r_+}, \end{aligned} $

(42) where B, which is the conjugate quantity of b, is regarded as the Born-Infeld vacuum polarization [63]. It must be stressed that M is not the internal energy but the enthalpy of the thermodynamic system, which relates to the internal energy through the following relation [63]:
$ M = U+YV+bB. $

(43) As the charged particle is absorbed by the black hole, the energy and charge are supposed to be conserved. In other words, the energy and charge of the particle are equal to the varied energy and charge of the black hole. According to Eq. (18), the energy of the particle is determined by the charge and radial momentum of the particle near the event horizon. Our goal is to obtain the first law of thermodynamics. Therefore, we must find some quantities that can be expressed by the charge and radial momentum of the particle.
Based on energy and charge conservation, we obtain
$ E = {\rm d}U = {\rm d}(M-YV-bB),\;\;\; e = {\rm d}Q. $

(44) The energy in Eq. (18) changes accordingly into
$ {\rm d}U = \frac{Q_2F_1\left(\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right)}{r_+}{\rm d}Q+|P^r_+|. $

(45) The variation in the event horizon of the black hole, denoted by
$ {\rm d}r_{+} $ , is determined by the charge, energy, and radial momentum of the absorbed particle, leading to changes in$ f(r) $ . However, near event horizon,$ {\rm d}f(r_{+})\equiv {\rm d}f_\text{+} $ will not change given that$ f(r_++{\rm d}r_{+}) = 0 $ , that is$ {\rm d}f_\text{+} = \frac{\partial f_\text{+}}{\partial M}{\rm d}M+\frac{\partial f_\text{+}}{\partial Q}{\rm d}Q+\frac{\partial f_\text{+}}{\partial l}{\rm d}l+\frac{\partial f_\text{+}}{\partial r_\text{+}}{\rm d}r_\text{+}+\frac{\partial f_\text{+}}{\partial b}{\rm d}b = 0. $

(46) In addition, with the help of Eq. (43), Eq. (45) can be expressed as
$ {\rm d}M-{\rm d}(YV+Bb) = \frac{Q_2F_1\left(\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right)}{r_+}{\rm d}Q+|P^r_+|.$

(47) From Eq. (46), we can obtain dl, and substituting dl into Eq. (47), we can delete it directly. Interestingly, dQ, db, and dM are also eliminated at the same time. In this case, there is only a relation between
$ |P^r_+| $ and$ {\rm d}r_{+} $ , which is$ {\rm d}r_\text{+} = \frac{-6 l^2 r_+^2(|P^r_+|+b {\rm d}B)}{4 l^2 Q^2 \, _2F_1\left(\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right)+l^2 \left(4 b^2 r_+^4 \left(\sqrt{\dfrac{Q^2}{b^2 r_+^4}+1}-1\right)-6 M r_+\right)+3 r_+^4}. $

(48) Therefore, the variations in entropy and volume of the black hole can be expressed as
$ {\rm d}S = \frac{-12 \pi l^2 (|P^r_+|+b {\rm d}B) r_+^3}{4 l^2 Q^2 \, _2F_1\left(\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right)+r_+^4 \left(4 b^2 l^2 \left(\sqrt{\dfrac{Q^2}{b^2 r_+^4}+1}-1\right)+3\right)-6 l^2 M r_+}, $

(49) $ {\rm d}V = \frac{-24 \pi l^2 (|P^r_+|+b {\rm d}B) r_+^4}{4 l^2 Q^2 \, _2F_1\left(\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right)+r_+^4 \left(4 b^2 l^2 \left(\sqrt{\dfrac{Q^2}{b^2 r_+^4}+1}-1\right)+3\right)-6 l^2 M r_+}. $

(50) Based on the above formulae, we obtain
$ T {\rm d}S-Y{\rm d}V-b {\rm d}B = |P^r_+|. $

(51) The internal energy in Eq. (45) will thus change into
$ {\rm d}U = \Phi {\rm d}Q + T {\rm d}S-Y{\rm d}V-b {\rm d}B.$

(52) In the extended phase space, the mass of the black hole is defined as the enthalpy. From Eq. (43), we can obtain the relation between the enthalpy and internal energy as
$ {\rm d}M = {\rm d} U+Y {\rm d}V+V{\rm d}Y+B{\rm d}b+b{\rm d}B. $

(53) Substituting Eq. (53) into Eq. (52), we obtain
$ {\rm d}M = T{\rm d}S+\Phi {\rm d}Q+V{\rm d}Y+B{\rm d}b, $

(54) which is evidently the first law of black hole thermodynamics in the extended phase space [62]. In other words, the first law of thermodynamics holds in the extended phase space of Born-Infeld-anti-de Sitter spacetime under a charged particle absorbtion.
Next, we focus on the second law of the thermodynamics in the extended phase space with Eq. (49). Note that, in Eq. (42), the variation dB is a function of
$ {\rm d}r_+, {\rm d}Q, {\rm d}b $ . However, the existence of dQ and db would affect the definition of$ \Phi $ and B, respectively. Thus, dQ and db may relate to$ {\rm d}r_+ $ , resulting in that dB is only a function of$ {\rm d}r_+ $ . Without loss of generality, we will regard dB as$ g h {\rm d}r_+ $ , in which$ g\equiv \partial B/ \partial r_+ $ and h are the contributions of$ \partial B/ \partial Q $ and$ \partial B/ \partial b $ , respectively. For simplicity, we set$ k = gh $ , where k is a positive parameter for the energy of the black hole, which increases as a charged particle is absorbed by the black hole②. In this case, Eq. (49) changes into$ {\rm d}S = \frac{-12 l^2 \pi |P^r_+| r_+^3}{3 r_+^4-6 M l^2r_+ +2 b l^2r_+^2 \left(3 k+2 b \left(-1+\sqrt{1+\dfrac{Q^2}{b^2 r_+^4}}\right) r^2\right)+4 l^2 Q^2 _2F_1\left[\dfrac{1}{4},\dfrac{1}{2};\dfrac{5}{4};-\dfrac{Q^2}{b^2 r_+^4}\right]}. $

(55) We use Eq. (55) to check the second law of thermodynamics.
For extremal black holes, Eq. (30) is substituted into Eq. (55), and we obtain
$ {\rm d}S_{\rm extreme} = -\frac{4 \pi l^2 |P^r_+| r_{\rm e}}{2 b k l^2+3 r_{\rm e}^2}<0, $

(56) in which
$ r_{\rm e} $ is the radius of horizon of the extremal black hole. It is evident that the variation in the entropy is always negative. In other words, the entropy of the black hole decreases, and the second law of black hole thermodynamics is violated for the extremal Born-Infeld-anti-de Sitter black hole.Regarding non-extremal black holes, Table 3 shows the variation in entropy for different values of k. For the case of
$ k = 0.01 $ , we found that the variation in the entropy is negative for$ M\leqslant 1.18 $ while it is positive for$ M>1.18 $ . As k increases to 0.05, the dividing point, which determines the negative or positive nature of dS, moves to 1.29.M $r_{+}$ 

dS(k = 0.01) dS(k = 0.05) dS(k = 0.1) 1.0302893 0.377831 −10.7015 −9.35242 −8.07927 1.06 0.559903 −26.6229 −21.4326 −17.2331 1.09 0.630175 −44.7806 −31.614 −23.3659 1.12 0.682279 −67.2451 −44.7716 −31.5792 1.15 0.725166 −115.771 −63.8534 −40.9168 1.18 0.762249 −261.085 −95.1325 −53.0124 1.21 0.795261 25611.5 −157.107 −69.5882 1.23 0.815527 446.991 −249.513 −84.645 1.26 0.843831 196.217 −1064.83 −117.876 1.29 0.870061 132.636 593.162 −177.586 1.32 0.894579 103.576 252.42 −316.98 1.35 0.917657 86.9155 167.913 −1018.35 Table 3. Numerical results of the variation in entropy in the extended phase space for different values of k with
$Q = 1, \;b = 0.8$ .Fig. 3 shows the relation between
$ f(r) $ and r. Note that there exist single horizon and double horizon black holes for different masses M. We are interested in the case$ M = 1.18, 1.29 $ , which is marked in red and black in Fig. 3. Clearly, for both cases, the black holes are single horizon black holes. Therefore, according to Table 3, we can conclude that the variations of entropy for all the double horizon black holes and part of the single horizon black holes are negative. In other words, all the double horizon black holes and part of the single horizon black holes violate the second law of black hole thermodynamics as a charged particle is absorbed by the black hole. As k increases, the mass of the black holes that violates the second law of black hole thermodynamics will be larger.To confirm our conclusion, we choose different charges and Born-Infeld parameters in the following. For the case
$ Q = 0.8, \;b = 0.8 $ , we found that the extremal black hole mass is$ M_{\rm e} = 0.7671287 $ . The variation in entropy and horizon for different masses are given in Table 4. For$ k = 0.01 $ , we found that the variation in the entropy is negative for the case$ M\leqslant 0.8 $ and positive for$ M>0.8 $ . As k increases to 0.05, the dividing point moves to 1.35. According to Fig. 4, in which the red and black curves represent cases for$ M = 0.8, \,0.85 $ , we found that the black holes are single horizon black holes for$ M = 0.8, 0.85 $ . Therefore, we can also conclude that all the double horizon black holes and part of the single horizon black holes violate the second law of black hole thermodynamics.M $r_{+}$ 

dS(k = 0.01) dS(k = 0.05) dS(k = 0.1) 0.7671287 0.257154 −15.0897 −11.6177 −9.0227 0.77 0.327056 −24.7011 −17.8392 −13.2413 0.78 0.399628 −46.5846 −29.2307 −19.9438 0.79 0.443068 −80.512 −41.8143 −26.1208 0.80 0.476571 −158.078 −58.7798 −32.9262 0.81 0.504592 579.968 −84.6206 −40.9266 0.82 0.529029 533.602 −129.248 −50.6305 0.83 0.550894 198.864 −237.174 −63.4017 0.84 0.570803 130.85 −781.178 −80.43 0.85 0.589163 100.887 788.852 −104.846 Table 4. Numerical results of the variation in entropy in the normal extended space for different values of k with
$Q = 0.8, \;b = 0.8$ . -
In the extended phase space, taking pressure, volume, and Born-Infeld vacuum polarization into account, we found that the first law of black hole thermodynamics is valid for both single horizon and double horizon black holes, but the second law is violated for double horizon black holes and part of the single horizon black holes. In this section, we check the weak cosmic censorship conjecture in the extended phase space for the Born-Infeld-anti-de Sitter. We want to know whether the horizon of the black hole will shrink to the singularity. As in the normal phase space, we focus only on double horizon black holes given that the weak cosmic censorship conjecture is always valid for single horizon black holes under a charged particle adsorbtion.
As a charged particle is absorbed by the black hole, the mass M, charge Q, Born-Infeld parameter b, and AdS radius l change into
$ (M+{\rm d}M, \;Q+{\rm d}Q,\; b+{\rm d}b,\; l+{\rm d}l) $ . Correspondingly, the locations of the minimum value and event horizon will change into$ r_{m}\rightarrow r_{m}+{\rm d}r_{m} $ ,$ r_{+}\rightarrow r_{+}+{\rm d}r_{+} $ . There is also a transformation for$ f(r) $ , which is labeled as$ {\rm d}f_{m} $ . At the new minimum point, according to Eq. (35), we can obtain$ {\rm d}f'_{m} = \frac{\partial f'_{m}}{\partial M}{\rm d}M+\frac{\partial f'_{m}}{\partial Q}{\rm d}Q+\frac{\partial f'_{m}}{\partial l}{\rm d}l+\frac{\partial f'_{m}}{\partial r_{m}}{\rm d}r_{m}+\frac{\partial f'_{m}}{\partial b}{\rm d}r_{b} = 0. $

(57) In addition, at this location,
$ f(r) $ would change into$ \begin{aligned}[b] f|_{r = r_{m}+{\rm d}r_{m}} =& f_{m}+{\rm d}f_{m} = \delta+\left(\frac{\partial f_{m}}{\partial M}{\rm d}M+\frac{\partial f_{m}}{\partial Q}{\rm d}Q\right.\\&\left.+\frac{\partial f_{m}}{\partial l}{\rm d}l+\frac{\partial f_{m}}{\partial b}{\rm d}b\right), \end{aligned}$

(58) where we have used
$ f'_{m} = 0 $ in Eq. (58). The next step is to find the solution of Eq. (58). We will analyze the extremal black hole, for which the horizon is located at$ r_m $ . Therefore, Eq. (47) can be used.Based on the condition
$ f'_{m} = 0 $ , we obtain the concrete form of dM as$ {\rm d}M = \frac{\partial M}{\partial r_m}{\rm d}r_m +\frac{\partial M}{\partial Q}{\rm d}Q+\frac{\partial M}{\partial l}{\rm d}l+\frac{\partial M}{\partial b} {\rm d}b. $

(59) Substituting Eq. (59) into Eq. (47), we obtain
$ {\rm d}r_{m} = \frac{-4 b^2{\rm d}b l^3 r_m^4 \left(\sqrt{\dfrac{Q^2}{b^2 r_m^4}+1}-1\right)+2 b \left(r_m \sqrt{\dfrac{Q^2}{b^2 r_m^4}+1} \left(3 {\rm d}l r_m^3-l^3|P^r_+|\right)+{\rm d}Q l^3 Q\right)+2 {\rm d}b l^3 Q^2}{b l r_m \left(2 b k l^2 \sqrt{\dfrac{Q^2}{b^2 r_m^4}+1}+4 b^2 l^2 r_m^2 \left(\sqrt{\dfrac{Q^2}{b^2 r_m^4}+1}-1\right)+9 r_m^2 \sqrt{\dfrac{Q^2}{b^2 r_m^4}+1}\right)}. $

(60) In addition, substituting Eq. (59) into Eq. (57), we obtain
$ {\rm d}r_{m} = 0 $ . Then, with Eq. (60), we obtain$ {\rm d}l = \frac{l^3 \left(2 b^2 {\rm d}b r_m^4 \left(\sqrt{\dfrac{Q^2}{b^2 r_m^4}+1}-1\right)+b \left(|P^r_+| r_m \sqrt{\dfrac{Q^2}{b^2 r_m^4}+1}-{\rm d}Q Q\right)-{\rm d}b Q^2\right)}{3 b r_m^4 \sqrt{\dfrac{Q^2}{b^2 r_m^4}+1}}. $

(61) Similarly, by substituting Eq. (59) into Eq. (58), f can be expressed as a function of
$ {\rm d}Q, \;{\rm d}l, \;{\rm d}r_{m}, \;{\rm d}b $ . With the obtained results in Eqs. (60) and (61), Eq. (58) can be finally simplified as$ f_{m}+{\rm d}f_{m} = -\frac{2 |P^r_+|}{r_{m}}. $

(62) Equation (62) shows that, as a charged particle is absorbed by the black hole, there is a shift of
$ f_m $ in the negative direction. Consequently, there always exist horizons to hide the singularity of the spacetime. In particular, extremal black holes will change into non-extremal black holes. Our result is different from the result in [66], according to which black holes are stable and extremal black holes are always extremal black holes in the extended phase space. -
In Born-Infeld-anti-de Sitter black holes, we investigated the motion of a charged particle around the black hole and obtained the relation between the energy and momentum of the particle near the horizon. Furthermore, we investigated the laws of thermodynamics and weak cosmic censorship conjecture in the normal phase space and extended phase space. As expected, the first law as well as second law of the thermodynamics hold, and the weak cosmic censorship conjecture is not violated in the normal phase space. This is consistent with the previous conclusion that the charged black hole cannot be over-spinning as the backreaction is considered, even for the extremal black holes. In the extended phase space, since the cosmological constant and Born-Infeld parameters are not a variable in the action and equations of the motion, the dynamical effect is not easy to predict with the extensive quantities Y, b. As the charged particle is absorbed by the black hole, we obtained the variation in the horizon of the black holes and further the variation in entropy and volume. We found that
$ T {\rm d}S-Y{\rm d}V- b {\rm d}B = |P^r_+| $ . Therefore, the relation between the energy and momentum can be written as the first law of thermodynamics in the extended phase space. It was already demonstrated that satisfying the first law of thermodynamics is a necessary condition to ensure the fulfillment of the second law of thermodynamics under a particle absorption [13, 14] in the normal phase space. However, satisfying the first law does not mean the second law is satisfied. Therefore, we also discussed the second law in the extended phase space. We found that the second law was violated for the double horizon black holes and part of the single horizon black holes. The violation of the second law of thermodynamics can be related to the weak cosmic censorship conjecture which is related to the stability of the horizon. The stability can be shown from the change in the minimal value of the function$ f(r) $ under the absorption. We found that the variation in the minimal value of$ f(r) $ in the extended phase space was consistent with that in the normal phase space, which is$ - {2 |P^r_+|}/{r_{m}} $ . In particular, extremal black holes will change into non-extremal black holes. Our results show that the singularity will always be hidden behind the horizons, which implies that the weak cosmic censorship conjecture is valid in the extended phase space. This is different from the results in [66], according to which black holes were stable and extremal black holes would always be extremal black holes. However, our results are consistent with those in the normal phase space, that is, extremal black holes will change into non-extremal black holes [13, 14].For extremal black holes in the normal phase space, the variation in the entropy is infinite, which implies that the horizon is infinity as well, according to the entropy area relation. Consequently, the singularity will always be hidden, which is consistent with the results obtained by the weak cosmic censorship conjecture. For extremal black holes in the extended phase space, the variation in the entropy is negative, and the horizons of black holes will shrink. However, the weak cosmic censorship conjecture holds in this case. Therefore, the horizon cannot shrink to the singularity. It would be interesting to investigate whether there exists a minimum value of the horizon where the black hole stops shrinking.
-
Xiao-Xiong Zeng would like to thank Bogeun Gwak and Hongbao Zhang for their helpful discussions.
Thermodynamics and weak cosmic censorship conjecture in Born-Infeld-anti-de Sitter black holes
- Received Date: 2020-02-02
- Available Online: 2021-02-15
Abstract: In this study, we examine the laws of thermodynamics and the weak cosmic censorship conjecture in the normal and extended phase spaces of Born-Infeld-anti-de Sitter black holes by considering a charged particle absorption. In the normal phase space, the first and second laws of thermodynamics as well as the weak cosmic censorship are still valid. However, in the extended phase space, the second law of thermodynamics is violated for double-horizon black holes and part of single-horizon black holes. The first law of thermodynamics and the weak cosmic censorship conjecture are still valid for all types of black holes. In addition, we found that the shift of the metric function, which determines the locations of the horizons, takes the same form at the minimum point in both the normal and extended phase spaces, indicating that the weak cosmic censorship conjecture is independent of the thermodynamic phase space.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: