Modified regular black holes with time delay and 1-loop quantum correction

Before establishing a complete theory of quantum gravity, it is desirable to construct regular black hole solutions that are non-singular everywhere and characterized by finite Kretschmann scalar curvature to understand the final stage of stellar collapse and black hole evaporation [1-8]. In literature [9-22], such regular black holes have been constructed by heuristically considering the quantum effects of gravity, and they can be classified into two categories based on their asymptotical behavior at the central core, which becomes regular. The first category is regular black holes with asymptotically de-Sitter cores, which includes the well known Bardeen black hole [9], Hayward black hole [10], and Frolov black hole [11]. The second category is regular black holes with asymptotically Minkowski cores, originally proposed in [18], and developed further in [20-22]. Recently, in [23], we proposed an exponentially suppressing form of mass dependent gravitational potential, such that the Kretschmann scalar curvature is bounded above by the Planck mass density, regardless of the mass of the black hole. Furthermore, we established a one-to-one correspondence between regular black holes with Minkowski cores and de-Sitter cores. This correspondence provides a scheme to construct new regular black holes with dS core as well.

With the aim of constructing effective metrics describing the evolution of black holes and the collapse of matter stars without a central singularity, in this study, we further develop the regular black holes proposed in [23] based on the following considerations. Firstly, at the Planck scale, quantum gravity effects are sufficiently strong to change the quantum mechanical behavior of matter, which is usually reflected by the generalized uncertainty principle (GUP). It is well known that GUP provides a lower bound for the size of any quantum object, whose size should be larger than the minimal length at Planck scale. As a result, any quantum object with finite size placed in a curved spacetime must be affected by tidal gravitational forces. In [23], we presented an alternative point of view on this scenario. One can assume that quantum objects still obey the usual Heisenberg's uncertainty relation, implying that quantum theory holds, but introduce an effective gravitational field strength accounting for the effects of gravity on the quantum object. In this scenario, the black hole background will be modified to a metric characterized by an effective Newton's constant, leading to the regular black holes constructed in [23]. Specifically, the regular black holes in [23] were constructed by considering strong quantum gravity effects such as GUP. In this study, we hypothesize that the effective metric not only contains strong quantum gravity effects from the GUP, but also 1-loop quantum corrections to the Newtonian potential via an effective field theory [24, 25]. Secondly, we expect that the effective metric leads to time delay between an observer at the central core and another observer at infinity. This should be a more practical setup, since any clock in a gravitational potential well should be slowed down in comparison to a clock in an asymptotically flat region. A similar modification has been performed on the Hayward black hole in [26]. Here, we follow up and improve this strategy to general regular black holes with spherical symmetry. In particular, we compare the distinct behavior of the Kretschmann curvature for these two types of black holes.

This paper is organized as follows. In next section we will present the general metric for regular black holes with spherical symmetry, with the basic features of these regular black holes reviewed in the Appendix. Then, we focus on the mass dependent behavior of the Kretschmann curvature when 1-loop quantum correction and time delay are taken into account. Next, we propose a scheme to evaluate the maximum time delay at the center by scanning the mass of black holes such that the sub-Plackian features of the Kretschmann curvature are preserved during the evaporation process. Then, from section three to section five, we numerically demonstrate the dependent behavior of the Kretschmann curvature on sevaral parameters in different regular black holes. The distinct behaviors are compared for regular black holes with asymptotically Minkowski cores and those with asymptotically de-Sitter cores. In particular, we find that the Kretschmann curvature can always be sub-Planckian, irrespective of the mass of black holes. Finally, we propose a scheme to fix the time delay parameter in the conclusion and discussion section.

We consider a static spherically symmetric black hole with a general form of the metric

with

where $ \phi(r) $ is the gravitational potential. Generally, we introduce $ F(r) $ to include the strong quantum gravity effects that modify the singularity at the Planck scale, while $ G(r) $ accounts for the weak quantum gravity effects as well as the finite time delay between an observer at the center and one at infinity. Thus, we assume that $ G(r) $ is a regular function of the radius, while the position of the horizon $ r_h $ is solely determined by $ g^{rr} = F(r_h) = 0 $. With this ansatz, it is straightforward to derive the Kretschmann scalar curvature which has been included in Appendix A.

In this study, we consider a specifical modification of the regular black hole proposed in [23] by adopting the strategy presented in [26]. Thus, the gravitational potential $ \phi(r) $ and modified function $ G(r) $ are specified as

where α, β, and γ are dimensionless constants. We have also set $ l_p = M_p = 1 $ throughout the paper, which implies that to recover the correct dimensions of any physical quantity, $ l_p $ or $ m_p $ should be inserted appropriately. The above form of $ \phi(r) $ was originally proposed by us in [23]. When x and n are specified with $ n>x\geqslant 0 $ and $ n\geqslant 1 $, it produces several regular black holes with asymptotically Minkowski cores. With $ G(r) = 1 $, the sub-Planckian and and thermodynamical features of the Kretschmann curvature have been investigated in detail in [23].

The above form of $ G(r) $ was first proposed in [26], resulting in a modified Hayward black hole. Here, we adopt the same form to introduce the 1-loop quantum correction to the gravitational potential and a time delay between the center and infinity. It is evident that with $ G(r) = 1 $, the regular black hole proposed in Ref. [23] is recovered. Now, with non-trivial $ G(r) $, it is also straightforward to obtain the location of the outer horizon and the thermodynamics of the above modified black holes, which are presented in Appendix B and Appendix C, respectively. Here, we intend to demonstrate how a 1-loop quantum correction and time delay can be incorporated by the function $ G(r) $. For such modified regular black holes, the metric component $ g_{00} $ at large scale behaves as

Furthermore, the leading quantum correction to the Newtonian potential has been perturbatively computed, and the large scale behavior of gravitational potential takes the following form [24, 25]

where the leading term is described with a positive sign. In this paper, we require that $ n\geqslant x \geqslant n/3 $ and $ n\geqslant 2 $ such that Kretschmann curvature can be sub-Planckian, irrespective of the mass of the black holes, as analyzed in [23]. Therefore, the exponential form of the gravitational potential has no contribution to the 1-loop quantum correction, and we simply set $ \beta = 41/(5 \pi) $ to reproduce such a 1-loop quantum correction^①.

Next, we explain how time delay is incorporated by $ G(r) $ with the parameter γ. First, we note that the metric component $ g_{00} $ at the center remains time-like, which is in contrast to the standard Schwarzschild black hole. Thus, we may compare the times for two clocks placed at the center and infinity. Specifically, the time delay may be defined as $ (\delta t_{\infty}-\delta t_{0})/\delta t_{\infty} = $$ 1-\sqrt{|g_{00}(0)}| $ as proposed in [26]. Before introducing the function $ G(r) $, it is easy to see that $ F(r)\rightarrow 1 $ as $ r\rightarrow 0 $, which means there is no time delay between these two clocks. This is an unusual feature, since the distribution of matter generally leads to time delay effects during stellar or matter collapse. Therefore, we introduce a parameter γ with $ 1> \gamma \geqslant 0 $ in $ G(r) $ to generate a desired time delay at the center. It is evident as $ r\rightarrow 0 $, $ G(r)\rightarrow 1-\gamma $ and $ F(r)\rightarrow 1 $, and then, the time delay between two clocks at the center and infinity is measured by γ.

Now, we are concerned with the effects of $ G(r) $ on the Kretschmann scalar curvature. As demonstrated in [23] with $ G(r) = 1 $, if $ n\geqslant x \geqslant n/3 $ and $ n\geqslant 2 $, the Kretschmann curvature can be always sub-Planckian, because its maximal value $K_{\max}$ is inversely proportional to the black hole mass. The saturated case is reached at $ x = n/3 $, where the maximal value $K_{\max}$ is independent of the mass of black holes. Specially, when $ n = 2 $ and $ n = 3 $ regular black holes with asymptotically Minkowski cores correspond to the Bardeen black hole and Hayward black hole, respectively, in the sense that they have the same asymptotic behavior at large scales. Now, once the function $ G(r) $ is introduced, it should be noted that the maximal value of the Kretschmann curvature generally becomes a function of the mass M, and parameters α and γ, denoted as $K^{\max}(m,\alpha, \gamma)$. In particular, in this form as $ \gamma \rightarrow 1 $in this form, the metric component $ g_{tt} $ becomes vanishing, such that the Kretschmann scalar curvature can easily exceed the Planckian mass density, as demonstrated explicitly in the next sections. This behavior is not unexpected, and implies that an arbitrarily large time delay is not possible. This is quite reasonable from physical perspectives, because any time delay induced by the matter distribution should be finite. Therefore, with a given α, we intend to define a maximal value of γ that saturates the bound of the Kretschmann scalar curvature by scanning the black hole mass with $K^{\max}( \gamma_{\max}) = 1$ for a certain mass m. More importantly, we note that in the region $ n\geqslant x \geqslant n/3 $ and $ n\geqslant 2 $, this assumption always holds, because $K^{\max}$ will not increase with the mass M forever in this region, but becomes saturated at large M for black holes. This will be justified by the numerical analysis described in the next sections. Therefore, for a given α, we can obtain the maximum time delay $\gamma_{\max}$ such that given a γ under the condition $\gamma_{\max} > \gamma\geqslant 0$, the Kretschmann curvature is maintained at the sub-Planckian scale for all black hole masses. This behavior is expected, because once all the parameters are specified in Eq. (3), the sub-Planckian feature of K is preserved during the evaporation process, in which the black hole mass changes. Therefore, we numerically plot $\gamma_{\max}$ as a function of α for typical regular black holes in Fig. 1. It can be seen in the figure that $\gamma_{\max}$ increases rapidly with increasing α, and then becomes saturated as $\gamma_{\max}\rightarrow 1$. In particular, for a Bardeen black hole it approaches unity rapidly in the region with smaller α. However, for the black holes described below, we consider the time delay with $\gamma_{\max} > \gamma\geqslant 0$, such that the sub-Planckian feature is always guaranteed for the Kretschmann scalar curvature.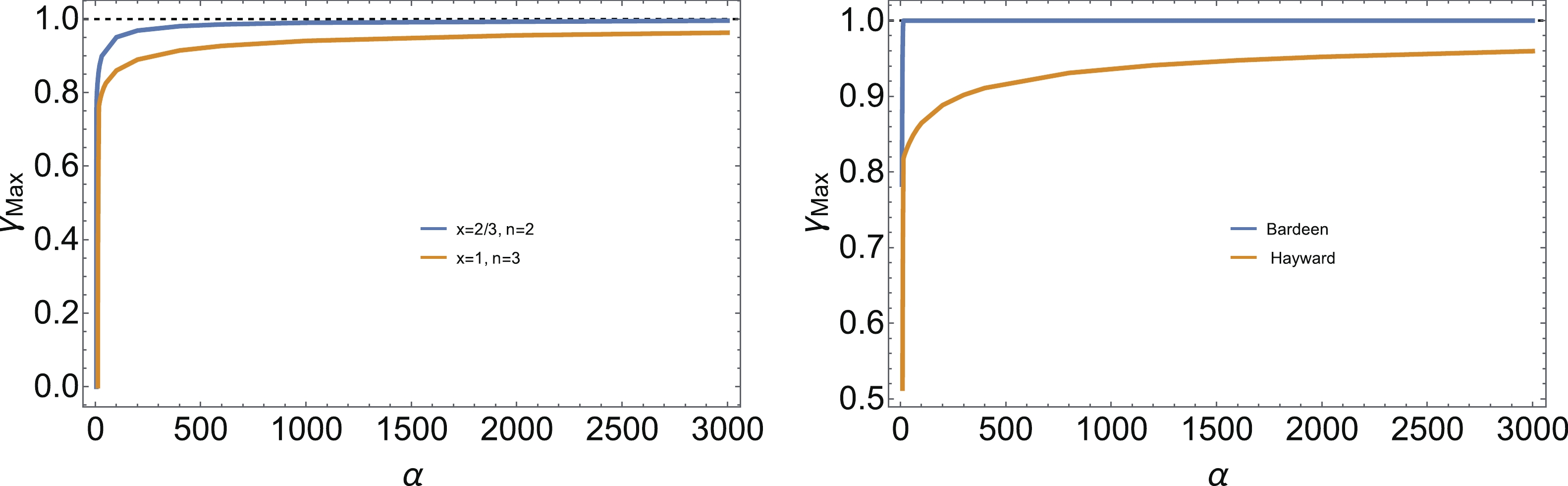

Figure 1.  (color online) $\gamma_{\max}$ as the function of α, which is defined as $K^{\max}( \gamma_{\max}) = 1$ and obtained by scanning the mass of black holes. The left plot is for the regular black holes with asymptotically Minkowski core while the right plot is for the regular black holes with asymptotically de-Sitter core.

We argue that our above treatment is a dramatic improvement in comparison with the scheme adoptedin [26], where the maximal value of γ is defined for a given mass. In the next sections, will show that for a given α and γ, the Kretschmann curvature is sub-Planckian at some large mass. However, this does not guarantee that it must be sub-Planckian at any mass, even if it becomes saturated in a large mass limit (which is generally true). On the contrary, the Kretschmann curvature may exceed the Planck scale easily when the mass decreases. For instance, in Fig. 6 of [26], which describes a modified Hayward black hole, K is sub-Planckian for $ M = 10^5 $. However, if the mass decreased with other parameters fixed, $K_{\max}$ can easily exceed unity. For instance, if $ M = 10^2 $, then $K_{\max}\simeq 6000$. In summary, the introduction of a $\gamma_{\max}$ independent of mass in this work enables specifying the parameter values such that the sub-Planckian feature of the Kretschmann curvature can be preserved during evaporation.

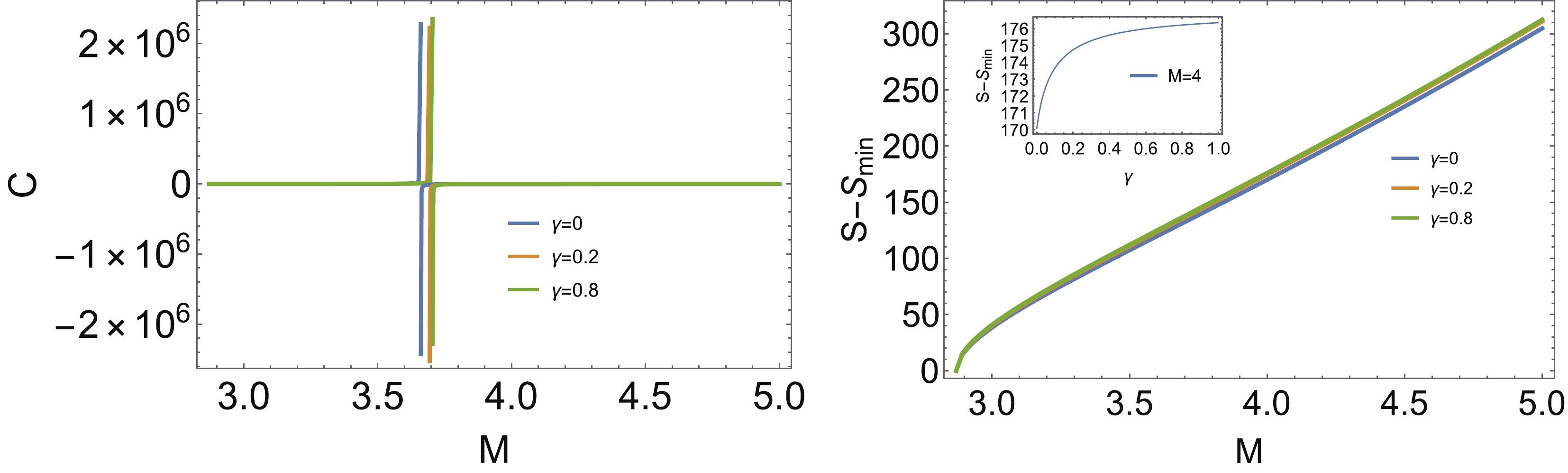
In this section, we describe the modified regular black hole with $ n = 2 $ and $ x = 1 $. The main features of this black hole with $ G(r) = 1 $ have been investigated in [23]. We note that the following features are maintained when the metric is modified by $ G(r) $. Firstly, the mass of the black hole is bounded by $ M \geqslant \dfrac{e \alpha}{2} $. In particular, when this bound is saturated, the black hole is characterized by the minimal radius $ r_h = \sqrt{e}\alpha_0 $, which may be treated as the remnant of the black hole evaporation, since the final stage of the black hole is characterized by $ M\rightarrow \dfrac{e \alpha_{0}}{2} $ (or $ r_h\rightarrow\sqrt{e}\alpha_0 $). This effect results from the exponential suppressing potential, and is controlled by the parameter α. In this limit, the Hawking temperature is always vanishing, even when 1-loop quantum correction and time delay are incorporated, as shown in Fig. 2. It can be seen that the maximal value of the temperature decreases with increasing γ. In addition, based on the equations in Appendix C, we plot the heat capacity and entropy as functions of the black hole mass. When the temperature reaches the maximal value, the heat capacity becomes divergent, as shown in Fig. 3. This means the black hole undergoes a transition from a system with negative heat capacity to a system with positive heat capacity during evaporation. Since the black hole has a remnant with the minimal mass with entropy $S_{\min}$, we also plot the entropy difference between the black hole with arbitrary mass and one with the minimal mass, as shownin Fig. 3. It is found that the entropy difference decreases monotonically with decreasing M, but does not change much with changing γ. The inset of Fig. 3 shows that the entropy increases slightly with increasing γ for a given mass.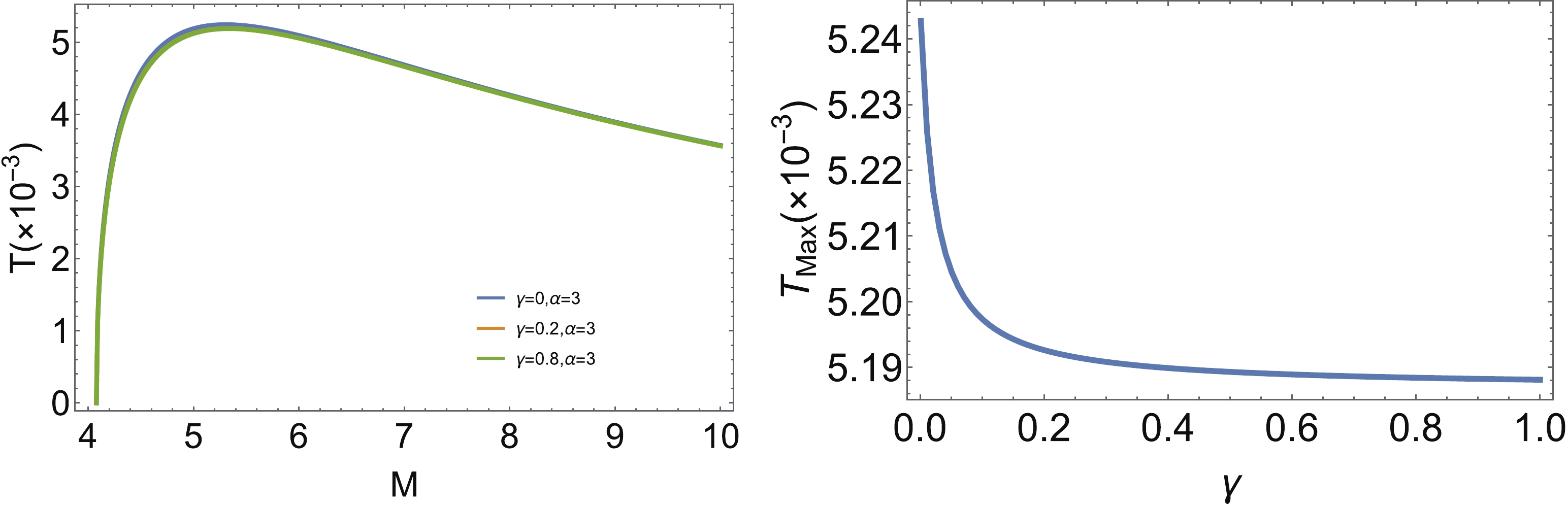

Figure 2.  (color online) Left: The temperature as the function of M. Right: The maximum value of temperature as the function of γ.

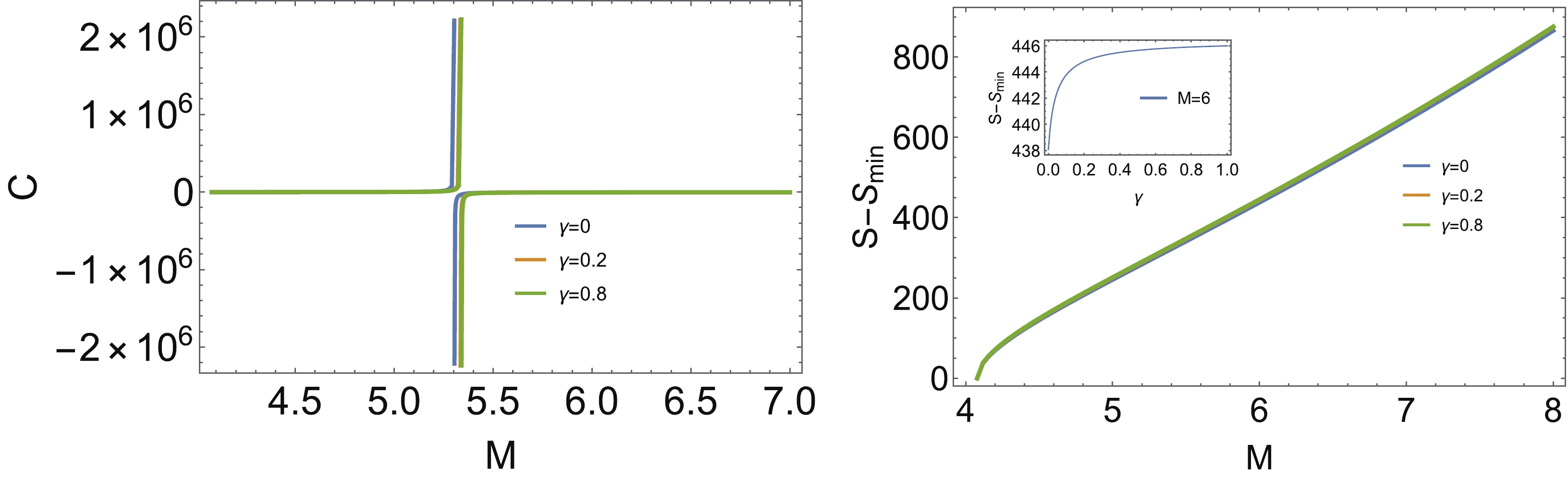
Figure 3.  (color online) Left: The heat capacity as the function of M. Right: The entropy as the function of M, while the inset shows the entropy as the function of γ with a given mass.

Secondly, these exists a minimal value for α at the Planck scale $\alpha_{\min}\simeq 2.747$, such that $K^{\max}(\alpha_{\min}) = 1$. When 1-loop quantum correction and time delay are incorporated, we find $\alpha_{\min}$ does not change. For $\alpha\geqslant \alpha_{\min}$, we may plot the Kretschmann curvature K as a function of the radial coordinate r, as shown in Fig. 4. In general, the maximal value of K appears at some position in space, and we denote it as $K_{\max}$. As in the case for $ G(r) = 1 $, we find that $ K(0) = 0 $ always, but the location of $K_{\max}$ moves to the right side with increasing M. We plot $K_{\max}$ as afunction of γ in the right plot of Fig. 4, indicating that it increases monotonously with the parameter γ once α is fixed. Therefore, we need to define a $\gamma_{\max}$ to preserve the ub-Planckian Kretschmann curvature.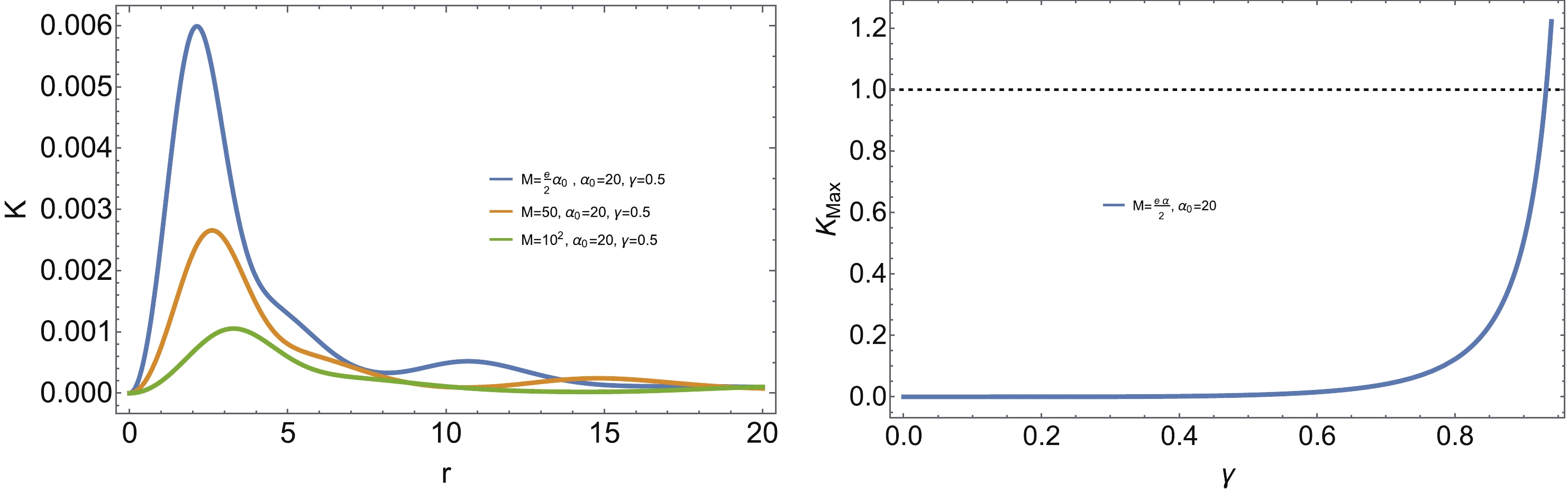

Figure 4.  (color online) Left: The Kretschmann scalar curvature K as the function of the radial coordinate r with $ \gamma = 0.5 $. Right: The maximum value of the Kretschmann scalar curvature K as the function of γ.

Finally, we illustrate the mass dependent behavior of $K_{\max}$ in Fig. 5. For $ G(r) = 1 $, we have demonstrated in [1] that $K_{\max}\propto 1/M$, such that the black hole with the minimal mass is described by the maximal $K_{\max}$. When $ G(r) $ is included, it can be seen in this figure that $K_{\max}$ mantains a linear relation with the logarithm of the mass, thus decaying with increasing mass. The main difference is that the value of $K_{\max}$ is increased due to the presence of γ.

Figure 5.  (color online) The maximum value of the Kretschmann scalar curvature K as the function of M.

In this section, we describe the modified regular black hole with $ n = 2 $ and $ x = 2/3 $, which corresponds to a Bardeen black hole at large scales. The gravitational potential $ \phi(r) $ of a Bardeen black hole is given as

It can be verified that these two black holes have the same expansion behavior for large radius. Nevertheless, they have distinct behavior near the central core. The former has an asymptotically Minkowski core, while Bardeen black hole has a de-Sitter core.

Similarly, we note that for the regular black hole with $ x = 2/3, \ n = 2 $, the mass is bounded by $M \geqslant $$ \left(\dfrac{e}{2}\right)^{3 / 4} \alpha^{3 /4}$, which is solely determined by the exponentially suppressing potential controlled by the parameter α. Thus, the presence of $ G(r) $ does not affect black hole evaporation significantly, and black hole remnants maintain the final stage. Again, α has the minimal value $\alpha_{\min} \simeq 0.875$, which is defined by $K_{\max}(\alpha_{\min}) = 1$ with $ \gamma = 0 $. However, for the Bardeen black hole, it is worth noting that $M \geqslant \left(\dfrac{9 \alpha }{4}\right)^3$, indicating that $M_{\min}$ increases with $ \alpha^3 $. Thus, $M_{\min}$ grows rapidly with $ \alpha>1 $. This behavior is in contrast with the other regular black holes described in this paper.

Now, we compare the Kretschmann scalar curvature K as a function of the radius r for these two black holes. In Fig. 6, we plot the Kretschmann curvature $ K(r) $ for $ \gamma = 0.5 $, which is much smaller than $\gamma_{\max}$. One finds $ K(0) = 0 $ for black holes with $ x = 2/3 $ and $ n = 2 $, while $K(0) = K_{\max}$ for Bardeen black holes, irrespective of the black hole mass . However, for γ close to $\gamma_{\max}$, for instance $ \gamma = 0.8 $, as illustrated in Fig. 7, the maximal value of K deviates from the center for the Bardeen black hole.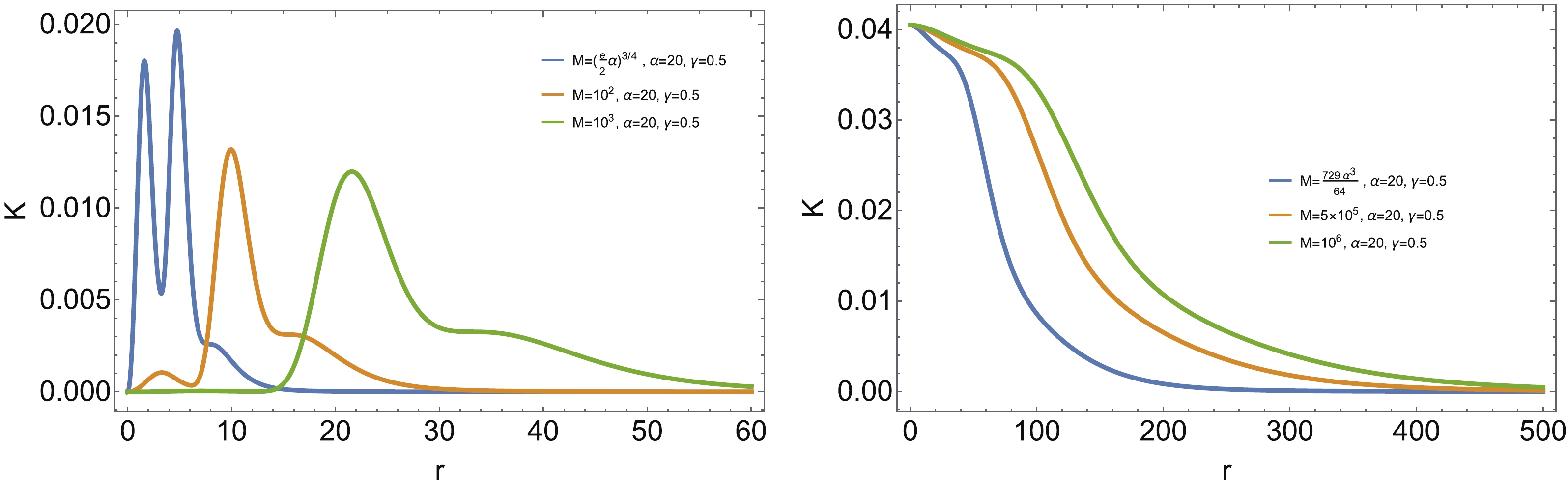

Figure 6.  (color online) Kretschmann curvature K as the function of the radial coordinate r for $ \gamma = 0.5 $. The left plot is for the regular black hole with $ x = 2/3, \ n = 2 $, while the right plot is for Bardeen black hole.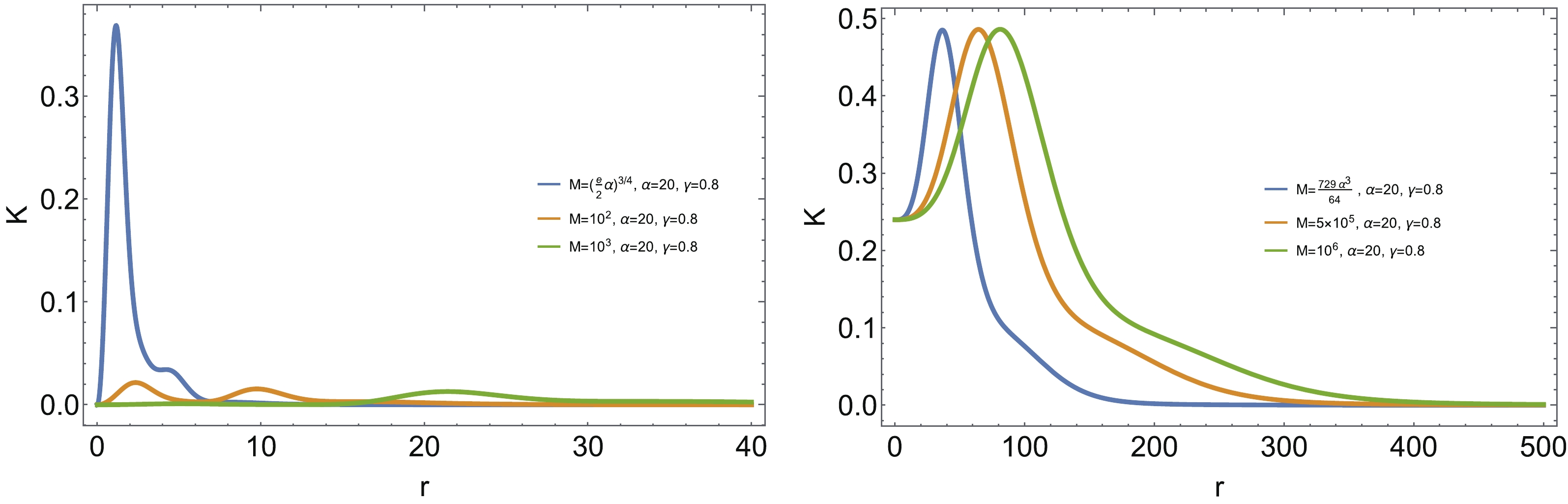

Figure 7.  (color online) Kretschmann curvature K as the function of the radial coordinate r for $ \gamma = 0.8 $. The left plot is for the regular black hole with $ n = 2, \ x = 2/3 $, while the right plot is for Bardeen black hole.

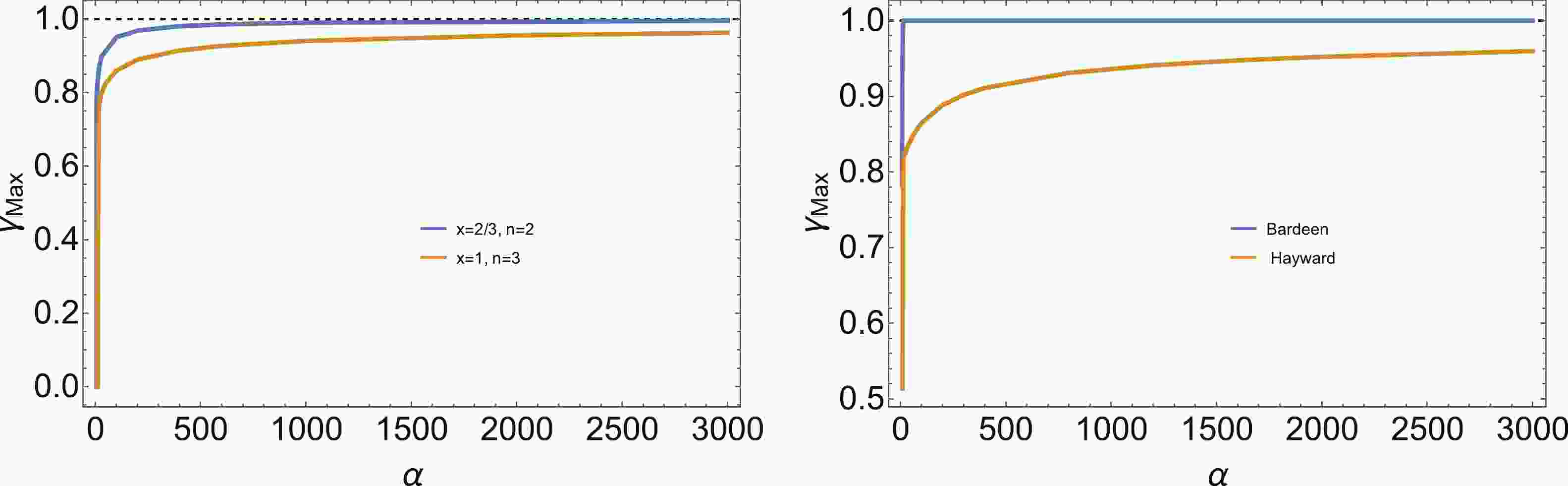
Next, we focus on the mass dependent behavior of $K_{\max}$ for these two black holes. It has been shown in [23] that when $ G(r) = 1 $, both black holes are characterized by the fact that $K_{\max}$ is independent of the black hole mass. However, when $ G(r) $ is included, we find that this feature does not hold anymore. This can be anticipated considering the fact that an arbitrarily large time delay renders the metric singular again. Therefore, in this case, we demonstrate the mass dependent behavior of $K_{\max}$ for different values of γ in Fig. 8. First, when $ G(r) = 1 $, i.e.,$ \gamma = 0 $, $K_{\max}$ is a constant (see the left plot of Fig. 8), while with increasing γ, we note that $K_{\max}$ becomes larger and mass dependent. In particular, it is observed that as γ approaches $ \gamma_{\max} $, $ K_{\max} $ with small masses becomes larger, and this phenomenon is observed for the black hole with $ x = 2/3, \ n = 2 $ and for the Bardeen black hole, as illustrated in Fig. 8 ($ \gamma = 0.4 $ in the left plot while $ \gamma = 1-3\times 10^{-5} $ in the right plot). Thus, $ K_{\max} $ with small masses always approaches unity at first, and determines the value of $\gamma_{\max}$ when scanning the mass of black holes. This tendency also makes it more difficult to figure out $\gamma_{\max}$ by scanning the mass of black holes, as shown in Fig. 1. Moreover, $K_{\max}$ always becomes saturated in the large mass limit. This feature is important in selecting $ \gamma_{\max} $ to preserve the sub-Planckian features of $ K_{\max} $. In addition, the mass dependent behavior of $ K_{\max} $ in Bardeen black holes does not change significantly until $ \gamma\rightarrow \gamma_{\max} $, and the mass scale is much larger than that for the black hole with $ x = 2/3, \ n = 2 $, which indicates that $M_{\min}\propto \alpha^3$, since we have set $ \alpha = 20 $.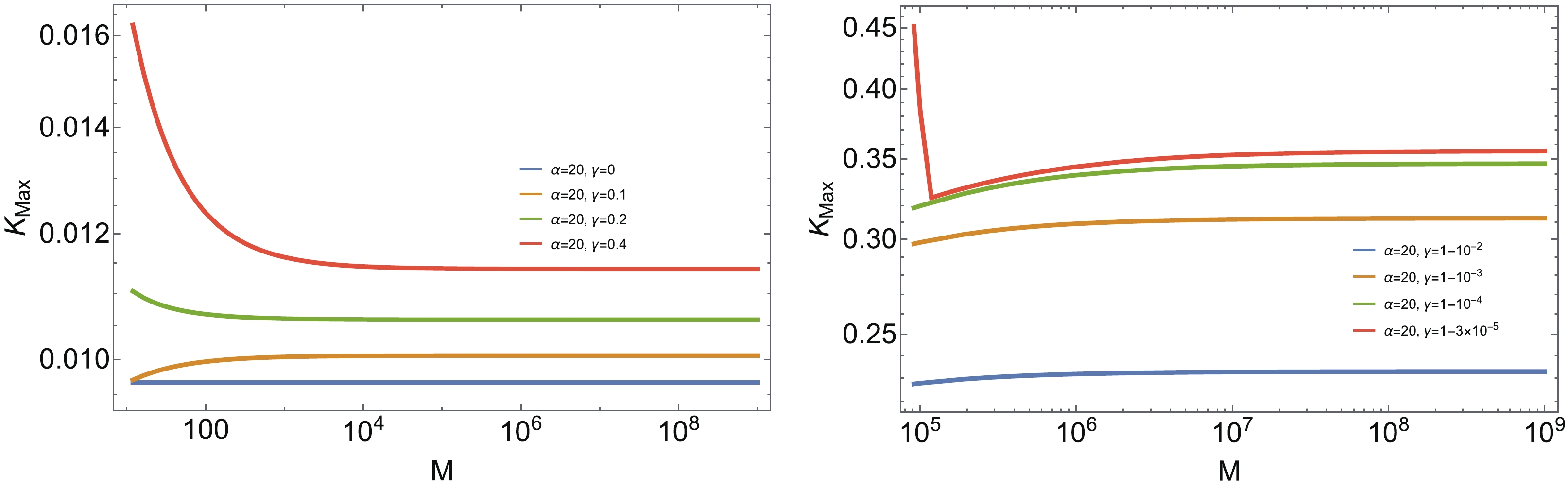

Figure 8.  (color online) The maximum value of Kretschmann curvature $K_{\max}$ as the function of M for the black hole with $ n = 2, \ x = 2/3 $ (left) and Bardeen black hole (right).

Finally, the thermodynamical behavior of the black hole is illustrated in Fig. 9 and Fig. 10. We find that the maximal value of the Hawking temperature decreases slightly with increasing γ, while the entropy increases slightly with increasing γ.

Figure 9.  (color online) Left: The temperature as the functions of M. Right: The maximum value of temperature as the functions of γ.

Figure 10.  (color online) Left: The heat capacity as the function of M. Right: The entropy as the function of M, while the inset shows the entropy as the function of γ with a given mass.

In this section, we describe the modified regular black hole with $ n = 3 $ and $ x = 1 $, which corresponds to a Hayward black hole at large scales. The gravitational potential for a Hayward black hole is given by

We plot the Kretschmann curvature K as a function of the radial coordinate r in Fig. 11, where $ M = \dfrac{1}{2} \sqrt{\dfrac{3 e \alpha}{2}} $ is the minimal value allowed for the regular black hole with $ x = 1 $ and $ n = 3 $, while $ M = \dfrac{3}{4} \sqrt{\dfrac{3 \alpha}{2}} $ is the minimal value allowed for the Hayward black hole. It is found that $K_{\max}$ moves to the right with larger radius as the mass increases for the black hole with $ x = 1 $ and $ n = 3 $, while for the Bardeen black hole $K_{\max}$ deviates from the center.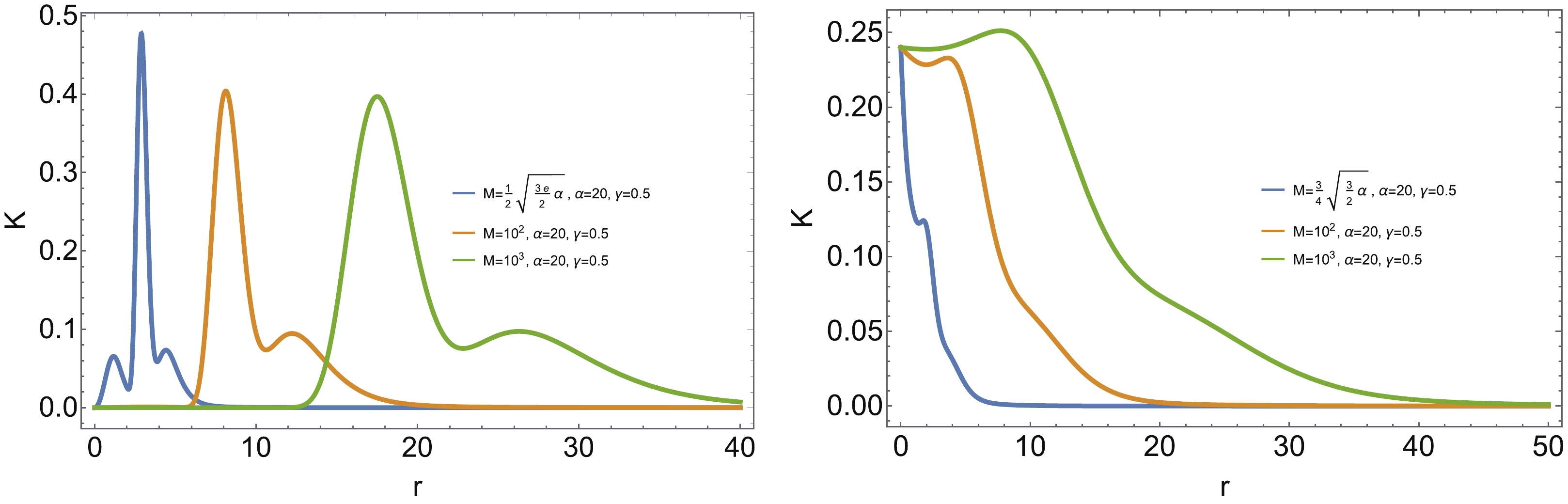

Figure 11.  (color online) The Kretschmann scalar curvature K as the functions of the radial coordinate r. The left plot is for the regular black hole with $ n = 3, \ x = 1 $, while the right plot is for Hayward black hole.

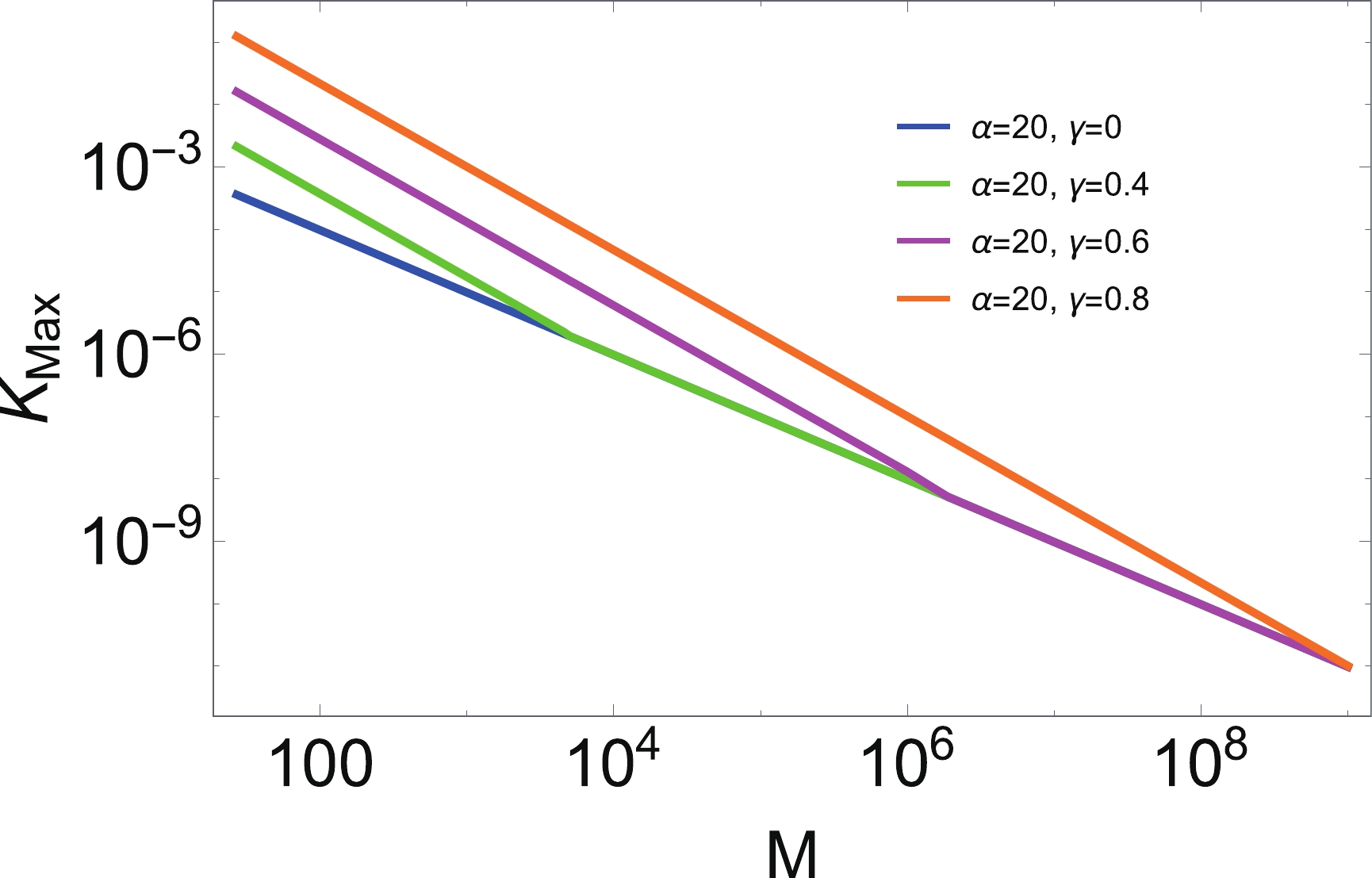
Next, we focus on the mass dependent behavior of $K_{\max}$. We plot $ K_{\max} $ as a function of M for both black holes, as illustrated in Fig. 12. The phenomenon is similar to that described in the previous section. This figure explicitly exhibits that $ K_{\max} $ does not depend on the mass of black holes when $ \gamma = 0 $, as expected. However, when the time delay parameter γ is included, for instance $ \gamma = 0.2 $ in the left plot and $ \gamma = 0.6, 0.7 $ in the right plot, we find $ K_{\max} $ increases with the mass and becomes saturated in the large mass limit. On increasing γ further, $ K_{\max} $ becomes larger on the side with small masses, for instance when $ \gamma = 0.3,0.4 $ in the left plot and $ \gamma = 0.8 $ in the right plot. In this situation, $ K_{\max} $ decreases with the mass and then becomes saturated in the large mass limit.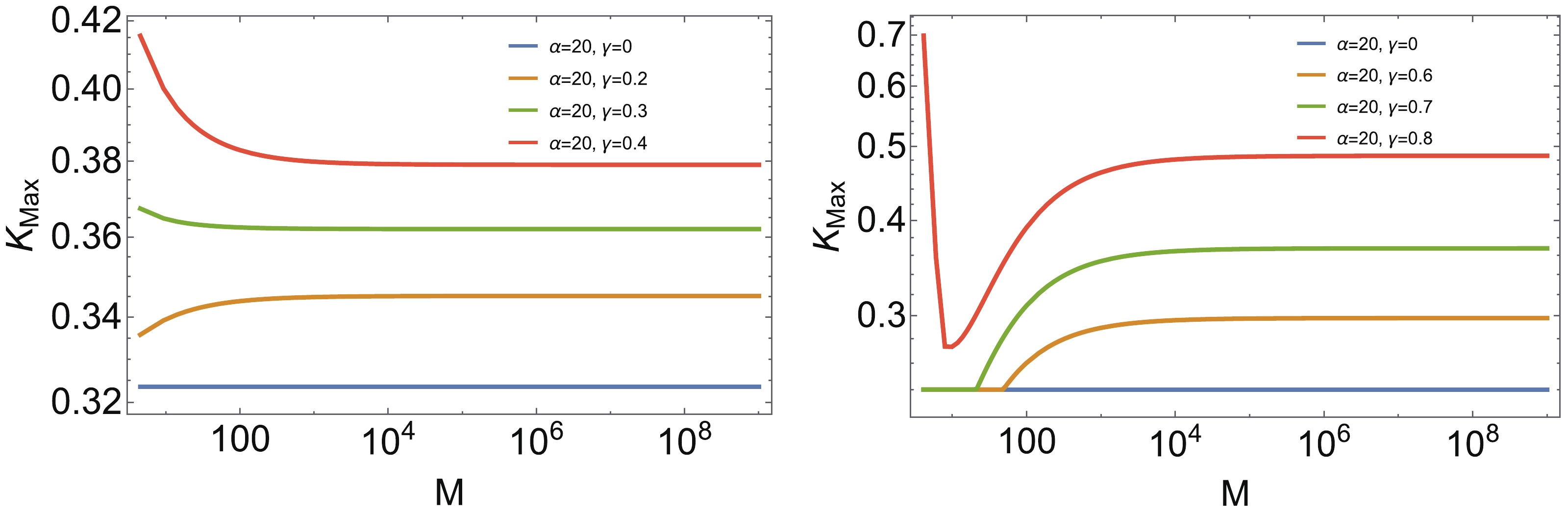

Figure 12.  (color online) The maximum value of the Kretschmann scalar curvature K as the function of M for $ n = 3, \ x = 1 $(left) and Hayward black hole(right).

Finally, we remark that the thermodynamical behavior of this modified regular black hole is similar to those described in previous sections. The maximal value of the Hawking temperature becomes slightly smaller with increasing γ, while the entropy becomes increases slightly with increasing γ.

In this study, we developed the regular black holes recently proposed in [1] by incorporating the 1-loop quantum correction to the gravitational potential and a time delay between an observer at the center and one at infinity. Our analysis covers two types of black holes. One is featured by an asymptotically Minkowski core, while the other is featured by an asymptotically de-Sitter core. We have proposed a scheme to determine the maximal time delay at the center by scanning the mass of the black holes such that the sub-Planckian feature of the Kretschmann curvature is preserved for black holes during the evaporation process. This improved the strategy presented in [26] significantly, where the maximal time delay is considered for a given mass in the context of a modified Hayward black hole. Therefore, such effective metrics may be more appropriate to describe the evolution of Planck stars or the evaporation of black holes. We have also compared the distinct behavior of the Kretschmann curvature for these two types of black holes. In general, we have found that the mass dependent behavior of $K_{\max}$ becomes complicated when the 1-loop quantum correction and time delay are taken into account. Nevertheless, it is still plausible to define a modified regular black hole with sub-Planckian curvature irrespective of the mass, owing to the saturating behavior of $K_{\max}$ in the large mass limit.

Next, it should be noted that the form of $ G(r) $ adopted in this paper is not unique. One may consider other forms of $ G(r) $, for instance, $G(r) = 1-\gamma+\gamma {\rm e}^{\frac{-\beta M}{\gamma r^3}}$ as proposed in [27], to introduce 1-loop quantum correction and time delay, and similar results may be obtained. More importantly, we may further improve the form of effective metric to describe stellar collapse or black holes more accurately. One prominent issue in all previous papers is that one just introduces the time delay by hand, since γ is introduced as a free parameter. A more realistic setup would be when the time delay is fixed to a specific value by the distribution of matter surrounding the center. At the phenomenological level, it implies that γ could be determined by other parameters or quantities. For instance, we could assume that $\gamma = 1-(\alpha_{\min}/\alpha)^{1/n}$ or $\gamma = 1-(\alpha_{\min}/\alpha)^{1/(n-1)}$; then, we remarkably find that this value is always smaller than $\gamma_{\max}$ for arbitrary value of α, such that a sub-Planckian Kretschmann scalar curvature is always guaranteed. We expect that this conjecture can be justified by more detailed investigations in future.

Finally, we have strictly considered regular black holes with spherical symmetry. We expect the proposed construction may be extended to rotating black holes, as demonstrated previously for Hayward black holes in [17, 27].

We are very grateful to Dr. Hong Guo and Prof. Xiang Li for helpful discussions.

For the ansatz in Eq. (1), it is straightforward to derive the Kretschmann scalar curvature as

Furthermore, if we consider that $ G(r) $ only affects the time delay at the center without changing the asymptotical behavior, it is reasonable to require that $ G'(0) = G''(0) = 0 $. Then, as $ r\rightarrow 0 $, we find that the Kretschmann scalar curvature behaves as

Remarkably, we find that the function $ G(r) $ would not change the value of the Kretschmann scalar curvature at the center under the condition $ G'(0) = G''(0) = 0 $.

In this section, we derive the location of the outer horizon for the modified regular black hole, where the metric components are specified by Eq. (3). First, we notice that the location of the outer horizon is not affected by $ G(r) $, and it is solely determined by $ F(r_h) = 0 $, which yields the relationship between $ r_h $ and M:

We rewrite the radius of the horizon $ r_h $ as

where

is the Lambert-W function with $ W(\theta)\geqslant -1 $. A real W requires $ \theta \geqslant -e^{-1} $, and thus, the mass of modified regular black hole is bounded by

For the modified black holes with non-trivial $ G(r) $, the black hole temperature and luminosity are respectively given by

Using Eqs. (11) and (14), the heat capacity can be derived as

Moreover, according to the first law of black hole thermodynamics, the entropy of the modified black hole is given by

Generally, due to the correction of the Hawking temperature, it is well known that the entropy of the modified black holes will deviate from the area law, and include higher order corrections. For instance, for the Hayward black hole in [28], the integrated form of the entropy can be expanded as

For the Bardeen black hole in [29], the integrated form of the entropy is given by

For the regular black hole in [18], the integrated form of the entropy can be written as

For the black hole discussed in this paper, such expansions become very complicated and we just present the numerical results in the main body of the text.