Production of $ {\boldsymbol{d}_{\boldsymbol{N\Omega}}} $ dibaryon in kaon induced reactions

In a strict sense, a dibaryon is a type of particle with baryon number $ B=2 $, which is composed of six quarks, typically two baryons. As a typical dibaryon, a deuteron consists of one proton and one neutron with a binding energy of $ 2.22 $ MeV. With the development of experimental techniques and the accumulation of experimental data, searching for dibaryon states other than the deuteron, composed of various baryons, has become an intriguing topic in hadron physics in recent decades.

The theoretical investigations of the dibaryon date back to 1964, when the dibaryon states were studied by Dyson and Xuong [1] with the SU(6) theory. Then, in 1977, Jaffe predicted the existence of the H and $ H^* $ particles with strangeness $ S= -2 $, which could be the bound state of $ \Lambda \Lambda $ and $ \Sigma \Sigma $, respectively. The investigations on two different quark models indicated that there should exist dibaryon states with strangeness of $ -3 $ [2] and stable for strong decay [2]. Later, the mass spectrum of low-lying dibaryons with strangeness of –1 were evaluated in the quark model [3]. Furthermore, some other models were extended to study the dibaryons, for example, the quark-cluster [4], Skyrme [5], quark potential [6], chiral SU(3) quark [7], quark delocalization and color screening [8–12], and realistic phenomenological nucleon-nucleon interaction [13, 14] models. In these models, a series of dibaryon states were investigated, such as the nonstrange dibaryon $ d^{\ast} $ with $ I(J^P)=0(3^+) $ and dibaryons composed of $ N\Xi^\prime $, $ N\Xi_{c} $, $ N\Xi_{cc} $, $ \Xi_{cc} \Xi_{cc} $ [13, 14], $ N\Omega $, and $ \Delta \Omega $ [15].

On the experimental side, the first breakthrough was the observation of $ d^\ast(2380) $, which was first observed in the cross sections for $ np \to d \pi \pi $ by the CELSIUS/WASA Collaboration in 2009 [16]. The discovery of $ d^\ast(2380) $ by the CELSIUS/WASA Collaboration encouraged the experimentists to search $ d^\ast(2380) $in more processes. With much better statistics and precision data samples, the WASA-at-COSY Collaboration found that the observed angular distributions for the deuterons and pions of the $ np \to d\pi^0 \pi^0 $ process in the center-of-mass system clearly preferred $ J=3 $ [17, 18] for $ d^\ast(2380) $, and then the $ I(J^{P}) $ quantum numbers were determined to be $ 0(3^+) $. Later on, the properties of $ d^\ast(2380) $ were investigated in various unpolarized $ np $ collision processes with more precise data samples, for example, $ np\rightarrow np \pi^0\pi^0 $, $ np\rightarrow pp\pi^0\pi^- $, $ np\rightarrow d \pi^0\pi^0 $ [19–21], and the polarized $ np $ scattering process [22].

The experimental observations of $ d^\ast(2380) $ attracted a significant interest in the exploration of its properties [23–30]. However, some dissenting opinions have been expressed. For example, in Refs. [31, 32], the authors claimed that the peak structure should be tied to a triangle singularity in the last step of the reaction. In any case, the experimental breakthrough has stimulate the interest of theorists in dibaryons states. Some dibaryon systems have been investigated in various models. For example, in a three-body hadronic model, the authors in Ref. [33] calculated the $ N\Delta $ and $ \Delta \Delta $ dibaryon states. In a pion exchange potential model, the H-like $ \Lambda_{c}\Lambda_{c} $ [34] and $ \Lambda_c N $ [35] dibaryons were researched. The possible $ \Lambda_{c}\Lambda_{c}/\Lambda_{b}\Lambda_{b} $ [36] and $ N\Sigma_{c,b} $ [37] dibaryon states were studied in the quark delocalization color screening model, and the possible $ \Delta^0\Delta^0 $, $ \Omega\Omega $, and $ \Xi\Xi $ dibaryons were investigated in Refs. [38–42].

As for the dibaryon states with strangeness $ S=-3 $, the possibilities of the existence of such type of dibaryons have been evaluated with various models. For example, the estimations in Ref. [43] indicated that there might exist two bound states, $ N\Omega $ and $ \Delta\Omega $ dibaryons, respectively, and in Ref. [15], the authors found that $ N\Omega $ and $ \Delta \Omega $ were weakly bound systems in the chiral quark model. The QCD sum rule estimations in Ref. [44] indicated that the $ N\Omega $ dibaryon with $ J^P=2^+ $ was stable for strong decay. In Ref. [45], the HAL QCD Collaboration calculated the $ N\Omega $ potential in $ 2+1 $ flavor Lattice QCD, and one bound state with binding energy of approximately 20 MeV was found. In 2019, the HAL QCD Collaboration updated their estimations of Ref. [45] near the physical point and they found that the binding energy of $ p\Omega(^5S_2) $ became $ 2.46(0.34)(^{+0.04}_{-0.11}) $ MeV. Stimulated by the most recent Lattice QCD estimations, the authors in Ref. [46] estimated the productions of Ω-dibaryons by utilizing a dynamical coalescence mechanism for the relativistic heavy-ion collisions, and the strong decays of $ d_{N\Omega} $ into conventional hadrons were evaluated [47].

Actually, experimentally producing the $ d_{N\Omega} $ dibaryon is the first step for investigating its properties. Thus, searching $ d_{N\Omega} $ experimentally becomes a pressing task. The key point of producing the $ d_{N\Omega} $ dibaryon is the production of the Ω baryon. In the high energy heavy-ion collision or $ pp $ collision processes, a large quantity of quarks with different flavors can be produced, where three strange quarks have a chance to form a Ω baryon and produce a $ d_{N\Omega} $ dibaryon by interacting with a nucleon. In 2018, the STAR Collaboration at RIHC investigated the proton-Ω interaction by measuring the corresponding correlation function in heavy-ion collisions at $ \sqrt{s_{NN}}=200 $ GeV [48]. By comparing the measured correlation ratio with the theoretical calculations, they concluded that the measurements slightly favored a proton-Ω bound system with a binding energy of $ \; 27 $ MeV [48]. Similarly, the ALICE Collaboration also proposed to investigate the strong interaction among hadrons, including proton-Ω, by using the ultrarelativistic proton-proton collisions at the LHC [49].

Besides the high energy heavy-ion collision and $ pp $ collision processes, the Ω baryon can be produced by kaon induced reactions as there is already a strange quark in the kaon. In Ref. [50], a project of extension of the Hadron Experimental Facility at J-PARC was proposed. By utilizing the secondary kaon beam with a typical momentum of approximately 3 GeV, the Ω baryon can be produced via the $ K^- p \to \Omega^- K^+ \bar{K}^{(\ast)0} $ reaction, and then, the $ d_{N\Omega} $ dibaryon can be investigated in the invariant mass spectrum of $ \Xi^- \Lambda $ of the $ \Omega^- d \to \Xi^- \Lambda p $ process.

In addition to the secondary kaon beam at J-PARC [51], high energy kaon beams with high quality are also available at COMPASS [52], OKA@U-70 [53], and SPS@CERN [54]. These high energy beams, especially those with momentum of approximately 10 GeV, may provide us another approach to directly produce $ d_{N\Omega} $ via the reaction $ K^- p \to d_{N\Omega}\bar{\Xi}^0 $, and then the $ d_{N\Omega} $ dibaryon can decay into $ \Xi \Lambda $ and $ \Xi \Sigma $. Thus, one can detect $ d_{N\Omega} $ in the $ \Xi\Lambda $ and $ \Xi\Sigma $ invariant mass spectra of the $ K^- p \to \bar{\Xi}^0 \Xi \Lambda $ and $ K^- p \to \bar{\Xi}^0 \Xi \Sigma $ processes, respectively. In the present work, we evaluated the possibility of observing the $ d_{N\Omega} $ dibaryon in these processes by estimating their cross sections.

This paper is organized as follows. After the introduction, the mechanism of $ d_{N\Omega} $ production in kaon induced reactions is presented. In Section III, the cross sections for the $ K^- p \rightarrow d_{N\Omega} \bar{\Xi}^0 $, $ K^- p \rightarrow \Xi^0\Lambda \bar{\Xi}^0 $, and $ K^- p \rightarrow \Xi^-\Sigma^+\bar{\Xi}^0 $ processes are presented, and the last section is devoted to a short summary.

In the present work, we consider that the $ d_{N\Omega} $ is a dibaryon composed of N and Ω with the $ J(J^P)=\frac{1}{2}(2^+) $, i.e., $ |d_{N\Omega}^0\rangle=|p\Omega\rangle $ and $ |d_{N\Omega}^-\langle=|n\Omega\rangle $. The dibayon $ d_{N\Omega} $ can be produced in the high energy $ K^-p $ interaction process. As indicated in Ref. [47], the dibaryon $ d_{N\Omega} $ could decay into $ \Lambda \Xi^0 $, which indicates the strong coupling between $ d_{N\Omega} $ and $ \Lambda \Xi^0 $. Thus, there exist the s channel contributions to $ K^-p\to \bar{\Xi}^0 d_{N\Omega} $, as shown in Fig. 1(a), where the initial $ K^- p $ and final $ d_{N\Omega} \bar{\Xi}^0 $ are connected by Λ. Moreover, there are contributions from the Ω baryon exchange process, which should be the u channel contribution in the strict sense. In the $ K^-p\to \bar{\Xi}^0 d_{N\Omega} $ process, there is no t channel diagram in the tree level. Empirically, in the high energy $ K^-p/\pi p $ scattering process, the contributions from the s channels are strongly suppressed [55–58]. Thus, the $ d_{N\Omega} $ production in the high energy $ K^-p $ scattering should occur dominantly by exchanging a Ω baryon as presented in Fig. 1(b), while the s channel contribution is ignored.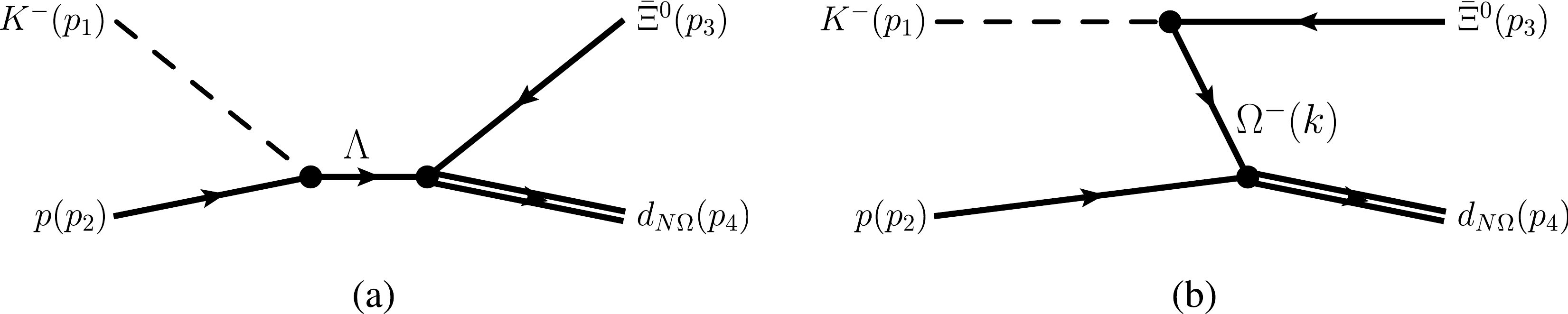

Figure 1.  (color online) Diagrams contributing to the process of $ K^-p \to d_{N\Omega}\bar{\Xi}^0 $, where the $ d_{N\Omega} $ is considered as a S-wave $ N\Omega $ dibaryon with $ J^P=2^+ $.

In the present work, we estimated the cross sections for $ K^-p \to d_{N\Omega} \bar{\Xi} $ in an effective Lagrangian approach. The interaction of the $ d_{N\Omega} $ dibayon and its components can be described as follows [47]:

where $ N^c=C\bar{N}^{T} $, $ \bar{N}^c=N^TC $, and $C= {\rm i} \gamma^2\gamma^0$ is the charge-conjugation matrix. T is the transpose transformation operator. From the above effective Lagrangian, the tensor field of $ d_{N\Omega} $ can be constructed by the appropriate combination of a Dirac field for the nucleon and a Rarita Schwinger field for Ω. The polarization tensor $ \epsilon^{\mu\nu}(\vec{p},\lambda) $ could be constructed by the combination of the Dirac field for spin-$ 1/2 $ and a Rarita Schwinger field for spin-$ 3/2 $, i.e,

with $ \lambda=(\pm2, \pm 1,0) $, $ \alpha=(\pm 3/2, \pm 1/2) $, and $ \beta=\pm 1/2 $, respectively. The polarization tensor satisfies

The effective Lagrangian for the $ \Omega \Xi K $ interaction reads [59–64]

With the above effective Lagrangians, we can obtain the amplitude corresponding to Fig. 1(b), which is

with $ S(k,m_{\Omega})_{\mu\beta} $ to be the propagator of the Ω baryon, which is

To depict the internal structure and the off shell effect of the exchanged Ω baryon, we introduce a form factor $ F(k^2, m^2_{\Omega}) $ in the amplitude, and its concrete form will be discussed later. With the amplitude in Eq. (5), one can obtain the cross section for $ K^- p \to d_{N\Omega} \bar{\Xi}^0 $ by

where $ s=(p_1+p_2)^2 $ is the center of mass energy and θ is the scattering angle, which refers to the angle of the outgoing $ d_{N\Omega} $ and the kaon beam direction in the center of mass frame. $ \vec{p}_i $ and $ \vec{p}_{f} $ are the momenta of the initial kaon beam and the final $ d_{N\Omega} $ dibaryon in the center of mass frame, respectively.

As indicated in Ref. [47], the dibayon $ d_{N\Omega} $ dominantly decays into $ \Lambda \Xi $ and $ \Xi \Sigma $. Thus, one can detect the $ d_{N\Omega} $ in the invariant mass spectrum of $ \Lambda \Xi^0 $ and $ \Xi^- \Sigma^+ $ of the $ K^- p \rightarrow \Xi^0\Lambda \bar{\Xi}^0 $ and $ K^- p \rightarrow \Xi^-\Sigma^+\bar{\Xi}^0 $ processes, respectively. To depict these processes, additional effective Lagrangians related to $ d_{N\Omega} \Xi \Lambda $ and $ d_{N\Omega} \Xi \Sigma $ are involved. As Ξ, Σ, and Λ have the same $ J^P $ quantum numbers, these two effective Lagrangians have the same form, which is

where $ Y_1 $and $ Y_2 $ could be Ξ, Σ, and Λ. Similar to the case of the tensor meson, we can choose $ F_{d_{N\Omega} Y_1Y_2}=0 $ with the tensor dominance hypothesis [65], and the values of the couplings $ G_{d_{N\Omega}Y_1 Y_2} $ will be discussed in the next section. With this additional effective Lagrangian, we can obtain the amplitudes corresponding to Fig. 2(a), which are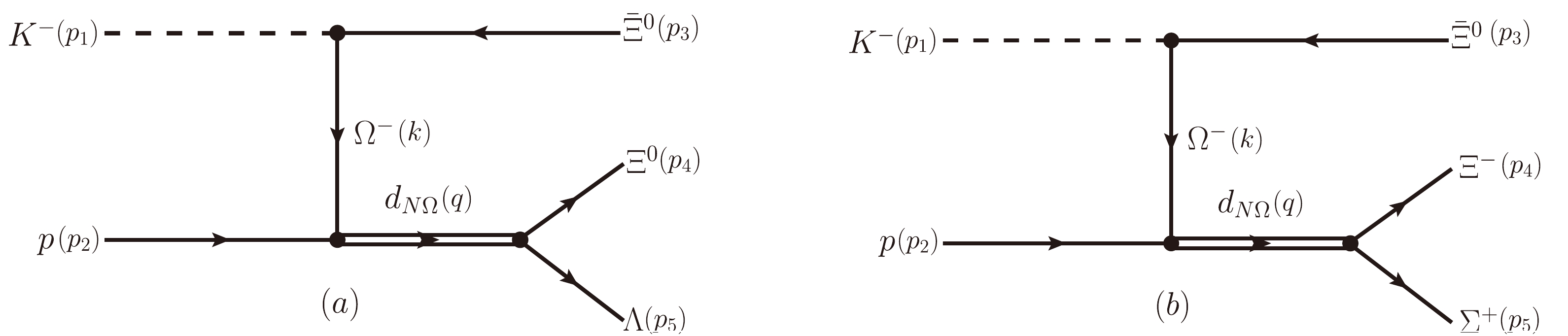

Figure 2.  (color online) Diagrams contributing to $ K^-p \to\Xi^0 \Lambda\bar{\Xi}^0 $ (diagram (a)) and $ K^- p \to \Xi^-\Sigma^+ \bar{\Xi}^0 $ (diagram (b)).

where $ \mathcal{P}_{d_{N\Omega}}^{\mu\nu \lambda \omega}(q,m_{d_{N\Omega}},\Gamma_{d_{N\Omega}}) $ is the propagator of the dibaryon $ d_{N\Omega} $, and its concrete form is

with $ \tilde{g}^{\mu \nu}= -g^{\mu\nu}+q^\mu q^\nu/m^2 $. In these amplitudes, an additional form factor $ F(q^2,m^2_{d_{N\Omega}}) $ is introduced to depict the internal structure and off shell effects of the $ d_{N\Omega} $ , and its concrete form will be discussed in the next section. In the same way, one can obtain the amplitude of $K^-p \to \bar{\Xi}^0 \Xi^- \Sigma^+$ corresponding to Fig. 2(b). With the amplitudes in Eq. (9), we can obtain the cross sections for the $ 2\to 3 $ processes by

where $ \Phi=2\sqrt{\lambda(s,m_1^2,m_2^2)}=4|\vec{p}_1|\sqrt{s} $ with $ \vec{p}_1 $ denoting the three momentums of the incident particle $ K^- $. $ p_3^0 $ is the energy of the outgoing $ \bar{\Xi}^0 $, whereas $ p_5^0 $ is the energy of Λ in the $ K^- p\to \Lambda \Xi^0 \bar{\Xi}^0 $ process and the energy of $ \Sigma^+ $ in the $ K^- p \to \bar{\Xi}^0\Xi^-\Sigma^+ $ process.

In the present work, we introduce two form factors to depict the internal structures and off-shell effects of the exchanging Ω baryon and intermediate $ d_{N\Omega} $ dibaryon. The specific expression of the factor is [66–69]

where Λ is a model parameter. In principle, the value of the model parameter Λ should be determined by comparing the theoretical estimations with the corresponding experimental measurements. However, the experimental data for the cross sections for the discussed processes are not available at the present time. In Ref. [69], the authors investigated the cross sections for $ \pi^- p \to K^{\ast 0} \Lambda $ and the parameter Λ was determined to be 0.55 GeV for the t channel and 0.60 GeV for the $ u/s $ channels by comparing the estimated cross sections with the experimental data. With this parameter, they also extended to estimate the cross sections for $ \pi^- p \to D^{\ast -} \Lambda_c^+ $. In the present work, we take a very similar parameter range, which is $ 0.55 \ \mathrm{GeV}< \Lambda < 0.65 $ GeV, to calculate the cross sections for the $K^- p\to d_{N\Omega} \bar{\Xi}^0$ process.

Before the estimations of the cross sections for the discussed processes, the relevant coupling constants should be clarified. As for the coupling constant $ g_{d_{N\Omega} N\Omega} $, it can be estimated by the compositeness condition of the composite state. In Ref. [47], the coupling constant $ g_{d_{N\Omega} N\Omega} $ was estimated to be approximately $ 1.88\sim 2.38 $ with the variation of the model parameter, where the binding energy was set to be $ 2.46 $ MeV. In the present estimation, we take $ g_{d_{N\Omega} N\Omega}=1.97 $. With this coupling constant, the partial decay widths of $ d_{N\Omega} \to \Lambda \Xi^0 $ and $ d_{N\Omega} \to \Sigma^+ \Xi^- $ are estimated to be $ 582 $ and $ 22.8 $ keV [47], respectively. Together with the effective Lagrangian in Eq. (8), one can obtain the amplitudes of $ d_{N\Omega} \to \Lambda \Xi^0 $ and $ d_{N\Omega} \to \Sigma^+ \Xi^- $, and then the corresponding partial width can be estimated by

where $ J=2 $ is the angular momentum of $ d_{N\Omega} $, $ |\vec{k}_f| $ denotes the three momentums of the daughter particles in the $ d_{N\Omega} $ rest frame. From Eq. (13) and the partial widths obtained in Ref. [47], one can estimate the corresponding effective coupling constants, which are $ g_{d_{N\Omega} \Lambda \Xi}=7.9\times10^{-2} $ and $g_{d_{N\Omega} \Sigma \Xi}= 2.5\times10^{-2}$, respectively. As for the coupling constant $ g_{K\Xi\Omega} $, we take $ g_{K\Xi\Omega}=2.12 $ as in Ref. [64].

With the above preparation, we can evaluate the cross sections for $ K^- p \to d_{N\Omega} \bar{\Xi}^0 $ depending on the beam energy and model parameter Λ. In Fig 3(a), the solid curve refers to the cross sections for $ K^- p \to d_{N\Omega} \bar{\Xi}^0 $ with $ \Lambda=0.60 $ GeV, whereas the uncertainties of the cross sections are obtained by the variation of the parameter Λ from 0.55 GeV to 0.65 GeV. From the figure, one can find that the cross sections for $ K^- p\to d_{N\Omega}\bar{\Xi}^0 $ increase sharply near the threshold of $ d_{N\Omega} \bar{\Xi}^0 $; however, when the beam energy is greater than 9 GeV, the cross sections increase very slowly with the increase in beam energy. In the considered parameter range, the cross sections are estimated to be $ 404^{+358}_ {-202}\ \mathrm{nb} $ at $ P_K=20 $ GeV, where the center value is estimated with $ \Lambda=0.60 $, while the uncertainties result from the variation of Λ from $ 0.55 $ GeV to 0.65 GeV. In Ref. [69], the cross sections for $ \pi p \to D^{\ast -}\Lambda_c^+ $ were estimated to be approximately 13 nb, whereas the present estimation indicates that the cross sections for $ K^- p \to d_{N\Omega} \bar{\Xi}^0 $ can reach 400 nb with the same model parameter, which is approximately 30 times larger than the one for $ \pi p \to D^{\ast -}\Lambda_c^+ $ [69].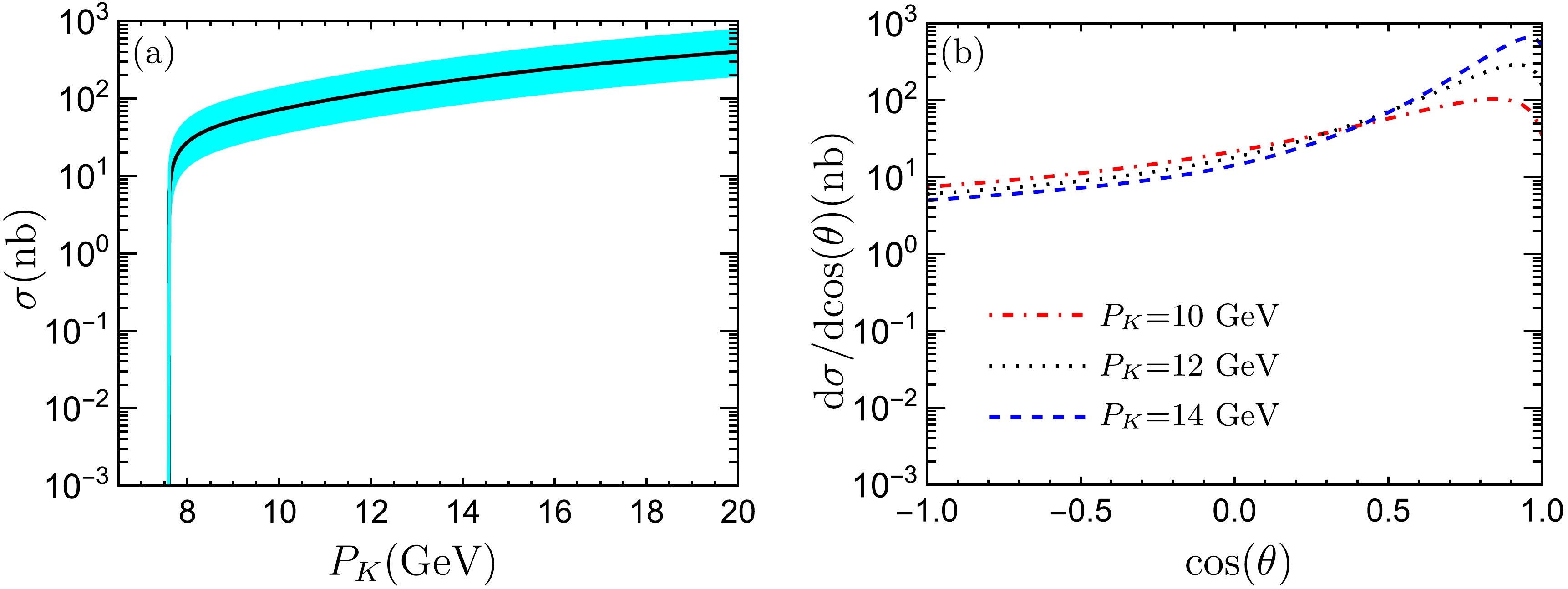

Figure 3.  (color online) Cross sections for the process $ K^-p\to d_{N\Omega} \bar{\Xi}^0 $ depending on the beam energy (diagram (a)), and differential cross sections depending on $ \cos(\theta) $ (diagram (b)).

In addition, we also present the differential cross sections depending on $ \cos (\theta) $ in Fig. 3(b). We select three typical beam energies as examples, which are $ P_K= $ 10, 12, 14 GeV with $ \Lambda=0.6 $ GeV. From the figure, one can find that more $ d_{N\Omega} $ dibaryons are concentrated in the forward angle area even in the case of $ P_K=10 $ GeV, which results from the Ω exchange.

Besides the $ K^- p \to d_{N\Omega} \bar{\Xi}^0 $ process, we estimated the beam energy dependences of the cross sections for $ K^- p\to \Xi^0 {\Lambda} \bar{\Xi}^0 $ and $ K^- p \to \Xi^- \Sigma^+ \bar{\Xi}^0 $, where $ \Xi^0 \Lambda $ and $ \Xi^- \Sigma^+ $ are the daughter particles of $ d_{N\Omega} $. As indicated in Ref. [47], the dibaryon $ d_{N\Omega} $ dominantly decays into $ \Lambda \Xi^0 $, and the branching ratio is estimated to be approximately $ 95\% $. Thus, one can experimentally detect $ d_{N\Omega} $ in the $ \Lambda \Xi^0 $ invariant mass distributions of the $ K^-p \to \Xi^0 {\Lambda} \bar{\Xi}^0 $ process, as shown in Fig. 2(a), where Λ can be reconstructed by $ p\pi^- $ and $ n\pi^0 $, while $ \Xi^0 $ can be reconstructed by the cascade decay processes $ \Xi^0 \to \Lambda \pi^0\to p \pi^- \pi^0 $ or $ \Xi^0 \to \Lambda \pi^0\to n \pi^0 \pi^0 $. Our estimations indicate that the cross sections for $K^-p \to \Xi^0 \Lambda \bar{\Xi}^0$ increase sharply near the threshold and become very weakly dependent on the beam energy as shown in Fig. 4(a) . In particular, the cross section is estimated to be $ 13^{+20}_{-7}\ \mathrm{n b} $ at $ P_K=20 $ GeV, where the center value is estimated with $ \Lambda=0.6 $, whereas the uncertainties result from the variation of Λ from 0.55 GeV to 0.65 GeV.

Figure 4.  (color online) Cross sections for $ K^-p \to\Xi^0 \Lambda\bar{\Xi}^0 $ (diagram (a)) and $ K^- p \to \Xi^-\Sigma^+ \bar{\Xi}^0 $ (diagram (b)) depending on the beam energy.

Furthermore, the branching ratio of $ d_{N\Omega}\to \Xi^- \Sigma^+ $ is sizable, and the final states are charged, which may be easier to be detected. Thus, in the present work, we also estimate the cross sections for $ K^- p \to \Xi^- \Sigma^+\bar{\Xi}^0 $. As shown in Fig. 4(b), the beam energy dependences of the cross sections for $ K^- p \to \Xi^- \Sigma^+\bar{\Xi}^0 $ are very similar to the ones for $ K^- p\to \Xi^0 \Lambda \bar{\Xi}^0 $ , and the magnitude of the cross section is estimated to be $ 0.5^{+0.5}_{-0.2}\ \mathrm{n b} $ at $ P_K=20 $ GeV.

The production of the dibaryon $ d_{N\Omega} $ is the crucial step for investigating its properties experimentally. The STAR Collaboration at RHIC detected the dibaryon $ d_{N\Omega} $ by measuring the proton-Ω correlation function in the high energy heavy-ion collision. The ALICE Collaboration at LHC also proposed to detect $ d_{N\Omega} $ in a very similar process. By utilizing the secondary kaon beam with a typical momentum of approximately 3 GeV, the Hadron experimental Facility at J-PARC proposed to produce $ d_{N\Omega} $ by two step reactions, i.e., $ K^-p \to \Omega^- K^+ K^{(\ast)0} $ and $\Omega d \to \Xi^- \Lambda p$, where the dibaryon $ d_{N\Omega} $ is expected to be observed in the $ \Xi^- \Lambda $ invariant mass spectrum.

Besides the above two types of production processes, in the present work, we propose to directly produce $ d_{N\Omega} $ in the $ K^- p \to d_{N\Omega}\bar{\Xi}^0 $ process using a secondary kaon beam with a typical momentum of approximately 10 GeV. The cross sections for $ K^- p \to d_{N\Omega} \bar{\Xi}^0 $ were estimated, and we found that the cross section is of approximately several hundreds nanobarns at $ P_K=20 $ GeV. Moreover, the estimated differential cross sections indicated that the produced $ d_{N\Omega} $ dibaryons were concentrated in the forward angle area.

Considering the fact that $ d_{N\Omega} $ dominantly decays into $ \Xi \Lambda $, we also estimated the cross sections for $K^- p \to \Xi^0 \Lambda \bar{\Xi}^0$ and $ K^- p \to \Xi^+ \Sigma^- \bar{\Xi}^0 $, where the $ d_{N\Omega} $dibaryon could be detected in the $ \Xi^0 \Lambda $ and $ \Xi^- \Sigma^+ $ invariant mass spectrum, respectively. In particular, the cross sections for $ K^- p \to \Xi^0 \Lambda \bar{\Xi}^0 $ were estimated to be approximately 10 nb at $ P_K=20 $ GeV, whereas the cross section for $ K^- p \to \Xi^- \Sigma^+ \bar{\Xi}^0 $ was approximately 20 times smaller than the one for $ K^- p \to \Xi^0 \Lambda \bar{\Xi}^0 $.