-
The discovery of the hyperon, a particle containing strange quarks, in 1953 sparked significant interest among experimental and theoretical physicists [1]. The ability of hyperons to enter the nucleus and form a system of hypernuclei makes them sensitive probes for studying the nuclear structure and specific nuclear features. Studies on hyperon behavior in the nucleus help us understand the baryon-baryon interaction in nuclear mediums and its effects on nuclear properties [2, 3]. In addition, hyperons are thought to be produced inside neutron stars [4−6]. The link between hypernucleus and neutron star properties benefits our understanding of the state of matter in extreme environments, as well as the strangeness-bearing nuclear force at high densities. In recent decades, a wealth of hypernuclear data have been generated through induced reactions of meson and electron beams at various radioactive beam facilities, including the Japan Proton Accelerator Research Complex (J-PARC) [7], Thomas Jefferson National Accelerator Facility (JLab) [8], and Facility for Antiproton and Ion Research (FAIR) [9]. These advanced facilities have played a pivotal role in advancing our understanding of strangeness in nuclear physics. Notably, single-Λ hypernuclei have been the most extensively studied, with experimental data covering hypernuclei from
${} ^{3}_\Lambda $ H to${} ^{208}_{\phantom{20}\Lambda}$ Pb in various laboratories [2, 3, 10, 11].When a Λ hyperon enters a nucleus, various phenomena can be observed. For instance, in
$ ^{7}_{\Lambda} $ Li, the size of the 6Li core has been found to be smaller than the free space 6Li nucleus, as suggested by the measurement of the γ-ray transition probability from$ E2(5/2^{+}\rightarrow1/2^{+} $ ) in$ ^{7}_{\Lambda} $ Li [12]. In addition, in$ ^{13}_{\phantom{1}\Lambda} $ C, it is hinted that the Λ spin-orbit splitting is considerably smaller than that of the nucleon [13]. Recently, the potential for producing neutron-rich hyperfragments at high-intensity heavy-ion accelerator facilities was discussed [14, 15]. The directed flow of hypernuclei ($^{3}_{\Lambda}$ H and${}^{4}_{\Lambda}$ H) recently observed at the RHIC for the first time in heavy-ion collisions provides insights into hyperon-nucleon interactions under finite pressure [16, 17]. These advances highlight the promising prospects of investigating hypernuclear structures using the forthcoming high-intensity heavy-ion accelerator facility, HIAF [18, 19]. To provide accurate predictions for these experiments, researchers have performed detailed theoretical studies on observables such as hypernuclear binding energy [20, 21], spin-orbit splitting [22−24], and hyperon and hypernuclear matter radius [25−29]. Overall, these efforts aim to provide valuable insights into the behavior of hypernuclei and deepen our understanding of in-medium baryon interactions.Owing to their ability to provide a self-consistent and unified description of almost all nuclei on the nuclear chart, both non-relativistic and relativistic mean-field theories are widely used in finite nuclei and nuclear matter calculations and have been extended to describe hypernuclear systems with strange degrees of freedom during the development of theoretical models [20, 22, 30−48]. As a key model utilized in this study, the relativistic mean-field theory has been extensively developed to investigate hypernuclear properties such as hyperon separation energy [20, 49], spin-orbit splitting [24, 40, 50, 51], hyperon halos [52], hypernuclear deformation [26, 53−57], cluster structure [58], and drip lines [59]. Although most theoretical models primarily emphasize nonlinear self-coupling interactions for the study of hypernuclei, a recent study explored the effective interactions for single-Λ hypernuclei within the density-dependent relativistic mean-field (DDRMF) model [60]. With three distinct fitting approaches, they proposed six new sets of effective
$ \Lambda N $ interactions and uncovered a significant linear correlation between the ratios$ R_{\sigma} $ and$ R_{\omega} $ , representing the scalar and vector coupling strengths, respectively, between these effective$ \Lambda N $ and$ NN $ interactions.Recently, a new type of DDRMF Lagrangian, DD-LZ1, was proposed, inspired by the restoration of pseudo-spin symmetry (PSS) and nuclear medium effects [61]. This new effective Lagrangian has produced satisfactory results in describing the properties of nuclear matter and finite nuclei. With its unique density-dependent form, DD-LZ1 eliminates the spurious shell closures that have appeared in previous RMF calculations and reasonably restores the PSS of the high orbital angular momentum near the Fermi energy [61]. Applications with this new RMF Lagrangian have been achieved for several nuclear many-body characteristics, in both finite nuclei with mass ranging from light to superheavy, and neutron star properties with densities ranging from low to high. For instance, a comprehensive macroscopic-microscopic model was developed to evaluate the total energies of even-even nuclei with proton numbers ranging from 8 to 110 [62]. Even with the appearance of a hyperon [63, 64], larger maximum masses of neutron stars could be obtained with DD-LZ1 than with several other RMF parameter sets, providing the possibility that the secondary object observed in GW190814 is a neutron star [65−67]. Utilizing the Thomas-Fermi approximation, different microscopic structures of nonuniform nuclear matter were calculated for the crust of neutron stars, and a unified equation of state was established in a vast density range [68, 69]. The different density-dependent behaviors of meson-nucleon couplings impact the microscopic structures of neutron star matter with DD-LZ1, which correspondingly affects the description of various physical processes and evolutions of neutron stars.
Apart from dealing with the different nuclear medium effects caused by the interactions themselves, the evolution of isospin leads to significant changes in the in-medium effects of hypernuclei, thereby affecting the description of their structural properties. In recent years, a series of refined theoretical studies have been conducted on hypernuclei in different isotopic chains using various interaction models. For instance, the no-core shell model has been employed to investigate the systematic evolution of ground and excited state energies in helium and lithium hyperisotopes [21]. The antisymmetrized molecular dynamics method has been applied to explore the low-lying level structure of hypernuclei in beryllium hyperisotopes [70]. The multidimensionally constrained RMF model has been used to study the shape evolution of hypernuclei in argon hyperisotopes [54]. The beyond mean-field approach has been utilized to discuss the evolution of p-state energies and composition in carbon hyperisotopes [24], as well as the hyperon halo structures in boron and carbon hyperisotopes [27, 29]. These studies revealed the significance of the role of isospin in the description of hypernuclear structure. In fact, with the development of hypernuclear spectroscopy, new experiments related to hypernuclei have been initiated, such as the planned measurements in the J-PARC project, aiming to study the Λ hyperon binding energies in the neutron-rich hyperisotopes of
${}^{124-136}_{\phantom{124-13}\Lambda}{\rm Sn}$ [71, 72]. These experiments will provide crucial information about the properties of hypernuclei associated with various isospin circumstances.In view of the essential role of nuclear in-medium effects on hypernuclear structure and their relevance to isotopic evolution, we aim to further expand the density-dependent RMF (DDRMF) model to investigate the structure of single-Λ hypernuclei in oxygen hyperisotopes. First, we introduce the theoretical framework of the hypernuclear RMF approach in Sec. II. Then, the induced Λ-nucleon (
$ \Lambda N $ ) effective interactions are determined by fitting Λ separation energies to the experimental data for the DD-LZ1 Lagrangian. The influence of nuclear in-medium effects on the isospin dependence of hypernuclear bulk properties, hyperon spin-orbit splitting, and matter/ hyperon radius is described in Sec. III. Finally, a summary is given in Sec. IV. -
To describe single-Λ hypernuclei within the meson-exchanged form of RMF theory, the covariant Lagrangian density serves as the foundation, which is
$ \begin{align} \mathscr{L} = \mathscr{L}_B + \mathscr{L}_{\varphi} + \mathscr{L}_I, \end{align} $

(1) where the free field terms read as
$ \begin{align} \mathscr{L}_B=&\sum_B\bar{\psi}_B\left({\rm i} \gamma^\mu\partial_\mu-M_B\right)\psi_B, \end{align} $

(2) $ \begin{aligned}[b] \mathscr{L}_{\varphi}=&+\frac{1}{2}\partial^\mu\sigma\partial_\mu\sigma-\frac{1}{2}m_\sigma^2\sigma^2-\frac{1}{4}\Omega^{\mu\nu}\Omega_{\mu\nu}+\frac{1}{2}m_\omega^2\omega^\mu\omega_\mu\\&-\frac{1}{4}\vec{R}^{\mu\nu}\cdot\vec{R}_{\mu\nu}+\frac{1}{2}m_\rho^2\vec{\rho}^{\,\mu}\cdot\vec{\rho}_\mu-\frac{1}{4}F^{\mu\nu}F_{\mu\nu}, \end{aligned} $

(3) where the index B (
$ B' $ ) represents the nucleon N (hyperon Λ), and the sum$ \sum_B $ is taken over both N and Λ. The masses of the baryon and mesons are denoted as$ M_B $ and$ m_\phi $ ($\phi=\sigma, \omega^{\mu}, \vec{\rho}^{\,\mu}$ ), respectively. Additionally,$ \Omega^{\mu\nu} $ ,$ \vec{R}^{\mu\nu} $ , and$ F^{\mu\nu} $ represent the field tensors of the vector mesons$ \omega^{\mu} $ and$\vec{\rho}^{\,\mu}$ and the photon$ A^\mu $ , respectively. The interaction between the nucleon (hyperon) and mesons (photons) is described by the Lagrangian$ \mathscr{L}_I $ ,$ \begin{aligned}[b] \mathscr{L}_I=&\sum_B\bar{\psi}_B\left(-g_{\sigma B}\sigma-g_{\omega B}\gamma^\mu\omega_\mu\right)\psi_B\\& +\bar{\psi}_N\left(-g_{\rho N}\gamma^\mu\vec{\tau}\cdot\vec{\rho}_\mu-e\gamma^\mu\frac{1-\tau_3}{2}A_\mu\right)\psi_N. \end{aligned} $

(4) Here, the Λ hyperon (namely,
$ \psi_B $ taken as$ \psi_\Lambda $ ), which is charge-neutral with isospin zero, only takes part in interactions that are spread by isoscalar mesons. The nuclear in-medium effects are introduced phenomenologically via the coupling strengths$ g_{\phi B} $ ($ g_{\phi N} $ ), which use baryon-density dependent functions in the DDRMF approach to define the strengths of different meson-baryon (meson-nucleon) couplings [61, 73].The effective Hamiltonian operator for Λ hypernuclei can be obtained by performing the general Legendre transformation on the Lagrange density
$ \mathscr{L} $ in Eq. (1) and can be written as the sum of the kinetic energy operator$ \hat{T} $ and potential energy operator$\hat{V}_{\varphi}$ ,$ \begin{aligned}[b] \hat{H}\equiv&\; \hat{T}+\sum_{\varphi}\hat{V}_\varphi\\ =&\int {\rm d} x \sum_{B} \bar{\psi}_{B}(x)(-{\rm i} \mathit{\boldsymbol{\gamma}}\cdot\mathit{\boldsymbol{\nabla}}+M_{B}) \psi_{B}(x)\\ &+ \frac{1}{2} \int {\rm d} x \sum_{B} \sum_{\varphi} \left[\bar{\psi}_{B} \mathscr{G}_{\varphi B} \psi_{B}\right]_{x} D_{\varphi}(x,x') \left[\bar{\psi}_{B'} \mathscr{G}_{\varphi B'} \psi_{B'}\right]_{x'}, \end{aligned} $

(5) where x is the four-vector
$(t,\boldsymbol{x})$ . Correspondingly, we define interaction vertices$ \mathscr{G}_{\varphi B}(x) $ for various meson (photon)-nucleon (hyperon) coupling channels, which for isoscalar σ and ω mesons are represented as$ \begin{align} \mathscr{G}_{\sigma B}(x) = &+g_{\sigma B}(x), \end{align}\tag{6a} $

$ \begin{align} \mathscr{G}_{\omega B}^\mu(x) = &+g_{\omega B}(x)\gamma^{\mu}. \end{align}\tag{6b} $

Notably, both nucleons and the Λ hyperon can contribute to the isoscalar meson fields. However, for the remaining isovector mesons and photon fields, it is expected that their interaction vertices solely connect to nucleons because of the isoscalar and charge-neutral nature of the Λ hyperon,
$ \begin{align} \mathscr{G}_{\rho N}^\mu(x) = &+g_{\rho N}(x) \gamma^{\mu} \vec{\tau}, \end{align}\tag{7a} $

$ \begin{align} \mathscr{G}_{A N}^\mu(x) = &+e\gamma^{\mu}\frac{1-\tau_{3}}{2}. \end{align}\tag{7b} $

Because the retardation effects can be neglected in the majority of RMF models, the meson (photon) propagators
$ D_{\phi} $ ($ D_{A} $ ) read as$ \begin{align} D_{\phi}(\boldsymbol{x},\boldsymbol{x}')=\frac{1}{4\pi}\frac{{\rm e}^{-m_\phi|\boldsymbol{x}-\boldsymbol{x}'|}}{|\boldsymbol{x}-\boldsymbol{x}'|},\quad D_A(\boldsymbol{x},\boldsymbol{x}')=\frac{1}{4\pi}\frac{1}{|\boldsymbol{x}-\boldsymbol{x}'|}. \end{align} $

(8) The baryon field operator
$ \psi_{B} $ in the Hamiltonian (5) can be second quantized in the positive-energy space under the no-sea approximation as$ \begin{align} \psi_B(x) &=\sum_if_i(\boldsymbol{x}){\rm e}^{-{\rm i}\epsilon_i t}c_i. \end{align} $

(9) Here,
$ f_i $ represents the Dirac spinor, and$ c_i $ denotes the annihilation operators for state i. Accordingly, the energy functional E is determined by evaluating the expectation value of the Hamiltonian with respect to a trial Hartree-Fock ground state$ |\Phi_0\rangle $ ,$ \begin{align} E & = \langle\Phi_{0}|\hat{H}| \Phi_{0}\rangle = \langle\Phi_{0}|\hat{T}| \Phi_{0}\rangle+\sum_{\varphi}\langle\Phi_{0}\left|\hat{V}_{\varphi}\right| \Phi_{0}\rangle. \end{align} $

(10) Then, the binding energy of a Λ hypernucleus is written as
$ \begin{align} E=&\sum_{B}(E_{\rm{kin},B} + E_{\sigma,B} + E_{\omega,B}) + E_{\rho,N}+E_{\rm{e.m.}} + E_{\rm{c.m.}} + E_{\rm{pair}}, \end{align} $

(11) where the kinetic energy functional of baryons is denoted as
$E_{{\rm kin},B}$ , the contributions of the potential energy functional from σ and ω are denoted by the variables$ E_{\sigma,B} $ and$ E_{\omega,B} $ ,$ E_{\rho,N} $ and$ E_{\rm{e.m.}} $ are used to represent the contributions from ρ and A, respectively, the center-of-mass adjustment to the mean-field is represented by the term$ E_{\rm{c.m.}} $ , and$ E_{\rm{pair}} $ takes into account the contribution from nucleon pairing correlations [74].The role of deformation in single-Λ hypernuclei has been discussed in various density functional models [24, 26, 75, 76], which may generate non-negligible effects on the single-particle energies, as seen in carbon hyperisotopes [24, 26, 76]. To describe single-Λ hypernuclei, particularly the oxygen hyperisotopes discussed hereafter, we restrict the RMF approach to spherical symmetry. Correspondingly, the Dirac spinor
$f_i(\boldsymbol{x})$ of the nucleon or hyperon in Eq. (9) has the following form:$ \begin{align} f_{n\kappa m}(\boldsymbol{x}) = \frac{1}{r} \left(\begin{array}{c}{\rm i} G_a(r)\Omega_{\kappa m}(\vartheta,\varphi)\\ F_a(r)\Omega_{-\kappa m}(\vartheta,\varphi) \end{array}\right), \end{align} $

(12) where the index a consists of the set of quantum numbers
$ (n\kappa) = (njl) $ , and$ \Omega_{\kappa m} $ is the spherical spinor. Meanwhile, the propagators can be expanded in terms of spherical Bessel and spherical harmonic functions as$ \begin{align} D_{\phi}(\boldsymbol{x},\boldsymbol{x}^{\prime}) = \sum_{L=0}^{\infty}\sum_{M=-L}^{L}(-1)^{M}R^{\phi}_{LL}\left( r, r^{\prime}\right) Y_{LM}\left(\boldsymbol\Omega\right)Y_{L-M}\left(\boldsymbol\Omega^{\prime}\right), \end{align} $

(13) where
$\boldsymbol\Omega=(\vartheta,\varphi)$ , and$ R_{LL} $ contains the modified Bessel functions I and K as$ \begin{align} R_{L L}^{\phi}\left(r, r^\prime\right)&=\sqrt{\frac{1}{rr^{\prime}}} I_{L+\frac{1}{2}}\left(m_{\phi}r_{<}\right) K_{L+\frac{1}{2}}\left(m_{\phi}r_{>}\right), \end{align} $

(14) $ \begin{align} R_{L L}^{A}\left(r, r^\prime\right)&=\frac{1}{2L+1}\frac{r_{<}^{L}}{r_{>}^{L+1}}. \end{align} $

(15) In the DDRMF approach, the meson-baryon coupling strengths are adopted as a function of baryon density
$ \rho_{b} $ , which are written as$ \begin{align} g_{\phi B}\left(\rho_{b}\right)=g_{\phi B}(0) f_{\phi B}(\xi) \quad\text{or}\quad g_{\phi B}\left(\rho_{b}\right)=g_{\phi B}(0) {\rm e}^{-a_{\phi B} \xi}, \end{align} $

(16) where
$ \xi=\rho_{b}/\rho_{0} $ , with$ \rho_{0} $ as the saturation density of nuclear matter, and$ \begin{align} f_{\phi B}(\xi)=a_{\phi B}\frac{1+b_{\phi B}(\xi+d_{\phi B})^2}{1+c_{\phi B}(\xi+d_{\phi B})^2}. \end{align} $

(17) The free coupling strength at
$ \rho_{b}=0 $ is represented by$ g_{\phi B}(0) $ in the above expression. To maintain the variational self-consistency between the energy density functional and single-particle properties, extra terms in the baryon self-energies, namely, rearrangement terms, will appear owing to the density dependence of the coupling strengths. The single-particle (nucleon or hyperon) properties can be determined by solving the Dirac equation,$ \begin{aligned}[b] & \varepsilon_{a,B} \begin{pmatrix} G_{a,B}(r) \\ F_{a,B}(r) \end{pmatrix} \\ = & \begin{pmatrix} \Sigma_+^B(r) & -\dfrac{\rm d}{{\rm d} r}+\dfrac{\kappa_{a,B}}{r} \\ \dfrac{\rm d}{{\rm d} r}+\dfrac{\kappa_{a,B}}{r} & -\left[2M_{B}-\Sigma_-^B(r)\right] \end{pmatrix} \begin{pmatrix} G_{a,B}(r) \\ F_{a,B}(r) \end{pmatrix}. \end{aligned} $

(18) Here, the self-energies
$ \Sigma_\pm^B=\Sigma_{0,B}\pm\Sigma_{S,B} $ are composed by the vector and scalar terms. The scalar self-energy$ \Sigma_{S,B} = \Sigma_{S,B}^{\sigma} $ , and the time component of the vector one is$ \begin{align} \Sigma_{0,B}(r) = \sum_{\phi}\Sigma_{0,B}^{\phi}(r)+\Sigma_{R}(r), \end{align} $

(19) where
$ \phi=\omega, \rho $ for nucleons, and$ \phi=\omega $ for Λ hyperons. The self-energies of nucleons or hyperons include a scalar one,$ \Sigma_{S,B} $ , and vector one,$ \Sigma_{0,B} $ , in which the coupling of isoscalar mesons contributes as follows:$ \begin{align} \Sigma_{S,B}^{\sigma}(r)&=-g_{\sigma B}(r)\sum_{B^\prime}\int r^{\prime2} {\rm d} r^\prime g_{\sigma B^\prime}(r^\prime)\rho_{s,B^\prime}(r^\prime)R^{\sigma}_{00}(r,r^\prime), \end{align} \tag{20a}$

$ \begin{align} \Sigma_{0,B}^{\omega}(r)&=+g_{\omega B}(r)\sum_{B^\prime}\int r^{\prime2} {\rm d} r^\prime g_{\omega B^\prime}(r^\prime)\rho_{b,B^\prime}(r^\prime)R^{\omega}_{00}(r,r^\prime). \end{align}\tag{20b} $

Here,
$ \rho_{s,B} $ and$ \rho_{b,B} $ represent the scalar and baryon densities, respectively [74]. Additionally, the rearrangement term$ \Sigma_R $ appears in the DDRMF approach, which contains the summation over all baryons for the isoscalar case of$ \phi=\sigma,\omega $ but only over nucleons for the isovector case. For example, the contribution from$ \sigma-S $ coupling is shown as$ \begin{align} \Sigma_{R,\sigma}(r)=\sum_{B}\frac{1}{g_{\sigma B}} \dfrac{\partial g_{\sigma B}}{\partial \rho_{b}}\rho_{s,B}\Sigma_{S,B}^{\sigma}(r). \end{align} $

(21) -
In recent years, there has been extensive theoretical research on hypernuclei, particularly focusing on the simplest single-Λ hypernuclei, using RMF and RHF theories. In this section, we aim to extend the effective interaction DD-LZ1 [61], which has been proven successful and promising in determining the properties of the nuclear structure in both bulk and single-particle aspects, to incorporate the Λ hyperon within the framework of the RMF model. To give a comparative study and illustrate the role of nuclear in-medium effects, the calculations with DD-LZ1 are accompanied by several existing effective
$ \Lambda N $ interactions within CDF models. These interactions have been significantly expanded to incorporate the degrees of freedom of the Λ hyperon and have yielded many successful findings in the study of hypernuclear structure and the properties of dense stars. Specifically, the density-dependent RMF effective interactions DD-LZ1 [61], PKDD [74], DD-ME2, TW99, and DDV [77]; the density-dependent RHF (DDRHF) effective interactions PKO1, PKO2, and PKO3 [74]; and the nonlinear RMF (NLRMF) effective interactions NL-SH [20] and PK1 [78] are selected. In these CDF functionals, the ω-tensor coupling, which has been proven essential in reducing the spin-orbit splitting of Λ in hypernuclei [51, 79−81], is ignored. The Dirac equation is solved using a radial box size of$ R=20 $ fm with a step size of 0.1 fm. For open-shell hypernuclei, we employ the BCS method to account for pairing correlations. Because the strength of hyperon pairing correlations remains uncertain and may become essential in multi-Λ hypernuclei, our current study solely considers pairing correlations between the$ nn $ and$ pp $ pairs using the finite-range Gogny force, D1S [82] (see Refs. [83−86] for details). In addition, the blocking effect should be taken into account for the last valence nucleon or hyperon (a detailed description can be found in Ref. [74]). -
For the theoretical study of hypernuclear structure, the
$ \Lambda N $ interaction must first be determined. Because the Λ hyperon is an electrically neutral particle with isospin zero, our focus lies on the coupling strengths between the isoscalar-scalar σ meson and isoscalar-vector ω meson with the Λ hyperon. For convenience, we introduce the ratio of the coupling strengths between the meson-hyperon and meson-nucleon,$ g_{\phi\Lambda}/g_{\phi N} $ . According to the näive quark model [87], we fix the ratio of the isoscalar-vector meson coupling strength$ g_{\omega\Lambda}/g_{\omega N} $ to 0.666, whereas the ratio of the isoscalar-scalar one$ g_{\sigma\Lambda}/g_{\sigma N} $ can be obtained by reproducing the Λ hyperon separation energy$ B_{\Lambda} $ experimental data for$^{16}_{\phantom{1}\Lambda}$ O,$^{40}_{\phantom{4}\Lambda}$ Ca, and$^{208}_{\phantom{20}\Lambda}$ Pb [3, 10]. In the fitting process, the hyperon is placed in the$ 1s_{1/2} $ ground state, and$ B_{\Lambda} $ is defined as follows:$ \begin{align} B_\Lambda(^{A}_\Lambda Z) = E(^{A-1}Z) - E(^{A}_\Lambda Z). \end{align} $

(22) Based on the effective interaction DD-LZ1, we finally obtain a new set of
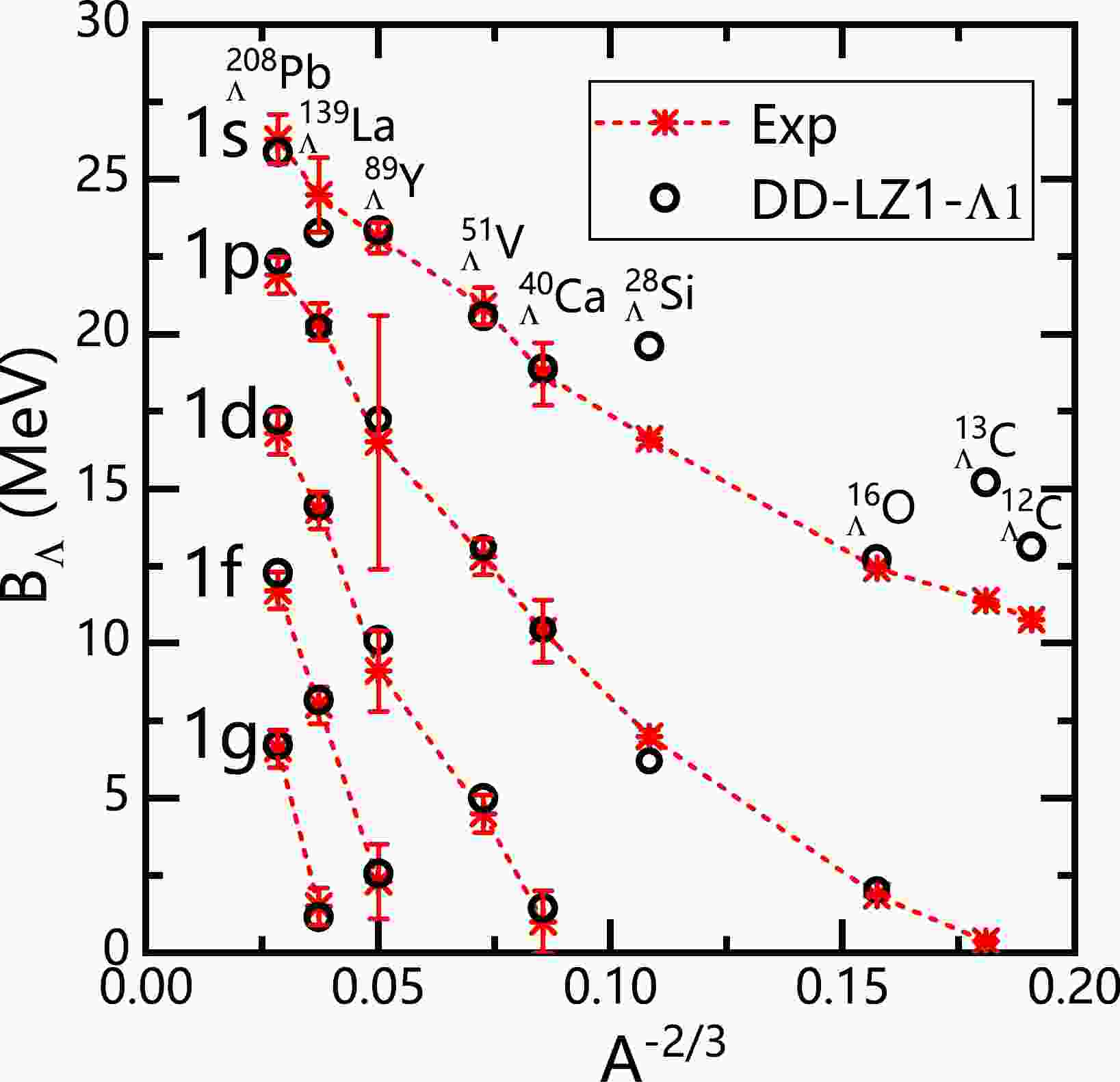
$ \Lambda N $ interactions, namely, DD-LZ1-$ \Lambda1 $ , after a fitting process of Levenberg-Marquardt minimization. Then, the Λ separation energy$ B_{\Lambda} $ and single-Λ energy are calculated, with the hyperon occupying the ground state$ 1s_{1/2} $ or possible excited states with higher angular momentum$ l_\Lambda $ . For the$ 1p $ ,$ 1d $ ,$ 1f $ , and$ 1g $ excited states,$ B_{\Lambda} $ is determined by averaging the values of Λ spin doublets with the same orbital angular momentum$ l_{\Lambda} $ . For$ B_{\Lambda} $ of DD-LZ1-$ \Lambda1 $ , a remarkable agreement with experimental data is found for most hypernuclei, except$^{28}_{\phantom{2}\Lambda}$ Si with significant deformation and carbon hyperisotopes with light mass, as shown in Fig. 1. In fact, a more accurate description of light-mass carbon hyperisotopes can be obtained by limiting the mass region of fitting and considering the deformation effects [60]. To investigate the deviation in describing the structural properties of single-Λ hypernuclei using different CDF effective interactions, the coupling strength of DD-LZ1-$ \Lambda1 $ in comparison with other selected CDF functionals is presented in Table 1. We can check the root-mean-square deviation Δ for$ B_{\Lambda} $ between theoretical calculations and experimental values, which is defined by
Figure 1. (color online) Calculated Λ separation energies
$ B_\Lambda $ for single-Λ hypernuclei with the RMF effective interaction DD-LZ1-$ \Lambda1 $ in comparison with experimental data taken from Refs. [3, 10]. For the$ 1p $ ,$ 1d $ ,$ 1f $ , and$ 1g $ states, the black circles are determined by averaging the separation energies of the Λ hyperon occupying spin doublets.DD-LZ1-Λ1 PKDD-Λ1 DD-ME2 TW99 DDV PKO1-Λ1 PKO2-Λ1 PKO3-Λ1 NL-SH PK1 $ g_{\sigma\Lambda}/g_{\sigma N} $ 

0.615 0.620 0.620 0.617 0.622 0.596 0.591 0.594 0.621 0.618 $ \Delta_{1} $ 

0.319 0.363 0.245 0.375 0.473 0.265 0.260 0.407 0.916 0.519 $ \Delta_{2} $ 

1.810 0.734 0.710 0.684 3.460 0.683 0.527 0.881 1.614 1.184 Table 1. σ-Λ coupling strengths
$ g_{\sigma\Lambda}/g_{\sigma N} $ fitted for the DDRMF effective interactions DD-LZ1-$ \Lambda1 $ , PKDD-$ \Lambda1 $ [74], DD-ME2, TW99, and DDV [77]; the DDRHF interactions PKO1-$ \Lambda1 $ , PKO2-$ \Lambda1 $ , and PKO3-$ \Lambda1 $ [74]; and the NLRMF interactions NL-SH [20] and PK1 [78] by minimizing the root-mean-square deviation$ \Delta_{1} $ (in MeV) from the experimental values of the Λ separation energies of$^{16}_{\phantom{1}\Lambda}$ O,$^{40}_{\phantom{4}\Lambda}$ Ca, and$^{208}_{\phantom{20}\Lambda}$ Pb, where the ω-Λ coupling is fixed as$ g_{\omega\Lambda}/g_{\omega N} = 0.666 $ .$ \Delta_{2} $ represents the root-mean-square deviation between the theoretical calculations and experimental values of Λ separation energies for all hypernuclei shown in Fig. 1.$ \begin{equation} \Delta\equiv\sqrt{\frac{1}{N}\sum\limits_{i=1}^N(B_{\Lambda,i}^{\rm{exp.}}-B_{\Lambda,i}^{\rm{cal.}})^2}. \end{equation} $

(23) To reveal the systematics, we define
$ \Delta_{1} $ as the deviation only for$^{16}_{\phantom{1}\Lambda}$ O,$^{40}_{\phantom{4}\Lambda}$ Ca, and$^{208}_{\phantom{20}\Lambda}$ Pb, as well as$ \Delta_{2} $ , which is suitable for all hypernuclei.As shown in Table 1, different CDF theoretical models have good descriptions for
$^{16}_{\phantom{1}\Lambda}$ O,$^{40}_{\phantom{4}\Lambda}$ Ca, and$^{208}_{\phantom{20}\Lambda}$ Pb, and most parameter sets have good consistency for hypernuclear theoretical calculations and experimental data over a large mass range from$^{12}_{\phantom{1}\Lambda}$ C to$^{208}_{\phantom{20}\Lambda}$ Pb. In addition, by comparing three different types of CDF effective interactions, we can find that when the ratio of the isospin scalar-vector meson coupling strength is fixed to the same value, the ratio of the isospin scalar-scalar meson coupling strength$ g_{\sigma\Lambda}/g_{\sigma N} $ may satisfy certain linear correlations with the ratio of the isospin scalar-vector meson coupling strength, which has been systematically explored in several studies [60, 64, 88]. It should be noted that the linear correlation of the meson-hyperon coupling strength ratios obtained in the RMF framework is obviously not suitable for DDRHF models [74].In the DDRMF approach, the in-medium effects of nuclear force are effectively embedded in the density-dependent shape of the meson-baryon coupling strength, playing the role in the nuclear structure via the equilibrium of nuclear dynamics from various coupling channels. In recent years, analyses based on the equilibrium of nuclear in-medium dynamics has been conducted to clarify the mechanism of PSS, shell evolution, the liquid-gas phase transition, and the spin-orbit splitting of hyperons in CDF models [61, 74, 85, 89, 90]. The delicate in-medium balance between nuclear attractive and repulsive interactions may be significantly altered by treating the density dependence of coupling strength differently, which impacts the description of the properties of nuclear matter and finite nuclei with different CDF effective interactions.
To provide a comprehensive understanding of in-medium equilibrium in hypernuclei, we present the density dependence of coupling strengths for selected CDF effective interactions in Fig. 2(a) and Fig. 2(b), corresponding to the isoscalar-scalar channel
$ g_{\sigma\Lambda} $ and isoscalar-vector channel$ g_{\omega\Lambda} $ . There are systematic divergences of the meson-hyperon coupling strengths with increasing density among the DDRMF, DDRHF, and NLRMF effective interactions. Notably, the density dependence of$ g_{\sigma\Lambda} $ and$ g_{\omega\Lambda} $ is significantly reduced in the DDRHF effective interaction compared to the DDRMF effective interaction. This pronounced reduction in density dependence also influences the description of single-particle properties in hypernuclei, such as Λ hyperon spin-orbit splitting [74]. Furthermore, in contrast with density-dependent interactions, the NLRMF effective interaction exhibits density-independent characteristics for$ g_{\sigma\Lambda} $ and$ g_{\omega\Lambda} $ . Consequently, when applying these three types of CDF effective interactions to single-Λ hypernuclei, systematic deviation can occur when describing the isospin dependence of the hypernuclear structure.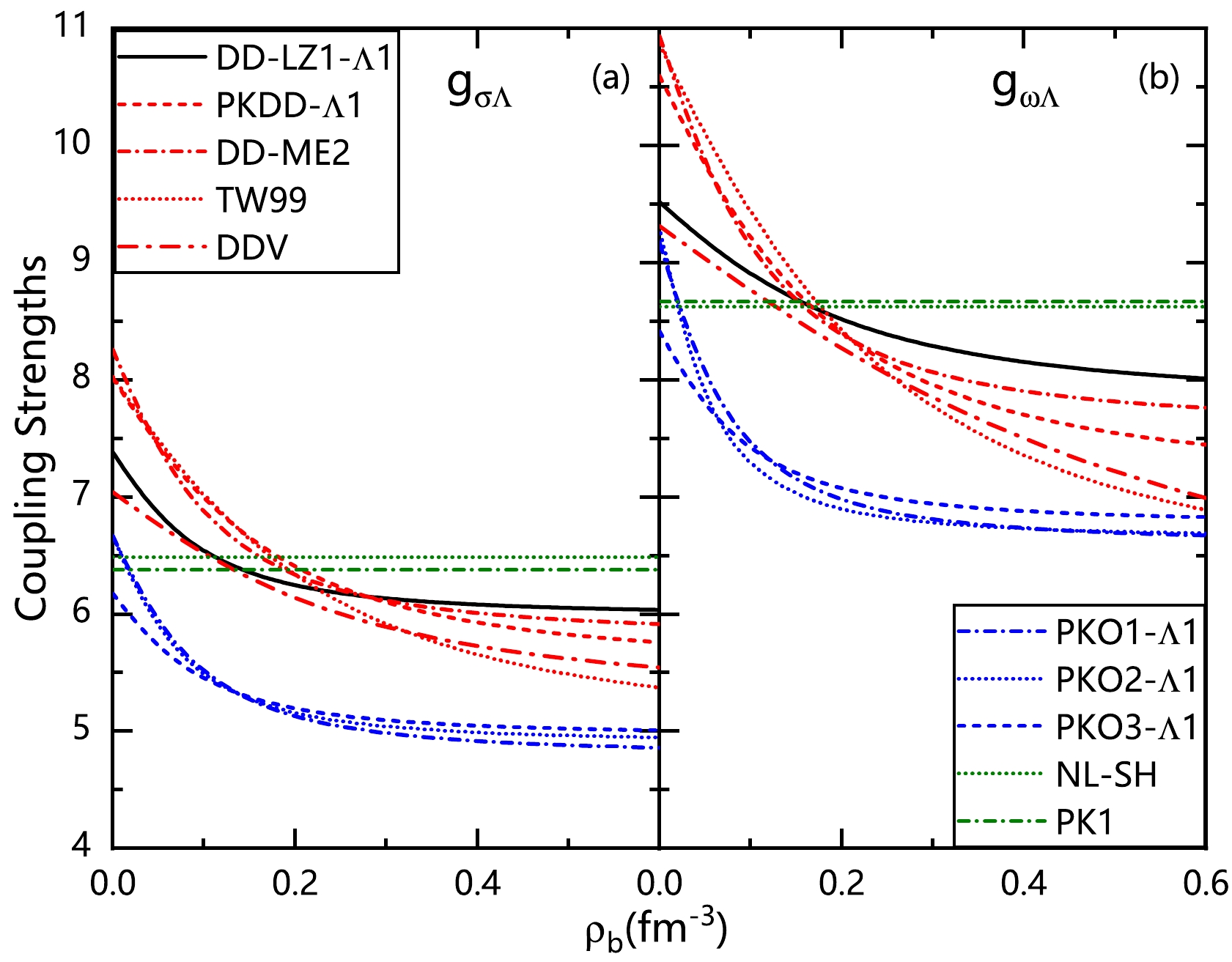
Figure 2. (color online) Meson-hyperon coupling strengths, namely, the isoscalar
$ g_{\sigma\Lambda} $ [panel (a)] and$ g_{\omega\Lambda} $ [panel (b)], as functions of baryonic density$ \rho_{b} $ ($ {\rm fm}^{-3} $ ) for the DDRMF effective interactions DD-LZ1-$ \Lambda1 $ , PKDD-$ \Lambda1 $ , DD-ME2, TW99, and DDV; the DDRHF interactions PKO1-$ \Lambda1 $ , PKO2-$ \Lambda1 $ , and PKO3-$ \Lambda1 $ ; and the NLRMF interactions NL-SH and PK1. -
To focus on the isospin dependence of single-particle properties, we choose the Λ hypernuclei and their nucleonic counterpart in oxygen (hyper)isotopes as examples because they usually take spherical symmetry. To check the accuracy of the chosen interactions in describing the properties of finite nuclei, we first calculate the binding energies
$ E_{B} $ , charge radii$ R_{c} $ , and matter radii$R_{m}$ for oxygen isotopes using the DD-LZ1 effective interaction. We compare the theoretical calculations with experimental measurements, which are taken from Refs. [91−93]. From the results in Table 2, we can see that the theoretical calculations and experimental measurements are in good agreement for both the binding energies$ E_{B} $ and charge radii$ R_{c} $ for the interaction DD-LZ1. The experimental values$R_{m}^{\rm{exp.}}$ of the total matter radius, unlike the charge radius, still have significant uncertainties with error bars, whereas the theoretical calculations$R_{m}$ reconcile with them qualitatively.Nucleus $E_{B} /{\rm{MeV} }$ 

$E_{B}^{\rm{exp.} } /{\rm{MeV} }$ 

$R_{c} /{\rm{fm} }$ 

$R_{\rm{c} }^{\rm{exp.} }/{\rm{fm} }$ 

$R_{m} /{\rm{fm} }$ 

$R_{m}^{\rm{exp.} }/{\rm{fm} }$ 

14O −99.699 −98.732 2.766 2.543 16O −128.215 −127.619 2.752 2.699 2.619 2.57(2) 18O −140.017 −139.808 2.749 2.773 2.761 2.64(8) 20O −150.687 −151.371 2.746 2.868 2.71(3) 22O −160.364 −162.028 2.746 2.955 2.90(5) 24O −168.802 −168.960 2.761 3.054 3.18(12) Furthermore, in Table 3, we summarize the systematics of the occupied energy level of the Λ hyperon, the single-particle energies of the Λ hyperon, the total binding energies, the charge radii, and the matter radii of hypernuclei in oxygen hyperisotopes. To give possible reference to hypernuclear experiments, we also calculate the strength of the electric dipole transition
$ B(E1) $ between the$ \Lambda1p $ and$ \Lambda1s $ occupation states. The transition strength is expressed asNucleus $ \Lambda(nlj) $ 

$\varepsilon_{\rm{s.p.} } /{\rm{MeV} }$ 

$E_{B} /{\rm{MeV} }$ 

$R_{c}/{\rm{fm} }$ 

$R_{\Lambda}/{\rm{fm} }$ 

$R_{m}/{\rm{fm} }$ 

$ B(E1) $ /(

$e^{2}\rm{fm}^2$ )

$ ^{15}_{\Lambda} $ O

$ 1s_{1/2} $ 

−14.330 −113.245 2.716 2.115 2.458 $ 1p_{1/2} $ 

−0.413 −99.590 2.772 5.265 2.813 0.095 $ 1p_{3/2} $ 

−1.582 −101.002 2.760 4.134 2.674 0.119 $ ^{17}_{\Lambda} $ O

$ 1s_{1/2} $ 

−13.086 −140.507 2.704 2.323 2.555 $ 1p_{1/2} $ 

−1.059 −128.927 2.756 4.609 2.780 0.109 $ 1p_{3/2} $ 

−2.278 −130.307 2.746 3.963 2.711 0.121 $ ^{19}_{\Lambda} $ O

$ 1s_{1/2} $ 

−14.170 −153.506 2.699 2.310 2.682 $ 1p_{1/2} $ 

−1.720 −141.540 2.751 4.291 2.861 0.090 $ 1p_{3/2} $ 

−3.036 −143.003 2.740 3.824 2.815 0.097 $ ^{21}_{\Lambda} $ O

$ 1s_{1/2} $ 

−15.394 −165.477 2.695 2.295 2.773 $ 1p_{1/2} $ 

−2.463 −153.079 2.744 4.062 2.927 0.075 $ 1p_{3/2} $ 

−3.890 −154.635 2.733 3.699 2.890 0.079 $ ^{23}_{\Lambda} $ O

$ 1s_{1/2} $ 

−16.804 −176.670 2.688 2.277 2.829 $ 1p_{1/2} $ 

−3.285 −163.703 2.737 3.882 2.977 0.063 $ 1p_{3/2} $ 

−4.841 −165.374 2.725 3.582 2.943 0.066 $ ^{25}_{\Lambda} $ O

$ 1s_{1/2} $ 

−17.634 −185.728 2.723 2.256 2.969 $ 1p_{1/2} $ 

−3.925 −172.669 2.757 3.836 3.079 0.052 $ 1p_{3/2} $ 

−5.522 −174.326 2.748 3.562 3.055 0.055 Table 3. Properties of single-Λ states in the hypernucleus
$^{Z+N+\Lambda}_{\phantom{Z+N+}\Lambda}$ O, calculated with the DDRMF effective interaction DD-LZ1-$ \Lambda1 $ , including single-particle energies$ \varepsilon_{\rm{s.p.}} $ , binding energies$ E_{B} $ , charge radii$ R_{c} $ , hyperon radii$ R_{\Lambda} $ , hypernuclear matter radii$R_{m}$ , and the$ B(E1) $ value of the transition from the excited$ (\Lambda1p) $ state to the ground$ (\Lambda1s) $ state.$ \begin{align} B(E1;J_{i}\longrightarrow J_{f})=\frac{3e^{2}_{\Lambda}}{4\pi}\langle f|r|i\rangle^{2}(2j_{f}+1) \begin{pmatrix} j_{f} & 1 & j_{i} \\ -\dfrac{1}{2} & 0 & \dfrac{1}{2} \end{pmatrix}^{2}, \end{align} $

(24) where
$ e_{\Lambda} $ represents the effective charge of the Λ hyperon. The integration$ \langle f|r|i\rangle $ can be computed using the radial wave functions of the initial and final single-Λ states (see Ref. [27] for details).In the framework of relativistic models, Dirac spinors with both upper and lower components may contribute to determining the value of
$ B(E1) $ . However, the contribution from the lower component is found to be negligible, especially for the non-charge exchange channel. Therefore, only the contribution from the upper component is preserved in current calculations for simplification. The inclusion of the Λ hyperon induces the so-called impurity effect inside hypernuclei [2]. When the Λ hyperon is filled in the$ 1s_{1/2} $ state, we can see from the comparison of the total matter radii in Tables 3 and 2 that the introduction of the hyperon causes a shrinkage effect on the hypernuclei, which is approximately$ 0.06-0.13 $ fm. Compared with the ground-state results, we observe a significant enhancement in the Λ root-mean-square radii when the hyperon is filled in the higher-lying$ 1p $ state. This change in the density distribution of the hyperon due to different level occupations leads to an overall expansion of the hypernuclear matter radii, different from the$ \Lambda1s $ case. Additionally, with the increase in neutron number, the hyperon radii, matter radii, and$ B(E_{1}) $ exhibit significant isospin dependence, which can be qualitatively explained by the density-dependence of the coupling strength. As indicated in Table 3, when the Λ hyperon occupies the$ 1p $ state, its density distribution spreads further outward than the nucleonic core. As the isospin evolves, more neutrons are filled and their attraction to the hyperon increases, leading to a significant reduction in the hyperon radius. The$ B(E_{1}) $ value is determined not only by the overlap between the initial and final states, which are sensitive to the neutron number, but also by the effective charge. As a result, the$ B(E_{1}) $ values increase slightly from$^{15}_{\phantom{1}\Lambda}$ O to$^{17}_{\phantom{1}\Lambda}$ O and decrease gradually as the isospin evolves after$ N=8 $ . -
Motivated by the connection between the density-dependent effective interactions of theoretical models and the isospin-dependent properties of nuclear structure, the spin-orbit splitting of the Λ hyperon in hypernuclei, as a promising observable in current hypernuclear spectroscopy, is discussed in this subsection with the newly developed DD-LZ1-
$ \Lambda1 $ and other selected CDF functionals. The Λ spin-orbit splitting is defined by the difference in Λ single-particle energies between a couple of spin partner states,$ \begin{align} \Delta E_{\rm{SO}}^\Lambda \equiv \varepsilon_{j_\Lambda=l_\Lambda-1/2} - \varepsilon_{j_\Lambda=l_\Lambda+1/2}. \end{align} $

(25) As shown in Fig. 3, the analysis is performed for the Λ spin partner states
$ 1p $ in oxygen hyperisotopes, with the Λ hyperon occupying its ground state.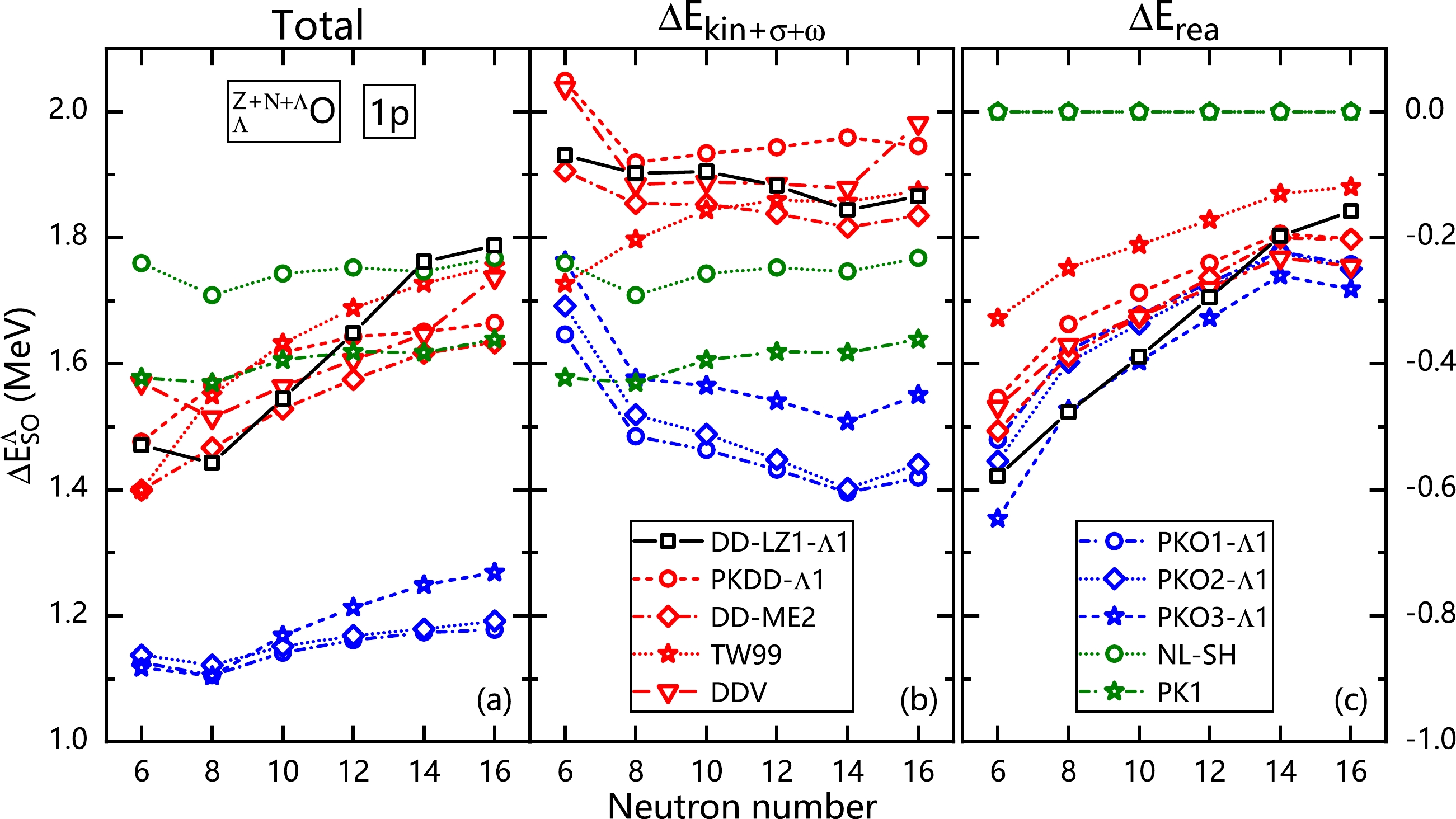
Figure 3. (Color Online) Spin-orbit splitting of
$ \Lambda 1p $ spin-partner states as a function of neutron number N for the ground state in$ ^{Z+N+\Lambda}_{\phantom{Z+N+}\Lambda} $ O hypernuclei [panel (a)], and its contribution$ \Delta E_{\rm{kin}+\sigma+\omega} $ from the sum of the kinetic energy, the density-independent potential energies of the σ and ω channels [panel (b)], and the rearrangement terms$ \Delta E_{\rm{rea}} $ due to density-dependent meson-hyperon couplings [panel (c)]. The results are extracted from the calculations with the DDRMF effective interactions DD-LZ1-$ \Lambda1 $ , PKDD-$ \Lambda1 $ , DD-ME2, TW99, and DDV, the DDRHF interactions PKO1-$ \Lambda1 $ , PKO2-$ \Lambda1 $ , and PKO3-$ \Lambda1 $ , and the NLRMF interactions NL-SH and PK1.As shown in Fig. 3(a), the isospin dependence of
$ \Delta E_{\rm{SO}}^\Lambda $ is clearly distinguished with the chosen CDF functionals. The curves from NLRMF models tend to be stable with increasing neutron number, whereas for DDRMF or DDRHF functionals the splitting enlarges generally with isospin. Among them, DD-LZ1-$ \Lambda1 $ exhibits the most significant isospin dependence. Moreover, it is clear that a smaller Λ spin-orbit splitting is predicted by DDRHF than by RMF, which is illustrated as a result in single-particle properties because the dynamical equilibrium between nuclear attraction and repulsion is dramatically changed with the appearance of Fock terms [74].To better understand the evolution of Λ spin-orbit splitting with isospin, we can decompose
$ \Delta E_{\rm{SO}}^\Lambda $ into various parts according to its source of kinetic or potential energy. The values are obtained by left-multiplying the transferred Dirac spinor to the Dirac equation, Eq. (18), and separating the integrated contributions from different self-energy terms. For instance,$ \Delta E_{\text{rea}} $ originates from the contribution of the rearrangement term$ \Sigma_R $ to the Λ self-energy$ \Sigma_{0,\Lambda} $ , as seen in Eq. (19), owing to the density dependence of meson-hyperon couplings. Consequently, the rest one from the kinetic energy and density-independent potential energies can be summed over; therefore,$ \Delta E_{\text{kin}+\sigma+\omega}\equiv\Delta E_{\rm{SO}}^\Lambda-\Delta E_{\text{rea}} $ , as discussed in Fig. 3(b).It is observed that the values of Λ spin-orbit splitting are primarily determined via
$ \Delta E_{\text{kin}+\sigma+\omega} $ . However, the isospin dependence of the splitting is weakly controlled by$ \Delta E_{\text{kin}+\sigma+\omega} $ , except for$ ^{15}_\Lambda $ O. Attributed to the occupation of the$ \nu 1p_{1/2} $ orbit, the Λ spin-orbit splitting predicted by various CDF functionals systematically decreases from$ ^{15}_\Lambda $ O to$ ^{17}_\Lambda $ O. As illustrated in Ref. [74], the spin-orbit coupling potential of the hyperon is determined mainly by the radial derivative of the self-energy$ \Sigma_-^\Lambda $ . In general, the more neutrons are filled into hypernuclei, the larger the density circumstance where the Λ hyperon is housed. Thus, if the model is density dependent, such as the DDRMFs and DDRHFs given in Fig. 2, the meson-hyperon coupling strength weakens and$ \Delta E_{\rm{SO}}^\Lambda $ should decrease as the neutron number increases. As shown in Fig. 3(b), such a reduction in$ \Delta E_{\text{kin}+\sigma+\omega} $ is remarkable from$ ^{15}_\Lambda $ O to$ ^{17}_\Lambda $ O and is relatively less significant at larger neutron numbers.In contrast with the NLRMF case, density-dependent CDFs introduce an extra contribution to reinforce the isospin dependence of the splitting, as demonstrated in Fig. 3(c), which cancels the reduction trend in
$ \Delta E_{\text{kin}+\sigma+\omega} $ overwhelmingly and finally leads to the enhancement of$ \Delta E_{\rm{SO}}^\Lambda $ with increasing neutron number in Fig. 3(a). In fact, the contribution$ \Delta E_{\text{rea}} $ to Λ spin-orbit splitting originates from the rearrangement terms of the self-energies, which depends on the density slope of the meson-baryon coupling strength, according to Eq. (21). As shown in Fig. 3(c),$ \Delta E_{\text{rea}} $ generates a suppressed contribution to the total Λ spin-orbit splitting in the whole oxygen hyperisotopes. As the neutron number increases, the density scenario where Λ lives may become more intense, leading to a weaker density dependence of the meson-hyperon coupling strength, a smaller density slope, and a suppressed value of$ \Delta E_{\text{rea}} $ . Therefore, the link between the isospin evolution of Λ spin-orbit splitting and the in-medium behavior of the$ \Lambda N $ interaction with baryon density is elucidated from the discussion on oxygen hyperisotopes. In consequence, possible experimental constraints on$ \Delta E_{\rm{SO}}^\Lambda $ along the hyperisotopes may assist us further in understanding the in-medium effects of nuclear force. -
In the properties of hypernuclear structure, it is not only Λ spin-orbit splitting but also the Λ impurity effect that can exhibit information on in-medium nuclear interactions. In Fig. 4(a), we select the DDRMF functionals DD-LZ1-
$ \Lambda1 $ and DD-ME2, DDRHF's PKO1-$ \Lambda1 $ , and NLRMF's PK1, to illustrate its influence on the matter radii of oxygen (hyper)isotopes, where the solid and dash-dotted lines correspond to the calculated results for single-Λ hypernuclei and their nucleonic counterpart in oxygen (hyper)isotopes, respectively. The matter radius$ R_m $ in hypernuclei increases monotonically as the neutron number increases, regardless of the specific model used, where a steep leap from$^{23}_\Lambda$ O to$^{25}_\Lambda $ O corresponds to the effect of new occupation in$ \nu 2s_{1/2} $ .
Figure 4. (color online) Variation in the matter radii of hypernuclei [Panel (a)] and their 16O core [Panel (b)] in oxygen (hyper)isotopes with respect to the neutron number, with the Λ hyperon occupying the
$ 1s_{1/2} $ ground state. The solid and dash-dotted lines represent the calculated results for hypernuclei and normal isotopes without a hyperon, respectively. The results are obtained with the CDF functionals DD-LZ1-$ \Lambda1 $ , DD-ME2, PKO1-$ \Lambda1 $ , and PK1.Although divergent values are given for oxygen isotopes without a hyperon, all of the selected models offer matter radii that are closer in size for hypernuclei, implying
$ R_m $ of hypernuclei as a possible model-independent observable. It is evident that the matter radii of oxygen hyperisotopes contract compared to their nucleonic counterparts, that is, size shrinkage due to the impurity effect of the Λ hyperon. However, the shrinkage magnitude appears to be strongly model dependent. Among them, the DDRMF effective Lagrangian DD-LZ1-Λ1 yields the largest difference between the solid and dash-dotted lines, whereas the NLRMF PK1 yields the smallest disparity. By checking the bulk properties of nuclear matter within these CDFs, we verify that the shrinkage magnitude correlates well with the incompressibility, which is 230.7 MeV for DD-LZ1, 250.8 MeV for DD-ME2, 250.2 MeV for PKO1, and 282.7 MeV for PK1 [61, 96, 97]. In fact, the larger the incompressibility K, the harder the nucleus is contracted by the exerted attraction from the filled hyperon inside, resulting in a weaker size shrinkage effect in the calculated matter radii. A similar relation can be found from Table 2 of a paper on the isoscalar giant monopole resonance of hypernuclei, in which the effective nuclear incompressibility modulus was extracted [98].To further distinguish the effects of different interactions on the description of hypernuclear structure, we investigate the isospin evolution of the Λ hyperon radius
$ R_\Lambda $ in oxygen hyperisotopes using all the selected CDF effective interactions, as shown in Fig. 5. It is tangibly observed that$ R_\Lambda $ evolves diversely along oxygen hyperisotopes with different CDF effective interactions. Some effective interactions, such as PKO3-$ \Lambda1 $ , DD-ME2, DDV, and DD-LZ1-$ \Lambda1 $ , exhibit a reduced$ R_\Lambda $ with increasing neutron number. In particular, DD-LZ1-$ \Lambda1 $ gives the smallest hyperon radii among all chosen CDFs and a strong declining trend. In fact, the core polarization effect due to the Λ hyperon plays a significant role in this evolution. When Λ occupies the$ 1s_{1/2} $ state, its density distribution is concentrated inside the hypernucleus. As a result, the coupling or attraction of Λ with the nucleons in the core (corresponding to$ ^{16} $ O) appears to be relatively stronger than that with the valence nucleons. Hence, the evolution of the hyperon radius can be understood more or less by the size change of the core with respect to neutron number.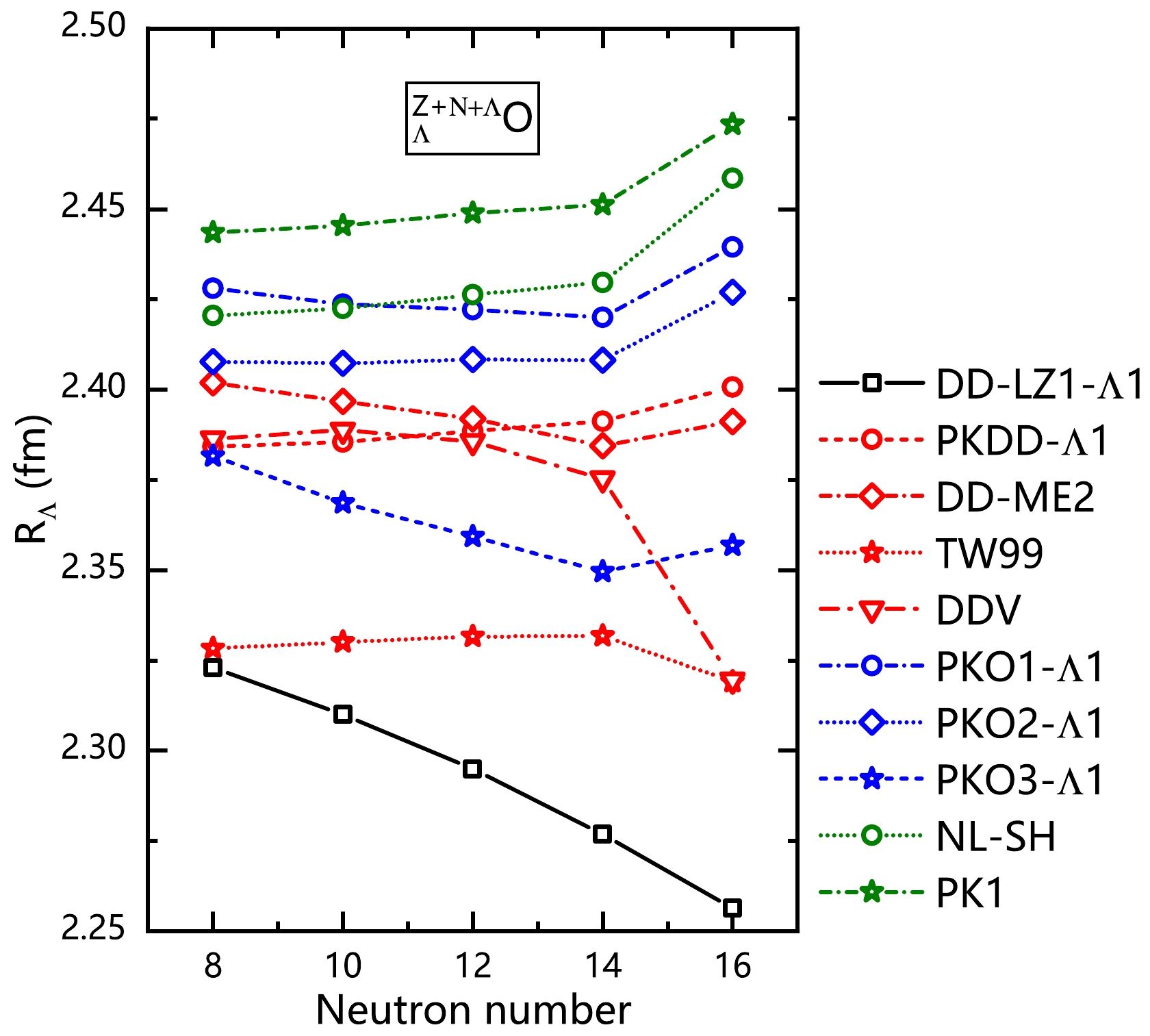
Figure 5. (color online) Variation in the Λ hyperon radius with respect to neutron number in oxygen hyperisotopes. The Λ hyperon is filled in the
$ 1s_{1/2} $ ground state. These results are obtained from calculations using all selected CDF effective interactions.The variation in the matter radii for the
$ ^{16} $ O core in oxygen (hyper)isotopes is plotted in Fig. 4(b) with respect to neutron number. From$ N=8 $ to 14, in contrast with the situation of the total matter radii$ R_m $ , there is no consistent isospin dependence for the selected CDFs in the core radius$ R_m^{\rm{core}} $ with increasing neutron number. The NLRMF functional PK1 exhibits a significant increasing trend with isospin, whereas the DDRMF functional DD-LZ1-Λ1 exhibits a noticeable decrease. Consequently, the hyperon radius$ R_\Lambda $ exhibits a similar isospin dependence resulting from the core polarization effect, determined mainly by the various isospin properties of CDF functionals in nucleon-nucleon channels. However, from$ N=14 $ to 16, the hyperon radii in DD-LZ1-Λ1, TW99, and DDV exhibit opposite trends compared to their core radii, with the presence of additional valence neutrons occupying the$ 2s_{1/2} $ orbital. After analyzing the contribution from various interaction matrix elements, it is found that the interaction between$ \nu1p_{1/2} $ and$ \Lambda 1s_{1/2} $ changes within these effective interactions as the neutron number increases from 14 to 16, that is, from attraction to repulsion. This alteration in the interaction dynamics results in extra suppression to the hyperon radius, such as in the case of DD-LZ1-Λ1. From such analysis, the importance of nuclear in-medium effects in affecting the hyperon radii is unveiled. Therefore, the divergent isospin evolution of$ R_\Lambda $ given by CDFs with different density dependent meson-baryon couplings makes it a valuable tool for clarifying the in-medium behavior of nuclear force. It is still difficult to directly measure the matter and hyperon radii experimentally owing to the limited lifetime of hypernuclei and the current reaction techniques. Therefore, theoretical studies on several radii of hypernuclei may be helpful for proposals of future experiments based on radioactive ion beam facilities, especially by revealing the correlations between the characteristic radii as well as the bulk properties of nuclear matter. -
In summary, considering the significance of nuclear in-medium effects in nuclear many-body problems, such as for eliminating spurious shell closures, we expand the newly developed DDRMF Lagrangian DD-LZ1 to incorporate the Λ hyperon degree of freedom and determine the
$ \Lambda N $ effective interaction by fitting the experimental data of Λ separation energies for several single-Λ hypernuclei. Subsequently, with several other CDF functionals, the features, including Λ separation energy and$ B(E1) $ transition, and evolution of spin-orbit splitting and the characteristic radii are analyzed in detail along oxygen (hyper)isotopes.By comparing the results obtained from different CDF models, we further investigate the crucial impact of nuclear in-medium effects on accurately describing the properties of hyperons, both in terms of their bulk and single-particle properties. For the
$ 1p $ spin-orbit splitting of the Λ hyperon, significant differences in the isospin dependence are observed among the selected CDF effective interactions in oxygen hyperisotopes. As the neutron number increases, the density circumstance where the hyperon is housed gradually increases, which causes the meson-hyperon coupling strengths that determine the hypernuclear properties to also change. In particular, the density-dependent CDF effective interactions introduce additional rearrangement terms that significantly enhance the isospin dependence of Λ spin-orbit splitting, leading to a more distinct variation in$ \Delta E_{\rm{SO}}^\Lambda $ with neutron number in the DDRMF and DDRHF models. It is worth noting that the given Λ spin-orbit splitting by DD-LZ1-Λ1 remains relatively large compared to typical values [99] because we focus mainly on elucidating the role of the density dependence of meson-baryon couplings in the isospin properties of hypernuclei. It has been suggested in CDF approaches that the predicted$ \Delta E_{\rm{SO}}^\Lambda $ could be reduced by including an extra ω-tensor coupling in the Λ channel [51, 79−81]. To provide a more thorough examination of the subject presented here, we propose to incorporate this term into our future work.The evolution of the hypernuclear matter radius with isospin is further investigated. A significant model dependence in the magnitude of size shrinkage due to the inclusion of the Λ hyperon is observed, where the DDRMF functional DD-LZ1-Λ1 exhibits the largest shrinkage effect. The result is then explained by an anticorrelation between the incompressibility coefficients K of nuclear matter and the hyperon radii
$ R_\Lambda $ , providing us with a possible way to constrain the hyperon distribution inside a hypernucleus from the better-determined bulk properties of nuclear matter. Additionally, we find that the isospin evolution of the hyperon radius is primarily influenced by the density-dependent behavior of the chosen CDF functional in the$ NN $ interaction channel via the procedure of core polarization. Thus, the sensitivity in depicting these hyperon-relevant properties in CDF models with different meson-baryon couplings offers great potential for elucidating the nuclear in-medium nature in both the$ \Lambda N $ and$ NN $ channels. -
The authors are grateful for the computational resources provided by the Supercomputing Center of Lanzhou University.
Density-dependent relativistic mean field approach and its application to single-Λ hypernuclei in oxygen hyperisotopes
- Received Date: 2023-07-10
- Available Online: 2023-12-15
Abstract: The in-medium feature of nuclear force, which includes both nucleon-nucleon (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: