-
The weak mixing angle,
$ \theta_W $ , is a fundamental parameter of the standard model (SM). It governs the relative strength of the axial-vector couplings to the vector couplings in the neutral-current interactions with Lagrangian$ \begin{eqnarray} \mathcal{L} = -{\rm i} \frac{g}{2\cos\theta_W}\bar{f}\gamma^\mu \left( g^f_V - g^f_A \gamma_5\right) f Z_\mu, \end{eqnarray} $

(1) where
$ g^f_A $ and$ g^f_V $ are the axial-vector and vector couplings, defined as$ g^f_A=I^f_3 $ and$ g^f_V = I^f_3 - 2Q_f\cdot \sin^2\theta_W $ , where$ I^f_3 $ and$ Q_f $ are the weak isospin component and the charge of the fermion f.$ Z_\mu $ describes the Z boson exchange. To include higher order electroweak radiative corrections, the effective weak mixing angles are defined as$ \begin{eqnarray} \sin^2\theta^f_\text{eff} = \kappa_f \sin^2\theta_W, \end{eqnarray} $

(2) where
$ \kappa_f $ is a flavor-dependent effective scaling factor absorbing the higher order corrections [1]. By doing this,$ \sin^2\theta^f_\text{eff} $ can be directly measured from the experimental observations; thus, it is very sensitive to both the precision validation of SM and the search for new physics beyond SM.It is customary to quote the leptonic effective weak mixing angle
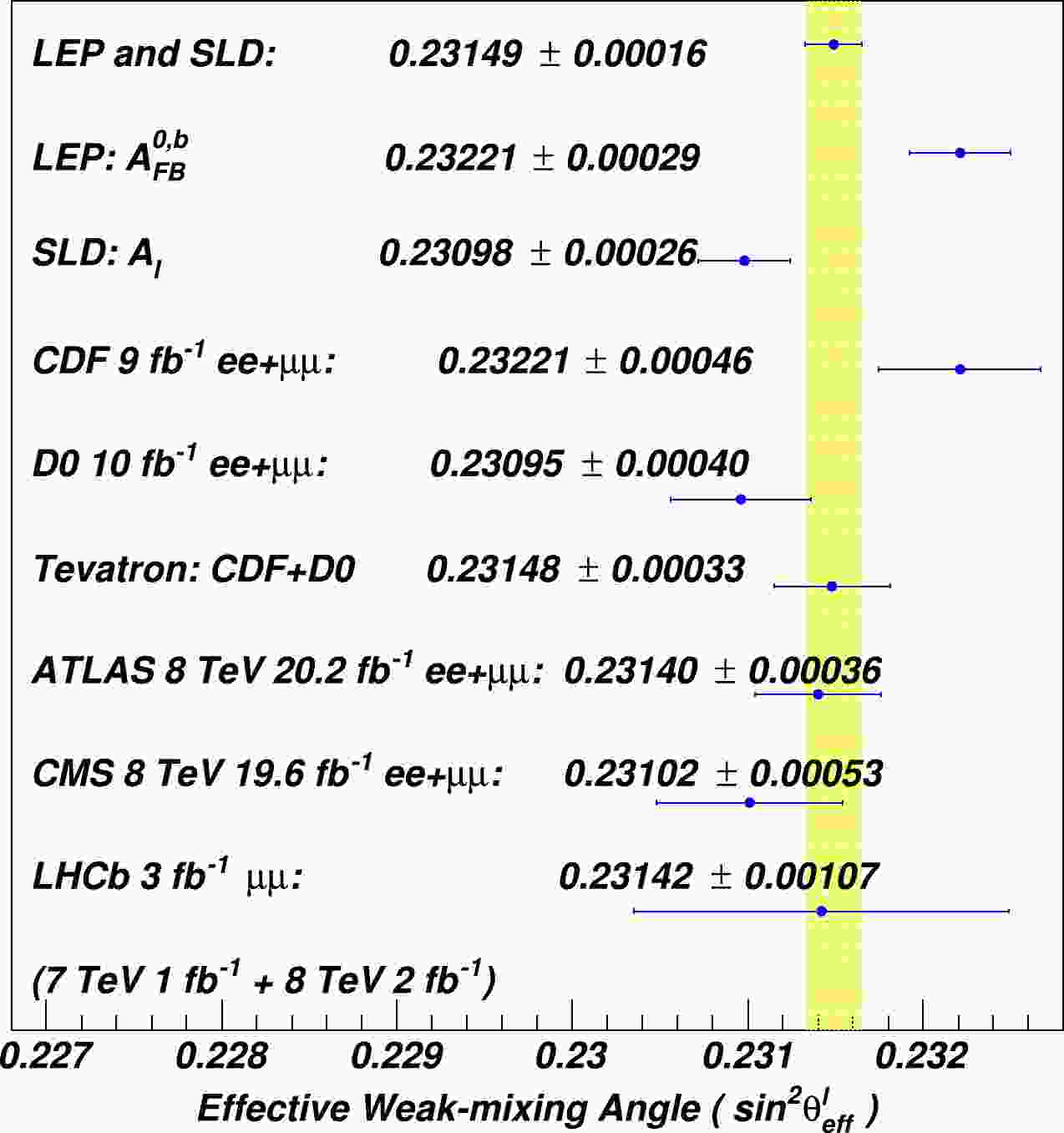
$ \sin^2\theta^\ell_\text{eff} $ , so that the measurements at the LEP, SLC, Tevatron, and LHC can be directly compared with each other. For this, shifts between$ \sin^2\theta^\ell_\text{eff} $ and$ \sin^2\theta^q_\text{eff} $ need to be calculated under the standard model assumptions. Herein, it is calculated using the ZFITTER package [2], which gives a shift of$ -0.0001 $ and$ -0.0002 $ for$ \sin^2\theta^u_\text{eff} $ and$ \sin^2\theta^d_\text{eff} $ with respect to$ \sin^2\theta^\ell_\text{eff} $ , respectively. For$ \sin^2\theta^b_\text{eff} $ as a special case, the shift is$ +0.0014 $ E. Such a calculation has a high precision as long as the energy of the interaction does not approach 160 GeV, where the correction from the box-diagrams becomes sizable [3].$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ has been measured in the past two decades using the$ f_i\bar{f_i}\rightarrow Z/\gamma^* \rightarrow f_j\bar{f_j} $ productions. The results are shown in Fig. 1. The most precise determinations of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ come from the electron-positron colliders, which are 0.23221$ \pm $ 0.00029 from the combined LEP b quark production, and 0.23098$ \pm $ 0.00026 from the SLD [1]. A similar precision was achieved at the proton-antiproton collider Tevatron as 0.23148$ \pm $ 0.00033 [4].$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ was also measured by ATLAS, CMS, and LHCb collaborations [5−7].$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ was extracted from the forward-backward charge asymmetry ($ A_{FB} $ , to be introduced in the following sections) in all the measurements above, except for the SLD result which also used the left-right polarization asymmetry.
Figure 1. (color online) Previously measured
$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ from LEP, SLD, Tevatron, and LHC.Previous measurements achieved a relative precision at
$\mathcal{O}(0.1\%)$ with respect to the central value of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ . It played an important role in the global fitting of the SM electroweak sector in the past years. However, the experimental precision, which is generally limited by the size of the data sample, is much worse than the precision of the theoretical calculations. At the two-loop level, the uncertainty in$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ calculation is reduced to 0.00004 [8]. It is essential to improve the experimental precision on$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ for it to be comparable to the theoretical calculations.Though a large data sample will be collected at the LHC in the next 10 years, it will be very difficult to reduce the uncertainty of
$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ to less than 0.00010 using the LHC data. At the hadron colliders, the initial state fermions of the neutral-current interactions are quarks and antiquarks that act as partons in the hadrons. Their effective momentum are described by the parton distribution functions (PDFs), which extrapolate large uncertainties to the$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ extraction. In the recent LHC measurements, the PDF-induced uncertainties of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ are greater than$ 0.00020 $ [5, 6], and it will become the most leading uncertainty in the future. Such uncertainty will not be naturally reduced as the LHC data is introduced in the PDF global analysis, owing to a strong correlation between the PDF and the$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ in the LHC observations [9]. The QCD-induced uncertainty is also greater than$ 0.00010 $ at the LHC [6], extrapolated via the soft-gluon radiations in the initial state. In conclusion, it would be most likely to achieve a high precision determination on$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ at the next generation electron-positron colliders, which are generally free from PDF and QCD and have the capability to generate a large data sample.In this paper, we study the measurement of
$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ at the proposed Circular Electron Positron Collider (CEPC). CEPC is a powerful machine providing physics interactions with high energy electron-positron initial state [10]. It is proposed to have a two-year running plan around the Z boson mass pole. We focus on the precision of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ in lepton and b quark final states, considering both statistical uncertainty and potential experimental systematics. -
The forward-backward charge asymmetry
$ A_{FB} $ of the$ f_i\bar{f_i} \rightarrow Z/\gamma^* \rightarrow f_j\bar{f_j} $ process is an ideal experimental observable to probe the electroweak interaction with a high precision. It is defined as$ \begin{eqnarray} A_{FB} = \frac{N_F - N_B}{N_F + N_B}, \end{eqnarray} $

(3) where
$ N_F $ and$ N_B $ are the numbers of the forward and backward events, respecitvely, judged by the scattering angle$ \theta_{ij} $ formed by the directions of the initial state negative charged electron beam and the final state fermion. Events with$ \cos\theta_{ij}>0 $ are classified as forward (F) and those with$ \cos\theta_{ij}<0 $ as backward (B). At the CEPC, the initial state fermions are electrons and positrons, while the final state fermions can be leptons and quarks. The asymmetry arises from the interference between the vector and axial vector coupling terms, and they are precisely governed by$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ . The value of$ A_{FB} $ changes with the center-of-mass energy$ \sqrt{s} $ . Figure 2 shows the$ A_{FB} $ spectrum as a function of$ \sqrt{s} $ for different productions. The predictions are calculated using the effective born approximation package zfitter corresponding to the next-to-next-to-leading order (NNLO) radiative corrections [2].$ A_{FB} $ is very sensitive to$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ around the Z mass pole. In the low mass region, the asymmetry approaches zero as$ \sqrt{s} $ reduces owing to the rising contribution of the photon exchange. In the high mass region, the asymmetry is roughly constant, dominated by the interference between the γ and Z boson exchanges. Therefore, the sensitivity of off-pole$ A_{FB} $ to$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ is significantly reduced. The sensitivity, defined as
Figure 2. (color online)
$ A_{FB} $ spectrum as a function of$ \sqrt{s} $ for$ e^+e^-\rightarrow Z/\gamma^* \rightarrow \ell^+\ell^- $ and$ e^+e^-\rightarrow Z/\gamma^* \rightarrow b\bar{b} $ productions.$ S = \partial A_{FB} / \partial {\sin^2\theta_{\text{eff}}^{{ \ell }}}, $

is given as a function of
$ \sqrt{s} $ in Fig. 3 for b quark and lepton productions as an example. Predictions are calculated using zfitter as well. In the following sections, we estimate the uncertainty of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ based on the sensitivity S of$ A_{FB} $ to$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ . -
The observed asymmetry, denoted as
$ A^\text{obs}_{FB} $ , could be biased because of the imperfect detector performance. Three major contributions of the potential experimental systematics are discussed in this work, which come from the$ \sqrt{s} $ determination, charge measurement, and inefficiency of particle reconstruction and selection. These systematics are generally small. At lepton colliders,$ \sqrt{s} $ of an event can be precisely controlled by the beam energy, instead of reconstructing from the final state particles measured in the detector. According to the CEPC conceptual design report, the uncertainty of the electron and positron beam energy can be controlled by around 100 keV [11], extrapolating the relative uncertainty of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ to be much lower than$0.01\%$ . The inefficiency of particle reconstruction and selection could have a large effect especially in quark productions. However,$ A_{FB} $ is defined as a relative asymmetry where the total cross section is perfectly cancelled. Therefore, the limited efficiency only enlarges the statistical uncertainty of the$ A_{FB} $ observation and$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ extraction and causes no systematics, as long as there is no difference between the forward and backward event efficiencies. With the large data sample of CEPC, the statistical uncertainty will be negligible anyway.A more complicated case is the charge mis-identification of the final state particles, which can increase both systematic extrapolation and statistical uncertainty. The forward and backward categories are classified according to the charge of the final state particles. If an event has a probability of f to be wrongly classified as forward or backward owing to the mis-identification of charge, the observed
$ A_{FB} $ will be diluted from the original$ A_{FB} $ , written as$ \begin{eqnarray} A^\text{mis-q}_{FB} = (1-2f) A_{FB}. \end{eqnarray} $

(4) When
$f=50\%$ , there will be no observed asymmetry. Such dilution causes reduction in the$ A_{FB} $ to$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ sensitivity, appearing as an enlarged statistical uncertainty. For the selected$ e^+e^- \rightarrow Z/\gamma^* \rightarrow f\bar{f} $ events, f can be determined from the following relationship:$ \begin{eqnarray} N_{ss} = 2\omega(1-\omega)\cdot N_\text{total}, \end{eqnarray} $

(5) where
$ N_{ss} $ is the number of selected events with the same charge sign as the final state fermions, while$ N_\text{total} $ is the total number of selected events. ω is the probability for mis-identifying the charge of a single fermion, and we have$ f = \omega^2/(\omega^2+(1-\omega)^2) $ . The precision of the f determination is dominated by the statistics. Considering the large data sample at the CEPC, f could be precisely determined by this data-driven method, and it causes very small systematics. Besides, the final state fermions should usually have opposite charge in order to suppress the mis-identification of the forward and backward categories.According to the definition of
$ A_{FB} $ in Eq. (4) and assuming that the value of$ A_{FB} $ around Z pole is close to zero, the statistical uncertainty of the observed asymmetry$ A^\text{obs}_{FB} $ is approximately written as$ \begin{eqnarray} \delta A^\text{obs}_{FB} = \sqrt{\frac{1-\left(A^\text{obs}_{FB}\right)^2}{N}} \approx \sqrt{\frac{1}{N}} , \end{eqnarray} $

(6) where N is the number of the selected events. Considering the above effects, the statistical uncertainty of
$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ measured from$ A_{FB} $ can be expressed as$ \begin{eqnarray} \delta {\sin^2\theta_{\text{eff}}^{{ \ell }}} = \sqrt{\frac{1}{N}} \cdot \sqrt{\frac{1}{\epsilon\cdot (1-2f)^2}} \cdot \frac{1}{|S|} , \end{eqnarray} $

(7) where
$ \epsilon $ is the overall efficiency of detecting and selecting an$ e^+e^-\rightarrow Z/\gamma^* \rightarrow \ell^+\ell^- $ event. The term$ \epsilon\cdot (1-2f)^2 $ is defined as the tagging power parameter. For the lepton final states, the overall efficiency is very close to$100$ %, and f is negligibly small. Therefore, the tagging power is almost$100\%$ [10]. It is considerably more complicated for the b quark final state. It is difficult to determine the b quark charge by measuring the final state jet. To obtain a better charge measurement, only a small part of the b quark production events, where b quarks decay to leptons or Kaons, could be used in the$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ measurement. Therefore, the tagging power parameter for the b quark productions needs to be optimized between the overall efficiency and the charge mis-identification probability. According to the CEPC simulation study [10, 12], with a selection of b quark with$98\%$ purity, the optimized tagging power for b quark production is 0.088.The number of the selected events N depends on the luminosity of the proposed running plan and the cross section of each channel of the Z boson decay. The latest CEPC studies propose a two-year running period around the Z boson mass pole, with 50 ab
$ ^{-1} $ integrated luminosity per year. That is, the CEPC can provide$1.7\times 10^{11}~ Z$ boson events every month. Considering the branching ratio [8] and Eq. (7), the expected statistical uncertainty of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ measured from the lepton final state ($ ee $ +$ \mu\mu $ ) is$ \delta {\sin^2\theta_{\text{eff}}^{{ \ell }}}(\ell) = 5 \times 10^{-6} $ using one month data. For b quark productions, the uncertainty is$\delta {\sin^2\theta_{\text{eff}}^{{ \ell }}}(b) = 4 \times 10^{-6}$ using one month data. This uncertainty can be further reduced by using the proposed two-year data sample. However, it would be more useful to run at different collision energy points off-pole rather than simply collecting data at the very peak of the Z mass line shape. When changing the collision energy in this study, the cross section of the Z boson production is altered according to its mass line shape. The drop of the instantaneous luminosity is estimated approximately as the third power of the increase in the collision energy [11]. The expected statistical uncertainties of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ with the one month data collection at different collision energy points are summarized in Table 1.collision energy/GeV $ \delta {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ in lepton

final state$ \delta {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ in b quark

final state70 $ 1.5\times 10^{-4} $ 

$ 4.1\times 10^{-5} $ 

75 $ 6.8\times 10^{-5} $ 

$ 3.3\times 10^{-5} $ 

92 $ 4.9\times 10^{-6} $ 

$ 3.5\times 10^{-6} $ 

105 $ 1.7\times 10^{-4} $ 

$ 2.7\times 10^{-5} $ 

115 $ 2.0\times 10^{-3} $ 

$ 4.8\times 10^{-5} $ 

130 $ 4.0\times 10^{-3} $ 

$ 9.8\times 10^{-5} $ 

Table 1. Expected statistical uncertainties on
$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ . Results are estimated according to one month data collection.As we can see, both the lepton final state and b quark final state can provide precise determination of
$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ at the Z boson mass pole. For the measurement of the energy running effect, b quark production has higher precision because the sensitivity S off-pole drops much slower than that for the lepton final state cases. To make a conservative estimation, the precision of the$ \sin^2\theta^\ell_\text{eff} $ determination, considering both the statistical uncertainty and the experimental systematics at the CEPC, can be 0.00001 in both the lepton and b quark productions with the one month data collection. The$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ can be measured as a function of the collision energy up to 130 GeV, with a precision of approximately$ 0.0001 $ from the b quark productions.Owing to the contribution of the t-channel and the s-t interference in the electron final state, the uncertainty of the theoretical calculation in the electron final state can be very large,
$ 0.00085 $ for the weak mixing angle according to Ref. [1]. However, such an uncertainty only affects the dielectron events. For other channels, the residual theoretical uncertainties can be much smaller,$ 0.00006 $ for the weak mixing angle [1]. Therefore, the best precision of the$ \sin^2\theta^\ell_\text{eff} $ determination relies on the muon channel. The uncertainty of the calculations of the$ e^+e^-\rightarrow f\bar{f} $ process is much greater than the statistical uncertainty and experimental systematics; thus, it will be the major source limiting the final precision of the experimental measurement of$ \sin^2\theta^\ell_\text{eff} $ . However, it will still be considerably better than the expected precision at the hadron colliders. -
Aside from electron, muon and b quark channel
$ A_{FB} $ measurement, other channels such as c quark can also be utilized to extract$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ . With the predicted sensitivity$ S_{f\bar{f}} $ listed in Table 2, the precision of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ from$ A_{FB} $ measurement can be predicted using Eq. (7), after investigating the performance of different final state particles. For instance, a recent CEPC simulation study [13] used leading particle and weighted jet charge combined information to achieve better performance of heavy flavor jet charge measurement, and the bare tagging power1 of b/c quark was determined. The tagging power of the b quark final state is doubled; therefore, the estimated$ \delta {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ with the b quark final state is$ 2.5\times10^{-6} $ (with the one month data collection at Z pole). However, for the c quark circumstance, owing to the low purity of c flavor tagging, the estimation will need a detailed simulation study of flavor tagging using$ Z\rightarrow q\bar{q} $ samples.$ \sqrt{s} $ /GeV

S of $ A_{FB}^{e/\mu} $ 

S of $ A_{FB}^{d} $ 

S of $ A_{FB}^{u} $ 

S of $ A_{FB}^{s} $ 

S of $ A_{FB}^{c} $ 

S of $ A_{FB}^{b} $ 

70 0.224 4.396 1.435 4.403 1.445 4.352 75 0.530 5.264 2.598 5.269 2.616 5.237 92 1.644 5.553 4.200 5.553 4.201 5.549 105 0.269 4.597 1.993 4.598 1.994 4.586 115 0.035 3.956 1.091 3.958 1.087 3.942 130 0.027 3.279 0.531 3.280 0.520 3.261 Table 2. Sensitivity S of different final state particles.
Tau lepton is the only final state fermion for which the polarizarion (
$ P_{\tau} $ ) can be measured at an unpolarized leptonic collider [1] with$ \begin{eqnarray*} P_{\tau}=\frac{\mathrm{d}(\sigma_r-\sigma_l)}{\mathrm{d}\cos{\theta}}\Big/ \frac{\mathrm{d}(\sigma_r+\sigma_l)}{\mathrm{d}\cos{\theta}}, \label{eq:PTauMeasurement} \end{eqnarray*} $

where
$ \sigma_{r/l} $ is the cross section for producing right/left-handed final state tau leptons.$ P_\tau $ is related to$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ by$ \begin{eqnarray} P_{\tau}=-\frac{\mathcal{A}_\tau\cdot(1+\cos^2{\theta})+\mathcal{A}_e\cdot(2\cos{\theta})} {(1+\cos^2{\theta})+\mathcal{A}_\tau\mathcal{A}_e\cdot(2\cos{\theta})}, \end{eqnarray} $

(8) where
$ \begin{eqnarray*} \mathcal{A}_f=\frac{2g_V^fg_A^f}{(g_V^f)^2+(g_A^f)^2}=\frac{2g_V^f/g_A^f}{1+(g_V^f/g_A^f)^2} \end{eqnarray*} $

is the asymmetry parameter. This property was utilized by LEP to perform an independent measurement for
$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ . Compared with the whole lepton channel, the statistics of the tau channel are small, and the efficiency and purity of tau reconstruction are low. However, with a very high sensitivity of$ P_{\tau} $ to$ \tau-Z $ vector coupling constant, a high precision extraction of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ can be achieved.The measurement of
$ P_{\tau} $ is based on the fact that τ has a short lifetime and that the kinematic spectrum of its decay production is different when tau has different helicity (shown in Fig. 4 and Fig. 5). We used the Pythia8 program [14] to generate$ e^{+}e^{-}\rightarrow \tau^{+}\tau^{-} $ events, and then, we used the TAUOLA interface [15] to decay the taus.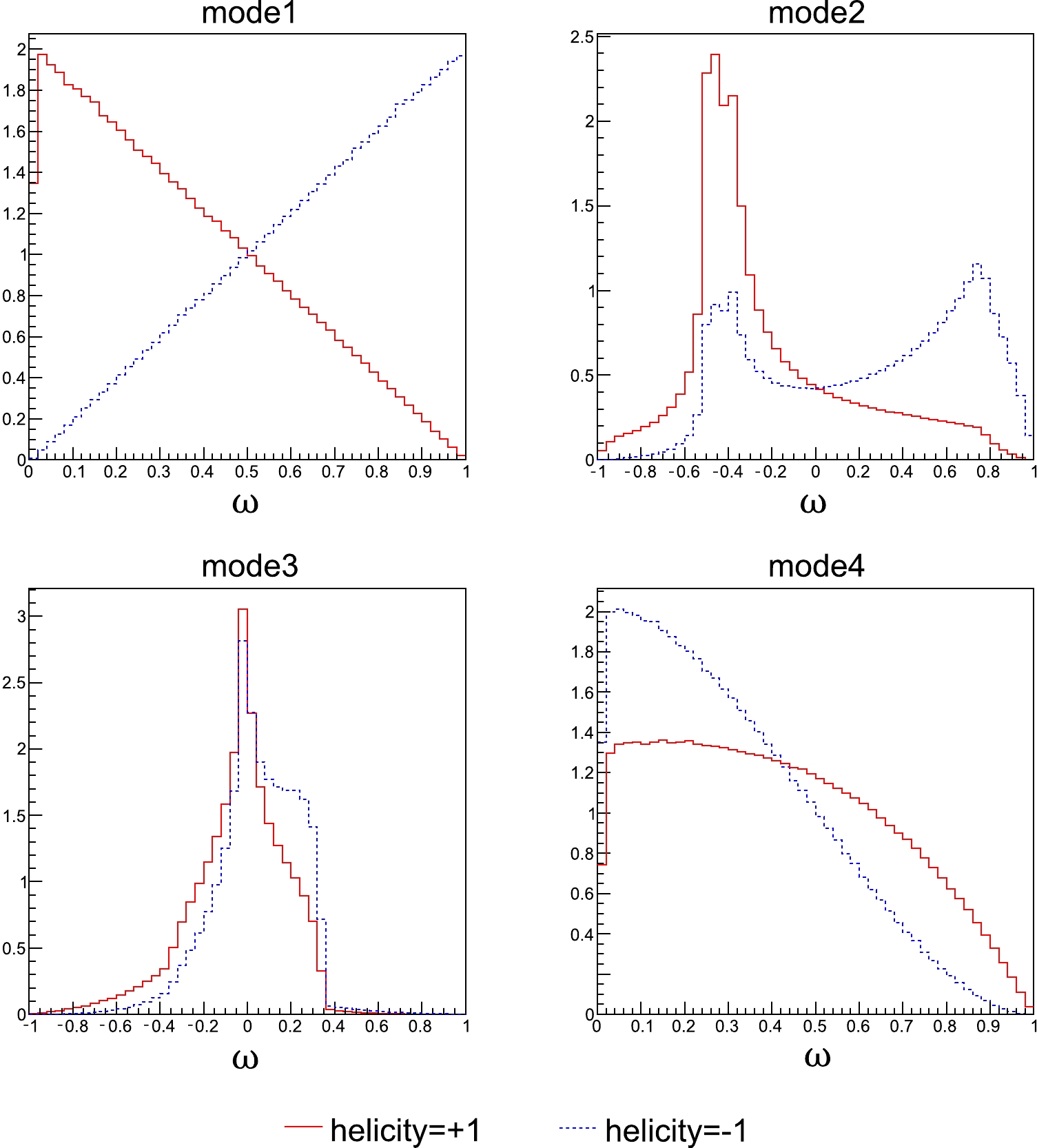
Figure 5. (color online) Kinematic spectrum of different tau decay modes. The red solid line and blue dashed line represent the kinematic spectrum of taus with
$ helicity=+1 $ and$ -1 $ , respectively. All the spectra are generated using Pythia8 genarator and TAUOLA interface.Using two templates with
$ helicity=+1 $ and$ -1 $ , respectively, we can fit to the pseudo-data, whose$ P_\tau $ is a given number. Owing to limited computing resources, only$2\times10^8~ Z\rightarrow \tau\bar{\tau}$ events are generated for the pseudo-data and each template. The extrapolation of the fitting results shows that the statistical uncertainty of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ with the one month data collection at the Z pole is$ 2.15\times 10^{-6} $ using the$ P_\tau $ measurement.Experimentally, the τ lepton is reconstructed from its daughter particles in the decay, thus relying on the precision of the measurement of the particle energy and the background control. This makes the detector systematics extrapolate more significantly to the weak mixing angle than that in other channels, According to the study of LEP [1], the systematics in the τ measurement is on an order of
$ \mathcal{O}(10^{-4}) $ for the weak mixing angle. Given that the statistical uncertainty at the CEPC would be much smaller, the total uncertaintt in the τ channel measurement will be dominated by the systematics. -
We present an estimation of the precision of
$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ determination at the CEPC in the lepton final state and b quark final state. With a high instantaneous luminosity, the statistical uncertainty can be reduced to be negligible. The experimental systematics are also negligible in general since$ A_{FB} $ is defined as a relative asymmetry so that the systematics cancel out. The dominant uncertainty arises from the theoretical calculation of the$ e^-e^+\rightarrow f\bar{f} $ process. As a result, the precision of$ \sin^2\theta^\ell_\text{eff} $ can be improved to$ \mathcal{O}(10^{-5}) $ , from the current precision of$ \mathcal{O}(10^{-4}) $ at the LEP, SLC, and Tevatron. Owing to a large model uncertainty from the QCD calculations and PDF modeling, it is difficult to achieve such precision using the LHC data in the future. This precision will, for the first time, be comparable to the precision of the theoretical calculation of$ \sin^2\theta^\ell_\text{eff} $ with radiative corrections at the two-loop level, meaning that the precision of the SM electroweak global fit can be significantly improved. Note that the high precision measurement of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ at the CEPC is essential to the QCD studies at the LHC. As discussed in the introduction section, the observation of the proton structure and electroweak symmetry breaking is highly correlated in$ pp(q\bar{q})\rightarrow Z/\gamma^* \rightarrow \ell^+\ell^- $ events. In Ref. [9], it is proved that the single Z boson production can provide unique information of the relative difference between the quarks and antiquarks. However, it is not available yet in the PDF global fitting because of the large uncertainty induced by the experimental determination of$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ . By using the electron-positron interaction from the CEPC, the measured$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ can be used as high precision input in the PDF global fitting, fixing the electroweak calculations for predicting the single Z boson production cross sections.Finally, our analysis uses high purity
$ b\bar{b} $ sample to exclude the contamination of other quark flavors. With a properly designed working point for jet flavor tagging, we can also use other quark flavors to measure$ {\sin^2\theta_{\text{eff}}^{{ \ell }}} $ . Future development of detector optimization and advanced reconstruction algorithm, especially those based on machine learning, for example such as those recently used at the CMS experiment [16], could also boost performance. -
We thank Dr. Zhijun Liang from the Institution of High Energy Physics Chinese Academy of Science for the helpful discussions.
-
$\sqrt{s}/\rm GeV$ 

$ \sigma_{\mu}/\rm mb $ 

$ \sigma_{d}/\rm mb $ 

$ \sigma_{u}/\rm mb $ 

$ \sigma_{s}/\rm mb $ 

$ \sigma_{c}/\rm mb $ 

$ \sigma_{b}/\rm mb $ 

70 0.039 0.032 0.066 0.031 0.058 0.028 75 0.039 0.047 0.073 0.046 0.065 0.043 92 1.196 5.366 4.228 5.366 4.222 5.268 105 0.075 0.271 0.231 0.271 0.227 0.265 115 0.042 0.135 0.122 0.135 0.118 0.132 130 0.026 0.071 0.068 0.071 0.066 0.069 Table A1. Cross section of process
$ e^{+}e^{-}\rightarrow f\bar{f} $ calculated using the zfitter package. Values of the fundamental parameters are set as$m_{Z}=91.1875~\mathrm{GeV}$ ,$ m_{t}=173.2~\mathrm{GeV} $ ,$ m_{H}=125~\mathrm{GeV} $ ,$ \alpha_{s}=0.118 $ and$ m_{W}=80.38~\mathrm{GeV} $ .
Measurement of the effective weak mixing angle at the CEPC
- Received Date: 2023-06-12
- Available Online: 2023-12-15
Abstract: We present a study of the measurement of the effective weak mixing angle parameter (






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: