Thermal pairing treatment within the path integral formalism

Pairing correlations are a crucial issue in nuclear structure theory and have been the subject of numerous studies since they were first highlighted at the end of the 1950s [1]. The theory of superfluid states in nuclei was then developed by adapting the Bardeen, Cooper, and Schrieffer (BCS) theory [2] to nuclear physics [3]. However, the typical BCS theory in nuclear physics is a zero-temperature theory. Since the early 1960s, the generalization of the study of nuclear superfluidity at finite temperature has been the subject of considerable attention. This interest has not diminished over the last 60 years, and the subject is still relevant, especially for the study of nuclear processes in hot stellar environments [4−6]. Several studies have been devoted to pairing correlations in heated nuclei. Some used a statistical method based on the BCS theory (see, e.g., Refs. [7−13]) or Hartree-Fock-Bogoliubov (HFB) theory (see, e.g., Refs. [14−18]), before or after particle-number projection. Other studies were based on the temperature dependent random phase approximation (RPA), see, e.g., Refs. [19−22]. For a review, see Ref. [23]. Pairing in hot nuclei has also been investigated in the relativistic case using the relativistic Hartree-Bogoliubov model [24], relativistic finite temperature quasiparticle RPA [6], and covariant density functional theory [25−29].

Recently, the Matsubara formalism [30] and self-consistent Green's function approach [31] have also been used to describe nuclear superfluidity at finite temperature.

Another possible approach for the treatment of pairing correlations in heated systems is based on the path integral representation of the partition function, which involves the shell-model Monte-Carlo method [32−34]. However, this method is not easy to apply, especially for heavy systems with large particle-numbers. Therefore, the static-path approximation (SPA) [35−41] is considered a convenient method of obtaining an approximation of the partition function.

In Ref. [42], Fletcher used the path integral technique, starting with an approximation in the pairing Hamiltonian and then linearizing it using the Hubbard-Stratonovitch transformation [43, 44]. He then showed that the standard finite temperature BCS (FTBCS) gap equations can be obtained via a saddle-point approximation in the path integral representation of the partition function of the system. This method has also been used in the neutron-proton pairing scenario [45−48].

In this study, we propose an alternative method to investigate pairing correlations at finite temperature within the path integral formalism. It is based on the polar decomposition of the creation and annihilation operators of pairs of paired particles in the Hamiltonian of a system. The pairing term in the Hamiltonian is then written in square form, which enables direct use of the Hubbard-Stratonovitch transformation.

The paper is organized as follows. Secs. II and III describe the Hamiltonian of the system and the derivation of the partition function, respectively. Expressions for the various statistical quantities are derived in Sec. IV. In Sec. V, the formalism is tested using the Richardson model, which enables comparison with an exact solution. Realistic cases are then considered using single-particle energies of a deformed Woods-Saxon mean-field. Finally, the main conclusions are summarized in Sec. VI.

In the second quantization formalism, the intrinsic motion of a system of paired particles (neutrons or protons) is described by the Hamiltonian

where $ \varepsilon_{\nu} $ is the single-particle energy of the state $ \vert \nu\rangle =a_{\nu}^{+} \;\; \vert 0\rangle $ and of its time reverse $ \vert \tilde{\nu}\rangle =a_{\tilde{\nu} }^{+} \;\; \vert 0\rangle $. $ \eta_{\nu} $ is defined by

The pairing strength G is assumed to be constant, and $ H_{p} $ is defined by

where

This method is based on the polar decomposition of the operators $ P^{+} $ and P to obtain the $ P^{+}P $ product on a square form, i.e.,

Therefore, we set $ \mathcal{S}_{\nu} $ the operator

where i is the imaginary unit.

$ \mathcal{S}_{\nu} $ obeys the following properties:

We set

where U is a unitary operator, which is also given by

It may then be easily shown that

with

In the same manner, we have

This is also the case reciprocally.

Eqs. (10) and (12) represent the generalization, in terms of operators, of the polar decomposition of complex numbers. Indeed,

Thus,

The calculation details of U, $ P^{+}P $ , and $ R^{2} $ are given in Appendix A.

To conserve the particle number on average, let us define the auxiliary Hamiltonian as

where

λ being the Fermi energy.

The grand partition function is given by

where β is the inverse of the temperature T of the system, and Tr is the trace over all the states of the system.

Note that $ H_{0} $ and $ H_{p} $ do not commute, thus

We now consider the operator $ \mathsf{S}\left(\beta\right) $ defined as

that is,

We can easily show that $ \mathsf{S}\left(\beta\right) $ satisfies the differential equation

where $ H_{p}\left(\beta\right) $ is the Heisenberg transform of $ H_{p} $

Eq. (21) is easily solved, considering the initial condition $ \mathsf{S}\left(\beta=0\right) =\mathbf{1}. $ The implicit solution is then

By proceeding by iteration, $ \mathsf{S}\left(\beta\right) $ may be formally written as

$ T_{\tau} $ is the chronological operator.

Then, Z may be expressed as

where

$ R\left(\tau\right) $ being the Heisenberg transform for the imaginary time τ of the operator R:

In the integral in Eq. (26), the interval $ \left[0,\beta\right] $ is divided into N intervals of length $ \dfrac{\beta}{N}.\ $Therefore, by definition,

because

where $ f\left(x\right) $ is any integrable function on the interval $ \left[0,\beta\right] $.

Thus,

Using the Hubbard-Stratonovitch transformation [42−44],

where O is a bounded Hermitian operator, and x is an external field, $ \mathsf{S}\left(\beta\right) $ may be written as

where we set

to simplify the notations.

Let us set

It is worth noting that $ X_{j} $ refers to $ X\left(\tau_{j}\right) $ and when the limit is taken, $ X_{j}\rightarrow X\left(\tau\right) $.

We then have

We set

Using the SPA [49], where it is assumed that $ \Delta\left(\tau\right) $ is independent of τ, i.e.,

Z reduces to an ordinary integral over the variable $ \Delta. $ It then reads as

After some algebra, it is given by

where we set

The eigenvalues of $ \eta_{\nu} $ are $ 0 $ and $ 1 $, which acts on a two-dimensional space. In its eigenbasis, its matrix $ \left(\eta_{\nu}\right) $ is

In the same manner, the eigenvalues of $ \eta_{\tilde{\nu}} $ are $ 0 $ and $ 1 $ and its matrix $ \left(\eta_{\tilde{\nu}}\right) $, in its eigenbasis, is given by

As for $ B_{\nu} $, knowing that $ B_{\nu}^{2}=\mathbf{1} $, its eigenvalues are $ \left(-1\right) $ and $ 1. $ Its matrix $ \left(B_{\nu}\right) $ is given, in its eigenbasis, by

The eigenbasis of $ h_{\nu} $ is the tensor product of the eigenbases of the three operators. The eigenvalues of $ \eta_{\nu} $, $ \eta_{\tilde{\nu}} $ , and $ B_{\nu} $ in this space are given in Table 1.

$ \eta_{\nu} $	$ 0 $	$ 0 $	$ 0 $	$ 0 $	$ 1 $	$ 1 $	$ 1 $	$ 1 $
$ \eta_{\widetilde{\nu}} $	$ 0 $	$ 0 $	$ 1 $	$ 1 $	$ 0 $	$ 0 $	$ 1 $	$ 1 $
$ B_{\nu} $	$ -1 $	$ 1 $	$ -1 $	$ 1 $	$ -1 $	$ 1 $	$ -1 $	$ 1 $
$ h_{\nu} $	$ 0 $	$ 0 $	$ \tilde{\varepsilon}_{\nu} $	$ \tilde {\varepsilon}_{\nu} $	$ \tilde{\varepsilon}_{\nu} $	$ \tilde {\varepsilon}_{\nu} $	$ 2\tilde{\varepsilon}_{\nu}-2\Delta $	$ \tilde{\varepsilon}_{\nu}+2\Delta $

Table 1.  Eigenvalues of $ \eta_\nu $, $ \eta_{\tilde{\nu}} $, $ B_\nu $ , and $ h_\nu $.

However, these three operators commute with each other and act on different spaces. Knowing the eigenvalues of $ \eta_{\nu} $, $ \eta _{\tilde{\nu}} $ , and $ B_{\nu} $, the eigenvalues of $ h_{\nu} $ can be deduced for a given ν using Table 1. Thus,

Next, to calculate the trace in Eq. (38), we assume, as an approximation, that $ h_{\nu} $ and $ h_{\mu} $ commute when $ \nu\neq\mu $. Indeed, the commutator $ \left[h_{\nu},h_{\mu }\right] $ is given by

It is thus the sum of a term proportional to G and a term proportional to $ \sqrt{G} $, because $ \Delta=X\sqrt{\pi G} $. The value of G is generally small compared to single-particle energies, justifying the approximation. This results in

As a consequence, the partition function may be written as

It is worth noting that this approach differs from the Fletcher method [42], which is recalled in Appendix B. In the latter, the pairing term in Eq. (B3) is written as a product $ \theta_{1}\theta_{2} $ and then converted into a square form to apply the Hubbard-Stratonovitch transformation. In the present study, the pairing term is in square form, enabling direct application of the Hubbard-Stratonovitch transformation.

However, in both approaches, an approximation is made because $ \theta_{1} $ and $ \theta_{2} $ are assumed to commute in the Fletcher method and $ h_{\nu } $ and $ h_{\mu} $, $ \nu\neq\mu, $ are assumed to commute in this study.

At this stage, it is difficult to determine whether the approximations are justified. However, a comparison of the numerical results of the various statistical quantities with exact values obtained within a schematic model will enable us to judge the validity of the approximations (see Sec. V).

The grand partition function can be used to determine various statistical quantities, such as energy, entropy, and heat capacity.

The free energy is obtained using the relation

and thus,

The quantity Δ is interpreted as the gap parameter. Hereafter, it is assumed to be real. It is found using the saddle point approximation [50]

Indeed, the dominant contribution to the partition function is found by determining the minimum value of the exponent in Eq. (47), resulting in

where

Because the grand potential Ω is given by

and the particle-number is defined by

we obtain

with

The system of Eqs. (50) and (54) constitutes the gap equations.

The quantity $ N_{\nu} $ may also be written as

The energy of the system is defined as

Then, after some algebra,

The entropy is defined by

After all calculations, it reads as

The heat capacity of the system is defined by

After some algebra, $ \dfrac{\partial S}{\partial\beta} $ may be written as

where

and $ \dfrac{\partial\left(\beta\Delta\right) }{\partial\beta} $ is deduced from the relation

Note that the obtained expressions for the various statistical quantities are different from those of the FTBCS approach, which are recalled in Appendix B.

The previously described formalism is first applied to the Richardson model, enabling comparison with an exact solution. Subsequently, it is applied to realistic cases.

In this section, we use the Richardson model with the same parameters as in Ref. [51], which refers to the exact solution of Ref. [52]. Thus, we consider $ N=10, ~ G=0.4 $ and doubly degenerated equidistant levels such that

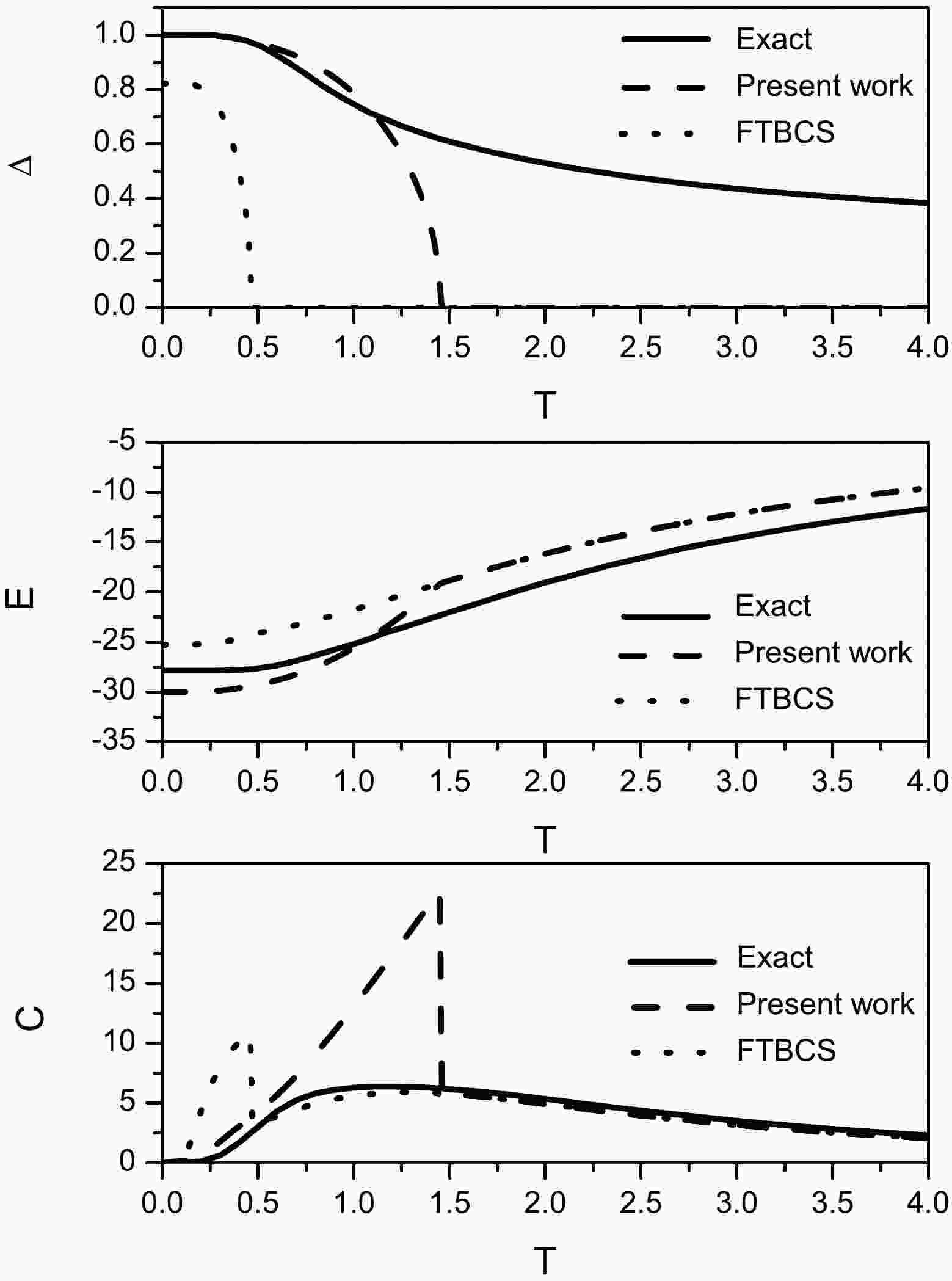
$ N_{or} $ is the total degeneracy of the levels, with $ N_{or}=10 $ and $ \Delta\varepsilon=1 $.

The various statistical quantities are then calculated as functions of temperature T using the approach in this study and compared with the exact solution and FTBCS results. The variations in the pairing gap parameter Δ, energy E, and heat capacity C are shown in Fig. 1.

Figure 1.  Variations in the pairing gap parameter Δ (upper part), energy E (middle), and heat capacity C (lower part) as functions of temperature T. The solid lines refer to the exact results, and the dashed and dotted lines refer to the results of this study and FTBCS, respectively.

As shown in the figure, the overall behavior of $ \Delta\left(T\right) $ is similar to the typical behavior in the FTBCS approach, i.e., exhibiting a plateau on a given interval at low temperatures and then decreasing until Δ vanishes at the critical temperature $ T_{c} $. The sharp phase transition at $ T=T_{c} $ is due to the approximations used in this study, i.e., the SPA (Eq. (36)), that of Eq. (45), and the saddle-point approximation (Eq. (49)). The inclusion of quantal and thermal fluctuations may lead to smoother behavior.

Furthermore, the agreement between the values of Δ from this study and the exact values is good for $ 0\leqslant T\leqslant0.5 $; a clear improvement in the Δ values of this study compared to the FTBCS values should be noted. Indeed, the FTBCS method predicts a Δ value of approximately $ 0.8 $ at low temperatures, whereas the present model reproduces the exact value $ \Delta=1 $.

Moreover, the $ T_{c} $ value of this study is clearly larger than that of the FTBCS approach. Consequently, our model better reproduces the exact values of Δ over a larger temperature interval. Indeed, our values are relatively close to the exact values until $ T\simeq1.2 $.

The behavior of $ E(T) $ at low temperatures is similar in the three cases. However, our model leads to a decrease in energy with respect to the exact values of approximately 7%, whereas the FTBCS method leads to an increase of approximately 9%. At higher temperatures, the difference in the Δ shape leads to a difference in the shape of the energy.

Finally, as shown in Fig. 1, the shape of the heat capacity C at low temperatures, i.e., at $ 0\leqslant T\leqslant0.5 $, is closer to that of the exact solution than that of the FTBCS method. Of course, the discontinuity at $ T=T_{c} $ still exists.

For large values of T, i.e., beyond the critical temperature of the FTBCS method and this study, the pairing vanishes. Thus, the energy is the same in both models. However, it may seem surprising that in this region, the C values of both models reproduce the exact values, whereas the exact value of Δ does not vanish. This is because the $ E(T) $ curves (and thus those of $ S(T) $) are parallel in this region; therefore, the value of the derivative is the same.

Next, we choose two nuclei as illustrative examples : $ ^{162} $Dy and $ ^{172} $Yb. These nuclei have semiexperimental heat capacity data, allowing comparisons with the current results. The single-particle energies are those of a Woods-Saxon deformed mean-field using the parameters described in Ref. [53], with a maximum number of shells $N_{\max}=12$.

To enable comparisons with the FTBCS approach, the pairing strength G is chosen to reproduce the pairing gap parameters Δ at zero temperature in both approaches, which are deduced from the even-odd mass differences and given by [54]

for the proton and neutron systems, respectively. $ M\left(Z,N\right) $ is the experimental mass value.

For the same reason, we consider the excitation energy $E_{\rm exc}$ defined as

rather than the energy of the system.

The variations in the gap parameter Δ, excitation energy $E_{\rm exc}$, and heat capacity C as functions of temperature T are shown in Figs. 2 and 3 for the proton and neutron systems of the two nuclei mentioned above. The FTBCS results are shown in the same figures.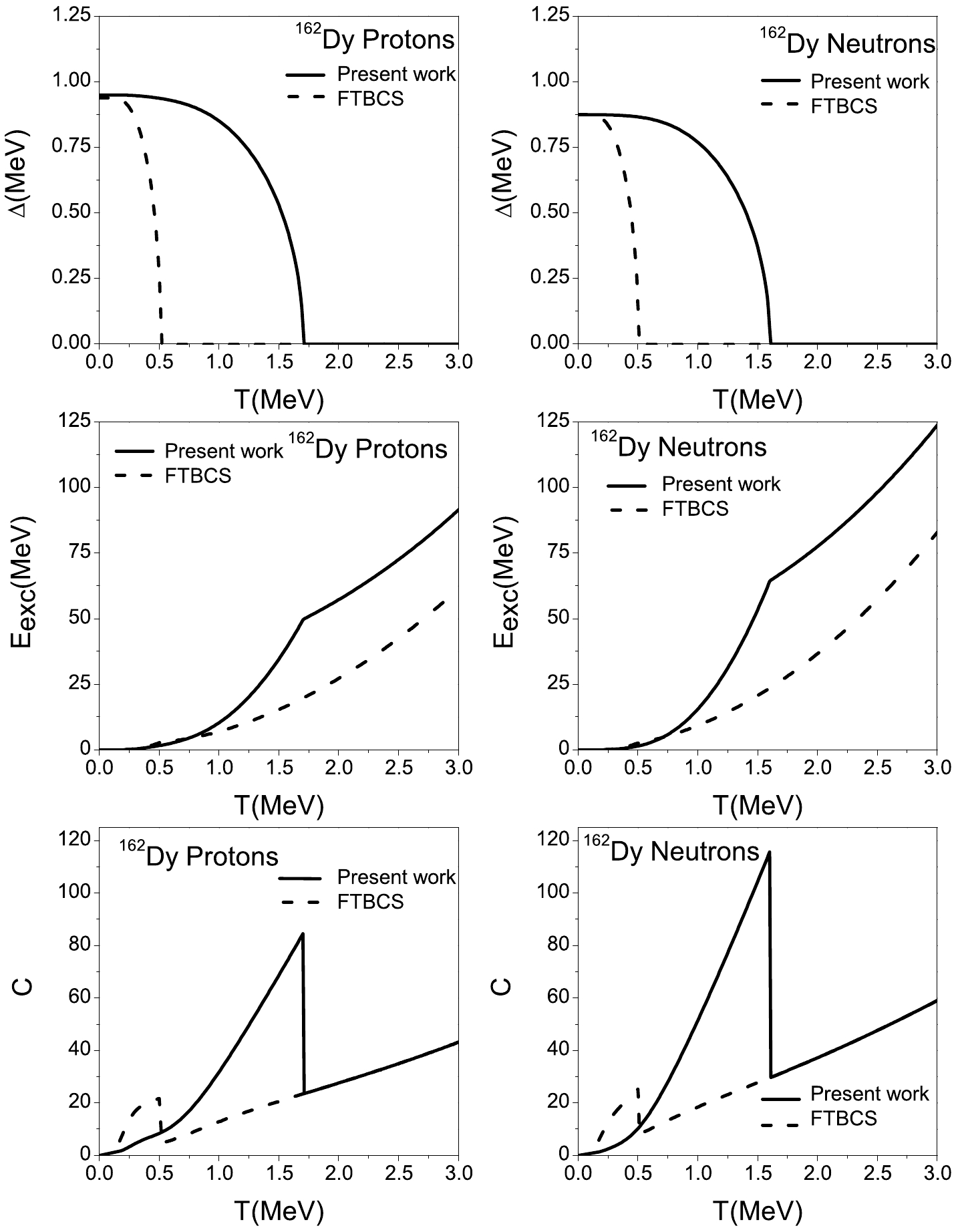

Figure 2.  Variations in the pairing gap parameter Δ (upper part), excitation energy $E_{\rm exc}$ (middle), and heat capacity C (lower part) as functions of temperature T for the proton (left) and neutron (right) systems of $ ^{162} $Dy. The solid lines refer to the results of this study, and the dashed lines are the FTBCS results.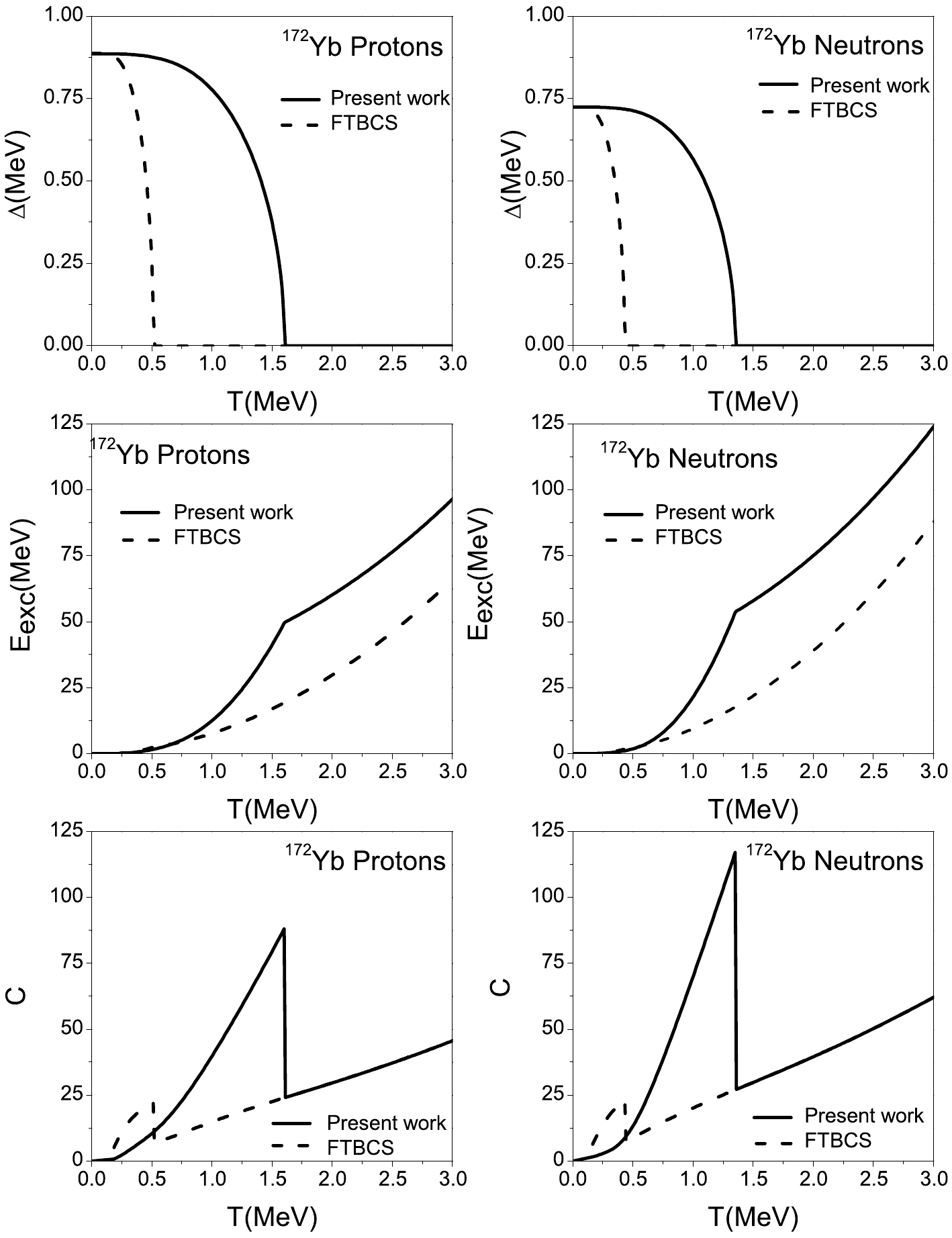

Figure 3.  Same as Fig. 2, but for ¹⁷²Yb.

In each case, the overall behavior of $ \Delta\left(T\right) $ is similar to the typical behavior in the FTBCS approach, as is the case in the schematic example. Once again, the $ T_{c} $ values of this study are clearly more important than those of the FTBCS approach. The ratio $T_{c}/\left(T_{c}\right) _{\rm FTBCS}$ is close to 3.

The behavior of the pairing parameters is reflected in the excitation energy, and the curves are similar in both approaches. We note a change in the slope at $ T=T_{c} $. In the region $T < \left(T_{c}\right) _{\rm FTBCS}$, $E_{\rm exc}$ increases more rapidly in the FTBCS approach than in this study. In the region $ \left(T_{c}\right)_{\rm FTBCS}<T<T_{c} $, $E_{\rm exc}$ in this study increases significantly faster than in the FTBCS case. In fact, in this region, the FTBCS pairing gap is nil. No explanation for this behavior is found, nor for $E_{\rm exc}$ being larger in the present model. Finally, when $ T>T_{c} $, the curves of the two approaches are parallel.

Regarding the heat capacity, we can draw the same conclusions regarding the general features of the curves deduced from the two approaches. The sharp discontinuity in C observed at $ T=T_{c} $ within the conventional FTBCS approach remains when using our formalism. However, it is worth noting that the graphs join beyond $ T_{c} $, when the pairing effects vanish.

Next, the total heat capacity $ C_{T} $ is evaluated as a function of temperature for both nuclei, making it possible to compare it with semiexperimental values. The latter are taken from Ref. [13], which refers to Refs. [55] and [56]. The corresponding results are shown in Figs. 4 and 5 for $ ^{162} $Dy and $ ^{172} $Yb, respectively. In both figures, the section within the interval $0\leqslant T\leqslant1 ~{\rm MeV}$, in which semiexperimental data are available, is enlarged in part (b) for clarity.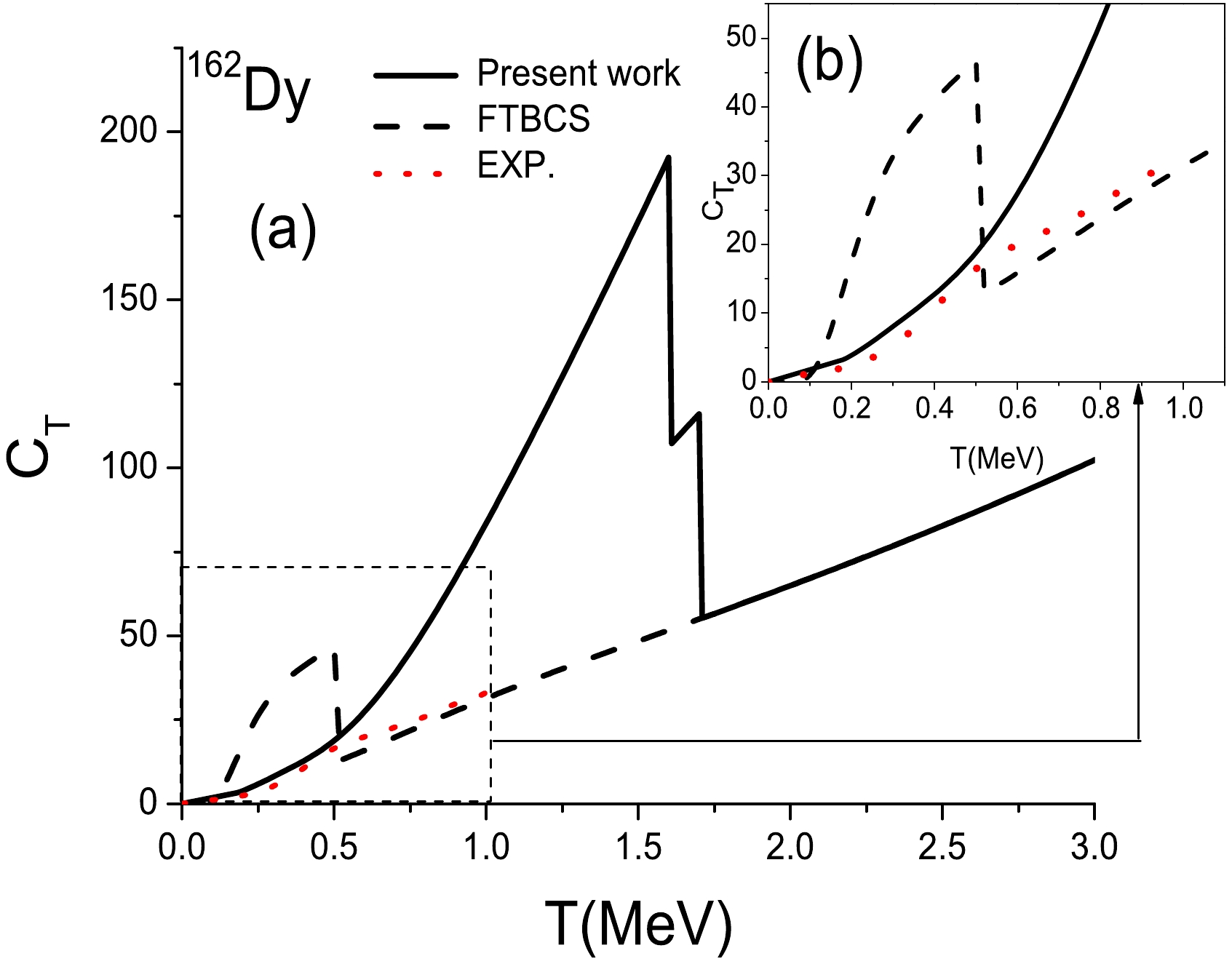

Figure 4.  (color online) Variation in the total heat capacity of $ ^{162} $Dy as a function of temperature T. The solid lines refer to the results of this study, the dashed lines are the FTBCS results, and the dotted lines are the values extracted from experimental data.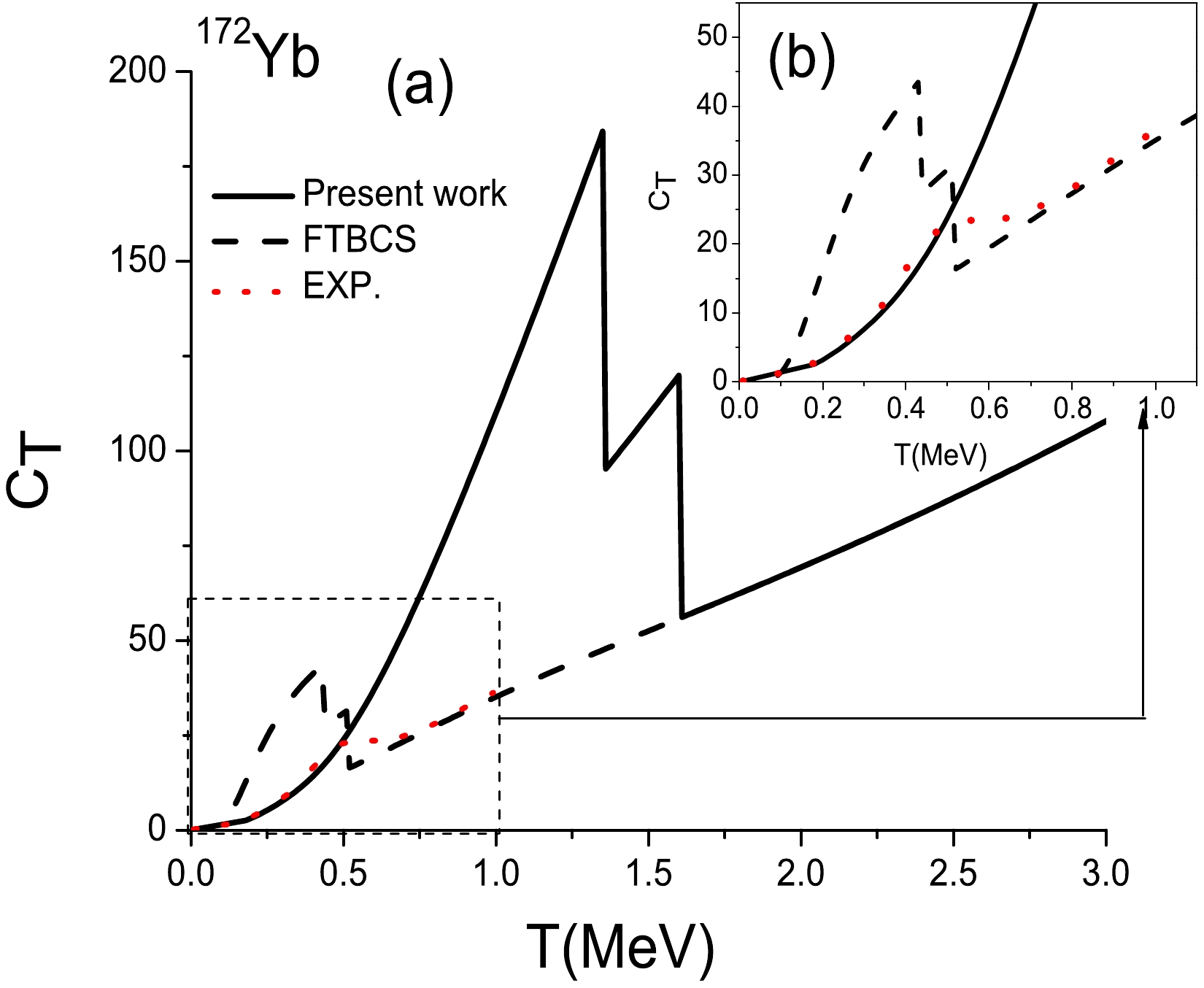

Figure 5.  (color online) Same as Fig. 4, but for$ ^{172} $Yb.

In each case (see Figs. 4 (a) and 5 (a)), two discontinuities are noted, corresponding to the neutron and proton critical temperatures, within the current model and FTBCS approach. In the $ ^{162} $Dy case, the two FTBCS critical temperatures are very close to each other, revealing only a discontinuity in the curve.

Note that the FTBCS curves of this study show, in each case, a sharp increase at low temperatures, whereas in Refs. [57] (for $ ^{162} $Dy) and [13] (for both $ ^{162} $Dy and $ ^{172} $Yb), C is flat in this region. This difference is likely due to the choice of the pairing-strength G value. In this study, we do not use the same value of G for the two approaches (i.e., the FTBCS and present approaches). As highlighted above, the G values are chosen to reproduce the Δ value at zero temperature in each case.

Moreover, for both nuclei, beyond the proton system critical temperature of the present model, the curves of the two models are superposed because there is no more pairing in this region.

As clearly shown in Figs. 4 (b) and 5 (b), at low temperatures, i.e., when $T\leqslant0.5~{\rm MeV}$, the agreement between the results of this study and the semiexperimental values is good, which is not the case for the FTBCS method. This observation is consistent with the conclusions drawn in the case of the Richardson model.

In addition, as in the schematic case, the good agreement between the values obtained using our model and the experimental (respectively exact) values is observed in the interval where Δ has a plateau shape.

Paradoxically, the FTBCS method seems to better reproduce the experimental values in the interval between the proton system critical temperatures of the two models. However, note that in this region, the FTBCS method predicts that the pairing effects vanish, suggesting that the entropy curves are parallel in this region, as is the case within the Richardson model.

However, in the present approach, the S shape of the experimental heat capacities is not reproduced. The model predicts a sharp transition when the temperature reaches its critical value. This shortcoming may be overcome by performing particle-number projection before variation (see, e.g., Refs. [13, 41, 57],). In our approach, thermal and quantal fluctuations should also be considered. One should then go beyond the SPA defined by Eq. (36).

We present a model for the treatment of nuclear pairing at finite temperature within the path integral formalism, based on the polar decomposition of the creation and annihilation operators of pairs of paired particles in the Hamiltonian of the system. The pairing term in the Hamiltonian is then written in square form, which enables direct use of the Hubbard-Stratonovitch transformation. This facilitates the derivation of the partition function of the system using the SPA.

A new expression for the partition function is established. Gap equations and expressions for various statistical quantities are then derived, which differ from those of the FTBCS approach because the used approximations are not of the same nature.

The model is first numerically tested using the Richardson schematic model, which enables a comparison with the exact solution. The results obtained using the present formalism are also compared to the FTBCS results. An improvement compared to the FTBCS model is noted at low temperatures for the values of the pairing gap parameter Δ. Indeed, our model can be used to reproduce the exact value of $\Delta$, which is not the case of the FTBCS model. An improvement is also noted for the energy E and heat capacity C. However, there is still a critical temperature $ T_{c} $ , which leads to discontinuities in the $ \Delta, \;\; E $ , and C curves. The $ T_{c} $ value of this study is found to be larger than that of FTBCS.

The model is then applied to realistic cases using the single-particle energies of a deformed Woods-Saxon mean-field. The various statistical quantities are evaluated for the proton and neutron systems of the $ ^{162} $Dy and $ ^{172} $Yb nuclei, which are chosen as illustrative examples. Compared to the FTBCS results, the overall behavior of the gap parameters and the various statistical quantities as functions of temperature is similar.

However, in the framework of our approach, the pairing effects persist at temperatures higher than those predicted by the FTBCS approach.

Because semiexperimental data of the heat capacity are available for these two nuclei, we compare them with the predictions of the present model and the FTBCS results. The model in our study better reproduces the experimental values at low temperatures. However, in the interval between the proton system critical temperatures of the two models, the FTBCS method appears to better reproduce the experimental values. This is paradoxical because FTBCS predicts that the pairing effects vanish in this region.

It would be interesting to consider the thermal and quantal fluctuations in the present model and perform particle-number projection. It would also be interesting to extend our formalism to the neutron-proton pairing case.

Recall that

where

Let us establish Eq. (9). Using Eq. (A2), we have

First, we establish that

Indeed,

However,

thus,

Similarly,

We then obtain

because $ a_{j} $ and $ a_{j}^{+} $ commute with $ a_{\tilde{_{j}}}\ $and $ a_{\tilde{j}}^{+} $.

That is,

Using Eq. (A1), we obtain

Let us calculate $ a_{\nu}^{+}a_{\tilde{\nu}}^{+}U $. We have

where we set

Similarly,

using the definition (4) of $ P^{+} $ and P, i.e.,

we then have

and

where we set

Hence,

We have

As

and

we obtain

To facilitate comparisons with our study, the Fletcher method [42] is recalled in this appendix.

We start with the Hamiltonian (1). To conserve the particle number on average, we define the auxiliary Hamiltonian as

where λ is the Fermi energy, and N is the particle number operator given by

The Hamiltonian H then reads as

with the notations

The grand partition function can be written as

where β is the inverse of the system temperature T, and Tr is the trace over all the states of the system.

Using the same treatment as in Sec. II, we obtain

where

$ T_{\tau} $ is the chronological operator, and $ H_{1}\left(\tau\right) $ is the Heisenberg transform of $ H_{1} $.

$ \mathsf{S}\left(\beta\right) $ may also be written as

where $ \tau_{j}=j\dfrac{\beta}{N}, $ $ j=1,2,...,N $.

To apply the Hubbard-Stratonovitch transformation (31), Fletcher assumes that $ H_{1}\left(\tau_{j}\right) $ in Eq. (B8) may be expressed as

with

Although $ \theta_{1} $ and $ \theta_{2} $ do not strictly commute because

for small G (which is the case as it represents a residual interaction),

because

By applying the Hubbard-Stratonovitch transformation to each exponential in Eq. (B12), we obtain

and

with the notations

Using the change of variables

Eq. (B12) takes the form

Let us introduce the notations

and

It is worth noting that when the limit is taken, $ X_{j}\rightarrow X\left(\tau\right) $ and $ Y_{j}\rightarrow Y\left(\tau\right) $.

We also define the complex function

As

and

where $ f\left(x\right) $ is any integrable function on the interval $ \left[0,\beta\right] $, we obtain

Finally, when replacing $ \theta_{1}\left(\tau\right) $ and $ \theta _{2}\left(\tau\right) $ with their respective expressions, and using Eq. (B6), the partition function becomes

where we set

In the case of the static path approximation, it is assumed that $ X\left(\tau\right) $ and $ Y\left(\tau\right), $ and thus $ z\left(\tau\right) $, are independent from the imaginary time τ. The functional integral in Eq. (B25) then reduces to an ordinary integral and is given by

where

The trace of ${\rm e}^{-\beta H^{\prime}}$ may be easily evaluated in its eigenbasis. Moreover, $ H^{\prime} $ may be written in the matrix form

where we set

The quantity Δ is interpreted as the gap parameter. Hereafter, it is assumed to be real.

The matrix $ A_{\nu} $ is diagonalized such that

where

with

The Hamiltonian $ H^{\prime} $ then takes the diagonal form

where

It is now possible to calculate the trace in Eq. (B27), which becomes

where the free energy F is given by

The saddle-point approximation reads as

Indeed, the dominant contribution to the partition function is found by determining the minimum value of the exponent in Eq. (B36). We then obtain

The latter equation is the typical FTBCS expression [7, 9, 46, 48]. The path integral method thus enables us to retrieve the standard FTBCS results by applying a saddle-point approximation.

The grand potential Ω is given by

and the particle-number is defined by Eq. (53).

We then have

The energy of the system is defined by Eq. (57). Thus,

As for the entropy, using definition (59), we have

Finally, the heat capacity of the system defined by

reads as

with