Effects of energy levels on the double-differential cross sections of outgoing charged particles for the n+¹⁹F reaction below 20 MeV

¹⁹F is the only stable isotope of the element fluorine, with a natural abundance of 100%. It demonstrates exceptional oxidizing capacity and high chemical reactivity and predominantly exists in compound forms in nature. In the realm of nuclear astrophysics, the isotope ¹⁹F takes part in nuclear reactions such as $ ^{19}\text{F}(n, \gamma $)$ ^{20}\text{F} $ and $ ^{19}\text{F}(n, p)^{19}\text{O} $ within high density neutron-rich environments, which include scenarios such as supernova explosions and neutron star mergers. These reactions have significant implications for understanding element synthesis processes in nuclear astrophysics and elucidating cosmic nucleosynthesis mechanisms [1, 2]. In nuclear engineering and technology, physical quantities (such as cross section, angular distribution, and double-differential cross section (DDCS)) for the n+¹⁹F reaction play a critical role in key areas, including the nuclear fuel cycle, nuclear waste management, and nuclear safety systems. For example, fluoride molten salt serves as both the coolant and fuel carrier in nuclear reactors, enabling the extraction, purification, recovery, and recycling of valuable nuclides, such as uranium and plutonium. This facilitates efficient nuclear fuel production and reprocessing while enhancing reactor safety and economic performance [3−7].

The DDCS is crucial for coupling energy and angular distributions of emitted particles, providing a concurrent description of neutron scattering and particle emission, handling numerous open reaction channels, and offering accurate distributions for particle transport, heat deposition, or radiation damage calculations [8]. Notably, the DDCS of outgoing charged particles is a fundamental value to estimate nuclear heating and material damages in fusion reactors [9]. Quantitatively describing the DDCS for neutron-induced light nucleus reactions is a challenging problem, not only due to the complexities of the reaction mechanisms but also the scarcity of data on the experimental DDCS of emitted charged particles. As the first nuclide in the 2s1d-shell, $ ^{19}\text{F} $ possesses 198 discrete energy levels [10], exhibiting nearly all the characteristics of 1p-shell nuclei. There are individual features of each energy level (including energy, spin, parity, width, and branching ratio), and the emission of particles between discrete energy levels is the most prominent characteristic for neutron-induced light nucleus reactions. Because of the light mass for nucleon-induced light nuclear reactions, the recoil effect must be strictly considered. Fortunately, the statistical theory for light nucleus reactions (STLN) was systematically described in 2015 [11], based on the unified Hauser-Feshbach and exciton model. STLN has been successfully applied to calculate the DDCSs of outgoing neutrons for neutron-induced reactions on ⁶Li [12], ⁷Li [13], ⁹Be [14, 15], ¹⁰B [16], ¹¹B [17], ¹²C [18−20], ¹³C [21], ¹⁴N [22], ¹⁶O [19, 23, 24], and ¹⁹F [25]. However, the DDCSs of outgoing charged particles in the aforementioned neutron-induced light nucleus reactions have scarcely been published, even though experimental measurements of the DDCSs for outgoing protons, deuterons, tritons, and α-particles for n+¹⁹F reaction were performed in 2011 [26]. These datasets have provided a critical benchmark for theoretical calculations of charged particle emission spectra.

Major international nuclear databases (including ENDF/B-VIII.1, JENDL-5, BROND-3.1, JEFF-3.3, TENDL-2023, and CENDL-3.2) have successively recommended the DDCSs of outgoing products for the n+¹⁹F reaction. In ENDF/B-VIII.1 [27] and BROND-3.1 [28], the DDCSs of outgoing protons and α-particles are evaluated using the TNG code [29], which employs the Hauser-Feshbach multi-step statistical model. These evaluations account for reaction channels including $ (n, n'), (n, p), (n, \alpha), (n, 2n), (n, np) $, and $ (n, n\alpha) $. In JENDL-5 [30], the DDCSs of outgoing primary protons, deuterons, tritons, and α from $ (n, n'), (n, p), (n, d), (n, t) $, and $ (n, \alpha $) reaction channels are evaluated using the Kalbach-Mann systematics [31, 32]. For secondary emitted protons, deuterons, and α from $ (n, np), (n, nd) $, and ($ n, n\alpha $) channels, evaluations are performed using the improved Kalbach-Mann systematics [33]. The file of the DDCS in JEFF-3.3 [34] was consistent with that in ENDF/B-VII. TENDL-2023 [35] data are generally generated using the well-known Talys code [36], but for the n+¹⁹F reaction, the data of ENDF/B-VIII.0 are directly adopted instead. The DDCS data derived from the major databases mentioned above heavily rely on statistical models or systematic approaches, resulting in insufficient characterization of secondary particle emission mechanisms. Based on STLN, CENDL-3.2 [37], including $ (n, p), (n, \alpha), (n, 2n), (n, np), (n, nd), (n, nt) $, and $ (n, n\alpha $) reaction channels, provided relatively accurate DDCSs of outgoing neutrons. However, the data of charged particles were only preliminarily estimated.

In this study, the pick-up mechanism of complex particles, one of the important components of STLN, is improved to describe the DDCSs of the outgoing charged particles at $ E_n=14.2 $MeV. In Sec. II, the theoretical framework for the DDCS of secondary particle emission between discrete energy levels is introduced for the n+¹⁹F reaction. In Sec. III, the analysis of reaction channels below 20 MeV is performed in detail, and the DDCSs of charged particles are calculated and compared with the experimental and evaluated data. A succinct summary is given in Sec. IV.

In the framework of STLN, a detailed description of the basic ideas for modeling the DDCS of outgoing nucleons and light charged particles can be found in Ref. [21]. The DDCS of outgoing light charged particle b with outgoing kinetic energy $ \varepsilon_b^c $ in the center-of-mass system (CMS) can be expressed as [21]

While the incident neutron energy $ E_n \leq 20 $ MeV, $ n_{\max}=3 $ can effectively describe the pre-equilibrium particle emission behavior [18].

The energy spectrum $ \dfrac{{\rm d} \sigma (n)}{{\rm d} \varepsilon_b^c} $ of the n-th exciton configuration at the pre-equilibrium stage can be expressed as

where $ \sigma_a^{j\pi} $ denotes the absorption cross section in the $ j\pi $ channel (j and π denote the angular momentum and parity in the final state, respectively). $ P^{j\pi}(n) $ denotes the occupation probability of the n-th exciton configuration at the pre-equilibrium stage. $ E^* $ denotes the excited energy of a compound nucleus. The emission rate of the emitted particle b with outgoing kinetic energy $ \varepsilon_{b}^c $ of the n-th exciton configuration at the pre-equilibrium stage $ W_{b}^{j\pi}(n, E^*,\varepsilon_{b}^c) $ can be expreesed as

Here, $ W_{b,k_1}^{j\pi}(n,E^*,\varepsilon_{b}^c) $ denotes the emission rate of emitted particle b with outgoing kinetic energy $ \varepsilon_{b}^c $ to discrete energy levels $ k_1 $ of the residual nucleus at the n-th exciton configuration and is expressed as

where $ \omega^{j\pi}(n,E^*) $ denotes the n-th exciton configuration density. $ T_l(\varepsilon_b^c,k_1) $ denotes the reduced penetration factor, which can be obtained by the optical model of the spherical nucleus. $ j_{k_1} $ denotes the angular momentum of the residual nucleus at energy level $ k_1 $. $ s_b $ denotes the spin of the emitted particle b. π and $ \pi_{k_1} $ denote the parities of compound nuclei and the first residual nucleus at the $ k_1 $th energy level, respectively. $ g_l(\pi, \pi_{k_1}) $ denotes the parity conservation function. The configuration $ [1, m] $ dominates the low-energy nuclear reactions [38]. $ F_{b\left[1, m \right]} (\varepsilon_b^c) $ denotes the pre-formation probabilities of complex particles b based on the improved Iwamoto-Harada model [39]. For convenience in model calculation, the pre-formation probabilities of the $ [1, m] $ configuration can be calculated using the following expression:

where $ \varepsilon = \varepsilon_b^c+B_b $, and $ B_b $ denotes the binding energy of a complex particle. The parameters $ a_1 $, $ a_2 $, $ b_1 $, $ b_2 $, $ c_1 $, and $ c_2 $ are listed in Table 2 of Ref. [39]. $ Q_{b\left[ 1,m \right]}(n) $, considering the effect of the incident particle memories for neutron-induced nucleus reactions, is the combination factor of the n-th exciton configuration, expressed as [40]

where $ A_T $, $ N_T $, and $ Z_T $ denote the mass, neutron, and proton numbers of the target, respectively. $ n_b $ and $ z_b $ denote the neutron and proton numbers of complex particles, respectively. p and h denote the particle number and hole number at the n-th exciton configuration. $ A_b = z_b +n_b =\lambda + m $ represents a configuration in which λ nucleons lie above the Fermi sea and m nucleons below it. The notation $ \binom{.}{.} $ denotes the binomial coefficient.

The total emission rate $ W_T^{j\pi}(n,E^*) $ at the pre-equilibrium stage can be expressed as

The normalized angular factor $ A(n, \varepsilon_b^c, \Omega^c) $ can be expressed as

where $ \tau_l(n, \varepsilon_b^c) $ denotes the lifetime of the l-th partial wave with outgoing particle energy $ \varepsilon_b^c $ emitted from the n-th exciton configuration, which can be derived by solving the generalized master equation. $ P_l (x) $ denotes the Legendre function. The geometric factor $ G_l(\varepsilon_b^c) $ can be expressed as [41]

where $ \varepsilon _F $ and $ p_F $ denote Fermi energy and Fermi momentum, respectively. $ x_1=p_1/p_F $, where $ p_1 $ is the momentum of the first nucleon in the outgoing composite particle b. $ x_b=p_b/p_F $, where $ p_b $ is the momentum of the outgoing composite particle. $ y=p_y/p_F $, where $ p_y $ is the total momentum of nucleons except the first nucleon in the outgoing composite particle b. The cosinoidal function is expressed as $ \cos \Theta = \dfrac{{x_b^2 + x_1^2 - {y^2}}}{{2{x_b}{x_1}}} $. $ {Z_b}(y) $ is a factor related to the emitted composite particle, expressed as

The geometric factor associated with the n-th exciton for the nucleon is equivalent to 1, i.e., $ G_l(\varepsilon_b^c)/G_0(\varepsilon_b^c) $= 1. The formulas given above are employed in this study to calculate the DDCSs of the outgoing neutron, proton, deuteron, triton, $ ^3 $He, α, and $ ^5 $He.

The energy spectrum at the equilibrium stage $ \dfrac{{\rm d} \sigma}{{\rm d} \varepsilon_b^c} $ can be expressed as

where $ Q^{j\pi}=1-\sum_{n=3}^{n_{\max}}P^{j\pi}(n) $ denotes the occupation probability of the equilibrium stage. $ W_{b}^{j\pi}(E^*,\varepsilon_{b}^c) $ and $ W_{T}^{j\pi}(E^*) $ denote the emission rate of particle b with outgoing energy $ \varepsilon_b^c $ and the total emission rate at the equilibrium stage, respectively. Their expressions are given by

where $ \rho^{j\pi}(E^*) $ denotes the energy level density. $ I_{M_1} $ denotes the spins of the first residual nucleus, and $ T_{Jl}(\varepsilon_b^c,k_1) $ denotes the penetration factor.

In the framework of STLN, a detailed description of the basic ideas for modeling the DDCS of outgoing nucleons and light charged particles can be found in Ref. [21]. The DDCS of outgoing light charged particle b with outgoing kinetic energy $ \varepsilon_b^c $ in the center-of-mass system (CMS) can be expressed as [21]

While the incident neutron energy $ E_n \leq 20 $ MeV, $ n_{\max}=3 $ can effectively describe the pre-equilibrium particle emission behavior [18].

The energy spectrum $ \dfrac{{\rm d} \sigma (n)}{{\rm d} \varepsilon_b^c} $ of the n-th exciton configuration at the pre-equilibrium stage can be expressed as

where $ \sigma_a^{j\pi} $ denotes the absorption cross section in the $ j\pi $ channel (j and π denote the angular momentum and parity in the final state, respectively). $ P^{j\pi}(n) $ denotes the occupation probability of the n-th exciton configuration at the pre-equilibrium stage. $ E^* $ denotes the excited energy of a compound nucleus. The emission rate of the emitted particle b with outgoing kinetic energy $ \varepsilon_{b}^c $ of the n-th exciton configuration at the pre-equilibrium stage $ W_{b}^{j\pi}(n, E^*,\varepsilon_{b}^c) $ can be expreesed as

Here, $ W_{b,k_1}^{j\pi}(n,E^*,\varepsilon_{b}^c) $ denotes the emission rate of emitted particle b with outgoing kinetic energy $ \varepsilon_{b}^c $ to discrete energy levels $ k_1 $ of the residual nucleus at the n-th exciton configuration and is expressed as

where $ \omega^{j\pi}(n,E^*) $ denotes the n-th exciton configuration density. $ T_l(\varepsilon_b^c,k_1) $ denotes the reduced penetration factor, which can be obtained by the optical model of the spherical nucleus. $ j_{k_1} $ denotes the angular momentum of the residual nucleus at energy level $ k_1 $. $ s_b $ denotes the spin of the emitted particle b. π and $ \pi_{k_1} $ denote the parities of compound nuclei and the first residual nucleus at the $ k_1 $th energy level, respectively. $ g_l(\pi, \pi_{k_1}) $ denotes the parity conservation function. The configuration $ [1, m] $ dominates the low-energy nuclear reactions [38]. $ F_{b\left[1, m \right]} (\varepsilon_b^c) $ denotes the pre-formation probabilities of complex particles b based on the improved Iwamoto-Harada model [39]. For convenience in model calculation, the pre-formation probabilities of the $ [1, m] $ configuration can be calculated using the following expression:

where $ \varepsilon = \varepsilon_b^c+B_b $, and $ B_b $ denotes the binding energy of a complex particle. The parameters $ a_1 $, $ a_2 $, $ b_1 $, $ b_2 $, $ c_1 $, and $ c_2 $ are listed in Table 2 of Ref. [39]. $ Q_{b\left[ 1,m \right]}(n) $, considering the effect of the incident particle memories for neutron-induced nucleus reactions, is the combination factor of the n-th exciton configuration, expressed as [40]

where $ A_T $, $ N_T $, and $ Z_T $ denote the mass, neutron, and proton numbers of the target, respectively. $ n_b $ and $ z_b $ denote the neutron and proton numbers of complex particles, respectively. p and h denote the particle number and hole number at the n-th exciton configuration. $ A_b = z_b +n_b =\lambda + m $ represents a configuration in which λ nucleons lie above the Fermi sea and m nucleons below it. The notation $ \binom{.}{.} $ denotes the binomial coefficient.

The total emission rate $ W_T^{j\pi}(n,E^*) $ at the pre-equilibrium stage can be expressed as

The normalized angular factor $ A(n, \varepsilon_b^c, \Omega^c) $ can be expressed as

where $ \tau_l(n, \varepsilon_b^c) $ denotes the lifetime of the l-th partial wave with outgoing particle energy $ \varepsilon_b^c $ emitted from the n-th exciton configuration, which can be derived by solving the generalized master equation. $ P_l (x) $ denotes the Legendre function. The geometric factor $ G_l(\varepsilon_b^c) $ can be expressed as [41]

where $ \varepsilon _F $ and $ p_F $ denote Fermi energy and Fermi momentum, respectively. $ x_1=p_1/p_F $, where $ p_1 $ is the momentum of the first nucleon in the outgoing composite particle b. $ x_b=p_b/p_F $, where $ p_b $ is the momentum of the outgoing composite particle. $ y=p_y/p_F $, where $ p_y $ is the total momentum of nucleons except the first nucleon in the outgoing composite particle b. The cosinoidal function is expressed as $ \cos \Theta = \dfrac{{x_b^2 + x_1^2 - {y^2}}}{{2{x_b}{x_1}}} $. $ {Z_b}(y) $ is a factor related to the emitted composite particle, expressed as

The geometric factor associated with the n-th exciton for the nucleon is equivalent to 1, i.e., $ G_l(\varepsilon_b^c)/G_0(\varepsilon_b^c) $= 1. The formulas given above are employed in this study to calculate the DDCSs of the outgoing neutron, proton, deuteron, triton, $ ^3 $He, α, and $ ^5 $He.

The energy spectrum at the equilibrium stage $ \dfrac{{\rm d} \sigma}{{\rm d} \varepsilon_b^c} $ can be expressed as

where $ Q^{j\pi}=1-\sum_{n=3}^{n_{\max}}P^{j\pi}(n) $ denotes the occupation probability of the equilibrium stage. $ W_{b}^{j\pi}(E^*,\varepsilon_{b}^c) $ and $ W_{T}^{j\pi}(E^*) $ denote the emission rate of particle b with outgoing energy $ \varepsilon_b^c $ and the total emission rate at the equilibrium stage, respectively. Their expressions are given by

where $ \rho^{j\pi}(E^*) $ denotes the energy level density. $ I_{M_1} $ denotes the spins of the first residual nucleus, and $ T_{Jl}(\varepsilon_b^c,k_1) $ denotes the penetration factor.

The opening of reaction channels, their corresponding reaction Q values, and the threshold energy $ E_{\rm th} $ significantly influence the DDCS of the emitted particles. Considering the emission processes from a compound nucleus to the discrete levels of the first residual nuclei and subsequently from these levels to the discrete levels of the secondary residual nuclei, with conservations of angular momentum and parity for the n+¹⁹F reaction, the following reaction channels are accessible at incident neutron energies $ E_n \leq 20 $ MeV:

Here, $ k_1 $ denotes the energy level of the first and secondary residual nuclei. The structural information of the target, compound nucleus, and first and secondary residual nuclei is taken from Refs. [10, 42−44].

After considering the contributions of the aforementioned reaction channels, the calculated DDCS of emitted neutrons is not only in good agreement with experimental data but also nearly consistent with the results of our previous study [25]. In this study, only values greater than $ 10^{-3} $ mb/sr/MeV are presented.

The opening of reaction channels, their corresponding reaction Q values, and the threshold energy $ E_{\rm th} $ significantly influence the DDCS of the emitted particles. Considering the emission processes from a compound nucleus to the discrete levels of the first residual nuclei and subsequently from these levels to the discrete levels of the secondary residual nuclei, with conservations of angular momentum and parity for the n+¹⁹F reaction, the following reaction channels are accessible at incident neutron energies $ E_n \leq 20 $ MeV:

Here, $ k_1 $ denotes the energy level of the first and secondary residual nuclei. The structural information of the target, compound nucleus, and first and secondary residual nuclei is taken from Refs. [10, 42−44].

After considering the contributions of the aforementioned reaction channels, the calculated DDCS of emitted neutrons is not only in good agreement with experimental data but also nearly consistent with the results of our previous study [25]. In this study, only values greater than $ 10^{-3} $ mb/sr/MeV are presented.

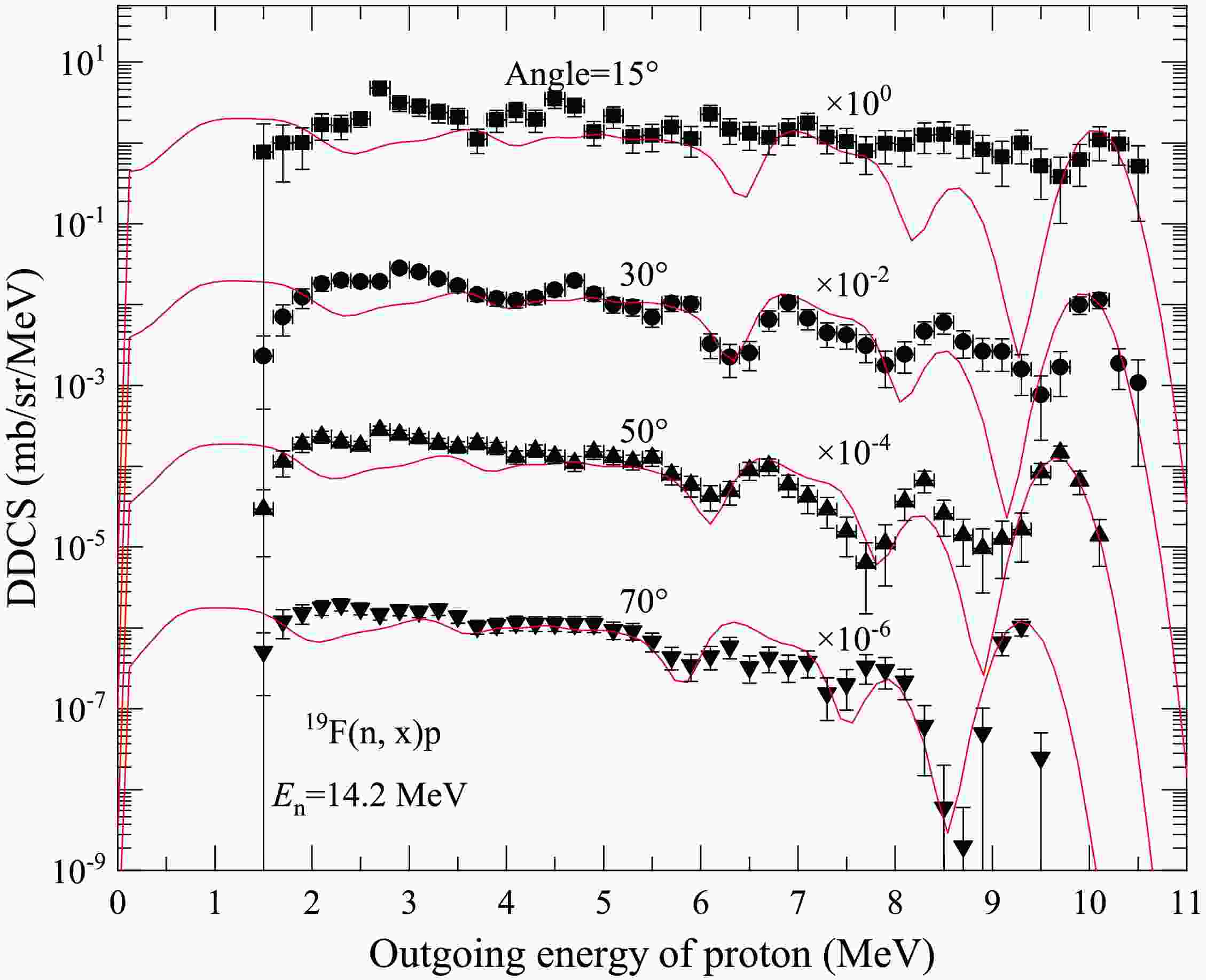
Comparisons are performed between the calculations and measurements of the total DDCS of the outgoing proton at an incident energy $ E_n = 14.2 $ MeV. The results are shown in Figs. 1 and 2 for outgoing angles of $ 15^{\circ} $, $ 30^{\circ} $, $ 50^{\circ} $, $ 70^{\circ} $, $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $. The black points represent the experimental data taken from Ref. [26], and the red solid lines represent the results of this study. Data are successively shifted downward by factors of $ 10^{0} $, $ 10^{-2} $, $ 10^{-4} $, and $ 10^{-6} $ for clarity. One can see that the calculated results agree reasonably well with the experimental data. At 15$ ^\circ $ in the 8–9 MeV outgoing energy region, the agreement between theoretical calculations and experimental data is slightly inferior. This is primarily due to the fact that the distance between the detector and sample at 15$ ^\circ $ is greater than that at other angles, as shown in Table 5 of Ref. [26]. This is the same case for the outgoing deuteron and triton.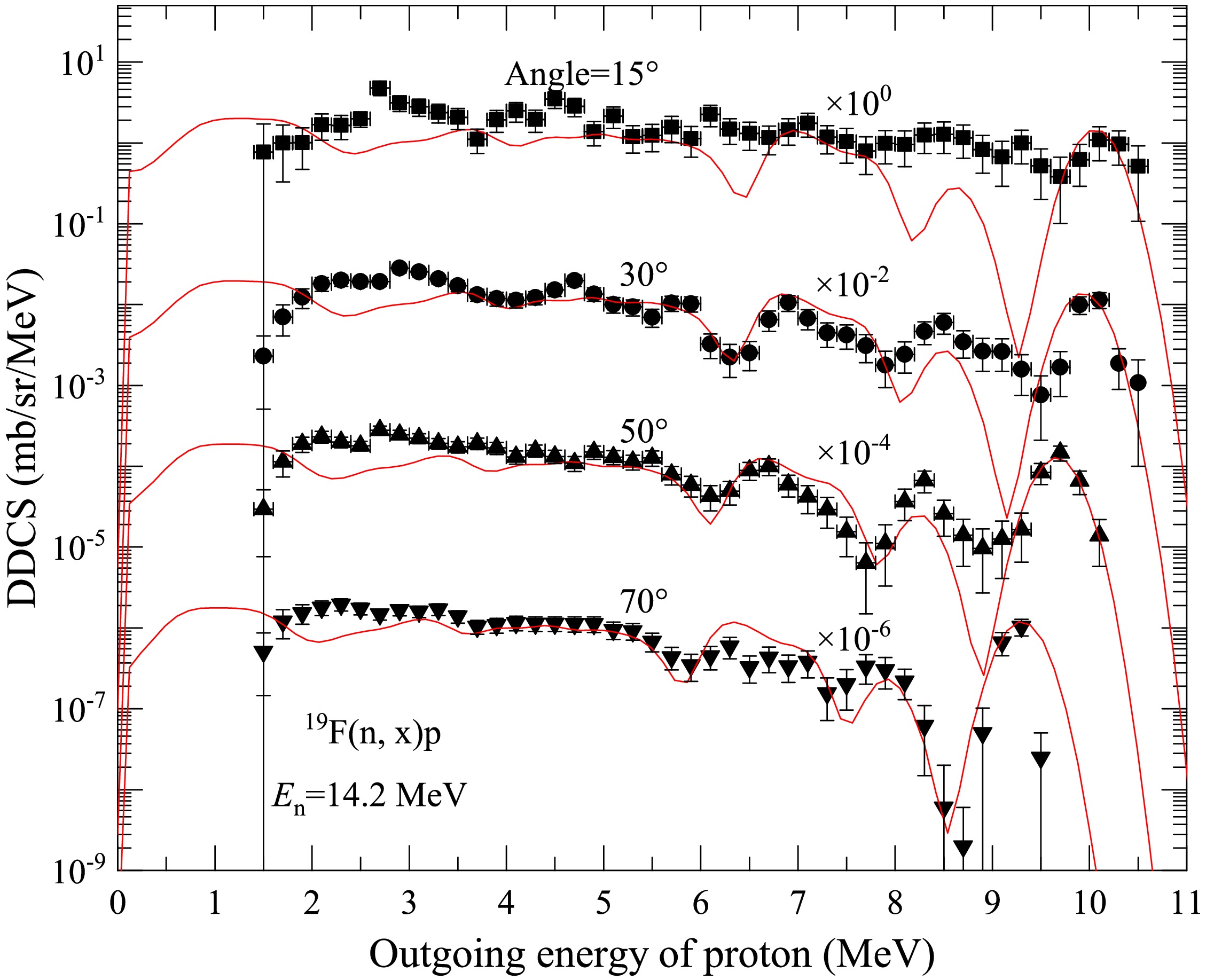

Figure 1.  (color online) Total DDCS of the outgoing proton for the $ \text{n} + ^{19}\text{F} $ reaction with outgoing angles $ 15^{\circ} $, $ 30^{\circ} $, $ 50^{\circ} $, and $ 70^{\circ} $ at $ E_n $ = 14.2 MeV in laboratory system (LS). The black points denote the experimental data taken from Ref. [26], and the red solid lines denote the results of this study.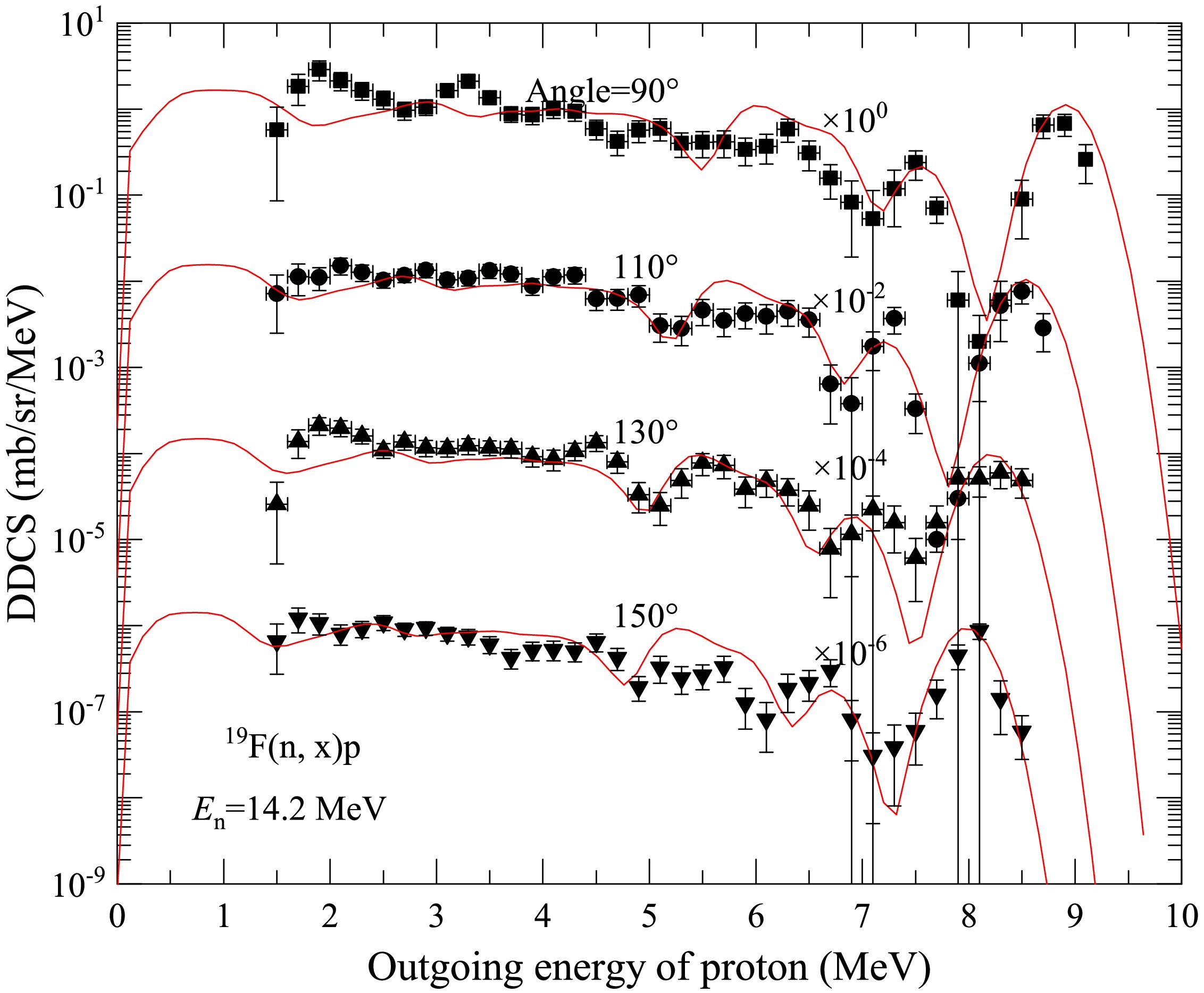

Figure 2.  (color online) Same as Fig. 1 but for outgoing angles $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $.

Taking the calculated DDCS of an outgoing proton with outgoing angle $ 90^{\circ} $ at $ E_n $ = 14.2 MeV as an example, the partial spectra are shown in Fig. 3. The blue dashed lines denote the partial spectra of the first outgoing protons from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to the 42nd excited state of the first residual nucleus $ ^{19}\text{O} $ (Fig. 3(a)). It is evident that the contribution of the reaction channel (n, p) dominates the DDCS of outgoing protons. Each experimentally observed discrete peak originates from the superposition of two or more energy levels, reflecting the energy level structure of the residual nucleus $ ^{19}\text{O} $, including both its ground and excited states. The examination of peak positions and shapes offers significant insights into the nuclear energy level structure of $ ^{19}\text{O} $, as well as its dynamic behavior throughout the reaction process. The green dashed lines denote the partial spectra of the secondary emitted protons from the compound nucleus $ ^{20}\text{F}^* $, which first emits a neutron to the 54th-148th excited energy levels of the first residual nucleus $ ^{19}\text{F}^* $ and then emits a proton to the ground state up to the 8th excited state of $ ^{18}\text{O} $ (Fig. 3(b)). It is also crucial to consider the contribution of the secondary emitted protons, especially in the low energy region.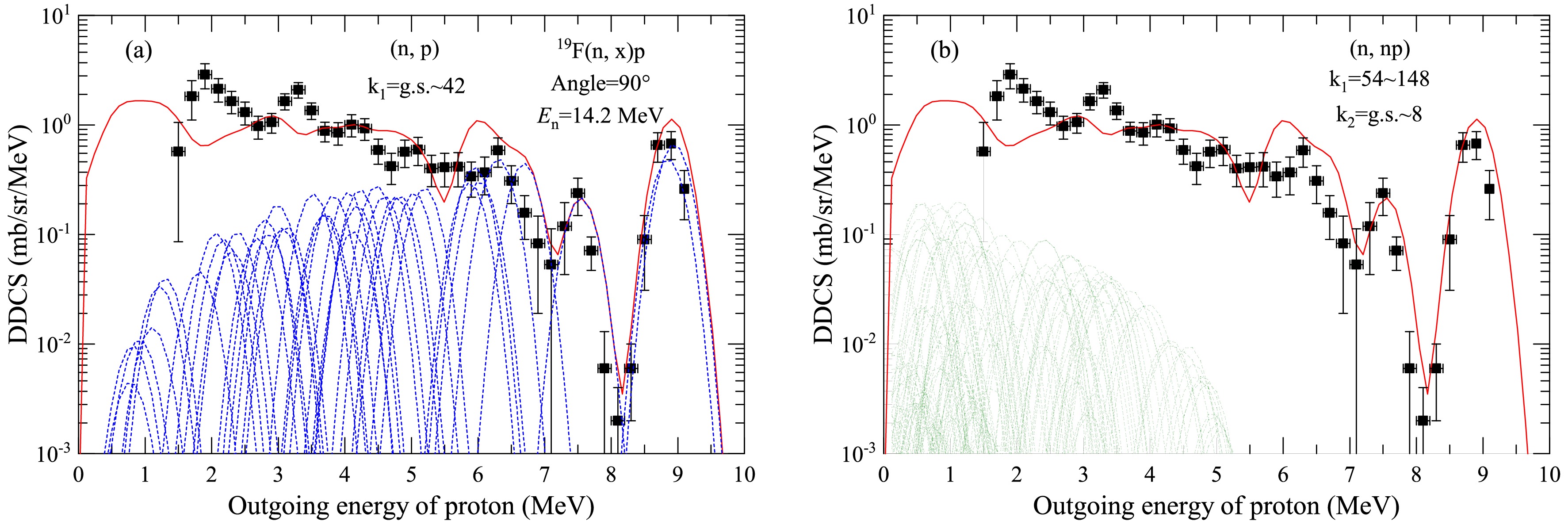

Figure 3.  (color online) Partial and total DDCSs of the outgoing proton for the n+¹⁹F reaction with an outgoing angle $ 90^{\circ} $ at $ E_n $ = 14.2 MeV in LS. The black points denote the experimental data taken from Ref. [26], and the red solid lines denote the results of this study. The blue dashed lines denote the partial spectra of the first outgoing protons from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to the 42nd excited state of the first residual nucleus $ ^{19}\text{O} $ (a). The green dashed lines denote the partial spectra of the secondary emitted protons from the compound nucleus $ ^{20}\text{F}^* $, which first emits a neutron to the 54th-148th excited energy levels of first residual nucleus $ ^{19}\text{F}^* $ and then emits a proton to the ground state up to the 8th excited state of $ ^{18}\text{O} $ (b).

Figure 4 shows a comparison of the DDCS of an outgoing proton calculated in this study versus those recommended by major international databases for n+¹⁹F at $ E_n $ = 14.2 MeV with a $ 90^{\circ} $ outgoing angle. The black points denote the experimental data taken from Ref. [26]. The red solid, pink dash-dotted, blue dashed, and green dotted lines denote the results of this study, ENDF/B-VIII.1, JENDL-5, and BROND-3.1, respectively. The results evaluated using ENDF/B-VIII.1 and BROND-3.1 can partly reproduce the experimental DDCS in the low energy region of outgoing protons. However, they fail to describe the discrete peaks in the high outgoing energy region. This discrepancy primarily stems from the assumption of isotropic angular distributions [27, 28], which neglects the influence of the energy level structure of the residual nucleus ¹⁹O. The results evaluated using JENDL-5 show significant discrepancies with respect to experimental data.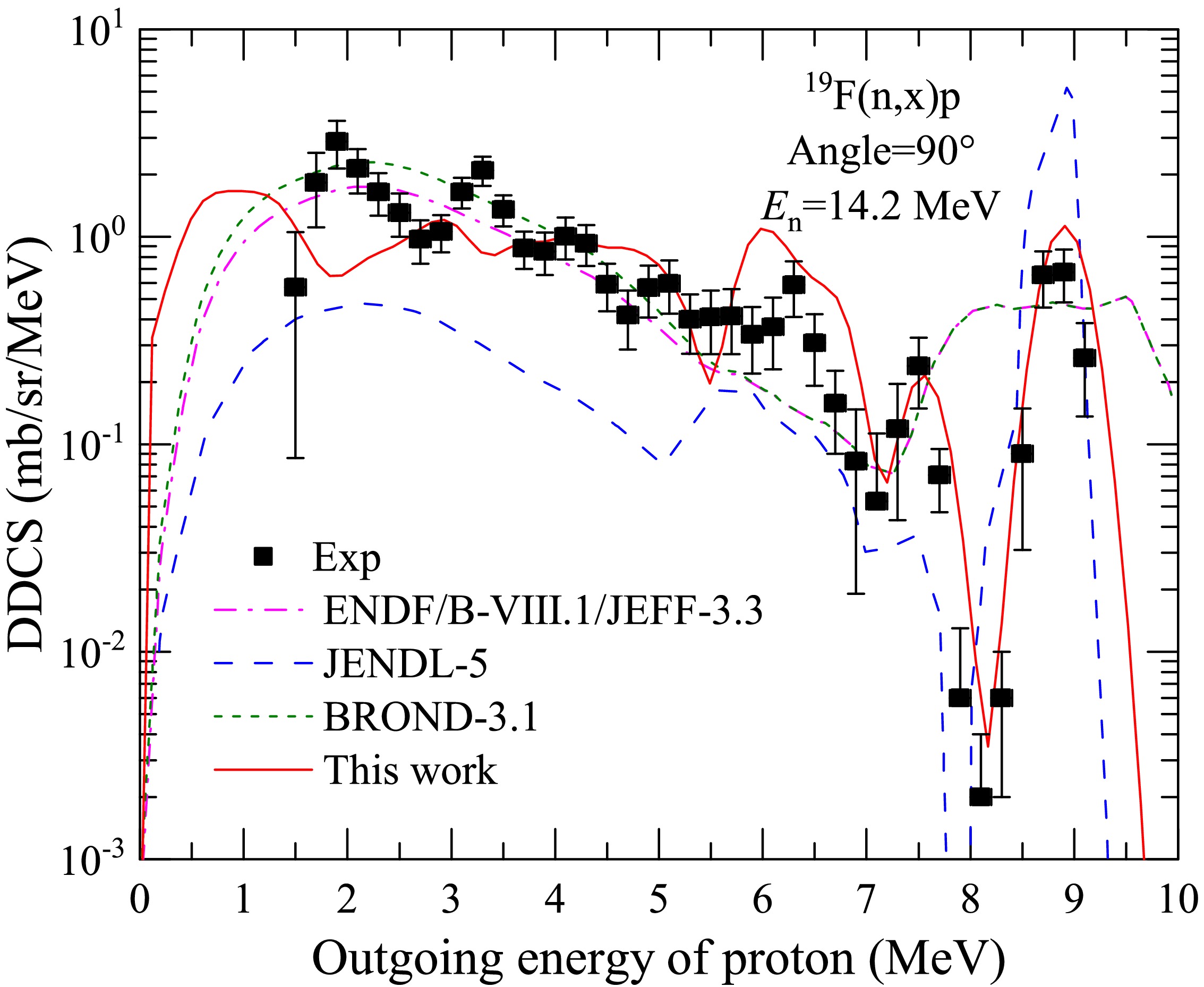

Figure 4.  (color online) Comparison of the DDCS of the emitted proton calculated in this study versus those recommended by major international databases for n+¹⁹F at $ E_n $ = 14.2 MeV with a $ 90^{\circ} $ outgoing angle. The black points denote the experimental data taken from Ref. [26]. The red solid, pink dash-dotted, blue dashed, and green dotted lines denote the results of this study, ENDF/B-VIII.1, JENDL-5, and BROND-3.1, respectively.

Comparisons are performed between the calculations and measurements of the total DDCS of the outgoing proton at an incident energy $ E_n = 14.2 $ MeV. The results are shown in Figs. 1 and 2 for outgoing angles of $ 15^{\circ} $, $ 30^{\circ} $, $ 50^{\circ} $, $ 70^{\circ} $, $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $. The black points represent the experimental data taken from Ref. [26], and the red solid lines represent the results of this study. Data are successively shifted downward by factors of $ 10^{0} $, $ 10^{-2} $, $ 10^{-4} $, and $ 10^{-6} $ for clarity. One can see that the calculated results agree reasonably well with the experimental data. At 15$ ^\circ $ in the 8–9 MeV outgoing energy region, the agreement between theoretical calculations and experimental data is slightly inferior. This is primarily due to the fact that the distance between the detector and sample at 15$ ^\circ $ is greater than that at other angles, as shown in Table 5 of Ref. [26]. This is the same case for the outgoing deuteron and triton.

Figure 1.  (color online) Total DDCS of the outgoing proton for the $ \text{n} + ^{19}\text{F} $ reaction with outgoing angles $ 15^{\circ} $, $ 30^{\circ} $, $ 50^{\circ} $, and $ 70^{\circ} $ at $ E_n $ = 14.2 MeV in laboratory system (LS). The black points denote the experimental data taken from Ref. [26], and the red solid lines denote the results of this study.

Figure 2.  (color online) Same as Fig. 1 but for outgoing angles $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $.

Taking the calculated DDCS of an outgoing proton with outgoing angle $ 90^{\circ} $ at $ E_n $ = 14.2 MeV as an example, the partial spectra are shown in Fig. 3. The blue dashed lines denote the partial spectra of the first outgoing protons from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to the 42nd excited state of the first residual nucleus $ ^{19}\text{O} $ (Fig. 3(a)). It is evident that the contribution of the reaction channel (n, p) dominates the DDCS of outgoing protons. Each experimentally observed discrete peak originates from the superposition of two or more energy levels, reflecting the energy level structure of the residual nucleus $ ^{19}\text{O} $, including both its ground and excited states. The examination of peak positions and shapes offers significant insights into the nuclear energy level structure of $ ^{19}\text{O} $, as well as its dynamic behavior throughout the reaction process. The green dashed lines denote the partial spectra of the secondary emitted protons from the compound nucleus $ ^{20}\text{F}^* $, which first emits a neutron to the 54th-148th excited energy levels of the first residual nucleus $ ^{19}\text{F}^* $ and then emits a proton to the ground state up to the 8th excited state of $ ^{18}\text{O} $ (Fig. 3(b)). It is also crucial to consider the contribution of the secondary emitted protons, especially in the low energy region.

Figure 3.  (color online) Partial and total DDCSs of the outgoing proton for the n+¹⁹F reaction with an outgoing angle $ 90^{\circ} $ at $ E_n $ = 14.2 MeV in LS. The black points denote the experimental data taken from Ref. [26], and the red solid lines denote the results of this study. The blue dashed lines denote the partial spectra of the first outgoing protons from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to the 42nd excited state of the first residual nucleus $ ^{19}\text{O} $ (a). The green dashed lines denote the partial spectra of the secondary emitted protons from the compound nucleus $ ^{20}\text{F}^* $, which first emits a neutron to the 54th-148th excited energy levels of first residual nucleus $ ^{19}\text{F}^* $ and then emits a proton to the ground state up to the 8th excited state of $ ^{18}\text{O} $ (b).

Figure 4 shows a comparison of the DDCS of an outgoing proton calculated in this study versus those recommended by major international databases for n+¹⁹F at $ E_n $ = 14.2 MeV with a $ 90^{\circ} $ outgoing angle. The black points denote the experimental data taken from Ref. [26]. The red solid, pink dash-dotted, blue dashed, and green dotted lines denote the results of this study, ENDF/B-VIII.1, JENDL-5, and BROND-3.1, respectively. The results evaluated using ENDF/B-VIII.1 and BROND-3.1 can partly reproduce the experimental DDCS in the low energy region of outgoing protons. However, they fail to describe the discrete peaks in the high outgoing energy region. This discrepancy primarily stems from the assumption of isotropic angular distributions [27, 28], which neglects the influence of the energy level structure of the residual nucleus ¹⁹O. The results evaluated using JENDL-5 show significant discrepancies with respect to experimental data.

Figure 4.  (color online) Comparison of the DDCS of the emitted proton calculated in this study versus those recommended by major international databases for n+¹⁹F at $ E_n $ = 14.2 MeV with a $ 90^{\circ} $ outgoing angle. The black points denote the experimental data taken from Ref. [26]. The red solid, pink dash-dotted, blue dashed, and green dotted lines denote the results of this study, ENDF/B-VIII.1, JENDL-5, and BROND-3.1, respectively.

Comparisons of the calculated total DDCS of the outgoing deuteron with the measured data are shown in Figs. 5 and 6 at $ E_n $=14.2 MeV for outgoing angles of $ 15^{\circ} $, $ 30^{\circ} $, $ 50^{\circ} $, $ 70^{\circ} $, $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $. The black points represent the experimental data taken from Ref. [26], and the red solid lines represent the results of this study. Similarly, the calculated results agree well with the experimental DDCS of the outgoing deuteron, except at the outgoing angle of 15$ ^\circ $. The theoretical calculations are evidently lower than the experimental data at the outgoing angle of 15$ ^\circ $in the 8–9 MeV outgoing energy region. The reason is the same as that for the outgoing proton mentioned above. In addition, the calculated results exhibit pronounced peaks at an outgoing deuteron energy of approximately 3 MeV only for outgoing angles of $ 110^\circ $ and $ 130^\circ $, indicating a scenario completely opposite to that of the experimental data. This discrepancy may have arisen from some unknown causes during the measurement process, and it is hoped that experimental physicists can further verify such data.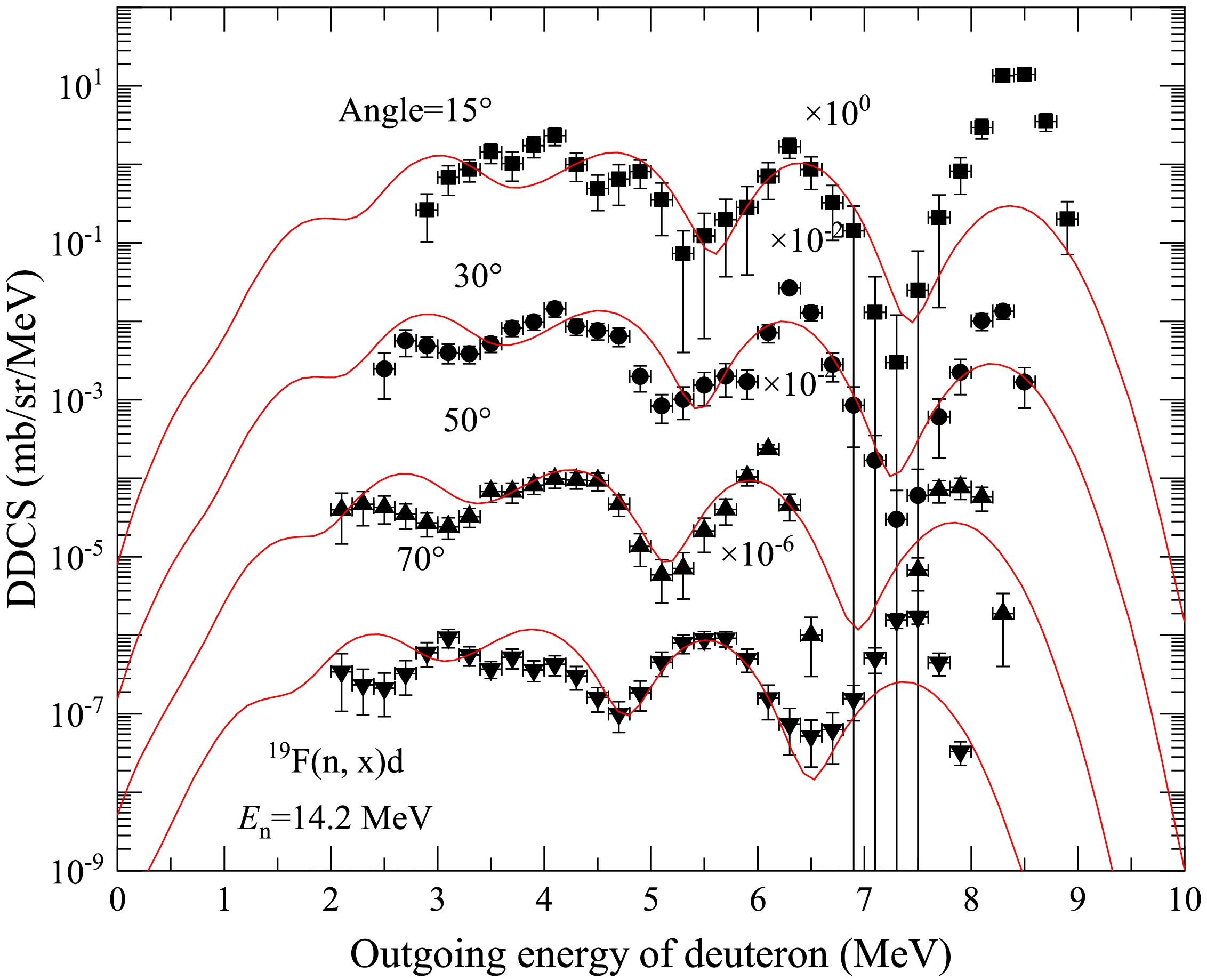

Figure 5.  (color online) Same as Fig. 1 but for the outgoing deuteron at angles $ 15^{\circ} $, $ 30^{\circ} $, $ 50^{\circ} $, and $ 70^{\circ} $.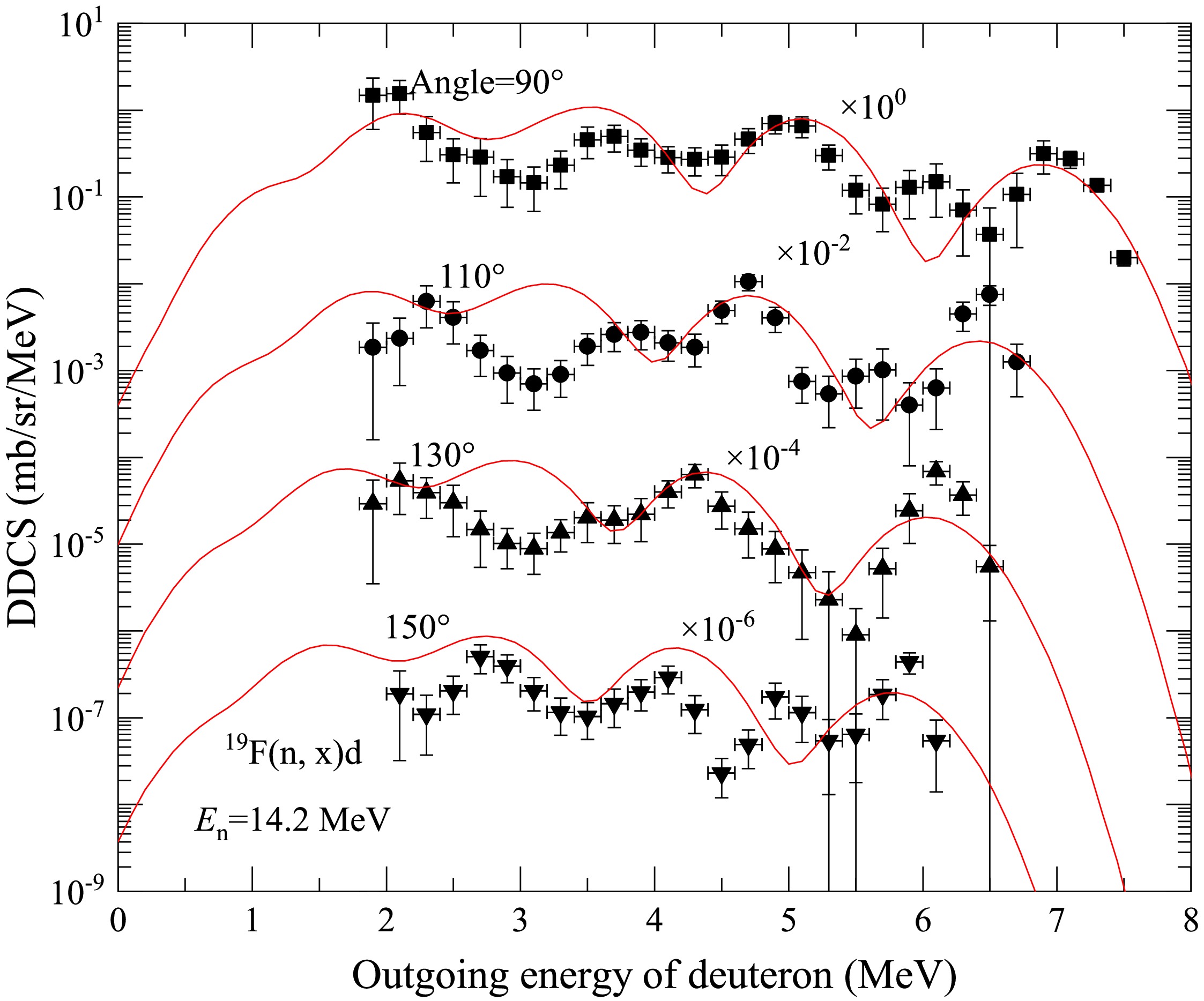

Figure 6.  (color online) Same as Fig. 1 but for the outgoing deuteron at angles $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $.

Figure 7 shows the partial and total DDCSs of the outgoing deuteron for the n+¹⁹F reaction with an outgoing angle of $ 90^{\circ} $ at $ E_n $ = 14.2 MeV in LS. The blue dashed lines denote the partial spectra of the first outgoing deuteron from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 15th excited state of the first residual nucleus $ ^{18}\text{O} $. These energy spectra from the $ (n, d) $ channel collectively contribute to the total DDCS of the outgoing deuteron. Each experimentally observed discrete peak reflects the influence of the energy level structure of the residual nucleus ¹⁸O.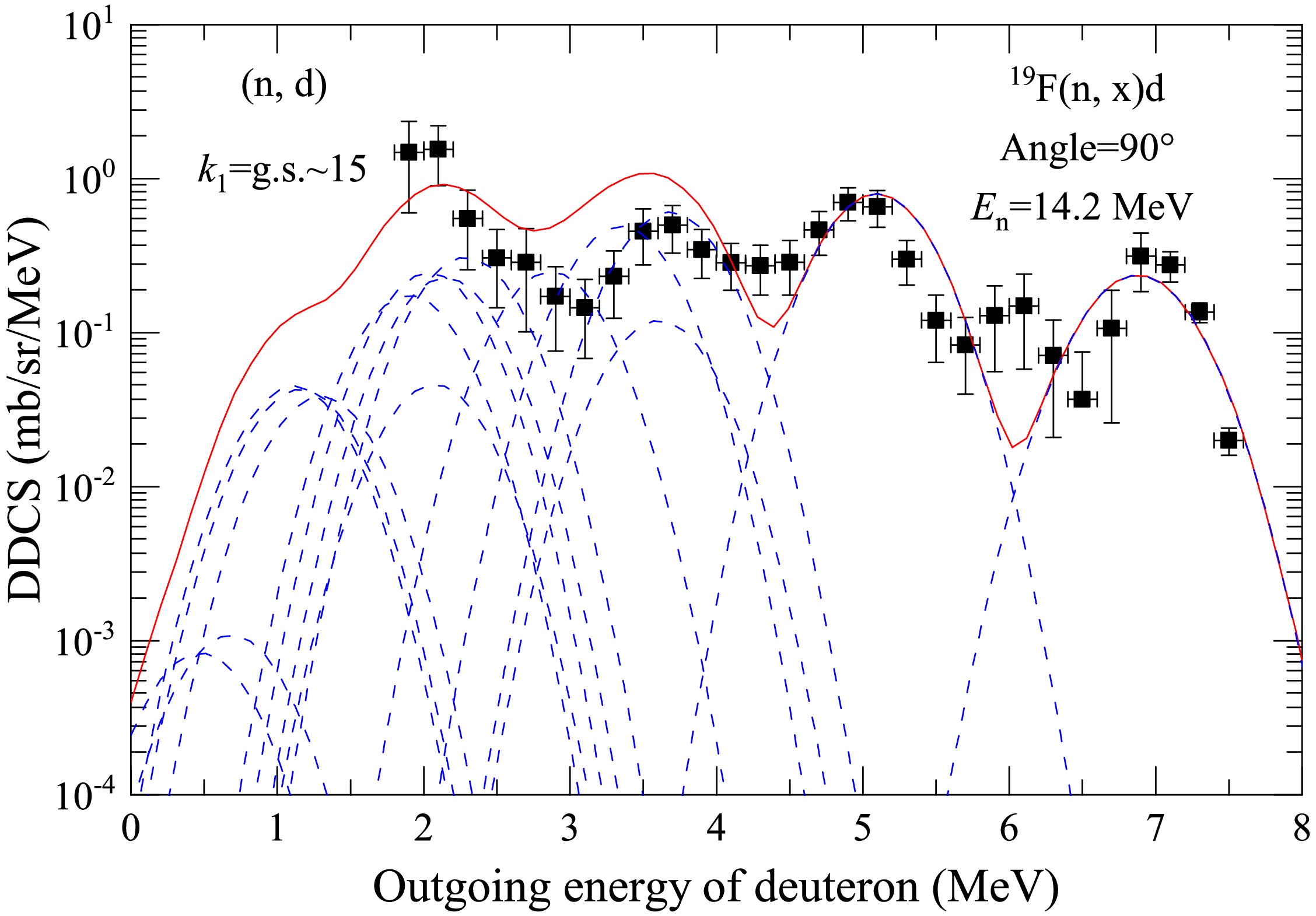

Figure 7.  (color online) Partial and total DDCSs of the outgoing deuteron for the $ {n} + ^{19}\text{F} $ reaction with $ 90^{\circ} $ outgoing angle at $ E_n $ = 14.2 MeV in LS. The black points denote the experimental data taken from Ref. [26], and the red solid line denotes the result of this study. The blue dashed lines denote the partial spectra of the first outgoing deuteron from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 15th excited state of the first residual nucleus $ ^{18}\text{O} $.

In Fig. 8, the calculated total DDCS of the outgoing deuteron is compared with the experimental and evaluated data from JENDL-5. The black points denote the experimental data taken from Ref. [26]. The red solid and blue dashed lines denote the results of this study and JENDL-5, respectively. The calculated results of this study and evaluated data from JENDL-5 both reasonably reproduce the measured data, but the former aligns more closely with the experimental data.

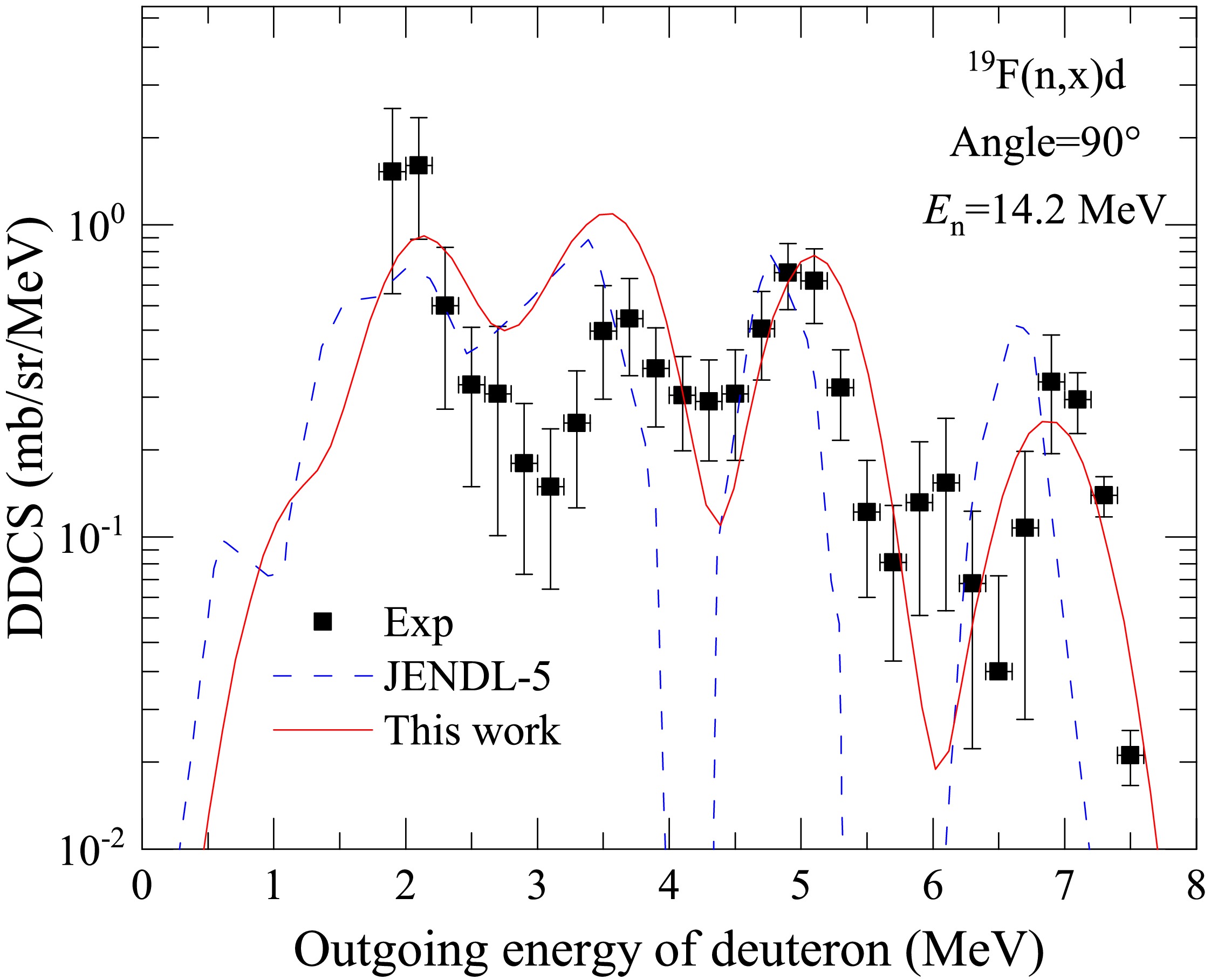
Figure 8.  (color online) Comparison of the calculated DDCS of the outgoing deuteron for the n+¹⁹F reaction with experimental data and evaluated results at $ E_n $ = 14.2 MeV with an outgoing angle of $ 90^{\circ} $. The black points denote the experimental data taken from Ref. [26]. The red solid and blue dashed lines denote the results of this study and JENDL-5, respectively.

Comparisons of the calculated total DDCS of the outgoing deuteron with the measured data are shown in Figs. 5 and 6 at $ E_n $=14.2 MeV for outgoing angles of $ 15^{\circ} $, $ 30^{\circ} $, $ 50^{\circ} $, $ 70^{\circ} $, $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $. The black points represent the experimental data taken from Ref. [26], and the red solid lines represent the results of this study. Similarly, the calculated results agree well with the experimental DDCS of the outgoing deuteron, except at the outgoing angle of 15$ ^\circ $. The theoretical calculations are evidently lower than the experimental data at the outgoing angle of 15$ ^\circ $in the 8–9 MeV outgoing energy region. The reason is the same as that for the outgoing proton mentioned above. In addition, the calculated results exhibit pronounced peaks at an outgoing deuteron energy of approximately 3 MeV only for outgoing angles of $ 110^\circ $ and $ 130^\circ $, indicating a scenario completely opposite to that of the experimental data. This discrepancy may have arisen from some unknown causes during the measurement process, and it is hoped that experimental physicists can further verify such data.

Figure 5.  (color online) Same as Fig. 1 but for the outgoing deuteron at angles $ 15^{\circ} $, $ 30^{\circ} $, $ 50^{\circ} $, and $ 70^{\circ} $.

Figure 6.  (color online) Same as Fig. 1 but for the outgoing deuteron at angles $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $.

Figure 7 shows the partial and total DDCSs of the outgoing deuteron for the n+¹⁹F reaction with an outgoing angle of $ 90^{\circ} $ at $ E_n $ = 14.2 MeV in LS. The blue dashed lines denote the partial spectra of the first outgoing deuteron from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 15th excited state of the first residual nucleus $ ^{18}\text{O} $. These energy spectra from the $ (n, d) $ channel collectively contribute to the total DDCS of the outgoing deuteron. Each experimentally observed discrete peak reflects the influence of the energy level structure of the residual nucleus ¹⁸O.

Figure 7.  (color online) Partial and total DDCSs of the outgoing deuteron for the $ {n} + ^{19}\text{F} $ reaction with $ 90^{\circ} $ outgoing angle at $ E_n $ = 14.2 MeV in LS. The black points denote the experimental data taken from Ref. [26], and the red solid line denotes the result of this study. The blue dashed lines denote the partial spectra of the first outgoing deuteron from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 15th excited state of the first residual nucleus $ ^{18}\text{O} $.

In Fig. 8, the calculated total DDCS of the outgoing deuteron is compared with the experimental and evaluated data from JENDL-5. The black points denote the experimental data taken from Ref. [26]. The red solid and blue dashed lines denote the results of this study and JENDL-5, respectively. The calculated results of this study and evaluated data from JENDL-5 both reasonably reproduce the measured data, but the former aligns more closely with the experimental data.

Figure 8.  (color online) Comparison of the calculated DDCS of the outgoing deuteron for the n+¹⁹F reaction with experimental data and evaluated results at $ E_n $ = 14.2 MeV with an outgoing angle of $ 90^{\circ} $. The black points denote the experimental data taken from Ref. [26]. The red solid and blue dashed lines denote the results of this study and JENDL-5, respectively.

Comparisons of the calculated total DDCS of the outgoing triton with the measured data are shown in Figs. 9 and 10 at the incident neutron energy $ E_n=14.2 $ MeV for outgoing angles of $ 15^{\circ} $, $ 30^{\circ} $, $ 50^{\circ} $, $ 70^{\circ} $, $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $, respectively. The black points represent the experimental data taken from Ref. [26], and the red solid lines represent the results of this study. One can see that the calculated results are in good agreement with the experimental data. However, there is an unknown peak around 4−4.5 MeV, as shown in Fig. 9, at outgoing angles of $ 15^{\circ} $, $ 30^{\circ} $, and $ 50^{\circ} $. The energy of the particle corresponds to an excited state of $ ^{17}\text{O} $ at approximately 2 MeV; however, it is not likely to be a real new excited state in $ ^{17}\text{O} $ because there is no corresponding state in the mirror nucleus $ ^{17}\text{F} $ [42]. It is still unclear what kind of mechanism contributes to the formation of this peak. It is expected that these unidentified peaks can be further confirmed through future experimental investigations.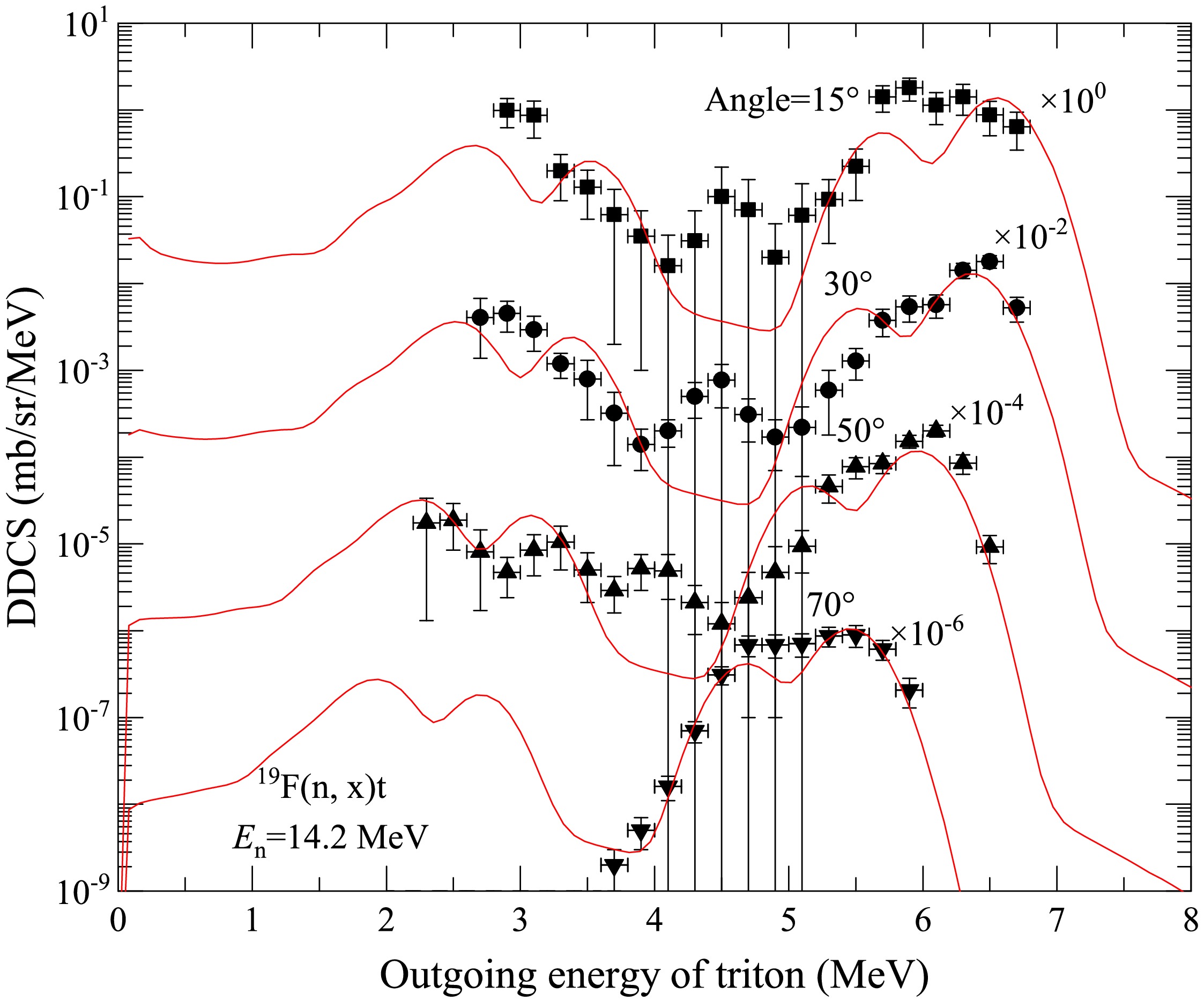

Figure 9.  (color online) Same as Fig. 1 but for the outgoing triton at angles $ 15^{\circ} $, $ 30^{\circ} $, $ 50^{\circ} $, and $ 70^{\circ} $.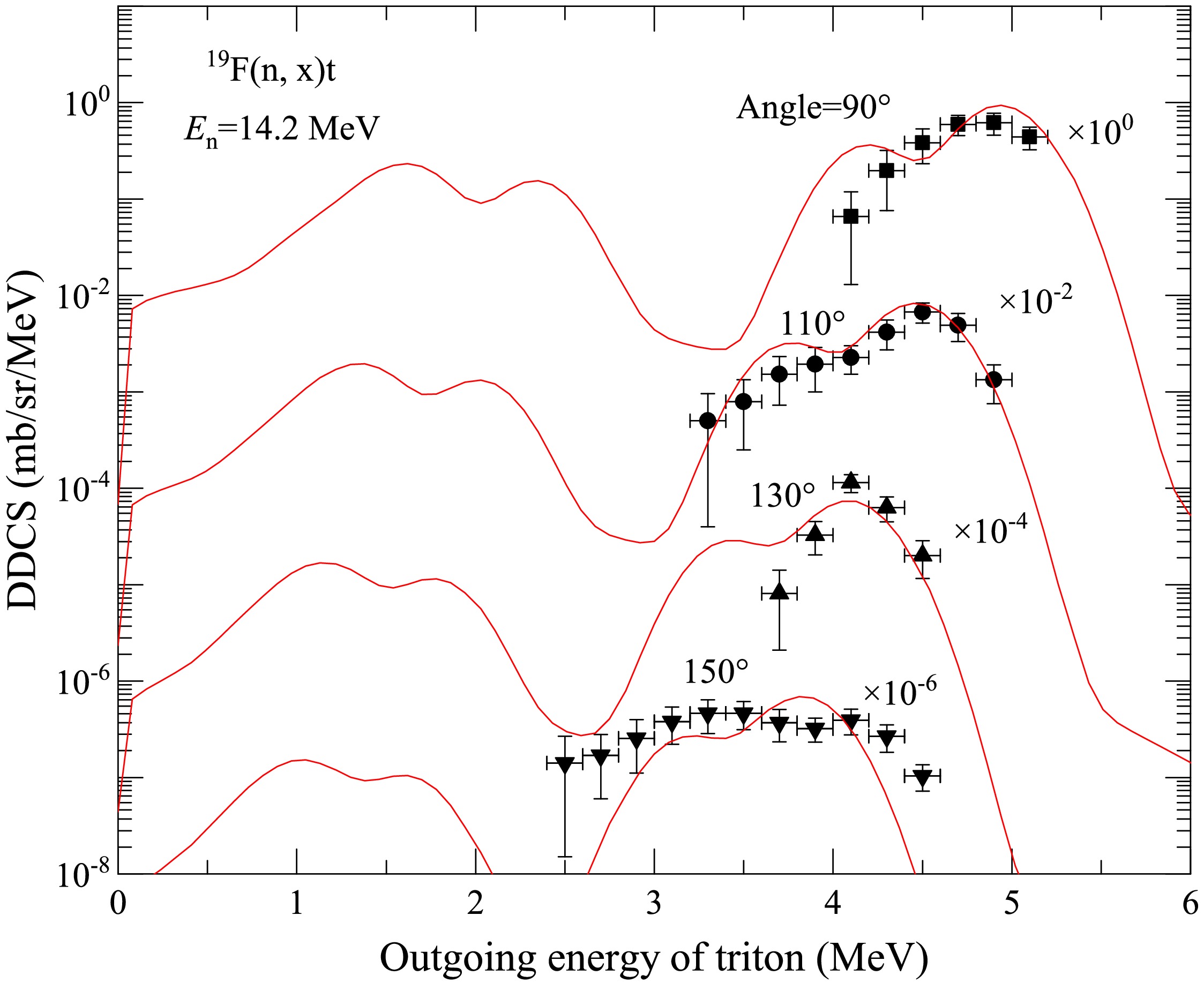

Figure 10.  (color online) Same as Fig. 1 but for the outgoing triton at angles $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $.

The partial and total DDCSs of the outgoing triton for the n+¹⁹F reaction are shown in Fig. 11 at $ E_n = 14.2 $ MeV with a $ 90^{\circ} $ outgoing angle. The blue dashed lines denote the partial spectra of the first outgoing tritons from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 8th excited state of the first residual nucleus $ ^{17}\text{O} $ (Fig. 11(a)). Each discrete peak matches an energy level of ¹⁷O. The green dashed lines denote the partial spectra of the secondary emitted tritons from the compound nucleus $ ^{20}\text{F}^* $, which first emits a neutron to the 130th−148th excited energy levels of the first residual nucleus $ ^{19}\text{F} $ and then emits a triton to the ground state of $ ^{16}\text{O} $ (Fig. 11(b)). Here, $ k_2 $ denotes the energy levels of the secondary residual nuclei. Although the reaction channel $ (n, nt) $ contributes less significantly to the overall spectra compared to the $ (n, t) $ channel, its influence extends over a broader range of outgoing energies.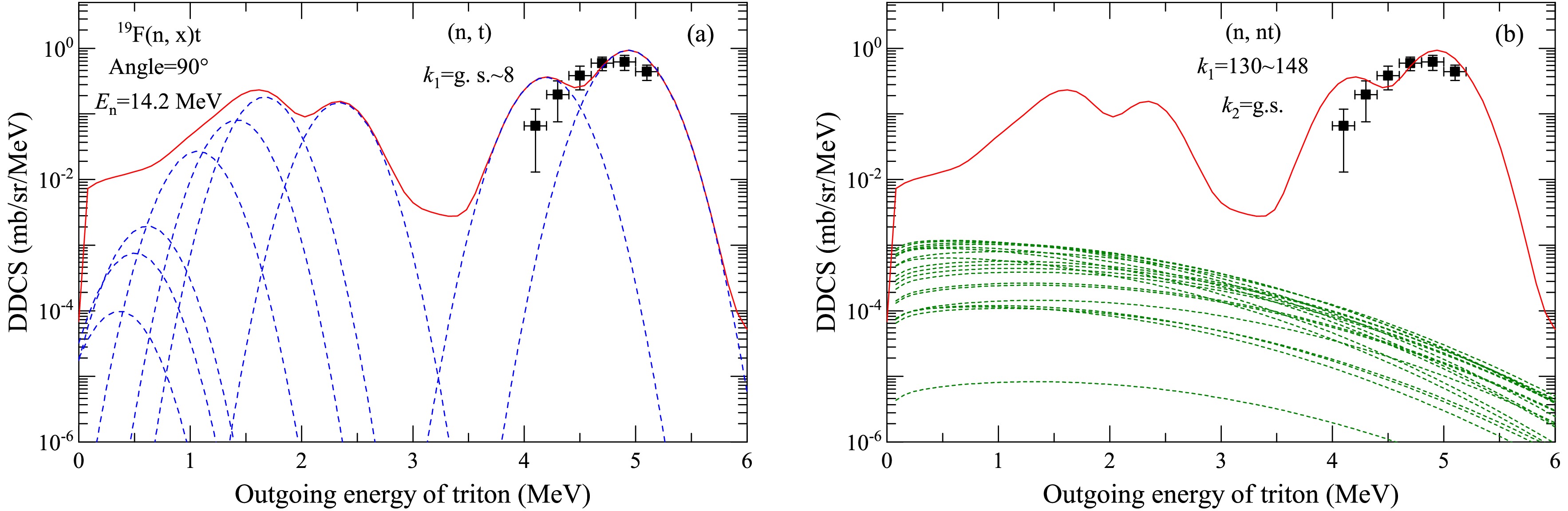

Figure 11.  (color online) Partial and total DDCSs of the outgoing triton for the n+¹⁹F reaction with an outgoing angle of $ 90^{\circ} $ at $ E_n $ = 14.2 MeV in LS. The black points denote the experimental data taken from Ref. [26], and the red solid lines denote the results of this study. The blue dashed lines denote the partial spectra of the first outgoing tritons from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 8th excited state of the first residual nucleus $ ^{17}\text{O} $ (a). The green dashed lines denote the partial spectra of the secondary emitted tritons from the compound nucleus $ ^{20}\text{F}^* $, which first emits a neutron to the 130th-148th excited energy levels of first residual nucleus $ ^{19}\text{F} $ and then emits a triton to the ground state of $ ^{16}\text{O} $ (b).

Figure 12 shows a comparison of the DDCS of the outgoing triton with the experimental data and evaluated results at $ E_n $ = 14.2 MeV with a $ 90^{\circ} $ angle for the n+¹⁹F reaction. The black points denote the experimental data taken from Ref. [26]. The red solid and blue dashed lines denote the results of this study and JENDL-5, respectively. The calculated results of this study and evaluated data from JENDL-5 both reasonably reproduce the measured data; however, the former aligns more closely with the experimental data.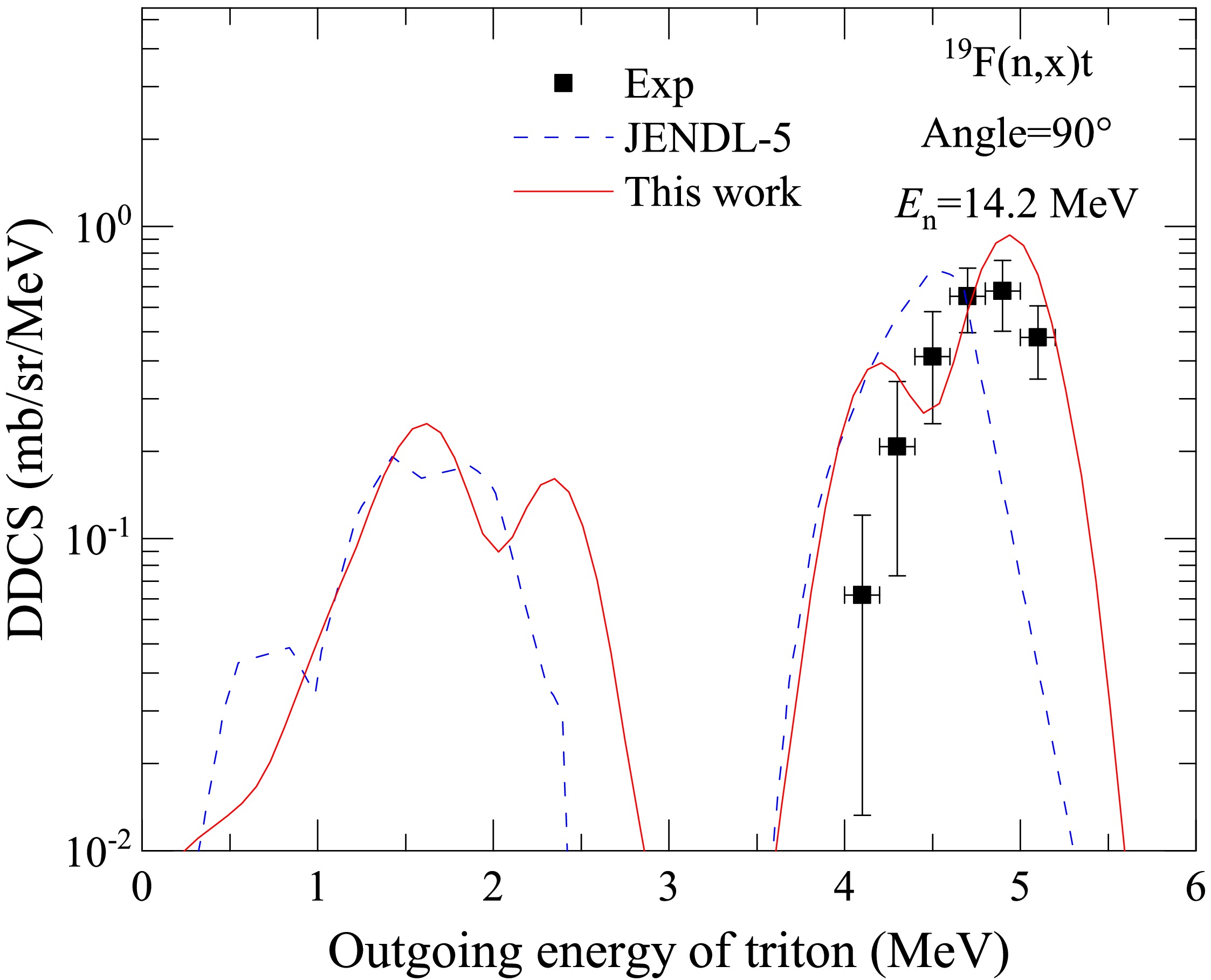

Figure 12.  (color online) Comparison of the calculated DDCS of outgoing triton at $ 90^{\circ} $ angle for the n+¹⁹F reaction with the experimental data and evaluated results at $ E_n $ = 14.2 MeV. The black points denote the experimental data taken from Ref. [26]. The red solid and blue dashed lines denote the results of this study and JENDL-5, respectively.

Comparisons of the calculated total DDCS of the outgoing triton with the measured data are shown in Figs. 9 and 10 at the incident neutron energy $ E_n=14.2 $ MeV for outgoing angles of $ 15^{\circ} $, $ 30^{\circ} $, $ 50^{\circ} $, $ 70^{\circ} $, $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $, respectively. The black points represent the experimental data taken from Ref. [26], and the red solid lines represent the results of this study. One can see that the calculated results are in good agreement with the experimental data. However, there is an unknown peak around 4−4.5 MeV, as shown in Fig. 9, at outgoing angles of $ 15^{\circ} $, $ 30^{\circ} $, and $ 50^{\circ} $. The energy of the particle corresponds to an excited state of $ ^{17}\text{O} $ at approximately 2 MeV; however, it is not likely to be a real new excited state in $ ^{17}\text{O} $ because there is no corresponding state in the mirror nucleus $ ^{17}\text{F} $ [42]. It is still unclear what kind of mechanism contributes to the formation of this peak. It is expected that these unidentified peaks can be further confirmed through future experimental investigations.

Figure 9.  (color online) Same as Fig. 1 but for the outgoing triton at angles $ 15^{\circ} $, $ 30^{\circ} $, $ 50^{\circ} $, and $ 70^{\circ} $.

Figure 10.  (color online) Same as Fig. 1 but for the outgoing triton at angles $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $.

The partial and total DDCSs of the outgoing triton for the n+¹⁹F reaction are shown in Fig. 11 at $ E_n = 14.2 $ MeV with a $ 90^{\circ} $ outgoing angle. The blue dashed lines denote the partial spectra of the first outgoing tritons from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 8th excited state of the first residual nucleus $ ^{17}\text{O} $ (Fig. 11(a)). Each discrete peak matches an energy level of ¹⁷O. The green dashed lines denote the partial spectra of the secondary emitted tritons from the compound nucleus $ ^{20}\text{F}^* $, which first emits a neutron to the 130th−148th excited energy levels of the first residual nucleus $ ^{19}\text{F} $ and then emits a triton to the ground state of $ ^{16}\text{O} $ (Fig. 11(b)). Here, $ k_2 $ denotes the energy levels of the secondary residual nuclei. Although the reaction channel $ (n, nt) $ contributes less significantly to the overall spectra compared to the $ (n, t) $ channel, its influence extends over a broader range of outgoing energies.

Figure 11.  (color online) Partial and total DDCSs of the outgoing triton for the n+¹⁹F reaction with an outgoing angle of $ 90^{\circ} $ at $ E_n $ = 14.2 MeV in LS. The black points denote the experimental data taken from Ref. [26], and the red solid lines denote the results of this study. The blue dashed lines denote the partial spectra of the first outgoing tritons from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 8th excited state of the first residual nucleus $ ^{17}\text{O} $ (a). The green dashed lines denote the partial spectra of the secondary emitted tritons from the compound nucleus $ ^{20}\text{F}^* $, which first emits a neutron to the 130th-148th excited energy levels of first residual nucleus $ ^{19}\text{F} $ and then emits a triton to the ground state of $ ^{16}\text{O} $ (b).

Figure 12 shows a comparison of the DDCS of the outgoing triton with the experimental data and evaluated results at $ E_n $ = 14.2 MeV with a $ 90^{\circ} $ angle for the n+¹⁹F reaction. The black points denote the experimental data taken from Ref. [26]. The red solid and blue dashed lines denote the results of this study and JENDL-5, respectively. The calculated results of this study and evaluated data from JENDL-5 both reasonably reproduce the measured data; however, the former aligns more closely with the experimental data.

Figure 12.  (color online) Comparison of the calculated DDCS of outgoing triton at $ 90^{\circ} $ angle for the n+¹⁹F reaction with the experimental data and evaluated results at $ E_n $ = 14.2 MeV. The black points denote the experimental data taken from Ref. [26]. The red solid and blue dashed lines denote the results of this study and JENDL-5, respectively.

Comparisons of the calculated total DDCS of the outgoing α particle with the measured data are shown in Figs. 13 and 14 at the incident neutron energy $ E_n $=14.2 MeV with outgoing angles of $ 30^{\circ} $, $ 50^{\circ} $, $ 70^{\circ} $, $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $. One can see that the calculated results agree well with the experimental data.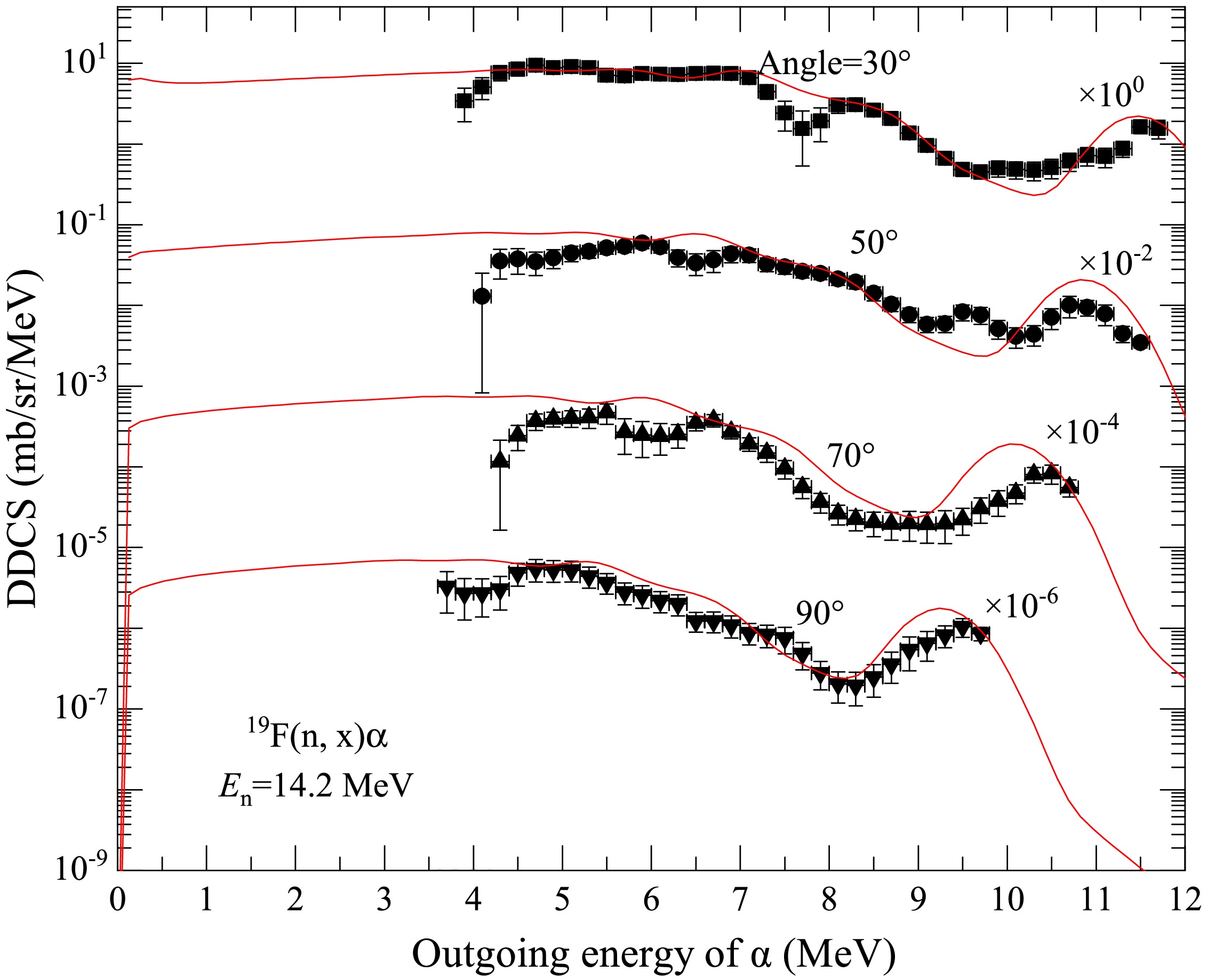

Figure 13.  (color online) Same as Fig. 1 but for the outgoing α at angles $ 30^{\circ} $, $ 50^{\circ} $, $ 70^{\circ} $, and $ 90^{\circ} $.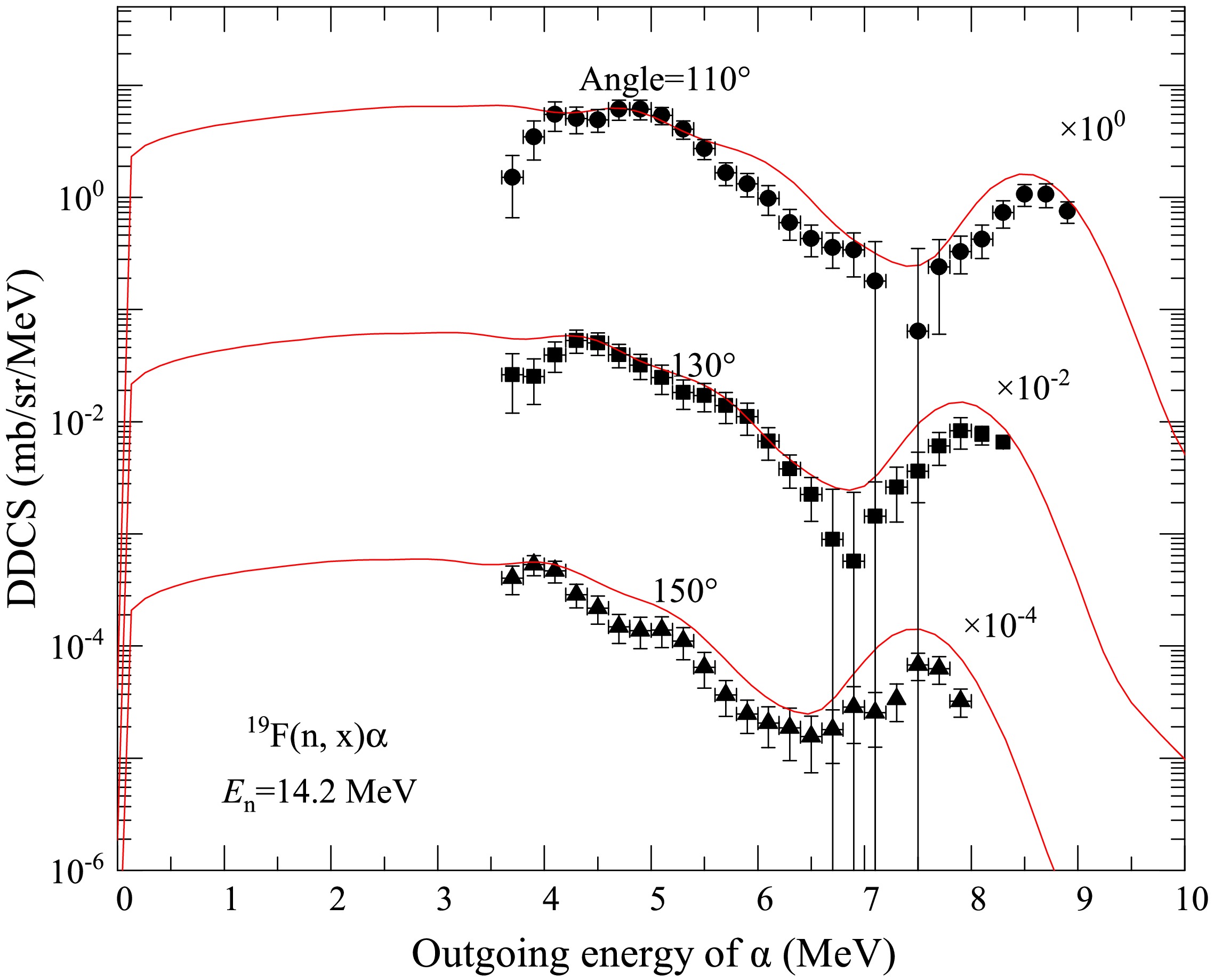

Figure 14.  (color online) Same as Fig. 1 but for the outgoing α at angles $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $.

Figure 15 shows the partial and total DDCSs of the outgoing α particle for the $ {n} + ^{19}\text{F} $ reaction with a $ 90^{\circ} $ outgoing angle at $ E_n $ = 14.2 MeV in LS. The black points denote the experimental data taken from Ref. [26], and the red solid lines denote the results of this study. The blue dashed lines denote the partial spectra of the first outgoing α from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 51st excited state of the first residual nucleus $ ^{16}\text{N} $ (Fig. 15(a)). Each experimentally observed discrete peak reflects the influence of the energy level structure of the residual nucleus $ ^{16}\text{N} $. The purple dashed lines denote the partial spectra of the first outgoing $ ^5\text{He} $ (which can break up into n and α) from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 6th excited state of the first residual nucleus $ ^{15}\text{N} $ (Fig. 15(b)). The green dashed lines denote the partial spectra of the secondary emitted α from the compound nucleus $ ^{20}\text{F}^* $, which first emits a neutron to the 12th−148th excited energy levels of first residual nucleus $ ^{19}\text{F} $ and then emits an α to the ground state up to the 12th excited state of $ ^{15}\text{N} $ (Fig. 15(c)). The yellow dashed lines denote the partial spectra of the secondary emitted α from the compound nucleus $ ^{20}\text{F}^* $, which first emits a deuteron to the 12th−15th excited energy levels of the first residual nucleus $ ^{18}\text{O} $ and then emits an α to the ground state of $ ^{14}\text{C} $ (Fig. 15(d)). It is evident that there are significant contributions from secondary particle emission to the DDCS of outgoing α particles for the n + ¹⁹F reaction.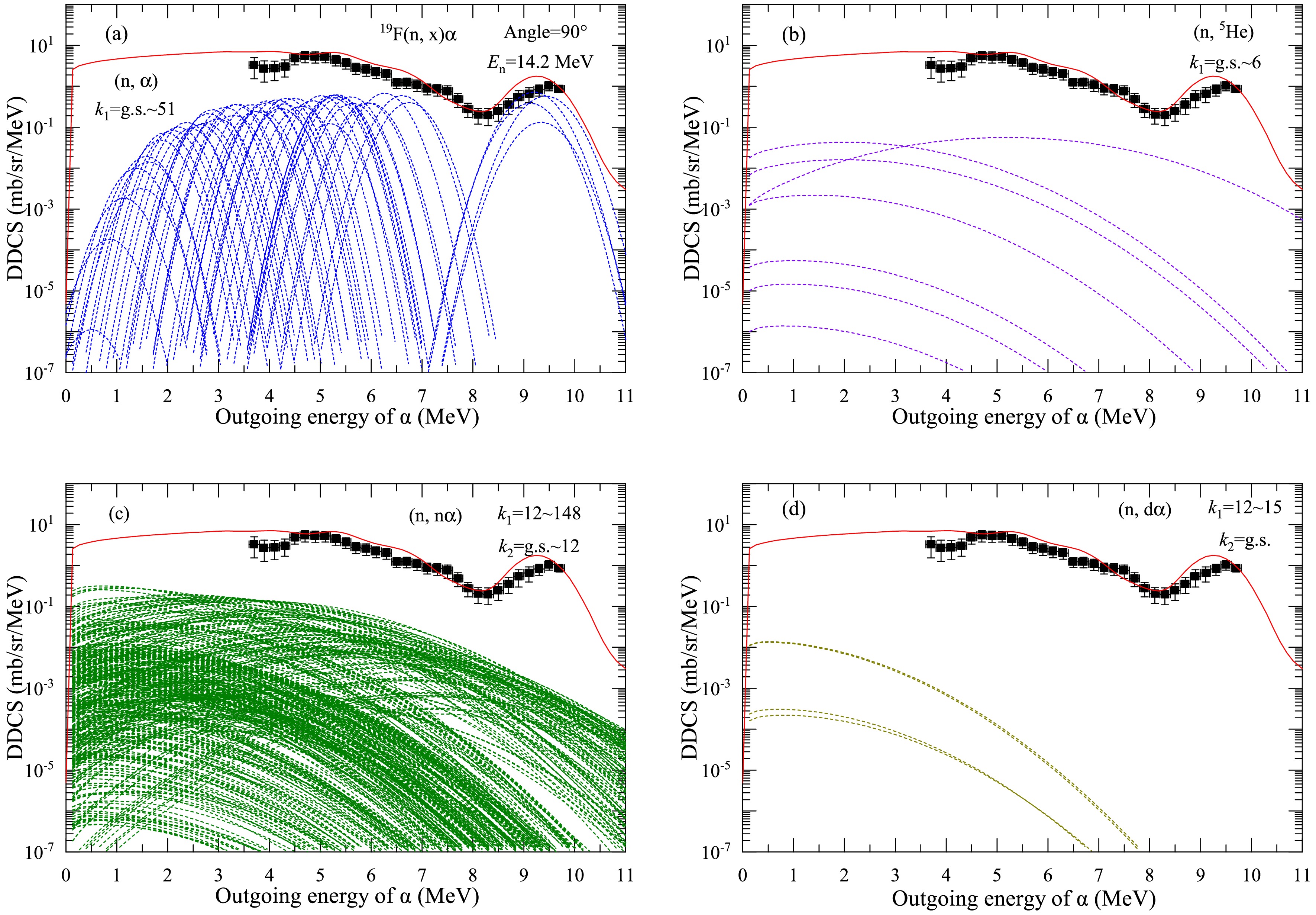

Figure 15.  (color online) Partial and total DDCSs of the outgoing α for the n+¹⁹F reaction with an outgoing angle of $ 90^{\circ} $ at $ E_n $ = 14.2 MeV in LS. The black points denote the experimental data taken from Ref. [26], and the red solid lines denote the results of this study. The blue dashed lines denote the partial spectra of the first outgoing α from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 51st excited state of the first residual nucleus $ ^{16}\text{N} $ (a). The purple dashed lines denote the partial spectra of the first outgoing $ ^5\text{He} $ (which can break up into n and α) from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 6th excited state of the first residual nucleus $ ^{15}\text{N} $ (b). The green dashed lines denote the partial spectra of the secondary emitted α from the compound nucleus $ ^{20}\text{F}^* $, which first emits a neutron to the 12th-148th excited energy levels of first residual nucleus $ ^{19}\text{F} $ and then emits an α to the ground state up to the 12th excited state of $ ^{15}\text{N} $ (c). The yellow dashed lines denote the partial spectra of the secondary emitted α from the compound nucleus $ ^{20}\text{F}^* $, which first emits a deuteron to the 12th-15th excited energy levels of first residual nucleus $ ^{18}\text{O} $ and then emits an α to the ground state of $ ^{14}\text{C} $ (d).

Figure 16 shows a comparison of the DDCS of the outgoing α for the n+¹⁹F reaction with the experimental data and evaluated results at $ E_n = 14.2$ MeV with a $ 90^{\circ} $ outgoing angle. The black points denote the experimental data taken from Ref. [26]. The red solid, pink dash-dotted, blue dashed, and green dotted lines denote the results of this study, ENDF/B-VIII.1, JENDL-5, and BROND-3.1, respectively. The evaluated data of ENDF/B-VIII.1, JENDL-5, and BROND-3.1 agree with the experimental DDCS in the low energy region of the outgoing α. However, the results of JENDL-5 overestimate the value at the first peak from the right side, while the results of ENDF/B-VIII.1 and BROND-3.1 fail to account for their corresponding tendencies at the same region.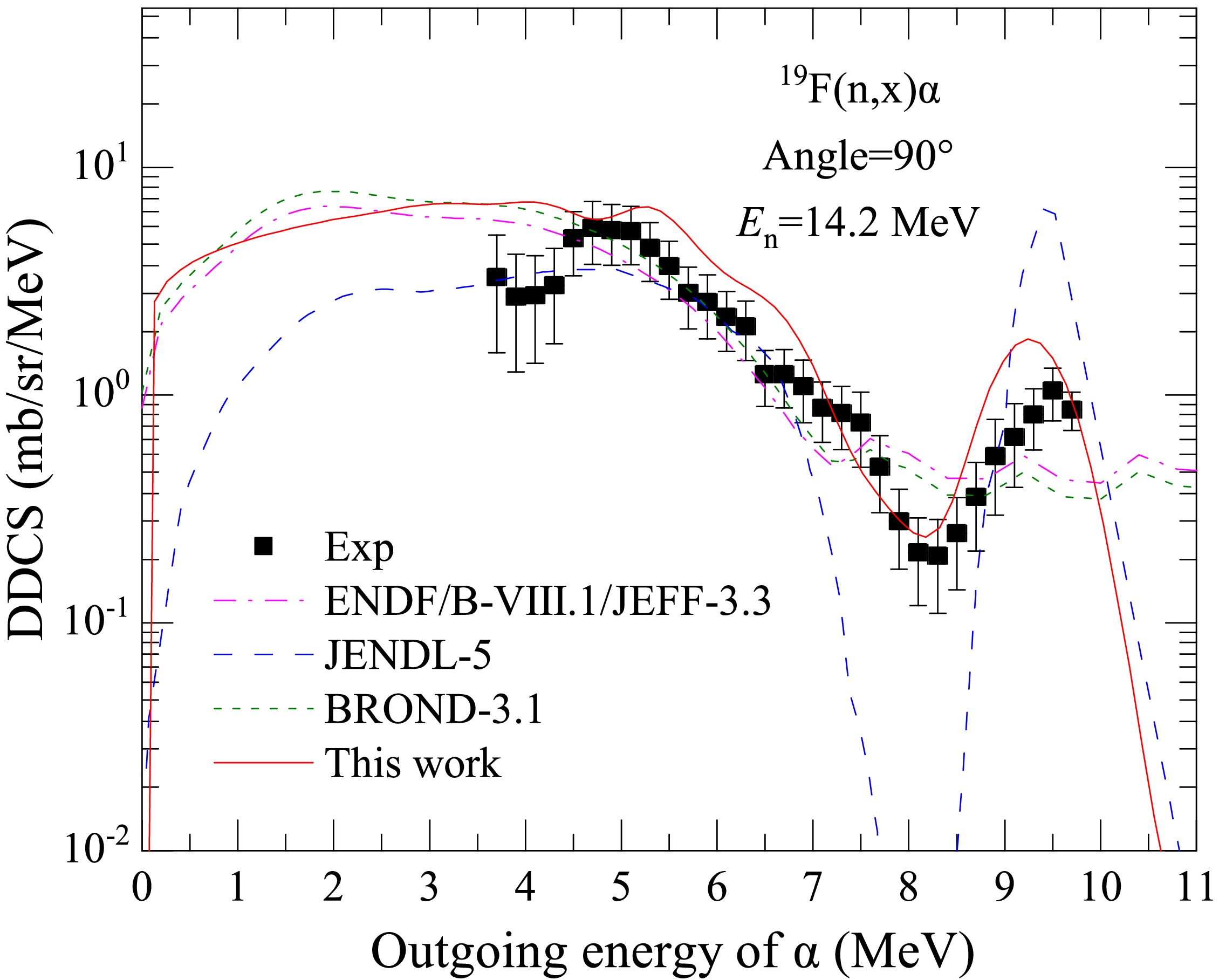

Figure 16.  (color online) Comparison of the calculated DDCS of the outgoing α for the n+¹⁹F reaction with the experimental data and evaluated results at $ E_n $ = 14.2 MeV with a $ 90^{\circ} $ outgoing angle. The black points denote the experimental data taken from Ref. [26]. The red solid, pink dash-dotted, blue dashed, and green dotted lines denote the results of this study, ENDF/B-VIII.1, JENDL-5, and BROND-3.1, respectively.

The data of the DDCSs for the n+¹⁹F reaction at low incident energies are of significance for the design of next-generation nuclear reactors. As an example, Fig. 17 shows the calculated results of the total DDCSs of the outgoing neutron and light charged particles for the n+¹⁹F reaction with an angle of 70$ ^\circ $ at $ E_n = 7 $ MeV in LS. The black solid, red dash-dot, blue dash, and green dot lines denote the predicted total DDCSs of the neutron, alpha, proton, and deutron, respectively. It is worth noting that, for the n+¹⁹F reaction, triton emission is energetically forbidden at $ E_n = 7 $ MeV. From the aforementioned figures, one can see that, among those of all light charged particles, the DDCS of α accounts for the largest proportion. This is consistent with the common phenomenon of α clusters in light nuclei.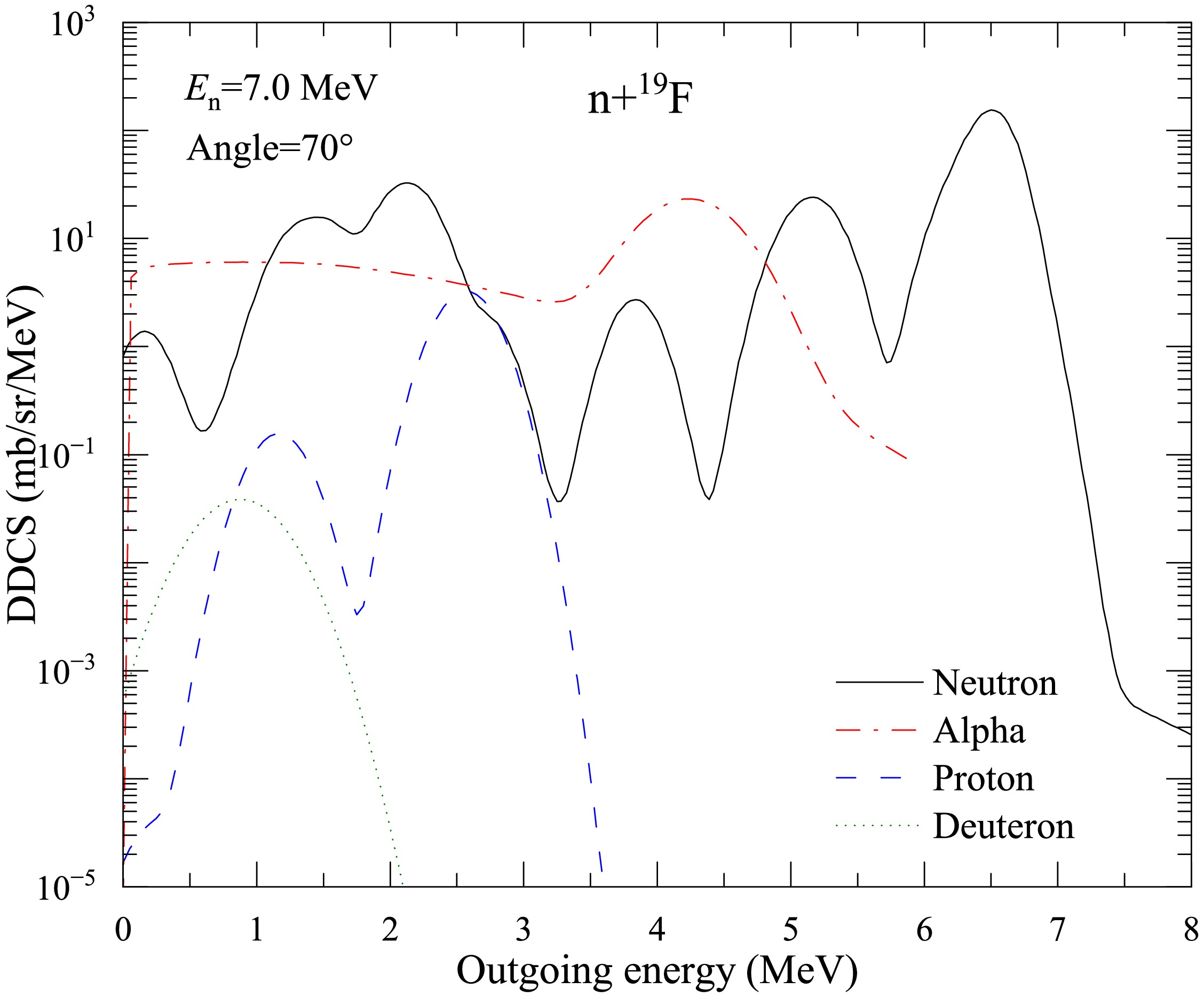

Figure 17.  (color online) Calculated total DDCSs of the outgoing neutron and light charged particles for the n+¹⁹F reaction with an angle of 70$ ^\circ $ at $ E_n $= 7 MeV in LS. The black solid, red dash-dot, blue dash, and green dot lines denote the predicted total DDCS of the neutron, alpha, proton, and deutron, respectively.

Comparisons of the calculated total DDCS of the outgoing α particle with the measured data are shown in Figs. 13 and 14 at the incident neutron energy $ E_n $=14.2 MeV with outgoing angles of $ 30^{\circ} $, $ 50^{\circ} $, $ 70^{\circ} $, $ 90^{\circ} $, $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $. One can see that the calculated results agree well with the experimental data.

Figure 13.  (color online) Same as Fig. 1 but for the outgoing α at angles $ 30^{\circ} $, $ 50^{\circ} $, $ 70^{\circ} $, and $ 90^{\circ} $.

Figure 14.  (color online) Same as Fig. 1 but for the outgoing α at angles $ 110^{\circ} $, $ 130^{\circ} $, and $ 150^{\circ} $.

Figure 15 shows the partial and total DDCSs of the outgoing α particle for the $ {n} + ^{19}\text{F} $ reaction with a $ 90^{\circ} $ outgoing angle at $ E_n $ = 14.2 MeV in LS. The black points denote the experimental data taken from Ref. [26], and the red solid lines denote the results of this study. The blue dashed lines denote the partial spectra of the first outgoing α from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 51st excited state of the first residual nucleus $ ^{16}\text{N} $ (Fig. 15(a)). Each experimentally observed discrete peak reflects the influence of the energy level structure of the residual nucleus $ ^{16}\text{N} $. The purple dashed lines denote the partial spectra of the first outgoing $ ^5\text{He} $ (which can break up into n and α) from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 6th excited state of the first residual nucleus $ ^{15}\text{N} $ (Fig. 15(b)). The green dashed lines denote the partial spectra of the secondary emitted α from the compound nucleus $ ^{20}\text{F}^* $, which first emits a neutron to the 12th−148th excited energy levels of first residual nucleus $ ^{19}\text{F} $ and then emits an α to the ground state up to the 12th excited state of $ ^{15}\text{N} $ (Fig. 15(c)). The yellow dashed lines denote the partial spectra of the secondary emitted α from the compound nucleus $ ^{20}\text{F}^* $, which first emits a deuteron to the 12th−15th excited energy levels of the first residual nucleus $ ^{18}\text{O} $ and then emits an α to the ground state of $ ^{14}\text{C} $ (Fig. 15(d)). It is evident that there are significant contributions from secondary particle emission to the DDCS of outgoing α particles for the n + ¹⁹F reaction.

Figure 15.  (color online) Partial and total DDCSs of the outgoing α for the n+¹⁹F reaction with an outgoing angle of $ 90^{\circ} $ at $ E_n $ = 14.2 MeV in LS. The black points denote the experimental data taken from Ref. [26], and the red solid lines denote the results of this study. The blue dashed lines denote the partial spectra of the first outgoing α from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 51st excited state of the first residual nucleus $ ^{16}\text{N} $ (a). The purple dashed lines denote the partial spectra of the first outgoing $ ^5\text{He} $ (which can break up into n and α) from the compound nucleus $ ^{20}\text{F}^* $ to the ground state up to 6th excited state of the first residual nucleus $ ^{15}\text{N} $ (b). The green dashed lines denote the partial spectra of the secondary emitted α from the compound nucleus $ ^{20}\text{F}^* $, which first emits a neutron to the 12th-148th excited energy levels of first residual nucleus $ ^{19}\text{F} $ and then emits an α to the ground state up to the 12th excited state of $ ^{15}\text{N} $ (c). The yellow dashed lines denote the partial spectra of the secondary emitted α from the compound nucleus $ ^{20}\text{F}^* $, which first emits a deuteron to the 12th-15th excited energy levels of first residual nucleus $ ^{18}\text{O} $ and then emits an α to the ground state of $ ^{14}\text{C} $ (d).

Figure 16 shows a comparison of the DDCS of the outgoing α for the n+¹⁹F reaction with the experimental data and evaluated results at $ E_n = 14.2$ MeV with a $ 90^{\circ} $ outgoing angle. The black points denote the experimental data taken from Ref. [26]. The red solid, pink dash-dotted, blue dashed, and green dotted lines denote the results of this study, ENDF/B-VIII.1, JENDL-5, and BROND-3.1, respectively. The evaluated data of ENDF/B-VIII.1, JENDL-5, and BROND-3.1 agree with the experimental DDCS in the low energy region of the outgoing α. However, the results of JENDL-5 overestimate the value at the first peak from the right side, while the results of ENDF/B-VIII.1 and BROND-3.1 fail to account for their corresponding tendencies at the same region.

Figure 16.  (color online) Comparison of the calculated DDCS of the outgoing α for the n+¹⁹F reaction with the experimental data and evaluated results at $ E_n $ = 14.2 MeV with a $ 90^{\circ} $ outgoing angle. The black points denote the experimental data taken from Ref. [26]. The red solid, pink dash-dotted, blue dashed, and green dotted lines denote the results of this study, ENDF/B-VIII.1, JENDL-5, and BROND-3.1, respectively.

The data of the DDCSs for the n+¹⁹F reaction at low incident energies are of significance for the design of next-generation nuclear reactors. As an example, Fig. 17 shows the calculated results of the total DDCSs of the outgoing neutron and light charged particles for the n+¹⁹F reaction with an angle of 70$ ^\circ $ at $ E_n = 7 $ MeV in LS. The black solid, red dash-dot, blue dash, and green dot lines denote the predicted total DDCSs of the neutron, alpha, proton, and deutron, respectively. It is worth noting that, for the n+¹⁹F reaction, triton emission is energetically forbidden at $ E_n = 7 $ MeV. From the aforementioned figures, one can see that, among those of all light charged particles, the DDCS of α accounts for the largest proportion. This is consistent with the common phenomenon of α clusters in light nuclei.

Figure 17.  (color online) Calculated total DDCSs of the outgoing neutron and light charged particles for the n+¹⁹F reaction with an angle of 70$ ^\circ $ at $ E_n $= 7 MeV in LS. The black solid, red dash-dot, blue dash, and green dot lines denote the predicted total DDCS of the neutron, alpha, proton, and deutron, respectively.

In our previous studies, STLN was used to calculate the DDCS of outgoing neutrons for the n+¹⁹F reaction, and the results were in good agreement with experimental data. In this study, the pick-up mechanism of complex particles, as one of the important components of STLN, is improved to describe the DDCSs of outgoing charged particles, considering the effects of energy levels with energy, angular momentum, and parity conservations. After reproducing the calculated DDCS of outgoing neutrons, the DDCSs of outgoing charged particles (including $ p, d, t, \alpha $) are self-consistently obtained. The results of this study are not only in good agreement with existing measurements at $ E_n=14.2 $ MeV but also superior to the data recommended by the current major nuclear databases. The results validate the effectiveness of STLN in describing the DDCSs of outgoing charged particles.

In our previous studies, STLN was used to calculate the DDCS of outgoing neutrons for the n+¹⁹F reaction, and the results were in good agreement with experimental data. In this study, the pick-up mechanism of complex particles, as one of the important components of STLN, is improved to describe the DDCSs of outgoing charged particles, considering the effects of energy levels with energy, angular momentum, and parity conservations. After reproducing the calculated DDCS of outgoing neutrons, the DDCSs of outgoing charged particles (including $ p, d, t, \alpha $) are self-consistently obtained. The results of this study are not only in good agreement with existing measurements at $ E_n=14.2 $ MeV but also superior to the data recommended by the current major nuclear databases. The results validate the effectiveness of STLN in describing the DDCSs of outgoing charged particles.