-
In 1973, Bekenstein first noticed the striking thermodynamic analogy of black holes. He then pioneered the concept of black hole entropy as a measure of the information inside a black hole and pointed out that the black hole entropy is proportional to the horizon area:
$S = {A \mathord{\left/ {\vphantom {A 4}} \right. } 4}$ [1]. Subsequently, Hawking used the semi-classical quantum field theory to prove that black holes indeed possess a temperature,$T = {\kappa \mathord{\left/ {\vphantom {\kappa {\left( {2\pi } \right)}}} \right. } {\left( {2\pi } \right)}}$ , where$\kappa $ is the surface gravity [2]. The discovery of Hawking radiation established a solid foundation for the four laws of black hole thermodynamics. In particular, for a Schwarzschild black hole, the first law of thermodynamics can be written as$ \mathrm{d}M=T\mathrm{d}S, $

(1) where
$M$ denotes the mass of the black hole. Studies on other black holes such as Reissner-Nordström and Kerr-Newmann black holes revealed that they also satisfy the first law of thermodynamics.However, when applying the first law of thermodynamics to calculate the entropy of regular black holes, one does not obtain an entropy proportional to the horizon area [3]. These black holes are characterized by having a regular core instead of a space-time singularity. Common examples of regular black holes include the Bardeen, Hayward, non-commutative, and vacuum non-singular black holes, among others; [4] and references therein provide a comprehensive overview of the thermodynamics of regular black holes. In [3], the authors pointed out that the reason why regular black holes do not satisfy the first law of thermodynamics is that the black hole mass cannot be regarded as internal energy. Based on this, the authors derived a corrected version of the first law of thermodynamics. By leveraging the corrected first law of thermodynamics, one can obtain an entropy that satisfies the Bekenstein-Hawking area law in regular black holes. In subsequent studies on the thermodynamics of regular black holes, the corrected first law of thermodynamics has been widely applied to static black holes [5−14]. These examples include common regular black holes such as the Bardeen, Hayward, vacuum non-singular, and non-commutative black holes. In addition, we include recently proposed non-singular black holes. The space-times of these black holes are all characterized by the absence of singularities.
It is known that black holes are all evolving, so it is necessary to investigate whether the first law of thermodynamics for dynamical regular black holes also requires correction. However, for dynamical black holes, the apparent and event horizons do not coincide, leading to different viewpoints on which horizon the thermodynamics should be based on. For example, in [15−17], the authors studied the entropy of a dynamical black hole using a thin-film model. By constructing the thin film outside the event horizon, they obtained an entropy proportional to the area of the event horizon. Similarly, [18−20] investigated Hawking radiation from the event horizon. By contrast, [21] suggested that thermodynamics should be established on the apparent horizon, as it serves as the boundary of negative energy states. Considering the collapse of a spherical shell, Hiscock proposed that one-quarter of the apparent horizon area must be deemed as the entropy of the black hole [22]. In [23] and [24], the authors demonstrated that the first law of thermodynamics can be successfully built on the apparent horizon. They treated the event horizon as a time-dependent perturbative hyper-surface of the apparent horizon and successfully established thermodynamics on the event horizon. In this study, we examined the corrected first law of thermodynamics on both horizons.
For the calculation of the temperature at the event horizon, we applied the conformal flat method [25, 26]. This is because, for a dynamical black hole space-time, there are no Killing vectors, and hence, it is difficult to directly calculate the temperature at the event horizon using the surface gravity method. In addition to the conformal flat method, another approach to calculating the temperature of a dynamical black hole is the radiation back-reaction method [18]. This method first calculates the expectation value of the renormalized energy-momentum tensor,
$\left\langle {{T_{ab}}} \right\rangle $ , in the Unruh vacuum state. Then, it examines the ingoing negative flux into the black hole. Finally, it determines the radiation temperature. However, this approach for studying thermal radiation from dynamical black holes is only applicable to asymptotically flat, spherically symmetric black holes and yields results with limited accuracy. Subsequently, Zhao et al. proposed the conformal flat approach, which can precisely determine the temperature and thermal spectrum of an evaporating black hole [25]. In this study, we employed this approach to investigate the temperature at the event horizon for a general spherically symmetric dynamical regular black hole. Regarding the apparent horizon, its surface gravity can be defined using the Kodama vector [27]. Therefore, we directly applied the surface gravity method to calculate the temperature associated to the apparent horizon.The structure of this paper is as follows. In Sec. II, we briefly introduce the dynamical regular black holes considered in this study and demonstrate their singularity-free nature by calculating their Kretschmann scalar. In Sec. III, we calculate the special ''surfaces'' for a general spherically symmetric dynamical regular black hole. In Sec. IV and V, we derive the corrected first law of thermodynamics on the event and apparent horizons, respectively. Finally, we summarize the main conclusions of this study.
-
In 1973, Bekenstein first noticed the striking thermodynamic analogy of black holes. He then pioneered the concept of black hole entropy as a measure of the information inside a black hole and pointed out that the black hole entropy is proportional to the horizon area:
$S = {A \mathord{\left/ {\vphantom {A 4}} \right. } 4}$ [1]. Subsequently, Hawking used the semi-classical quantum field theory to prove that black holes indeed possess a temperature,$T = {\kappa \mathord{\left/ {\vphantom {\kappa {\left( {2\pi } \right)}}} \right. } {\left( {2\pi } \right)}}$ , where$\kappa $ is the surface gravity [2]. The discovery of Hawking radiation established a solid foundation for the four laws of black hole thermodynamics. In particular, for a Schwarzschild black hole, the first law of thermodynamics can be written as$ \mathrm{d}M=T\mathrm{d}S, $

(1) where
$M$ denotes the mass of the black hole. Studies on other black holes such as Reissner-Nordström and Kerr-Newmann black holes revealed that they also satisfy the first law of thermodynamics.However, when applying the first law of thermodynamics to calculate the entropy of regular black holes, one does not obtain an entropy proportional to the horizon area [3]. These black holes are characterized by having a regular core instead of a space-time singularity. Common examples of regular black holes include the Bardeen, Hayward, non-commutative, and vacuum non-singular black holes, among others; [4] and references therein provide a comprehensive overview of the thermodynamics of regular black holes. In [3], the authors pointed out that the reason why regular black holes do not satisfy the first law of thermodynamics is that the black hole mass cannot be regarded as internal energy. Based on this, the authors derived a corrected version of the first law of thermodynamics. By leveraging the corrected first law of thermodynamics, one can obtain an entropy that satisfies the Bekenstein-Hawking area law in regular black holes. In subsequent studies on the thermodynamics of regular black holes, the corrected first law of thermodynamics has been widely applied to static black holes [5−14]. These examples include common regular black holes such as the Bardeen, Hayward, vacuum non-singular, and non-commutative black holes. In addition, we include recently proposed non-singular black holes. The space-times of these black holes are all characterized by the absence of singularities.
It is known that black holes are all evolving, so it is necessary to investigate whether the first law of thermodynamics for dynamical regular black holes also requires correction. However, for dynamical black holes, the apparent and event horizons do not coincide, leading to different viewpoints on which horizon the thermodynamics should be based on. For example, in [15−17], the authors studied the entropy of a dynamical black hole using a thin-film model. By constructing the thin film outside the event horizon, they obtained an entropy proportional to the area of the event horizon. Similarly, [18−20] investigated Hawking radiation from the event horizon. By contrast, [21] suggested that thermodynamics should be established on the apparent horizon, as it serves as the boundary of negative energy states. Considering the collapse of a spherical shell, Hiscock proposed that one-quarter of the apparent horizon area must be deemed as the entropy of the black hole [22]. In [23] and [24], the authors demonstrated that the first law of thermodynamics can be successfully built on the apparent horizon. They treated the event horizon as a time-dependent perturbative hyper-surface of the apparent horizon and successfully established thermodynamics on the event horizon. In this study, we examined the corrected first law of thermodynamics on both horizons.
For the calculation of the temperature at the event horizon, we applied the conformal flat method [25, 26]. This is because, for a dynamical black hole space-time, there are no Killing vectors, and hence, it is difficult to directly calculate the temperature at the event horizon using the surface gravity method. In addition to the conformal flat method, another approach to calculating the temperature of a dynamical black hole is the radiation back-reaction method [18]. This method first calculates the expectation value of the renormalized energy-momentum tensor,
$\left\langle {{T_{ab}}} \right\rangle $ , in the Unruh vacuum state. Then, it examines the ingoing negative flux into the black hole. Finally, it determines the radiation temperature. However, this approach for studying thermal radiation from dynamical black holes is only applicable to asymptotically flat, spherically symmetric black holes and yields results with limited accuracy. Subsequently, Zhao et al. proposed the conformal flat approach, which can precisely determine the temperature and thermal spectrum of an evaporating black hole [25]. In this study, we employed this approach to investigate the temperature at the event horizon for a general spherically symmetric dynamical regular black hole. Regarding the apparent horizon, its surface gravity can be defined using the Kodama vector [27]. Therefore, we directly applied the surface gravity method to calculate the temperature associated to the apparent horizon.The structure of this paper is as follows. In Sec. II, we briefly introduce the dynamical regular black holes considered in this study and demonstrate their singularity-free nature by calculating their Kretschmann scalar. In Sec. III, we calculate the special ''surfaces'' for a general spherically symmetric dynamical regular black hole. In Sec. IV and V, we derive the corrected first law of thermodynamics on the event and apparent horizons, respectively. Finally, we summarize the main conclusions of this study.
-
In this section, we briefly introduce the two dynamical regular black holes used as specific examples in this study, particularly by calculating their Kretschmann scalars to clearly demonstrate that they do not possess curvature singularities at the origin. The first example is the dynamical Hayward black hole, whose line element is given by [28]
$ \mathrm{d}s^2=-\left[1-\frac{2M\left(v\right)r^2}{r^3+2\alpha M\left(v\right)}\right]\mathrm{d}v^2+2\mathrm{d}v\mathrm{d}r+r^2\mathrm{d}\theta^2+r^2\sin^2\theta\mathrm{d}\varphi^2, $

(2) where
$ v $ is the advanced Eddington coordinate and$\alpha $ characterizes quantum gravity effects, having the order of squared Planck length. In the following, for brevity, we sometimes abbreviate$M(v)$ as$M$ . The line element expressed by Eq. (2) is a Vaidya-type generalization of the Hayward black hole using the advanced Eddington coordinate. It can also be derived from the Vaidya black hole with an effective Newton constant$G' = {G \mathord{\left/ {\vphantom {G {\left( {1 + \alpha {p^2}} \right)}}} \right. } {\left( {1 + \alpha {p^2}} \right)}}$ , which is inspired by the generalized uncertainty principle [29]. After careful calculations, the representative geometric invariants are given by$ \mathcal{R} = \frac{{24\alpha {M^2}\left( { - {r^3} + 4\alpha M} \right)}}{{{{\left( {{r^3} + 2\alpha M} \right)}^3}}}, \quad {\mathcal{R}_{\mu \nu }}{\mathcal{R}^{\mu \nu }} = \frac{{288{\alpha ^2}{M^4}\left( {5{r^6} - 4\alpha {r^3}M + 8{\alpha ^2}{M^2}} \right)}}{{{{\left( {{r^3} + 2\alpha M} \right)}^6}}}, $

$ {\mathcal{R}_{\mu \nu \tau \sigma }}{\mathcal{R}^{\mu \nu \tau \sigma }} = - \frac{{4M\left[ {{r^9} + 8\left( { - 10 + \alpha } \right){\alpha ^2}{M^3} - 8\alpha \left( { - 2 + 3\alpha } \right){M^2}{r^3} - 4\left( {2 + 3\alpha } \right)M{r^6}} \right]}}{{{{\left( {{r^3} + 2\alpha M} \right)}^4}}}. $

(3) Here,
$ {\mathcal{R}_{\mu \nu \tau \sigma }}{\mathcal{R}^{\mu \nu \tau \sigma }} $ is also known as the Kretschmann scalar$K$ , used to determine the existence of curvature singularities. It is evident that the presence of$\alpha $ ensures the absence of a singularity at the origin of the dynamical Hayward black hole. By setting$\alpha = 0$ , Eq. (3) reduces to the Kretschmann scalar of the Vaidya black hole,$ {K_{\rm Vaidya}} = \frac{{4M\left( {8M - {r^3}} \right)}}{{{r^6}}}, $

(4) which diverges at the origin. In [30], a dynamical extension of the non-commutative Schwarzschild black hole was proposed:
$ \begin{aligned}[b]\mathrm{d}s^2= & -\left[1-\frac{4M\left(v\right)}{\sqrt{\pi}r}\gamma\left(\frac{3}{2},\frac{r^2}{4\vartheta}\right)\right]\mathrm{d}v^2 \\ & +2\mathrm{d}v\mathrm{d}r+r^2\mathrm{d}\theta^2+r^2\sin^2\theta\mathrm{d}\varphi^2,\end{aligned} $

(5) where the lower incomplete gamma function is defined by
$ \gamma\left(\frac{3}{2},\frac{r^2}{4\vartheta}\right)=\int_0^{r^2\mathord{\left/\vphantom{r^24\vartheta}\right.}4\vartheta}t^{1\mathord{\left/\vphantom{12}\right.}2}\mathrm{e}^{-t}\mathrm{d}t. $

(6) Here,
$ \vartheta $ is the non-commutative parameter with dimensions of Planck length squared, representing the smeared structure of space. In a non-commutative space, geometric points that describe positions are replaced by regions with a minimum width on the order of the Planck length. Therefore, the method of defining point mass density using the Dirac delta function is no longer applicable; instead, a Gaussian distribution is used. The line element given by Eq. (5) gradually approaches that of a Vaidya black hole as$r$ increases. For a dynamical non-commutative black hole, we can also calculate the geometric invariants:$\begin{aligned}[b] \mathcal{R} &= - \frac{{{{\rm e}^{ - \frac{{{r^2}}}{{4\vartheta }}}}M({r^2} - 8\vartheta )}}{{2\sqrt \pi {\vartheta ^{5/2}}}}, \\ {\mathcal{R}_{\mu \nu }}{\mathcal{R}^{\mu \nu }} &= \frac{{{{\rm e}^{ - \frac{{{r^2}}}{{2\vartheta }}}}{M^2}\left( {{r^4} - 8{r^2}\vartheta + 32{\vartheta ^2}} \right)}}{{8\pi {\vartheta ^5}}}, \end{aligned} $

$ \begin{aligned}[b] {\mathcal{R}_{\mu \nu \tau \sigma }}{\mathcal{R}^{\mu \nu \tau \sigma }} =& \frac{M}{{2\pi }}\left\{ \frac{{{{\rm e}^{ - \frac{{{r^2}}}{{2\vartheta }}}}}}{{{\vartheta ^3}}}\left( {8M + \sqrt {\pi \vartheta } {r^2}{{\rm e}^{\frac{{{r^2}}}{{4\vartheta }}}}} \right) \right.\\ &- \frac{{16}}{{{r^3}}}\left( {\sqrt \pi + \frac{{4M{{\rm e}^{ - \frac{{{r^2}}}{{4\vartheta }}}}}}{{{\vartheta ^{3/2}}}}} \right)\gamma \left( {\frac{3}{2},\frac{{{r^2}}}{{4\vartheta }}} \right) \\ &\left. { + \frac{{256M}}{{{r^6}}}{{\left[ {\gamma \left( {\frac{3}{2},\frac{{{r^2}}}{{4\vartheta }}} \right)} \right]}^2}} \right\}. \end{aligned} $

(7) For small values of
$r$ , using the definition of the gamma function, we have$ \gamma \left( {\frac{3}{2},\frac{{{r^2}}}{{4\vartheta }}} \right) \approx \int_0^{{{{r^2}} \mathord{\left/ {\vphantom {{{r^2}} {4\vartheta }}} \right. } {4\vartheta }}} {{t^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}{\rm d}t} = \frac{2}{3}{\left( {\frac{{{r^2}}}{{4\vartheta }}} \right)^{{3 \mathord{\left/ {\vphantom {3 2}} \right. } 2}}} = \frac{{{r^3}}}{{12{\vartheta ^{{3 \mathord{\left/ {\vphantom {3 2}} \right. } 2}}}}}, $

(8) which implies that the Kretschmann scalar is finite at the origin. When
$r \to 0$ , we have$ \mathop {\lim }\limits_{r \to 0} \left( {{\mathcal{R}_{\mu \nu \tau \sigma }}{\mathcal{R}^{\mu \nu \tau \sigma }}} \right) = \frac{{2M\left( {10M - 3\sqrt \pi {\vartheta ^{{3 \mathord{\left/ {\vphantom {3 2}} \right. } 2}}}} \right)}}{{9\pi {\vartheta ^3}}}, $

(9) which shows that the non-commutative factor
$\vartheta $ ensures the absence of a curvature singularity. Additionally, when$\vartheta \to 0$ , we can similarly obtain the Kretschmann scalar for the Vaidya black hole. Figure 1 shows the relationship between the Kretschmann scalar and$ r $ for two types of dynamical black holes. It can be seen that there is no curvature singularity at the origin in both cases. -
In this section, we briefly introduce the two dynamical regular black holes used as specific examples in this study, particularly by calculating their Kretschmann scalars to clearly demonstrate that they do not possess curvature singularities at the origin. The first example is the dynamical Hayward black hole, whose line element is given by [28]
$ \mathrm{d}s^2=-\left[1-\frac{2M\left(v\right)r^2}{r^3+2\alpha M\left(v\right)}\right]\mathrm{d}v^2+2\mathrm{d}v\mathrm{d}r+r^2\mathrm{d}\theta^2+r^2\sin^2\theta\mathrm{d}\varphi^2, $

(2) where
$ v $ is the advanced Eddington coordinate and$\alpha $ characterizes quantum gravity effects, having the order of squared Planck length. In the following, for brevity, we sometimes abbreviate$M(v)$ as$M$ . The line element expressed by Eq. (2) is a Vaidya-type generalization of the Hayward black hole using the advanced Eddington coordinate. It can also be derived from the Vaidya black hole with an effective Newton constant$G' = {G \mathord{\left/ {\vphantom {G {\left( {1 + \alpha {p^2}} \right)}}} \right. } {\left( {1 + \alpha {p^2}} \right)}}$ , which is inspired by the generalized uncertainty principle [29]. After careful calculations, the representative geometric invariants are given by$ \mathcal{R} = \frac{{24\alpha {M^2}\left( { - {r^3} + 4\alpha M} \right)}}{{{{\left( {{r^3} + 2\alpha M} \right)}^3}}}, \quad {\mathcal{R}_{\mu \nu }}{\mathcal{R}^{\mu \nu }} = \frac{{288{\alpha ^2}{M^4}\left( {5{r^6} - 4\alpha {r^3}M + 8{\alpha ^2}{M^2}} \right)}}{{{{\left( {{r^3} + 2\alpha M} \right)}^6}}}, $

$ {\mathcal{R}_{\mu \nu \tau \sigma }}{\mathcal{R}^{\mu \nu \tau \sigma }} = - \frac{{4M\left[ {{r^9} + 8\left( { - 10 + \alpha } \right){\alpha ^2}{M^3} - 8\alpha \left( { - 2 + 3\alpha } \right){M^2}{r^3} - 4\left( {2 + 3\alpha } \right)M{r^6}} \right]}}{{{{\left( {{r^3} + 2\alpha M} \right)}^4}}}. $

(3) Here,
$ {\mathcal{R}_{\mu \nu \tau \sigma }}{\mathcal{R}^{\mu \nu \tau \sigma }} $ is also known as the Kretschmann scalar$K$ , used to determine the existence of curvature singularities. It is evident that the presence of$\alpha $ ensures the absence of a singularity at the origin of the dynamical Hayward black hole. By setting$\alpha = 0$ , Eq. (3) reduces to the Kretschmann scalar of the Vaidya black hole,$ {K_{\rm Vaidya}} = \frac{{4M\left( {8M - {r^3}} \right)}}{{{r^6}}}, $

(4) which diverges at the origin. In [30], a dynamical extension of the non-commutative Schwarzschild black hole was proposed:
$ \begin{aligned}[b]\mathrm{d}s^2= & -\left[1-\frac{4M\left(v\right)}{\sqrt{\pi}r}\gamma\left(\frac{3}{2},\frac{r^2}{4\vartheta}\right)\right]\mathrm{d}v^2 \\ & +2\mathrm{d}v\mathrm{d}r+r^2\mathrm{d}\theta^2+r^2\sin^2\theta\mathrm{d}\varphi^2,\end{aligned} $

(5) where the lower incomplete gamma function is defined by
$ \gamma\left(\frac{3}{2},\frac{r^2}{4\vartheta}\right)=\int_0^{r^2\mathord{\left/\vphantom{r^24\vartheta}\right.}4\vartheta}t^{1\mathord{\left/\vphantom{12}\right.}2}\mathrm{e}^{-t}\mathrm{d}t. $

(6) Here,
$ \vartheta $ is the non-commutative parameter with dimensions of Planck length squared, representing the smeared structure of space. In a non-commutative space, geometric points that describe positions are replaced by regions with a minimum width on the order of the Planck length. Therefore, the method of defining point mass density using the Dirac delta function is no longer applicable; instead, a Gaussian distribution is used. The line element given by Eq. (5) gradually approaches that of a Vaidya black hole as$r$ increases. For a dynamical non-commutative black hole, we can also calculate the geometric invariants:$\begin{aligned}[b] \mathcal{R} &= - \frac{{{{\rm e}^{ - \frac{{{r^2}}}{{4\vartheta }}}}M({r^2} - 8\vartheta )}}{{2\sqrt \pi {\vartheta ^{5/2}}}}, \\ {\mathcal{R}_{\mu \nu }}{\mathcal{R}^{\mu \nu }} &= \frac{{{{\rm e}^{ - \frac{{{r^2}}}{{2\vartheta }}}}{M^2}\left( {{r^4} - 8{r^2}\vartheta + 32{\vartheta ^2}} \right)}}{{8\pi {\vartheta ^5}}}, \end{aligned} $

$ \begin{aligned}[b] {\mathcal{R}_{\mu \nu \tau \sigma }}{\mathcal{R}^{\mu \nu \tau \sigma }} =& \frac{M}{{2\pi }}\left\{ \frac{{{{\rm e}^{ - \frac{{{r^2}}}{{2\vartheta }}}}}}{{{\vartheta ^3}}}\left( {8M + \sqrt {\pi \vartheta } {r^2}{{\rm e}^{\frac{{{r^2}}}{{4\vartheta }}}}} \right) \right.\\ &- \frac{{16}}{{{r^3}}}\left( {\sqrt \pi + \frac{{4M{{\rm e}^{ - \frac{{{r^2}}}{{4\vartheta }}}}}}{{{\vartheta ^{3/2}}}}} \right)\gamma \left( {\frac{3}{2},\frac{{{r^2}}}{{4\vartheta }}} \right) \\ &\left. { + \frac{{256M}}{{{r^6}}}{{\left[ {\gamma \left( {\frac{3}{2},\frac{{{r^2}}}{{4\vartheta }}} \right)} \right]}^2}} \right\}. \end{aligned} $

(7) For small values of
$r$ , using the definition of the gamma function, we have$ \gamma \left( {\frac{3}{2},\frac{{{r^2}}}{{4\vartheta }}} \right) \approx \int_0^{{{{r^2}} \mathord{\left/ {\vphantom {{{r^2}} {4\vartheta }}} \right. } {4\vartheta }}} {{t^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}{\rm d}t} = \frac{2}{3}{\left( {\frac{{{r^2}}}{{4\vartheta }}} \right)^{{3 \mathord{\left/ {\vphantom {3 2}} \right. } 2}}} = \frac{{{r^3}}}{{12{\vartheta ^{{3 \mathord{\left/ {\vphantom {3 2}} \right. } 2}}}}}, $

(8) which implies that the Kretschmann scalar is finite at the origin. When
$r \to 0$ , we have$ \mathop {\lim }\limits_{r \to 0} \left( {{\mathcal{R}_{\mu \nu \tau \sigma }}{\mathcal{R}^{\mu \nu \tau \sigma }}} \right) = \frac{{2M\left( {10M - 3\sqrt \pi {\vartheta ^{{3 \mathord{\left/ {\vphantom {3 2}} \right. } 2}}}} \right)}}{{9\pi {\vartheta ^3}}}, $

(9) which shows that the non-commutative factor
$\vartheta $ ensures the absence of a curvature singularity. Additionally, when$\vartheta \to 0$ , we can similarly obtain the Kretschmann scalar for the Vaidya black hole. Figure 1 shows the relationship between the Kretschmann scalar and$ r $ for two types of dynamical black holes. It can be seen that there is no curvature singularity at the origin in both cases. -
To calculate the horizon radius of a general spherically symmetric dynamical black hole, we assume its line element to be
$ \mathrm{d}s^2=-f(v,r)\mathrm{d}v^2+2\mathrm{d}v\mathrm{d}r+r^2\mathrm{d}\theta^2+r^2\sin^2\theta\mathrm{d}\varphi^2, $

(10) where
$f\left( {v,r} \right) = 1 - {{2m\left( {v,r} \right)} \mathord{\left/ {\vphantom {{2m\left( {v,r} \right)} r}} \right. } r}$ . The determinant and non-vanishing contravariant components of the metric are given, respectively, by$\begin{aligned}[b] & g = - {r^4}{\sin ^2}\theta ,\quad {g^{vr}} = {g^{rv}} = 1, \quad{g^{rr}} = f(v,r), \\ & {g^{\theta \theta }} = \frac{1}{{{r^2}}}, \quad{g^{\varphi \varphi }} = \frac{1}{{{r^2}{{\sin }^2}\theta }}. \end{aligned}$

(11) The line element described by Eq. (10) can also be rewritten as
$ \mathrm{d}s^2=h_{ab}\mathrm{d}x^a\mathrm{d}x^b+r^2\mathrm{d}\Omega^2 $ , with${x^a} = \left( {v,r} \right)$ . In general, a dynamical black hole is characterized by different special “surfaces:” the time-like limit surface, trapped horizon, and apparent and event horizons. The definition of the time-like limit surface of a dynamical black hole is the same as that in a stationary black hole:${g_{vv}} = 0$ . Therefore, the radius of the time-like limit surface satisfies$f(v,{r_{TLS}}) = 0$ . According to the definition of the trapped horizon,${h^{ab}}{\partial _a}r{\partial _b}r = 0$ , we obtain that the radius of the trapped horizon also satisfies$f(v,{r_{TH}}) = 0$ . The apparent horizon is the outermost marginally trapped surface and is defined as$\Theta = l_{;\mu }^\mu - \kappa = 0$ , where$\Theta $ is the expansion of a congruence of null geodesics and$\kappa = {l_{\mu ;\nu }}{n^\mu }{l^\nu }$ reduces to the surface gravity in the stationary case. Additionally,${n^\mu }$ and${l^\nu }$ are null tetrads. For the spherically symmetric dynamical black hole described by the line element expressed by Eq. (10), we calculate the radius of its apparent horizon in Appendix A. Here, we directly use the result. The radius satisfies$ f\left( {v,{r_{AH}}} \right) = 0 $ , that is,$ {r_{AH}} = m\left( {v,{r_{AH}}} \right) $ . Note that for an arbitrary spherically symmetric dynamical black hole, the trapped and apparent horizons coincide. Therefore, in this paper, we denote their radii uniformly as${r_{AH}}$ . Next, we proceed to calculate the radius of the event horizon. The event horizon is defined as a special hyper-surface where the norm of the normal vector is zero (while the normal vector itself is non-zero). It is also referred to as a null hyper-surface, which preserves the symmetries of the space-time. For the spherically symmetric space-time described by Eq. (10), the event horizon can be assumed to be of the form$F\left( {v,r} \right)$ , with the normal vector defined as${n_\mu } = {\partial _\mu }F\left( {v,r} \right)$ . From the condition that the normal vector is null, we obtain$ {n_\mu }{n^\mu } = {g^{\mu \nu }}\frac{{\partial F}}{{\partial {x^\mu }}}\frac{{\partial F}}{{\partial {x^\nu }}} = 0. $

(12) Using the null surface equation
$F\left( {v,r} \right) = 0$ , we have that$ \frac{\mathrm{d}r}{\mathrm{d}v}\frac{\partial F}{\partial r}+\frac{\partial F}{\partial v}=0. $

(13) Substituting Eq. (13) into Eq. (12), we find that the event horizon radius
${r_H}$ satisfies$ f\left( {v,{r_H}} \right) - 2{\dot r_H} = 0. $

(14) In this paper, we denote the event horizon radius as
${r_H}$ . Given that${\dot r_H}$ is a small quantity, it is easy to see that the event and apparent horizons are very close to each other. -
To calculate the horizon radius of a general spherically symmetric dynamical black hole, we assume its line element to be
$ \mathrm{d}s^2=-f(v,r)\mathrm{d}v^2+2\mathrm{d}v\mathrm{d}r+r^2\mathrm{d}\theta^2+r^2\sin^2\theta\mathrm{d}\varphi^2, $

(10) where
$f\left( {v,r} \right) = 1 - {{2m\left( {v,r} \right)} \mathord{\left/ {\vphantom {{2m\left( {v,r} \right)} r}} \right. } r}$ . The determinant and non-vanishing contravariant components of the metric are given, respectively, by$\begin{aligned}[b] & g = - {r^4}{\sin ^2}\theta ,\quad {g^{vr}} = {g^{rv}} = 1, \quad{g^{rr}} = f(v,r), \\ & {g^{\theta \theta }} = \frac{1}{{{r^2}}}, \quad{g^{\varphi \varphi }} = \frac{1}{{{r^2}{{\sin }^2}\theta }}. \end{aligned}$

(11) The line element described by Eq. (10) can also be rewritten as
$ \mathrm{d}s^2=h_{ab}\mathrm{d}x^a\mathrm{d}x^b+r^2\mathrm{d}\Omega^2 $ , with${x^a} = \left( {v,r} \right)$ . In general, a dynamical black hole is characterized by different special “surfaces:” the time-like limit surface, trapped horizon, and apparent and event horizons. The definition of the time-like limit surface of a dynamical black hole is the same as that in a stationary black hole:${g_{vv}} = 0$ . Therefore, the radius of the time-like limit surface satisfies$f(v,{r_{TLS}}) = 0$ . According to the definition of the trapped horizon,${h^{ab}}{\partial _a}r{\partial _b}r = 0$ , we obtain that the radius of the trapped horizon also satisfies$f(v,{r_{TH}}) = 0$ . The apparent horizon is the outermost marginally trapped surface and is defined as$\Theta = l_{;\mu }^\mu - \kappa = 0$ , where$\Theta $ is the expansion of a congruence of null geodesics and$\kappa = {l_{\mu ;\nu }}{n^\mu }{l^\nu }$ reduces to the surface gravity in the stationary case. Additionally,${n^\mu }$ and${l^\nu }$ are null tetrads. For the spherically symmetric dynamical black hole described by the line element expressed by Eq. (10), we calculate the radius of its apparent horizon in Appendix A. Here, we directly use the result. The radius satisfies$ f\left( {v,{r_{AH}}} \right) = 0 $ , that is,$ {r_{AH}} = m\left( {v,{r_{AH}}} \right) $ . Note that for an arbitrary spherically symmetric dynamical black hole, the trapped and apparent horizons coincide. Therefore, in this paper, we denote their radii uniformly as${r_{AH}}$ . Next, we proceed to calculate the radius of the event horizon. The event horizon is defined as a special hyper-surface where the norm of the normal vector is zero (while the normal vector itself is non-zero). It is also referred to as a null hyper-surface, which preserves the symmetries of the space-time. For the spherically symmetric space-time described by Eq. (10), the event horizon can be assumed to be of the form$F\left( {v,r} \right)$ , with the normal vector defined as${n_\mu } = {\partial _\mu }F\left( {v,r} \right)$ . From the condition that the normal vector is null, we obtain$ {n_\mu }{n^\mu } = {g^{\mu \nu }}\frac{{\partial F}}{{\partial {x^\mu }}}\frac{{\partial F}}{{\partial {x^\nu }}} = 0. $

(12) Using the null surface equation
$F\left( {v,r} \right) = 0$ , we have that$ \frac{\mathrm{d}r}{\mathrm{d}v}\frac{\partial F}{\partial r}+\frac{\partial F}{\partial v}=0. $

(13) Substituting Eq. (13) into Eq. (12), we find that the event horizon radius
${r_H}$ satisfies$ f\left( {v,{r_H}} \right) - 2{\dot r_H} = 0. $

(14) In this paper, we denote the event horizon radius as
${r_H}$ . Given that${\dot r_H}$ is a small quantity, it is easy to see that the event and apparent horizons are very close to each other. -
In this section, we use the so-called conformal flat approach to calculate the temperature of dynamical regular black holes. The core idea of this approach is that, in a general static or stationary space-time, one can employ the tortoise coordinate transformation to render the space-time explicitly conformal to Minkowski space near the horizon. As a result, the dynamical equations describing particles can be reduced to their traditional form near the horizon. Zhao et al. applied the conformal flat approach to a dynamical black hole to calculate the temperature, yielding a more accurate result than the widely used radiation back-reaction method [25].
We start with the Klein-Gordon equation describing the motion of a scalar field with mass
${m_0}$ $ \frac{1}{{\sqrt { - g} }}{\partial _\mu }\left( {\sqrt { - g} {g^{\mu \nu }}{\partial _\nu }\psi } \right) - m_0^2\psi = 0. $

(15) In conjunction with the line element described by Eq. (10), the Klein-Gordon equation can be explicitly written as
$ \begin{aligned}[b] & f\frac{{{\partial ^2}\psi }}{{\partial {r^2}}} + 2\frac{{{\partial ^2}\psi }}{{\partial v\partial r}} + \frac{2}{r}\frac{{\partial \psi }}{{\partial v}} + \left( {\frac{{2f}}{r} + f'} \right)\frac{{\partial \psi }}{{\partial r}} \\ & \quad + \frac{1}{{{r^2}}}\left[ {\frac{1}{{\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{{\partial \psi }}{{\partial \theta }}} \right) + \frac{1}{{{{\sin }^2}\theta }}\frac{{{\partial ^2}\psi }}{{\partial {\varphi ^2}}}} \right] - m_0^2\psi = 0. \end{aligned} $

(16) In the dynamical regular black hole space-time, we separate the variables of the wave function as
$ \psi = \frac{1}{r}R\left( {v,r} \right){Y_{lm}}\left( {\theta ,\varphi } \right). $

(17) Substituting separated wave function
$\psi $ into Eq. (16), we obtain the radical and angular components of the field equations as$ f\frac{{{\partial ^2}R}}{{\partial {r^2}}} + 2\frac{{{\partial ^2}R}}{{\partial v\partial r}} + f'\frac{{\partial R}}{{\partial r}} - \left[ { \frac{{f'}}{r} - \frac{{l\left( {l + 1} \right)}}{{{r^2}}} + m_0^2} \right]R = 0, $

$ \left[ {\frac{1}{{\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{\partial }{{\partial \theta }}} \right) + \frac{1}{{{{\sin }^2}\theta }}\frac{{{\partial ^2}}}{{\partial {\varphi ^2}}} - l\left( {l + 1} \right)} \right]{Y_{lm}} = 0. $

(18) Here,
$l$ is the angular quantum number of the particle. Given that the angular equation is not relevant to our discussion, the following analysis focuses on the radial part. Next, consider the coordinate transformation$ {r_*} = \frac{1}{{2\kappa \left( {{v_0}} \right)}}\ln \left| {\frac{{r - {r_H}\left( v \right)}}{{{r_H}\left( {{v_0}} \right)}}} \right|, \quad {v_*} = v - {v_0}, $

(19) where
$ {v_0} $ represents the moment of a particle when it escapes from the horizon and$ \kappa \left({v}_{0}\right) $ is a function to be determined. Both$r\left( {{v_0}} \right)$ and$\kappa \left( {{v_0}} \right)$ represent the values of the corresponding quantities at the moment the particle leaves the horizon. Therefore, they can be treated as constants under the coordinate transformation. Differentiating Eq. (19), we obtain$ \begin{aligned}[b] & \mathrm{d}r_*=\frac{1}{2\kappa\left(r-r_H\right)}\mathrm{d}r-\frac{\dot{r}_H}{2\kappa\left(r-r_H\right)}\mathrm{d}v, \\ & \mathrm{d}v_*=\mathrm{d}v.\end{aligned} $

(20) Then, the transformation of the differential operator under the tortoise coordinate transformation can be further obtained as
$ \begin{aligned}[b] \frac{\partial }{{\partial r}} = &\frac{1}{{2\kappa \left( {r - {r_H}} \right)}}\frac{\partial }{{\partial {r_*}}}, \frac{\partial }{{\partial v}} = \frac{\partial }{{\partial {v_*}}} - \frac{{{{\dot r}_H}}}{{2\kappa \left( {r - {r_H}} \right)}}\frac{\partial }{{\partial {r_*}}}, \\ \frac{{{\partial ^2}}}{{\partial {r^2}}} =& {\left[ {\frac{1}{{2\kappa \left( {r - {r_H}} \right)}}} \right]^2}\frac{{{\partial ^2}}}{{\partial r_*^2}} - \frac{1}{{2\kappa {{\left( {r - {r_H}} \right)}^2}}}\frac{\partial }{{\partial {r_*}}}, \\ \frac{{{\partial ^2}}}{{\partial r\partial v}} =& \frac{1}{{2\kappa \left( {r - {r_H}} \right)}}\frac{{{\partial ^2}}}{{\partial {r_*}\partial {v_*}}} - \frac{{{{\dot r}_H}}}{{{{\left[ {2\kappa \left( {r - {r_H}} \right)} \right]}^2}}}\frac{{{\partial ^2}}}{{\partial r_*^2}}\\ &+ \frac{{{{\dot r}_H}}}{{2\kappa {{\left( {r - {r_H}} \right)}^2}}}\frac{\partial }{{\partial {r_*}}}. \end{aligned} $

(21) Using this transformation of the differential operator, the radial equation of motion for the particle can be rewritten as
$ \begin{aligned}[b] &\frac{{f - 2{{\dot r}_H}}}{{2\kappa \left( {r - {r_H}} \right)}}\frac{{{\partial ^2}R}}{{\partial r_*^2}} + \left( { - \frac{{f - 2{{\dot r}_H}}}{{r - {r_H}}} + f'} \right)\frac{{\partial R}}{{\partial {r_*}}} + 2\frac{{{\partial ^2}R}}{{\partial {r_*}\partial {v_*}}} \\ & \quad - 2\kappa \left( {r - {r_H}} \right)\left[ { \frac{{f'}}{r} + \frac{{l\left( {l + 1} \right)}}{{{r^2}}} + m_0^2} \right]R = 0. \end{aligned} $

(22) According to the spirit of the conformal flat approach, the coefficient of
$ {{{\partial ^2}R} \mathord{\left/ {\vphantom {{{\partial ^2}R} {\partial r_*^2}}} \right. } {\partial r_*^2}} $ should be equal to$1$ near the event horizon at the moment${v_0}$ when the particle escapes from the event horizon. At the same time, note that$ \mathop {\lim }\limits_{\scriptstyle r \to {r_H}({v_0})\atop \scriptstyle v \to {v_0}} \left[ {f\left( {v,r} \right) - 2{{\dot r}_H}} \right] = 0,$

(23) where we have used the relation satisfied by the horizon radius, that is, Eq. (14). Therefore, we can apply L’Hôpital’s rule to evaluate the coefficient of
$ {{{\partial ^2}R} \mathord{\left/ {\vphantom {{{\partial ^2}R} {\partial r_*^2}}} \right. } {\partial r_*^2}} $ $ \mathop {\lim }\limits_{\scriptstyle r \to {r_H}\left( {{v_0}} \right)\atop \scriptstyle v \to {v_0}} \left[ {\frac{{f\left( {v,r} \right) - 2{{\dot r}_H}}}{{2\kappa \left( {{v_0}} \right)\left( {r - {r_H}} \right)}}} \right] = \mathop {\lim }\limits_{\scriptstyle r \to {r_H}\left( {{v_0}} \right)\atop \scriptstyle v \to {v_0}} \left[ {\frac{{f'\left( {v,r} \right)}}{{2\kappa \left( {{v_0}} \right)}}} \right]{\kern 1pt} {\kern 1pt} = 1. $

(24) Using the above expression, we can finally determine
$\kappa \left( v \right)$ at any given advanced Eddington time:$ \kappa \left( v \right) = \frac{1}{2}f'\left( {v,{r_H}} \right). $

(25) Meanwhile, using L’Hôpital’s role, we can also prove that
$\mathop {\lim }\limits_{\scriptstyle r \to {r_H}({v_0})\atop \scriptstyle v \to {v_0}} \left[ { - \frac{{f\left( {v,r} \right) - 2{{\dot r}_H}}}{{r - {r_H}}}} \right] = - \mathop {\lim }\limits_{\scriptstyle r \to {r_H}({v_0})\atop \scriptstyle v \to {v_0}} f'\left( {v,r} \right). $

(26) As a result, the coefficient of
${{\partial R} \mathord{\left/ {\vphantom {{\partial R} {\partial {r_*}}}} \right. } {\partial {r_*}}}$ vanishes in the above limit. It is not difficult to show that the coefficient of$R$ also breaks down near the horizon. Therefore, the radial equation of motion reduces to the traditional form:$ \frac{{{\partial ^2}R}}{{\partial r_*^2}} + 2\frac{{{\partial ^2}R}}{{\partial {v_*}\partial {r_*}}} = 0. $

(27) The two linearly independent solutions of Eq. (27) are
$ R_{\omega}^{in}=\mathrm{e}^{-\mathrm{i}\omega v_*},\quad R_{\omega}^{out}=\mathrm{e}^{-\mathrm{i}\omega v_*+2\mathrm{i}\omega r_*}. $

(28) Following the approach of Damour and Ruffini [31] and Sannan [32], we can obtain the spectral distribution of the outgoing wave:
$ N_{\omega}=\frac{\Gamma_{\omega}}{\mathrm{e}^{\omega\mathord{\left/\vphantom{\omega T_H}\right.}T_H}\pm1}, $

(29) with
$ {T_H} = \frac{\kappa }{{2\pi }}. $

(30) Here, ''
$ + $ '' corresponds to fermions, ''$ - $ '' represents bosons, and${\Gamma _\omega }$ is the transmission coefficient associated to the gravitational field barrier outside the horizon. From Eqs. (29) and (30), we conclude that$\kappa $ should be identified as the surface gravity at the horizon. Substituting Eq. (25) into Eq. (30), we can express the temperature at the event horizon as$ {T_H} = \frac{\kappa }{{2\pi }} = \frac{{f'\left( {v,{r_H}} \right)}}{{4\pi }} = \frac{{1 - 2{{\dot r}_H}}}{{4\pi {r_H}}} - \frac{{m'\left( {v,{r_H}} \right)}}{{2\pi {r_H}}}. $

(31) Next, we specifically calculate the temperature at the event horizon of the two dynamically regular black holes introduced in Sec. II. For the dynamical Hayward black hole, using Eq. (14), we obtain that its event horizon radius satisfies
$ r_H^3 - \left( {\frac{{2M}}{{1 - 2{{\dot r}_H}}}} \right)r_H^2 + 2\alpha M = 0, $

(32) which provides the relationship between the black hole mass and event horizon radius:
$ M = \frac{{\left( {1 - 2{{\dot r}_H}} \right)r_H^3}}{{2\left[ {r_H^2 + \left( {2{{\dot r}_H} - 1} \right)\alpha } \right]}}. $

(33) In conjunction with Eq. (31), we obtain the temperature at the event horizon as
$ {T_H} = \frac{\kappa }{{2\pi }} = \frac{{\left( {1 - 2{{\dot r}_H}} \right)\left[ {r_H^2 + 3\left( {2{{\dot r}_H} - 1} \right)\alpha } \right]}}{{4\pi r_H^3}}. $

(34) Similarly, the event horizon radius of the dynamical non-commutative black hole satisfies
$ 1 - \frac{{4M}}{{\sqrt \pi {r_H}}}\gamma \left( {\frac{3}{2},\frac{{r_H^2}}{{4\vartheta }}} \right) - 2{\dot r_H} = 0. $

(35) The temperature is expressed as
$ \begin{aligned}[b]T_H & =\frac{\kappa}{2\pi}=\frac{1}{4\pi}f'\left(v,r_H\right) \\ & =\frac{\left(2\dot{r}_H-1\right)}{16\pi r_H}\left[-4+r_H^3\vartheta^{-\frac{3}{2}}\mathrm{e}^{-\frac{r_H^2}{4\vartheta}}\gamma^{-1}\left(\frac{3}{2},\frac{r_H^2}{4\vartheta}\right)\right].\end{aligned} $

(36) By contrast, the corresponding temperatures of the dynamical Hayward black hole and dynamical non-commutative black hole given by the first law of black hole thermodynamics are respectively
$ \begin{aligned}[b] {\tilde T_H} &= \frac{{\partial M}}{{\partial {S_H}}} = \frac{{\partial {r_H}}}{{\partial {S_H}}}\frac{{\partial M}}{{\partial {r_H}}} \\ &= \frac{{\left( {1 - 2{{\dot r}_H}} \right)\left[ {r_H^2 + 3\left( {2{{\dot r}_H} - 1} \right)\alpha } \right]{r_H}}}{{4\pi {{\left[ {r_H^2 + \left( {2{{\dot r}_H} - 1} \right)\alpha } \right]}^2}}}, \end{aligned}$

(37) $\begin{aligned}[b] {\tilde T_H} &= \frac{{\partial M}}{{\partial {S_H}}} \\ &= \frac{{2{{\dot r}_H} - 1}}{{32\sqrt \pi {r_H}}}\left[ {r_H^3{\vartheta ^{ - \frac{3}{2}}}{e^{ - \frac{{r_H^2}}{{4\vartheta }}}} - 4\gamma \left( {\frac{3}{2},\frac{{r_H^2}}{{4\vartheta }}} \right)} \right]{\gamma ^{ - 2}}\left( {\frac{3}{2},\frac{{r_H^2}}{{4\vartheta }}} \right). \end{aligned}$

(38) The relation
${S_H} = \pi r_H^2$ [23, 24] was used in the derivation above. It can be clearly seen that the temperature obtained from the first law of thermodynamics is different from that obtained using the conformal flat method. Similar to the case of static black holes [3, 5−14], this inspired us to search for the corrected first law of thermodynamics for dynamical black holes. -
In this section, we use the so-called conformal flat approach to calculate the temperature of dynamical regular black holes. The core idea of this approach is that, in a general static or stationary space-time, one can employ the tortoise coordinate transformation to render the space-time explicitly conformal to Minkowski space near the horizon. As a result, the dynamical equations describing particles can be reduced to their traditional form near the horizon. Zhao et al. applied the conformal flat approach to a dynamical black hole to calculate the temperature, yielding a more accurate result than the widely used radiation back-reaction method [25].
We start with the Klein-Gordon equation describing the motion of a scalar field with mass
${m_0}$ $ \frac{1}{{\sqrt { - g} }}{\partial _\mu }\left( {\sqrt { - g} {g^{\mu \nu }}{\partial _\nu }\psi } \right) - m_0^2\psi = 0. $

(15) In conjunction with the line element described by Eq. (10), the Klein-Gordon equation can be explicitly written as
$ \begin{aligned}[b] & f\frac{{{\partial ^2}\psi }}{{\partial {r^2}}} + 2\frac{{{\partial ^2}\psi }}{{\partial v\partial r}} + \frac{2}{r}\frac{{\partial \psi }}{{\partial v}} + \left( {\frac{{2f}}{r} + f'} \right)\frac{{\partial \psi }}{{\partial r}} \\ & \quad + \frac{1}{{{r^2}}}\left[ {\frac{1}{{\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{{\partial \psi }}{{\partial \theta }}} \right) + \frac{1}{{{{\sin }^2}\theta }}\frac{{{\partial ^2}\psi }}{{\partial {\varphi ^2}}}} \right] - m_0^2\psi = 0. \end{aligned} $

(16) In the dynamical regular black hole space-time, we separate the variables of the wave function as
$ \psi = \frac{1}{r}R\left( {v,r} \right){Y_{lm}}\left( {\theta ,\varphi } \right). $

(17) Substituting separated wave function
$\psi $ into Eq. (16), we obtain the radical and angular components of the field equations as$ f\frac{{{\partial ^2}R}}{{\partial {r^2}}} + 2\frac{{{\partial ^2}R}}{{\partial v\partial r}} + f'\frac{{\partial R}}{{\partial r}} - \left[ { \frac{{f'}}{r} - \frac{{l\left( {l + 1} \right)}}{{{r^2}}} + m_0^2} \right]R = 0, $

$ \left[ {\frac{1}{{\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{\partial }{{\partial \theta }}} \right) + \frac{1}{{{{\sin }^2}\theta }}\frac{{{\partial ^2}}}{{\partial {\varphi ^2}}} - l\left( {l + 1} \right)} \right]{Y_{lm}} = 0. $

(18) Here,
$l$ is the angular quantum number of the particle. Given that the angular equation is not relevant to our discussion, the following analysis focuses on the radial part. Next, consider the coordinate transformation$ {r_*} = \frac{1}{{2\kappa \left( {{v_0}} \right)}}\ln \left| {\frac{{r - {r_H}\left( v \right)}}{{{r_H}\left( {{v_0}} \right)}}} \right|, \quad {v_*} = v - {v_0}, $

(19) where
$ {v_0} $ represents the moment of a particle when it escapes from the horizon and$ \kappa \left({v}_{0}\right) $ is a function to be determined. Both$r\left( {{v_0}} \right)$ and$\kappa \left( {{v_0}} \right)$ represent the values of the corresponding quantities at the moment the particle leaves the horizon. Therefore, they can be treated as constants under the coordinate transformation. Differentiating Eq. (19), we obtain$ \begin{aligned}[b] & \mathrm{d}r_*=\frac{1}{2\kappa\left(r-r_H\right)}\mathrm{d}r-\frac{\dot{r}_H}{2\kappa\left(r-r_H\right)}\mathrm{d}v, \\ & \mathrm{d}v_*=\mathrm{d}v.\end{aligned} $

(20) Then, the transformation of the differential operator under the tortoise coordinate transformation can be further obtained as
$ \begin{aligned}[b] \frac{\partial }{{\partial r}} = &\frac{1}{{2\kappa \left( {r - {r_H}} \right)}}\frac{\partial }{{\partial {r_*}}}, \frac{\partial }{{\partial v}} = \frac{\partial }{{\partial {v_*}}} - \frac{{{{\dot r}_H}}}{{2\kappa \left( {r - {r_H}} \right)}}\frac{\partial }{{\partial {r_*}}}, \\ \frac{{{\partial ^2}}}{{\partial {r^2}}} =& {\left[ {\frac{1}{{2\kappa \left( {r - {r_H}} \right)}}} \right]^2}\frac{{{\partial ^2}}}{{\partial r_*^2}} - \frac{1}{{2\kappa {{\left( {r - {r_H}} \right)}^2}}}\frac{\partial }{{\partial {r_*}}}, \\ \frac{{{\partial ^2}}}{{\partial r\partial v}} =& \frac{1}{{2\kappa \left( {r - {r_H}} \right)}}\frac{{{\partial ^2}}}{{\partial {r_*}\partial {v_*}}} - \frac{{{{\dot r}_H}}}{{{{\left[ {2\kappa \left( {r - {r_H}} \right)} \right]}^2}}}\frac{{{\partial ^2}}}{{\partial r_*^2}}\\ &+ \frac{{{{\dot r}_H}}}{{2\kappa {{\left( {r - {r_H}} \right)}^2}}}\frac{\partial }{{\partial {r_*}}}. \end{aligned} $

(21) Using this transformation of the differential operator, the radial equation of motion for the particle can be rewritten as
$ \begin{aligned}[b] &\frac{{f - 2{{\dot r}_H}}}{{2\kappa \left( {r - {r_H}} \right)}}\frac{{{\partial ^2}R}}{{\partial r_*^2}} + \left( { - \frac{{f - 2{{\dot r}_H}}}{{r - {r_H}}} + f'} \right)\frac{{\partial R}}{{\partial {r_*}}} + 2\frac{{{\partial ^2}R}}{{\partial {r_*}\partial {v_*}}} \\ & \quad - 2\kappa \left( {r - {r_H}} \right)\left[ { \frac{{f'}}{r} + \frac{{l\left( {l + 1} \right)}}{{{r^2}}} + m_0^2} \right]R = 0. \end{aligned} $

(22) According to the spirit of the conformal flat approach, the coefficient of
$ {{{\partial ^2}R} \mathord{\left/ {\vphantom {{{\partial ^2}R} {\partial r_*^2}}} \right. } {\partial r_*^2}} $ should be equal to$1$ near the event horizon at the moment${v_0}$ when the particle escapes from the event horizon. At the same time, note that$ \mathop {\lim }\limits_{\scriptstyle r \to {r_H}({v_0})\atop \scriptstyle v \to {v_0}} \left[ {f\left( {v,r} \right) - 2{{\dot r}_H}} \right] = 0,$

(23) where we have used the relation satisfied by the horizon radius, that is, Eq. (14). Therefore, we can apply L’Hôpital’s rule to evaluate the coefficient of
$ {{{\partial ^2}R} \mathord{\left/ {\vphantom {{{\partial ^2}R} {\partial r_*^2}}} \right. } {\partial r_*^2}} $ $ \mathop {\lim }\limits_{\scriptstyle r \to {r_H}\left( {{v_0}} \right)\atop \scriptstyle v \to {v_0}} \left[ {\frac{{f\left( {v,r} \right) - 2{{\dot r}_H}}}{{2\kappa \left( {{v_0}} \right)\left( {r - {r_H}} \right)}}} \right] = \mathop {\lim }\limits_{\scriptstyle r \to {r_H}\left( {{v_0}} \right)\atop \scriptstyle v \to {v_0}} \left[ {\frac{{f'\left( {v,r} \right)}}{{2\kappa \left( {{v_0}} \right)}}} \right]{\kern 1pt} {\kern 1pt} = 1. $

(24) Using the above expression, we can finally determine
$\kappa \left( v \right)$ at any given advanced Eddington time:$ \kappa \left( v \right) = \frac{1}{2}f'\left( {v,{r_H}} \right). $

(25) Meanwhile, using L’Hôpital’s role, we can also prove that
$\mathop {\lim }\limits_{\scriptstyle r \to {r_H}({v_0})\atop \scriptstyle v \to {v_0}} \left[ { - \frac{{f\left( {v,r} \right) - 2{{\dot r}_H}}}{{r - {r_H}}}} \right] = - \mathop {\lim }\limits_{\scriptstyle r \to {r_H}({v_0})\atop \scriptstyle v \to {v_0}} f'\left( {v,r} \right). $

(26) As a result, the coefficient of
${{\partial R} \mathord{\left/ {\vphantom {{\partial R} {\partial {r_*}}}} \right. } {\partial {r_*}}}$ vanishes in the above limit. It is not difficult to show that the coefficient of$R$ also breaks down near the horizon. Therefore, the radial equation of motion reduces to the traditional form:$ \frac{{{\partial ^2}R}}{{\partial r_*^2}} + 2\frac{{{\partial ^2}R}}{{\partial {v_*}\partial {r_*}}} = 0. $

(27) The two linearly independent solutions of Eq. (27) are
$ R_{\omega}^{in}=\mathrm{e}^{-\mathrm{i}\omega v_*},\quad R_{\omega}^{out}=\mathrm{e}^{-\mathrm{i}\omega v_*+2\mathrm{i}\omega r_*}. $

(28) Following the approach of Damour and Ruffini [31] and Sannan [32], we can obtain the spectral distribution of the outgoing wave:
$ N_{\omega}=\frac{\Gamma_{\omega}}{\mathrm{e}^{\omega\mathord{\left/\vphantom{\omega T_H}\right.}T_H}\pm1}, $

(29) with
$ {T_H} = \frac{\kappa }{{2\pi }}. $

(30) Here, ''
$ + $ '' corresponds to fermions, ''$ - $ '' represents bosons, and${\Gamma _\omega }$ is the transmission coefficient associated to the gravitational field barrier outside the horizon. From Eqs. (29) and (30), we conclude that$\kappa $ should be identified as the surface gravity at the horizon. Substituting Eq. (25) into Eq. (30), we can express the temperature at the event horizon as$ {T_H} = \frac{\kappa }{{2\pi }} = \frac{{f'\left( {v,{r_H}} \right)}}{{4\pi }} = \frac{{1 - 2{{\dot r}_H}}}{{4\pi {r_H}}} - \frac{{m'\left( {v,{r_H}} \right)}}{{2\pi {r_H}}}. $

(31) Next, we specifically calculate the temperature at the event horizon of the two dynamically regular black holes introduced in Sec. II. For the dynamical Hayward black hole, using Eq. (14), we obtain that its event horizon radius satisfies
$ r_H^3 - \left( {\frac{{2M}}{{1 - 2{{\dot r}_H}}}} \right)r_H^2 + 2\alpha M = 0, $

(32) which provides the relationship between the black hole mass and event horizon radius:
$ M = \frac{{\left( {1 - 2{{\dot r}_H}} \right)r_H^3}}{{2\left[ {r_H^2 + \left( {2{{\dot r}_H} - 1} \right)\alpha } \right]}}. $

(33) In conjunction with Eq. (31), we obtain the temperature at the event horizon as
$ {T_H} = \frac{\kappa }{{2\pi }} = \frac{{\left( {1 - 2{{\dot r}_H}} \right)\left[ {r_H^2 + 3\left( {2{{\dot r}_H} - 1} \right)\alpha } \right]}}{{4\pi r_H^3}}. $

(34) Similarly, the event horizon radius of the dynamical non-commutative black hole satisfies
$ 1 - \frac{{4M}}{{\sqrt \pi {r_H}}}\gamma \left( {\frac{3}{2},\frac{{r_H^2}}{{4\vartheta }}} \right) - 2{\dot r_H} = 0. $

(35) The temperature is expressed as
$ \begin{aligned}[b]T_H & =\frac{\kappa}{2\pi}=\frac{1}{4\pi}f'\left(v,r_H\right) \\ & =\frac{\left(2\dot{r}_H-1\right)}{16\pi r_H}\left[-4+r_H^3\vartheta^{-\frac{3}{2}}\mathrm{e}^{-\frac{r_H^2}{4\vartheta}}\gamma^{-1}\left(\frac{3}{2},\frac{r_H^2}{4\vartheta}\right)\right].\end{aligned} $

(36) By contrast, the corresponding temperatures of the dynamical Hayward black hole and dynamical non-commutative black hole given by the first law of black hole thermodynamics are respectively
$ \begin{aligned}[b] {\tilde T_H} &= \frac{{\partial M}}{{\partial {S_H}}} = \frac{{\partial {r_H}}}{{\partial {S_H}}}\frac{{\partial M}}{{\partial {r_H}}} \\ &= \frac{{\left( {1 - 2{{\dot r}_H}} \right)\left[ {r_H^2 + 3\left( {2{{\dot r}_H} - 1} \right)\alpha } \right]{r_H}}}{{4\pi {{\left[ {r_H^2 + \left( {2{{\dot r}_H} - 1} \right)\alpha } \right]}^2}}}, \end{aligned}$

(37) $\begin{aligned}[b] {\tilde T_H} &= \frac{{\partial M}}{{\partial {S_H}}} \\ &= \frac{{2{{\dot r}_H} - 1}}{{32\sqrt \pi {r_H}}}\left[ {r_H^3{\vartheta ^{ - \frac{3}{2}}}{e^{ - \frac{{r_H^2}}{{4\vartheta }}}} - 4\gamma \left( {\frac{3}{2},\frac{{r_H^2}}{{4\vartheta }}} \right)} \right]{\gamma ^{ - 2}}\left( {\frac{3}{2},\frac{{r_H^2}}{{4\vartheta }}} \right). \end{aligned}$

(38) The relation
${S_H} = \pi r_H^2$ [23, 24] was used in the derivation above. It can be clearly seen that the temperature obtained from the first law of thermodynamics is different from that obtained using the conformal flat method. Similar to the case of static black holes [3, 5−14], this inspired us to search for the corrected first law of thermodynamics for dynamical black holes. -
From the above calculations, we conclude that, similar to static regular black holes, dynamical regular black holes do not satisfy the first law of thermodynamics. In the following, we aim to find a corrected version of the first law of thermodynamics. To this end, we rewrite the relation satisfied by the event horizon as
$ m\left( {v,{r_H}} \right) = \frac{{{r_H}}}{2}\left( {1 - {{\dot r}_H}} \right). $

(39) The Einstein field equations corresponding to the line element expressed by Eq. (10) are
$ \frac{{\partial m\left( {v,r} \right)}}{{\partial v}} = 4\pi {r^2}T_v^r. $

$ \frac{{\partial m\left( {v,r} \right)}}{{\partial r}} = - 4\pi {r^2}T_v^v. $

(40) Using Eq. (40), we can rewrite the temperature as
$ T = \frac{{1 - 2{{\dot r}_H}}}{{4\pi {r_H}}} + 2{r_H}T_v^v. $

(41) Integrating Eq. (40), we obtain
$ m\left(v,r\right)=M\left(v\right)+4\pi\int_r^{\infty}r^2T_v^v\mathrm{d}r. $

(42) At the event horizon, Eq. (42) gives
$ M\left(v\right)=m\left(v,r_H\right)-4\pi\int_{r_H}^{\infty}r^2T_v^v\mathrm{d}r. $

(43) Differentiating Eq. (43), one can obtain
$ \mathrm{d}M(v)=\mathrm{d}\left[\frac{r_H}{2}\left(1-2\dot{r}_H\right)\right]-4\pi\mathrm{d}\left(\int_{r_H}^{\infty}r^2T_v^v\mathrm{d}r\right). $

(44) For regular black holes,
$T_v^v$ is a function of$M\left( v \right)$ . Therefore, the differential of the second term on the right-hand side of the above equation becomes$ \begin{aligned}[b] & -4\pi\mathrm{d}\left(\int_{r_H}^{\infty}r^2T_v^v\mathrm{d}r\right) \\ = & -4\pi T_v^vr_H^2\mathrm{d}r_H-4\pi\left[\int_{r_H}^{\infty}r^2\frac{\partial T_v^v}{\partial M(v)}\mathrm{d}r\right]\mathrm{d}M\left(v\right).\end{aligned} $

(45) We can rearrange Eq. (44) as
$ \begin{aligned}[b] & \left[1+4\pi\int_{r_H}^{\infty}r^2\frac{\partial T_v^v}{\partial M(v)}\mathrm{d}r\right]\mathrm{d}M(v) \\ = & \left[\frac{1-2\dot{r}_H}{4\pi r_H}+2r_HT_v^v\right]\mathrm{d}\left(\frac{A_H}{4}\right).\end{aligned} $

(46) In conjunction with the temperature expression given by Eq. (41), the above equation can be simplified to
$ \left[1+4\pi\int_{r_H}^{\infty}r^2\frac{\partial T_v^v}{\partial M(v)}\mathrm{d}r\right]\mathrm{d}M(v)=T_H\mathrm{d}S_H. $

(47) This is the corrected first law of thermodynamics for the dynamical regular black hole, and its form is the same as that in the case of a static black hole. The correction factor in the above expression is
$ 1+ 4\pi\displaystyle\int_{r_H}^{\infty}r^2\partial T_v^v/\partial M(v)\mathrm{d}r $ . For application convenience, we use Eq. (42) to rewrite the corrected first law of black hole thermodynamics as$ {\left. {{\rm d}\mathcal{M}\left( v \right)} \right|_{r = {r_H}}} = \left[ {{{\left. {\frac{{\partial m\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_H}}}} \right]{\rm d}M(v) = {T_H}{\rm d}{S_H}. $

(48) We can clearly see that the relationship between
${T_H}$ and${\tilde T_H}$ is given by$ {T_H} = \left[ {{{\left. {\frac{{\partial m\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_H}}}} \right]{\tilde T_H}. $

(49) When additional variables appear in the expression for
$T_v^v\left( {r,M(v),\alpha ,\beta , \ldots } \right)$ , that is, in the presence of other fields, we can readily express the modified first law of thermodynamics as$\begin{aligned}[b] {\left. {{\rm d}\mathcal{M}\left( v \right)} \right|_{r = {r_H}}} & = \left[ {{{\left. {\frac{{\partial m\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_H}}}} \right]{\rm d}M(v) \\ &= {T_H}{\rm d}{S_H} + \Phi _H^\alpha d\alpha + \Phi _H^\beta {\rm d}\beta + \cdots . \end{aligned}$

(50) For dynamical Hayward black holes, the correction factor to the first law of thermodynamics can be expressed as
$\begin{aligned}[b] F\left( {v,{r_H},\alpha } \right) &= {\left. {\frac{{\partial m\left( {v,r,\alpha } \right)}}{{\partial M\left( v \right)}}} \right|_{r = {r_H}}} \\ &= {\left. {\left[ {\frac{\partial }{{\partial M\left( v \right)}}\left( {\frac{{M\left( v \right){r^3}}}{{{r^3} + 2\alpha M\left( v \right)}}} \right)} \right]} \right|_{r = {r_H}}} \\ &= \frac{1}{{r_H^4}}{\left[ {r_H^2 + \left( {2{{\dot r}_H} - 1} \right)\alpha } \right]^2}. \end{aligned} $

(51) The product of
${T_H}$ and the correction factor$ F\left( {v,{r_H},\alpha } \right) $ exactly gives${\tilde T_H}$ . Similarly, for dynamical non-commutative black holes, the correction factor is given by$\begin{aligned}[b] F\left( {v,{r_H},\vartheta } \right) &= {\left. {\frac{{\partial m\left( {v,r,\vartheta } \right)}}{{\partial M\left( v \right)}}} \right|_{r = {r_H}}} \\ &= {\left. {\left\{ {\frac{\partial }{{\partial M\left( v \right)}}\left[ {\frac{{2M\left( v \right)}}{{\sqrt \pi }}\gamma \left( {\frac{3}{2},\frac{{{r^2}}}{{4\vartheta }}} \right)} \right]} \right\}} \right|_{r = {r_H}}} \\ &= \frac{2}{{\sqrt \pi }}\gamma \left( {\frac{3}{2},\frac{{r_H^2}}{{4\vartheta }}} \right). \end{aligned} $

(52) A direct calculation can also verify that
${T_H} = F\left( {v,{r_H},\vartheta } \right){\tilde T_H}$ , which demonstrates the validity of the corrected first law of thermodynamics. -
From the above calculations, we conclude that, similar to static regular black holes, dynamical regular black holes do not satisfy the first law of thermodynamics. In the following, we aim to find a corrected version of the first law of thermodynamics. To this end, we rewrite the relation satisfied by the event horizon as
$ m\left( {v,{r_H}} \right) = \frac{{{r_H}}}{2}\left( {1 - {{\dot r}_H}} \right). $

(39) The Einstein field equations corresponding to the line element expressed by Eq. (10) are
$ \frac{{\partial m\left( {v,r} \right)}}{{\partial v}} = 4\pi {r^2}T_v^r. $

$ \frac{{\partial m\left( {v,r} \right)}}{{\partial r}} = - 4\pi {r^2}T_v^v. $

(40) Using Eq. (40), we can rewrite the temperature as
$ T = \frac{{1 - 2{{\dot r}_H}}}{{4\pi {r_H}}} + 2{r_H}T_v^v. $

(41) Integrating Eq. (40), we obtain
$ m\left(v,r\right)=M\left(v\right)+4\pi\int_r^{\infty}r^2T_v^v\mathrm{d}r. $

(42) At the event horizon, Eq. (42) gives
$ M\left(v\right)=m\left(v,r_H\right)-4\pi\int_{r_H}^{\infty}r^2T_v^v\mathrm{d}r. $

(43) Differentiating Eq. (43), one can obtain
$ \mathrm{d}M(v)=\mathrm{d}\left[\frac{r_H}{2}\left(1-2\dot{r}_H\right)\right]-4\pi\mathrm{d}\left(\int_{r_H}^{\infty}r^2T_v^v\mathrm{d}r\right). $

(44) For regular black holes,
$T_v^v$ is a function of$M\left( v \right)$ . Therefore, the differential of the second term on the right-hand side of the above equation becomes$ \begin{aligned}[b] & -4\pi\mathrm{d}\left(\int_{r_H}^{\infty}r^2T_v^v\mathrm{d}r\right) \\ = & -4\pi T_v^vr_H^2\mathrm{d}r_H-4\pi\left[\int_{r_H}^{\infty}r^2\frac{\partial T_v^v}{\partial M(v)}\mathrm{d}r\right]\mathrm{d}M\left(v\right).\end{aligned} $

(45) We can rearrange Eq. (44) as
$ \begin{aligned}[b] & \left[1+4\pi\int_{r_H}^{\infty}r^2\frac{\partial T_v^v}{\partial M(v)}\mathrm{d}r\right]\mathrm{d}M(v) \\ = & \left[\frac{1-2\dot{r}_H}{4\pi r_H}+2r_HT_v^v\right]\mathrm{d}\left(\frac{A_H}{4}\right).\end{aligned} $

(46) In conjunction with the temperature expression given by Eq. (41), the above equation can be simplified to
$ \left[1+4\pi\int_{r_H}^{\infty}r^2\frac{\partial T_v^v}{\partial M(v)}\mathrm{d}r\right]\mathrm{d}M(v)=T_H\mathrm{d}S_H. $

(47) This is the corrected first law of thermodynamics for the dynamical regular black hole, and its form is the same as that in the case of a static black hole. The correction factor in the above expression is
$ 1+ 4\pi\displaystyle\int_{r_H}^{\infty}r^2\partial T_v^v/\partial M(v)\mathrm{d}r $ . For application convenience, we use Eq. (42) to rewrite the corrected first law of black hole thermodynamics as$ {\left. {{\rm d}\mathcal{M}\left( v \right)} \right|_{r = {r_H}}} = \left[ {{{\left. {\frac{{\partial m\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_H}}}} \right]{\rm d}M(v) = {T_H}{\rm d}{S_H}. $

(48) We can clearly see that the relationship between
${T_H}$ and${\tilde T_H}$ is given by$ {T_H} = \left[ {{{\left. {\frac{{\partial m\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_H}}}} \right]{\tilde T_H}. $

(49) When additional variables appear in the expression for
$T_v^v\left( {r,M(v),\alpha ,\beta , \ldots } \right)$ , that is, in the presence of other fields, we can readily express the modified first law of thermodynamics as$\begin{aligned}[b] {\left. {{\rm d}\mathcal{M}\left( v \right)} \right|_{r = {r_H}}} & = \left[ {{{\left. {\frac{{\partial m\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_H}}}} \right]{\rm d}M(v) \\ &= {T_H}{\rm d}{S_H} + \Phi _H^\alpha d\alpha + \Phi _H^\beta {\rm d}\beta + \cdots . \end{aligned}$

(50) For dynamical Hayward black holes, the correction factor to the first law of thermodynamics can be expressed as
$\begin{aligned}[b] F\left( {v,{r_H},\alpha } \right) &= {\left. {\frac{{\partial m\left( {v,r,\alpha } \right)}}{{\partial M\left( v \right)}}} \right|_{r = {r_H}}} \\ &= {\left. {\left[ {\frac{\partial }{{\partial M\left( v \right)}}\left( {\frac{{M\left( v \right){r^3}}}{{{r^3} + 2\alpha M\left( v \right)}}} \right)} \right]} \right|_{r = {r_H}}} \\ &= \frac{1}{{r_H^4}}{\left[ {r_H^2 + \left( {2{{\dot r}_H} - 1} \right)\alpha } \right]^2}. \end{aligned} $

(51) The product of
${T_H}$ and the correction factor$ F\left( {v,{r_H},\alpha } \right) $ exactly gives${\tilde T_H}$ . Similarly, for dynamical non-commutative black holes, the correction factor is given by$\begin{aligned}[b] F\left( {v,{r_H},\vartheta } \right) &= {\left. {\frac{{\partial m\left( {v,r,\vartheta } \right)}}{{\partial M\left( v \right)}}} \right|_{r = {r_H}}} \\ &= {\left. {\left\{ {\frac{\partial }{{\partial M\left( v \right)}}\left[ {\frac{{2M\left( v \right)}}{{\sqrt \pi }}\gamma \left( {\frac{3}{2},\frac{{{r^2}}}{{4\vartheta }}} \right)} \right]} \right\}} \right|_{r = {r_H}}} \\ &= \frac{2}{{\sqrt \pi }}\gamma \left( {\frac{3}{2},\frac{{r_H^2}}{{4\vartheta }}} \right). \end{aligned} $

(52) A direct calculation can also verify that
${T_H} = F\left( {v,{r_H},\vartheta } \right){\tilde T_H}$ , which demonstrates the validity of the corrected first law of thermodynamics. -
In a dynamical spherically symmetric space-time, the Kodama vector can be used to describe the symmetry of the space-time. When the dynamical space-time reduces to a static one, the Kodama vector also reduces to the Killing vector. The Kodama vector is defined as
$ {K}^{a}=-{\epsilon }^{ab}{\nabla }_{b}r $ , where$ {\epsilon }^{ab} $ denotes the volume form [27]. For the metric given by Eq. (2), the Kodama vector is expressed as${K^a} = {\left( {{\partial _v}} \right)^a}$ . Given that the Kodama vector is divergence free, that is,${\nabla _a}{K^a} = 0$ , there exists a conserved current${J^a} = T_b^a{K^b}$ , and the conserved charge is$ E= -\displaystyle\int_{\sigma}^{ }J^a\mathrm{d}\sigma_a $ , which is equal to the Misner-Sharp energy. Using the Kodama vector, Hayward defined the surface gravity on the apparent horizon as$ \kappa = \dfrac{1}{2}{\nabla ^a}{\nabla _a}r $ . Therefore, we can directly use the surface gravity method to calculate the temperature at the apparent horizon. In combination with the line element expressed by Eq. (2), we obtain the surface gravity associated to the apparent horizon as$ \begin{aligned}[b] \kappa = {\left. {\frac{1}{2}{\nabla ^a}{\nabla _a}r} \right|_{r = {r_{AH}}}} &= {\left. {\left[ {\frac{1}{{2\sqrt { - h} }}{\partial _i}\left( {\sqrt { - h} {h^{ij}}{\partial _j}r} \right)} \right]} \right|_{r = {r_{AH}}}} \\ & = {\left. {\left[ {\frac{1}{{2\sqrt { - h} }}{\partial _r}\left( {\sqrt { - h} {h^{rr}}} \right)} \right]} \right|_{r = {r_{AH}}}} \\ & = \frac{1}{2}f'\left( {v,{r_{AH}}} \right). \end{aligned} $

(53) Here,
$i$ and$j$ range from$0$ to$1$ . The temperature derived from the surface gravity method is given by$ {T_{AH}} = \frac{\kappa }{{2\pi }} = \frac{{f'(v,{r_{AH}})}}{{4\pi }} = \frac{1}{{4\pi {r_{AH}}}} - \frac{{m'\left( {v,{r_{AH}}} \right)}}{{2\pi {r_{AH}}}}. $

(54) The last step for Eq. (54) makes use of the condition satisfied by the radius of the apparent horizon:
$ {r_{AH}} = 2m\left( {v,{r_{AH}}} \right) $ . Next, we address the calculations related to the dynamical regular black holes discussed in this paper. For dynamical Hayward black holes, the relation between$M(v)$ and${r_{AH}}$ is$ M\left( v \right) = \frac{{r_{AH}^3}}{{2\left( {r_{AH}^2 - \alpha } \right)}}. $

(55) In conjunction with Eq. (54), we can obtain the temperature at the apparent horizon:
$ {T_{AH}} = \frac{{r_{AH}^2 - 3\alpha }}{{4\pi r_{AH}^3}}. $

(56) Following the same approach, the temperature at the apparent horizon for the dynamical non-commutative black hole is given by
$ T_{AH}=\frac{1}{16\pi r_{AH}}\left[4-r_{AH}^3\vartheta^{-\frac{3}{2}}\mathrm{e}^{-\frac{r_{AH}^2}{4\vartheta}}\gamma^{-1}\left(\frac{3}{2},\frac{r_{AH}^2}{4\vartheta}\right)\right]. $

(57) Next, we use the first law of thermodynamics [23,24] to obtain the temperature at the apparent horizons for both black holes:
$ {\tilde T_{AH}} = \frac{{\partial M}}{{\partial {S_{AH}}}} = \frac{{\partial {r_{AH}}}}{{\partial {S_{AH}}}}\frac{{\partial M}}{{\partial {r_{AH}}}} = \frac{{{r_{AH}}\left( {r_{AH}^2 - 3\alpha } \right)}}{{4\pi {{\left( {r_{AH}^2 - \alpha } \right)}^2}}}, $

(58) $\begin{aligned}[b] {\tilde T_{AH}} = &\frac{1}{{32\sqrt \pi {r_{AH}}}}\left[ r_{AH}^3{\vartheta ^{ - \frac{3}{2}}}{{\rm e}^{ - \frac{{r_{AH}^2}}{{4\vartheta }}}} \right.\\ &\left. - 4\gamma \left( {\frac{3}{2},\frac{{r_{AH}^2}}{{4\vartheta }}} \right) \right]{\gamma ^{ - 2}}\left( {\frac{3}{2},\frac{{r_{AH}^2}}{{4\vartheta }}} \right). \end{aligned}$

(59) Note that, similar to the case at the event horizon, the temperatures obtained from the surface gravity and the first law of thermodynamics on the apparent horizon are different. Next, we follow a procedure similar to that in the previous section to derive the corrected first law of thermodynamics on the apparent horizon. First, using Eq. (40), the temperature can be expressed as
$ {T_{AH}} = \frac{1}{{4\pi {r_{AH}}}} + 2{r_{AH}}T_v^v. $

(60) On the apparent horizon, Eq. (42) gives
$ M\left( v \right) = m\left( {v,{r_{AH}}} \right) - 4\pi \int_{{r_{AH}}}^\infty {{r^2}T_v^v{\rm d}r.} $

(61) Substituting
$ m\left( {v,{r_{AH}}} \right) = {{{r_{AH}}} \mathord{\left/ {\vphantom {{{r_{AH}}} 2}} \right. } 2} $ and differentiating Eq. (61), we obtain$ {\rm d}M(v) = {\rm d}\left( {\frac{1}{2}{r_{AH}}} \right) - 4\pi {\rm d}\left( {\int_{{r_{AH}}}^\infty {{r^2}T_v^v{\rm d}r} } \right). $

(62) Eq. (62) finally leads to the following result:
$\begin{aligned}[b] &\left[ {1 + 4\pi \int_{{r_{AH}}}^\infty {{r^2}\frac{{\partial T_v^v}}{{\partial M(v)}}{\rm d}r} } \right]{\rm d}M(v) \\ =& \left[ {\frac{1}{{4\pi {r_{AH}}}} + 2{r_{AH}}T_v^v} \right]{\rm d}\left( {\frac{{{A_{AH}}}}{4}} \right). \end{aligned}$

(63) In conjunction with the temperature expression given by Eq. (60), Eq. (63) can be simplified to
$ \left[1+4\pi\int_{r_{AH}}^{\infty}r^2\frac{\partial T_v^v}{\partial M(v)}\mathrm{d}r\right]\mathrm{d}M(v)=T_{AH}\mathrm{d}S_{AH}. $

(64) Using Eq. (42), we finally obtain the corrected first law of thermodynamics on the apparent horizon as
$ {\left. {{\rm d}\mathcal{M}\left( v \right)} \right|_{r = {r_{AH}}}} = \left[ {{{\left. {\frac{{\partial m\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_{AH}}}}} \right]{\rm d}M(v) = {T_{AH}}{\rm d}{S_{AH}}. $

(65) When other fields are present, Eq. (65) can be generalized as
$\begin{aligned}[b] {\left. {{\rm d}\mathcal{M}\left( v \right)} \right|_{r = {r_{AH}}}} &= \left[ {{{\left. {\frac{{\partial m\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_{AH}}}}} \right]{\rm d}M(v) \\ &= {T_{AH}}{\rm d}{S_{AH}} + \Phi _{AH}^\alpha {\rm d}\alpha + \Phi _{AH}^\beta {\rm d}\beta + \cdots . \end{aligned} $

(66) At the apparent horizon,
${T_{AH}}$ and${\tilde T_{AH}}$ are also related by the corrected factor:$ {T_{AH}} = \left[ {{{\left. {\frac{{\partial m\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_{AH}}}}} \right]{\tilde T_{AH}}. $

(67) For the dynamical Hayward and dynamical non-commutative black holes, the correction factors are respectively given by
$ \begin{aligned}[b] F\left( {v,{r_{AH}},\alpha } \right) &= {\left. {\frac{{\partial m\left( {v,r,\alpha } \right)}}{{\partial M\left( v \right)}}} \right|_{r = {r_{AH}}}} \\ &= {\left. {\left[ {\frac{\partial }{{\partial M\left( v \right)}}\left( {\frac{{M\left( v \right){r^3}}}{{{r^3} + 2\alpha M\left( v \right)}}} \right)} \right]} \right|_{r = {r_{AH}}}} \\ &= \frac{1}{{r_{AH}^4}}{\left( {r_{AH}^2 - \alpha } \right)^2}, \end{aligned} $

(68) $\begin{aligned}[b] F\left( {v,{r_{AH}},\vartheta } \right) &= {\left. {\frac{{\partial m\left( {v,r,\vartheta } \right)}}{{\partial M\left( v \right)}}} \right|_{r = {r_h}}}\\ &= {\left. {\left\{ {\frac{\partial }{{\partial M\left( v \right)}}\left[ {\frac{{2M\left( v \right)}}{{\sqrt \pi }}\gamma \left( {\frac{3}{2},\frac{{{r^2}}}{{4\vartheta }}} \right)} \right]} \right\}} \right|_{r = {r_{AH}}}}\\ &= \frac{2}{{\sqrt \pi }}\gamma \left( {\frac{3}{2},\frac{{r_{AH}^2}}{{4\vartheta }}} \right). \end{aligned}$

(69) The product of
${T_{AH}}$ and the correction factor exactly gives${\tilde T_{AH}}$ , which satisfies Eq. (67). This verifies the validity of the corrected first law of thermodynamics on the apparent horizon. -
In a dynamical spherically symmetric space-time, the Kodama vector can be used to describe the symmetry of the space-time. When the dynamical space-time reduces to a static one, the Kodama vector also reduces to the Killing vector. The Kodama vector is defined as
$ {K}^{a}=-{\epsilon }^{ab}{\nabla }_{b}r $ , where$ {\epsilon }^{ab} $ denotes the volume form [27]. For the metric given by Eq. (2), the Kodama vector is expressed as${K^a} = {\left( {{\partial _v}} \right)^a}$ . Given that the Kodama vector is divergence free, that is,${\nabla _a}{K^a} = 0$ , there exists a conserved current${J^a} = T_b^a{K^b}$ , and the conserved charge is$ E= -\displaystyle\int_{\sigma}^{ }J^a\mathrm{d}\sigma_a $ , which is equal to the Misner-Sharp energy. Using the Kodama vector, Hayward defined the surface gravity on the apparent horizon as$ \kappa = \dfrac{1}{2}{\nabla ^a}{\nabla _a}r $ . Therefore, we can directly use the surface gravity method to calculate the temperature at the apparent horizon. In combination with the line element expressed by Eq. (2), we obtain the surface gravity associated to the apparent horizon as$ \begin{aligned}[b] \kappa = {\left. {\frac{1}{2}{\nabla ^a}{\nabla _a}r} \right|_{r = {r_{AH}}}} &= {\left. {\left[ {\frac{1}{{2\sqrt { - h} }}{\partial _i}\left( {\sqrt { - h} {h^{ij}}{\partial _j}r} \right)} \right]} \right|_{r = {r_{AH}}}} \\ & = {\left. {\left[ {\frac{1}{{2\sqrt { - h} }}{\partial _r}\left( {\sqrt { - h} {h^{rr}}} \right)} \right]} \right|_{r = {r_{AH}}}} \\ & = \frac{1}{2}f'\left( {v,{r_{AH}}} \right). \end{aligned} $

(53) Here,
$i$ and$j$ range from$0$ to$1$ . The temperature derived from the surface gravity method is given by$ {T_{AH}} = \frac{\kappa }{{2\pi }} = \frac{{f'(v,{r_{AH}})}}{{4\pi }} = \frac{1}{{4\pi {r_{AH}}}} - \frac{{m'\left( {v,{r_{AH}}} \right)}}{{2\pi {r_{AH}}}}. $

(54) The last step for Eq. (54) makes use of the condition satisfied by the radius of the apparent horizon:
$ {r_{AH}} = 2m\left( {v,{r_{AH}}} \right) $ . Next, we address the calculations related to the dynamical regular black holes discussed in this paper. For dynamical Hayward black holes, the relation between$M(v)$ and${r_{AH}}$ is$ M\left( v \right) = \frac{{r_{AH}^3}}{{2\left( {r_{AH}^2 - \alpha } \right)}}. $

(55) In conjunction with Eq. (54), we can obtain the temperature at the apparent horizon:
$ {T_{AH}} = \frac{{r_{AH}^2 - 3\alpha }}{{4\pi r_{AH}^3}}. $

(56) Following the same approach, the temperature at the apparent horizon for the dynamical non-commutative black hole is given by
$ T_{AH}=\frac{1}{16\pi r_{AH}}\left[4-r_{AH}^3\vartheta^{-\frac{3}{2}}\mathrm{e}^{-\frac{r_{AH}^2}{4\vartheta}}\gamma^{-1}\left(\frac{3}{2},\frac{r_{AH}^2}{4\vartheta}\right)\right]. $

(57) Next, we use the first law of thermodynamics [23,24] to obtain the temperature at the apparent horizons for both black holes:
$ {\tilde T_{AH}} = \frac{{\partial M}}{{\partial {S_{AH}}}} = \frac{{\partial {r_{AH}}}}{{\partial {S_{AH}}}}\frac{{\partial M}}{{\partial {r_{AH}}}} = \frac{{{r_{AH}}\left( {r_{AH}^2 - 3\alpha } \right)}}{{4\pi {{\left( {r_{AH}^2 - \alpha } \right)}^2}}}, $

(58) $\begin{aligned}[b] {\tilde T_{AH}} = &\frac{1}{{32\sqrt \pi {r_{AH}}}}\left[ r_{AH}^3{\vartheta ^{ - \frac{3}{2}}}{{\rm e}^{ - \frac{{r_{AH}^2}}{{4\vartheta }}}} \right.\\ &\left. - 4\gamma \left( {\frac{3}{2},\frac{{r_{AH}^2}}{{4\vartheta }}} \right) \right]{\gamma ^{ - 2}}\left( {\frac{3}{2},\frac{{r_{AH}^2}}{{4\vartheta }}} \right). \end{aligned}$

(59) Note that, similar to the case at the event horizon, the temperatures obtained from the surface gravity and the first law of thermodynamics on the apparent horizon are different. Next, we follow a procedure similar to that in the previous section to derive the corrected first law of thermodynamics on the apparent horizon. First, using Eq. (40), the temperature can be expressed as
$ {T_{AH}} = \frac{1}{{4\pi {r_{AH}}}} + 2{r_{AH}}T_v^v. $

(60) On the apparent horizon, Eq. (42) gives
$ M\left( v \right) = m\left( {v,{r_{AH}}} \right) - 4\pi \int_{{r_{AH}}}^\infty {{r^2}T_v^v{\rm d}r.} $

(61) Substituting
$ m\left( {v,{r_{AH}}} \right) = {{{r_{AH}}} \mathord{\left/ {\vphantom {{{r_{AH}}} 2}} \right. } 2} $ and differentiating Eq. (61), we obtain$ {\rm d}M(v) = {\rm d}\left( {\frac{1}{2}{r_{AH}}} \right) - 4\pi {\rm d}\left( {\int_{{r_{AH}}}^\infty {{r^2}T_v^v{\rm d}r} } \right). $

(62) Eq. (62) finally leads to the following result:
$\begin{aligned}[b] &\left[ {1 + 4\pi \int_{{r_{AH}}}^\infty {{r^2}\frac{{\partial T_v^v}}{{\partial M(v)}}{\rm d}r} } \right]{\rm d}M(v) \\ =& \left[ {\frac{1}{{4\pi {r_{AH}}}} + 2{r_{AH}}T_v^v} \right]{\rm d}\left( {\frac{{{A_{AH}}}}{4}} \right). \end{aligned}$

(63) In conjunction with the temperature expression given by Eq. (60), Eq. (63) can be simplified to
$ \left[1+4\pi\int_{r_{AH}}^{\infty}r^2\frac{\partial T_v^v}{\partial M(v)}\mathrm{d}r\right]\mathrm{d}M(v)=T_{AH}\mathrm{d}S_{AH}. $

(64) Using Eq. (42), we finally obtain the corrected first law of thermodynamics on the apparent horizon as
$ {\left. {{\rm d}\mathcal{M}\left( v \right)} \right|_{r = {r_{AH}}}} = \left[ {{{\left. {\frac{{\partial m\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_{AH}}}}} \right]{\rm d}M(v) = {T_{AH}}{\rm d}{S_{AH}}. $

(65) When other fields are present, Eq. (65) can be generalized as
$\begin{aligned}[b] {\left. {{\rm d}\mathcal{M}\left( v \right)} \right|_{r = {r_{AH}}}} &= \left[ {{{\left. {\frac{{\partial m\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_{AH}}}}} \right]{\rm d}M(v) \\ &= {T_{AH}}{\rm d}{S_{AH}} + \Phi _{AH}^\alpha {\rm d}\alpha + \Phi _{AH}^\beta {\rm d}\beta + \cdots . \end{aligned} $

(66) At the apparent horizon,
${T_{AH}}$ and${\tilde T_{AH}}$ are also related by the corrected factor:$ {T_{AH}} = \left[ {{{\left. {\frac{{\partial m\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_{AH}}}}} \right]{\tilde T_{AH}}. $

(67) For the dynamical Hayward and dynamical non-commutative black holes, the correction factors are respectively given by
$ \begin{aligned}[b] F\left( {v,{r_{AH}},\alpha } \right) &= {\left. {\frac{{\partial m\left( {v,r,\alpha } \right)}}{{\partial M\left( v \right)}}} \right|_{r = {r_{AH}}}} \\ &= {\left. {\left[ {\frac{\partial }{{\partial M\left( v \right)}}\left( {\frac{{M\left( v \right){r^3}}}{{{r^3} + 2\alpha M\left( v \right)}}} \right)} \right]} \right|_{r = {r_{AH}}}} \\ &= \frac{1}{{r_{AH}^4}}{\left( {r_{AH}^2 - \alpha } \right)^2}, \end{aligned} $

(68) $\begin{aligned}[b] F\left( {v,{r_{AH}},\vartheta } \right) &= {\left. {\frac{{\partial m\left( {v,r,\vartheta } \right)}}{{\partial M\left( v \right)}}} \right|_{r = {r_h}}}\\ &= {\left. {\left\{ {\frac{\partial }{{\partial M\left( v \right)}}\left[ {\frac{{2M\left( v \right)}}{{\sqrt \pi }}\gamma \left( {\frac{3}{2},\frac{{{r^2}}}{{4\vartheta }}} \right)} \right]} \right\}} \right|_{r = {r_{AH}}}}\\ &= \frac{2}{{\sqrt \pi }}\gamma \left( {\frac{3}{2},\frac{{r_{AH}^2}}{{4\vartheta }}} \right). \end{aligned}$

(69) The product of
${T_{AH}}$ and the correction factor exactly gives${\tilde T_{AH}}$ , which satisfies Eq. (67). This verifies the validity of the corrected first law of thermodynamics on the apparent horizon. -
In this subsection, we provide some remarks regarding the corrected first law of thermodynamics. From the differential form of the field equation (Eq. (40)) or its integral form (Eq. (42)), it is not difficult to find that
$m\left( {v,r} \right)$ appearing in the correction factor is given by$ m\left(v,r\right)=-4\pi\int_0^rr^2T_v^v\mathrm{d}r. $

(70) This form suggests that it is likely related to the energy enclosed within a sphere of radius
$r$ . In fact, we can verify that the Misner-Sharp energy within a sphere of radius$r$ is exactly equal to$ m\left( {v,r} \right) $ . This can be verified using the definition of Misner-Sharp energy:$ {E_{MS}}\left( {v,r} \right) = \frac{r}{2}\left( {1 - {h^{ab}}{\partial _a}r{\partial _b}r} \right) = \frac{r}{2}\left[ {1 - f(v,r)} \right] = m\left( {v,r} \right). $

(71) Therefore, the corrected first law of thermodynamics for spherically symmetric dynamical regular black hole can be written as
$ \begin{aligned}[b] &\left[ {{{\left. {\frac{{\partial {E_{MS}}\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_{\left( A \right)H}}}}} \right]{\rm d}M(v) \\ = &{T_{{r_{\left( A \right)H}}}}{\rm d}{S_{{r_{\left( A \right)H}}}} + \Phi _{\left( A \right)H}^\alpha {\rm d}\alpha + \Phi _{\left( A \right)H}^\beta {\rm d}\beta + \cdots . \end{aligned}$

(72) For static spherically symmetric black holes, the correction factor can also be expressed in the same form. Here, the reason why we chose the Misner-Sharp energy is that it is a conserved charge associated with the Kodama vector. However, a more physically intuitive explanation for why the corrected factor of spherically symmetric regular black holes is related to the Misner-Sharp energy still remains to be developed.
Additionally, by examining the forms of Eqs. (50) and (66), we conclude that, in general,
$ \mathrm{d}\mathcal{M}\left(v\right) $ is not an exact differential form. Only when${{\partial T_v^v} \mathord{\left/ {\vphantom {{\partial T_v^v} {\partial M}}} \right. } {\partial M}}\left( v \right) = 0$ , that is, when$ \mathrm{d}\mathcal{M}\left(v\right)=\mathrm{d}M\left(v\right) $ , does it become an exact differential form. In this way, the corrected first law of thermodynamics reduces to the traditional first law of thermodynamics for singular black holes.Another aspect to be discussed is that, given that we can successfully establish a corrected first law of thermodynamics on both the event and apparent horizons, a question arises: which one should be considered more fundamental? Refs. [23, 24] treated the event horizon as a time-dependent perturbation of the apparent horizon and showed that thermodynamics can also be established on the event horizon. Therefore, the authors concluded that the thermodynamics associated with the apparent horizon should be regarded as more fundamental. However, if we think reversely, the apparent horizon can also be viewed as a time-dependent perturbation of the event horizon. Hence, the explanation given in [23, 24] is mostly a mathematical interpretation. Regarding this issue, we would like to highlight the following two points. The first concerns the definition of the event horizon itself, which can only be defined in asymptotically flat space-times. However, the universe may not be asymptotically flat, so the existence of an event horizon is questionable. Even if the universe were asymptotically flat, an observer with a finite lifespan would not be able to verify such a global property [33]. The second point is related to Ref. [21], in which the author considered the collapse process of a spherical shell and suggested that the Hawking effect is associated with the apparent horizon rather than the event horizon. The reason was that the apparent horizon constitutes the boundary of the ergoregion, and if Hawking radiation originates from regions near the ergoregion, then the apparent horizon is associated with Hawking radiation. Another conclusion reached in [21] is even more significant: Hawking radiation survives even in the absence of an event horizon. Therefore, in this study, we are inclined to believe that the corrected first law of thermodynamics on the apparent horizon is more fundamental.
-
In this subsection, we provide some remarks regarding the corrected first law of thermodynamics. From the differential form of the field equation (Eq. (40)) or its integral form (Eq. (42)), it is not difficult to find that
$m\left( {v,r} \right)$ appearing in the correction factor is given by$ m\left(v,r\right)=-4\pi\int_0^rr^2T_v^v\mathrm{d}r. $

(70) This form suggests that it is likely related to the energy enclosed within a sphere of radius
$r$ . In fact, we can verify that the Misner-Sharp energy within a sphere of radius$r$ is exactly equal to$ m\left( {v,r} \right) $ . This can be verified using the definition of Misner-Sharp energy:$ {E_{MS}}\left( {v,r} \right) = \frac{r}{2}\left( {1 - {h^{ab}}{\partial _a}r{\partial _b}r} \right) = \frac{r}{2}\left[ {1 - f(v,r)} \right] = m\left( {v,r} \right). $

(71) Therefore, the corrected first law of thermodynamics for spherically symmetric dynamical regular black hole can be written as
$ \begin{aligned}[b] &\left[ {{{\left. {\frac{{\partial {E_{MS}}\left( {v,r} \right)}}{{\partial M\left( v \right)}}} \right|}_{r = {r_{\left( A \right)H}}}}} \right]{\rm d}M(v) \\ = &{T_{{r_{\left( A \right)H}}}}{\rm d}{S_{{r_{\left( A \right)H}}}} + \Phi _{\left( A \right)H}^\alpha {\rm d}\alpha + \Phi _{\left( A \right)H}^\beta {\rm d}\beta + \cdots . \end{aligned}$

(72) For static spherically symmetric black holes, the correction factor can also be expressed in the same form. Here, the reason why we chose the Misner-Sharp energy is that it is a conserved charge associated with the Kodama vector. However, a more physically intuitive explanation for why the corrected factor of spherically symmetric regular black holes is related to the Misner-Sharp energy still remains to be developed.
Additionally, by examining the forms of Eqs. (50) and (66), we conclude that, in general,
$ \mathrm{d}\mathcal{M}\left(v\right) $ is not an exact differential form. Only when${{\partial T_v^v} \mathord{\left/ {\vphantom {{\partial T_v^v} {\partial M}}} \right. } {\partial M}}\left( v \right) = 0$ , that is, when$ \mathrm{d}\mathcal{M}\left(v\right)=\mathrm{d}M\left(v\right) $ , does it become an exact differential form. In this way, the corrected first law of thermodynamics reduces to the traditional first law of thermodynamics for singular black holes.Another aspect to be discussed is that, given that we can successfully establish a corrected first law of thermodynamics on both the event and apparent horizons, a question arises: which one should be considered more fundamental? Refs. [23, 24] treated the event horizon as a time-dependent perturbation of the apparent horizon and showed that thermodynamics can also be established on the event horizon. Therefore, the authors concluded that the thermodynamics associated with the apparent horizon should be regarded as more fundamental. However, if we think reversely, the apparent horizon can also be viewed as a time-dependent perturbation of the event horizon. Hence, the explanation given in [23, 24] is mostly a mathematical interpretation. Regarding this issue, we would like to highlight the following two points. The first concerns the definition of the event horizon itself, which can only be defined in asymptotically flat space-times. However, the universe may not be asymptotically flat, so the existence of an event horizon is questionable. Even if the universe were asymptotically flat, an observer with a finite lifespan would not be able to verify such a global property [33]. The second point is related to Ref. [21], in which the author considered the collapse process of a spherical shell and suggested that the Hawking effect is associated with the apparent horizon rather than the event horizon. The reason was that the apparent horizon constitutes the boundary of the ergoregion, and if Hawking radiation originates from regions near the ergoregion, then the apparent horizon is associated with Hawking radiation. Another conclusion reached in [21] is even more significant: Hawking radiation survives even in the absence of an event horizon. Therefore, in this study, we are inclined to believe that the corrected first law of thermodynamics on the apparent horizon is more fundamental.
-
Inspired by the corrected first law of thermodynamics for static spherically symmetric regular black holes, we investigated the corrected first law of thermodynamics for dynamical regular black holes. First, we calculated the apparent and event horizon radii for an arbitrary spherically symmetric dynamical regular black hole and found that they are very close to each other. Then, for the event and apparent horizons, we obtained the corresponding temperatures using the conformal flat and surface gravity methods, respectively. However, the temperature derived from the first law of thermodynamics differs from those obtained by the two methods mentioned above. This indicates that, similar to the static case, the first law of thermodynamics also needs to be corrected for dynamical regular black holes. Following the idea proposed in [23, 24], that thermodynamics can be built on both horizons, we successfully established the corrected first law of thermodynamics on both horizons using the Einstein field equations. Moreover, we found that they share the same form. Finally, we found that for both spherically symmetric dynamical and static regular black holes, the correction factor is related to the derivative of the Misner-Sharp energy with respect to the mass
$M\left( v \right)$ . A deeper physical meaning behind this relation requires further investigation. -
Inspired by the corrected first law of thermodynamics for static spherically symmetric regular black holes, we investigated the corrected first law of thermodynamics for dynamical regular black holes. First, we calculated the apparent and event horizon radii for an arbitrary spherically symmetric dynamical regular black hole and found that they are very close to each other. Then, for the event and apparent horizons, we obtained the corresponding temperatures using the conformal flat and surface gravity methods, respectively. However, the temperature derived from the first law of thermodynamics differs from those obtained by the two methods mentioned above. This indicates that, similar to the static case, the first law of thermodynamics also needs to be corrected for dynamical regular black holes. Following the idea proposed in [23, 24], that thermodynamics can be built on both horizons, we successfully established the corrected first law of thermodynamics on both horizons using the Einstein field equations. Moreover, we found that they share the same form. Finally, we found that for both spherically symmetric dynamical and static regular black holes, the correction factor is related to the derivative of the Misner-Sharp energy with respect to the mass
$M\left( v \right)$ . A deeper physical meaning behind this relation requires further investigation. -
In this appendix, we explicitly calculate the apparent horizon radius for the dynamical black hole described by the line element expressed by Eq. (10). First, for computational convenience, we rewrite it in a metric signature of (+, −, −, −) as
$ {\rm d}{s^2} = f(v,r){\rm d}{v^2} - 2{\rm d}v{\rm d}r - {r^2}{\rm d}{\theta ^2} - {r^2}{\sin ^2}\theta {\rm d}{\varphi ^2}. $

(A1) The determinant and non-vanishing contravariant components of the metric are given, respectively, by
$ \begin{aligned}[b] & g = - {r^4}{\sin ^2}\theta , \quad {g^{vr}} = {g^{rv}} = - 1, \quad {g^{rr}} = - f(v,r),\\ &{g^{\theta \theta }} = - \frac{1}{{{r^2}}}, \quad {g^{\varphi \varphi }} = - \frac{1}{{{r^2}{{\sin }^2}\theta }}. \end{aligned} $

(A2) From the line element given by Eq. (A.1), we can obtain the non-vanishing components of the affine connections as
$ \begin{aligned}[b] \Gamma _{vv}^v &= \frac{1}{2}f', \Gamma _{\theta \theta }^v = - r, \Gamma _{\varphi \varphi }^v = - r{\sin ^2}\theta , \\ \Gamma _{vr}^r &= \Gamma _{rv}^r = - \frac{1}{2}f', \Gamma _{vv}^r = \frac{1}{2}\left( { - \dot f + ff'} \right), \\ \Gamma _{\theta \theta }^r &= - f \cdot r, \Gamma _{\varphi \varphi }^r = - f \cdot r{\sin ^2}\theta , \\ \Gamma _{r\theta }^\theta &= \Gamma _{\theta r}^\theta = \frac{1}{r}, \Gamma _{\varphi \varphi }^\theta = - \sin \theta \cos \theta , \\ \Gamma _{r\varphi }^\varphi &= \Gamma _{\varphi r}^\varphi = \frac{1}{r}, \Gamma _{\theta \varphi }^\varphi = \Gamma _{\varphi \theta }^\varphi = \cot \theta . \end{aligned} $

(A3) Next, we choose the following null tetrad:
$ \begin{aligned}[b] & {l_\mu } = \left( {\frac{f}{2}, - 1,0,0} \right) , \quad {n_\mu } = \left( {1,0,0,0} \right), \\ & {m_\mu } = \frac{r}{{\sqrt 2 }}\left( {0,0,1,{\rm i} \sin \theta } \right), \\ & {{\bar m}_\mu } = \frac{r}{{\sqrt 2 }}\left( {0,0,1, - {\rm i} \sin \theta } \right), \end{aligned} $

(A4) and their contravariant forms are given by
$ \begin{aligned}[b] & {l^\mu } = \left( {1,\frac{f}{2},0,0} \right) , \quad {n^\mu } = \left( {0, - 1,0,0} \right), \\ & {m^\mu } = \frac{1}{{\sqrt 2 r}}\left( {0,0, - 1, - \frac{{\rm i} }{{\sin \theta }}} \right) , \\ & {{\bar m}^\mu } = \frac{1}{{\sqrt 2 r}}\left( {0,0, - 1,\frac{{\rm i} }{{\sin \theta }}} \right). \end{aligned} $

(A5) One can verify that they satisfy the condition of the null tetrad frame:
$ \begin{aligned}[b] & {n_\mu }{n^\mu } = {l_\mu }{l^\mu } = {m_\mu }{m^\mu } = {{\bar m}_\mu }{{\bar m}^\mu } = 0, \\ & {n_\mu }{l^\mu } = - {m_\mu }{{\bar m}^\mu } = 1, \\ & {n_\mu }{m^\mu } = {n_\mu }{{\bar m}^\mu } = {l_\mu }{m^\mu } = {l_\mu }{{\bar m}^\mu } = 0. \end{aligned} $

(A6) Using the components of the affine connection and null tetrads, we can calculate
$ l_{;\mu }^\mu $ and$\kappa $ :$ \begin{aligned}[b] l_{;\mu }^\mu &= l_{,\mu }^\mu + \Gamma _{\sigma \mu }^\mu {l^\sigma } = \frac{1}{{\sqrt { - g} }}\frac{\partial }{{\partial {x^\mu }}}\left( {\sqrt { - g} {l^\mu }} \right) \\ &= \frac{1}{{\sqrt { - g} }}\left[ {\frac{\partial }{{\partial v}}\left( {\sqrt { - g} {l^v}} \right) + \frac{\partial }{{\partial r}}\left( {\sqrt { - g} {l^r}} \right)} \right] = \frac{{rf' + 2f}}{{2r}}, \end{aligned} $

(A7) $ \begin{aligned}[b] \kappa &= \left( {{l_{\mu ,\nu }} - \Gamma _{\mu \nu }^\sigma {l_\sigma }} \right){n^\mu }{l^\nu } = {l_{\mu ,\nu }}{n^\mu }{l^\nu } - \Gamma _{\mu \nu }^\sigma {l_\sigma }{n^\mu }{l^\nu } \\ &= \left( {{l_{r,v}}{n^r}{l^v} + {l_{r,r}}{n^r}{l^r}} \right) - \Gamma _{rv}^r{l_r}{n^r}{l^v} = \frac{{f'}}{2}. \end{aligned}$

(A8) Therefore, we obtain
$ \Theta = l_{;\mu }^\mu - \kappa = {{f\left( {v,r} \right)} \mathord{\left/ {\vphantom {{f\left( {v,r} \right)} r}} \right. } r} $ . Setting$\Theta = 0$ , we finally obtain that the radius of the apparent horizon satisfies$ f\left( {v,{r_{AH}}} \right) = 0 $ . -
In this appendix, we explicitly calculate the apparent horizon radius for the dynamical black hole described by the line element expressed by Eq. (10). First, for computational convenience, we rewrite it in a metric signature of (+, −, −, −) as
$ {\rm d}{s^2} = f(v,r){\rm d}{v^2} - 2{\rm d}v{\rm d}r - {r^2}{\rm d}{\theta ^2} - {r^2}{\sin ^2}\theta {\rm d}{\varphi ^2}. $

(A1) The determinant and non-vanishing contravariant components of the metric are given, respectively, by
$ \begin{aligned}[b] & g = - {r^4}{\sin ^2}\theta , \quad {g^{vr}} = {g^{rv}} = - 1, \quad {g^{rr}} = - f(v,r),\\ &{g^{\theta \theta }} = - \frac{1}{{{r^2}}}, \quad {g^{\varphi \varphi }} = - \frac{1}{{{r^2}{{\sin }^2}\theta }}. \end{aligned} $

(A2) From the line element given by Eq. (A.1), we can obtain the non-vanishing components of the affine connections as
$ \begin{aligned}[b] \Gamma _{vv}^v &= \frac{1}{2}f', \Gamma _{\theta \theta }^v = - r, \Gamma _{\varphi \varphi }^v = - r{\sin ^2}\theta , \\ \Gamma _{vr}^r &= \Gamma _{rv}^r = - \frac{1}{2}f', \Gamma _{vv}^r = \frac{1}{2}\left( { - \dot f + ff'} \right), \\ \Gamma _{\theta \theta }^r &= - f \cdot r, \Gamma _{\varphi \varphi }^r = - f \cdot r{\sin ^2}\theta , \\ \Gamma _{r\theta }^\theta &= \Gamma _{\theta r}^\theta = \frac{1}{r}, \Gamma _{\varphi \varphi }^\theta = - \sin \theta \cos \theta , \\ \Gamma _{r\varphi }^\varphi &= \Gamma _{\varphi r}^\varphi = \frac{1}{r}, \Gamma _{\theta \varphi }^\varphi = \Gamma _{\varphi \theta }^\varphi = \cot \theta . \end{aligned} $

(A3) Next, we choose the following null tetrad:
$ \begin{aligned}[b] & {l_\mu } = \left( {\frac{f}{2}, - 1,0,0} \right) , \quad {n_\mu } = \left( {1,0,0,0} \right), \\ & {m_\mu } = \frac{r}{{\sqrt 2 }}\left( {0,0,1,{\rm i} \sin \theta } \right), \\ & {{\bar m}_\mu } = \frac{r}{{\sqrt 2 }}\left( {0,0,1, - {\rm i} \sin \theta } \right), \end{aligned} $

(A4) and their contravariant forms are given by
$ \begin{aligned}[b] & {l^\mu } = \left( {1,\frac{f}{2},0,0} \right) , \quad {n^\mu } = \left( {0, - 1,0,0} \right), \\ & {m^\mu } = \frac{1}{{\sqrt 2 r}}\left( {0,0, - 1, - \frac{{\rm i} }{{\sin \theta }}} \right) , \\ & {{\bar m}^\mu } = \frac{1}{{\sqrt 2 r}}\left( {0,0, - 1,\frac{{\rm i} }{{\sin \theta }}} \right). \end{aligned} $

(A5) One can verify that they satisfy the condition of the null tetrad frame:
$ \begin{aligned}[b] & {n_\mu }{n^\mu } = {l_\mu }{l^\mu } = {m_\mu }{m^\mu } = {{\bar m}_\mu }{{\bar m}^\mu } = 0, \\ & {n_\mu }{l^\mu } = - {m_\mu }{{\bar m}^\mu } = 1, \\ & {n_\mu }{m^\mu } = {n_\mu }{{\bar m}^\mu } = {l_\mu }{m^\mu } = {l_\mu }{{\bar m}^\mu } = 0. \end{aligned} $

(A6) Using the components of the affine connection and null tetrads, we can calculate
$ l_{;\mu }^\mu $ and$\kappa $ :$ \begin{aligned}[b] l_{;\mu }^\mu &= l_{,\mu }^\mu + \Gamma _{\sigma \mu }^\mu {l^\sigma } = \frac{1}{{\sqrt { - g} }}\frac{\partial }{{\partial {x^\mu }}}\left( {\sqrt { - g} {l^\mu }} \right) \\ &= \frac{1}{{\sqrt { - g} }}\left[ {\frac{\partial }{{\partial v}}\left( {\sqrt { - g} {l^v}} \right) + \frac{\partial }{{\partial r}}\left( {\sqrt { - g} {l^r}} \right)} \right] = \frac{{rf' + 2f}}{{2r}}, \end{aligned} $

(A7) $ \begin{aligned}[b] \kappa &= \left( {{l_{\mu ,\nu }} - \Gamma _{\mu \nu }^\sigma {l_\sigma }} \right){n^\mu }{l^\nu } = {l_{\mu ,\nu }}{n^\mu }{l^\nu } - \Gamma _{\mu \nu }^\sigma {l_\sigma }{n^\mu }{l^\nu } \\ &= \left( {{l_{r,v}}{n^r}{l^v} + {l_{r,r}}{n^r}{l^r}} \right) - \Gamma _{rv}^r{l_r}{n^r}{l^v} = \frac{{f'}}{2}. \end{aligned}$

(A8) Therefore, we obtain
$ \Theta = l_{;\mu }^\mu - \kappa = {{f\left( {v,r} \right)} \mathord{\left/ {\vphantom {{f\left( {v,r} \right)} r}} \right. } r} $ . Setting$\Theta = 0$ , we finally obtain that the radius of the apparent horizon satisfies$ f\left( {v,{r_{AH}}} \right) = 0 $ .
Corrected first law of thermodynamics for dynamical regular black holes
- Received Date: 2025-06-22
- Available Online: 2025-12-15
Abstract: In this study, we establish the corrected first law of thermodynamics for dynamical regular black holes on both the event and apparent horizons. We found that the temperature of dynamical regular black holes derived from the traditional first law differs from that obtained through other approaches. This indicates that, similar to static cases, the first law of thermodynamics requires correction. We derived the corrected first law of thermodynamics from the Einstein field equations. Our analysis reveals that the corrected factor originates from the fact that the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

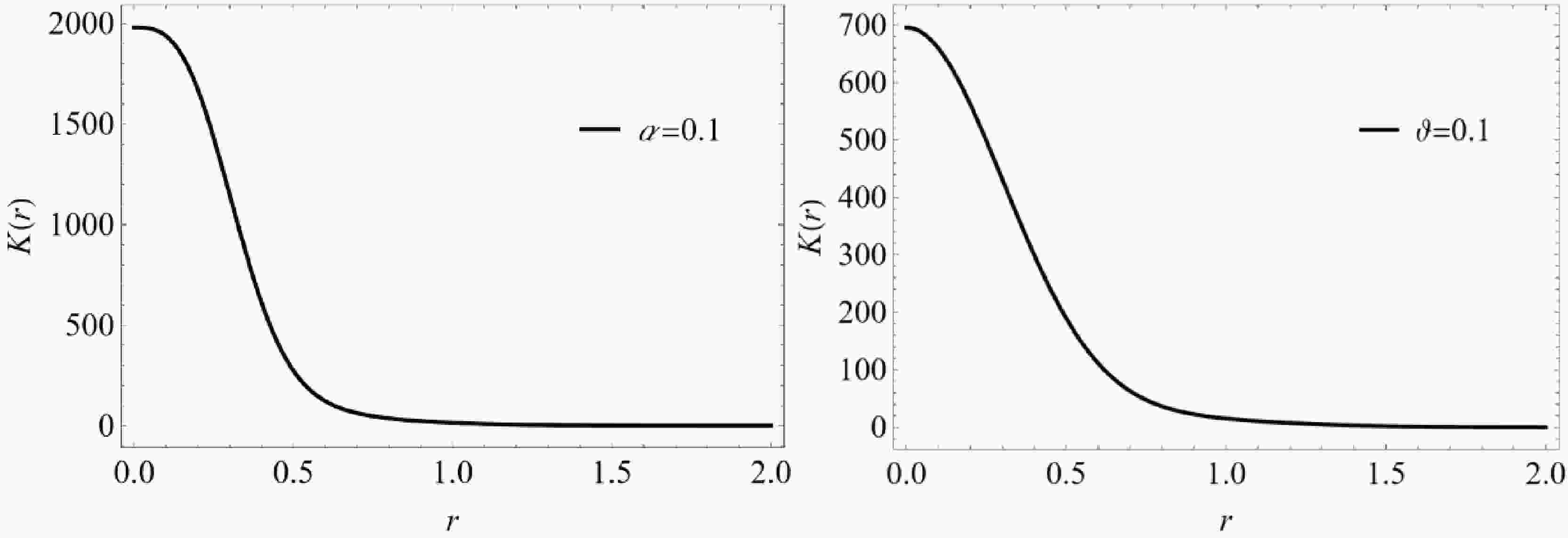










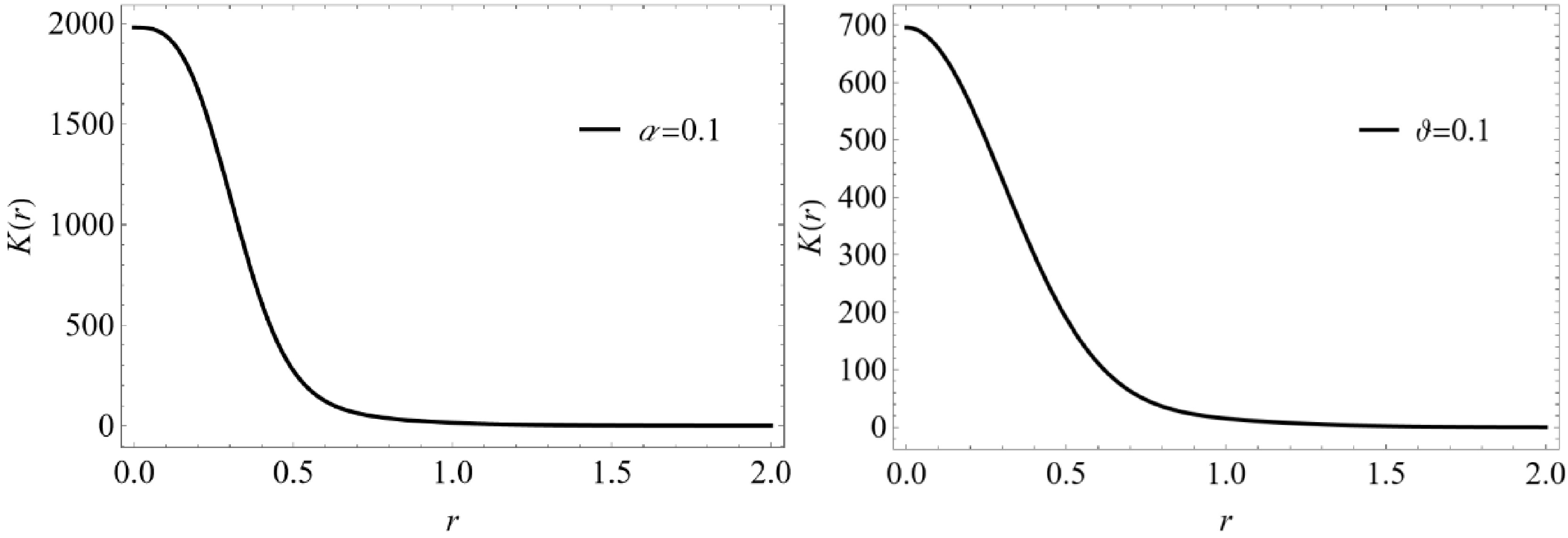



 DownLoad:
DownLoad: