-
Detectable signals from mergers of compact stars, such as those involving black holes and neutron stars, provide insights into their internal composition and dynamic evolution, thereby opening a new avenue for astronomical outreach. Fortunately, the detection of binary neutron star (BNS) mergers by the LIGO-Virgo Collaboration and electromagnetic (EM) observer partners, GW170817 [1], has imposed new limitations on the maximum mass of neutron stars (NSs). In addition, it significantly influences our understanding of gravity, specifically the physics of dense matter above
$ \sim $ 1-2$ n_0 $ (being$ n_0 = 0.16 $ fm$ ^{-3} $ the nuclear saturation density). Therefore, accurately characterizing the equation of state (EOS) of dense matter is still challenging when attempting to infer the interior composition of neutron stars (NSs). Among the various proposed interior structures discussed in the literature, the quark star (QS), which comprises quark matter, has emerged as a potential candidate. Therefore, QSs in such environments offer a platform for investigating high-density matter beyond nuclear saturation.Theoretically, quark matter (QM) treated as the true ground state of dense matter was proposed by E. Witten in 1984 [2] (following Bodmer's important precursor [3]). The hypothesis concerning QM and particularly strange QM consisting of u, d, and s quarks, also called strange quark matter (SQM), posits that it represents the most energetically favourable state of matter. However, some research [4, 5] has explored the flavor-dependent effects of quark gas on the QCD vacuum, suggesting that
$ u, d $ quark matter ($ ud\mathrm{QM} $ ) is typically more stable than SQM. Notably, at sufficiently high baryon numbers,$ ud\mathrm{QM} $ can surpass the stability of ordinary nuclei and extend beyond the periodic table. This finding has led to an increase in recent experimental pursuits [6−8] and phenomenological research [9−14].Along these lines, the MIT bag model [15] has been widely employed by many authors to describe massive neutron stars (NSs), i.e., NSs with a quark matter core, which have been detected in the past decade [16−19]. A modified version of this model, incorporating vector interactions and drawing features from quantum hadrodynamics (QHD) [20], has also been proposed and applied to strange quark matter (SQM) and quark stars [21−24]. Building on these developments, Zhang et al [25] introduced an EoS for quark matter that incorporates perturbative QCD (pQCD) corrections and color superconductivity. This model has the notable advantage of producing massive quark stars with larger radii consistent with recent astrophysical constraints. An additional feature is that, through a single parameter, the EoS can be rescaled into a dimensionless form, thereby reducing the number of free parameters and characterizing the relative strength of strong interaction effects [26−28].
However, in the presence of enormous densities and pressures in the interiors of such stars, one can expect that the pressure could be anisotropic, with the radial pressure differing from that in the azimuthal directions. In addition to these nuclear interactions [30], viscosity effects [31], pion condensation [32], and some kinds of phase transitions [33] may contribute to the presence of pressure anisotropy. Considering local anisotropy, QSs or NSs have been studied to extract information regarding their internal structure and nuclear physics(see, e.g., [34−45]). These investigations suggest that pressure anisotropy has a significant impact on the mass-radius relationship and the internal properties of stars, including the maximum surface redshift and maximum compactness. It's also important to note that the presence of anisotropy influences the stability of the configuration by supporting outwardly increasing energy density within the star core [46].
The above discussion suggests that investigations of anisotropic systems are typically conducted within the framework of Einstein's theory of gravity. Here, we study the stability of anisotropic QSs in gravity's rainbow. Gravity's rainbow [47] has been treated as an extension of the principles of doubly special relativity (DSR) [48] to curved spacetimes. This theory suggests a modification of the spacetime metric by introducing energy-dependent rainbow functions,
$ \Xi(x) $ and$ \Sigma(x) $ , that are characterised by the dimensionless ratio of the total energy of the probe particle E to the Planck energy$ E_p $ . This approach helps alter the relativistic dispersion relations. It allows for a deeper understanding of the relation between quantum mechanics and general relativity at high energy scales, particularly near the Planck scale [49, 50]. By incorporating energy-dependent effects into curved spacetimes, gravity's rainbow attempts to address some of the conceptual issues, like black hole solutions and their properties [51−56], gravastar, and wormhole solutions [57, 58]. Another intriguing finding in this context is the dark star [59] and NSs [60], which also analyse their stability-related issues.In summary, this work thoroughly investigates the possible existence of QSs with pressure anisotropy, emphasizing the interaction between strongly interacting quark matter and gravity's rainbow, where strongly interacting quark matter is considered. Focusing on understanding how these concepts affect the stability and detectability of QSs, and building upon recent theoretical works, we aim to gain a collective understanding of their fundamental properties. Inside these stars, the EoS strongly influences maximum mass and drives their internal structure, and it is susceptible to the strong interactions of quark matter. Conversely, Gravity's Rainbow alters the gravitational field at high energies, leading to modifications in compactness and, therefore, in the observational properties of the QSs. The theory of gravity and high matter interactions is varied in an attempt to study their combined effects on mass-radius relations, pulsar emissions, and gravitational wave signatures. Furthermore, it contributes to the knowledge of these constructs in broad astrophysics. This helps us even if we do not know the correct model yet, since it has some ideas for testing quantum gravity models in extreme astrophysical environments. In this work, we investigate the properties of QSs with modified parameters and anisotropic pressures within Gravity's Rainbow, focusing on their internal structure and stability in response to perturbations. Although the study by Zhang and Mann [25] provides a unified EoS for isotropic interacting quark matter (IQM) and discusses the corresponding QS solutions within general relativity, our work presents an important extension in two directions: First, we consider pressure anisotropy in the stellar matter configuration, which is physically motivated in ultra-dense regimes due to strong interaction effects, viscosity, or phase transitions; second, we introduce gravity's rainbow formalism by modifying spacetime geometry via energy-dependent rainbow functions that can capture possible Lorentz-violating effects at high energies. With this combined framework, we investigate how anisotropic pressures and quantum gravity-inspired corrections jointly impact the mass-radius relation, compactness, and stability criteria of quark stars, extending the description beyond what conventional isotropic models can achieve.
This paper is structured in the following manner: In Sec. II, we provide a detailed description of the perturbative QCD-motivated EoS, and the derivation of the modified Tolman-Oppenheimer-Volkoff (TOV) equations is also included. In Sec. III, we present the results of the numerical computation, illustrating the impact of the model parameters on the mass-radius relationships. Sec. IV comprehensively examines the static stability criterion, adiabatic index, and sound velocity. Finally, we discuss the results in Sec. V.
-
Detectable signals from mergers of compact stars, such as those involving black holes and neutron stars (NSs), provide insights into their internal composition and dynamic evolution, thereby opening a new avenue for astronomical outreach. Fortunately, the detection of binary NS (BNS) mergers by the LIGO-Virgo Collaboration and electromagnetic (EM) observer partners, such as GW170817 [1], has imposed new limitations on the maximum mass of NSs. In addition, it significantly influences our understanding of gravity, specifically, the physics of dense matter above
$ \sim $ 1-2$ n_0 $ ($ n_0 = 0.16 $ fm$ ^{-3} $ represents the nuclear saturation density). Therefore, accurately characterizing the equation of state (EOS) of dense matter is still challenging when attempting to infer the interior composition of NSs. Among the various proposed interior structures discussed in literature, the quark star (QS), which comprises quark matter, has emerged as a potential candidate. Therefore, QSs in such environments offer a platform for investigating high-density matter beyond nuclear saturation.Theoretically, quark matter (QM) treated as the true ground state of dense matter was proposed by E. Witten in 1984 [2] (following Bodmer's important precursor [3]). The hypothesis concerning QM and particularly strange QM consisting of u, d, and s quarks, also called strange quark matter (SQM), posits that it represents the most energetically favorable state of matter. However, some studies [4, 5] have explored the flavor-dependent effects of quark gas on the QCD vacuum, suggesting that
$ u, d $ quark matter ($ u{\rm d}\mathrm{QM} $ ) is typically more stable than SQM. Notably, at sufficiently high baryon numbers,$ u{\rm d}\mathrm{QM} $ can surpass the stability of ordinary nuclei and extend beyond the periodic table. This finding has led to an increase in recent experimental pursuits [6−8] and phenomenological research [9−14].Along these lines, the MIT bag model [15] has been widely employed by several authors to describe massive NSs, i.e., NSs with a quark matter core, which have been detected in the past decade [16−19]. A modified version of this model, incorporating vector interactions and drawing features from quantum hadrodynamics (QHD) [20], has also been proposed and applied to SQM and QSs [21−24]. Building on these developments, Zhang et al. [25] introduced an EoS for QM that incorporates perturbative quantum chromodynamics (QCD) (pQCD) corrections and color superconductivity. This model has the notable advantage of producing massive QSs with larger radii consistent with recent astrophysical constraints. An additional feature is that, through a single parameter, the EoS can be rescaled into a dimensionless form, thereby reducing the number of free parameters and characterizing the relative strength of strong interaction effects [26−28].
However, in the presence of enormous densities and pressures in the interiors of such stars, one can expect that the pressure could be anisotropic, with the radial pressure differing from that in the azimuthal directions. In addition to these nuclear interactions [29], viscosity effects [30], pion condensation [31], and some kinds of phase transitions [32] may contribute to the presence of pressure anisotropy. Considering local anisotropy, QSs or NSs have been studied to extract information regarding their internal structure and nuclear physics (see, e.g., [33−44]). These investigations suggest that pressure anisotropy has a significant influence on the mass-radius relationship and the internal properties of stars, including the maximum surface redshift and maximum compactness. Note that the presence of anisotropy influences the stability of the configuration by supporting outwardly increasing energy density within the star core [45].
The above discussion suggests that investigations of anisotropic systems are typically conducted within the framework of Einstein's theory of gravity. Here, we study the stability of anisotropic QSs in gravity's rainbow. Gravity's rainbow [46] has been treated as an extension of the principles of doubly special relativity (DSR) [47] to curved spacetimes. This theory suggests a modification of the spacetime metric by introducing energy-dependent rainbow functions,
$ \Xi(x) $ and$ \Sigma(x) $ , which are characterized by the dimensionless ratio of the total energy of the probe particle E to the Planck energy$ E_p $ . This approach helps alter the relativistic dispersion relations. It allows for a deeper understanding of the relation between quantum mechanics and general relativity at high energy scales, particularly near the Planck scale [48, 49]. By incorporating energy-dependent effects into curved spacetimes, gravity's rainbow attempts to address some of the conceptual issues, such as black hole solutions and their properties [50−55], gravastars, and wormhole solutions [56, 57]. Other intriguing findings in this context are the studies on dark star [58] and NSs [59], which also analyze their stability-related issues.In summary, this study thoroughly investigates the possible existence of QSs with pressure anisotropy, emphasizing the interaction between strongly interacting QM and gravity's rainbow, where strongly interacting QM is considered. Focusing on understanding how these concepts affect the stability and detectability of QSs, and building upon recent theoretical works, we aim to gain a collective understanding of their fundamental properties. Inside these stars, the EoS strongly influences maximum mass and drives their internal structure, and it is susceptible to the strong interactions of QM. Conversely, gravity's rainbow alters the gravitational field at high energies, leading to modifications in compactness and, therefore, in the observational properties of the QSs. The theory of gravity and high matter interactions is varied in an attempt to study their combined effects on mass-radius relations, pulsar emissions, and gravitational wave signatures. Furthermore, it contributes to the knowledge of these constructs in broad astrophysics. This helps us even if we do not know the correct model yet, as it has some ideas for testing quantum gravity models in extreme astrophysical environments. In this study, we investigate the properties of QSs with modified parameters and anisotropic pressures within gravity's rainbow, focusing on their internal structure and stability in response to perturbations. Although the study by Zhang and Mann [25] provides a unified EoS for isotropic interacting QM and discusses the corresponding QS solutions within general relativity, our study presents an important extension in two directions: First, we consider pressure anisotropy in the stellar matter configuration, which is physically motivated in ultra-dense regimes owing to strong interaction effects, viscosity, or phase transitions; second, we introduce the gravity's rainbow formalism by modifying spacetime geometry via energy-dependent rainbow functions that can capture possible Lorentz-violating effects at high energies. With this combined framework, we investigate how anisotropic pressures and quantum gravity-inspired corrections jointly influence the mass-radius relation, compactness, and stability criteria of QSs, extending the description beyond what conventional isotropic models can achieve.
The remainder of this paper is structured in the following manner. In Sec. II, we provide a detailed description of the perturbative QCD-motivated EoS, and the derivation of the modified Tolman-Oppenheimer-Volkoff (TOV) equations is also included. In Sec. III, we present the results of the numerical computation, illustrating the influence of the model parameters on the mass-radius relationships. Sec. IV comprehensively examines the static stability criterion, adiabatic index, and sound velocity. Finally, we discuss the results in Sec. V.
-
Detectable signals from mergers of compact stars, such as those involving black holes and neutron stars (NSs), provide insights into their internal composition and dynamic evolution, thereby opening a new avenue for astronomical outreach. Fortunately, the detection of binary NS (BNS) mergers by the LIGO-Virgo Collaboration and electromagnetic (EM) observer partners, such as GW170817 [1], has imposed new limitations on the maximum mass of NSs. In addition, it significantly influences our understanding of gravity, specifically, the physics of dense matter above
$ \sim $ 1-2$ n_0 $ ($ n_0 = 0.16 $ fm$ ^{-3} $ represents the nuclear saturation density). Therefore, accurately characterizing the equation of state (EOS) of dense matter is still challenging when attempting to infer the interior composition of NSs. Among the various proposed interior structures discussed in literature, the quark star (QS), which comprises quark matter, has emerged as a potential candidate. Therefore, QSs in such environments offer a platform for investigating high-density matter beyond nuclear saturation.Theoretically, quark matter (QM) treated as the true ground state of dense matter was proposed by E. Witten in 1984 [2] (following Bodmer's important precursor [3]). The hypothesis concerning QM and particularly strange QM consisting of u, d, and s quarks, also called strange quark matter (SQM), posits that it represents the most energetically favorable state of matter. However, some studies [4, 5] have explored the flavor-dependent effects of quark gas on the QCD vacuum, suggesting that
$ u, d $ quark matter ($ u{\rm d}\mathrm{QM} $ ) is typically more stable than SQM. Notably, at sufficiently high baryon numbers,$ u{\rm d}\mathrm{QM} $ can surpass the stability of ordinary nuclei and extend beyond the periodic table. This finding has led to an increase in recent experimental pursuits [6−8] and phenomenological research [9−14].Along these lines, the MIT bag model [15] has been widely employed by several authors to describe massive NSs, i.e., NSs with a quark matter core, which have been detected in the past decade [16−19]. A modified version of this model, incorporating vector interactions and drawing features from quantum hadrodynamics (QHD) [20], has also been proposed and applied to SQM and QSs [21−24]. Building on these developments, Zhang et al. [25] introduced an EoS for QM that incorporates perturbative quantum chromodynamics (QCD) (pQCD) corrections and color superconductivity. This model has the notable advantage of producing massive QSs with larger radii consistent with recent astrophysical constraints. An additional feature is that, through a single parameter, the EoS can be rescaled into a dimensionless form, thereby reducing the number of free parameters and characterizing the relative strength of strong interaction effects [26−28].
However, in the presence of enormous densities and pressures in the interiors of such stars, one can expect that the pressure could be anisotropic, with the radial pressure differing from that in the azimuthal directions. In addition to these nuclear interactions [29], viscosity effects [30], pion condensation [31], and some kinds of phase transitions [32] may contribute to the presence of pressure anisotropy. Considering local anisotropy, QSs or NSs have been studied to extract information regarding their internal structure and nuclear physics (see, e.g., [33−44]). These investigations suggest that pressure anisotropy has a significant influence on the mass-radius relationship and the internal properties of stars, including the maximum surface redshift and maximum compactness. Note that the presence of anisotropy influences the stability of the configuration by supporting outwardly increasing energy density within the star core [45].
The above discussion suggests that investigations of anisotropic systems are typically conducted within the framework of Einstein's theory of gravity. Here, we study the stability of anisotropic QSs in gravity's rainbow. Gravity's rainbow [46] has been treated as an extension of the principles of doubly special relativity (DSR) [47] to curved spacetimes. This theory suggests a modification of the spacetime metric by introducing energy-dependent rainbow functions,
$ \Xi(x) $ and$ \Sigma(x) $ , which are characterized by the dimensionless ratio of the total energy of the probe particle E to the Planck energy$ E_p $ . This approach helps alter the relativistic dispersion relations. It allows for a deeper understanding of the relation between quantum mechanics and general relativity at high energy scales, particularly near the Planck scale [48, 49]. By incorporating energy-dependent effects into curved spacetimes, gravity's rainbow attempts to address some of the conceptual issues, such as black hole solutions and their properties [50−55], gravastars, and wormhole solutions [56, 57]. Other intriguing findings in this context are the studies on dark star [58] and NSs [59], which also analyze their stability-related issues.In summary, this study thoroughly investigates the possible existence of QSs with pressure anisotropy, emphasizing the interaction between strongly interacting QM and gravity's rainbow, where strongly interacting QM is considered. Focusing on understanding how these concepts affect the stability and detectability of QSs, and building upon recent theoretical works, we aim to gain a collective understanding of their fundamental properties. Inside these stars, the EoS strongly influences maximum mass and drives their internal structure, and it is susceptible to the strong interactions of QM. Conversely, gravity's rainbow alters the gravitational field at high energies, leading to modifications in compactness and, therefore, in the observational properties of the QSs. The theory of gravity and high matter interactions is varied in an attempt to study their combined effects on mass-radius relations, pulsar emissions, and gravitational wave signatures. Furthermore, it contributes to the knowledge of these constructs in broad astrophysics. This helps us even if we do not know the correct model yet, as it has some ideas for testing quantum gravity models in extreme astrophysical environments. In this study, we investigate the properties of QSs with modified parameters and anisotropic pressures within gravity's rainbow, focusing on their internal structure and stability in response to perturbations. Although the study by Zhang and Mann [25] provides a unified EoS for isotropic interacting QM and discusses the corresponding QS solutions within general relativity, our study presents an important extension in two directions: First, we consider pressure anisotropy in the stellar matter configuration, which is physically motivated in ultra-dense regimes owing to strong interaction effects, viscosity, or phase transitions; second, we introduce the gravity's rainbow formalism by modifying spacetime geometry via energy-dependent rainbow functions that can capture possible Lorentz-violating effects at high energies. With this combined framework, we investigate how anisotropic pressures and quantum gravity-inspired corrections jointly influence the mass-radius relation, compactness, and stability criteria of QSs, extending the description beyond what conventional isotropic models can achieve.
The remainder of this paper is structured in the following manner. In Sec. II, we provide a detailed description of the perturbative QCD-motivated EoS, and the derivation of the modified Tolman-Oppenheimer-Volkoff (TOV) equations is also included. In Sec. III, we present the results of the numerical computation, illustrating the influence of the model parameters on the mass-radius relationships. Sec. IV comprehensively examines the static stability criterion, adiabatic index, and sound velocity. Finally, we discuss the results in Sec. V.
-
Detectable signals from mergers of compact stars, such as those involving black holes and neutron stars (NSs), provide insights into their internal composition and dynamic evolution, thereby opening a new avenue for astronomical outreach. Fortunately, the detection of binary NS (BNS) mergers by the LIGO-Virgo Collaboration and electromagnetic (EM) observer partners, such as GW170817 [1], has imposed new limitations on the maximum mass of NSs. In addition, it significantly influences our understanding of gravity, specifically, the physics of dense matter above
$ \sim $ 1-2$ n_0 $ ($ n_0 = 0.16 $ fm$ ^{-3} $ represents the nuclear saturation density). Therefore, accurately characterizing the equation of state (EOS) of dense matter is still challenging when attempting to infer the interior composition of NSs. Among the various proposed interior structures discussed in literature, the quark star (QS), which comprises quark matter, has emerged as a potential candidate. Therefore, QSs in such environments offer a platform for investigating high-density matter beyond nuclear saturation.Theoretically, quark matter (QM) treated as the true ground state of dense matter was proposed by E. Witten in 1984 [2] (following Bodmer's important precursor [3]). The hypothesis concerning QM and particularly strange QM consisting of u, d, and s quarks, also called strange quark matter (SQM), posits that it represents the most energetically favorable state of matter. However, some studies [4, 5] have explored the flavor-dependent effects of quark gas on the QCD vacuum, suggesting that
$ u, d $ quark matter ($ u{\rm d}\mathrm{QM} $ ) is typically more stable than SQM. Notably, at sufficiently high baryon numbers,$ u{\rm d}\mathrm{QM} $ can surpass the stability of ordinary nuclei and extend beyond the periodic table. This finding has led to an increase in recent experimental pursuits [6−8] and phenomenological research [9−14].Along these lines, the MIT bag model [15] has been widely employed by several authors to describe massive NSs, i.e., NSs with a quark matter core, which have been detected in the past decade [16−19]. A modified version of this model, incorporating vector interactions and drawing features from quantum hadrodynamics (QHD) [20], has also been proposed and applied to SQM and QSs [21−24]. Building on these developments, Zhang et al. [25] introduced an EoS for QM that incorporates perturbative quantum chromodynamics (QCD) (pQCD) corrections and color superconductivity. This model has the notable advantage of producing massive QSs with larger radii consistent with recent astrophysical constraints. An additional feature is that, through a single parameter, the EoS can be rescaled into a dimensionless form, thereby reducing the number of free parameters and characterizing the relative strength of strong interaction effects [26−28].
However, in the presence of enormous densities and pressures in the interiors of such stars, one can expect that the pressure could be anisotropic, with the radial pressure differing from that in the azimuthal directions. In addition to these nuclear interactions [29], viscosity effects [30], pion condensation [31], and some kinds of phase transitions [32] may contribute to the presence of pressure anisotropy. Considering local anisotropy, QSs or NSs have been studied to extract information regarding their internal structure and nuclear physics (see, e.g., [33−44]). These investigations suggest that pressure anisotropy has a significant influence on the mass-radius relationship and the internal properties of stars, including the maximum surface redshift and maximum compactness. Note that the presence of anisotropy influences the stability of the configuration by supporting outwardly increasing energy density within the star core [45].
The above discussion suggests that investigations of anisotropic systems are typically conducted within the framework of Einstein's theory of gravity. Here, we study the stability of anisotropic QSs in gravity's rainbow. Gravity's rainbow [46] has been treated as an extension of the principles of doubly special relativity (DSR) [47] to curved spacetimes. This theory suggests a modification of the spacetime metric by introducing energy-dependent rainbow functions,
$ \Xi(x) $ and$ \Sigma(x) $ , which are characterized by the dimensionless ratio of the total energy of the probe particle E to the Planck energy$ E_p $ . This approach helps alter the relativistic dispersion relations. It allows for a deeper understanding of the relation between quantum mechanics and general relativity at high energy scales, particularly near the Planck scale [48, 49]. By incorporating energy-dependent effects into curved spacetimes, gravity's rainbow attempts to address some of the conceptual issues, such as black hole solutions and their properties [50−55], gravastars, and wormhole solutions [56, 57]. Other intriguing findings in this context are the studies on dark star [58] and NSs [59], which also analyze their stability-related issues.In summary, this study thoroughly investigates the possible existence of QSs with pressure anisotropy, emphasizing the interaction between strongly interacting QM and gravity's rainbow, where strongly interacting QM is considered. Focusing on understanding how these concepts affect the stability and detectability of QSs, and building upon recent theoretical works, we aim to gain a collective understanding of their fundamental properties. Inside these stars, the EoS strongly influences maximum mass and drives their internal structure, and it is susceptible to the strong interactions of QM. Conversely, gravity's rainbow alters the gravitational field at high energies, leading to modifications in compactness and, therefore, in the observational properties of the QSs. The theory of gravity and high matter interactions is varied in an attempt to study their combined effects on mass-radius relations, pulsar emissions, and gravitational wave signatures. Furthermore, it contributes to the knowledge of these constructs in broad astrophysics. This helps us even if we do not know the correct model yet, as it has some ideas for testing quantum gravity models in extreme astrophysical environments. In this study, we investigate the properties of QSs with modified parameters and anisotropic pressures within gravity's rainbow, focusing on their internal structure and stability in response to perturbations. Although the study by Zhang and Mann [25] provides a unified EoS for isotropic interacting QM and discusses the corresponding QS solutions within general relativity, our study presents an important extension in two directions: First, we consider pressure anisotropy in the stellar matter configuration, which is physically motivated in ultra-dense regimes owing to strong interaction effects, viscosity, or phase transitions; second, we introduce the gravity's rainbow formalism by modifying spacetime geometry via energy-dependent rainbow functions that can capture possible Lorentz-violating effects at high energies. With this combined framework, we investigate how anisotropic pressures and quantum gravity-inspired corrections jointly influence the mass-radius relation, compactness, and stability criteria of QSs, extending the description beyond what conventional isotropic models can achieve.
The remainder of this paper is structured in the following manner. In Sec. II, we provide a detailed description of the perturbative QCD-motivated EoS, and the derivation of the modified Tolman-Oppenheimer-Volkoff (TOV) equations is also included. In Sec. III, we present the results of the numerical computation, illustrating the influence of the model parameters on the mass-radius relationships. Sec. IV comprehensively examines the static stability criterion, adiabatic index, and sound velocity. Finally, we discuss the results in Sec. V.
-
Current astronomical observations suggest that massive pulsars may have a core composed of QM rather than dense nuclear matter. Consequently, studying the internal properties of matter subjected to extreme conditions of density and temperature is an attractive area of research, along with identifying the associated EOS. This study uses the pQCD correction and color superconductivity to characterize the QM EoS, as outlined in Ref. [25]. The EoS can be rescaled into a dimensionless form, allowing it to depend on a single parameter. The rescaled procedure notably reduces the degrees of freedom, thereby enabling the relative size of strong interaction effects to be more accurately assessed. Thus, the EoS can be formulated as [25, 26]
$ P=\ \frac{1}{3}(\rho-4B_{{\rm{eff}}}) + \frac{4\lambda^2}{9\pi^2}\left[ -1+ {\rm sgn}(\lambda) \sqrt{1+3\pi^2 \frac{(\rho-B_{{\rm{eff}}})}{\lambda^2}} \right], $

(1) where ρ refers to the energy density associated with the homogeneously distributed QM, and P denotes the pressure variation along the radial direction. Here,
$ B_{{\rm{eff}}} $ is the effective bag constant, representing the non-perturbative contribution from the QCD vacuum; it acts as a confining pressure that stabilizes QM and, in general, may be flavor-dependent [25]. An additional significant quantity is$ {\rm sgn}(\lambda) $ , denoting the sign of λ,$ \lambda=\frac{\xi_{2a} \Delta^2-\xi_{2b} m_s^2}{\sqrt{\xi_4 a_4}}, $

(2) where
$ m_s $ denotes the mass of the strange quark, and Δ represents the gap parameter. Color superconductivity is a phase of cold, dense QM in which quarks form Cooper-like pairs owing to attractive strong interactions, analogous to electron pairing in conventional superconductors. This pairing modifies the EoS, enhancing the stiffness of QM and significantly influencing the macroscopic structure of QSs [60]. Moreover, the quartic coefficient$ a_4 $ can vary within the range$ a_4 \in (0,1) $ owing to pQCD contributions, whereas$ a_4 =1 $ denotes the case of noninteracting quarks. In this case,$ {\rm sgn}(\lambda) $ denotes the sign of λ with a positive value when$ \Delta^2/m_s^2>\xi_{2b}/\xi_{2a} $ . The constant coefficients in λ are$ \begin{array}{*{20}{l}} (\xi_4,\xi_{2a}, \xi_{2b}) =\\ \left\{ \begin{array} {ll} \Bigg(\Bigg( \left(\dfrac{1}{3}\right)^{\frac{4}{3}}+ \left(\dfrac{2}{3}\right)^{\frac{4}{3}}\Bigg)^{-3},1,0\Bigg), & \rm{2SC phase},\\ (3,1,3/4), & \rm{2SC+s phase},\\ (3,3,3/4),& \rm{CFL phase}. \end{array} \right. \end{array} $

In the present analysis, we restrict our attention to the positive λ space, which is favored by astrophysical models and observational findings [25, 61]. In this scenario, to eliminate the effective bag constant
$ B_{{\rm{eff}}} $ , we apply a dimensionless rescaling as proposed in [25],$ \bar{\lambda}=\frac{\lambda^2}{4B_{{\rm{eff}}}}= \frac{(\xi_{2a} \Delta^2-\xi_{2b} m_s^2)^2}{4\,B_{{\rm{eff}}}\xi_4 a_4}, $

(3) and
$ \bar{\rho} =\frac{\rho}{4\,B_{{\rm{eff}}}}, \; \; \bar{P} =\frac{P}{4\,B_{{\rm{eff}}}}, $

(4) thus introducing Eqs. (3) and (4) in Eq. (1), we have the following dimensionless form:
$ \bar{P} =\ \frac{1}{3}(\bar{\rho}-1) + \frac{4\bar{\lambda}}{9\pi^2} \left[-1+ \sqrt{1+ \frac{3\pi^2}{\bar{\lambda}} \left(\bar{\rho}-\frac{1}{4}\right)}\right] . $

(5) When examining the scenario where
$ \bar{\lambda} \to 0 $ , we can obtain the rescaled conventional noninteracting QM EoS represented by$ \bar{P}=\dfrac{1}{3}(\bar{\rho}-1) $ . In contrast, for extremely large positive values of$ \bar{\lambda} $ , the above expression has the following form:$ \bar{P}\vert_{\bar{\lambda}\to \infty}=\bar{\rho}-\frac{1}{2}. $

(6) or, equivalently,
$ P={\rho}-2B_{{\rm{eff}}} $ , using Eq. (4). According to Refs. [25, 26], positive increasing values of$ \bar{\lambda} $ result in a stiffer EoS, whereas$ \bar{\lambda} =0 $ represents noninteracting QM. The regularized$ 4D $ Einstein Gauss-Bonnet theory of gravity was also examined; for further information, see Refs. [28, 62]. -
Current astronomical observations suggest that massive pulsars may have a core composed of QM rather than dense nuclear matter. Consequently, studying the internal properties of matter subjected to extreme conditions of density and temperature is an attractive area of research, along with identifying the associated EOS. This study uses the pQCD correction and color superconductivity to characterize the QM EoS, as outlined in Ref. [25]. The EoS can be rescaled into a dimensionless form, allowing it to depend on a single parameter. The rescaled procedure notably reduces the degrees of freedom, thereby enabling the relative size of strong interaction effects to be more accurately assessed. Thus, the EoS can be formulated as [25, 26]
$ P=\ \frac{1}{3}(\rho-4B_{{\rm{eff}}}) + \frac{4\lambda^2}{9\pi^2}\left[ -1+ {\rm sgn}(\lambda) \sqrt{1+3\pi^2 \frac{(\rho-B_{{\rm{eff}}})}{\lambda^2}} \right], $

(1) where ρ refers to the energy density associated with the homogeneously distributed QM, and P denotes the pressure variation along the radial direction. Here,
$ B_{{\rm{eff}}} $ is the effective bag constant, representing the non-perturbative contribution from the QCD vacuum; it acts as a confining pressure that stabilizes QM and, in general, may be flavor-dependent [25]. An additional significant quantity is$ {\rm sgn}(\lambda) $ , denoting the sign of λ,$ \lambda=\frac{\xi_{2a} \Delta^2-\xi_{2b} m_s^2}{\sqrt{\xi_4 a_4}}, $

(2) where
$ m_s $ denotes the mass of the strange quark, and Δ represents the gap parameter. Color superconductivity is a phase of cold, dense QM in which quarks form Cooper-like pairs owing to attractive strong interactions, analogous to electron pairing in conventional superconductors. This pairing modifies the EoS, enhancing the stiffness of QM and significantly influencing the macroscopic structure of QSs [60]. Moreover, the quartic coefficient$ a_4 $ can vary within the range$ a_4 \in (0,1) $ owing to pQCD contributions, whereas$ a_4 =1 $ denotes the case of noninteracting quarks. In this case,$ {\rm sgn}(\lambda) $ denotes the sign of λ with a positive value when$ \Delta^2/m_s^2>\xi_{2b}/\xi_{2a} $ . The constant coefficients in λ are$ \begin{array}{*{20}{l}} (\xi_4,\xi_{2a}, \xi_{2b}) =\\ \left\{ \begin{array} {ll} \Bigg(\Bigg( \left(\dfrac{1}{3}\right)^{\frac{4}{3}}+ \left(\dfrac{2}{3}\right)^{\frac{4}{3}}\Bigg)^{-3},1,0\Bigg), & \rm{2SC phase},\\ (3,1,3/4), & \rm{2SC+s phase},\\ (3,3,3/4),& \rm{CFL phase}. \end{array} \right. \end{array} $

In the present analysis, we restrict our attention to the positive λ space, which is favored by astrophysical models and observational findings [25, 61]. In this scenario, to eliminate the effective bag constant
$ B_{{\rm{eff}}} $ , we apply a dimensionless rescaling as proposed in [25],$ \bar{\lambda}=\frac{\lambda^2}{4B_{{\rm{eff}}}}= \frac{(\xi_{2a} \Delta^2-\xi_{2b} m_s^2)^2}{4\,B_{{\rm{eff}}}\xi_4 a_4}, $

(3) and
$ \bar{\rho} =\frac{\rho}{4\,B_{{\rm{eff}}}}, \; \; \bar{P} =\frac{P}{4\,B_{{\rm{eff}}}}, $

(4) thus introducing Eqs. (3) and (4) in Eq. (1), we have the following dimensionless form:
$ \bar{P} =\ \frac{1}{3}(\bar{\rho}-1) + \frac{4\bar{\lambda}}{9\pi^2} \left[-1+ \sqrt{1+ \frac{3\pi^2}{\bar{\lambda}} \left(\bar{\rho}-\frac{1}{4}\right)}\right] . $

(5) When examining the scenario where
$ \bar{\lambda} \to 0 $ , we can obtain the rescaled conventional noninteracting QM EoS represented by$ \bar{P}=\dfrac{1}{3}(\bar{\rho}-1) $ . In contrast, for extremely large positive values of$ \bar{\lambda} $ , the above expression has the following form:$ \bar{P}\vert_{\bar{\lambda}\to \infty}=\bar{\rho}-\frac{1}{2}. $

(6) or, equivalently,
$ P={\rho}-2B_{{\rm{eff}}} $ , using Eq. (4). According to Refs. [25, 26], positive increasing values of$ \bar{\lambda} $ result in a stiffer EoS, whereas$ \bar{\lambda} =0 $ represents noninteracting QM. The regularized$ 4D $ Einstein Gauss-Bonnet theory of gravity was also examined; for further information, see Refs. [28, 62]. -
Current astronomical observations suggest that massive pulsars may have a core composed of QM rather than dense nuclear matter. Consequently, studying the internal properties of matter subjected to extreme conditions of density and temperature is an attractive area of research, along with identifying the associated EOS. This study uses the pQCD correction and color superconductivity to characterize the QM EoS, as outlined in Ref. [25]. The EoS can be rescaled into a dimensionless form, allowing it to depend on a single parameter. The rescaled procedure notably reduces the degrees of freedom, thereby enabling the relative size of strong interaction effects to be more accurately assessed. Thus, the EoS can be formulated as [25, 26]
$ P=\ \frac{1}{3}(\rho-4B_{{\rm{eff}}}) + \frac{4\lambda^2}{9\pi^2}\left[ -1+ {\rm sgn}(\lambda) \sqrt{1+3\pi^2 \frac{(\rho-B_{{\rm{eff}}})}{\lambda^2}} \right], $

(1) where ρ refers to the energy density associated with the homogeneously distributed QM, and P denotes the pressure variation along the radial direction. Here,
$ B_{{\rm{eff}}} $ is the effective bag constant, representing the non-perturbative contribution from the QCD vacuum; it acts as a confining pressure that stabilizes QM and, in general, may be flavor-dependent [25]. An additional significant quantity is$ {\rm sgn}(\lambda) $ , denoting the sign of λ,$ \lambda=\frac{\xi_{2a} \Delta^2-\xi_{2b} m_s^2}{\sqrt{\xi_4 a_4}}, $

(2) where
$ m_s $ denotes the mass of the strange quark, and Δ represents the gap parameter. Color superconductivity is a phase of cold, dense QM in which quarks form Cooper-like pairs owing to attractive strong interactions, analogous to electron pairing in conventional superconductors. This pairing modifies the EoS, enhancing the stiffness of QM and significantly influencing the macroscopic structure of QSs [60]. Moreover, the quartic coefficient$ a_4 $ can vary within the range$ a_4 \in (0,1) $ owing to pQCD contributions, whereas$ a_4 =1 $ denotes the case of noninteracting quarks. In this case,$ {\rm sgn}(\lambda) $ denotes the sign of λ with a positive value when$ \Delta^2/m_s^2>\xi_{2b}/\xi_{2a} $ . The constant coefficients in λ are$ \begin{array}{*{20}{l}} (\xi_4,\xi_{2a}, \xi_{2b}) =\\ \left\{ \begin{array} {ll} \Bigg(\Bigg( \left(\dfrac{1}{3}\right)^{\frac{4}{3}}+ \left(\dfrac{2}{3}\right)^{\frac{4}{3}}\Bigg)^{-3},1,0\Bigg), & \rm{2SC phase},\\ (3,1,3/4), & \rm{2SC+s phase},\\ (3,3,3/4),& \rm{CFL phase}. \end{array} \right. \end{array} $

In the present analysis, we restrict our attention to the positive λ space, which is favored by astrophysical models and observational findings [25, 61]. In this scenario, to eliminate the effective bag constant
$ B_{{\rm{eff}}} $ , we apply a dimensionless rescaling as proposed in [25],$ \bar{\lambda}=\frac{\lambda^2}{4B_{{\rm{eff}}}}= \frac{(\xi_{2a} \Delta^2-\xi_{2b} m_s^2)^2}{4\,B_{{\rm{eff}}}\xi_4 a_4}, $

(3) and
$ \bar{\rho} =\frac{\rho}{4\,B_{{\rm{eff}}}}, \; \; \bar{P} =\frac{P}{4\,B_{{\rm{eff}}}}, $

(4) thus introducing Eqs. (3) and (4) in Eq. (1), we have the following dimensionless form:
$ \bar{P} =\ \frac{1}{3}(\bar{\rho}-1) + \frac{4\bar{\lambda}}{9\pi^2} \left[-1+ \sqrt{1+ \frac{3\pi^2}{\bar{\lambda}} \left(\bar{\rho}-\frac{1}{4}\right)}\right] . $

(5) When examining the scenario where
$ \bar{\lambda} \to 0 $ , we can obtain the rescaled conventional noninteracting QM EoS represented by$ \bar{P}=\dfrac{1}{3}(\bar{\rho}-1) $ . In contrast, for extremely large positive values of$ \bar{\lambda} $ , the above expression has the following form:$ \bar{P}\vert_{\bar{\lambda}\to \infty}=\bar{\rho}-\frac{1}{2}. $

(6) or, equivalently,
$ P={\rho}-2B_{{\rm{eff}}} $ , using Eq. (4). According to Refs. [25, 26], positive increasing values of$ \bar{\lambda} $ result in a stiffer EoS, whereas$ \bar{\lambda} =0 $ represents noninteracting QM. The regularized$ 4D $ Einstein Gauss-Bonnet theory of gravity was also examined; for further information, see Refs. [28, 62]. -
Current astronomical observations suggest that massive pulsars may have a core composed of quark matter rather than dense nuclear matter. As a result, studying the internal properties of matter subjected to extreme conditions of density and temperature is an attractive area of research, along with identifying the associated EOS. This article will use the perturbative QCD (pQCD) correction and color superconductivity to characterise the QM EoS, as outlined in Ref. [25]. The EoS can be rescaled into a dimensionless form, allowing it to depend on a single parameter. The rescaled procedure notably reduces the degrees of freedom, thereby allowing for the relative size of strong interaction effects to be more accurately assessed. Taking this into account, the EoS can be formulated as [25, 26]:
$ P=\ \frac{1}{3}(\rho-4B_{{\rm{eff}}}) + \frac{4\lambda^2}{9\pi^2}\left[ -1+ {\rm sgn}(\lambda) \sqrt{1+3\pi^2 \frac{(\rho-B_{{\rm{eff}}})}{\lambda^2}} \right], $

(1) where ρ refers to the energy density associated with the homogeneously distributed QM, and P denotes the pressure variation along the radial direction. Here,
$ B_{{\rm{eff}}} $ is the effective bag constant, representing the non-perturbative contribution from the QCD vacuum; it acts as a confining pressure that stabilizes quark matter and, in general, may be flavor-dependent [25]. An additional significant quantity is the$ {\rm sgn}(\lambda) $ , denoting the sign of λ,$ \lambda=\frac{\xi_{2a} \Delta^2-\xi_{2b} m_s^2}{\sqrt{\xi_4 a_4}}, $

(2) where
$ m_s $ denotes the mass of the strange quark and Δ represents the gap parameter. Color superconductivity is a phase of cold, dense quark matter in which quarks form Cooper-like pairs due to attractive strong interactions, analogous to electron pairing in conventional superconductors. This pairing modifies the equation of state, enhancing the stiffness of quark matter and significantly influencing the macroscopic structure of quark stars [61]. Moreover, the quartic coefficient$ a_4 $ can change within the range$ a_4 \in (0,1) $ due to pQCD contributions, while$ a_4 =1 $ denotes the case of noninteracting quarks. In this case,$ {\rm sgn}(\lambda) $ denotes the sign of λ with a positive value when$ \Delta^2/m_s^2>\xi_{2b}/\xi_{2a} $ . The constant coefficients in λ are$ \begin{array}{*{20}{l}} (\xi_4,\xi_{2a}, \xi_{2b}) =\\ \left\{ \begin{array} {ll} \Bigg(\Bigg( \left(\dfrac{1}{3}\right)^{\frac{4}{3}}+ \left(\dfrac{2}{3}\right)^{\frac{4}{3}}\Bigg)^{-3},1,0\Bigg) & \rm{2SC phase}\\ (3,1,3/4) & \rm{2SC+s phase}\\ (3,3,3/4)& \rm{CFL phase} \end{array} \right. \end{array} $

In the present analysis, we restrict our attention to the positive λ space, which is favored by astrophysical models and observational findings [25, 62]. In this scenario, to eliminate the effective bag constant
$ B_{{\rm{eff}}} $ , we apply a dimensionless rescaling as proposed in [25],$ \bar{\lambda}=\frac{\lambda^2}{4B_{{\rm{eff}}}}= \frac{(\xi_{2a} \Delta^2-\xi_{2b} m_s^2)^2}{4\,B_{{\rm{eff}}}\xi_4 a_4}, $

(3) and
$ \bar{\rho} =\frac{\rho}{4\,B_{{\rm{eff}}}}, \; \; \bar{P} =\frac{P}{4\,B_{{\rm{eff}}}}, $

(4) thus introducing (3) and (4) in Eq. (1), we have the following dimensionless form:
$ \bar{P} =\ \frac{1}{3}(\bar{\rho}-1) + \frac{4\bar{\lambda}}{9\pi^2} \left[-1+ \sqrt{1+ \frac{3\pi^2}{\bar{\lambda}} \left(\bar{\rho}-\frac{1}{4}\right)}\right] . $

(5) When examining the scenario where
$ \bar{\lambda} \to 0 $ , we can obtain the rescaled conventional noninteracting QM EoS represented by$ \bar{P}=\dfrac{1}{3}(\bar{\rho}-1) $ . In contrast, for extremely large positive values of$ \bar{\lambda} $ , the above expression has the following form$ \bar{P}\vert_{\bar{\lambda}\to \infty}=\bar{\rho}-\frac{1}{2}. $

(6) or, equivalently,
$ P={\rho}-2B_{{\rm{eff}}} $ , using Eq. (4). According to Ref. [25, 26], it was noted that for positive increasing values of$ \bar{\lambda} $ result in stiffer EoS, while$ \bar{\lambda} =0 $ represents noninteracting QM. The regularized$ 4D $ Einstein Gauss-Bonnet theory of gravity was also examined; for further information, see Ref. [28, 29]. -
In this section, we derive the equations of hydrostatic equilibrium in rainbow gravity, assuming a static,
$ 4D $ spherically symmetric metric that is substituted with a rainbow metric represented as follows: [46],$ {\rm d}s^{2} = -\frac{{\rm e}^{2\Phi(r)}}{\Xi^{2}(x)}\, {\rm d}t^{2} + \frac{{\rm e}^{2\lambda(r)}}{\Sigma^{2}(x)}\, {\rm d}r^{2} + \frac{r^{2}}{\Sigma^{2}(x)}\, {\rm d}\Omega^{2}, $

(7) where
$ \Phi(r) $ and$ \lambda(r) $ are radial functions to be determined, and$ {\rm d}\Omega^{2} = {\rm d}\theta^{2} + \sin^{2}\theta\, {\rm d}\phi^{2} $ denotes the metric on the unit 2-sphere. The rainbow functions$ \Xi(x) $ and$ \Sigma(x) $ depend only on the dimensionless ratio$ x = E/E_{p} $ , with E denoting the total energy of the particle and$ E_{p} $ the Planck energy, defined as$ E_{p} = \sqrt{\hbar c^{5}/G} $ . They are independent of the spacetime coordinates$ (t,r,\theta,\phi) $ .Motivated by [63, 64], we explore the possible existence of a QS with anisotropic pressure in the context of rainbow gravity. Therefore, we define the fluid in the matter sector as locally anisotropic and express the energy-momentum tensor as follows:
$ \begin{array}{*{20}{l}} T_{\mu\nu}=(\rho+P_{\perp})u_\mu u_\nu+ P_{\perp} g_{\mu\nu}+\left(P-P_{\perp}\right)\chi_{\mu}\chi_{\nu}, \end{array} $

(8) where
$ u^\mu $ denotes the (timelike) 4-velocity of the fluid, and$ \chi_{\mu} $ represents a unit radial vector that fulfills$ \chi_{\mu} \chi^{\mu} = 1 $ . Indeed, P denotes the radial pressure, and$ P_{\perp} $ represents the transverse pressure. Furthermore, we express the generalized EoS for the tangential pressure as follows [63]:$ \begin{aligned}[b] P_{\perp}=\;& P_c +\dfrac{1}{3}\left(\rho-4B_{{\rm{eff}}, \perp}\right) \\&+ \frac{4\lambda_{\perp}^2}{9\pi^2}\left[ -1+\sqrt{1+3\pi^2 \frac{(\rho-B_{{\rm{eff}}, \perp})}{\lambda_{\perp}^2}} \right] \\ & -\dfrac{1}{3}\left(\rho_c-4B_{{\rm{eff}}, \perp}\right) \\&- \frac{4\lambda_{\perp}^2}{9\pi^2}\left[ -1+\sqrt{1+3\pi^2 \frac{(\rho_c-B_{{\rm{eff}}, \perp})}{\lambda_{\perp}^2}} \right], \end{aligned} $

(9) where
$ P_c $ and$ \rho_c $ in Eq. (9) represent the radial pressure (Eq. (5)) and energy density, respectively, at the center of the star. At the core of the star, specifically at$ r=0 $ , it is observed that the radial and tangential pressures are equivalent when the conditions$ B_{\rm{eff}} = B_{\rm{eff}}, \perp $ and$ \lambda=\lambda_{\perp} $ are satisfied. This condition indicates that the fluid attains isotropy at the center of the star. Additionally, the parameters$ B_{\rm{eff}}, \perp $ and$ \lambda_{\perp} $ contribute to the tangential pressure and are within the same value ranges as$ B_{{\rm{eff}}} $ and λ, respectively. Note that, in this setup, the parameters for the radial and tangential directions, written as λ and$ \lambda_\perp $ , respectively, are allowed to differ. This does not imply that the underlying microscopic physics changes with direction; rather, it provides a way to capture how strong interactions, possible phase transitions, or collective stresses might manifest as anisotropic behavior. At the stellar center, we impose$ \lambda=\lambda_\perp $ , thereby restoring isotropy, whereas controlled deviations arise only away from the center. In this sense, the construction is analogous in spirit to other anisotropy models considered in literature. Still, here it is cast in a more compact and microphysically motivated form, naturally embedded within the gravity’s rainbow framework. In contrast to the commonly used Bowers–Liang [65] or quasi-local models [45], which introduce anisotropy through externally prescribed stress profiles$ \Delta(r) $ , our formulation emerges as a direct extension of the interacting QM EoS. This approach naturally permits distinct couplings for radial and tangential pressures, while ensuring isotropy at the center, thereby providing a consistent way to incorporate strong-interaction corrections. Further, we remove the$ B_{{\rm{eff}}, \perp} $ parameter by applying dimensionless rescaling as follows:$ \bar{P}_\perp =\frac{P_\perp}{4\,B_{{\rm{eff}}}}, \; \bar{\lambda}_{\perp}=\frac{\lambda^2_{\perp}}{4B_{{\rm{eff}}}} \; \text{and}\; \bar{B} = \frac{B_{{\rm{eff}}, \perp}}{B_{{\rm{eff}}}}, $

(10) and ultimately, we obtain the pressure in the transverse direction in the following dimensionless form:
$ \begin{aligned}[b] \bar{P}_{\perp} =\;& \bar{P}_{c} + \frac{1}{3}(\bar{\rho} - \bar{B}) \\&+ \frac{4\bar{\lambda}_{\perp}}{9\pi^2} \left[-1+ \sqrt{1+ \frac{3\pi^2}{\bar{\lambda}_{\perp}} \left(\bar{\rho}-\frac{\bar{B}}{4}\right)}\right] \\ & -\frac{1}{3}(\bar{\rho}_{c} - \bar{B}) - \frac{4\bar{\lambda}_{\perp}}{9\pi^2} \left[-1+ \sqrt{1+ \frac{3\pi^2}{\bar{\lambda}_{\perp}} \left(\bar{\rho}_{c}-\frac{\bar{B}}{4}\right)}\right]. \end{aligned} $

(11) Here, we rescale the mass and radius into a dimensionless form,
$ \begin{array}{*{20}{l}} \bar{m} = m \sqrt{{4\,B_{{\rm{eff}}}}} \; ~{\rm and}~\; \bar{r} = r \sqrt{{4\,B_{{\rm{eff}}}}}\; . \end{array} $

(12) Here, the parameters are rescaled with respect to the effective bag constant, which sets the natural energy scale of the QM system. This rescaling reduces the number of free parameters and allows the EoS to be cast in a compact dimensionless form. It also ensures that the formulation connects smoothly to the standard GR limit in the absence of rainbow corrections, while retaining the effects of strong interactions in a controlled manner. Finally, using Eqs. (7) and (8), the modified TOV equations are [46, 59] (we work with natural units
$ G = \hslash= c = 1 $ )$ M_{\rm{eff}}(r, x)= \int^{r}_{0} \frac{4 \pi r^2 \rho(r)}{\Sigma^{2}(x)} {\rm d}r \equiv \frac{m(r)}{\Sigma^{2}(x)}, $

(13) $ P' = -(\rho+P_{r})\Phi'+ \frac{2}{r}\left(P_{\bot}-P\right), $

(14) $ \Phi'(r)=\frac{M_{\rm{eff}}(r, x) \Sigma^{2}(x)+4\pi r^3 P}{r\left(r-2M_{\rm{eff}}(r, x) \right)\Sigma^{2}(x)}, $

(15) where the prime denotes the derivative with respect to the radial coordinate r. We can also transform it into a dimensionless form by substituting the non-barred symbols with their corresponding barred counterparts. Note that the normal relation
$ (M, R) $ can be recovered by introducing$ (M, R) $ =$ (\bar{M}/ \sqrt{{4\,B_{{\rm{eff}}}}}, \bar{R}/ \sqrt{{4\,B_{{\rm{eff}}}}}) $ , and we present$ M-R $ relations in normalized form. -
In this section, we derive the equations of hydrostatic equilibrium in rainbow gravity, assuming a static,
$ 4D $ spherically symmetric metric that is substituted with a rainbow metric represented as follows: [46],$ {\rm d}s^{2} = -\frac{{\rm e}^{2\Phi(r)}}{\Xi^{2}(x)}\, {\rm d}t^{2} + \frac{{\rm e}^{2\lambda(r)}}{\Sigma^{2}(x)}\, {\rm d}r^{2} + \frac{r^{2}}{\Sigma^{2}(x)}\, {\rm d}\Omega^{2}, $

(7) where
$ \Phi(r) $ and$ \lambda(r) $ are radial functions to be determined, and$ {\rm d}\Omega^{2} = {\rm d}\theta^{2} + \sin^{2}\theta\, {\rm d}\phi^{2} $ denotes the metric on the unit 2-sphere. The rainbow functions$ \Xi(x) $ and$ \Sigma(x) $ depend only on the dimensionless ratio$ x = E/E_{p} $ , with E denoting the total energy of the particle and$ E_{p} $ the Planck energy, defined as$ E_{p} = \sqrt{\hbar c^{5}/G} $ . They are independent of the spacetime coordinates$ (t,r,\theta,\phi) $ .Motivated by [63, 64], we explore the possible existence of a QS with anisotropic pressure in the context of rainbow gravity. Therefore, we define the fluid in the matter sector as locally anisotropic and express the energy-momentum tensor as follows:
$ \begin{array}{*{20}{l}} T_{\mu\nu}=(\rho+P_{\perp})u_\mu u_\nu+ P_{\perp} g_{\mu\nu}+\left(P-P_{\perp}\right)\chi_{\mu}\chi_{\nu}, \end{array} $

(8) where
$ u^\mu $ denotes the (timelike) 4-velocity of the fluid, and$ \chi_{\mu} $ represents a unit radial vector that fulfills$ \chi_{\mu} \chi^{\mu} = 1 $ . Indeed, P denotes the radial pressure, and$ P_{\perp} $ represents the transverse pressure. Furthermore, we express the generalized EoS for the tangential pressure as follows [63]:$ \begin{aligned}[b] P_{\perp}=\;& P_c +\dfrac{1}{3}\left(\rho-4B_{{\rm{eff}}, \perp}\right) \\&+ \frac{4\lambda_{\perp}^2}{9\pi^2}\left[ -1+\sqrt{1+3\pi^2 \frac{(\rho-B_{{\rm{eff}}, \perp})}{\lambda_{\perp}^2}} \right] \\ & -\dfrac{1}{3}\left(\rho_c-4B_{{\rm{eff}}, \perp}\right) \\&- \frac{4\lambda_{\perp}^2}{9\pi^2}\left[ -1+\sqrt{1+3\pi^2 \frac{(\rho_c-B_{{\rm{eff}}, \perp})}{\lambda_{\perp}^2}} \right], \end{aligned} $

(9) where
$ P_c $ and$ \rho_c $ in Eq. (9) represent the radial pressure (Eq. (5)) and energy density, respectively, at the center of the star. At the core of the star, specifically at$ r=0 $ , it is observed that the radial and tangential pressures are equivalent when the conditions$ B_{\rm{eff}} = B_{\rm{eff}}, \perp $ and$ \lambda=\lambda_{\perp} $ are satisfied. This condition indicates that the fluid attains isotropy at the center of the star. Additionally, the parameters$ B_{\rm{eff}}, \perp $ and$ \lambda_{\perp} $ contribute to the tangential pressure and are within the same value ranges as$ B_{{\rm{eff}}} $ and λ, respectively. Note that, in this setup, the parameters for the radial and tangential directions, written as λ and$ \lambda_\perp $ , respectively, are allowed to differ. This does not imply that the underlying microscopic physics changes with direction; rather, it provides a way to capture how strong interactions, possible phase transitions, or collective stresses might manifest as anisotropic behavior. At the stellar center, we impose$ \lambda=\lambda_\perp $ , thereby restoring isotropy, whereas controlled deviations arise only away from the center. In this sense, the construction is analogous in spirit to other anisotropy models considered in literature. Still, here it is cast in a more compact and microphysically motivated form, naturally embedded within the gravity’s rainbow framework. In contrast to the commonly used Bowers–Liang [65] or quasi-local models [45], which introduce anisotropy through externally prescribed stress profiles$ \Delta(r) $ , our formulation emerges as a direct extension of the interacting QM EoS. This approach naturally permits distinct couplings for radial and tangential pressures, while ensuring isotropy at the center, thereby providing a consistent way to incorporate strong-interaction corrections. Further, we remove the$ B_{{\rm{eff}}, \perp} $ parameter by applying dimensionless rescaling as follows:$ \bar{P}_\perp =\frac{P_\perp}{4\,B_{{\rm{eff}}}}, \; \bar{\lambda}_{\perp}=\frac{\lambda^2_{\perp}}{4B_{{\rm{eff}}}} \; \text{and}\; \bar{B} = \frac{B_{{\rm{eff}}, \perp}}{B_{{\rm{eff}}}}, $

(10) and ultimately, we obtain the pressure in the transverse direction in the following dimensionless form:
$ \begin{aligned}[b] \bar{P}_{\perp} =\;& \bar{P}_{c} + \frac{1}{3}(\bar{\rho} - \bar{B}) \\&+ \frac{4\bar{\lambda}_{\perp}}{9\pi^2} \left[-1+ \sqrt{1+ \frac{3\pi^2}{\bar{\lambda}_{\perp}} \left(\bar{\rho}-\frac{\bar{B}}{4}\right)}\right] \\ & -\frac{1}{3}(\bar{\rho}_{c} - \bar{B}) - \frac{4\bar{\lambda}_{\perp}}{9\pi^2} \left[-1+ \sqrt{1+ \frac{3\pi^2}{\bar{\lambda}_{\perp}} \left(\bar{\rho}_{c}-\frac{\bar{B}}{4}\right)}\right]. \end{aligned} $

(11) Here, we rescale the mass and radius into a dimensionless form,
$ \begin{array}{*{20}{l}} \bar{m} = m \sqrt{{4\,B_{{\rm{eff}}}}} \; ~{\rm and}~\; \bar{r} = r \sqrt{{4\,B_{{\rm{eff}}}}}\; . \end{array} $

(12) Here, the parameters are rescaled with respect to the effective bag constant, which sets the natural energy scale of the QM system. This rescaling reduces the number of free parameters and allows the EoS to be cast in a compact dimensionless form. It also ensures that the formulation connects smoothly to the standard GR limit in the absence of rainbow corrections, while retaining the effects of strong interactions in a controlled manner. Finally, using Eqs. (7) and (8), the modified TOV equations are [46, 59] (we work with natural units
$ G = \hslash= c = 1 $ )$ M_{\rm{eff}}(r, x)= \int^{r}_{0} \frac{4 \pi r^2 \rho(r)}{\Sigma^{2}(x)} {\rm d}r \equiv \frac{m(r)}{\Sigma^{2}(x)}, $

(13) $ P' = -(\rho+P_{r})\Phi'+ \frac{2}{r}\left(P_{\bot}-P\right), $

(14) $ \Phi'(r)=\frac{M_{\rm{eff}}(r, x) \Sigma^{2}(x)+4\pi r^3 P}{r\left(r-2M_{\rm{eff}}(r, x) \right)\Sigma^{2}(x)}, $

(15) where the prime denotes the derivative with respect to the radial coordinate r. We can also transform it into a dimensionless form by substituting the non-barred symbols with their corresponding barred counterparts. Note that the normal relation
$ (M, R) $ can be recovered by introducing$ (M, R) $ =$ (\bar{M}/ \sqrt{{4\,B_{{\rm{eff}}}}}, \bar{R}/ \sqrt{{4\,B_{{\rm{eff}}}}}) $ , and we present$ M-R $ relations in normalized form. -
In this section, we derive the equations of hydrostatic equilibrium in rainbow gravity, assuming a static,
$ 4D $ spherically symmetric metric that is substituted with a rainbow metric represented as follows: [46],$ {\rm d}s^{2} = -\frac{{\rm e}^{2\Phi(r)}}{\Xi^{2}(x)}\, {\rm d}t^{2} + \frac{{\rm e}^{2\lambda(r)}}{\Sigma^{2}(x)}\, {\rm d}r^{2} + \frac{r^{2}}{\Sigma^{2}(x)}\, {\rm d}\Omega^{2}, $

(7) where
$ \Phi(r) $ and$ \lambda(r) $ are radial functions to be determined, and$ {\rm d}\Omega^{2} = {\rm d}\theta^{2} + \sin^{2}\theta\, {\rm d}\phi^{2} $ denotes the metric on the unit 2-sphere. The rainbow functions$ \Xi(x) $ and$ \Sigma(x) $ depend only on the dimensionless ratio$ x = E/E_{p} $ , with E denoting the total energy of the particle and$ E_{p} $ the Planck energy, defined as$ E_{p} = \sqrt{\hbar c^{5}/G} $ . They are independent of the spacetime coordinates$ (t,r,\theta,\phi) $ .Motivated by [63, 64], we explore the possible existence of a QS with anisotropic pressure in the context of rainbow gravity. Therefore, we define the fluid in the matter sector as locally anisotropic and express the energy-momentum tensor as follows:
$ \begin{array}{*{20}{l}} T_{\mu\nu}=(\rho+P_{\perp})u_\mu u_\nu+ P_{\perp} g_{\mu\nu}+\left(P-P_{\perp}\right)\chi_{\mu}\chi_{\nu}, \end{array} $

(8) where
$ u^\mu $ denotes the (timelike) 4-velocity of the fluid, and$ \chi_{\mu} $ represents a unit radial vector that fulfills$ \chi_{\mu} \chi^{\mu} = 1 $ . Indeed, P denotes the radial pressure, and$ P_{\perp} $ represents the transverse pressure. Furthermore, we express the generalized EoS for the tangential pressure as follows [63]:$ \begin{aligned}[b] P_{\perp}=\;& P_c +\dfrac{1}{3}\left(\rho-4B_{{\rm{eff}}, \perp}\right) \\&+ \frac{4\lambda_{\perp}^2}{9\pi^2}\left[ -1+\sqrt{1+3\pi^2 \frac{(\rho-B_{{\rm{eff}}, \perp})}{\lambda_{\perp}^2}} \right] \\ & -\dfrac{1}{3}\left(\rho_c-4B_{{\rm{eff}}, \perp}\right) \\&- \frac{4\lambda_{\perp}^2}{9\pi^2}\left[ -1+\sqrt{1+3\pi^2 \frac{(\rho_c-B_{{\rm{eff}}, \perp})}{\lambda_{\perp}^2}} \right], \end{aligned} $

(9) where
$ P_c $ and$ \rho_c $ in Eq. (9) represent the radial pressure (Eq. (5)) and energy density, respectively, at the center of the star. At the core of the star, specifically at$ r=0 $ , it is observed that the radial and tangential pressures are equivalent when the conditions$ B_{\rm{eff}} = B_{\rm{eff}}, \perp $ and$ \lambda=\lambda_{\perp} $ are satisfied. This condition indicates that the fluid attains isotropy at the center of the star. Additionally, the parameters$ B_{\rm{eff}}, \perp $ and$ \lambda_{\perp} $ contribute to the tangential pressure and are within the same value ranges as$ B_{{\rm{eff}}} $ and λ, respectively. Note that, in this setup, the parameters for the radial and tangential directions, written as λ and$ \lambda_\perp $ , respectively, are allowed to differ. This does not imply that the underlying microscopic physics changes with direction; rather, it provides a way to capture how strong interactions, possible phase transitions, or collective stresses might manifest as anisotropic behavior. At the stellar center, we impose$ \lambda=\lambda_\perp $ , thereby restoring isotropy, whereas controlled deviations arise only away from the center. In this sense, the construction is analogous in spirit to other anisotropy models considered in literature. Still, here it is cast in a more compact and microphysically motivated form, naturally embedded within the gravity’s rainbow framework. In contrast to the commonly used Bowers–Liang [65] or quasi-local models [45], which introduce anisotropy through externally prescribed stress profiles$ \Delta(r) $ , our formulation emerges as a direct extension of the interacting QM EoS. This approach naturally permits distinct couplings for radial and tangential pressures, while ensuring isotropy at the center, thereby providing a consistent way to incorporate strong-interaction corrections. Further, we remove the$ B_{{\rm{eff}}, \perp} $ parameter by applying dimensionless rescaling as follows:$ \bar{P}_\perp =\frac{P_\perp}{4\,B_{{\rm{eff}}}}, \; \bar{\lambda}_{\perp}=\frac{\lambda^2_{\perp}}{4B_{{\rm{eff}}}} \; \text{and}\; \bar{B} = \frac{B_{{\rm{eff}}, \perp}}{B_{{\rm{eff}}}}, $

(10) and ultimately, we obtain the pressure in the transverse direction in the following dimensionless form:
$ \begin{aligned}[b] \bar{P}_{\perp} =\;& \bar{P}_{c} + \frac{1}{3}(\bar{\rho} - \bar{B}) \\&+ \frac{4\bar{\lambda}_{\perp}}{9\pi^2} \left[-1+ \sqrt{1+ \frac{3\pi^2}{\bar{\lambda}_{\perp}} \left(\bar{\rho}-\frac{\bar{B}}{4}\right)}\right] \\ & -\frac{1}{3}(\bar{\rho}_{c} - \bar{B}) - \frac{4\bar{\lambda}_{\perp}}{9\pi^2} \left[-1+ \sqrt{1+ \frac{3\pi^2}{\bar{\lambda}_{\perp}} \left(\bar{\rho}_{c}-\frac{\bar{B}}{4}\right)}\right]. \end{aligned} $

(11) Here, we rescale the mass and radius into a dimensionless form,
$ \begin{array}{*{20}{l}} \bar{m} = m \sqrt{{4\,B_{{\rm{eff}}}}} \; ~{\rm and}~\; \bar{r} = r \sqrt{{4\,B_{{\rm{eff}}}}}\; . \end{array} $

(12) Here, the parameters are rescaled with respect to the effective bag constant, which sets the natural energy scale of the QM system. This rescaling reduces the number of free parameters and allows the EoS to be cast in a compact dimensionless form. It also ensures that the formulation connects smoothly to the standard GR limit in the absence of rainbow corrections, while retaining the effects of strong interactions in a controlled manner. Finally, using Eqs. (7) and (8), the modified TOV equations are [46, 59] (we work with natural units
$ G = \hslash= c = 1 $ )$ M_{\rm{eff}}(r, x)= \int^{r}_{0} \frac{4 \pi r^2 \rho(r)}{\Sigma^{2}(x)} {\rm d}r \equiv \frac{m(r)}{\Sigma^{2}(x)}, $

(13) $ P' = -(\rho+P_{r})\Phi'+ \frac{2}{r}\left(P_{\bot}-P\right), $

(14) $ \Phi'(r)=\frac{M_{\rm{eff}}(r, x) \Sigma^{2}(x)+4\pi r^3 P}{r\left(r-2M_{\rm{eff}}(r, x) \right)\Sigma^{2}(x)}, $

(15) where the prime denotes the derivative with respect to the radial coordinate r. We can also transform it into a dimensionless form by substituting the non-barred symbols with their corresponding barred counterparts. Note that the normal relation
$ (M, R) $ can be recovered by introducing$ (M, R) $ =$ (\bar{M}/ \sqrt{{4\,B_{{\rm{eff}}}}}, \bar{R}/ \sqrt{{4\,B_{{\rm{eff}}}}}) $ , and we present$ M-R $ relations in normalized form. -
In this section, we proceed to derive the equations of hydrostatic equilibrium in rainbow gravity, assuming a static,
$ 4D $ spherically symmetric metric that is substituted with a rainbow metric represented as follows [47],$ ds^{2} = -\frac{e^{2\Phi(r)}}{\Xi^{2}(x)}\, dt^{2} + \frac{e^{2\lambda(r)}}{\Sigma^{2}(x)}\, dr^{2} + \frac{r^{2}}{\Sigma^{2}(x)}\, d\Omega^{2}, $

(7) where
$ \Phi(r) $ and$ \lambda(r) $ are radial functions to be determined, and$ d\Omega^{2} = d\theta^{2} + \sin^{2}\theta\, d\phi^{2} $ denotes the metric on the unit 2-sphere. The rainbow functions$ \Xi(x) $ and$ \Sigma(x) $ depend only on the dimensionless ratio$ x = E/E_{p} $ , with E denoting the total energy of the particle and$ E_{p} $ the Planck energy, defined as$ E_{p} = \sqrt{\hbar c^{5}/G} $ . They are independent of the spacetime coordinates$ (t,r,\theta,\phi) $ .Motivated by [63, 65], we explore the possible existence of a quark star with anisotropic pressure in the context of rainbow gravity. Therefore, we define the fluid in the matter sector as locally anisotropic and express the energy-momentum tensor as follows:
$ \begin{array}{*{20}{l}} T_{\mu\nu}=(\rho+P_{\perp})u_\mu u_\nu+ P_{\perp} g_{\mu\nu}+\left(P-P_{\perp}\right)\chi_{\mu}\chi_{\nu}, \end{array} $

(8) where
$ u^\mu $ denotes the (timelike) 4-velocity of the fluid and$ \chi_{\mu} $ represents a unit radial vector that fulfills$ \chi_{\mu} \chi^{\mu} = 1 $ . Indeed, P denotes the radial pressure, while$ P_{\perp} $ represents the transverse pressure. Furthermore, we write down the generalized EoS for the tangential pressure [63]$ \begin{aligned}[b] P_{\perp}=\;& P_c +\dfrac{1}{3}\left(\rho-4B_{{\rm{eff}}, \perp}\right) \\&+ \frac{4\lambda_{\perp}^2}{9\pi^2}\left[ -1+\sqrt{1+3\pi^2 \frac{(\rho-B_{{\rm{eff}}, \perp})}{\lambda_{\perp}^2}} \right] \\ & -\dfrac{1}{3}\left(\rho_c-4B_{{\rm{eff}}, \perp}\right) \\&- \frac{4\lambda_{\perp}^2}{9\pi^2}\left[ -1+\sqrt{1+3\pi^2 \frac{(\rho_c-B_{{\rm{eff}}, \perp})}{\lambda_{\perp}^2}} \right], \end{aligned} $

(9) where
$ P_c $ and$ \rho_c $ of Eq. (9) represent the radial pressure (5) and energy density, respectively, at the center of the star. At the core of the star, specifically at$ r=0 $ , it is observed that the radial and tangential pressures are equivalent when the conditions$ B_{\rm{eff}} = B_{\rm{eff}}, \perp $ and$ \lambda=\lambda_{\perp} $ are satisfied. This condition indicates that the fluid attains isotropy at the center of the star. Additionally, it is noteworthy that the parameters$ B_{\rm{eff}}, \perp $ and$ \lambda_{\perp} $ contribute to the tangential pressure and are within the same value ranges as$ B_{{\rm{eff}}} $ and λ, respectively. {It is worth noting that in this setup the parameters for the radial and tangential directions, written as λ and$ \lambda_\perp $ , are allowed to differ. This does not imply that the underlying microscopic physics changes with direction; rather, it provides a way to capture how strong interactions, possible phase transitions, or collective stresses might manifest as anisotropic behavior. At the stellar center we impose$ \lambda=\lambda_\perp $ , thereby restoring isotropy, while controlled deviations arise only away from the center. In this sense, the construction is analogous in spirit to other anisotropy models considered in the literature. Still, here it is cast in a more compact and microphysically motivated form, naturally embedded within the gravity’s rainbow framework. In contrast to the commonly used Bowers–Liang [64] or quasi-local models [46], which introduce anisotropy through externally prescribed stress profiles$ \Delta(r) $ , our formulation emerges as a direct extension of the interacting quark matter EoS. This approach naturally permits distinct couplings for radial and tangential pressures, while still ensuring isotropy at the center, thereby providing a consistent way to incorporate strong-interaction corrections. Further, we remove the$ B_{{\rm{eff}}, \perp} $ parameter by applying dimensionless rescaling as follows:$ \bar{P}_\perp =\frac{P_\perp}{4\,B_{{\rm{eff}}}}, \; \bar{\lambda}_{\perp}=\frac{\lambda^2_{\perp}}{4B_{{\rm{eff}}}} \; \text{and}\; \bar{B} = \frac{B_{{\rm{eff}}, \perp}}{B_{{\rm{eff}}}}, $

(10) and ultimately, we obtain the pressure in the transverse direction in the following dimensionless form
$ \begin{aligned}[b] \bar{P}_{\perp} =\;& \bar{P}_{c} + \frac{1}{3}(\bar{\rho} - \bar{B}) \\&+ \frac{4\bar{\lambda}_{\perp}}{9\pi^2} \left[-1+ \sqrt{1+ \frac{3\pi^2}{\bar{\lambda}_{\perp}} \left(\bar{\rho}-\frac{\bar{B}}{4}\right)}\right] \\ & -\frac{1}{3}(\bar{\rho}_{c} - \bar{B}) - \frac{4\bar{\lambda}_{\perp}}{9\pi^2} \left[-1+ \sqrt{1+ \frac{3\pi^2}{\bar{\lambda}_{\perp}} \left(\bar{\rho}_{c}-\frac{\bar{B}}{4}\right)}\right]. \end{aligned} $

(11) Here, we proceed to rescale the mass and radius into a dimensionless form,
$ \begin{array}{*{20}{l}} \bar{m} = m \sqrt{{4\,B_{{\rm{eff}}}}} \; {\rm and}\; \bar{r} = r \sqrt{{4\,B_{{\rm{eff}}}}}. \end{array} $

(12) Here, the parameters are rescaled with respect to the effective bag constant, which sets the natural energy scale of the quark matter system. This rescaling reduces the number of free parameters and allows the EoS to be cast in a compact dimensionless form. It also ensures that the formulation connects smoothly to the standard GR limit in the absence of rainbow corrections, while retaining the effects of strong interactions in a controlled manner. Finally, using (7) and (8), the modified Tolman-Oppenheimer-Volkoff (TOV) equations are [47, 60] (we work in natural units
$ G = \hslash= c = 1 $ )$ M_{\rm{eff}}(r, x)= \int^{r}_{0} \frac{4 \pi r^2 \rho(r)}{\Sigma^{2}(x)} dr \equiv \frac{m(r)}{\Sigma^{2}(x)}, $

(13) $ P' = -(\rho+P_{r})\Phi'+ \frac{2}{r}\left(P_{\bot}-P\right), $

(14) $ \Phi'(r)=\frac{M_{\rm{eff}}(r, x) \Sigma^{2}(x)+4\pi r^3 P}{r\left(r-2M_{\rm{eff}}(r, x) \right)\Sigma^{2}(x)}, $

(15) where prime denotes the derivative with respect to the radial coordinate r. We can also transform it into a dimensionless form by substituting the non-barred symbols with their corresponding barred counterparts. It should be noted that the normal relation
$ (M, R) $ can be recovered by introducing$ (M, R) $ =$ (\bar{M}/ \sqrt{{4\,B_{{\rm{eff}}}}}, \bar{R}/ \sqrt{{4\,B_{{\rm{eff}}}}}) $ , and we present$ M-R $ relations in normalized form. -
In this section, we outline methods for solving the differential Eqs. (13)−(15) using a fourth-order Runge-Kutta method with adaptive step size control, in conjunction with the specified EOSs (Eqs. (11) and (5)). To achieve this, we need to specify the appropriate boundary conditions and subsequently integrate them, starting at the star's center and extending to a specific radius where the radial pressure equals zero, i.e.,
$ P(R) = 0 $ . The initial conditions are given by$ \begin{array}{*{20}{l}} \rho(0) = \rho_c, & m(0) = 0, \end{array} $

(16) where
$ \rho_c $ represents the value of the central energy density. Additionally, we need an exterior Schwarzschild solution [66] to match this interior spacetime, given by$ {\rm e}^{2\Phi(R)} = 1-\frac{2M}{R}, $

(17) with
$ M = m(r=R) $ being the total mass of the star. In this study on QSs, we examine the influences of three parameters, specifically, Σ,$ \bar{\lambda} $ , and$ \bar{\lambda}_{\perp} $ . The parameter$ \bar{\lambda} $ characterizes the strength of strong interaction effects in radial pressure by color superconductivity and pQCD corrections. In contrast,$ \bar{\lambda}_\perp $ influences transverse pressure under an anisotropic environment. Both parameters are rescaled with respect to the effective bag constant to represent a dimensionless form of the EoS. The rainbow parameter Σ, which is derived from gravity's rainbow, encodes high-energy modifications to spacetime curvature, influencing the equilibrium structure of compact stars. We adopt a phenomenological choice for Σ within the narrow range$ 0.9 \leq \Sigma \leq 1.1 $ , following earlier studies of gravity's rainbow [59]. This range captures possible Planck-scale modifications to spatial geometry while ensuring smooth recovery of general relativity in the low-energy limit and permitting measurable corrections in the ultra-dense regime of compact stars. Here, we present the relations$ (M-R) $ by choosing the bag constant$ B = B_{\perp}= 70 $ MeV/fm3 and$ \bar{\lambda} $ ,$ \bar{\lambda}_{\perp} $ $ \in [0, 1] $ . Together, these parameters allow us to investigate how strong interactions, anisotropy, and quantum gravity-inspired corrections jointly affect the structure and stability of QSs. -
In this section, we outline methods for solving the differential Eqs. (13)-(15) are solved using a fourth-order Runge-Kutta method with adaptive step size control, in conjunction with the specified equations of state (11) and (5). To achieve this, we need to specify the appropriate boundary conditions and subsequently integrate them, starting at the star's center and extending to a specific radius where the radial pressure equals zero, i.e.,
$ P(R) = 0 $ . The initial conditions are given by$ \begin{array}{*{20}{l}} \rho(0) &= \rho_c, & m(0) &= 0, \end{array} $

(16) where
$ \rho_c $ represents the value of the central energy density. Additionally, we need an exterior Schwarzschild solution [66] to match this interior spacetime, given by$ e^{2\Phi(R)} = 1-\frac{2M}{R} $

(17) with
$ M = m(r=R) $ being the total mass of the star. In this work on QSs, we examine the impacts of three parameters, specifically, Σ,$ \bar{\lambda} $ , and$ \bar{\lambda}_{\perp} $ . Since, the parameter$ \bar{\lambda} $ characterizes the strength of strong interaction effects in radial pressure by colour superconductivity and pQCD corrections. In contrast,$ \bar{\lambda}_\perp $ is the parameter that influences transverse pressure under an anisotropic environment. Both parameters are rescaled with respect to the effective bag constant to represent a dimensionless form of the EoS. The rainbow parameter Σ, which is derived from gravity's rainbow, encodes high-energy modifications to spacetime curvature, influencing the equilibrium structure of compact stars. We adopt a phenomenological choice for Σ within the narrow range$ 0.9 \leq \Sigma \leq 1.1 $ , following earlier studies of gravity's rainbow [60]. This range captures possible Planck-scale modifications to spatial geometry while ensuring smooth recovery of general relativity in the low-energy limit and permitting measurable corrections in the ultra-dense regime of compact stars. Here, we present the relations$ (M-R) $ by choosing the bag constant$ B = B_{\perp}= 70 $ MeV/fm3 and$ \bar{\lambda} $ ,$ \bar{\lambda}_{\perp} $ $ \in [0, 1] $ . Together, these parameters allow us to investigate how strong interactions, anisotropy, and quantum gravity-inspired corrections jointly affect the structure and stability of QSs. -
In this section, we outline methods for solving the differential Eqs. (13)−(15) using a fourth-order Runge-Kutta method with adaptive step size control, in conjunction with the specified EOSs (Eqs. (11) and (5)). To achieve this, we need to specify the appropriate boundary conditions and subsequently integrate them, starting at the star's center and extending to a specific radius where the radial pressure equals zero, i.e.,
$ P(R) = 0 $ . The initial conditions are given by$ \begin{array}{*{20}{l}} \rho(0) = \rho_c, & m(0) = 0, \end{array} $

(16) where
$ \rho_c $ represents the value of the central energy density. Additionally, we need an exterior Schwarzschild solution [66] to match this interior spacetime, given by$ {\rm e}^{2\Phi(R)} = 1-\frac{2M}{R}, $

(17) with
$ M = m(r=R) $ being the total mass of the star. In this study on QSs, we examine the influences of three parameters, specifically, Σ,$ \bar{\lambda} $ , and$ \bar{\lambda}_{\perp} $ . The parameter$ \bar{\lambda} $ characterizes the strength of strong interaction effects in radial pressure by color superconductivity and pQCD corrections. In contrast,$ \bar{\lambda}_\perp $ influences transverse pressure under an anisotropic environment. Both parameters are rescaled with respect to the effective bag constant to represent a dimensionless form of the EoS. The rainbow parameter Σ, which is derived from gravity's rainbow, encodes high-energy modifications to spacetime curvature, influencing the equilibrium structure of compact stars. We adopt a phenomenological choice for Σ within the narrow range$ 0.9 \leq \Sigma \leq 1.1 $ , following earlier studies of gravity's rainbow [59]. This range captures possible Planck-scale modifications to spatial geometry while ensuring smooth recovery of general relativity in the low-energy limit and permitting measurable corrections in the ultra-dense regime of compact stars. Here, we present the relations$ (M-R) $ by choosing the bag constant$ B = B_{\perp}= 70 $ MeV/fm3 and$ \bar{\lambda} $ ,$ \bar{\lambda}_{\perp} $ $ \in [0, 1] $ . Together, these parameters allow us to investigate how strong interactions, anisotropy, and quantum gravity-inspired corrections jointly affect the structure and stability of QSs. -
In this section, we outline methods for solving the differential Eqs. (13)−(15) using a fourth-order Runge-Kutta method with adaptive step size control, in conjunction with the specified EOSs (Eqs. (11) and (5)). To achieve this, we need to specify the appropriate boundary conditions and subsequently integrate them, starting at the star's center and extending to a specific radius where the radial pressure equals zero, i.e.,
$ P(R) = 0 $ . The initial conditions are given by$ \begin{array}{*{20}{l}} \rho(0) = \rho_c, & m(0) = 0, \end{array} $

(16) where
$ \rho_c $ represents the value of the central energy density. Additionally, we need an exterior Schwarzschild solution [66] to match this interior spacetime, given by$ {\rm e}^{2\Phi(R)} = 1-\frac{2M}{R}, $

(17) with
$ M = m(r=R) $ being the total mass of the star. In this study on QSs, we examine the influences of three parameters, specifically, Σ,$ \bar{\lambda} $ , and$ \bar{\lambda}_{\perp} $ . The parameter$ \bar{\lambda} $ characterizes the strength of strong interaction effects in radial pressure by color superconductivity and pQCD corrections. In contrast,$ \bar{\lambda}_\perp $ influences transverse pressure under an anisotropic environment. Both parameters are rescaled with respect to the effective bag constant to represent a dimensionless form of the EoS. The rainbow parameter Σ, which is derived from gravity's rainbow, encodes high-energy modifications to spacetime curvature, influencing the equilibrium structure of compact stars. We adopt a phenomenological choice for Σ within the narrow range$ 0.9 \leq \Sigma \leq 1.1 $ , following earlier studies of gravity's rainbow [59]. This range captures possible Planck-scale modifications to spatial geometry while ensuring smooth recovery of general relativity in the low-energy limit and permitting measurable corrections in the ultra-dense regime of compact stars. Here, we present the relations$ (M-R) $ by choosing the bag constant$ B = B_{\perp}= 70 $ MeV/fm3 and$ \bar{\lambda} $ ,$ \bar{\lambda}_{\perp} $ $ \in [0, 1] $ . Together, these parameters allow us to investigate how strong interactions, anisotropy, and quantum gravity-inspired corrections jointly affect the structure and stability of QSs. -
In this subsection, we present the results of our analysis of the mass-radius
$ (M-R) $ and mass-compactness$ (M-M/R) $ relations, as shown in Fig. 1, for different Σ values. For this investigation, we selected$ B_{{\rm{eff}}}= B_{{\rm{eff}}, \perp} = $ 70 MeV/fm3, with the additional parameters set as$ \bar{\lambda} =0.2 $ and$ \bar{\lambda}_{\perp}= 0.5 $ . As evident from Fig. 1, the parameter Σ can influence the maximum gravitational mass$ M_{\rm max} $ of QSs, which reaches 2.30$ M_\odot $ with a corresponding radius$ R=13.30 $ km at$ \Sigma =1.10 $ . Furthermore, we compare our results with the predicted masses and radii of the pulsars, specifically PSR J0952-0607 with a mass$ M = 2.35 \pm 0.17\; M_{\odot} $ (yellow) [67], PSR J0740+6620 with a mass$ M = 2.08 \pm 0.07 $ $ M_{\odot} $ (orange) [68], and PSR J0348+0432 with a mass$ M = 2.01 \pm 0.04\; M_{\odot} $ (pink) [69]. For completeness, we also compute the$ (M-R) $ relation for the GR solution, i.e., when$ \Sigma =1.0 $ . Based on the results presented in Table 1, it is observed that the maximum mass may exceed its GR counterpart when$ \Sigma > 1 $ . Finally, the bottom panel of Fig. 1 illustrates how Σ influences the characteristics of maximum compactness. The findings indicate that the maximum compactness is invariant to the value of Σ, maintaining a constant ratio of$ \dfrac{M}{R} \sim 0.257 $ , as listed in Table 1. Moreover, our findings indicate that the Buchdahl limit is maintained, such that$ M/R < 4/9 $ .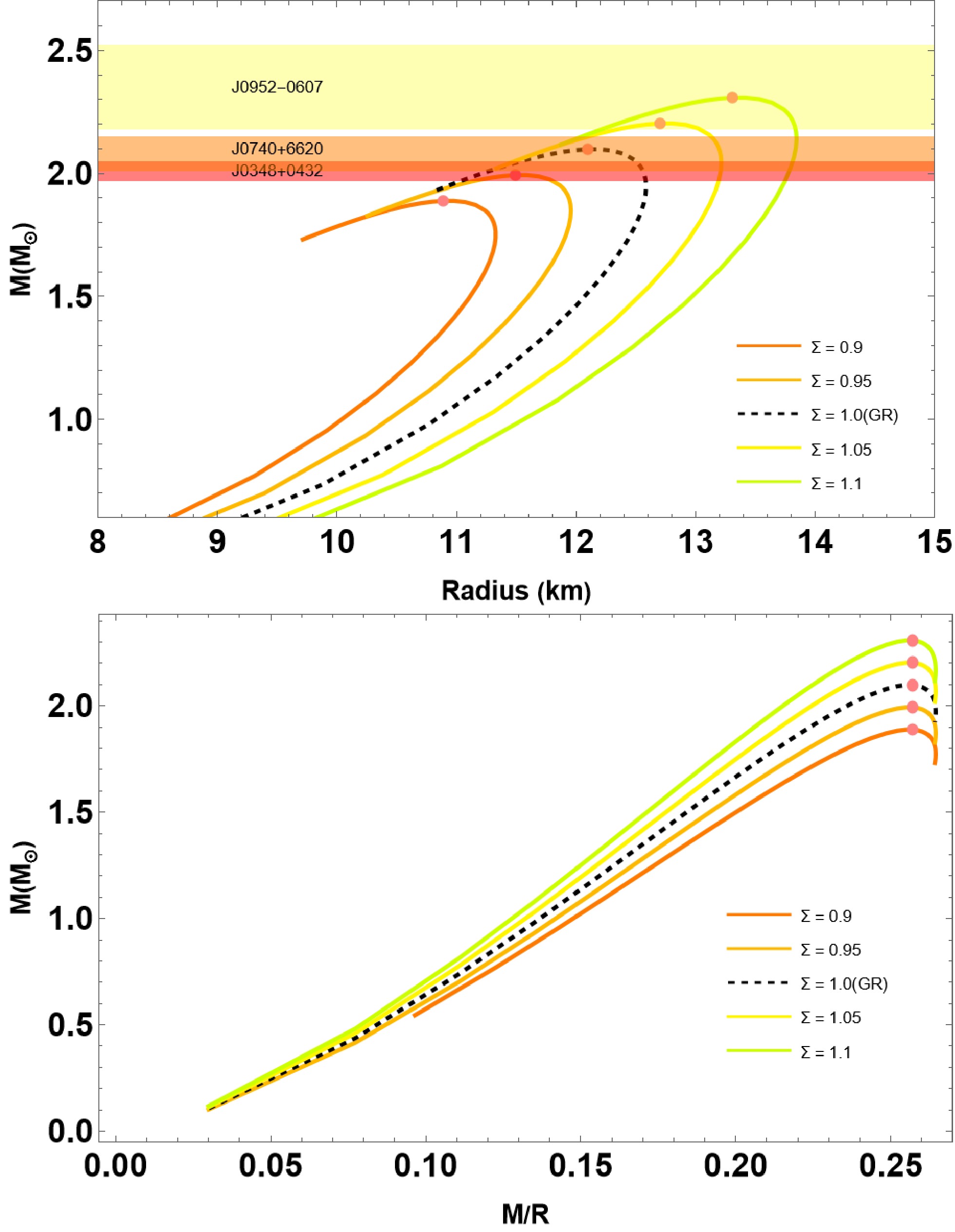
Figure 1. (color online) The mass-radius and compactness relationships of QSs for the given EoSs (Eqs. (5) and (11)) are presented in Table 1 for various values of the rainbow function Σ. We draw graphs for
$ B_{{\rm{eff}}}=B_{{\rm{eff}}, \perp} = 60 $ MeV/fm3 with the other parameters being$ \bar{\lambda} =0.2 $ and$ \bar{\lambda}_{\perp}= 0.5 $ . The color bands illustrate the MR constraints from PSR J0952-0607 (yellow) [67], PSR J0740+6620 (orange) [68], and PSR J0348+0432 (pink) [69]. The black dashed line indicates the GR solution.Σ M R $ \rho_c $ 

$ M/R $ 

$/ M_{\odot} $ 

/km /(MeV/fm3) 0.90 1.89 10.89 788 0.257 0.95 2.00 11.49 788 0.257 1.00 2.09 12.09 788 0.257 1.05 2.20 12.70 788 0.257 1.10 2.30 13.30 788 0.257 Table 1. Properties of QSs for varying values of the effective bag constant. Here,
$ B \equiv B_{{\rm{eff}}} $ and$ B_{\rm \perp} \equiv B_{{\rm{eff}}, \perp} $ . We use the same parameter set as that indicated in Fig. 1. -
In this subsection, we present the results of our analysis of the mass-radius
$ (M-R) $ and mass-compactness$ (M-M/R) $ relations, as shown in Fig. 1, for different Σ values. For this investigation, we selected$ B_{{\rm{eff}}}= B_{{\rm{eff}}, \perp} = 70 $ MeV/fm3, with the additional parameters set as$ \bar{\lambda} =0.2 $ and$ \bar{\lambda}_{\perp}= 0.5 $ , respectively. As evident from Fig. 1, the Σ parameter can influence the maximum gravitational mass$ M_{\rm max} $ of QSs, and this value reaches 2.30$ M_\odot $ with a corresponding radius$ R=13.30 $ km at$ \Sigma =1.10 $ . Furthermore, we compare our results with the predicted masses and radii of the pulsars, specifically PSR J0952-0607 with mass$ M = 2.35 \pm 0.17 M_{\odot} $ (Yellow) [68], PSR J0740+6620 with the pulsar mass$ M = 2.08 \pm 0.07 $ $ M_{\odot} $ (Orange) [69] and PSR J0348+0432 with the mass of$ M = 2.01 \pm 0.04 M_{\odot} $ (Pink) [70]. For completeness, we also compute the$ (M-R) $ relation for the GR solution, i.e., when$ \Sigma =1.0 $ . Based on the results presented in Table 1, it is observed that the maximal mass may exceed its GR counterpart when$ \Sigma > 1 $ . Finally, the bottom panel of Fig. 1 illustrates how Σ influences the characteristics of maximal compactness. The findings indicate that the maximum compactness is invariant to the value of Σ, maintaining a constant ratio of$ \dfrac{M}{R} \sim 0.257 $ , as shown in Table 1. Moreover, our findings indicate that the Buchdahl limit is maintained, such that$ M/R < 4/9 $ .
Figure 1. (color online) The mass-radius and compactness relationships of QSs for the given EoSs (5) and (11) are presented in Table 1 for various values of the rainbow function Σ. We draw graphs for
$ B_{{\rm{eff}}}=B_{{\rm{eff}}, \perp} = 60 $ MeV/fm3 with the other parameters being$ \bar{\lambda} =0.2 $ and$ \bar{\lambda}_{\perp}= 0.5 $ , respectively. The color bands illustrate the MR constraints from PSR J0952-0607 (Yellow) [68], PSR J0740+6620 (Orange) [69] and PSR J0348+0432 (Pink) [70]. The black dashed line indicates the GR solution.Σ M R $ \rho_c $ 

$ M/R $ 

$ M_{\odot} $ 

km MeV/fm3 0.90 1.89 10.89 788 0.257 0.95 2.00 11.49 788 0.257 1.00 2.09 12.09 788 0.257 1.05 2.20 12.70 788 0.257 1.10 2.30 13.30 788 0.257 Table 1. Properties of QSs for varying the effective bag constant. Here,
$ B \equiv B_{{\rm{eff}}} $ and$ B_{\rm \perp} \equiv B_{{\rm{eff}}, \perp} $ . We use the same parameter set as indicated in Fig. 1. -
In this subsection, we present the results of our analysis of the mass-radius
$ (M-R) $ and mass-compactness$ (M-M/R) $ relations, as shown in Fig. 1, for different Σ values. For this investigation, we selected$ B_{{\rm{eff}}}= B_{{\rm{eff}}, \perp} = $ 70 MeV/fm3, with the additional parameters set as$ \bar{\lambda} =0.2 $ and$ \bar{\lambda}_{\perp}= 0.5 $ . As evident from Fig. 1, the parameter Σ can influence the maximum gravitational mass$ M_{\rm max} $ of QSs, which reaches 2.30$ M_\odot $ with a corresponding radius$ R=13.30 $ km at$ \Sigma =1.10 $ . Furthermore, we compare our results with the predicted masses and radii of the pulsars, specifically PSR J0952-0607 with a mass$ M = 2.35 \pm 0.17\; M_{\odot} $ (yellow) [67], PSR J0740+6620 with a mass$ M = 2.08 \pm 0.07 $ $ M_{\odot} $ (orange) [68], and PSR J0348+0432 with a mass$ M = 2.01 \pm 0.04\; M_{\odot} $ (pink) [69]. For completeness, we also compute the$ (M-R) $ relation for the GR solution, i.e., when$ \Sigma =1.0 $ . Based on the results presented in Table 1, it is observed that the maximum mass may exceed its GR counterpart when$ \Sigma > 1 $ . Finally, the bottom panel of Fig. 1 illustrates how Σ influences the characteristics of maximum compactness. The findings indicate that the maximum compactness is invariant to the value of Σ, maintaining a constant ratio of$ \dfrac{M}{R} \sim 0.257 $ , as listed in Table 1. Moreover, our findings indicate that the Buchdahl limit is maintained, such that$ M/R < 4/9 $ .
Figure 1. (color online) The mass-radius and compactness relationships of QSs for the given EoSs (Eqs. (5) and (11)) are presented in Table 1 for various values of the rainbow function Σ. We draw graphs for
$ B_{{\rm{eff}}}=B_{{\rm{eff}}, \perp} = 60 $ MeV/fm3 with the other parameters being$ \bar{\lambda} =0.2 $ and$ \bar{\lambda}_{\perp}= 0.5 $ . The color bands illustrate the MR constraints from PSR J0952-0607 (yellow) [67], PSR J0740+6620 (orange) [68], and PSR J0348+0432 (pink) [69]. The black dashed line indicates the GR solution.Σ M R $ \rho_c $ 

$ M/R $ 

$/ M_{\odot} $ 

/km /(MeV/fm3) 0.90 1.89 10.89 788 0.257 0.95 2.00 11.49 788 0.257 1.00 2.09 12.09 788 0.257 1.05 2.20 12.70 788 0.257 1.10 2.30 13.30 788 0.257 Table 1. Properties of QSs for varying values of the effective bag constant. Here,
$ B \equiv B_{{\rm{eff}}} $ and$ B_{\rm \perp} \equiv B_{{\rm{eff}}, \perp} $ . We use the same parameter set as that indicated in Fig. 1. -
In this subsection, we present the results of our analysis of the mass-radius
$ (M-R) $ and mass-compactness$ (M-M/R) $ relations, as shown in Fig. 1, for different Σ values. For this investigation, we selected$ B_{{\rm{eff}}}= B_{{\rm{eff}}, \perp} = $ 70 MeV/fm3, with the additional parameters set as$ \bar{\lambda} =0.2 $ and$ \bar{\lambda}_{\perp}= 0.5 $ . As evident from Fig. 1, the parameter Σ can influence the maximum gravitational mass$ M_{\rm max} $ of QSs, which reaches 2.30$ M_\odot $ with a corresponding radius$ R=13.30 $ km at$ \Sigma =1.10 $ . Furthermore, we compare our results with the predicted masses and radii of the pulsars, specifically PSR J0952-0607 with a mass$ M = 2.35 \pm 0.17\; M_{\odot} $ (yellow) [67], PSR J0740+6620 with a mass$ M = 2.08 \pm 0.07 $ $ M_{\odot} $ (orange) [68], and PSR J0348+0432 with a mass$ M = 2.01 \pm 0.04\; M_{\odot} $ (pink) [69]. For completeness, we also compute the$ (M-R) $ relation for the GR solution, i.e., when$ \Sigma =1.0 $ . Based on the results presented in Table 1, it is observed that the maximum mass may exceed its GR counterpart when$ \Sigma > 1 $ . Finally, the bottom panel of Fig. 1 illustrates how Σ influences the characteristics of maximum compactness. The findings indicate that the maximum compactness is invariant to the value of Σ, maintaining a constant ratio of$ \dfrac{M}{R} \sim 0.257 $ , as listed in Table 1. Moreover, our findings indicate that the Buchdahl limit is maintained, such that$ M/R < 4/9 $ .
Figure 1. (color online) The mass-radius and compactness relationships of QSs for the given EoSs (Eqs. (5) and (11)) are presented in Table 1 for various values of the rainbow function Σ. We draw graphs for
$ B_{{\rm{eff}}}=B_{{\rm{eff}}, \perp} = 60 $ MeV/fm3 with the other parameters being$ \bar{\lambda} =0.2 $ and$ \bar{\lambda}_{\perp}= 0.5 $ . The color bands illustrate the MR constraints from PSR J0952-0607 (yellow) [67], PSR J0740+6620 (orange) [68], and PSR J0348+0432 (pink) [69]. The black dashed line indicates the GR solution.Σ M R $ \rho_c $ 

$ M/R $ 

$/ M_{\odot} $ 

/km /(MeV/fm3) 0.90 1.89 10.89 788 0.257 0.95 2.00 11.49 788 0.257 1.00 2.09 12.09 788 0.257 1.05 2.20 12.70 788 0.257 1.10 2.30 13.30 788 0.257 Table 1. Properties of QSs for varying values of the effective bag constant. Here,
$ B \equiv B_{{\rm{eff}}} $ and$ B_{\rm \perp} \equiv B_{{\rm{eff}}, \perp} $ . We use the same parameter set as that indicated in Fig. 1. -
Subsequently, we conduct our analysis based on the variation of
$ \bar{\lambda} $ and present the$ (M-R) $ and$ (M-M/R) $ relations in Fig. 2. For numerical calculations, we set$ B_{{\rm{eff}}}= B_{{\rm{eff}}, \perp} = 70 $ MeV/fm3, whereas the other parameters are$ \Sigma =0.9 $ and$ \bar{\lambda}_{\perp}= 0.5 $ . By increasing the value of$ \bar{\lambda} $ , we observe that the maximum gravitational mass of the QSs increases and reaches the value of$ M_{\rm max} =2.77\; M_\odot $ with a corresponding radius$ R=13.12 $ km at$ \bar{\lambda}= 0.8 $ . To verify the consistency of our solution, we utilize the same astrophysics constraints described in the caption of Fig. 1. In addition to the mass and radius constraints, we include the GW190814 event (green) [70], consistent with the maximum masses obtained from our calculation. Our results are presented in Table 2. In addition, the lower panel of Fig. 3 demonstrates the variation in maximum compactness across different$ \bar{\lambda} $ values. As indicated in Table 1, the maximum compactness$ M/R $ of the star increases with$ \bar{\lambda} $ , and at$ \bar{\lambda} = 0.8 $ , this value is$ M/R= 0.312 $ . Notably, the obtained values adhere to the Buchdahl limit of$ M/R < 4/9 $ . This consistency ensures that the configurations under consideration do not exhibit apparent horizons, thereby classifying them as stable, compact objects rather than black holes. In particular, an increase in$ \bar{\lambda} $ enhances the stiffness of pressure support, thereby shifting stellar configurations toward higher masses and greater compactness.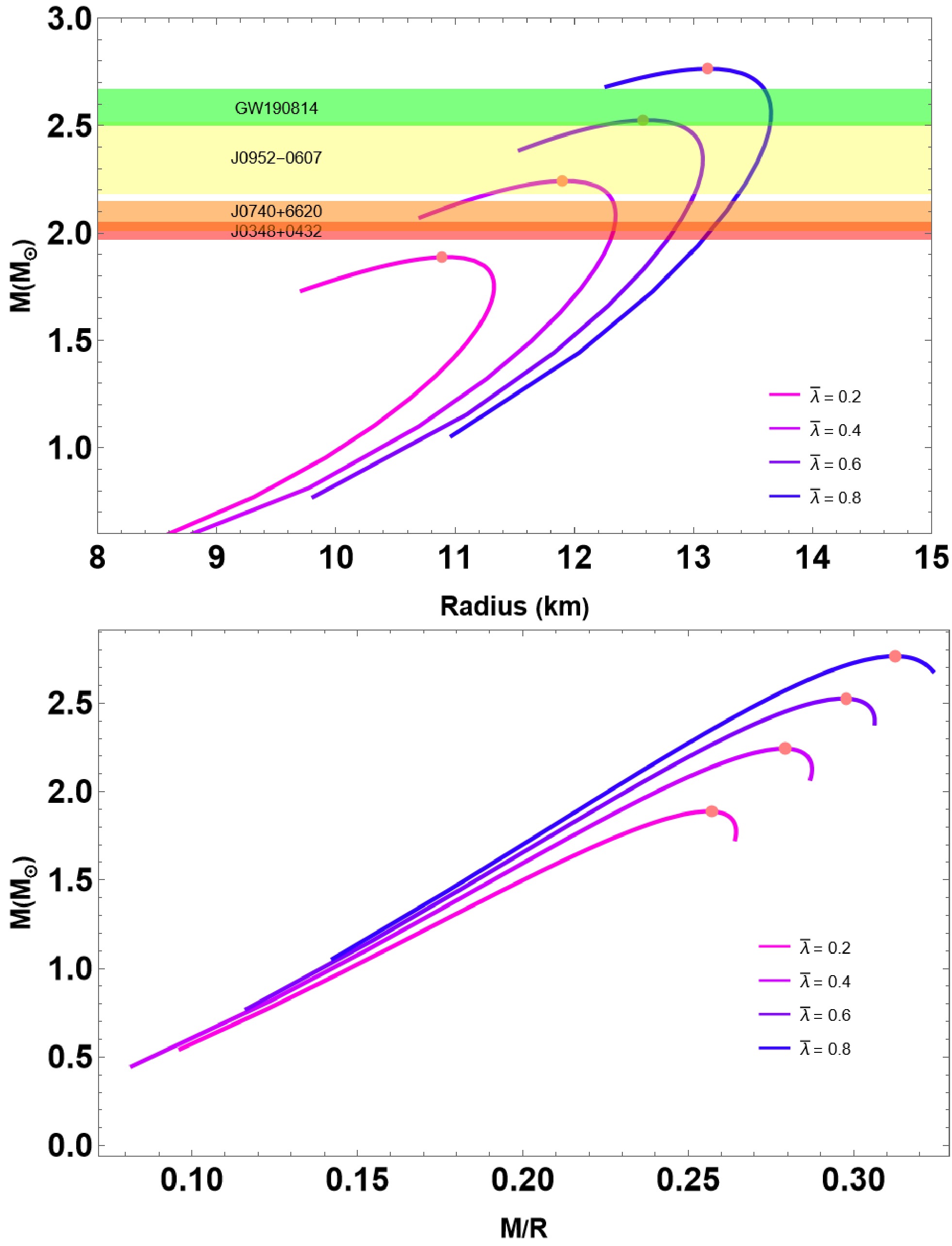
Figure 2. (color online) The mass-radius and compactness relationships of QSs for the given EoSs (Eqs. (5) and (11)) are presented in Table 2 for various values of
$ \bar{\lambda} $ . We draw graphs for$ B_{{\rm{eff}}}=B_{{\rm{eff}}, \perp} = 70 $ MeV/fm3 with the other parameters being$ \Sigma =0.9 $ and$ \bar{\lambda}_{\perp}= 0.5 $ . The color bands illustrate the MR constraints from PSR J0952-0607 (yellow) [67], PSR J0740+6620 (orange) [68], and PSR J0348+0432 (pink) [69]. We also include the GW190814 event, as indicated by the green horizontal band [70].$ \bar{\lambda} $ 

M R $ \rho_c $ 

$ M/R $ 

$ /M_{\odot} $ 

/km /(MeV/fm3) 0.2 1.89 10.89 788 0.257 0.4 2.24 11.90 731 0.280 0.6 2.53 12.57 731 0.298 0.8 2.77 13.12 731 0.312 Table 2. Properties of QSs for varying
$ \bar{\lambda} $ . We use the same parameter set as that indicated in Fig. 2.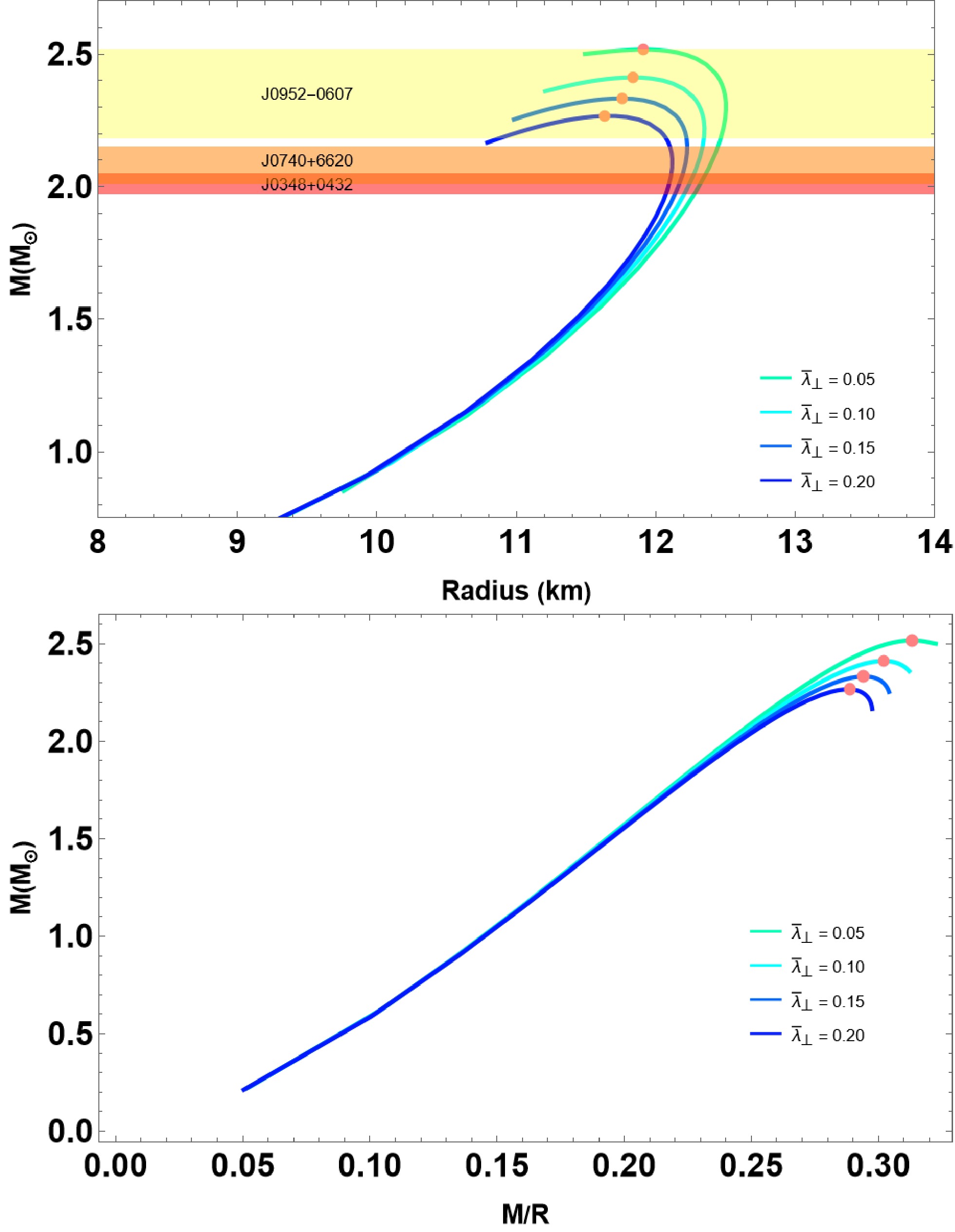
Figure 3. (color online) The mass-radius and compactness relationships of QSs for the given EoSs (Eqs. (5) and (11)) are shown in Table 3 for different values of
$ \bar{\lambda}_{\perp} $ . We draw graphs for$ B_{{\rm{eff}}}=B_{{\rm{eff}}, \perp} = 60 $ MeV/fm3 with the other parameters being$ \Sigma =0.9 $ and$ \bar{\lambda}= 0.25 $ . The color bands illustrate the MR constraints from PSR J0952-0607 (yellow) [67], PSR J0740+6620 (orange) [68], and PSR J0348+0432 (pink) [69]. -
Subsequently, we conduct our analysis based on the variation of
$ \bar{\lambda} $ and present the$ (M-R) $ and$ (M-M/R) $ relations in Fig. 2. For numerical calculations, we set$ B_{{\rm{eff}}}= B_{{\rm{eff}}, \perp} = 70 $ MeV/fm3, whereas the other parameters are$ \Sigma =0.9 $ and$ \bar{\lambda}_{\perp}= 0.5 $ . By increasing the value of$ \bar{\lambda} $ , we observe that the maximum gravitational mass of the QSs increases and reaches the value of$ M_{\rm max} =2.77\; M_\odot $ with a corresponding radius$ R=13.12 $ km at$ \bar{\lambda}= 0.8 $ . To verify the consistency of our solution, we utilize the same astrophysics constraints described in the caption of Fig. 1. In addition to the mass and radius constraints, we include the GW190814 event (green) [70], consistent with the maximum masses obtained from our calculation. Our results are presented in Table 2. In addition, the lower panel of Fig. 3 demonstrates the variation in maximum compactness across different$ \bar{\lambda} $ values. As indicated in Table 1, the maximum compactness$ M/R $ of the star increases with$ \bar{\lambda} $ , and at$ \bar{\lambda} = 0.8 $ , this value is$ M/R= 0.312 $ . Notably, the obtained values adhere to the Buchdahl limit of$ M/R < 4/9 $ . This consistency ensures that the configurations under consideration do not exhibit apparent horizons, thereby classifying them as stable, compact objects rather than black holes. In particular, an increase in$ \bar{\lambda} $ enhances the stiffness of pressure support, thereby shifting stellar configurations toward higher masses and greater compactness.
Figure 2. (color online) The mass-radius and compactness relationships of QSs for the given EoSs (Eqs. (5) and (11)) are presented in Table 2 for various values of
$ \bar{\lambda} $ . We draw graphs for$ B_{{\rm{eff}}}=B_{{\rm{eff}}, \perp} = 70 $ MeV/fm3 with the other parameters being$ \Sigma =0.9 $ and$ \bar{\lambda}_{\perp}= 0.5 $ . The color bands illustrate the MR constraints from PSR J0952-0607 (yellow) [67], PSR J0740+6620 (orange) [68], and PSR J0348+0432 (pink) [69]. We also include the GW190814 event, as indicated by the green horizontal band [70].$ \bar{\lambda} $ 

M R $ \rho_c $ 

$ M/R $ 

$ /M_{\odot} $ 

/km /(MeV/fm3) 0.2 1.89 10.89 788 0.257 0.4 2.24 11.90 731 0.280 0.6 2.53 12.57 731 0.298 0.8 2.77 13.12 731 0.312 Table 2. Properties of QSs for varying
$ \bar{\lambda} $ . We use the same parameter set as that indicated in Fig. 2.
Figure 3. (color online) The mass-radius and compactness relationships of QSs for the given EoSs (Eqs. (5) and (11)) are shown in Table 3 for different values of
$ \bar{\lambda}_{\perp} $ . We draw graphs for$ B_{{\rm{eff}}}=B_{{\rm{eff}}, \perp} = 60 $ MeV/fm3 with the other parameters being$ \Sigma =0.9 $ and$ \bar{\lambda}= 0.25 $ . The color bands illustrate the MR constraints from PSR J0952-0607 (yellow) [67], PSR J0740+6620 (orange) [68], and PSR J0348+0432 (pink) [69]. -
Subsequently, we conduct our analysis based on the variation of
$ \bar{\lambda} $ and present the$ (M-R) $ and$ (M-M/R) $ relations in Fig. 2. For numerical calculations, we set$ B_{{\rm{eff}}}= B_{{\rm{eff}}, \perp} = 70 $ MeV/fm3, while the other parameters are$ \Sigma =0.9 $ and$ \bar{\lambda}_{\perp}= 0.5 $ , respectively. By increasing the value of$ \bar{\lambda} $ , we see that the maximum gravitational mass of the QSs is increasing, and this could reach the value of$ M_{\rm max} =2.77 M_\odot $ with a corresponding radius$ R=13.12 $ km at$ \bar{\lambda}= 0.8 $ . To verify the consistency of our solution, we utilize the same astrophysics constraints described in the caption of Fig. 1. In addition to the mass and radius constraints, we include the GW190814 event (Green) [67], consistent with the maximum masses obtained from our calculation. Our results are presented in Table 2. In addition, the lower panel of Figure 3 demonstrates the variation in maximum compactness across different$ \bar{\lambda} $ values. As indicated in Table 1, the maximum compactness$ M/R $ of the star increases with$ \bar{\lambda} $ , and at$ \bar{\lambda} = 0.8 $ , this value could be$ M/R= 0.312 $ . Notably, the obtained values adhere to the Buchdahl limit of$ M/R < 4/9 $ . This consistency ensures that the configurations under consideration do not exhibit apparent horizons, thereby classifying them as stable, compact objects rather than black holes. In particular, an increase in$ \bar{\lambda} $ enhances the stiffness of pressure support, thereby shifting stellar configurations toward higher masses and greater compactness.
Figure 2. (color online) The mass-radius and compactness relationships of QSs for the given EoSs (5) and (11) are presented in Table 2 for various values of
$ \bar{\lambda} $ . We draw graphs for$ B_{{\rm{eff}}}=B_{{\rm{eff}}, \perp} = 70 $ MeV/fm3 with the other parameters being$ \Sigma =0.9 $ and$ \bar{\lambda}_{\perp}= 0.5 $ , respectively. The color bands illustrate the MR constraints from PSR J0952-0607 (Yellow) [68], PSR J0740+6620 (Orange) [69] and PSR J0348+0432 (Pink) [70]. We also include the GW190814 event, as indicated by the green horizontal band [67].$ \bar{\lambda} $ 

M R $ \rho_c $ 

$ M/R $ 

$ M_{\odot} $ 

km MeV/fm3 0.2 1.89 10.89 788 0.257 0.4 2.24 11.90 731 0.280 0.6 2.53 12.57 731 0.298 0.8 2.77 13.12 731 0.312 Table 2. Properties of QSs for varying
$ \bar{\lambda} $ . We use the same parameter set as indicated in Fig. 2.
Figure 3. (color online) The mass-radius and compactness relationships of QSs for the given EoSs (5) and (11) are shown in Table 3 for different values of
$ \bar{\lambda}_{\perp} $ . We draw graphs for$ B_{{\rm{eff}}}=B_{{\rm{eff}}, \perp} = 60 $ MeV/fm3 with the other parameters being$ \Sigma =0.9 $ and$ \bar{\lambda}= 0.25 $ , respectively. The color bands illustrate the MR constraints from PSR J0952-0607 (Yellow) [68], PSR J0740+6620 (Orange) [69] and PSR J0348+0432 (Pink) [70]. -
Subsequently, we conduct our analysis based on the variation of
$ \bar{\lambda} $ and present the$ (M-R) $ and$ (M-M/R) $ relations in Fig. 2. For numerical calculations, we set$ B_{{\rm{eff}}}= B_{{\rm{eff}}, \perp} = 70 $ MeV/fm3, whereas the other parameters are$ \Sigma =0.9 $ and$ \bar{\lambda}_{\perp}= 0.5 $ . By increasing the value of$ \bar{\lambda} $ , we observe that the maximum gravitational mass of the QSs increases and reaches the value of$ M_{\rm max} =2.77\; M_\odot $ with a corresponding radius$ R=13.12 $ km at$ \bar{\lambda}= 0.8 $ . To verify the consistency of our solution, we utilize the same astrophysics constraints described in the caption of Fig. 1. In addition to the mass and radius constraints, we include the GW190814 event (green) [70], consistent with the maximum masses obtained from our calculation. Our results are presented in Table 2. In addition, the lower panel of Fig. 3 demonstrates the variation in maximum compactness across different$ \bar{\lambda} $ values. As indicated in Table 1, the maximum compactness$ M/R $ of the star increases with$ \bar{\lambda} $ , and at$ \bar{\lambda} = 0.8 $ , this value is$ M/R= 0.312 $ . Notably, the obtained values adhere to the Buchdahl limit of$ M/R < 4/9 $ . This consistency ensures that the configurations under consideration do not exhibit apparent horizons, thereby classifying them as stable, compact objects rather than black holes. In particular, an increase in$ \bar{\lambda} $ enhances the stiffness of pressure support, thereby shifting stellar configurations toward higher masses and greater compactness.
Figure 2. (color online) The mass-radius and compactness relationships of QSs for the given EoSs (Eqs. (5) and (11)) are presented in Table 2 for various values of
$ \bar{\lambda} $ . We draw graphs for$ B_{{\rm{eff}}}=B_{{\rm{eff}}, \perp} = 70 $ MeV/fm3 with the other parameters being$ \Sigma =0.9 $ and$ \bar{\lambda}_{\perp}= 0.5 $ . The color bands illustrate the MR constraints from PSR J0952-0607 (yellow) [67], PSR J0740+6620 (orange) [68], and PSR J0348+0432 (pink) [69]. We also include the GW190814 event, as indicated by the green horizontal band [70].$ \bar{\lambda} $ 

M R $ \rho_c $ 

$ M/R $ 

$ /M_{\odot} $ 

/km /(MeV/fm3) 0.2 1.89 10.89 788 0.257 0.4 2.24 11.90 731 0.280 0.6 2.53 12.57 731 0.298 0.8 2.77 13.12 731 0.312 Table 2. Properties of QSs for varying
$ \bar{\lambda} $ . We use the same parameter set as that indicated in Fig. 2.
Figure 3. (color online) The mass-radius and compactness relationships of QSs for the given EoSs (Eqs. (5) and (11)) are shown in Table 3 for different values of
$ \bar{\lambda}_{\perp} $ . We draw graphs for$ B_{{\rm{eff}}}=B_{{\rm{eff}}, \perp} = 60 $ MeV/fm3 with the other parameters being$ \Sigma =0.9 $ and$ \bar{\lambda}= 0.25 $ . The color bands illustrate the MR constraints from PSR J0952-0607 (yellow) [67], PSR J0740+6620 (orange) [68], and PSR J0348+0432 (pink) [69]. -
In the final stage of our investigation, we employ the variation in
$ \bar{\lambda}_{\perp} $ to carry out our analysis. The resulting correlations$ (M-R) $ and$ (M-M/R) $ are illustrated in Fig. 3. The figure demonstrates that the maximum mass and its corresponding radius increase as the values of$ B_{{\rm{eff}}, \perp} $ decrease, while$ B_{{\rm{eff}}} $ remains constant. The figure demonstrates that the maximum mass and its corresponding radius increase as the values of$ B_{{\rm{eff}}, \perp} $ decrease, while$ B_{{\rm{eff}}} $ remains constant. This observation is consistent with previous findings in Ref. [63]. From Fig. 3, we can also clearly see that the maximum mass exceeds$ M_{\rm{max}}> $ 2$ M_{\odot} $ depending on the model parameters, and reaches a value of$ M_{\rm max} =2.51 M_\odot $ with a corresponding radius$ R=11.91 $ km at$ \bar{\lambda}_{\perp}=0.05 $ . The results are shown in Table 3, demonstrating an excellent agreement in mass-radius measurements across various pulsars. This alignment is consistent with the astrophysical constraints outlined in the caption accompanying Fig. 1. Finally, we demonstrate how$ \bar{\lambda}_{\perp} $ affects the properties of the$ (M-M/R) $ relations in the lower panel of Fig. 4. Regarding the$ (M-M/R) $ curves, the trend is analogous to that of$ (M-R) $ , wherein the curves are indistinguishable in the low mass region but exhibit significant differences in the high mass region. Table 3 reveals that the maximum gravitational compactness increases with decreasing values of$ \bar{\lambda}_{\perp} $ , spanning over$ 0.289 < M/R < 0.313 $ .$ \bar{\lambda}_{\perp} $ 

M R $ \rho_c $ 

$ M/R $ 

$ M_{\odot} $ 

km MeV/fm3 0.05 2.51 11.91 1013 0.313 0.10 2.41 11.86 900 0.302 0.15 2.33 11.76 844 0.294 0.20 2.27 11.63 844 0.289 Table 3. Properties of QSs for varying
$ \bar{\lambda}_{\perp} $ . We use the same parameter set as indicated in Fig. 3.For comparison with the Einstein gravity case studied in Ref. [63], we note that the overall qualitative features of the sequences remain unchanged; however, quantitative deviations are evident. In particular, the maximum mass, the corresponding stellar radius, and the compactness exhibit systematic upward shifts once the rainbow parameter is introduced. These deviations, while modest in scale, are consistent across the parameter space explored and indicate that gravity’s rainbow extends the viable astrophysical window for stable quark star configurations beyond that obtained in general relativity.
-
In the final stage of our investigation, we employ the variation in
$ \bar{\lambda}_{\perp} $ to perform our analysis. The resulting correlations$ (M-R) $ and$ (M-M/R) $ are illustrated in Fig. 3. The figure demonstrates that the maximum mass and its corresponding radius increase as the values of$ B_{{\rm{eff}}, \perp} $ decrease, whereas$ B_{{\rm{eff}}} $ remains constant. This observation is consistent with previous findings in Ref. [63]. From Fig. 3, we can also observe that the maximum mass exceeds$ M_{\rm{max}}> $ $2\;M_{\odot} $ depending on the model parameters and reaches a value of$ M_{\rm max} =2.51\; M_\odot $ with a corresponding radius$ R=11.91 $ km at$ \bar{\lambda}_{\perp}=0.05 $ . The results are shown in Table 3, demonstrating an excellent agreement in mass-radius measurements across various pulsars. This alignment is consistent with the astrophysical constraints outlined in the caption accompanying Fig. 1. Finally, we demonstrate how$ \bar{\lambda}_{\perp} $ affects the properties of the$ (M- M/R) $ relations in the lower panel of Fig. 4. Regarding the$ (M-M/R) $ curves, the trend is analogous to that of$ (M-R) $ , wherein the curves are indistinguishable in the low mass region but exhibit significant differences in the high mass region. Table 3 reveals that the maximum gravitational compactness increases with decreasing values of$ \bar{\lambda}_{\perp} $ , spanning over$ 0.289 < M/R < 0.313 $ .$ \bar{\lambda}_{\perp} $ 

M R $ \rho_c $ 

$ M/R $ 

$ /M_{\odot} $ 

/km /(MeV/fm3) 0.05 2.51 11.91 1013 0.313 0.10 2.41 11.86 900 0.302 0.15 2.33 11.76 844 0.294 0.20 2.27 11.63 844 0.289 Table 3. Properties of QSs for varying
$ \bar{\lambda}_{\perp} $ . We use the same parameter set as that indicated in Fig. 3.In comparison with those from the Einstein gravity case reported in Ref. [63], the overall qualitative features of the sequences remain unchanged; however, quantitative deviations are evident. In particular, the maximum mass, corresponding stellar radius, and compactness exhibit systematic upward shifts once the rainbow parameter is introduced. These deviations, while modest in scale, are consistent across the parameter space explored and indicate that gravity’s rainbow extends the viable astrophysical window for stable QS configurations beyond that obtained in general relativity.
-
In the final stage of our investigation, we employ the variation in
$ \bar{\lambda}_{\perp} $ to perform our analysis. The resulting correlations$ (M-R) $ and$ (M-M/R) $ are illustrated in Fig. 3. The figure demonstrates that the maximum mass and its corresponding radius increase as the values of$ B_{{\rm{eff}}, \perp} $ decrease, whereas$ B_{{\rm{eff}}} $ remains constant. This observation is consistent with previous findings in Ref. [63]. From Fig. 3, we can also observe that the maximum mass exceeds$ M_{\rm{max}}> $ $2\;M_{\odot} $ depending on the model parameters and reaches a value of$ M_{\rm max} =2.51\; M_\odot $ with a corresponding radius$ R=11.91 $ km at$ \bar{\lambda}_{\perp}=0.05 $ . The results are shown in Table 3, demonstrating an excellent agreement in mass-radius measurements across various pulsars. This alignment is consistent with the astrophysical constraints outlined in the caption accompanying Fig. 1. Finally, we demonstrate how$ \bar{\lambda}_{\perp} $ affects the properties of the$ (M- M/R) $ relations in the lower panel of Fig. 4. Regarding the$ (M-M/R) $ curves, the trend is analogous to that of$ (M-R) $ , wherein the curves are indistinguishable in the low mass region but exhibit significant differences in the high mass region. Table 3 reveals that the maximum gravitational compactness increases with decreasing values of$ \bar{\lambda}_{\perp} $ , spanning over$ 0.289 < M/R < 0.313 $ .$ \bar{\lambda}_{\perp} $ 

M R $ \rho_c $ 

$ M/R $ 

$ /M_{\odot} $ 

/km /(MeV/fm3) 0.05 2.51 11.91 1013 0.313 0.10 2.41 11.86 900 0.302 0.15 2.33 11.76 844 0.294 0.20 2.27 11.63 844 0.289 Table 3. Properties of QSs for varying
$ \bar{\lambda}_{\perp} $ . We use the same parameter set as that indicated in Fig. 3.In comparison with those from the Einstein gravity case reported in Ref. [63], the overall qualitative features of the sequences remain unchanged; however, quantitative deviations are evident. In particular, the maximum mass, corresponding stellar radius, and compactness exhibit systematic upward shifts once the rainbow parameter is introduced. These deviations, while modest in scale, are consistent across the parameter space explored and indicate that gravity’s rainbow extends the viable astrophysical window for stable QS configurations beyond that obtained in general relativity.
-
In the final stage of our investigation, we employ the variation in
$ \bar{\lambda}_{\perp} $ to perform our analysis. The resulting correlations$ (M-R) $ and$ (M-M/R) $ are illustrated in Fig. 3. The figure demonstrates that the maximum mass and its corresponding radius increase as the values of$ B_{{\rm{eff}}, \perp} $ decrease, whereas$ B_{{\rm{eff}}} $ remains constant. This observation is consistent with previous findings in Ref. [63]. From Fig. 3, we can also observe that the maximum mass exceeds$ M_{\rm{max}}> $ $2\;M_{\odot} $ depending on the model parameters and reaches a value of$ M_{\rm max} =2.51\; M_\odot $ with a corresponding radius$ R=11.91 $ km at$ \bar{\lambda}_{\perp}=0.05 $ . The results are shown in Table 3, demonstrating an excellent agreement in mass-radius measurements across various pulsars. This alignment is consistent with the astrophysical constraints outlined in the caption accompanying Fig. 1. Finally, we demonstrate how$ \bar{\lambda}_{\perp} $ affects the properties of the$ (M- M/R) $ relations in the lower panel of Fig. 4. Regarding the$ (M-M/R) $ curves, the trend is analogous to that of$ (M-R) $ , wherein the curves are indistinguishable in the low mass region but exhibit significant differences in the high mass region. Table 3 reveals that the maximum gravitational compactness increases with decreasing values of$ \bar{\lambda}_{\perp} $ , spanning over$ 0.289 < M/R < 0.313 $ .$ \bar{\lambda}_{\perp} $ 

M R $ \rho_c $ 

$ M/R $ 

$ /M_{\odot} $ 

/km /(MeV/fm3) 0.05 2.51 11.91 1013 0.313 0.10 2.41 11.86 900 0.302 0.15 2.33 11.76 844 0.294 0.20 2.27 11.63 844 0.289 Table 3. Properties of QSs for varying
$ \bar{\lambda}_{\perp} $ . We use the same parameter set as that indicated in Fig. 3.In comparison with those from the Einstein gravity case reported in Ref. [63], the overall qualitative features of the sequences remain unchanged; however, quantitative deviations are evident. In particular, the maximum mass, corresponding stellar radius, and compactness exhibit systematic upward shifts once the rainbow parameter is introduced. These deviations, while modest in scale, are consistent across the parameter space explored and indicate that gravity’s rainbow extends the viable astrophysical window for stable QS configurations beyond that obtained in general relativity.
-
This section focuses on evaluating the stability of the proposed model. To perform this assessment, we employ the static stability criterion, adiabatic index, and speed of sound. Each stability-related condition is methodically analyzed and depicted graphically.
-
This section focuses on evaluating the stability of the proposed model. To perform this assessment, we employ the static stability criterion, adiabatic index, and speed of sound. Each stability-related condition is methodically analyzed and depicted graphically.
-
This section focuses on evaluating the stability of the proposed model. To perform this assessment, we employ the static stability criterion, adiabatic index, and speed of sound. Each stability-related condition is methodically analyzed and depicted graphically.
-
This part focuses on evaluating the proposed model's stability. To perform this assessment, we employ the static stability criterion, the adiabatic index, and the speed of sound. Each stability-related condition is methodically analyzed and depicted graphically.
-
We now assess the viability of the configuration by checking its stability criteria. For our analysis, we apply the static stability criterion [71, 72]. This criterion facilitates the determination of the dynamic stability of a stellar configuration through the analysis of the relationship between the total mass M of the star and its central energy density
$ \rho_c $ , specifically at the turning point where$ \dfrac{{\rm d}M}{{\rm d}\rho_c} = 0 $ . We define the following inequalities:$ \begin{array}{*{20}{l}} \dfrac{{\rm d}M}{{\rm d}\rho_c} < 0 &\; \rightarrow \text{unstable configuration}, \end{array} $

(18) $ \begin{array}{*{20}{l}} \dfrac{{\rm d}M}{{\rm d}\rho_c} > 0 &\; \rightarrow \text{stable configuration}. \end{array} $

(19) Notably, this condition is necessary but insufficient for stability. Under these circumstances, the point
$ (M_{\text{max}}, R_{M_{\text{max}}}) $ is classified as a boundary point that distinguishes the stable region from the unstable region. Figure 4 displays the$ M-\rho_c $ relationships for the three scenarios previously discussed, wherein the pink points denote the boundary point. -
We now proceed to assess the viability of the configuration by checking its stability criteria. For our analysis, we apply the static stability criterion [71, 72]. This criterion facilitates the determination of the dynamic stability of a stellar configuration through the analysis of the relationship between the total mass M of the star and its central energy density
$ \rho_c $ , specifically at the turning point where$ \dfrac{dM}{d\rho_c} = 0 $ . We define the following inequalities as:$ \begin{array}{*{20}{l}} \dfrac{dM}{d\rho_c} < 0 &\; \rightarrow \text{unstable configuration}, \end{array} $

(18) $ \begin{array}{*{20}{l}} \dfrac{dM}{d\rho_c} > 0 &\; \rightarrow \text{stable configuration}. \end{array} $

(19) We must emphasize that this condition is necessary but insufficient for stability. Under these circumstances, the point
$ (M_{\text{max}}, R_{M_{\text{max}}}) $ is classified as a boundary point that distinguishes the stable region from the unstable region. Figure 4 displays the$ M-\rho_c $ relationships for the three scenarios previously discussed, wherein the pink points denote the boundary point. -
We now assess the viability of the configuration by checking its stability criteria. For our analysis, we apply the static stability criterion [71, 72]. This criterion facilitates the determination of the dynamic stability of a stellar configuration through the analysis of the relationship between the total mass M of the star and its central energy density
$ \rho_c $ , specifically at the turning point where$ \dfrac{{\rm d}M}{{\rm d}\rho_c} = 0 $ . We define the following inequalities:$ \begin{array}{*{20}{l}} \dfrac{{\rm d}M}{{\rm d}\rho_c} < 0 &\; \rightarrow \text{unstable configuration}, \end{array} $

(18) $ \begin{array}{*{20}{l}} \dfrac{{\rm d}M}{{\rm d}\rho_c} > 0 &\; \rightarrow \text{stable configuration}. \end{array} $

(19) Notably, this condition is necessary but insufficient for stability. Under these circumstances, the point
$ (M_{\text{max}}, R_{M_{\text{max}}}) $ is classified as a boundary point that distinguishes the stable region from the unstable region. Figure 4 displays the$ M-\rho_c $ relationships for the three scenarios previously discussed, wherein the pink points denote the boundary point. -
We now assess the viability of the configuration by checking its stability criteria. For our analysis, we apply the static stability criterion [71, 72]. This criterion facilitates the determination of the dynamic stability of a stellar configuration through the analysis of the relationship between the total mass M of the star and its central energy density
$ \rho_c $ , specifically at the turning point where$ \dfrac{{\rm d}M}{{\rm d}\rho_c} = 0 $ . We define the following inequalities:$ \begin{array}{*{20}{l}} \dfrac{{\rm d}M}{{\rm d}\rho_c} < 0 &\; \rightarrow \text{unstable configuration}, \end{array} $

(18) $ \begin{array}{*{20}{l}} \dfrac{{\rm d}M}{{\rm d}\rho_c} > 0 &\; \rightarrow \text{stable configuration}. \end{array} $

(19) Notably, this condition is necessary but insufficient for stability. Under these circumstances, the point
$ (M_{\text{max}}, R_{M_{\text{max}}}) $ is classified as a boundary point that distinguishes the stable region from the unstable region. Figure 4 displays the$ M-\rho_c $ relationships for the three scenarios previously discussed, wherein the pink points denote the boundary point. -
This analysis focuses on the stability of astrophysical models by examining the adiabatic index, γ. This approach, initially proposed by Chandrasekhar [73], aimed to evaluate the dynamical stability of equilibrium configurations. Additionally, the study presented in [74] investigated the stability of compact stars under the framework of rainbow gravity. The radial adiabatic index γ is characterized by
$ {\gamma}= \left(1+\frac{\rho}{P}\right){v_s^2}, $

(20) where
$ {v_s^2} $ is the speed of sound. The adiabatic index γ is associated with a critical value, known as$ <\gamma> >\gamma_{cr} $ , which is essential for determining the instability of a static spherically symmetric configuration. Here,$ <\gamma> $ represents the averaged adiabatic index [75]. Extensive studies have been conducted on the static stability criterion and the significance of the adiabatic index γ in [76−79]. In pure Newtonian gravity, one must recognize that the value of$ \gamma_{cr} $ always equals$ 4/3 $ , whereas this value exceeds$ 4/3 $ when the effects of GR are considered. Utilizing Eq. (20), Fig. 5 presents the dependence of γ with respect to the radius for various selected values of$ \left(\Sigma, \bar{\lambda}_{\perp}, \bar{\lambda}\right) $ . The figures indicate that all situations meet the criterion$ \gamma > 4/3 $ . This finding confirms that QSs are stable against radial adiabatic infinitesimal perturbations. -
This analysis focuses on the stability of astrophysical models by examining the adiabatic index, γ. This approach, initially proposed by Chandrasekhar [73], aimed to evaluate the dynamical stability of equilibrium configurations. Additionally, the study presented in [74] investigated the stability of compact stars under the framework of rainbow gravity. The radial adiabatic index γ is characterized by
$ {\gamma}= \left(1+\frac{\rho}{P}\right){v_s^2}, $

(20) where
$ {v_s^2} $ is the speed of sound. The adiabatic index γ is associated with a critical value, known as$ <\gamma> >\gamma_{cr} $ , which is essential for determining the instability of a static spherically symmetric configuration. Here,$ <\gamma> $ represents the averaged adiabatic index [75]. Extensive studies have been conducted on the static stability criterion and the significance of the adiabatic index γ in [76−79]. In pure Newtonian gravity, one must recognize that the value of$ \gamma_{cr} $ always equals$ 4/3 $ , whereas this value exceeds$ 4/3 $ when the effects of GR are considered. Utilizing Eq. (20), Fig. 5 presents the dependence of γ with respect to the radius for various selected values of$ \left(\Sigma, \bar{\lambda}_{\perp}, \bar{\lambda}\right) $ . The figures indicate that all situations meet the criterion$ \gamma > 4/3 $ . This finding confirms that QSs are stable against radial adiabatic infinitesimal perturbations. -
This analysis focuses on the stability of astrophysical models by examining the adiabatic index, γ. This approach, initially proposed by Chandrasekhar [73], aimed to evaluate the dynamical stability of equilibrium configurations. Additionally, the research presented in [74] investigates the stability of compact stars under the framework of rainbow gravity. The radial adiabatic index γ is characterized by
$ {\gamma}= \left(1+\frac{\rho}{P}\right){v_s^2}, $

(20) where
$ {v_s^2} $ is the sound speed. Since the adiabatic index γ is associated with a critical value, known as$ <\gamma> >\gamma_{cr} $ , which is essential for determining the instability of a static spherically symmetric configuration. Here,$ <\gamma> $ represents the averaged adiabatic index [75]. Extensive research has been conducted on the static stability criterion and the significance of the adiabatic index γ in [76−79]. In pure Newtonian gravity, one must recognize that the value of$ \gamma_{cr} $ always equals$ 4/3 $ , whereas this value exceeds$ 4/3 $ when the effects of GR are considered. Utilizing Eq. (20), Fig. 5 presents the dependence of γ with respect to the radius for various selected values of$ \left(\Sigma, \bar{\lambda}_{\perp}, \bar{\lambda}\right) $ . The figures indicate that all situations meet the criterion$ \gamma > 4/3 $ . This finding confirms that QSs are stable against radial adiabatic infinitesimal perturbations. -
This analysis focuses on the stability of astrophysical models by examining the adiabatic index, γ. This approach, initially proposed by Chandrasekhar [73], aimed to evaluate the dynamical stability of equilibrium configurations. Additionally, the study presented in [74] investigated the stability of compact stars under the framework of rainbow gravity. The radial adiabatic index γ is characterized by
$ {\gamma}= \left(1+\frac{\rho}{P}\right){v_s^2}, $

(20) where
$ {v_s^2} $ is the speed of sound. The adiabatic index γ is associated with a critical value, known as$ <\gamma> >\gamma_{cr} $ , which is essential for determining the instability of a static spherically symmetric configuration. Here,$ <\gamma> $ represents the averaged adiabatic index [75]. Extensive studies have been conducted on the static stability criterion and the significance of the adiabatic index γ in [76−79]. In pure Newtonian gravity, one must recognize that the value of$ \gamma_{cr} $ always equals$ 4/3 $ , whereas this value exceeds$ 4/3 $ when the effects of GR are considered. Utilizing Eq. (20), Fig. 5 presents the dependence of γ with respect to the radius for various selected values of$ \left(\Sigma, \bar{\lambda}_{\perp}, \bar{\lambda}\right) $ . The figures indicate that all situations meet the criterion$ \gamma > 4/3 $ . This finding confirms that QSs are stable against radial adiabatic infinitesimal perturbations. -
In our final analysis, we examined the causality condition. This condition requires that the speed of sound, represented by
$ \begin{array}{*{20}{l}} v_{r,{\bot}}^2=dP_{\{r,{\bot}\}}/d\rho, \end{array} $

(21) must not surpass the speed of light in a vacuum, expressed as
$ v_{r,{\bot}}^2 \leq 1 $ . The relationship between sound velocity and distance r in radial and transverse directions is illustrated in Figs. 6 and 7, respectively. These graphs show the results for various representative values of Σ,$ \bar{\lambda}_{\perp} $ , and$ \bar{\lambda} $ , ensuring adherence to the causality condition and validating the physical feasibility of the solutions.Before concluding, we briefly comment on the role of anisotropy in the broader context of compact star stability. As shown in our analysis, allowing for
$ \bar{\lambda} \neq \bar{\lambda}_{\perp} $ introduces controlled deviations between radial and tangential pressures, which directly influence the equilibrium configurations. In particular, anisotropy can either enhance or reduce the effective pressure support, thereby modifying the maximum mass and compactness of quark stars. Such behavior has been widely connected with the stability properties of compact objects, where anisotropic stresses may delay the onset of collapse or, conversely, trigger instabilities under certain conditions. We further note that the study of radial oscillation modes has long been recognized as a powerful tool for probing the stability and EOS of compact stars, including strange stars [80] and strangeon stars [81]. While a full oscillation analysis lies beyond the scope of the present work, our results provide a complementary step in this direction by clarifying how anisotropy, when embedded in gravity’s rainbow, affects the stellar structure in equilibrium. -
In our final analysis, we examined the causality condition. This condition requires that the speed of sound, represented by
$ \begin{array}{*{20}{l}} v_{r,{\bot}}^2={\rm d}P_{\{r,{\bot}\}}/{\rm d}\rho, \end{array} $

(21) must not surpass the speed of light in vacuum, expressed as
$ v_{r,{\bot}}^2 \leq 1 $ . The relationship between sound velocity and distance r in radial and transverse directions is illustrated in Figs. 6 and 7, respectively. These graphs show the results for various representative values of Σ,$ \bar{\lambda}_{\perp} $ , and$ \bar{\lambda} $ , ensuring adherence to the causality condition and validating the physical feasibility of the solutions.Before concluding, we briefly comment on the role of anisotropy in the broader context of compact star stability. As shown in our analysis, allowing for
$ \bar{\lambda} \neq \bar{\lambda}_{\perp} $ introduces controlled deviations between radial and tangential pressures, which directly influence the equilibrium configurations. In particular, anisotropy can either enhance or reduce the effective pressure support, thereby modifying the maximum mass and compactness of QSs. Such behavior has been widely connected with the stability properties of compact objects, where anisotropic stresses may delay the onset of collapse or, conversely, trigger instabilities under certain conditions. We further note that the study of radial oscillation modes has long been recognized as a powerful tool for probing the stability and EOS of compact stars, including strange stars [80] and strangeon stars [81]. While a full oscillation analysis lies beyond the scope of the present study, our results provide a complementary step in this direction by clarifying how anisotropy, when embedded in gravity’s rainbow, affects the stellar structure in equilibrium. -
In our final analysis, we examined the causality condition. This condition requires that the speed of sound, represented by
$ \begin{array}{*{20}{l}} v_{r,{\bot}}^2={\rm d}P_{\{r,{\bot}\}}/{\rm d}\rho, \end{array} $

(21) must not surpass the speed of light in vacuum, expressed as
$ v_{r,{\bot}}^2 \leq 1 $ . The relationship between sound velocity and distance r in radial and transverse directions is illustrated in Figs. 6 and 7, respectively. These graphs show the results for various representative values of Σ,$ \bar{\lambda}_{\perp} $ , and$ \bar{\lambda} $ , ensuring adherence to the causality condition and validating the physical feasibility of the solutions.Before concluding, we briefly comment on the role of anisotropy in the broader context of compact star stability. As shown in our analysis, allowing for
$ \bar{\lambda} \neq \bar{\lambda}_{\perp} $ introduces controlled deviations between radial and tangential pressures, which directly influence the equilibrium configurations. In particular, anisotropy can either enhance or reduce the effective pressure support, thereby modifying the maximum mass and compactness of QSs. Such behavior has been widely connected with the stability properties of compact objects, where anisotropic stresses may delay the onset of collapse or, conversely, trigger instabilities under certain conditions. We further note that the study of radial oscillation modes has long been recognized as a powerful tool for probing the stability and EOS of compact stars, including strange stars [80] and strangeon stars [81]. While a full oscillation analysis lies beyond the scope of the present study, our results provide a complementary step in this direction by clarifying how anisotropy, when embedded in gravity’s rainbow, affects the stellar structure in equilibrium. -
In our final analysis, we examined the causality condition. This condition requires that the speed of sound, represented by
$ \begin{array}{*{20}{l}} v_{r,{\bot}}^2={\rm d}P_{\{r,{\bot}\}}/{\rm d}\rho, \end{array} $

(21) must not surpass the speed of light in vacuum, expressed as
$ v_{r,{\bot}}^2 \leq 1 $ . The relationship between sound velocity and distance r in radial and transverse directions is illustrated in Figs. 6 and 7, respectively. These graphs show the results for various representative values of Σ,$ \bar{\lambda}_{\perp} $ , and$ \bar{\lambda} $ , ensuring adherence to the causality condition and validating the physical feasibility of the solutions.Before concluding, we briefly comment on the role of anisotropy in the broader context of compact star stability. As shown in our analysis, allowing for
$ \bar{\lambda} \neq \bar{\lambda}_{\perp} $ introduces controlled deviations between radial and tangential pressures, which directly influence the equilibrium configurations. In particular, anisotropy can either enhance or reduce the effective pressure support, thereby modifying the maximum mass and compactness of QSs. Such behavior has been widely connected with the stability properties of compact objects, where anisotropic stresses may delay the onset of collapse or, conversely, trigger instabilities under certain conditions. We further note that the study of radial oscillation modes has long been recognized as a powerful tool for probing the stability and EOS of compact stars, including strange stars [80] and strangeon stars [81]. While a full oscillation analysis lies beyond the scope of the present study, our results provide a complementary step in this direction by clarifying how anisotropy, when embedded in gravity’s rainbow, affects the stellar structure in equilibrium. -
In this study, we explored the characteristics of QSs with anisotropic pressures utilizing a model that includes interquark effects such as pQCD corrections and color superconductivity. The EoS has been transformed into a dimensionless form depending on a single parameter
$ \bar{\lambda} $ . The entire configuration adheres to the principles of gravity's rainbow, where the energy-dependent rainbow functions$ \Xi(x) $ and$ \Sigma(x) $ modify the spacetime geometry and dispersion relations at high energies. Subsequently, equations (13)-(15) were derived as modified TOV equations, forming the basis for investigating the properties of QSs.Next, we solved equations (13)-(15) numerically, paying particular attention to anisotropic QS configurations subjected to appropriate boundary conditions. Our study systematically investigates the role of key parameters - B,
$ B_{\perp} $ ,$ \bar{\lambda} $ , and$ \bar{\lambda}_{\perp} $ -on the$ M-R $ and the compactness relations of QSs, making full use of their respective flexible frameworks. By thoroughly examining the$ M-R $ curves, we demonstrate how variations in these parameters impact the QSs' maximum mass and radius. Notably, our findings revealed that QSs can have masses greater than$ 2M_{\odot} $ ; these results align closely with recent observational constraints from pulsar timing, such as PSR J0740+6620 and PSR J0952-0607, as well as gravitational wave detection like GW190814. In addition, anisotropic effects lead to considerable deviations from the isotropic QS models and particularly enhance the maximum mass and radius without requiring any exotic assumptions. The parameter$ \bar{\lambda}_\perp $ , characterized by the transverse pressure profile, plays a crucial role in tuning the compactness and stability of the configuration. We also investigate the gravitational compactness, demonstrating the consistency of our findings with satisfying the Buchdahl limit, i.e.,$ M/R < 4/9 $ . The used methodology further examines the stability of the configuration in Section 4, where we perform static stability criteria, evaluate adiabatic indices, and sound speed profiles for QSs with varying parameters. These analyses substantiate the stability of QS configurations, thereby reinforcing their viability as astrophysical models. In contrast to the Einstein gravity analysis in Ref. [63], our results indicate that incorporating gravity’s rainbow functions induces systematic shifts in stellar parameters, including an enhancement of the maximum mass, radius, and compactness. Although the qualitative behavior remains similar, these quantitative deviations demonstrate that rainbow gravity broadens the astrophysical parameter space accessible to stable quark star models. Beyond the structural properties, quark stars may also manifest through distinctive electromagnetic phenomena. For instance, crustal collapses in quark stars have been proposed as potential sources of repeating fast radio bursts [82]. Quark star engines have also been linked to gamma-ray bursts [83] and superbursts [84]. Although such emission mechanisms lie outside the primary scope of this work, our results on stellar stability and compactness provide a theoretical foundation that could be extended to explore these astrophysical signatures in future studies.In summary, by extending interacting quark matter with pressure anisotropy to the framework of gravity’s rainbow, we find systematic modifications to the stellar equilibrium relative to Einstein gravity. In particular, the sequences exhibit modest increases in the maximum mass, the corresponding radius, and the compactness, while remaining causal and stable over the explored parameter ranges. These quantitative shifts delineate where rainbow effects become appreciable, yet the overall qualitative trends remain similar to the GR baseline.
-
In this study, we explored the characteristics of QSs with anisotropic pressures by utilizing a model that includes interquark effects, such as pQCD corrections and color superconductivity. The EoS was transformed into a dimensionless form depending on a single parameter
$ \bar{\lambda} $ . The entire configuration adheres to the principles of gravity's rainbow, where the energy-dependent rainbow functions$ \Xi(x) $ and$ \Sigma(x) $ modify the spacetime geometry and dispersion relations at high energies. Subsequently, Eqs. (13)−(15) were derived as modified TOV equations, forming the basis for investigating the properties of QSs.Next, we solved Eqs. (13)−(15) numerically, paying particular attention to anisotropic QS configurations subjected to appropriate boundary conditions. Our study systematically investigates the role of key parameters, namely, B,
$ B_{\perp} $ ,$ \bar{\lambda} $ , and$ \bar{\lambda}_{\perp} $ , on the$ M-R $ and compactness relations of QSs, making full use of their respective flexible frameworks. By thoroughly examining the$ M-R $ curves, we demonstrate how variations in these parameters influence the maximum masses and radii of QSs. Notably, our findings revealed that QSs can have masses greater than$ 2\;M_{\odot} $ ; these results align closely with recent observational constraints from pulsar timing, such as PSR J0740+6620 and PSR J0952-0607, as well as gravitational wave detection, such as GW190814. In addition, anisotropic effects lead to considerable deviations from the isotropic QS models and particularly enhance the maximum mass and radius without requiring any exotic assumptions. The parameter$ \bar{\lambda}_\perp $ , characterized by the transverse pressure profile, plays a crucial role in tuning the compactness and stability of the configuration. We also investigated the gravitational compactness, demonstrating the consistency of our findings by satisfying the Buchdahl limit, i.e.,$ M/R < 4/9 $ . The used methodology further examines the stability of the configuration in Section 4, where we analyzed static stability criteria, adiabatic indices, and sound speed profiles for QSs with varying parameters. These analyses substantiate the stability of QS configurations, thereby reinforcing their viability as astrophysical models. In contrast to the Einstein gravity analysis in Ref. [63], our results indicate that incorporating gravity’s rainbow functions induces systematic shifts in stellar parameters, including an enhancement of the maximum mass, radius, and compactness. Although the qualitative behavior remains similar, these quantitative deviations demonstrate that rainbow gravity broadens the astrophysical parameter space accessible to stable QS models. Beyond their structural properties, QSs may also manifest through distinctive electromagnetic phenomena. For instance, crustal collapses in QSs have been proposed as potential sources of repeating fast radio bursts [82]. QS engines have also been linked to gamma-ray bursts [83] and superbursts [84]. Although such emission mechanisms lie outside the primary scope of this study, our results on stellar stability and compactness provide a theoretical foundation that could be extended to explore these astrophysical signatures in future studies.In summary, by extending interacting QM with pressure anisotropy to the framework of gravity’s rainbow, we find systematic modifications to the stellar equilibrium relative to Einstein gravity. In particular, the sequences exhibit modest increases in the maximum mass, corresponding radius, and compactness, while remaining causal and stable over the explored parameter ranges. These quantitative shifts delineate where rainbow effects become appreciable; nevertheless, the overall qualitative trends remain similar to those of the GR baseline.
-
In this study, we explored the characteristics of QSs with anisotropic pressures by utilizing a model that includes interquark effects, such as pQCD corrections and color superconductivity. The EoS was transformed into a dimensionless form depending on a single parameter
$ \bar{\lambda} $ . The entire configuration adheres to the principles of gravity's rainbow, where the energy-dependent rainbow functions$ \Xi(x) $ and$ \Sigma(x) $ modify the spacetime geometry and dispersion relations at high energies. Subsequently, Eqs. (13)−(15) were derived as modified TOV equations, forming the basis for investigating the properties of QSs.Next, we solved Eqs. (13)−(15) numerically, paying particular attention to anisotropic QS configurations subjected to appropriate boundary conditions. Our study systematically investigates the role of key parameters, namely, B,
$ B_{\perp} $ ,$ \bar{\lambda} $ , and$ \bar{\lambda}_{\perp} $ , on the$ M-R $ and compactness relations of QSs, making full use of their respective flexible frameworks. By thoroughly examining the$ M-R $ curves, we demonstrate how variations in these parameters influence the maximum masses and radii of QSs. Notably, our findings revealed that QSs can have masses greater than$ 2\;M_{\odot} $ ; these results align closely with recent observational constraints from pulsar timing, such as PSR J0740+6620 and PSR J0952-0607, as well as gravitational wave detection, such as GW190814. In addition, anisotropic effects lead to considerable deviations from the isotropic QS models and particularly enhance the maximum mass and radius without requiring any exotic assumptions. The parameter$ \bar{\lambda}_\perp $ , characterized by the transverse pressure profile, plays a crucial role in tuning the compactness and stability of the configuration. We also investigated the gravitational compactness, demonstrating the consistency of our findings by satisfying the Buchdahl limit, i.e.,$ M/R < 4/9 $ . The used methodology further examines the stability of the configuration in Section 4, where we analyzed static stability criteria, adiabatic indices, and sound speed profiles for QSs with varying parameters. These analyses substantiate the stability of QS configurations, thereby reinforcing their viability as astrophysical models. In contrast to the Einstein gravity analysis in Ref. [63], our results indicate that incorporating gravity’s rainbow functions induces systematic shifts in stellar parameters, including an enhancement of the maximum mass, radius, and compactness. Although the qualitative behavior remains similar, these quantitative deviations demonstrate that rainbow gravity broadens the astrophysical parameter space accessible to stable QS models. Beyond their structural properties, QSs may also manifest through distinctive electromagnetic phenomena. For instance, crustal collapses in QSs have been proposed as potential sources of repeating fast radio bursts [82]. QS engines have also been linked to gamma-ray bursts [83] and superbursts [84]. Although such emission mechanisms lie outside the primary scope of this study, our results on stellar stability and compactness provide a theoretical foundation that could be extended to explore these astrophysical signatures in future studies.In summary, by extending interacting QM with pressure anisotropy to the framework of gravity’s rainbow, we find systematic modifications to the stellar equilibrium relative to Einstein gravity. In particular, the sequences exhibit modest increases in the maximum mass, corresponding radius, and compactness, while remaining causal and stable over the explored parameter ranges. These quantitative shifts delineate where rainbow effects become appreciable; nevertheless, the overall qualitative trends remain similar to those of the GR baseline.
-
In this study, we explored the characteristics of QSs with anisotropic pressures by utilizing a model that includes interquark effects, such as pQCD corrections and color superconductivity. The EoS was transformed into a dimensionless form depending on a single parameter
$ \bar{\lambda} $ . The entire configuration adheres to the principles of gravity's rainbow, where the energy-dependent rainbow functions$ \Xi(x) $ and$ \Sigma(x) $ modify the spacetime geometry and dispersion relations at high energies. Subsequently, Eqs. (13)−(15) were derived as modified TOV equations, forming the basis for investigating the properties of QSs.Next, we solved Eqs. (13)−(15) numerically, paying particular attention to anisotropic QS configurations subjected to appropriate boundary conditions. Our study systematically investigates the role of key parameters, namely, B,
$ B_{\perp} $ ,$ \bar{\lambda} $ , and$ \bar{\lambda}_{\perp} $ , on the$ M-R $ and compactness relations of QSs, making full use of their respective flexible frameworks. By thoroughly examining the$ M-R $ curves, we demonstrate how variations in these parameters influence the maximum masses and radii of QSs. Notably, our findings revealed that QSs can have masses greater than$ 2\;M_{\odot} $ ; these results align closely with recent observational constraints from pulsar timing, such as PSR J0740+6620 and PSR J0952-0607, as well as gravitational wave detection, such as GW190814. In addition, anisotropic effects lead to considerable deviations from the isotropic QS models and particularly enhance the maximum mass and radius without requiring any exotic assumptions. The parameter$ \bar{\lambda}_\perp $ , characterized by the transverse pressure profile, plays a crucial role in tuning the compactness and stability of the configuration. We also investigated the gravitational compactness, demonstrating the consistency of our findings by satisfying the Buchdahl limit, i.e.,$ M/R < 4/9 $ . The used methodology further examines the stability of the configuration in Section 4, where we analyzed static stability criteria, adiabatic indices, and sound speed profiles for QSs with varying parameters. These analyses substantiate the stability of QS configurations, thereby reinforcing their viability as astrophysical models. In contrast to the Einstein gravity analysis in Ref. [63], our results indicate that incorporating gravity’s rainbow functions induces systematic shifts in stellar parameters, including an enhancement of the maximum mass, radius, and compactness. Although the qualitative behavior remains similar, these quantitative deviations demonstrate that rainbow gravity broadens the astrophysical parameter space accessible to stable QS models. Beyond their structural properties, QSs may also manifest through distinctive electromagnetic phenomena. For instance, crustal collapses in QSs have been proposed as potential sources of repeating fast radio bursts [82]. QS engines have also been linked to gamma-ray bursts [83] and superbursts [84]. Although such emission mechanisms lie outside the primary scope of this study, our results on stellar stability and compactness provide a theoretical foundation that could be extended to explore these astrophysical signatures in future studies.In summary, by extending interacting QM with pressure anisotropy to the framework of gravity’s rainbow, we find systematic modifications to the stellar equilibrium relative to Einstein gravity. In particular, the sequences exhibit modest increases in the maximum mass, corresponding radius, and compactness, while remaining causal and stable over the explored parameter ranges. These quantitative shifts delineate where rainbow effects become appreciable; nevertheless, the overall qualitative trends remain similar to those of the GR baseline.
-
We thank the anonymous reviewers for their constructive comments and insightful suggestions, which helped us improve the clarity and scope of this manuscript.
-
We thank the anonymous reviewers for their constructive comments and insightful suggestions, which helped us to improve the clarity and scope of this manuscript. J.R. acknowledges the Grant No. F-FA-2021-510 of the Ministry of Innovative Development of Uzbekistan.
-
We thank the anonymous reviewers for their constructive comments and insightful suggestions, which helped us improve the clarity and scope of this manuscript.
-
We thank the anonymous reviewers for their constructive comments and insightful suggestions, which helped us improve the clarity and scope of this manuscript.
Existence of quark stars in gravity's rainbow: the significance of strongly interacting quark matter
- Received Date: 2025-07-20
- Available Online: 2025-12-15
Abstract: This study explores the internal composition and equation of state (EoS) of quark stars (QSs) characterized by pressure anisotropy, considering recent astrophysical findings within the framework of gravity's rainbow. By employing perturbative quantum chromodynamics corrections and the concept of color superconductivity, the EoS is formulated as a dimensionless function reliant on a single parameter, thereby offering an in-depth analysis of the effects of strong interactions. The study is further extended by rescaling the EoS and applying dimensionless variables, thus covering the range from non-interacting quark matter to extreme stiffness characterized by a parameter





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

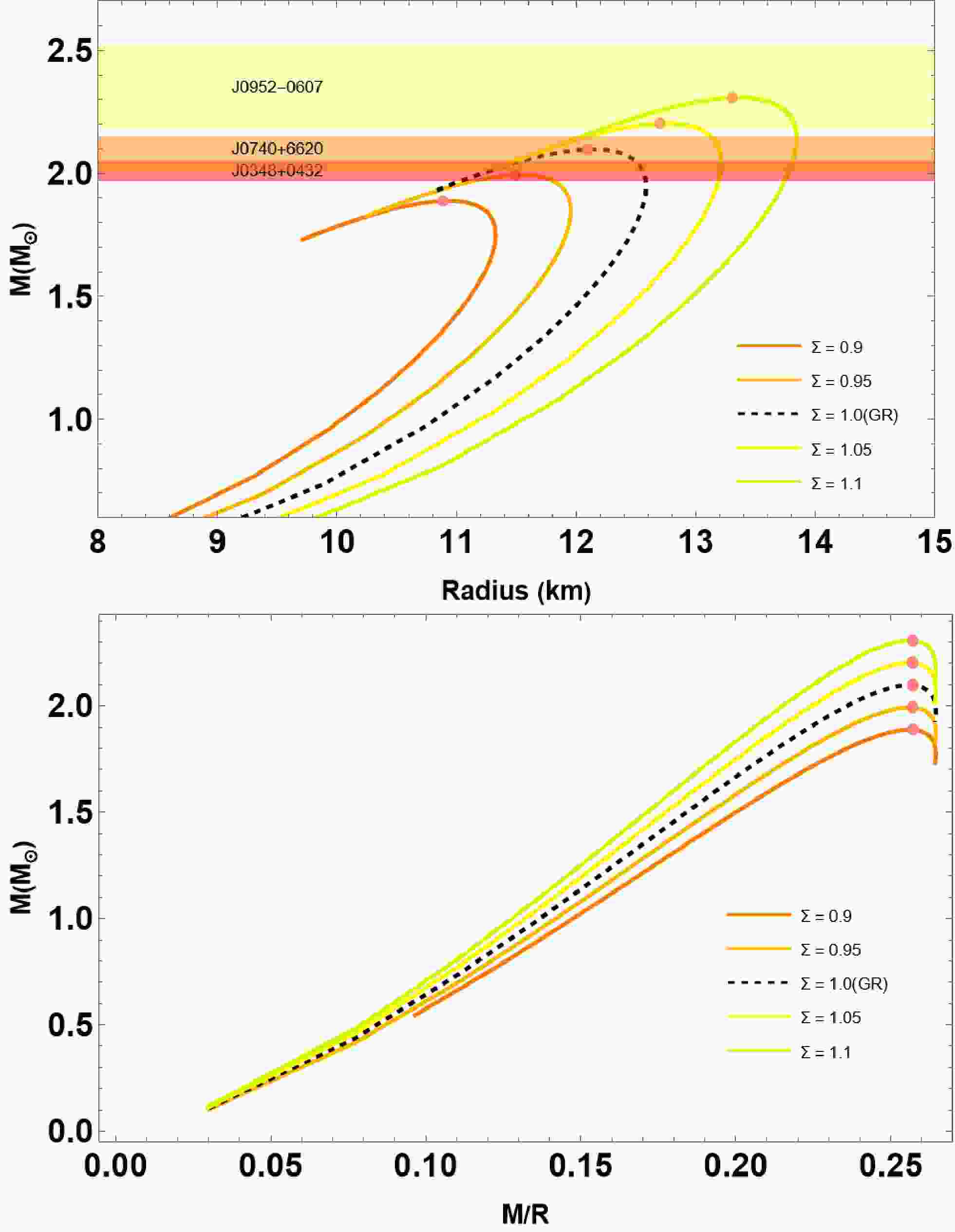










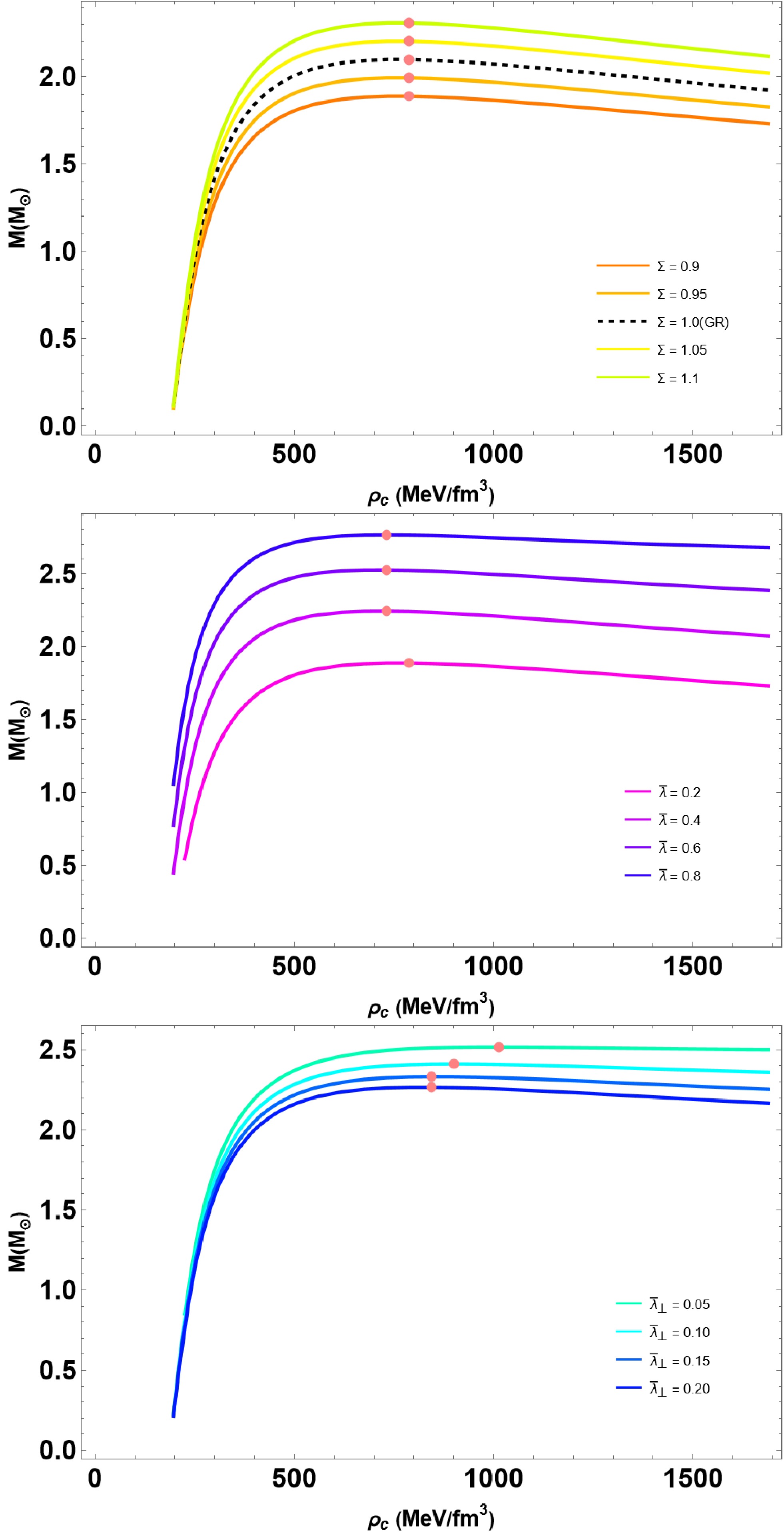
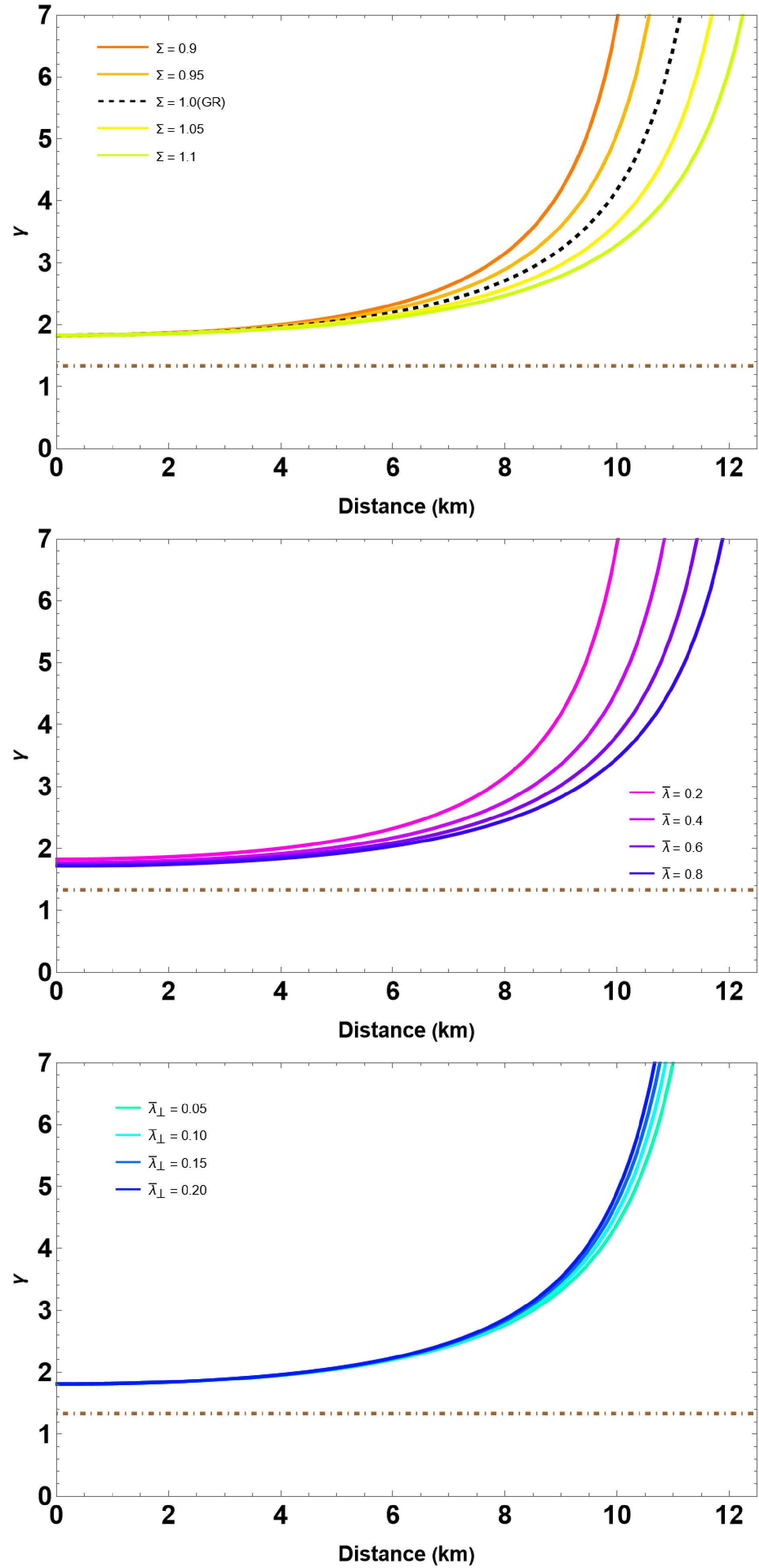
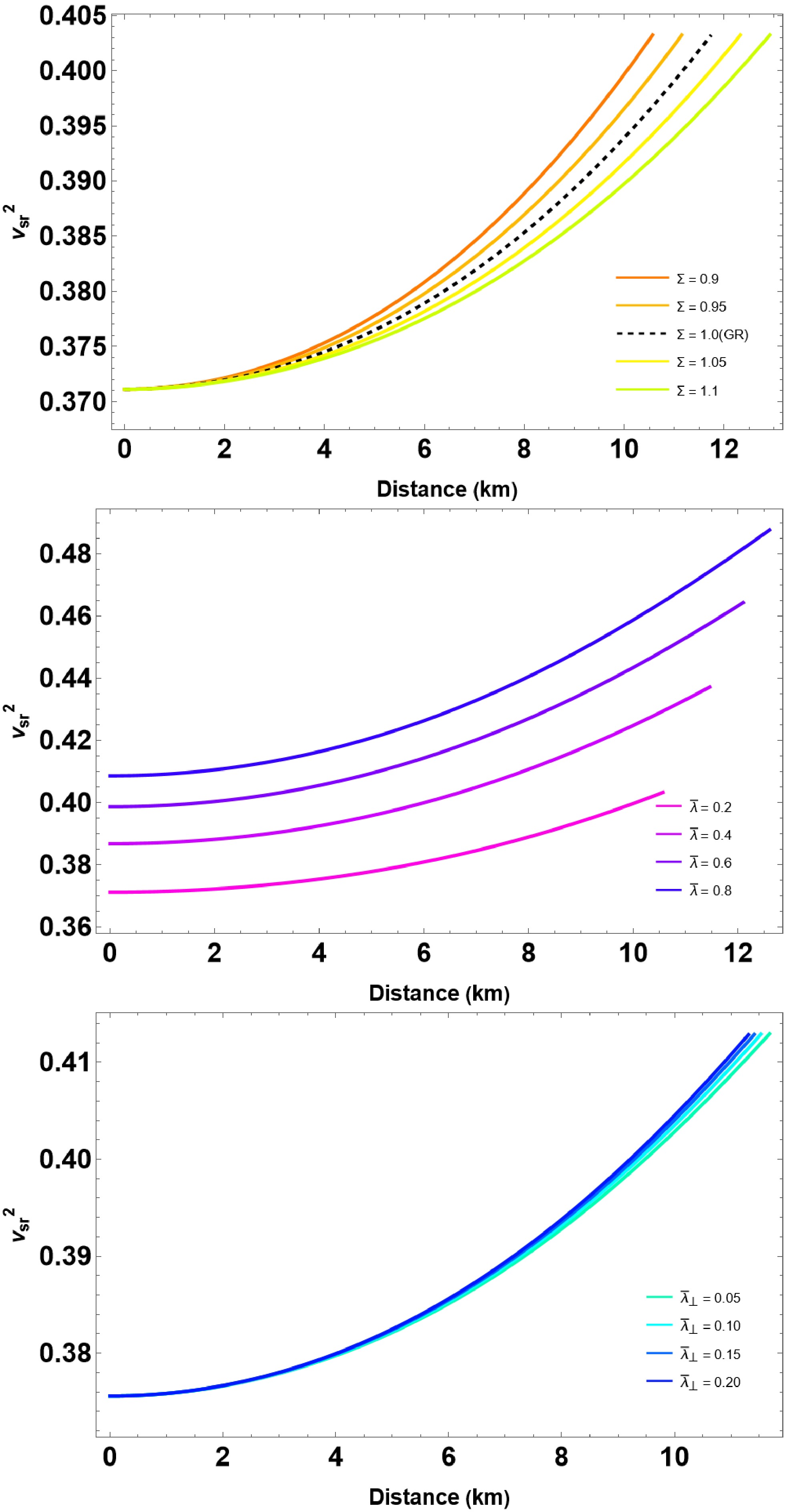
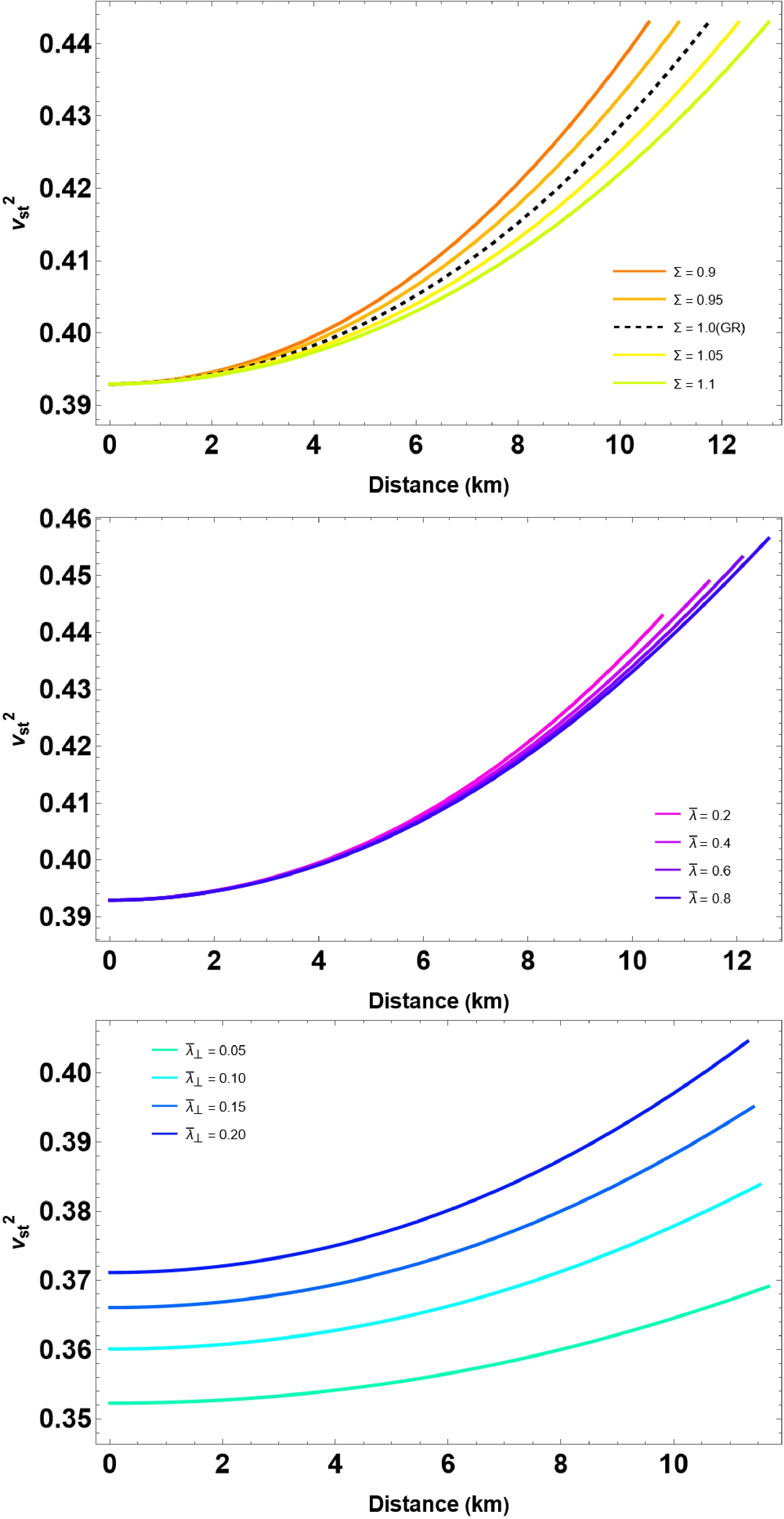



 DownLoad:
DownLoad: