-
The exploration of the microscopic properties of black holes is a hot topic in theoretical physics. Traditional general relativity holds that there is no matter structure inside a black hole, other than the singularity. However, the proposal of the black hole temperature and area entropy has provided a new perspective for reinterpreting the properties of black holes [1-3]. With the development of black hole thermodynamics [4-8], and specifically the introduction of extended phase space [9], black holes have been found to show abundant critical behaviors [10-13], indicating that they possess some unknown microscopic characteristics.
Recently, based on the Ruppeiner thermodynamic geometry [14], a new abstract concept of a "black hole molecule" was proposed [15], which provides a new perspective by which the microscopic behavior of black holes can be studied roughly and phenomenologically. The proponents of this concept describe the interior of a black hole as a kind of fluid composed of black hole molecules that represent its microstructure. This is similar to the atomic hypothesis put forward by Boltzmann more than a century ago. Although we do not know exactly what these black hole molecules are, as a preliminary exploration of black hole microstructure, this abstract concept is very useful for understanding certain microscopic properties of black holes. Among these properties, the role of the Ruppeiner geometry is particularly important. It introduces a thermodynamic metric for representing the thermodynamic fluctuation theory. Meanwhile, the components of the inverse thermodynamic metric correspond to second moments in the fluctuation theory of equilibrium thermodynamics. The original form of the thermodynamic metric is the second derivative of the entropy with respect to other generalized coordinates (or other thermodynamic quantities).
When studying the Ruppeiner geometry of black holes, the thermodynamic curvature is the most important physical quantity. It has two important roles:
● Analyzing the phase transition. The divergence of the thermodynamic curvature is believed to correspond to some kind of phase transition within the system. There are two ways to understand the divergence. On the one hand, the divergence of the thermodynamic curvature corresponds to the configuration of an extremal black hole, or perhaps, the black hole/extremal black hole transition [15-27]. Alternatively, the divergence of the thermodynamic curvature corresponds to the divergence of the heat capacity, i.e., a second-order phase transition [28-37]. However, at present, there is no theoretical requirement that the divergent point of the thermodynamic curvature must correspond to the divergence of the heat capacity or the configuration of an extremal black hole. Irrespective of what the divergent point of the thermodynamic curvature corresponds to, both ideas can be regarded as reasonable and feasible ways to explain the divergent behavior of the thermodynamic curvature.
● Discussing the interaction in a thermodynamic system. As with any new physical quantity, we only care about the role of thermodynamic curvature itself in the context of the microscopic behavior of the system. In certain statistical mechanics models, there is an empirical, yet hypothetical, observation from the view of thermodynamic geometry, that is, the thermodynamic curvature can have a corresponding relationship with the interactions between the constituent molecules of the system [38,39]. However, for the black hole system, the situation is slightly different, and we need to explain the logic for exploring its microscopic behavior. In statistical mechanics, it is generally accepted that if we know the microscopic dynamics of a system, its thermodynamic properties can be derived from the statistical physics of the system. In general, the inverse process does not hold, namely we cannot know the micro-dynamics of the system from its thermodynamics. Turning to the black hole thermodynamic system, although its thermodynamic properties have been discussed at length, its micro-dynamic behavior is still being explored owing to the lack of a theory of quantum gravity. Therefore, if we want to explore the microscopic properties of black holes, we need to make some appropriate assumptions. In comparison with the mature research system of well-established statistical mechanical models, we can consider applying the abovementioned inverse process to the black hole system. Coincidentally, the underlying idea behind this inverse process is reflected in the exploration of the microscopic behavior of black holes by the Ruppeiner thermodynamic geometry. Although certain aspects of this scheme remain the subject of debate within the research community, there appears to be no method that is more suitable from the perspective of thermodynamics. Aided by the abstract concept of the black hole molecule, through analogy, we can assume that there is an interaction among the molecules comprising a black hole, and thus, the above empirical observation also applies to black holes. The physical meaning of the thermodynamic curvature in a black hole system was provided by Ruppeiner [40]. Furthermore, Refs. [19,41] point out that the absolute value of the thermodynamic curvature measures the strength of the interactions among black hole molecules phenomenologically or qualitatively. Recently, for a class of black hole systems with zero heat capacity at constant volume, two methods have been posited to deal with the thermodynamic curvature. The first introduces the normalized thermodynamic curvature by treating the heat capacity at constant volume as a constant very close to zero [41-43]. The second regards the entropy in the thermodynamic metric as a function of the mass (i.e., enthalpy) and other thermodynamic quantities of AdS black holes [24-27]. Both these schemes can well analyze the interaction among molecules of the black hole system.
Therefore, thermodynamic geometry can be considered as one of the best methods for exploring the microscopic properties of black holes solely from the perspective of thermodynamics. Previously, only the positive/negative of the thermodynamic curvature was used to analyze the type of interaction occurring between black hole molecules in the black hole thermodynamic system, while the magnitude of the thermodynamic curvature was used to describe the strength of the interaction qualitatively. We know that, at the microscopic level, the interactions among the constituent molecules of the system always compete with the thermal motion of the molecules themselves. Hence, for the black hole thermodynamic system, this competition should exist. This study focuses on how best to describe this competition.
Under the black hole molecule hypothesis, the product of the temperature and entropy of a black hole can reflect the thermal motion of black hole molecules in terms of the theory of molecular thermal motion. At the same time, using thermodynamic geometry, we can approximate the thermodynamic curvature as a measure of the interactions among black hole molecules. In our previous work [24], via analysis of the microscopic thermal behavior of the Reissner-Nordström black hole, we speculated on the relation between the thermal motion of black hole molecules and their interactions. In this paper, with the help of these two important tools, we propose a preliminary and coarse-grained description of the relation between the interactions among black hole molecules and their thermal motion using the AdS background, taking the AdS black holes as examples, with the aim of elucidating the possible microscopic behavior of black holes. We use the proposed description to identify the transition point between the state dominated by the interaction and that dominated by thermal motion in the black hole system, further revealing the mechanism of black hole phase transition at the microscopic level entirely from the perspective of thermodynamics.
The paper is organized as follows. Section II provides a brief introduction to the Ruppeiner thermodynamic geometry. In section III, we introduce a dimensionless ratio to characterize the relation between the interaction and thermal motion of molecules in AdS black holes. Finally, section IV presents our conclusions.
-
The Ruppeiner thermodynamic geometry originates from the fluctuation theory of equilibrium thermodynamics [14,40]. Consider an equilibrium isolated thermodynamic system with total entropy
$ S $ , and divide it into a small subsystem$ S_B $ and a large subsystem$ S_E $ . Additionally, we require that$ S_B \ll S_E \sim S $ . Then, the total entropy of the system reads as$ \begin{array}{l} S(x^0,x^1,\cdots) = S_B(x^0,x^1,\cdots)+S_E(x^0,x^1,\cdots), \end{array} $

(1) where the parameters
$ x^0 $ ,$ x^1 $ ,$ \cdots $ are independent thermodynamic variables. For a system in equilibrium, the entropy$ S $ has a local maximum value$ S_0 $ at$ x_0^\mu $ ($ \mu = 0,1,2,\cdots $ ). Therefore, in the vicinity of the local maximum, the entropy is expressed as$ \begin{aligned}[b] S =& S_0+\frac{\partial S_B}{\partial x_B^\mu}\Delta x^\mu_B +\frac{\partial S_E}{\partial x_E^\mu}\Delta x^\mu_E +\frac{1}{2}\frac{\partial^2 S_B}{\partial x_B^\mu \partial x_B^\nu}\Delta x^\mu_B \Delta x^\nu_B \\ & +\frac{1}{2}\frac{\partial^2 S_E}{\partial x_E^\mu \partial x_E^\nu}\Delta x^\mu_E \Delta x^\nu_E +\cdots. \end{aligned} $

(2) The first derivative terms in Eq. (2) cancel each other owing to the conservation of entropy for the equilibrium isolated system. Compared with the second derivative term for
$ S_B $ , the corresponding$ S_E $ term can be ignored because$ S_E $ is of the same order as the whole system ($ S_E \sim S $ ). Finally, we arrive at$ \Delta S = S_0-S \approx -\frac{1}{2}\frac{\partial^2 S_B}{\partial x_B^\mu \partial x_B^\nu}\Delta x^\mu_B \Delta x^\nu_B. $

(3) Then, according to the fluctuation probability given by Einstein’s formula
$ P\propto e^{S} $ , we obtain$ P(x^0,x^1,\cdots)\propto \exp\left(-\frac12 \Delta l^2\right) , $

(4) where
$ \Delta l^2 = -\frac{\partial^2 S}{\partial x^\mu \partial x^\nu}\Delta x^\mu \Delta x^\nu, $

(5) is referred to as the metric of the Ruppeiner thermodynamic geometry (here, we omit subscript
$ B $ ).For a system comprising a black hole and its surrounding infinite environment, the black hole itself is a small subsystem of the above. Returning to the example of an AdS black hole, the first law of thermodynamics is
${\rm d}M = T{\rm d}S+V{\rm d}P+\text{other terms}$ . For the situation in which all other terms are fixed, we can adjust the first law of thermodynamics slightly to obtain$ {\rm d}S = \frac{1}{T}{\rm d}M-\frac{V}{T}{\rm d}P, $

(6) which describes the entropy as a function of enthalpy (or mass) and thermodynamic pressure. Now, we set
$ x^{\mu} = (M,P) $ , with the conjugate quantities corresponding to$ x^{\mu} $ given by$ y_{\mu} = \partial S/\partial x^{\mu} = (1/T,-V/T) $ . Then, the line element Eq. (5) becomes$ \Delta l^2 = -\Delta y_{\mu} \Delta x^{\mu} $ . Finally, we can write this line element in a universal form for the AdS black hole [25]:$ \Delta l^2 = \frac{1}{T}\Delta T \Delta S+\frac{1}{T}\Delta V \Delta P. $

(7) The phase space of the AdS black hole is
$ \{T, P, S, V\} $ . For the theory of thermodynamic geometry, we use a space of generalized coordinates, such as$ \{T, P\} $ ,$ \{S, V\} $ ,$ \{T, V\} $ , and$ \{S, P\} $ for the AdS black hole. As the thermodynamic curvatures obtained in these coordinate spaces are same, we can take the coordinate space$ \{S,P\} $ as an example for the subsequent calculations and analyses in this paper. According to Eq. (7), the line element of the Ruppeiner geometry for the AdS black hole takes the following form in the coordinate space$ \{S,P\} $ :$ \Delta l^2 = \frac{1}{T}\left(\frac{\partial T}{\partial S}\right)_P \Delta S^2+\frac{2}{T}\left(\frac{\partial T}{\partial P}\right)_S \Delta S \Delta P+\frac{1}{T}\left(\frac{\partial V}{\partial P}\right)_S \Delta P^2, $

(8) where we have used the Maxwell relation
$ (\partial T/\partial P)_{_S} = (\partial V/\partial S)_{_P} $ based on the first law of thermodynamics.In addition, we use the Christoffel symbols,
$ \Gamma^{\alpha}_{\beta\gamma} = \frac12 g^{\mu\alpha}\left(\partial_{\gamma}g_{\mu\beta}+\partial_{\beta}g_{\mu\gamma}-\partial_{\mu}g_{\beta\gamma}\right), $

(9) to express the Riemannian curvature tensor,
$ \begin{array}{l} {R^{\alpha}}_{\beta\gamma\delta} = \partial_{\delta}\Gamma^{\alpha}_{\beta\gamma}-\partial_{\gamma}\Gamma^{\alpha}_{\beta\delta}+ \Gamma^{\mu}_{\beta\gamma}\Gamma^{\alpha}_{\mu\delta}-\Gamma^{\mu}_{\beta\delta}\Gamma^{\alpha}_{\mu\gamma}. \end{array} $

(10) Consequently, we can obtain the thermodynamic (scalar) curvature,
$ \begin{array}{l} R = g^{\mu\nu}{R^{\xi}}_{\mu\xi\nu}. \end{array} $

(11) -
To study the relationship between the interactions among black hole molecules and their thermal motion, as a preliminary and coarse-grained description, we define the following dimensionless ratio to characterize the strength between the interactions and the thermal motion:
$ \eta: = \frac{\rm{Interaction}}{\rm{Thermal\; motion}} \approx \frac{\rm{The\; magnitude\; of\; thermodynamic\; curvature \times Planck\; volume}}{\rm{Temperature\; \times\; entropy}}. $

(12) There are several important points that must be considered here:
● In regular thermodynamics, the key notion used to describe the phase transition is the free energy, which measures the competition between interactions and the thermal motions. In particular, for the free energy, the degree of the thermal motion is measured by the product of the temperature and entropy of the system.
● First, through analysis, it can be seen that the temperature, entropy, and volume have dimensions of
$ [\text{length}]^{-1} $ ,$ [\text{length}]^{2} $ , and$ [\text{length}]^{3} $ , respectively. Meanwhile, the thermodynamic curvature has the dimension of$ [\text{length}]^{-2} $ , which is consistent with the dimension of thermodynamic pressure in the natural system of units. To retain the same dimension as that of the measurement (the product of the temperature and entropy) of the thermal motion, analogous to the$ PV $ term in ordinary thermodynamics, we posit that the combination of the thermodynamic curvature and a certain volume may be a suitable physical quantity to describe the degree of the interaction between black hole molecules. Second, Ruppeiner [40] proposed that if we imagine the fluid as separate pieces, each with volume$ v $ ,$ |R| $ is the average number of correlated "pixels." Next, we assume that each pixel occupies approximately one Planck volume, because the Planck length is often suggested as a physical constant for quantum gravity. Therefore, we can approximate that the product of the absolute value of thermodynamic curvature and the size of each pixel qualitatively reflects the interaction strength. Again, this is only a preliminary exploration and, at present, there is no direct evidence for such a conjecture.● The dimensions of the numerator and denominator in Eq. (12) are consistent. When the interaction represented by the numerator and the thermal motion represented by the denominator are in balance with each other, the ratio
$ \eta $ is a fixed constant, and a fixed constant can always be set to 1. Thus,$ \eta = 1 $ is special and important.● If
$ \eta>1 $ , the interactions between molecules dominate the black hole system.● If
$ \eta<1 $ , the thermal motion of molecules dominates the black hole system.● If
$ \eta = 1 $ , the interactions between molecules and the thermal motion of molecules reach a competitive balance, and the whole system will be in transition from the interaction state to the thermal motion state, or vice versa.Next, we use the newly introduced measurement to investigate the microscopic behaviors of several kinds of AdS black holes. In the following discussion, we often set the value of Planck volume as a unit.
-
We start by considering a four-dimensional charged AdS black hole, the metric of which can be expressed as [11,12,30]
$ {\rm d} s^2 = -f(r){\rm d}t^2+\frac{{\rm d} r^2}{f(r)}+r^2({\rm d}\theta^2+\sin^2 \theta {\rm d}\varphi^2), $

(13) where the function
$ f(r) = 1-2M/r+r^2/l^2+q^2/r^2 $ , in which$ M $ is the mass of the black hole,$ l $ is the curvature radius of the AdS spacetime, and$ q $ is the total charge of the black hole. The horizon radius$ r_h $ is regarded as the largest root of equation$ f(r) = 0 $ . Then, the temperature of the black hole can be written as$ T = \frac{8P S^2+S-\pi q^2}{4S\sqrt{\pi S}}, $

(14) where the entropy is
$ S = \pi r_h^2 $ , and thermodynamic pressure is$ P = 3/(8\pi l^2) $ . Furthermore, the thermodynamic volume is$ V = 4\pi r_h^3/3 $ . Hence, according to Eq. (11), we obtain the thermodynamic curvature of the four-dimensional charged AdS black hole:$ R = \frac{2\pi q^2-S}{S(8P S^2+S-\pi q^2)}. $

(15) For the sake of convenience, we introduce some dimensionless reduced parameters as follows [11,19]:
$ t: = \frac{T}{T_c}, \;\;\;\; s: = \frac{S}{S_c}, \;\;\;\; p: = \frac{P}{P_c}, \;\;\;\; \zeta: = \left|\frac{R}{R_c}\right|, $

(16) where
$ T_c = \frac{\sqrt{6}}{18\pi q}, \;\;\; S_c = 6\pi q^2, \;\;\; P_c = \frac{1}{96\pi q^2}, \;\;\; R_c = -\frac{1}{12\pi q^2}. $

(17) Next, we can determine the dimensionless ratio between the dimensionless measurement
$ ts $ of the thermal motion and the dimensionless measurement$ \zeta $ of the interaction:$ \eta = \left|\frac{32(1-3s)}{\sqrt{s}(3ps^2+6s-1)^2}\right|. $

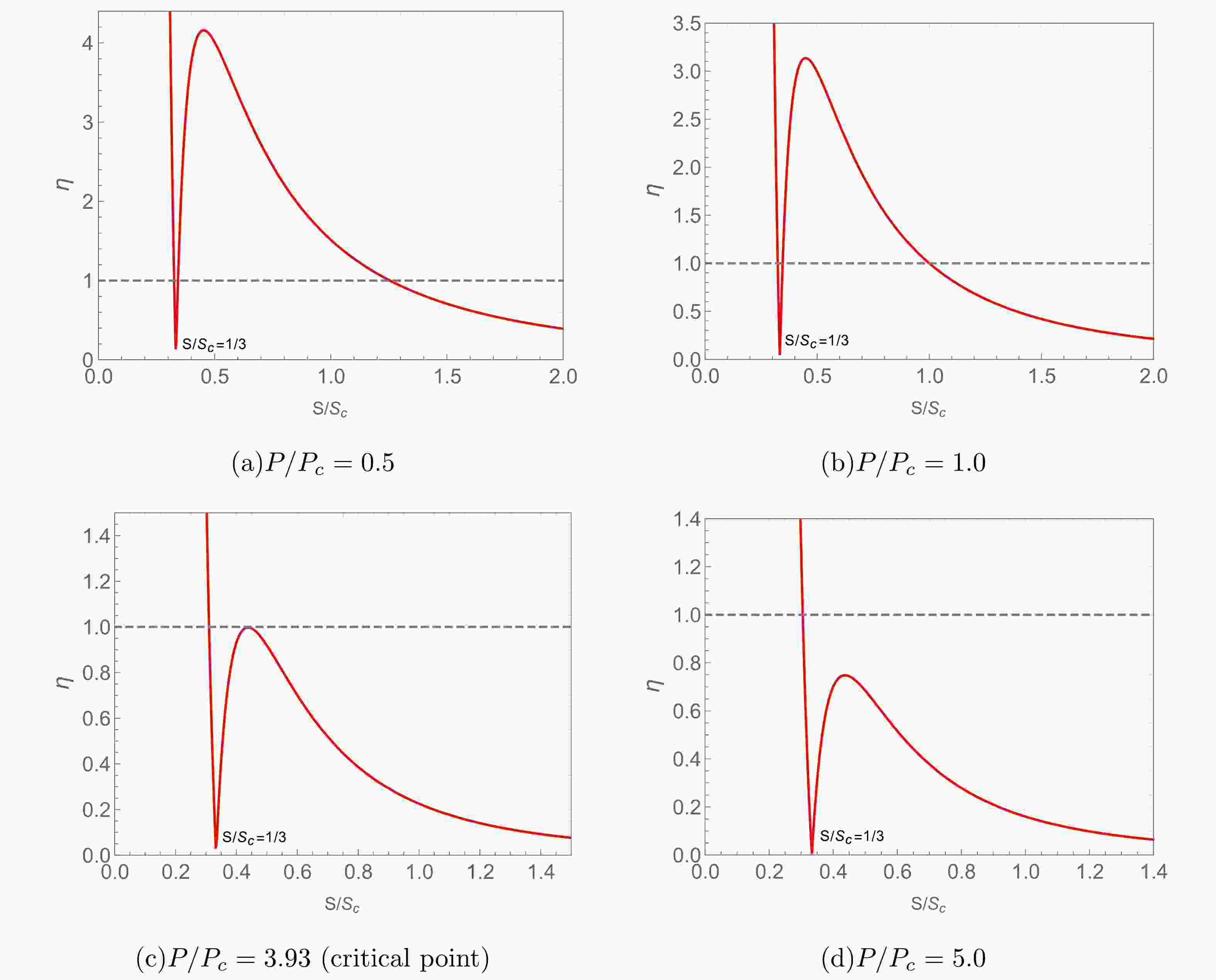
(18) Figure 1 shows plots of the behavior of the dimensionless ratio
$ \eta $ with respect to the dimensionless entropy$ s $ at different values of the dimensionless pressure$ p $ . Using these plots, we can analyze some novel properties of the thermal microscopic behaviors of charged AdS black holes:
Figure 1. (color online) The dimensionless ratio
$ \eta $ between the interaction and the thermal motion with respect to the dimensionless entropy$ S/S_c $ at the different dimensionless pressures$ P/P_c $ for a charged AdS black hole.● For the charged AdS black hole system, there is indeed competition between the interactions among black hole molecules and their thermal motion.
● At
$ s = 1/3 $ , the thermodynamic curvature equals zero. Therefore, we can divide the microscopic behaviors of the black hole into two branches. Branch-1 (B1) corresponds to the interval of$ 0<s<1/3 $ , while branch-2 (B2) corresponds to the interval of$ s>1/3 $ .● In B1, we can see that regardless of the value of the dimensionless pressure
$ p $ , as the dimensionless entropy$ s $ increases, the dimensionless ratio$ \eta $ decreases monotonically and always has an intersection with the curve$ \eta = 1 $ . This implies that the black hole always experiences a transition from the interaction state to the thermal motion state.● In B2, as the dimensionless entropy
$ s $ increases, the dimensionless ratio$ \eta $ shows a trend of first increasing and then decreasing, while its intersection with the curve$ \eta = 1 $ depends on the value of the dimensionless pressure$ p $ . Numerical calculation yields a new critical dimensionless pressure of$ p\approx 3.93 $ . When$ 0< p < 3.93 $ , two intersections are observed. The first intersection represents the transition from the thermal motion state to the interaction state, while the second intersection signifies the transition from the interaction state to the thermal motion state. When$ p\geqslant 3.93 $ , the two intersections merge and disappear, indicating that the black hole will always be in the thermal motion state. -
The Schwarzschild-AdS black hole is a special case of the charged AdS black hole for which
$ q = 0 $ . The temperature and thermodynamic curvature of the Schwarzschild-AdS black hole are [25]$ T = \frac{8P S+1}{4\sqrt{\pi S}}, \;\;\;\; R = -\frac{1}{8P S^2+S}. $

(19) To these expressions, we introduce a dimensionless quantity
$ u = 8PS $ , enabling the temperature, entropy, and the thermodynamic curvature to be expressed as the rescaled temperature$ t $ , entropy$ s $ , and thermodynamic curvature$ \zeta$ $ t = \frac{T}{\sqrt{8\pi P}} = \frac{u+1}{4\pi\sqrt{u}}, \;\;\; s = 8\pi PS = \pi u, \;\;\; \zeta = \left|\frac{R}{8P}\right| = \frac{1}{u(u+1)}. $

(20) Subsequently, the dimensionless ratio
$ \eta $ can be written as$ \eta = \frac{4}{u^{3/2}(u+1)}. $

(21) The behavior of the dimensionless ratio
$ \eta $ between the thermal motion and the interaction with respect to the quantity$ u $ is plotted in Fig. 2. We can clearly see that as$ u $ increases, the dimensionless ratio$ \eta $ decreases monotonically and always has an intersection with the curve$ \eta = 1 $ at$ u = 1 $ . This implies that the Schwarzschild-AdS black hole always experiences a transition from the interaction state to the thermal motion state. -
The metric of the Gauss-Bonnet AdS black hole in
$ d $ dimensions is [44]$ {\rm d}s^2 = -f(r){\rm d}t^2+\frac{1}{f(r)}{\rm d}r^2+r^2 {\rm d}\Omega^2, $

(22) in which
$ f(r) = 1+\frac{r^2}{2\alpha_0}\left(1-\sqrt{1+\frac{64\pi\alpha_0 {\cal M}}{(d-2)r^{d-1}\Sigma}-\frac{64\pi\alpha_0 P}{(d-1)(d-2)}}\right), $

where
$ \mathrm{d}\Omega^2 $ is the square of line element on a$ (d-2) $ -dimensional maximally symmetric Einstein manifold with volume$ \Sigma $ . The black hole mass is$ \cal M $ , and the pressure is$ P = (d-1)(d-2)/(16\pi l^2) $ . The auxiliary symbol$ \alpha_0 $ is related to the Gauss-Bonnet coefficient$ \alpha_{_{\mathrm{GB}}} $ via$ \alpha_0 = (d-3) \times(d-4)\alpha_{_{\mathrm{GB}}} $ for compactness.When
$ d = 5 $ , the temperature and entropy of the Gauss-Bonnet AdS black hole take the following forms in terms of the horizon radius$ r_h $ [44,45]:$ T = \frac{8\pi P r_h^3+3r_h}{6\pi(r_h^2+2\alpha_0)}, \qquad S = \frac{\pi^2 r_h(r_h^2+6\alpha_0)}{2}. $

(23) Meanwhile, the thermodynamic curvature for the five-dimensional Gauss-Bonnet AdS black hole in terms of the horizon radius
$ r_h $ is [46]$ R = -\frac{4}{\pi^2 r_h(r_h^2+2\alpha_0)(8\pi P r_h^2+3)}. $

(24) Similarly, the dimensionless temperature
$ t $ , entropy$ s $ , and thermodynamic curvature$ \zeta $ can be written as$ t = \frac{p x^3+3x}{3x^2+1}, \;\;\; s = \frac{x^3+x}{2}, \;\;\; \zeta = \frac{4}{(3x^2+1)(p x^3+3x)}, $

(25) in which
$ t = T/T_c $ ,$ s = S/S_c $ ,$ p = P/P_c $ ,$ \zeta = |R/R_c| $ , and$ x = r_h/r_c $ , where [44-46]$ \begin{aligned}[b] T_c =& \frac{1}{2\pi\sqrt{6\alpha_0}}, \;\;\; r_c = \sqrt{6\alpha_0}, \;\;\; S_c = 6 \pi^2 \alpha_0 \sqrt{6\alpha_0}, \\ P_c =& \frac{1}{48\pi \alpha_0}, \;\;\; R_c = -\frac{1}{8\pi^2 \alpha_0 \sqrt{6\alpha_0}}. \end{aligned} $

Thus, the dimensionless ratio between the thermal motion and the interaction is
$ \eta = \frac{8}{(p x^3+3x)^2(x^3+x)}. $

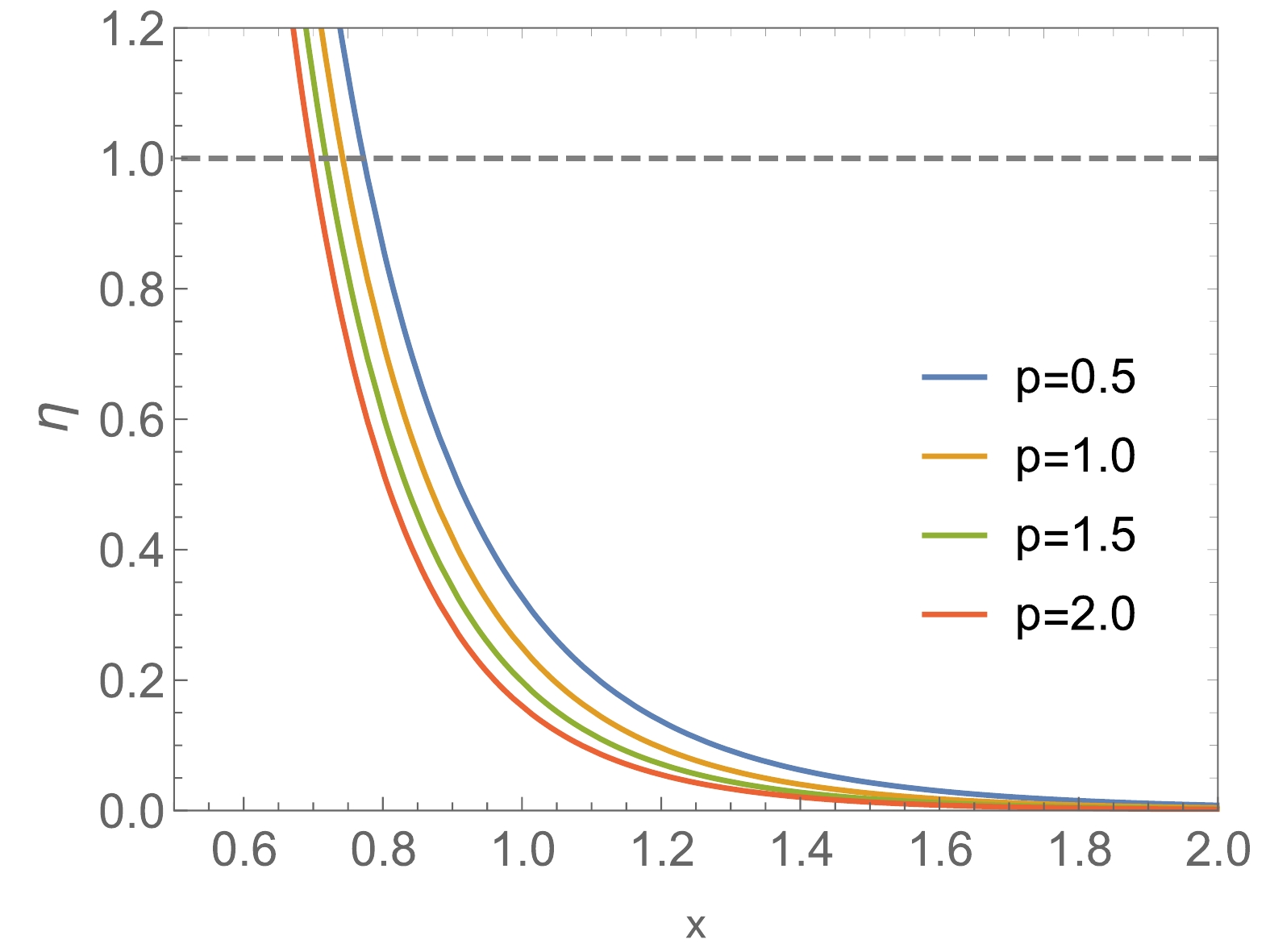
(26) The behavior of the ratio
$ \eta $ with respect to$ x $ for different dimensionless pressures$ p $ is presented in Fig. 3. Clearly, as$ x $ increases, the dimensionless ratio$ \eta $ decreases monotonically and always has an intersection with the curve$ \eta = 1 $ . This implies that the five-dimensional Gauss-Bonnet AdS black hole always experiences a transition between the interaction state and the thermal motion state. -
In the absence of a complete theory of quantum gravity, thermodynamic geometry is a strong candidate as an effective means to study the microscopic properties of black holes from the perspective of thermodynamics. In [24], by introducing a new generalized coordinate, we provided a preliminary solution to the puzzle of whether the Reissner-Nordström black hole is an interacting system or not. Our analysis of the microscopic behavior of the Reissner-Nordström black hole yielded some insights into relation between the thermal motion of black hole molecules and their interaction. Then, in [25], we proposed a scheme to solve the problem of the singularity of thermodynamic geometry for static spherically symmetric AdS black holes. We identified enthalpy as the basic thermodynamic potential of thermodynamic geometry for such black holes, from which we can obtain the thermodynamic curvature. The ideas outlined in [25] were an important basis for the analysis presented herein. Our method differs from others in the literature [41] by introducing the normalized thermodynamic curvature to address the divergence of the thermodynamic curvature, while the internal energy is regarded as the basic thermodynamic potential. In [26], supported by the scheme proposed in [25], we analyzed the behavior of the thermodynamic curvature for the BTZ black hole and provided a framework to discriminate between different thermodynamic calculation schemes from the point of view of the thermodynamic geometry of the BTZ black hole.
In this paper, using the concept of black hole molecules, we introduce a dimensionless ratio (Eq. (12)) to characterize the relation between the interactions and the thermal motion of the AdS black holes. Using this preliminary and coarse-grained description, we find that there is indeed competition between the interactions among black hole molecules and their thermal motion. As such, we present the following conclusions:
● For the charged AdS black hole, the microscopic behaviors of the black hole can be divided into two branches (B1 and B2). In B1, the black hole always experiences a transition from the interaction state to the thermal motion state, whereas in B2, the transition point between the interaction state and the thermal motion state depends on the value of the dimensionless pressure
$ p $ . Below the critical dimensionless pressure$ p = 3.93 $ , two transitions occur. In contrast, above the critical dimensionless pressure, the transition disappears, and the black hole is always in the thermal motion state.● For the Schwarzschild-AdS black hole, there is always a transition between the interaction state and the thermal motion state. Meanwhile, the transition point satisfies
$ 8PS = 1 $ exactly.● For the five-dimensional Gauss-Bonnet AdS black hole, a transition always occurs between the interaction state and the thermal motion state.
In addition, our current approach is extendable to other types of black holes, such as (charged) Kerr (-AdS) black holes, thereby offering a versatile approach to analyze certain new microscopic thermal information of various black holes.
-
The authors would like to thank the anonymous reviewers for the helpful comments that greatly improved this work.
A new measure of thermal micro-behavior for the AdS black hole
- Received Date: 2020-05-22
- Accepted Date: 2020-08-17
- Available Online: 2021-01-15
Abstract: Inspired by the hypothesis of the black hole molecule, with the help of the Hawking temperature, entropy, and the thermodynamic curvature of black holes, we propose a new measure of the relation between the interaction and the thermal motion of molecules of the AdS black hole as a preliminary and coarse-grained description. The proposed measure introduces a dimensionless ratio to characterize this relation and shows that there is indeed competition between the interactions of black hole molecules and their thermal motion. For a charged AdS black hole, below the critical dimensionless pressure, there are three transitions between the interaction and thermal motion states. In contrast, above the critical dimensionless pressure, only one transition takes place. For the Schwarzschild-AdS and five-dimensional Gauss-Bonnet AdS black holes, a transition always occurs between the interaction and thermal motion states.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: